1 引言
单脉冲测角是一种常用的测角方法,它利用多个天线同时接收回波信号,通过比较回波信号的幅度或相位来获得目标的角度位置信息。根据从回波信号中提取目标的角信息方式将单脉冲测角分为比幅法和比相法两种,通常采用比幅法[1-3]。单脉冲测角方法具有操作简单,实时性强,测角精度高,特别是和差波束比较单脉冲测角方法,不局限于波束关于中心射轴完全对称,减少测角误差来源,广泛应用在雷达、声呐、无线通信、无源探测等领域[4-7]。
常规的单脉冲测角算法是建立在单个目标的应用场景上,当存在干扰时,特别是干扰靠近目标时会产生很大的角度估计误差[8-9]。为了存在干扰的同时也能精确的进行单脉冲测角,引入了现代数字波束形成(Digital Beam Forming,DBF)技术抑制干扰,即有了自适应单脉冲测角技术[10-13]。为了在干扰抑制的同时使得和差波束形状不变形,保持单脉冲测角曲线线性性能,保证测角精度,研究了针对应用场景与对象增加不同约束条件的约束类自适应单脉冲测角方法[14-16],以及基于平面相控阵、共形天线等的单脉冲测角方法[17-19]。上述方法都能在抑制干扰的同时保持单脉冲测角精度,但算法仅适用于窄带信号应用场景,在宽带信号应用场景,算法难以保证测角精度。
宽带波束合成常规方法主要有空频方法和空时方法两种,空频方法又可以分为非相干处理和相干处理两种方法[20-22]。空频处理基本思想就是将宽带时域信号通过傅里叶变换转变成频域信号,然后采用窄带的方法对各个子频带进行处理[23]。基于空频处理方式的和差测向方法中,非相干处理方法,直接对每个子频带进行自适应单脉冲测角;相干处理方法,需要将宽带信号通过聚焦的方式投影到某个频点,然后在这个频点的基础上进行自适应单脉冲测角[24-25]。空频处理方法需对每个频点的数据做期望信号的检测,而低信噪比时关于期望信号的检测和角度的测量易出错,且非相干处理方法由于需在多个频点上做存在干扰时的单脉冲测向,计算量也较大,而相干处理方法中聚焦矩阵的计算和聚焦变换也会引入巨大的计算量[26-27]。
文献[21]提出的空时波束自适应形成算法是经典的空时处理方法,该方法会对接收信号进行预延迟处理来补偿各阵元间期望信号的相位差和时延差,随后再进行自适应的波束形成来抑制干扰[21];文献[28]也提出了使用频域约束条件而无需进行预处理的宽带空时波束形成方法[28]。为了采用和差测向方法,需进行两次预处理以获得左右波束的输出,以此来构建和波束与差波束输出,此时需要对应的形成两次完全不相同的自适应波束形成,大大增加了计算量,而且和差自适应处理所对应的鉴角曲线的线性度会变差[29-30]。
本文提出了一种基于空时架构的无需额外预延迟处理的宽带自适应和差波束形成和测角方法,论文主要内容包括:章节2通过多点约束的窄带单脉冲测角,以及宽带信号模型与测角提出论文的研究问题;章节3对无需预延迟处理宽带自适应和差波束形成、单脉冲测角以方法实现进行推导分析;章节4通过仿真分析验证算法可行性及性能分析;最后章节对论文研究内容进行总结。
2 问题的提出
2.1 多点约束的窄带单脉冲测角
假设有Kr个干扰信号入射,则M个均匀线阵阵列接收干扰信号模型为
z(n)=As(n)+v(n), n=1,2,…,N
(1)
其中N为快拍数,v(n)为独立同分布加性高斯白噪声矢量。干扰信号向量s(n)和方向矩阵A分别定义为s(n)=[s1(n),s2(n),…,sKr(n)]T∈CKr×1和A=[a(θ1),a(θ2),…,a(θKr)]∈CM×Kr。
常规的自适应单脉冲算法能很好地处理窄带信号。以均匀线阵为例,假设θ0是波束指向,信号来向为(θ=θ0+Δθ)。当存在干扰时,通常采用自适应数字波束形成(Adaptive Digital Beam Forming,ADBF)抑制干扰,改善输出的信干噪比,提高对目标的检测性能。自适应单脉冲技术,是和通道计算得到自适应权后,然后对和波束方向矢量进行修正得到差通道的权值。根据MVDR(Minimum Variance Distortionless Response)准则,和波束自适应权为
wΣ=R-1aΣ(θ0)∈CM×1
(2)
其中,R是干扰加噪声的协方差矩阵,aΣ(θ0)是静态和波束权且有aΣ(θ0)=a(θ0)。在实际应用中,R通常采用采样矩阵估计得到,即
(3)
对差波束权值提出两点约束:一是约束后的自适应单脉冲比趋近常规静态单脉冲比;二是最小化干扰和噪声的输出功率。由于不可能对鉴角曲面上的每一个点进行约束,因此,只是选取离散的几点做约束,假定选取0、±Δθ′三点做为约束点,其中Δθ′为约束间隔。对单脉冲比做如下约束
(4)
其中,k为线性比值常数,在实现时可以自己定义大小。Σ(θ)为自适应和波束响应,Δ(θ)为自适应差波束响应
(5)
其中,wΔ为差波束自适应权值。代入上式约束条件可以写成矩阵的形式
(6)
其中,约束矩阵H和响应矩阵ρ为
H=[a(θ0+Δθ′) a(θ0) a(θ0-Δθ′)]∈CM×3
(7)

(8)
差波束权值wΔ必须使差波束输出的干扰功率最小,这个极值问题可以描述为
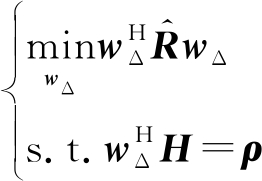
(9)
得到自适应差波束权值
(10)
该线性约束使得自适应波束形成的和差比可以保持好的线性关系。
2.2 宽带信号模型与和差测角
对于宽带阵列信号,当有Kr个远场信号s1(t),s2(t),…,sKr(t),分别来自θ1,θ2,…,θKr方向,则第m个阵元的输出是
(11)
式中τm(θi)是第i个信号到达第m个阵元相对其到达参考阵元的时间延迟,νm(t)为第m个阵元上的加性噪声。
对时域的宽带信号做傅里叶变换,可得频域下的信号接收向量为
Z( fj)=A( fj)S( fj)+V( fj)
(12)
其中S( fj)=[S1( fj),S2( fj),…,SKr( fj)]T,A( fj)=[a( fj,θ1),a( fj,θ2),…,a( fj,θD)],V( fj)是对应的噪声向量,a( fj,θi)=[1,ejφ( fj,θi),…,ej(M-1)φ( fj,θi)]T, fj表示对应频带的频率。式(12)是阵列输出的宽带频域模型,它与窄带时域模型很相似。
空频信号模型下,由于频域信号模型表达式与窄带时域类似,所以可以直接采用多点约束的和差测向方法。但是空频结构需要对每个频点作期望信号的检测,对有期望信号的多个频点作自适应处理,使得计算量大大增加,且低信噪比时,分散在每个频点的期望信号功率更低,测向结果会很差。空时结构下,由于信号模型的问题,不可以采用窄带的自适应多点约束方法。
3 宽带自适应和差波束形成与测角
3.1 空时处理下的宽带信号模型
雷达信号处理时,干扰是连续的,即一直都存在,而期望信号可以不是一直存在的。所提方法是基于空时处理结构实现的,并且是先用信号不存在时的接收信号来进行波束权向量计算的,此时接收到的是干扰加噪声。假设K为时间抽头阶数,则n时刻的空时二维的干扰加噪声数据可以表示为
(13)
其中zk(n)=[z1,k(n) z2,k(n) … zM,k(n)],k=1,2,…,K,zm,k(n)表示为第m 个阵元第k个抽头在n时刻的数据。由于抽头主要是处理延时,则第k个抽头向量zk(n)与第1个抽头上向量z1(n)满足zm,k(n)=zm,1(n+(k-1))。快拍数据n+(k-1)≤N,所以时域快拍数应为n≤N-K+1。
理论上,干扰信号的空时自相关矩阵为
(14)
在实际情况下,采用有限次样本计算相关矩阵RST的时间平均估计![]() 数据协方差矩阵
数据协方差矩阵![]() 可由下式计算
可由下式计算
(15)
3.2 无需预延迟处理的空时波束形成
当信号入射方向和频率分别为θ,Ts为延迟时间,一般也是采样周期。此时假设第m个阵元上收到的信号为
xm(t)=s(t-τm(θ))ejω0(t-τm(θ))+nm(t), m=1,2,…,M
(16)
其中τm(θ)为第m个阵元相对于参考阵元的延时。ω0是该信号的角中心频率。nm(t)是噪声(无干扰)或者干扰加噪声(有干扰)。所以第m个阵元第k个抽头上的基带信号为
xm,l(n)=xm(n-kTs)= s(n-τm(θ)-k/Ts)e-jω0(-τm(θ)+kTs)+nm(t), m=1,2,…,M
(17)
忽略噪声情况下,对于不存在预延迟处理的信号来说,空时结构的信号经加权处理以后每一个阵元经K 个时域抽头后有
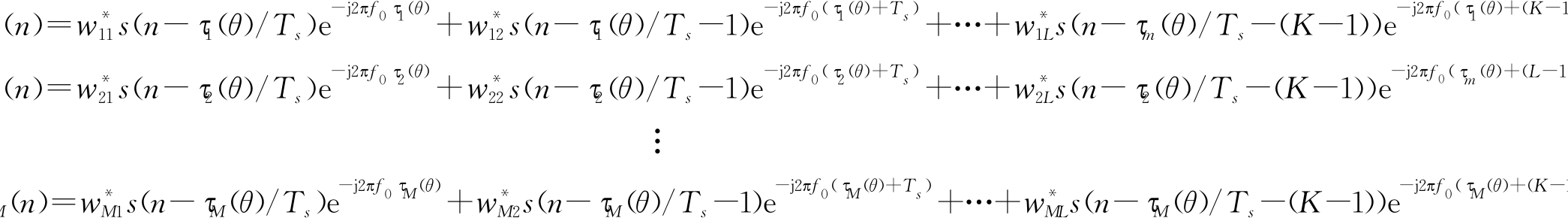
(18)
最终波束形成输出为
(19)
其对应的频域信号为
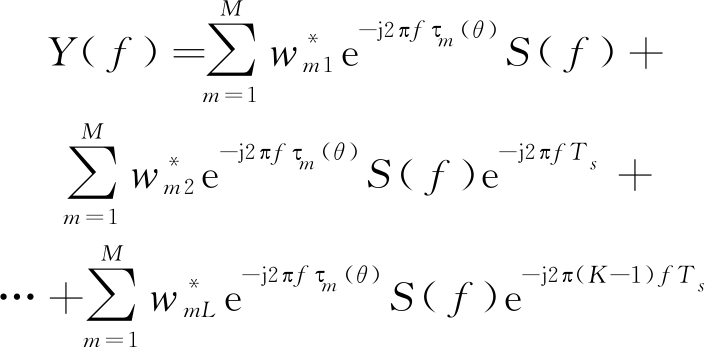
(20)
根据上式可以得到期望信号从空域转换到频域的响应函数:
![]() wHast(θ, f )
wHast(θ, f )
(21)
其中![]() 是空时二维权向量。空时二维向量ast(θ, f )为
是空时二维权向量。空时二维向量ast(θ, f )为
ast(θ, f )=at( f )⊗as(θ, f )∈CMK×1 at( f )=[1 e-j2πf Ts … e-j2πf(L-1)Ts]T ![]()
(22)
⊗为Hadamard积,as(θ0, f )是频率为f时的空域导向矢量,at( f )是时间导向矢量。为使期望信号输出无损失,可使
Hd( f )=e-j2πfL
(23)
忽略噪声情况下,此时空时滤波输出为y(n)=s(n-L)。由时延滤波器的处理原理,L=(K-1)/2 时最佳。
从以上分析可以看出,只要权向量对信号带宽范围内的所有频点都满足如下约束条件
wHast(θ, f )=e-j2πfL
(24)
则可实现无需预延迟处理的期望信号的滤波输出,即期望信号经空时二维处理后为s(n-(K-1)/2)。当存在有干扰信号时,此时无需预延迟处理的权向量可以通过如下优化问题来求解最优权向量以使期望信号无失真通过的同时抑制干扰。优化问题为:
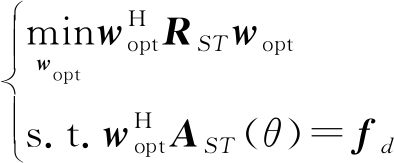
(25)
其中
AST(θ)=[ast(θ, f1) ast(θ, f2)…ast(θ, fL)]∈CMK×L
(26)
ast(θ0, f )=at( f )⊗as(θ0, fl)∈CMK×1
(27)
at( fl)=[1 e-j2πflTs … e-j2πfl(K-1)Ts]T
(28)
fd=[e-j2πf1(K-1)/2 e-j2πf2(K-1)/2 … e-j2πfL(K-1)/2]T ∈CL×1
(29)
其中fl(l=1,2,…,L) 为宽带信号频率范围内均匀取的L个频点[f1, f2,…, fL]。此时最优权向量为
(30)
3.3 无需预延迟的空时自适应和差波束形成
当波束指向和频率分别为θ0、f,空时二维导向矢量为
ast(θ0, f )=at( f )⊗as(θ0, f )∈CMK×1
(31)
其中as(θ0, f )是频率为f时的空域导向矢量。
空时二维导向矩阵是
AST(θ0)=[ast(θ0, f1) ast(θ0, f2)…ast(θ0, fL)] ∈CMK×L
(32)
要使和波束输出功率最小的条件下保持约束条件,对和波束权值wopt做以下约束
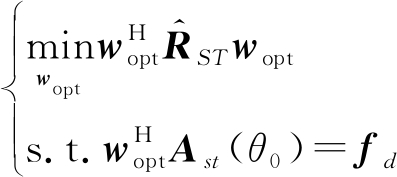
(33)
应用拉格朗日乘子法可解得和波束权值
(34)
对和波束权值wopt采取与窄带类似的方法对L个频点[f1, f2,…, fL]修正鉴角曲面得到差波束权值wdiff。约束矩阵为
(35)
其中,约束矩阵![]() 和响应矩阵
和响应矩阵![]() 为
为
(36)
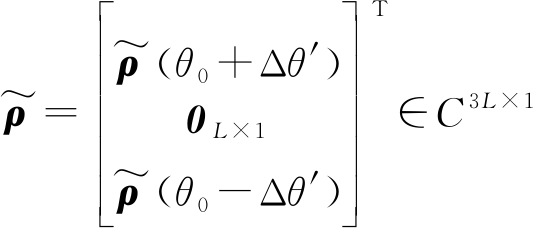
(37)
其中
h(θ0+Δθ′)=[ast(θ0+Δθ′, f1) ast(θ0+Δθ′, f2) … ast(θ+Δθ′, fL)]T h(θ0)=[ast(θ0, f1) ast(θ0, f2) … ast(θ, fL)]T h(θ0-Δθ′)=[ast(θ0-Δθ′, f1) ast(θ0-Δθ′, f2) … ast(θ-Δθ′, fL)]T
(38)
![]()
![]()
(39)
差波束权值wdiff必须使差波束输出的干扰功率最小。这个极值问题可以描述为

(40)
应用拉格朗日乘子法,可求得约束下的自适应差波束权值
(41)
3.4 单脉冲和差比幅测角
对接收到的信号做与前面相同阶数的时域抽头处理,则接收到的空时二维信号向量为
(42)
其中xk(n)=[x1,k(n) x2,k(n) … xM,k(n)],k=1,2,…,K,xm,k(n)表示为第m个阵元第k个抽头在n时刻的上的信号数据。第k个抽头向量xk(n)与第1个抽头上向量x1(n)满足xk(n)=x1(n+(k-1))。此时空时二维接收信号数据矩阵为
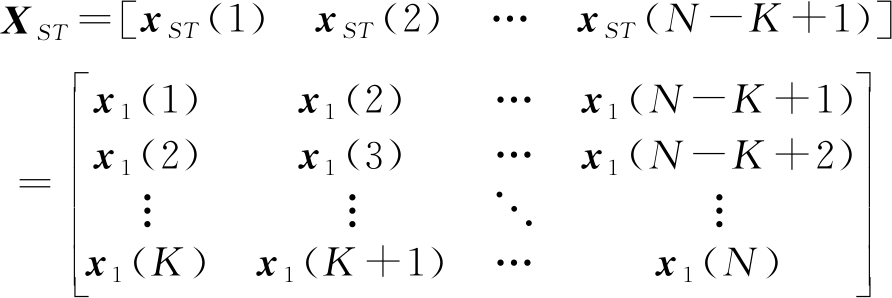
(43)
利用和波束权得到的和波束输出为
(44)
利用差波束权得到的差波束输出为
(45)
所以,每个样本的和差比值是
(46)
其中./点除表示向量中的每个数分别对应相除。
通过取平均的方式计算最后的结果,所以最后求取的和差单脉冲测角角度为
(47)
3.5 方法具体实现步骤
基于均匀线阵阵列接收物理结构,无需预延迟处理的空时宽带自适应和差波束形成与测角方法的具体实现步骤可以概括为:
1)计算物理均匀线阵阵列接收干扰信号的空时自相关矩阵
对阵列干扰信号接收模型进行空时抽头计算其自相关矩阵,采用接收干扰信号的有限次快拍数据先对其进行空时抽头,然后再对抽头后的数据进行时间平均估计作为接收信号的空时自相关矩阵的估计值,即利用干扰信号数据协方差矩阵作为干扰信号自相关矩阵的估计。
2)用无需预延迟的空时自适应波束形成方法计算得到和波束权向量
利用步骤1)中得到的物理线阵阵列下接收干扰信号的数据协方差矩阵约束在给定波束指向上的空时二维向量保持不变的条件下使输出功率最小计算得到和波束权向量。
3)对和波束权向量进行修正得到差波束权向量
在宽带信号带宽内均匀取出多个频点,对取出来频点的空时二维向量采取与窄带类似的方法修正和波束权向量得到差波束权向量。
4)对每个样本进行和差比幅
利用步骤2)和步骤3)中得到的和差波束权向量对物理线阵阵列下接收信号的数据做了时间抽头以后的数据进行和差波束形成,然后对和差波束形成后的每个快拍进行和差比幅。
5)计算单脉冲测角角度
对步骤4)中计算得到的和差比值求平均计算得到信号偏离角度,将信号偏离角度与波束指向角相加得到单脉冲测角角度。
4 仿真分析
仿真分析试验1 仿真中假设采用16阵元的均匀线阵,阵元间距为信号最高频率的半波长,波束指向10°,干扰来向分别为-30°、40°,其中,信噪比SNR=0 dB,信号中心频率f0=1 GHz,带宽B=300 MHz,采样频率fs=2*B,样本快拍数snap=5000,两个干扰干噪比JNR=40 dB,干扰中心频率分别为f1=1.1 GHz、 f2=0.9 GHz,干扰带宽分别为B1=100 MHz、B2=150 MHz。
仿真中选取的约束角度间隔Δθ′=4°,在选择频率点的分布和数量应当合理选择,频率划分点数越多,最后的测角误差越小,但是频率点数越多消耗的自由度数越多,抽样时间阶数也必须随之增加使得K>L,同时频率点的分布应该覆盖整个频带尽可能的均匀。在本次仿真过程中选取的时间抽头阶数统一为K=15,频率点数统一为L=10在信号带宽范围内均匀选择。图1是归一化和波束图,图 2是归一化差波束图,图 3为信号带宽内自适应单脉冲鉴角曲面图。
图1表明和波束权值向量能保持信号的同时可抑制干扰,图 2表明差波束权向量能使信号在波束指向方向上形成很深的零陷,与自适应单脉冲和差比幅测角原理是一致的,和波束与差波束可在干扰方向自适应置零。由仿真图 3可以看出,单脉冲和差比幅比在波束指向±4°范围内的整个频带上有很好的聚焦性,虽然鉴角曲线有一定的幅度波动,这与修正得到差波束权值时只选取了L个频点有关,但可近似的认为单脉冲比为偏离中心角Δθ斜率为1的线性函数。
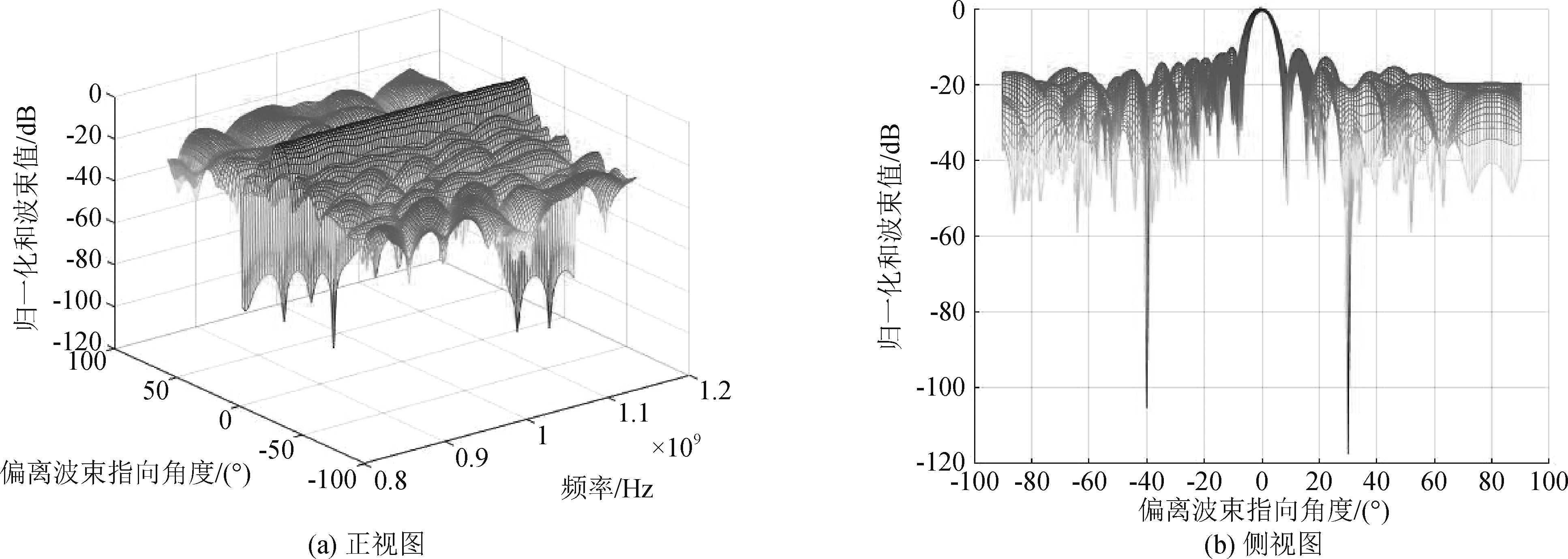
图1 归一化和波束图
Fig.1 Normalization sum beam pattern
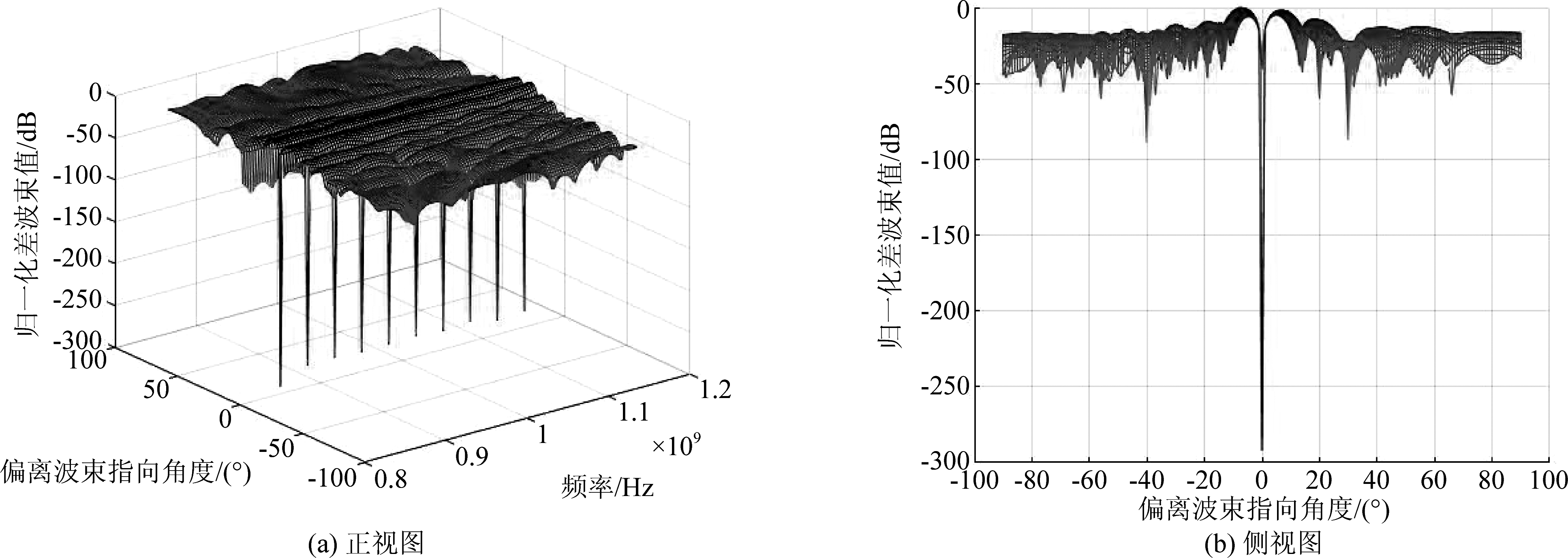
图2 归一化差波束图
Fig.2 Normalization difference beam pattern

图3 空时宽带自适应单脉冲鉴角曲面
Fig.3 Space time wideband adaptive monopulse angle discrimination surface
仿真分析试验2 保持仿真分析实验 1中其他实验条件不变,改变第一个干扰方向为7°。对于波束指向为10° 时,均匀线阵的波束3 dB宽度约为6.45°。可以看出7°方向的干扰在此时的主瓣范围内。改变信号方向在波束指向方向±4°范围内变化,用所提方法进行单脉冲测角,Monte-Carlo试验次数为100次。
此仿真条件下,所提方法鉴角曲面如图 4,仿真测角均方根误差如图 5。
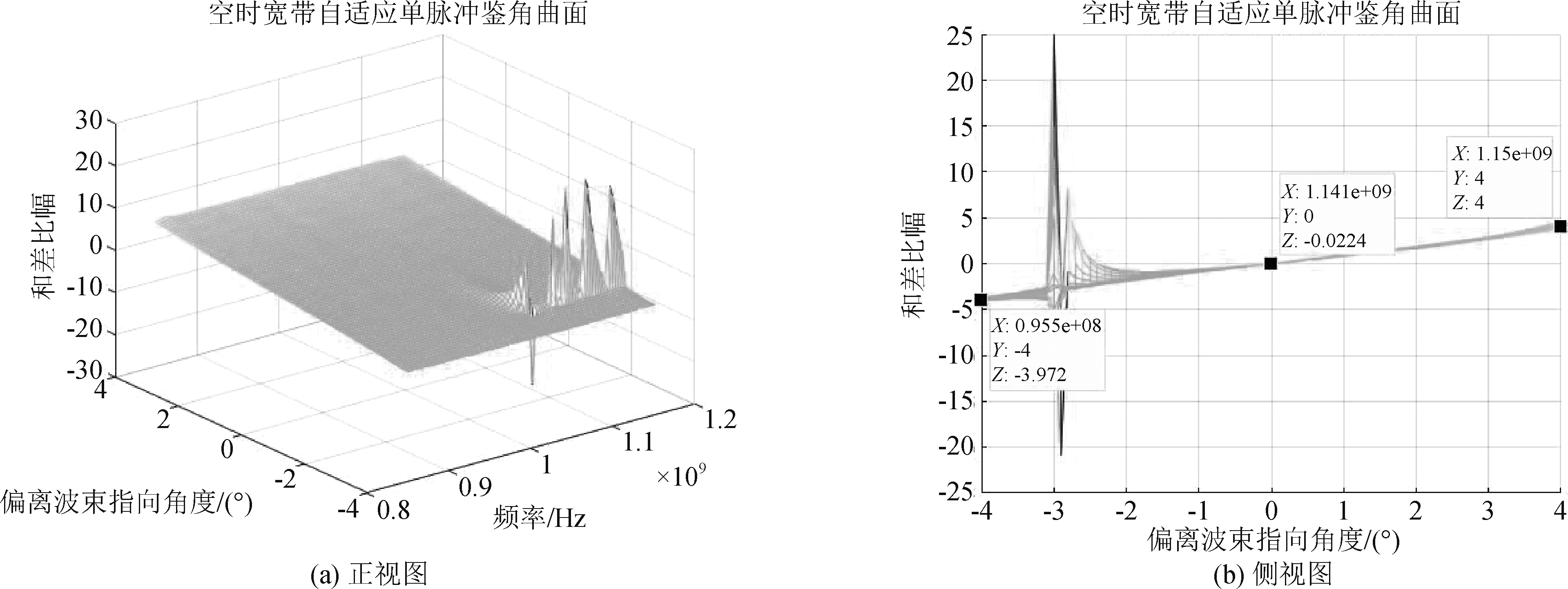
图4 存在主瓣干扰的空时宽带自适应单脉冲鉴角曲面
Fig.4 Space time wideband adaptive monopulse angle discrimination surface with main lobe interference
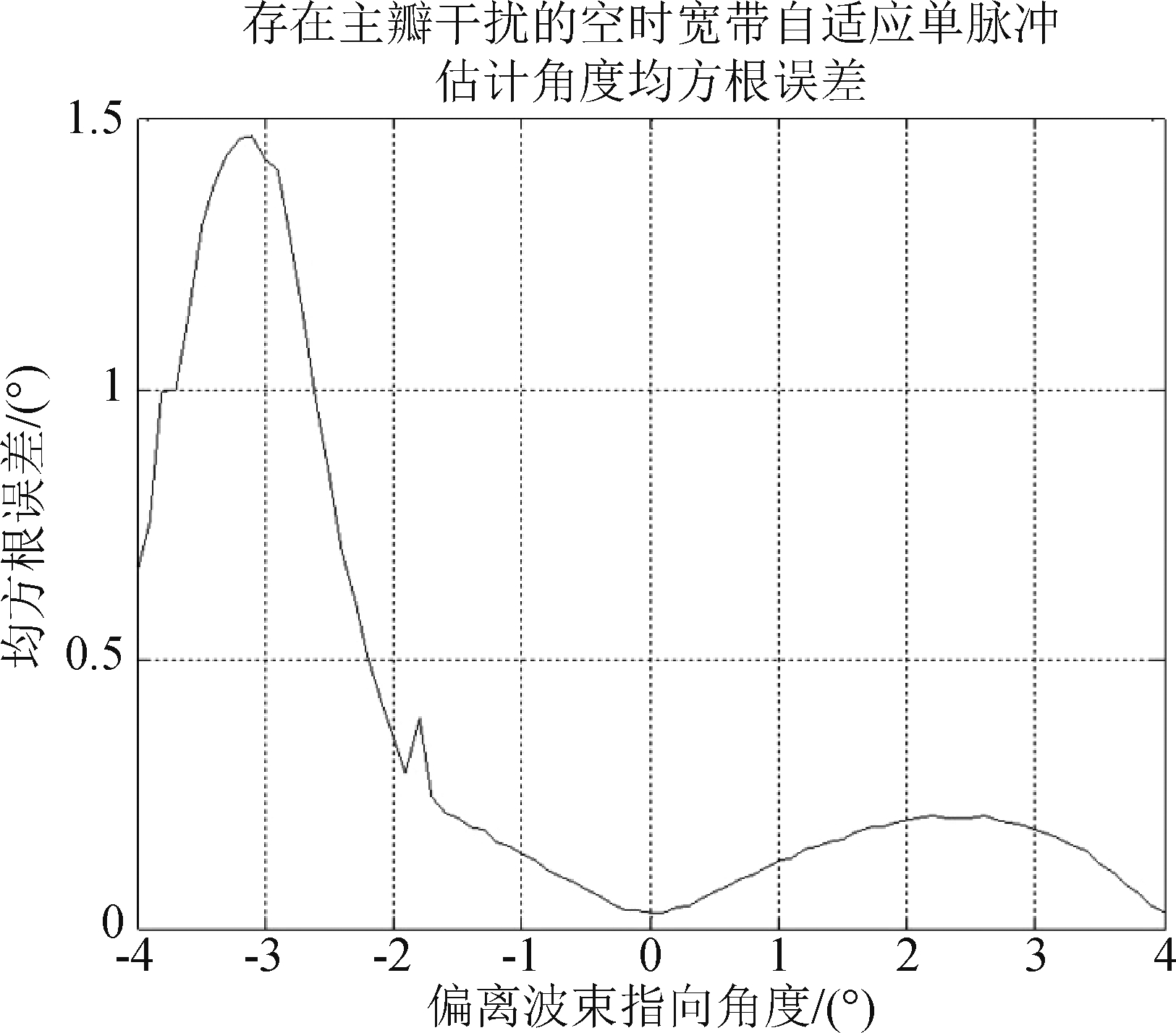
图5 存在主瓣干扰的空时宽带自适应单脉冲 估计角度均方根误差
Fig.5 Root mean square error of space-time broadband adaptive monopulse angle estimation with main lobe interference
仿真分析结果图4表明当干扰在主瓣波束3 dB内,鉴角曲面会在干扰位置出现偏差,在修正角位置±4°、0°是与理论值吻合的,在其他角度区域仍然能保持斜率为1的线性关系,所以当存在主瓣干扰时,所提方法的鉴角曲面在干扰以外的角度区域仍然能保持良好的线性关系。图5表明当干扰在主瓣波束3 dB内,所提方法除了在主瓣干扰附近无法有效测角,在其他角度区域范围仍然能精确测角,说明了所提方法具有存在主瓣干扰时仍然能精确测角的优点。
仿真分析试验3 保持仿真分析实验1中的条件不变,将信号方向固定为偏离波束指向-4°,即信号来向6°,改变一个干扰方向为7°,此时该干扰距离期望信号非常近。改变信噪比,观察存在主瓣干扰时SNR变化对估计误差的影响,用所提方法进行单脉冲测角,Monte-Carlo试验次数为100次。
仿真结果如图6所示,从图中可以看出,测角性能受SNR影响明显,由于主瓣干扰的存在使得测向对期望信号的SNR要求较高,当SNR大于5dB时,测向的均方根误差会低于0.2°,展示良好测角性能。
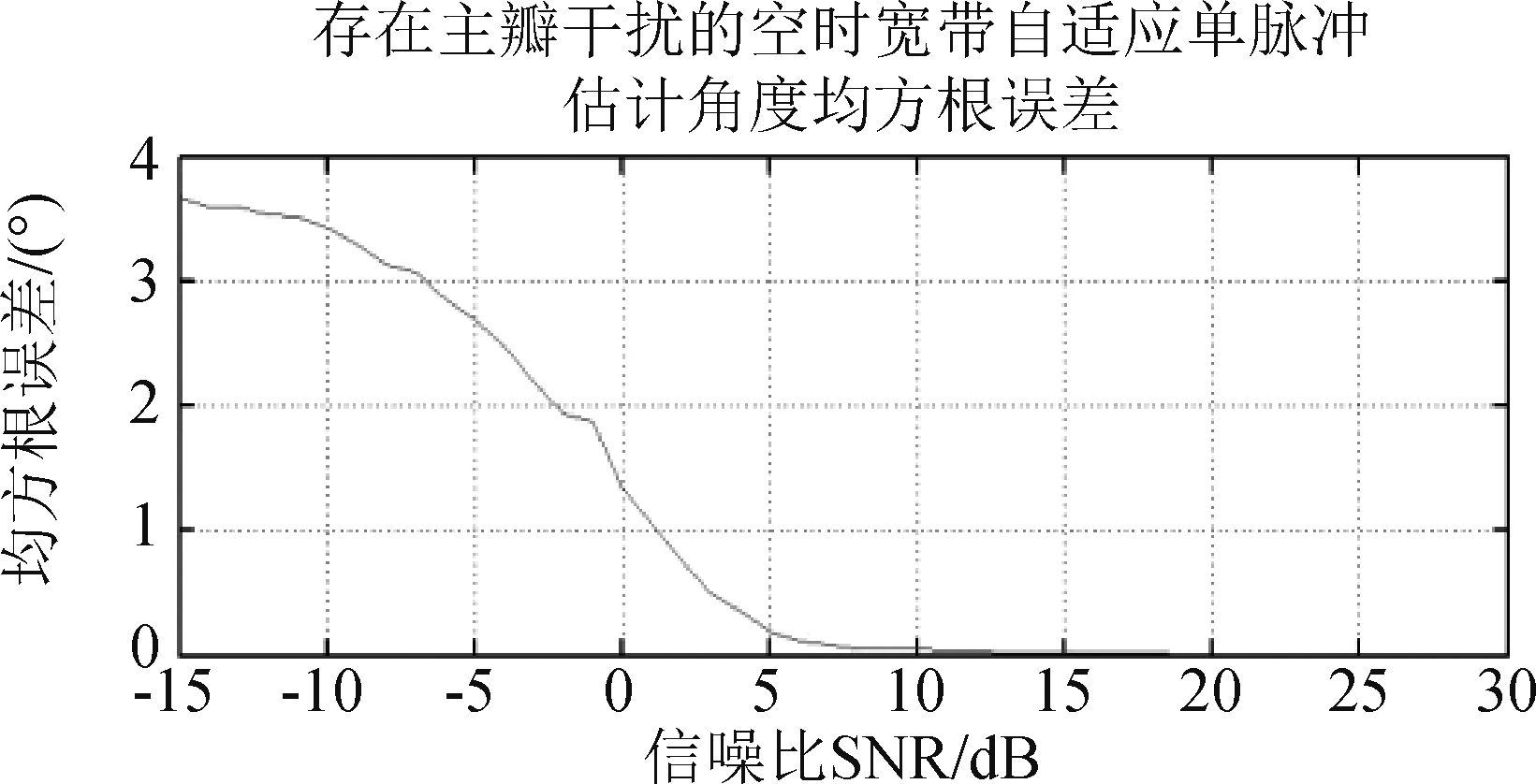
图6 存在主瓣干扰时不同信噪比下估计角度均方根误差
Fig.6 Root mean square error of angle estimation under different SNR
仿真分析试验4 保持仿真分析试验1中条件不变,选取的子带划分个数J=100,为了让每个子带内有足够多的样本数据,将仿真1中样本快拍数增加为snap=20000,为了让每个子带都有信号,在做空频处理时用fs1=B对信号采样。改变信号方向在波束指向方向±4°范围内变化,Monte-Carlo试验次数为100次,采用均方根误差(RMSE)来进行空时宽带自适应方法与空频相干、非相干处理方法的单脉冲角度误差的比较。
在上述仿真分析条件下,三种方法的均方根误差如图7所示,表明所提方法在低信噪比SNR=0 dB时仍然能精确测角,而与此同时采用常规的空频处理实现自适应单脉冲测角无法精确测角,并且所提方法在约束角度处趋近于0,与理论吻合,说明了所提方法具有在低信噪比下在波束指向3 dB内精确测角的优点。
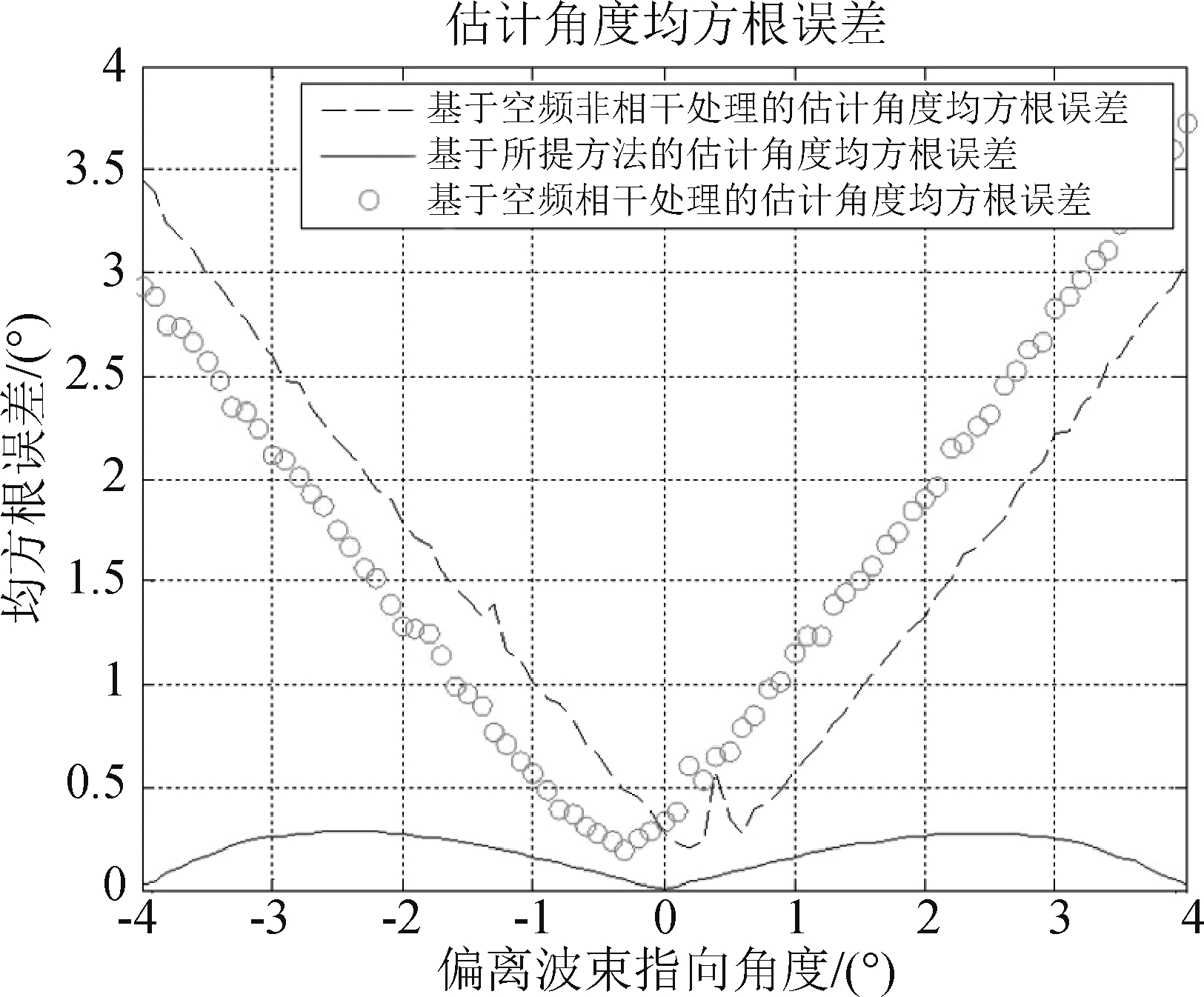
图7 不同方位估计角度均方根误差比较
Fig.7 Comparison of root mean square error of different azimuth estimation angles
仿真分析试验5 保持仿真分析实验4中的条件不变,将信号方向固定为偏离波束指向-4°,即信号来向6°,改变信噪比,在同等条件下比较宽带空时与空频相干、非相干处理的测角性能如图8所示。
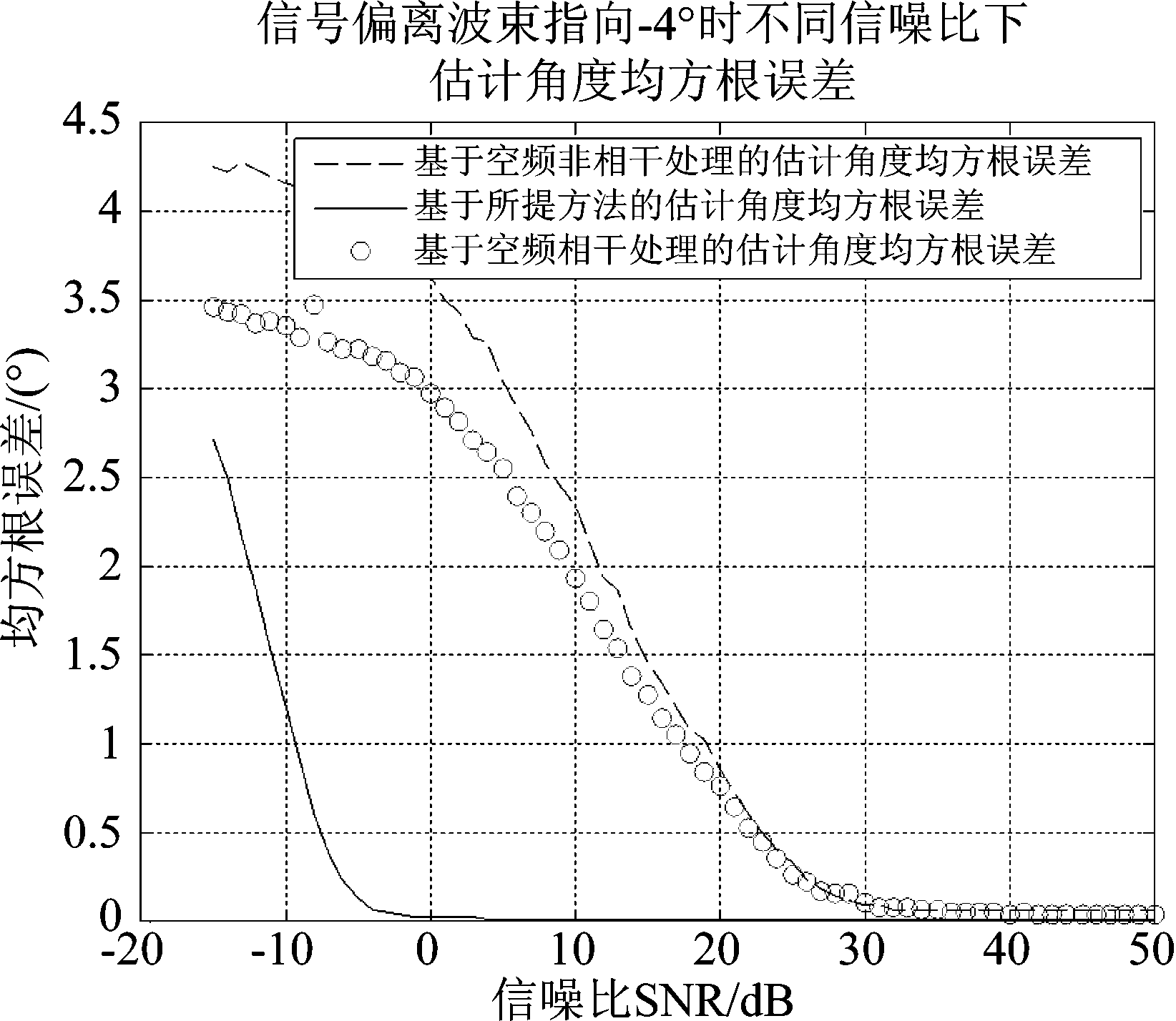
图8 不同信噪比下估计角度均方根误差比较
Fig.8 Comparison of root mean square error of angle estimation under different SNR
在上述仿真分析条件下,三种方法在不同信噪比下的均方根误差如图8所示,表明所提算法能在较低的信噪比-10 dB下实现精确的测角,在-5 dB以后估计角度均方根误差已经能够趋近于平稳,其远远优于同等条件下基于空频处理的宽带单脉冲测角精度,说明了同等条件下所提算法能在更低信噪比下精确测角的优势。观察图中每条曲线最后的收敛值,所提方法和两种空频处理的方法均方根误差近乎相同接近于0,这与修正间隔Δθ′=4°是相符的。
5 结论
本文提出了一种无需预延迟处理的宽带空时自适应干扰抑制的和差波束形成,以及单脉冲比幅测角的方法。该方法基于空时结构,利用线性约束最小方差求得和波束权,对和波束权向量进行修正得到差波束权向量,在有效的抑制干扰宽带自适应波束形成的同时还可以对期望信号的来波方向进行精确估计。本方法有着能充分利用空时法对宽带信号进行整体处理的特点,相比于传统空频处理方法无需对每个频带做信号检测,具有所需信噪比小、计算量小的优势。仿真分析结果表明,所提方法在信号的信噪比大于-5 dB情况下即可精确测角,而且在存在主瓣干扰的条件下仍然能进行有效的单脉冲测角。接下来研究重点将是把无需预延迟处理的宽带空时处理方法引入到二维阵、共形阵等的和差波束形成与测角。
[1]Samuel M. Sherman, David C. Barton. 单脉冲测向原理与技术[M]. 国防工业出版社, 2013.
Samuel M. Sherman, David C. Barton. Monopulse Principles and Techniques[M]. National Defense Industry Press, 2013.(in Chinese)
[2]谢俊好, 熊卫明. 传统单脉冲方法的数学原理及工程实现[J]. 系统工程与电子技术, 2004, 26(4): 467- 473.
Xie Junhao, Xiong Weiming. Mathematical principle and practical implementation of conventional monopulse[J]. Systems Engineering and Electronics, 2004, 26(4): 467- 473.(in Chinese)
[3]Nickel U. Overview of generalized monopulse estimation[J]. IEEE Aerospace and Electronic Systems Magazine, 2006, 21(6): 27-56.
[4]郭琨毅, 牛童瑶, 盛新庆. 散射中心属性对单脉冲雷达测角的影响研究[J]. 电子与信息学报, 2017, 39(9): 2238-2244.
Guo Kunyi, Niu Tongyao, Sheng Xinqing. Influence of Multiple Scattering Centers with Various Attributeson Radar Angular Measurements[J]. Journal of Electronics & Information Technology, 2017, 39(9): 2238-2244.(in Chinese)
[5]陈新亮, 曾涛, 郑乐. 基于极大似然估计的高分辨雷达测角方法[J]. 信号处理, 2012, 28(9): 1241-1247.
Chen Xinliang, Zeng Tao, Zheng Le. An angle measurement method for high resolution radar based on maximum likelihood estimation[J]. Signal Processing, 2012, 28(9): 1241-1247.(in Chinese)
[6]López-Pastor J A, Gómez-Alcaraz A, Ca ete-Rebenaque D, et al. Near-Field Monopulse DoA Estimation for Angle-Sensitive Proximity WiFi Readers[J]. IEEE Access, 2019, 7(3): 88450- 88460.
ete-Rebenaque D, et al. Near-Field Monopulse DoA Estimation for Angle-Sensitive Proximity WiFi Readers[J]. IEEE Access, 2019, 7(3): 88450- 88460.
[7]Galy J, Chaumette E, Larzabal P. Joint Detection Estimation Problem of Monopulse Angle Measurement[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(1): 397- 413.
[8]Liu W, Zhang H,Liu Q. Monopulse angle measurement with mainlobe interference based on the auxiliary array[J]. The Journal of Engineering, 2019, 2019(19): 5873-5876.
[9]Nickel U. Monopulse estimation with adaptive arrays[J]. Radar & Signal Processing Iee Proceedings F, 1993, 140(5): 303-308.
[10]Fante R L. Synthesis of adaptive monopulse patterns[J]. IEEE Transactions on Antennas and Propagation, 1999, 47(5): 773-774.
[11]朱林. 单脉冲测角和差波束形成算法研究与实现[D]. 南京理工大学, 2018.
Zhu Lin. Research and implementation of monopulse angle measurement and difference beamforming algorithm[D]. Nanjing University of Science&Technology, 2018.(in Chinese)
[12]马晓峰, 沈爱松, 盛卫星, 等. 可控测角精度和范围的数字阵列单脉冲和差波束优化[J]. 电子与信息学报, 2016, 38(12): 3107-3113.
Ma Xiaofeng, Shen Aisong, Sheng Weixing, et al. Sum and Difference Patterns Optimization for Digital Array with Controllable Accuracy and Range of Angle Estimation[J]. Journal of Electronics & Information Technology, 2016, 38(12): 3107-3113.(in Chinese)
[13]Takahashi R, Inaba T, Takahashi T, et al. Digital Monopulse Beamforming for Achieving the CRLB for Angle Accuracy[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(1): 315-323.
[14]许京伟, 廖桂生, 朱圣棋. 基于幅相线性约束的自适应和差波束形成方法研究[J]. 电子学报, 2013, 41(9): 1724-1729.
Xu Jingwei, Liao Guisheng, Zhu Shengqi. Approach of Adaptive Sum and Difference Beamforming Based on Magnitude and Phase Linear Constrain[J]. Acta Electronica Sinica, 2013, 41(9): 1724-1729.(in Chinese)
[15]曹运合, 曾丽, 王宇. 基于特征空间的子阵级自适应和差波束测角方法[J]. 吉林大学学报(工学版), 2019, 49(5): 1735-1744.
Cao Yunhe, Zeng Li, Wang Yu. Adaptive sum and difference beam angel measurement method at subarray level based on feature space[J]. Journal of Jilin University (Engineering and Technology Edition), 2019, 49(5): 1735-1744.(in Chinese)
[16]李永伟, 谢文冲. 端射阵机载雷达STAP单脉冲测角方法[J]. 系统工程与电子技术, 2020, 42(2): 322-330.
Li Yongwei, Xie Wenchong. Monopulse angel estimation method for end-fire array airborne radar based on STAP[J]. Systems Engineering and Electronics, 2020, 42(2): 322-330.(in Chinese)
[17]冯林高. 一种全空域电扫球面相控阵单脉冲角跟踪方法[J]. 电讯技术, 2019, 59(11): 1293-1298.
Feng Lingao. A Monopulse Angle Tracking Method for Electronically Scanned Spherical Phased Array in Hemispherical[J]. Telecommunication Engineering, 2019, 59(11): 1293-1298.(in Chinese)
[18]向巍, 葛志强, 崔剑, 等. 多通道相控阵自适应数字单脉冲合成方法[J]. 系统工程与电子技术, 2019, 41(4): 765-771.
Xiang Wei, Ge Zhiqiang, Cui Jian, et al. Adaptive digital monopulse beamforming for multi-channel phased array[J]. Systems Engineering and Electronics, 2019, 41(4): 765-771.(in Chinese)
[19]Cheng Z, He Z, Duan X, et al. Adaptive Monopulse Approach With Joint Linear Constraints for Planar Array at Subarray Level[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(3): 1432-1441.
[20]Raabe H P. Fast Beamforming with Circular Receiving Arrays[J]. IBM Journal of Research & Development, 1976, 20(4): 398- 408.
[21]Frost. An algorithm for linearly constrained adaptive array processing [J]. Proc. IEEE, 1972, 60(8): 926-935.
[22]Anbiyaei M R, Liu W, McLernon D C. White noise reduction for wideband linear array signal processing[J]. IET Signal Processing, 2018, 12(3): 335-345.
[23]Su G, Morf M. The signal subspace approach for multiple wide-band emitter location[J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1983, 31(6): 1502-1522.
[24]Allam M, Moghaddamjoo A. Two-dimensional DFT projection for wideband direction-of-arrival estimation[J]. IEEE Transactions on Signal Processing, 2002, 43(7): 1728-1732.
[25]Wang H, Kaveh M. Coherent signal-subspace processing for the detection and estimation of angles of arrival of multiple wide-band sources[J]. Acoustics Speech & Signal Processing IEEE Transactions on, 1985, 33(4): 823- 831.
[26]Wang Guan, Shen Mingwei, Li Jianfeng, et al. Wideband transmitting adaptive digital beamforming based on sub-band multiple linear constrained minimum variance method[J]. Progress In Electromagnetics Research M, 2018, 75(2): 113-120.
[27]陈亮, 盛卫星, 韩玉兵, 等. 改进贝叶斯聚焦的宽带自适应单脉冲算法[J]. 电波科学学报, 2013, 28(2): 35- 46.
Chen Liang, Sheng Weixing, Han Yubing, et al. Wideband adaptive monopulse algorithm based on improved Bayesian focusing [J]. Chinese Journal of Radio Science, 2013, 28(2): 35- 46.(in Chinese)
[28]Reza Ebrahimi, Saeid R. Seyhnejad. Elimination of Pre-Steering Delays in Space-Time Broadband Beamforming Using Frequency Domain Constraints [J]. IEEE Communication Letters, 2013, 17(4): 769-772.
[29]Zoltowski M D. Synthesis of sum and difference patterns processing common nulls for monopulse bearing estimation with line array[J]. IEEE Transactions on Antennas and Propagation, 1992, 40(1): 25-37.
[30]何松华, 蒋政胜, 张军. 弹载宽带相控阵单脉冲雷达通道级STAP与ATBF研究[J]. 信号处理, 2016, 32(9): 1108-1116.
He Songhua, Jiang Zhengsheng, Zhang Jun. Channel-level STAP and ATBF for Missile-borne Wideband Phased-array Mono-pulse Radar[J]. Journal of Signal Processing, 2016, 32(9): 1108-1116.(in Chinese)


