1 引言
在飞机精密进近过程中,陆基增强系统(GBAS)的地面子系统为机载设备提供包含伪距改正量、完好性检测和最终进场航道等在内的信息,以满足国际民航组织(ICAO)规定的所需导航性能(RNP)[1]。其中,GBAS的完好性异常检测是确保精密进近是否成功的关键技术之一。
对于地面子系统来说,基准站异常检测是地面完好性检测的重要一环。通常利用多台基准站采集到的观测量进行交叉冗余计算,将计算得到的B值与相应阈值进行比较[2-3],即多参考一致性检测(MRCC)。如果B值超过阈值,则代表对应的基准站存在问题。斯坦福大学的谢刚等人搭建完好性测试平台对MRCC算法进行实验测试[4]。
目前,大多数GBAS地面子系统布设3个或4个基准站,虽然存在备用基准接收机可供使用,若在不了解故障具体情况下直接减少基准站个数也将导致系统性能下降。为解决这类问题,Jie Hu等人提出一种基于S值辅助信息的MRCC算法,可以有效排除由故障卫星引起的基站数据异常情况[5]。李斌、杨文辉等人采用高斯膨胀法设定阈值,提升系统完好性[6-7]。孙淑光等利用小波多分辨技术改进MRCC故障监测流程[8]。现有的改进方法都在一定程度上提高了GBAS系统的可用性,但却无法识别出基站故障的异常程度和具体信息。而且,从地面基准站发生故障开始,往往需要一段时间的延迟,MRCC才能将异常检测出来。
本文引入希尔伯特—黄变换对B值数据进行异常诊断,通过对异常数据的分解和其模态分量的频谱分析,能有效识别由电离层误差引起的基站数据异常情况,同时得到异常的程度及其局部信息。同时该算法在自适应分解过程中直接分离出有效信号,减少了系统检测时延,为GBAS地面站完好性检测提供一种新的技术手段和有效的数据支撑。
2 传统多参考一致性检测
为排除存在较大伪距改正量误差的接收机通道,通常利用多参考一致性检测算法对B值进行计算,检测某一基准站与其他基准站数据的一致性。将引起B值数据异常的基准站排除在播发的伪距改正数(PRC)之外,以此保证地面系统的完好性。将基准站获得的伪距同卫星与基准站天线的真实距离做差,可以得到伪距改正值。多个地面基准站所得伪距改正数的平均值为
(1)
式中,PRCRXi为第i个基准站的伪距改正数, M为GBAS基准站的数目,系统通常采用4基准站模式。通过伪距改正数可以计算得到B值,即
(2)
其中, j对应第j颗可见卫星,Bi, j为第i号基准站接收第j颗卫星信号所获得的B值,M为基准站数目,PRC c, j为广播的第j颗卫星的伪距改正值,PRCRXk, j表示第k号基准站接收第j颗卫星计算出的伪距改正值。
式(2)表示每个基准站对应每颗卫星都有一个B参数。斯坦福(Stanford)大学提出的MRCC阈值为[9]
(3)
σpr_lg f=0.16+1.07e-θi, j×90.0/π/15.5
(4)
式中,θi, j为卫星仰角,单位为弧度。
影响GBAS完好性参数B值异常的主要因素是地面基准站故障,为研究GBAS地面基准站与B参数之间的关系,分别仿真了无基准站故障情况下的B值(如图1所示)、3号基准站4000 s处出现瞬时故障下的B值(如图2所示)以及某一单个基准站长时间故障下的B值变化情况(如图3所示)。
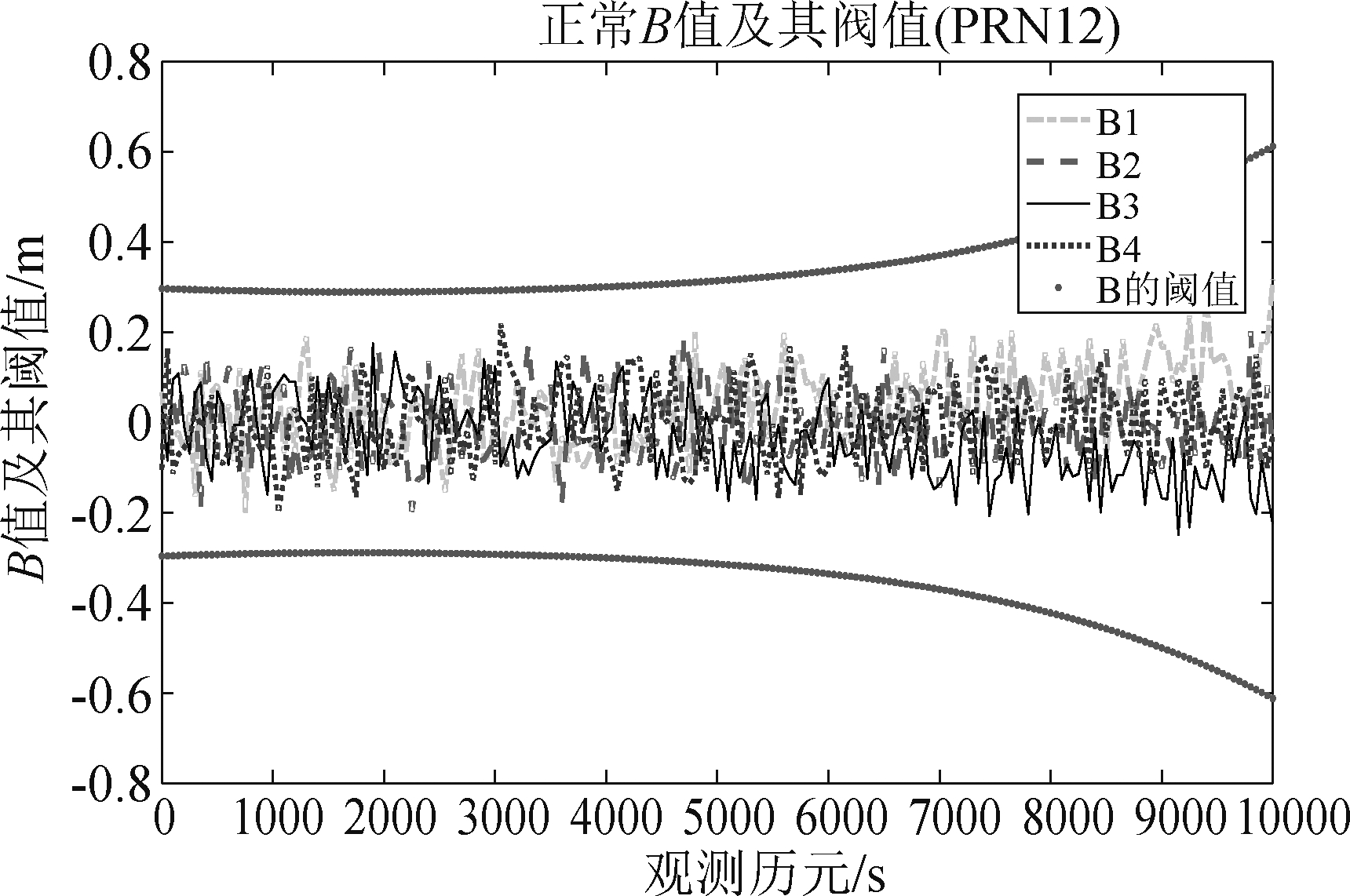
图1 正常情况下基准站对应B值变化情况
Fig.1 Change of B values corresponding to the ground reference station under normal circumstances
具体实验场景采用GBAS典型的4基准站布设要求,基准站坐标设在天津滨海国际机场内,分别为(N1:[E39.10972,N117.34148,98 m] N2: [E39.40972,N117.34148,58 m] N3: [E39.40972,N117.64148,18 m] N4: [E39.10972,N117.64148,18 m])。实验的历书数据采用GPS第1000周历书,仿真起始时间为世界协调时2018年10月23日16时,仿真时长10000 s,采样频率1 Hz,将高度角大于5°的卫星视为可见卫星,获得观测时间内4个基准站B值及相应阈值的变化情况,具体检测结果如图1所示。为观测基准站的异常情况,实验人为的在3号基准站计算的B值数据上添加大小为1.2 m的故障,并且在1号基准站的伪距改正值上添加大小为0.6 m误差,仿真结果分别如图2和图3 所示。
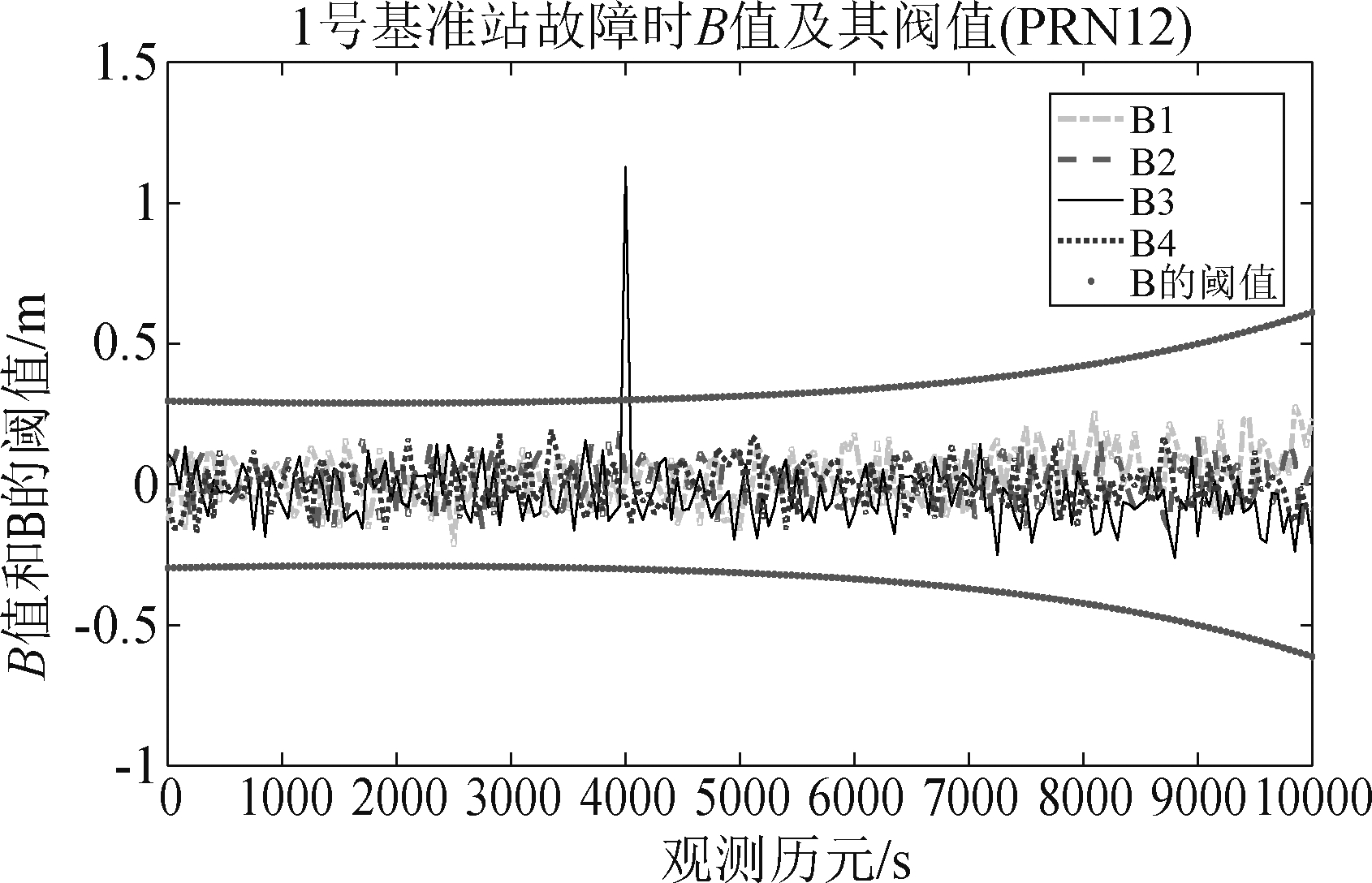
图2 3号基准站瞬时故障时对应B值变化情况
Fig.2 Change of B values during instantaneous failure of No.3 ground reference station
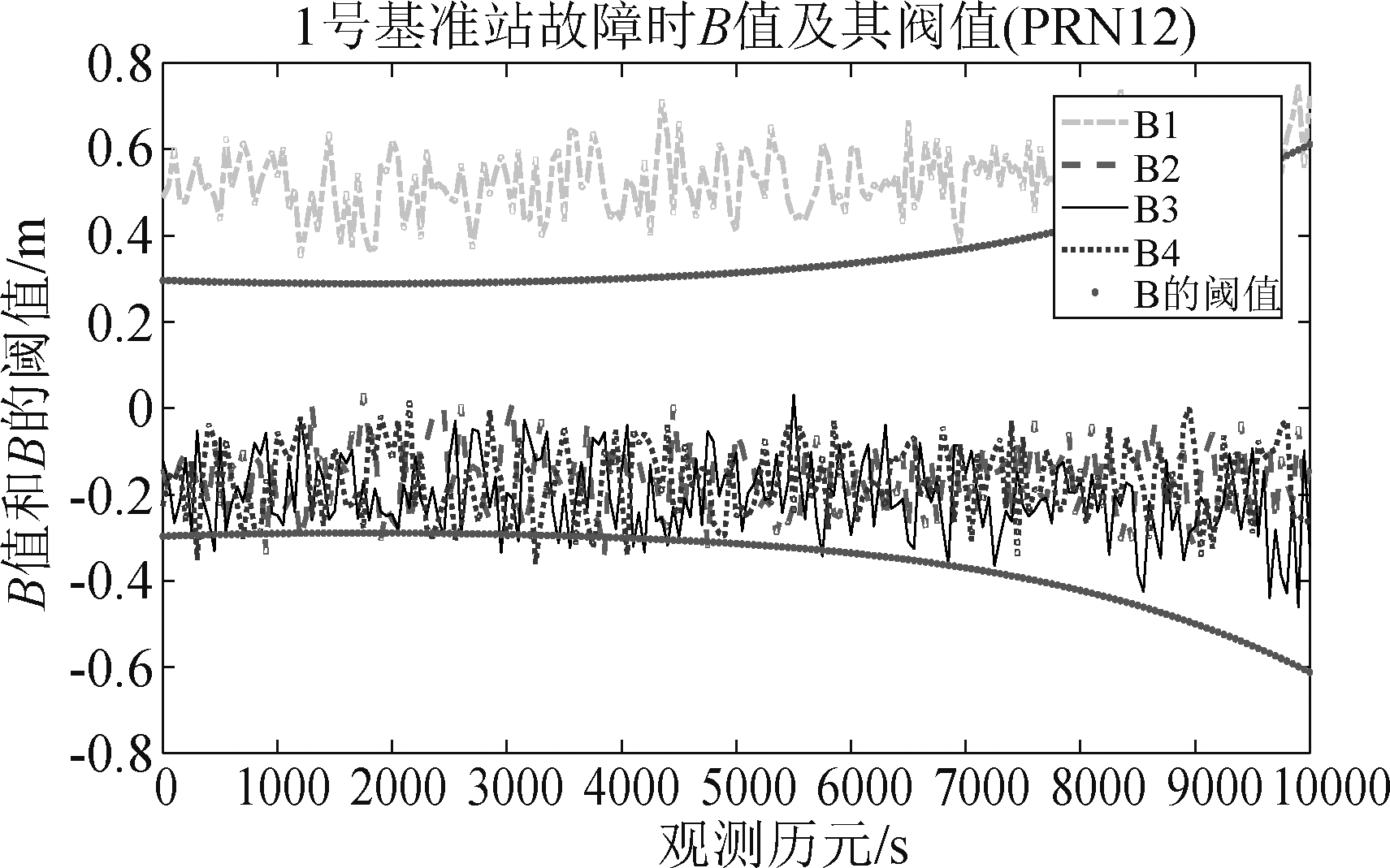
图3 1号基准站长时间故障的B值变化情况
Fig.3 Change of B values for a long-term failure of the No.1 ground reference station
由图1、图2可以看出,在传统的MRCC中,当基准站无故障时,整个观测时间内的B值变化范围在 0.3 m左右,并未超出相应阈值。当基准站发生瞬时故障时,对应基站的B值会在某一时刻跳出阈值,引发告警。图3显示了基准站B值之间的相关性。在B值交叉冗余的过程中会发生同一卫星对应不同基准站或者同一基准站对应不同卫星的情况。当1号基准站长时间出现问题时,其他基站的B值也会受到影响,进而影响整个GBAS系统地面接收机的检测情况。上述仿真结果显示,B值会随基准站的故障情况实时变化,通过对B值的检测即可监视基准站的完好性。
3 GBAS系统故障分类
在对B值数据进行分析研究之前,本文首先对GBAS基准站的故障类型进行分析,考虑其可能存在的故障模型。GBAS地面子系统存在三种类型故障,即卫星测距源故障、单个基准接收机故障和电离层异常。这三种故障类型存在的误差峰值和有效错误阈值有所不同。在GBAS进近服务类型D(GAST D)模式中[10],卫星测距源故障又分为信号形变、加速度误差、码载波偏离、低功率信号引起的误差以及星历误差。
3.1 卫星测距源故障
(1)信号形变。是指由卫星故障引发的传输信号C/A码错乱,进而导致信号相关峰的变形[11]。信号形变导致的典型结果是机载端和地面端测距结果不同,出现差分伪距误差。美国航空无线电技术委员会(RTCA)发布的《局域增强系统机载设备最低运行标准》(DO-253D)中包括了检测此误差特性的约束区域,得到的差分伪距误差可用载波平滑导致的指数阶跃响应表示[12]。
E(t)=(1-e-at)A
(5)
式中,A决定了响应的初始斜率,范围在1~35 m/s以内; a=1/τ=1/30,τ为伪距载波相位平滑时间常数。
该阶跃响应故障的限制条件是差分伪距误差在2.5 s告警时间内不超过1.6 m的风险概率是10-9。如图4所示。
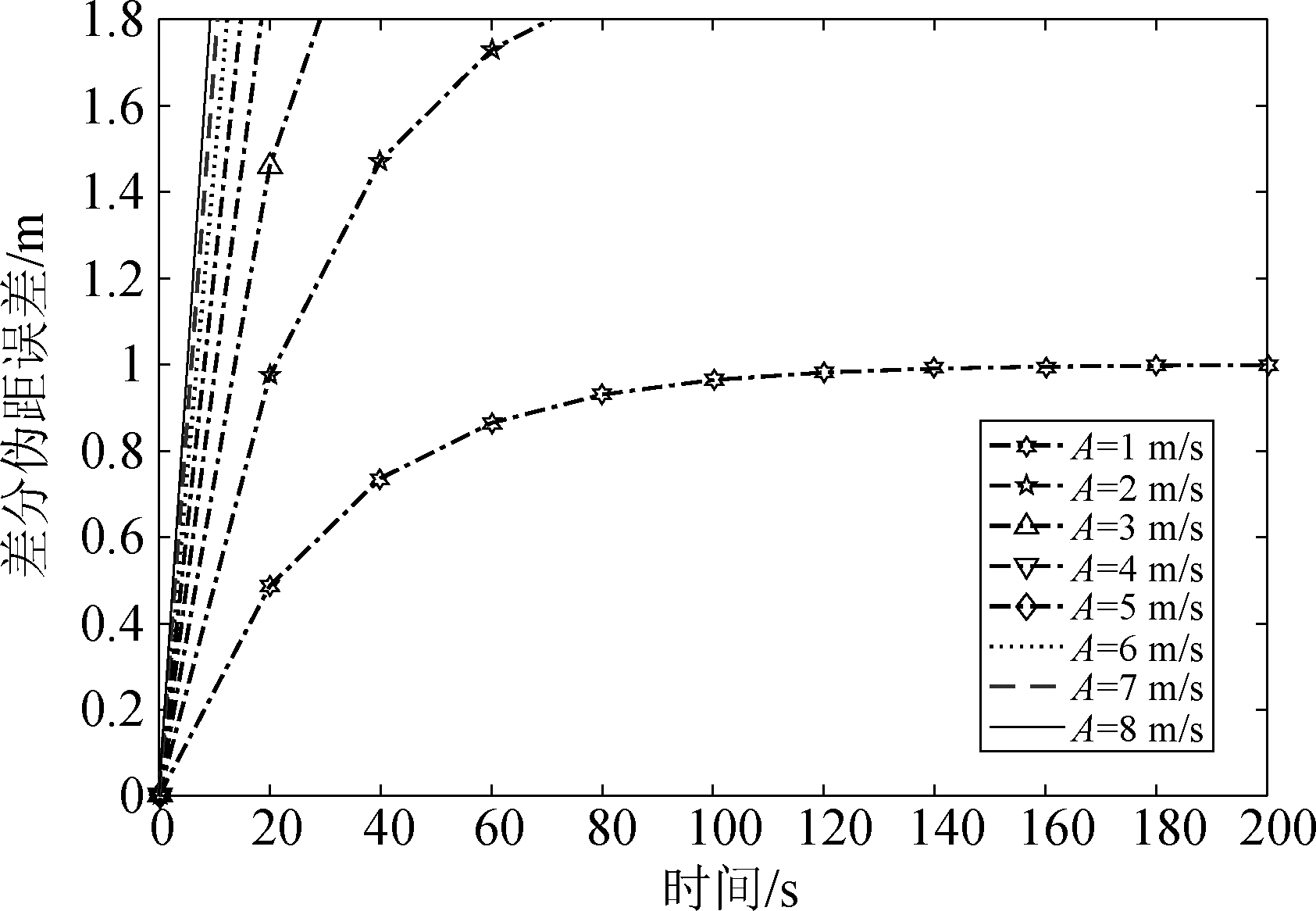
图4 信号形变瞬态故障
Fig.4 Signal deformation malfunction transient
图4可以看出,曲线初始斜率越大,伪距误差越快到达1.6 m。在误差低于1.6 m的范围内,信号形变故障近似为一个斜坡形态。
(2)加速度误差。由于地面子系统向机载用户广播差分改正信息时存在一定程度的延迟,卫星产生的信号加速度会同时影响到地面设备和机载接收机,使二者在估算用户位置时产生一个误差[13-14]。即
E=0.5×A×t2,0<t≤τ
(6)
其中,t为采样时间,τ为地面站与机载接收机之间的通信延时(2.5 s),信号加速度A变化范围为0.1~1 m/s2。
当t>τ时,由信号加速度导致的伪距误差为
E=0.5×A×τ(τ+0.5),t>τ
(7)
额外的0.5 s误差与差分修正率的形成有关,一般在计算中可忽略。加速度误差约束范围为1.6 m,若误差超过1.6 m系统会自动排除此颗卫星数据。
图5反映了信号加速度产生的误差形态。随着伪距加速度的增大,产生的差分误差也逐渐增大,但是当采样时间大于2.5 s时,误差变为恒定。
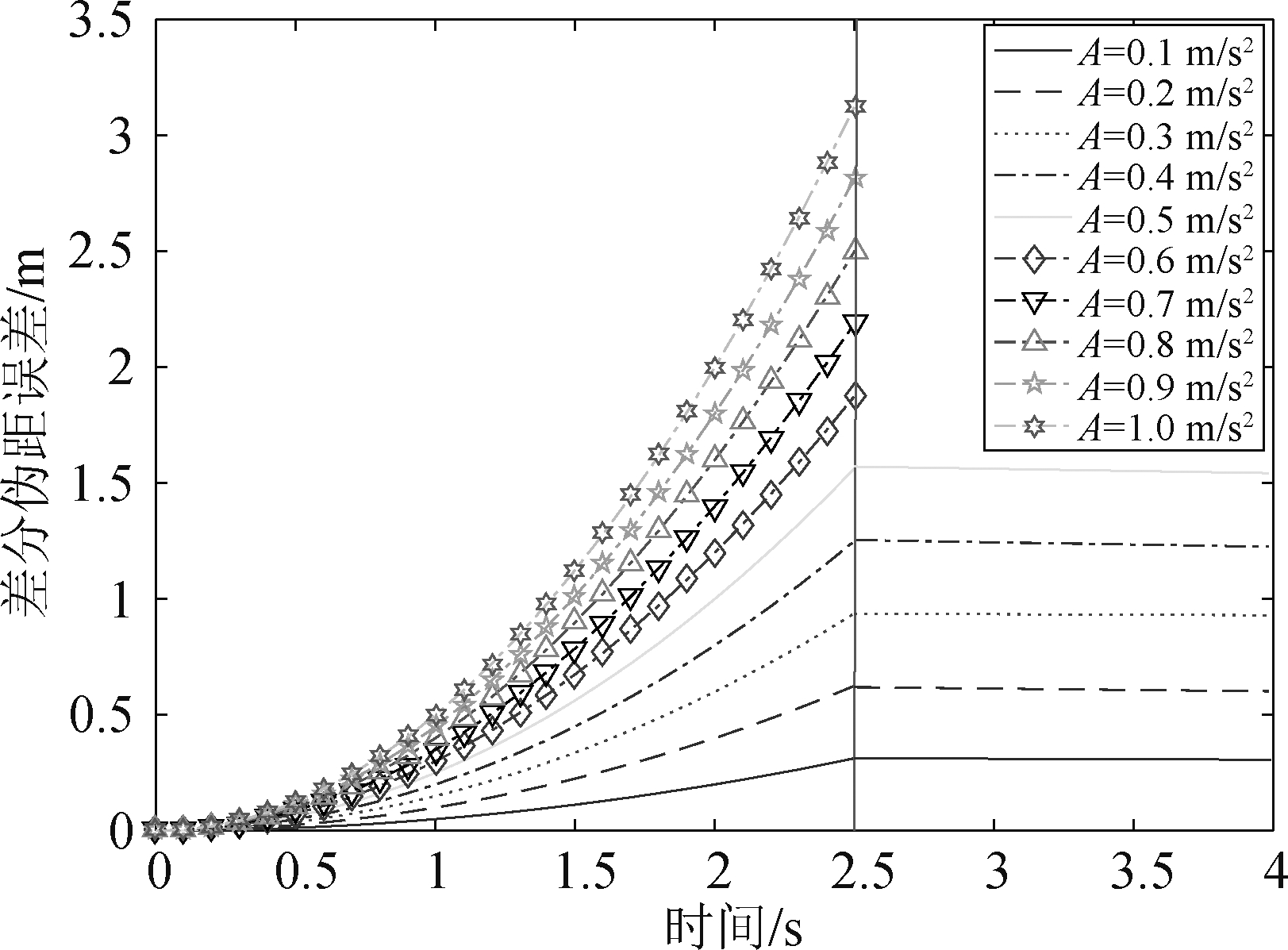
图5 加速度伪距误差
Fig.5 Acceleration pseudorange error
(3)码载波偏离误差。该误差是由卫星故障引起的导航信号的码载波偏差率超过载波驱动率,从而使信号在传输过程中产生偏离[13]。若故障发生在接收机平滑滤波初始化30 s以后,测距码和载波的平滑时间相同,可以消除相互之间的影响。所以当偏差发生时,卫星会进入延迟状态直到30 s以后,确保系统有足够的时间消除码载波偏差。
图6可以看出码载波偏差率越大,引起的差分伪距误差变化越剧烈。偏差率的变化形态以斜坡开始,继而逐渐衰减。因此在30 s平滑时间内,可以将偏差结果保守地建模为一个斜坡。
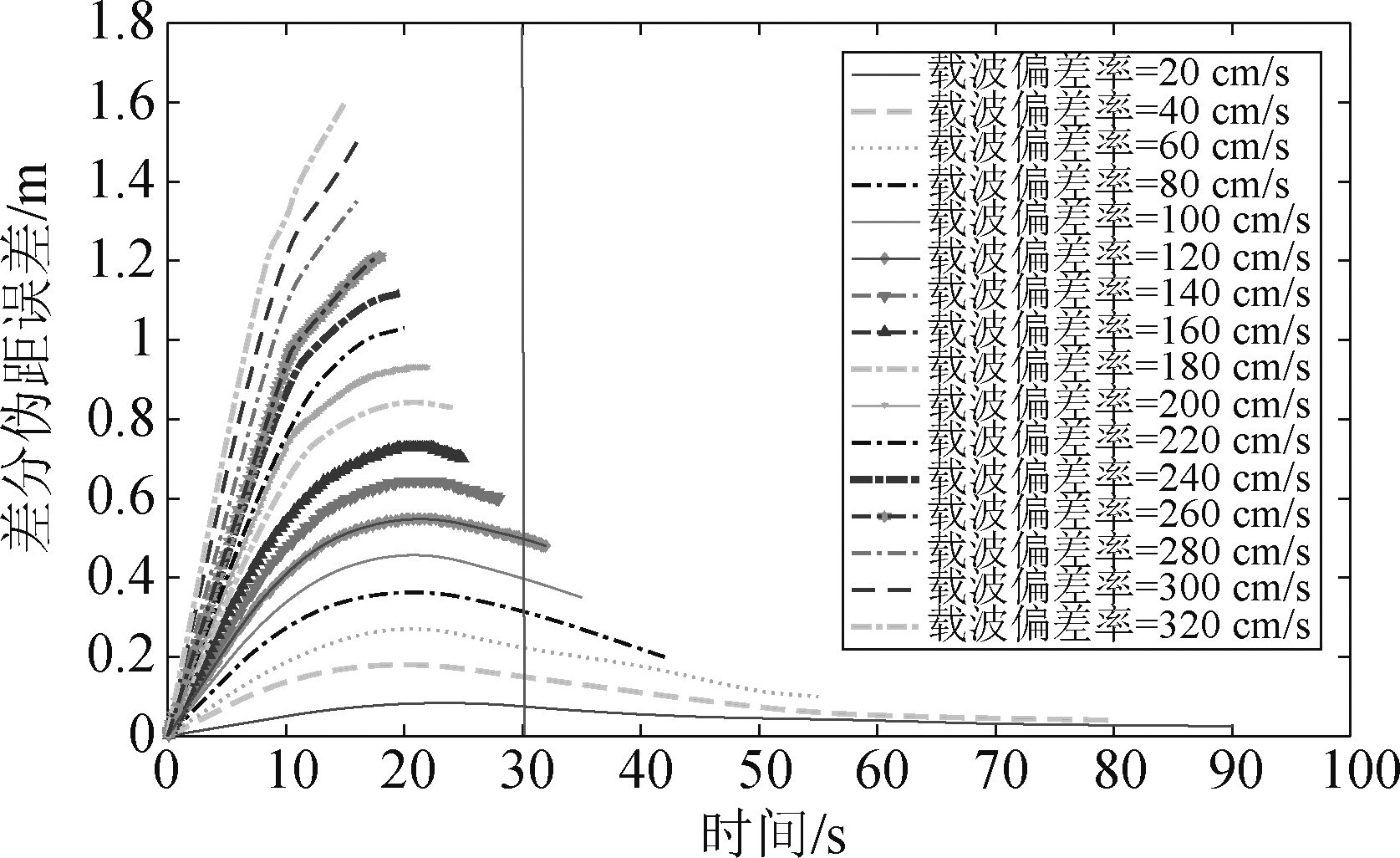
图6 码载波偏离误差
Fig.6 Code carrier deviation error
(4)低功率信号误差。信号功率和卫星测距误差存在着紧密的联系。当信号功率过低,信噪比比接收机预先设定的临界值低,接收机很难将信号从噪声中分离开来,导致测距误差增大,完好性风险概率随之增加[15]。一般情况下,临界值的设定由接收机的天线位置,天线增益变化,电缆损耗,硬件配置等因素决定。
(5)星历误差。指进行卫星定位时,星历给出的卫星空间位置与实际位置之间的误差。一般情况下卫星每运行10 km至少会出现1.6 m左右的径向误差,此误差也可用一个缓慢的斜坡来表示。
3.2 单个基准接收机故障
国际民航组织在相关的“标准和建议措施(SARPs)”中定义了基准接收机故障检测(RRFM)的漏检率[16-17]。当给定单个基准接收机出现故障时,用户可以接受的最大漏检概率是10-9,RRFM在GAST D情况下垂直和水平上的最大告警门限分别为9.35 m和35.9 m。
3.3 电离层延迟误差
电离层延迟误差是影响伪距精度的重要因素之一[18]。局部电离层的变化过程十分复杂,可将电离层风暴看作是等电子密度的梯形区域,随着电离层风暴的向前推进,会逐渐穿透该梯形区域形成伪距误差。其中,伪距误差的大小随电离层风暴向前推进的速度不断变化,它在推进过程中表现出斜坡变化的趋势。
表1给出了GAST D标准下各类故障的具体参数指标。根据各故障模式的斜率不同可以有效确定电离层误差带来的系统影响。
表1 Ⅱ/Ⅲ类GBAS故障瞬态性能指标
Tab.1 Transient performance indicators for CAT Ⅱ/Ⅲ GBAS faults

故障类型服务类型斜率m/s垂直告警限水平告警限Emax/m有效阈值/m卫星测距源误差GAST D0~∞1.6×Svert1.6×Slat视情况0.75×Svert/0.75×Slat单个基准接收机误差GAST D0~∞9.3535.9视情况6.5/24.5电离层误差GAST D0~2N/AN/A2.75×Svert/2.75×SlatN/A
*: Svert/Slat表示任一卫星的最大垂直/横向系数大小,该参数确保飞机性能能够支持故障模式下的最大误差值Emax,也与故障检测的有效告警限有关,一般由飞机制造商设定。
3.4 GBAS接收机故障模型
通过对Ⅱ/Ⅲ类GBAS故障类型的分析,可以得出结论,几乎每种故障模式都可建模为斜坡表示。Honeywell公司根据这些参数指标建立了具体的故障模型[13],如图7所示。该模型适用于系统中只含有一个故障的情形。故障的大小往往由其假定的斜坡斜率和故障响应时间共同决定。在总曝光时间(Tmax)一定的情况下,系统故障(Emax)越大,其相应的斜率k越大。系统误差随着模型斜率的增大而增大,两者关系如式(8)所示。
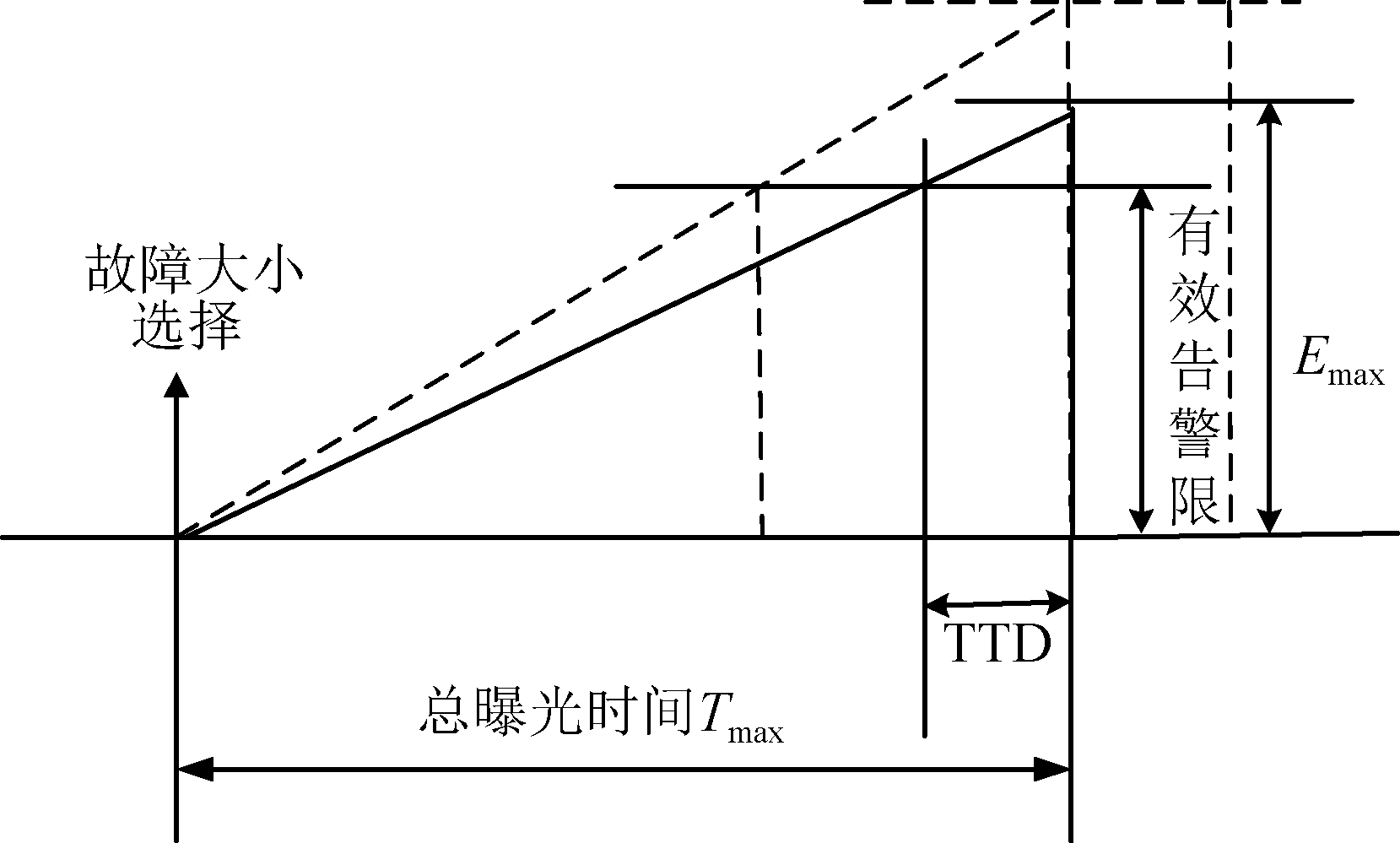
图7 GBAS基准站故障误差模型
Fig.7 The fault error model of GBAS ground reference station
根据前面观察到的故障特征,可以推出斜率k为
(8)
因此,斜坡信号足以作为系统故障模型用于后续实验的进行。
4 算法流程及机理
根据上文对MRCC算法的分析,不难发现该方法无法得到不同GBAS基准站故障的具体信息。本节在对B值数据进行分析的过程中则需要考虑如何获得突变数据的局部信息。
希尔伯特—黄变换是一种可以反应信号局部时频特性的变换方法,主要用于非线性、非平稳信号的处理。该方法在多种时频分析方法的对比研究和实际应用中表现出优势,目前被广泛应用于海洋、地震、雷达、声纳的研究中[19, 21]。HHT主要由经验模态分解(EMD)和Hilbert谱分析(HSA)两部分组成,核心技术是EMD。简单来说,HHT首先利用EMD将给定的数据按照不同尺度的波动分解成若干固有模态函数(IMF);然后,对分解后的分量进行Hilbert变换,得到Hilbert谱,根据变换后信号的频谱变化对故障特征进行识别。HHT在时频域上的检测精度很高,这使它非常适用于提取异常信号的特征。图8表示了利用HHT进行GBAS地面基准站故障检测的整个流程。
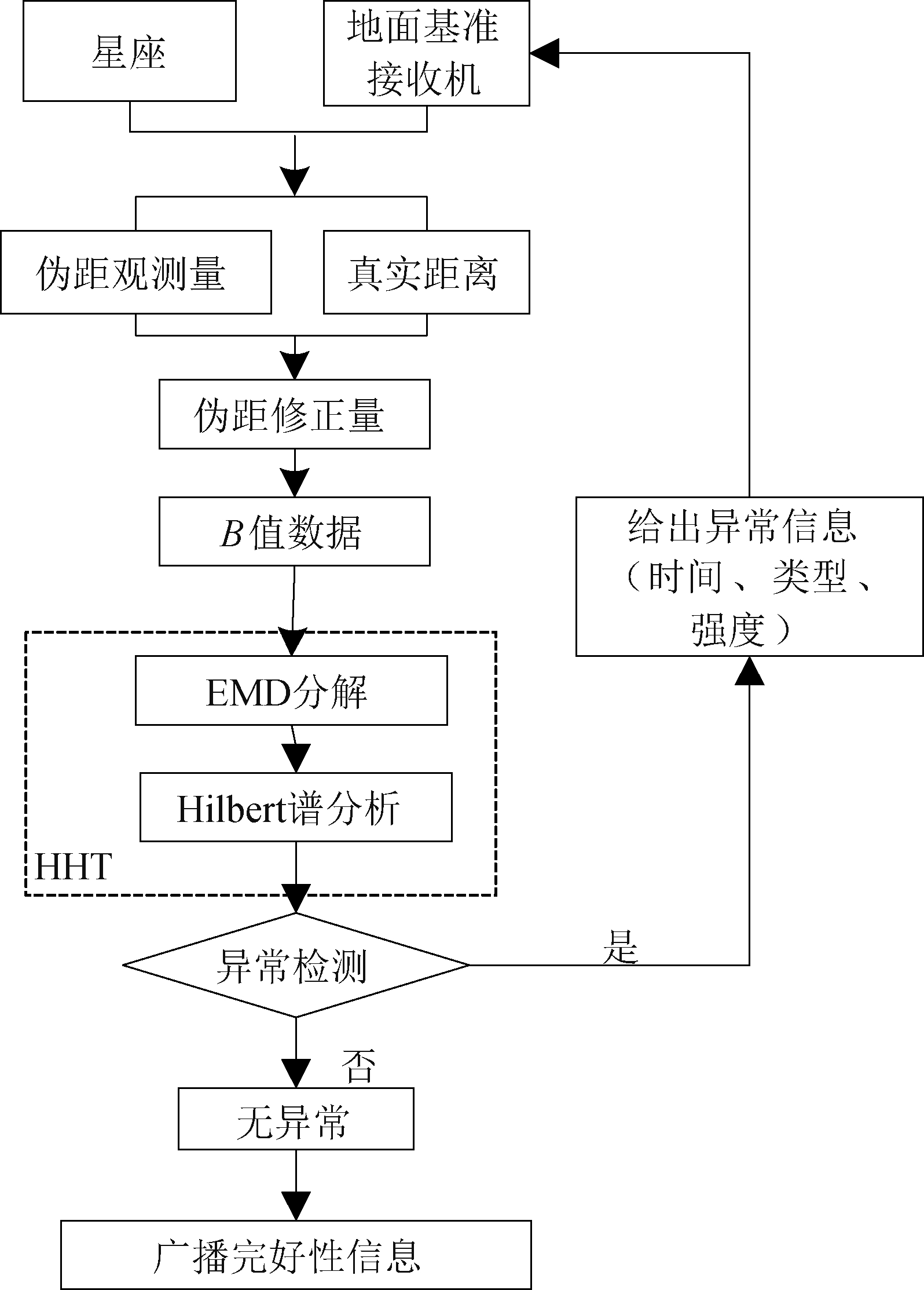
图8 利用HHT进行GBAS地面基准站故障检测的操作流程
Fig.8 Operation procedure of GBAS ground reference station fault detection using HHT
当GBAS基站发生斜坡故障时,B值数据会产生相应的斜坡变化。利用HHT方法对B值数据进行多级分解,将系统信号与系统各项噪声分离,得到基站信号的一系列异常信息,包括异常发生时间、异常信号幅值等。各分量曲线在异常区间内会发生较大的幅值变化,在某一时刻出现模极大值,利用信号的最大幅值等信息即可求得异常信号斜率。通过对信号的频谱分析即可检测出故障的强度。因此可以利用HHT来处理异常B值数据进而确定引发基站故障的具体信息。
4.1 经验模态分解
EMD是一种有效的信号分解方法,在信号与噪声的分离、信号分解以及故障提取等方面应用广泛。EMD将B值信号分解为有限个imf分量的具体过程如下:
(1)找出B值信号的极值点,利用3次样条插值函数对局部极值点拟合成原始信号x(t)的上下包络线。
(2)求出上、下包络的平均值m1,并用原始B信号x(t)减去m1得到差值,即新的信号h1
h1=x(t)-m1
(9)
成为IMF分量必须满足的两个条件:一是整个信号时域范围内的极点数和零点数至多相差一个;二是由极值点形成的上、下包络线在局部范围内均值为零。如果h1达不到这两个条件,那么h1将重复步骤(1)~(2),连续筛选k次,直至满足IMF条件。此时的h1k(t)即为第一个imf分量
h1k(t)=h1(k-1)(t)-m1k(t)
(10)
式中,h1(k-1)(t)为筛选k-1次后的信号;m1k(t)为筛选k次后的上下包络平均值。
B信号经过分解后得到第一个分量,记为imf1(t)
imf1(t)=h1k(t)
(11)
(3)从原始信号x(t)中减去imf1(t),得到一阶剩余信号r1(t)
r1(t)=x(t)-imf1(t)
(12)
(4)重复步骤(1)~(3)计算,计算第二个分量imf2(t),连续重复可以得到
r2(t)=r1(t)-imf2(t) …… rn(t)=rn-1(t)-imfn(t)
(13)
直至rn(t)成为一个单调残余函数时退出循环,于是有
(14)
式中rn(t)为分解后的剩余残差,可忽略不计。
每一个imfi(t)分量的能量都来自于原始B信号,前L个分量主要含有噪声等干扰信号,层层分解后n-L个分量逐渐逼近于原始信号[21],故后者能量值更高。经EMD分解后的每一个imf能量为
(15)
4.2 故障特征提取
Hilbert变换强调信号的特征提取[23]。基准站发生故障后的B值特征信息主要集中在imf分量中。对imf分量进行Hilbert变换后,消除了信号中的高频干扰分量,其他含有缺陷的激励分量a(t)代替原始信号x(t)进行频谱分析,进而提取有效故障信息。
对于式(13)中任一固有模态函数c(t)进行Hilbert变换为
(16)
c(t)的解析信号为
z(t)=c(t)+jH[c(t)]=a(t)ej φ(t)
(17)
式中,P为柯西主值, τ为时间差值,t为时间, a(t)和φ(t)分别为变换后c(t)的瞬时振幅和瞬时相位。
(18)
(19)
HHT谱反映的是信号振幅在频率-时间域上的变化情况,即
(20)
若对H(ω,t)进行时间上积分,可得B值分量的边际谱为
h(ω)=![]() H(ω,t)dt
H(ω,t)dt
(21)
根据式(18)可以对每个频率的振幅进行量测,从而得到异常信号的局部特征。
5 仿真实验及分析
5.1 经验模态分解对故障B信号的检测
仿真实验环境设置和 “2 传统多参考一致性检测”的一致,为比较不同斜率故障下的检测情况,在3号基准站第2000~4000 s观测时间内分别引入斜率为0.005、0.05和0.5的斜坡故障,图9展示了对不同斜率的斜坡故障进行EMD分解得到的模态分量曲线,图10为各分量对应的能量图。
图9可以看出,经过EMD分解后的B值信号分离了噪声项影响,频带宽度变窄,故障信息越发明显。imf 1~imf 9各模态分量频率从上到下逐渐降低,由于故障信息反映在波形上往往是幅度很大的信号尖峰值,各分量在4000 s左右出现幅度最大值。图10显示了各分量的能量分布图,能量较高的分量为imf 7~imf 9,当信号分解至imf 7~imf 9时,故障信号逐渐从噪声项中分离出来。imf 9能量占比最大,最逼近原始故障信号,其在2000 s时分量幅度模值大于0,数据出现突变,信号故障响应的持续时间为2000 s。根据EMD分解原则,分量信号每一时刻幅值由原始故障数据的上下包络求平均得到,故分量最大幅值的2倍即为系统的最大故障Emax,结合式(8)的斜率计算公式,即可求得斜率为 0.005043。

图9 斜坡故障信号EMD波形分解图
Fig.9 Exploded view of EMD waveform of ramp fault signal
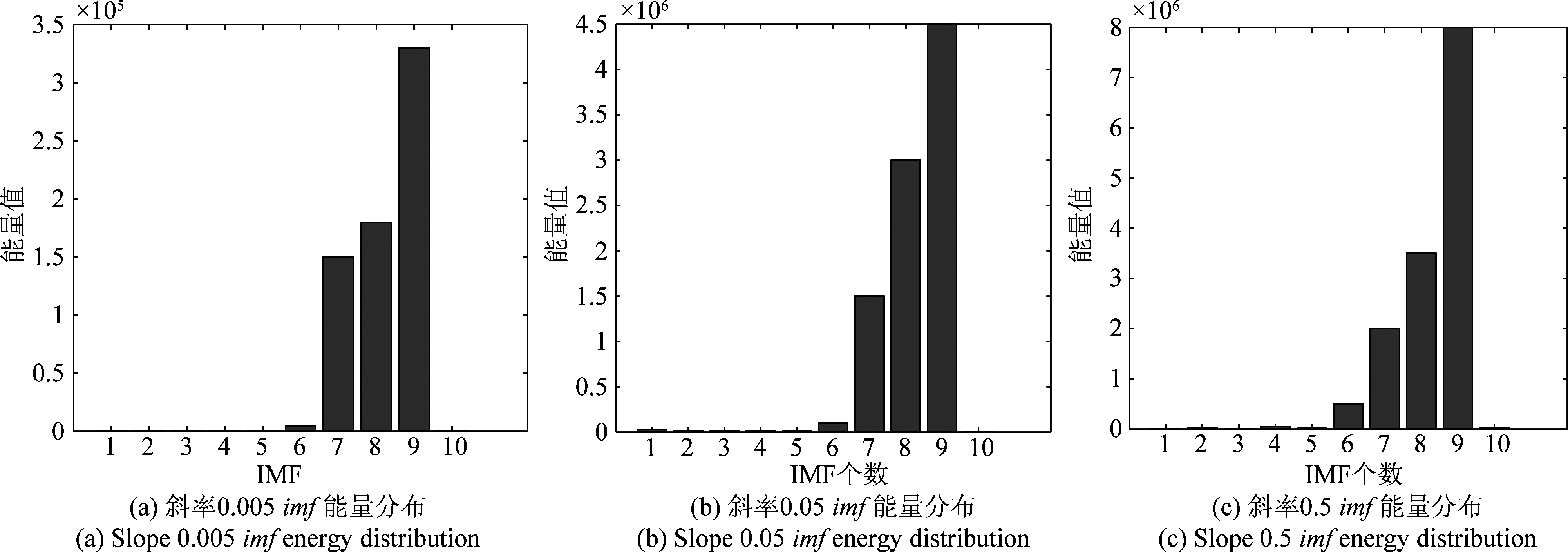
图10 斜坡故障各imf能量分布图
Fig.10 Energy distribution diagram of each imf of slope fault signal
由于EMD工作过程中,信号的两个端点不可能同时为极大值或极小值,分解时上、下两个包络在序列两端会发散,且这种发散现象随着分解的进行而逐渐严重,进而影响整个数据序列的分解。为避免这种问题,挑选端点效应影响较小且信号能量较高的分量进行研究,以便有效观察故障信息。图11截取了斜率为0.005、0.05和0.5斜坡故障分解下的imf 8分量,得到不同斜率下信号的幅度最大值。
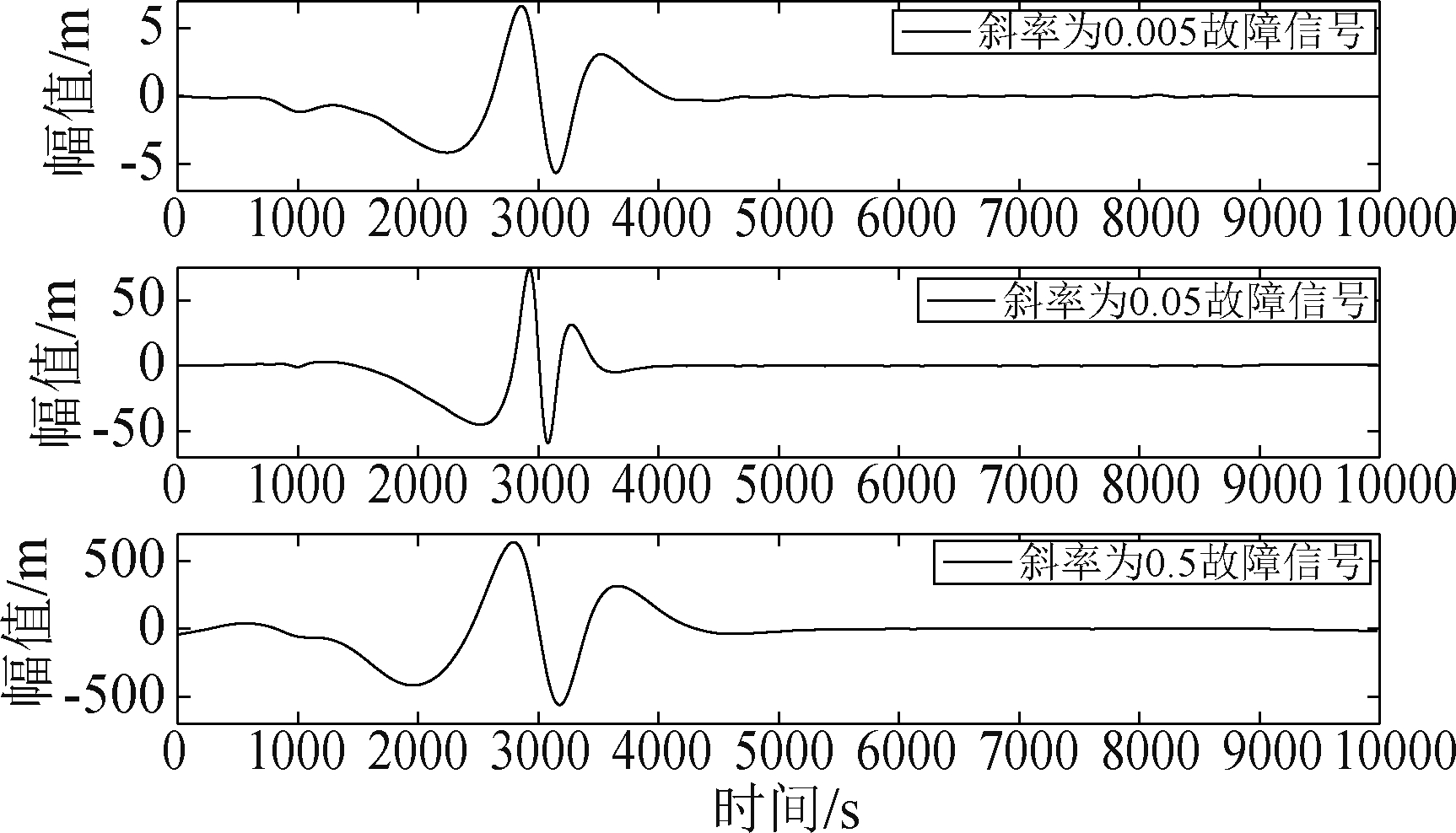
图11 不同斜率故障的imf 8分量
Fig.11 Different slope faults of imf 8
通过式(8)公式计算可得,故障幅值Emax与故障持续响应时间的比值即为斜坡故障斜率值。0.005、0.05以及0.5的斜坡故障经过EMD分解之后检测出的斜率分别为0.005043、0.051358和0.5133915。这些故障斜率都在0~2以内,属于电离层引起误差的斜率范畴,因此可以通过斜率有效判别基准站故障中的电离层误差。
5.2 Hilbert谱分析
边际谱是根据B值信号在整个频段的变化情况来判定故障强度的。为分析异常信号随频率的变化情况,以斜率为0.005故障B信号为例,图12和图13给出了故障B信号Hilbert谱变化和边际谱曲线。实验环境和参数设置和上文一致,数据采用“5.1 经验模态分解对故障B信号的检测”中分解出的各固有模态分量。
图12和图13的Hilbert频谱分析能精确的表现出信号实际的频率成分。作为对比,图13同时给出了无故障情况下的信号边际谱。图中可以看出B值信号频率主要集中在在0~70 Hz以内。当基准站发生故障后,边际谱曲线在频率0~10 Hz以内发生明显变化,无故障B信号边际谱幅值非常小且变化稳定。将所有检测数据汇总于表2,得到3种不同斜率故障信号的性能检测对比。
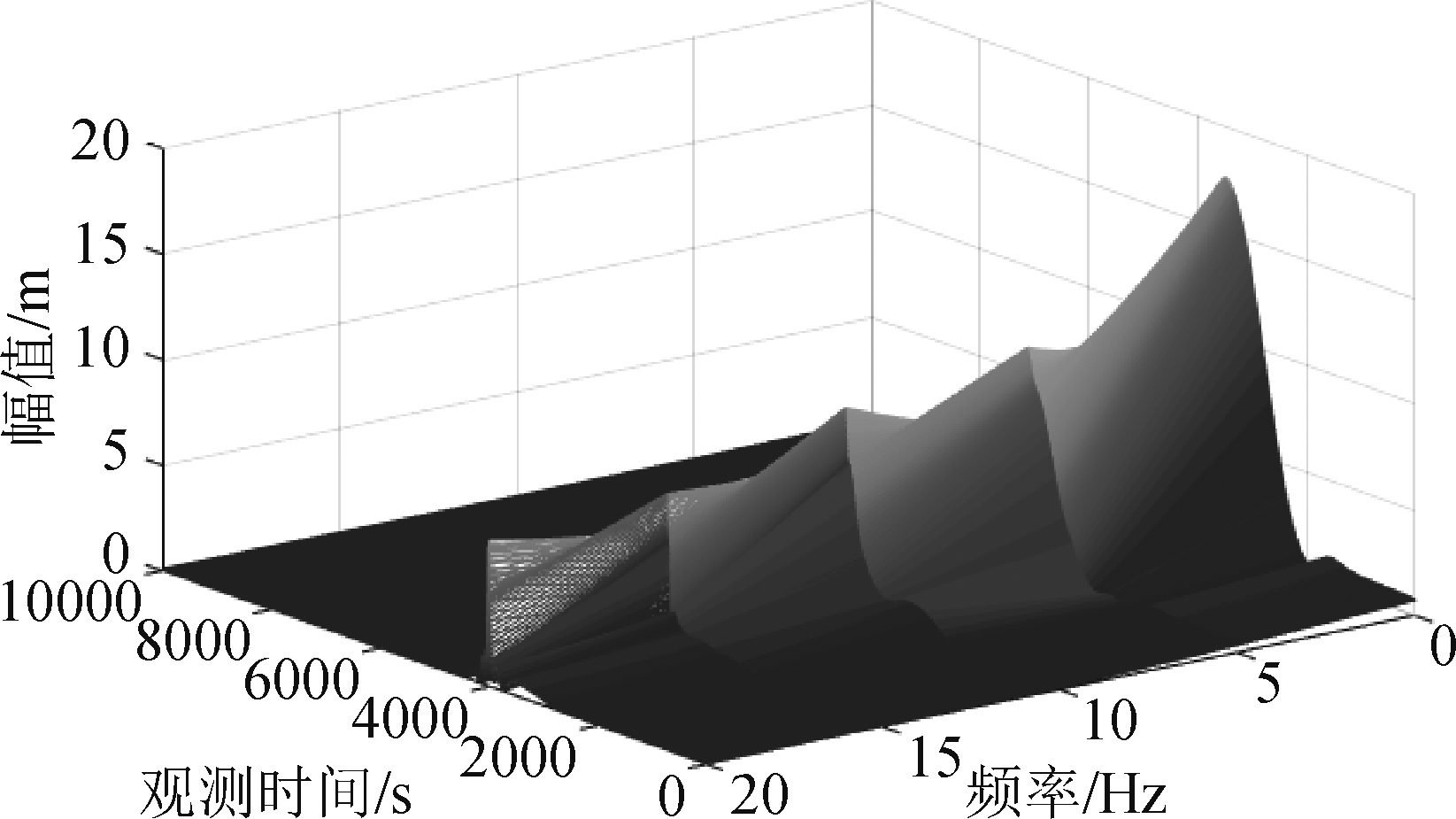
图12 斜率为0.005的斜坡故障B信号Hilbert三维谱
Fig.12 Hilbert three-dimensional spectrum of a slope fault B signal with a slope of 0.005
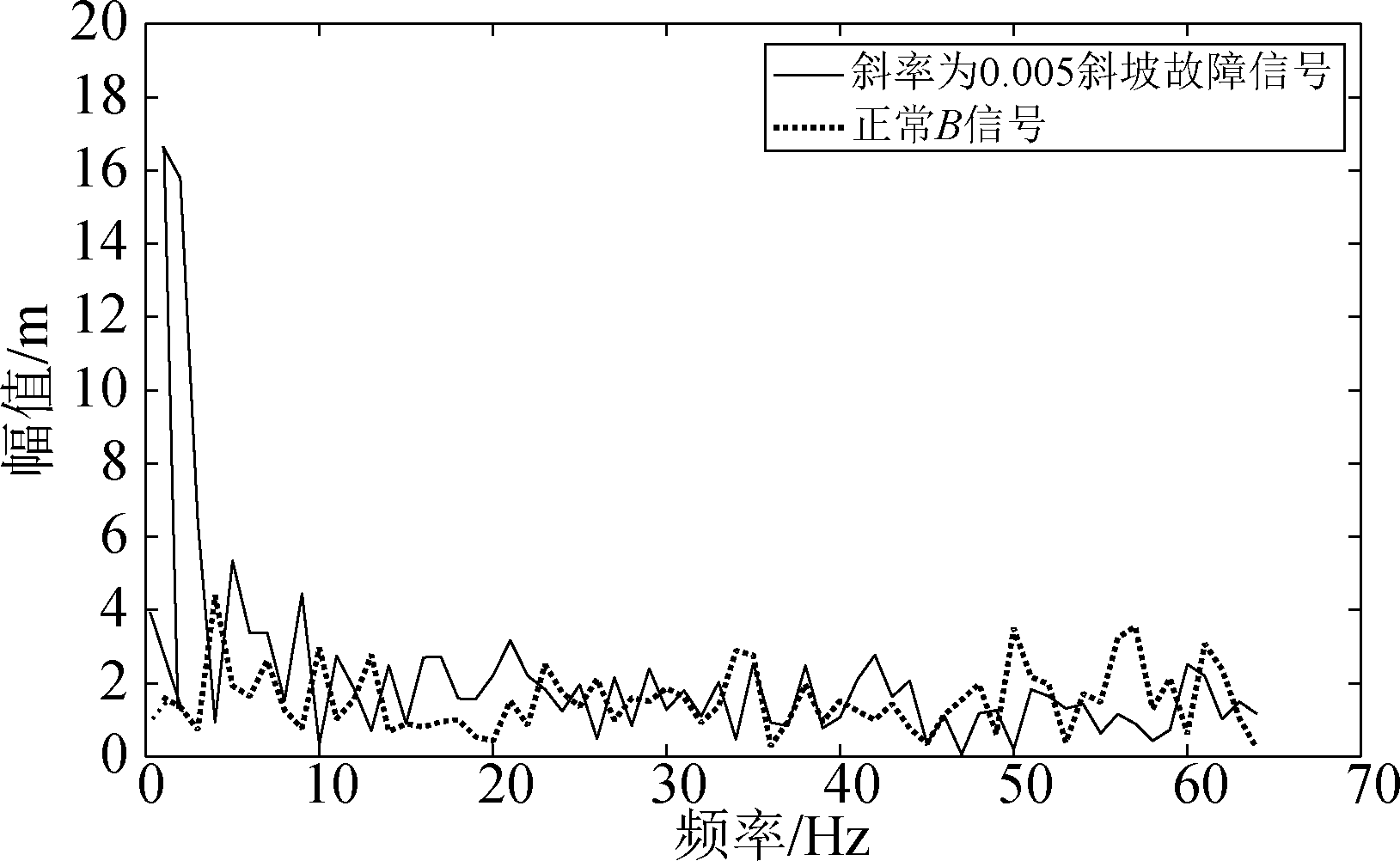
图13 斜率为0.005斜坡故障B信号边际谱波形
Fig.13 Marginal spectrum waveform of slope fault B signal with slope of 0.005
表2 采用HHT对不同斜率故障信号的检测性能对比
Tab.2 Comparison of detection performance of different fault slope signals using HHT
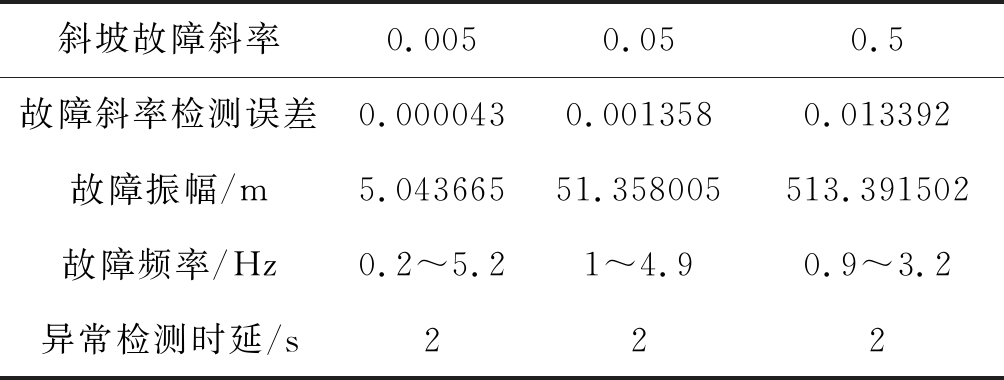
斜坡故障斜率0.0050.050.5故障斜率检测误差0.0000430.0013580.013392故障振幅/m5.04366551.358005513.391502故障频率/Hz0.2~5.2 1~4.90.9~3.2异常检测时延/s222
分析表2数据看出,采用HHT可以得到较为精确的故障斜坡估计量和异常信号的频谱特性,该方法的本质是对原始信号的逼近和细节描述。三种不同斜率的故障信号通过EMD的自适应分解,排除了其他干扰的影响,得到较为精确的故障斜率估计值。与MRCC相比,HHT检测幅值可以精确到小数点后6位,为验证该方法的有效性,随机抽取0~2范围内斜率不同的50例斜坡故障信号进行检测,其检测误差均低于3%。由于卫星测距源误差和单个基准接收机误差斜率范围一样且范围过大,目前该方法仅能识别电离层异常情况。三种信号的边际谱在一定频率范围内出现突变,表示斜坡故障在该频率段内存在且具有能量。通过对故障信号的Hilbert谱分析可以看出,故障斜率越大,其幅值越大,故障强度也越大。经过实验统计得到,EMD在实验仿真平台上运行时间总计为2.065009 s,检测时延平均值为2 s。
6 结论
本文利用HHT检测从多个方面对不同斜率基准站故障数据进行分析,结合理论和仿真讨论了故障信号的时频特征及局部特性,得到以下结论:
(1)EMD分解能够根据自身特性对基站故障数据进行有效分解,将系统误差和噪声项分开,识别敏感的IMF分量,根据故障斜率排除电离层误差成分,并且其时域局部定位能力较强。
(2)将HHT方法用于动态变化的B信号的分析,可以敏感的捕捉到B值信号能量突变点的信息。相应频率的幅值随着故障的能量一直改变,由于HHT边际谱将大部分能量集中于一定范围的时间-频率域内,相较于整个时频空间,可以在局部真实的反映非线性序列的本质特征,即达到识别故障信息的目的。
(3)HHT对B值信号具有良好的处理效果,其分解速度较快,通过对故障信息的分析可以得到较短的检测时延,同时完整的实现了故障的检测、诊断和强度识别,确保了地面子系统的完好性。
采用HHT可以在一定程度上摆脱传统信号处理方法对于基底信号的束缚,使故障信号的检测在时域和频域范围内都能达到较好的效果,其检测结果为基准站提供了一定的数据支持。
[1]Yun Y, Chao J, Heo M B, et al. GBAS Reference Receiver Clock Adjustment Effects on Continuity and Integrity Performance[J]. IEEE Transactions on Aerospace & Electronic Systems, 2012, 48(1): 693-707.
[2]刘军, 牟绍君, 张立, 等. GBAS中基于导航星监测的B值修正算法[J]. 东北大学学报, 2016, 37(8): 1075-1078.
Liu Jun, Mou Shaojun, Zhang Li, et al. B Correction Algorithm in GABS Based on Navigation Satellites Monitoring Information[J]. Journal of Northeastern University (Natural Science), 2016, 37(8): 1075-1078.(in Chinese)
[3]Liang L, Mohammed Q, Stephen I, et al. Multiple Reference Consistency Check for LAAS: A Novel Position Domain based Approach[J]. GPS Solutions, 2012, 16(2): 209-220.
[4]Gang Xie. Optimal on-airport Monitoring of the Integrity of GPS-based Landing Systems[D]. Stanford University, 2004(3): 20- 80.
[5]Jie Hu, Qi Weisun, Xiao zhushi. Multiple Reference Consistency Check Algorithm in GBAS Based on S-Values Auxiliary[C]∥2018 37th Chinese Control Conference (CCC), 2018.
[6]李斌, 王党卫, 杨明. 一种地基增强系统(GBSA)B值得分析与处理技术[J]. 现代导航, 2013, 2(1): 19-23.
Li Bin, Wang Dangwei, Yang Ming. Analysis and Processing of B-Values for GNSS GBAS[J]. Modern Navigation, 2013, 2(1): 19-23.(in Chinese)
[7]杨文辉, 周保军. LAAS地面系统中多基准一致性检测算法的分析[J]. 电子学报, 2006(3): 469- 471.
Yang Wenhui, Zhou Baojun. Analysis of Multiple Reference Consistency Check on LAAS Ground Facility[J]. Acta Electronica Sinica, 2006(3): 469- 471.(in Chinese)
[8]孙淑光, 郑杨, 王崇岩. 基于小波多分辨技术的GBAS地面接收机故障检测[M]. 中国科技信息. 2018(11): 82- 85.
Sun Shuguang, Zhen Yang, Wang chongyan. GBAS Ground Receiver Fault Detection Based on Wavelet Multi-resolution Technology[M]. China Science and Technology Information, 2018(11): 82- 85.(in Chinese)
[9]Xie G, Pullen S, Luo M, et al. Integrity Design and Updated Test Results for the Stanford LAAS Integrity Monitor Testbed[C]∥Proceedings of the 57th Annual Meeting of The Institute of Navigation, 2001: 681- 693.
[10]Ravier C, Azoulai L, Rambach D. Vertical Criterion for GAST D Failures Assessment[J]. Pres to RTCA SC 159 WG 2C and WG 4, June 2010.
[11]ICAO. Annex 10-Aeronautical Telecommunications Volume Ⅰ Radio Navigation Aids(Six Edition) [S]. Montreal Canada: ICAO, July 2018.
[12]RTCA SC-159. Minimum Operational Performance Standards for GPS Local Area Augmentation System Airborne Equipment[S]. Washington D. C, DO-253D, 13 July, 2017.
[13]Murphy T, Harris M, Shively C, et al. Fault Modeling for GBAS Airworthiness Assessments [J]. Navigation, 2012, 59(2): 145-161.
[14]Neri P, Macabiau C, Azoulai L, et al. GBAS NSE Model for CAT Ⅱ/Ⅲ Autoland Simulations[J]. IEEE/ION Position, Location and Navigation Symposium, 2010, 14(2): 233-241.
[15]陈丹. 基于地基北斗地基增强系统完好性算法的设计和仿真[D]. 西安电子科技大学, 2015(12): 1-59.
Chen Dan. Design and Simulation of BEIDOU Ground Augmentation System Integrity Algorithm[D]. XIDIAN University, 2015(12): 1-59.(in Chinese)
[16]ICAO Paper GNSSP-WP- 8, Validation of GBAS CAT I Accuracy: A GLS Model and Autoland Simulations for Boeing Airplanes[S]. Presented at the ICAO Global Navigation Satellite Systems Panel, Working Group B Meeting, Seattle, WA, May 29-June 9, 2000.
[17]ICAO NSP May 2010 WP 59. Development Baseline SARPs Proposal[S]. Pres by Tim Murphy, Montreal, 17-28 May 2010.
[18]焦卫东, 王艳群, 沈笑云, 等. BDS/GPS组合导航RAIM 可用性分析[J]. 信号处理, 2015, 31(9): 1165-1172.
Jiao Weidong, Wang Yanyun, Shen Xiaoyun, et al. Anaiysis of RAIM Availability for BDS/GPS Integrated Navigation[J]. Journal of Signal Processing, 2015, 31(9): 1165-1172.(in Chinese)
[19]庞春颖, 韩立喜, 刘记奎. HHT和提升小波包相结合的心音信号识别研究[J]. 信号处理, 2014, 30(1): 112-118.
Pang Chunying, Han Lixi, Liu Jikui. Study on Heart Sound Identification Based on Connection of HHT and Lifting Wavelet Package[J]. Journal of Signal Processing, 2014, 30(1): 112-118.(in Chinese)
[20]刘明亮, 丁克良, 宋子超, 等. 基于地基干涉雷达的超高层动态变形监测[J]. 北京测绘, 2019, 33(7): 829- 834.
Liu Mingliang, Ding Keliang, Song Zichao, et al. Super High-rise Dynamic Deformation Monitoring Based on Ground-based Interferometric Radar[J]. Beijing Surveying and Mapping, 2019, 33(7): 829- 834.(in Chinese)
[21]焦向东, 唐建, 戴波, 等. 基于Hilbert-Huang变换的管道超声检测信号处理[J]. 上海交通大学学报, 2016, 50(10): 1646-1650.
Jiao Xiangdong, Tang Jian, Dai Bo, et al. Pipeline Ulteasonic Testing Signal Processing Based on Hilbert-Huang Transform[J]. Journal of Shanghai Jiao Tong University, 2016, 50(10): 1646-1650.(in Chinese)
[22]卢丹, 陈涛. 基于EMD的单天线ADS-B交织信号自检测与分离算法[J]. 信号处理, 2019, 35(10): 1680-1689.
Lu Dan, Chen Tao. Single-antenna Overlapped ADS-B Signal Self-detection and Separation Algorithm Based on EMD[J]. Journal of Signal Processing, 2019, 35(10): 1680-1689.(in Chinese)
[23]罗昕炜, 方世良. 基于HHT的宽带幅度非平稳调制信号特征提取[J]. 信号处理, 2011, 27(6): 950-955.
Luo Xinwei, Fang Shiliang. Feature Extraction from Non-stationary Ampltitude Modulated Broad-band Signal Using the Hilbert-Huang Transform[J]. Journal of Signal Processing, 2011, 27(6): 950-955.(in Chinese)

