1 引言
认知无线电技术(Cognitive Radio,CR)是一种无线频谱资源智能分配技术,该技术让认知用户(Secondary User,SU)能够在授权用户(Primary User,PU)空闲时使用频谱资源进行通信。PU使用频率管理部门专门分配的特定管理频段进行通信。在PU不通信时,SU可以在不影响其他PU使用的前提下按照一定规则使用已授权的频谱资源。PU对频谱的使用具有更高的优先权,那么检测PU的存在与否成为关键问题,因此提出频谱感知技术。
频谱感知技术出现以来,频谱感知算法不断更新。传统频谱感知算法有能量检测(Energy Detection,ED),匹配滤波器检测和循环平稳特征检测等多种办法[1]。这些方法的提出为频谱感知问题提供解决方案,但也存在一些问题。能量检测算法的精确度受噪声不确定性干扰较大[2-3],匹配滤波器对同步要求高[4],循环平稳特征检测算法计算量大[5]。近年来,一些新的频谱感知算法被提出,例如:利用采样样本的协方差矩阵特征值及其特征向量进行特征检测,将最大特征值与最小特征值之比与主特征向量之积定义为检验统计量,实验结果表明此算法在信噪比-14 dB时检测概率仍能达到90%以上[6];采用过零双门限协作频谱感知算法降低感知系统虚警概率Pf, 将过零检测算法与双门限能量检测算法结合,对在双门限能量检测过程中能量统计值位于双门限之间的认知用户采用过零算法进行判决,实验结果表明此算法提高了检测准确度[7];利用盲检测算法中的检验统计量作为特征构造出特征向量,输入支持向量机进行训练得到模型进行频谱感知,此算法无需计算检测门限值,在低信噪比-10 dB时检测概率可达94.5%[8];利用样本协方差矩阵的最大特征值与迹线的比率进行拟合优度检测,仿真结果表明此算法在信噪比为-7 dB时检测概率可达90%以上[9];将人工神经网络(Artificial Neural Network,ANN)用作单个CR感知数据的决策融合块和权重分配单元,训练得到新的融合方案进行感知,实验结果显示该基于ANN的频谱感知算法在信噪比为-15 dB时检测概率约为59%[10];利用卷积神经网络(Convolutional Neural Network,CNN)以及接收信号协方差矩阵进行频谱感知,实现结果表明,在信噪比为-13 dB,SU个数为40个时,检测概率为0.94[11]。这些方法都在传统方法上做出了改进,提高了检测效率,指出了许多新的研究方向。信号的特征值是识别信号的关键,对此有学者提出利用拟合优度(Goodness of Fit,GoF)算法判断加性高斯白噪声(Additive White Gaussian Noise,AWGN)信号的累积概率分布从而判断授权信号的存在与否,实验结果表明拟合优度Anderson-Darling(AD)检测在信噪比为-2 dB,样本点数为28时检测概率可达93.54%,并指出PU信号可能因调制等因素存在非独立问题[12],即PU信号存在相关性时,GoF算法性能不理想。
上述方法实现了频谱感知,但其检测性能还有待提高,主要是该方法对数据的灵敏度不高,并且传统GoF算法是以PU不存在下接收信号的瞬时值分布为基础。因为PU信号存在相关性影响了传统GoF算法的性能,而LSTM神经网络能够处理具有时间先后顺序的序列,即对有序序列进行分类,这个特性便为减小PU信号相关性,提高系统性能提供了可行性。针对上述问题,本文提出一种基于信号能量拟合优度的长短时记忆网络(Long Short-Term Memory,LSTM)频谱感知算法(SNEG-LSTM)。本文的其他部分按照以下安排:第2节介绍基于能量分布拟合优度距离值的新频谱感知模型,第3节介绍本文采用的拟合优度检验算法,第4节介绍LSTM神经网络模型,第5节是实验结果及分析,在第6节总结全文。
2 系统模型
认知无线电系统由授权用户和认知用户组成,那么该系统可以描述为一个二元假设检验问题,如下所示:
(1)
其中y(t)表示检测端接收信号,H0表示PU信号不存在,即接收信号中只有噪声,H1表示PU信号存在,即接收信号中包含PU信号和噪声。n(t)表示AWGN,其均值为0,方差为σ2,s(t)表示PU信号,N为采样点数。本文研究的是PU信号经过AWGN信道后检测信号能量值的分布,能量统计值G的计算公式如下式(2):
(2)
其中|·|代表求取信号的绝对值。
当N足够大时,信号统计能量值G近似服从如式(3)的正态分布[13]:
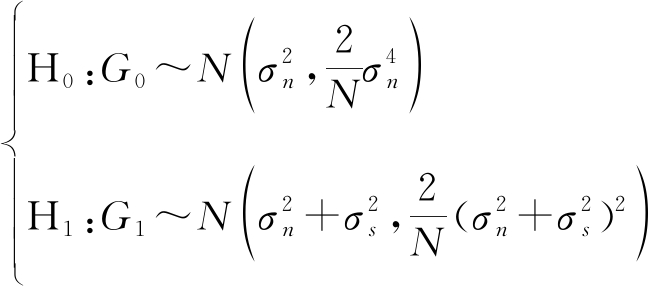
(3)
其中
表示噪声方差,
表示PU信号平均功率,N为采样点数。这样通过拟合优度算法分析,将二元假设问题转化为分析检测信号能量分布是否与主用户存在时信号能量分布符合的问题,如果符合,则PU信号存在,否则PU信号不存在,如式(4)所示:
(4)
其中F(y)表示检测信号能量统计值的累积概率分布, f1(y)表示授权用户在AWGN信道中能量值的累积概率分布。
3 拟合优度算法
拟合优度算法计算的是检测模型和假设模型之间的拟合程度,如果检测模型偏离假设模型一定程度,那么拒绝原假设,即检测模型不符合假设模型。假设X1, X2,…,Xn是一组独立同分布(i.i.d.)数据,该组数据的假设分布为F1,检测所得分布为FN,拟合优度算法检验的就是:
D=ξ(F1, fN)
(5)
其中D是计算累积分布函数FN和假设检验分布F1间距离值,ξ(·)是距离值的计算函数。
根据拟合准则的不同,距离值D的计算函数也不同。常见的拟合准则主要有Kolmogorov-Smirnov(KS)准则,Ctamer-von Mises(CM)准则和Anderson-Darling(AD)准则。
3.1 KS准则
KS准则的定义为两个累积分布函数之间绝对距离值的最大值。在KS检验中,距离值的定义为:
(6)
式(6)中,
其中,zi=F1(yi),N为样本量。当距离DN小于设定的阈值λ时,认为FN未偏离F1,即H1成立,否则FN偏离F1,即H0成立。
当样本量足够大时,KS 检验的检测概率一定满足下式:
(7)
其中
为置信度。当N趋向于无穷大时,式(7)趋向于1。因此样本量越大,KS检验的检测概率趋于1越快。
3.2 CM准则
CM准则的定义为两个累积分布函数差值平方的积分函数。在CM检验中,距离值的定义为:
(8)
上式可以被简化为:
(9)
其中zi=F1(yi),N为样本量。当距离值WN小于给定阈值λ时,认为FN未偏离F1,即H1成立,否则FN偏离F1,即H0成立。对比于KS检验,CM检验运算量大,复杂度高,但拟合效果好[14]。
由式(8)可得:
(10)
根据三角不等式,上式可以进一步变形得到:
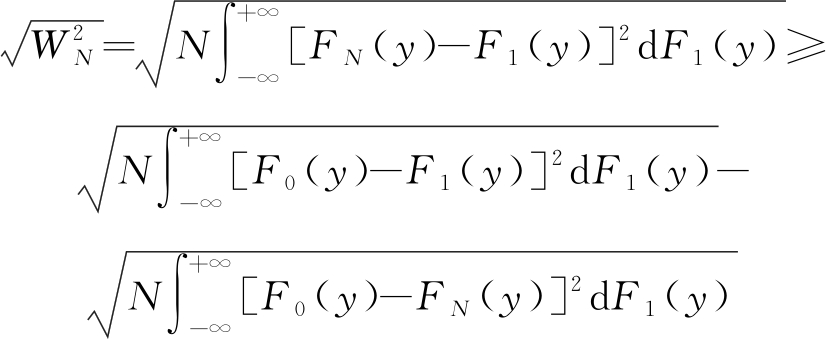
(11)
为了方便起见,令:
(12)
(13)
因此式(8)化简后得到
CM检验的检测概率为:
(14)
其中t0为判决门限,本文提出的SNEG-LSTM算法不需要求取判决门限,故不对其进行展开讨论。上式中:
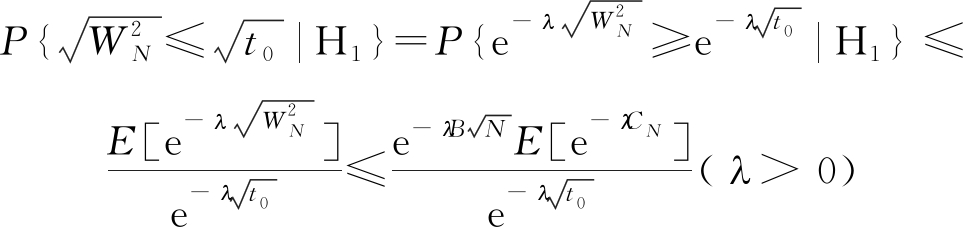
(15)
其中第一个不等式由马尔科夫不等式得到。当N→∞时,E[e-λCN]有界,
趋向于0,因此, CM检验的检测概率以
的速度趋向于1。
3.3 AD准则
AD准则相对复杂,在AD检验中,距离值的定义为:
(16)
其中,zi=F1(yi),N为样本量。当距离值
小于给定阈值λ时,认为FN未偏离F1,即H1成立,否则FN偏离F1,即H0成立。
不妨设上式中
(17)
则式(16)可以改写为:
(18)
接下来的推导和CM检验相同,可得到
其中
(19)
(20)
AD检验的检测概率为:
(21)
其中t0为判决门限,本文提出的SNEG-LSTM算法不需要求取判决门限,故不对其进行展开讨论。上式中
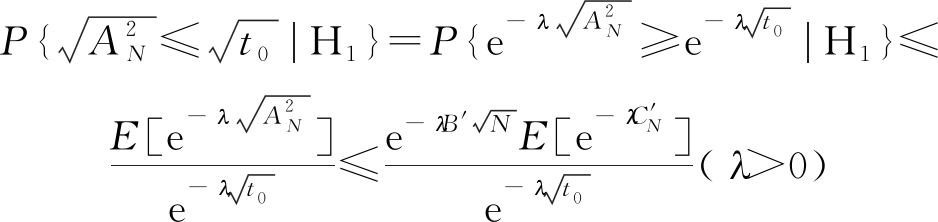
(22)
当N→∞时,
趋向于0,因此,AD检验的检测概率以
的速度趋向于1。
3.4 拟合准则的选取
根据上述关于KS准则,CM准则和AD准则的检测概率的推导得出的结论:当样本量越大,KS准则的检验概率趋向于1越快;CM准则的检验概率以
的速度趋向于1;AD准则的检验概率以的速度趋向于1。其中,B和B′决定了CM准则和AD准则之间收敛速度的大小,式(12)和式(19)为对应的定义,又因为F1(y)时是连续的,并且0<F1(y)<1,由此可得:F1(y)(1-F1(y))≤1/4,最后推得B′≥2B。因此AD检验的检测概率PAD比PCM更快的趋于1,即AD准则的性能优于CM准则的性能。
KS准则的检验概率收敛速度取决于样本量的大小,当固定样本量的大小为28时,KS准则的检测性能明显低于CM准则[15]。文献[15]的实验结果也证明了这一点。当样本量较小时,KS准则的检测概率收敛速度慢于CM准则。综上可得,在样本量相同且较小时,AD准则具有优于其他准则的性能,因此本文采用AD准则计算拟合优度距离。
4 LSTM神经网络
传统循环神经网络(Recurrent neural network,RNN)是时序神经网络,能够处理时序序列或者带有时间先后顺序的数据。传统的RNN对长时间数据的处理不够理想,表现为RNN存在梯度消失问题[16]。为了改善这类问题,在不改变结构的前提下,LSTM对传统RNN的细胞单元进行了改进。LSTM增加了遗忘门,输入门和输出门来控制信息传递和结果计算,LSTM网络结构如下图1所示。
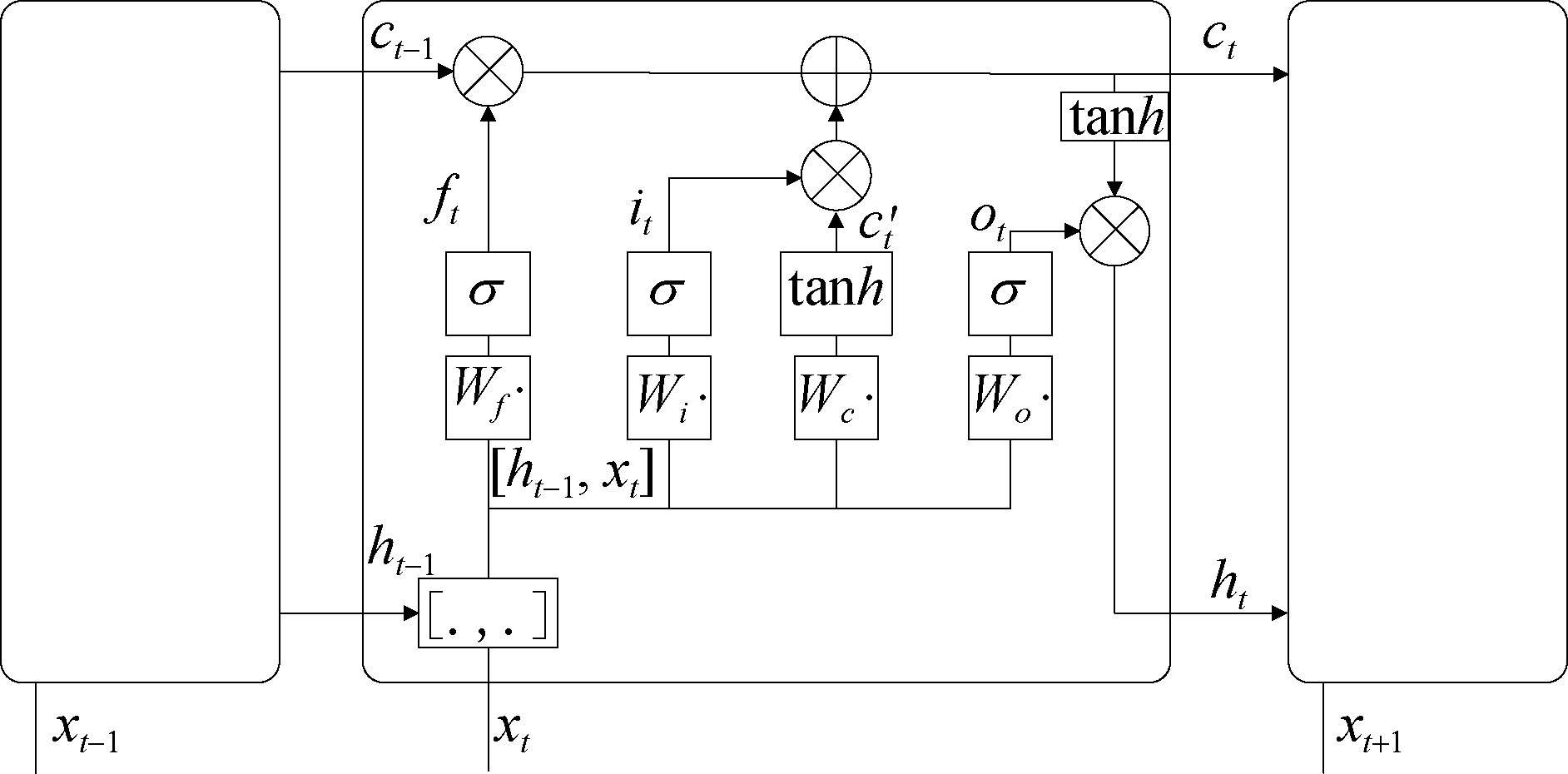
图1 LSTM神经元结构图
Fig.1 Structure of LSTM neuron
上图中ft代表遗忘门,it代表输入门,ot代表输出门,ht代表当前输出,ht-1代表上一时刻隐含层的输出,ct代表当前单元状态,ct-1代表前一时刻单元状态,xt为当前输入层输入值,σ为sigmoid函数,tanh为双曲正切函数。Wf,Wi,Wc,Wo分别是遗忘门权重矩阵,输入门权重矩阵,输出门权重矩阵和计算单元状态的权重矩阵。下面详细介绍遗忘门,输入门,输出门的计算公式:
4.1 遗忘门
遗忘门控制前一时刻单元状态ct-1能保留到当前单元状态ct的程度。其计算公式为:
ft=σ(Wf[ht-1,xt]+bf)
(23)
其中bf为遗忘门偏置。
4.2 输入门
输入门控制当前输入层的输入值xt能保存到当前单元状态ct的程度。其计算公式为:
it=σ(Wi[ht-1,xt]+bi)
(24)
其中bi为输入门偏置。
4.3 输出门
输出门控制当前单元状态ct能输出到当前输出ht的程度。其计算公式为:
ot=σ(Wo[ht-1,xt]+bo)
(25)
其中bo为输出门偏置。
LSTM网络不仅具备神经网络的高运算速度,强自适应性,强自组织能力等特点,并且在对时间序列的处理上有着突出表现。文献[9]中指出了授权信号因调制方式等因素可能不是独立的,即当前信号值的产生可能和前n时刻的值有一定关系,LSTM神经网络正具备这样的“记忆”功能[17]。
本文采用LSTM神经网络作为数据处理的模型,将检测信号能量分布拟合优度距离值作为模型训练数据的主要来源。首先对已知信噪比的接收信号进行采样,采样的样本量为20或28,与传统GoF算法不同的是,传统GoF算法只提取信号瞬时值,本文SNEG-LSTM算法需计算每个样本的信号能量,然后对该组样本中的信号能量数据拟合得到该组信号能量的近似分布,再对比近似分布模型与式(3)提出的理论分布模型,最后用AD准则提取能量分布的拟合优度距离。获得信号能量分布及拟合优度距离的过程如下图2所示。
图2中,信号仅为示意图,信号样本量N为20或28,28样本量的选取传统GoF算法已经进行了证明,本文因篇幅限制不过多讨论,选取最优的28样本量以基础,进一步提升系统性能。
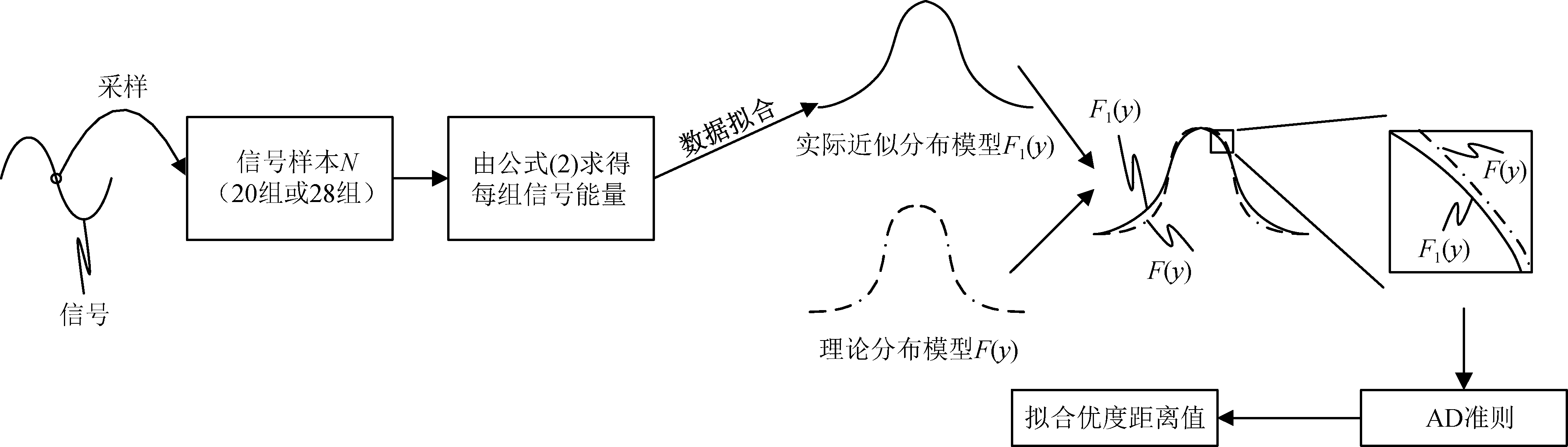
图2 信号能量分布及拟合优度距离的提取过程图
Fig.2 Extraction process chart of signal energy distribution and GoF distance
得到拟合优度距离值后,构造特征向量集,分成了训练数据集和测试数据集,然后输入LSTM模型进行训练并不断优化准确率,最后得到良好的频谱感知模型。模型建立和训练的流程图如下图3。
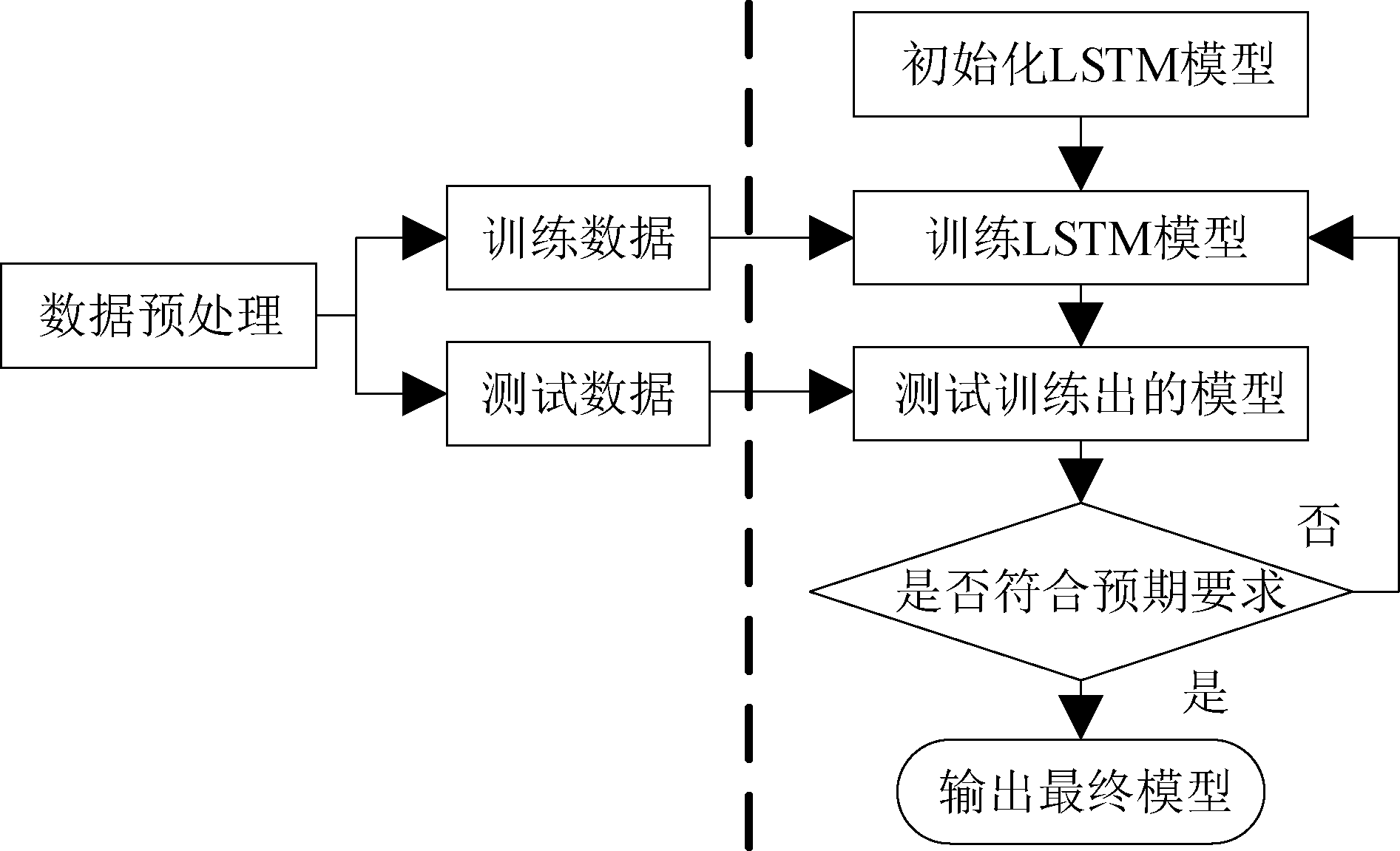
图3 频谱感知模型训练和建立流程图
Fig.3 Flow chart of spectrum sensing model’s training and building
LSTM网络模型中输入层数为4,LSTM神经网络的输出层为2,LSTM隐含层节点个数为64,隐含层层数为1。设拟合优度距离值
信号能量值为E,AD检验的临界值为CV,观察到观极端检验统计量的概率P,特征向量便由以上四个分量组成,其中概率P定义为:当原假设为真时,比所得到的样本观察结果更极端的结果出现的概率,即检验原假设成立或表现更严重的可能性。统计学中P值反映了结果的真实程度,本文中P值衡量了距离值
的可信程度,为LSTM处理一些极端数据时提供判断依据,从而能够提升分类效果。LSTM神经网络的输出的是对主信号存在与否的分类结果,在程序中表现为输出“0”和“1”,所以LSTM神经网络的输出层为2。LSTM隐含层节点个数影响模型的训练时间和准确率,隐含层节点个数与输入序列长度有关,一般为2n(n为整数),且接近输入序列长度的一半,本文中特征向量分量的长度为50～100,故选取隐含层64节点个数;实验仿真中发现隐含层层数对实验结果的影响不大,为了节约时间成本,故隐含层层数选取1层。因篇幅限制,相关参数的选取过程不作过多展开。LSTM神经网络为实现分类效果,需在网络模型中加入Softmax Layer[18]以达到分类效果。本文中研究的是频谱感知问题,即授权用户存在与否的问题,在模型中就简化为‘0’和‘1’的问题。
5 实验结果及分析
检测概率Pd和虚警概率Pf是频谱感知算法的衡量标准。固定虚警概率Pf前提下,检测概率Pd高于90%及以上,则认为该感知算法有较好性能。实验仿真基于MATLAB R2018a和其中的机器学习工具箱。首先利用MATLAB生成信号,拟合能量值分布并提取特征值GoF距离;然后利用MATLAB设置LSTM模型参数,向模型中输入特征向量训练模型,然后输入测试集进行分类,查看分类结果,如果性能不佳,则改变模型参数,重新训练并测试。
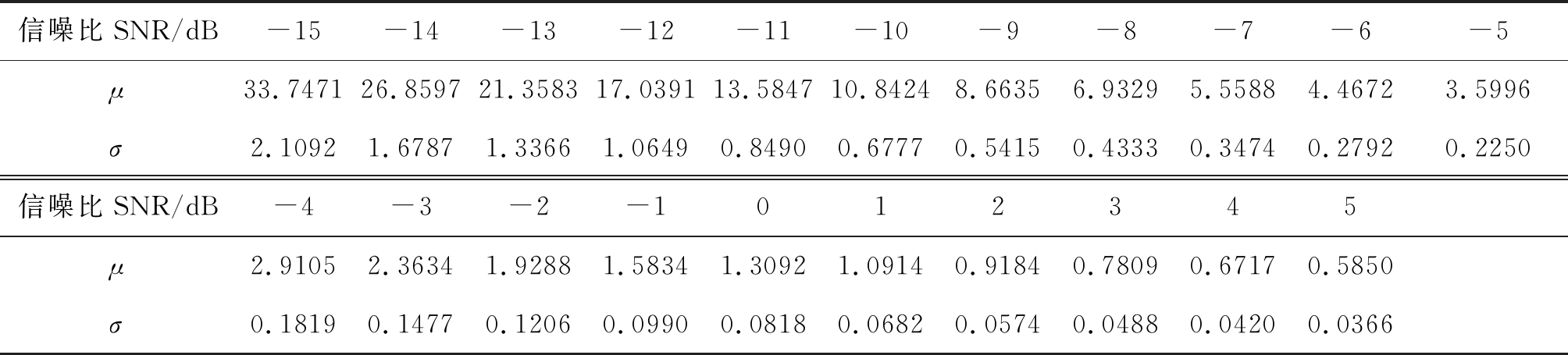
在本实验仿真中,PU信号以AM信号为例,噪声信号为AWGN。首先根据式(3)求出已知不同信噪比下AM信号能量服从的正态分布的数学期望μ和标准差σ,为了保证数值的稳定,进行了100000次计算求取均值,具体数值如下表1。
表1 信号能量服从的数学期望μ和标准差σ
Tab.1 Mean μ and standard deviation σ of signal energy
信噪比SNR/dB-15-14-13-12-11-10-9-8-7-6-5μ33.747126.859721.358317.039113.584710.84248.66356.93295.55884.46723.5996σ2.10921.67871.33661.06490.84900.67770.54150.43330.34740.27920.2250信噪比SNR/dB-4-3-2-1012345μ2.91052.36341.92881.58341.30921.09140.91840.78090.67170.5850σ0.18190.14770.12060.09900.08180.06820.05740.04880.04200.0366
求得对应的数学期望μ和标准差σ后,即可得到信号能量符合的假设分布N(μ,σ2)。随后对信号样本进行20点和28点采样,并用AD检验求得拟合优度距离值
则SNEG-LSTM模型的特征向量可由距离值
信号能量值为E,AD检验的临界值为CV,观察到观极端检验统计量的概率P表示,表示为
即其维数为4维,且4个分量之间无特定时间特性。假设当前时刻为i,前一时刻为i+1,后一时刻为i-1,当前时刻i下的
组成了4维特征向量的一组数据,然后下一时刻i-1来临,得到
以此类推,最后将得到的50～100个连续时刻的数据按时间先后顺序排列,得到特征向量。其中因为LSTM神经网络具有输入特征向量序列长度非固定数值的特性,所以可采用50～100长度的数据。所以特征向量每一维里是一组带有时间先后顺序的数据,且每一维的数据长度相同,其结构示意图如下图4所示。
图4 特征向量数据结构图
Fig.4 Structure of data in eigenvector
特征向量
分别组成了训练集XTrain和测试集XTest。其中XTrain共有4000个特征向量,包括2000个H0状态下的特征向量集XTrain_0和2000个H1状态下的特征向量集XTrain_1,并且XTrain有相对应的标签集XLabel,XTrain_0和XTrain_1对应的标签分别为“0”和“1”。测试集XTest共有10000个特征向量,包括5000个H0状态下的特征向量集和5000个H1状态下的特征向量集,也有相应的标签集YLabel。训练测试一般过程示意图如下图5所示。
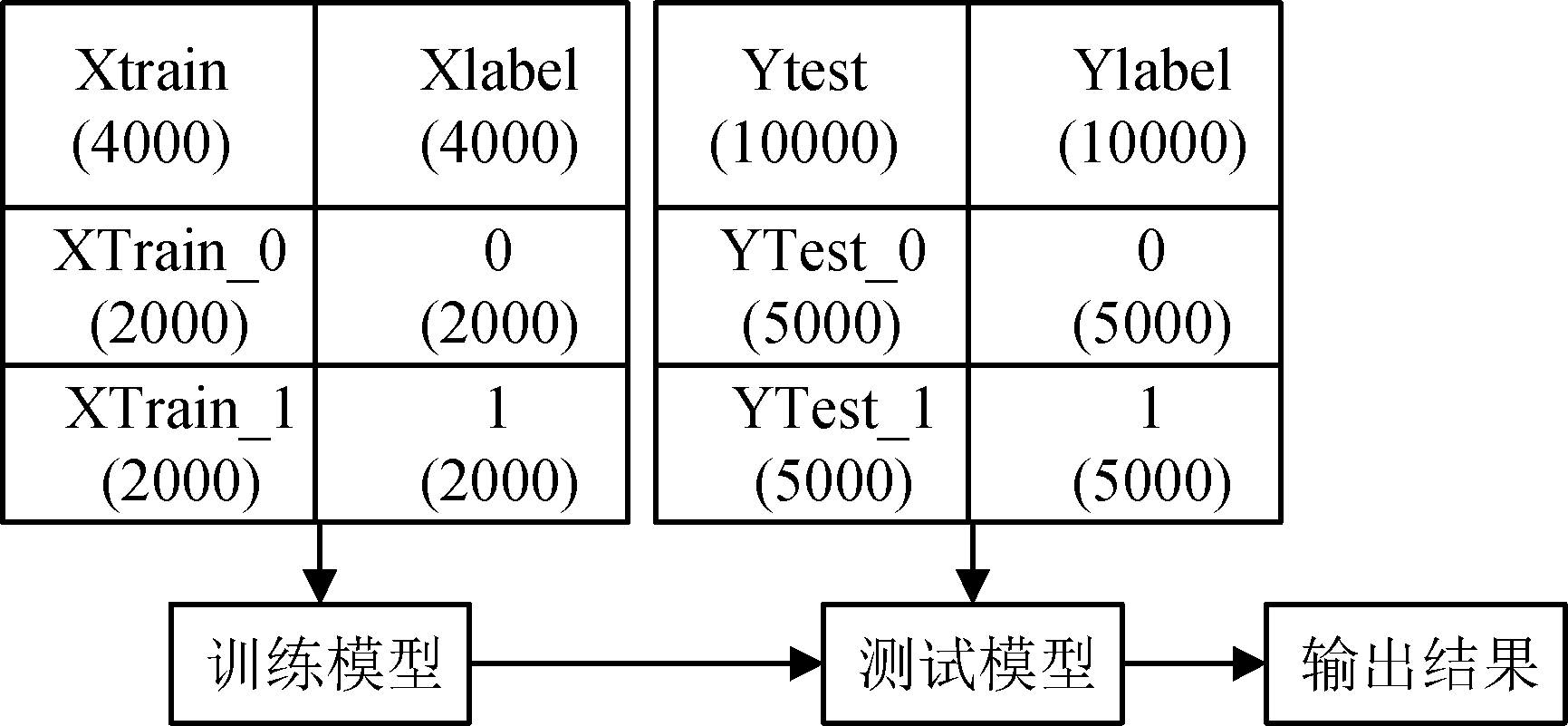
图5 训练测试一般过程图
Fig.5 General flow chart of training and testing
下面分别对传统ED算法,传统GoF算法,基于噪声能量分布的拟合优度LSTM算法(NEG-LSTM)和本文中提出的SNEG-LSTM算法进行了仿真,其中,假设系统要求的虚警概率Pf为0.1,结果如图6所示。
图6(a)是SNEG-LSTM算法与传统GoF算法,ED算法对比,其中根据ED算法的特性,256点样本的算法性能肯定高于256点以下样本量的算法性能。从图中可以看出,在低信噪比-15 dB时,SNEG-LSTM算法检测概率可达0.86,而相同信噪比下ED算法检测概率仅为0.22,GoF算法的检测概率仅为0.15,说明了SNEG-LSTM算法明显优于ED算法和传统GoF算法。
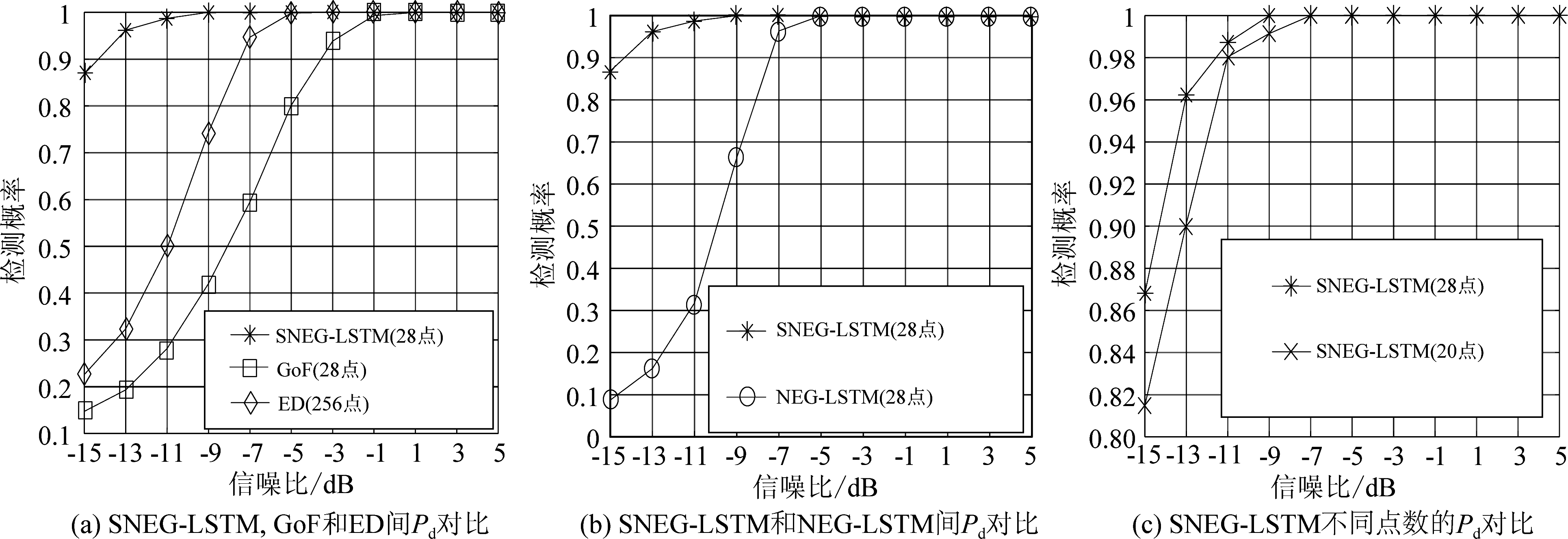
图6 频谱感知算法性能对比
Fig.6 Comparison of spectrum sensing algorithms’ performance
图6(b)是SNEG-LSTM与NEG-LSTM算法对比,从图可以看出,NEG-LSTM是基于只有噪声存在时能量分布为基础。通过对比可以发现,以主用户信号存在时的信号能量分布为基础的SNEG-LSTM算法检测概率更高,这体现了LSTM神经网络很好的利用了PU信号的时间相关性,起到了提高检测性能的作用,把传统GoF算法认为的弊端转化为解决频谱感知的优点。
图6(c)是SNEG-LSTM算法不同样本量对检测概率的影响,该图证明了相同信噪比条件下,采样样本量越大,检测概率越高,检测性能越好。
考虑到输入信号对算法性能的影响,本文分别采用AM信号,PSK信号和QAM信号输入神经网络进行性能分析,预设样本量均为28点,网络模型参数不变,得到结果如图7所示。
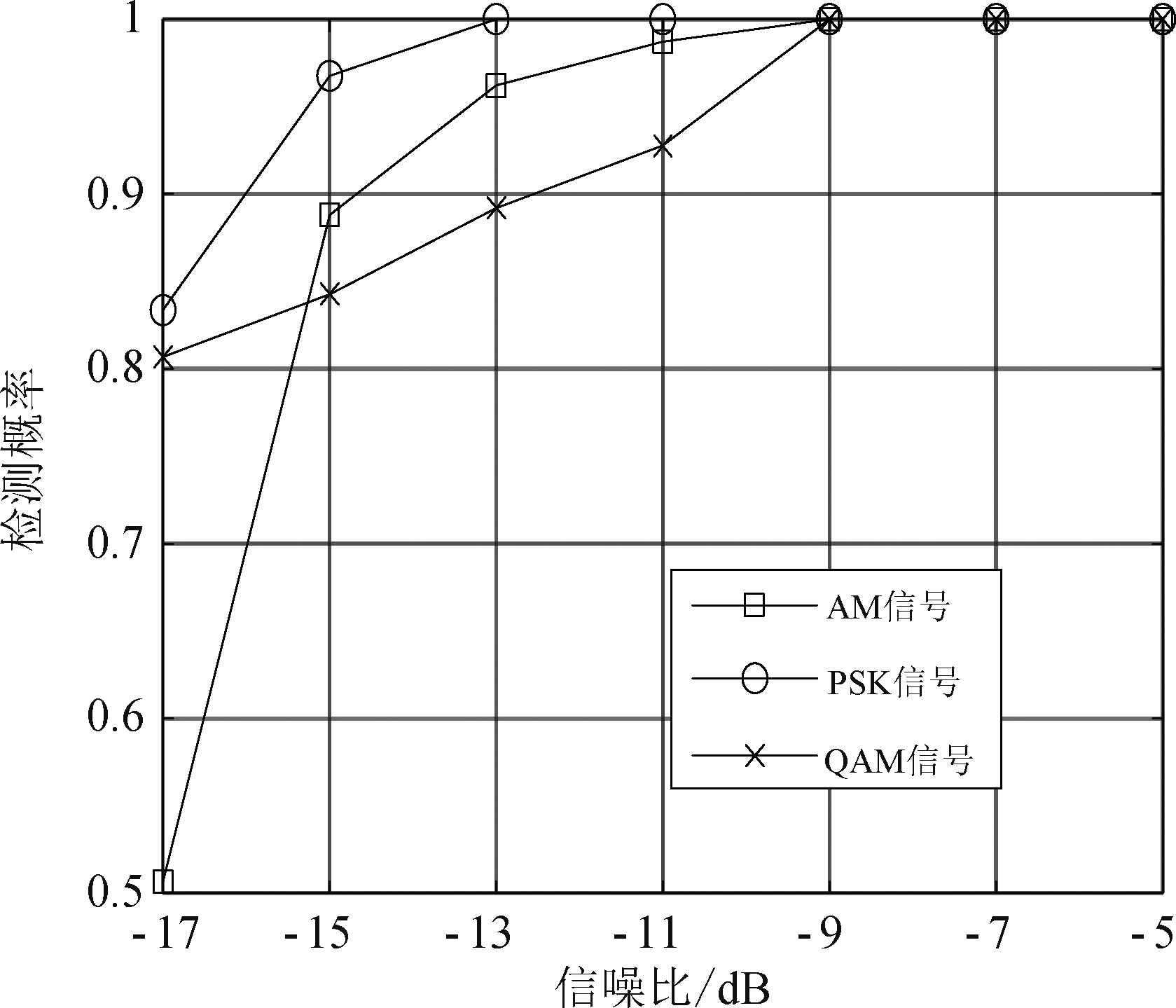
图7 不同输入信号下SNEG-LSTM性能对比
Fig.7 Comparison of different signals in SNEG-LSTM
图7表明,在样本量和网络模型参数相同的情况下,PSK调制信号的检测性能最优,其检测概率在-15 dB时仍能达到0.9以上;QAM调制信号的检测性能略差,其检测概率在-13 dB时为0.892;输入信号为AM的SNEG-LSTM算法在信噪比小于-15 dB后性能不理想,出现了恶化。图7证明了不同调制方式信号对SNEG-LSTM算法性能影响不同,PSK信号性能略优于AM信号和QAM信号,并且SNEG-LSTM算法总体性能在信噪比-13 dB及以上情况下表现较好。
因为神经网络直接对数据进行处理,不能像传统频谱感知算法一样提前设置虚警概率,本文提出的模型在不同信噪比下有不同的虚警概率,可固定传统ED算法的虚警概率并与之比较,结果如下图8所示。
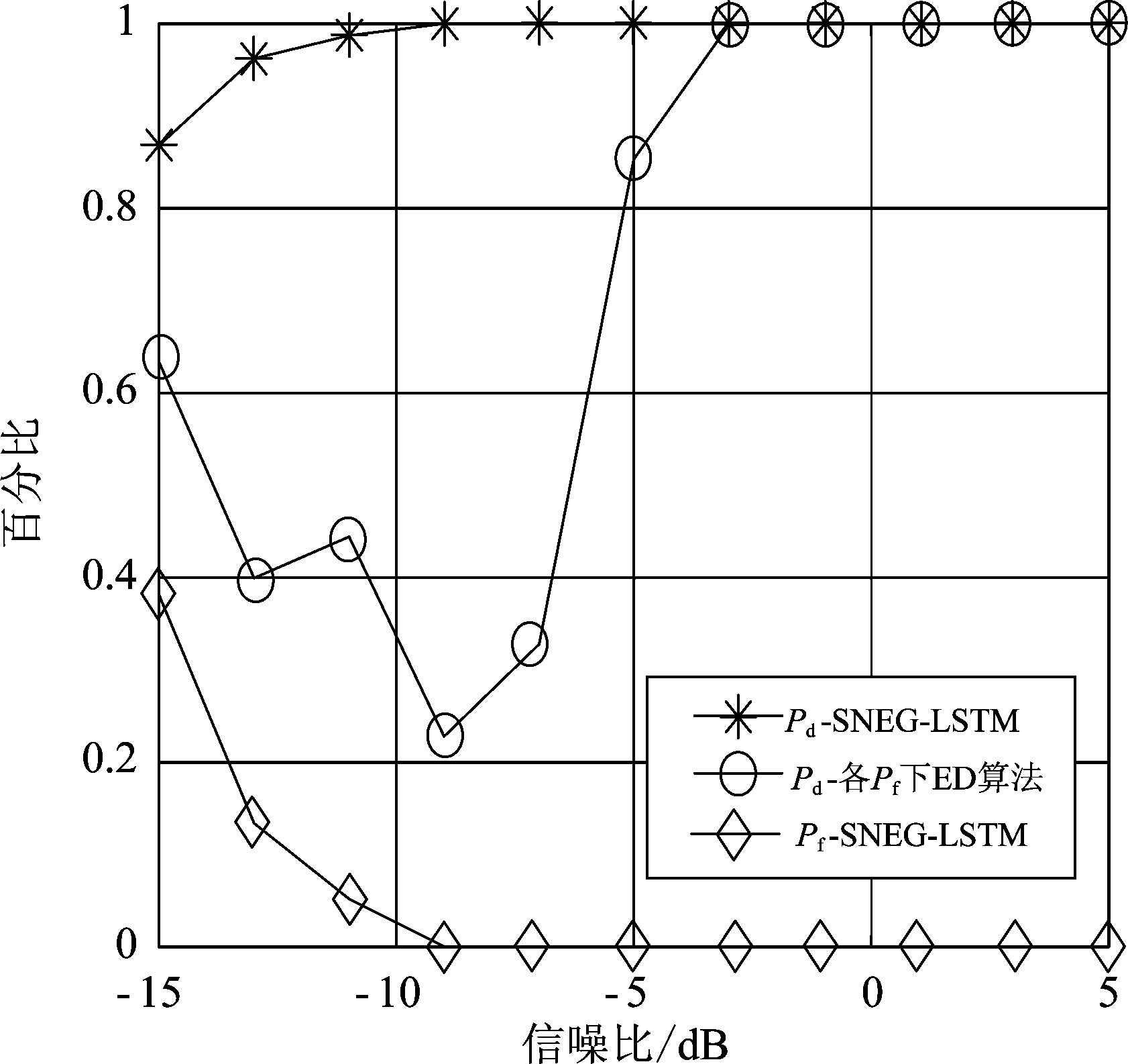
图8 SNEG-LSTM与同Pf的ED性能对比
Fig.8 Comparison of SNEG-LSTM and ED at the same Pf
由图8可以看出,SNEG-LSTM算法不同信噪比下虚警概率不同,因此预设ED算法的虚警概率进行对比。相同信噪比,相同虚警概率条件下,SNEG-LSTM算法的检测概率明显优于ED算法。图8表明,本文提出的新算法的虚警概率随着信噪比增大而降低,最后在信噪比为-10 dB时趋于0,但是虚警概率变化过快,导致在该虚警概率条件下的ED算法性能不同步。
6 结论
传统的ED算法,传统的GoF算法和基于噪声能量分布的拟合优度LSTM算法,在低信噪比时都没有较好的检测概率。本文提出的基于LSTM的频谱感知算法在信噪比-13 dB,采样点数28时,检测概率能达到96.21%。检测概率随着采样点数的增大而增大。通过实验仿真,在相同的信噪比条件下,本文提出的算法性能明显优于传统ED算法,传统GoF算法和基于噪声能量分布的拟合优度LSTM算法,体现了神经网络应用在频谱感知方面的可行性。
[1]Gafoor R A, Kuriakose R, Sibila M, et al. A Survey on traditional and advanced spectrum sensing techniques in cognitive radio networks[C]∥ 2018 International Conference on Control, Power, Communication and Computing Technologies, Kannur, 2018: 65-72.
[2]Kumar A, Thakur P, Pandit S, et al. Fixed and dynamic threshold selection criteria in energy detection for cognitive radio communication systems[C]∥ 2017 Tenth International Conference on Contemporary Computing, Noida, 2017: 1- 6.
[3]Rani R, Kumar K, Kumar R, et al. Evaluation of spectrum sensing process through energy detection technique[C]∥ 2017 International Conference on Computing and Communication Technologies for Smart Nation, Gurgaon, 2017: 348-351.
[4]Sansoy M, Buttar A S. Spectrum sensing algorithms in Cognitive Radio: A survey[C]∥ 2015 IEEE International Conference on Electrical, Computer and Communication Technologies, Coimbatore, 2015: 1-5.
[5]Anyim I G, Chiverton J, Filip M, et al. The Implementation of wideband Cyclostationary Feature Detector with receiver constraints[C]∥ 2017 European Conference on Networks and Communications, Oulu, 2017: 1-5.
[6]Chen Y, Gao Y. Dual-Feature Spectrum Sensing Exploiting Eigenvalue and Eigenvector of the Sampled Covariance Matrix[J]. Communications, Signal Processing, and Systems. 2019, 516(1): 855- 862.
[7]徐国强, 王孟, 李英华, 等. 过零双门限协作频谱感知算法[J]. 西安科技大学学报, 2019, 39(1): 145-151.
Xu Guoqiang, Wang Meng, Li Yinghua, et al. Zero-crossing dual-threshold cooperative spectrum sensing algorithm[J]. Journal of Xi’an University of Science and Technology, 2019, 39(1): 145-151.(in Chinese)
[8]姚迪, 刘会杰, 刘洁, 等. 基于支持向量机的认知无线电频谱感知[J]. 电子设计工程, 2018, 26(21): 1-5.
Yao Di, Liu Huijie, Liu Jie, et al. Support vector machine based spectrum sensing algorithm in cognitive radio[J]. Electronic Design Engineering, 2018, 26(21): 1-5.(in Chinese)
[9]Liu C, Wang J, Liu X, et al. Maximum Eigenvalue-Based Goodness-of-Fit Detection for Spectrum Sensing in Cognitive Radio[J]. IEEE Transactions on Vehicular Technology, 2019, 68(8): 7747-7760.
[10]Varma A K, Mitra D. A Neural Network Approach to Decision Fusion for Wideband Cooperative Sensing[C]∥ 2018 Conference on Information and Communication Technology, India, 2018: 1-5.
[11]鲁华超, 赵知劲, 尚俊娜, 等. 利用卷积神经网络和协方差的协作频谱感知算法[J]. 信号处理, 2019, 35(10): 1700-1707.
Lu Huachao, Zhao Zhijin, Shang Junna, et al. Cooperative Spectrum Sensing Algorithm Using Convolutional Neural Networks and Covariance[J]. Journal of Signal Processing, 2019, 35(10): 1700-1707.(in Chinese)
[12]Wang H, Yang E, Zhao Z, et al. Spectrum sensing in cognitive radio using goodness of fit testing[J]. IEEE Transactions on Wireless Communications, 2009, 8(11): 5427-5430.
[13]Zhang Ling-ling, Huang Jian-guo, Tang Cheng-kai. Novel energy detection scheme in cognitive radio[C]∥ 2011 IEEE International Conference on Signal Processing, Communications and Computing, Xi’an, 2011: 1- 4.
[14]陈亚芹. 认知无线电中基于协方差检测的盲感知算法的研究[D]. 北京邮电大学, 2019: 44- 46.
Chen Yaqin. Research on Blind Sensing Algorithm Based on Covariance Detection in Cognitive Radio[D]. Beijing University of Posts and Telecommunications, 2019: 44- 46.(in Chinese)
[15]Lei S, Wang H, Shen L. Spectrum sensing based on goodness of fit tests[C]∥ 2011 International Conference on Electronics, Communications and Control. Ningbo, 2011: 485- 489.
[16]令狐王丹. ISM频段认知无线电的自话应接入[D]. 北京邮电大学, 2018: 19-21.
Linghu Wangdan. Adaptive Access for ISM Band Cognitive Radio[D]. Beijing University of Posts and Telecommunications, 2018: 19-21.(in Chinese)
[17]刘云, 尹传环, 胡迪, 等. 基于循环神经网络的通信卫星故障检测[J]. 计算机科学, 2019: 1-10.
Liu Yun, Yin Chuanhuan, Hu Di, et al. Communication Satellite Fault Detection Based on Recurrent Neural Network[J]. Computer Science, 2019: 1-10.(in Chinese)
[18]Simone Totaro, Amir Hussain, Simone Scardapane. A non-parametric softmax for improving neural attention in time-series forecasting[J]. Neurocomputing, 2019.
