1 引言
随着战争形态向信息化网络化智能化的演变,为促进航空作战平台效能发挥,研究者们提出航空集群作战的概念[1]。航空集群由一定数量的有人/无人航空平台组成,能够根据作战需求进行高效灵活的组织协同[2],通过平台间优势互补来获取航空作战效能的提升[3]。然而航空集群作战场景下电磁环境较为复杂,且用户数量以及需要传输信息较多,数据链频谱资源愈发紧张,在高负载时会由于信道资源不足而产生信息时延高,吞吐量低等问题[4-5]。
关于提升数据链系统的频谱利用率的研究已经有一段时间。文献[6]基于轮询提出了一种新的控制协议,通过缩短各站点的等待时间来提高系统实时性。文献[7]对TDMA系统整个时间域资源的统筹管理,通过通信资源动态占有的方式,提升系统的使用效能。文献[8]通过动态博弈的方式优化功率控制问题,提高了数据链系统的公平性与稳定性。但这些优化策略未能突破数据链系统原有的时域频域基础,高负载情况下频谱资源紧张的问题仍十分严重。
作为5G移动通信系统的关键技术之一,非正交多址接入(non-orthogonal multiple access,NOMA)技术在原有时域频域的基础上引入了功率域,并通过功率分配算法实现多用户的功率域复用[9-10]。在NOMA系统中,发送端使用叠加编码(Superposition Coding,SC)技术发送信息,在接收端需使用干扰删除(successive interference cancellation,SIC)技术获取需要的信息[11],可以有效提高频谱利用率[12]。NOMA技术的出现为解决数据链频谱资源紧张问题提供了新的思路。
研究者们在移动通信系统中对NOMA系统进行了广泛的研究。文献[13]研究了用户随机部署的蜂窝下行链路NOMA网络的性能。研究结果表明与传统的OMA相比,NOMA可以获得更高的系统速率且通过适当的功率分配算法可以降低系统的中断概率。文献[14]分析了仅具有部分信道状态信息的情况下,NOMA系统的中断概率,研究结果表明NOMA技术可以有效提高系统的频谱效率。文献[15-16]分别研究了SISO与MISO场景中NOMA系统安全性以及最大传输速率的问题。文献[17-18]分别研究了单天线与多天线协作传输场景中,天线选择对NOMA系统中断性能的影响。文献[19]研究了系统中存在窃听节点的情况下NOMA系统的性能,并提出了优化功率分配方案。文献[20]研究了在考虑非理想的条件下,自干扰因素对系统性能的影响。文献[21-22]研究了认知无线电网络中NOMA的中断性能,并分别设计了两级中继选择方案与功率分配算法。然而,上述研究均是在民用移动通信场景中对NOMA系统进行研究分析。与移动通信系统相比,航空集群作战场景中电磁环境更复杂,用户间通信距离远、各用户移动速度快,且通信时存在敌方干扰的风险[23-24]。目前还很少有文献研究NOMA技术在航空集群作战场景中的应用。
本文在航空集群作战背景下分析NOMA系统性能,考虑了敌方干扰因素对NOMA系统性能的影响,提出了干扰条件下的基于NOMA技术的航空数据链系统模型(Aviation Data link system based on NOMA technology under interference,ADLS-NOMA-I),与移动通信系统不同的是,在ADLS-NOMA-I模型中,各个节点间距离较远且衰落信道满足莱斯衰落,同时系统中存在干扰节点,对接收端进行干扰。本文推导了ADLS-NOMA-I系统中断概率的闭合表达式,为分析集群作战场景中NOMA系统的性能提供了快速有效的方法。仿真结果表明,ADLS-NOMA-I系统具有一定的抗干扰能力,且系统中断概率受到我方发射功率及信道状态与到敌方干扰信号的共同影响,当敌方干扰严重时,可以通过增大发射功率,调整功率分配系数以及降低数据速率等手段保障信息的成功传输。
2 系统模型
假设某一时刻飞机编队S需向多个飞机编队发送不同指令信息时,之前的做法是通过轮询的方式依次向各飞机编队发送指令信息,但由于集群作战场景中业务量较大,且电磁环境复杂,轮询或频分等方式会导致指令信息的时延较大,频谱资源不足等问题。而通过将NOMA技术,飞机编队S可以在相同的时间频率资源上,向不同的飞机编队发送信息,接收端通过SIC技术对需要的信息进行解码,可以有效降低时延,提高频谱效率。由于发送端发送信号叠加的越多,接收端使用SIC技术解码难度越高,算法复杂度越大,目前在民用移动通信中研究NOMA技术时,发送端通常采用两用户信号叠加的方式发送信息,当需要向多用户发送信息时,会先将各用户两两分组,不同组间信号仍采用时分或频分的方式加以区分,因此本文中飞机编队S同样以两用户信号叠加的方式发送指令信息。假设在飞机编队S发送指令信息时,将飞机编队A与飞机编队B分为一组,在某一时刻利用NOMA技术以广播的形式发送给飞机编队A、B的指令信息,飞机编队B受到了敌方干扰机N的干扰,其系统模型如图2所示。
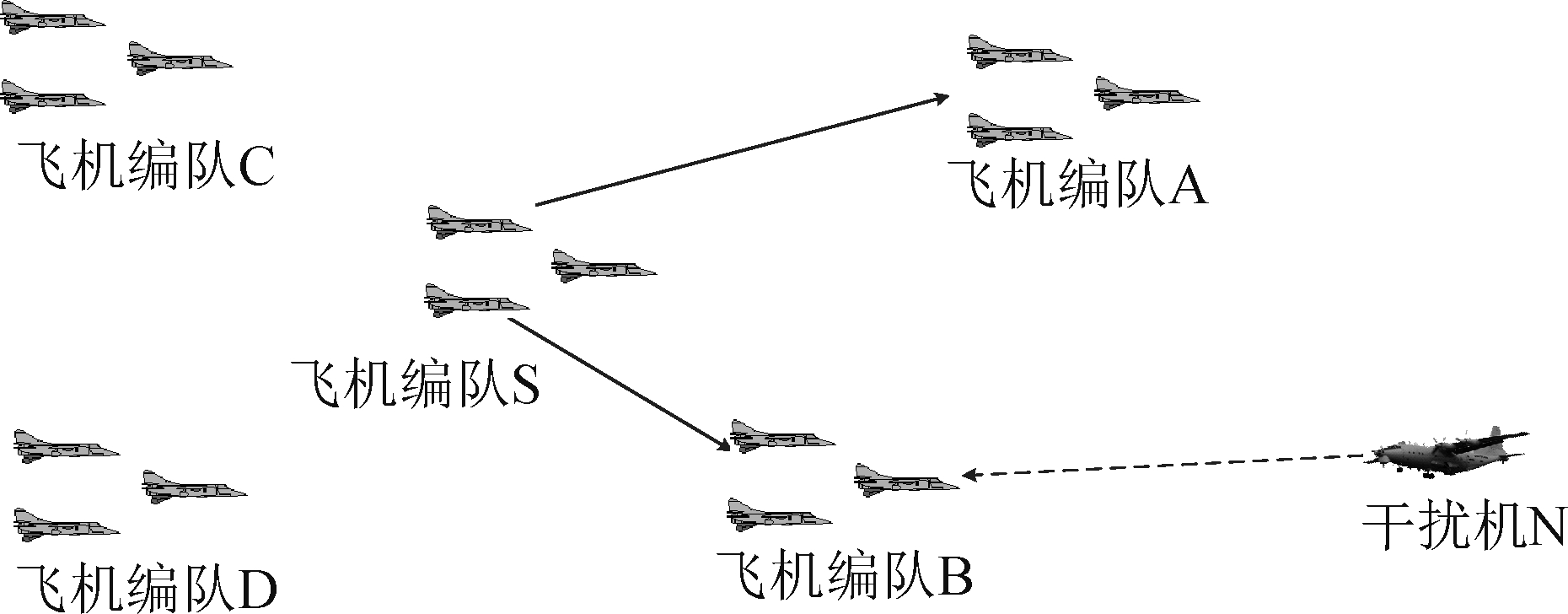
图1 航空集群作战场景图
Fig.1 Aviation cluster operation scenario
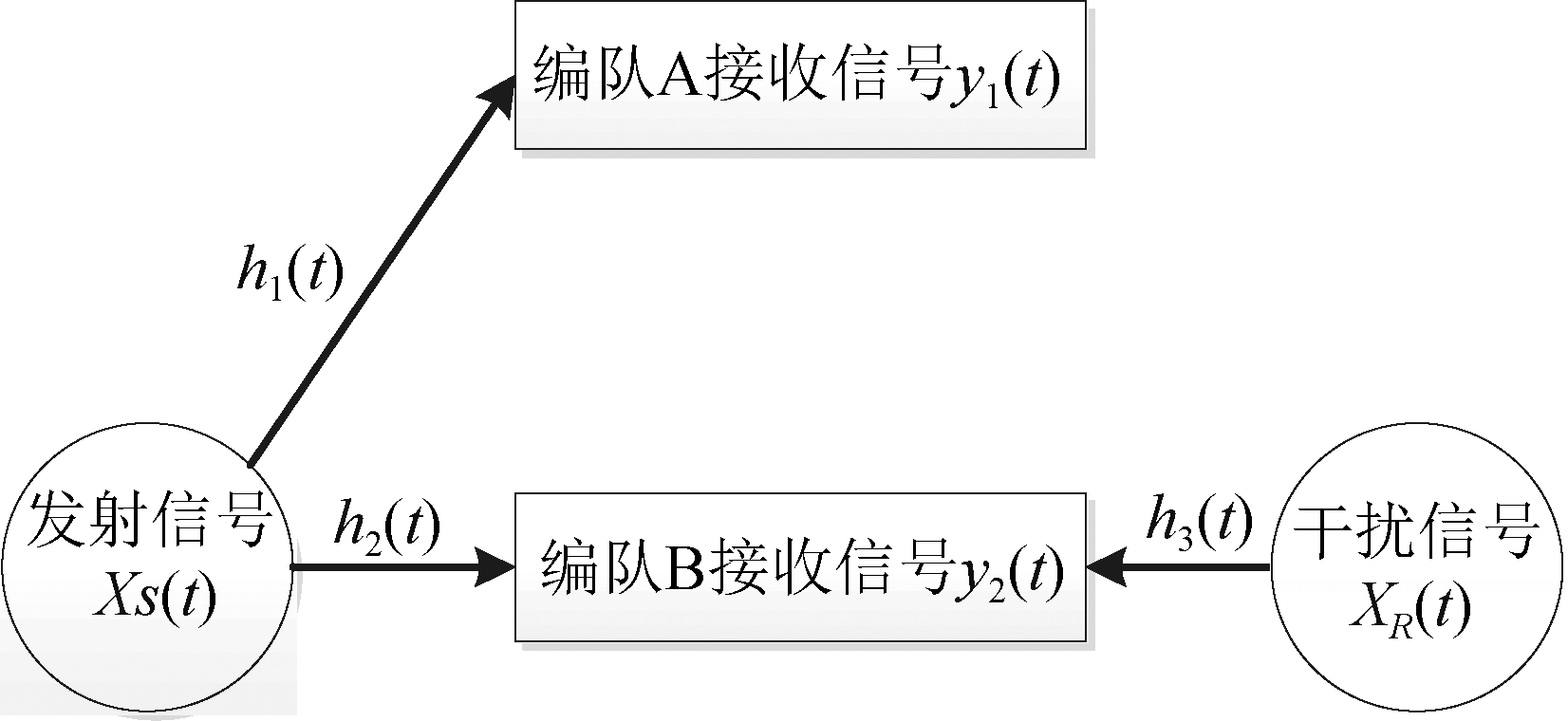
图2 ADLS-NOMA-I系统模型
Fig.2 ADLS-NOMA-I system model
在ADLS-NOMA-I系统中,飞机编队S通过广播的方式同时向两个我机编队发送信息,信息中既包括发给A的信号x1(t),又包括发给编队B的信息x2(t),飞机编队S发送的信号xs(t)可以表示为
(1)
其中α1,α2分别为信号x1(t),x2(t)的功率分配系数,且α1+α2=1,α1>α2,Ps为S的发射信号的功率,E[|X1(t)|2]=1,E[|X2(t)|2]=1。
编队A接收到的信号 y1(t)可以表示为:
(2)
其中h1(t)为飞机编队S与编队A之间信道衰落系数,![]() 为高斯白噪声。
为高斯白噪声。
编队B在收到飞机编队S发送信号的同时,也会接收到N发送的干扰信号xR(t),设干扰机的发射功率为PR,则编队B收到的信号y2(t)可以表示为:
(3)
其中h2(t)为飞机编队S与编队B之间信道衰落系数,h3(t)为干扰机N与编队B之间信道衰落系数,![]() 为高斯白噪声。
为高斯白噪声。
本文中不考虑阴影衰落的影响,其路径衰减系数 hi(t)=di(t)-γgi(t),其中di(t)-γ为路径衰减系数,di(t)为信号传输距离,γ为路径损耗指数,gi(t)为莱斯衰减系数,为方便表达,后文中hi(t)均使用hi表示,di(t)均使用di表示。
在ADLS-NOMA-I系统中,由于编队A接收到的是S发送的NOMA信号,其中包含了x1(t)和x2(t)两个用户的信号,因此,其需要使用SIC技术对其解调。由于S与编队A之间的链路状态信号较差,需分配更大的功率,因此在设计功率分配参数时,设α1>α2,信号x1(t)的功率高于信号x2(t)的功率,编队A在接收到S发送的数据后,可以直接对x1(t)进行解调,可达速率为:
(4)
在编队B对S发送的信号进行解调时,由于信号x2(t)的功率低于信号x1(t)的功率,需先使用SIC技术提取出x1(t)信号,再在剩余信号中对x2(t)信号进行解码,其提取x1(t)信号的可达速率如下表示:
(5)
当R对x2(t)成功解码后,将把x2(t)从接收到的信号提取出来,并在提取后的信号中对x1(t)进行检测。剩余的信号可以表示为:
(6)
因此,编队B对x2(t)进行解码时可获得的信息速率为:
(7)
综合公式(6)和(7),编队B可获得的最大信息速率为:
CB=min{CAx1,CBx2}
(8)
综合公式(4)和(8)可以得到,ADLS-NOMA-I系统可获得的最大信息速率为:
Cmax=min{CA,CB}
(9)
3 性能分析
在移动通信系统中,研究者通常使用中断概率分析NOMA系统的性能。本文同样采用中断概率分析干扰条件下数据链系统的性能。在ADLS-NOMA-I系统中,以下两种情况会造成系统产生中断:
(1) 编队A无法对x1(t)进行解码。编队A可以成功的对x1(t)进行解码的条件为A的对信号x1(t)的解码速度快于信号传输的速率。在本文中用R来表示系统能够正常运行所需求的最低传输速率,则A发生中断的概率可以表示为:
P=Pr{CA<R}
(10)
(2) 编队B无法对x2(t)进行解码。编队B可以成功的对x2(t)进行解码的条件是要求其既可对x1(t)成功解码同时,对信号x2(t)也能解码成功。其发生中断的概率可以表示为:
P=Pr{CB<R}
(11)
结合公式(3)到(10),ADLS-NOMA-I系统的中断概率可如下计算:
 Pr(min(X1,X2,X3)<2R-1)=1-Pr(X1≥2R-1)Pr(X2≥2R-1)Pr(X3≥2R-1)
Pr(min(X1,X2,X3)<2R-1)=1-Pr(X1≥2R-1)Pr(X2≥2R-1)Pr(X3≥2R-1)
(12)
本文飞机间链路均服从莱斯衰落,即小尺度衰落系数gi服从于莱斯分布,信道衰落系数hi的概率密度如下表示:
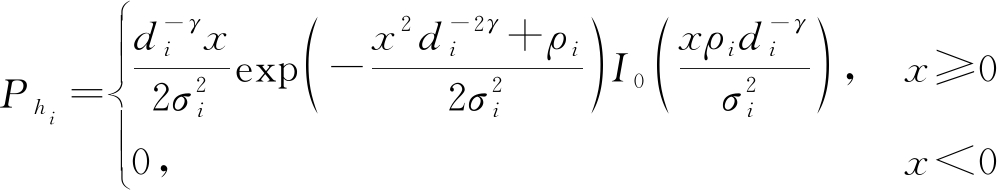
(13)
其中I0(·)为第一类修正Bessel函数,![]() 为莱斯信道多径分量信号的功率,ρi为直射信号峰值。由此可以推导出:
为莱斯信道多径分量信号的功率,ρi为直射信号峰值。由此可以推导出:
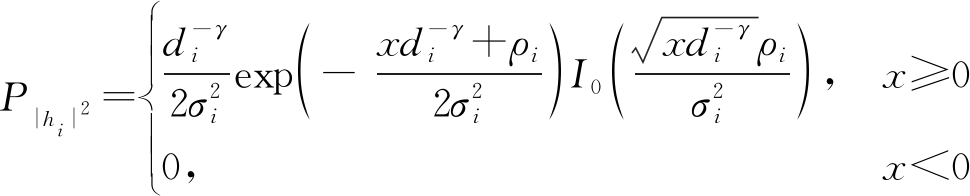
(14)
X1的分布函数FX1(x)可以表示为:
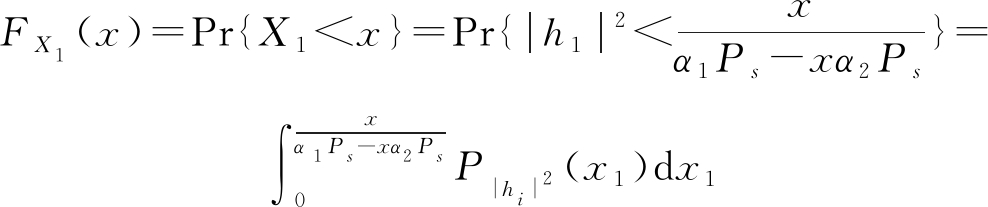
(15)
由于公式(15)中的积分难以精确求解,可采用复合高斯求积公式求其近似解:
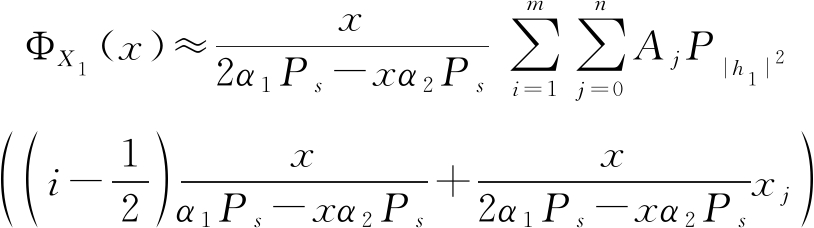
(16)
其中,m为使用高斯求积分是子区间的个数,n为插值节点个数,系数Aj与坐标xj均可根据n查表得到。
由于S与A之间的链路状态|h1|2与N与B之间的链路状态|h3|2相互独立,故其联合概率密度可直接由概率密度相乘得到,即联合概率密度概率密度函数f(x2,x3)如下:
f(x2,x3)=P|h2|2(x1)P|h3|2(x3)
(17)
X2的分布函数FX2(x)可以表示为:
FX2(x)=Pr{X2<x}=Pr{l|h2|2-PRx|h3|2
![]()
(18)
其中l=α1Ps-xα2Ps。公式中二重积分难以求出其精确解,可采用复合辛普森公式对其进行简化估计:
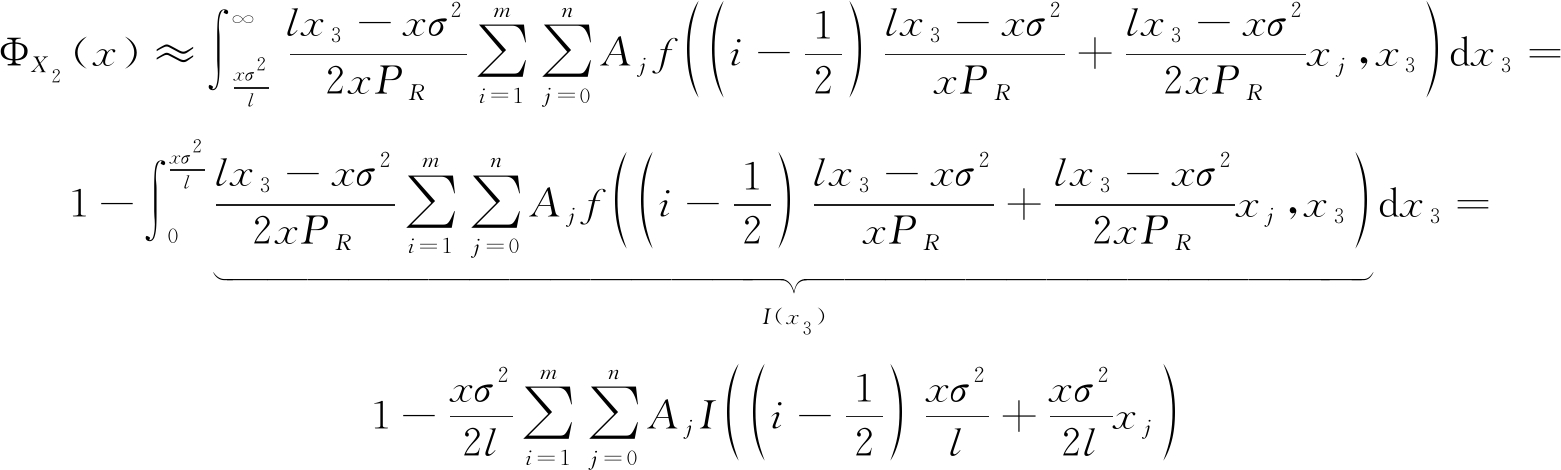
(19)
同理,X3的分布函数FX3(x)可以表示为:
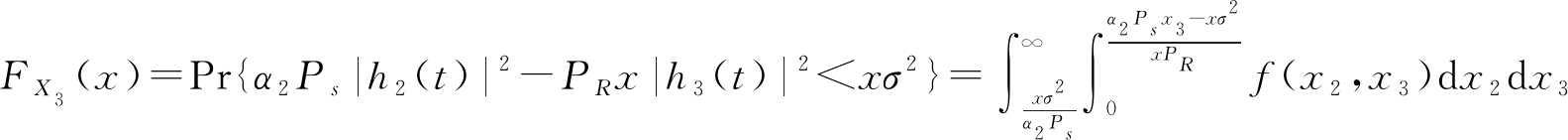
(20)
其近似解可表示为:
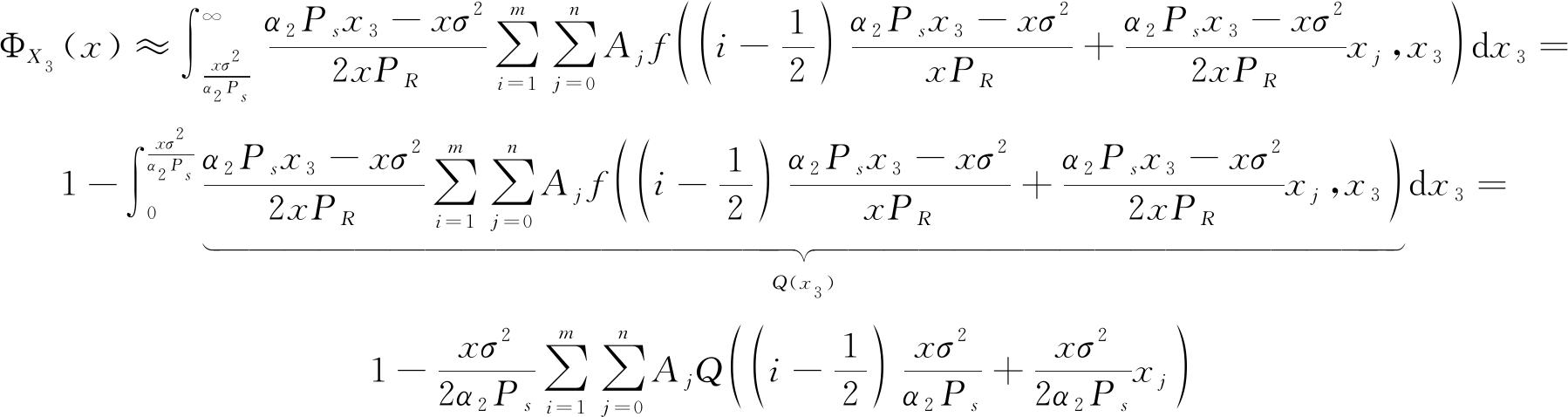
(21)
结合公式(12)、(16)、(19)、(21),即可求出系统的中断概率:
Pout=1-(1-ΦX1(2R-1))· (1-ΦX2(2R-1))·(1-ΦX3(2R-1))
(22)
4 仿真结果及分析
本文针对所提出的ADLS-NOMA-I系统,重点分析了存在敌方干扰的情况下基于NOMA技术的航空数据链系统的中断性能,通过Matlab对推导公式进行仿真验证及分析。根据航空集群作战场景的实际情况,假设所有链路均服从莱斯衰落,如无特殊说明,系统仿真参数如表1所示。为验证航空集群作战场景下NOMA系统的可行性,下面分别分析发射功率、传输距离、干扰功率以及信号数据速率四个方面对系统中断概率的影响。
表1 仿真参数
Tab.1 Simulation parameters
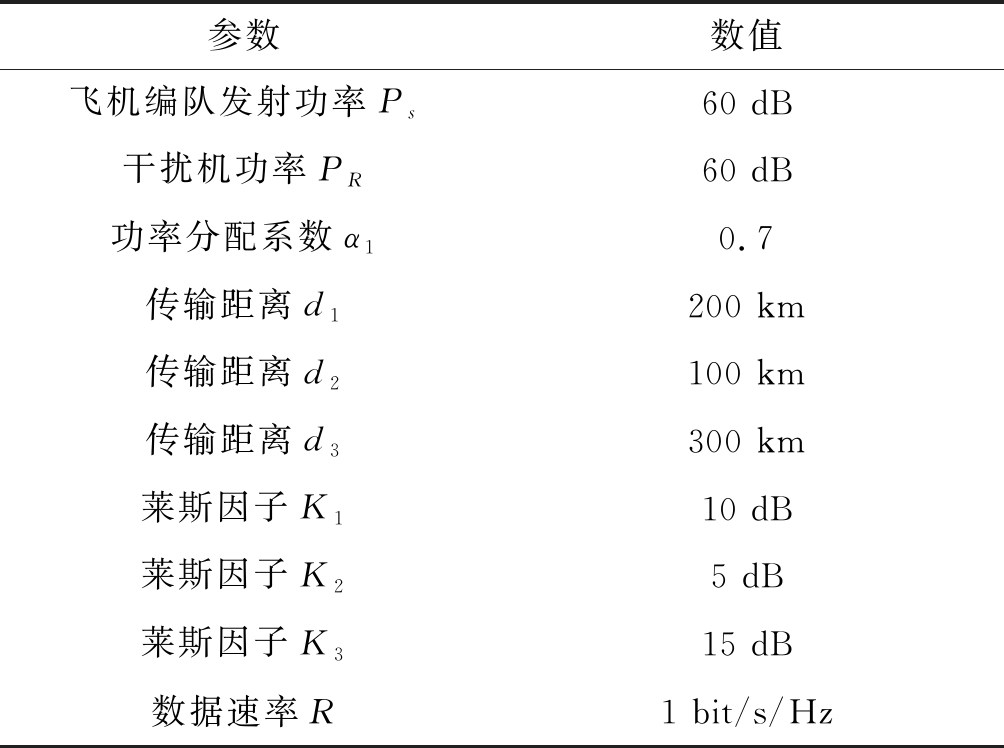
参数数值飞机编队发射功率Ps60 dB干扰机功率PR60 dB功率分配系数α10.7传输距离d1200 km传输距离d2100 km传输距离d3300 km莱斯因子K110 dB莱斯因子K25 dB莱斯因子K315 dB数据速率R1 bit/s/Hz
4.1 发射功率
发射功率对ADLS-NOMA-I系统的中断概率影响较大,仿真结果如图3所示。从仿真结果可以看出,当发射功率小于40 dB时,系统中断概率基本为1,这是信号的大尺度衰落导致的。由于传输距离较长,当发射功率较小时,接收端接收信号的信噪比会较小,导致信号无法被成功解调。发射功率的增加导致接收端接收信号的信噪比增加,信号被成功解调的概率变大,系统的中断概率降低。

图3 中断概率随发射功率变化情况图
Fig.3 Change of outage probability with transmit power
同时从图中的数据还可以看出,不同的功率分配系数对系统的中断概率有着很大的影响,这是由于在 S与编队B受到敌方干扰,更容易发生中断现象, 故而通过调整功率分配系数, 为其分配更大的发射功率, 可以有效降低系统的中断概率。
4.2 传输距离
传输距离对ADLS-NOMA-I系统的中断概率的影响主要体现在路径损耗上,仿真结果如图4所示。由于存在路径损耗,传输距离越远,接收端接收到信号的功率越小,导致信噪比变小,系统中断概率增加。根据图4(a)中数据可以看出,当发射功率为50 dB时,S与编队A之间的距离对中断概率影响较大,这是因为路径损耗的过大,导致编队A接收信号信噪比小于编队B,在整个系统中,编队A发生中断的可能性更大。当发射功率为60 dB或更大时,虽然编队A发生中断的可能性也会随着通信距离增加,但是此时系统发生中断主要由编队B引起的,故而中断概率受影响较小。图4(b)中数据可以看出飞机编队S与飞机编队B之间的距离对系统中断概率影响较大,这是由于飞机编队B受到了敌方干扰,相较于编队A而言,更容易发生中断,此时接收信号功率的减小更容易引起系统发生中断。
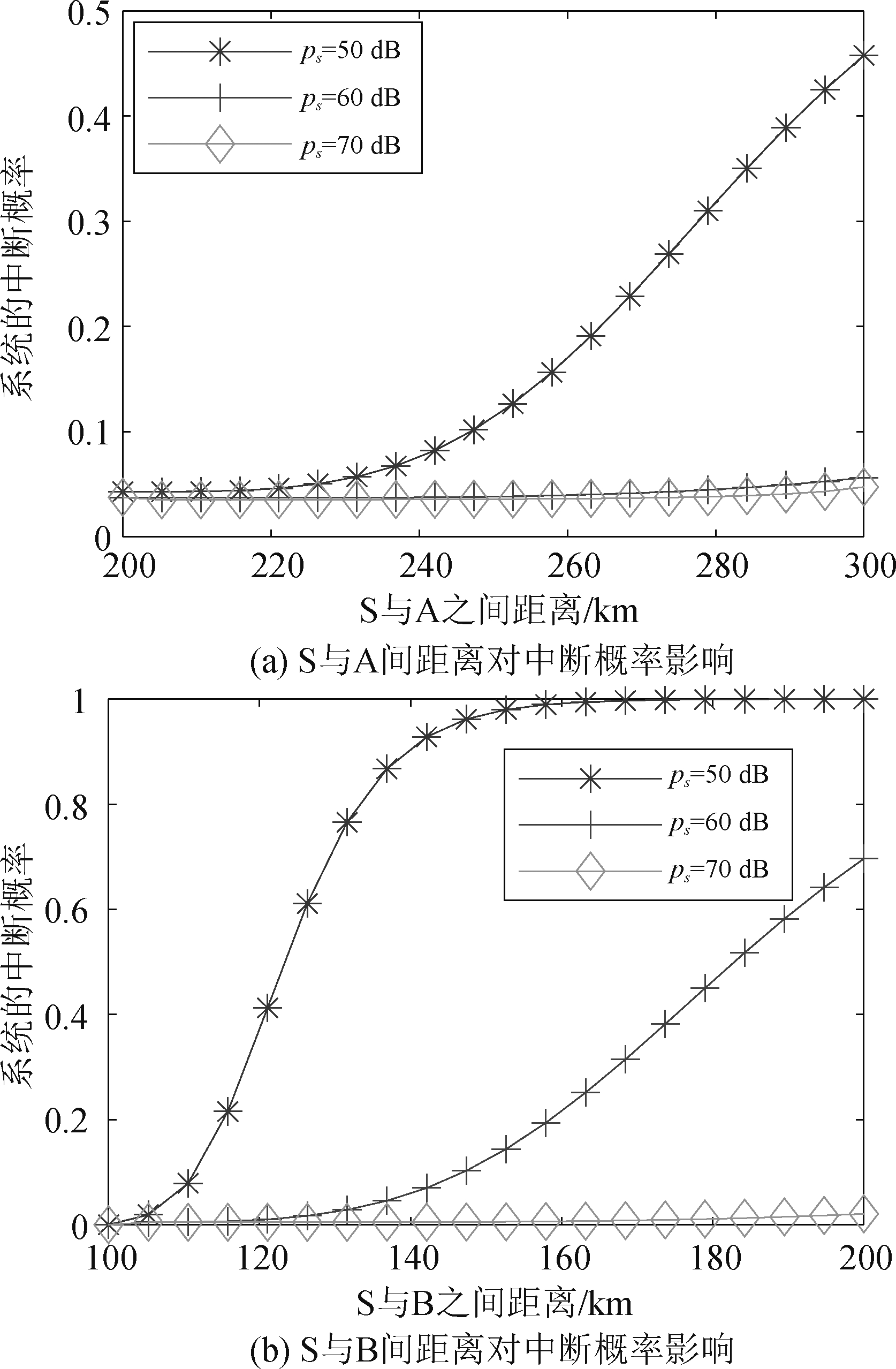
图4 中断概率随传输距离变化情况
Fig.4 Change of outage probability with transmission distance
4.3 干扰信号功率
图5所示为敌方干扰信号对系统中断概率的影响。根据图5中的数据可以看出,当敌方干扰功率为0,也就是未进行干扰时,根据当前的系数设置,系统几乎不会发生中断。随着敌方干扰机的干扰功率逐渐增强,系统的中断概率也在缓慢增加,这个结果也很明显,在我方接收到的信号一定的情况下,敌方的干扰信号越强,我方越不容易解调出正确的信息,系统成功传输可达的最大速率就越小,更加容易发生中断。图5(a)对比了不同发送功率与分配系数下,干扰信号对中断概率的影响,从图中数据可以看出,为提高系统抗干扰能力,在发射端应该向被干扰端分配更高的功率。图5(b)对比了信号下, 干扰信号对中断概率的影响, 从图中数据可以看出, 当敌方干扰严重时, 可以通过降低信号数据速率降低到1 bit/s/Hz以下, 来保证数据链通信系统的抗干扰能力。
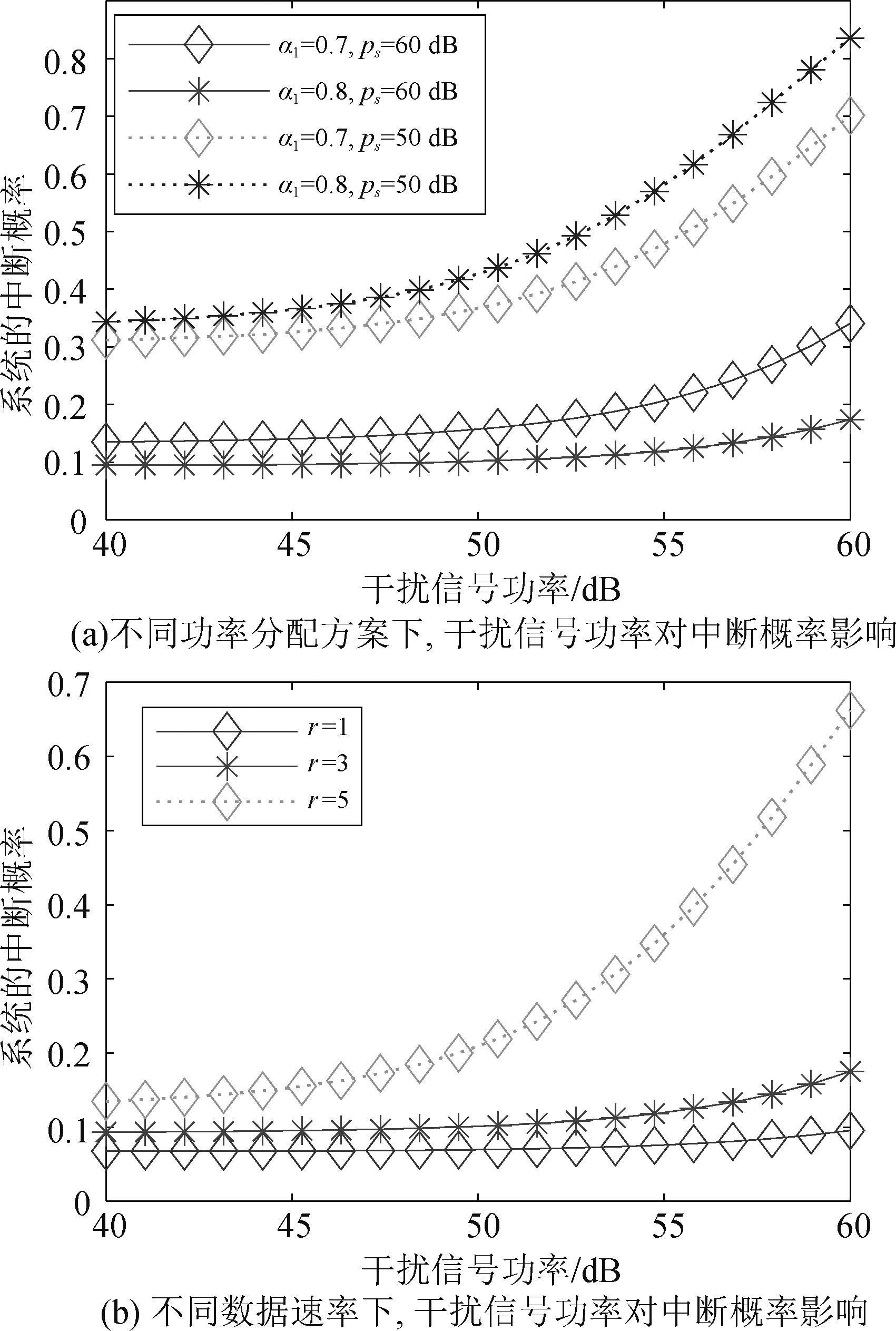
图5 中断概率随干扰信号功率变化情况
Fig.5 Change of interruption probability with interference signal power
4.4 数据速率
在ADLS-NOMA-I系统中,信号数据速率的大小对中断概率有较大影响,仿真结果如图6所示。根据图6中的数据可以看出,目标数据速率越大,系统发生中断的可能性越大,敌方干扰对系统的影响严重。这是由于目标数据速率越高,对系统的解码速率要求就越高。通过不同发射功率与分配系数下,目标数据速率的对比,可以看出能够通过提高发射功率和提高被干扰目标的功率分配系数的方式,系统可以获取更高的数据速率。这是由于改变发射功率与功率分配系数,使接收端接收信号的信噪比发生了变化,进而导致系统的最大信息速率发生改变。从图中的数据可以看出,通过为被干扰端分配更多的功率,可以有效提高系统的最大信息速率,保证数据的高速率传输。
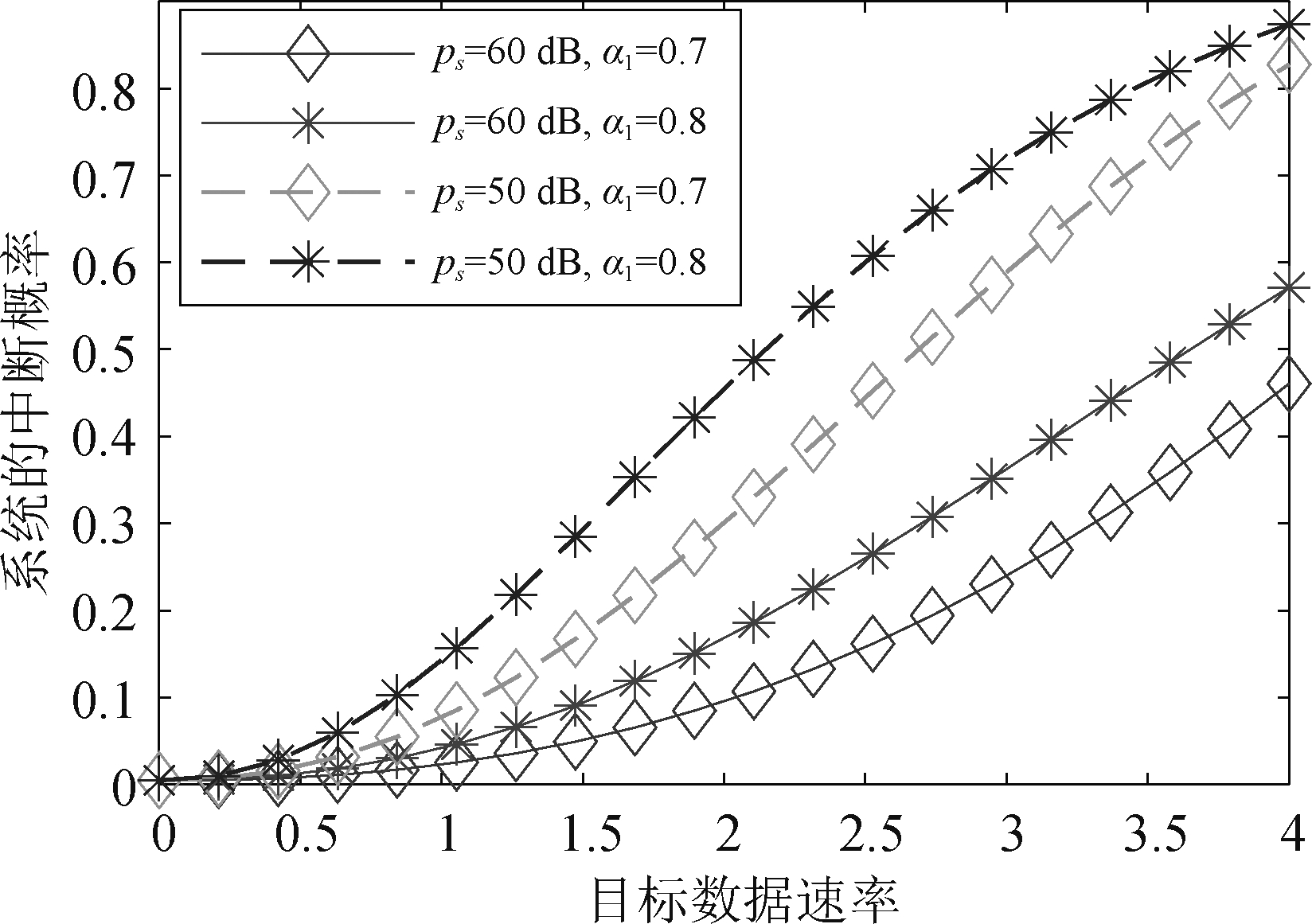
图6 中断概率随目标数据速率变化情况
Fig.6 Change of outage probability with target data rate
综合上述分析可以看出,ADLS-NOMA-I系统具有一定的抗干扰能力,通过NOMA技术对现有数据链技术进行优化具有一定可行性,将NOMA技术应用于数据链系统中具有一定的研究价值。
5 结论
NOMA技术作为5G的重要技术之一,将其应用于数据链系统中,将有助于提高系统的频谱利用率。本文分析了基于NOMA的数据链通信系统的性能,从系统中断概率的角度分析了敌方干扰对数据链系统安全中断性能的影响;推导了系统中断概率表达式,为基于NOMA的数据链通信系统的性能评估和设计功率分配方案提供了参考和依据。仿真结果表明, 将NOMA技术应用在数据链系统中具有一定的可行性, 并且在敌方干扰严重时, 可以通过增大发射功率、调整功率分配系数、降低数据速率等方案保证信息的成功传输。
[1]梁晓龙, 何吕龙, 张佳强, 等. 航空集群构型控制及其演化方法[J]. 中国科学: 技术科学, 2019, 49(3): 277-287.
Liang Xiaolong, He Lvlong, Zhang Jiaqiang, et al. Configuration control and evolutionary mechanism of aircraft swarm[J]. Scientia Sinica Technologica, 2019, 49(3): 277-287.(in Chinese)
[2]景晓年, 梁晓龙, 张佳强, 等. 航空集群作战编队优化控制研究 [J]. 计算机仿真, 2017, 34(4): 90-94.
Jing Xiaonian, Liang Xiaolong, Zhang Jiaqiang, et al. Research on Optimized Control for Aircraft Swarms Combat Formation[J]. Computer Simulation, 2017, 34(4): 90-94.(in Chinese)
[3]赵尚弘, 陈柯帆, 吕娜, 等. 软件定义航空集群机载战术网络[J]. 通信学报, 2017, 38(8): 140-155.
Zhao Shanghong, Chen Kefan, Lv Na, et al. A software defined airborne tactical network for aeronautic[J]. Journal on Communications, 2017, 38 (8): 140-155.(in Chinese)
[4]Baek H, Lim J. Spectrum Sharing for Coexistence of Fixed Satellite Services and Frequency Hopping Tactical Data Link[J]. IEEE Journal on Selected Areas in Communications, 2016: 1-1.
[5]Baek H, Lim J. Design of Future UAV-Relay Tactical Data Link for Reliable UAV Control and Situational Awareness[J]. IEEE Communications Magazine, 2018, 56(10): 144-150.
[6]Ding H, Li C, Bao L, et al. Research on multi-level priority polling MAC protocol in FPGA tactical data chain[J]. IEEE Access, 2019, 7: 33506-33516.
[7]Zhuo S, Wang Z, Song Y Q, et al. A traffic adaptive multi-channel MAC protocol with dynamic slot allocation for WSNs[J]. IEEE Transactions on Mobile Computing, 2015, 15(7): 1600-1613.
[8]董玉浩, 赵学军, 袁修久, 等. 数据链中功率控制的改进算法[J]. 兵器装备工程学报, 2019, 40(7): 144-147.
Dong Yuhao, Zhao Xuejun, Yuan Xiujiu, et al, Improved Algorithm for Power Control in Data-Link System[J]. Journal of Ordnance Equipment Engineering, 2019, 40(7): 144-147.(in Chinese)
[9]Liu F, Petrova M. Proportional fair scheduling for downlink single-carrier NOMA systems[C]∥ GLOBECOM 2017-2017 IEEE Global Communications Conference. IEEE, 2017: 1-7.
[10]Islam S M R, Avazov N, Dobre O A, et al. Power-domain non-orthogonal multiple access (NOMA) in 5G systems: Potentials and challenges[J]. IEEE Communications Surveys & Tutorials, 2016, 19(2): 721-742.
[11]Ding Z G, Liu Y W, Choi J H, et al. Application of non-orthogonal multiple access in LTE and 5G Networks[J]. IEEE Communications Magazine, 2017, 55(2): 185-191.
[12]Al-Imari M, Xiao P, Imran M A, et al. Uplink non-orthogonal multiple access for 5G wireless networks[C]∥2014 11th International Symposium on Wireless Communications Systems (ISWCS). IEEE, 2014: 781-785.
[13]Ding Z, Yang Z, Fan P, et al. On the performance of non-orthogonal multiple access in 5G systems with randomly deployed users[J]. IEEE Signal Processing Letters, 2014, 21(12): 1501-1505.
[14]Yang Z, Ding Z, Fan P, et al. On the Performance of Non-orthogonal Multiple Access Systems With Partial Channel Information[J]. Communications, IEEE Transactions on, 2016, 64(2): 654- 667.
[15]Zhang Y, Wang H M, Yang Q, et al. Secrecy sum rate maximization in non-orthogonal multiple access[J]. IEEE Communications Letters, 2016, 20(5): 930-933.
[16]Li Y, Jiang M, Zhang Q, et al. Secure beamforming in downlink MISO non-orthogonal multiple access systems [J]. IEEE Transactions on Vehicular Technology, 2017, 66(8): 7563-7567.
[17]He B, Liu A, Yang N. On the design of secure non-orthogonal multiple access systems[J]. IEEE Journal on Selected Areas in Communications, 2017, 35(10): 2196-2206.
[18]Liu Y, Qin Z, Elkashlan M, et al. Enhancing the Physical Layer Security of Non-Orthogonal Multiple Access in Large-Scale Networks[J]. IEEE Transactions on Wireless Communications, 2017, 16(3): 1656-1672.
[19]Chen J, Yang L, Alouini M. Physical Layer Security for Cooperative NOMA Systems[J]. IEEE Transactions on Vehicular Technology, 2018, 67(5): 4645- 4649.
[20]李美玲, 李莹, Sami M, 等. 非理想干扰删除下全双工中继NOMA系统的物理层安全性能研究[J]. 电子学报, 2019, 47(1): 183-189.
Li Meiling, Li Ying, Sami M, et al. Physical Layer Security for NOMA-Based Full Duplex Relay Networks with Non-ldeal Interference Cancellation [J]. Acta Electronica Sinica, 2019, 47(l): 183-189.(in Chinese)
[21]乔宇航, 贺玉成, 杨键泉, 等. 两级中继选择的协作CR-NOMA网络性能分析[J]. 信号处理, 2020, 36(2): 196-202.
Qiao Yuhang, He Yucheng, Yang Jianquan, et al. Performance Analysis for Cooperative CR-NOMA with Two-Stage Relay Selection[J]. Journal of Signal Processing, 2020, 36(2): 196-202.(in Chinese)
[22]时安谊, 杨震. 针对NOMA和CR网络的功率分配方法[J]. 信号处理, 2019, 35(7): 1224-1234.
Shi Anyi, Yang Zhen. Power Allocation Method for Non-Orthogonal Multiple Access and Cognitive Radio Network[J]. Journal of Signal Processing, 2019, 35(7): 1224-1234.(in Chinese)
[23]Bellido-Manganell M A, Gräupl T, Schnell M. Impact Assessment of the L-Band Digital Aeronautical Communications System on the Joint Tactical Information Distribution System[J]. IEEE Transactions on Vehicular Technology, 2019, 68(4): 3629-3641.
[24]Riihonen T, Korpi D, Turunen M, et al. Tactical communication link under joint jamming and interception by same-frequency simultaneous transmit and receive radio[C]∥MILCOM 2018-2018 IEEE Military Communications Conference (MILCOM). IEEE, 2018: 1-5.


