1 引言
上世纪三十年代,德国物理学家 Paul Leug 首次提出了噪声的主动控制方法(Active Noise Control, ANC)[1]。该方法通过波形相消原理人为发出次级声波,以达到将噪声声波抵消的目的。ANC技术与传统的噪声控制相比更为灵巧且成本低廉,在过去的20年里在人们的生活与生产中有着广泛的应用[2- 4]。ANC的控制算法对于噪声的控制效果有着至关重要的作用。经典的滤波-最小均方误差算法(Filtered x Least Mean Square,FxLMS)在噪声主动控制中得到了相当广泛的应用。然而实际情况中大多数噪声控制系统都是非线性的,传统的线性控制算法尤其是FxLMS算法难以满足控制需求。
ANC中的非线性扰动主要由以下三种情况导致:输入为混沌噪声或噪声超过电子器件动态范围的非线性饱和;主通道为非线性结构,如管道声压较大时产生的非线性失真;由扬声器产生的次级通道为非线性结构。传统的FxLMS 控制器算法在非线性条件下的性能急剧下降,甚至会产生额外噪声。Li Zhe Tan 与 Jean Jiang等人基于二阶Volterra滤波器提出了多通道噪声的主动控制器的VFxLMS(VFxLMS)算法[5]。该算法首次将自适应非线性滤波器引入噪声的主动控制,来解决主通道为非线性结构的问题。使用Volterra非线性滤波器的噪声的主动控制器对主通道非线性问题有着很好的控制效果,然而其结构较为复杂且计算复杂度高,算法的实施对硬件的要求更高。Nithin V. George 与Ganapati Panda将函数连接型神经网络(Functional Link Artificial Neural Network,FLANN)结构嵌入主动噪声控制模型。对输入进行非线性展开提出了FsLMS算法,并给出了其快速实现方法[6]。该算法考虑到实际情况下的动力系统产生的噪声是非线性的、随机的、有色的以及非最小相位次级通道的问题,然而它的展开式不含交叉项,其性能还有一定的改进空间。
近年来,随着信息论的发展,核方法以其坚实的数学基础和成功的应用而受到广泛欢迎[7]。核方法被验证了是解决非线性系统识别[8]、非线性信道均衡[9]、多输入多输出传输系统[10]以及非线性声回波抵消[11]等问题的强有力工具。核方法的主要思想是将非线性系统映射到一个高维再生核希尔伯特空间(Reproducing Kernel Hilbert Space,RKHS)中,再在高维空间中用线性方法去处理。Hua Bao与Issa M.S. Panahi首次将核方法引入主动噪声控制系统,使用核自适应滤波器对输入噪声信号进行处理[12]。但由于没有考虑到系统中次级通道的影响,算法并未得到推广。Liu Yuqi等人将(Kernel Adaptive Filter,KAF)引入到具有次级通道的ANC系统中,并提出了核-滤波最小均方误差算法(Kernel Filtered x Least Mean Square,KFxLMS)[13]。KFxLMS算法中的核映射包含了输入信号无限维的特征,这使得算法能够更精确的适用于解决非线性ANC问题。然而KFxLMS算法存在一个较大的缺陷,即算法更新所需的内存随着自适应迭代次数的增加而增加,且计算量会相当庞大。设定一定的稀疏准则筛选新信号能够适当的降低计算量[13],但同时也会降低算法的收敛性能。
为进一步改进KFxLMS算法,本文基于非线性主动噪声控制系统模型,提出一种随机傅里叶特征核滤波最小均方误差算法(Random Fourier Feature - Kernel Filtered x Least Mean Square,RFF-KFxLMS)。该算法使用随机傅里叶特征[14]近似核映射,将原始输入数据映射到有限维随机傅里叶特征空间(Random Fourier Feature Space,RFFS),并利用变换后的输入数据和一组固定大小的线性参数来估计输出。此外,随机傅里叶特征有着明确的映射关系,与核方法相比它的映射关系更加直观。因此,RFF-KFxLMS算法的更新公式计算简单,极大地减轻了计算负担,且不再需要对输入信号稀疏化。在噪声通道为非线性的情况下,本文对含有不同频率分量的正弦噪声进行仿真,实验结果表明提出的算法与已有算法相比,具有较好的控制效果。
2 非线性主动噪声控制
2.1 核方法
非线性问题可通过一连续的输入-输出展开来表示f:Rm×1→R
y=f(u),u∈U⊂Rm×1,y∈R
(1)
其中u表示m维输入向量,y表示输出向量。输入输出对用序列表示为![]() 作为一种可以有效的重构非线性展开的方法,核方法通过将原始输入数据映射到一个高维特征空间来逼近非线性函数,映射关系为:
作为一种可以有效的重构非线性展开的方法,核方法通过将原始输入数据映射到一个高维特征空间来逼近非线性函数,映射关系为:
(2)
其中κ(·,·)表示Mercer核,Mercer核是具有连续性、对称性和正定性的函数κ:U×U⊂R。
采用最典型的核函数高斯核来逼近非线性映射,则有
(3)
其中σ>0表示的是高斯核的核宽度参数。
根据Mercers定理,任意一个Mercers核κ(u(i),u(j))对应着从U映射到高维的RKHS的非线性展开,即有
Φ(u(i))TΦ(u(j))=κ(u(i),u(j))
(4)
其中Φ(·)表示该Mercers核所对应的非线性展开关系。
2.2 非线性主动噪声控制系统
本文采用单通道非线性主动噪声控制的系统[13],其控制框图如图1所示。其中P(z)表示噪声通道的系统响应;权向量w(n)=[w1(n),w2(n),...,wN(n)]T表示自适应FIR滤波器的权系数;S(z)表示次级通道的系统响应。向量x(n)=[x(n),x(n-1),...,x(n-N+1)]T是由输入噪声经采样得到的输入信号,其中n为时间指标,N为自适应FIR滤波器的长度。d(n)为在对消点观测到的期望信号值。
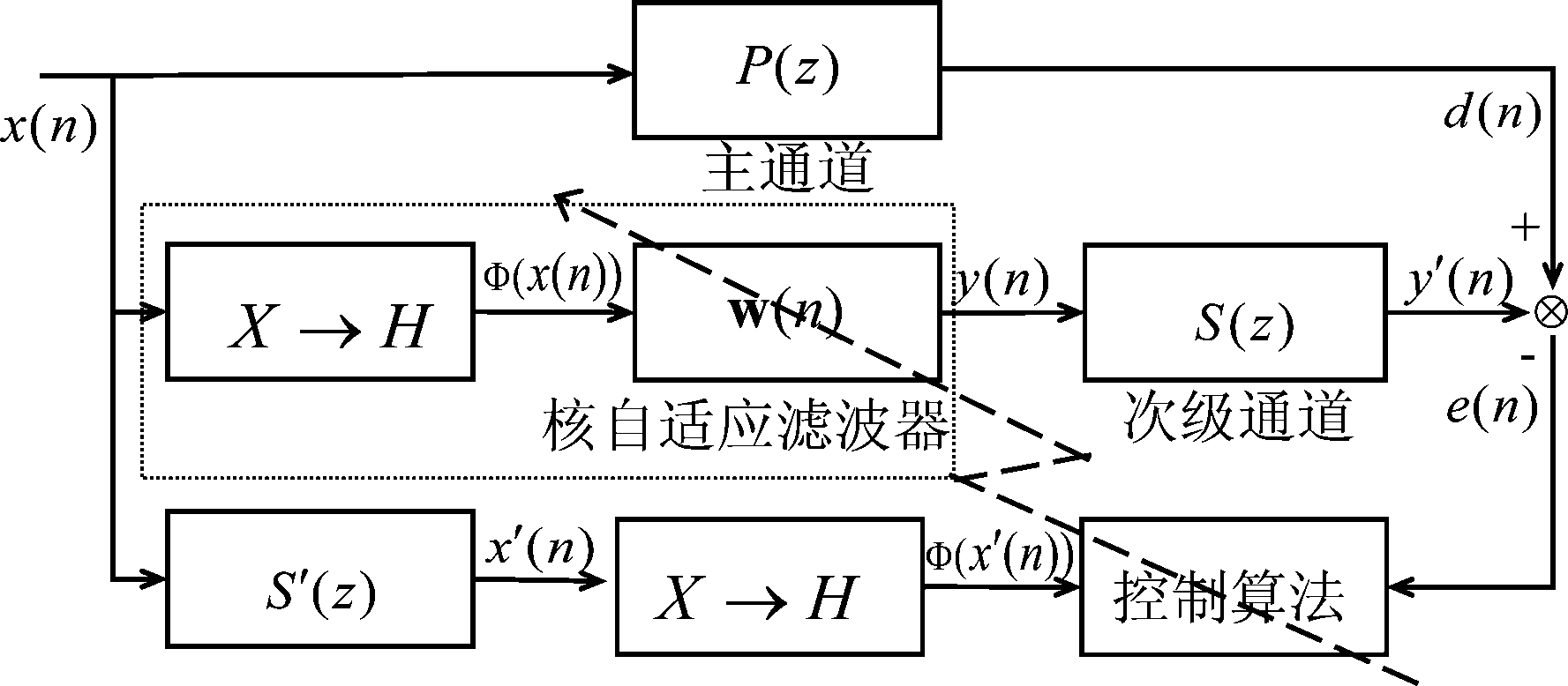
图1 基于核自适应滤波器的单通道非线性主动噪声控制系统框图
Fig.1 The block diagram of Single channel NANC based on KAFs
X→H表示非线性转换模块,该非线性模块通过核方法将输入信号映射到RKHS,即输入信号x(n)(x(n)∈X)通过非线性展开模块展开为Φ(x(n))(Φ(x(n))∈H),再将非线性问题转化为线性问题处理。
输入信号x(n)通过非线性展开模块X→H处理,并经过自适应滤波后得到y(n):
y(n)=wT(n)Φ(x(n))
(5)
期望信号与输出信号在扬声器到误差麦克风之间的声电通路叠加后得到残差信号e(n),该通道为次级通道,它的响应表示为S(z)。残差信号e(n)由经过次级通道后的y ′(n)与期望信号d(n)相叠加而得到,即:
e(n)=d(n)-y′(n)=
d(n)-s(n)*[wT(n)Φ(x(n))]
(6)
基于最小均方误差准则[16],控制自适应滤波器权值系数更新的KFxLMS算法的代价函数表示为:
ξ=E[e2(n)]
(7)
滤波器权值向量使用梯度下降法进行更新,当前时刻n的梯度向量为 ξ,
ξ,
![]()
(8)
则滤波器下一时刻的权系数向量为w(n+1),w(n+1)=w(n)+μe(n)Φ(x′(n)),其中x′(n)=s(n)*x(n) 。
将等式进一步展开,得到
w(n)=w(n-1)+μe(n-1)Φ(x′(n-1))=
[w(n-2)+μe(n-2)Φ(x′(n-2))]+
μe(n-1)Φ(x′(n-1))
⋮![]()
![]()
(9)
从上式中可以看到,当前时刻的权向量可以通过所有过去和当前的输入数据的展开,并乘以相应的预测误差和系数 μ 得到。将等式(9)带入等式(5)可以得到输出的表达式
(10)
根据Mercers定理,Φ(x′(i))TΦ(x(n))=κ(x′(i),x(n)),则有
(11)
当前时刻的滤波器输出是由前n个时刻的误差e(i)与κ(x′(i),x(n))的乘积求和得到,一旦采样点数(样本)非常多,随着迭代次数的增加,每次迭代所需的计算量也会随之不断增大。
3 随机傅里叶特征滤波算法
3.1 随机傅里叶特征
随机傅里叶特征是对核函数的一种近似估计,以典型的高斯核![]() 为例,高斯核函数κ(x-y)的傅里叶变换p(ω)仍服从高斯分布,可表示为:
为例,高斯核函数κ(x-y)的傅里叶变换p(ω)仍服从高斯分布,可表示为:
(12)
p(ω)经傅里叶反变换后得到核函数:
(13)
上式亦可看作ej(wT(x-y))的数学期望,根据数学期望的定义,令ej(wTx)=zw(x),则得到核函数的无偏估计![]() 为了得到一个实值特征映射,基于核的对称性,zw(x)可用余弦函数近似表示为[15]
为了得到一个实值特征映射,基于核的对称性,zw(x)可用余弦函数近似表示为[15]
ej(wTx)=zw(x)≈z(x)=
(14)
其中ωk=[ω1,...,ωL],k=1,...,D服从均值为0和协方差矩阵为ε2I高斯分布;φk,k=1,...,D在区间[0,2π]内服从均匀分布。该近似z(x)为随机傅里叶特征。
3.2 提出算法
基于RFF滤波器的非线性主动噪声控制的系统框图如图2所示。基于上述随机傅里叶变换,L维输入向量x(n)经过RF(ωk,φk)模块进行运算ωkx(n)+φk,k=1,...,D;再经过余弦模块后得到D维展开向量z(x(n))=[z1(x(n)),…,zD(x(n))]T,其中zk(x(n))=cos(ωkx(n)+φk),k=1,...,D。将展开信号再通过权向量为w(n)=[w1(n),w2(n),...,wN(n)]T的滤波器,得到输出为y(n)=wT(n)z(x(n));系统输出的次级声源信号为y′(n)=s(n)*(wT(n)z(x(n)));残余噪声表示为e(n)=d(n)-y′(n)。
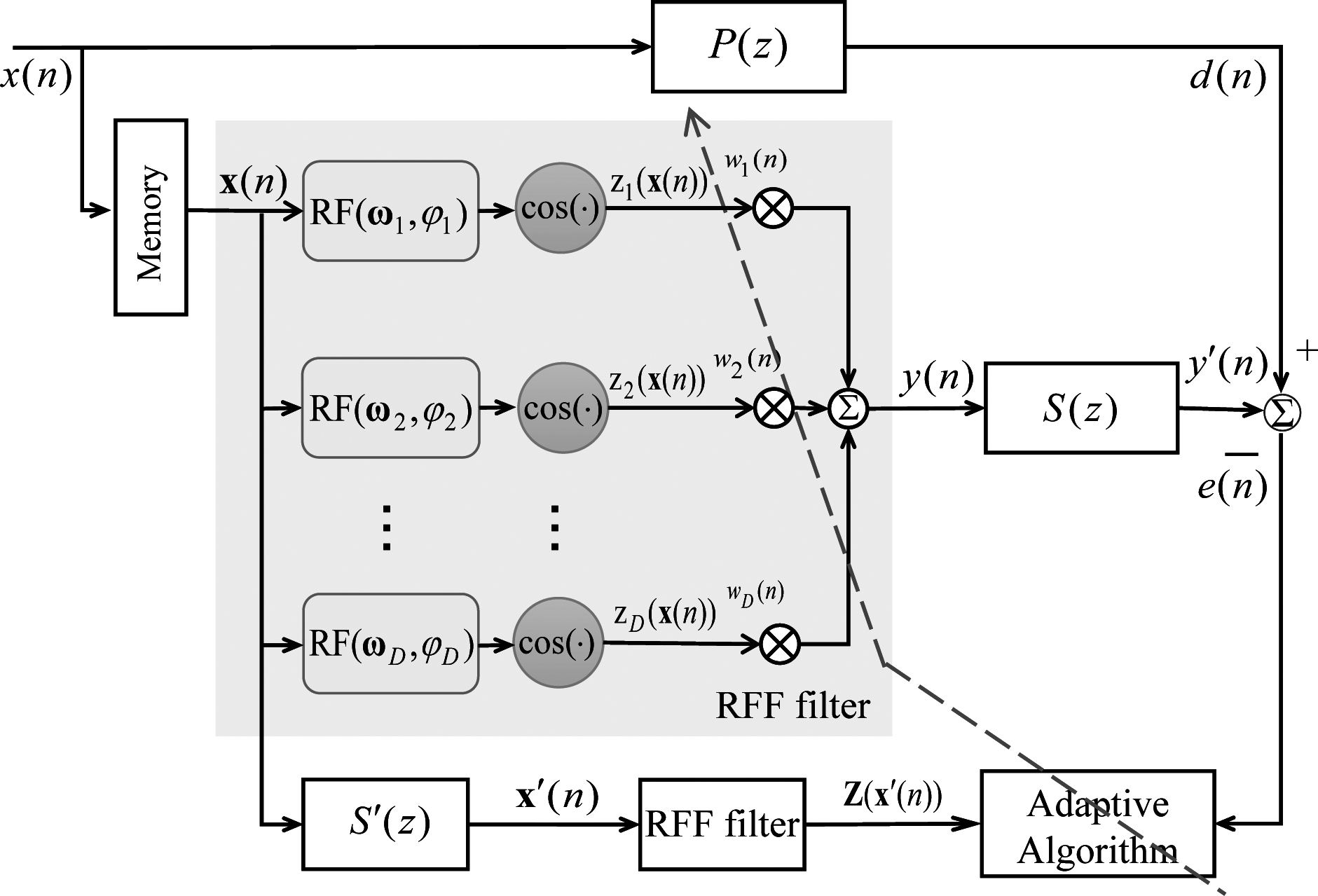
图2 基于RFF滤波器的单通道非线性主动噪声控制的系统框图
Fig.2 The block diagram of Single channel NANC based on KAFs
基于最小均方误差准则,控制自适应滤波器权值系数更新的RFF-KFxLMS算法的代价函数为:
ζ=E[e2(n)]
(15)
滤波器权值向量使用梯度下降法进行更新,当前时刻n的梯度向量为 ξ,
ξ,
![]()
(16)
则滤波器的权值更新公式如下所示
w(n)=w(n-1)+μe(n-1)z(x′(n-1))
(17)
其中x′(n)=s(n)*x(n) 。
4 仿真验证
为验证所提出的非线性算法的有效性,考虑噪声通道存在非线性失真的情况,本节在不同情况的噪声环境下进行仿真。本节将提出的RFF-KFxLMS算法与已有的VFxLMS算法[5]、FsLMS算法[6]、KFxLMS算法[13]进行对比。非线性的噪声主通道由以下三阶多项式建模:
d(n)=u(n-2)+0.08*u2(n-2)-
0.04*u3(n-2)
(18)
其中u(n)为输入信号x(n)经过有限脉冲响应滤波器Q(z),Q(z)=z-3-0.3z-4+0.2z-5。
采用平均噪声余量(Average Noise Reduction, ANR)评估算法的性能,定义如下:
(19)
其中Ae(n)=θAe(n-1)+(1-θ)|e(n)|,Ad(n)=θAd(n-1)+(1-θ)|d(n)|;遗忘因子θ=0.999。仿真结果取30次蒙特卡罗平均值。
4.1 参数讨论
为进一步研究D的取值对于算法性能的影响,本节定性的分析了不同D值的条件下对随机傅里叶变换近似程度的影响。算法的核宽度参数默认为ε=0.5,实验采用D维随机傅里叶特征的内积〈z(x),z(0)〉来近似高斯核函数κ(x,0),维数分别取(a) D=100,(b) D=500,(c) D=1000,(d) D=5000。如图3所示,随机傅里叶特征的内积近似高斯核的偏差随着D的增大而减小,且在D取1000时可以获得较好的估计效果。然而,较大的D值在提高的滤波精度的同时会增加计算量。一味的提高D值并不总能够提高滤波精度,图4为不同D值条件下的稳态ANR和单次运行消耗时间曲线,其中稳态ANR通过对最后200次迭代进行平均得到。可以看出,D的增加可以提高滤波精度,但代价是计算时间的增加。当D大于300时,稳态ANR的变化逐渐趋于平稳,而计算时间近乎正比例上升。因此,为了平衡精度和计算成本,在以下实验中D取500。
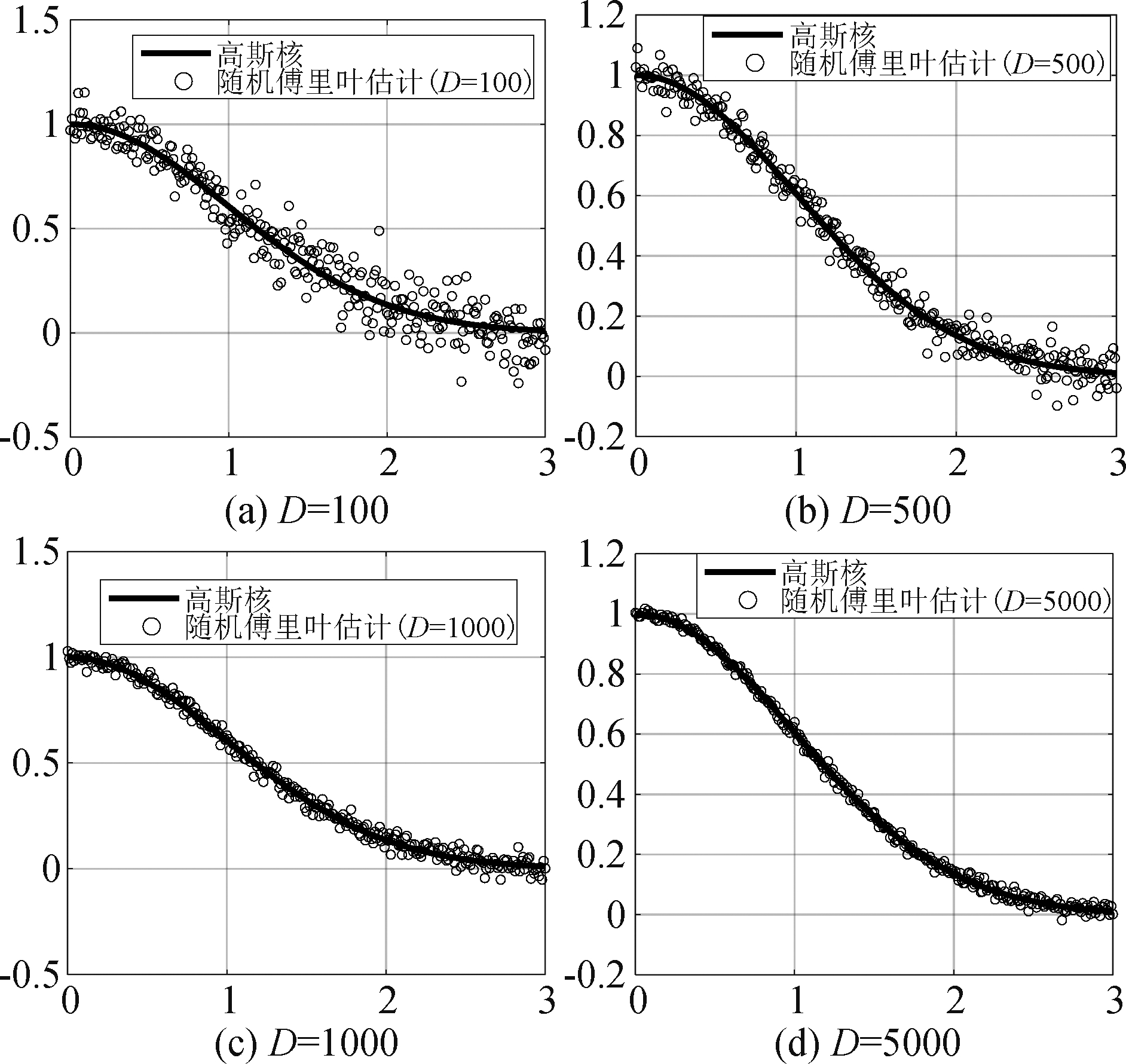
图3 高斯核的随机傅里叶特征(RFF)内积近似。曲线显示了精确的高斯函数;散点图显示了D取不同值时的近似程度
Fig.3 Qualitative view of the random Fourier feature (RFF) inner product approximation of the Gaussian kernel. The black curve shows the exact Gaussian function. The scatter plot shows the approximation, for different values of D

图4 RFF-KFxLMS算法在不同D取值条件下的稳态平均噪声余量与平均单次运行消耗时间
Fig.4 The steady-state ANR and mean consumed time of RFF-KFxLMS algorithm under different D values
4.2 实验一
本实验采用500 Hz,采样频率为8000采样点/秒的正弦波作为输入信号,即
(20)
其中ν(n)为信噪比为40 dB的高斯白噪声。
系统的噪声通道传递函数如等式(18)所示,次级通道的传递函数设置为:
(21)
单一正弦波噪声输入情况下的平均噪声余量对比如图5所示。图中横坐标表示迭代次数,实验迭代次数共5000次,纵坐标表示平均噪声余量以衡量算法对噪声的控制效果。随着迭代次数的增加,算法在2000次迭代后逐渐达到稳态。可以明显的看出在该实验条件下,对比算法都能够收敛,而VFxLMS算法的控制能力较弱。FsLMS算法、KFxLMS算法与本文所提出的算法控制效果接近,ANR都能够接近-30 dB。此外,算法的平均单次运行消耗时间的对比如表1所示。FsLMS算法的计算耗时最少,单次运行仅需0.11 s。KFxLMS算法单次运行需要达到11.759 s。而本文提出的算法单次运行耗时2.526 s,大幅减轻了KFxLMS算法的计算负担,降低了算法的实际应用成本。
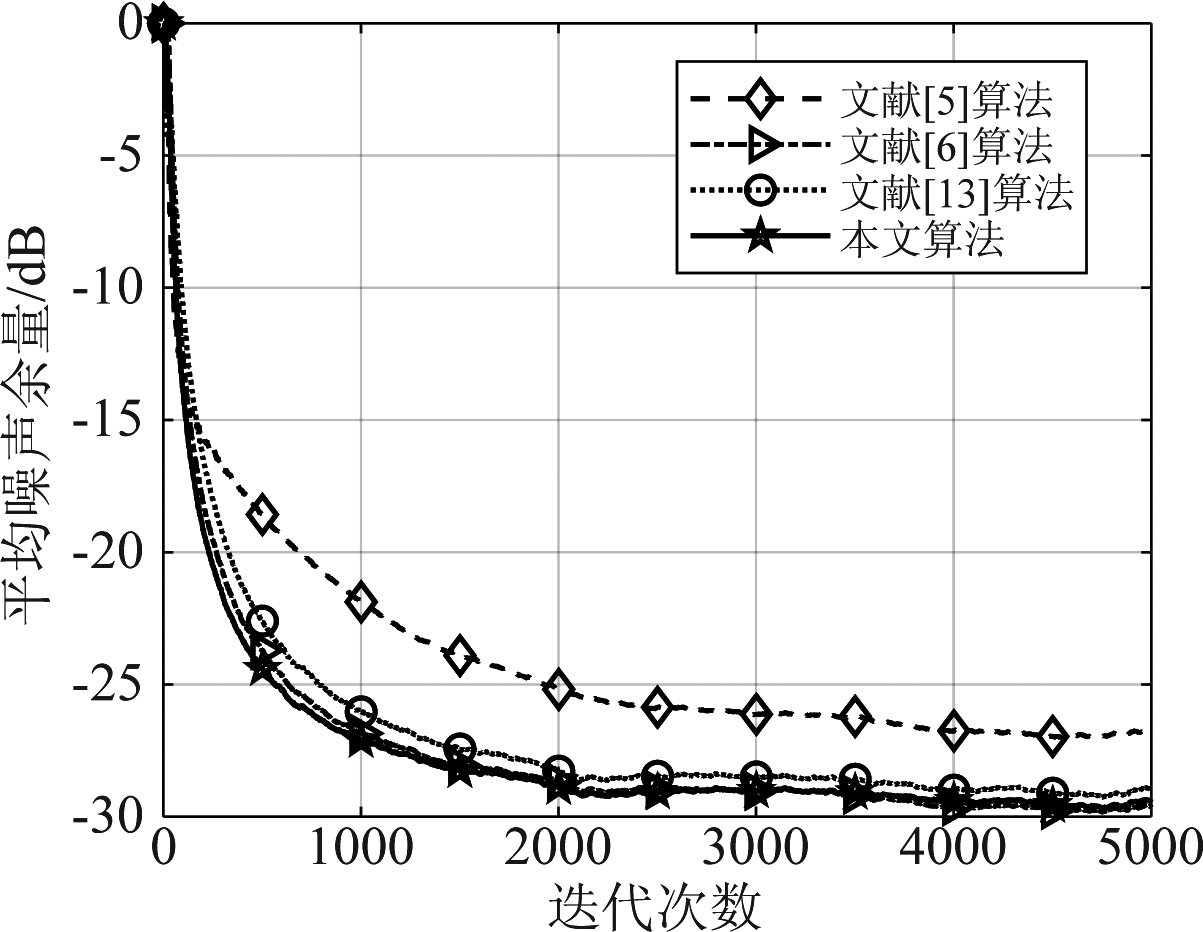
图5 单一正弦波噪声输入情况下的平均噪声余量对比图
Fig.5 Comparison curves of the ANR under sinusoidal noise input
表1 迭代次数5×103的平均单次运行消耗时间
Tab.1 Comparison of averaged consumed time over 5×103 iterations

算法平均单次运行消耗时间/sVFxLMS算法[5]0.746FsLMS算法[6]0.110KFxLMS算法[13]11.759RFF-KFxLMS算法2.526
4.3 实验二
本实验采用包含三个频率分量的正弦噪声作为参考信号。噪声的表达式如下:
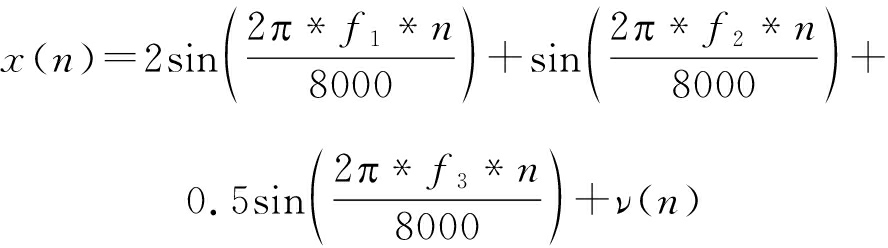
(22)
其中ν(n)为信噪比为40 dB的加性高斯白噪声。
三组包含不同频率分量的正弦噪声波形分别如图6所示。其中图6(a)所示信号的频率分量为f1=160 Hz、 f2=320 Hz、 f3=480 Hz;图6(b)对应的频率分量为f1=250 Hz、 f2=500 Hz、 f3=750 Hz;图6(c)对应的频率分量为f1=400 Hz、 f2=800 Hz、 f3=1200 Hz。
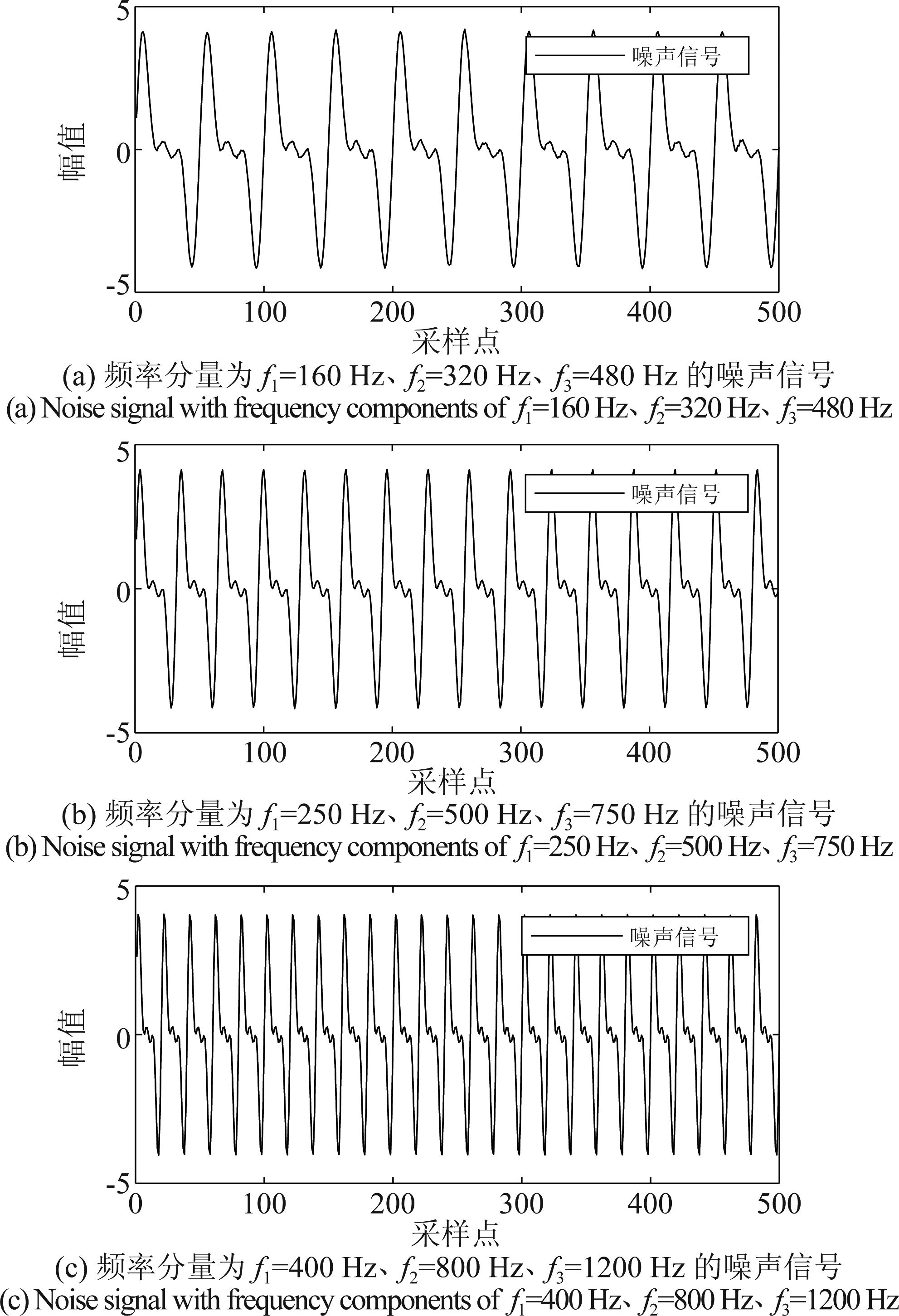
图6 三组包含三个频率分量的正弦噪声信号
Fig.6 Three sinusoidal noise signals containing different frequency components
采用与实验一相同的系统条件,非线性主通道模型如等式(18),次级通道的传递函数如等式(21)所示。图7显示了噪声频率为f1=160 Hz、 f2=320 Hz、 f3=480 Hz时算法的平均噪声余量对比,可以看到在该条件下采用VFxLMS算法与FsLMS算法的ANR在-15 dB左右,而KFxLMS算法以及提出的算法在接近稳态时可以达到-30 dB。可见采用核方法的控制算法的效果较普通算法有着明显的性能优势。参考噪声包含频率分量f1=250 Hz、 f2=500 Hz、 f3=750 Hz的算法对比如图8所示,在该噪声条件下本文提出的算法较收敛曲线对比的稳态误差更小,即能够达到更佳的控制效果。图9显示了在参考噪声频率分量为f1=400 Hz、 f2=800 Hz、 f3=1200 Hz情况下的收敛曲线对比,直观体现了提出的算法的性能提升。与VFxLMS算法相比噪声控制效果提升了约25 dB,与FsLMS算法相比提升了10 dB,且较KFxLMS算法提升了4 dB。
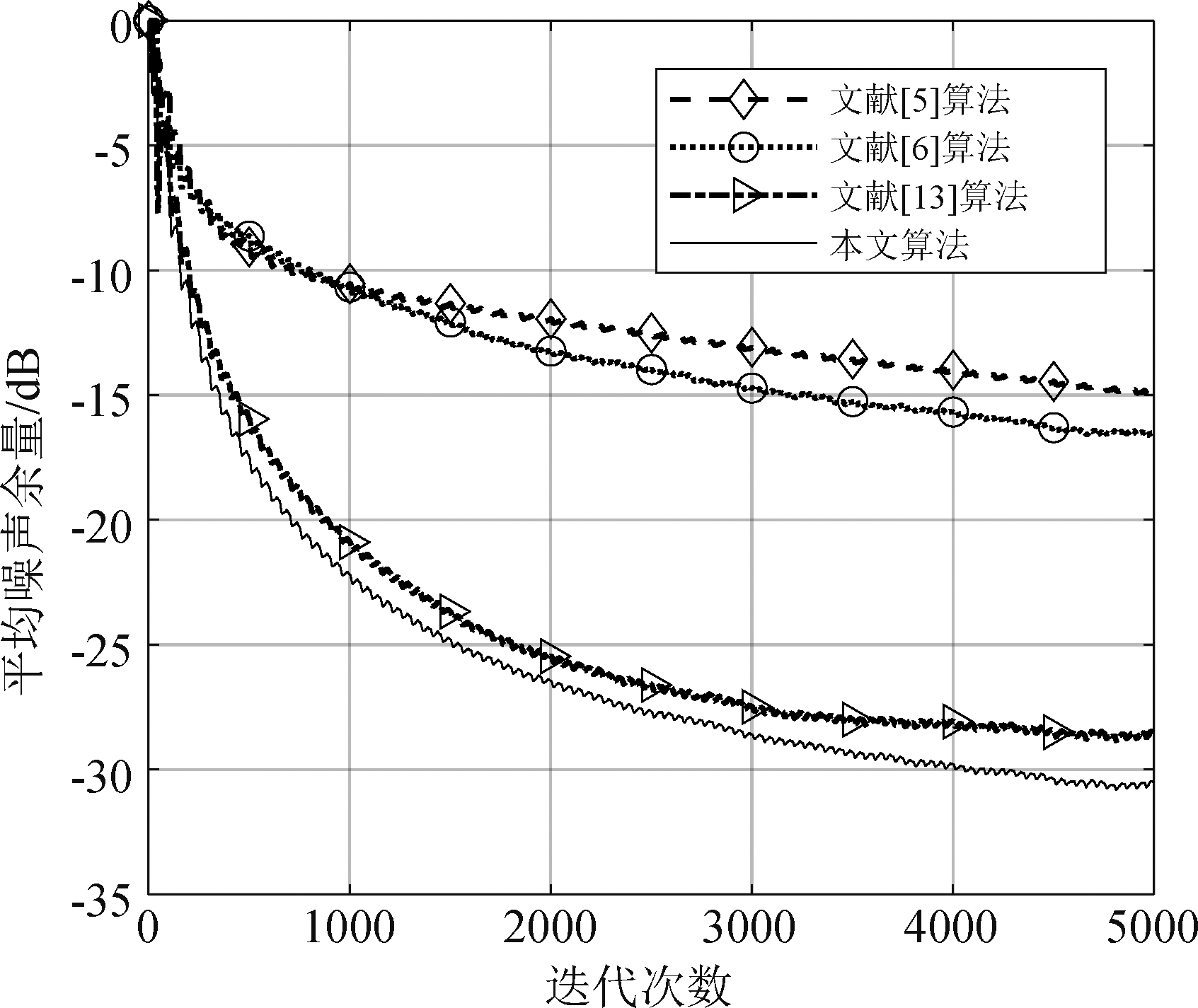
图7 参考噪声频率分量为f1=160 Hz、 f2=320 Hz、f3=480 Hz下各算法的平均噪声余量收敛曲线对比
Fig.7 Comparison curves of the ANR under Noise signal with frequency components of f1=160 Hz、 f2=320 Hz、 f3=480 Hz
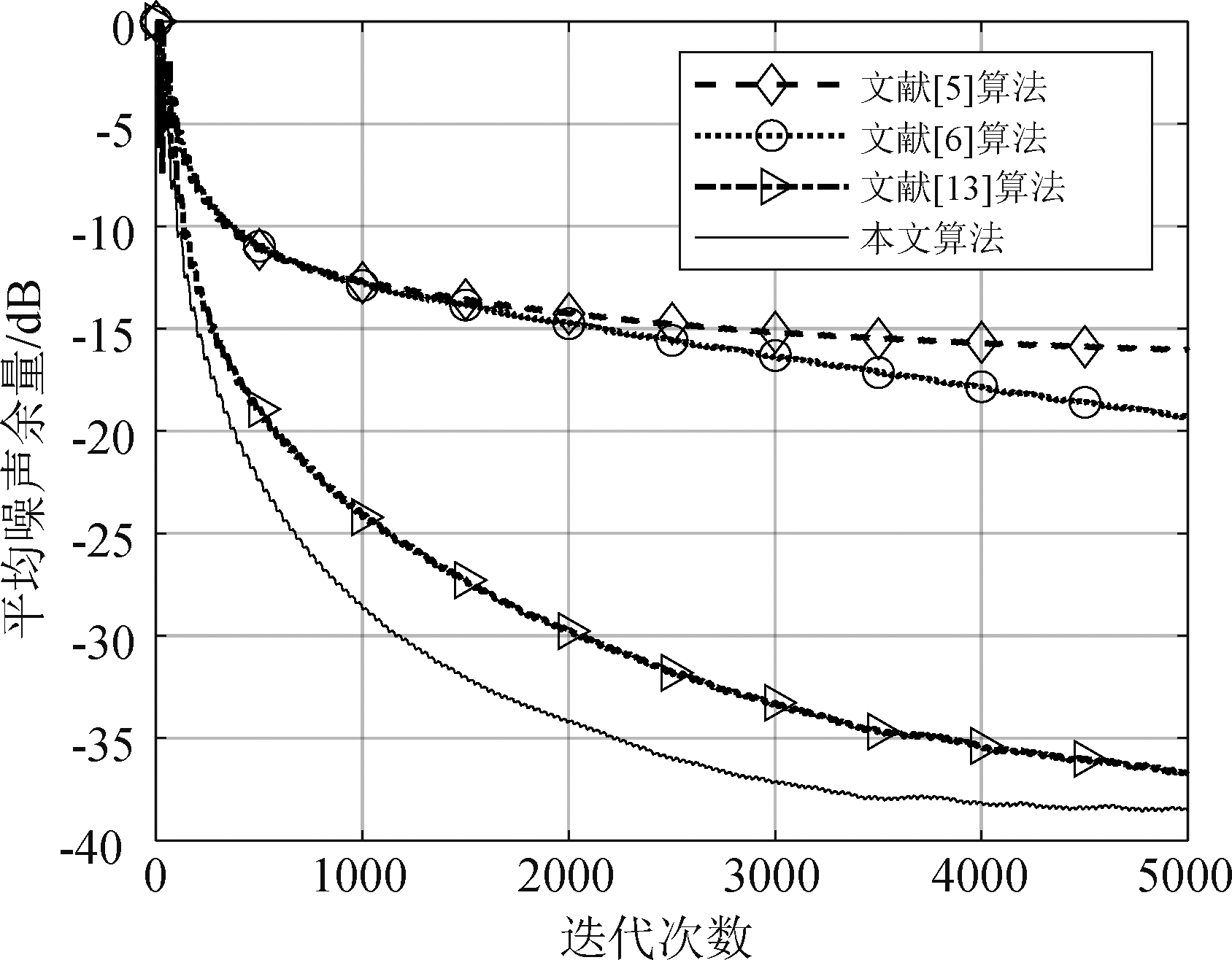
图8 参考噪声频率分量为f1=250 Hz、 f2=500 Hz、f3=750 Hz下各算法的平均噪声余量收敛曲线对比
Fig.8 Comparison curves of the ANR under Noise signal with frequency components of f1=250 Hz、 f2=500 Hz、 f3=750 Hz
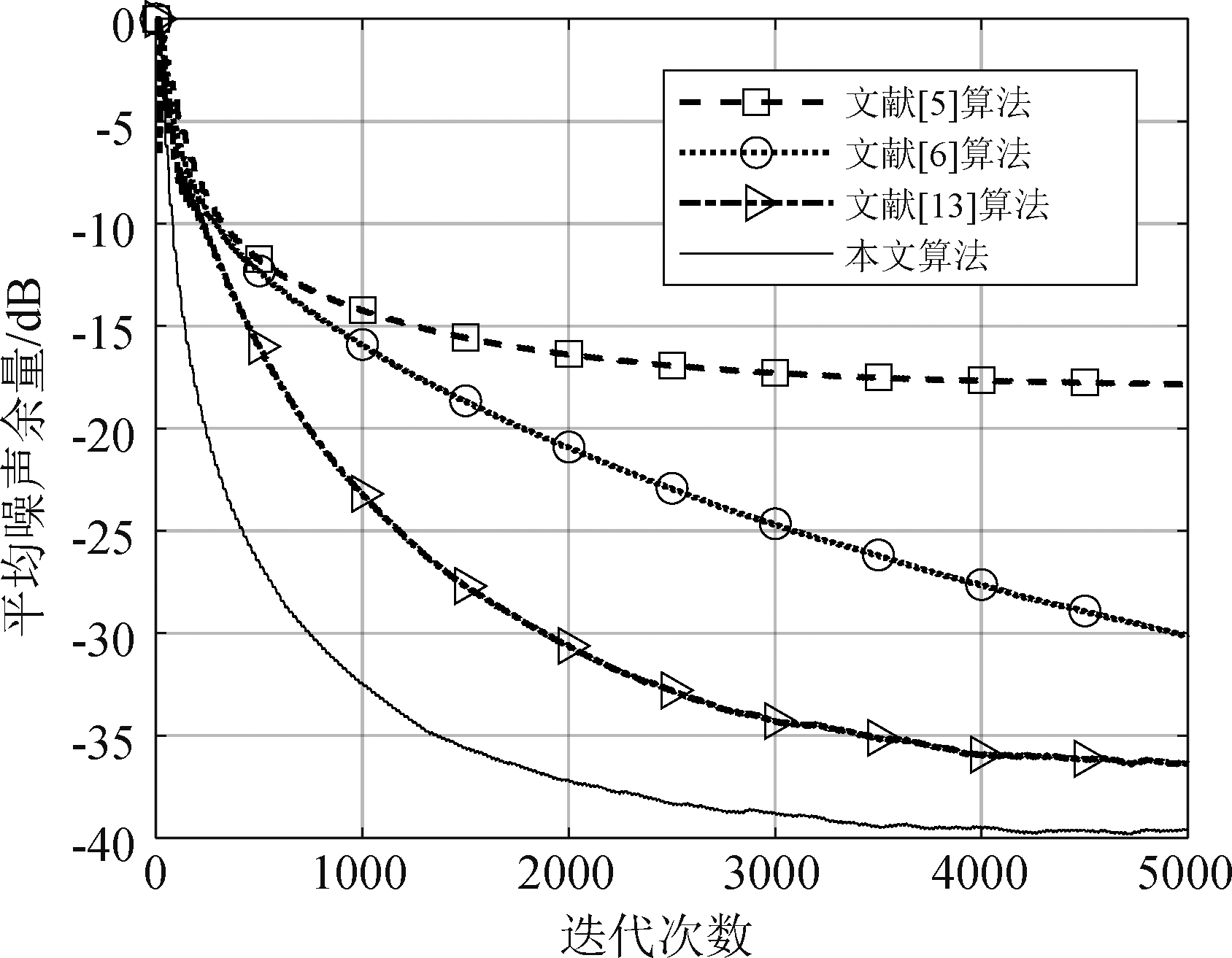
图9 参考噪声频率分量为f1=400 Hz、 f2=800 Hz、f3=1200 Hz下各算法的平均噪声余量收敛曲线对比
Fig.9 Comparison curves of the ANR under Noise signal with frequency components of f1=400 Hz、 f2=800 Hz、 f3=1200 Hz
4.4 实验三
上述两个实验的参考信号为人工的仿真噪声,为进一步验证算法对于实际噪声下的性能,本节采用实际噪声进行实验。实际噪声在嘈杂的餐厅中录制获得,其波形如图10所示。非线性主通道模型见等式(18),次级通道的传递函数见等式(21)。图11显示了参考噪声为实际噪声时算法的平均噪声余量对比,可以看到在噪声信号为实际采样噪声的情况下,提出的算法能够有较好的控制效果,尤其是较KFxLMS算法的平均噪声余量有5 dB左右的降低。从本次实验的结果来看,提出的RFF-KFxLMS 算法与几种现存典型的非线性控制算法相比控制效果非常可观。不仅如此,本文提出的RFF-KFxLMS算法的计算复杂度与KFxLMS算法相比要低的多,这意味着该算法的进一步改进与应用会更容易实现。
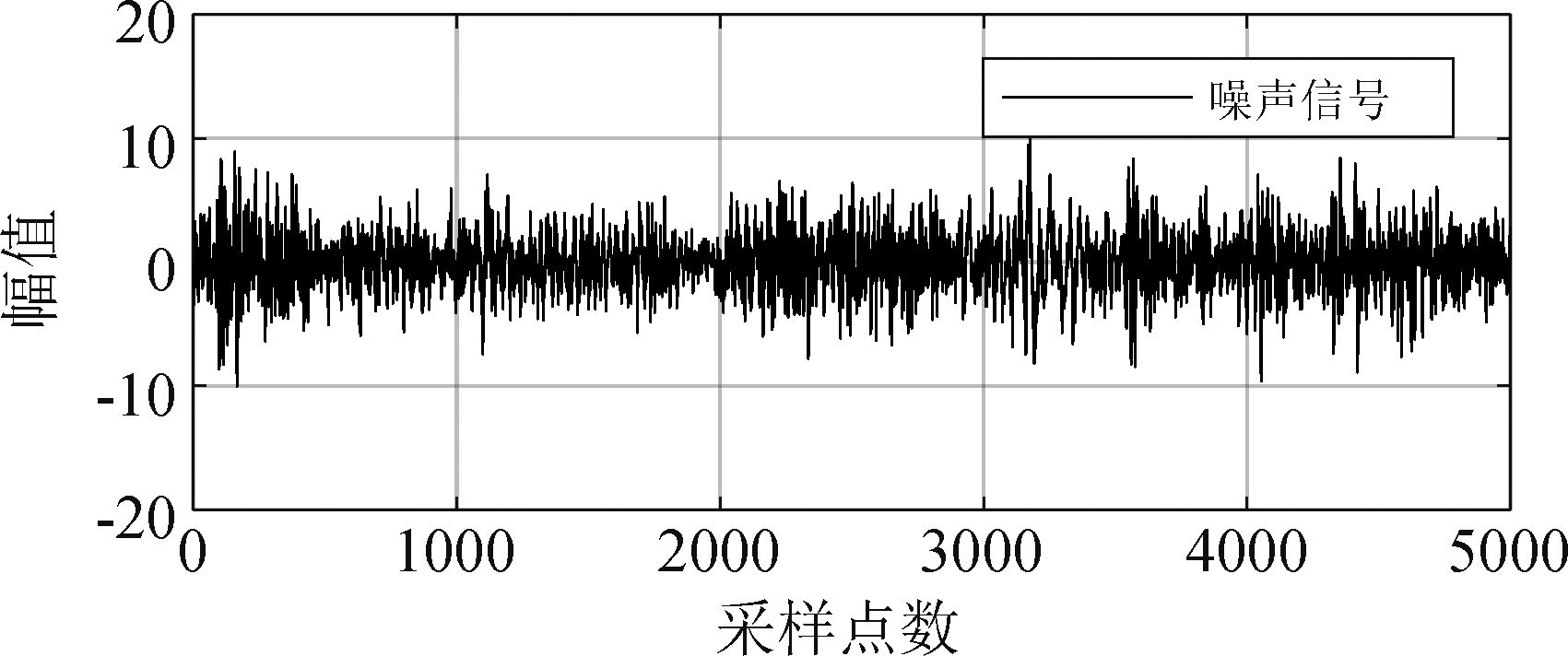
图10 参考噪声波形
Fig.10 Waveform of the real noise signal
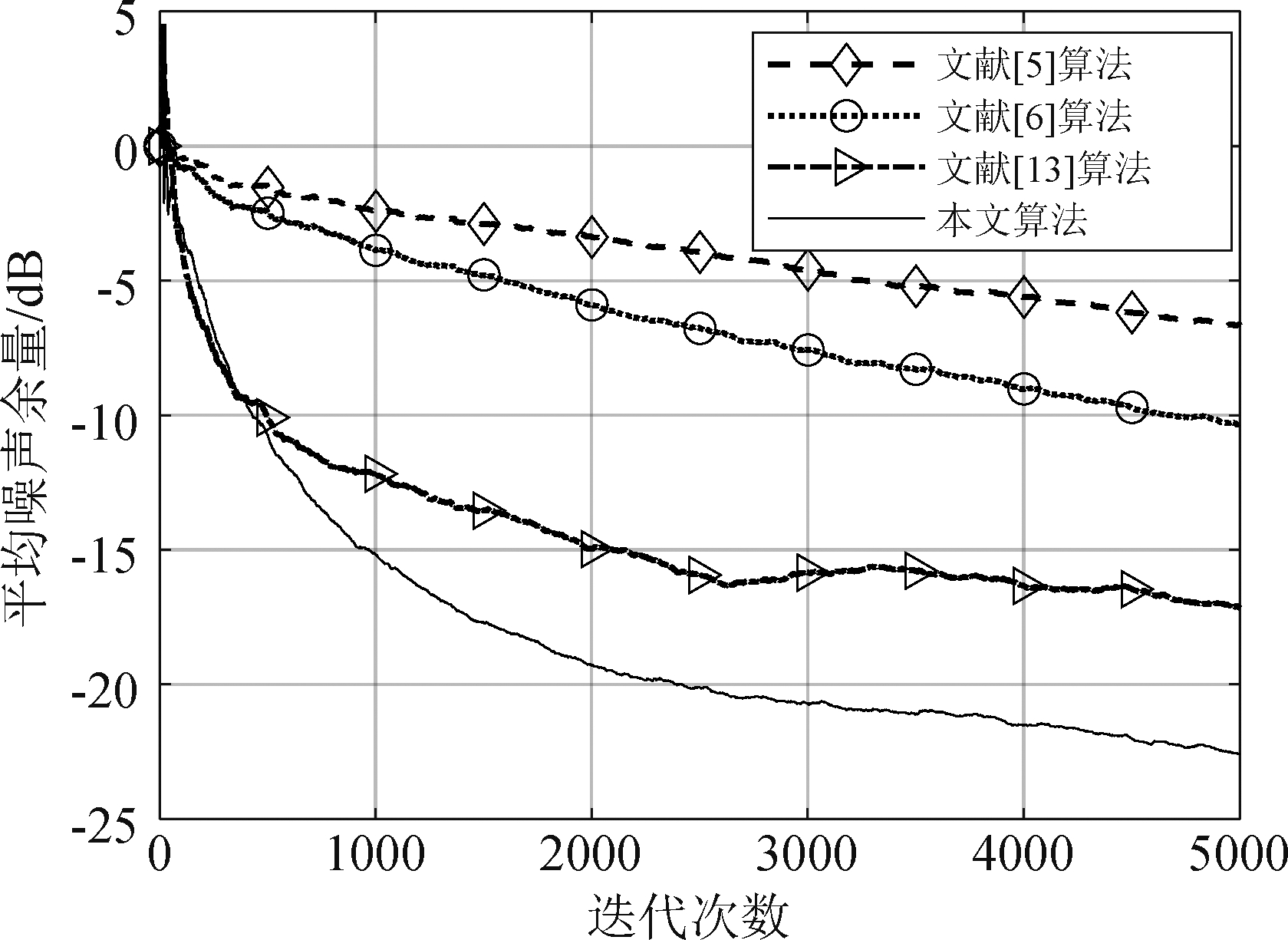
图11 参考噪声为实际噪声时各算法的平均噪声余量收敛曲线对比
Fig.11 Comparison curves of the ANR under real noise signal
5 结论
本文针对非线性的主动噪声控制系统,提出了一种基于随机傅里叶变换的非线性控制算法RFF-KFxLMS算法。该算法将采样后的输入噪声信号进行随机傅里叶变换映射至有限维的随机傅里叶特征空间,再通过自适应滤波器得到次级声源达到噪声抵消的目的。与基于核方法的KFxLMS算法相比,当前时刻的滤波器权向量的求取需要过去所有时刻的数据。本文提出的RFF-KFxLMS算法将输入信号显式地变换到高维RFFS,仅需要当前时刻的数据即可完成自适应滤波器的权值更新,极大的减轻了核方法的计算负担。此外,通过仿真对比实验,验证了提出的算法较已有算法对噪声的控制效果更佳。
[1] Leug P. Process of silencing sound oscillations[P]. US Patent: 2043416, 1936-09-06.
[2] Martin V, Gronier C. Minimum attenuation guaranteed by an active noise control system in presence of errors in the spatial distribution of the primary field[J]. Journal of Sound & Vibration, 1998, 217(5): 827- 852.
[3] Zhao Tong, Liang Jiabi, Zou Liang, et al. A New FXLMS Algorithm With Offline and Online Secondary-Path Modeling Scheme for Active Noise Control of Power Transformers[J]. Industrial Electronics, IEEE Transactions on, 2017, 64(8): 6432- 6442.
[4] Cheer J, Daley S. An Investigation of Delayless Subband Adaptive Filtering for Multi-Input Multi-Output Active Noise Control Applications[J]. Audio, Speech, and Language Processing, IEEEACM Transactions on, 2017, 25(2): 359-373.
[5] Tan Li, Jiang J. Filtered-X second-order Volterra adaptive algorithms[J]. Electronics Letters, 1997, 33(8): 671- 672.
[6] George N V, Panda G. A robust filtered-s LMS algorithm for nonlinear active noise control[J]. Applied Acoustics, 2012, 73(8): 836- 841.
[7] Liu Weifeng, Pokharel P P, Principe J C. The Kernel Least-Mean-Square Algorithm[J]. IEEE Transactions on Signal Processing, 2008, 56(2): 543-554.
[8] Chen Jie, Gao Wei, Richard C, et al. Convergence analysis of kernel LMS algorithm with pre-tuned dictionary[C]∥2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). Florence, 2014: 7243-7247.
[9] Pulido M, Van Leeuwen P J, Posselt D J, et al. Kernel Embedded Nonlinear Observational Mappings in the Variational Mapping Particle Filter[C]∥International Conference on Computational Science. Springer, Cham, 2019: 141-155.
[10] Tan Weiqiang, Matthaiou M, Jin Shi, et al. Spectral Efficiency of DFT-Based Processing Hybrid Architectures in Massive MIMO[J]. IEEE Wireless Communications Letters, 2017, 6(5): 586-589.
[11] Gil-Cacho J M, Waterschoot T V, Moonen M, et al. Nonlinear acoustic echo cancellation based on a parallel-cascade kernel affine projection algorithm[C]∥IEEE International Conference on Acoustics, Speech & Signal Processing. IEEE, 2012.
[12] Bao Hua, Panahi I M S. Active Noise Control based on Kernel Least-Mean-Square algorithm[C]∥2009 Conference Record of the Forty-Third Asilomar Conference on Signals, Systems and Computers, 2009: 642- 644.
[13] Liu Yuqi, Sun Chao, Jiang Shouda. Kernel Filtered-x LMS Algorithm for Active Noise Control System with Nonlinear Primary Path[J]. Circuits Systems & Signal Processing, 2018, 37(3): 5576-5594.
[14] Rahimi A, Recht B. Random Features for Large-Scale Kernel Machines[C]∥Proceedings of the 20th International Conference on Neural Information Processing Systems. Vancouver, British Columbia, Canada: Curran Associates Inc., 2007: 1177-1184.
[15] Bliek L, Verstraete H R, Verhaegen M, et al. Online Optimization With Costly and Noisy Measurements Using Random Fourier Expansions[J]. IEEE Transactions on Neural Networks, 2018, 29(1): 167-182.
[16] Gaur S, Gupta V K. A review on filtered-x LMS algorithm[J]. International Journal of Signal Processing Systems, 2016, 4(2): 172-176.

