1 引言
随着工业的不断发展,噪声的污染也越来越多,从而造成了一些机械设备的损坏以及影响人们的生活。因此,消除或减少噪声的影响是非常重要的。主动噪声控制(active noise control,ANC)是一种众所周知的抑制噪声的技术[1]。该技术基于叠加原理,也就是说,噪声可以被振幅相同但相位相反的另一种噪声抵消。由于其在低频噪声控制应用中的潜在用途,它已经受到越来越多的关注[2-3]。自适应滤波算法在主动噪声控制中起着关键作用,其中最受欢迎的自适应滤波算法之一是滤波x最小均方(filtered-x least mean square,FxLMS)算法,由于其结构简单,易于在ANC系统中实现[4- 6]。
在过去的几十年中,ANC取得了很大的进步,但实际应用有限,其中一个重要的挑战来自于脉冲噪声的控制。实际上,脉冲噪声的产生通常具有低概率、幅值大的特性。为了消除脉冲噪声,人们专门研究了一些针对脉冲噪声的ANC技术[7-13]。1995年,Leahy等人提出了以误差信号的分数阶为代价函数(目标函数)的滤波x最小均方p范数(filtered-x least mean p-norm, FxLMP)算法[7],但是,它需要知道噪声的先验知识才能选择参数。后来,Wu等人开发了滤波x对数误差最小均方算法(filtered-x logarithmic error least mean square, FxlogLMS)算法[10],该算法克服了基于幅度阈值的方法的缺点,并且不需要任何先验知识或噪声估计。2012年,George和Panda基于功能链接人工神经网络的自适应控制器设计了一种鲁棒的滤波s最小均方算法(robust filtered-s least mean square, RFsLMS)算法[12]并使用在非线性ANC系统中,该算法对高斯噪声和非高斯噪声具有相似的效率水平。为了发展一种性能好的自适应算法,最大相关熵准则(maximum correntropy criterion,MCC)通常被用作代价函数。最近,Kurian等人提出了一种基于最大相关熵准则的代价函数滤波s最大相关熵准则(filtered-s maximum correntropy criterion, FsMCC)算法[13], 该算法显示好的降噪性能和收敛速度在非线性ANC系统中。
然而,传统的相关熵具有单一的高斯核。在许多实际问题中,数据属性在特征空间中的分布往往是不同的、异常的、非平坦的,因此我们考虑将不同类型的核函数组合在一起以获得更好的结果[14]。2018年,Chen等人提出了最大混合相关熵准则(maximum mixture correntropy criterion,MMCC)[15],一个混合熵使用两个不同核参数的高斯核的准则。然而,不同的内核有不同的属性。当面对更复杂的数据,特别是那些对核参数不敏感的数据时,单个高斯核函数可能是不够的。因此,本文的目的是将最大混合相关熵准则使用到ANC系统中去处理脉冲噪声信号,并通过计算机仿真来评估该算法的收敛速度和降噪性能。
2 提出的算法
2.1 ANC模型
如图1所示是单通道前馈ANC系统框图,其中x(n)是参考信号,它由靠近噪声源的参考传感器采样得到的,d(n)是需要消除的初级噪声,P(z)表示主通道传递函数,S(z)是次级通道的传递函数,W(z)是ANC控制器(自适应滤波器),y(n)是自适应滤波器的输出信号,y′(n)表示次级噪声,e(n)是残余噪声可以通过误差传感器观察得到。![]() 是次级通道S(z)的估计值可以使用离线或在线辅助路径建模技术并通过自适应滤波器来进行估计。
是次级通道S(z)的估计值可以使用离线或在线辅助路径建模技术并通过自适应滤波器来进行估计。
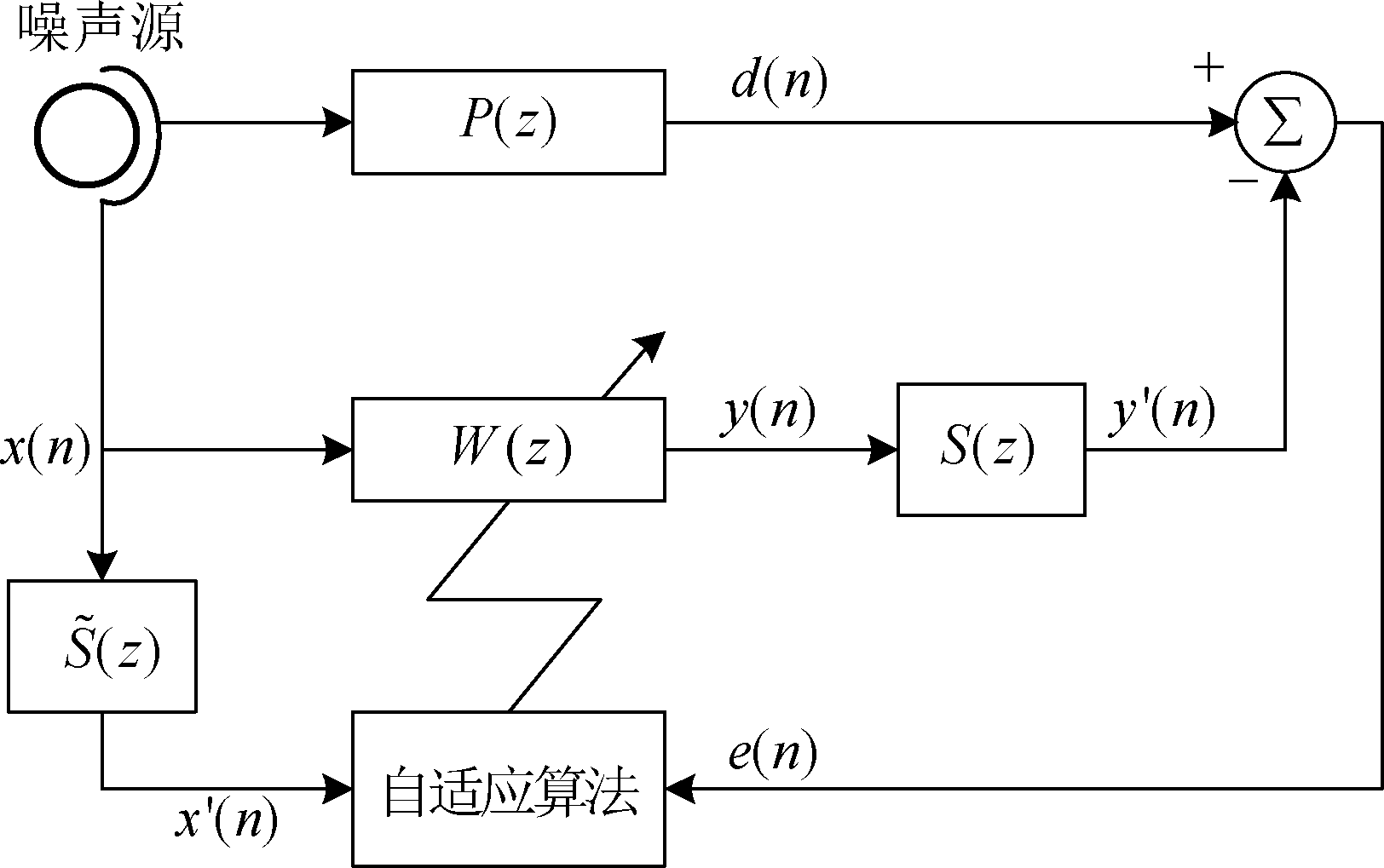
图1 单通道前馈ANC系统的框图
Fig.1 Block diagram of a single-channel feed-forward ANC system
自适应滤波器的输出信号y(n)为
y(n)=wT(n)x(n)
(1)
其中x(n)=[x(n),x(n-1),...,x(n-L+1)]T是参考信号向量,w(n)=[w0(n),w1(n),…,wL-1(n)]T是自适应滤波器的权重向量,L是滤波器长度。
残余噪声e(n)被计算为
e(n)=d(n)-y′(n)
(2)
其中d(n)=x(n)*p(n),y′(n)=y(n)*s(n),s(n)是S(z)的脉冲响应,*表示离散卷积运算符。
2.2 混合相关熵
在给出混合熵的定义之前,首先回顾一下相关熵的定义。熵是测量两个随机变量X和Y的一种相似度,被定义为
V(X,Y)=E[κ(X,Y)]
(3)
其中E[·]表示取均值操作,κ(X,Y)表示一个移位不变的Mercer核,给定随机变量X和Y的N个样本![]() 那么经验相关熵估算为:
那么经验相关熵估算为:
(4)
熵使用最广泛的核是以下高斯核:
(5)
其中e=X-Y,σ>0表示核宽度。
具体来说,混合熵定义为[15]:
M(X,Y)=E[λGσ1(e)+(1-λ)Gσ2(e)]
(6)
其中σ1和σ2是高斯函数Gσ1(·)和Gσ2(·)的核宽度,并且0≤λ≤1是混合系数,图2显示了不同λ的混合高斯函数的曲线,当λ=0或λ=1,它就是单一的高斯核。
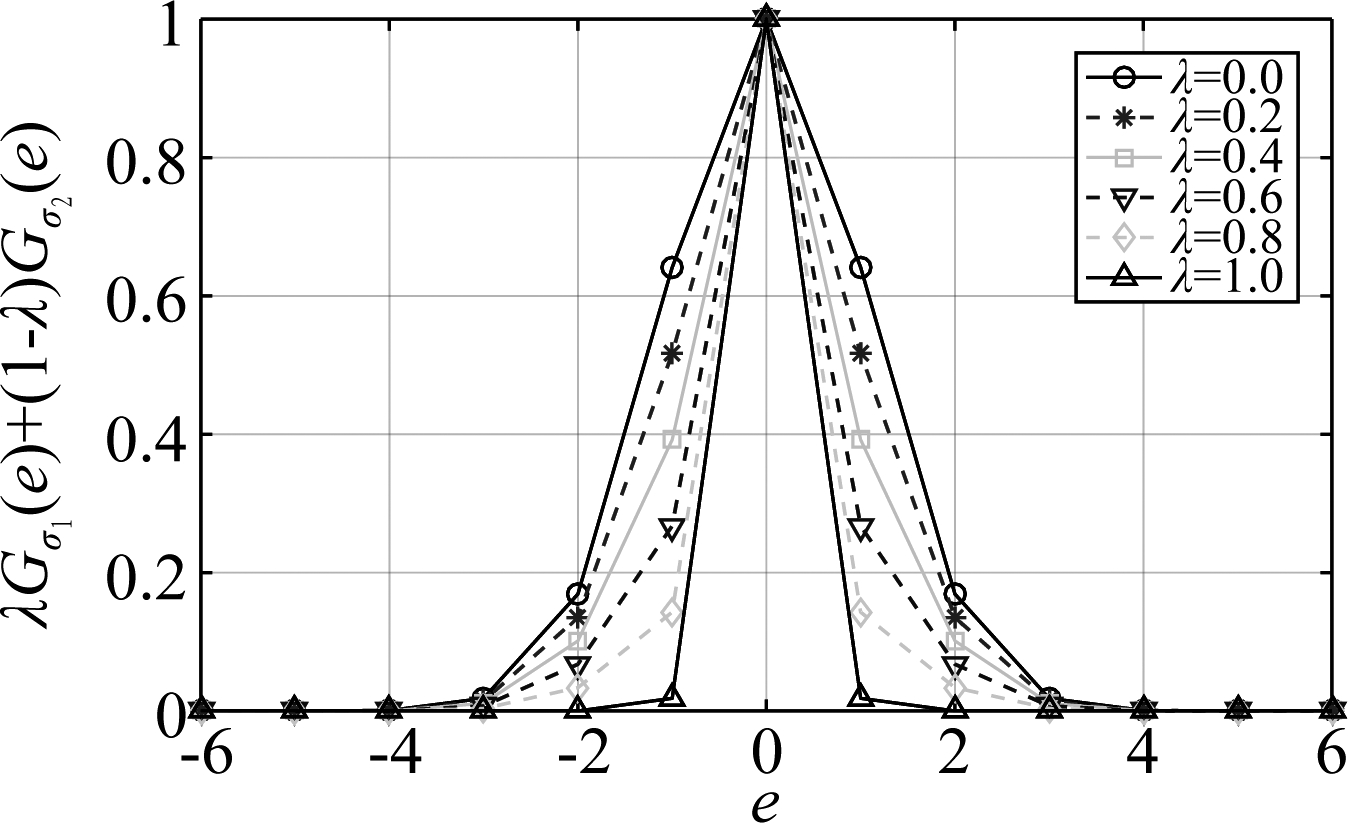
图2 具有不同λ的混合高斯函数(σ1=0.5,σ2=1.5)
Fig.2 Mixture Gaussian functions with different λ (σ1=0.5,σ2=1.5)
2.3 本文算法
由于传统的FxMCC算法的降噪性能易受到核宽度的取值的影响。为了提高单通道前馈ANC系统的降噪性能,本文采用最大混合相关熵准则,提出了滤波x最大混合相关熵准则(filtered-x maximum mixture correntropy criterion,FxMMCC)算法,为了方便阅读,本文算法被总结在表1中。
FxMMCC算法的代价函数由以下关系式给出[14]
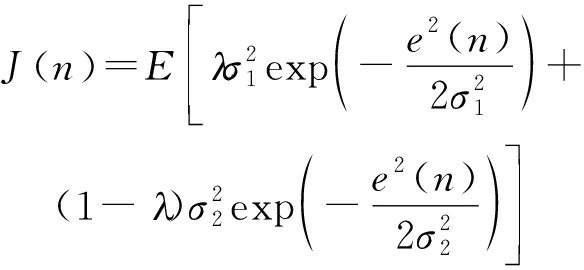
(7)
然后,FxMMCC算法的代价函数的瞬时梯度向量为
![]() =
=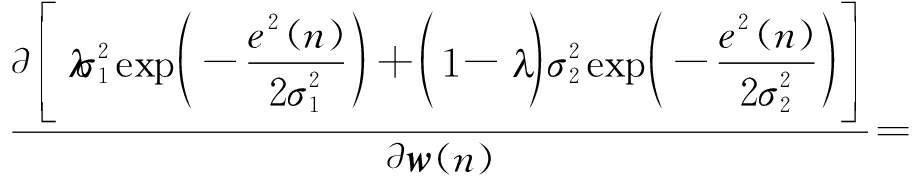
![]()
![]()
![]()
![]()
![]()
![]()
(8)
最后,本文提出的FxMMCC算法的权向量更新方程为
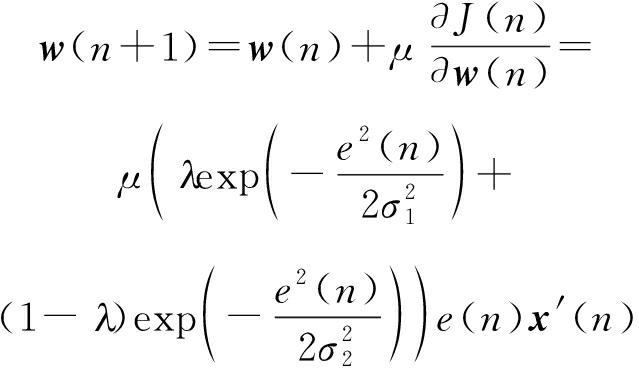
(9)
其中x′(n)=x(n)*s(n)是滤波后的输入向量;σ1是大的核宽度,σ2是小的核宽度,u为步长参数,λ是混合参数其取值为0~1,它主要控制算法的收敛速度和降噪性能。
注释1 当混合参数λ取值为0或1时,本文的FxMMCC算法可以变成为FxMCC算法[13],即
(10)
其中σ是核宽度,其取值规则为:核宽度σ取值越大,那么算法的收敛速度越快,但是算法的稳态误差就越高;与之相反,核宽度σ取值越小,那么算法的收敛速度越慢,但是算法的稳态误差就越低。
注释2 本文采用自动更新混合参数λ(n)来进一步完善算法的收敛性能,如下所示:
λ(n)=1-exp(-βe2(n))
(11)
其中β是大于零的调整参数,图3是取不同调整参数的λ(n)函数曲线图。该参数的取值主要依赖于脉冲噪声的强度,其选取准则如下:(1)在高的脉冲噪声下,稳态时残余噪声e(n)比较大,则选取较小的β值,从而可以得到较小的混合参数λ(n),那么小的核宽度σ2在公式(9)FxMMCC算法的权向量更新中,所占权重比较大,从而来降低稳态误差;(2)与之相反,在低的脉冲噪声下,稳态时残余噪声e(n)相对比较小,则选取较大的β值来提高算法的收敛速度。
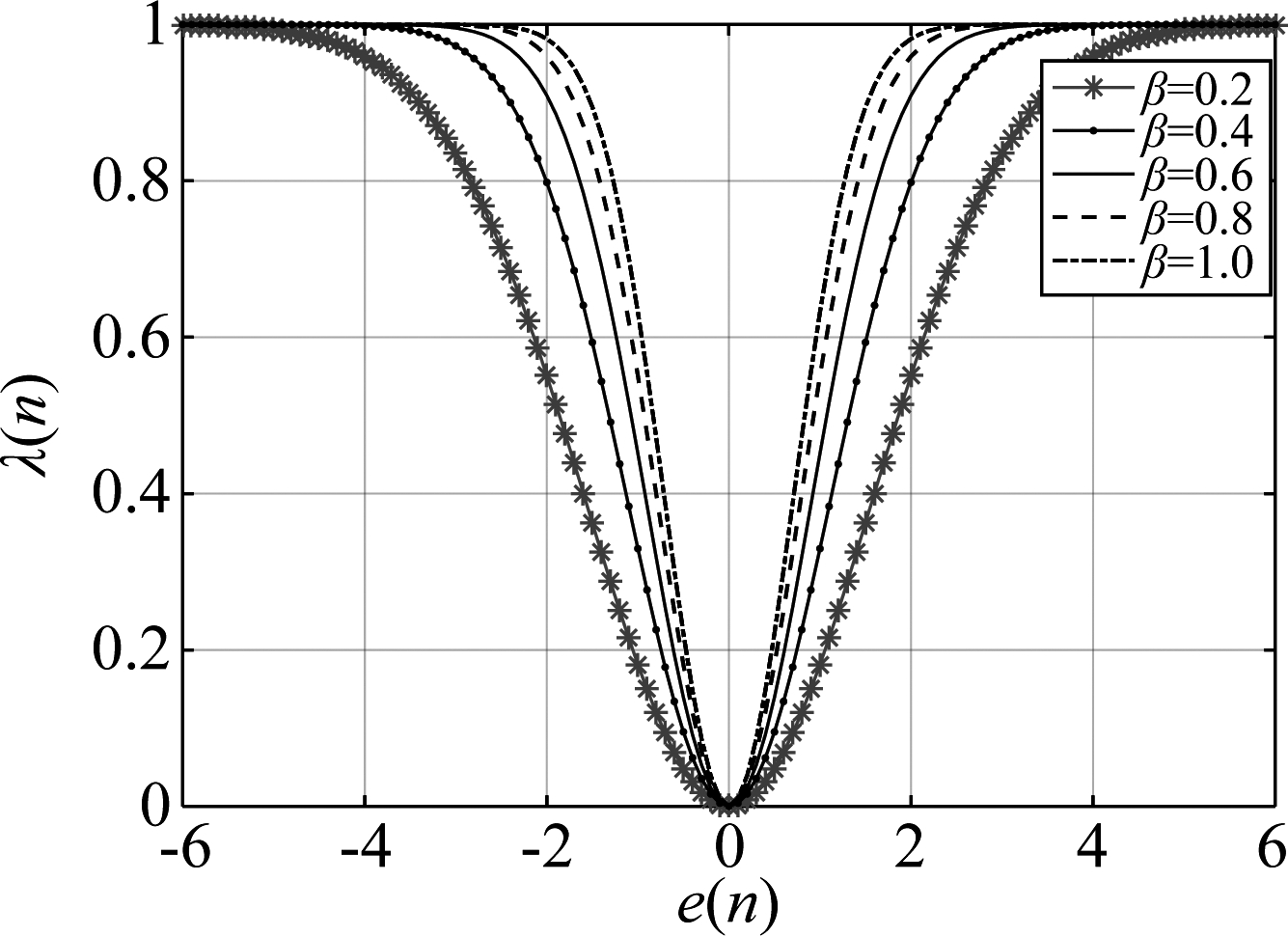
图3 具有不同β的混合参数曲线图
Fig.3 Mixture parameter curves with different β
表1 FxMMCC算法的伪代码
Tab.1 Pseudocode of FxMMCC algorithm

3 计算机仿真
为了评估本文算法的性能,假定自适应滤波器的长度为L=128,其中主通道P(z)和次级通道S(z)分别由长度为N=256和M=100的FIR滤波器建模,它们的频率响应如图4所示,平均噪声衰减量(averaged noise reduction, ANR)被定义为[16-18]
(12)
其中Ae(n)=ηAe(n-1)+(1-η)|e(n)|和Ad(n)=ηAd(n-1)+(1-η)|d(n)|具有初始值Ae(0)=0,Ad(0)=0并且η=0.999是遗忘因子。
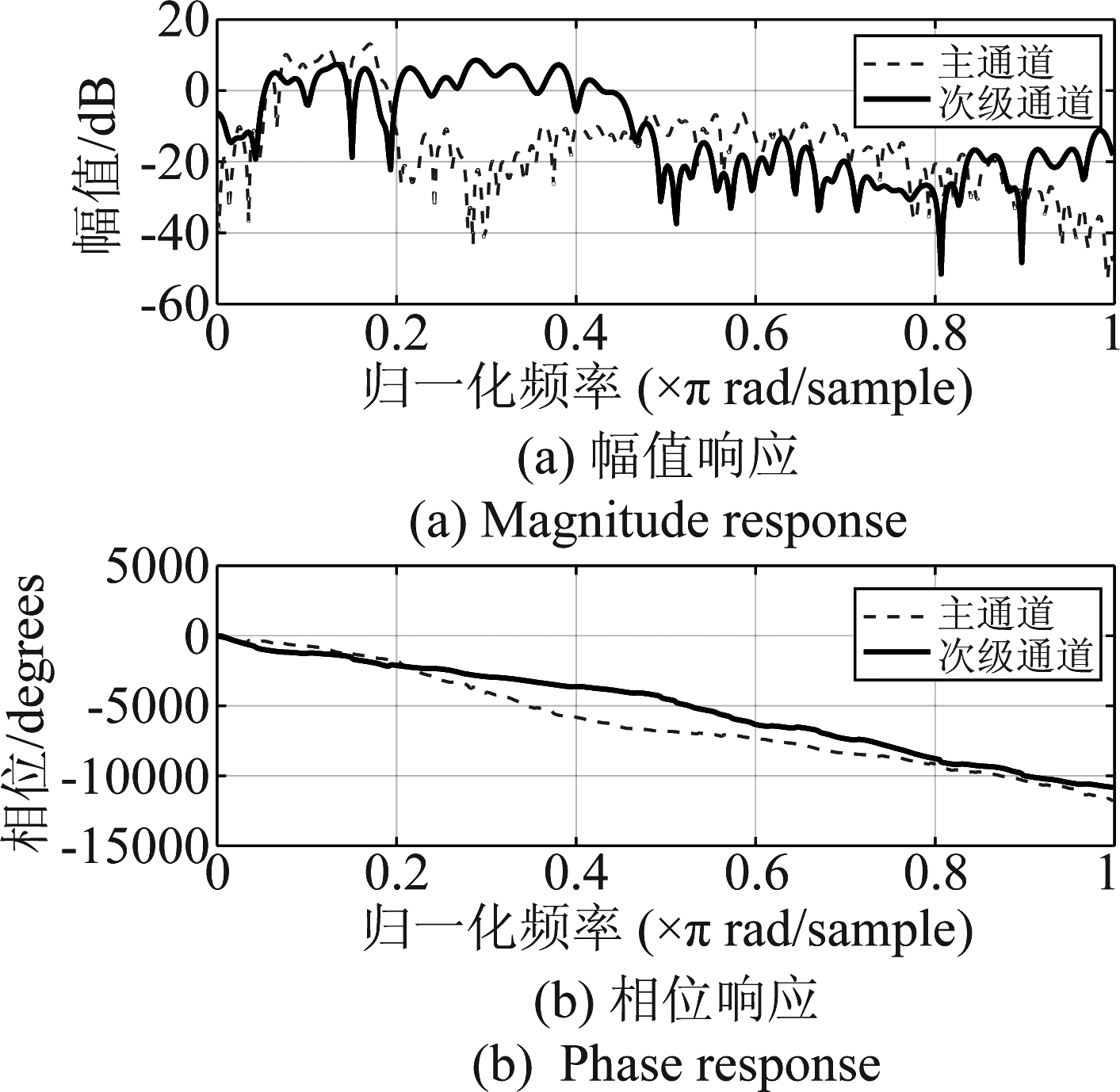
图4 计算机仿真中使用的主通道与次级通道的频率响应
Fig.4 Frequency response of primary and secondary paths used in computer simulations
在实际环境中,脉冲噪声通常是由于噪声干扰的发生概率较低,但幅度较大,因此可以通过稳定的非高斯分布来模拟脉冲噪声。在计算机仿真中脉冲噪声采用的是服从标准对称α稳定(symmetric α-stable,SαS)分布,它的概率密度函数f(x)通过其特征函数定义[16-17]
φ(t)=exp(-|t|α)
(13)
由图5可知,α值越大,噪声信号拖尾就越短,波峰越平滑,近似服从正态分布,代表噪声信号的冲击性较弱;相反,α值越小,噪声信号拖尾就越长,波峰越尖锐,代表噪声信号的冲击性较强。
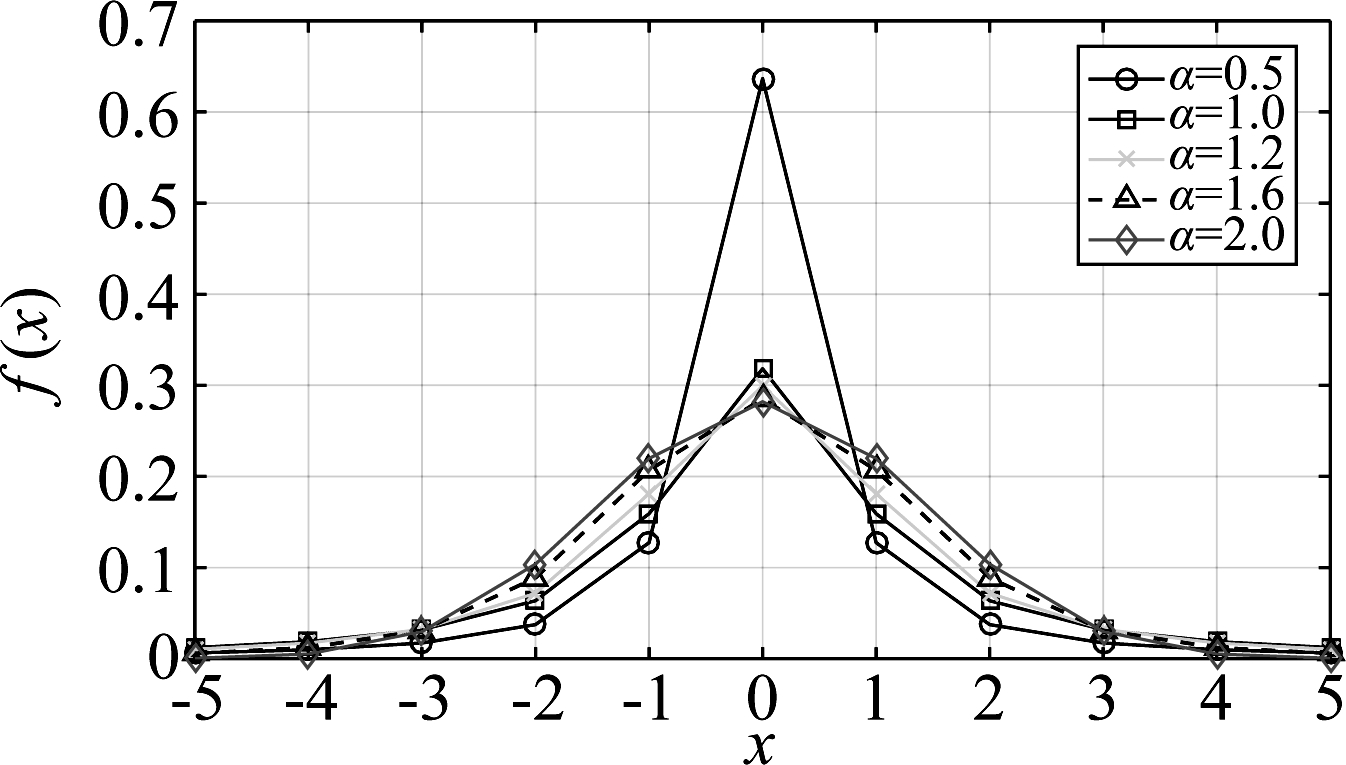
图5 对于不同α值时标准的SαS分布的概率密度函数
Fig.5 Probability density function of standard SαS distribution for different α values
3.1 例子1
如图6所示,计算机仿真分别取α=1.4和α=1.8服从标准的SαS分布的脉冲噪声来验证算法的性能。各算法的仿真曲线是独立运行100次后取平均获得的,其中σ1=3,σ2=1其余的仿真参数被设置在表2中。
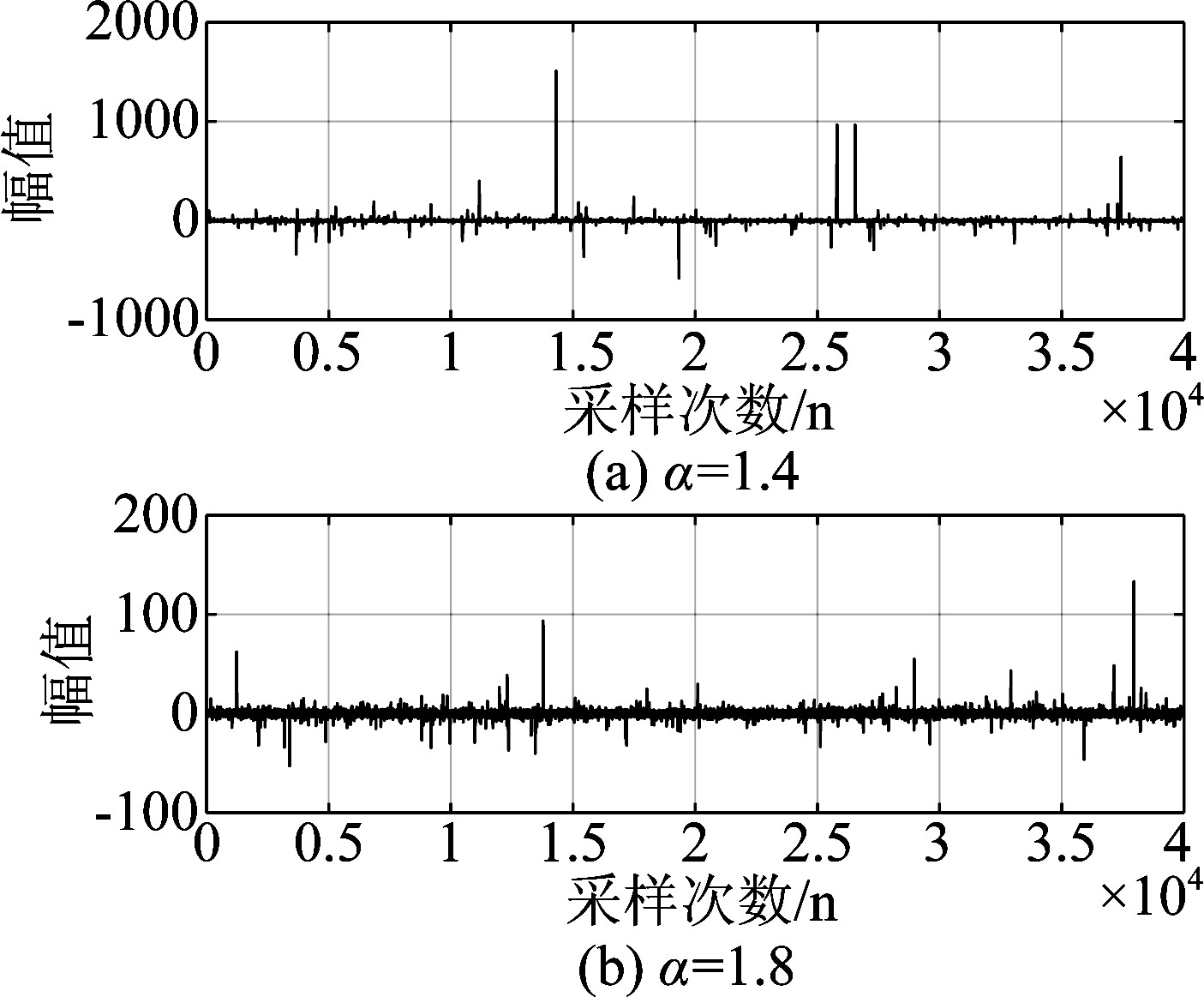
图6 参考信号x(n)采用的是标准的SαS分布
Fig.6 The reference signal x(n) uses standard SαS distribution
表2 仿真参数
Tab.2 Simulation parameters

ANC算法参数设置(α=1.4)参数设置(α=1.6)参数设置(α=1.8) 文献[4]算法μ=0.00001μ=0.0001μ=0.0001文献[13]算法μ=0.0002,σ=3μ=0.0002,σ=3μ=0.0003,σ=3文献[12]算法μ=0.001,σ=1μ=0.001,σ=1μ=0.001,σ=1本文算法μ=0.0002, β=0.2μ=0.0002, β=0.3μ=0.0003, β=0.4
图7是在α=1.4的脉冲噪声环境下各算法之间的降噪性能比较的仿真曲线图。文献[4]算法的权系数向量更新公式为w(n+1)=w(n)+μe(n)x′(n);文献[12]算法的权系数向量更新公式为w(n+1)=w(n)+μe(n)/(e2(n)+2σ2)x′(n);文献[13]算法的权系数向量更新公式为w(n+1)=w(n)+μexp(-e2(n)/2σ2)e(n)x′(n);从图7可以得出,文献[4]算法收敛性能衰退,甚至发散;在采样次数为1×104时,本文算法平均噪声衰减量为-3 dB,相比于文献[12]算法的-2.5 dB降低了0.5 dB,相比于文献[13]算法-2.2 dB降低了0.8 dB,可见,本文算法具有更小的稳态误差,显示很好的降噪性能。
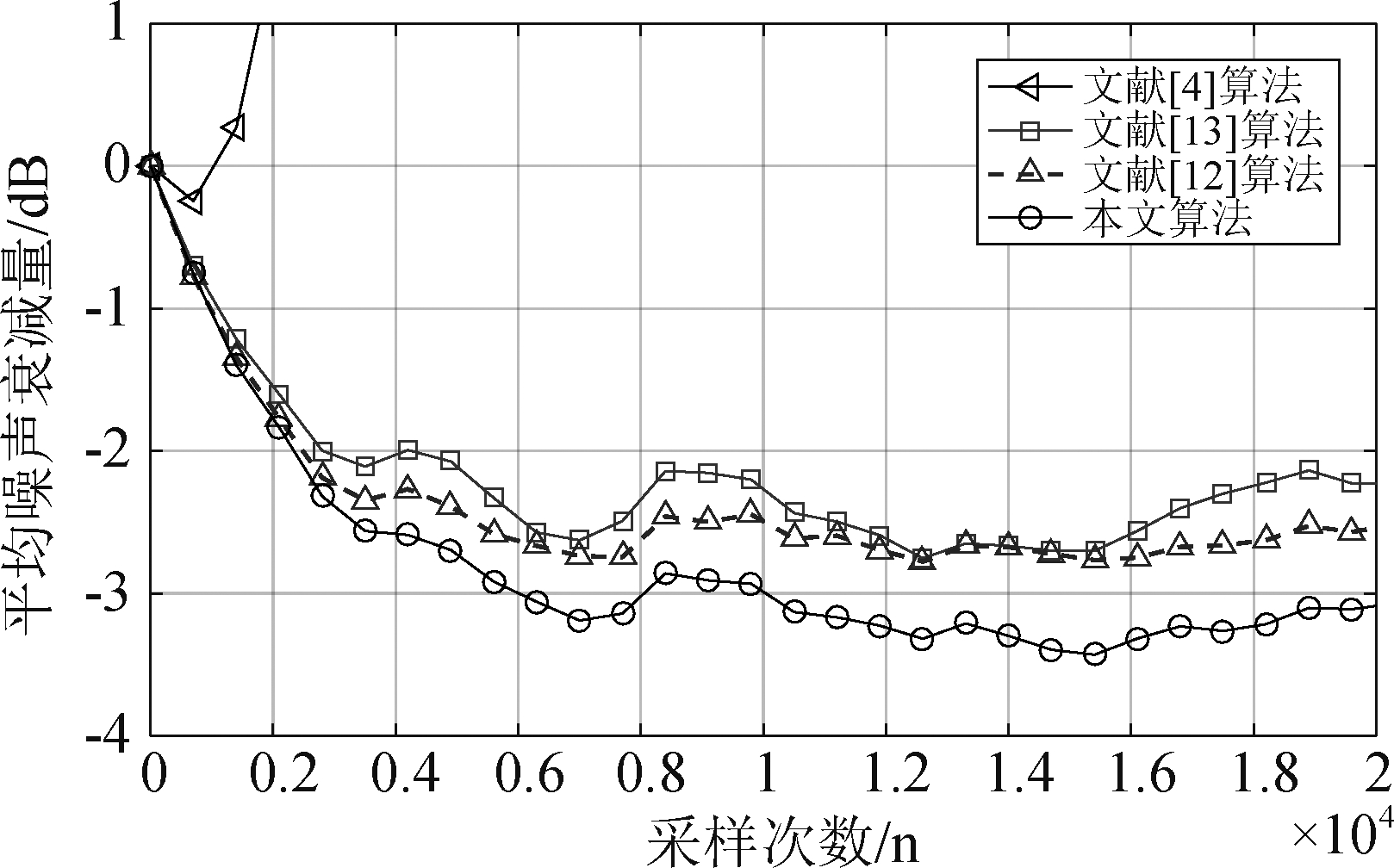
图7 各算法之间的平均噪声衰减量的曲线图(α=1.4)
Fig.7 Curve of averaged noise reduction between algorithms (α=1.4)
图8是在α=1.8的脉冲噪声环境下各算法之间的降噪性能比较的仿真曲线图。在图8中,文献[4]算法可以收敛但是平均噪声衰减量高至-4 dB;在采样次数为1×104时,本文算法平均噪声衰减量低至-7.2 dB,相比于文献[13]算法的-6.8 dB降低了0.4 dB,相比于文献[12]算法的-7 dB降低了0.2 dB。从而得出本文算法在脉冲噪声控制中具有比较好的降噪性能。
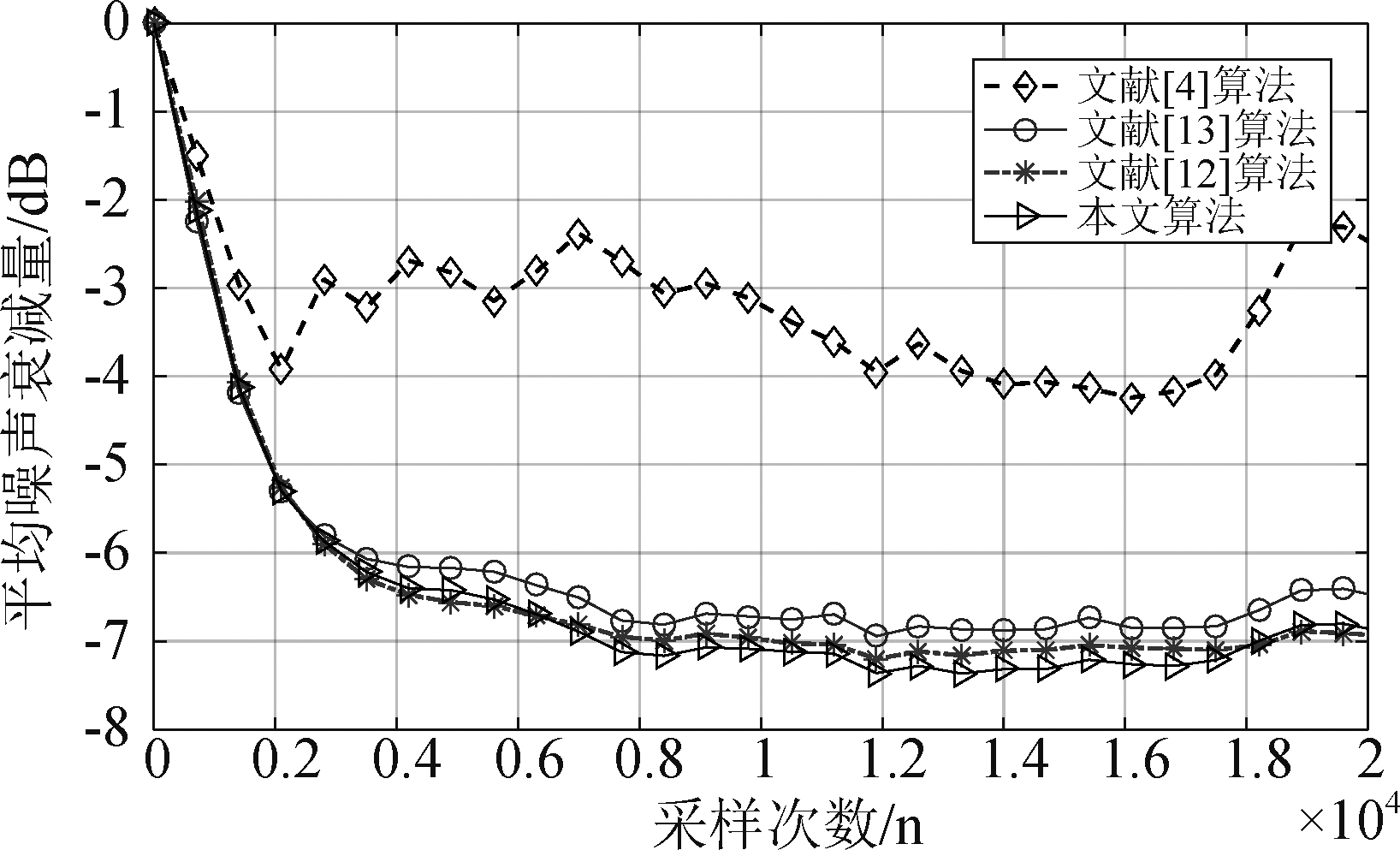
图8 各算法之间的平均噪声衰减量的曲线图(α=1.8)
Fig.8 Curve of averaged noise reduction between algorithms (α=1.8)
3.2 例子2
为了进一步验证本文算法的降噪性能,其参考信号x(n)为混合噪声,如下所示:
(14)
其中υ(n)是脉冲噪声服从标准的SαS分布,α取值为1.6。
图9参考信号x(n)是混合噪声采用的是正弦信号和脉冲噪声的混合;图10是在混合噪声输入下,各算法之间的平均噪声衰减量的曲线图,其中σ1=3,σ2=1,其余的仿真参数被设置在表2中。在采样次数为1×104时,本文算法平均噪声衰减量低至-4.5 dB,相比于文献[13]算法的-4 dB降低了0.5 dB,相比于文献[12]算法的-3.7 dB降低了0.8 dB,从而验证了本文算法在混合脉冲噪声控制中具有比较好的降噪性能。
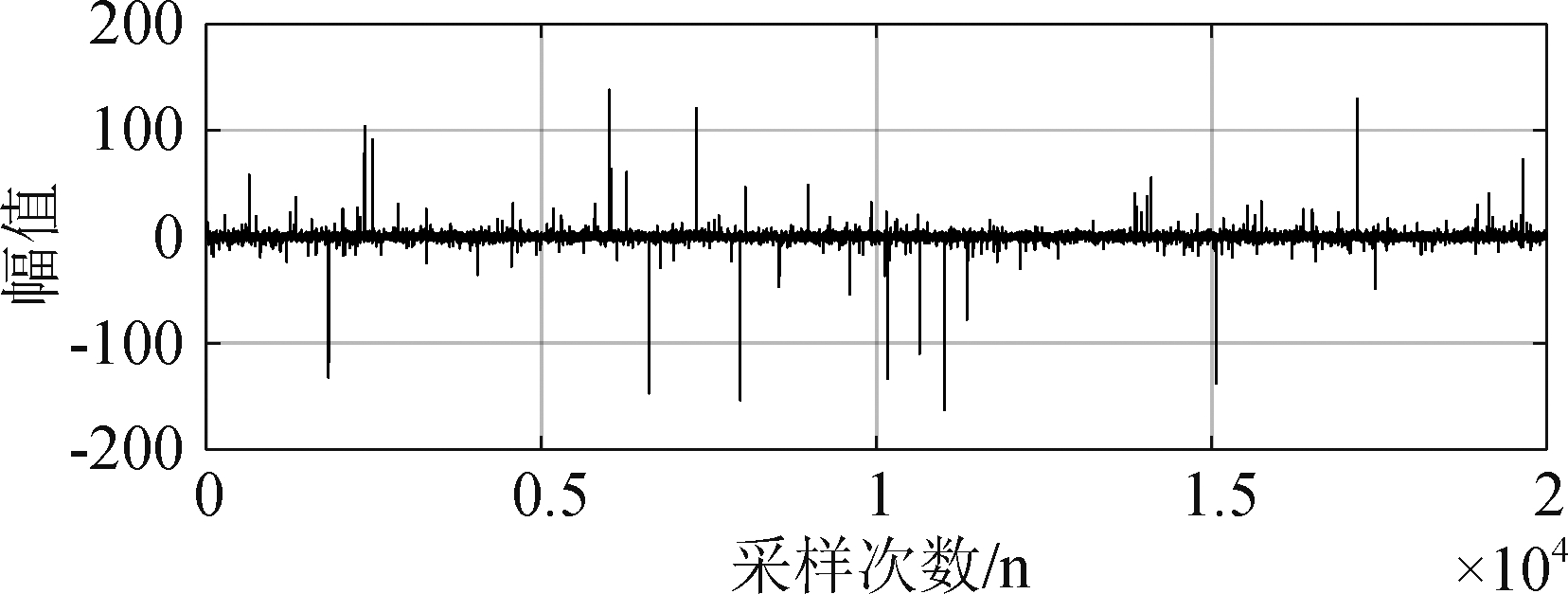
图9 参考信号x(n)采用的是正弦信号和脉冲噪声的混合
Fig.9 The reference signal x(n) uses mixture of sinusoidal and impulsive noise
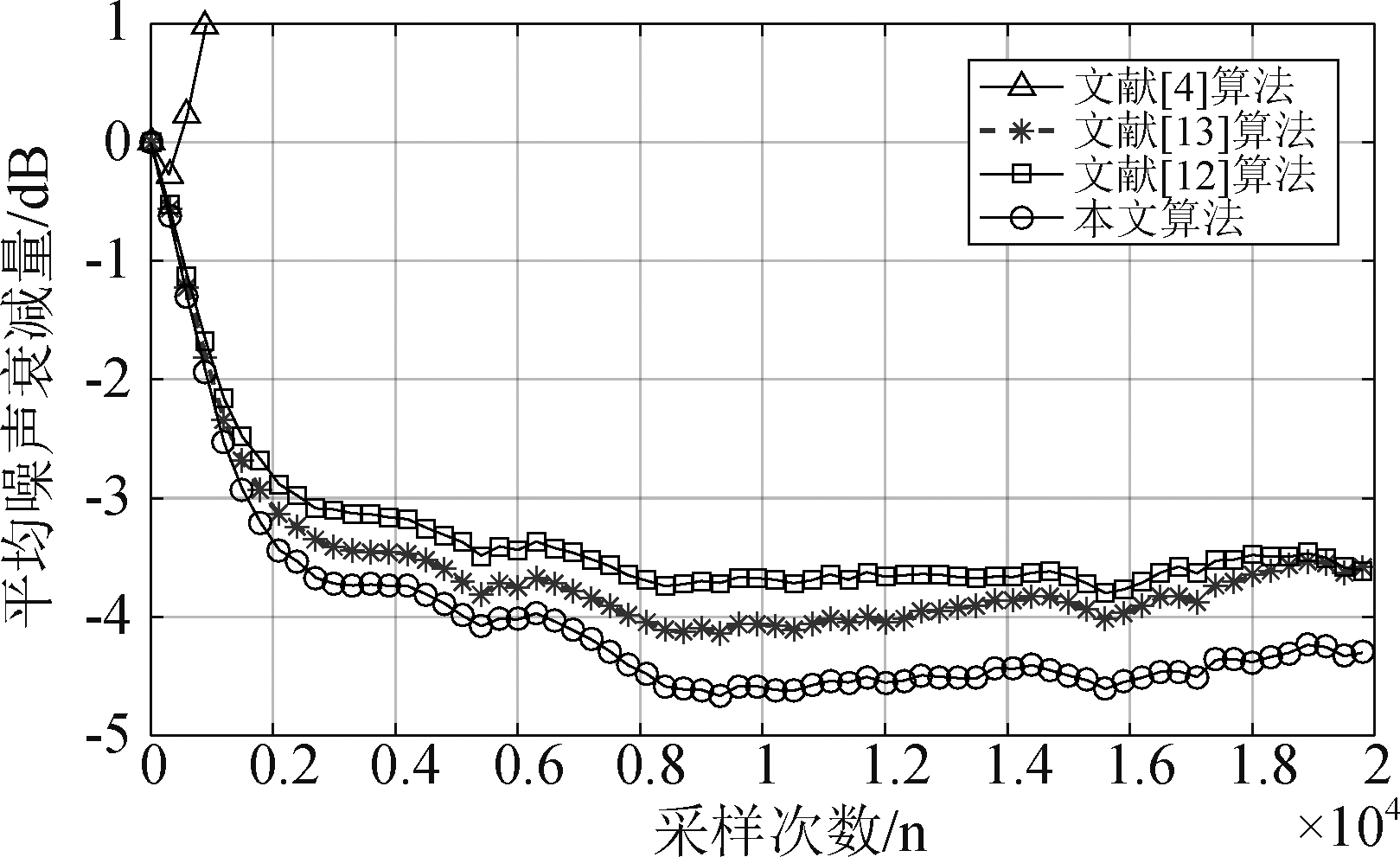
图10 各算法之间的平均噪声衰减量的曲线图(α=1.6)
Fig.10 Curve of averaged noise reduction between algorithms (α=1.6)
4 结论
针对标准的SαS分布的非高斯噪声的前馈主动噪声控制,采用最大混合相关熵准则为目标函数,在此基础上,提出了一种滤波x最大混合相关熵准则算法,并从理论推导和仿真验证对比了本文算法与已有算法的性能之间的比较。已有滤波x最大相关熵准则算法的降噪性能以及收敛速度对于核宽度的参数设置影响较大,尤其在脉冲噪声控制中,本文的算法改进了该算法的这种局限性,具有更好的降噪性能和更快的收敛速度。
[1] Hinamoto Y, Sakai H. A filtered-X LMS algorithm for sinusoidal reference signals—effects of frequency mismatch[J]. IEEE Signal Processing Letters, 2007, 14(4): 259-262.
[2] Kuo S M, Morgan D R. Active noise control: a tutorial review[J]. Proceedings of the IEEE, 1999, 87(6): 702-943.
[3] Zhang Ming, Lan Hui, Ser W. Cross-updated active noise control system with online secondary path modeling[J]. IEEE Transactions on Speech and Audio Processing, 2001, 9(5): 598- 602.
[4] Ardekani I T, Abdulla W H. Theoretical convergence analysis of FxLMS algorithm[J]. Signal Processing, 2010, 90(12): 3046-3055.
[5] Tobias O J, Bermudez J C M, Bershad N J. Mean weight behavior of the filtered-x LMS algorithm[J]. IEEE Transactions on Signal Processing, 2000, 48(4): 1061-1075.
[6] Gaur S, Gupta V K. A review on filtered-x LMS algorithm[J]. International Journal of Signal Processing Systems, 2016, 4(2): 172-176.
[7] Leahy R, Zhou Z, Hsu Y C. Adaptive filtering of stable processes for active attenuation of impulsive noise[C]∥1995 International Conference on Acoustics, Speech, and Signal Processing. IEEE, 1995, 5: 2983-2986.
[8] Sun Xu, Kuo S M, Meng Guang. Adaptive algorithm for active control of impulsive noise[J]. Journal of Sound and Vibration, 2006, 291(1-2): 516-522.
[9] Akhtar M T, Mitsuhashi W. Improving performance of FxLMS algorithm for active noise control of impulsive noise[J]. Journal of Sound and Vibration, 2009, 327(3-5): 647- 656.
[10] Wu Lifu, He Hongshen, Qiu Xiaojun. An active impulsive noise control algorithm with logarithmic transformation[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2011, 19(4): 1041-1044.
[11] Sun G, Li M, Lim T C. A family of threshold based robust adaptive algorithms for active impulsive noise control[J]. Applied Acoustics, 2015, 97: 30-36.
[12] George N V, Panda G. A robust filtered-s LMS algorithm for nonlinear active noise control[J]. Applied Acoustics, 2012, 73(8) : 836- 841.
[13] Kurian N C, Patel K, George N V. Robust active noise control: an information theoretic learning approach[J]. Applied Acoustics, 2017, 117: 180-184.
[14] Wang Yidan, Yang Liming, Ren Qiangqiang. A robust classification framework with mixture correntropy[J]. Information Sciences, 2019, 491: 306-318.
[15] Chen Badong, Wang Xin, Lu Na, et al. Mixture correntropy for robust learning[J]. Pattern Recognition, 2018, 79: 318-327.
[16] Song Pucha, Zhao Haiquan. Filtered-x generalized mixed norm (FXGMN) algorithm for active noise control[J]. Mechanical Systems and Signal Processing, 2018, 107: 93-104.
[17] Song Pucha, Zhao Haiquan. Filtered-x least mean square/fourth (FXLMS/F) algorithm for active noise control[J]. Mechanical Systems and Signal Processing, 2019, 120: 69- 82.
[18] 王文益, 伊雪. 基于改进语音存在概率的自适应噪声跟踪算法[J]. 信号处理, 2020, 36(1): 33- 41.
Wang Wenyi, Yi Xue. An Adaptive Noise Tracking Algorithm Using Improved Speech Presence Probability [J]. Journal of Signal Processing, 2020, 36(1): 33- 41.(in Chinese)

