1 引言
音质(Timbre)是指听者能够区分两种具有相同响度、音高、空间位置和持续时间的声音的多维属性特征[1]。音质是音频信息检索、言语识别和医学领域检测病人听觉能力的重要特征[2-3]。因此,探索声音精细结构,寻找有效的音质特征提取方法具有重要意义。
大量的心理、生理和物理学实验表明音质是多维度的,为音质特征提取方法提供了理论支持与研究方向。音质与音频的时间相关特征、频谱相关特征和频谱随时间的演化特征有关[4- 6]。当前的音质特征提取方法主要基于短时平稳假设,通过短时傅里叶变换(Short Time Fourier Transform, STFT)、Gabor展开和小波变换(Wavelet Transform,WT)等时频分析方法从多个维度提取音质特征[7-9]。Peeters等学者通过分析总结前人对音质特征提取方法的研究,采用不同的音频分析技术(如短时傅里叶变换、谐波正弦分量、基于等效矩形带宽概念的听觉模型、能量包络线等),提取了能够描述音频的时域、频域和时频域的特征[7]。Adeli等学者利用耳蜗滤波器组、横向抑制模块和调制滤波器组构建了音质的层次模型,来提取信号的频谱、时间和振幅调制特征,并在5种乐器的分类实验中取得了一定的效果[8]。Pons 等研究人员利用卷积神经网络(Convolutional Neural Networks,CNN)捕捉STFT和Mel等时频谱图中的音质特征,并成功应用到歌唱语音音素分类、乐器识别和音乐自动标注等应用中[10]。
在实际应用中,音乐和语音信号多数是非平稳的时变信号,具有丰富的频率成分和时间上的节奏变化,同时还可能含有大量的背景声,对时空分辨率和鲁棒性要求较高。而前述的传统音质特征提取方法不能同时得到时间和频率上的良好分辨率,而且对音频的非平稳特性没有很好地进行挖掘。同时STFT、Gabor展开和小波变换等方法需要预先设定基函数,对非平稳非线性的音频信号分析时缺乏自适应性[9]。经验模态分解(Empirical Mode Decomposition,EMD)技术因其对复杂时序信号的良好的自适应分解被广泛应用于信号处理领域[11]。例如,应用在共振峰跟踪、说话人识别和语音情感识别当中,且经过EMD分解得到的有限个固有模态函数(Intrinsic Mode Function,IMFs)已经被证明能够捕获共振峰结构和声门声源特征,可以挖掘信号中的非线性信息[12-14]。
本文工作专注于音质精细特征的提取,挖掘非线性非平稳音频信号中更精确的音质属性。在方法上,采用可以有效解决EMD模态混叠问题的时变滤波经验模态分解(Time Varying Filtering based EMD,TVF-EMD)技术对音频进行时频分析,提取音质特征,以期降低音质表示的复杂性,提高音质表征的准确性。并在不同复杂度乐曲的乐器识别中验证本文特征提取方法的有效性和鲁棒性。
本文后续内容安排如下:在第2节中介绍基于TVF-EMD的音质特征提取方法,第3节给出乐器分类实验的数据集和实验流程介绍,第4节为在不同复杂度的乐器音乐数据集上进行实验的结果分析,验证本文方法的有效性,最后给出了本文的结论。
2 基于TVF-EMD的音质特征提取方法
研究表明:应用EMD技术分析语音信号时,IMFs能够捕获信号的共振峰结构和声门声源特征,且乐器的发声模型与语音的源滤波器模型相似,即乐器的振动部件是声源(如弦和簧片),乐器的不同形状构成了不同的滤波器和谐振体。因此,本节通过TVF-EMD方法分解得到乐器演奏音频的IMFs,通过挖掘不同IMF频带的时频信息,给出了不同乐器音质相关的特征。本文共构建了两大类音质特征:希尔伯特频谱分布特征和希尔伯特轮廓特征。
2.1 基于TVF-EMD的音乐信号希尔伯特谱分析
EMD方法通过一系列筛选步骤将原始信号分解成有限个从高频模态到低频模态的IMF分量和一个残差,其中IMF需要满足的条件为:1)全局窄带要求:数据序列极值点的数目和过零点的数目相等或至多相差一个;2)局部零均值条件:在任意时间点,局部极大值包络线和局部极小值包络线均值为零。EMD算法通过筛选得到一个IMF的过程如下所示:
(1)输入信号s(t);
(2)通过三次样条插值法求解信号的上下包络线,并求解上下包络线的平均值;
(3)从信号中减去平均值,得到r(t),判断r(t)是否满足IMF条件。是,则r(t)为一个IMF;否则,s(t)=r(t),转到(1)执行循环,直至满足IMF条件。
由于信号经常出现由噪声或信号突然中断引起的频率跳变,以及频谱成分在一个八度范围内(两个频率的比在0.5到2之间)不可分的问题,导致EMD存在模态混叠。TVF-EMD方法在筛选过程使用基于B样条的时变滤波器,更适应非线性非平稳的时变信号,且有效解决了EMD方法的模态混叠问题,没有引入噪声,计算效率高。因此本文使用TVF-EMD对音频信号进行分解,TVF-EMD方法的筛选步骤主要包括以下3个步骤,详细的步骤和相关参数计算方法参见论文[11]。
(1)利用解析法估计信号的局部截止频率;
(2)调整局部截止频率,利用局部截止频率构建B样条节点,通过B样条估计得到局部均值;
(3)从原始信号s(t) 中减去局部均值,得到r(t),判断r(t)是否满足IMF为局部窄带的条件。
图1为乐器长号的A4单音音频的TVF-EMD分解结果。从图1(d) 中可以看出,IMF8边际谱中的频率为440 Hz,对应该音频的基频,从下往上各维IMF的频率依次增加约为类基频IMF频率的整数倍。从图中还可以看出各维IMF之间模态混叠现象较少,因此在分析频谱分布时可靠性更高。
经过TVF-EMD分解,原始信号s(t)被分解成一系列的从高频模态到低频模态的IMF分量,记为rj(t)(j=1,2,...,m),m为IMF维数。对每一个固有模态函数rj(t)进行希尔伯特变换(Hilbert Transform, HT),固有模态函数rj(t)的希尔伯特变换yj(t)定义如下所示。
(1)
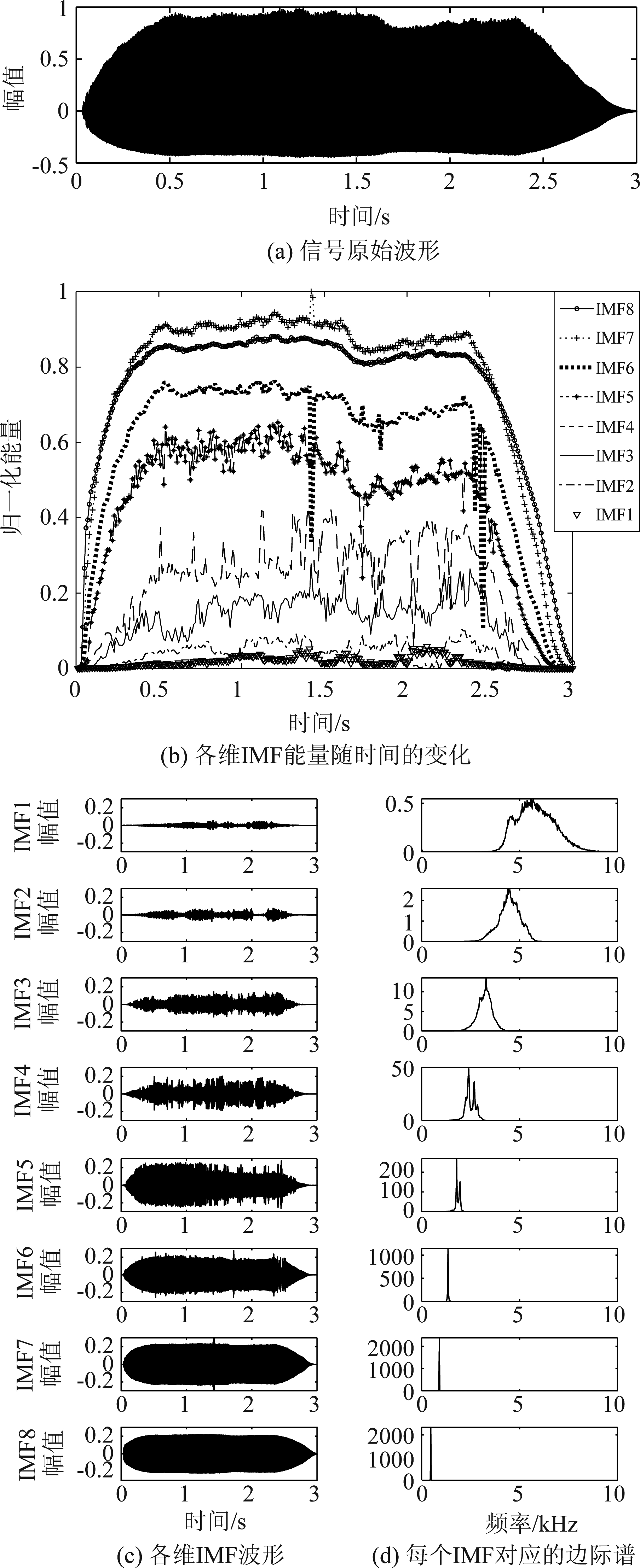
图1 乐器长号的A4单音原始波形及TVF-EMD分解结果
Fig.1 TVF-EMD decomposition results of A4 pitch monophonic audio of the trombone
将各维固有模态函数rj(t)和式(1)中的yj(t)组合成解析信号zj(t):
zj(t)=rj(t)+iyj(t)=aj(t)eiφj(t)
(2)
其中,瞬时幅值aj(t)(瞬时幅值随时间变化的曲线即为时域包络)和瞬时相位φj(t)分别为:
(3)
(4)
则,瞬时频率可定义如下:
(5)
由HT得到的瞬时振幅与瞬时频率均为时间的函数,振幅随频率-时间的分布图即为Hilbert振幅谱,简称Hilbert谱,记为H(ω,t):
(6)
对Hilbert谱先求幅值的平方,然后再对时域积分,即可得到Hilbert能量谱:
EH(ω)=![]() H2(ω,t)dt
H2(ω,t)dt
(7)
通过Hilbert谱分析可以得到信号的瞬时幅值、瞬时能量与频谱能量。
2.2 希尔伯特频谱分布特征
通过TVF-EMD这个自适应的滤波器,将时变信号分解为含有不同频率成分的IMF,这些IMF中携带有关信号生成过程的潜在和有意义的信息。例如,从图1(b)的长号A4音高单音的不同维IMF归一化能量随时间的变化图可以看出,不同频带的IMF能量分布不同,且低频带的IMF能量包络与原始信号的能量包络相似;从图1(d)又可看出各维IMF的频率分布有一定的规律。研究表明音质与音频的频谱能量分布有关。因此,挖掘信号不同频带IMF的能量分布关系。
对于Hilbert能量谱中的质心频率,类比物理学中的质心的概念,定义如下Fj的计算方法:
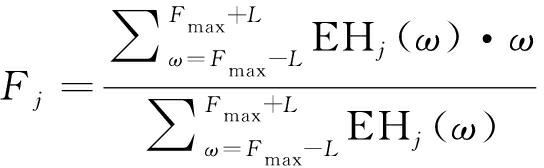
(8)
对上式,Fmax为每维IMF的Hilbert谱中能量最大的瞬时频率。其中2L代表通过对每维IMF对应的Hilbert谱中主峰分布区间的长度。对于Hilbert能量谱中的能量,定义如下与每个IMF质心频率Fj对应的频谱质心能量Ej(j=1,2,...,m):
(9)
定义如下对Hilbert频谱分布进行描述的统计矩(Statistical Moments)特征[7],特征计算如下:
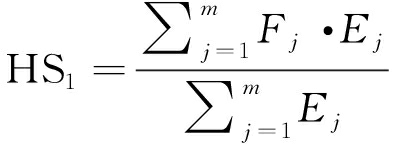
(10)
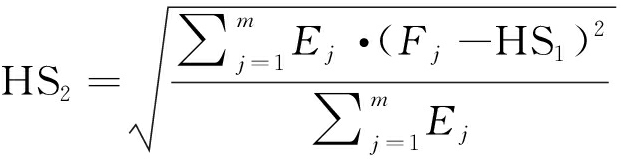
(11)
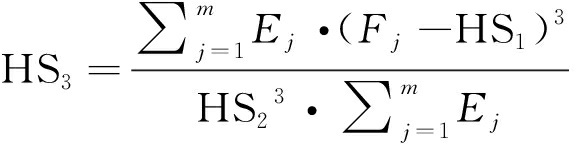
(12)
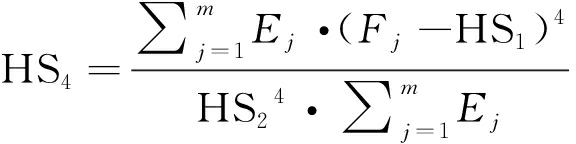
(13)
其中,HS1为Hilbert频带谱质心,主要与幅值较大的共振峰有关;HS2为Hilbert频谱标准差,描述了频谱分布的分散程度;HS3为Hilbert频谱偏度,为频谱在其平均值附近的不对称性;HS4为Hilbert频谱峰度,为频谱在其质心附近的平坦度。这4个特征是对音频不同频带Hilbert频谱分布结构的刻画,称之为希尔伯特频谱分布特征。
2.3 希尔伯特轮廓特征
音质不仅与频谱分布有关,还与时间模式有关。不同乐器能量包络的启动(Attack)、衰变(Decay)、维持(Sustain)和释放(Release)阶段的比例分布不同,即ADSR包络不同。弓弦乐器、木管乐器和铜管乐器属于持续类乐器,包含完整的ADSR四个阶段,而打击乐器属于衰减类乐器,没有维持阶段。
下图2为音高、响度和空间位置一致的情况下单簧管、长笛和萨克斯A4单音的不同维度IMF归一化能量随时间的变化对比图,为了更好地比较不同乐器的特点,在共同的图例中均用IMF8代表最低维度IMF(基频),其他各维IMF依次从低频向高频排列(IMF1频率最高)。从图2可以看到,虽然三种乐器均属于持续类乐器,频谱成分丰富,但是从时域看,长笛的能量包络存在较多波动,并不像单簧管和萨克斯一样较为稳定。
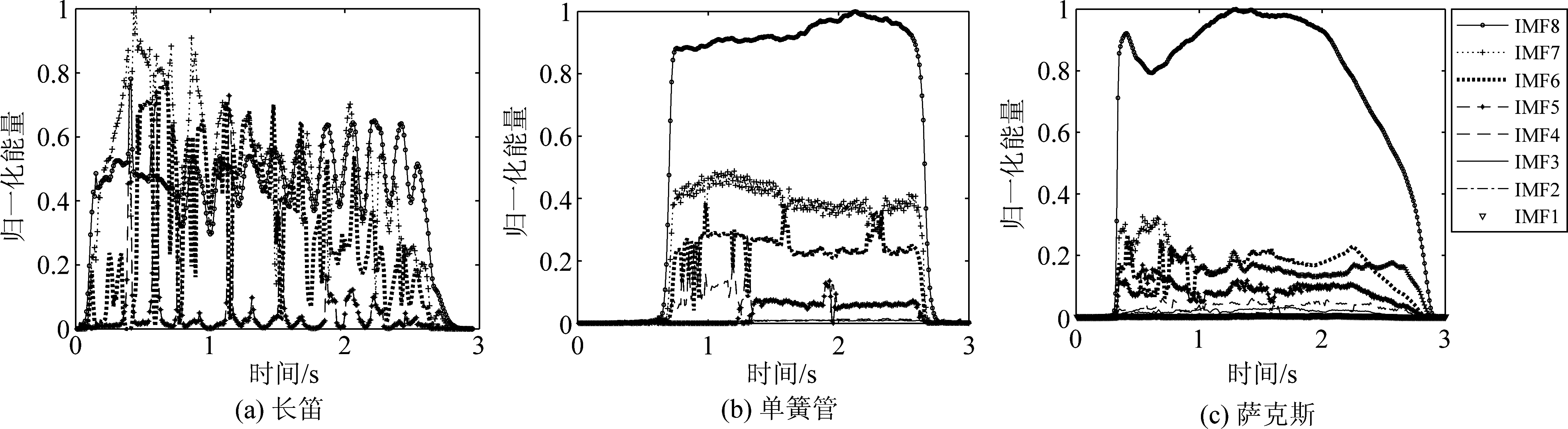
图2 长笛、单簧管和萨克斯A4单音的各维IMF归一化能量随时间的变化
Fig.2 Comparison of the normalized energy of IMFs of flute, clarinet and saxophone over time
对经过预处理的音频信号s(t)进行加窗平滑,目的是对每维IMF的能量包络进行平滑,更好地突出包络的变化,同时减少随机性造成的影响,提高特征的表达能力。经过统计,不同样本经过TVF-EMD分解后的IMF个数不同,因此对每个单位时间内的不同IMF之间的特征求解统计值。
其中,通过对乐器单音音频分析发现,信号能量最大的IMF与原始信号的相关性较大,且其能量包络的ADSR改变位置与原始信号的ADSR包络对应的时间一致。对于一些复杂的乐曲(如,3.1节介绍的IRMAS音频数据库),乐曲片段不是纯净的单一乐器演奏片段,其中包含了噪声和各种调音修饰且随时间不断变化,仅通过对原始信号时域波形求解或者对最大Ej对应的IMF分析误差较大。因此,通过下述的轮廓提取方法可以较为准确地捕捉信号中的动态特性。
对s(t)的第k个平滑窗的信号sk(t)的第j维IMF rjk(t)(j=1,2,...,m),其质心频率Fjk与质心能量Ejk分别为:
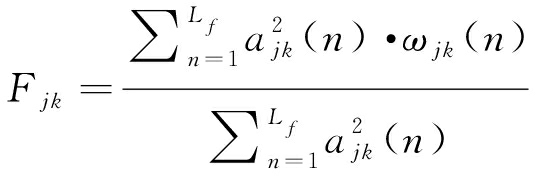
(14)
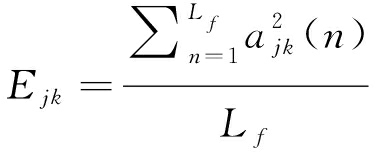
(15)
其中,Lf为每个平滑窗的长度,n代表一个平滑窗内的信号中的第n个采样点。
通过定位每个单位时间内的主频IMF(Ejk最大)并求其随时间的变化曲线分析能量随时间的变化规律。求解方法如下:
(16)
SEN=[E1max,E2max,...,Eimax,..., ENmax]
(17)
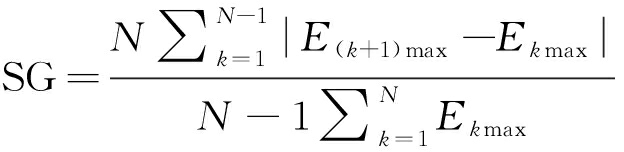
(18)
其中,N为信号的总平滑窗个数,Ekmax为第k个平滑窗中m维IMF的质心能量的最大值,SE为由每一个平滑窗的Ekmax构成的序列,对SE求一阶差分ΔSE和二阶差分Δ2SE,表征能量随时间的变化,这两个特征为时序特征;SG表征了信号整体的能量波动趋势。因为该类特征是基于HHT得到的瞬时幅值和频率求解的,且刻画了ADSR包络的变化信息,因此称为希尔伯特轮廓特征。
3 基于TVF-EMD音质特征的乐器分类
3.1 数据源介绍
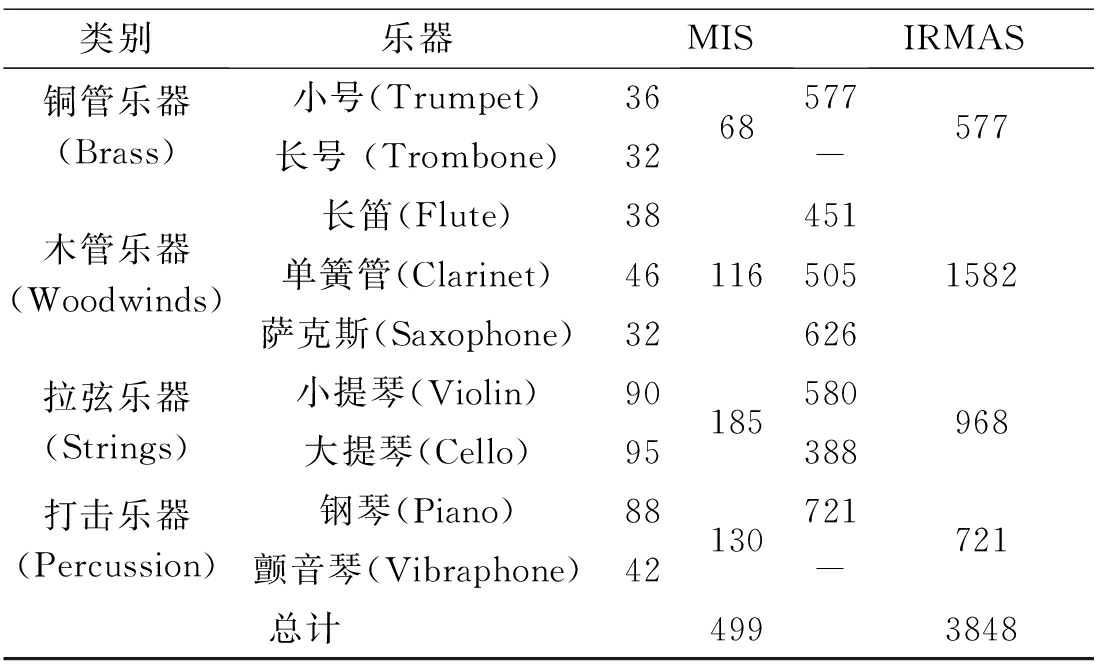
本文使用的数据库共有两个,分别为:1)The University of IOWA Musical Instrument Samples(MIS):共选取4大类9种乐器的单音演奏片段,所有样本均为16 bit,采样频率为44.1 kHz[15]。2)IRMAS数据库:选取7种乐器分别为主乐器的演奏片段,数据涵盖了不同的乐器类型、表演者、表达方式以及一般录音和制作风格。所有样本均为16 bit,采样频率为44.1 kHz。不同乐器的种类及乐曲片段数目如表1所示[16]。
表1 MIS和IRMAS数据库乐器类别及样本个数统计表
Tab.1 The statistical table of instrument category and sample number in MIS and IRMAS
类别乐器MISIRMAS铜管乐器(Brass)木管乐器(Woodwinds)拉弦乐器(Strings)打击乐器(Percussion)小号(Trumpet)长号 (Trombone)长笛(Flute)单簧管(Clarinet)萨克斯(Saxophone)小提琴(Violin)大提琴(Cello)钢琴(Piano)颤音琴(Vibraphone)36323846329095884268116185130577-451505626580388721-5771582968721总计4993848
3.2 实验流程
将本文提取的希尔伯特频谱分布特征和希尔伯特轮廓特征应用于乐器分类实验中,验证提取特征的有效性。实验设置如下:
(1)原始音频信号的预处理
对多通道样本,采用平均多通道数据的方法,保证空间位置的一致性。所有音频去除静音段的方法采用基于短时能量的双门限端点检测。对MIS数据集音频进行裁剪,保证所有样本时长均为3 s;IRMAS数据集的样本长度均为3 s,不需要再处理。为了去除响度的影响,对原始波形的幅值进行归一化。
(2)IMF筛选
对MIS数据集,由于其音频较为纯净且只含有单音,且通过对MIS样本分析发现最后一维IMF频率基本与单音的基频对应,因此对MIS数据集使用所有的IMF。对IRMAS数据集,该数据集为乐曲片段,包括了外部声音的修饰及少量噪声。从该数据集中提取出的IMF包含了大量的低频IMF,由于大多数乐器音高的频率范围在60 Hz以上,且60 Hz以下的频率段一般是房间或厅堂的谐振频率,不是乐器的固有频率,所以本文将IMF频率在60 Hz以下的部分舍去。
(3)特征选择
本文所提基于TVF-EMD的特征有7维,包括:希尔伯特频谱分布特征共4维(HS1、 HS2、HS3和HS4),希尔伯特轮廓特征3维(ΔSE、Δ2SE和SG),对这两类特征设置平滑窗长为441个采样点, 重叠为221个采样点。其中,对希尔伯特频谱分布特征,对每一个平滑窗内的信号段基于公式(14)的Fjk和公式(15)的Ejk分别求解HS1、HS2、HS3和HS4,并按时间顺序组成4维时序特征。
对比特征有:a)基于文献[7]的Timbre工具箱的全局描述特征(Global descriptors)和基于STFT的时变描述特征(Time-varying descriptors)共35维,简称为时频域特征;b)12维梅尔频率倒谱系数(Mel Frequency Cepstrum Coefficient, MFCC)及11维梅尔差分倒谱系数(△MFCC)共23维,简称为MFCC特征。在特征提取中,帧长取46 ms,帧移取23 ms。其中,Timbre工具箱是提取音乐音质特征的常用工具箱,而MFCC特征被证明是提取语音和音乐等多种音频音质的有效特征[17]。
(4)分类器设计
不同类别特征的对比实验:对所有数据集均采用原始数据集的20%作为测试集,剩下80%为训练集和验证集,采用10倍交叉验证训练SVM分类器进行分类。对所有特征中的时序特征均采用提取其统计值(平均值,标准差,偏态,峰度,25%和75%分位数)的方法。
时序分类器设计:音质的一个重要属性依赖于频谱随时间的演化,而长短时记忆网络能够较好地表示时序数据中的长距离依赖关系[18]。因此,为了能够对音质时序特性进行建模,构建了基于双向长短时记忆网络(Bi-directional Long Short-Term Memory,BiLSTM)的时序分类器对IRMAS数据集进行乐器分类。其中,网络的输入为特征序列,网络隐层采用两层单元个数均为200的双向长短时记忆网络层,然后连接一个大小为7的全连接层、一个softmax层和一个7类的分类层;网络的训练使用自适应矩估计 (Adaptive Moment Estimation, ADAM) 求解器[19]。
(5)结果评价方法
本文采用精确率(Precision,P),召回率(Recall,R) 和 F1测度(F1-Measure,F1)进行分类结果的评估[20]。Precision是精确性的度量,表示被分为正例的示例中实际为正例的比例。Recall是覆盖面的度量,度量有多少个正例被分为正例。F1-Measure是准确率和召回率的调和平均,用于计算系统的整体性能。三个指标的计算公式如下:
(19)
(20)
(21)
其中,tPl、 fPl和fnl分别为L个标签中某个标签l中的真阳性(True positive)、假阳性(False positive)和假阴性(False negative)的样本数。
本文使用的数据集不同类别样本数量不均衡,因此为了更好地体现样本不均衡条件下,不同类别的总体分类效果,使用加权的精确率(Pmacro),召回率(Rmacro)和F1值(W-F1)表示对不同类别的总体评估:
(22)
(23)
(24)
其中,wl为标签为l的样本的个数,|L|为所有样本的总数。
综上,本文的音质特征提取及乐器分类流程如图3所示。
4 实验结果分析
表2是基于不同类别特征对MIS数据集的9种乐器类别进行分类的结果。
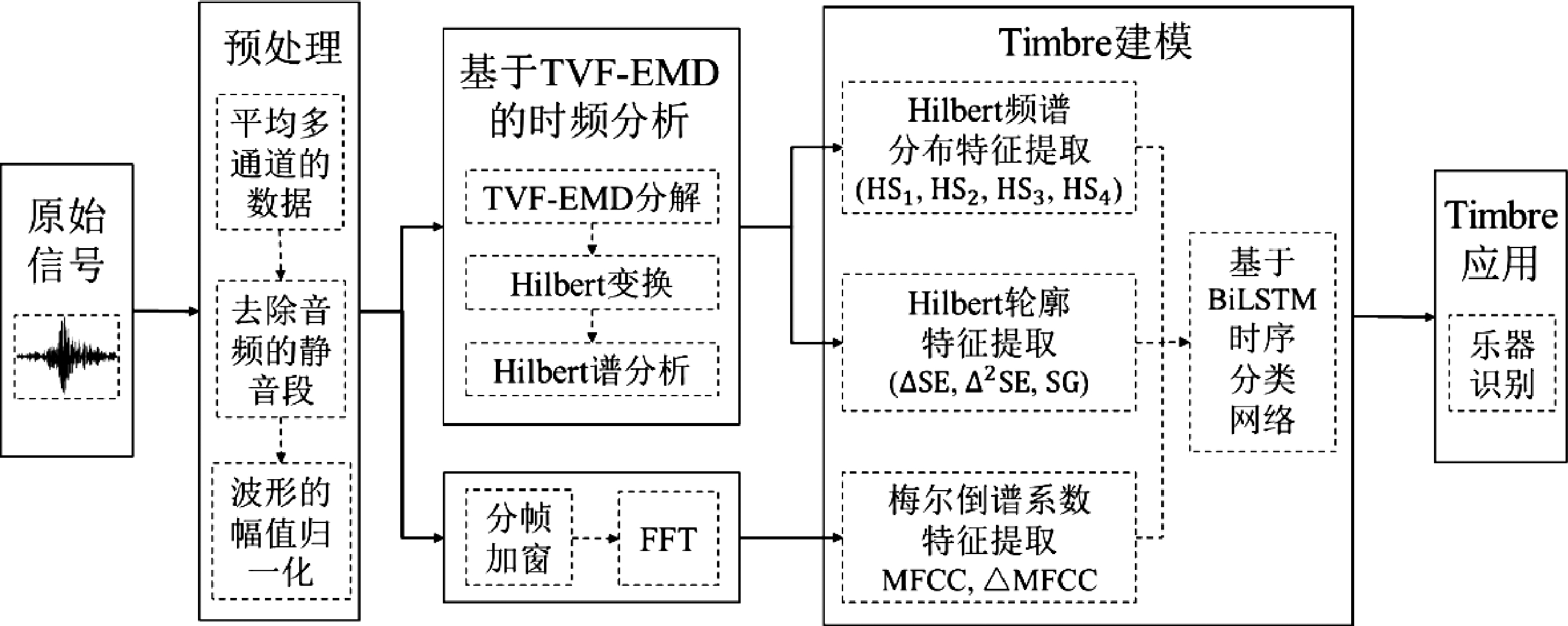
图3 特征提取及识别流程图
Fig.3 Flow chart of the feature extraction and recognition
表2 基于不同类别特征对MIS数据集的分类结果
Tab.2 The classification results of MIS based on different features
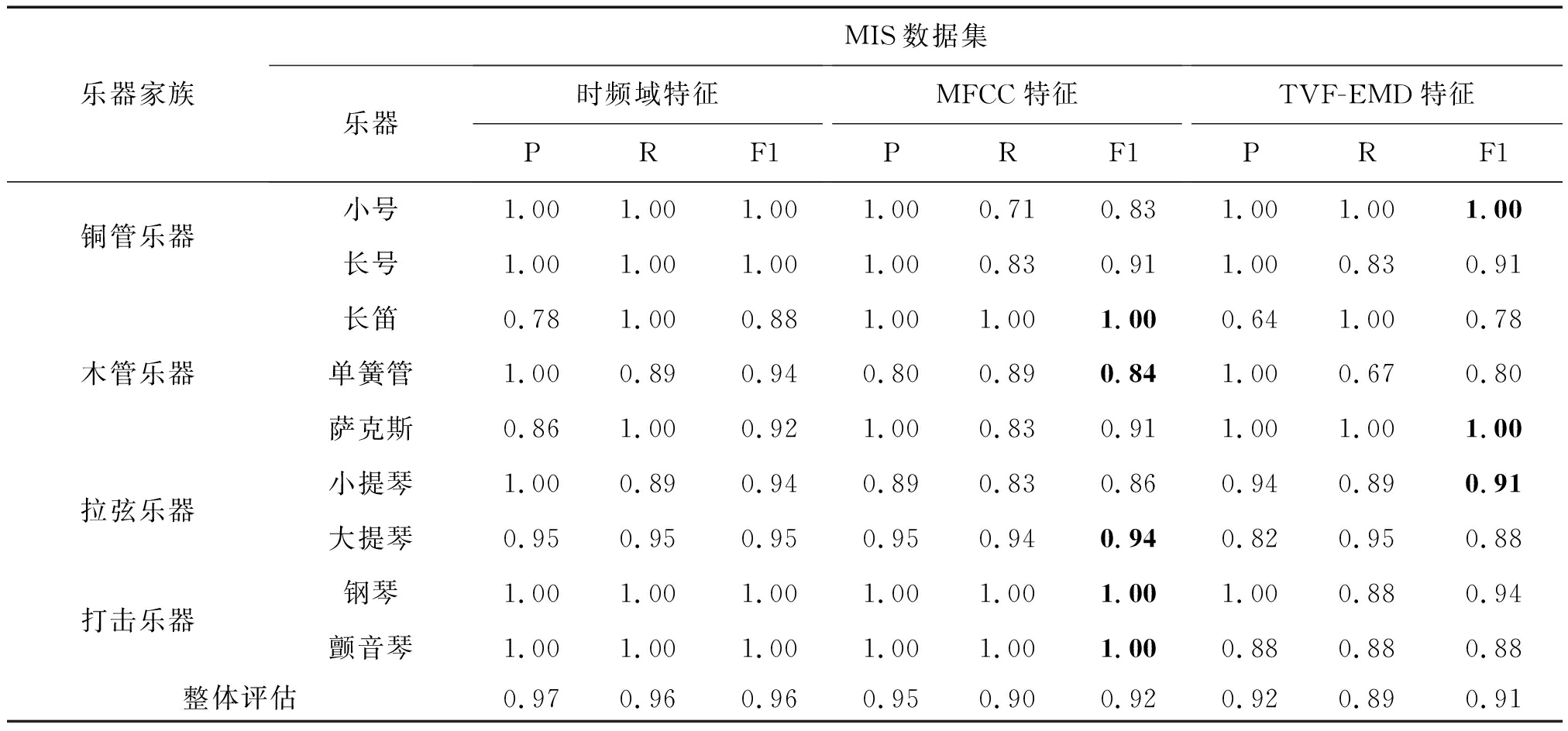
乐器家族MIS数据集乐器时频域特征PRF1MFCC特征PRF1TVF-EMD特征PRF1铜管乐器小号1.001.001.001.000.710.831.001.001.00长号1.001.001.001.000.830.911.000.830.91木管乐器长笛0.781.000.881.001.001.000.641.000.78单簧管1.000.890.940.800.890.841.000.670.80萨克斯0.861.000.921.000.830.911.001.001.00拉弦乐器小提琴1.000.890.940.890.830.860.940.890.91大提琴0.950.950.950.950.940.940.820.950.88打击乐器钢琴1.001.001.001.001.001.001.000.880.94颤音琴1.001.001.001.001.001.000.880.880.88整体评估0.970.960.960.950.900.920.920.890.91
上表2 中加粗的数字表示MFCC特征和TVF-EMD特征相比,二者中的最优解。基于Timbre工具箱的时频域特征对9种乐器的整体分类性能要高于单独使用MFCC特征和单独使用TVF-EMD特征。说明TVF-EMD特征和MFCC特征单独使用并不能完整的表征音质特征。对TVF-EMD特征和MFCC特征分类结果对比可知:TVF-EMD特征和MFCC特征对不同乐器的分类结果各有优势,TVF-EMD特征在识别萨克斯、小提琴和小号时结果优于MFCC特征,在识别长号时与MFCC特征识别效果一样。
MFCC特征是从音频感知的角度设计的,基于TVF-EMD的特征处理的是音频的非线性非平稳特征。两者从不同方面捕捉音频的音质特性。将MFCC特征和TVF-EMD特征组成组合特征对MIS数据集9种乐器进行分类,识别结果为100%,所有乐器均被正确分类,可见MFCC与TVF-EMD特征互相之间具有互补作用,二者相结合可以很好地用来进行音质特征的提取,且优于基于Timbre工具箱的时频特征。
从上文对MIS数据集的实验可以看出TVF-EMD与MFCC的组合特征可以有效对乐器的音质进行分类,下面通过乐器演奏的实际乐曲样本验证该组合特征的有效性。其中对比方法采用文献[7]的Timbre工具箱,共有63维特征。
从表3中可以看出MFCC和TVF-EMD的组合特征的识别效果优于Timbre工具箱的识别效果,从整体上W-F1值提高3%,对单类乐器来说,识别效果最好的是单簧管和萨克斯,分别较Timbre工具箱F1值提升10%,验证了本文方法在处理较为复杂乐曲片段的乐器识别中的有效性。
针对IRMAS数据集,对MFCC和TVF-EMD组合特征使用3.2节中设计的基于BiLSTM的时序分类器进行分类,分类结果的混淆矩阵如图4所示。其中图4中乐器的缩写分别代表如下乐器:大提琴(cel),单簧管(cla),长笛(flu),钢琴(pia),萨克斯(sax),小号(tru)和小提琴(vio)。从图4与表3对比可以看出,7类乐器的准确率和召回率均有提升。
表3 基于不同类别特征对IRMAS数据集的分类结果
Tab.3 The classification results of IRMAS based on different features
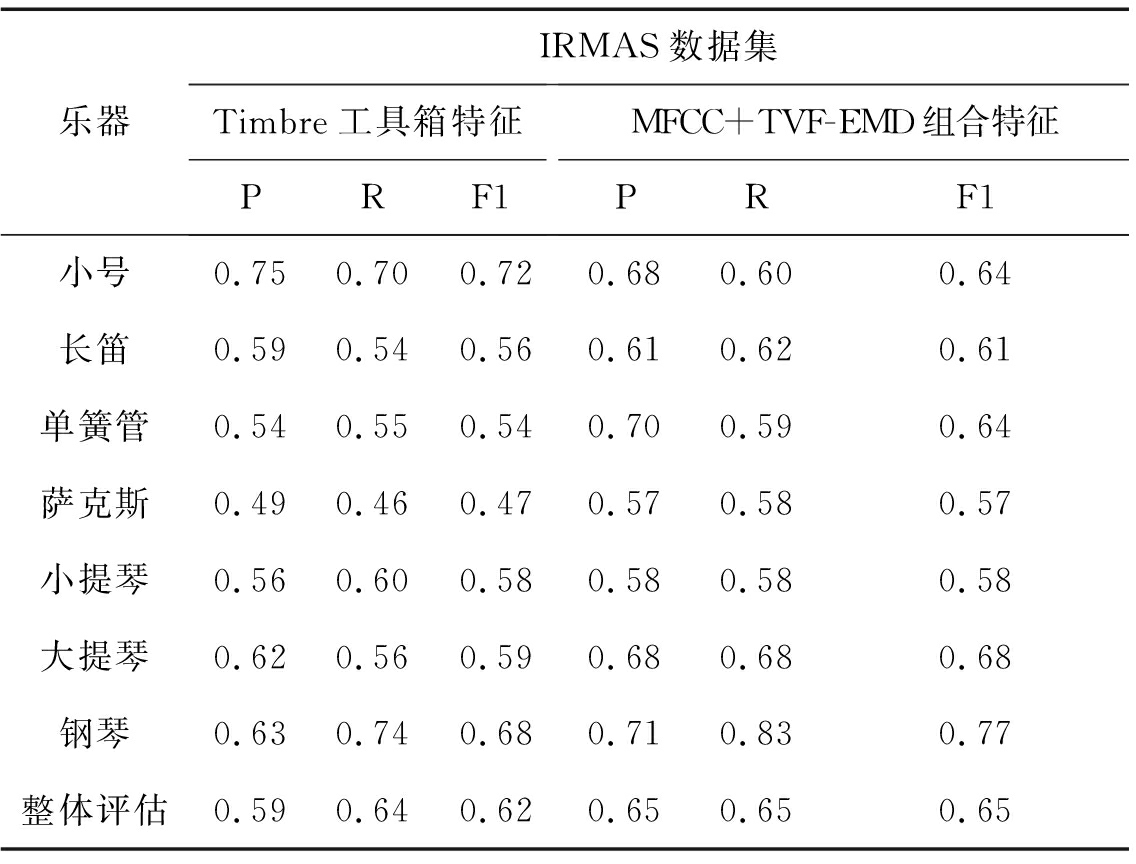
乐器IRMAS数据集Timbre工具箱特征PRF1MFCC+TVF-EMD组合特征PRF1小号0.750.700.720.680.600.64长笛0.590.540.560.610.620.61单簧管0.540.550.540.700.590.64萨克斯0.490.460.470.570.580.57小提琴0.560.600.580.580.580.58大提琴0.620.560.590.680.680.68钢琴0.630.740.680.710.830.77整体评估0.590.640.620.650.650.65
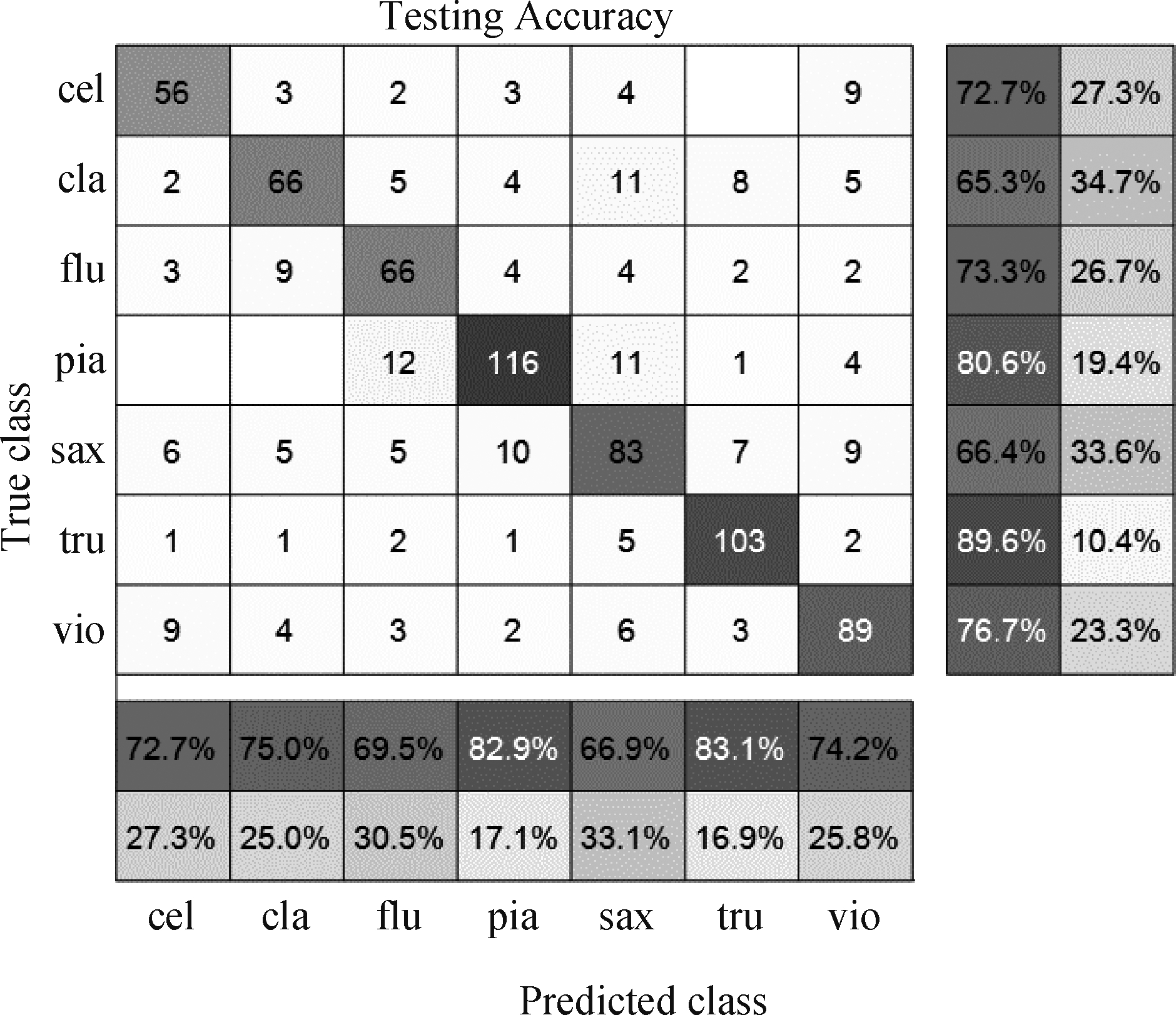
图4 使用组合特征和BiLSTM识别结果混淆矩阵
Fig.4 The confusion matrix of recognition results using BiLSTM and the combination of features
为了更进一步验证本文方法的有效性,将本文方法与文献[21]和文献[22]中的方法进行对比,结果见表4。
从表4可以看出对IRMAS数据集,本文提出的方法优于对比的方法。同时,基于BiLSTM的总体分类结果W-F1值比基于SVM的方法提高了11%,说明基于BiLSTM的分类网络捕捉到了信号的时序信息,也进一步说明了时序特征是表征音质的重要特征。
表4 对IRMAS数据集使用不同方法分类结果对比表
Tab.4 The comparison of classification results using different methods for IRMAS
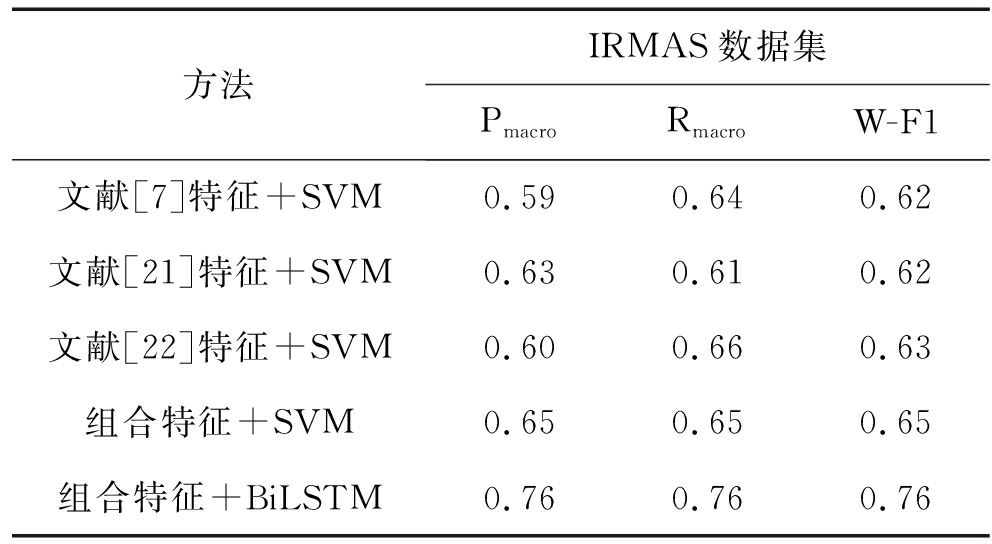
方法IRMAS数据集PmacroRmacroW-F1文献[7]特征+SVM0.590.640.62文献[21]特征+SVM0.630.610.62文献[22]特征+SVM0.600.660.63组合特征+SVM0.650.650.65组合特征+BiLSTM0.760.760.76
5 结论
本文基于TVF-EMD技术提出了面向非平稳音频信号的音质提取方法,提取了希尔伯特频谱分布特征和希尔伯特轮廓特征共两大类特征,并在不同复杂度的乐器分类实验中验证了本文所提方法的有效性。本文提出的音质特征可以补充Mel倒谱特征等传统特征中没有提取到的非线性非平稳信息,将本文所提音质特征与MFCC特征有效结合,实现了在9类乐器单音数据集上基于SVM分类器达到100%的准确率;在7类不同乐器演奏的复调乐曲中,相较于传统方法有了进一步提升。证明了所提出的方法在编码音频的音质特征方面具有很高的潜力,并且适用于不同复杂度的信号中。本文的方法补充了传统音质特征提取方法对非线性非平稳信息提取不足的方面,使得音质特征提取方法可以适应各种复杂音频场景。本文仅对频率随时间演化的特征做了初步的分析,未来将深入研究时频联合解析方法,并将应用扩展到音频生成、多乐器演奏音乐音频分离中,提升对多乐器演奏的音频的乐器识别效果。
[1] ANSI.S1.1—2013, American National Standard Acoustical Terminology[S]. New York: American National Standards Institute, 2013.
[2] 李伟, 李子晋, 高永伟. 理解数字音乐——音乐信息检索技术综述[J]. 复旦学报:自然科学版, 2018, 57(3): 271-313.
Li Wei, Li Zijin, Gao Yongwei. Understanding Digital Music-A Review of Music Information Retrieval Technology[J]. Journal of Fudan University: Natural Science Edition, 2018, 57 (3): 271-313.(in Chinese)
[3] Spreadborough K L, Anton-Mendez I. It’s not what you sing, it’s how you sing it: How the emotional valence of vocal timbre influences listeners’ emotional perception of words[J]. Psychology of Music, 2019, 47(3): 407- 419.
[4] Elliott T M, Hamilton L S, Theunissen F E. Acoustic Structure of the Five Perceptual Dimensions of Timbre in Orchestral Instrument Tones[J]. Journal of the Acoustical Society of America, 2013, 133(1): 389- 404.
[5] Allen E J, Moerel M, Lage-Castellanos A, et al. Encoding of Natural Timbre Dimensions in Human Auditory Cortex[J]. Neuroimage, 2017, 166: 60-70.
[6] Caclin A, Brattico E, Tervaniemi M, et al. Separate Neural Processing of Timbre Dimensions in Auditory Sensory Memory[J]. Journal of Cognitive Neuroscience, 2006, 18(12): 1959-1972.
[7] Peeters G, Giordano B L, Susini P, et al. The Timbre Toolbox: Extracting audio descriptors from musical signals[J]. Journal of the Acoustical Society of America, 2011, 130(5): 2902-2916.
[8] Adeli M, Rouat J, Wood S, et al. A Flexible Bio-inspired Hierarchical Model for Analyzing Musical Timbre[J]. I IEEE-ACM Transactions on Audio Speech and Language Processing, 2016, 24(5): 875- 889.
[9] Sharma R, Vignolo L, Schlotthauer G, et al. Empirical Mode Decomposition for adaptive AM-FM analysis of Speech: A Review[J]. Speech Communication, 2017, 88: 39- 64.
[10] Pons J, Slizovskaia O, Gong R, et al. Timbre Analysis of Music Audio Signals with Convolutional Neural Networks[C]∥2017 25th European Signal Processing Conference. New York: IEEE, 2017: 2744-2748.
[11] Li H, Li Z, Mo W. A Time Varying Filter Approach for Empirical Mode Decomposition[J]. Signal Processing, 2017, 138: 146-158.
[12] Schlotthauer G, Torres M E, Rufiner H L. Voice Fundamental Frequency Extraction Algorithm Based on Ensemble Empirical Mode Decomposition and Entropies[J]. IFMBE Proceedings, 2010, 25(4): 984-987.
[13] Sharma R, Bhukya R K, Prasanna S R M. Analysis of the Hilbert Spectrum for Text-Dependent Speaker Verification[J]. Speech Communication, 2018, 96: 207-224.
[14] Mo S S, Niu J W, Su Y M, et al. A Novel Feature Set for Video Emotion Recognition[J]. Neurocomputing, 2018, 291: 11-20.
[15] Sarimollaoglu M, Bayrak C. Musical Instrument Classification Using Neural Networks[C]∥5th Wseas International Conference on Signal Processing. USA: World Scientific and Engineering Academy and Society (WSEAS), 2006: 151-154.
[16] Bosch J J, Janer J, Fuhrmann F, et al. A Comparison of Sound Segregation Techniques for Predominant Instrument Recognition in Musical Audio Signals[C]∥Proceedings of the 13th International Society for Music Information Retrieval Conference, ISMIR, 2012: 559-564.
[17] Sharma R, Prasanna S R M, Bhukya R K, et al. Analysis of the Intrinsic Mode Functions for Speaker Information[J]. Speech Communication, 2017, 91: 1-16.
[18] 冯天艺, 杨震. 采用多任务学习和循环神经网络的语音情感识别算法[J]. 信号处理, 2019, 35(7): 1133-1140.
Feng Tianyi, Yang Zhen. Speech Emotion Recognition Algorithm Based on Multi Task Learning and Recurrent Neural Network[J]. Journal of Signal Processing, 2019, 35 (7): 1133-1140.(in Chinese)
[19] Sun Yingyi, Zhang Wei, Gu Hao, et al. Convolutional Neural Network Based Models for Improving Super-Resolution Imaging[J]. IEEE Access, 2019, 7: 43042- 43051.
[20] Han Y, Kim J, Lee K. Deep Convolutional Neural Networks for Predominant Instrument Recognition in Polyphonic Music[J]. IEEE-ACM Transactions on Audio Speech and Language Processing, 2017, 25(1): 208-221.
[21] Slizovskaia O, Gómez E, Haro G. Automatic musical instrument recognition in audiovisual recordings by combining image and audio classification strategies[C]∥13th Sound and Music Computing Conference. Germany, 2016: 442- 447.
[22] Racharla K, Kumar V, Jayant C B, et al. Predominant Musical Instrument Classification based on Spectral Features[C]∥7th International Conference on Signal Processing and Integrated Networks. India, 2020: 617- 622.




