1 引言
现如今,移动智能设备的免提交互是非常普遍的。由于尺寸的限制,这些设备只能使用小型扬声器。为了产生较大的音量,这些扬声器常常工作在饱和区附近,这会导致很明显的非线性声学回声问题。这些回声无法用线性AEC算法中消除。在一般的回声抵消系统中,即使扬声器信号和麦克风拾取的信号之间存在很小的非线性失真,线性自适应滤波器的收敛也会受到严重影响[1-2]。因此如何处理非线性回声成为一个极具挑战的问题。
处理非线性回声问题的一般方法是对非线性回声路径[3- 4]进行建模,从而将非线性问题转化为线性的形式,例如Volterra级数模型[5-9]和神经网络(Neural Networks,简写为NN)模型[10-12]。Volterra级数将非线性关系表示为多项式的形式,该模型一般都需要高阶的滤波器系数才能有效的建模非线性路径,这会带来巨大的计算量。NN模型作为一种数据驱动型模型,往往需要大量的激励信号和回声信号去充分的训练模型,然而由于电声系统的非线性特性和声学回声路径耦合在一起,该模型的普适性也成为一个挑战。这两种解决方法的最大争议在于非线性回声的特点和形成原因很复杂且缺乏一般的表达形式。另外,后置滤波也是处理非线性回声的一种方法,但这种方法往往会影响语音质量[13-14]。文献[15]中还提到了一种工程上使用的方法,但是其与特定设备相关,普适性也有待考虑。所以非线性回声的问题仍待研究。
在本文中,我们采用了不同的思路,并非去对非线性回声路径建模,而是将全带AEC问题转换为子带AEC问题,把非线性失真转换成子带内的加性噪声。扬声器的非线性主要表现为谐波失真和互调失真,这会导致高频出现众多的高次谐波[16-17]。对于全带自适应滤波器而言,由于代价函数定义在全带上,频谱上任何一部分出现非线性关系都会影响全带误差,进而影响自适应滤波器的收敛。然而对于子带方法,因为每个子带独立更新且取决于各个子带自身的误差信号,出现在高频的谐波成分仅仅是那些子带上的“加性噪声”。因此没有谐波成分的子带可以正常收敛,有谐波成分的子带的收敛情况取决于“加性噪声”的大小程度[19]。这种方法的最大好处是具有普适性,可以与其他各种非线性回声抵消方法结合,而且与具体的扬声器失真无关。
本文首先分析了AEC系统中的非线性问题和传统方法处理该问题的局限性,进而提出了基于多相滤波器组的子带AEC方法。为了证实子带方法处理非线性回声的有效性,我们在仿真数据和真实数据上均进行了AEC实验。实验证明,正常音量下,子带方法的ERLE不低于全带方法;当非线性较明显时,子带方法的优势会显现出来。最后,将本文所提方法和目前主流的两个回声抑制模块(WebRTC和Speex)进行实际数据下的性能对比,正常音量(扬声器1 m距离处的声压级为60 dB~70 dB)下,子带方法与主流AEC算法的性能基本一致;当扬声器音量达到90 dB时,子带方法的性能损失明显小于这两种回声抑制方案。
2 回声抵消系统中的非线性
2.1 回声抵消模型和传统算法
回声抵消系统的基本结构如图1所示,送往扬声器播放的信号是x(n), 假设扬声器单元是线性的,那么扬声器实际播放出来的信号也是ax(n),a是放大倍数,该信号经过房间冲激响应h(n) (假设h(n)也是线性的),得到回声信号ye(n), 房间的其余噪声为ν(n),此时麦克风拾取到的信号记为y(n)。图1中,![]() 是自适应滤波器,其作用是,在x(n)和y(n)的驱动下,尽可能的逼近真实的回声路径h(n),从而使得自适应滤波器的输出
是自适应滤波器,其作用是,在x(n)和y(n)的驱动下,尽可能的逼近真实的回声路径h(n),从而使得自适应滤波器的输出![]() 接近于y(n),进而达到使残差信号e(n)尽可能小的目的。此时的e(n)就是回声抵消之后的信号。整个过程概括为一句话就是:根据信号x(n),自适应地合成回声
接近于y(n),进而达到使残差信号e(n)尽可能小的目的。此时的e(n)就是回声抵消之后的信号。整个过程概括为一句话就是:根据信号x(n),自适应地合成回声![]() 并从麦克风拾取到的信号中减去该回声。
并从麦克风拾取到的信号中减去该回声。

图1 单通道回声抵消基本结构
Fig.1 The basic structure of single-channel echo cancellation
在回声抵消模型中,最重要的步骤就是估计回声路径系统函数,这就用到了自适应滤波器技术。最早的自适应滤波器研究工作可以追溯到上世纪50年代末,到现在以线性自适应滤波器为代表的经典算法已经有了很多,时域的自适应滤波算法有最小均方算法(LMS)[18]、归一化最小均方算法(NLMS)等,频域的自适应滤波算法有频域LMS算法(FLMS)和多延迟块自适应滤波器算法(MDF)等[19-20]。
2.2 回声抵消系统中的非线性通路
线性AEC最基本的思想就是使用线性自适应滤波器去估计回声路径,并且将滤波器输出的回声估计信号从麦克风记录的信号中减去,达到回声抵消的目的,如果抵消不彻底则会留下残余回声。这其中,最重要的基本要求就是从D/A转换器到A/D转换器之间的信号通路必须是线性的。一个完整的信号通路包含四部分,从(A)到(D)[21],如图2所示,(A)D/A转换器,(B)扬声器单元(功率放大器和扬声器),(C)声学回声路径,和(D) A/D转换器。
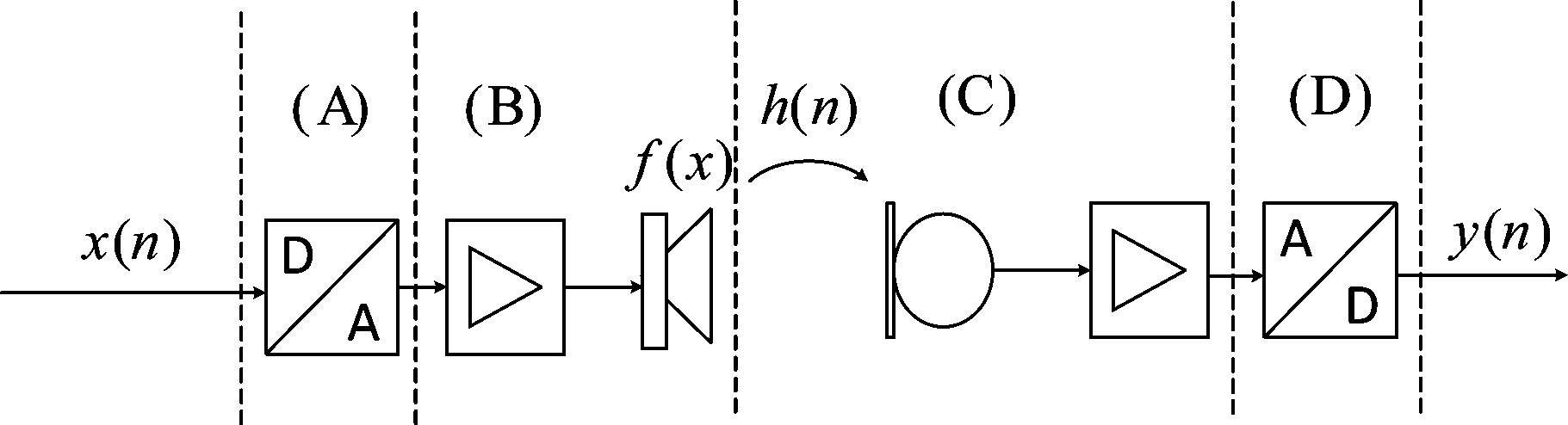
图2 非线性回声路径模型
Fig.2 Model of the nonlinear echo path
在现代数字通信系统中,D/A转换器和A/D转换器的精度已经越来越高,由这两部分引起的非线性失真可以忽略不计。(C)部分中的麦克风不需要功率放大,一般只需要阻抗匹配即可,其能承受的最大声压远超过一般的语音应用,因此可以认为是线性系统;回声路径h(n)在一般的语音应用中都属于小振幅线性声学范畴,可以由线性自适应滤波器来辨识。因此导致非线性失真的主要原因是扬声器单元,该单元是一个将电信号转化为声信号的电声器件,属于功率放大器件,一般都有线性的工作范围,一旦超出这一范围,就会出现明显的非线性失真。
扬声器的非线性特性主要表现为谐波失真和互调失真,表现在频域上即为高频的高次谐波。经过大量实验证实,扬声器单元的失真大小与音量放大倍数和信号频率都有关系。当扬声器的音量越大时,扬声器系统由于性能过载会呈现出明显的非线性,尤其是当其音量越接近于饱和区时。另外,扬声器系统在同等声压级下,低频信号的非线性失真要比高频信号的非线性失真明显得多。
2.3 传统方法的局限性
非线性回声最大的问题在于从扬声器到麦克风的信号通路上存在非线性部分,这使线性滤波器无法准确的建模。这种情况下麦克风采集到的回声中会出现一些“多余”的频率成分,我们叫做非线性成分。非线性成分可能是“无中生有”——即扬声器输入信号本身不含这些频率成分,也可能与扬声器输入信号频率重叠,此时麦克风采集的回声信号中,非线性成分将和线性回声混合在一起,导致回声路径不再是一个理想的线性模型。更为棘手的是,在语音和音频应用中,由于馈给扬声器的信号不断随时间变化,动态范围很大,频谱范围宽,因此这些非线性现象也随着时间不断地变化,给回声路径建模造成极大的困难。
图3给出500 Hz单频信号在一种非线性情况(截辐)下的谐波失真情况。
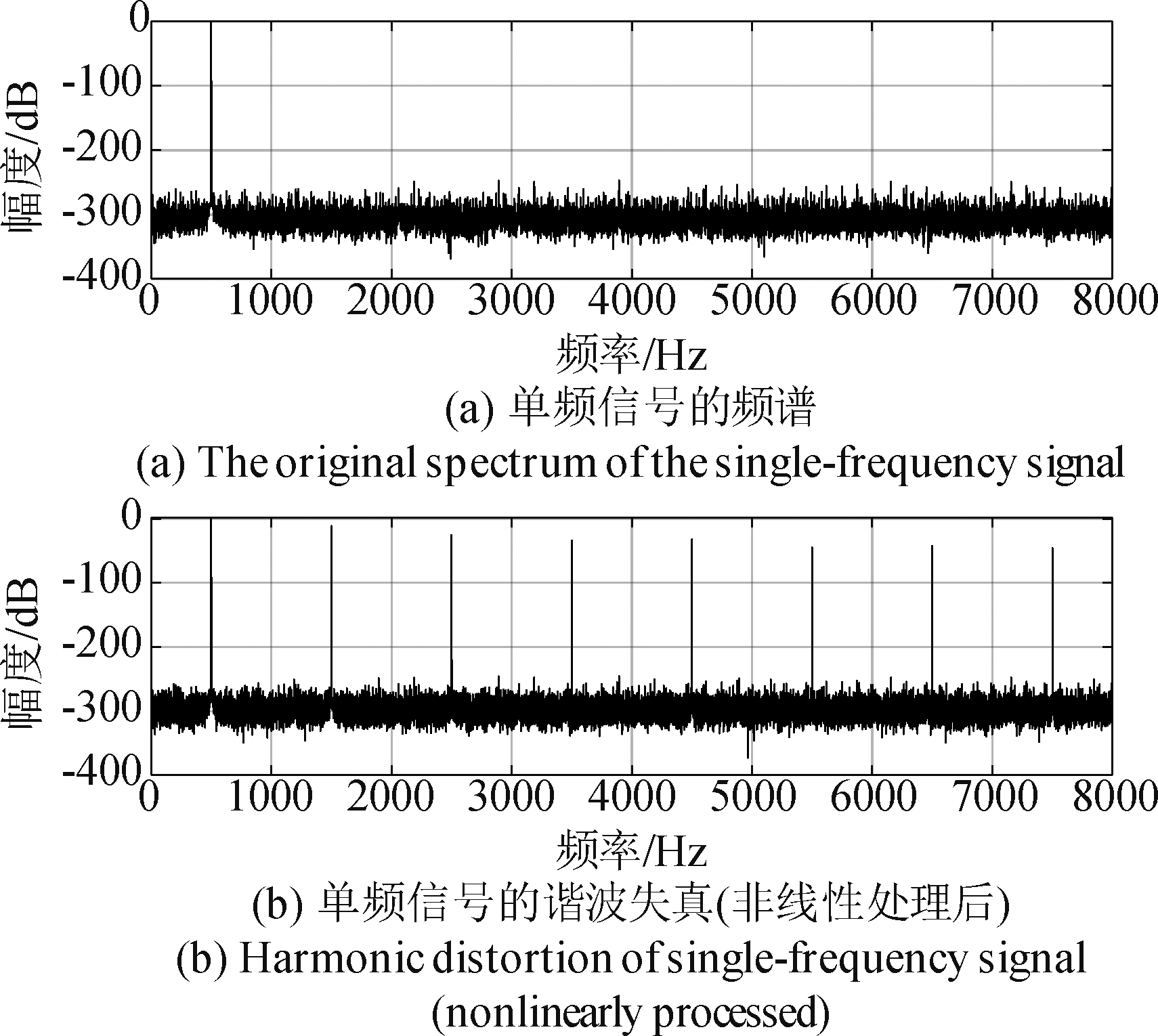
图3 单频信号的谐波失真
Fig.3 Harmonic distortion of single-frequency signal
传统的自适应滤波算法在学习这种非线性回声路径会存在一些问题。对于时域的算法(以NLMS为例[1-2]),每次更新滤波器时,都需要计算当前的误差e(n)。从时间统计上,当前误差e(n)是所有频率成分产生的综合误差。因此,滤波器每次更新的增量几乎都会受到所有非线性成分的干扰。对于频域的算法(以FLMS为例[19-20]),由于其是在频域更新滤波器,且先进的算法中各个频率还有独立的学习因子,所以在最理想的情况下,其各个频率应该单独收敛互不干扰,即使部分频带存在非线性成分,也不会影响其他频率的收敛。但是事实上,因为频域算法进行了分块操作,这种分块操作相当于对信号加矩形窗,会造成较大的频谱泄露,导致滤波器在某一频率上的收敛一定会干扰附近的其他频率。如果需要保证较小的处理延迟,通常还需要更小的分块(如MDF算法),这会造成更加明显的频谱泄露。
正是由于传统方法处理非线性回声的局限性,本文提出基于多相滤波器组的子带处理方法。我们考虑将信号分解到不同的频带上,在保证带间混叠较小的情况下,各频带采用独立的自适应滤波器,可以根据自己频带的误差信号独立收敛。
3 基于多相滤波器组的子带回声抵消
3.1 子带方法的优势
为了简单起见,我们假设参考信号x(n)有两个频率成分组成,分别为fa和fb。频域信号分量为X(fa)和X(fb)。如果信号路径是线性的,并且用H( f )表示,那么麦克风信号y(n)在频域可表示为Y( f ),其也包含两个频率分量Y(fa)和Y(fb),且满足,
Y(fa)=X(fa)·H(fa),Y(fb)=X(fb)·H(fb)
(1)
将X( f )作为输入信号,Y( f )作为输出信号,H( f )在fa和fb处的模型可以很容易的辨识。
然而,如果将一个非线性函数f(·)加在信号路径中,比起线性情况下,麦克风信号y(n)中将会有更多的谐波分量,例如Mfa±Nfb,M和N是和非线性特性相关的整数。所以,对于这些新的频率成分,在线性系统辨识的理论里,由于没有相应频率的输入信号,全带方法的误差是无法收敛的,所以全带自适应滤波器将会发散。
如果将全带方法变换到子带上,假设子带被定义为B0,B1等,则新的频率成分连同原先的频率成分将会被分到不同的子带上,尤其是在高频,谐波分量会很稀疏。如果子带足够小,y(n)分解后的子带上将会出现以下几种情况:(1)只有原始的频率成分之一,例如fa,或者(2)包含原始信号的频率成分之一和与其他子带相关的干扰成分,例如fb+Mfa,或者(3)仅仅只有干扰成分,例如Nfb,或者(4)没有有效的频率成分。因为子带方法中每个子带上的自适应滤波器是独立收敛的,所以情况(1)将会正常收敛,情况(2)可以认为是含有加性噪声的线性辨识问题,其收敛将会受到该子带上SNR的影响,情况(3)将无法收敛,情况(4)中,没有有效的信息可以学习,但是也没有残余回声。综上,子带方法的收敛一定比全带方法更好。而且将信号分解到子带,自适应滤波器的长度更短,因此具有较快的收敛速度和追踪速度[22-23]。
显然,子带方法无法解决非线性问题,但是通过将信号分解到不同的子带上,可以让输入和输出在某些子带上保持线性关系,所以在这些子带上可以正常进行回声抵消。这说明,不仅限于回声抵消,任何全带的非线性问题都可以用上述的子带方法来改善。子带方法将信号分解到若干个子带上,然后各个子带独立地按照AEC的思路进行收敛,这种做法最突出的特点就是令各个子带的误差分别独立地最小化,这也是子带方法与全带方法最根本的区别。这一区别改变了全带算法中自适应滤波器的收敛路径,主要有两个好处:(1) 避免各子带间的干扰,尤其是非线性失真的干扰;(2) 加快收敛速度。
3.2 子带回声抵消
一般的子带AEC系统的结构如图4所示[24],即每个子带都有其独立的自适应滤波器,并且每个子带独立收敛。分析滤波器组将参考信号x(n)和麦克风信号y(n)分解到若干个子带上,然后每个子带经过独立回声抵消算法消除各子带上的回声,每个子带上的残余回声信号经过综合滤波器组综合作为最终的残差信号。理论上,语音信号的频率成分相对集中于中低频,因此集中处理中低频一定有利于AEC在语音通话时的性能表现,但是这要结合应用场景进行算法的调整优化。如果目标是音乐信号,针对语音信号的优化可能就无法起到应有的作用。因此本文中,各子带是相同的处理方法和过程,具体到应用中要根据信号特点进行灵活调整。
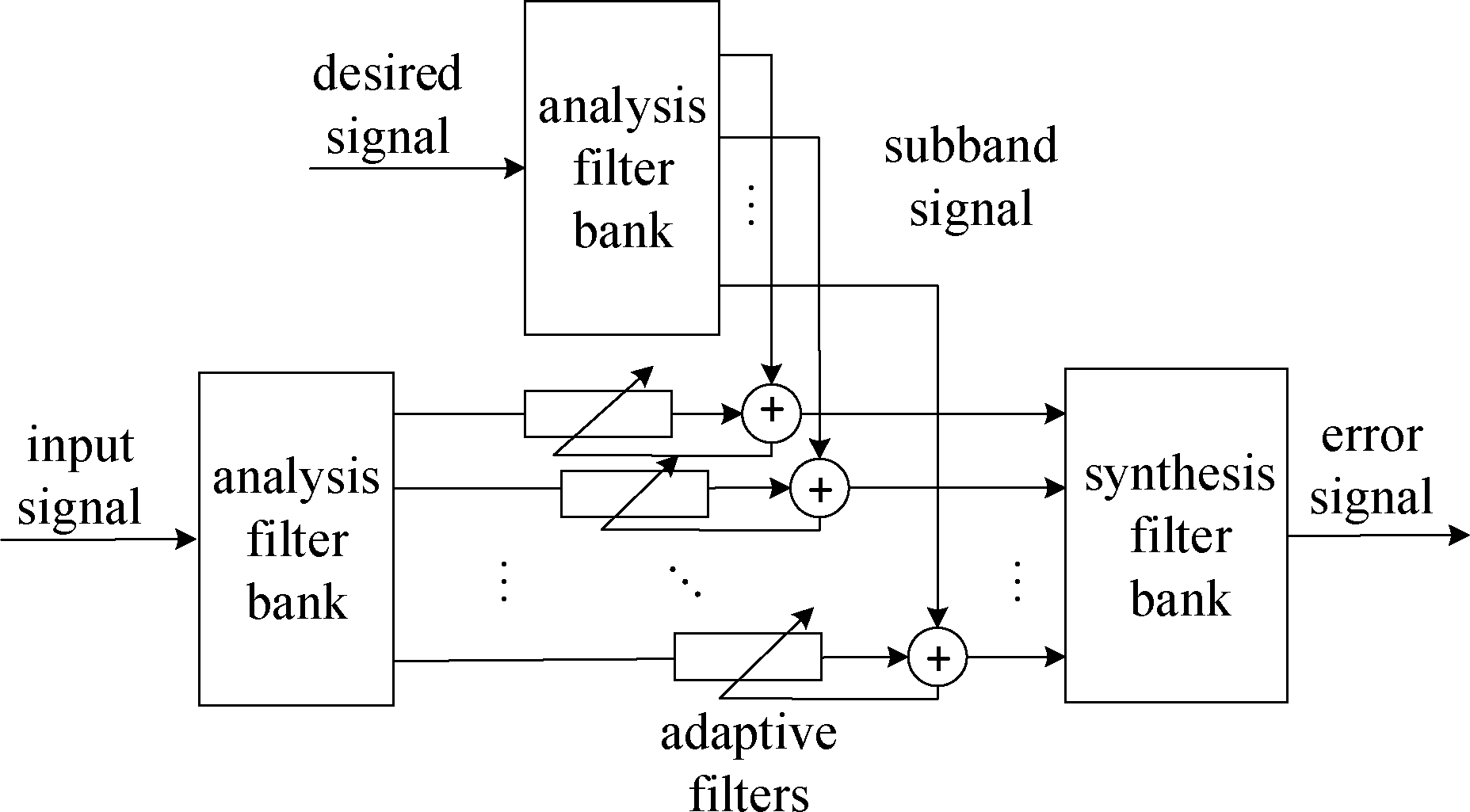
图4 子带回声消除的结构
Fig.4 Set-up of the subband echo cancellation
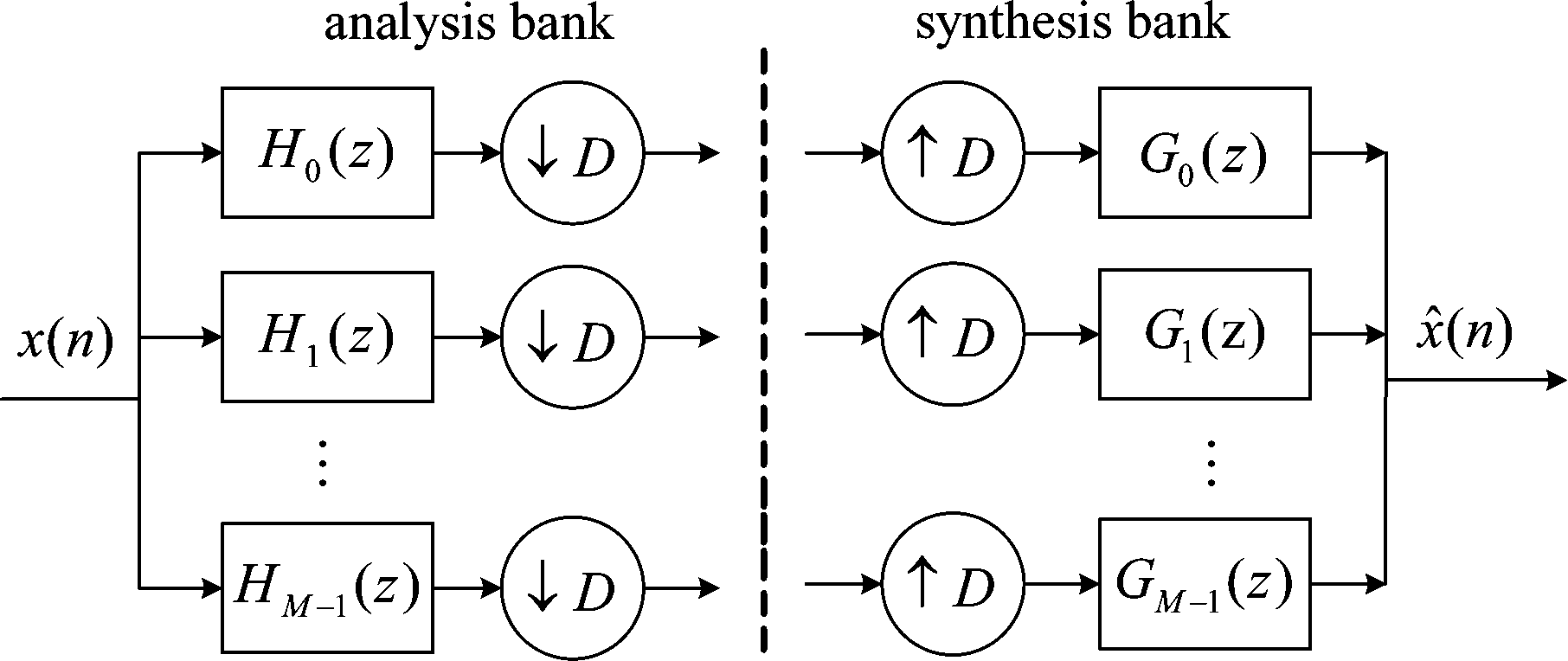
图5 子带个数为M,降采样为D的子带系统
Fig.5 Analysis and synthesis branch of a M-channel filter bank with subbands decimated by D
从图4中可以看出,分解后的子带信号和分解前的全带信号有相同的采样点个数,即就是,如果按图4中的结构直接实现系统并且计算的话,子带算法的计算量是全带算法的M(子带个数)倍。鉴于此,因为经过滤波器组分解后,每个子带均为窄带信号,故可以进行降采样操作。图5中是子带个数为M,降采样为D的子带系统。其中的关键问题是:如何降低相邻子带间的混叠和减小系统的重构误差[25]?高效实现子带滤波器组最常见的方法是多相结构[26]。
3.3 使用多相结构来高效实现
本文中使用的多相滤波器组为DFT调制滤波器组。其中,原型滤波器一般要求具有较窄的过渡带、较大的阻带衰减等,然后将其调制到不同的频带上来得到分析滤波器组。假设一个调制滤波器组由M个滤波器构成,这些滤波器分别为h0(n1T1),h1(n1T1),…,hk(n1T1),…,hM-1(n1T1),T1为采样间隔。其中h0(n1T1)是一个低通滤波器,其余的滤波器具有如下的结构:
(2)
其中D是降采样数。这种滤波器组最大的优势就是可以用多相结构和FFT单元来加速分解和综合过程中的计算。
结合子带分解和综合的理论以及多相结构的实现,可以推导出高效的实现过程。图6给出了计算方法,(a)图是子带分解过程,(b)图是子带重构过程。其中hproto是原型滤波器,![]() 是hproto的时间翻转形式[19]。对于子带分解,输入信号先通过原型滤波器加窗,然后将得到的数据进行分组,进行FFT 操作,进而得到子带数据。子带综合和子带分解是相反的操作。
是hproto的时间翻转形式[19]。对于子带分解,输入信号先通过原型滤波器加窗,然后将得到的数据进行分组,进行FFT 操作,进而得到子带数据。子带综合和子带分解是相反的操作。

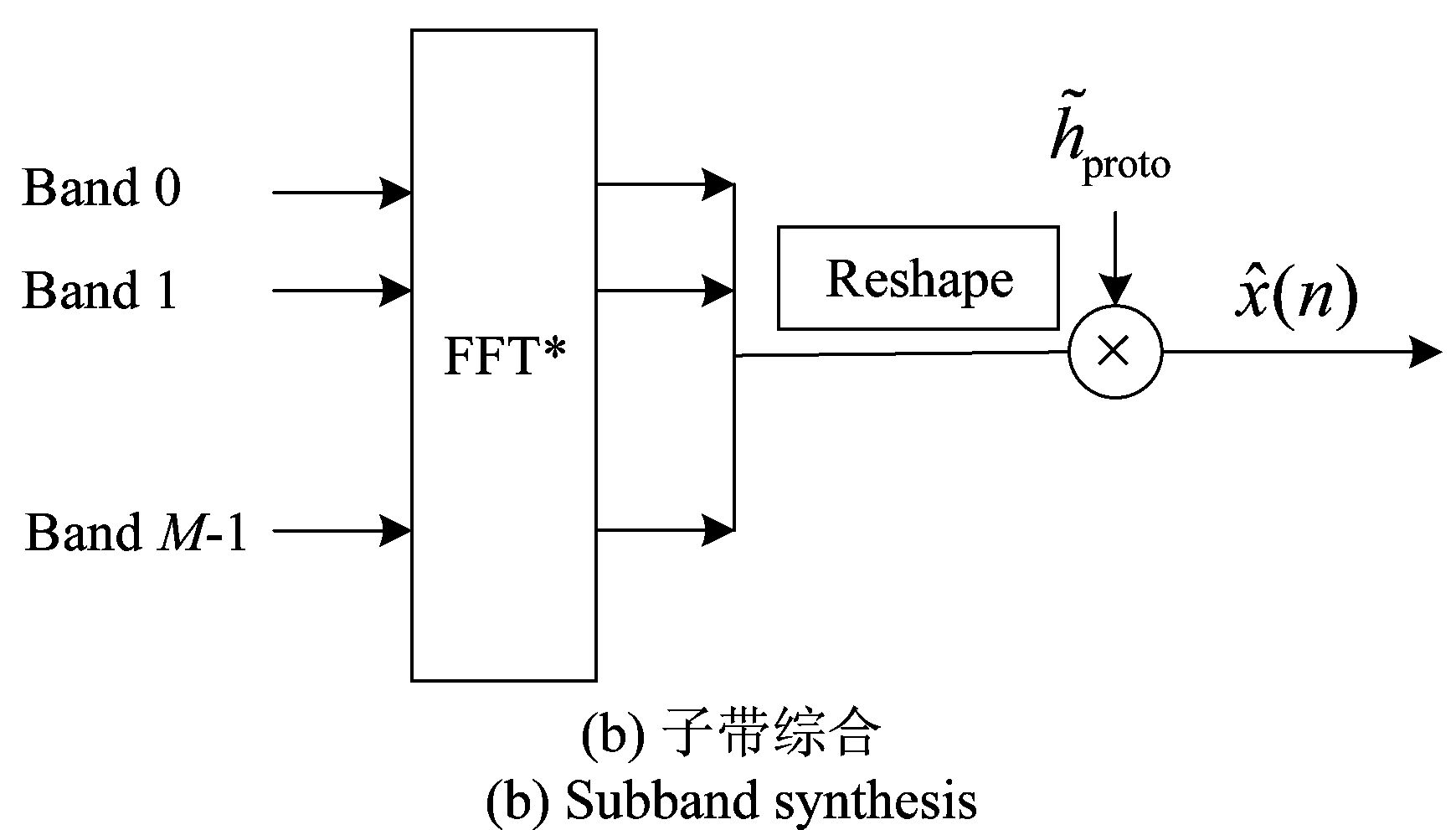
图6 DFT调制多相滤波器组进行子带分解和综合
Fig.6 The subband analysis and synthesis using DFT-modulated polyphase filter bank
一般来说,我们需要尽可能多的子带、相邻子带间没有混叠且能完全重构的滤波器组。然而这些要求无法同时满足,在实际应用中需要折衷选择。由式(2)可以看出,子带系统中的所有滤波器都是由原型滤波器调制而来,所以滤波器组的性能取决于原型滤波器的特性[27]。
3.4 原型滤波器的设计
原型滤波器需要满足以下设计原则[28]:(1)阻带衰减尽可能大:阻带衰减不够会带来过高的混叠,严重时甚至会造成自适应算法不收敛;(2)较窄的过渡带:过渡带太宽也会带来混叠,并且过宽的过渡带会使得信号的特征值分散度增大,从而降低自适应算法的收敛速度;(3)线性相位:可以保证信号通过该滤波器组时没有相位失真。就这一点而言,FIR 型的原型滤波器更容易做到线性相位。原型滤波器的阻带衰减越大并且过渡带越窄,就越能保证由该原型滤波器调制的滤波器组的各个子带越独立,算法收敛越好。
已经有许多研究工作讨论原型滤波器的设计问题,这是个典型的优化问题,且和特定的应用相关。常用的设计原型滤波器的方法有窗函数法,特征值法等。在本文中,我们使用最小二乘迭代法[28],其基本的思想就是选择目标函数,不断修正参数,使目标函数最小化。详细讨论原型滤波器设计超出了本文的关注范围,我们采用文献[28]中的设计方法,该方法可以灵活的控制滤波器的各项参数。
对于子带AEC而言,混叠是很重要的问题[25]。为了减小混叠,要求原型滤波器的过渡带尽可能窄,所以滤波器会较长且重构误差也要放大。另外,对阻带衰减的要求也要放宽。我们实验中使用的原型滤波器和滤波器组的频响曲线如图7所示。将0 Hz~fsHz(本文中fs=16 kHz)分成64个子带,降采样数D=32,原型滤波器长度为512。重构误差约为-100 dB,混叠约为-92 dB。
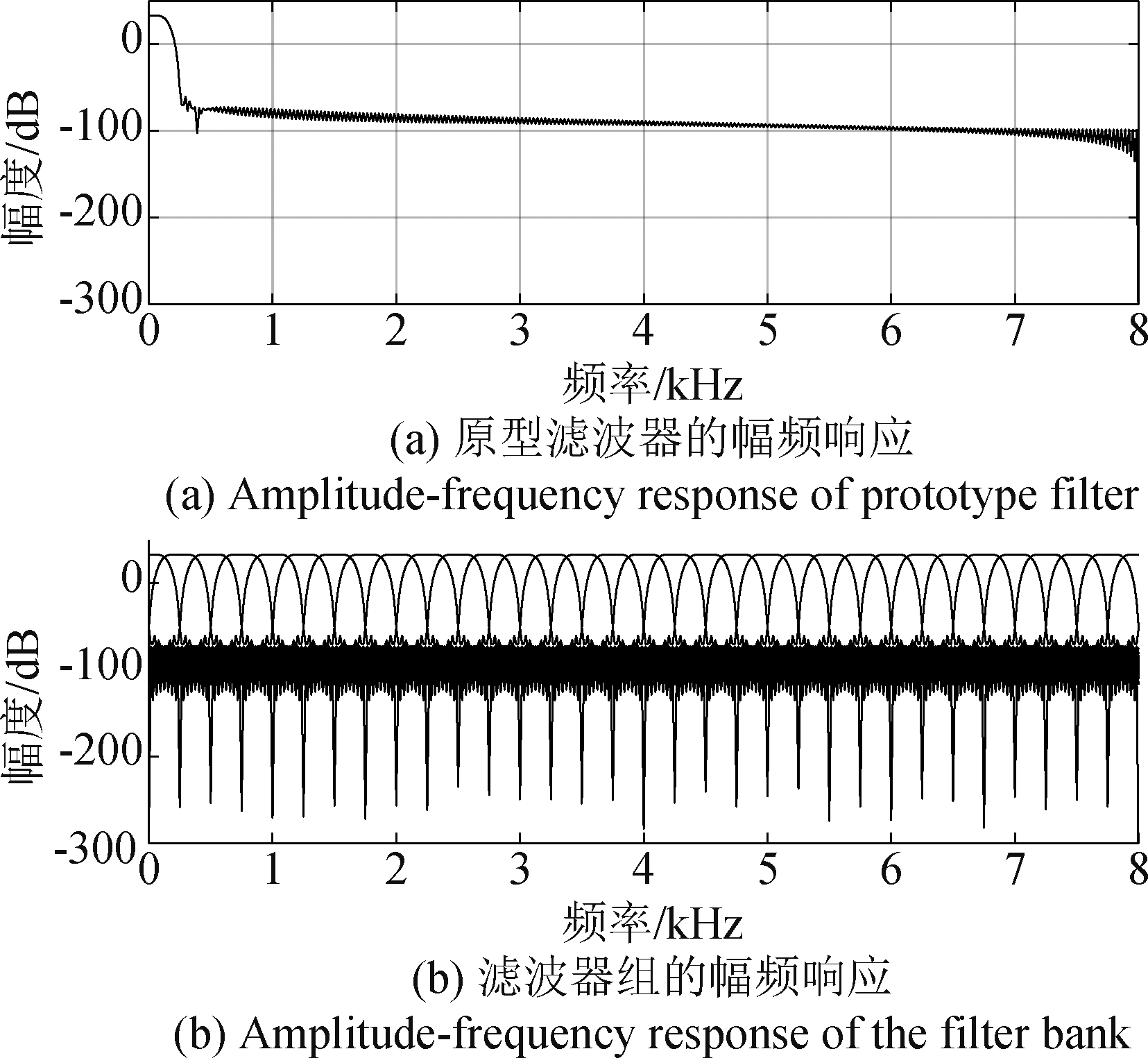
图7 原型滤波器和滤波器组的幅频响应
Fig.7 Amplitude-frequency response of the prototype filter and filter bank
从理论上说,子带划分越多,某些频率的非线性谐波分量就越有可能被分解到其他的子带上,从而受干扰的频带会越少,子带AEC算法的性能也会越好。但是子带划分的数量有两方面限制:(1)子带划分过多会导致原型滤波器的设计很难满足阻带衰减和过渡带宽度的要求;(2)子带划分过多会导致子带分解和综合系统的误差变大。本文是在这两个限制条件下,选择了尽可能多的子带数量。
4 实验
在这节中,我们通过四个实验来验证前面的分析,不仅能够说明不同数据下的处理效果,还能够说明不同算法下的处理效果。4.1小节使用仿真数据,仿真采用一种典型的非线性函数:截幅,信号是单频信号和白噪声信号。该实验的目的是观察非线性处理之后,出现在高频的谐波成分,并且观察在这种理想的情况下不同信号的回声抵消效果。4.2小节使用在消声室中录制的非线性数据,这些数据可以比较准确的反映扬声器的非线性特性,避免了复杂回声路径的影响。实验采用笔记本电脑扬声器数据来进行非线性AEC实验,笔记本电脑型号为DELL G7 7588,使用AWA 5636声级计来测量扬声器正前方约10 cm处的声压级。在4.3小节中,我们在普通的会议室中录制数据并比较子带方法和全带方法的区别,为了使实验结果更具有说服力,这里的数据包括了语音信号和音乐信号。笔记本和声压级校准与4.2小节一样。4.4小节主要对比子带方法和目前主流的两个回声抑制模块之间的性能。
需要指出的是,本节实验只比较全带方法和子带方法处理非线性回声消除的性能,不考虑复杂的AEC算法优化和Double-Talk检测。两种方法下均使用学习率为1的NLMS算法。AEC的性能用ERLE来衡量,定义,
(3)
其中,e(n)是残余回声信号。ERLE越高,则e(n)越小,即AEC性能越好。注意分子和分母不是纯粹的回声信号和残余回声信号,而是麦克风拾取的信号与全部残余信号,这与ERLE的理论定义有所不同。ERLE的理论公式是计算回声信号和残余回声信号的功率比,但是通常我们只能获取到麦克风信号,而无法获取到纯粹的回声信号。并且即使在未发生双讲时,麦克风信号中也包含了背景噪声和回声信号,且无法分离。本文的实验主要考虑大音量下的非线性回声问题,因此在麦克风信号中,回声信号的功率远高于实验条件下(消声室和会议室)的背景噪声功率,并且通常至少高出40 dB~50 dB。因此在式(3)中,我们直接用麦克风信号替代了回声信号,在上述条件下,这可以很好的近似理论公式的结果。ERLE也是行业内评价AEC算法性能的重要指标。
这里特别说明一点,在本文的实验部分里,我们使用NLMS算法(注意全带算法使用的是NLMS算法,分解后的各个子带上使用参数一致的NLMS算法)。在这样的对比下,本文证明了子带分解能够提高AEC算法在非线性回声下的性能。在实际应用中,也可以将子带上的自适应算法换成频域算法等其他AEC算法。这与子带的分解综合是不冲突的。
4.1 仿真数据的结果对比
该仿真数据中,截幅函数为,

(4)
其中,a是控制截幅大小的因子。单频信号是1000 Hz的正弦信号,此时a=1.5;白噪声时,a=6。对于这两种信号,均约有40%的采样点被截幅。截幅后的信号再卷积房间冲激响应(使用镜像声源法计算得到)得到麦克风信号y(n)。采样率均为16000 Hz。信号长度均为20 s。如图8所示,截幅后的信号在高频出现很多的谐波成分,例如3000 Hz、5000 Hz和7000 Hz,这将会严重影响全带AEC的收敛。当使用子带方法时,不同的频率成分被分解到不同的子带上,原始频率1000 Hz被单独的分解到第5个子带上,则在该子带上保持线性关系。

图8 原始信号x(n)的频谱和f(x)(非线性处理后的信号)的频谱
Fig.8 The original spectrum of the x(n) and the spectrum of the f(x)(nonlinearly processed signal)
图9是两种方法下的ERLE。显然,全带NLMS算法几乎没有收敛,但是子带NLMS 算法却正常工作。因为自适应滤波器足够长,所以在线性情况下,ERLE可以充分收敛。然而,在白噪声下,如图10所示,两种方法的性能区别不大。原因是白噪声中包含太多的频率成分,即使在子带方法中,也几乎不存在理想的线性情况的子带。
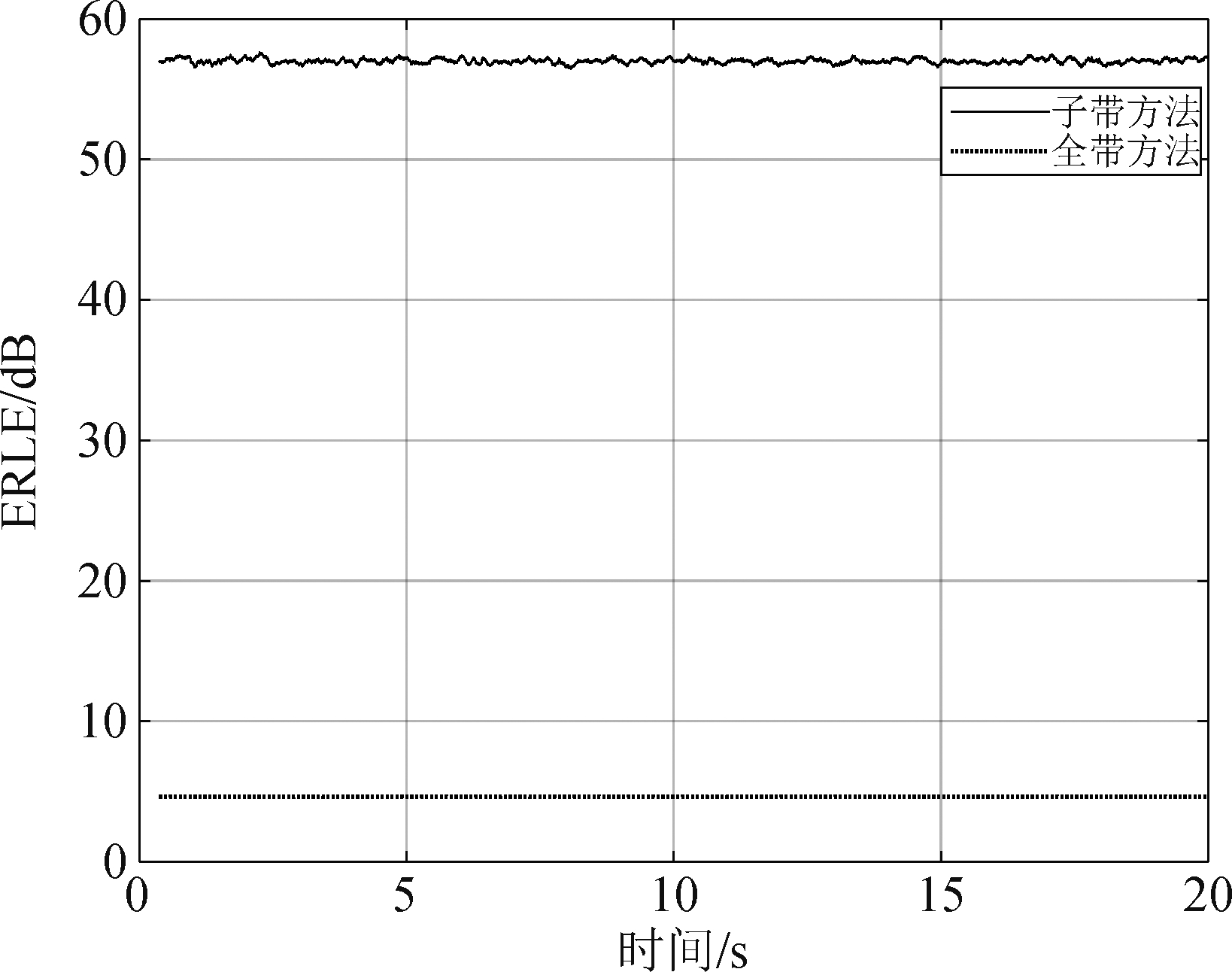
图9 信号x(n)是1000 Hz的单频信号
Fig.9 Signal x(n) is a 1000 Hz single-frequency signal
4.2 消声室数据的结果对比
在该实验中,我们主要观察笔记本电脑的扬声器的非线性特性。测试信号是在消声室中录制的1000 Hz正弦信号和白噪声信号。此时声学回声路径对扬声器非线性特性的影响可以忽略不计。调节笔记本电脑系统的音量以实现不同声压级(声级计测量)。然后将该信号与仿真的房间脉冲响应进行卷积以获得最终的麦克风信号y(n)。对于正弦信号和白噪声信号,不同声压级下的ERLE分别如图10和图11所示。
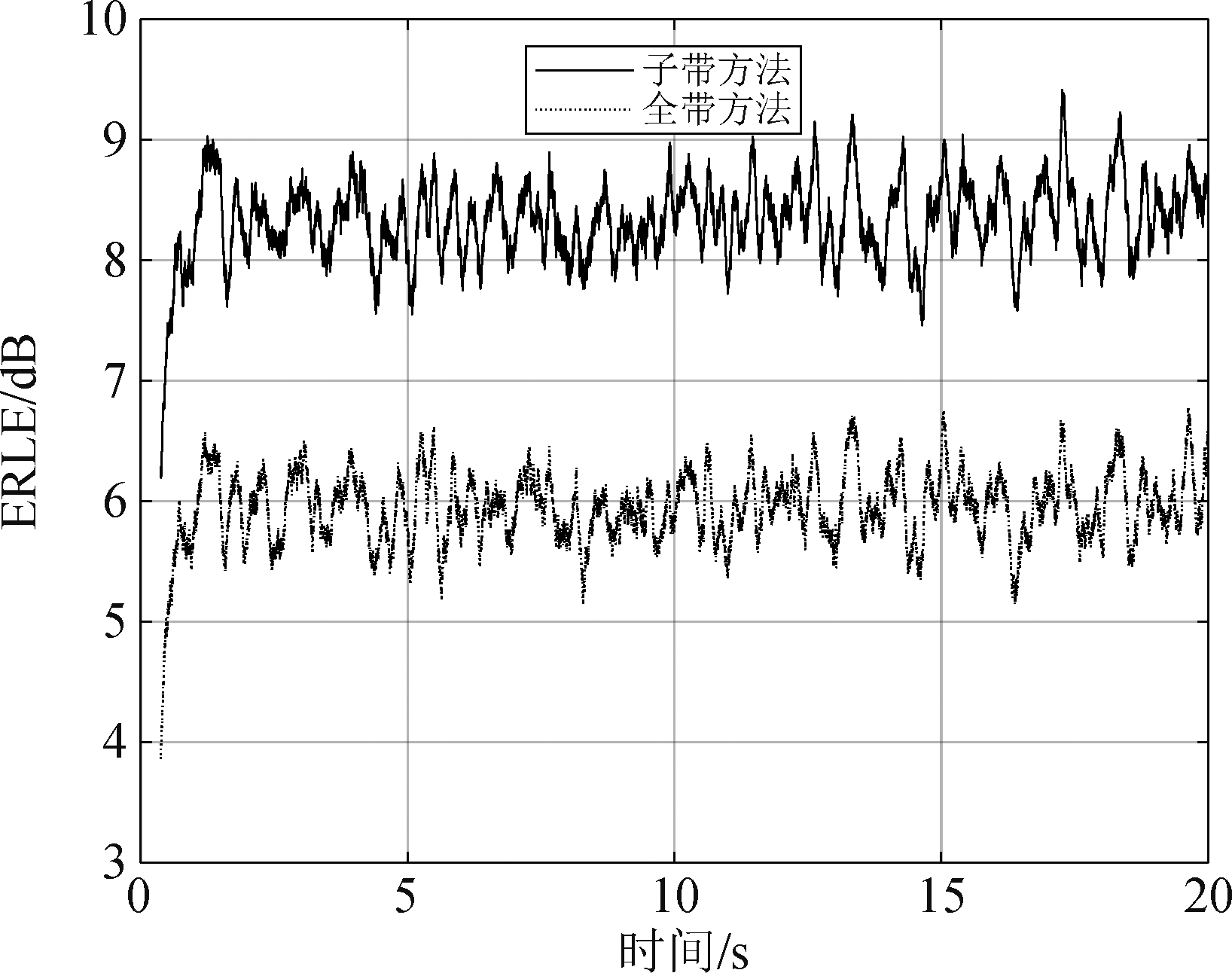
图10 信号x(n)是白噪声
Fig.10 Signal x(n) is a white noise signal
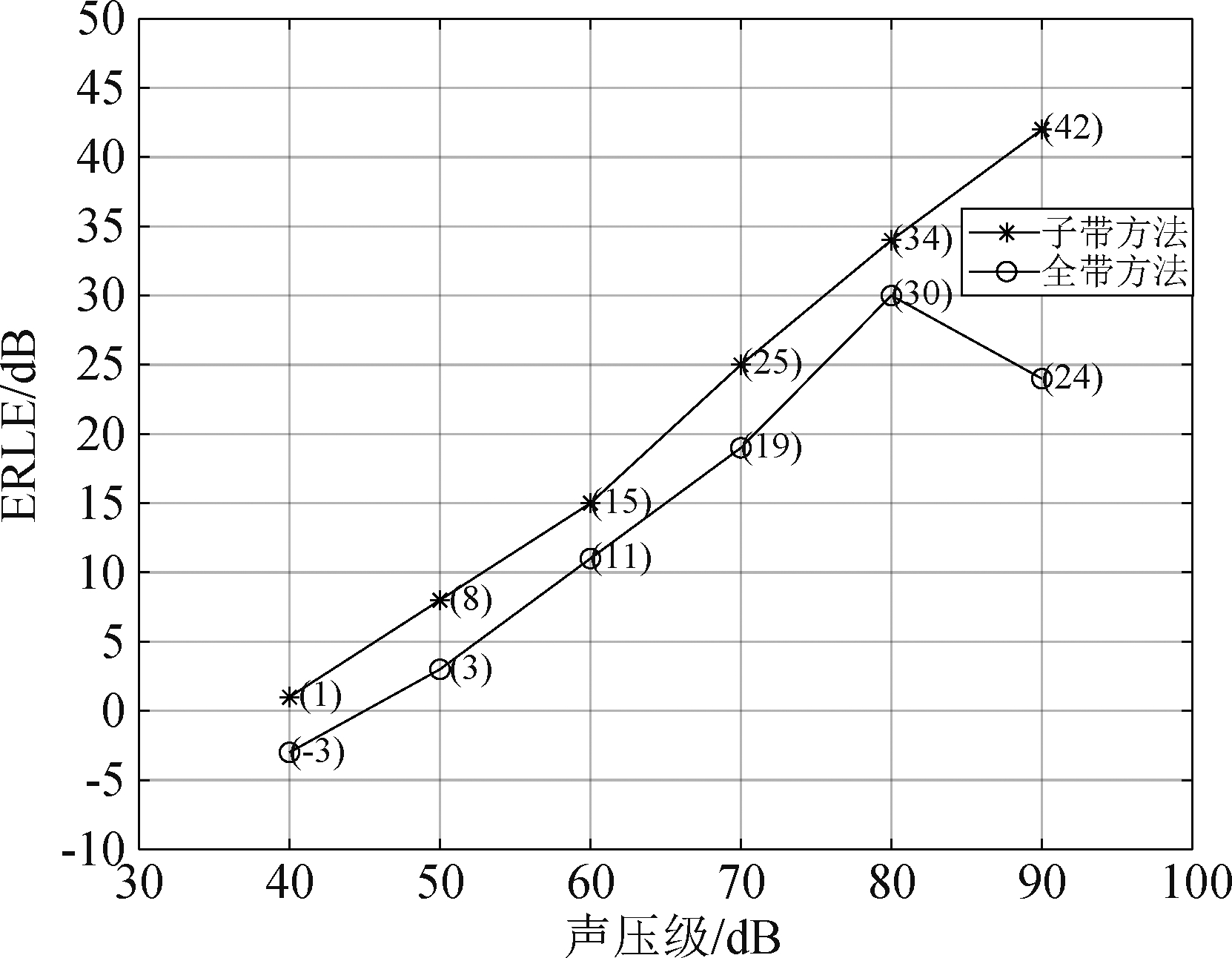
图11 信号x(n)是1000 Hz正弦信号
Fig.11 Signal x(n) is a 1000 Hz single-frequency signal
在图11中,可以发现从40 dB到80 dB,全带方法和子带方法都实现了ERLE的稳定提升。原因是随着SPL的增加,回声能量与环境噪声能量的比值随之增加,此时的环境噪音主要来自笔记本电脑的风扇。正如预期的那样,当SPL(Sound Pressure Level)接近90 dB(几乎是笔记本电脑正常放音的最大音量)时,由于扬声器性能饱和引起的非线性,导致全带方法的性能显著下降,但是子带方法的性能仍在提高。白噪声的结果略有不同,如图12所示。与4.1节实验结果相似,子带方法处理白噪声的效果不如线谱信号。但是,随着SPL的增加,子带方法和全带方法之间的ELRE差异会略微增加。
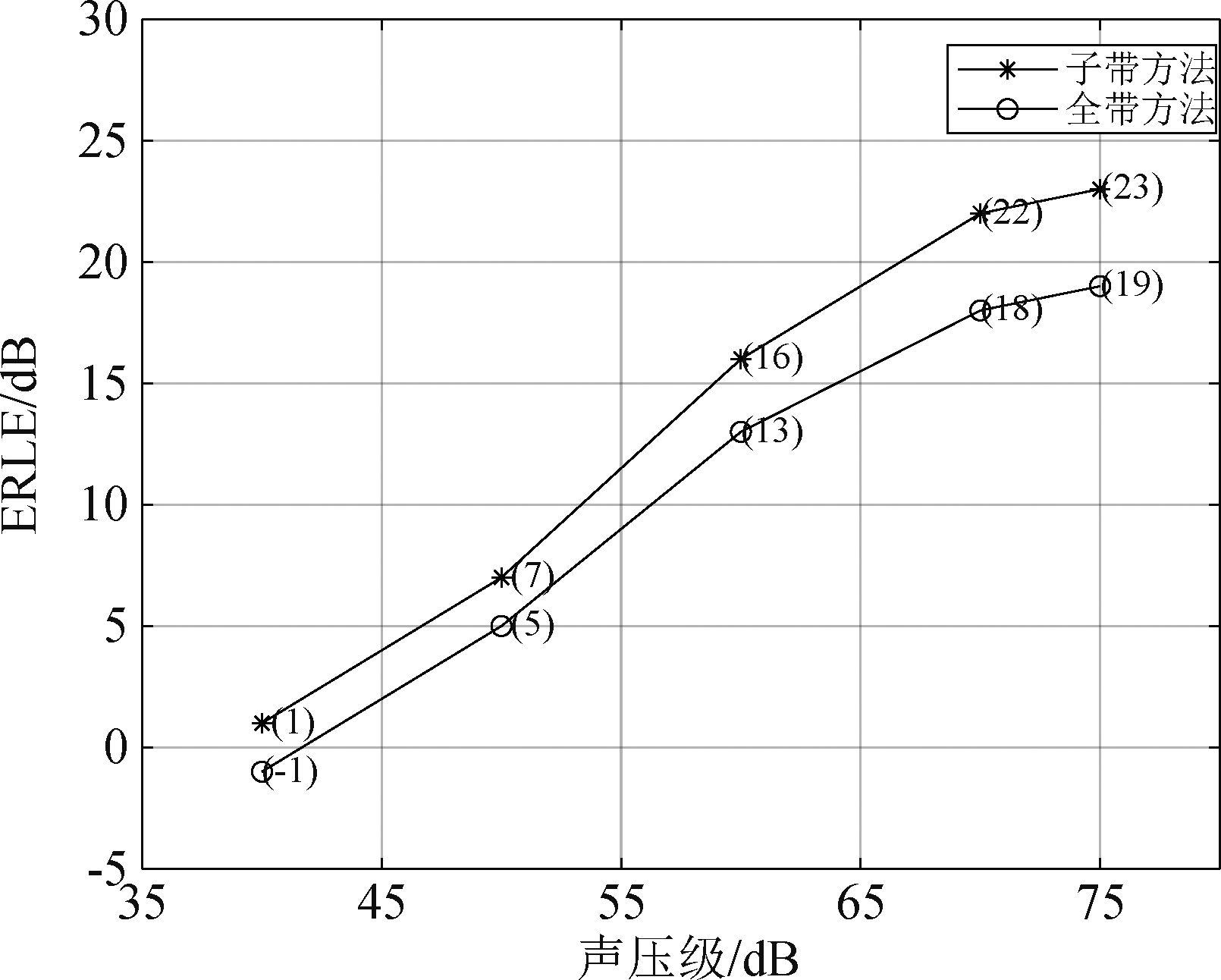
图12 信号x(n)是白噪声
Fig.12 Signal x(n) is a white noise signal
4.3 真实房间数据的结果对比
在该实验中,我们在安静的普通办公室中录制回声数据来测试AEC性能。测试信号不仅有之前使用的1000 Hz正弦信号和白噪声信号,还有另外一种由两个频率成分组成的线谱信号:1000 Hz和2500 Hz的组合线谱信号,目的是测试笔记本电脑扬声器的互调失真的影响。调节笔记本电脑系统的音量以实现不同声压级,实验结果如图13~15所示。
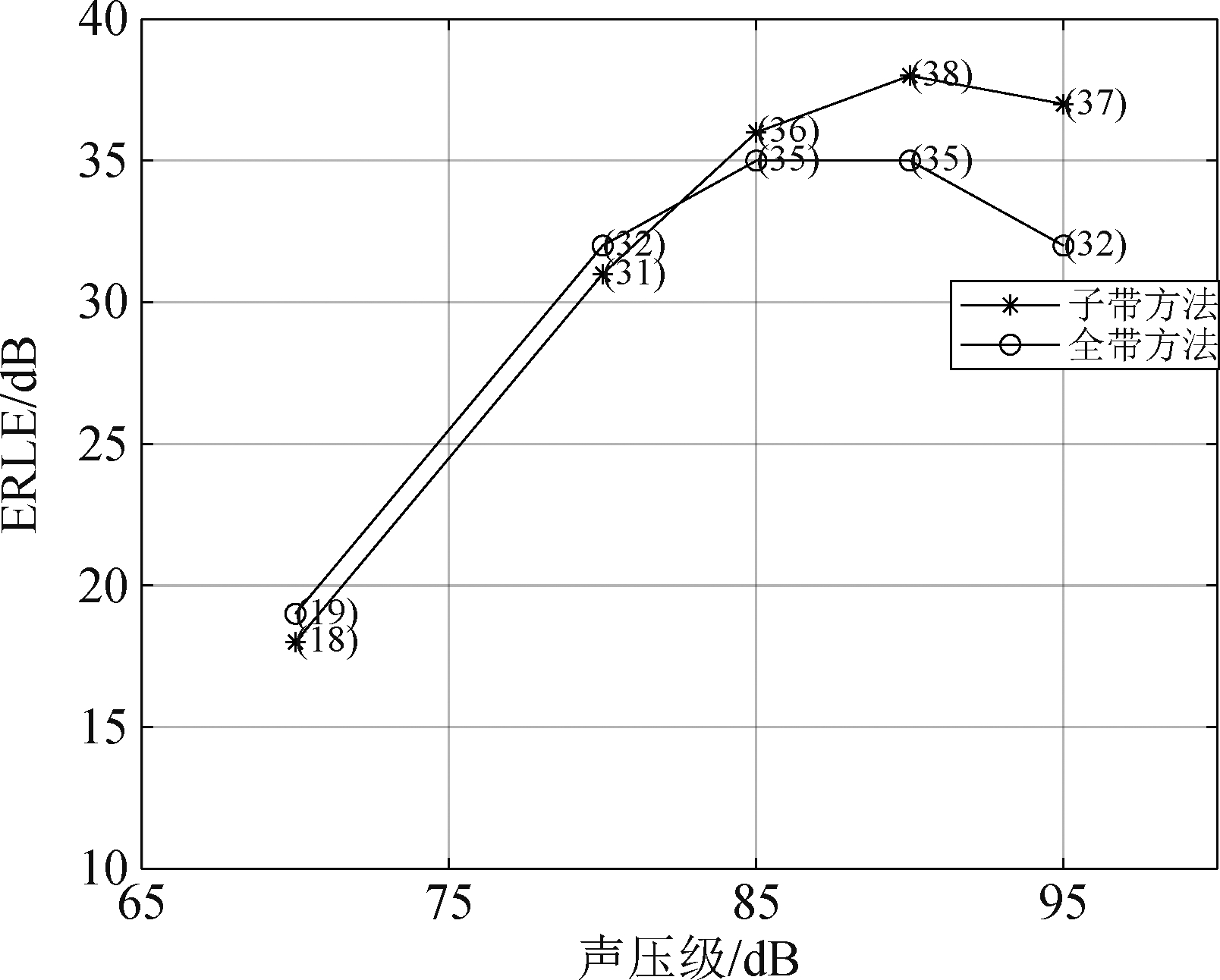
图13 信号x(n)是1000 Hz正弦信号
Fig.13 Signal x(n) is a 1000 Hz single-frequency signal

图14 信号x(n)是白噪声
Fig.14 Signal x(n) is a white noise signal
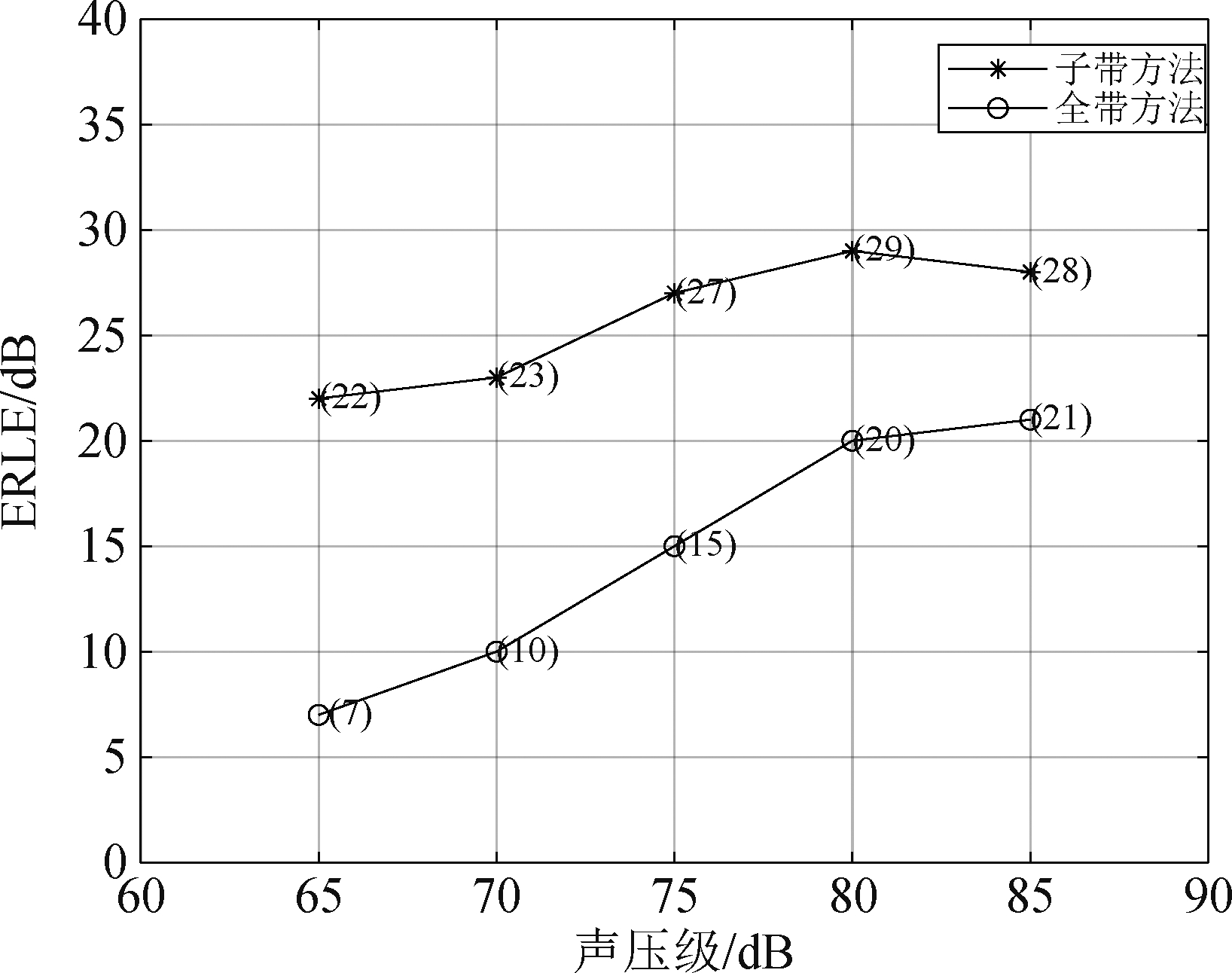
图15 信号x(n)是1000 Hz+2500 Hz(互调失真)
Fig.15 Signal x(n) is a 1000 Hz+2500 Hz signal(intermodulation distortion)
在图13中,使用的是1000 Hz单频信号,得到的结果与实验2类似。当SPL低于80 dB时,ERLE随着SPL的增加而增加,两种方法都能正常工作。 但是当SPL进一步增加到85 dB以上时,全带方法的性能会停止增加甚至下降,但是子带表现出更好的性能并且下降缓慢。在图14中,如预期的那样,对于白噪声信号,两种方法在非线性严重的情况下都会失效。在图15中的信号中出现了互调失真。这组数据的总体性能比单频信号差,但子带方法仍然表现出更好的性能。值得注意的是,即使声压级适中,全带方法也表现不佳。这意味着全带方法对互调失真更敏感。
图16和图17分别是语音信号和音乐信号在两种方法下的 ERLE对比。这两个结果中,信号的声压级都在80~85 dB附近, 即非线性失真比较严重。
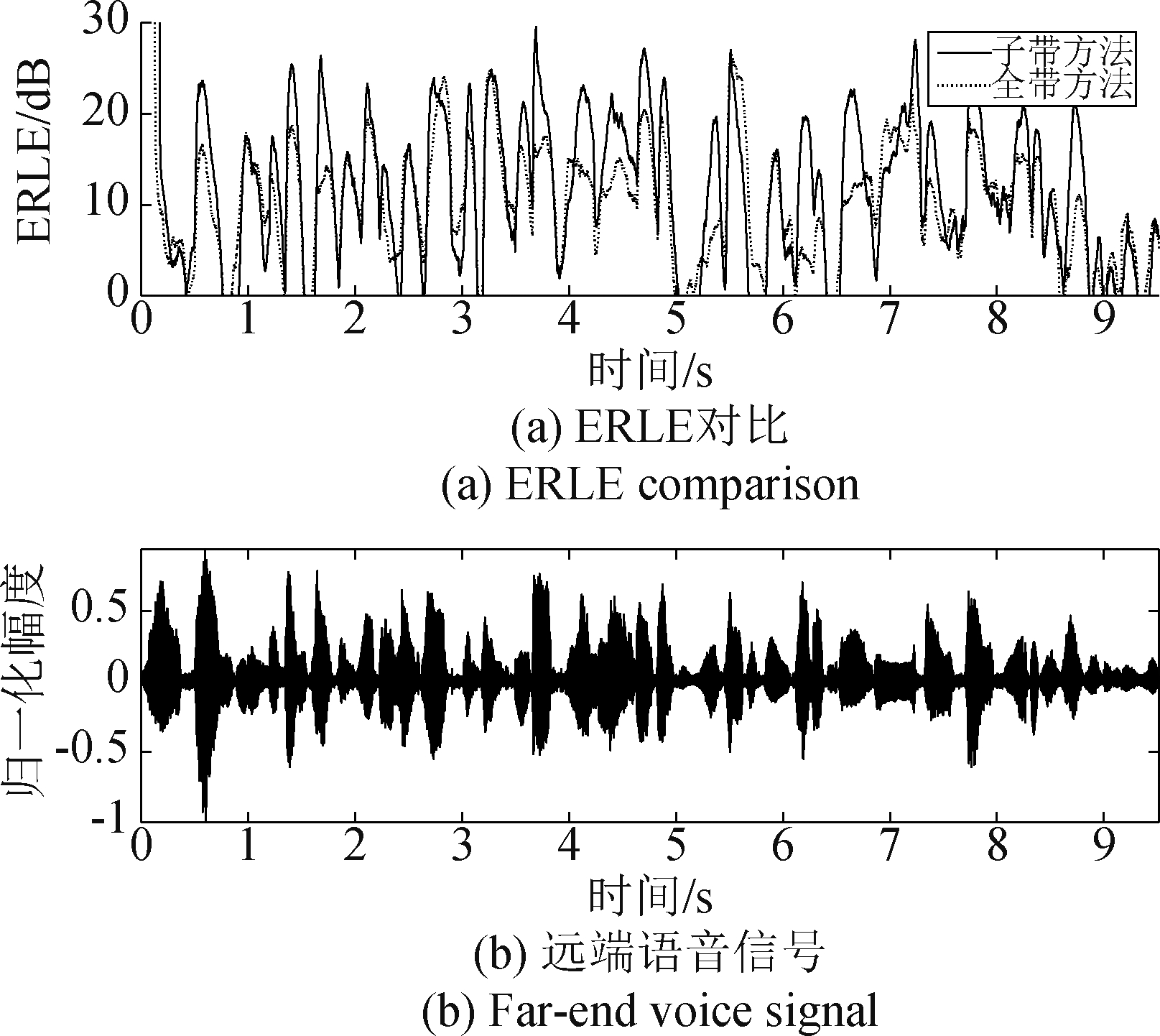
图16 信号x(n)是语音信号
Fig.16 Signal x(n) is a voice signal
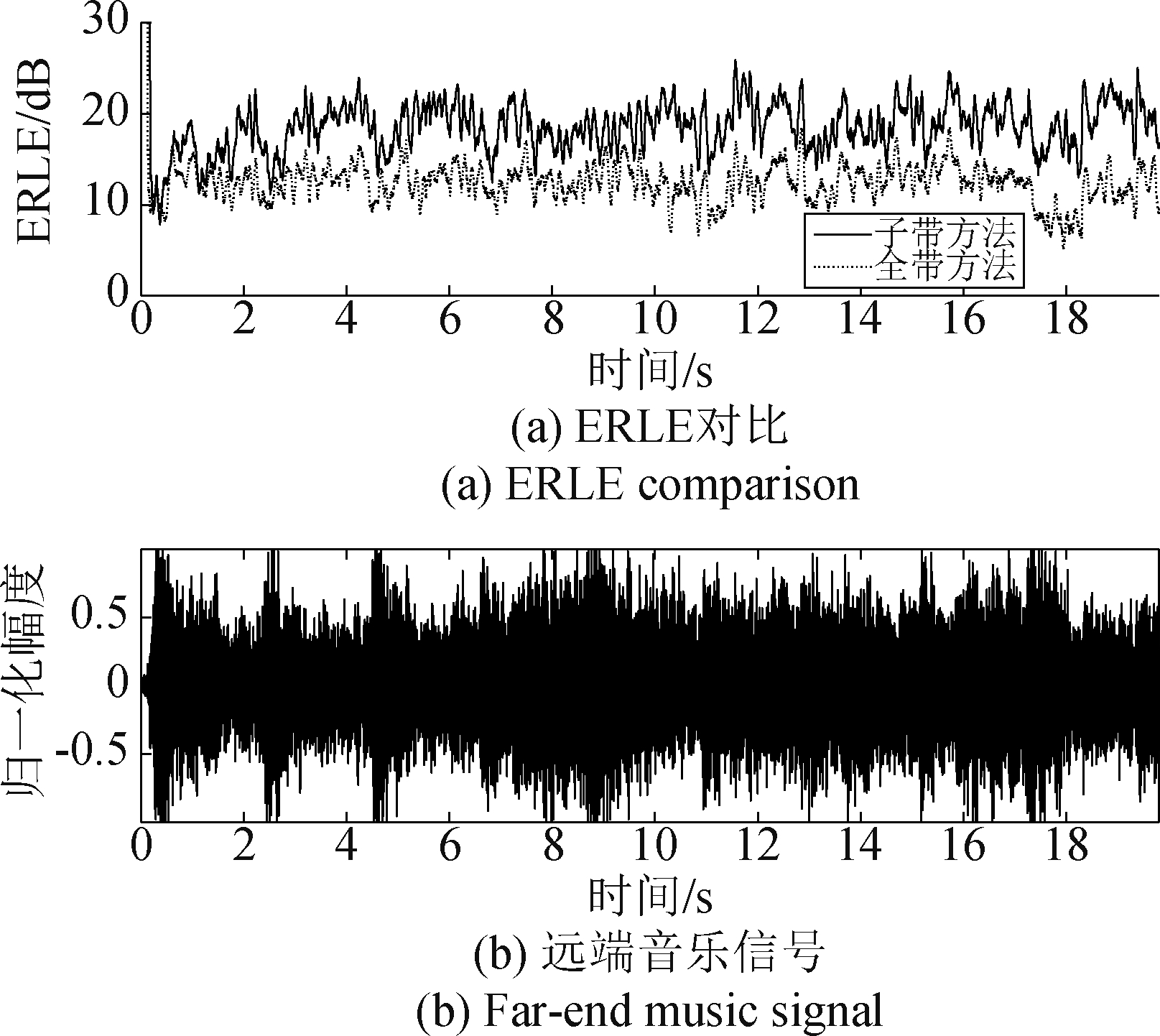
图17 信号x(n)是音乐信号
Fig.17 Signal x(n) is a music signal
对于语音信号,子带方法的ERLE普遍高于全带方法的ERLE。尤其是在语音能量较大的时候,子带方法的ERLE比全带方法的ERLE提升约10 dB。不难发现,两者在音量较大部分的差异更加明显,说明非线性程度不断地随时间变化。对于音乐信号,子带方法的 ERLE 普遍高于全带方法的ERLE。在音乐能量较大的时候,子带方法的 ERLE比全带方法的ERLE提升5~8 dB。
4.4 子带方法与Speex、WebRTC的AEC性能对比
目前最流行的回声抑制算法模块是WebRTC和Speex的AEC模块。WebRTC是Google的开源项目,其包括的AudioProcessing模块包含各种算法,如NoiseSuppression、Beamforming、AGC和AEC等,其中AEC包含三个版本,分别是aec、aec3和aecm。本文中使用的是aec回声消除算法代码。WebRTC中的AEC模块的处理流程主要分为四部分,输入数据缓存、自适应滤波、后置滤波以及添加舒适噪声。注意该算法的自适应回声抵消比较简单,主要起作用的是回声抑制,前者是后者的基础。Speex是另一个主流的开源项目,其中自适应滤波算法用到MDF算法,也应用到最优步长策略和Two-path模型等,是目前最常用的AEC算法模块。
本节中,我们主要是对比子带方法和目前主流的这两个AEC处理模块之间的性能。使用的数据是语音信号和音乐信号,录音地点为消声室。为了使音量的可调范围较大,放音设备选为JBL音箱(型号为JBL LSR 306P MKII),录音设备为笔记本电脑。笔记本约在音箱的正前方1 m处录制。回声的非线性主要来自JBL音箱。录制的数据包括语音信号和音乐信号各四条,音量从小到大。最小音量大约为60 dB, 最大音量约为90 dB。为了保证对比的公平性,(A)关闭开源代码WebRTC、Speex的AEC模块中的后处理部分,仅留下线性滤波部分; (B)滤波器长度统一选择2048;(C)Speex中有对信号的预处理步骤 (比如陷波和预加重),在子带算法处理之前也加上类似的操作。对比结果如图18~19所示。

图18 语音信号的结果对比
Fig.18 Comparison of results of speech signals
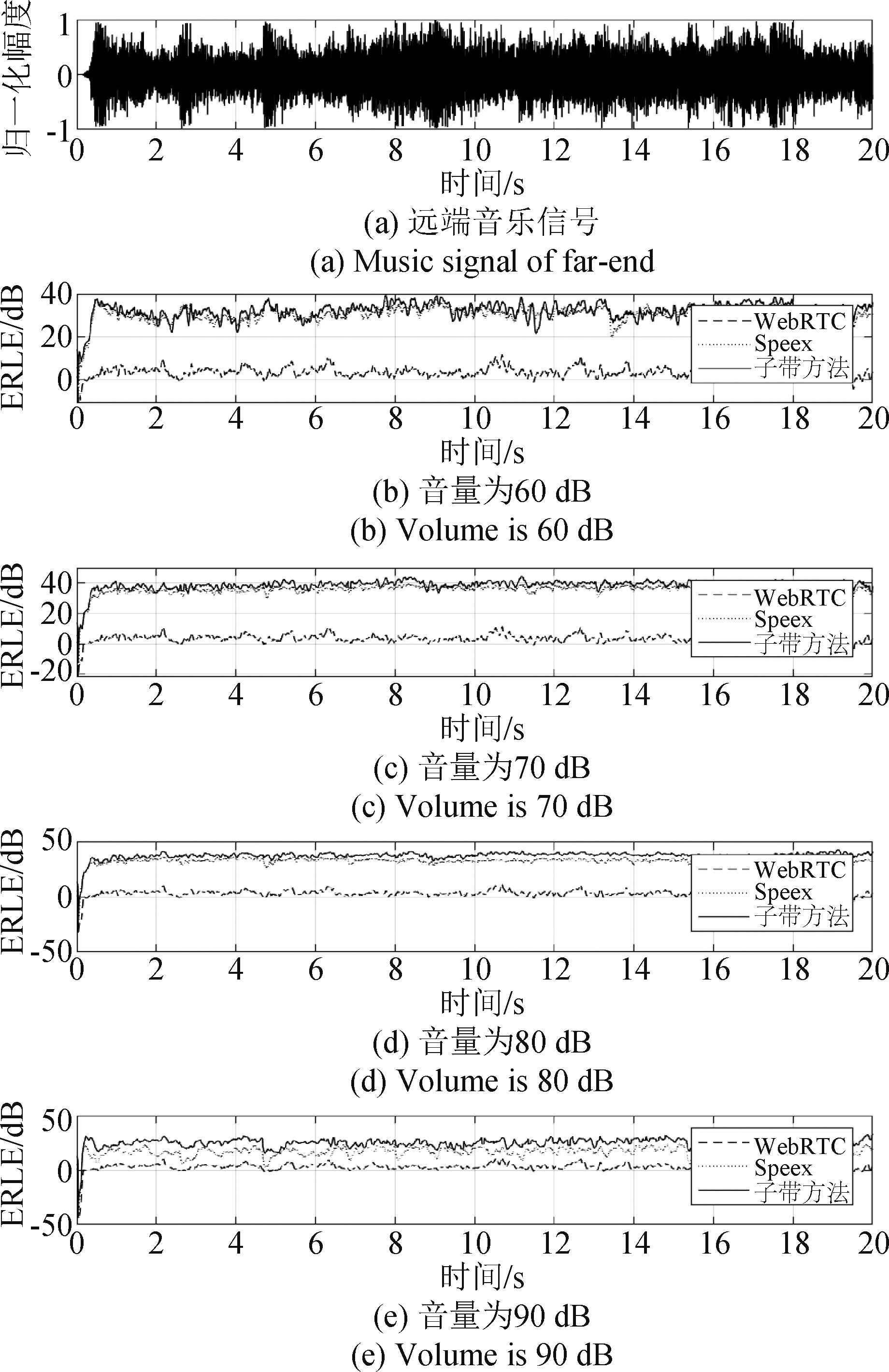
图19 音乐信号的结果对比
Fig.19 Results comparison of music signals
需要特别指出的是,WebRTC的策略主要是靠后处理来消除回声。由于这里都去掉了后处理部分,所以WebRTC 基本上不起作用。故可以主要比较子带方法和Speex模块的性能。
图18中可以看出:(A)音量为60 dB时,子带方法和Speex模块的ERLE的两条曲线基本上在一个水平,子带方法并未显现出明显的优势。(B)当音量超过70 dB时,两种方法的ERLE的值已经开始有区别,尤其是在音量变大的时候,可以看出子带方法的ERLE有3~5 dB的优势。(C)当音量继续增大到约90 dB时,子带方法的优势更加明显。ERLE的两条曲线已经完全分开,在音量最大时,子带方法有约10 dB的优势。
通过观察图19中音乐信号的结果,可以得到和语音信号类似的结论:(A)音量为60 dB时,子带方法已经表现出优势。这是因为在同等音量下,音乐信号的非线性失真比语音信号更明显。(B)随着音量持续增加到90 dB,子带方法的优势进一步增大。音量最大时,子带方法的ERLE有超过10 dB 的优势。
综上所述,该方法在语音信号和音乐信号下的结论均符合预期。即在正常音量时,子带方法不比Speex模块差(子带方法的ERLE值大于或等于Speex模块的ERLE值);在音量较大(非线性失真比较严重)时,子带方法的性能优于Speex模块。
5 结论
本文主要研究非线性回声抵消问题。我们不考虑对复杂的非线性系统进行建模,而是使用多相滤波器组来实现子带AEC的解决方案。全带自适应滤波器的收敛由全带误差信号控制,但子带方法取决于每个子带中的误差信号。我们认为,当转换到子带方法后,非线性特性在某些子带中会弱化或消失,从而这些子带中的自适应滤波器可以收敛,因此提升了AEC性能。我们还着重分析了传统方法的局限性和子带方法的优势。所有分析结果均在本文的实验中得到验证。我们发现随着声压级接近扬声器的饱和区,其非线性特性会更加显着,此时子带AEC方法呈现出比全带方法更高的ERLE,无论是对于线谱信号还是实际语音和音乐信号均有性能提升。在非线性失真明显的情况下,子带方法的ERLE比经典的全带AEC方法高出10 dB。该方法的优点还在于可以与其他处理非线性回声的方法结合使用。
[1] Costa M H, Bermudez J C M, Bershad N J. Statistical analysis of the LMS algorithm with a zero-memory nonlinearity after the adaptive filter[C]∥IEEE International Conference on Acoustics. IEEE, 1999.
[2] Bershad N J. On error-saturation nonlinearities in LMS adaptation[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1988, 36(4): 440- 452.
[3] Schrammen, Matthias, et al. Efficient Nonlinear Acoustic Echo Cancellation by Dual-stage Multi-channel Kalman Filtering[C]∥ICASSP 2019-2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 2019.
[4] Halimeh, Mhd Modar, Christian Huemmer, and Walter Kellermann. Nonlinear acoustic echo cancellation using elitist resampling particle filter[C]∥2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 2018.
[5] Kiich F, Kellermann W. Nonlinear line echo cancellation using a simplified second order Volterra filter[C]∥IEEE International Conference on Acoustics. IEEE, 2009.
[6] Stenger A, Trautmann L, Rabenstein R. Nonlinear acoustic echo cancellation with 2nd order adaptive Volterra filters[C]∥Icassp. IEEE Computer Society, 1999.
[7] Mossi M. Non-linear acoustic echo cancellation with loudspeaker modelling and pre-processing[D]. Ph. D. dissertation, Thesis, 10 2012, 2012.
[8] Huang Y, Skoglund J, Luebs A. Practically efficient nonlinear acoustic echo cancellers using cascaded block RLS and FLMS adaptive filters[C]∥ICASSP 2017-2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 2017.
[9] Hofmann C, Guenther M, Huemmer C, et al. Efficient nonlinear acoustic echo cancellation by partitioned-block significance-aware Hammerstein group models[C]∥2016 24th European Signal Processing Conference (EUSIPCO). IEEE, 2016: 1783-1787.
[10] Birkett A N, Goubran R A. Acoustic echo cancellation using NLMS-neural network structures[C]∥Icassp. IEEE Computer Society, 1995.
[11] Birkett A N, Goubran R A. Nonlinear echo cancellation using a partial adaptive time delay neural network[C]∥Neural Networks for Signal Processing[1995] V. Proceedings of the 1995 IEEE Workshop. IEEE, 1995.
[12] Muller M, Jansky J, Bohac M, et al. Linear acoustic echo cancellation using deep neural networks and convex reconstruction of incomplete transfer function[C]∥2017 IEEE International Workshop of Electronics, Control, Measurement, Signals and their Application to Mechatronics (ECMSM). IEEE, 2017.
[13] Ykhlef F, Ykhlef H. A post-filter for acoustic echo cancellation in frequency domain[C]∥Complex Systems. IEEE, 2015.
[14] Schalk-Schupp I, Faubel F, Buck M, et al. Approximation of a Nonlinear Distortion Function for Combined Linear and Nonlinear Residual Echo Suppression[C]∥2016 IEEE International Workshop on Acoustic Signal Enhancement (IWAENC). IEEE, 2016.
[15] Huang Y A, Skoglund J, Luebs A. Bi-magnitude processing framework for nonlinear acoustic echo cancellation on Android devices[C]∥IEEE International Workshop on Acoustic Signal Enhancement. IEEE, 2016.
[16] Morgan D R, Hall J L, Benesty J. Investigation of several types of nonlinearities for use in stereo acoustic echo cancellation[J]. Speech & Audio Processing IEEE Transactions on, 2001, 9(6): 686- 696.
[17] Birkett A N, Goubran R A. Limitations of handsfree acoustic echo cancellers due to nonlinear loudspeaker distortion and enclosure vibration effects[C]∥Applications of Signal Processing to Audio and Acoustics, 1995. IEEE ASSP Workshop on. IEEE, 1995.
[18] Albu I, Anghel C, Paleologu C. Adaptive filtering in acoustic echo cancellation systems—A practical overview[C]∥2017 9th International Conference on Electronics, Computers and Artificial Intelligence (ECAI). IEEE, 2017.
[19] Benesty J, Gaensler T, Morgan D R, et al. Advances in Network and Acoustic Echo Cancellation[M]. Springer,2001.
[20] Haykin S. Adaptive Filter Theory, Fifth Edition[M]. Pearson Education, Inc. 2014.
[21] Kuech F, Mitnacht A, Kellermann W. Nonlinear acoustic echo cancellation using adaptive orthogonalized power filters[C]∥Acoustics, Speech, and Signal Processing, 2005. Proceedings. (ICASSP′05). IEEE International Conference on. IEEE, 2005.
[22] 闫震海, 杨飞然, 杨军. 一种变正则化矩阵的改进多带结构子带自适应滤波算法[J]. 电子学报, 2017, 45(8): 2019-2025.
Yan Zhenghai, Yang Feiran, Yang Jun. An improved multiband structure subband adaptive filtering algorithm with variable regularization matrix[J]. Chinese Journal of Electronics, 2017, 45(8): 2019-2025.(in Chinese)
[23] Shin J W , Yoo J W , Park P G . Adaptive regularisation for normalised subband adaptive filter: mean-square performance analysis approach[J]. IET Signal Processing, 2018, 12(9):1146-1153.
[24] Weiss S, Lampe L, Stewart R W. Efficient subband adaptive filtering with oversampled GDFT filter banks[C]∥In IEE Colloquium Adaptive Signal Processing for Mobile Communication Systems (Ref. No.1997/383). 1997: 4/1- 4/9.
[25] Kellermann W. Analysis and Design of Multirate Systems for Cancellation of Acoustical Echos[C]∥Acoustics, Speech, and Signal Processing, 1988. ICASSP- 88. 1988 International Conference on. IEEE, 1988.
[26] Vaidyanathan P P. Multirate digital filters, filter banks, polyphase networks, and applications: a tutorial[J]. Proceedings of the IEEE, 1990, 78(1): 56-93.
[27] 宗孔德. 多抽样率信号处理[M]. 清华大学出版社,1996.
Zong Kongde. Multi-sampling rate signal processing[M]. Tsinghua University Press,1996.(in Chinese)
[28] Harteneck M, Weiss S, Stewart R W. Design of near perfect reconstruction oversampled filter banks for subband adaptive filters[J]. IEEE Transactions on Circuits and Systems II: Analog and Digital, Signal Processing, 1999, 46(8): 1081-1085.

