1 引言
在信息化时代中,复杂多变的信息蕴含在同样复杂多变的信号当中,有效信息获取得准确与否,关键在于对相应信号中重要属性特征的正确处理。音频信号作为时变信号中的典型代表,一直是众多学者的热门研究对象,有着明显的非线性非平稳特征,但是这些随机变化的特征与其蕴含的信息是有着稳定的对应关系。对音频信号而言,主要是稳态成分和含有较多目标信息的突变成分所组成,而两者在属性特征上具有明显的差异[1]。因此,如果想要获取到音频信号中的目标信息、实现稳态成分与突变成分的分离,那就需要有效地检测出突变成分并将其尽可能完整地提取出来。
自从信号处理领域单独作为研究方向以来,已经发展出了众多的信号处理方法,检测提取出信号成分的方法便是近年来从传统信号处理方法中发展出的一个分支。关欣等研究人员利用乐器在时间序列上的累积能量,提出了一种乐器分离算法[2]。翟鹏的团队将非负矩阵分解算法和经验模态分解算法相结合,实现了多乐器混合音频中检测出特定乐器的目标[3]。还有一些学者,使用非负张量分解技术对音频信号进行处理[4]。王冬冬等研究人员通过节拍和关键背景建立模型完成了音频信号的分类与音频信号成分的检测,经实验证实方法可行有效[5]。在2018年,徐金才等学者就利用乐器音频信号的对数功率谱作为特征参数,提出了三种可用于音源分离的神经网络模型,并且都具有不错的效果[6]。孙慧芳等人将过零率和频谱幅值作为特征应用到语音音乐的处理中,并通过实验验证了所提取特征的有效性[7]。在语音音频检测方面,兰琼琼和陆志华等研究人员根据声学特征之间的不同特性,对时频域特征选择并组合后,利用深度神经网络实现了检测并分离混合语音中的特定语音[8]。Arijit Ghosal的团队认为音频分类和检索的关键在于特征提取,经验模态分解便是分开音频信号中丰富频率分量的最佳方法[9]。在分析语音和音乐音频时,提取其中的频谱信息是必不可少的,Birajdar G K的研究团队提出了一种基于IIR-CQT频谱图的分析方法[10]。
在信号分析中,对信号端点检测得准确与否便直接决定了信号成分提取的准确性,因此端点检测的精确度是制约该类方法发展的最大考验。要想获取到精确的端点信息,就需要明确稳态成分和突变成分的本质区别,即频率和能量。经验模态分解方法便可以在无需预设基函数的情况下,将原始音频信号分解成按频率划分的成分,并且可以进一步地从分解后的成分中挖掘各点的信息[11]。
在音频信号中,以混合乐器音频为例,常常是一些乐器已经开始演奏,然后其他的乐器再开始演奏,而后来演奏的乐器旋律对于已经开始演奏的乐器旋律来说,是一种突变成分。如何从混合乐器音频中检测并分离出后加入演奏的乐器,就需要将该乐器从发声到结束的位置检测出来。从理论上知道,各种乐器有着不同的发声频率以及各异的声波能量[9]。因此,本文提出一种基于启发式掩模经验模态分解(Empirical Mode Decomposition,EMD)的音频突变成分检测方法,该方法中的启发式掩模EMD能够在缓解EMD分解信号后产生模态混叠现象的同时,提取出音频信号中各点维度一致的瞬时频率和瞬时能量,将这两者作为检测特征,从而精准检测出音频突变成分的起止点,此外该检测方法将根据突变成分自身的信息定义了窗长自适应更新策略,从而完整精确地检测出突变成分。
在这里,对本文的工作框架进行简要叙述。文章的第2部分将对经验模态分解进行较为详细地介绍,以便了解经验模态分解的利弊所在;第3部分详细阐述了启发式掩模经验模态分解方法的理论优势,并在此基础上提出了结合窗长自适应更新策略的音频突变成分检测方法;第4部分将首先对启发式掩模经验模态分解的优势进行实验验证,进而通过实验展示检测方法的应用效果。最后,对本文的所用方法进行总结,同时对未来的研究内容与研究方向进行了展望。
2 经验模态分解
经验模态分解(Empirical Mode Decomposition,EMD)是Norden E. Huang在1998年提出的一种适用于非线性非稳态时变信号的信号处理方法。本征模态函数(Intrinsic Mode Function,IMF)作为EMD处理信号后的分解成分,有两个特性,这两个特性也是EMD算法中判定分解成分是否为IMF的条件:一个是在整个时间范围内,局部极值点的数目与过零点的数目相差不超过一个,另一个是在任意时间点,局部极大值的包络线与局部极小值的包络线的均值为零[11]。在信号x(t)经过EMD处理后,得到的各个IMF和最后不满足IMF条件的残基r(t),这些分解后的成分可以用式(1)来重构原始信号
x(t) = ∑ni=1imfi(t)+r(t)
(1)
式中的imfi(t)为信号分解后产生的各个IMF,n为IMF个数。
该方法应用范围广、通用性强,无需像小波分解提前预设小波基函数,也不像傅里叶变换在分析频域信息时提前预设谐波函数,将信号分解后得到的IMFs经希尔伯特变换(Hilbert Transform,HT)即可得到信号中各点相应的瞬时信息,构造边际谱便可研究频域信息。但同时EMD也存在着自身的问题,即模态混叠问题和信号分解后的IMFs维度不一致问题。模态混叠致使信号分解后的部分IMFs中在频率分布上有交叠部分,难以划分清楚某一段频率分布于哪个IMF中;而维度不一致则会导致相同帧长的源信号经分解后产生不同数量的IMF,进而导致所需的特征向量维度不匹配,难以进行后续的信号分析处理。这两个问题在多元经验模态分解方法的处理有所缓解,具体操作则是要加入多个辅助信号通道来干预所分析信号的分解[12-13],这就势必会造成信号分解的时间成本过高。
3 基于启发式掩模经验模态分解的音频突变成分检测方法
3.1 稳态成分与突变成分
在开始进行音频信号中突变成分的检测工作之前,首先需要明确音频信号中稳态成分与突变成分的含义与区别,为尽可能通俗易懂地阐述清楚这两种成分之间的差异,将从统计概率和差异信息这两个方面进行综合考量。
从统计概率理论的角度来看,稳态成分可以被认为是一种在信号当中自始至终都出现的成分,而突变成分则是一种在信号中偶发性出现的成分,两种成分可分别表示为式(2)、(3)的形式,式中的Ps和Pm分别表示稳态成分和突变成分在一段信号中出现的频率。
Ps ≈ 1
(2)
Ps ≫ Pm
(3)
从差异信息理论的角度来看,稳态成分与突变成分在属性特征方面有着明显的差异,这些差异则可以认定这两种成分属于不同的种类,而不是同一种类中成分之间的属性特征波动,可表示为式(4)的形式,式中的F(·)表示一种获取信号成分属性特征的一种方法,Xs和Xm分别表示稳态成分和突变成分,δ即为两种成分在某些属性特征方面差异的临界值,其值需根据具体的属性特征而确定。
F(Xs)-F(Xm)>δ
(4)
综合这两种理论来对信号成分进行考虑,能够对稳态成分与突变成分的含义与区别有进一步的理解。接下来便是要根据这两种成分的含义与区别将突变成分从音频信号中检测出来以便后续的研究分析,在混合乐器音频中,乐器之间的差异往往反映在发声频率与声波能量当中,因此需要一种能够获取音频信号中各点瞬时频率与瞬时能量的有效方法。
3.2 启发式掩模经验模态分解
根据上述内容可知,EMD分解后的IMFs进行HT便可以获取音频信号中的瞬时信息,但同时需要一种方法对EMD分解信号时出现的缓解模态混叠现象和维度不一致问题进行改善,而掩模EMD便可以做到。简单来说,掩模EMD就是在EMD对原始信号处理的过程中加入掩模信号来干预原始信号的分解[14]。这一点与集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)中为缓解模态混叠问题而在原始信号中加入适当的高斯白噪声相似[15],但EEMD计算量大,需要时常人为调整高斯白噪声的属性,并且高斯白噪声会在信号分解出的IMFs中留下痕迹,难以彻底消除高斯白噪声的残留影响,从而致使信号复原精度不够高。
造成EMD中模态混叠现象产生的一个主要原因可以简述为,当两个纯净信号(即信号的频率固定且单一)的频率分布在同一个八度音阶中并进行叠加时,这两个信号会表现为一个调制信号,而EMD无法将这两个纯净信号从调制信号中分离,这就会导致所分解出的部分成分彼此之间有交叉。可用一个简单的数学模型说明,
x1(t)=a1sin(2πf1t)
(5)
x2(t)=a2sin(2πf2t)
(6)
式(5)、(6)则分别表示为两个纯净信号, f1不等于f2,当这两个信号叠加时便有式(7),
x(t)=a1sin(2πf1t)+a2sin(2πf2t)
(7)
进一步地,当这两个信号幅值相同时,即满足式(8),
a1=a2=a
(8)
根据和差化积公式,信号x(t)可以表示为式(9)的形式。
x(t)=2asin(πt(f1+f2))cos(πt(f1-f2))
(9)
而每隔八度音阶,对应的频率变化一倍,表示为式(10)。
0.5<f1/f2<2
(10)
总的来说,便是当有两个信号进行叠加且它们的频率满足式(10)时,这两个信号会表现为一个调制信号,EMD在分解这个调制信号后的成分中会有明显的模态混叠现象。而音频信号是由多种频率不一的信号叠加在一起的复杂信号,势必会满足式(10)的条件,因此EMD在分解音频信号时,必然会出现模态混叠现象。
要使得信号分解后的成分之间交叠现象不明显,则要充分利用式(10)。让加入到原始信号中的掩模信号频率依次确定在各IMF中瞬时频率分布的中心线附近,同时结合非线性度(Degree of Nonlinearity,DN)评价原始信号加入掩模信号后的特征及掩模信号的优劣,式(11)给出了非线性度的数学表示,
(11)
式中的IF(t)为时刻t对应的瞬时频率,IFm为信号的瞬时频率均值,DN的数值越大则说明非线性的程度越大,不难看出当信号各时刻的瞬时频率接近信号的瞬时频率均值时,信号的非线性程度降低,便于分析处理。
因此,本文提出对原始掩模EMD[14]的一种改进方法——启发式掩模EMD,其中掩模信号的形式如式(12)所示,式中的幅值am和频率fm是原始信号经EMD分解后第一个IMF的瞬时幅值均值和瞬时频率均值,可按式(13)和式(14)计算,而瞬时幅值与瞬时频率为IMFs经HT求得,式(15)中h(t)为原始信号x(t)经HT后获得的信号,式(16)、(17)给出了瞬时幅值与瞬时相位的计算方法,而瞬时频率则是对瞬时相位求一阶导数,如式(18)所示。
s(t)=amsin(2πfmt)
(12)
(13)
(14)
(15)
(16)
(17)
(18)
在通常的概念中,启发式是指自我发现、自我学习的能力,而在这个方法中,启发式便体现在掩模信号中的参数完全由所分析信号的数据内容而自适应设定并学习调整,无需人为干预,在理论上和性能上与原始掩模EMD相比有着明显的优势。
在原始掩模EMD当中,掩模信号的频率由瞬时幅值加权计算获得,不能够保证所获得的频率确定在IMF中瞬时频率分布的中心线附近,而且幅值固定为定值2,显然不适合于音频信号这个复杂多变的信号种类。而本文构造的掩模信号的频率为IMF中瞬时频率的均值,可以确保在IMF中瞬时频率分布的中心线附近,受此启发,幅值也确定为IMF中瞬时幅值的均值,可自适应多种信号内容,充分利用信号自身的本质属性来构造掩模信号。另外,将两种掩模信号加入到原始信号后所计算的DN有如下关系:
DNori/DNpro>1
(19)
DNori和DNpro分别为原始掩模EMD中掩模信号和启发式掩模EMD的掩模信号的非线性度,可以通过式(19)看出,所提的掩模信号构造方法远胜于原始掩模EMD的掩模信号构造方法。
启发式掩模经验模态分解算法的具体流程如算法1所示。
算法1 启发式掩模经验模态分解
Algorithm 1 Heuristic empirical mode decomposition with a masking signal

3.3 窗长自适应更新策略
音频信号在经过启发式掩模EMD和HT处理后,便可以得到信号中各点的瞬时信息,从相邻点中找到有显著差异的点便可以认为是突变成分的起止点。但仅仅获取到突变成分的起止点是不能够保证精确地检测出完整的突变成分,这是因为突变成分起止点会有获取精确度不高以及误识的情况,因此需要合理合适的窗长来将这些情况加以弥补。同时,还应确保突变成分能够完整被计算出的窗长所包含从而不会遗漏突变成分信息,也便于进行后续的分析处理,将当前获悉的突变成分窗长均值设定为最适宜的突变成分窗长,从而根据信号的数据内容不断自适应地调整突变成分窗长。现给出窗长自适应更新算法,如算法2。
算法2 窗长自适应更新
Algorithm 2 Window adaptive update

窗长自适应更新(Window Adaptive Updating)输入:信号x(t)输出:窗长(Window,W) 1 根据信号x(t)的段长划分,确定数据段个数为S; 2 令变量begin=0,W=0,c=0; 3 对S个数据段执行第4~7步; 4 对数据段内每个点i执行第5~7步; 5 判断该点是否有标记p,若有则执行第6步,否则在i=i+1后执行第4步; 6 判断begin是否为0,若为0,则pb=i,begin=1,保留p标记,若为1,则pe=i,begin=0,去除p标记,c=c+1; 7 更新W=(W * (c-1)+(pe-pb))c,i=i+1,返回第4步。
3.4 音频突变成分检测方法
在要求高精度检测出音频突变成分的情况下,就需要精准地获取突变成分的起止点并根据数据内容自适应学习出最适宜的突变成分窗长,该部分将详细描述检测方法的步骤。
将原始信号分解后产生的IMFs做HT,获取每个IMF中各采样点的瞬时信息,使用其中的瞬时频率与瞬时能量,组成检测特征,即[瞬时频率,瞬时能量]。为保证由所分析的各段信号提取的检测特征维度一致,此处所选用的信号分解方法为本文提出的启发式掩模EMD。
由于音频信号中的稳态成分与突变成分在瞬时频率和瞬时能量上有着明显的差异,故将检测特征作为判断音频信号中稳态成分与突变成分的特征向量,训练支持向量机(Support Vector Machine, SVM),以期达到分界线一侧为稳态成分采样点集合,另一侧为突变成分采样点集合,最接近分界线上的采样点集合即为突变成分起止点集合的效果,并对突变成分起止点加以标记。
将SVM分类处理后的信号经过窗长自适应更新策略获取突变成分的最适宜窗长,同时结合由SVM检测出的初步突变成分起止点来确定精确的突变成分起止点,将连续多个过短的突变成分视作一个突变成分,将一个过长的突变成分视作多个突变成分,这样便可以获得更为精确的突变成分起始点,再结合已得到的突变成分最适宜窗长,即可将突变成分从信号中检测出来。
至此,音频信号中突变成分的检测方法已经详细介绍完毕,这里给出该方法的流程图辅以理解,如图1所示。
4 基于启发式掩模EMD的音频突变成分检测方法的验证实验结果
为验证启发式掩模EMD方法的效果以及音频突变成分检测方法的效果,实验所用数据来源为IOWA的乐器音频数据集,采样率为44100 Hz,在实验时将原始数据降采样到11025 Hz后进行验证。首先进行实验验证启发式掩模EMD的效果,然后采用相同来源的音频实验数据观察基于启发式掩模EMD的音频突变成分检测方法的效果。

图1 音频信号中突变成分的检测方法流程图
Fig.1 The flow of mutant component detection in audio signal
4.1 启发式掩模EMD分解信号的结果
在该部分实验验证中,从原始音频数据集中分别截取出100段0.4 s长的长笛乐器音频和100段0.15 s长的排钟乐器音频,然后在截取出的长笛音频中的随机位置混入0.15 s长的排钟音频作为实验数据,所用的截取音频均是在原始音频中静音段结束后即乐器开始发声时截取的。在实验中,选取原始掩模EMD与Norden E. Huang团队的改进掩模EMD[16]进行对照实验,通过对实验数据的分解结果分析,本文提出的启发式掩模EMD和Norden E. Huang团队的改进掩模EMD在信号复原精度方面明显优于原始掩模EMD,这是因为原始掩模EMD中的掩模信号没有充分利用原始信号中的数据内容。而在信号分解速度方面,启发式掩模EMD胜于Norden E. Huang团队的改进掩模EMD,这是因为在他们的改进方案中,构造了四个掩模信号并添加了相位信息,一旦加入额外的相位信息,尽管会在信号复原精度上有提升,但却需要另外的相位信息来消除先前加入的相位信息对原始信号分解造成的影响,增加了许多额外的计算量,不符合奥坎姆剃刀原理。因此,本文所提的启发式掩模比这两者更加合理有效,具体结果可从信号数据的平均误差与平均分解时间看出,如表1所示。
表1 三种不同掩模EMD的实验结果
Tab.1 The results of three different EMD with a masking signal
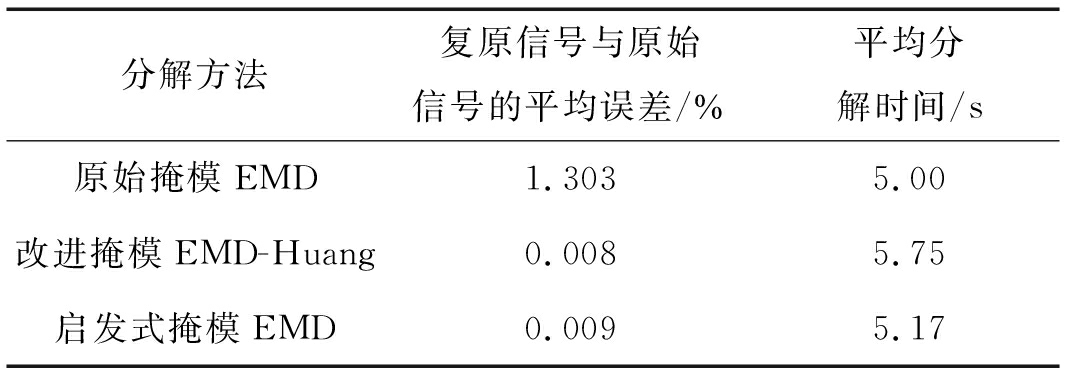
分解方法复原信号与原始信号的平均误差/%平均分解时间/s原始掩模EMD1.303 5.00改进掩模EMD-Huang0.008 5.75启发式掩模EMD0.009 5.17
同时,将EMD、原始掩模EMD与本文提出的启发式掩模EMD这三种信号处理方法对同样的实验数据进行分解,实验结果如表2所示。
表2 EMD、原始掩模EMD与启发式掩模EMD分解实验数据结果
Tab.2 The decomposition results of EMD, original and heuristic EMD with a masking signal

方法模态混叠现象维度不一致现象平均分解时间/sEMD一般不可控,不稳定0.31原始掩模EMD较少可控,稳定5.00启发式掩模EMD很少可控,稳定5.17
可以看出,尽管EMD可以在很短的时间内完成信号的分解,但是分解出的IMFs维度完全不可控,不利于后续的特征提取,并且存在着模态混叠问题,如图2所示,图中横坐标表示频率,纵坐标表示幅值,虚线为IMF3,实线为IMF4,这里为了清楚地看到模态混叠发生的部分,只对模态混叠显著的部分绘制边际谱图,而没有绘制完整的边际谱图,可以看出从50 Hz到600 Hz这两条线彼此之间均有重叠,在50 Hz附近尤为明显;原始掩模EMD可以保证分解出的IMFs维度一致,但是结合表1可以看出,由原始掩模EMD分解出的IMFs在复原精度方面不如启发式掩模EMD;而启发式掩模EMD就可以保证在分解出的IMFs维度一致的情况下,减少模态混叠现象,快速地分解信号,并且精度有所保障。图3即为与图2中相同的实验信号数据经启发式掩模EMD得到IMF3-IMF4的边际谱图,对照图2可以看出,图3中这两个IMF在边际谱图中的重叠部分明显减少,重叠现象仅发生在300~400 Hz之间,而且并不明显,即模态混叠现象明显改善。

图2 EMD分解实验信号数据后IMF3-IMF4的边际谱图
Fig.2 The marginal spectrum of IMF3-IMF4 obtained by EMD in signal data
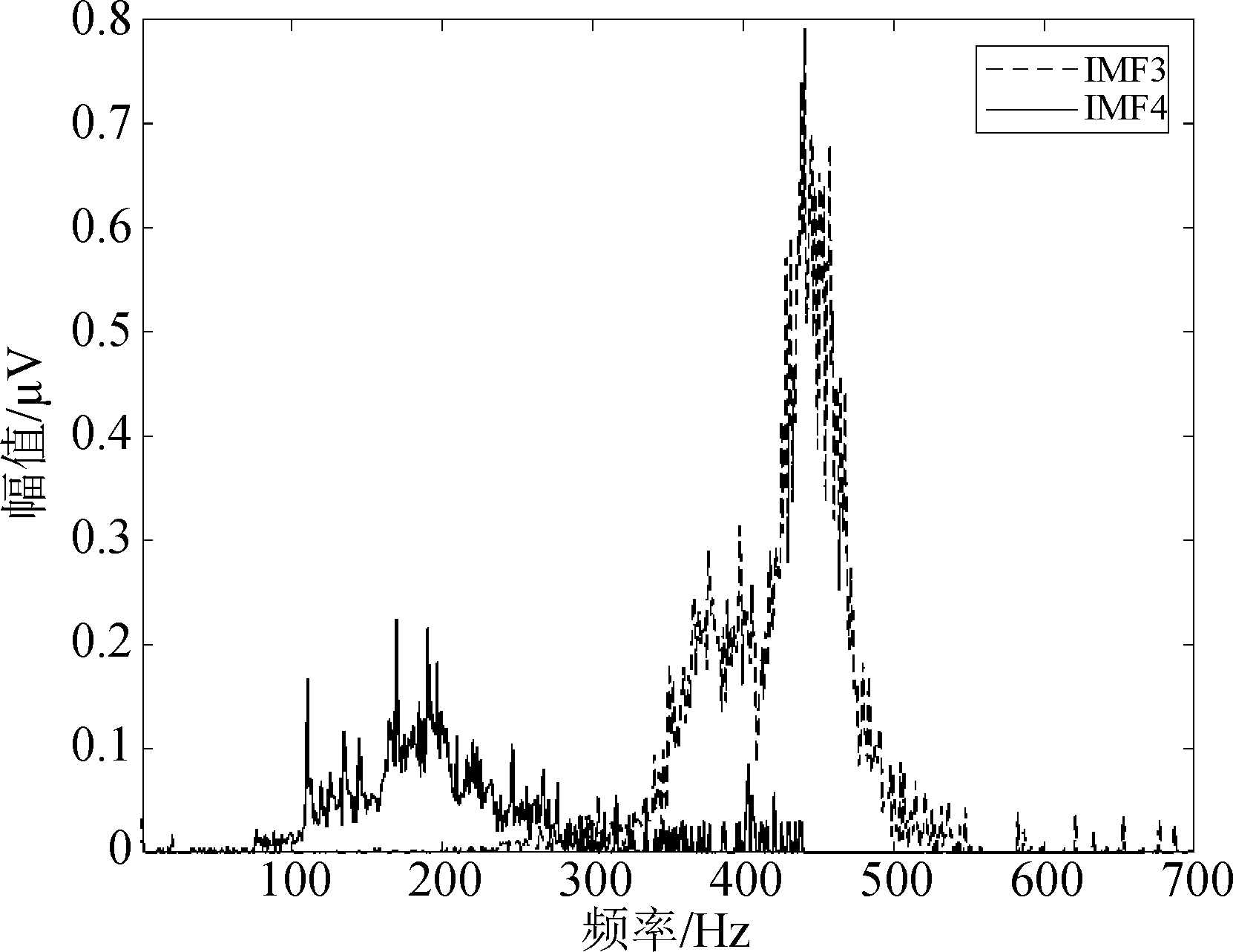
图3 启发式掩模EMD分解实验信号数据后IMF3-IMF4的边际谱图
Fig.3 The marginal spectrum of IMF3-IMF4 obtained by heuristic EMD with a masking signal in signal data
4.2 检测结果及分析
在该部分实验验证中,需要提供训练集和测试集。训练集和测试集均是由两种数据构成,一种是单一乐器音频数据,另一种是在单一乐器发声中有其他乐器混入的音频数据,而混入的乐器声即为突变成分。在训练集中,包含100段0.4 s长的长笛音频数据和100段在0.4 s中随机位置混入长度在0.1 s~0.2 s之间的排钟音频数据。在测试集中,两种数据各50段。所用音频数据均是在原始音频数据中静音段结束后立刻截取的,并对所有实验数据进行能量归一化处理。
采用检测精确率P、检测召回率R和综合特征F来评价检测方法的性能,三项指标分别按式(20)、(21)、(22)计算得出
(20)
(21)
(22)
式中的TP表示为检测正确的正例,FP表示为检测错误的正例,FN表示为检测为错误的负例。由于突变成分的长度是由采样点的个数来计量,故在计算上述指标中的正例与负例均是针对点而言。
在该部分实验中,调整由随机选择样本构成的测试集,对测试集重复进行30次实验,同时为了说明启发式掩模EMD与窗长自适应更新策略的有效性,选用原始掩模EMD与0.2 s定长窗长进行对照实验,窗长设定为突变成分可能的最大长度是为了确保突变成分的信息不会遗漏,其具体实验结果如表3所示。
表3 检测方法结果
Tab.3 The results of detection methods
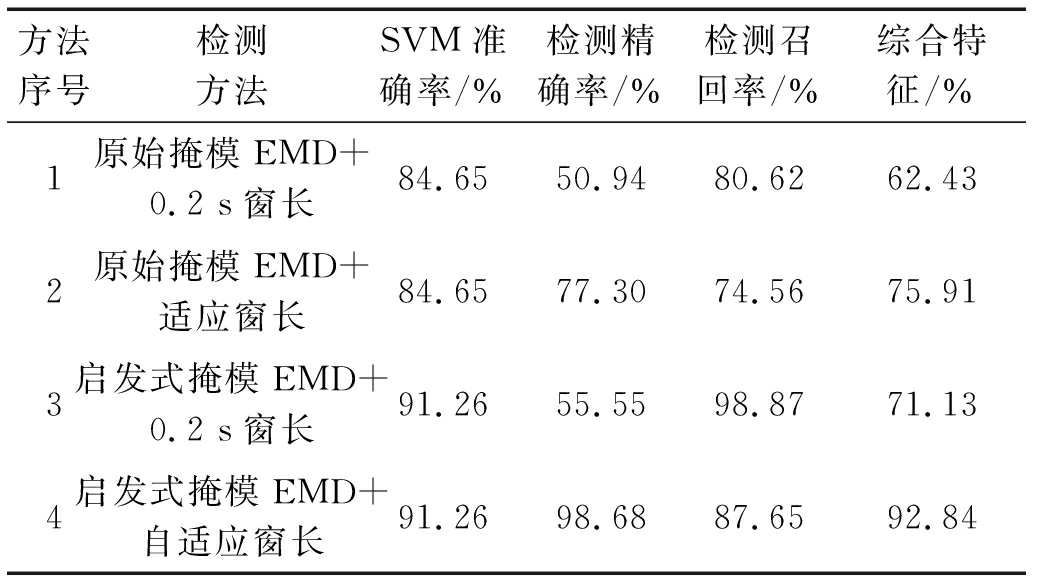
方法序号检测方法SVM准确率/%检测精确率/%检测召回率/%综合特征/%1原始掩模EMD+0.2 s窗长84.6550.9480.6262.432原始掩模EMD+适应窗长84.6577.3074.5675.913启发式掩模EMD+0.2 s窗长91.2655.5598.8771.134启发式掩模EMD+自适应窗长91.2698.6887.6592.84
表3中的SVM准确率和综合特征数据均是在测试集中最好的实验结果,而检测精确率和检测召回率是在综合特征达到最好结果时相应的数据。观察表中的SVM准确率,可以看出影响该数据的因素是所选用的信号分解方法,SVM准确率将直接影响到初步检测出的突变成分起止点,由此可以看出方法1和方法2的综合特征分别低于方法3和方法4,这说明启发式掩模EMD在分解信号和获取检测特征方面优于原始掩模EMD。同时,分别对比方法1、2和方法3、4,不难发现采用窗长自适应策略的检测方法在综合特征方面和检测精确率方面高于0.2 s定长窗长的检测方法,而检测召回率低于0.2 s定长窗长的检测方法,这是因为突变成分的最大可能长度为0.2 s,将此数值作为突变成分窗长会将一些稳态成分检测为突变成分,最好的证明就是方法1、3中的检测精确率会由于FP的增加而大幅降低,而采用自适应窗长的检测方法则会最大程度保证检测到的突变成分不含有稳态成分,而且检测召回率不会过低,从而达到更佳的检测效果。对比方法2、3可以看出,即使由SVM获得的初步突变成分起止点准确率不高,但在窗长自适应更新策略的弥补下,方法2的综合特征超过了方法3的综合特征,即方法2的检测效果优于方法3。
由此,可以看到启发式掩模EMD+自适应窗长的音频突变成分检测方法效果最好,绘制PR曲线图用以直接观察检测精确率与检测召回率的关系,同时绘制综合特征F的变化图以找到最佳效果,分别如图4和图5所示。当综合特征F=92.84%取得最大值时,P=98.68%,R=87.65%,因此该方法在音频突变成分的检测方面有着不错的效果。
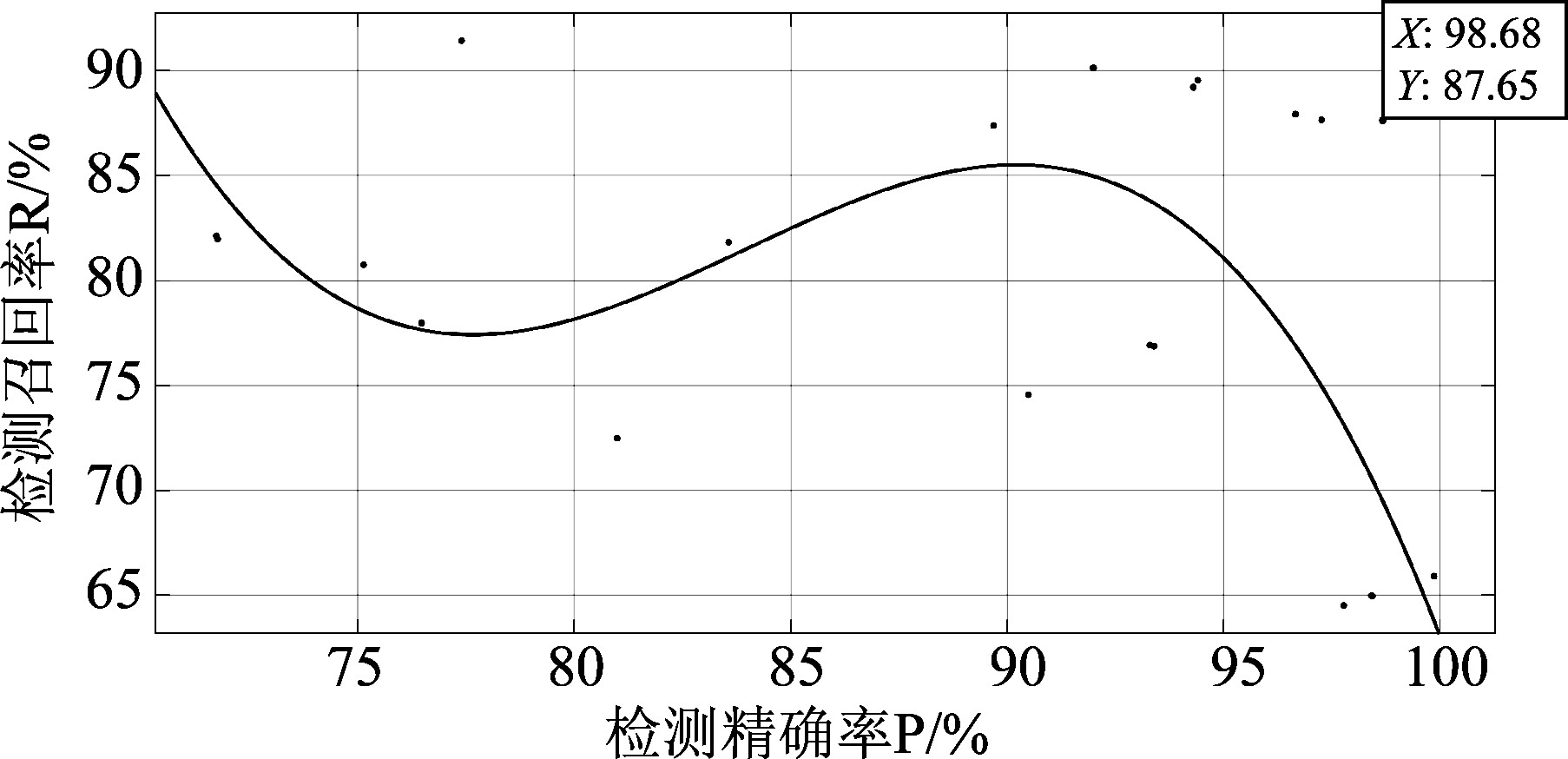
图4 PR曲线图
Fig.4 PR curve
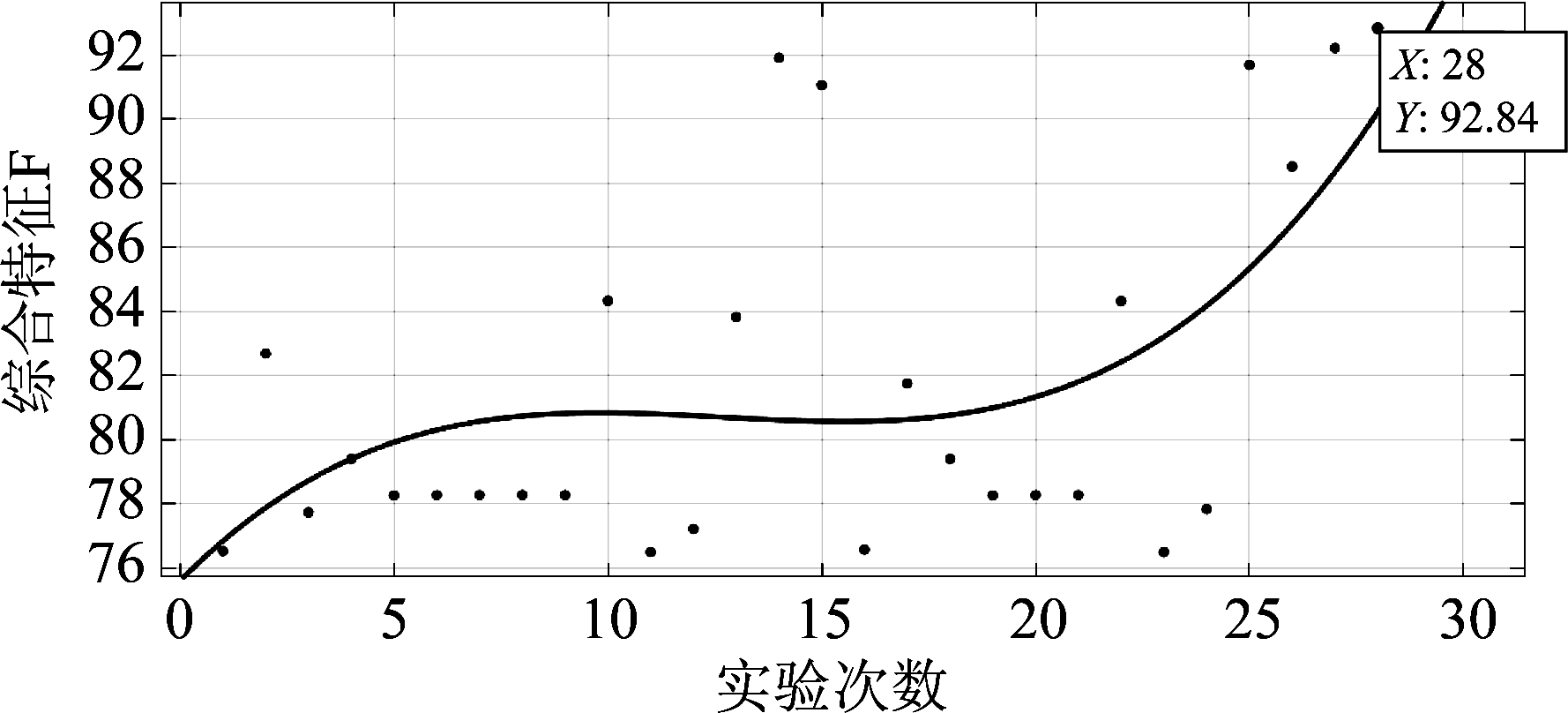
图5 综合特征F变化图
Fig.5 The variation of comprehensive feature F
5 结论
在本文中,提出了一种启发式掩模EMD用于音频信号的分解,与原始掩模EMD和其他掩模EMD的改进方法相比,启发式掩模EMD能够简洁有效地利用所分析信号的数据内容来确定掩模信号的幅值和频率,无需人为干预或提前设定,并通过在公开数据集上的实验证明启发式掩模EMD在信号复原精度和分解速度方面均有着明显的优势。
基于此信号分解方法,本文进一步地设计了一种音频突变成分检测方法。将音频信号经启发式掩模EMD分解后并提取检测特征,同时结合在检测方法中定义的窗长自适应更新策略获取突变成分的最适宜窗长,即可完成音频信号中突变成分的检测工作。该检测方法在执行时,无需有关信号的先验信息来调整参数,而是完全由所分析信号的数据内容来设定参数,在公开数据集上证明了该检测方法能够精确有效地检测出音频信号中的突变成分。此外,所检测出的突变成分维度一致,便于后续的信号处理操作,如特征提取、识别分类等。
在未来的工作中,可从两个方面着手:第一个是检测特征的提取,目前仅使用了最能反映音频信号中稳态成分与突变成分差异的瞬时频率和瞬时能量这两项作为检测特征,可进一步深入挖掘稳态成分与突变成分的差异,从而设计出更佳的检测特征;第二个是突变成分起止点的获取,本文使用简单易行的SVM作为起止点获取的工具,但在SVM的准确率到达92%之后就难以进一步提高,可试用其他更为精确的方法来获取突变成分的起止点。
[1] 李伟, 李硕. 理解数字声音——基于一般音频/环境声的计算机听觉综述[J]. 复旦学报:自然科学版, 2019, 58(3): 269-313.
Li Wei, Li Shuo. Understanding Digital Audio-A Review of General Audio/Ambient Sound Based Computer Audition[J]. Journal of Fudan University: Natural Science, 2019, 58(3): 269-313.(in Chinese)
[2] 关欣, 李锵, 郭继昌, 等. 二、四阶时延统计量多乐器盲分离[J]. 计算机工程与应用, 2010, 46(30): 121-124.
Guan Xin, Li Qiang, Guo Jichang, et al. Blind Musical Instrument Separation Using 2nd and 4th Combined Time Delay Statistic[J]. Computer Engineering and Application, 2010, 46(30): 121-124.(in Chinese)
[3] 翟鹏. 基于非负矩阵分解的单通道音乐分离研究[D]. 成都: 西南交通大学, 2013.
Zhai Peng. Single Channel Music Separation Based on Nonnegative Matrix Factorization[D]. Chengdu: Southwest Jiaotong University, 2013.(in Chinese)
[4] 杨立东. 基于张量分析的多因素音频信号建模与应用研究[D]. 北京: 北京理工大学, 2016.
Yang Lidong. Study on Multifactor Audio Signal Modeling and Applications Based on Tensor Analysis[D]. Beijing: Beijing Institute of Technology, 2016.(in Chinese)
[5] 王冬冬. 基于节拍和关键背景模型的音频分类与分割[D]. 哈尔滨: 哈尔滨工业大学, 2017.
Wang Dongdong. Audio Classification and Segmentation Method Based on Beats and Key Background Modes[D]. Harbin: Harbin Institute of Technology, 2017.(in Chinese)
[6] 徐金才. 基于深度神经网络的音频信号分离的研究[D]. 北京: 北京邮电大学, 2018.
Xu Jincai. Research on Separation of Audio Signal Based on Deep Neural Network[D]. Beijing: Beijing University of Posts and Telecommunications, 2018.(in Chinese)
[7] 孙慧芳, 龙华, 邵玉斌, 等. 基于过零率及频谱的语音音乐分类算法[J]. 云南大学学报:自然科学版, 2019, 41(5): 925-931.
Sun Huifang, Long Hua, Shao Yubin, et al. Speech Music Classification Algorithm Based on Zero-crossing Rate and Spectrum[J]. Journal of Yunnan University: Natural Science Edition, 2019, 41(5): 925-931.(in Chinese)
[8] 兰琼琼, 陆志华, 叶庆卫, 等. 基于特征组合的多目标监督性语音分离研究[J]. 无线通信技术, 2019, 28(3): 17-22.
Lan Qiongqiong, Lu Zhihua, Ye Qingwei, et al. Multi-targets for Supervised Speech Separation Based on Feature Combination[J]. Wireless Communication Technology, 2019, 28(3): 17-22.(in Chinese)
[9] Ghosal A, Dhara B C, Saha S K. Speech/Music Classification Using Empirical Mode Decomposition[C]∥2011 Second International Conference on Emerging Applications of Information Technology. Kolkata: IEEE, 2011: 49-52.
[10] Birajdar G K, Patil M D. Speech and Music Classification Using Spectrogram Based Statistic Descriptors and Extreme Learning Machine[J]. Multimedia Tools and Applications, 2019, 78(11): 15141-15168.
[11] Norden E Huang, Zheng Shen, Steven R Long, et al. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis[J]. Proceedings of The Royal Society A, 1998, 454(1971): 903-995.
[12] Rehman N, Mandic D P. Multivariate Empirical Mode Decomposition[J]. Proceedings of The Royal Society A, 2010, 466(2117): 1291-1302.
[13] Rehman N, Mandic D P. Filter Bank Property of Multivariate Empirical Mode Decomposition[J]. IEEE Transactions on Signal Processing, 2011, 59(5): 2421-2426.
[14] Deering R, Kaiser J F. The Use of a Masking Signal to Improve Empirical Mode Decomposition[C]∥Acoustics, Speech, And Signal Processing. Philadelphia: IEEE, 2005: 485- 488.
[15] 黎恒, 李智, 莫玮, 等. 噪声干扰环境下抑制EMD模态混叠方法[J]. 信号处理, 2015, 31(8): 956-961.
Li Heng, Li Zhi, Mo Wei, et al. Resolving the mode-mixing problem of EMD in the presence of noise[J]. Journal of Signal Processing, 2015, 31(8): 956-961.(in Chinese)
[16] Tsai F-F, Fan S-Z, Lin Y-S, et al. Investigating Power Density and the Degree of Nonlinearity in Intrinsic Components of Anesthesia EEG by the Hilbert-Huang Transform: An Example Using Ketamine and Alfentanil[J]. PLOS ONE, 2016, 11(12): e0168108-e0168123.




