1 引言
自电话发明以来,声信号的拾取与处理就一直是信号信息领域的一个重要研究方向。经过一个多世纪的发展,相关技术取得了长足进步,成功地解决了手持式或近距离拾音系统(如电话、扩放、播音等)中的很多难题,不仅推动了语音通信从单工到双工、从窄带到宽带、从有线到无线、从双端到多端、从单通道到立体声再到空间声的重大转变,也促进了人机交互和人工智能等技术的快速发展。但是随着语音通信与交互应用的不断推广,拾音系统面临的挑战也越来越大[1]。首先,拾音距离不断增大,在传统的通信系统中,声源距麦克风传感器的距离一般只有几个到几十个厘米,但随着电话会议、远程合作、智慧大屏、智能家居、安防监控等系统的出现,声源距麦克风传感器之间的距离会增大到几米甚至几十米。由于声传播服从逆平方定律,随拾音距离增大,传感器观测信号中期望声源信号的能量大幅下降,信噪比也随之大幅下降。一般来讲,拾音距离每增加1倍,信噪比下降至少6个分贝。其次,和传统的电话、扩放、播音等应用相比,智慧大屏、智能家居、安防监控等新的应用所面临的声学环境更为复杂,除了噪声、回声外,还存在多源干扰、多径效应和大量晚期反射造成的混响。再次,受温度、风速、声源的动态特性、拾音系统本身的移动(如可移动机器人)等多种因素的影响,声学环境呈现出快速时变和高度非平稳等特性。另外,声学系统所需完成的功能也越来越多,目前的大多数声学系统都需要具备远程拾音、双工通信、唤醒、识别等多种功能。受以上挑战的影响,单传感器系统已无法胜任目前通信与交互应用中的拾音需求,使用多个麦克风传感器已成为拾音系统的发展趋势。
和单传感器拾音系统相比,多传感器系统可感知声场空间信息,结合适当的处理算法,可以实现声源的定向/定位、空间声场分析与重构、盲信道辨识/均衡、盲源分离、信号增强、去混响等功能[2]。一般来讲,多传感器系统可分为两大类,即麦克风阵列和分布式多通道系统(通常也称作分布式传感网络)。两者的主要区别在于前者由相同特性的麦克风传感器按一定的拓扑结构组成,各传感器的前置放大倍数相同并共享同一个A/D时钟;而后者则一般没有严格的拓扑结构,每个通道的传感器特性、前放倍数、时钟也可以不同。相较而言,麦克风阵列方面的研究时间较长,处理方法也比较体系化,而分布式系统方面的研究还刚刚起步,理论基础尚未体系化,所以本文主要聚焦在麦克风阵列方面的工作。
麦克风阵列一般由两个关键部分组成:①由多个相同特性的麦克风传感器组成的物理阵列, ②利用传感器观测信号来实现一个或多个功能的阵列信号处理单元。前者的设计涉及到传感器的选择与校正、阵形的选择与优化、自动增益控制、前置放大与滤波以及多通道A/D的设计等,这些与具体应用的需求密切相关。后者则涉及到算法的设计、选择与优化。尽管两者是一个有机的整体,但是目前大多数关于麦克风阵列的研究都集中在处理方法和算法的研发方面。阵列信号处理方法有很多种,根据功能的不同可以分为声源定向/定位(包括时延估计)[2- 4]、 信道辨识与均衡[5]、信号增强(包括降噪、混响抑制等)[6]、声源分离[7- 8]等,也可以根据所利用的先验知识/假设不同而分为基于阵列拓扑结构和空间信息的波束形成[2,9]、 基于信号时空统计特性的多通道增强[10-12]、基于独立成分分析的盲源分离[8]、 基于数据驱动的学习方法等[13-14]。由于篇幅有限,本文集中讨论波束形成方面的工作。
波束形成作为阵列信号处理的一种基本方法,其用途很广,即可以用于定位/定向,信号的参数估计,也可以用于信号的增强和分离。其基本原理是利用麦克风阵列中传感器所携带的空间信息,构造一个增益随方位角甚至距离变化的空域滤波器[9,15]。和雷达、声纳、地震检测、无线通信等领域的波束形成相比,用于拾音的波束形成需要面对如下挑战:①由于语音、音频等声信号的频率范围很大,从20 Hz到20 kHz, 如何在如此大的带宽内获取一致的阵列响应是一个极具挑战性的难题,如果在不同频率上的阵列响应不一致,很容易造成信号畸变;②在大多数电子产品中,受空间、成本等因素的限制,阵列的孔径和阵元数目都不会很大,如何在小阵列上获取足够高的性能增益,尤其是在低频部分获取足够高的性能增益,难度很大;③由于声学环境和噪声环境快速时变且高度非平稳,如何解决阵列处理方法的鲁棒性也是一个难题。
针对以上挑战,人们提出了很多方法,本文简要介绍几种主要方法,包括延迟求和波束形成、超指向波束形成、差分波束形成、正交级数展开波束形成、Kronecker波束形成和自适应波束形成。几类波束形成方法从设计思路上都各不相同:延迟求和波束形成的设计思想是对阵列观测信号中的期望声源信号成分进行相干叠加;超指向波束形成是使阵列在空间上获得最高指向性;差分波束形成通过测量微分声场使阵列获得不随频率变化的指向性;正交级数展开方法是一种面向小孔径阵列的波束图逼近方法;Kronecker波束形成的思想是任务分解;自适应波束形成则从优化的角度解决阵列设计问题。论文聚焦在方法的基本原理、实现框架和优缺点,旨在为领域的研发人员提供一些基础知识,启发更多的兴趣,从而研发更好的解决方法。
2 信号模型
波束形成的过程如图1(a)所示,基本由滤波和叠加两个过程组成[16],各通道对应的滤波器共同组成了波束形成器,其响应特性决定了阵列的性能。波束形成器可以在时域设计,也可以在频域(大多是短时傅里叶变换域)设计,目前多数实用的麦克风阵列波束形成方法是在短时傅里叶变换域实现的,因为在该域不仅有复杂度小的优势,而且更适合处理和分析非平稳声信号。频域波束形成的过程如图1(b)所示。若将给定时刻和频带上的阵列观测信号叠成一个向量(为了表达的简便,我们在公式中省略了时间变量),可得

图1 时域和频域波束形成结构
Fig.1 Beamforming frameworks
y(ω) [Y1(ω) Y2(ω) … YM(ω)]T
[Y1(ω) Y2(ω) … YM(ω)]T
(1)
其中M是麦克风阵列的阵元个数,ω代表频率,上标T表示矩阵或向量的转置。波束形成器的输出可以写成如下的形式:
(2)
=hH(ω)y(ω)
(3)
其中上标*代表共轭,上标H代表矩阵或向量的共轭转置,h(ω) [H1(ω) H2(ω) … HM(ω)]T是阵列的波束形成滤波器,它是一个与y(ω)维度相同的复向量。给定h(ω)时,阵列的空域响应定义为:
[H1(ω) H2(ω) … HM(ω)]T是阵列的波束形成滤波器,它是一个与y(ω)维度相同的复向量。给定h(ω)时,阵列的空域响应定义为:
![]() ϑ)
ϑ) hH(ω)d(ω,ϑ)
hH(ω)d(ω,ϑ)
(4)
其中ϑ代表方向,通常由方位角φ∈[0,2π]和俯仰角θ∈[0,π]组成;d(ω, ϑ)是阵列的导向矢量,由阵列几何结构、方向和频率共同确定。空域响应反映了阵列对来自不同方向信号的响应特性。通常情况下,人们希望空域响应在期望声源方向的幅度是最大的,对其他方向的信号会产生不同程度的衰减。如果将空域响应的幅度随方向的变化曲线画出来,可得到通常所说的波束图,如图2所示,在这个示意图中,0°方向的为主瓣,其他方向的为旁瓣。通常情况下,波束形成器的主瓣越窄、旁瓣越低越好,可以通过指向性因子来衡量这一性能,其定义如下:
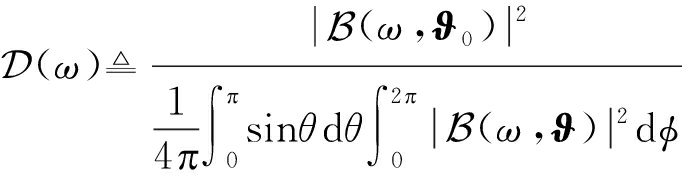
(5)
(6)
其中ϑ0代表期望的导向方向,Γ(ω)是各向同性噪声的协方差矩阵[17]。人们常说的指向性指数是对数尺度下的指向性因子,即![]() 对于小孔径阵列而言,指向性指数高的波束形成器可能对麦克风传感器的自噪声或阵元之间的不匹配非常敏感,衡量这一敏感度的指标是白噪声增益,其定义如下:
对于小孔径阵列而言,指向性指数高的波束形成器可能对麦克风传感器的自噪声或阵元之间的不匹配非常敏感,衡量这一敏感度的指标是白噪声增益,其定义如下:
(7)
白噪声增益越高,波束形成器的鲁棒性越好,反之,越差。在实际系统中,白噪声增益的dB数可以是负的,白噪声增益与鲁棒性之间的关系取决于麦克风传感器的自噪声水平以及传感器之间的不匹配程度。自噪声水平越低,达到同样的鲁棒性所需的白噪声增益可以越小。目前大多数麦克风传感器的自噪声水平在20 dB~30 dB 之间,只要白噪声增益大于-10 dB,系统通常不会出现由信号放大产生的白噪声问题,换句话说,具有很好的鲁棒性。另外,在音频和语音处理中,为了避免波束形成器对方向性信号造成频谱失真,人们通常希望波束图不随频率ω 的变化而变化。
3 延迟求和波束形成
顾名思义,延迟求和波束形成就是将各麦克风的观测信号引入适当的延迟,再将延迟后的信号叠加起来。引入时延的目的是使得各通道中来自期望声源的信号成分在时间上是同步的,各通道的时延量取决于声源相对阵列的方位。在频域,延迟求和波束形成器可非常简洁地表示为:
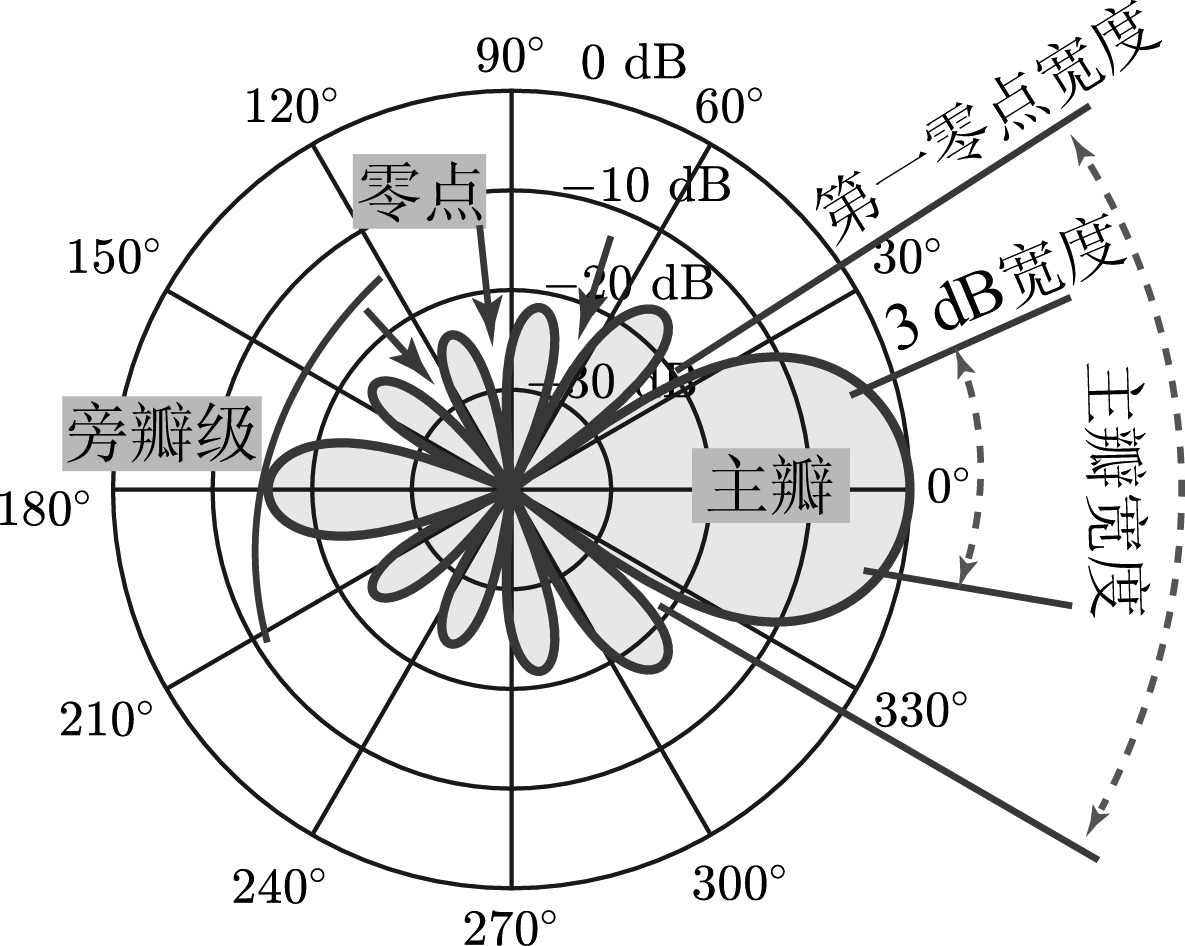
图2 波束图示意图
Fig.2 Illustration of a beampattern
![]() ϑ0)
ϑ0)
(8)
其中ϑ0代表期望的导向方向(应该和期望声源的方向一致)。
将(8)代入(4),可得到延迟求和波束形成器的空域响应为:
![]() ϑ
ϑ![]() ϑ0)d(ω,ϑ)
ϑ0)d(ω,ϑ)
(9)
可以验证,![]() ϑ0)=1,也就是说,来自期望声源方向ϑ0的信号会无失真地保留;而任意ϑ 方向阵列的响应取决于ϑ和ϑ0方向阵列导向矢量的内积。
ϑ0)=1,也就是说,来自期望声源方向ϑ0的信号会无失真地保留;而任意ϑ 方向阵列的响应取决于ϑ和ϑ0方向阵列导向矢量的内积。
图3给出了一个基于均匀线形麦克风阵列的延迟求和波束形成器在不同频率上的波束图,阵元个数为M=5,相邻阵元之间的间距为1 cm,极坐标的极轴为阵元的连线(0°~180°),导向方向为0°。由于阵列的空间响应是以阵列的轴向为对称的,因此,二维波束图就能完全反应阵列的空域响应。由图可见:①导向方向(0°)响应最大,因此能够保证来自导向方向的信号不被衰减;②低频段波束图指向性差,见图3(a)和(b),所以该波束形成器在低频段的噪声抑制能力差;③阵列的波束图随频率变化而变化,波束图的频率一致性差,因此,若将延迟求和波束形成器用于处理宽带音频或语音信号,很容易引入信号畸变。
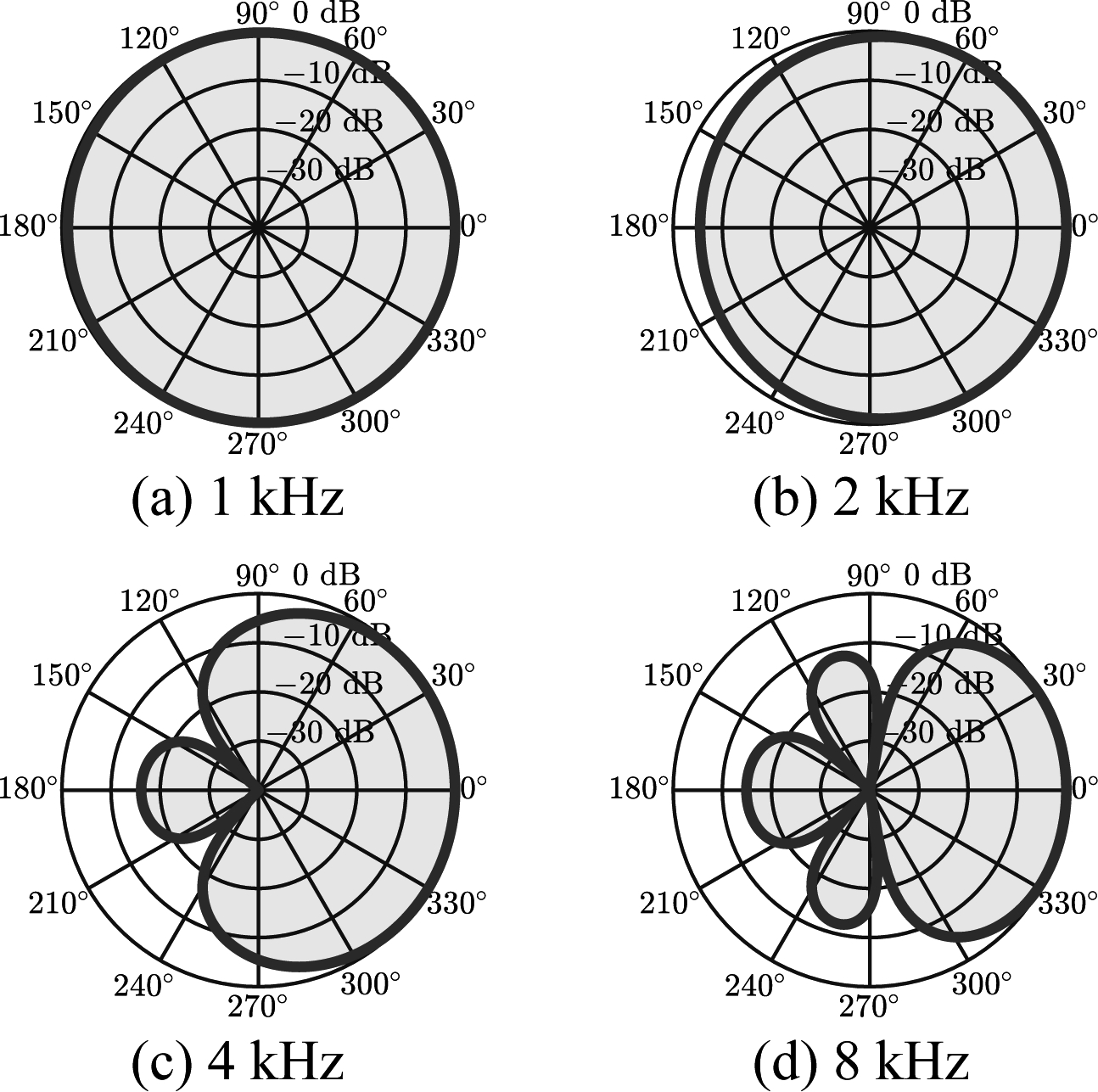
图3 延迟求和波束形成器的波束图
Fig.3 Beampatterns of the delay-and-sum beamformer at different frequencies
4 超指向波束形成
为了更好地抑制来自导向方向以外的噪声,人们希望波束形成器的指向性越高越好,一种直接的思路是极大化指向性因子,相应的波束形成器被称为超指向波束形成器。根据式(6)中指向性因子的定义, 结合期望声源方向的无失真约束,超指向波束形成器的优化问题可以描述为:
![]() ϑ0)=1
ϑ0)=1
(10)
可以求得:
(11)
超指向波束形成器的波束图如图4(a), (c)和(d)所示,其中阵列参数与图3中的相同。超指向波束形成有很多优点:①对于小孔径阵列,波束图具有非常好的频率一致性,因此适合处理宽带信号;②波束图具有类似等旁瓣级的特性,使得来自各方向的噪声都能得到较好程度的抑制;③具有最大的阵列指向性,对于小孔径均匀线阵,指向性因子可达M2。 事实上,超指向波束形成的原理还可以从其他多个角度去解释。由于它是差分波束形成的一种特例,差分波束形成测量微分声场,故超指向波束形成实质上也是对微分声场响应。超指向波束形成还是自适应MVDR波束形成在各向同性噪声下的特例,根据MVDR波束形成的原理,超指向波束形成实质上也是在约束期望声源方向信号不失真的条件下,尽可能多地抑制来自所有其他方向的信号[18]。
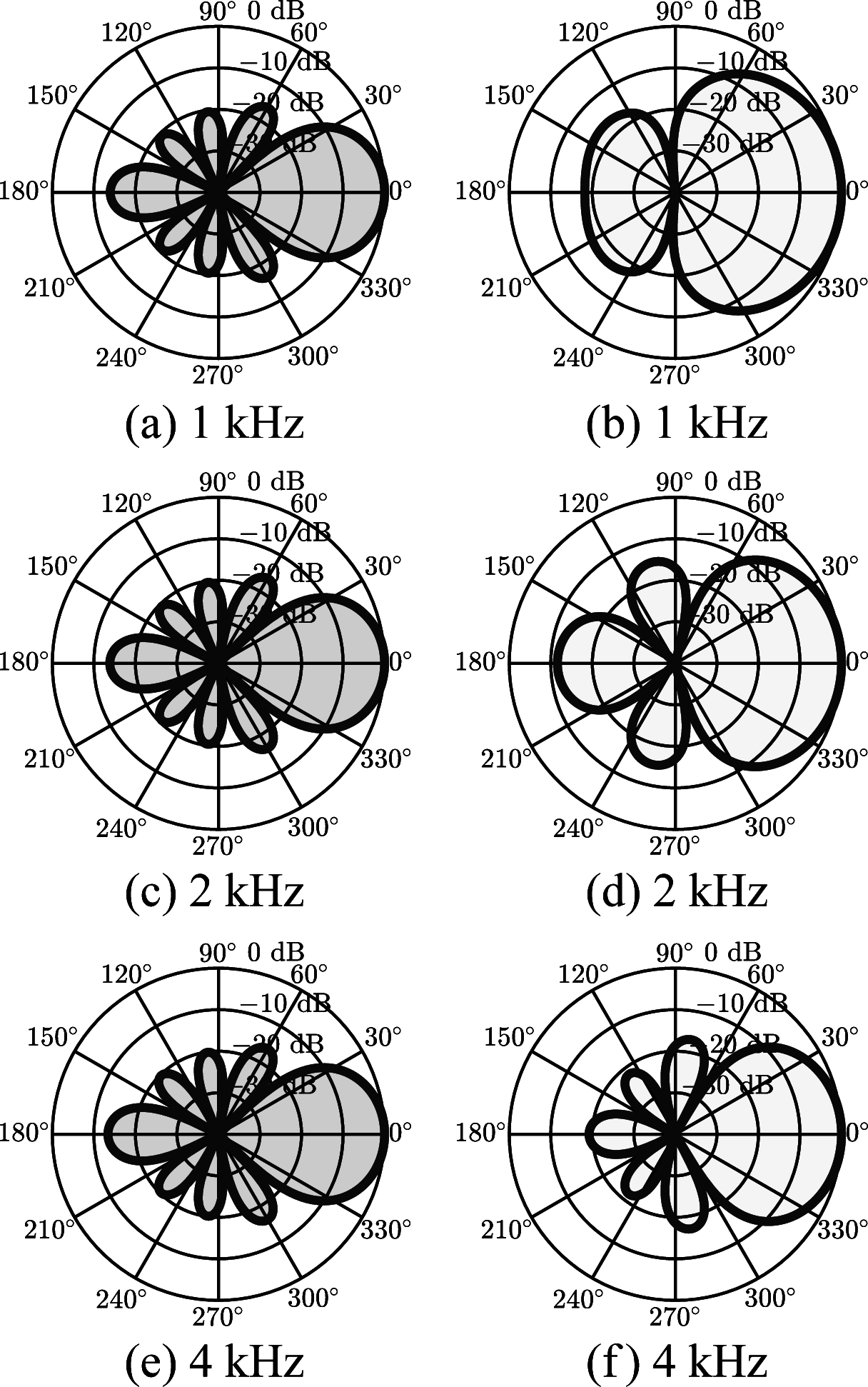
图4 不同频段超指向波束形成的波束图:左边一列对应经典超指向波束形成;右边一列对应基于对角加载的稳健超指向波束形成
Fig.4 Beampatterns of the superdirective beamformer at different frequencies: subfigures on the left-hand side plot the beampatterns of the superdirective beamformer; subfigures on the right-hand side plot the beamptterns of the robust superdirective beamformer (with diagonal loading)
但是,超指向波束形成存在一个严重的缺点:白噪声增益低,对阵列的自噪声非常敏感,稳健性差。针对超指向阵列白噪声增益低的问题,相关的研究已经很多[19-24],对白噪声增益改善的途径也多种多样,如:①考虑到延迟相加波束形成具有最大的白噪声增益,文献[25]提出了一种结合超指向性波束形成和延时相加波束形成的方法,从而获得阵列指向性和白噪声增益之间的折衷;②文献[26-28]从子空间分解的角度研究了如何在指向性和白噪声增益之间找到合适的折衷;③在对最优波束形成器(11)中的协方差矩阵Γ(ω)求逆时进行对角加载[24],从MVDR波束形成的角度看,该方法等价于阵列协方差矩阵中除了考虑各向同性噪声的贡献外,还有一部分来自自噪声的贡献,在建模的时候引入自噪声,故而能够获得对抗自噪声的稳健波束形成器。④在优化问题中引入对白噪声增益的约束,根据白噪声增益的定义,该约束等价于在(10)中对波束形成器的范数进行约束[19],这类方法通常没有解析解,需要借助凸优化工具、或者利用迭代的方式求解最优解。改善超指向波束形成稳健性的途径还很多,这里不一一列举。然而,大多数经典方法在改善阵列白噪声增益时,都会严重损失波束图的频率一致性,使其不再适合处理语音信号这类宽带信号。图4(b), (d)和(f)展示了基于对角加载的稳健超指向波束形成方法的波束图,其中阵列参数与图3中的阵列参数相同,对角加载的数值是10-3;由图可见,波束图频率一致性较差。
改善波束图频率一致性最为直接的方法在优化问题中约束阵列波束图与期望波束图之间的误差。文献[29]提供了一种解决方案,在优化问题中同时考虑阵列波束图的频率一致性、白噪声增益和指向性因子。然而,根据实验结果,这类联合优化的方法所能得到的波束图指向性较低,且单项性能指标通常需要经过大量的尝试才能获得一个合理的解。文献[30]提出了一种两级级联的超指向波束形成方法,其波束形成器是两个子滤波器的卷积,波束形成器的波束图是级联滤波器波束图的乘积。这种分解下,波束形成器的两个子滤波器分别设计,一个用于最大化阵列的指向性,另一个用于提升阵列的白噪声增益。通过级联结构分级优化,超指向阵列能够在提升白噪声增益时,保持阵列的频率一致性。这种级联结构[18,31]后来被推广成了一种更通用的Kronecker波束形成方法。
5 差分波束形成
差分波束形成的原理类似于压差式麦克风[32],通过测量声压场的微分场来获取不随频率变化的空间指向性。由于麦克风阵列中的传感器只能测量到空间离散点的声压,所以差分波束形成利用有限阶空间差分来逼近声压场的微分[9,33]。为了保证逼近的准确性,要求阵列中阵元间距足够小,远小于频段中最小的波长。这种波束形成方法从原理上非常适合设计小孔径阵列的波束形成器;由于波束图频率一致性好,它也适合用于处理宽带声信号;除此之外,和延迟求和波束形成器相比,差分波束形成在相同数目阵元的情况下可获得更高的指向性因子,前面介绍的超指向波束形成是差分波束形成的一个特例。
传统的差分波束形成方法如图5所示,一阶差分波束形成通过将两路麦克风观测信号相减得到,二阶差分波束形成通过对两个一阶差分波束形成器的输出再相减得到,以此类推,任意N阶差分波束形成可通过对两个N-1阶差分波束形成器的输出进行相减而得。在这种多级级联的结构下,N阶差分波束形成需要N+1个压强式麦克风,阵列的波束图通过控制图5中的时延参数来调整。差分波束形成的指向性与其阶数有关,阶数越高,可获得的指向性越高,因此在实际应用中我们希望阶数越高越好。但差分波束形成也有一个非常大的缺点:因为差分操作会放大白噪声,而且频率越低,白噪声放大问题越严重,所以差分波束形成稳健性差,对传感器的自噪声非常敏感。对于高阶差分波束形成,如果不加以克服,放大的自噪声可淹没观测信号中的期望声源信号,因此白噪声放大问题阻碍了高阶差分波束形成的应用。
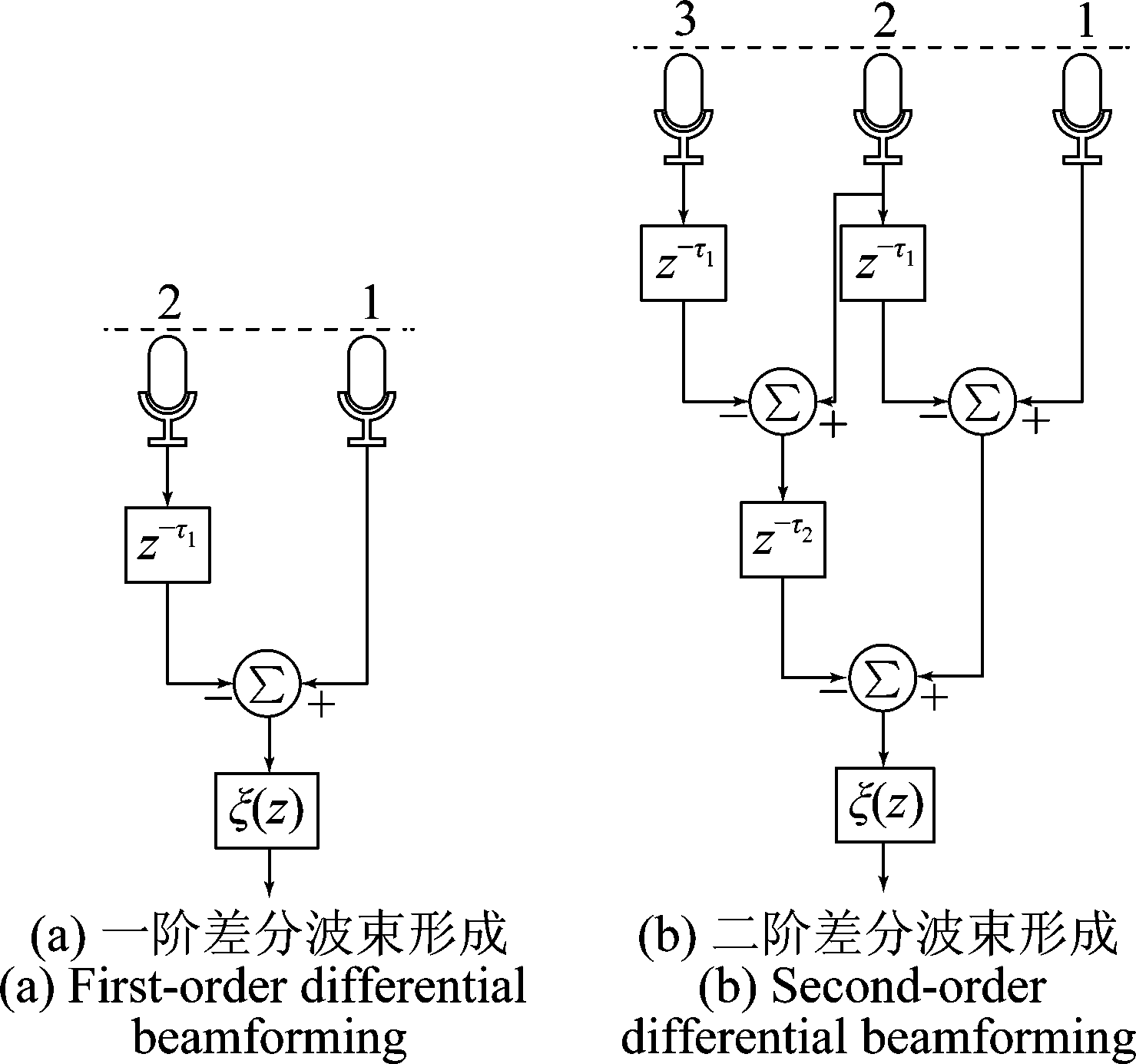
图5 差分波束形成的基本原理
Fig.5 Fundamental of differential beamforming
图5中给出的传统差分波束形成设计结构是固定的,很难解决稳健性问题;而且,这种多级结构不同于经典的滤波求和、加权求和波束形成结构,不便分析高阶差分阵列的性能。为了克服级联型差分阵列设计方法存在的问题,Benesty和Chen基于均匀线形阵列提出了一种零点约束差分波束形成方法[17,34]。这种设计方法在子带上根据理想波束图的零点位置来构造一系列零点约束关系,这些零点约束方程加上期望方向不失真约束组成一个线性系统,求解这个线性系统,便可得到差分波束形成的滤波器[17]。具体而言,对于有M个阵元的均匀线列阵,希望形成N阶的差分波束(M≥N+1),其波束形成的约束条件为
D(ω,α)h(ω)=β
(12)
其中α和β是由预设的波束图的零点信息和期望声源方向而定,D(ω,α)是由阵列零点及导向方向上的导向矢量构成的(N+1)×M维矩阵。当M>N+1时,可利用(12)中波束形成器剩余的自由度最大化阵列的白噪声增益,即:
(13)
其解
hDMA(ω)=DH(ω,α)[D(ω,α)DH(ω,α)]-1β
(14)
为最大化白噪声增益的稳健零点约束差分波束形成器。相比传统方法,基于零点约束的设计方法可以方便灵活地设计各种波束图,尤其重要的是,该方法能够通过增加麦克风数目来提升白噪声增益,从而解决制约差分阵列应用的白噪声放大瓶颈问题。在现有的框架下,文献[18,31]对零点约束差分波束形成和传统多级差分波束形成做了深入分析,提出了一种更加通用的多级级联结构,为差分波束形成的分析与深入理解提供了新的视角。多级级联结构的研究表明:①给定M元均匀线阵,若按图5的多级级联结构进行N 阶的差分波束形成,理论上等价于(12)中的线性约束差分波束形成器;②多级级联结构中,相邻的多个级可以合并成单级的结构,单级结构下的波束形成器等于多级结构下各级子滤波器的线性卷积;③多级级联结构下,阵列的波束图等于各级子滤波器波束图的乘积;④稳健的差分波束形成器可以分解成两级级联的结构,一级用于实现差分波束形成,另一级用于提升阵列的稳健性。利用性质③和④,文献[31]中的工作发现如果阵元数目过大,最大白噪声增益差分波束形成方法波束图在高频段会逐渐出现额外零点,因此阵列输出在高频段会存在高阶声场的成分,需要约束差分波束形成的阶数以保证波束图的频率一致性。除此之外,多级级联结构的分级设计思想还启发了超指向波束形成和Kronecker波束形成。
差分波束形成方法可以形成一系列些经典的波束图,如双极形(dipole)、心形(cardioid)、超心形(supercardioid)、锐心形(Hypercardioid)和切比雪夫形等。图6给出了几个典型的2阶和3阶波束图。这些波束图适合不同的应用场景,实际中选取哪种波束图要视应用需求和场景而定。上述方法通过零点的位置来设计波束图,设计方法简便,不需要预知目标波束图,但零点的选取有一些范围限制[35],理论上,N 阶差分波束形成的最小零点不能小于π/(2N)。
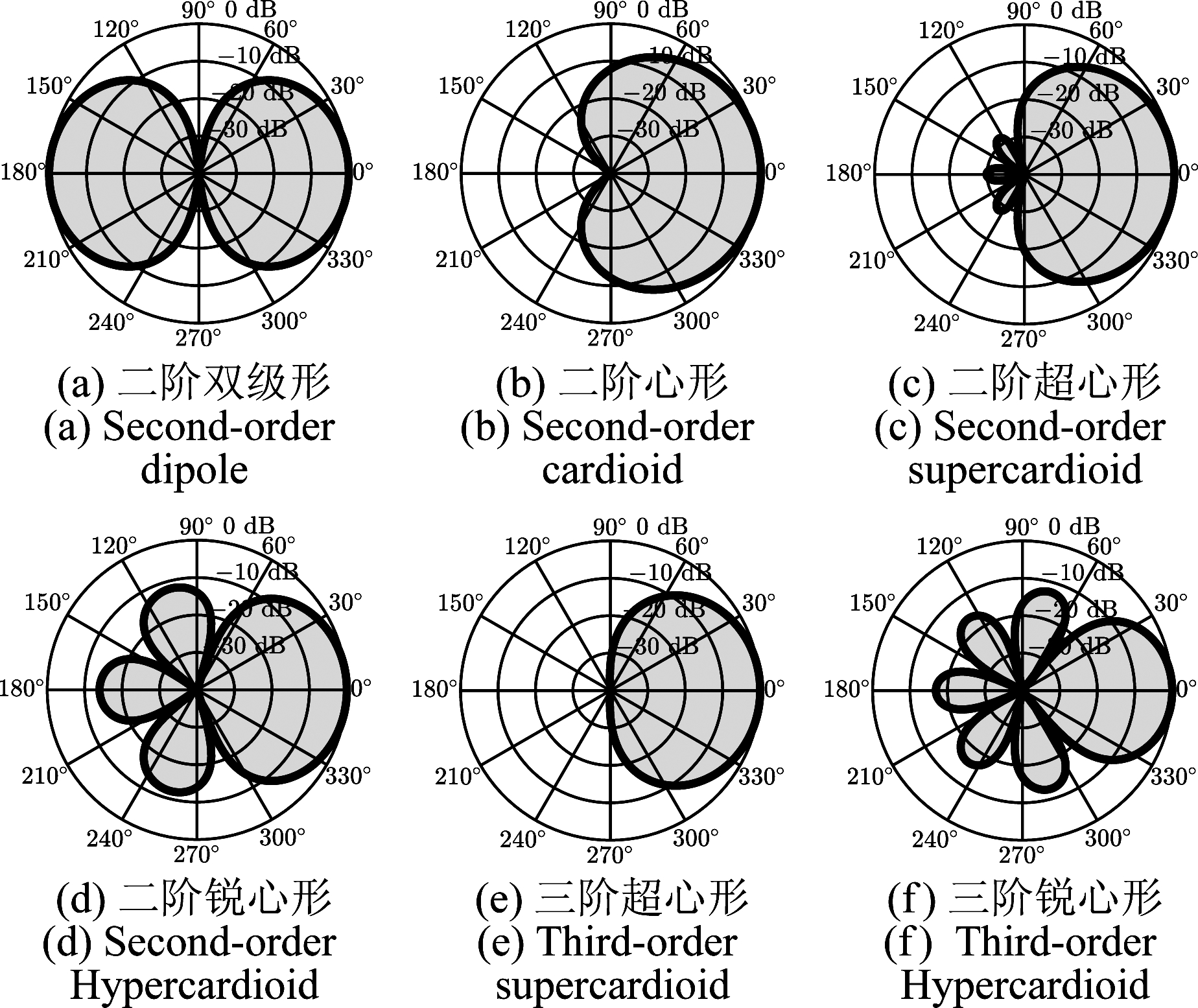
图6 典型的差分波束形成的波束图
Fig.6 Typical beampatterns of the differential beamformer
基于线性阵列的差分波束形成通常设定端射方向为导向方向,如其他方向为导向方向时,受物理结构的限制,可能无法形成有效的波束图,换而言之,线形阵列差分波束形成的调向能力有限,其波束图随导向方向的变化而变化,若导向方向不在端射方向上,其增益可能会小于其他方向的增益,导致负增益。为了获得好的调向能力,Benesty等将线形差分阵列设计的理论和方法推广到了环形阵列,提出了基于均匀环形麦克风阵列的零点约束环形差分波束形成方法[36]。但是,这种环形差分波束形成方法只能提供有限的波束调向选择。针对该问题,文献[37-38]从波束图逼近的角度,以差分阵列的理想波束图为目标波束图,提出了基于雅克比级数展开的环形差分阵列设计方法。这种方法设计的波束能在阵元所在平面内实现任意方位的调向,且从理论上保证了波束的频不变性和对称性。为了提高环形差分波束形成的性能,文献[39- 41]提出了基于同心圆环阵列的差分波束形成方法,能显著改善差分波束形成在高频的频不变性、稳健性和指向性。
此外,以上差分波束形成方法只能设计整数阶的差分,在给定麦克风数目的情况下,如果N阶差分波束形成器存在较严重的白噪声放大问题,无法使用,则只能选择N-1阶或更低的整数阶。为改善这一现象,文献[42]提出了一种分数阶的差分波束形成方法,推导了分数阶阶数与预设指向性因子和白噪声增益之间的关系,解决了传统差分波束形成只能设计整数阶波束图的局限。该方法还能够根据给定的指向性因子或白噪声增益算出具体的分数阶数,用于设计稳健的差分波束形成器,使其白噪声增益不低于给定的阈值。当然,也可以通过其他方法来取得指向性因子和白噪声增益之间的折衷,如文献[43]将传统的级联型差分波束形成方法和基于滤波求和的差分波束形成相结合,构成一个两级级联型波束形成架构,第一级通过不同阶数的差分算子得到差分信号,第二级对得到的差分信号进行滤波。通过使用不同的优化准则,可以得到不同的差分波束形成器。
除了基本原理、稳健设计方法、调向能力等方面的研究外,差分波束形成其他方面的研究还包括:文献[44- 46]将差分波束形成方法推广到任意结构的平面阵列;文献[47]研究了时域差分波束形成;文献[46,48-53]对不同阵列结构下差分波束形成波束(或主瓣)的调向能力、稳健性和计算复杂度等进行了探讨。
6 正交级数展开波束形成
正交级数展开波束形成的基本原理是波束图逼近。通过级数展开建立阵列波束图和目标波束图的等价关系,求解滤波器系数,使得阵列波束图逼近目标波束图。这类波束形成方法中,目标波束图往往是正交级数的函数,如何选取正交级数、以及如何利用级数设计/表示目标波束图是首要问题。对于小孔径阵列,差分波束形成目标波束图的函数形式为:
![]() ϑ
ϑ![]() ϑ)
ϑ)
(15)
其中Pn(ϑ) 是角度θ和角度φ的函数,与频率无关,Pn(ϑ)具有按某个非负权函数ψ(ϑ) 正交的特性,具体而言,
![]() ϑ)Pn′(ϑ)ψ(ϑ) dϑ
ϑ)Pn′(ϑ)ψ(ϑ) dϑ![]()
(16)
对于线阵,Pn(ϑ) 是cos θ的n阶多项式,L=N为波束图的阶数;对于一般阵列形状,级数可能更加复杂,并且L>N不再等于波束图的阶数。典型的正交级数有切比雪夫级数、勒让德级数、雅可比级数、球谐函数等。给定一组完备的正交级数,阵列的导向矢量可以展开为:
d(ω,ϑ![]() ϑ)
ϑ)
![]() ϑ)
ϑ)
(17)
阵列波束图可通过如下线性方程设计:
C(ω)h(ω)=β
(18)
其中C(ω)是一个(L+1)×M的矩阵,它的第i行为![]() 向量β的第i个元素为βi-1,∀i=1,2,…, L+1。为方便起见,定义矩阵
向量β的第i个元素为βi-1,∀i=1,2,…, L+1。为方便起见,定义矩阵
![]() ϑ)dH(ω,ϑ)ψ(ϑ)dϑ
ϑ)dH(ω,ϑ)ψ(ϑ)dϑ
(19)
理论证明,最小化hH(ω)Γψ(ω)h(ω)可控制阵列波束图和期望波束图之间的误差[54],从而获得频率一致的阵列响应。考虑对白噪声增益的约束,正交级数展开波束形成的优化问题可以表述为[54]:
(20)
其中Γψ , 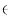 (ω)
(ω) Γψ(ω)+
Γψ(ω)+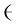 I, 参数
I, 参数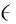 用于控制阵列的白噪声增益。其对应的波束形成器可以表示为:
用于控制阵列的白噪声增益。其对应的波束形成器可以表示为:
(21)
一般来讲,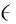 的值越大,波束形成器的稳健性越好,但是波束图的频率一致性将变差。当
的值越大,波束形成器的稳健性越好,但是波束图的频率一致性将变差。当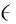 =0时,波束形成器能够从均方误差的角度对目标波束图进行最优逼近,但是阵列波束形成器的稳健性通常比较差。实际中通过调整
=0时,波束形成器能够从均方误差的角度对目标波束图进行最优逼近,但是阵列波束形成器的稳健性通常比较差。实际中通过调整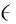 值的大小可在指向性、波束图频率一致性和白噪声增益之间找到一个折衷,阵列波束图与目标波束图之间的误差则通过调整权函数ψ(ϑ) 来控制[54]。
值的大小可在指向性、波束图频率一致性和白噪声增益之间找到一个折衷,阵列波束图与目标波束图之间的误差则通过调整权函数ψ(ϑ) 来控制[54]。
文献[37,55]提出了基于雅各比级数展开的环形阵列频不变波束形成方法,并证明了利用雅各比级数对阵列波束图逼近时具有最小均方误差。其还从理论上给出了环形阵列频不变波束形成性能(波束图、指向性因子和白噪声增益)和麦克风数目、阵列半径等的解析关系,为优化环形阵列频不变波束形成提供了理论指导。当期望调向方向为φs时,环形阵列的滤波器系数可以表示为:
(22)
其中bN,n是由目标波束图决定的系数,Jn(![]() ) 表示n阶第一类贝塞尔函数,
) 表示n阶第一类贝塞尔函数,![]() =ωr/c,r是环形阵列半径,c是声波在空气中的传播速度,φm 表示第m个麦克风对应的方位角。当系数
=ωr/c,r是环形阵列半径,c是声波在空气中的传播速度,φm 表示第m个麦克风对应的方位角。当系数![]() 时,环形阵列频不变波束形成等价于传统的圆环谐波分解波束形成[56-57](圆环谐波分解波束形成经过近几十年的发展,出现了很多新的更加灵活、鲁棒的算法[20,58])。
时,环形阵列频不变波束形成等价于传统的圆环谐波分解波束形成[56-57](圆环谐波分解波束形成经过近几十年的发展,出现了很多新的更加灵活、鲁棒的算法[20,58])。
根据(22),当贝塞尔函数Jn( ![]() )趋于零时(通常在高频段出现),滤波器系数将会趋向无穷大,从而使波束形成器出现奇异,阵列性能在该频段显著下降。针对该问题, 文献[38,40- 41,59]提出了一种基于同心圆环阵列的频不变波束形成方法,能很好解决高频奇异并改善白噪声放大问题。文献[40]还发现了阶数越低的贝塞尔函数引入的奇异问题越严重。因此,可在环形阵列中心增加一个麦克风来改善零阶贝塞尔函数引起的奇异问题能显著提高频不变波束形成的性能。同时,文献[40]中提出的同心圆环阵列结构非常灵活,可以用不同阶数的雅各比级数来近似不同圆环阵列对应的波束图,实际中可以在靠外的圆环上放置更多的麦克风,用来支持设计波束中的高阶分量,在靠内的圆环上放置更少的麦克风,用来支持设计波束中的低阶分量。而且在这种结构下,不同环形阵列上的麦克风不需要对齐,既可以增加阵列结构的灵活性,减小制造工艺的复杂性,又可以提高波束形成方法的鲁棒性。
)趋于零时(通常在高频段出现),滤波器系数将会趋向无穷大,从而使波束形成器出现奇异,阵列性能在该频段显著下降。针对该问题, 文献[38,40- 41,59]提出了一种基于同心圆环阵列的频不变波束形成方法,能很好解决高频奇异并改善白噪声放大问题。文献[40]还发现了阶数越低的贝塞尔函数引入的奇异问题越严重。因此,可在环形阵列中心增加一个麦克风来改善零阶贝塞尔函数引起的奇异问题能显著提高频不变波束形成的性能。同时,文献[40]中提出的同心圆环阵列结构非常灵活,可以用不同阶数的雅各比级数来近似不同圆环阵列对应的波束图,实际中可以在靠外的圆环上放置更多的麦克风,用来支持设计波束中的高阶分量,在靠内的圆环上放置更少的麦克风,用来支持设计波束中的低阶分量。而且在这种结构下,不同环形阵列上的麦克风不需要对齐,既可以增加阵列结构的灵活性,减小制造工艺的复杂性,又可以提高波束形成方法的鲁棒性。
此外,正交级数展开波束形成方法在球形麦克风阵列中也有大量的研究[60- 65],最具代表性的是Eigenmike系统中基于球谐波分解的波束形成[62- 63]。 这种球谐波分解波束形成通常分为两步:①分解获取不同阶数的球谐波;②按一定的权系数线性组合球谐波形成期望波束。但是,为了满足球谐波函数采样的正交性,球谐波分解通常对阵元位置的布放有严格的要求[64]。相较而言,基于正交级数展开的波束形成中,通常对阵元位置的布放没有严格要求,利用(21)均可实现频不变波束形成的设计,阵列设计上可以更加灵活。
7 Kronecker波束形成
设计波束形成器时,一方面希望能够形成频率一致性好的波束图,另一方面希望能够充分利用阵列的自由度获取最高的指向性和合理的白噪声增益。但是实际中,当约束阵列的白噪声增益时,往往很难控制指向性因子和波束图的频率一致性。针对这个问题,限定阶数差分波束形成[31]和两级级联超指向波束形成[30]提供了一种解决思路:将波束形成器分解成两个子滤波器,一个子滤波器设计期望的波束图,另一个子滤波器改善阵列的白噪声增益。Kronecker波束形成将该思想推广成一种更为通用的方法[66- 67]。
当阵列的几何结构满足一定的条件时,阵列的导向矢量可以分解成两个子阵导向矢量的直积(Kronecker积):
d(ω,ϑ)=d1(ω,ϑ)⊗d2(ω,ϑ)
(23)
其中⊗表示直积,d1(ω, ϑ)和d2(ω, ϑ)分别是长度为M1和M2 的向量,且有M=M1M2。向量d1(ω, ϑ)和d2(ω, ϑ)可以看成是两个子阵的导向矢量。与子阵导向矢量d1(ω, ϑ) 和d2(ω, ϑ)相对应,可以定义两个子滤波器h1(ω)和h2(ω);它们的长度与对应子阵的导向矢量相同,两个子滤波器可以看作是两个子阵的波束形成器。Kronecker波束形成通过子滤波器的直积来得到总的波束形成器:
h(ω)=h1(ω)⊗h2(ω)
(24)
将(23)和(24)代入(4),利用直积的性质,可以求得:
![]() ϑ
ϑ![]() ϑ
ϑ![]() ϑ)]
ϑ)]
(25)
根据(25),阵列的波束图等于两个子阵波束图的乘积。因此,在设计波束图时,可通过优化其中一个子滤波器设计期望的波束图,同时,约束另一个子滤波器响应不随角度的变化而变化(平坦的空间全通滤波器)来保证阵列整体波束图的频率一致性。例如可以利用孔径小的子阵设计频不变的波束图,用孔径大的子阵优化阵列的白噪声增益。由于约束波束图平坦在低频段并不会占用阵列的自由度,Kronecker波束形成器能够在低频段充分的利用冗余的自由度提升阵列的白噪声增益。Kronecker波束形成提供了一种小孔径阵列频不变波束形成的框架,它可以非常灵活地与其他波束形成方法进行结合,设计频不变波束图,提升波束形成器的稳健性。文献[68]将Kronecker波束形成推广到可适用于任意阵元个数的均匀线列阵。文献[69-70]进一步将Kronecker波束形成推广到具有灵活调向能力的平面阵列。
Kronecker波束形成方法有很多优点。从设计复杂性的角度,它可以将一个复杂的阵列分解成两个简单的子阵列,每个子阵列的波束形成器设计起来更为简便。从设计灵活性的角度,Kronecker 波束形成方法可以非常灵活的将不同种类的波束形成方法结合起来,如固定波束形成和自适应波束形成。以自适应波束形成为例,最优滤波器通常是阵列观测信号的协方差矩阵的函数。当阵元数较大时,协方差矩阵维度很高,求逆非常耗费计算资源;另外,由于语音信号非平稳、声学环境时变,准确地估计协方差矩阵通常十分困难,维度越高,估计的误差也越大。利用Kronecker分解,可以将矩阵分解成一个小孔径阵列和一个大孔径阵列的直积。小孔径阵列利用自适应波束形成方法设计,充分利用观测信号中噪声的相关性实现高增益;大孔径阵列中,噪声的相关性弱,直接采用延迟求和波束形成便可实现最优滤波。如此一来,最优波束形成器变成低维协方差矩阵的函数,估计容易,求解速度快,阵列稳健性可得到大幅提升。
8 自适应波束形成
前面介绍的都是固定波束形成,波束形成器的系数一旦确定后,不随应用环境的变化而变化。固定波束形成的优点是稳健性好而且复杂度低,但噪声抑制性能一般是次优的。为了获得更好的噪声抑制能力,需要考虑声场或噪声场的特性,因此出现了自适应波束形成。一种最为经典的自适应波束形成是在保证期望信号不失真的条件下最小化阵列输出中残余噪声的方差,相应的自适应波束形成方法通常称作为最小方差无失真(MVDR)波束形成器。MVDR波束形成器通常具有如下的函数形式:
(26)
其中Φ(ω)是观测信号或者噪声的协方差矩阵,d(ω, ϑ0)是阵列的导向矢量。理论上,自适应波束形成器可以获得最佳的降噪效果,因为它可以根据噪声的统计特性自适地调整波束形成滤波器的系数[71]。 但在实际系统中设计这类波束形成器需要解决很多参数估计问题,如期望声源的方位、导向矢量、干扰信号或背景噪声协方差矩阵等[2,72]。在单声源、平稳噪声、混响较弱的声学场景下,对这些参数的估计相对容易;在多声源、非平稳噪声、强混响、时变声学环境下,对这些参数的估计往往非常困难。参数估计不准确一方面会导致噪声抑制性能下降,另一方面会引起信号的自对消,从而产生畸变。因此,参数估计和稳健的实现方法一直是自适应波束形成的研究热点[73]。
在室内声学环境中,阵列除了接收到期望声源的直达声信号以外,还会收到经过界面反射的源信号。反射信号分为两部分:早期反射和晚期反射。早期反射的声信号包含了房间的声学特性、声源的空间特性,在拾音中通常希望能够保留这些成分,所以实际中阵列真正的导向矢量并不是一个只与方位有关的函数,最佳的导向矢量建模方法需要用到房间声学、心理声学和信号处理等多个学科的知识。针对该问题,过去有过很多尝试,典型的方法有:①相对传递函数方法[74-75],这类方法假定在麦克风观测信号之间存在一个相对传递函数,设计波束形成器时用相对传递函数构成的向量替代(26)中的导向矢量,以期解决模型导向矢量与真实导向矢量不匹配的问题;②多通道滤波方法[2,76],将波束形成器导向矢量的估计问题转换成协方差矩阵的估计问题,绕开声源定位和导向矢量建模问题,将波束形成器的设计问题转换成多通道滤波器设计问题。尽管如此,如何对导向矢量进行精准建模仍是一个需要深入研究的问题。
除了MVDR波束形成外,线性约束最小方差(LCMV)波束形成器也是一种常见的自适应波束形成器[77],它在约束期望方向信号不失真外,通常还会约束其他若干方向阵列的响应[78]。另一种常用的自适应波束形成方法为广义旁瓣对消(GSC)算法[79],大致由三部分构成:固定波束形成器,阻塞滤波器和自适应对消器。当滤波器收敛后,GSC和MVDR是等价的,两者的区别在于GSC将MVDR中的带约束的波束形成优化问题转换成不带约束的噪声对消优化问题,因此,GSC可以看作是MVDR的一种稳健实现方法[80]。值得一提的是,在特定的噪声环境下,自适应波束形成器可以退化为固定波束形成器[18],例如:白噪声环境下,MVDR波束形成器退化成延迟求和波束形成器;在各向同性噪声环境下,MVDR波束形成器退化成超指向波束形成器;在各向同性噪声和白噪声同时存在的情况下,MVDR波束形成器等价于稳健的超指向波束形成器;在点源噪声环境下,MVDR波束形成器与LCMV波束形成器、差分波束形成器等都存在很强的内在联系。
9 总结
本文简要讨论了麦克阵列波束形成的基本方法,包括延迟求和、超指向、差分、正交级数展开、Kronecker和自适应波束形成方法,这些方法在实际系统和产品中已经获得了广泛的应用。因为各类方法的原理不同,各有优缺点,在特定应用中选择哪一种方法需要根据具体需求而定。但这些方法尚不能完全解决实际声学环境中远距离拾音面临的诸多问题,进一步深入研究是势在必行。需研究的问题很多,包括:
高增益:固定波束形成的优点是稳健,但其指向性的上限为阵元数目的平方,当阵元数目较小时,其指向性无法满足实际应用的需求,如何突破这一上限,值得探索;
白噪声放大: 差分波束形成、超增益波束形成具有很多好的特性,但存在白噪声放大问题,如何从根本上解决这一问题,需要新的方法;
频不变性:波束图频率一致性对高保真拾音非常重要,如何衡量频不变性和设计真正的频不变波束形成器,需要新的理论支持;
动态阵列拓扑优化:随着机器人、智能化设备的普及,阵列拓扑结构不再是固定的,如何利用载体的运动在线优化阵列的拓扑结构,从而更好地实现参数估计和信号获取,相关方面的研究目前还很少;
麦克风传感网络:随着传感器的微型化和芯片处理能力的持续增强,构建传感网络越来越容易,但相关的处理方法目前很少,需要理论与方法方面的突破。
[1] Huang Y, Chen J, Benesty J. Immersive audio schemes[J]. IEEE Signal Process. Mag., 2010, 28(1): 20-32.
[2] Benesty J, Chen J, Huang Y. Microphone Array Signal Processing[M]. Berlin, Germany: Springer-Verlag, 2008.
[3] Long T, Chen J, Huang G, et al. Acoustic source localization based on geometric projection in reverberant and noisy environments[J]. IEEE J. Select. Topics Signal Process., 2018, 13(1): 143-155.
[4] Chen J, Benesty J, Huang Y. Time delay estimation in room acoustic environments: an overview[J]. EURASIP Journal on Applied Signal Processing, 2006(1): 170-170.
[5] Huang Y, Benesty J, Chen J. Acoustic MIMO Signal Processing[M]. Berlin, Germany: Springer-Verlag, 2006.
[6] Nakatani T, Yoshioka T, Kinoshita K, et al. Speech dereverberation based on variance-normalized delayed linear prediction[J]. IEEE Trans. Audio, Speech, Lang. Process., 2010, 18(7): 1717-1731.
[7] Makino S. Audio Source Separation[M]. Springer International, 2018.
[8] Kitamura D, Ono N, Sawada H, et al. Determined blind source separation unifying independent vector analysis and nonnegative matrix factorization[J]. IEEE/ACM Trans. Audio, Speech, Lang. Process., 2016, 24(9): 1626-1641.
[9] Elko G W, Meyer J. Microphone arrays[G]∥Benesty J, Sondhi M M, Huang Y. Springer Handbook of Speech Processing. Berlin, Germany: Springer-Verlag, 2008: 1021-1041.
[10] Chen J, Benesty J, Huang Y, et al. New insights into the noise reduction Wiener filter[J]. IEEE Trans. Audio, Speech, Lang. Process., 2006, 14: 1218-1234.
[11] Benesty J, Chen J, Habets E A. Speech Enhancement in the STFT Domain[M]. Berlin, Germany: Springer-Verlag, 2011.
[12] Huang G, Benesty J, Long T, et al. A family of maximum SNR filters for noise reduction[J]. IEEE/ACM Trans. Audio, Speech, Lang. Process., 2014, 22(12): 2034-2047.
[13] Xu Y, Du J, Dai L-R, et al. An experimental study on speech enhancement based on deep neural networks[J]. IEEE Signal Process. Lett., 2014, 21(1): 65- 68.
[14] Wang D, Chen J. Supervised speech separation based on deep learning: An overview[J]. IEEE/ACM Trans. Audio, Speech, Lang. Process., 2018, 26(10): 1702-1726.
[15] Van Veen B D, Buckley K M. Beamforming: A versatile approach to spatial filtering[J]. IEEE ASSP Mag., 1988, 5: 4-24.
[16] Trees H V. Optimum Array Processing: Part IV of Detection, Estimation, and Modulation theory[M]. New York, John Wiley Sons, Inc, 2002.
[17] Benesty J, Chen J. Study and Design of Differential Microphone Arrays[M]. Berlin, Germany: Springer-Verlag, 2012.
[18] Pan C. Study of Microphone Array Beamforming for Speech Communication[D]. Xi’an, China: Northwestern Polytechnical University, 2018.
[19] Yan S, Ma Y. Robust supergain beamforming for circular array via second-order cone programming[J]. App. Acous., 2005, 66(9): 1018-1032.
[20] Yan S. Optimal design of modal beamformers for circular arrays[J]. J. Acoust. Soc. Am., 2015, 138(4): 2140-2151.
[21] Ma Y, Yang Y, He Z, et al. Theoretical and practical solutions for high-order superdirectivity of circular sensor arrays[J]. IEEE Trans. Industrial Electronics, 2013, 60(1): 203-209.
[22] Wang Y, Yang Y, Ma Y, et al. Robust high-order superdirectivity of circular sensor arrays[J].J.Acoust. Soc. Am., 2014, 136(4): 1712-1724.
[23] Doclo S, Moonen M. Superdirective beamforming robust against microphone mismatch[J]. IEEE Trans. Acoust., Speech, Signal Process., 2007, 15(2): 617- 631.
[24] Cox H, Zeskind R M, Kooij T. Practical supergain[J]. IEEE Trans.Acoust.,Speech,Signal Process.,1986,34(3): 393-398.
[25] Berkun R, Cohen I, Benesty J. Combined beamformers for robust broadband regularized superdirective beamforming[J]. IEEE/ACM Trans. Audio, Speech, Lang. Process., 2015, 23(5): 877- 886.
[26] Li C, Benesty J, Huang G, et al. Subspace superdirective beamformers based on joint diagonalization[C]∥Proc. IEEE ICASSP, 2016: 400- 404.
[27] Huang G, Benesty J, Chen J. Subspace superdirective beamforming with uniform circular microphone arrays[C]∥Proc. IEEE IWAENC, 2016: 1-5.
[28] Huang G, Benesty J, Chen J. Superdirective beamforming based on the Krylov matrix[J]. IEEE/ACM Trans. Audio, Speech, Lang. Process., 2016, 24(12): 2531-2543.
[29] Crocco M, Trucco A. Design of robust superdirective arrays with a tunable tradeoff between directivity and frequency-invariance[J]. IEEE Trans. Signal Process., 2011, 59(5): 2169-2181.
[30] Pan C, Chen J, Benesty J. Reduced-order robust superdirective beamforming with uniform linear microphone arrays[J].IEEE/ACM Trans.Audio,Speech,Lang.Process., 2016, 24(9): 1548-1559.
[31] Pan C, Chen J, Benesty J. Theoretical analysis of differential microphone array beamforming and an improved solution[J].IEEE/ACM Trans.Audio,Speech,Lang. Process., 2015, 23(11): 2093-2105.
[32] Olson H F. Gradient microphones[J]. J. Acoust. Soc. Am., 1946, 17(3): 192-198.
[33] Elko G W. Differential microphone arrays[G]∥Audio Signal Processing for Next-Generation Multimedia Communication Systems. Springer, 2004: 11- 65.
[34] Chen J, Benesty J, Pan C. On the design and implementation of linear differential microphone arrays[J].J.Acoust.Soc.Am., 2014, 136: 3097-3113.
[35] Pan C, Chen J, Benesty J, et al. On the design of target beampatterns for differential microphone arrays[J]. IEEE/ACM Trans.Audio,Speech,Lang.Process., 2019, 27(8): 1295-1307.
[36] Benesty J, Chen J, Cohen I. Design of Circular Differential Microphone Arrays[M]. Berlin, Germany: Springer-Verlag, 2015.
[37] Huang G, Benesty J, Chen J. On the design of frequency-invariant beampatterns with uniform circular microphone arrays[J].IEEE/ACM Trans.Audio,Speech,Lang.Process., 2017, 25(5): 1140-1153.
[38] Huang G. Study of Microphone Array Speech Enahancement for Speech Communication and Human-machine Interface[D]. Xi’an, China: Northwestern Polytechnical University, 2018.
[39] Huang G, Benesty J, Chen J. Design of robust concentric circular differential microphone arrays[J].J.Acoust.Soc.Am., 2017, 141(5): 3236-3249.
[40] Huang G, Chen J, Benesty J. Insights into frequency-invariant beamforming with concentric circular microphone arrays[J].IEEE/ACM Trans.Audio,Speech,Lang.Process., 2018, 26(12): 2305-2318.
[41] Zhao X, Huang G, Chen J, et al. An improved solution to the frequency-invariant beamforming with concentric circular microphone arrays[C]∥Proc. IEEE ICASSP, 2020: 556-560.
[42] Huang G, Chen J, Benesty J. Design of planar differential microphone arrays with fractional orders[J]. IEEE/ACM Trans. Audio, Speech, Lang. Process., 2019, 28: 116-130.
[43] Huang G, Benesty J, Cohen I, et al. A simple theory and new method of differential beamforming with uniform linear microphone arrays[J]. IEEE/ACM Trans. Audio, Speech, Lang. Process., 2020, 28(1): 1079-1093.
[44] Huang G, Chen J, Benesty J. On the design of differential beamformers with arbitrary planar microphone array[J]. J.Acoust.Soc.Am.,2018, 144(1): EL66-EL70.
[45] Huang G, Benesty J, Cohen I, et al. Differential beamforming on graphs[J].IEEE/ACM Trans.Audio,Speech,Lang.Process., 2020, 28(1): 901-913.
[46] Borra F, Bernardini A, Antonacci F, et al. Efficient implementations of first-order steerable differential microphone arrays with arbitrary planar geometry[J]. IEEE/ACM Trans. Audio, Speech, Lang. Process., 2020.
[47] Buchris Y, Cohen I, Benesty J. On the design of time-domain differential microphone arrays[J]. Applied Acoustics, 2019, 148: 212-222.
[48] Borra F, Bernardini A, Antonacci F, et al. Uniform linear arrays of first-order steerable differential microphones[J].IEEE/ACM Trans.Audio,Speech,Lang.Process., 2019, 27(12): 1906-1918.
[49] Lovatello J, Alberto B, Augusto S. Steerable circular differential microphone arrays[C]∥Proc. EUSIPCO, 2018: 1245-1249.
[50] Bernardini A, D. Aria M, Sannino R, et al. Efficient continuous beam steering for planar arrays of differential microphones[J]. IEEE Signal Process. Lett., 2017, 24(6): 794-798.
[51] Bernardini A, Antonacci F, Sarti A. Wave digital implementation of robust first-order differential microphone arrays[J]. IEEE Signal Process. Lett., 2018, 25(2): 253-257.
[52] Byun J, Park Y C, Park S W. Continuously steerable second-order differential microphone arrays[J].J.Acoust.Soc.Am., 2018, 143(3): EL225-EL230.
[53] Wu X, Chen H, Zhou J, et al. Study of the mainlobe misorientation of the first-order steerable differential array in the presence of microphone gain and phase errors[J]. IEEE Signal Process. Lett., 2014, 21(6): 667- 671.
[54] Pan C, Benesty J, Chen J. Design of robust differential microphone arrays with orthogonal polynomials[J]. J. Acoust. Soc. Am., 2015, 138(2): 1079-1089.
[55] Huang G, Zhao X, Chen J, et al. Properties and limits of the minimum-norm differential beamformers with circular microphone arrays[C]∥Proc. IEEE ICASSP, 2019: 426- 430.
[56] Meyer J. Beamforming for a circular microphone array mounted on spherically shaped objects[J]. J. Acoust. Soc. Am., 2001, 109: 185-193.
[57] Tiana-Roig E, Jacobsen F, Grande E F. Beamforming with a circular microphone array for localization of environmental noise sources[J].J.Acoust.Soc.Am., 2010, 128(6): 3535-3542.
[58] Yan S, Ma Y, Hou C. Optimal array pattern synthesis for broadband arrays[J].J.Acoust.Soc.Am.,2007, 122(5): 2686-2696.
[59] Huang G, Chen J, Benesty J. On the design of robust steerable frequency-invariant beampatterns with concentric circular microphone arrays[C]∥Proc.IEEE ICASSP, 2018: 506-510.
[60] Yan S, Sun H, Ma X, et al. Time-Domain implementation of broadband beamformer in spherical harmonics domain[J].IEEE Trans.Acoust.,Speech,Signal Process.,2011, 19: 1221-1230.
[61] Yan S, Sun H, Svensson U P, et al. Optimal modal beamforming for spherical microphone arrays[J]. IEEE Trans. Acoust., Speech, Signal Process., 2011, 19: 361-371.
[62] Meyer J, Elko G. Spherical harmonic modal beamforming for an augmented circular microphone array[C]∥Proc. IEEE ICASSP, 2008: 5280-5283.
[63] Meyer J, Elko G. A highly scalable spherical microphone array based on a orthonormal decomposition of the soundfield[C]∥Proc. IEEE ICASSP, 2002: II178-II1784.
[64] Rafaely B. Fundamentals of Spherical Array Processing[M]. Berlin, Germany: Springer-Verlag, 2015.
[65] Huang G, Chen J, Benesty J. A flexible high directivity beamformer with spherical microphone arrays[J]. J. Acoust.Soc.Am., 2018, 143(5): 3024-3035.
[66] Benesty J, Cohen I, Chen J. Array Processing: Kronecker Product Beamforming[M]. Berlin, Germany: Springer-Verlag, 2019.
[67] Cohen I, Benesty J, Chen J. Differential Kronecker product beamforming[J]. IEEE/ACM Trans. Audio, Speech, Lang. Process., 2019, 27(5): 892-902.
[68] Yang W, Huang G, Benesty J, et al. On the design of flexible Kronecker product beamformers with linear microphone arrays[C]∥Proc. IEEE ICASSP, 2019: 441- 445.
[69] Huang G, Chen J, Benesty J, et al. Robust and steerable Kronecker product differential beamforming with rectangular microphone arrays[C]∥Proc. IEEE ICASSP, 2020.
[70] Huang G, Cohen I, Benesty J, et al. Kronecker product beamforming with multiple differential microphone arrays[C]∥Proc. IEEE SAM, 2020.
[71] Pan C, Chen J, Benesty J. Performance study of the MVDR beamformer as a function of the source incidence angle[J].IEEE/ACM Trans.Audio,Speech,Lang. Process., 2013, 22(1): 67-79.
[72] Higuchi T, Ito N, Araki S, et al. Online MVDR beamformer based on complex Gaussian mixture model with spatial prior for noise robust ASR[J].IEEE/ACM Trans.Audio,Speech,Lang.Process.,2017,25(4): 780-793.
[73] Li J, Stoica P. Robust adaptive beamforming[M]. Wiley Online Library, 2006.
[74] Gannot S, Burshtein D, Weinstein E. Signal enhancement using beamforming and nonstationarity with applications to speech[J]. IEEE Trans. Signal Process., 2001, 49(8): 1614-1626.
[75] Talmon R, Cohen I, Gannot S. Relative transfer function identification using convolutive transfer function approximation[J].IEEE Trans.Audio,Speech,Lang.Process., 2009, 17(4): 546-555.
[76] Chen J, Benesty J, Huang Y. A minimum distortion noise reduction algorithm with multiple microphones[J]. IEEE Trans.Audio,Speech,Lang.Process.,2008,16(3): 481- 493.
[77] Frost III O L. An algorithm for linearly constrained adaptive array processing[J]. Proc. IEEE, 1972, 60: 926-935.
[78] Gannot S, Burshtein D, Weinstein E. Beamforming methods for multi-channel speech enhancement[C]∥Proc. IEEE IWAENC, 1999: 96-99.
[79] Gannot S, Burshtein D, Weinstein E. Analysis of the power spectral deviation of the general transfer function GSC[J]. IEEE Trans. Signal Process., 2004, 52: 1115-1120.
[80] Werner S, Apolin rio Jr J A, de Campos M L. On the equivalence of RLS implementations of LCMV and GSC processors[J].IEEE Signal Process.Lett.,2003,10: 356-359.
rio Jr J A, de Campos M L. On the equivalence of RLS implementations of LCMV and GSC processors[J].IEEE Signal Process.Lett.,2003,10: 356-359.


