1 引言
语音增强作为语音信号处理的重要组成部分,旨在抑制噪声污染,提升各种以语音为媒介的应用在噪声环境下的性能,比如移动电话,智能家电,视频会议,助听器,语音识别,语音编码等。语音增强的目标是通过信号处理和数学的方法,从被噪声污染的语音信号中尽可能恢复出原始的纯净语音信号,从而提升人们的主观听觉质量(Speech quality)和语音的可懂度(Intelligibility)[1]。
在最近的几十年里,人们对单通道语音增强方法进行了广泛的研究,迄今为止已经开发出了众多的语音增强方法[1],这些语音增强方法大体上可以分为基于语音和噪声先验知识的语音增强方法和无先验知识的语音增强方法两大类。无先验知识的方法主要包括谱减法[2-3],维纳滤波法[4],基于统计模型的方法[5- 6]和基于子空间的方法[7]等等几类经典的方法。这些经典的语音增强方法对平稳噪声的去除能力还可以接受,而对非平稳噪声却有不足。利用语音和噪声先验知识的语音增强方法包括基于隐马尔科夫模型(Hidden Markov model, HMM)的方法[8-9],码本驱动(Codebook driven)的方法[10-11],基于深度神经网络(Deep neural networks, DNN)的方法[12-13]以及基于非负矩阵分解(Nonnegative matrix factorization, NMF)的方法[25- 44]等等。这些方法利用语音和噪声的先验信息,在线从带噪语音信号中提取相应的语音和噪声模型参数,然后用得到的语音和噪声参数进行语音增强。由于用到了先验信息,这些方法对非平稳噪声的处理效果明显比经典的无先验知识的方法要好。
基于非负矩阵分解的语音增强方法[25- 44]是目前一种具有代表性的数据驱动的有先验知识的语音增强技术,其通过训练语音和噪声的基矩阵来存储语音和噪声的先验信息,在非平稳噪声环境下取得了令人满意的增强效果。通常,该类方法首先离线训练语音和噪声的基矩阵,然后把带噪语音的频谱矢量投影到语音和噪声联合的基矩阵中进而获得相应的语音和噪声编码矢量,最后用语音和噪声的基矩阵和估计的编码矢量构建维纳滤波器来实现语音增强。
本文第2部分对非负矩阵分解理论做了一个深入的概述。随后,本文在第3部分详细描述了基于非负矩阵分解的语音增强方法的基本原理,并进行了一些实验。最后在第4部分,本文对现有的一些基于非负矩阵分解的语音增强算法做了一个总结,并分别对其进行了简单的介绍。
2 非负矩阵分解理论概述
非负矩阵分解思想自从由Lee和Seung在1999年提出以来[14],便即得到快速的发展。非负矩阵分解对数据矩阵施加非负性约束,该约束在合成矩阵时只允许加法组合,而不允许减法组合,从而导致基于“部分(Parts)”的(而非“整体”的)表示。非负矩阵分解学习基于部分的表示和人的大脑对事物的感知是基于部分的生理学和心理学依据相契合,展现了数学原理和人脑感知的内在联系。对数据施加非负性约束是存在一定的道理的,比如语音的幅度频谱,图像的像素值都不可能是负数。目前为止,非负矩阵分解已被成功应用到各个领域,包括图像识别[15],文本语义分析[14],音乐信号处理[16-17]以及本文的核心语音增强[25- 44]等等。
非负矩阵分解可以学习对象的部分。文献[14]中,作者通过NMF对人脸图像的数据集进行分解,结果证明每张人脸图像都可以表示为一些基础图像的线性叠加组合,而这些基础图像正好对应于人脸的局部特征,诸如鼻子、眼睛、嘴巴等。可以知道这些基础图像就是学习到的人脸图像的部分。非负矩阵分解由于施加了非负性约束,因此和由部分构成整体的概念相契合。
2.1 非负矩阵分解模型
定义一个非负矩阵为V∈Re×m,非负矩阵分解旨在找到一个非负矩阵T∈Re×r和一个非负矩阵C∈Rr×m,使其满足下面的矩阵方程[18]:
(1)
vμ≈Tcμ
(2)
式中,V是待分解的矩阵, Ai,j代表矩阵A的第i行第j列的元素,vμ为矩阵V的第μ列,T称为基矩阵,又叫字典,它的每一列叫做基矢量,C称为编码矩阵,又叫系数矩阵或激活矩阵,cμ为矩阵C的第μ列,又叫编码矢量,e,m,r代表矩阵的维数,R代表实数域空间。
非负矩阵分解常用于多变量数据的统计分析,即在式(1)中,矩阵V∈Re×m的每一列都是一个e维的数据矢量,m则为数据矢量的个数。把式(1)写成一列列的形式就成了式(2),由此可见,矩阵V的每一列都可建模为矩阵T中所有列矢量的加性组合,其中编码矢量cμ为加权系数。因此,矩阵T的每一列都可以看成构成矩阵V中列矢量的部分,称之为基矢量。由于这些基矢量的线性组合也能表示其他的数据矢量,因此分解得到的基矩阵可用于数据的重构。通常r选取的比e和m要小,以得到低秩的表达,但若r过小,则得到的基矩阵将失去对原始数据的建模能力。
2.2 代价函数的定义
非负矩阵分解常用迭代梯度下降(Iterative gradient descent)法和期望最大(Expectation-maximization, EM)算法进行求解[18]。随后,Lee和Seung提出了一种乘法迭代公式进行非负矩阵分解[18],这是目前最简单和最常用的非负矩阵分解方法,下面对其进行详细介绍。
首先定义代价函数(Cost function)来度量矩阵分解的近似程度,直观上,直接用两个非负矩阵之间某些距离就可以。文献[18]中给出了两种简单且有用的代价函数,其一是用V和TC之间的欧几里德距离(Euclidean distance)的平方:
(3)
另外一种代价函数就是V和TC之间的广义KL散度(Generalized Kullback-Leibler divergence),可以写为:
(4)
这两种代价函数![]() V-TC
V-TC![]() 2和D(V
2和D(V![]() TC)都以零为下限,并且当且仅当V=TC时等于零。
TC)都以零为下限,并且当且仅当V=TC时等于零。
2.3 乘法更新准则
针对不同的代价函数,文献[18]给出了解决非负矩阵分解的对应的乘法更新准则。在下面的更新准则下,随着不断的迭代,欧几里德距离![]() V-TC
V-TC![]() 2的值将会不断减小,直到收敛得到局部最优解:
2的值将会不断减小,直到收敛得到局部最优解:
式中,符号AT代表矩阵A的转置矩阵。
而D(V![]() TC)的局部最小则是通过下面更新准则不断迭代直到收敛得到:
TC)的局部最小则是通过下面更新准则不断迭代直到收敛得到:
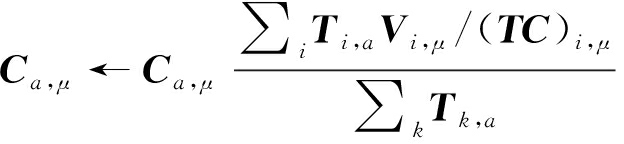
(6)
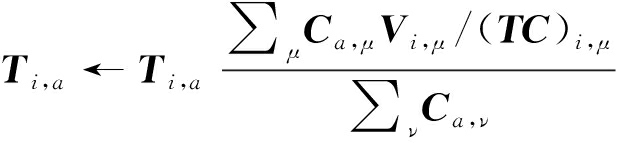
(7)
这两种乘法更新准则单调收敛的性质在文献[18]中给出了严格的证明,本文在此不做过多叙述。值得注意的是,文献[19]给出了另一种形式的乘法迭代公式,其作用和式(5)~式(7)一致,其中对应于广义KL散度的迭代公式为:
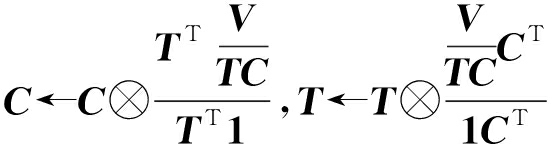
(8)
式中,⊗和![]() 分别代表基于元素的乘法和除法,1代表一个和V同维度的元素全是1的矩阵。
分别代表基于元素的乘法和除法,1代表一个和V同维度的元素全是1的矩阵。
对于某些数据集,有学者发现上面提到的NMF方法并不能得到基于部分的表示,因此改进的NMF方法也层出不穷。比如,Hoyer提出了一种稀疏性约束的非负矩阵分解算法[20],该算法可以人为地控制基矩阵的稀疏度,进而得到基于部分的表示。
3 基于NMF的语音增强方法的基本原理
在基于NMF的语音增强中,待分解矩阵V一般为语音信号或噪声信号的幅度频谱(或功率频谱),V的每一列都为一帧的频谱。通过分解语音和噪声的频谱矩阵,可得到语音源和噪声源的基矩阵,然后才能进一步实现语音增强。其实语音基矩阵就是非负矩阵分解学习到的语音频谱的部分,语音基矩阵中所有基矢量的线性组合可以近似任意一帧的语音频谱,噪声基矩阵亦然。本文一律使用幅度谱。
3.1 语音和噪声基矩阵的训练
干净语音信号常被加性噪声源污染,假设语音和噪声信号相互独立,则有
y(n)=x(n)+w(n)
Y(k,τ)=X(k,τ)+W(k,τ)
(9)
式中,y(n),x(n)和w(n)分别为带噪语音信号,纯净语音信号和噪声信号,n为时域采样点索引。Y(k,τ),X(k,τ),W(k,τ)为对应的短时傅里叶变换系数,k和τ分别为频点索引和帧索引。
在训练阶段,需要通过非负矩阵分解分别训练语音源和各种类型的噪声源的基矩阵。以语音基矩阵的训练为例,图1是训练语音基矩阵的原理框图。
图1 语音基矩阵的训练原理框图
Fig.1 Training diagram of the basis matrix of speech
首先,把训练用的纯净语音通过短时傅里叶变换(Short-time Fourier transform, STFT)从时域转换到频域,获得每帧语音的频谱进而得到语音的幅度频谱矩阵Xtrain∈RE×M(E和M分别代表每帧的频点数和语音帧的数量)。矩阵Xtrain的每一列都为一帧语音的幅度谱,也就是说元素(Xtrain)k,τ代表训练语音的第τ帧的第k个频点的幅度谱。然后,通过式(6)和式(7)分解Xtrain为:
(10)
式中,TX为分解得到的语音基矩阵,CX为相应的编码矩阵。语音基矩阵和编码矩阵的每个元素在迭代前都随机初始化为0到1之间的随机数,而选取D(Xtrain![]() TC)作为NMF的代价函数是因为其在先前研究中被证明对语音分离很有效[27]。把训练阶段的编码矩阵CX舍弃,而保留得到的语音基矩阵TX。在基于NMF的语音增强中,基矩阵的每一列在每次迭代后都会被归一化,保证每一列的和都为1。对于各种噪声源的基矩阵,采取相似的方法,得到噪声基矩阵TW。
TC)作为NMF的代价函数是因为其在先前研究中被证明对语音分离很有效[27]。把训练阶段的编码矩阵CX舍弃,而保留得到的语音基矩阵TX。在基于NMF的语音增强中,基矩阵的每一列在每次迭代后都会被归一化,保证每一列的和都为1。对于各种噪声源的基矩阵,采取相似的方法,得到噪声基矩阵TW。
3.2 线上语音增强
线上增强原理框图如图2所示。在增强阶段,首先水平组合语音基矩阵和噪声基矩阵来获得带噪语音的基矩阵,即:
(11)
式中,TY为增强阶段的基矩阵。
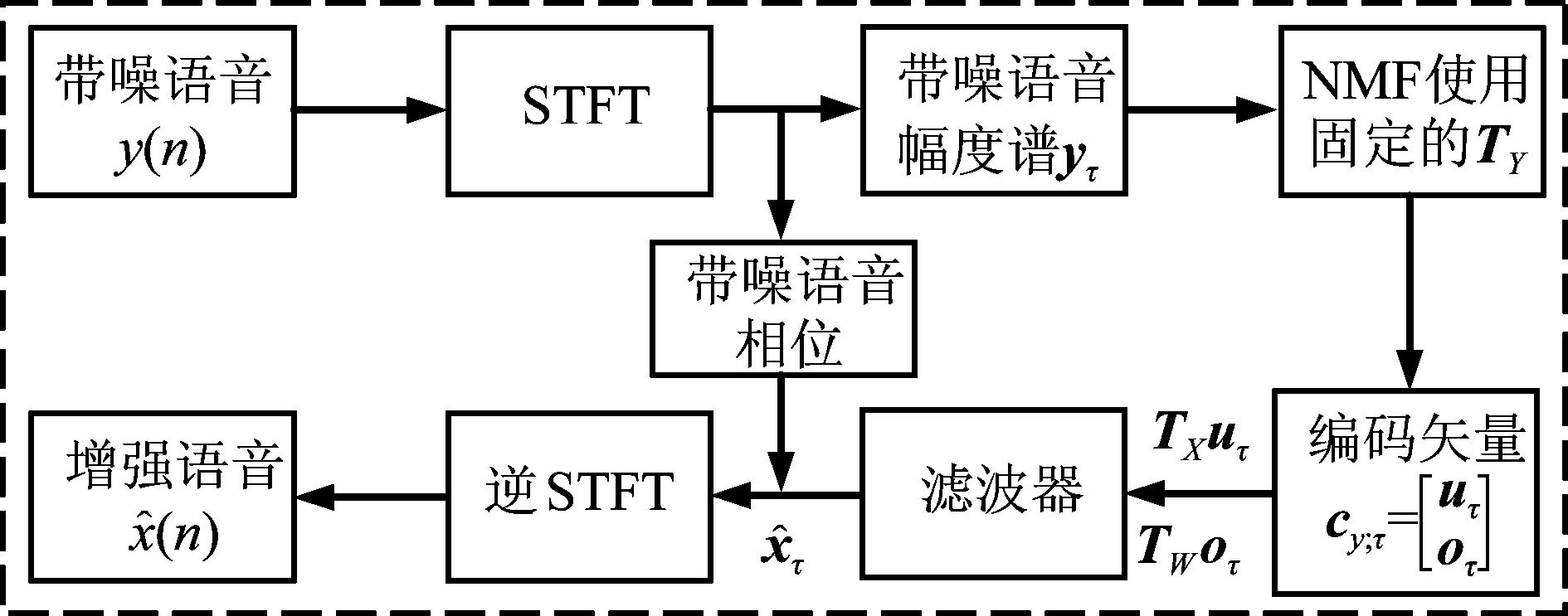
图2 基于NMF的线上语音增强原理框图
Fig.2 Block diagram of on-line speech enhancement based on NMF
由于带噪语音的幅度谱可近似等于语音幅度谱和噪声幅度谱的和,而连接的矩阵中既包含语音基矢量又包含噪声基矢量,所以矩阵TY的列矢量就可以看成构成带噪语音幅度谱的部分。
图2中, yτ为第τ帧的带噪语音幅度谱列矢量。cy;τ为yτ在固定的基矩阵TY中分解获得的编码矢量,uτ和oτ分别代表估计的语音编码矢量和噪声编码矢量。![]() 为增强的第τ帧的语音幅度谱矢量。
为增强的第τ帧的语音幅度谱矢量。
首先,通过短时傅里叶变换获得每一帧带噪语音的频谱,进而求取每一帧带噪语音的幅度谱和相位。然后把每一帧的带噪语音幅度谱在连接的基矩阵TY中进行分解,如第τ帧的带噪语音幅度谱矢量yτ可以分解如下:
(12)
式中,TY保持不变,而编码矢量cy;τ需不断根据式(6)迭代更新。
式(12)中待分解的是一个矢量,而非一个矩阵,不过迭代公式(6)同样适用,只是相应地变化了维度。编码矢量cy;τ被不断更新,最后得到最优的近似,其中uτ和oτ分别对应于语音基矩阵和噪声基矩阵。因此,第τ帧带噪语音中的语音和噪声分量可以分别表示为TXuτ和TWoτ。最后在得到估计的语音和噪声分量后,通常通过构建如下的维纳滤波形式来实现语音增强:
(13)
式中,(·)2代表基于元素的平方,![]() 是维纳滤波器估计的语音幅度谱矢量。除了构建上述维纳滤波器,语音增强还可通过其他途径实现,如文献[29]提出的线性最小均方误差滤波器(Linear Minimum mean-square error, LMMSE),该滤波器通过使用文献[5]中的判决-引导法求得,可以获得优越的性能。
是维纳滤波器估计的语音幅度谱矢量。除了构建上述维纳滤波器,语音增强还可通过其他途径实现,如文献[29]提出的线性最小均方误差滤波器(Linear Minimum mean-square error, LMMSE),该滤波器通过使用文献[5]中的判决-引导法求得,可以获得优越的性能。
3.3 线上语音重构
要实现基于非负矩阵分解的语音信号重构,只需在语音基矩阵中分解纯净语音的幅度谱即可。给定一段语音信号,先通过短时傅里叶变换获得每一帧语音的频谱,进而求取每一帧语音的幅度谱和相位。然后把每一帧语音的幅度谱在训练得到的语音基矩阵中进行分解,如第τ帧的语音幅度谱矢量xτ可以分解如下:
(14)
式中,TX保持不变,cx;τ为不断根据式(6)迭代更新获得的最优解,即xτ≈TXcx;τ,因此,第τ帧的语音幅度谱可以估计为![]()
3.4 实验设置和实验结果分析
本小节首先实现了基于非负矩阵分解的语音信号重构实验,测试了不同维度的语音基矩阵对语音幅度谱的建模能力。然后实现了基于维纳滤波器的非负矩阵分解语音增强算法,并和基于线性最小均方误差滤波器的方法[29]进行了对比。下面给出具体的实验设置和结果评估,本文用LMMSE-NMF代表基于最小均方误差滤波器的方法,而用WIENER-NMF代表使用维纳滤波器的方法。本文从TIMIT数据库选取语音信号,从Noisex-92数据库选取噪声信号,这些信号的采样率都调整为8 kHz。
TIMIT数据库中的6300段语音来自美国8个主要方言地区的630位男性和女性,其中,每个人讲10句话,这些讲话者包含了各个地区的不同发音。TIMIT数据库使用的文本材料包括方言类型的句子,说话紧凑的句子,发音多样的句子。在每个人所读的10句话中,2句话来自相同的方言文本材料,5句话来自说话紧凑型文本材料,其中每个人所读文本存在部分重叠,而3句话来自发音多样型文本材料,这3句话的文本每个人都完全不同。TIMIT数据库的训练集和测试集的说话者相互独立。TIMIT数据库包含所有的音素,即使在跨语言的情况下,由TIMIT数据库训练得到的语音基矩阵也能够建模其他数据库的语音信号。
在语音重构实验中,从TIMIT数据库的训练集中随机选取语音信号并组成大约持续一个小时的干净语音作为训练语音基矩阵的训练集。为了比较不同维度的语音基矩阵对语音信号的建模能力及计算负载,分别训练基矢量个数为20、40、60、80的不同维度的语音基矩阵。本实验从TIMIT数据库的测试集中随机选择200段来进行语音重构。
在语音增强实验中,选择四种噪声类型,即多人说话噪声(Babble)、工厂噪声(Factory)、歼击机噪声(F16)和白噪声(White),被污染的测试语音信号的信噪比分别为-5 dB,0 dB,5 dB和10 dB。本实验对选取的四种噪声类型分别训练噪声基矩阵,产生噪声基矩阵的训练噪声信号持续时间为半个小时。而语音基矩阵和语音信号重构实验中的保持一致。语音和噪声基矩阵的维数都选为20,因为实验证明20可以取得较好的增强效果。为什么基矩阵维数选为20比选为40时的效果好呢?那是因为随着基矩阵维数的增大,算法虽然有效地提高了重构的精度,但语音和噪声源之间的混淆问题也更加突出。本实验用语音信号重构实验中的200段测试语音来评估语音增强方法的性能。方法LMMSE-NMF的参数设置和文献[29]保持一致。
在短时傅里叶变换中,本文选择汉明窗(Hamming),窗长为32 ms,即256个采样点。相邻帧之间的重叠为50%。傅里叶变换的长度是每帧256个点,由于这256个频点的幅度是对称的,所以获得的幅度频谱矩阵Xtrain以及Wtrain的每一列有129维。语音和噪声基矩阵在训练时的迭代次数设置为1000次以保证收敛。通过实验验证,增强时迭代次数设置为20次可以取得不错的效果。
图3和图4给出了基矢量个数为20的语音基矩阵的各个基矢量的图解。
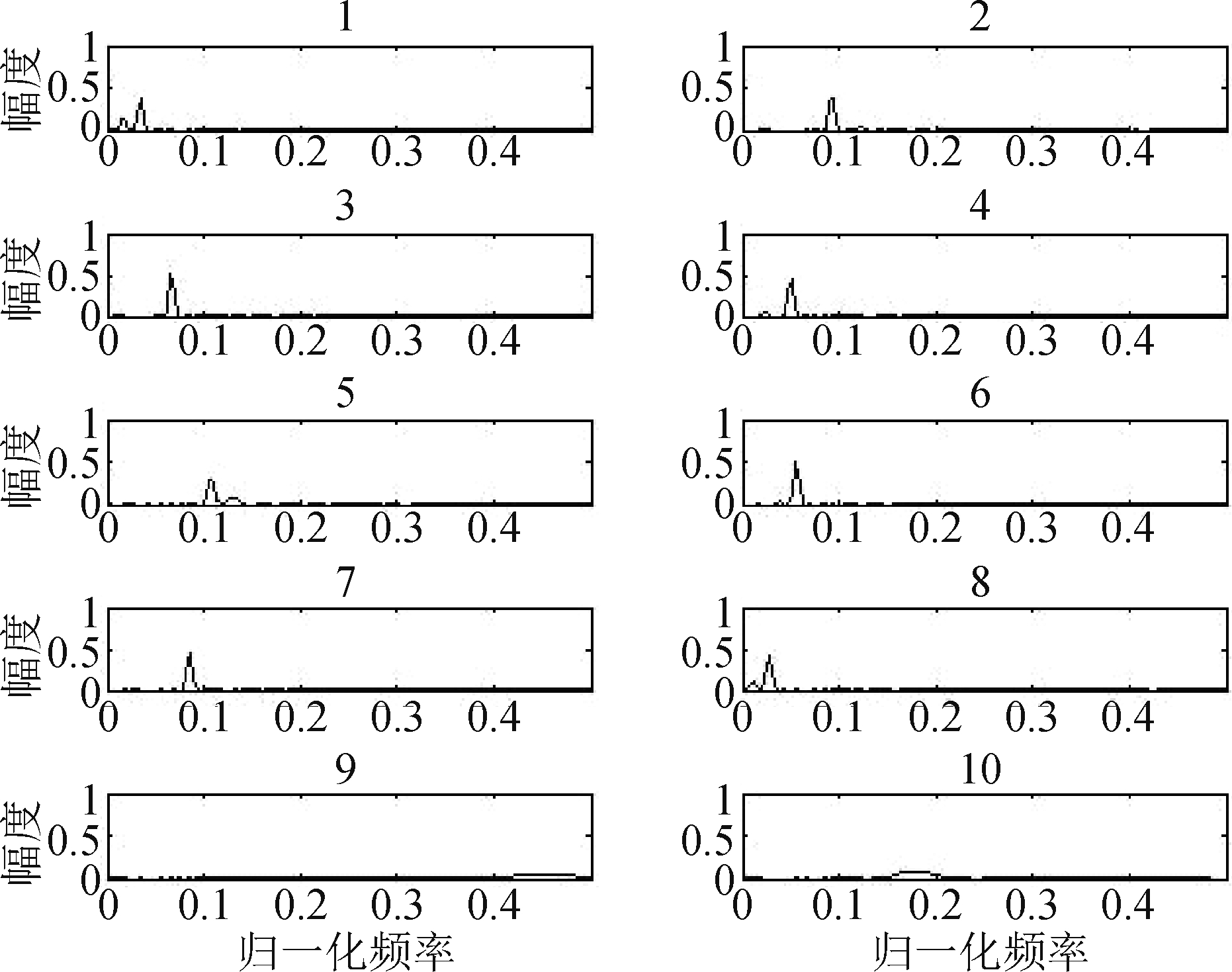
图3 维度为20的语音基矩阵的前10个基矢量
Fig.3 The first 10 basis vectors of the 20-dimensional speech basis matrix
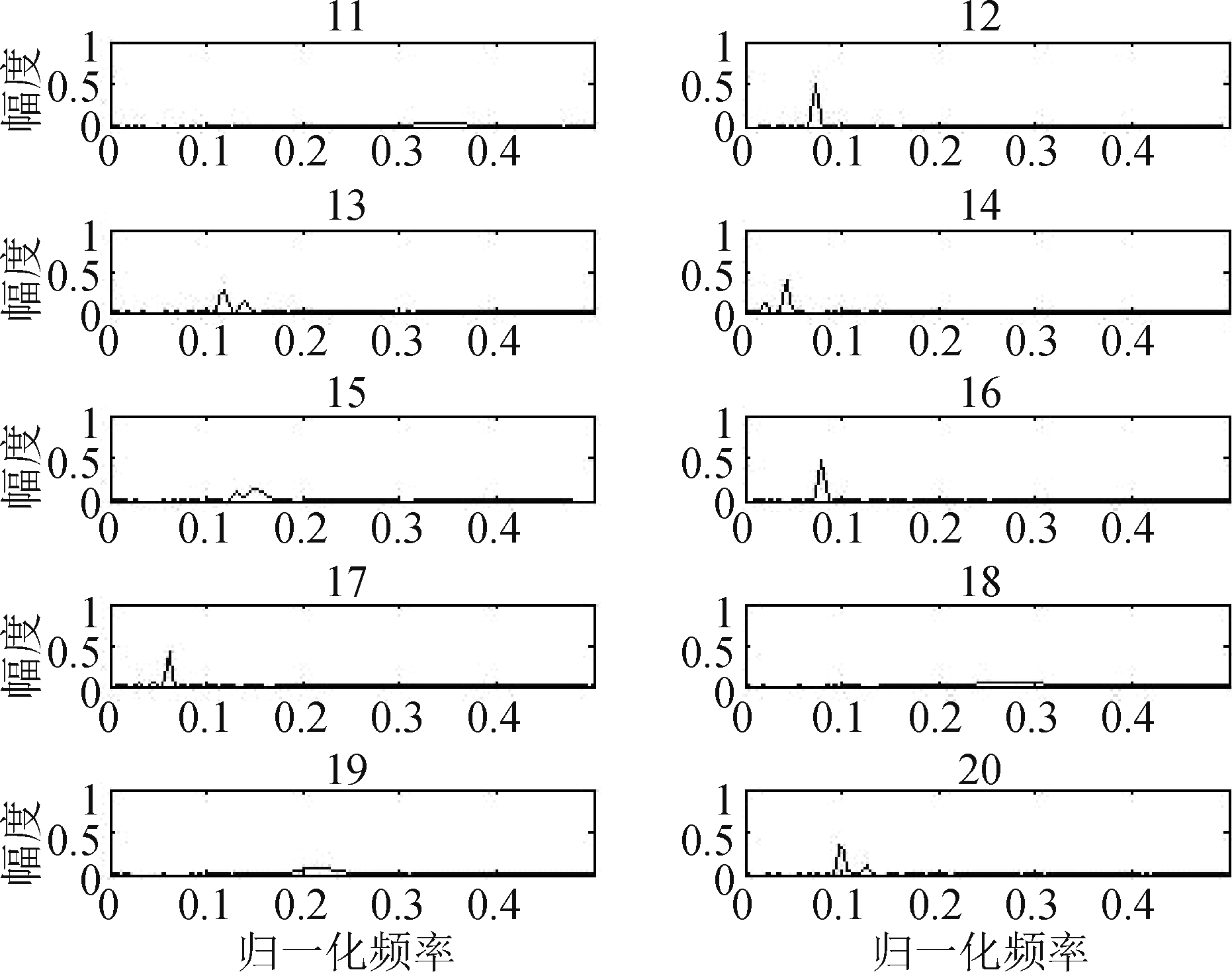
图4 维度为20的语音基矩阵的后10个基矢量
Fig.4 The last 10 basis vectors of the 20-dimensional speech basis matrix
从图3和图4中可以看到,每个基矢量都可以看成构成语音幅度谱的部分,它们展现出NMF的“部分”特征。由于在训练时,本文对基矩阵的列进行了归一化,所以图解的纵轴值在0到1之间。
在进行语音重构时,为了验证算法的收敛和迭代次数的关系,实验随机抽取了1000帧语音,并且记录了其在非负矩阵分解过程中达到收敛时的迭代次数。此外,本实验还随机抽取若干帧,记录了其重构语音幅度和实际语音幅度的广义KL散度D(xτ![]() TXcx;τ)随着迭代次数的变化。图5给出了具体的实验结果(此实验的基矩阵维数为60)。
TXcx;τ)随着迭代次数的变化。图5给出了具体的实验结果(此实验的基矩阵维数为60)。
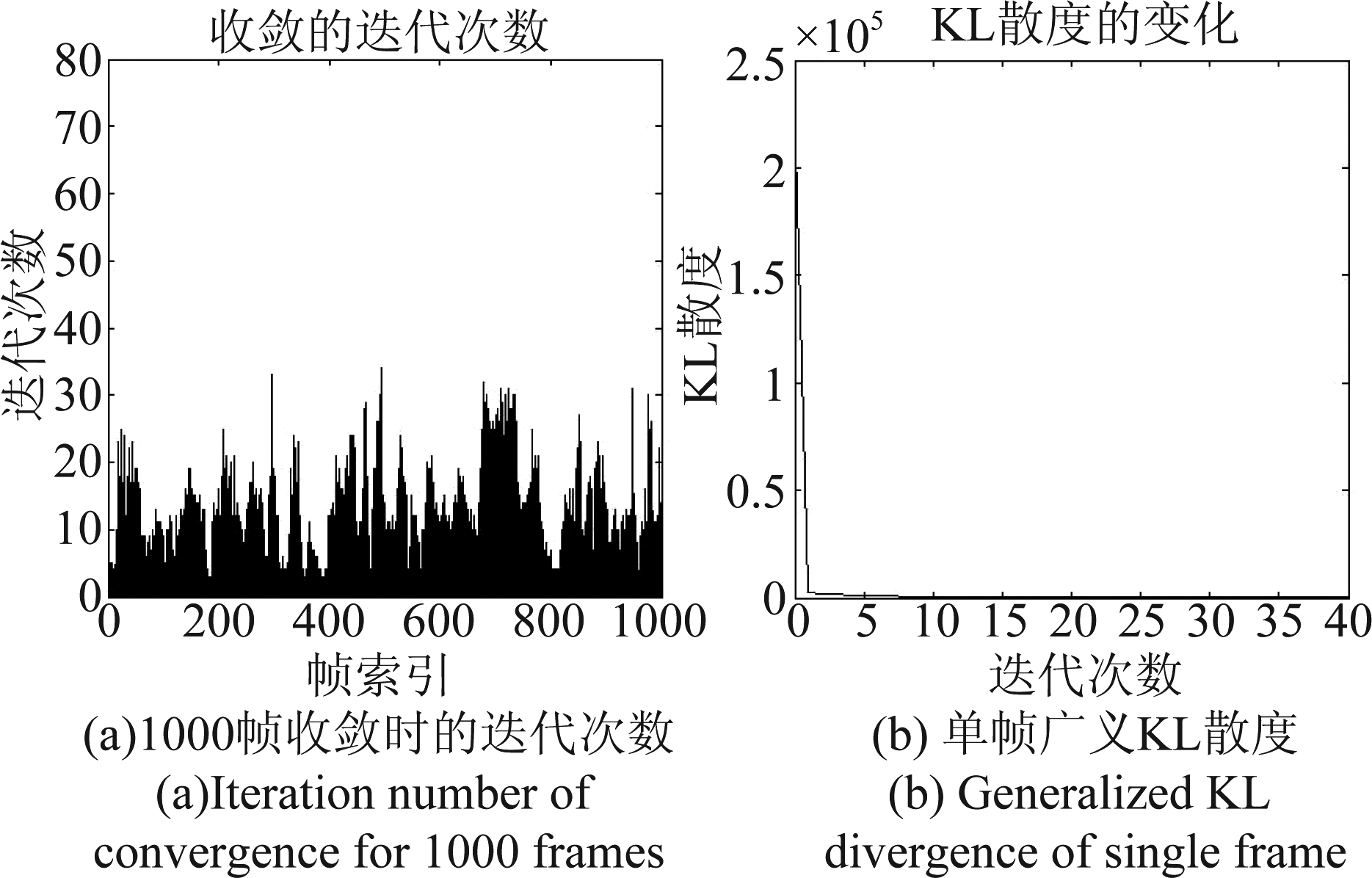
图5 多帧收敛迭代次数与单帧KL散度示例
Fig.5 Iteration number of convergence of multi-frames and the generalized KL divergence of single frame
从图5中可以看到,在进行语音重构时,迭代次数选为50已经足够保证收敛。而且随着迭代次数的增加,代价函数的值迅速减小,最后收敛到一个值。
语音重构实验使用语音感知质量(Perceptual evaluation of speech quality, PESQ)[22]和短时客观可懂度(Short-time objective intelligibility, STOI)[23]来评估算法的重构性能。表1给出了在不同维度的语音基矩阵下的测试结果,结果为200段语音的平均值。
表1 基于NMF的语音重构的测试结果
Tab.1 Test results of the NMF-based speech reconstruction

基矩阵维度20406080PESQ3.1343.8754.1664.255STOI0.91880.96790.99070.9944
从表1中可以看到,随着基矢量个数的增加,重构语音的质量以及可懂度不断提高,并且在基矩阵维度为80时,重构语音已经很接近真实的语音了。
在增强实验中,使用分段信噪比提升(Segment signal-to-noise ratio improvement, SSNRI)[21]、语音感知质量(PESQ)[22]以及扩展的短时客观可懂度(Extended short-time objective intelligibility, ESTOI)[24]对两种算法的性能进行评估,结果为200段语音的平均值。表2和表3给出了部分实验结果。
表2 在White噪声下的测试结果
Tab.2 Test results for White noise environment

信噪比评估度量5 dBSSNRIPESQESTOI10 dBSSNRIPESQESTOINoisy-1.6640.5263-2.0010.6900WIENER-NMF5.692.0830.50844.322.3940.6437LMMSE-NMF7.542.3360.58946.292.6210.7285
表3 在F16噪声下的测试结果
Tab.3 Test results for F16 noise environment

信噪比评估度量5 dBSSNRIPESQESTOI10 dBSSNRIPESQESTOINoisy-2.0010.5689-2.3250.7114WIENER-NMF5.742.3170.59253.882.6260.6957LMMSE-NMF8.082.5480.66906.792.8640.7759
由表2和表3可见,在两种噪声环境的两种信噪比下,LMMSE-NMF的性能在三种度量下都比WIENER-NMF要好。此外,WIENER-NMF虽然有效地提升了语音的质量以及信噪比,却降低了语音的可懂度,而LMMSE-NMF 可有效地提升可懂度。
此外,图6给出了使用两种方法的增强语音的语谱图比较。由图6可见,WIENER-NMF虽然在一定程度上抑制了背景噪声,但是残留噪声仍然较多,这就导致听觉体验不佳。相比之下,LMMSE-NMF方法在更大程度上抑制了背景噪声,且没有引入语音失真,大幅度地提升了语音的质量和可懂度。
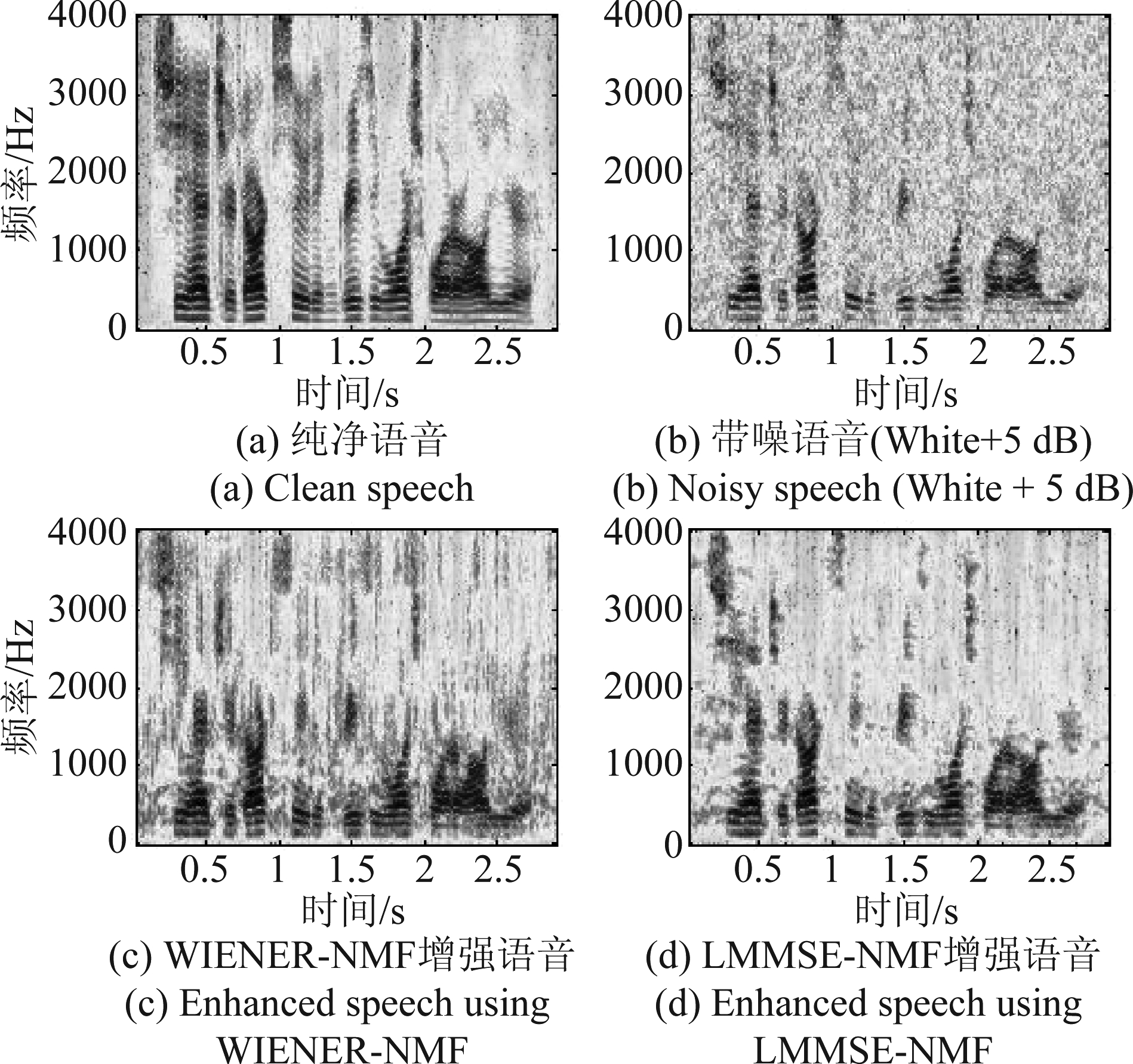
图6 语谱图对比
Fig.6 Spectrogram comparison
在另外两种噪声条件下以及-5 dB和0 dB低信噪比条件下,所得结论一致。这里只为说明基于非负矩阵分解的语音增强方法的有效性,LMMSE-NMF方法在其他条件下的实验结果详见第4部分。
4 基于非负矩阵分解的语音增强方法综述
4.1 传统方法的不足及改进方案
虽然上述描述的基于非负矩阵分解的语音增强方法在一定程度上抑制了背景噪声,提升了语音的质量和可懂度,但方法存在两个固有的不足。第一就是当语音和干扰噪声的频谱结构相似时,训练得到的语音基矩阵和噪声基矩阵也会相似,以至于产生重叠。在增强时,就可能出现语音分量被噪声基矢量表示;噪声分量被语音基矢量表示这样的源混淆问题。在实际中,语音和噪声的基矩阵几乎不可能正交,多多少少存在着重叠,这就严重影响了算法的性能。第二就是此类算法需要匹配的噪声基矩阵,需要尽可能多的不同种类的噪声来训练出一个通用的噪声基矩阵。当然为了提升算法的性能,通常需要对噪声进行分类,即分别对每种噪声类型训练对应的基矩阵,但是噪声的类型无穷无尽,就算同种类型的噪声也是不断变化的,而且背景噪声的类型和特性也不是总能提前预知,所以总会出现无训练噪声数据可用的情况。如果增强时的噪声基矩阵和背景噪声的类型不匹配,就会严重降低算法的性能。
为了解决上面的问题,研究者们提出了不少改进的算法[25-28,30-35,37- 45,47- 49,51]。为了减少语音和噪声的源混淆,一般会在代价函数上面加上正则项(Regularization term),其中建模输入数据的时间动力学特征和编码矩阵的稀疏性是设计约束项的两个常见的动机[25-28,30-32,38,41,45]。而为了解决噪声基矩阵不匹配的问题所提出的方法主要是如何在事先不知道噪声训练集的情况下,在线更新出需要的噪声基矩阵[26,33-35,39- 41,43- 44]。这种噪声训练集事先不可用的情况又称为半监督(Semi-supervised)的语音增强。从专业上来说,语音和噪声中一种训练集不可用的情况都可称为半监督的语音增强,语音和噪声训练集都不可用的情况被称为无监督(Unsupervised)的语音增强,而语音和噪声训练集都可用的情况被称为有监督(Supervised)的语音增强[41]。
2008年,Schmidt等提出了一种基于NMF的无监督语音增强算法[26],该算法假设带噪信号的全部信息可用,在语音暂停时学习噪声的基矩阵,在语音活动期间,保持噪声基矩阵不变,迭代更新语音基矩阵以及语音和噪声的系数矩阵,最后利用维纳型的滤波器得到增强语音,该算法还对系数矩阵施加了稀疏性约束。然而该算法对语音活动检测(Voice activity detector, VAD)模块的性能过于敏感。同年,Wilson等提出了一种基于NMF的去噪算法[27-28],该算法在训练阶段额外计算了语音和噪声编码矩阵的均值和方差,根据获得的编码矩阵的统计分布在增强阶段对代价函数施加约束,强制数据矩阵按照统计分布分解,使分解更加准确。2011年,Mohammadiha等针对基于NMF的语音增强提出了一种线性最小均方误差估计器[29],该算法针对语音和噪声的P次方频谱进行分解,并推导出了一种线性最优的估计器。在增强阶段,获得每帧估计的语音和噪声分量后,该算法给出了一种获得增强语音的有效途径。同年,Mohammadiha等又提出了一种基于约束非负矩阵分解的语音增强算法[30]来估计噪声的功率谱,该算法在代价函数上施加了一个L2范数惩罚项来利用观测信号的时间相关性,强制矩阵分解得到语音和噪声编码矢量的平滑估计。Raj等提出了一种音素依赖的(Phoneme-dependent)非负矩阵分解语音增强算法[31],该算法学习一系列的基矢量作为每个音素的先验信息,通过组合一个迭代的基于NMF的增强器和一个自动语音识别器来估计纯净语音。2012年,Mohammadiha等提出了一种基于贝叶斯非负矩阵分解(Bayesian NMF, BNMF)的语音增强算法[32],为了利用语音和噪声的时间连续性,该算法通过扩大前一时间帧的NMF系数矩阵的后验分布来引入适当的先验分布。2012年,Weninger等提出了一种基于NMF的半监督语音增强方法,并且和基于NMF的有监督的方法做了比较[33],该方法在线估计噪声的基矩阵,能够适应不匹配的噪声环境,有效地解决了噪声基矩阵不匹配的问题。2012年,Joder等开发了一套基于半监督非负矩阵分解的实时语音分离系统[34],该方法利用一个滑动窗口(Sliding window),能够逐帧更新噪声基矩阵,并实时实现语音增强。2013年,Mohammadiha等又完善了基于BNMF的方法[35],该方法在前面的方法的基础上又增加了一个基于HMM的噪声分类方案,而且还提出了一种在线学习噪声字典的方法。2014年,Fan等提出了一种基于分段非负矩阵分解的方法[36],该方法把频谱整个频带一分为二,分段进行训练增强,这样更加有利于精确捕获语音和噪声的局部谐波结构。而在时域,用一个时间窗包含相邻帧的频谱,更有利于捕获语音和噪声不变的结构。2014年,张立伟等提出了一种基于稀疏卷积非负矩阵分解(Sparse convolutive NMF, SCNMF)的语音增强算法[37],该算法应用卷积非负矩阵分解,并且进一步考虑到了语音信号频谱具有稀疏性的特点。2014年,Wang等提出了一种基于有判别学习的非负矩阵分解语音增强方法[38],该方法能够判别式地学习语音和噪声的编码矢量,有效缓解了语音和噪声基矩阵相混淆的问题。2015年,Kwon等结合了基于NMF的方法和基于统计模型的方法[39- 40],并且利用语音存在概率(Speech presence probability, SPP)在线更新语音和噪声基矩阵,该方法结合基于NMF和统计模型方法的优点,在性能上更好。同年,Kim等利用多个局部字典的混合(Mixture of Local Dictionaries, MLD)来进行语音增强[41],该混合字典的各个局部块能够代表声源的多样性,因此更具有判别力,此外,该算法利用块稀疏约束保证混合字典在给定时间只有一个或少量的块是活动的。2016年,Chung等在增强阶段使用额外的语音和噪声自由基矢量来捕获训练数据中没有的特征[42],该算法假设语音服从伽马分布来获得语音基矢量,用正则化的方法获得与训练得到的语音和噪声基矢量正交的噪声基矢量。2016年,Jeon等提出了一种基于局部稀疏度的在线字典学习的非负矩阵分解语音增强算法[43],该算法首先通过基于局部稀疏度的MMSE滤波器估计噪声频谱,然后通过一种判别式的NMF学习方案在线学习噪声字典,该方法不需要任何噪声先验知识且可以适应变化的噪声类型。2017年,Lee等把利用对数谱幅度估计器估计的语音存在概率结合到基于NMF的语音增强中[44],进一步消除了残余噪声,并且提出了一套无监督的噪声基矩阵学习方法,缓解了噪声基矩阵不匹配的问题。2018年,针对传统的基于NMF的信号分解完全依赖通过短时傅里叶变换得到的频谱矩阵,Fagot等提出了一种新颖的分解方法[45],该方法制定了一个类似于传统NMF的正则化优化问题,但将待分解频谱矩阵作为额外的未知参数。该方法不再依赖通过固定变换得到的频谱数据,而是在分解过程中学习短时正交变换(Short-time orthogonal transform)。将提出的分解方法用于语音增强实验,证明了该方法得到的语音和噪声基矩阵更具有正交性,可以获得更好的增强性能。2018年,Kavalekalam等提出了一种基于参数化NMF的语音增强方法[46],该方法用自回归(Auto-regressive, AR)系数来参数化语音和噪声基矢量,而频谱基矢量的参数化表示包含了语音生成模型的信号特征,该方法实验结果优于传统的基于非参数NMF的方法。2018年,Bai等提出了一种基于码本(Codebook)约束的非负矩阵分解语音增强方法[47],在训练阶段,该方法训练一个语音码本对语音的幅度谱进行建模。在增强阶段,该方法首先估计噪声的幅度谱,然后用其和码本中的语音码字构造增强阶段的基矩阵。该方法不用预先训练语音和噪声的基矩阵,因此不存在语音和噪声的源混淆问题和噪声基矩阵不匹配问题。
此外,结合DNN和NMF的语音增强方法也是近年来的一大研究热点。2014年,Kang等提出了一种结合DNN的基于NMF的语音增强方法[48- 49],该方法利用DNN来建模带噪语音频谱和相应编码矢量之间的映射关系,有效地提高了语音和噪声编码矢量估计的准确性。2015年,Tseng等提出了一种组合稀疏非负矩阵分解和DNN的基于分类的语音增强算法[50],该算法利用NMF对带噪语音进行特征提取,并利用DNN来估计理想二值掩膜(Ideal binary mask, IBM),进而实现语音增强。2016年,Vu等提出了一种新的结合稀疏非负矩阵分解和DNN的语音增强算法[51],该算法利用DNN来学习带噪语音编码矢量和语音编码矢量之间的非线性映射函数,获得了更好的性能。2016年,Nie等提出了一种利用频谱时间结构的基于DNN的语音增强算法[52],该算法使用NMF来利用幅度谱的频谱时间结构,并在DNN的输出层加了一个NMF层,提升了算法的性能。2018年,Bando等提出了一种基于变分自编码器(Variational autoencoder, VAE)和NMF的半监督语音增强方法[53],该方法制定了一个统一的带噪语音的概率生成模型,包括一个基于VAE的非线性语音概率生成模型和一个基于NMF的噪声概率生成模型,其中噪声模型自适应环境噪声,实验表明该方法优于有监督的基于DNN的方法。
4.2 实验设置和实验结果分析
本小节实现了4.1小节论述的两个具有代表性的方法,一是基于半监督非负矩阵分解的语音分离方法[34],二是有监督的基于LMMSE滤波器的方法[29]。文献[34]的方法表示为S-NMF,文献[29]的方法表示为L-NMF。此外,本小节还实现了一个很具代表性的基于DNN的语音增强方法,并和基于NMF的方法进行了对比分析。基于DNN的方法为基于回归的对数能量谱估计方法[54]。
对于S-NMF和L-NMF,实验设置和3.4小节保持一致,包括数据库、噪声类型、训练数据、语音和噪声基矩阵的维度、测试数据以及短时傅里叶变换的设置等,其中S-NMF不用提前训练噪声基矩阵。这两个方法中的参数都通过大量实验调整为最优。
对于基于DNN的方法,为了和基于NMF的方法公平的比较,本实验对每种噪声类型分别训练单独的DNN模型。连接TIMIT训练集中所有的4620句语音信号,组成训练的纯净语音。这段纯净语音时长大约为4个小时,其被四种噪声污染,信噪比为-5 dB,0 dB,5 dB和10 dB。对于每种噪声,连接具有不同信噪比的带噪语音,就可以产生大约16个小时的带噪语音,用其作为DNN的训练集。DNN训练50个周期,其中前十个周期的学习率为0.1,后面每过一个周期,学习率下降10%。每个批次的大小为128。丢包率(Dropout rate)为0.2。具体设置见文献[54]。
本小节仍然使用SSNRI[21]、PESQ[22]以及ESTOI[24]对算法的性能进行评估,结果为200段语音的平均值。
在四种噪声的各个信噪比条件下的SSNRI的测试结果如表4所示,SSNRI主要表征对背景噪声的抑制能力。和S-NMF相比,方法L-NMF的增强效果更好,虽然S-NMF实现了噪声的自适应,但增强效果却不如有监督的方法L-NMF。基于DNN的方法的性能在大多数条件下比L-NMF好,除了在10 dB的White,F16和Factory噪声条件下,这就说明基于DNN的方法在高信噪比下对噪声的抑制能力稍弱。同样是在10 dB条件下,基于DNN的方法对Babble噪声的抑制效果却比L-NMF好,这主要是因为Babble噪声的频谱结构很接近语音的频谱结构,会导致源混淆问题。
在四种噪声的各个信噪比条件下的PESQ的测试结果如表5所示,PESQ表征的是语音的感知质量。在大多数条件下,基于DNN的方法的性能比L-NMF好,除了F16噪声的-5 dB条件下,原因是F16噪声的谐波结构很有规律,容易被NMF所捕获,因此基于NMF的方法会实现较好的性能。方法L-NMF的性能在大多数条件下优于S-NMF,除了White和Babble噪声的低信噪比条件下,这主要是因为L-NMF在低信噪比条件下会产生更多的源混淆,而S-NMF在线更新噪声基矩阵虽然会产生源混淆,但信噪比对其影响不是很大。同样,虽然方法S-NMF实现了噪声自适应,但是性能却不如有监督的方法L-NMF。
表4 SSNRI的测试结果
Tab.4 Test results of SSNR improvement
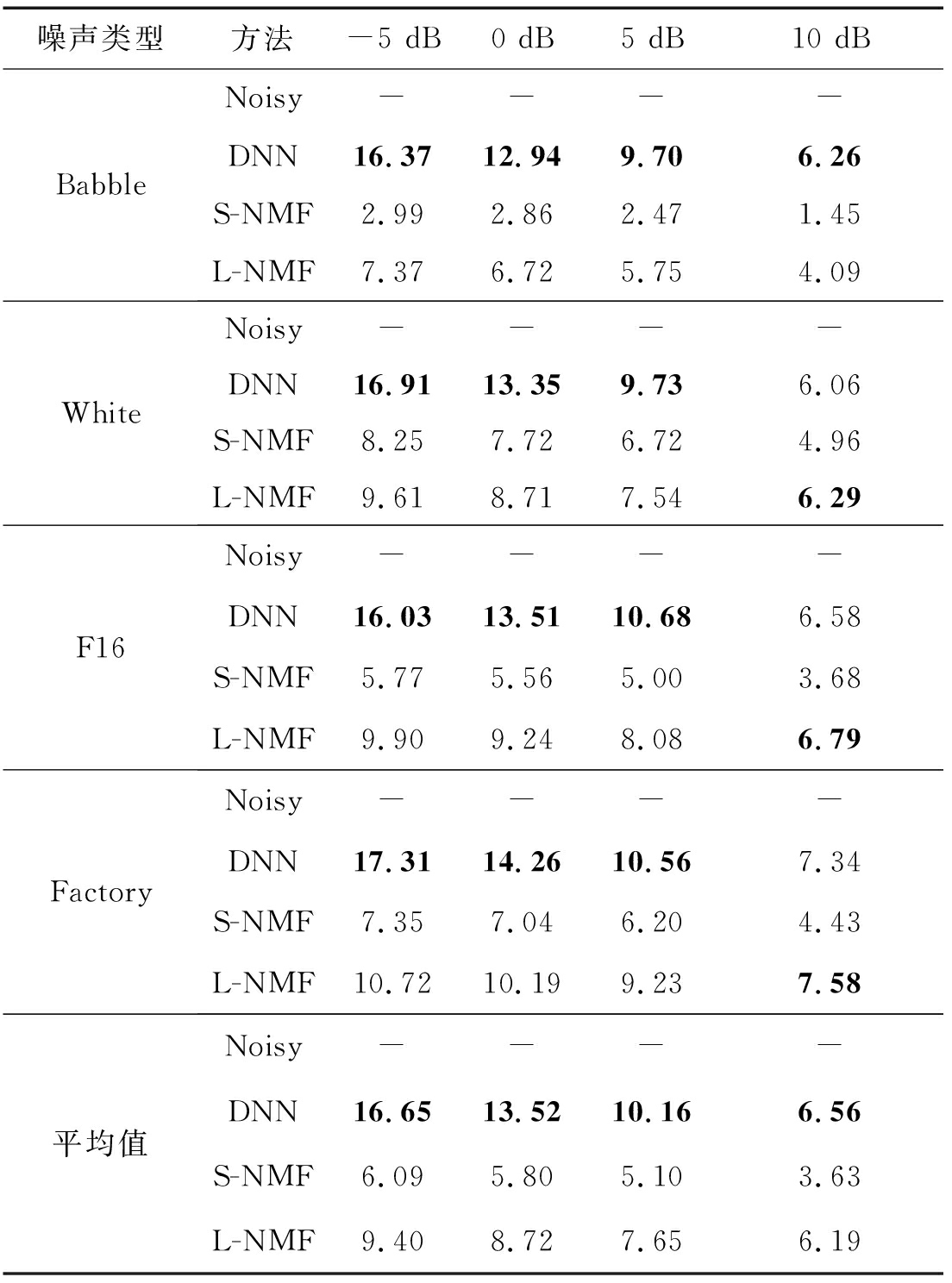
噪声类型方法-5 dB0 dB5 dB10 dBBabbleNoisy----DNN16.3712.949.706.26S-NMF2.992.862.471.45L-NMF7.376.725.754.09WhiteNoisy----DNN16.9113.359.736.06S-NMF8.257.726.724.96L-NMF9.618.717.546.29F16Noisy----DNN16.0313.5110.686.58S-NMF5.775.565.003.68L-NMF9.909.248.086.79FactoryNoisy----DNN17.3114.2610.567.34S-NMF7.357.046.204.43L-NMF10.7210.199.237.58平均值Noisy----DNN16.6513.5210.166.56S-NMF6.095.805.103.63L-NMF9.408.727.656.19
表5 PESQ的测试结果
Tab.5 Test results of PESQ
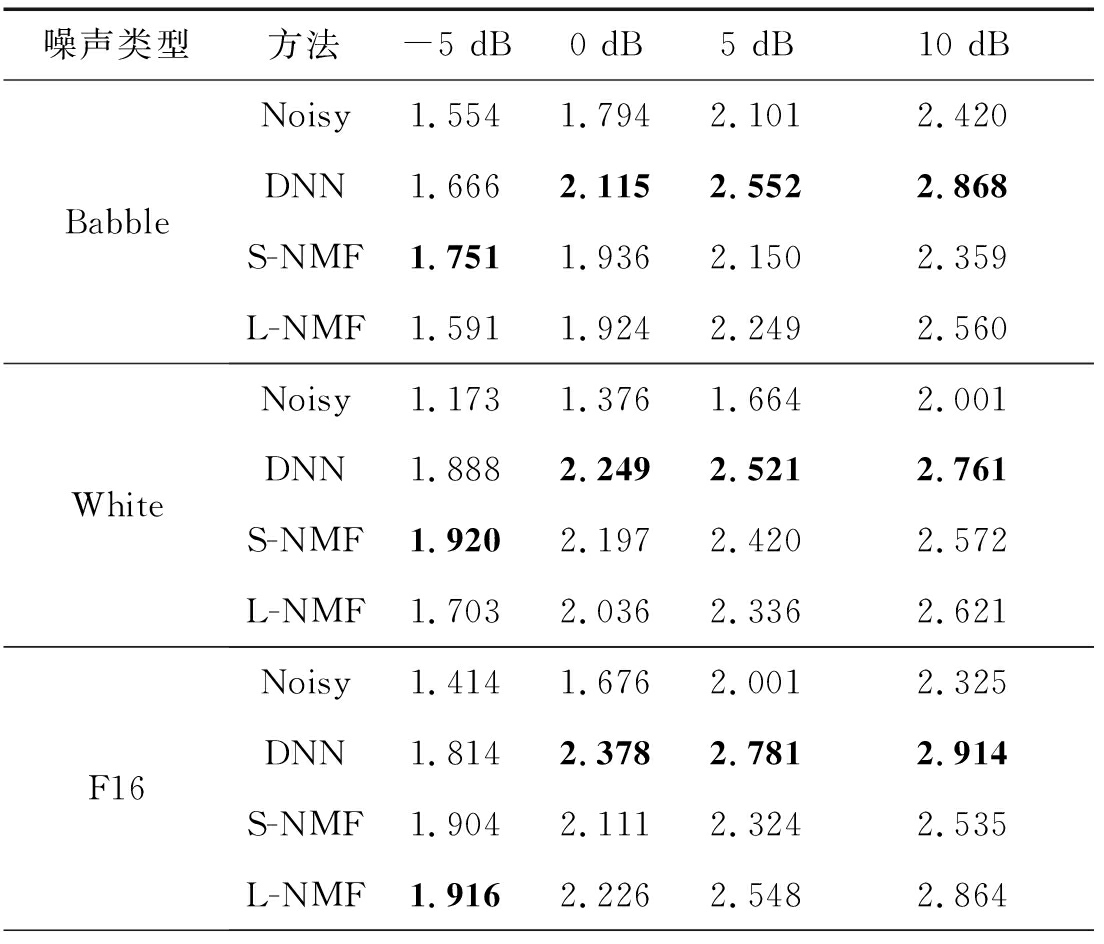
噪声类型方法-5 dB0 dB5 dB10 dBBabbleNoisy1.5541.7942.1012.420DNN1.6662.1152.5522.868S-NMF1.7511.9362.1502.359L-NMF1.5911.9242.2492.560WhiteNoisy1.1731.3761.6642.001DNN1.8882.2492.5212.761S-NMF1.9202.1972.4202.572L-NMF1.7032.0362.3362.621F16Noisy1.4141.6762.0012.325DNN1.8142.3782.7812.914S-NMF1.9042.1112.3242.535L-NMF1.9162.2262.5482.864
续表5
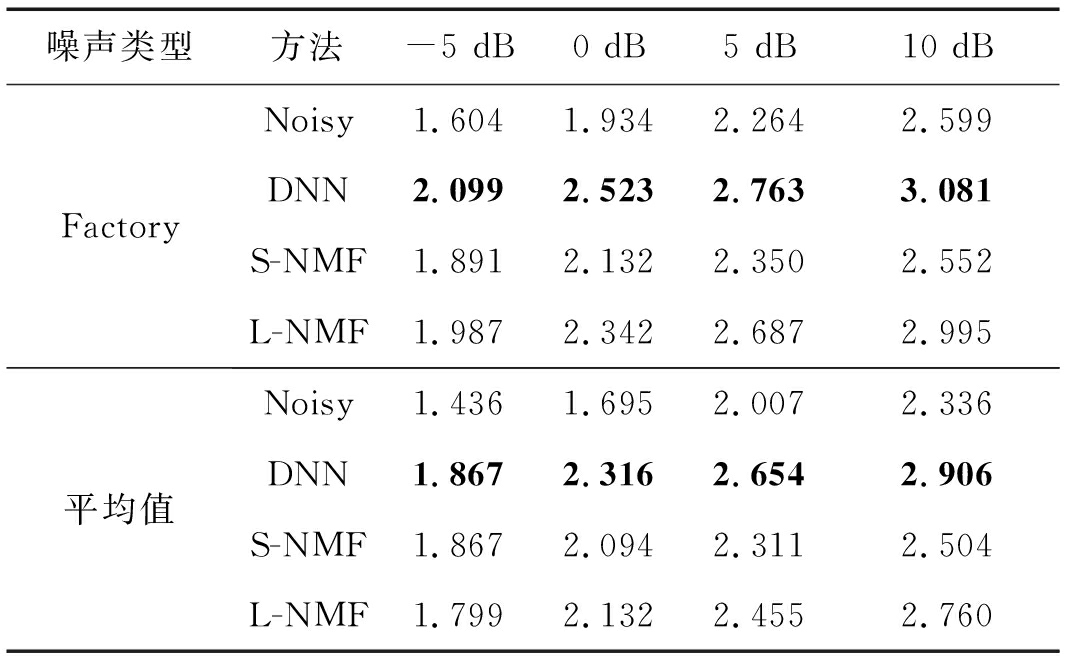
噪声类型方法-5 dB0 dB5 dB10 dBFactoryNoisy1.6041.9342.2642.599DNN2.0992.5232.7633.081S-NMF1.8912.1322.3502.552L-NMF1.9872.3422.6872.995平均值Noisy1.4361.6952.0072.336DNN1.8672.3162.6542.906S-NMF1.8672.0942.3112.504L-NMF1.7992.1322.4552.760
三种方法在四种噪声的各个信噪比条件下的ESTOI的测试结果如表6所示,ESTOI主要表征语音可懂度。在所有条件下,基于DNN的方法的性能比L-NMF好,而L-NMF优于S-NMF。实验结果的趋势和SSNRI以及PESQ一致。
表6 ESTOI的测试结果
Tab.6 Test results of ESTOI
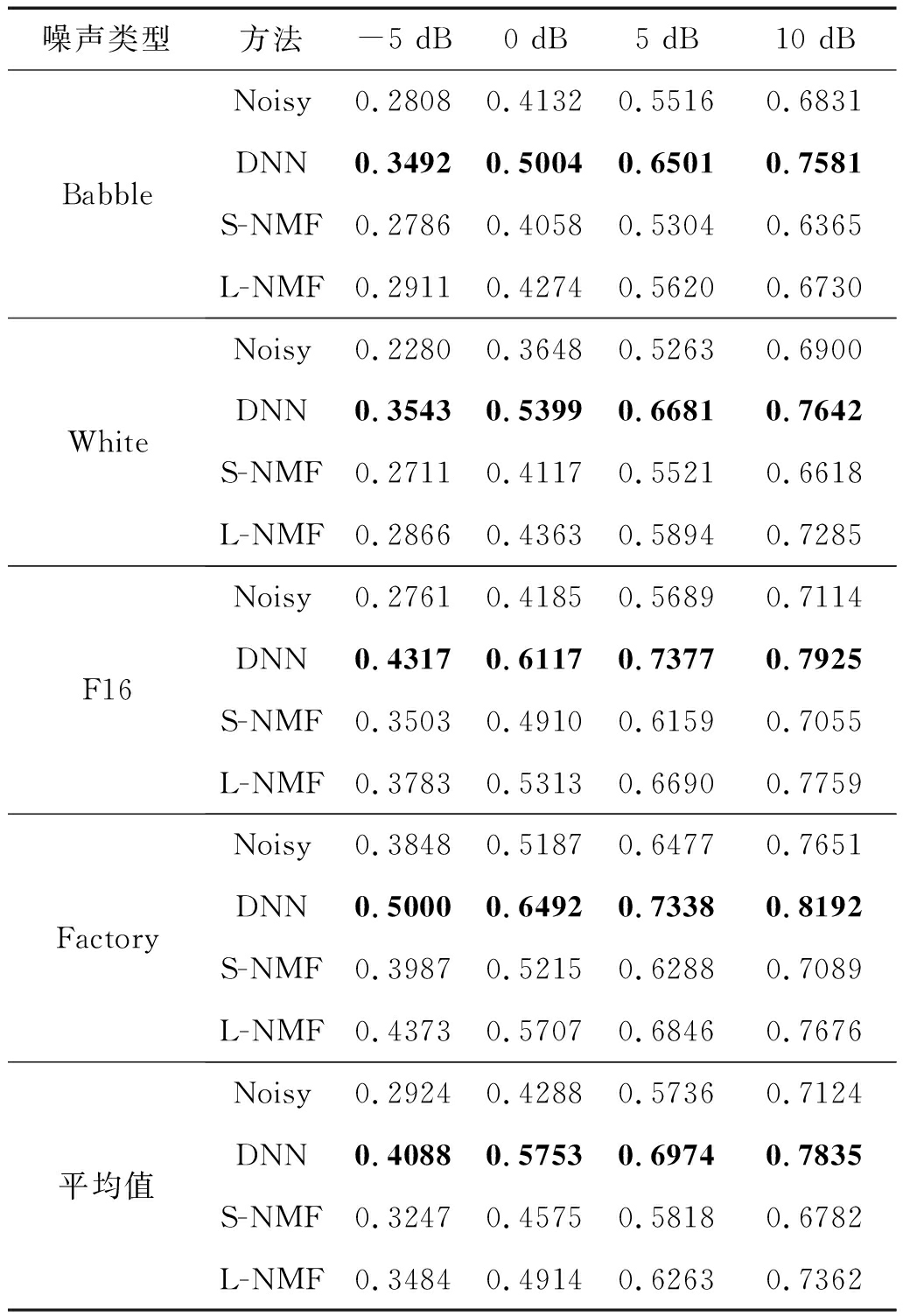
噪声类型方法-5 dB0 dB5 dB10 dBBabbleNoisy0.28080.41320.55160.6831DNN0.34920.50040.65010.7581S-NMF0.27860.40580.53040.6365L-NMF0.29110.42740.56200.6730WhiteNoisy0.22800.36480.52630.6900DNN0.35430.53990.66810.7642S-NMF0.27110.41170.55210.6618L-NMF0.28660.43630.58940.7285F16Noisy0.27610.41850.56890.7114DNN0.43170.61170.73770.7925S-NMF0.35030.49100.61590.7055L-NMF0.37830.53130.66900.7759FactoryNoisy0.38480.51870.64770.7651DNN0.50000.64920.73380.8192S-NMF0.39870.52150.62880.7089L-NMF0.43730.57070.68460.7676平均值Noisy0.29240.42880.57360.7124DNN0.40880.57530.69740.7835S-NMF0.32470.45750.58180.6782L-NMF0.34840.49140.62630.7362
5 结论
本文对基于非负矩阵分解的语音增强方法进行了介绍。首先,本文详细介绍了非负矩阵分解理论,给出了常用的实现非负矩阵分解的乘法更新准则。由于非负性约束的使用,非负矩阵分解可以导致基于部分的表示,其和由部分构成整体的概念相契合。然后,本文把非负矩阵分解引入到语音增强领域,对基于非负矩阵分解的语音增强方法的基本原理作了一个详细介绍,并实现了基于维纳滤波器的方法和基于线性最小均方误差滤波器的方法,给出了两种方法的增强结果和分析。此外,还实现了基于非负矩阵分解的语音信号重构,实验证明,语音基矩阵的每一列都可以看成构成语音幅度谱的部分,它们展现出了NMF的“部分”结构。随着基矩阵中基矢量的增多,语音基矩阵对语音幅度谱的建模能力不断增加。最后,本文总结了传统方法的不足之处,对现有的一些基于非负矩阵分解的算法做了一个整理,并对其分别进行了简单的概述,还给出了其中部分方法的实验结果,并和基于深度神经网络的方法进行了比较。
基于非负矩阵分解的语音增强方法在一定程度上有效地抑制了非平稳的背景噪声,而且很多改进的方法在一定程度上解决了传统方法存在的两点不足,然而这两个问题依然没有很好地得到解决。通过为代价函数添加正则化项来建模语音信号的时间依赖性或者为非负矩阵分解增加稀疏性约束都只是缓解了该类方法的不足。此外,利用非负矩阵分解在线更新噪声基矩阵也免不了更新过程中带来的源混淆,有些方法还利用噪声估计算法来解决噪声未知的情况,但是噪声估计算法的性能在低信噪比下却不尽人意。即使如此,基于非负矩阵分解的语音增强方法的研究前景依然很是乐观。未来,把非负矩阵分解模型和其他模型相结合为一个很好的方向,各个模型可以取长补短,比如DNN模型和隐马尔可夫模型(Hidden Markov model, HMM)等。从文献[48-53]来看,研究者已经开始尝试和DNN进行结合了。此外,对于噪声未知的情况,由于语音总是存在着自然地停顿,而停顿间隔的带噪语音信号就只包含背景噪声,所以充分利用带噪语音的说话间隙是一个很好的选择,只不过现存的端点检测算法还没有很好的性能,不过肯定是一个很好的研究方向。
[1] Loizou P. Speech enhancement: theory and practice[M]. CRC Press, 2007.
[2] Boll S. Suppression of acoustic noise in speech using spectral subtraction[J]. IEEE Transactions on Acoustic, Speech, and Signal Processing, Apr. 1979, ASSP-27(2): 113-120.
[3] Berouti M, Schwartz M, Makhoul J. Enhancement of speech corrupted by acoustic noise[C]∥IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Washington, DC, USA, 2- 4 April 1979: 208-211.
[4] Chen J, Benesty Huang J, et al. New insights into the noise reduction Wiener filter[J]. IEEE Transactions on Audio, Speech, and Language Processing, July 2006, 14(4): 1218-1233.
[5] Ephraim Y, Malah D. Speech enhancement using a minimum mean-square error short-time spectral amplitude estimator[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1984, ASSP-32(6): 1109-1121.
[6] 邹霞, 陈亮, 张雄伟. 基于Gamma语音模型的语音增强算法[J]. 通信学报, 2006, 27(10): 118-123.
Zou Xia,Chen Liang,Zhang Xiongwei. Speech enhancement with Gamma speech modeling[J]. Journal on Communications, 2006, 27(10): 118-123.(in Chinese)
[7] Ephraim Y, Trees H. A signal subspace approach for speech enhancement[J]. IEEE Transactions on Speech and Audio Processing, July 1995, 3(4): 251-266.
[8] 高珍珍, 鲍长春. 能量匹配的MFS-HMM语音增强方法[J]. 信号处理, 2016, 32(8): 937-944.
Gao Zhenzhen,Bao Changchun. MFS-HMM speech enhancement with the matched energy[J]. Journal of Signal Processing, 2016, 32(8): 937-944.(in Chinese)
[9] Deng F, Bao C, Kleijn W B. Sparse hidden markov models for speech enhancement in non-stationary noise environments[J]. IEEE/ACM Transactions on Audio, Speech, and Language Processing, November 2015, 23(11): 1973-1987.
[10] Srinivasan S, Samuelsson J, Kleijn W B. Codebook-based Bayesian speech enhancement for nonstationary environments[J]. IEEE Transactions on Audio, Speech, and Language Processing, Feb. 2007, 15(2): 441- 452.
[11] Huang Q, Bao C, Wang X. Improved codebook-based speech enhancement based on MBE model[C]∥2017 Annual Conference of the International Speech Communication Association (INTERSPEECH 2017), Stockholm, Sweden, 20-24 August 2017: 3627-3631.
[12] Wang D, Chen J. Supervised speech separation based on deep learning: an overview[J]. IEEE/ACM Transactions on Audio, Speech, and Language Processing, Oct. 2018, 26(10): 1702-1726.
[13] Yang Y, Bao C. DNN-based AR-Wiener filtering for speech enhancement[C]∥2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15-20 April 2018: 2901-2905.
[14] Lee D, Seung H. Learning the parts of objects by non-negative matrix factorization[J]. Nature, October 1999, 401(21): 788-791.
[15] Teoh A, Neo H, Ngo D. Sorted locally confined non-negative matrix factorization in face verification[C]∥2005 International Conference on Communications, Circuits and Systems, Hong Kong, China, 27-30 May 2005: 820- 824.
[16] Smaragdis Brown P. Non-negative matrix factorization for polyphonic music transcription[C]∥IEEE Workshop on Applications of Signal Processing to Audio and Acoustics, New Paltz, NY, USA, 19-22 Oct. 2003: 177-180.
[17] Smaragdis P. From learning music to learning to separate[C]∥Forum Acusticum, 2005.
[18] Lee D, Seung H. Algorithms for non-negative matrix factorization[J]. Advances in Neural Information Processing Systems, 2001, 13(6): 556-562.
[19] F′evotte C, Bertin N, Durrieu J. Nonnegative matrix factorization with the Itakura-Saito divergence: with application to music analysis[J]. Neural Computation, March 2009, 21(3): 793- 830.
[20] Hoyer P. Non-negative matrix factorization with sparseness constraints[J]. Journal of Machine Learning Research, April 2004, 5(1): 1457-1469.
[21] Quackenbush S, Barnwell T, Clements M. Objective measures of speech quality. Englewood Cliffs, NJ: Prentice Hall, 1988.
[22] Perceptual evaluation of speech quality (PESQ), an objective method for end-to-end speech quality assessment of narrow-band telephone networks and speech codecs. ITU-T Recommendation, P.862, February 2001.
[23] Taal C, Hendriks R, Heusdens R, et al. A short-time objective intelligibility measure for time-frequency weighted noisy speech[C]∥IEEE International Conference on Acoustics, Speech and Signal Processing, 2010: 4214- 4217.
[24] Jensen J, Taal C. An algorithm for predicting the intelligibility of speech masked by modulated noise maskers[J]. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2016, 24(11): 2009-2022.
[25] Virtanen T. Monaural sound source separation by nonnegative matrix factorization with temporal continuity and sparseness criteria[J]. IEEE Transactions on Audio, Speech, and Language Processing, March 2007, 15(3): 1066-1074.
[26] Schmidt M, Larsen J. Reduction of non-stationary noise using a non-negative latent variable decomposition[C]∥IEEE Workshop on Machine Learning for Signal Processing (MLSP), Cancun, Mexico, 16-19 Oct. 2008: 486- 491.
[27] Wilson K, Raj B, Smaragdis P, et al. Speech denoising using nonnegative matrix factorization with priors[C]∥2008 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Las Vegas, NV, USA, 31 March- 4 April 2008: 4029- 4032.
[28] Wilson K, Raj B, Smaragdis P. Regularized non-negative matrix factorization with temporal dependencies for speech denoising[C]∥INTERSPEECH 2008, Brisbane Australia, 22-26 September 2008: 411- 414.
[29] Mohammadiha N, Gerkmann T, Leijon A. A new linear MMSE filter for single channel speech enhancement based on nonnegative matrix factorization[C]∥2011 IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA), New Paltz, NY, USA, 16-19 Oct. 2011: 45- 48.
[30] Mohammadiha N, Gerkmann T, Leijon A. A new approach for speech enhancement based on a constrained nonnegative matrix factorization[C]∥2011 International Symposium on Intelligent Signal Processing and Communications Systems (ISPACS), Chiang Mai, Thailand, 7-9 Dec. 2011: 1-5.
[31] Raj B, Singh R, Virtanen T. Phoneme-dependent NMF for speech enhancement in monaural mixtures[C]∥INTERSPEECH 2011, Florence, Italy, 28-31 August 2011: 1217-1220.
[32] Mohammadiha N, Taghia J, Leijon A. Single channel speech enhancement using Bayesian NMF with recursive temporal updates of prior distributions[C]∥IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25-30 March 2012: 4561- 4564.
[33] Weninger F, Feliu J, Schuller B. Supervised and semi-supervised suppression of background music in monaural speech recordings[C]∥IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25-30 March 2012: 61- 64.
[34] Joder C, Weninger F, Eyben F, et al. Real-time speech separation by semi-supervised nonnegative matrix factorization[C]∥International Conference on Latent Variable Analysis and Signal Separation (LVA ICA), Tel Aviv, Israel, 2012: 322-329.
[35] Mohammadiha N, Smaragdis P, Leijon A. Supervised and unsupervised speech enhancement using nonnegative matrix factorization[J]. IEEE Transactions on Audio, Speech, and Language Processing, Oct. 2013, 21(10): 2140-2151.
[36] Fan H, J. Hung W, X. Lu X, et al. Speech enhancement using segmental nonnegative matrix factorization[C]∥2014 IEEE International Conference on Acoustic, Speech and Signal Processing (ICASSP), Florence, Italy, 4-9 May 2014: 4483- 4487.
[37] 张立伟, 贾冲, 张雄伟, 等. 稀疏卷积非负矩阵分解的语音增强算法[J]. 数据采集与处理, 2014, 29(2): 259-264.
Zhang Liwei,Jia Chong,Zhang Xiongwei, et al. Speech enhancement based on convolutive nonnegative matrix factorization with sparseness constraints[J]. Journal of Data Acquisition and Processing, 2014, 29(2): 259-264.(in Chinese)
[38] Wang Z, Sha F. Discriminative non-negative matrix factorization for single-channel speech separation[C]∥2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4-9 May 2014: 3749-3753.
[39] Kwon K, Shin J, Sonowal S, et al. Speech enhancement combining statistical models and NMF with update of speech and noise bases[C]∥2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4-9 May 2014: 7103-7107.
[40] Kwon K, Shin J, Kim N. NMF-based speech enhancement using bases update[J]. IEEE Signal Processing Letters, April 2015, 22(4): 450- 454.
[41] Kim M, Smaragdis P. Mixtures of local dictionaries for unsupervised speech enhancement[J]. IEEE Signal Processing Letters, March 2015, 22(3): 293-297.
[42] Chung H, Plourde E, Champagne B. Basis compensation in non-negative matrix factorization model for speech enhancement[C]∥2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20-25 March 2016: 2249-2253.
[43] Jeon K, Kim H. Local sparsity based online dictionary learning for environment-adaptive speech enhancement with nonnegative matrix factorization[C]∥INTERSPEECH 2016, San Francisco, USA, 8-12 September 2016: 2861-2865.
[44] Lee S, Han D, Ko H. Single-channel speech enhancement method using reconstructive NMF with spectrotemporal speech presence probabilities[J]. Applied Acoustics, 2017, 117: 257-262.
[45] Fagot D, Wendt H, Févotte C. Nonnegative matrix factorization with transform learning[C]∥2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15-20 April 2018: 2431-2435.
[46] Kavalekalam M, Nielsen J, Shi J, et al. Online parametric NMF for speech enhancement[C]∥2018 26th European Signal Processing Conference (EUSIPCO), Rome, Italy, 3-7 Sept. 2018: 2320-2324.
[47] Bai Z, Bao C, Yan B. Speech enhancement based on codebook constrained nonnegative matrix factorization[C]∥2018 International Conference on Audio, Language and Image Processing (ICALIP), Shanghai, China, 16-17 July 2018: 361-365.
[48] Kang T, Kwon K, Shin J, et al. NMF-based speech enhancement incorporating deep neural network[C]∥INTERSPEECH 2014, Singapore, 14-18 September 2014: 2843-2846.
[49] Kang T, Kwon T, Shin J, et al. NMF-based target source separation using deep neural network[J]. IEEE Signal Processing Letters, February 2015, 22(2): 229-233.
[50] Tseng H, Hong M, Luo Z. Combining sparse NMF with deep neural network: a new classification-based approach for speech enhancement[C]∥2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brisbane, QLD, Australia, 19-24 April 2015: 2145-2149.
[51] Vu T, Bigot B, Chng E. Combining non-negative matrix factorization and deep neural networks for speech enhancement and automatic speech recognition[C]∥2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20-25 March 2016: 499-503.
[52] Nie S, Liang S, Li H, et al. Exploiting spectro-temporal structures using NMF for DNN-based supervised speech separation[C]∥2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20-25 March 2016: 469- 473.
[53] Bando Y, Mimura M, Itoyama K, et al. Statistical speech enhancement based on probabilistic integration of variational autoencoder and non-negative matrix factorization[C]∥2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15-20 April 2018: 716-720.
[54] Xu Y, Du J, Dai L, et al. A regression approach to speech enhancement based on deep neural networks[J]. IEEE/ACM Transactions on Audio, Speech, and Language Processing, January 2015, 23(1): 7-19.

