1 引言
基于位置的定位导航服务在室内环境中扮演着重要的角色。然而,由于建筑物的遮挡、多楼层等复杂环境因素的影响,传统的全球导航系统(Global Positioning System,GPS)无法在室内环境中发挥作用;基于传感器[1]的技术虽然能有效地实现室内定位,但由于在实施过程中,需要配置大量传感器节点,费时费力,不具备环境适应性;基于摄像头[2]的方法只能定向跟踪视距线(Line of Sight,LoS)范围内的运动,并且侵犯了用户隐私;基于声音[3]的解决方案容易受到环境噪声的影响,覆盖范围也非常小;超声波在实际应用中存在着成本昂贵等问题。相比之下,WiFi的室内覆盖范围在逐年增加,我们可以利用现有的商用WiFi设备,不再增加多余的成本来实现室内导航。WiFi凭借这一优势吸引了越来越多的研究人员。
对于基于WiFi的室内定位与跟踪技术,已经开发了有源[4]和无源[5]两种解决方案。其中,有源定位主要是指通过用户携带智能手机或其他可穿戴设备主动定位跟踪用户,无源定位则是指用户无需携带任何设备便可以得到其位置信息。相比之下,有源定位需要用户携带设备,这不仅大大增加了成本,而且给用户带来了不便,并不适合应用于某些场景中,例如安防监控。此外,早期的研究主要利用接收信号强度(Received Signal Strength Indication,RSSI)来实现定位[6,7]。但由于WiFi信号在传播过程中存在多径效应,影响了最终的定位精度。研究人员发现了物理层的信道状态信息(Channel State Information,CSI)能够描述信道的细粒度信息,因此利用CSI进行室内定位与轨迹跟踪的技术得到了广泛的关注。DeepFi[8]将CSI幅值作为指纹,利用一个带有四个隐层的基于深度学习的神经网络算法,实现室内指纹定位识别;PhaseFi[9]利用CSI相位作为指纹,使用神经网络算法进行目标位置匹配识别;WiDeo[10]在WARP软件定义的无线电平台上,通过从WiFi反向散射后的每个反射中提取幅度、飞行时间和到达角度等信息,并使用稀疏感知优化算法来精确查找反向散射参数,实现了细粒度的运动跟踪;WiDar[11]利用具有不同空间特征的多个WiFi链路来获得多普勒频移,进一步得到移动方向和位置信息来进行轨迹跟踪。
本文提出一种用户无需携带设备,仅仅利用一台路由器作为发射端,一台装有CSI Tools的台式电脑作为接收端的轨迹定位系统。通过建立一个统一的模型来计算达到角度(Angle-of-Arrival,AoA)、飞行时间(Time-of-Flight,ToF)和多普勒频移(Doppler Frequency Shift,DFS)等多维参数,随后利用图匹配算法筛选其中与路径相关的部分,进而得到精确的位置信息。同时,实验人员无需提前采集环境数据,仅仅利用采集到的路径数据中包含的环境动态参数来修正定位所需要的参数信息,以达到了更为精准的轨迹跟踪效果。
2 基本原理
2.1 CSI多参数估计模型
由于室内多径效应的影响,无线信号在时间t、频率f和传感器s处有以下测量值:
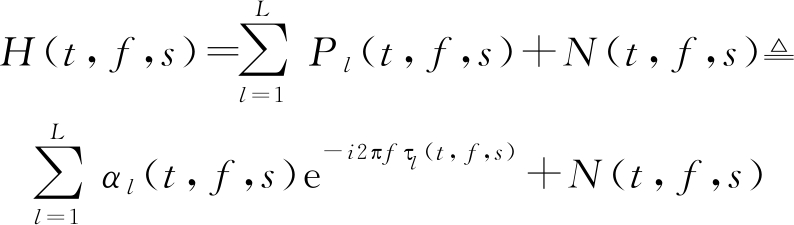
(1)
其中,L表示多径总数,Pl表示第l条多径下的信号,N表示环境中的背景噪声(主要是高斯白噪声),αl和τl表示的是第l条多径的复衰减因子和传播延迟。在WIFI的信号状态信息CSI中,幅值信息所表示的含义是能量衰减,相位信息所表示的含义是传播延迟。结合公式(1)可以将CSI的测量值H(i, j,k)在以H(0,0,0)为基准时的相位信息表示为:
fcτl+Δfjτl+fcΔsk·φl-fDlΔti
(2)
其中,i、 j、k分别表示数据包、子载波、接收天线, fc为信道的载波频率,Δti,Δfj,Δsk分别表示H(i, j,k)与H(0,0,0)之间的时间差、频率差和空间位置差,τl,φl, fDl分别表示第l条多径的ToF、AoA、DFS。
我们将多径的信号的第l条参数表示为θl=(αl,τl,φl, fDl)。那么,多参数估计问题就可以转化为最大似然估计问题。由于θ本身维度很高,且不存在闭式解,无法直接利用软件计算。为了解决这个问题,我们采用空间交替广义期望最大化(Space Alternating Generalized Expectation-maximization,SAGE)算法[12]来减少整体的搜索空间。算法的主要核心是每次迭代仅估计一个子集,同时保持其他组件估计不变,因此我们将原本对θ的估计转化为对单个参数ToF、AoA、DFS和衰减的估计。
2.2 共轭乘法纠正相位信息
由于室内环境复杂,商用WiFi容易受到室内环境变化的影响,采集到CSI不仅包含信道响应,还包含收发器之间的异步和硬件缺陷引起的各种相位噪声,并不能直接使用上述算法。
另外,我们发现由定时偏移(Timing Offset,TO)和载波偏移(Carrier Frequency Offset,CFO)引起的CSI相位噪声仅在时间和频率上变化,而不在空间上变化。即同一网卡的所有接收天线在同一个时刻经历相同的未知噪声。我们考虑选择一根接收天线作为参考值(例如第k0根天线),计算每根天线与参考天线的共轭乘法C(m)[13]来清除不相关噪声:
(3)
其中
然后,我们将多径信号分为静态(fD=0)路径Ps和动态(fD≠0)路径Pd,则公式(3)可以改写成:
C(m)=(Ps+Pd)*(Ps0+Pd0)*=
(4)
其中,由于静态路径比动态路径的信号强得多,所以第三个求和项的阶数比前两个项弱,可以忽略不计。
2.3 图形匹配算法
参数估计算法的输入由多径信号的参数组成,需要一个筛选程序来确定与轨迹相关的参数。然而,多路径参数杂乱无章并携带了各种噪声信息。为了克服这些问题,我们使用一种基于图的路径匹配算法(Graph-based Path Matching,GPM)。算法原理如图1,假设考虑N个CSI段的估计,并且每个CSI段中都包含L条多径(图中实线)的参数,由此,我们可以得到一个加权的N分图为:
G=(V,E,W)
(5)
其中,νij∈V表示第i个CSI的第j条路径的参数θij的估计。
表示Vi1j1与Vi2j2之间的边(图中的实线与虚线部分)。
表示边
的权重,物理含义为参数间的距离,可以表示为:
(6)
其中,c是不同参数ToF、AoA、DFS和衰减进行归一化后的系统向量。此外,
为二进制变量,用来指示是否选择边进行匹配。那么,目标函数可写为:
xopt=arg minxwTx
(7)
其中,w、x分别表示矢量化后的权重与变量。为了确保选定的边可以形成L个N阶完整图,应需满足以下几个条件:
(1)不得选择第i部分的内边,即
(2)第i1部分中选定边的数量必须等于其余部分中的顶点数,即
(3)顶点Vi1j1与第i2部分顶点之间的边不得超过1,即
(4)如果选择
和
那么必须选择
即
由此,公式(7)的目标函数再加上以上四个约束条件,形成了一个二元整数规划(Binary Integer Programming,BIP)问题,可以通过例如YALMIP[14]的BIP解算器来求解。在进行图匹配之后,会存在少量异常值,为了去除这些异常值,我们对匹配后的结果做了Hample滤波处理。
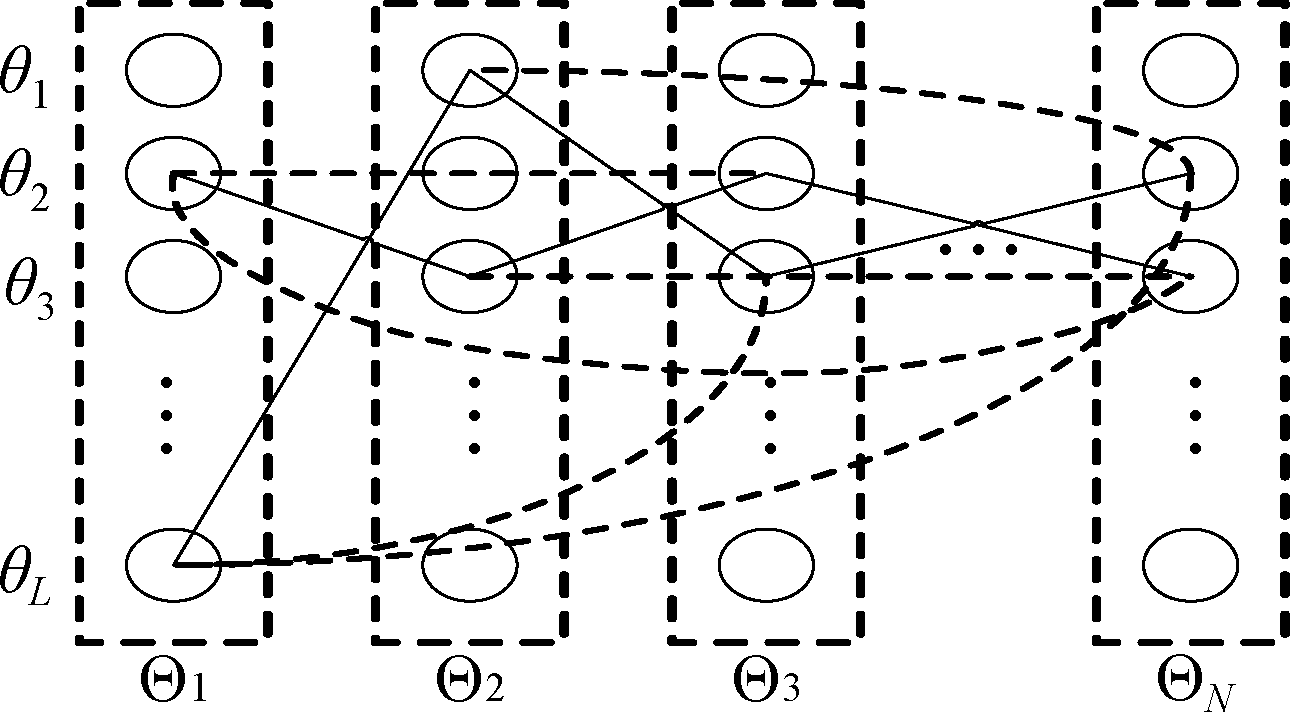
图1 图匹配原理
Fig.1 The principle of Graph matching
2.4 定位算法
理论上,ToF乘上光速可以表示实际路径的数值,我们将发射端到用户以及用户到接收端之间的距离和为实际路径,如图2所示。然而,由于强噪声和低分辨率对ToF的影响,距离的估计是波动的,不能直接用于定位。为此,我们将粗粒度的ToF与相对细粒度的DFS结合,具体来说就是将DFS通过
转换为路径变化率ν,其中λ为信号的波长。
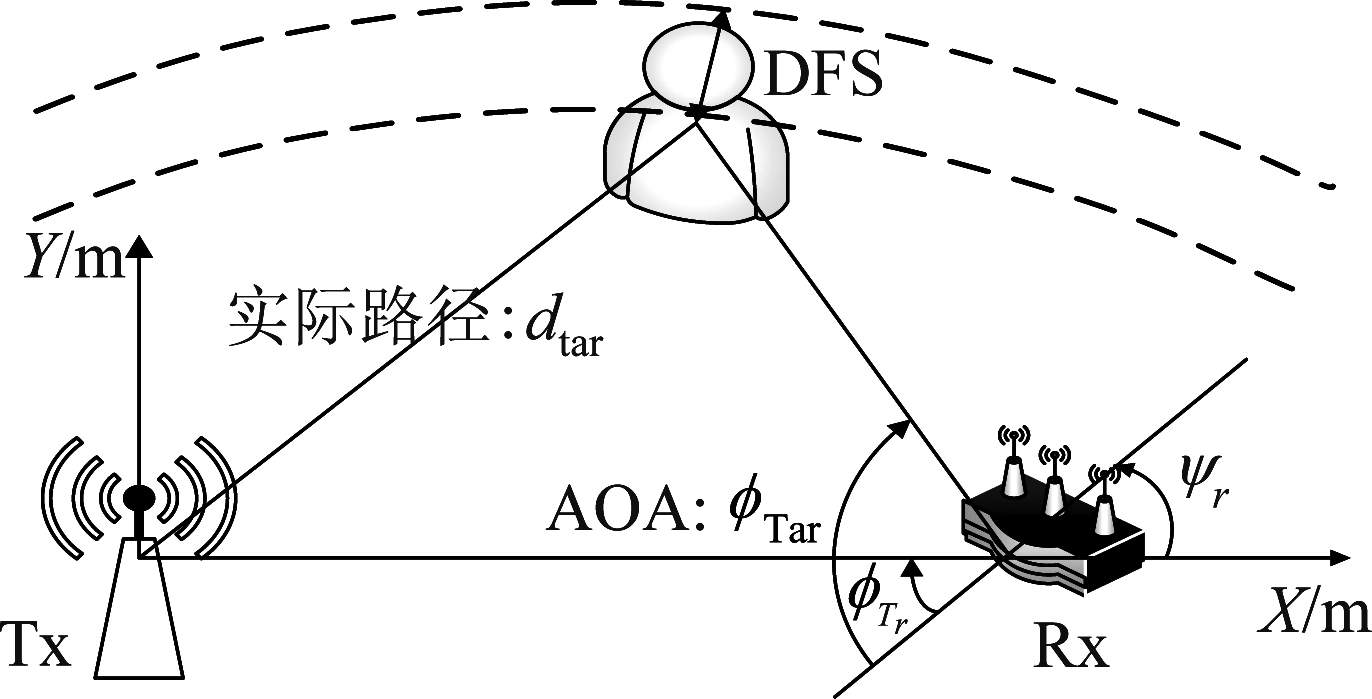
图2 定位原理图
Fig.2 The principle of positioning
有了这些理论基础,我们利用卡尔曼平滑器通过DFS估计的路径范围变化率对从ToF中提取的距离进行修正,从而得到用于定位的实际路径的绝对范围。
随后,我们就可以综合实际路径与AoA得到位置信息,原理图如图2所示。我们将发射端、接收端和目标位置分别表示为o=(0,0)、lr=(xr,yr)和l=(x,y)。接收天线的偏向角ψr可以通过φTr和(xr,yr)计算得到。另外,坐标之间的关系可以用如下方程组表示:
(y-yr)cos(ψr-φTar)=(x-xr)sin(ψr-φTar)
(8)
其中,dTar和φTar分别表示实际路径和AoA信息,我们可以利用由实际路径确定的半椭圆和AoA所在直线的交点来确定位置信息。位置坐标表示如下:
y=tanφ(x-xr)+yr
(9)
其中,φ=ψr-φTar,sr=sgn{(x-xr)cos φ}。
3 算法改进
3.1 环境参考角
本文2.4小节定位算法中,我们设定发射端为坐标系原点,发射端与接收端的连线为坐标系X轴。那么φTr我们可以理解为由环境状况和噪声共同造成的一个环境参考角。环境参考角容易受到环境状况以及其他用电器的干扰。在原先算法的设定中,假设参考角φTr是恒定不变的,然而室内环境复杂,一定存在噪声干扰或环境不稳定等因素,为了得到更加精准的轨迹结果,φTr的大小与变化需要进一步探究。
为了验证环境参考角的变化情况,我们采集相同环境(空房间)、不同时间(时间差不大)的CSI数据并分析其时频图。如图3所示,图3(a)显示的是t1时刻采集到的CSI数据的时频图,图3(b)显示的是t2时刻采集到的CSI数据的时频图。
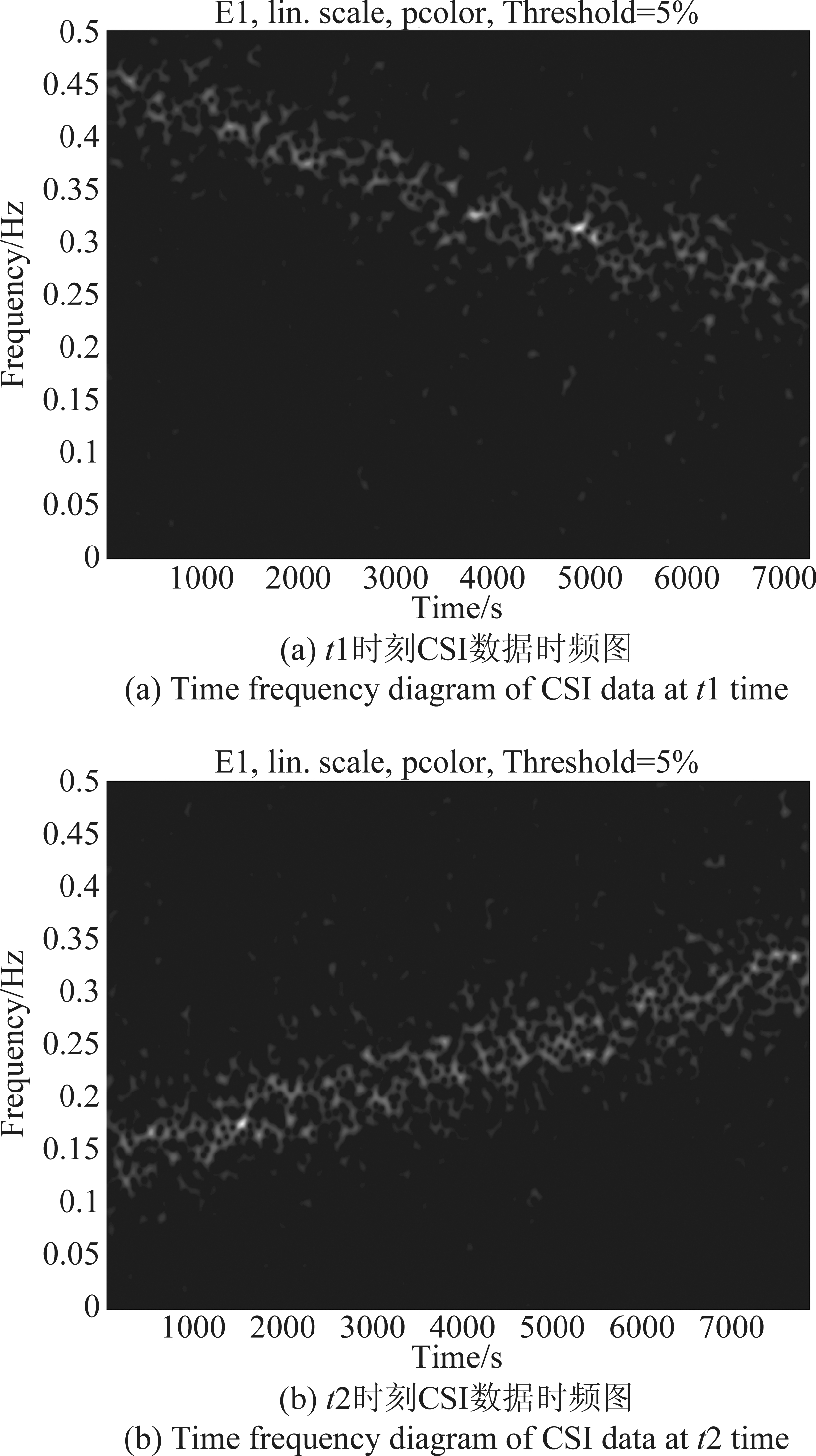
图3 不同时刻CSI数据时频图
Fig.3 The principle of positioning
从图中可以明显看出:(1)不同时刻的环境状态不一致;(2)环境参考角不是恒定的,是动态变化的。这样看来,恒定不变的环境参考角势必会影响我们的定位跟踪结果,为此我们将在3.2节继续讨论如何提取环境参考角信息,以及如何利用环境动态参考角对AoA信息进行修正。
3.2 到达角度(AoA)的修正
本文2.2小节的相位纠正算法中,我们首先假设实验环境是稳定不变的,也就是说静态路径随时间的变化是恒定的。从而可以将公式(4)中的第一个求和公式
通过高通滤波器去除。然而,在3.1节中我们已经讨论并验证了环境并非稳定不变,那么仅仅采用高通滤波器过滤掉的静态路径中包含有可以反映路径变化的部分。
此外,我们将公式(4)中第二部分的求和公式与公式(1)、(2)相结合,改写为:
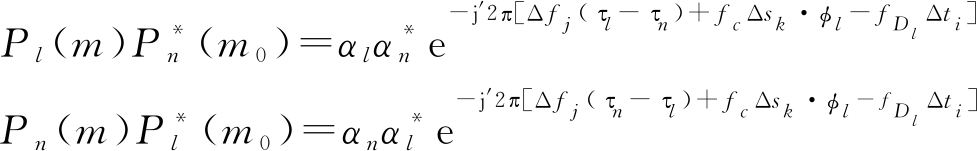
(10)
其中, j′代表虚部表示符。由于
中的
中e-j′2πfcΔsk0·φl对于所有多径测量值都是恒定的,并且不影响参数估计,可以忽略不计。
观察公式(10)中的两个等式,我们可以发现,除去表示ToF的(τl-τn),其余部分具有相同的结构。我们假设Pl、Pn分别为目标实际路径和视距线传播路径,那么由于收发器的位置是固定并且已知的,我们便可利用链路距离直接计算出ToF值τn,从而进一步计算出ToF值τl。
对于共轭乘法的副产物(公式(10)中的第二个等式
其具有不真实的ToF值(τn-τl)、AoA值φn、DFS值fDl。为了这些副产物,我们将所有CSI的幅值减去一个常数β,并添加定值γ到参考天线的CSI中。那么当m≠m0时,我们有:
(11)
由此,共轭乘法的副产物就可以去除了。在做了振幅调整与高通滤波后,共轭乘法C(m)中就只剩下
其中l∈Pd、n∈Ps,与CSI测量值H(m)具有相同的结构,可以将多参数估计算法直接应用于C(m)中。
同理,我们可以得到与H(m)也具有相同的结构。我们将经过如图4的处理流程。将
和分别经过参数估计、路径匹配后得到ToF、DFS、AoA与环境参考角。利用环境动态参考角来修正AoA得到轨迹AoA,再与2.4小节中得到的实际路径结合起来,即可得到轨迹结果。
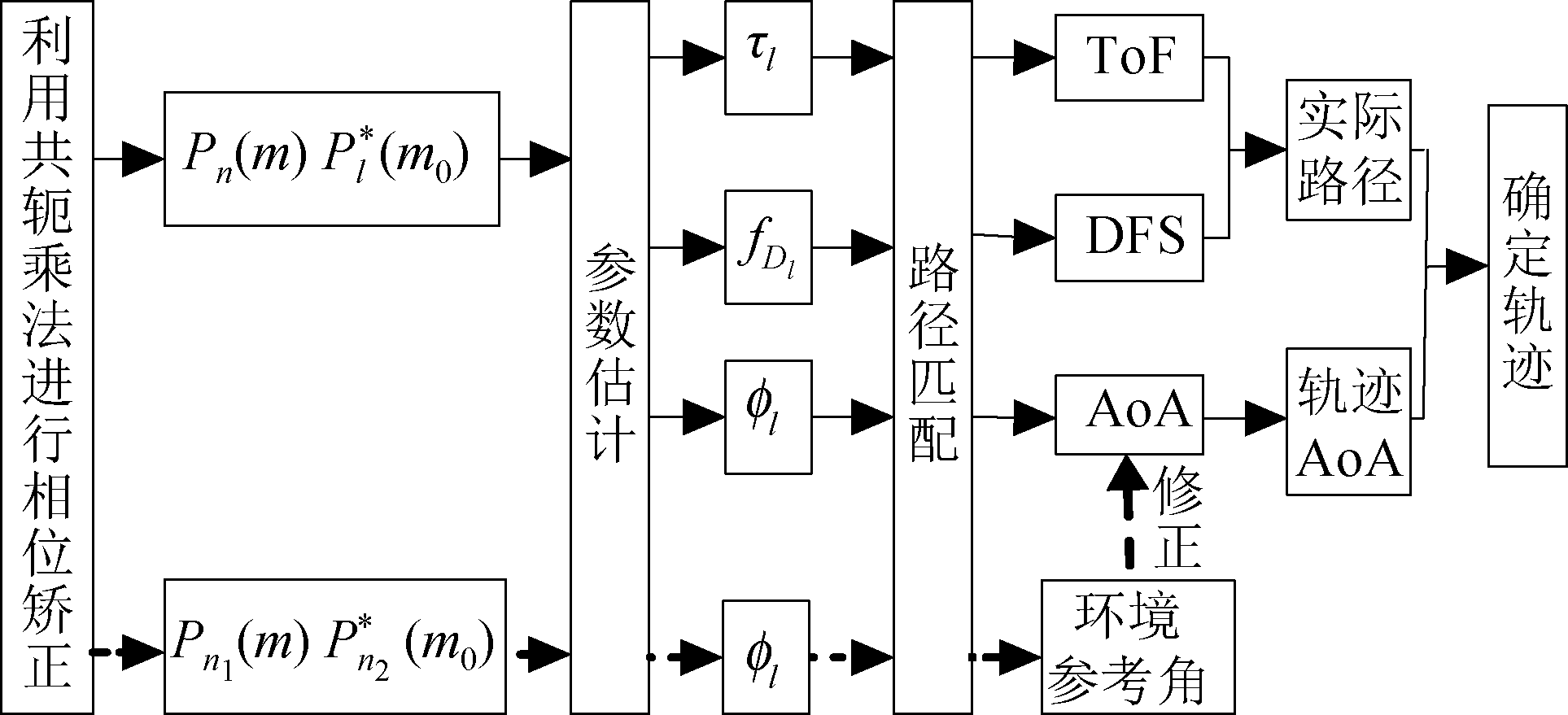
图4 系统流程图
Fig.4 System flowchart
结果如图5(a)所示,散点表示的是多路径AoA,圆圈表示的是图匹配后的AoA,散点表示环境恒定参考角修正后的轨迹AoA,实线表示环境动态参考角修正后的轨迹AoA,可以明显看出,实线数据比散点数据更能体现图匹配后AoA的特征。图5(b)显示了在两种处理方法后的轨迹结果,其中,虚线小点为真实轨迹,虚线大点为环境恒定参考角矫正后的轨迹,实线为环境动态参考角矫正后的轨迹。结果显示,利用环境动态参考角得到的轨迹更贴合真实轨迹。
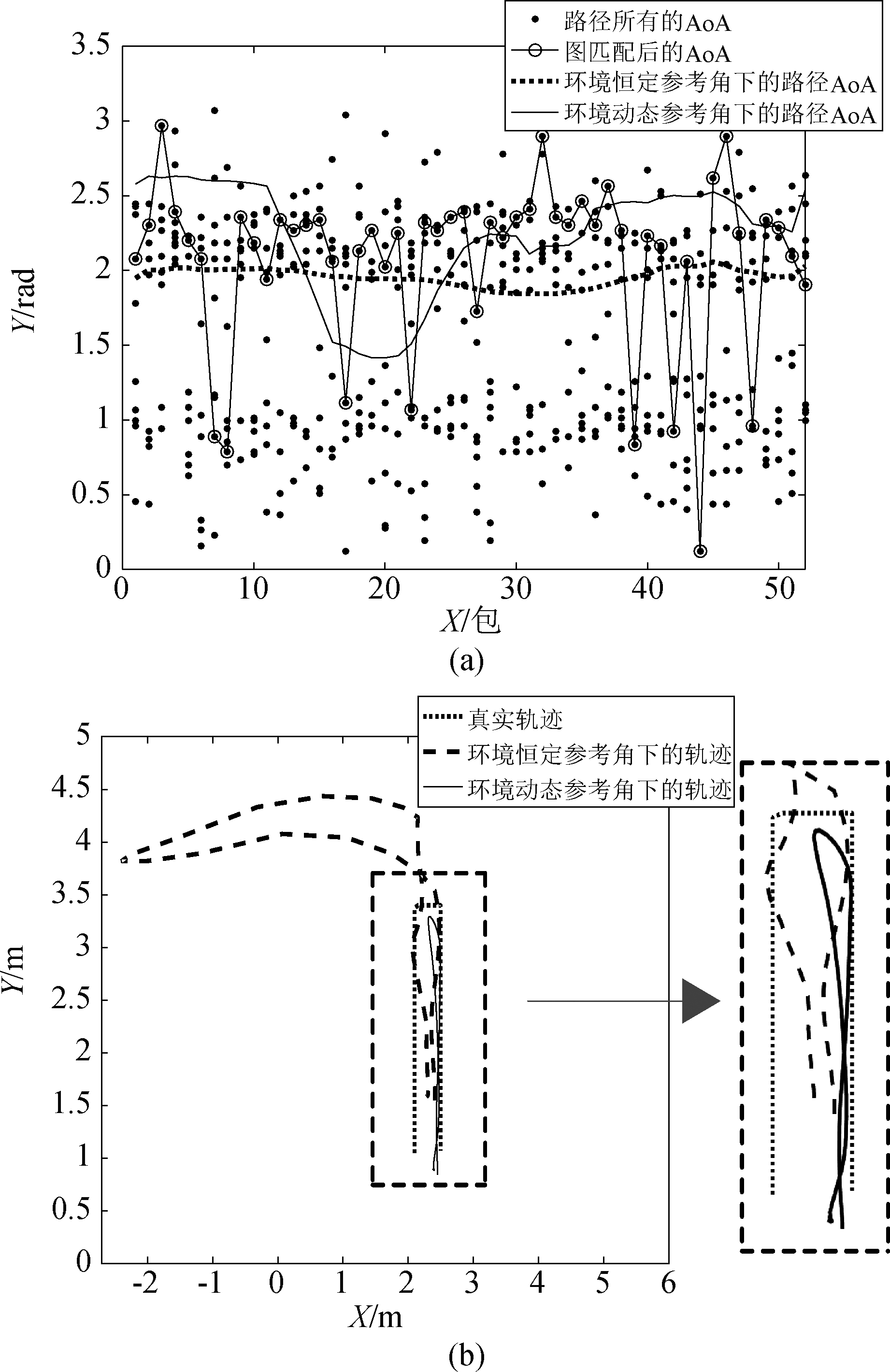
图5 环境动态参考角修正
Fig.5 Environment dynamic reference angle correction
4 实验场景与轨迹跟踪结果
4.1 实验场景与系统性能
我们使用一台支持802.11协议的TP-Link路由器作为WiFi接入点,即发射端(AP)。选取165信道5.825 GHz的频段信号,并将数据传输速率设置为1000 Hz。一台安装inter5300网卡的台式机作为接收端(MP)。其中接收端有三根天线,可以形成一个均匀的线性阵列,接收端电脑安装Ubuntu11.04系统,导入CSI Tools工具包,并配置相关内核参数,通过ping命令对信号进行收发,并利用CSI Tools工具包将接收到的CSI数据保存到目标文件中,使用MATLAB对CSI数据进行处理。
为了充分评估系统的性能,我们选取环境复杂的实验室作为实验环境,房间大小约为7.5 m×8.7 m。另外,实验共有三名实验员(1名男性2名女性)参与,他们分别沿直线来回、P型、N型等不同的形状随意行走。图6显示了轨迹跟踪的结果。其中,虚线表示真实轨迹,实线表示通过我们的轨迹跟踪系统得到的轨迹。
为了更全面的评估系统性能,首先,我们对比了环境恒定参考角与环境动态参考角的定位精度,结果如图7(a)所示,通过验证了使用环境动态参考角的方法确实可以提高系统定位精度,其中值定位误差达到了0.65 m。此外,将我们的系统与现用轨迹跟踪系统Dynamic-Music[15]和IndoTrack[16]的定位精度进行对比。结果如图7(b)所示,可以看出,我们的定位精度明显高于其他两种轨迹跟踪系统。
4.2 参数研究
行走速度:为了评估行走速度对系统性能的影响,我们进行了不同速度自由行走的实验。图8(a)显示了不同行走速度的定位误差分布。经验证,在行走速度变化的情况下,我们的定位误差可以稳定在0.65 m左右,但随着行走速度的增加,定位误差逐渐减小,这是因为较大的行走速度会在接收端引起较大的频偏,有助于校准过程中提取反射信号。
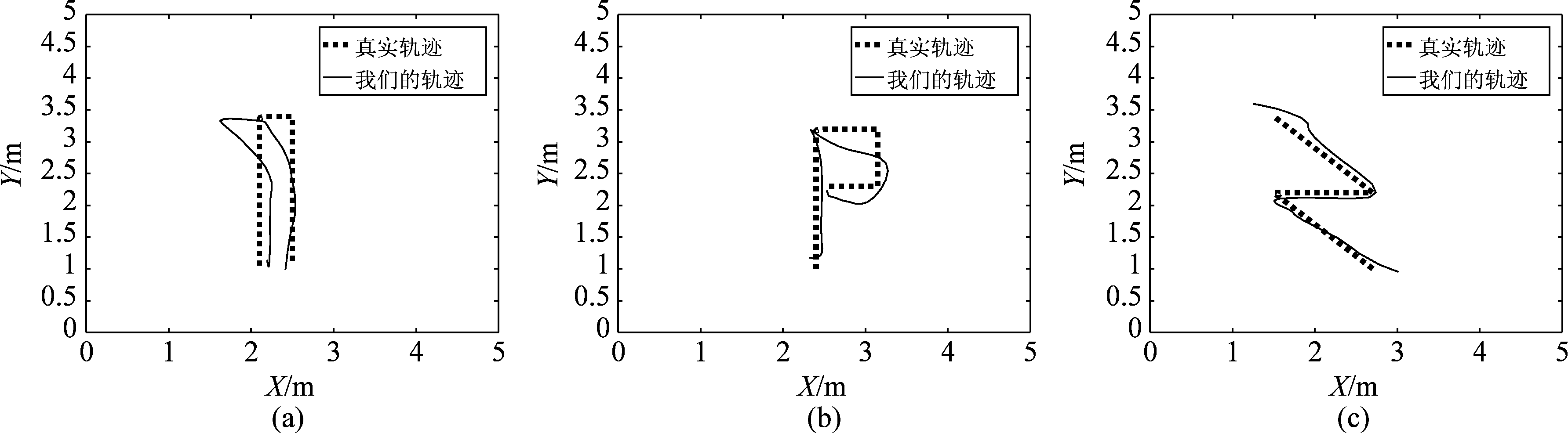
图6 轨迹结果图
Fig.6 The result of trajectory
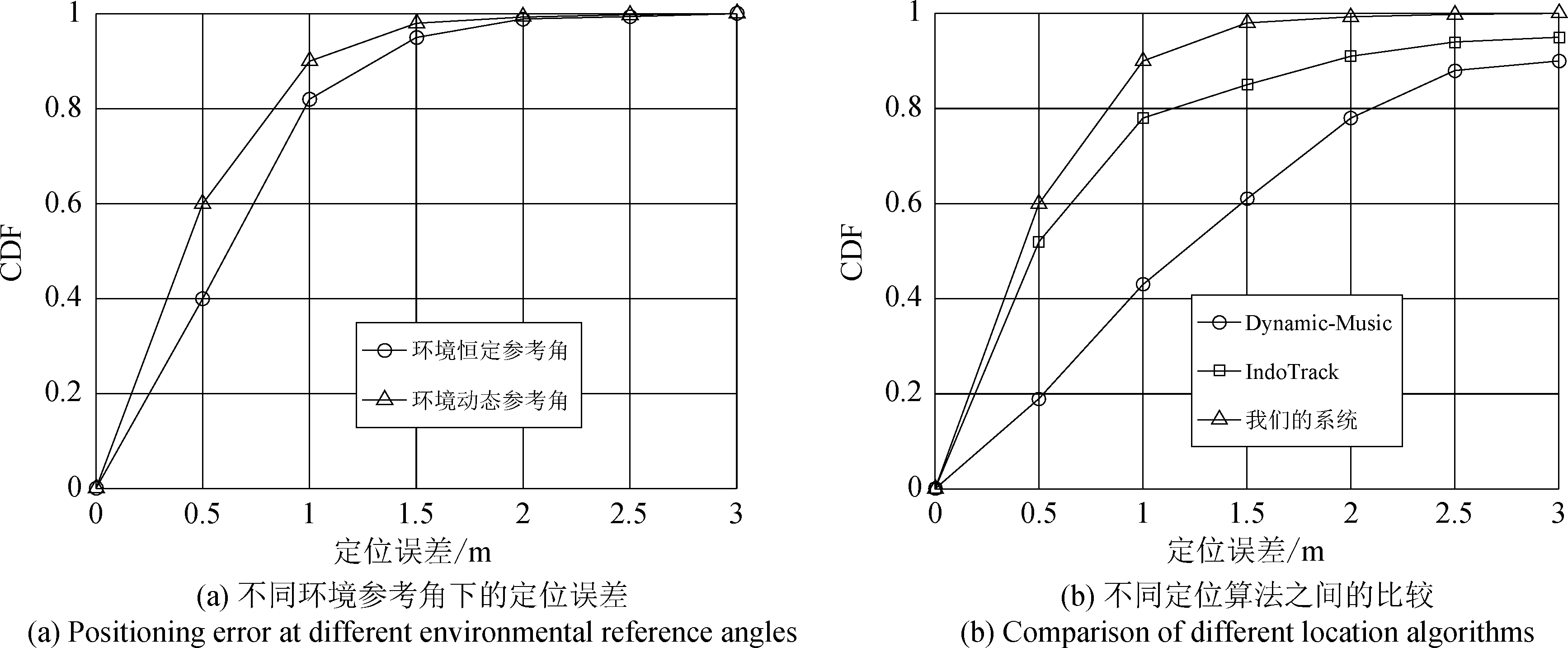
图7 性能对比
Fig.7 Performance comparison
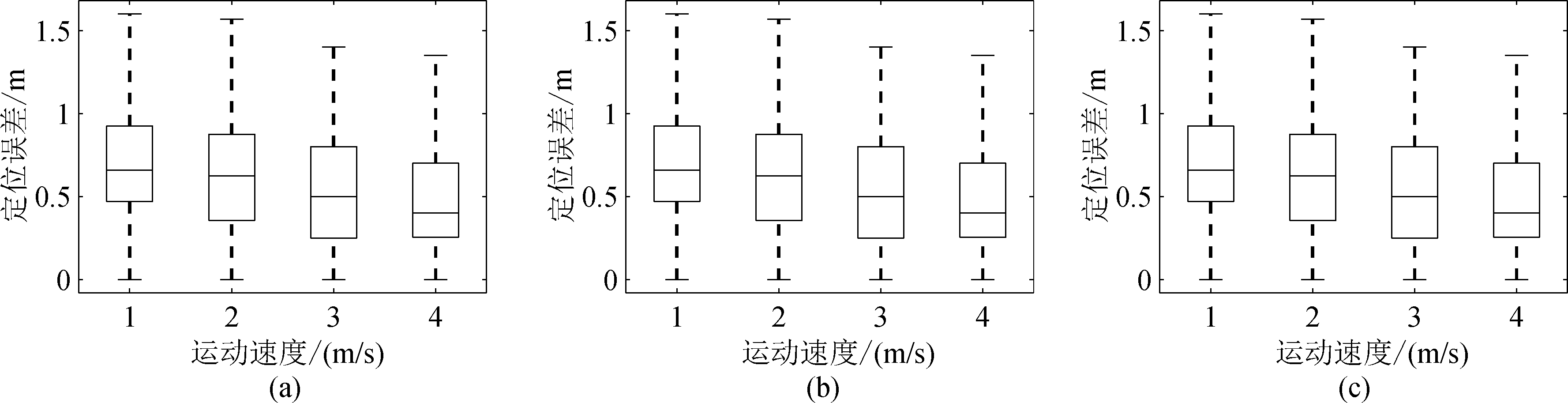
图8 不同参数下的定位误差
Fig.8 Positioning errors at different parameters
发包率:为了找出算法的最佳发包率,我们在Linux系统上利用命令将路由器的发包率设定为200 Hz、400 Hz、600 Hz、800 Hz、1000 Hz五个频段。图8(b)显示了不同发包率下的定位误差。可以看出,在这个范围的不同发包率下,定位误差几乎不变。然而在理论上,如果再进一步降低发包率,定位误差将会明显下降。这是由于较低的发包率造成DFS估计的混叠引起的。结果表明,我们的系统具有适当的发包率,适用于WiFi的传输。
不同实验人员:为了确保我们的系统在不同用户使用时都具有较好的跟踪效果,我们让四名不同性别、身高和体型的人员参与实验(2名男性2名女性)。在实验开始前,仅仅只向参与实验的人员介绍基本的实验设置,如跟踪区域和典型的行走路线。同时,参与实验的人员并未经过专门的训练,行走习惯也不一致。图8(c)显示了不同实验人员参与下的定位误差。可以看出,我们的系统在不了解参与实验人员的特征的情况下,定位误差可以稳定在0.65 m左右。
5 结论
在本文中,我们介绍了一个轨迹跟踪系统,充分利用人在行走时采集到的CSI数据。通过环境动态参考角对轨迹信息进行矫正,从而达到了更精准的轨迹跟踪效果,并提高了跟踪系统对环境的适应性。结果表明,我们的跟踪系统在7.5 m×8.7 m范围内实现了0.65 m的中值定位误差。
[1] Zhuang Y, Yang J, Li Y, et al. Smartphone-Based Indoor Localization with Bluetooth Low Energy Beacons[J]. Sensors, 2016, 16(5): 596.
[2] 曹凯悦, 阮秋琦. 大型追踪系统的多摄像头协同[J]. 信号处理, 2018, 34(4): 494-502.
Cao Kaiyue, Ruan Qiuqi. Multi-camera Coordination in Large-scale Intelligent Tracking System[J]. Journal of Signal Processing, 2018, 34(4): 494-502.(in Chinese)
[3] 居太亮, 邵怀宗, 彭启琮, 等. 基于任意麦克风阵列的近场声源三维定位算法研究[J]. 信号处理, 2007,23(2): 231- 234.
Ju Tailiang, Shao Huaizong, Peng Qicong, et al. Speech Source 3D localization MUSIC Algorithm in near field[J]. Signal Processing, 2007 , 23(2): 231- 234.(in Chinese)
[4] Li J, Li Y, Ji X. A novel method of Wi-Fi indoor localization based on channel state information[C]∥International Conference on Wireless Communications & Signal Processing. IEEE, 2016: 1-5.
[5] 王磊, 周慧, 蒋国平, 等. 基于WiFi的自适应匹配预处理WKNN算法[J]. 信号处理, 2015, 31(9): 1067-1074.
Wang Lei, Zhou Hui, Jiang Guoping, et al. WiFi-based Self-adaptive Matching and Preprocessing WKNN Algorithm[J]. Journal of Signal Processing, 2015, 31(9): 1067-1074.(in Chinese)
[6] Bandirmali N, Torlak M. ERLAK: On the Cooperative Estimation of the Real-Time RSSI Based Location and K Constant Term[J]. Wireless Personal Communications, 2017, 95(4): 1-10.
[7] Labinghisa B A, Lee D M. Indoor localization algorithm based on behavior-driven predictive learning in crowdsourced Wi-Fi environments[J]. Modern Physics Letters B, 2019, 33(14n15): 1940036.
[8] Wang X, Gao L, Mao S, et al. DeepFi: Deep learning for indoor fingerprinting using channel state information[C]∥Wireless Communications and NETWORKING Conference. IEEE, 2015: 1666-1671.
[9] Wang X, Gao L, Mao S. CSI Phase Fingerprinting for Indoor Localization With a Deep Learning Approach[J]. IEEE Internet of Things Journal, 2017, 3(6): 1113-1123.
[10] Kiran Joshi, Dinesh Bharadia, Manikanta Kotaru, et al. WiDeo: Fine-grained Device-free Motion Tracing UsingRF Backscatter[C]∥In Proceedings of the 12th USENIX Conference on Networked Systems Design and Implementation (NSDI ‘15), 2015: 189-204.
[11] Qian Kun, Wu Chenshu, Yang Zheng, et al. Widar: Decimeter-Level Passive Tracking via Velocity Monitoring with Commodity WiFi[C]∥ACM, 2017.
[12] Fessler J A, Hero A O. Space-alternating generalized expectation-maximization algorithm[J]. IEEE Transactions on Signal Processing, 1994, 42(10): 2664-2677.
[13] Qian Kun, Wu Chenshu, Zhou Zimu, et al. Inferring Motion Direction Using Commodity Wi-Fi for Interactive Exergames[C]∥ACM, 2017.
[14] Lofberg J. YALMIP: a toolbox for modeling and optimization in MATLAB[C]∥2004 IEEE International Conference on Robotics and Automation (IEEE Cat. No. 04CH37508). IEEE, 2005.
[15] Li X, Li S, Zhang D, et al. Dynamic-MUSIC: accurate device-free indoor localization[C]∥the 2016 ACM International Joint Conference. ACM, 2016.
[16] Li Xiang, Zhang Daqing, Qin Lv, et al. IndoTrack: Device-Free Indoor Human Tracking with Commodity Wi-Fi[C]∥ACM, 2017.
