1 引言
正交频分复用(orthogonal frequency division multiplexing, OFDM)技术已广泛应用到数字音视频广播以及第四代移动通信等领域。但是OFDM技术具有带外辐射高、频偏敏感和频谱效率低等问题,无法满足5G异步多址、超低延迟和高可靠性的应用场景[1- 2]。而滤波器组多载波(filter-bank multi-carrier, FBMC)技术能满足未来无线通信的应用需求,采用交错正交幅度调制(offset quadrature amplitude modulation, OQAM)的FBMC系统具有灵活的时频分配、超高频谱利用率和超低的带外辐射,其相邻混叠载波间不需要严格的正交,是极具有应用价值的多载波传输技术[3- 4]。
在非协作通信背景下,载波参数是通信信号自适应解调的重要参数。目前关于FBMC-OQAM信号参数估计的文献较少,许多学者关注的是原型滤波器设计和优化问题[5-8],以提升传输性能,降低计算复杂度,抵抗载波和信道干扰为目标设计原型滤波器。仅有文献[9]运用自相关二阶矩和循环自相关算法对FBMC-OQAM信号的有用符号周期进行盲估计。目前对OFDM信号参数盲估计的研究已相对成熟,文献[10]通过计算接收信号自相关矩阵,根据特征值的特性判断子载波数目,但该方法不能估计出载波频率。文献[11]利用功率二次谱估计载波参数和载波间隔。文献[12]运用哈尔小波改进倒谱法,并联合随机共振增强微弱信号抑制噪声的方法,利用频谱的波纹周期性来估计子载波数,该方法主要用于微弱信号处理且复杂度高。文献[13-14]利用四阶循环累积量算法对MC-CDMA和OFDM信号的子载波频率和数目进行盲估计。二次谱法和倒谱法利用了循环前缀引入的自相关特性,通过检测循环前缀在频谱上的特征点来估计载波参数,而四阶累积量不需利用循环前缀就能估计载波参数。
为了解决滤波器组的子载参数估计问题,本文在高斯白噪声信道下提出四阶累积量估计FBMC-OQAM 信号的子载波频率和数目。首先分析FBMC-OQAM 系统模型,以及滤波器组通过多相网络实现加窗操作;然后根据循环频率算出同步后信号的四阶累积量,分析发现四阶累积量受原型滤波器响应系数影响;最后仿真发现重叠因子奇偶引起四阶累积量的凹凸变化。
2 FBMC-OQAM系统模型
FBMC-OQAM系统被认为是未来5G物理层主要的多载波通信方式。输入的高速码字经过串并变换后成为并行的低速码字,传统的QAM基带映射会引起子载波间的混叠干扰,所以利用OQAM映射能有效抑制混叠干扰。经过IFFT和多相网络(poly phase network, PPN)构成综合滤波器组(synthesis filter bank, SFB),在接收端FFT和PPN构成分析滤波器组(analysis filter bank, AFB)[15],系统框图如图1。
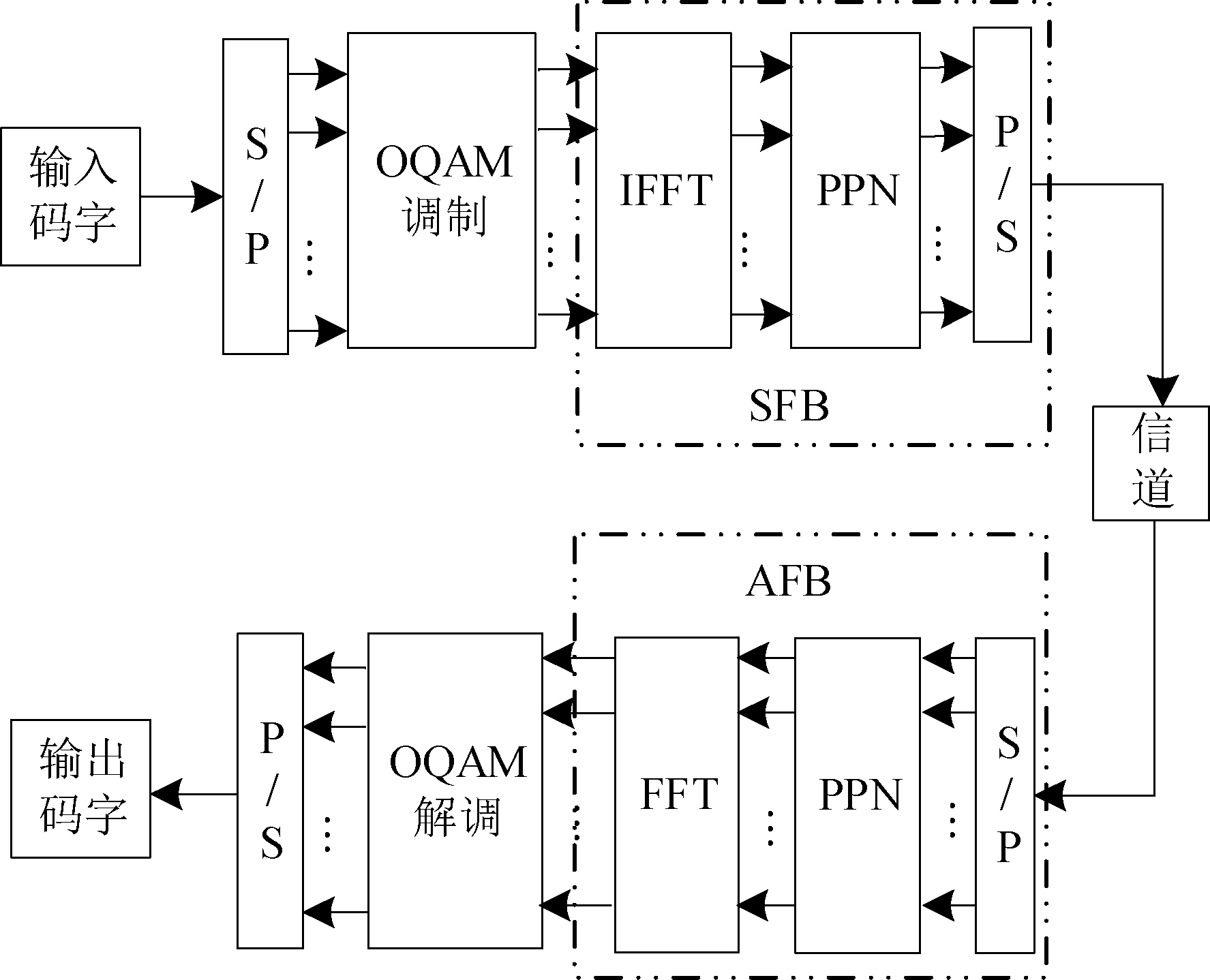
图1 FBMC-OQAM系统框图
Fig.1 FBMC-OQAM system block diagram
其发送端FBMC-OQAM信号可表示为
(1)
cn,i=dn,2iejθn,2i+dn,2i+1ejθn,2i+1
(2)
式中:i表示符号变量;n表示子载波变量;N表示信号的多载波数;cn,i表示第n个用户的第i个复数符号,第i个FBMC符号由N个子载波构成,即CN,i={c0,i,c1,i,…,cN-1,i}T。式(2)将cn,i拆分为实部和虚部偏移半个符号周期传输,用dn,i表示拆分后的实值符号,可见符号数加倍,偏移的相位旋转因子用θn,i表示,即
原型滤波器h(m)采用频域采样技术设计,重叠因子用K表示,则滤波器长度为L=KN。所设计滤波器能使信号完美重构且频谱旁瓣衰减快速下降,频率采样点的系数为Hk满足对称性和奈奎斯特准则[16-17],即系数满足如下等式:
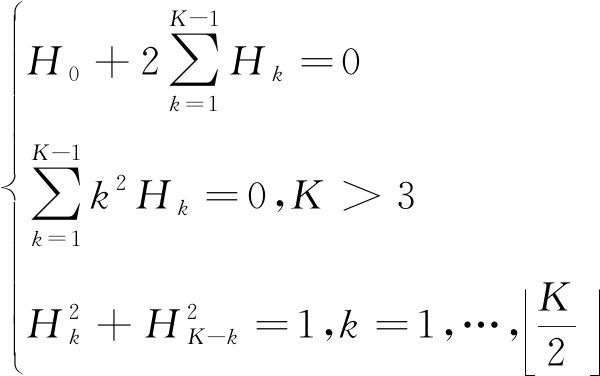
(3)
表1 采样点系数
Tab.1 Sampling point coefficient
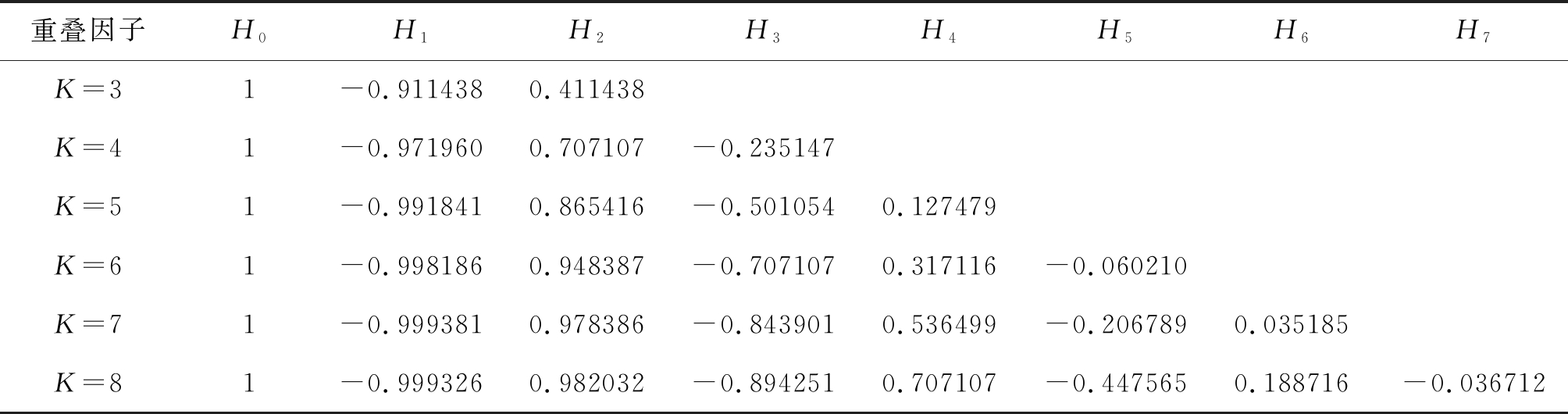
重叠因子H0H1H2H3H4H5H6H7K=31-0.9114380.411438K=41-0.9719600.707107-0.235147K=51-0.9918410.865416-0.5010540.127479K=61-0.9981860.948387-0.7071070.317116-0.060210K=71-0.9993810.978386-0.8439010.536499-0.2067890.035185K=81-0.9993260.982032-0.8942510.707107-0.4475650.188716-0.036712
通过式(3)可推导出滤波器频域系数如表1,然后内插得到原型滤波器的频域响应形式,经过傅里叶反变换求得时域信号,按重叠因子3归一化的不同重叠因子时域响应如图2所示。重叠因子K越大,其时域幅值越大,t∈[-L/2,L/2],当t=0时,时域系数取得最大值。
(4)
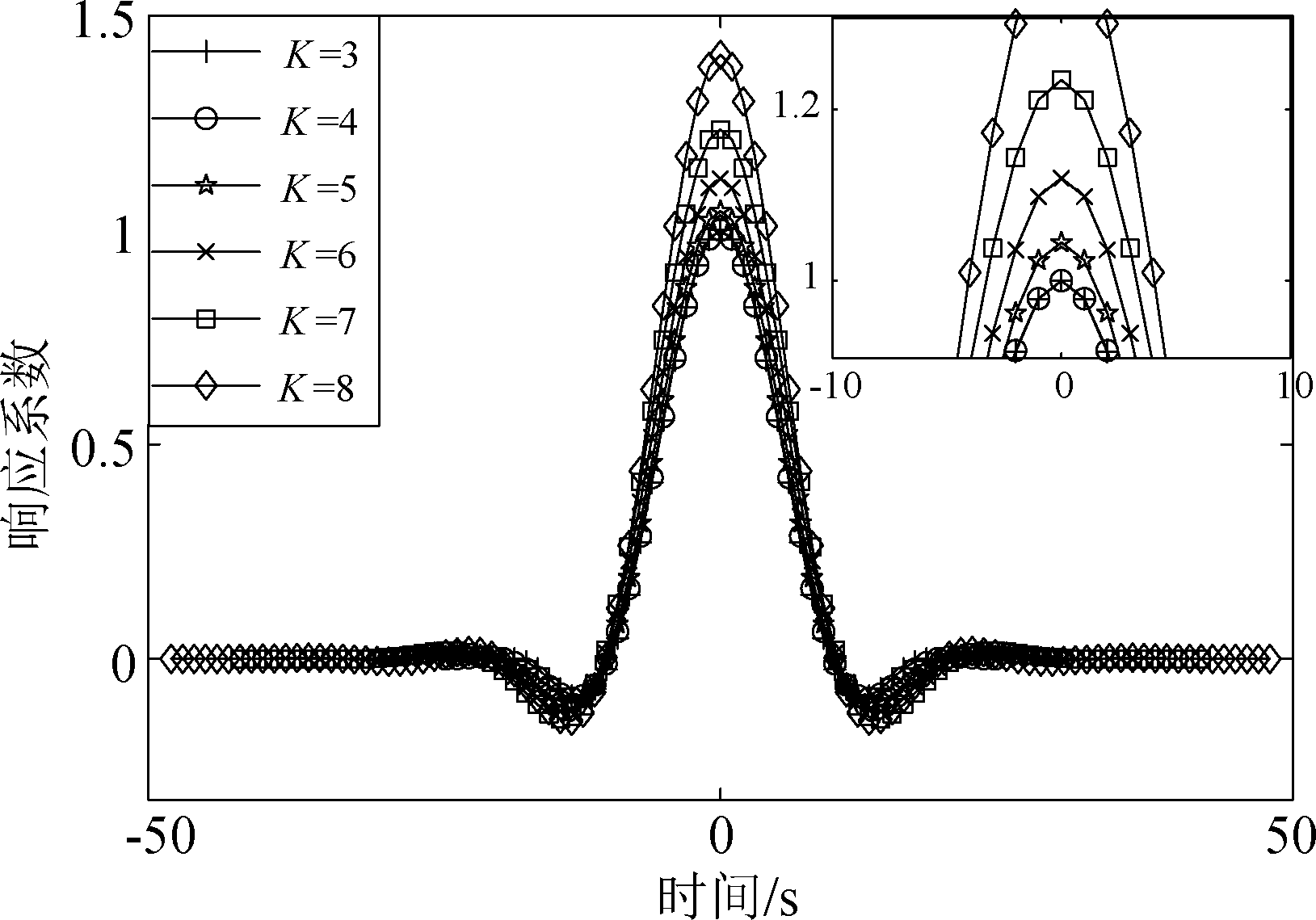
图2 不同K的时域脉冲响应
Fig.2 The time domain impulse response of different K
滤波器组可从频域和时域实现,然而频域扩展的复杂度高于时域加窗,后者能有效减小系统硬件资源开销[18]。时域加窗的实现原理是将实数符号通过离散傅里叶反变换后,再由多相网络结构展开完成时域加窗操作。当重叠因子为4时,滤波器组的多相网络实现结构如图3所示。发射机第i路载波Z域实现方式可表示为
(5)
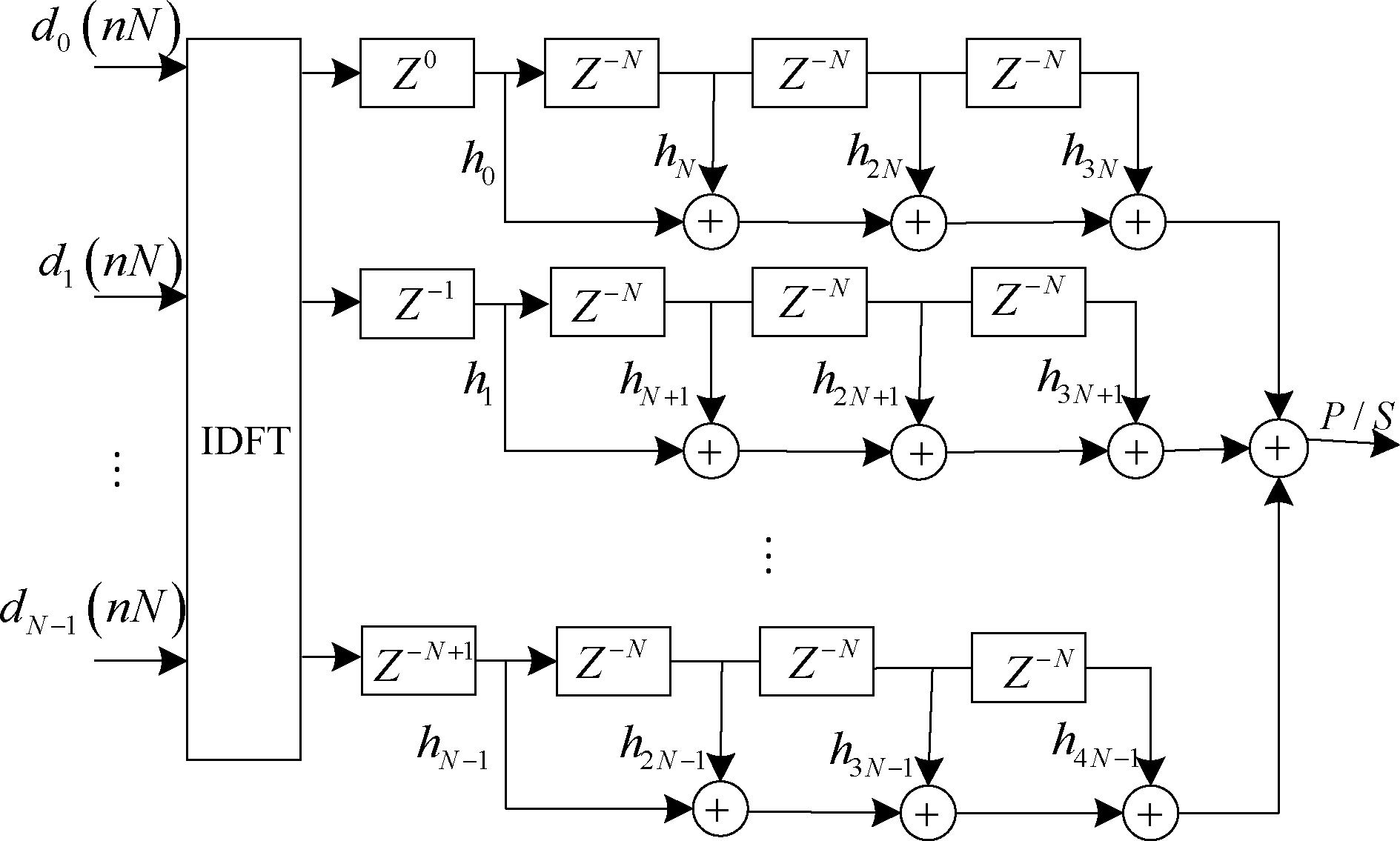
图3 IDFT-PPN结构(K=4)
Fig.3 IDFT-PPN structure(K=4)
设接收端截获的FBMC-OQAM信号经过同步后的连续带噪信号表示为
(6)
(7)
其中An表示n路子载波的幅度值,φn表示初始相位偏差,信号的符号周期用T表示,t0表示信号的起始时刻,第n路子载波频率为fn,其中fn=fc-nΔf, fc表示载波初始频率,Δf表示相邻载波间的间隔,w(t)表示均值为0,方差为σ2的窄带高斯白噪声。
3 FBMC-OQAM信号的高阶循环累积量分析
假设x(t)为随机信号,根据循环矩的原始定义知,随机信号x(t)随循环频率变化的k阶循环矩的傅里叶系数为
即:
〈x(n)x(n+τ1)…x(n+τk-1)e-j2πkαt〉t
(8)
式中:α表示循环频率,循环矩的阶数用k表示,T表示信号时间平均长度, 用τ1,τ2,…,τk-1表示固有时延,N表示平均时间内的采样数,符号n=0,1,…,N-1,符号〈·〉t表示求时间平均。设随机变量为零均值,根据循环矩定义,式(8)可得随机信号的四阶累积量为
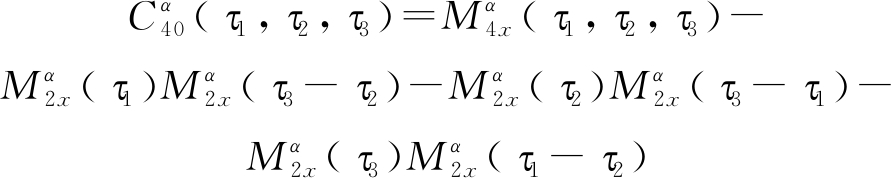
(9)
当且仅当τ1=τ2=τ3=0时,式(8)和式(9)可推导出随机信号的四阶累积量为
(10)
由于通信信号FBMC-OQAM具有随机平稳的特性[9],故本文基于高阶循环累积量分析此信号是一种有效的算法。当循环矩阶数大于二阶时高斯随机变量信号恒为零,因此截获的带高斯白噪声信号的四阶累积量仅存在s(t)信号,即
将式(6)代入式(10)可得FBMC-OQAM信号的四阶累积量为
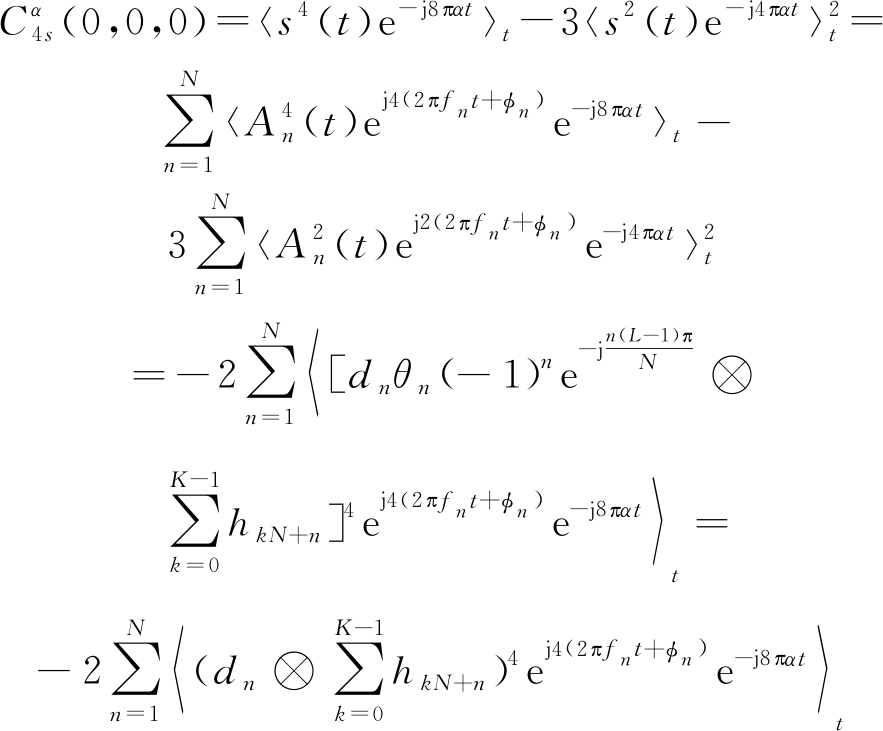
(11)
式中,⊗表示卷积运算。
根据循环累积量的性质可知,不同子载波间相互独立,因此可以分别对其中某一路子载波独立求和。根据截获信号的功率谱估计循环频率的范围,再遍历循环频率代入式(11)计算出信号的四阶累积量。
当α=fn时,由式(11)化简得第n路子载波的部分累积量为:
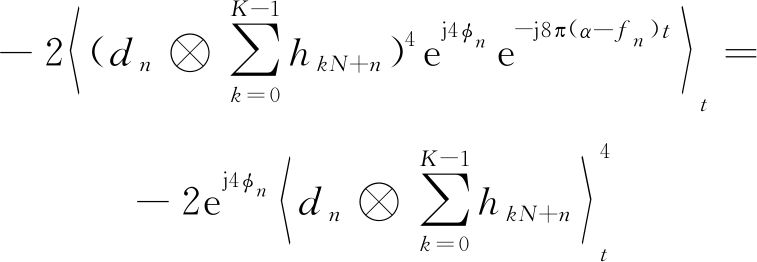
(12)
当α≠fn时,FBMC-OQAM信号的四阶累积量为
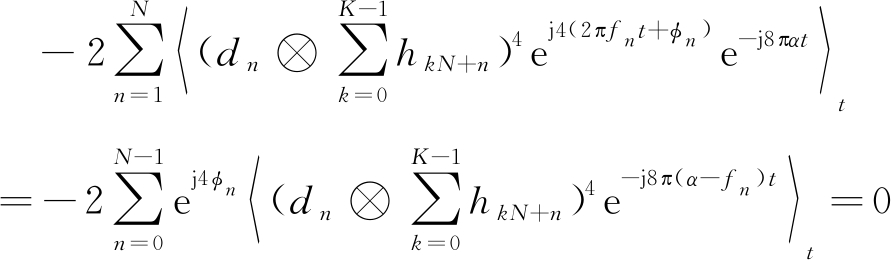
(13)
本文理论研究了方形16QAM调制方式,假设星座点等概率出现且均值为零,经过OQAM调制后实部与虚部拆分的传输符号dn∈{±1,±3,±i,±3i},综合式(12)和(13)可得FBMC-OQAM信号的四阶累积量为:
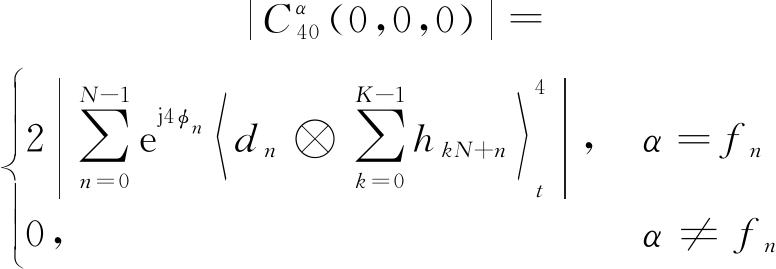
(14)
当α=fn时,仅存在调制数据符号和原型滤波器系数的代数关系;当α≠fn时,不同频率的随机序列相互独立,组合后的四阶累积量理论上等于零。由式(14)可知,四阶累积量的值与原型滤波器的响应系数相关,该系数随多相网络的结构变化而变化。当hkN+n取得最大值时,
对应取得最大值。当重叠因子为偶数时,滤波器响应系数h(0)max在α=f0处取得最大值;当重叠因子为奇数时,滤波器响应系数h(0)max在α=fN/2处取得最大值。
综上所述:FBMC-OQAM信号四阶累积量的子载波参数盲估计步骤如下:
1)先利用截获的信号功率谱频率去估计循环频率的大致范围f0≤α≤fN-1;
2)根据1)估计的循环频率代入式(14)算出信号的四阶循环累积量值并得到曲线
3)最后检测曲线峰值的位置能有效估计FBMC-OQAM信号的子载波参数。
4 仿真实验
在高斯白噪声下,验证FBMC-OQAM信号载波参数估计性能。
实验1 通过仿真分析循环频率估计FBMC信号的四阶累积量。仿真条件:用户输入的每段码元个数为3200个,载波个数12和载波间隔100 Hz,码元采用16OQAM调制方式,设重叠因子为4,子载波的初始频率2 kHz,数据采样频率8 kHz,将数据分成50段对每一段数据求和后取平均值。当SNR=2 dB、6 dB时,循环频率α与归一化四阶累积量幅值如图4所示。
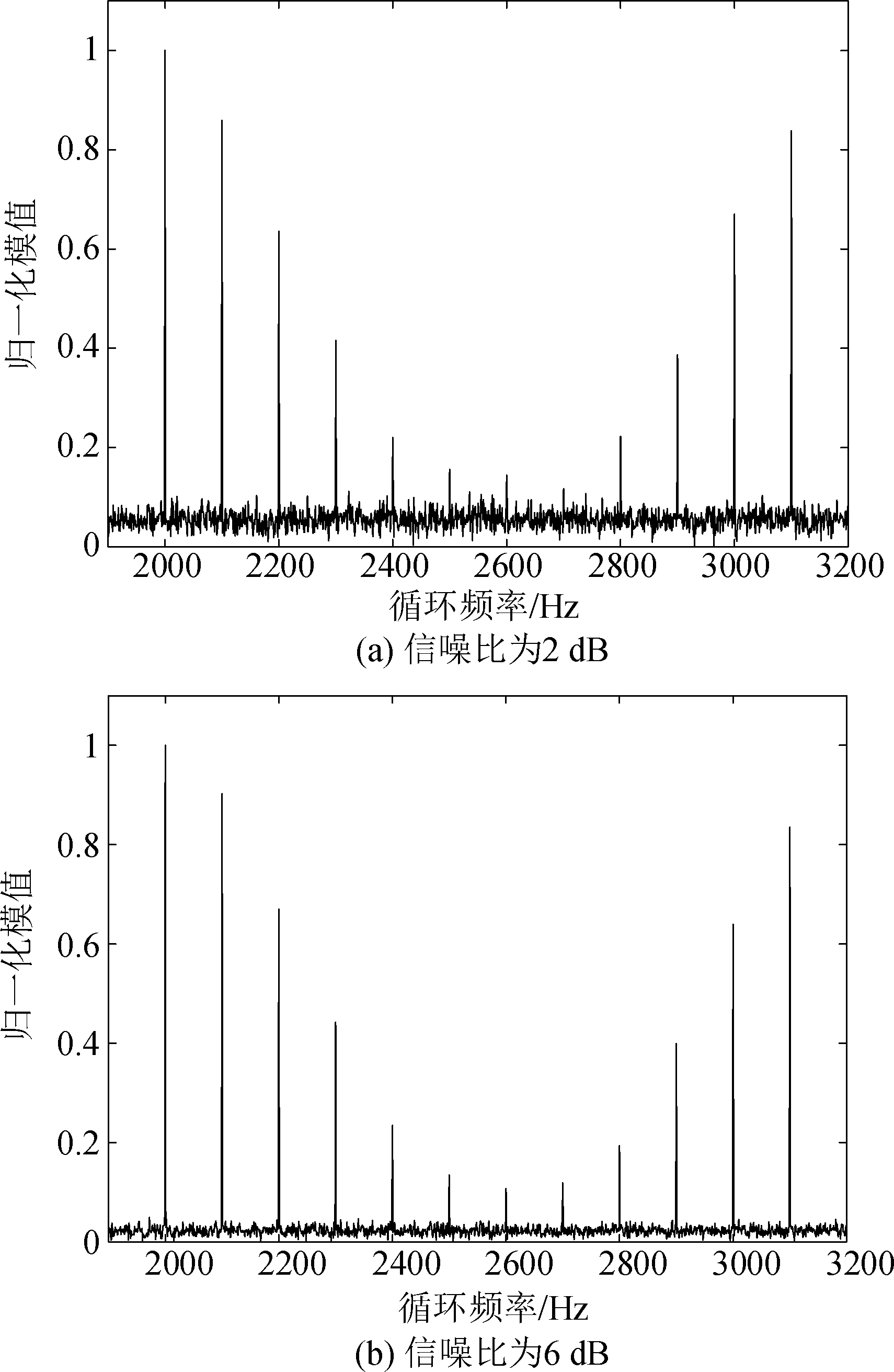
图4 不同信噪比的影响
Fig.4 Influence of different signal to noise ratios
检测
曲线峰值个数估计子载波数为12,检测相邻峰值距离估计相邻载波间隔Δf=100 Hz,峰值对应的循环频率就是载波频率,与预设的仿真条件一致。由于原型滤波器时域响应的影响,重叠因子为偶数时,四阶累积量在α=f0处值最大,导致截获信号的四阶累积量呈现凹型变化。在信噪比较大时如图4(b)可以更加清楚的检测载波参数,该实验效果与理论分析一致。
当重叠因子为奇数时,在不同重叠因子情况下对比估计载波数目和频率的影响。当信噪比SNR=4 dB时,图5(a)、(b)分别表示重叠因子为3和7的归一化四阶循环累积量,四阶累积量的最大值在循环频率中央α=fN/2=2.6 kHz处,向两边逐渐减小,随着重叠因子的增加,时域响应系数增加导致四阶累积量也增加,验证滤波器响应系数与四阶累积量的相关性。
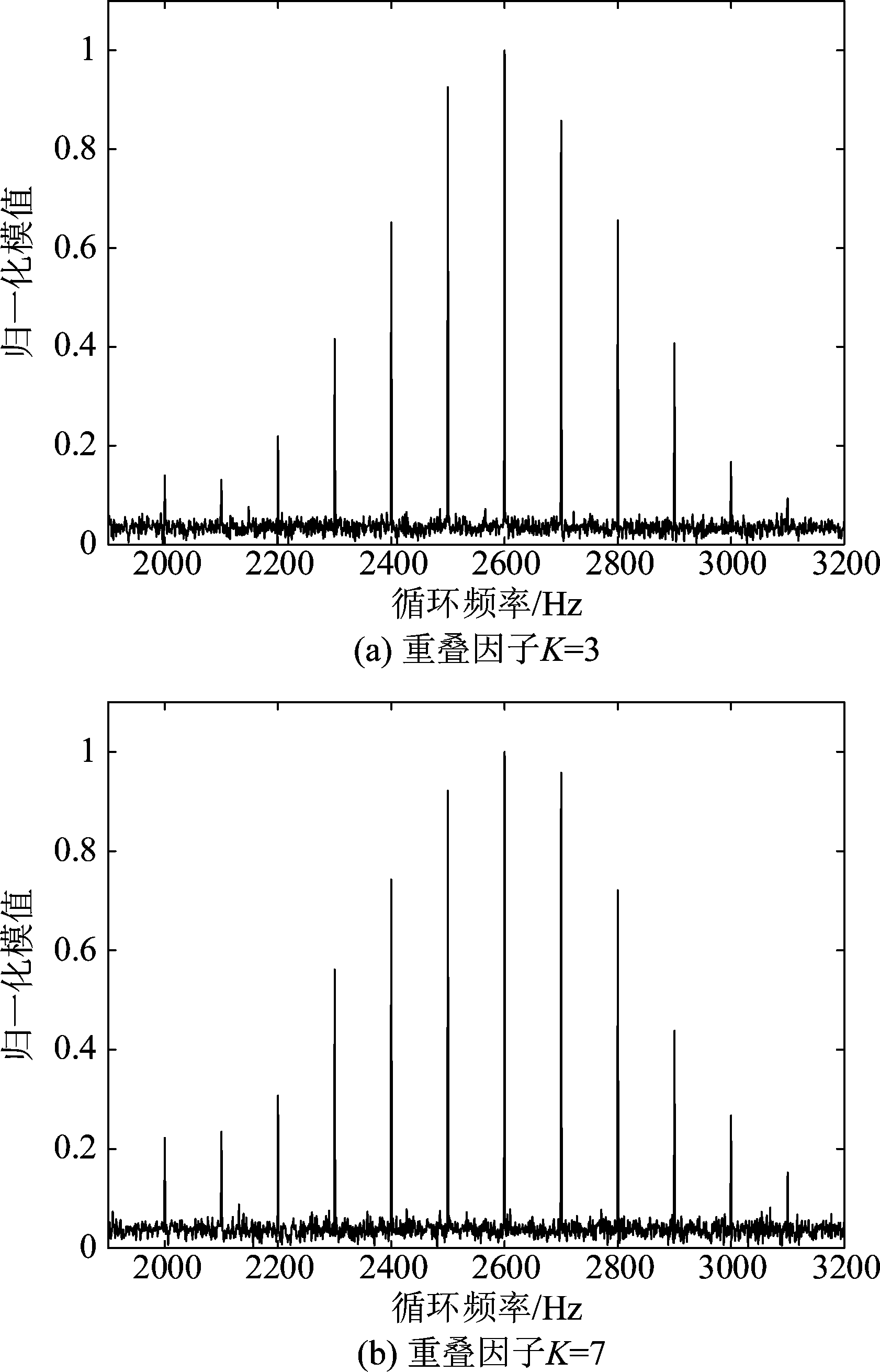
图5 重叠因子对四阶累积量的影响
Fig.5 Influence of K on fourth-order cumulants
实验2 在调制阶数、累加次数以及码元个数变化的条件下,子载波频率和数目的正确估计概率。码元符号分别采用16/64/256 OQAM的阶数调制,重叠因子为K=4,子载波数为N=12,其他仿真条件参照实验1。将截获的信息码分为20段,每段取2000个信息码累加求和取平均,蒙特卡洛实验次数为500次。
由图6可知,调制阶数对四阶累积量估计子载波参数影响并不大。当信噪比大于6.5 dB时,调制阶数不影响载波参数正确估计概率。
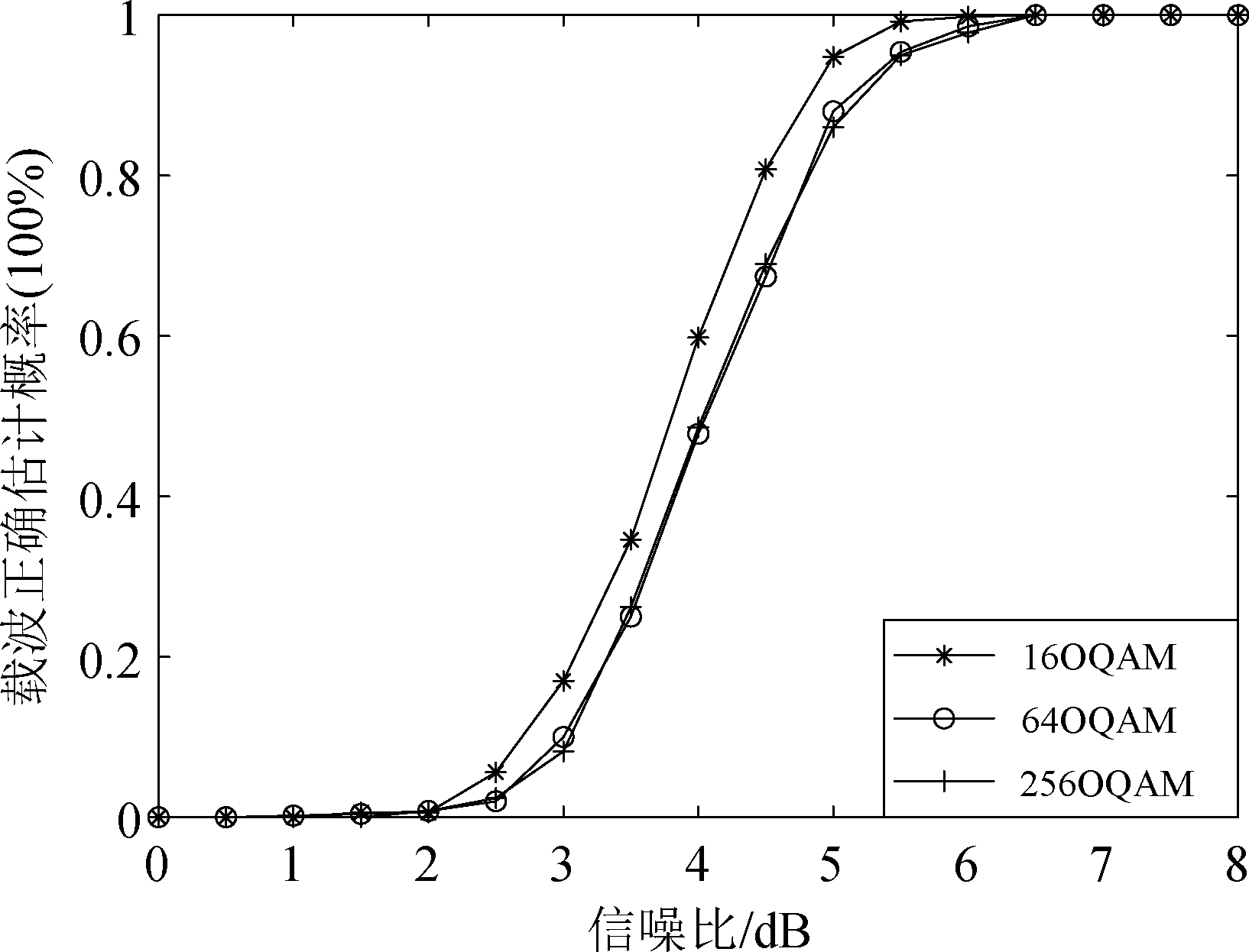
图6 不同调制阶数的载波正确估计曲线
Fig.6 Carrier accurate estimation curve with different modulation orders
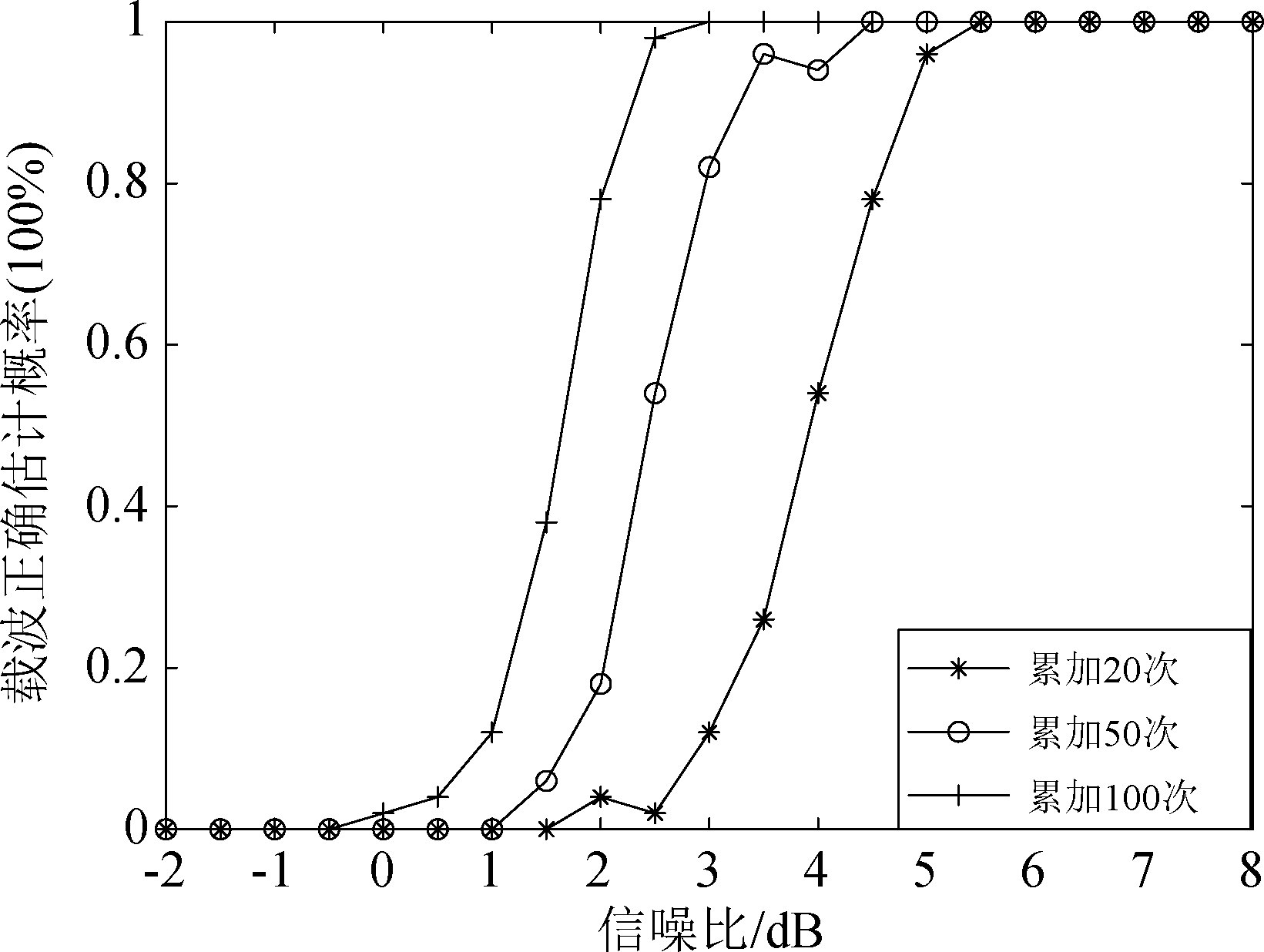
图7 不同累加次数的载波正确估计曲线
Fig.7 Carrier estimation accuracy curve under different accumulative times
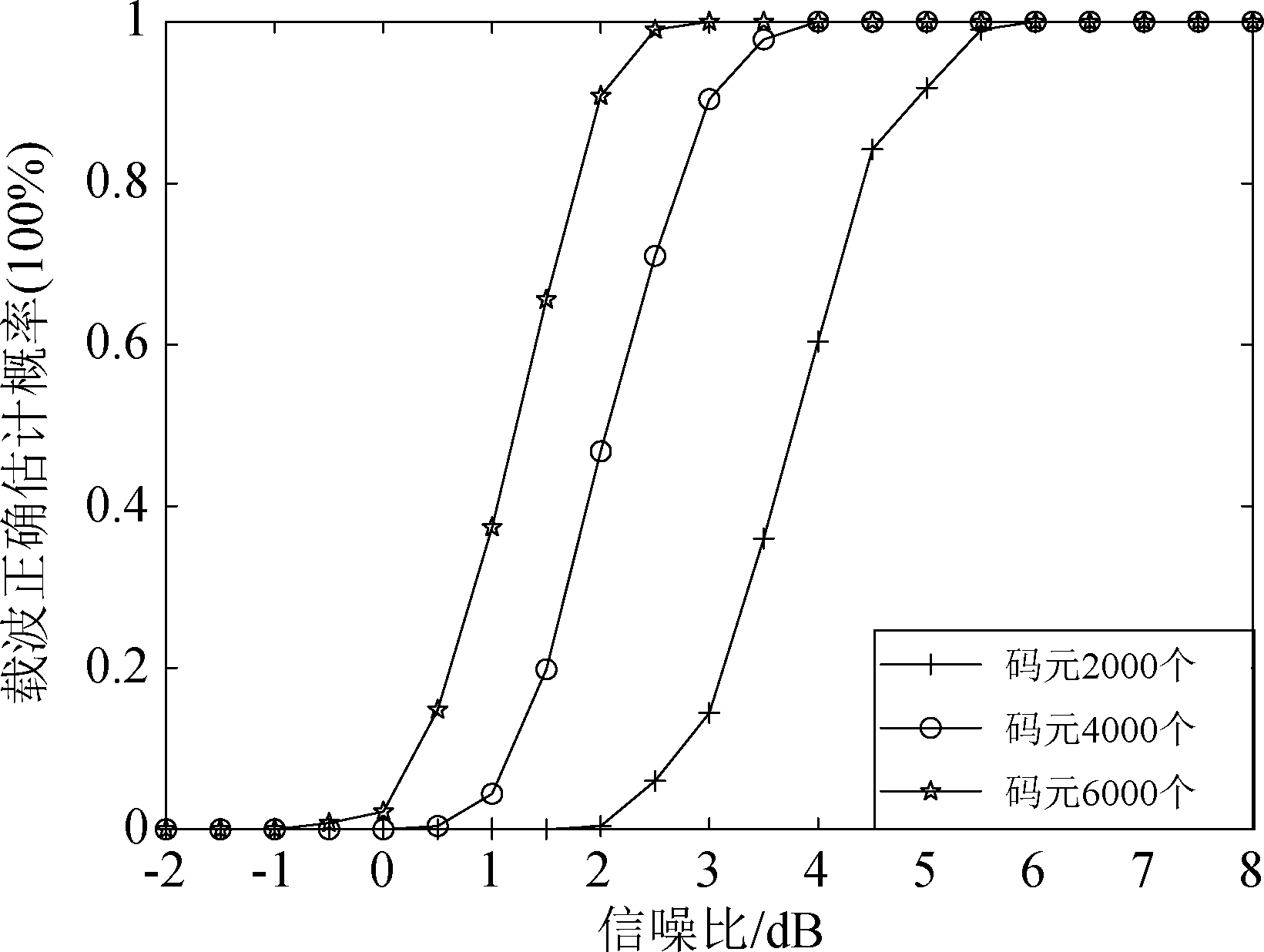
图8 码元个数估计载波正确率曲线
Fig.8 Carrier number estimation carrier correct rate curve
图7验证了累加次数对FBMC-16OQAM信号载波频率和数目估计的正确概率,被截获的信号每段包括2000个信息码元,分别累加20、50、100次求平均值来估计子载波的正确估计率,蒙特卡洛实验次数为200次。仿真图表明:累加次数越多,抗噪声性能越好,因为累加求平均值能够有效的抑制噪声对算法的影响,当累加100次时,载波参数估计在SNR≥3 dB时达100%;累加20次时SNR≥6 dB才达到100%。图8说明了码元个数对载波估计正确率的影响,码元个数分别取2000、4000、6000,采用累加20次求平均估计载波参数, 蒙特卡洛实验次数为500次。曲线表明:截获码元越多正确概率越高。
实验3 不同重叠因子下设计的原型滤波器对子载波频率和数目估计的曲线比较。仿真条件:码元采用16OQAM调制,设每段截获2000个信息码元,累加30次求四阶累积量的平均,蒙特卡洛仿真500次,其他条件参考实验1。
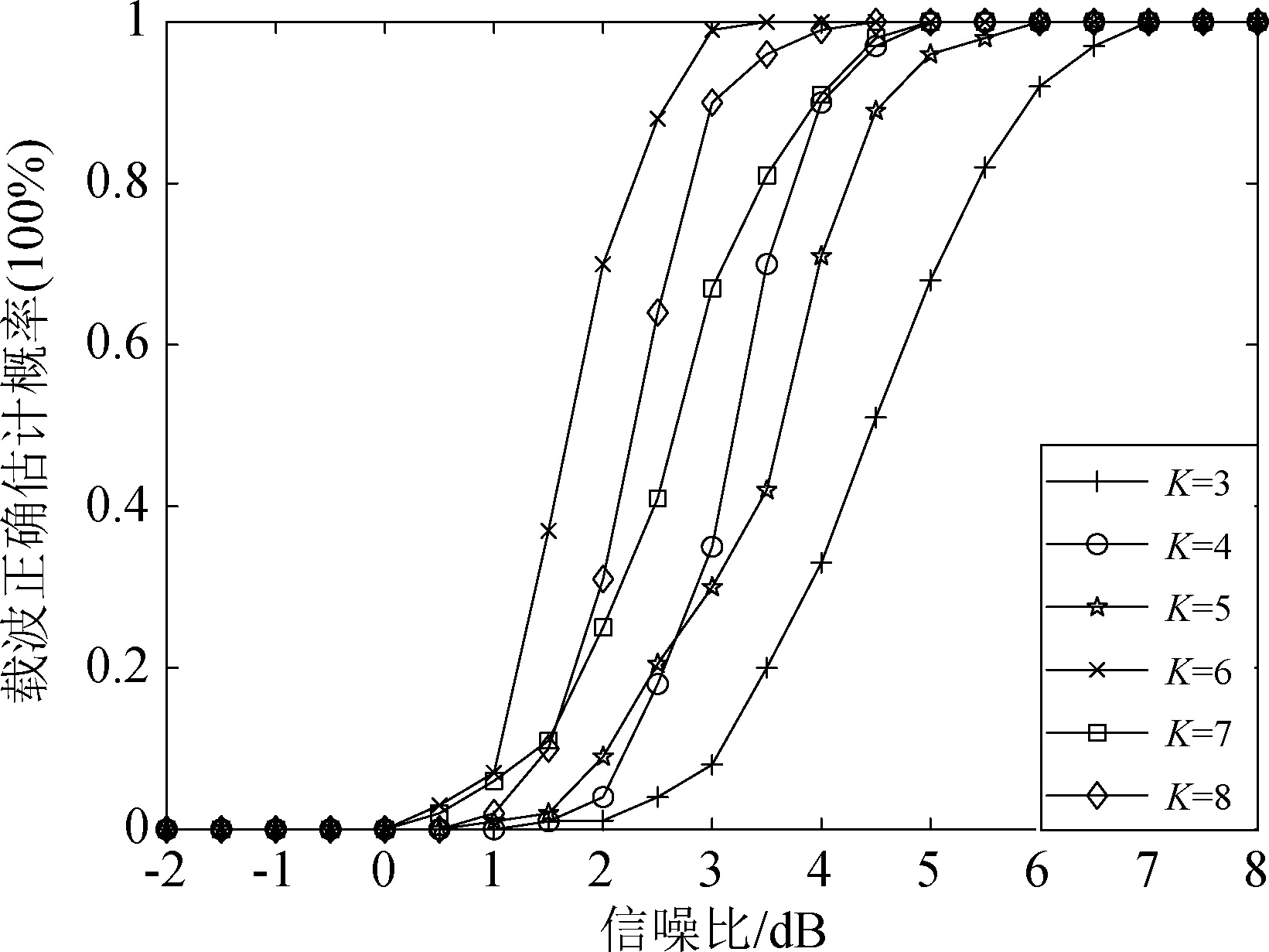
图9 不同重叠因子的载波正确估计曲线
Fig.9 Correct estimation curve of carriers with different overlapping factors
图9表明:在相同信噪比情况下,随着重叠因子的增加,四阶累积量幅值方差逐渐减小,载波正确估计概率有所上升,然而K越大滤波器组的传输符号时间越长,传输速率越低。当重叠因子为3时,SNR=7 dB时,载波正确估计概率为98%以上;当重叠因子为6或8时,载波正确估计概率在SNR=4 dB时就达到98%。
在仿真条件相同条件下,图10描述了本文载波数估计算法与文献[10]中估计算法的性能对比。在重叠因子K=4、6时,对两种估计算法的性能分析。定义估计偏差函数为均方根误差(root mean square error, RMSE) 函数,即:
为蒙特卡洛次数为500。
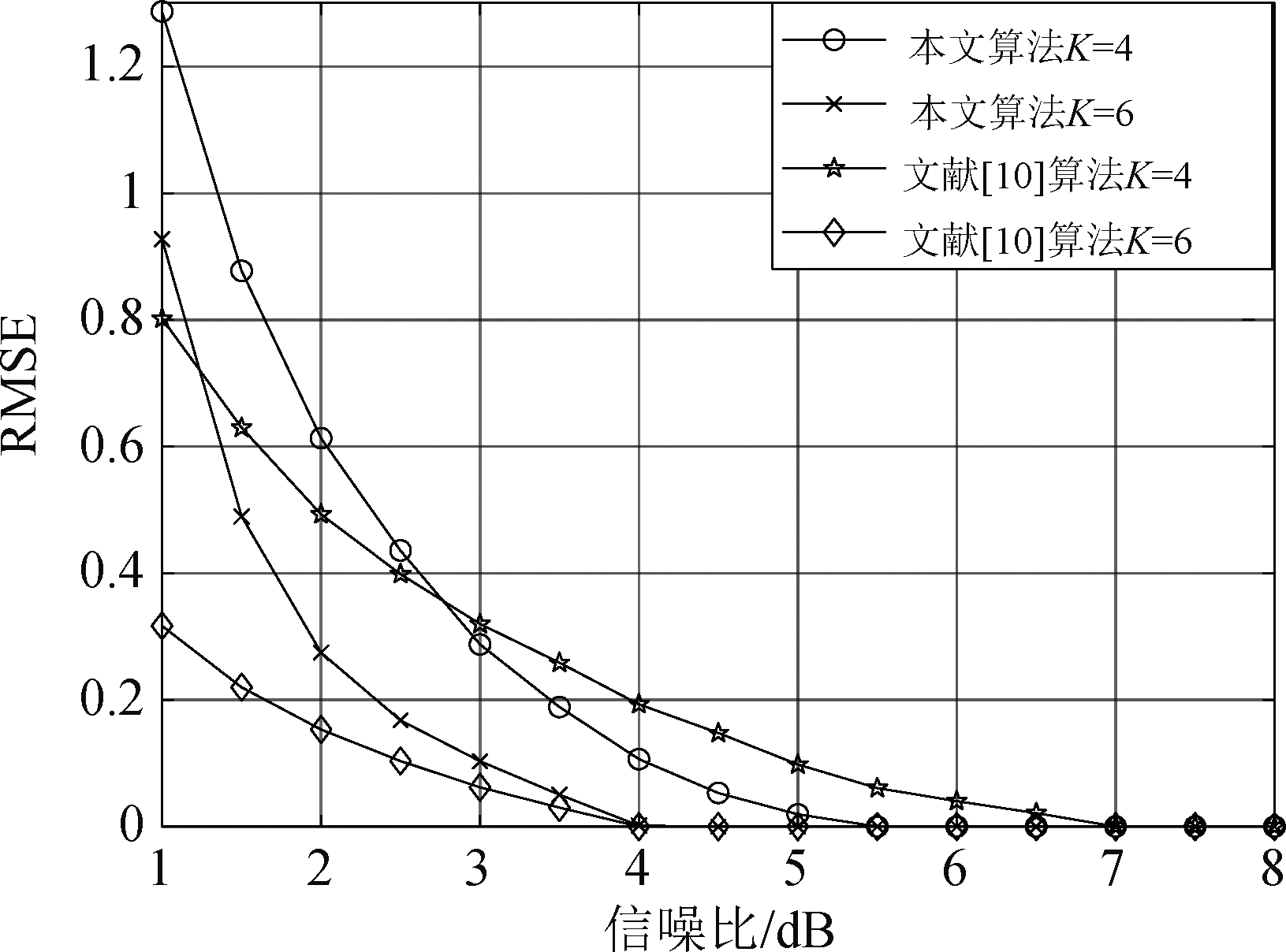
图10 载波数估计的均方根误差
Fig.10 Root mean square error of carrier number estimation
仿真结果表明:在低信噪比下,本文算法的四阶累积量最小值不易被检测,RMSE的值大于自相关矩阵算法。随着重叠因子的增加,文献[10]的算法更优于四阶累积量算法,但系统硬件要求提高了且不能有效估计载波频率。当重叠因子K为4,信噪比SNR>3 dB时,本文算法的估计偏差优于文献[10],在5.5 dB就能准确估计。针对重叠因子小和高信噪比情况下,四阶累积量估计载波数目是可行的。
5 结论
在非协作通信应用中,接收端将截获的信号后处理得到子载波参数给解调带来便利。本文运用四阶累积量方法估计FBMC-OQAM信号载波参数,理论表明FBMC-OQAM信号的四阶循环累积量与原型滤波器时域响应系数相关,通过多相网络实现滤波处理时,引起响应系数随重叠因子变化而变化。当重叠因子为偶数时,FBMC-OQAM信号的四阶累积量曲线呈凹形变化;当重叠因子为奇数时,四阶累积量曲线呈凸形变化,两种情况下均能对信号的载波频率和数目盲估计。在低信噪比下,仅能估计较大峰值的四阶累积量值确定载波参数。
[1] Ladislav P, Tomas K. Measurement and Evaluation of IQ-Imbalances in DVB-T and DVB-T2-Lite OFDM Modulators[C]∥2017 40th International Conference on Telecommunications and Signal Processing (TSP). Barcelona, Spain: IEEE, 2017: 555-558.
[2] David L, Arie R. Filter bank multi carrier modulation performance[C]∥2017 IEEE International Conference on Microwaves Antennas Communications and Electronic Systems (COMCAS). Tel-Aviv, Israel: IEEE, 2017: 1- 6.
[3] Ronald N, Stefan S, Markus R. Filter Bank Multicarrier Modulation Schemes for Future Mobile Communications[J]. IEEE Journal on Selected Areas in Communications, 2017, 35(8): 1768-1782.
[4] Banelli P, Buzzi S, Colavolpe G, et al. Modulation Formats and Waveforms for 5G Networks: Who Will Be the Heir of OFDM? An overview of alternative modulation schemes for improved spectral efficiency[J]. IEEE Signal Processing Magazine, 2014, 31(6): 80-93.
[5] Alphan S, Ismail G, Huseyin A. A Survey on Multicarrier Communications: Prototype Filters, Lattice Structures, and Implementation Aspects[J]. IEEE Communications Surveys & Tutorials, 2014, 16(3): 1312-1338.
[6] 蒋俊正, 杨玉琳, 穆亚起, 等. FBMC-OQAM中原型滤波器的快速设计[J]. 华中科技大学学报:自然科学版, 2019, 47(7): 73-78.
Jiang Junzheng, Yang Yulin, Mu Yaqi, et al. Fast Design of Prototype Filter for FBMC-OQAM[J]. Journal of Huazhong University of Science and Technology:Natural Science Edition, 2019, 47(7): 73-78.(in Chinese)
[7] David G L, Sheeba V S, Chunkath J, et al. Performance Analysis of Fast Convolution Based FBMC-OQAM system[C]∥2016 International Conference on Communication Systems and Networks (ComNet), Thiruvananthapuram, India: IEEE, 2016: 65-70.
[8] Jeremy N, Charbel A N, Amer B. Design and Evaluation of a Novel Short Prototype Filter for FBMC-OQAM Modulation[J]. IEEE Access, Mar 2018, 6(23): 19610-19625.
[9] 张天骐, 王胜, 李群, 等. 基于相关性的FBMC-OQAM信号的符号周期盲估计[J]. 系统工程与电子技术, 2019, 41(6): 1402-1407.
Zhang Tianqi, Wang Sheng, Li Qun, et al. Symbol Period Blind Estimation of FBMC-OQAM Signals Based on Correlation[J]. Systems Engineering and Electronics, 2019, 41(6): 1402-1407.(in Chinese)
[10] 张海川, 雷迎科. 一种新颖的OFDM信号子载波数估计方法[J]. 计算机应用研究, 2017, 34(1): 211-213.
Zhang Haichuan, Lei Yingke. Novel Blind Estimation Method of Number of OFDM Subcarriers[J]. Application Research of Computers, 2017, 34(1): 211-213.(in Chinese)
[11] Zhang H Y, Yuan C W. A Method for Blind Detection of OFDM Signal Based on Power Spectrum Reprocessing[C]∥Eighth ACIS International Conference on Software Engineering, Artificial Intelligence, Networking, and Parallel/Distributed Computing (SNPD 2007). Qingdao, China: IEEE, 2007: 181-186.
[12] 张政, 马金全, 王学成. 基于随机共振的微弱OFDM子载波数估计改进算法[J]. 信号处理, 2018, 34(9): 1086-1093.
Zhang Zheng, Ma Jinquan, Wang Xuecheng. An Improved Algorithm for Estimating the Number of Weak OFDM Subcarriers Based on Stochastic resonance[J]. Journal of Signal Processing, 2018, 34(9): 1086-1093.(in Chinese)
[13] 杨凯, 张天骐, 赵亮, 等. MC-CDMA信号子载波参数盲估计[J]. 计算机工程与设计, 2018, 39(2): 311-315.
Yang Kai, Zhang Tianqi, Zhao Liang, et al. Blind Estimation of Subcarrier Parameters for MC-CDMA Signal[J]. Computer Engineering and Design, 2018, 39(2): 311-315.(in Chinese)
[14] 郑文秀, 赵国庆, 罗明. 基于高阶循环累积量的OFDM子载波盲估计[J]. 电子与信息学报, 2008(2): 346-349.
Zheng Wenxiu, Zhao Guoqing, Luo Ming. Blind Estimation of OFDM Subcarrier Frequencies Based on the High-Order Cyclic Cumulants[J]. Journal of Electronics & Information Technology, 2008(2): 346-349.(in Chinese)
[15] Ari V, Tero I, Tobias H S, et al. Prototype Filter Design for Filter Bank Based Multicarrier Transmission[C]∥2009 17th European Signal Processing Conference. Glasgow, UK: IEEE, 2009: 1359-1363.
[16] Mirabbasi S, Martin K. Overlapped Complex-modulated Transmultiplexer Filters with Simplified Design and Superior Stopbands[J]. IEEE Transactions on Circuits and Systems II: Analog and Digital Signal Processing, 2003, 50(8): 456- 469.
[17] Maurice B. FBMC physical layer: A primer, PHYDYAS project[EB/OL]. http:∥www.ict-phydyas.org,Jan.2010.
[18] 罗潇景. 基于滤波器组的多载波(FBMC)调制系统的研究及实现[D]. 成都: 电子科技大学, 2016.
Luo Xiaojing. Research and implementation of optimization algorithm for modulation based on FBMC[D]. Chengdu: University of Electronic Science and Technology of China, 2016.(in Chinese)
