1 引言
在地面无线定位系统中,信号从发射机到达接收机通常有两种传播方式,一种是视距(Line-of-Sight, LOS)传播,另一种是非视距(Non-Line-of-Sight, NLOS)传播。在NLOS传播环境下如何有效克服非视距误差的不利影响从而取得较高的定位精度一直是一个难题[1]。为此,国内外学者针对抗NLOS误差定位算法开展了广泛深入研究,目前主要有残差加权法、约束最优化法和基于散射体信息法等非视距抑制算法。基于散射体信息的抗NLOS误差定位算法主要可以分为两类:一类是基于散射传播模型的定位算法。这类算法主要通过对圆环、圆盘和高斯散射模型等传播模型的研究,获得各种信号参数的统计分布特性,再对NLOS误差进行抑制来提高定位精度[2-5];另一类是基于散射体几何位置的定位算法。这类算法利用基站(Base station, BS)、移动台(Mobile station, MS) 和散射体三者之间的几何位置关系,建立某种模型以减小NLOS误差的影响从而提高定位精度。例如使用单基站进行定位时,先通过定位单次散射体,然后将其作为虚拟基站,再使用多基站定位算法对移动台进行定位[6-7];或者利用散射体的相关信息,将NLOS问题转化为LOS问题,再使用LOS下的相关算法进行定位[8-10]。
但是,现有研究在NLOS环境中一般假定信号仅经过一次散射,较少考虑甚至完全忽略了可能存在的二次以上多次散射的情况,因此在实际应用环境中必然造成算法性能下降。目前仅出现一种基于移动台可能位置线(Line of Possible Mobile Device, LPMD)的算法[11-12]对NLOS环境中的单次与多次散射路径进行了识别,但识别性能在宏蜂窝环境下比较有限。
目前有少量针对LOS和NLOS传播路径进行识别的研究[13-15],还鲜有文献研究NLOS环境中如何区分、识别单次与二次以上散射路径信号,通过先识别、定位单次散射体,再将其作为虚拟基站以进一步提升算法定位性能。为此,借鉴文献[15]识别LOS和NLOS传播路径的基本思想,本文参考单次散射圆环模型首次构建了一种二次散射圆环模型,对其二次散射信号统计特征进行分析,再根据单次和二次这两种散射信号统计特征的差别,基于信号统计检测理论对单次散射路径和二次散射路径进行区分识别。仅将识别出的单次散射路径及单次散射体的相关信息与诸如文献[8-10]的基于散射体信息的NLOS定位算法结合使用,将有利于提高NLOS环境下的定位精度。
2 单次与二次散射圆环模型
NLOS环境中,信号在移动台和基站之间传播时可能会经过一次或多次散射,散射体通常会以一定的特征分布在移动台周围,目前宏蜂窝环境下主要的散射体信道模型有单次散射条件下的圆环散射模型(Risk of Scatter, ROS)和圆盘散射模型(Disk of Scatter, DOS)。为此,本文参考单次散射圆环模型建立一种二次散射圆环模型,并应用到后续的单次与二次散射信号检测中。
2.1 单次散射圆环模型
ROS圆环散射模型如下图所示。
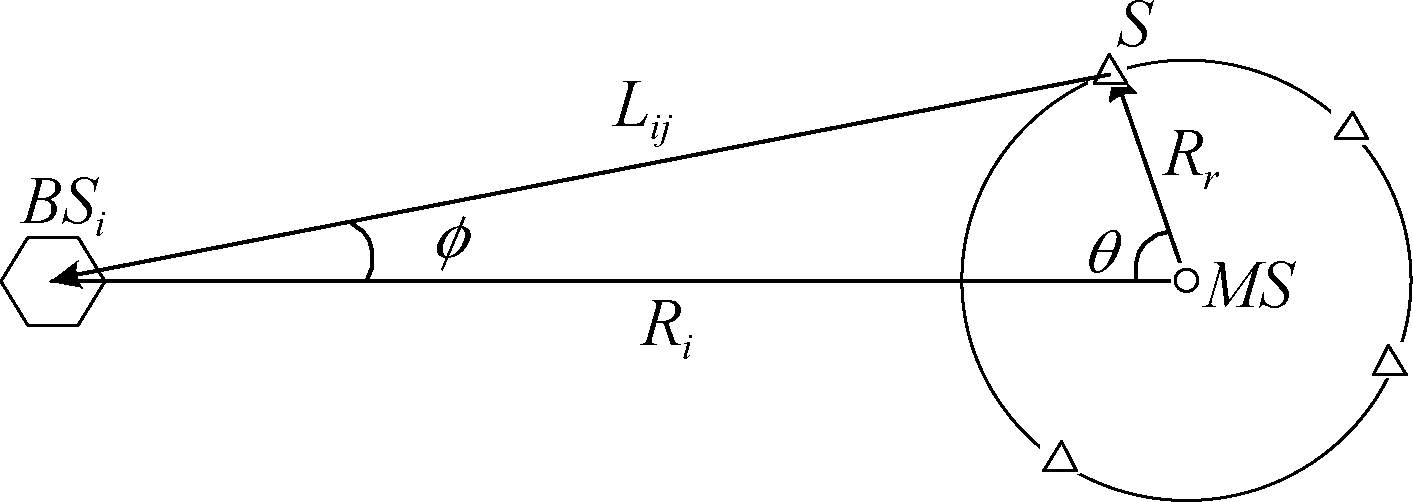
图1 单次散射圆环模型示意图
Fig.1 Schematic diagram of a single scattering ring model
ROS模型中,假定散射体均匀分布在移动站周围半径为Rr的圆环上,θ角服从[0,2π]上的均匀分布。设移动站与第i个基站的视距距离为Ri,基站与移动站之间第j条多径分量的距离为Lij,NLOS误差为ηij=Lij-Ri,可以得到该NLOS测量值的概率密度函数[16]:
(1)
其中
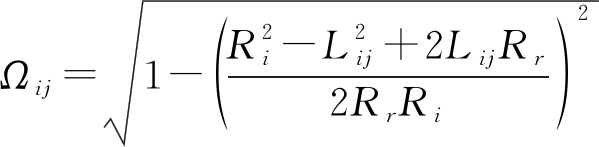
(2)
将Lij=ηij+Rr代入式(1),可得NLOS误差ηij的概率密度函数:
(3)
其中
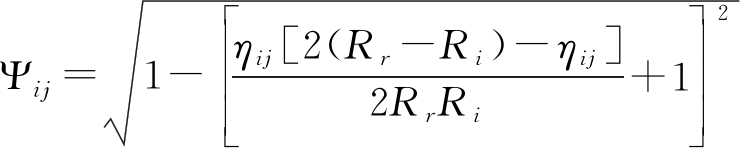
(4)
2.2 二次散射圆环模型
为了更全面地考虑NLOS环境下的信号二次散射问题,本文以单次ROS模型[17]上的每个散射体分别为第二个散射圆环的圆心,然后在此基础上分别再构建一个圆环模型,形成二次散射圆环模型,如图2所示。其中散射体S1、S2分别随机均匀分布在半径为R1、R2的两个圆环上,S2与S1的距离为R2,由此S2将存在于以R1-R2与R1+R2为半径构成的环形区域内,即图中两个虚线所绘的圆环之间。

图2 二次散射圆环模型示意图
Fig.2 Schematic diagram of the secondary scattering ring model
在二次散射模型中,信号从移动台经散射体S1散射,再经散射体S2散射,最终到达基站。假设移动台与第i个基站的视距距离为Ri,散射体S1到基站的LOS距离为mi,散射体S2到基站的LOS距离为hi,散射角θ和α均服从[0,2π]上的均匀分布。
移动台发出的信号经S1散射然后到达基站的传播过程可以视作第一次散射过程。信号从S1处开始,经S2散射,然后到达基站的传播过程可以视作第二次散射过程。信号由移动台出发,经S1、S2散射体再到基站的信号传播过程可以视作二次散射过程。上述三个过程对应的第j条多径分量造成的NLOS误差分别为ηij1、ηij2和ηij。从图2中可知:
ηij1=mi+R1-Ri
(5)
ηij2=hi+R2-mi
(6)
ηij=hi+R1+R2-Ri
(7)
由上式可以推出二次散射的非视距误差为
ηij=ηij1+ηij2
(8)
在式(3)基础上,假设第一次散射与第二次散射的NLOS误差概率密度函数分别为pROS(ηij1)和pROS(ηij2),由于第一次散射与第二次散射过程是相互统计独立的,因此pROS(ηij1)和pROS(ηij2)可以分别作为第一次散射和第二次散射的边缘概率密度,在式(8)的基础上,对二者求解联合概率密度,即可得到二次散射圆环NLOS误差概率密度函数为
(9)
2.3 单次与二次散射路径检测模型
假定进行检测时N次NLOS测量值均服从独立同分布,在检测时间内,MS位置没有发生变化。根据上述单次和二次散射圆环模型下NLOS距离测量值的组成分析,可将其表示为以下假设检验:
(10)
其中H0、H1分别是单次散射和二次散射的假设,ri为第i次系统测量值,d为基站与移动台的LOS距离,nS、nD分别为单次、二次散射的NLOS误差,ni为测量噪声。
若已知检测模型中单次散射NLOS误差、二次散射NLOS误差以及测量噪声的统计特性,即可以使用信号统计检测理论进行单次与二次散射路径的检测。假设测量噪声服从N(0,σ2),单次散射NLOS误差服从![]() 二次散射NLOS误差服从
二次散射NLOS误差服从![]() 则检测模型的条件假设的概率密度函数分别为:
则检测模型的条件假设的概率密度函数分别为:
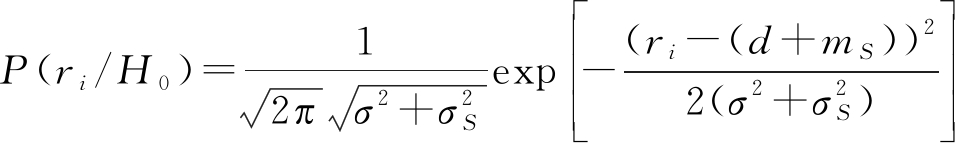
(11)
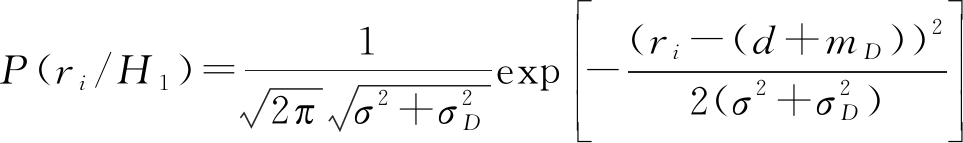
(12)
3 散射路径检测算法
本文中单次与二次散射路径的检测识别问题可转化为信号统计检测理论中带确定性参数的复合假设检验。根据对NLOS传播环境中产生单次及二次散射的先验概率P(H0)和P(H1)的了解程度,可将检测问题分为先验概率已知和未知两种情况分别讨论。
3.1 先验概率已知
在一些特定的NLOS传播环境中,如果能基于测试估计出先验概率P(H0)和P(H1),并且希望使用确定性参数进行复合假设检验,可以使用广义似然比检验进行门限判决。广义似然比检验是一种相对于经典似然比检验使用场景更加广泛的似然比检验,下面将给出先验概率已知情况下信号检测算法的设计和分析。
在N次测量值统计独立的情况下,单次散射与二次散射假设下观测距离矢量r的概率密度函数分别为:
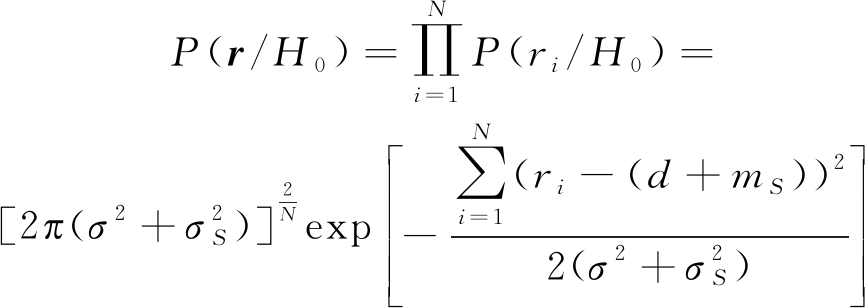
(13)
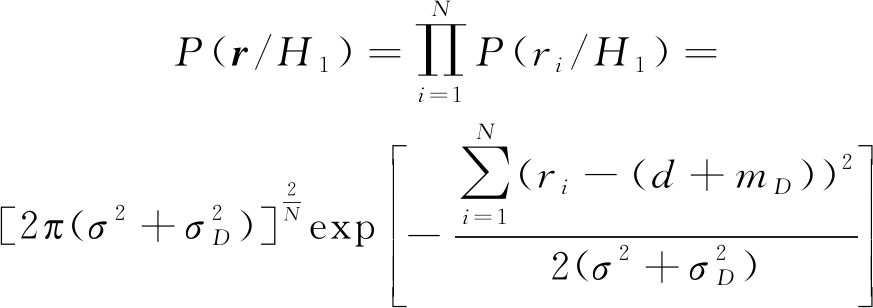
(14)
因此,广义似然比检验可以表示为:
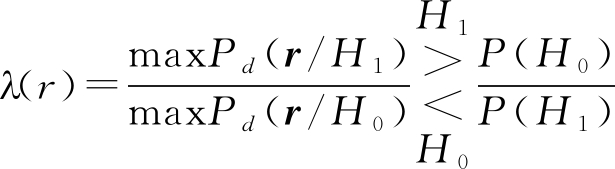
(15)
对上式中的分子和分母分别采用极大似然估计方法求d的最大值,可分别得到
(16)
(17)
带入式(15)化简可得广义似然比检验为:
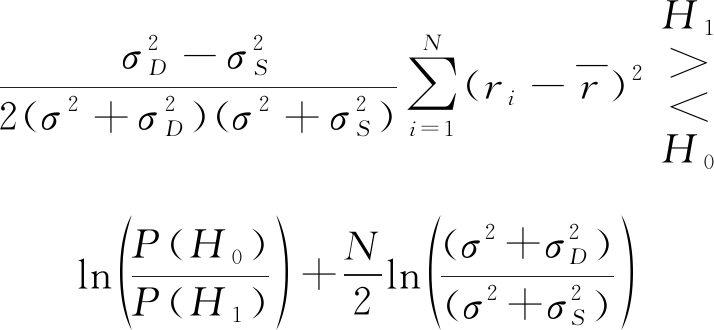
(18)
其中
(19)
3.2 先验概率未知
在实际NLOS传播环境中,一般难以确知两种先验概率。在未知先验概率的情况下,我们可以使用虚警概率作为检测指标,采用奈曼皮尔逊准则来对单次散射路径与二次散射路径进行检测。
在式(18)的基础上进行变换,可得到判决表达式:
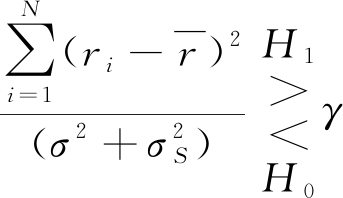
(20)
其中

(21)
由于在先验概率未知情况下,P(H0)和P(H1)未知,因此可将整个表达式用γ表示,作为待求判决门限值。
根据奈曼皮尔逊准则,判决门限γ可以表示为:
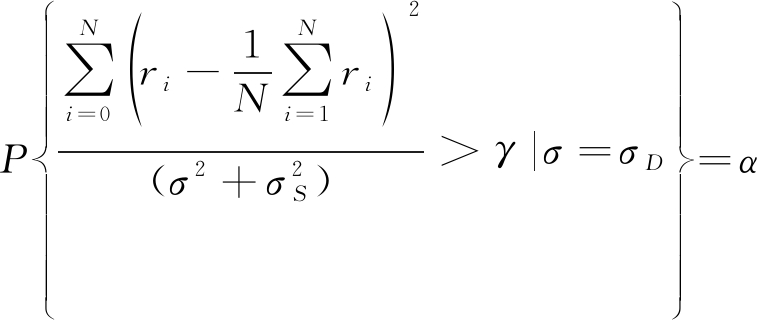
(22)
其中α为检测的虚警概率,可独立于测量值设置。由概率统计理论可知,在统计量的样本数量为N,统计量的自由度为N-1情况下,式(20)左侧服从自由度为N-1的χ2卡方分布,可以通过下式求得判决门限γ:
(23)
3.3 算法主要步骤和流程图
本文中单次与二次散射路径检测算法主要分为以下几步。首先,根据不同地理环境,预先评估本次检测中是否已知单次与二次散射的先验概率。当先验概率已知时,通过广义似然比检验完成对单次与二次散射路径的识别;当先验概率未知时,基于假定的虚警概率,通过奈曼皮尔逊准则完成对单次与二次散射路径的识别。算法流程图如图3所示。
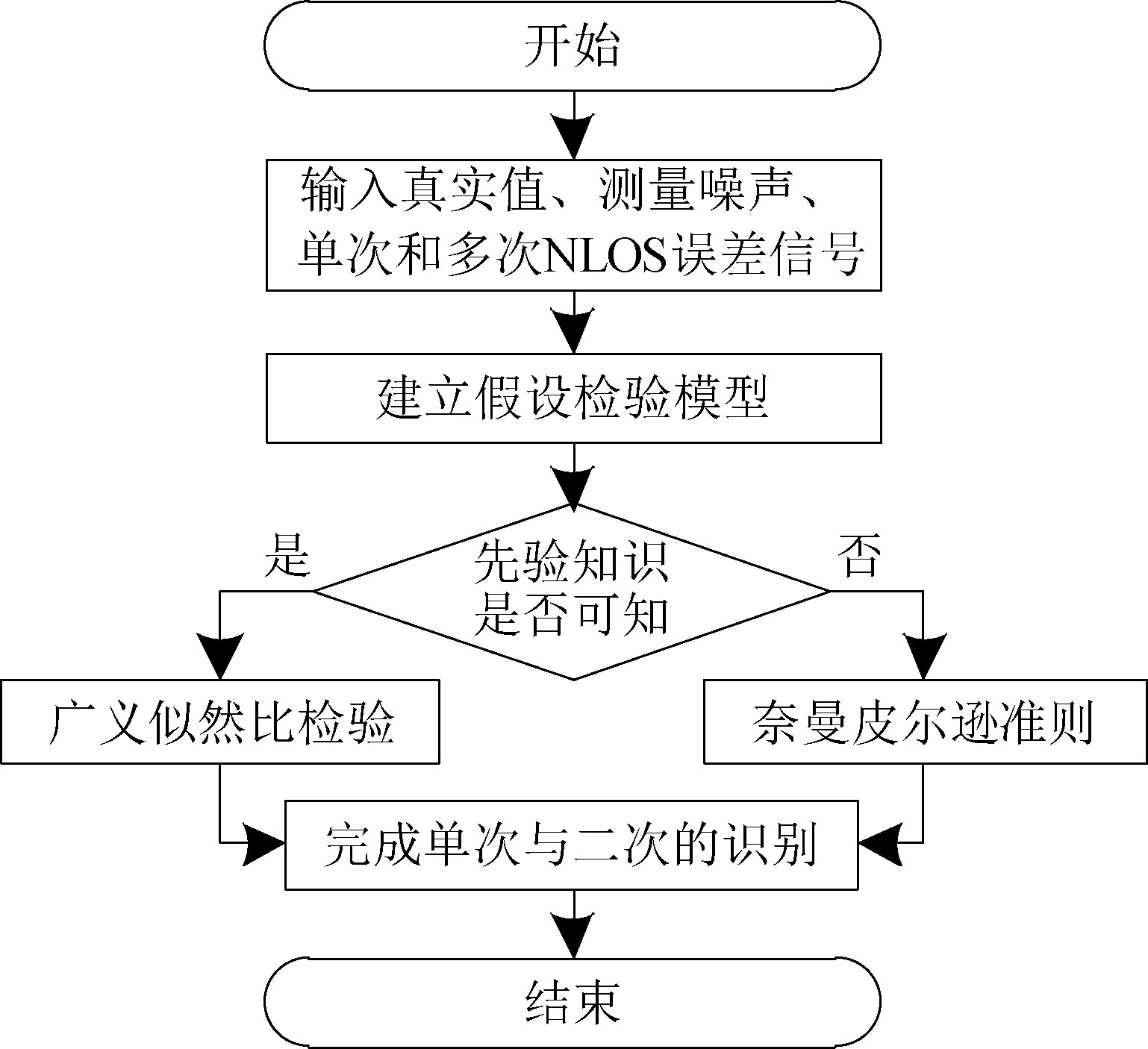
图3 算法流程图
Fig.3 Algorithm flow graph
4 算法仿真与分析
本文参考Nokia公司现场测量数据,对检测算法性能进行仿真分析。根据文献[18-20]和Nokia公司的测量结果,在各基站间距离约为5000 m,基站与移动台相距约2500 m的情况下,其测量噪声和NLOS环境下的统计特性均服从高斯分布,其中测量噪声服从均值为0 m,标准差为150 m的高斯分布,NLOS误差信号服从均值为513 m,标准差为409 m的高斯分布。本节将参照以上场景进行仿真,测量噪声服从N(0,σ2),其中σ=150。假设第一个圆环散射半径为530 m,可以通过单次散射圆环模型得到信号经过单次散射的NLOS误差服从![]() 其中mS=557,σS=373,与Nokia公司测量数据的统计特性相接近。在此基础上假设第二个圆环散射半径为500 m,并可以通过二次散射圆环模型得到信号经过两次散射后的NLOS误差服从
其中mS=557,σS=373,与Nokia公司测量数据的统计特性相接近。在此基础上假设第二个圆环散射半径为500 m,并可以通过二次散射圆环模型得到信号经过两次散射后的NLOS误差服从![]() 以上均为先验概率已知和未知两种情况的仿真场景,本节最后将给出LPMD算法与信号检测算法的仿真场景及对比分析。
以上均为先验概率已知和未知两种情况的仿真场景,本节最后将给出LPMD算法与信号检测算法的仿真场景及对比分析。
(1)先验概率已知
第一个仿真场景是在先验概率已知的情况下,算法对单次散射信号与二次散射信号测量值进行检测识别。图4给出了当先验概率为P(H0)=0.5,P(H1)=0.5时,信号检测算法对单次与二次散射信号测量值的识别结果,其中横轴为测量次数,纵轴为式(18)中的计算结果。图5则给出了当P(H0)=0.8,P(H1)=0.2时,P(H0)=0.5,P(H1)=0.5时以及P(H0)=0.2,P(H1)=0.8时,信号检测算法的识别率随测量次数的变化情况。
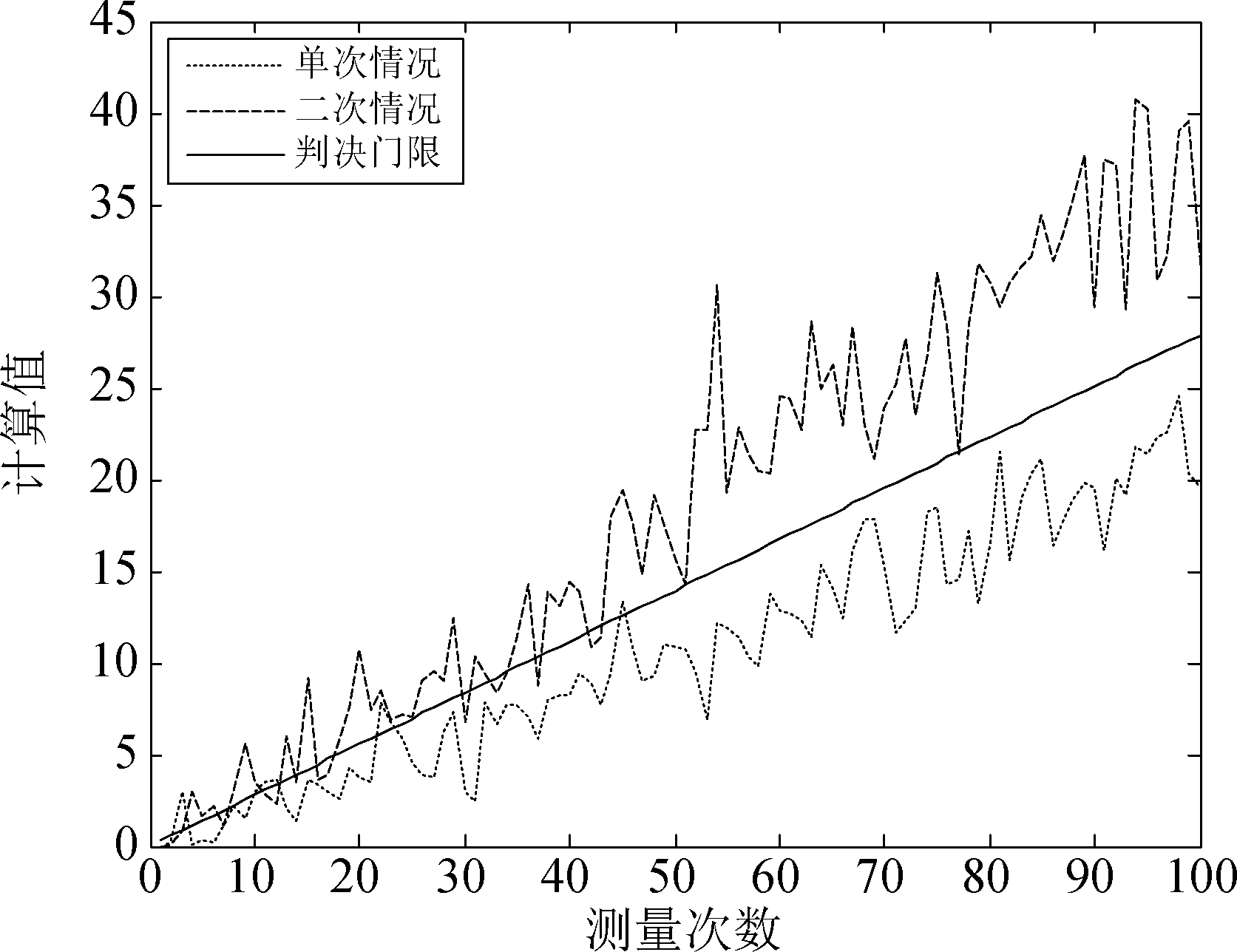
图4 单次与二次散射先验概率相等时信号检测算法的识别结果
Fig.4 Recognition results of signal detection algorithm when single and second scattering prior probabilities are equal
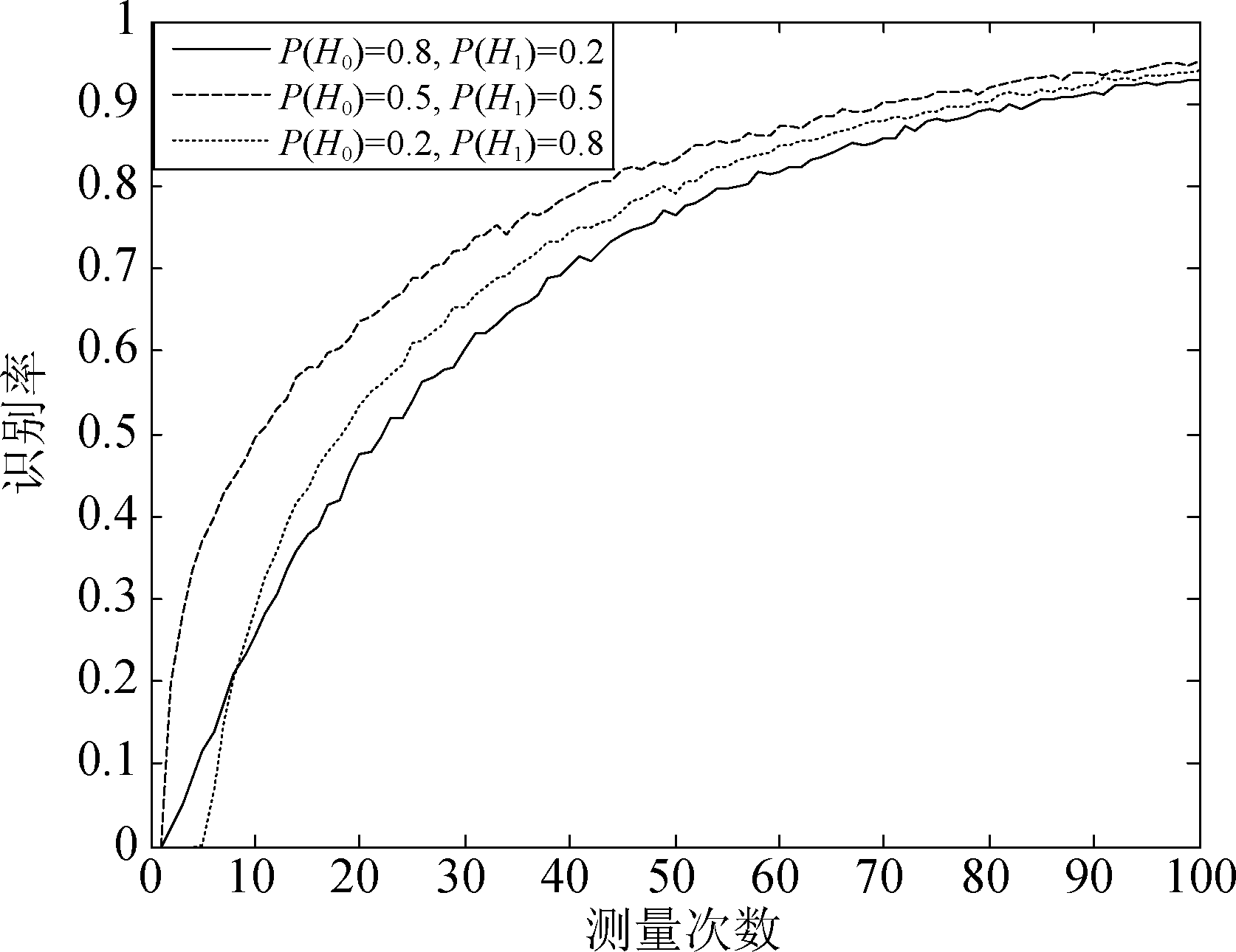
图5 不同先验概率下信号检测算法的识别率
Fig.5 Recognition rate of signal detection algorithm under different prior probabilities
由图4可知,在单次散射路径与二次散射路径概率相近的情况下,算法求得的门限值位于单次散射计算值和二次散射计算值之间,且与二者均保持着一定的距离,测量次数接近50次即可进行准确识别。由图5可知,在三种不同先验概率下,单次散射信号与二次散射信号比例相近时识别效果最好,而当仅有单次散射信号或者仅有二次散射信号在系统环境占据主导地位时,其统计检测量会分别向判决门限靠近而导致漏警概率或虚警概率增大,从而使得识别率下降。在上述情况中,算法在测量次数较少的情况下,会存在一定的误判概率,这是因为测量数据过少而使得算法不稳定。随着测量次数的增加,算法识别性能趋于稳定,单次和二次散射信号检测统计量与判决门限的距离随之增大,识别效果也更好。
(2)先验概率未知
第二个仿真场景是在先验概率未知的情况下,预先设置系统的虚警概率,然后对单次散射信号与二次散射信号测量值进行检测识别。图6是在虚警概率α=0.1时的仿真结果,其中横轴为测量次数,纵轴为式(20)中的计算结果。图7则给出了在虚警概率分别为α=0.2、α=0.1和α=0.05时,信号检测算法的识别率随测量次数的变化情况。
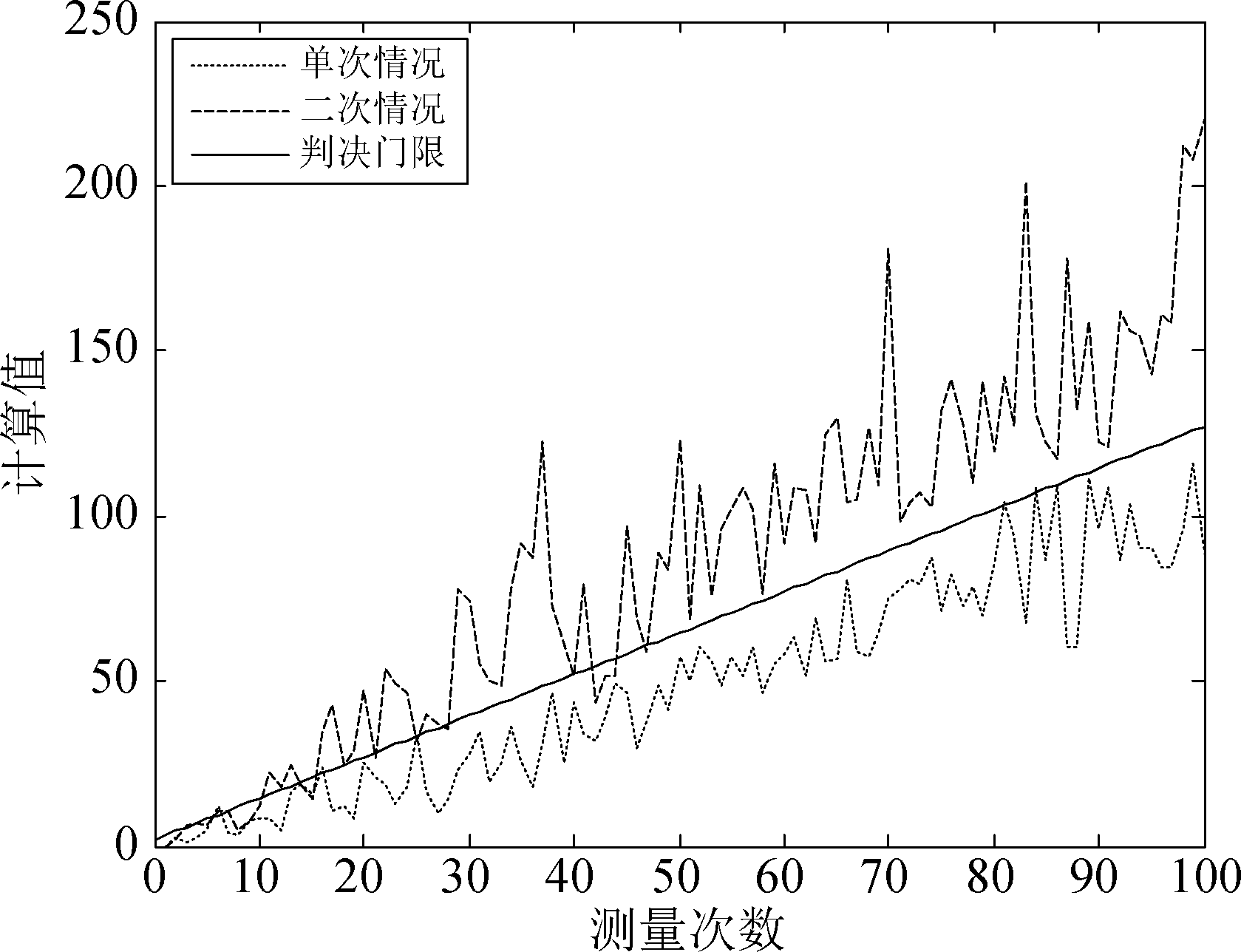
图6 虚警概率为0.1时信号检测算法的识别结果
Fig.6 Recognition result of signal detection algorithm when false alarm probability is 0.1

图7 不同虚警概率下信号检测算法的识别率
Fig.7 Recognition rate of signal detection algorithm under different false alarm probabilities
从图6可知,单次散射信号检测统计量和二次散射信号检测统计量均与门限值保持着一定的距离,算法在预设的虚警概率下能较好地区分单次散射与二次散射路径。由图7可知,在测量次数较大时,随着虚警概率的减小,算法的检测性能也有所增加。在测量次数较少的情况下,算法同样存在不稳定的情况,不过随着测量次数的增加,单次和二次散射的检测统计量与判决门限的距离随之拉大,识别效果也越好。因此,在先验概率未知的情况下,该算法同样具有良好的单次与二次散射信号检测识别性能。
(3) LPMD算法与信号检测算法性能比较
本次仿真将对LPMD算法与本文信号检测识别算法进行对比分析。仿真中假设单次散射概率与二次散射概率相等,散射半径依次增大。即在LPMD算法仿真中,单次散射与二次散射路径数相等,散射体服从ROS圆环散射,半径依次增大。在信号检测算法仿真中,假设P(H0)=0.5,P(H1)=0.5,两个圆环半径之和与前者保持相等,且保持相同比例,取测量次数为50次。算法均独立仿真1000次。图8分别给出了两种识别算法的虚警概率、漏警概率和正确识别率。
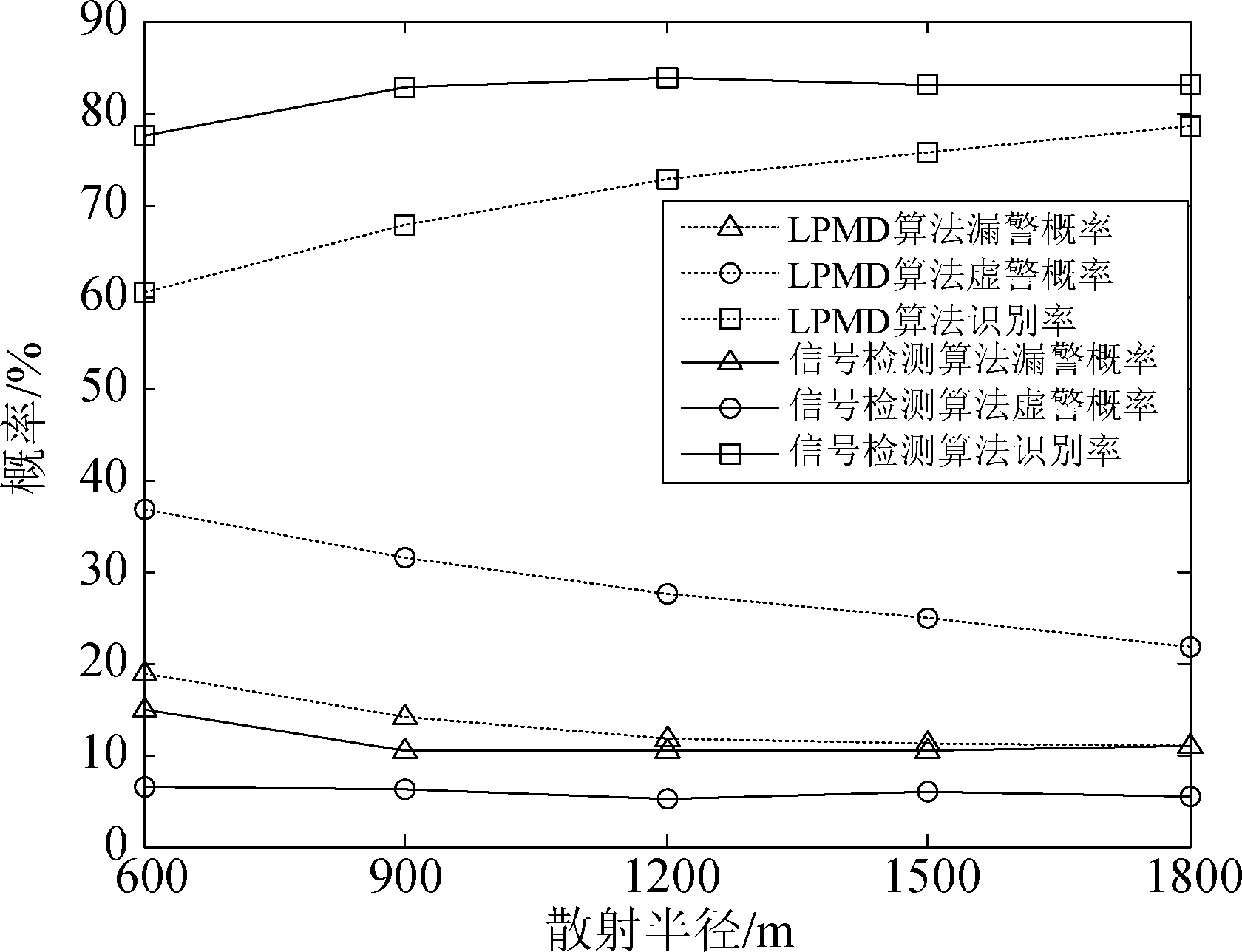
图8 LPMD算法与信号检测算法的识别性能比较
Fig.8 Comparison of recognition performance between LPMD algorithm and signal detection algorithm
从图8中可以看出,随着散射半径的增加,基于LPMD的识别算法和基于信号检测的识别算法的识别率均随之增加,虚警概率和漏警概率均随之减少,且后者相较于前者在识别率上有所提升,而虚警概率和漏警概率有所下降。因此,在一定的测量次数下,相对于传统的LPMD识别算法,信号检测算法具有更好的识别效果。
5 结论
本文针对传统NLOS散射模型中忽略多次散射路径,将多径散射简化而统一看作单次散射这一问题,建立了一种基于ROS的二次散射模型,并提出一种信号统计检测算法,基于是否已知先验概率对单次与二次散射路径进行识别,甄别出产生单次散射路径的散射体,为单次散射体定位打下良好基础。
从仿真结果可见,无论先验概率是否已知,基于信号检测的单次与二次散射信号的识别算法均具有良好的识别性能,并且随着测量次数的增加,算法趋于稳定,检测性能也越来越高。需要注意的是,算法中对于测量次数的取值不宜过小或过大,过小会由于测量数据太少而导致误判概率增大,过大则会增加时间成本,因此可以根据实际需求适当选取,使得时间成本较低的同时,也能保证算法具有较高的识别率。
如何获取实际NLOS环境中的散射半径等信息,并将本文算法与多种基于散射体信息和散射模型的抗NLOS误差定位算法进行融合,以进一步提升NLOS环境下对MS的定位性能,是后续需要研究的重要课题。
[1] Hsu L. Analysis and Modeling GPS NLOS Effect in Highly Urbanized Area[J]. GPS Solutions, 2018, 22(7): 1-12.
[2] Liu Lin, Deng Ping, Fan Pingzhi. A TOA Reconstruction Method Based on Ring of Scatterers Model[C]∥Proceedings of the Fourth International Conference on Parallel and Distributed Computing, Applications and Technologies. IEEE, 2003: 375-377.
[3] Liu Lin, Fan Pingzhi. An Improved NLOS Error Mitigation TOA Reconstruction Method[C]∥2006 IET International Conference on Wireless, Mobile and Multimedia Networks. IEEE, 2006: 1-3.
[4] Zhang Weiyi, Chen Xiuwan, Wan Jiahuan, et al. GPS/Cellular Network Hybrid Positioning Method Based on Two Scatter Model[C]∥2012 International Conference on Computer Science and Electronics Engineering. IEEE, 2012: 98-103.
[5] 田增山, 舒月月, 周牧, 等. 基于B-LM圆环模型的NLOS信息约束单基站定位算法[J]. 电子与信息学报, 2018, 40(10): 2316-2322.
Tian Zengshan, Shu Yueyue, Zhou Mu, et al. Single Base Station Localization Algorithm Based on B-LM Ring of Scattering Model Using NLOS Information[J]. Journal of Electronics & Information Technology, 2018, 40(10): 2316-2322.(in Chinese)
[6] Yang Tianchi, Jin Liang. Single Station Location Method in NLOS Environment: The Circle Fitting Algorithm[J]. Science China Information Sciences, 2011, 54(2): 381-385.
[7] Zhang Rui, Xia Weiwei, Yan Feng, et al. A Single-Site Positioning Method Based on TOA and DOA Estimation Using Virtual Stations in NLOS Environment[J]. China Communications, 2019, 16(2): 146-159.
[8] Kim J. Fast Non-Line-of-Sight Receivers Conjecturing Method in TDOA Localisation Using Obstacle Information[J]. IET Radar, Sonar & Navigation, 2019, 13(3): 347-351.
[9] Ma Yongtao, Wang Bobo, Pei Shuyang, et al. An Indoor Localization Method Based on AOA and PDOA Using Virtual Stations in Multipath and NLOS Environments for Passive UHF RFID[J]. IEEE Access, 2018, 6(1): 31772-31782.
[10] Liu Deliang, Wang Ying, He Peng, et al. TOA Localization for Multipath and NLOS Environment with Virtual Stations[J]. EURASIP Journal on Wireless Communications and Networking, 2017, 104(1): 1-7.
[11] Seow C K, Tan S Y. Non-Line-of-Sight Localization in Multipath Environments[J]. IEEE Transactions on Mobile Computing, 2008, 7(5): 647- 660.
[12] 邓平, 芮洋, 邓水发. 一种新的基于LPMD的散射路径识别算法[J]. 西南交通大学学报, 2018, 1(1): 182-188.
Deng Ping, Rui Yang, Deng Shuifa. A Novel Scattering Path Recognition Algorithm Based on LPMD[J]. Journal of Southwest Jiaotong University, 2018, 1(1): 182-188.(in Chinese)
[13] Hu Boyang, Tian Hui, Fan Shaoshuai. Millimeter Wave LOS/NLOS Identification and Localization via Mean-Shift Clustering[C]∥2019 IEEE 30th Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC). IEEE, 2019: 1-7.
[14] Zhan Shigeng, Yang Chengwei, Jiang Danming, et al. Nothing Blocks Me: Precise and Real-Time LOS/NLOS Path Recognition in RFID Systems[J]. IEEE Internet of Things Journal, 2019, 6(3): 5814-5824.
[15] 颜俊, 陈亮, 吴乐南. 基于信号检测法的NLOS识别[J]. 信号处理, 2009, 25(12): 1848-1852.
Yan Jun, Chen Liang, Wu le-nan. NLOS Identification via Signal Detection Algorithm[J]. Journal of Signal Processing, 2009, 25(12): 1848-1852.(in Chinese)
[16] Jazzar S A, Caffery J, You H R. A Scattering Model Based Approach to NLOS Mitigation in TOA Location Systems[C]∥IEEE 55th Vehicular Technology Conference. IEEE, 2002: 861- 865.
[17] Ertel R B, Reed J H. Angle and Time of Arrival Statistics for Circular and Elliptical Scattering Models[J]. IEEE Journal on Selected Areas in Communications, 1999, 17(11): 1829-1840.
[18] Liao J F, Chen B S. Robust Mobile Location Estimator with NLOS Mitigation using Interacting Multiple Model Algorithm[J]. IEEE Transactions on Wireless Communications, 2006, 5(11): 3002-3006.
[19] Wylie M P, Holtzman J. The Non-Line of Sight Problem in Mobile Location Estimation[C]∥Proceedings of ICUPC-5th International Conference on Universal Personal Communications. IEEE, 1996: 827- 831.
[20] Silventoinen M I, Rantalainen T. Mobile Station Emergency Locating in GSM[C]∥1996 IEEE International Conference on Personal Wireless Communications Proceedings and Exhibition. IEEE, 1996: 232-238.

