1 引言
波束形成系统是一个空域滤波处理系统。常规波束形成方法用期望信号的导向矢量作为权矢量,使阵列输出在对应角度方向的信号增益最大,但即使对其进行低旁瓣加权处理也不能抑制较强的旁瓣干扰。而自适应波束形成方法根据接收到的数据,通过相应的自适应方法,使阵列形成一个很窄的对准期望信号的主波束,在干扰方向形成零陷,提高输出信号干扰比[1-5]。在实际工程应用中,自适应波束形成方法的性能会因为诸如有限快拍数、信号方向估计偏差、阵元校正误差、远近场效应等因素的影响而严重下降[6-7]。由于水下航行器的工作环境复杂,要求在强干扰背景下提取期望信号的同时抑制干扰信号,本文假设DOA是服从先验分布的一个随机变量,提出了一种基于均匀先验分布的Bayesian自适应波束形成方法,对观测信号方向误差具有较好的宽容性,该方法将对期望信号的估计转化为一个Bayesian后验分布和条件最小均方误差估计的组合问题,其中最小均方误差估计是给定均匀先验分布时阵列接收数据的条件均值,然后计算得到权矢量。最后通过一系列计算机仿真分析了方法的阵列方向图以及观测方向误差、输入信噪比和快拍数对输出信干噪比的影响。
2 阵列信号模型
假设P个远场窄带点目标信号源入射到阵元数为M,阵元间距为入射波长一半的均匀线列阵上,则可以得到第m个阵元t时刻的输出可以表示为[8]
m=1,2,…,M
(1)
其中τmi表示第i个目标信号到达第m个阵元时相对于参考阵元的时延。nm(t)表示第m个阵元在t时刻的噪声,于是,M个阵元的1次快拍接收数据矢量形式表示为
x(t)=A(θ)s(t)+n(t)
(2)
式中
s(t)=[s1(t),s2(t),…,sP(t)]T
(3)
是空间信号的P×1维矢量;
n(t)=[n1(t),n2(t),…,nM(t)]T
(4)
是M×1维加性噪声数据矢量;
(5)
是M×P维阵列流型矩阵,其中a(θi)(i=1,2,…,P)称为方向矢量,对于均匀线列阵
(6)
其中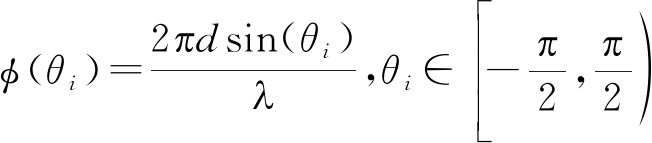
是信号源相对于阵列法线的入射方位。
阵列N次快拍接收数据可以表示为
X=AS+N
(7)
式中X=[x(1),x(2),…,x(N)]是阵列接收数据,S=[s(1),s(2),…,s(N)]是信号矩阵,N=[n(1),n(2),…,n(N)]是加性噪声矩阵。
3 基于均匀先验分布的Bayesian自适应波束形成方法
传统的自适应波束形成方法,有的没有考虑水下存在观测信号方向误差,比如CBF方法、MVDR方法等,有的不能自适应的抑制强干扰,比如CBF方法。而在工程实际中,期望信号的方向往往是不确定的,将信号方向向量的不确定性当做约束条件,假设DOA是服从先验分布p(θ)的随机变量,p(θ)定义在先验参数空间Θ上,反应DOA不确定程度。在此约束条件下,各阵元的接收数据是独立同分布的,对于N次快拍数据x(t),(t=1,…,N),协方差矩阵为
(8)
期望信号s(t)的最小均方误差估计是给定接收数据时x(t)的条件均值,即
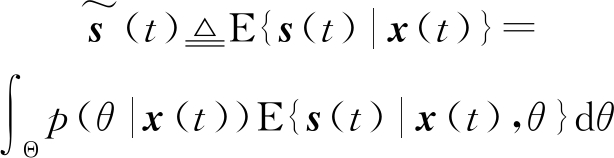
(9)
式中p(θ|x(t))是给定x(t)时的θ后验分布。由于N次快拍数据是独立同分布的,所以条件最小均方误差估计E{s(t)|x(t),θ}与E{sk|xk,θ}相等,其中sk和xk分别为一次快拍的M×1维信号向量和接收数据向量[9]。定义
(10)
式(9)可以重新写为
(11)
上式可以看做一个条件最小均方误差估计和后验分布的组合问题。假定θ是一个定义在先验参数空间Θ={θ1,…,θL}上的离散变量,最小均方误差估计变为
(12)
下面给出求解过程。选用文献[10]的Bayesian后验分布
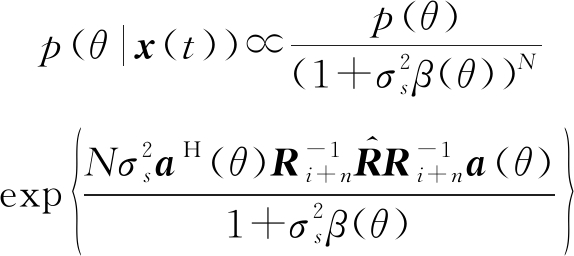
(13)
式中
表示二者成正比例,即二者只相差一个常数因子。
指数项可以展开为
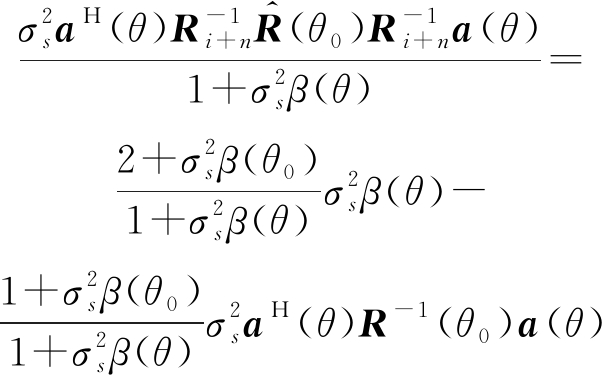
(14)
后验分布近似为
(15)
式中α是确保函数积分为1的正则化参数。对于高斯信号和噪声,方向的维纳滤波是最小均方误差,即
(16)
把式(15)和式(16)带入式(11),Bayesian自适应波束形成器可以描述为
(17)
(18)
式中
称为Bayesian方向矢量。
假定DOA是分布在Θ={θ1,…,θL}上的离散随机变量,θ1,…,θL是均匀分布在[-π,π]上的离散点(L>M)。给出Bayesian自适应波束形成方法的步骤如下:
(1) 初始化DOA的先验参数空间Θ={θ1,…,θL},从[-π,π]中选出期望信号可能出现的区域,仿真中根据一般经验选取先验角度[-30°,30°],按照均匀分布从中抽样出L个离散点。
(2) 计算先验参数空间Θ的Bayesian方向矢量
(19)
(3) 将计算所得的Bayesian方向矢量代入式(18)得到权矢量
(20)
4 UB方法性能分析
通过一系列仿真实验验证基于均匀分布的Bayesian自适应波束形成方法的性能。首先定义输出信干噪比SINR为
(21)
仿真中先验参数空间Θ均为从[-30°,30°]的均匀分布中抽取L=61个离散点作为DOA的先验点集。
4.1 观测方向误差对方向图的影响
仿真模型:假设10元均匀线列阵,目标信号从0°方向入射,输入信噪比SNR为0 dB,两个干扰信号分别从-40°和50°方向入射,干噪比均为30 dB,阵元间距为半波长,快拍数为300。观测方向误差Δ=4°时,各方法方向图如图1所示,图2是目标附近和干扰附近的放大图。
图1 观测方向误差对方向图的影响
Fig.1 Effect of steering vector mismatch
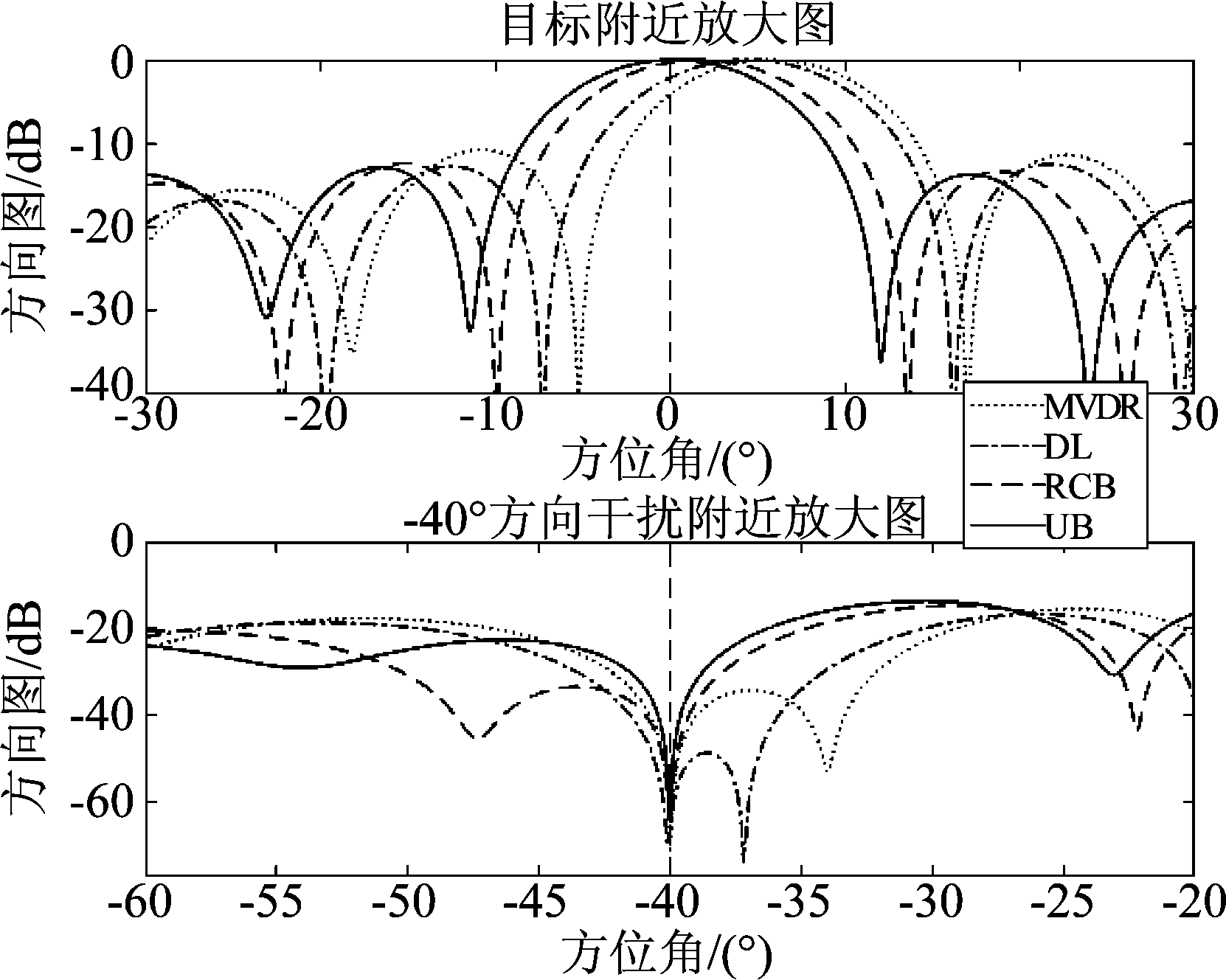
图2 局部放大图
Fig.2 Local amplification figure
由图1和图2可以看出,当观测方向有误差时,四种方法均能有效抑制干扰,本文的基于均匀分布的Bayesian自适应波束形成方法的主波束与信号方向对得最准,RCB自适应波束形成方法稍有偏差,MVDR自适应波束形成方法和DL自适应波束形成方法则偏离了期望信号方向。
4.2 观测方向误差对输出信干噪比的影响
仿真模型:假设10元均匀线列阵,目标信号从0°方向入射,输入信噪比SNR为10 dB,两个干扰信号分别从-40°和50°方向入射,干噪比均为30 dB,阵元间距为半波长,快拍数为300,观测方向误差Δ从1°变化到10°,每个观测方向误差下做100次Monte-Carlo仿真取平均值。各方法的输出信干噪比SINR随观测方向误差的变化情况如图3所示。
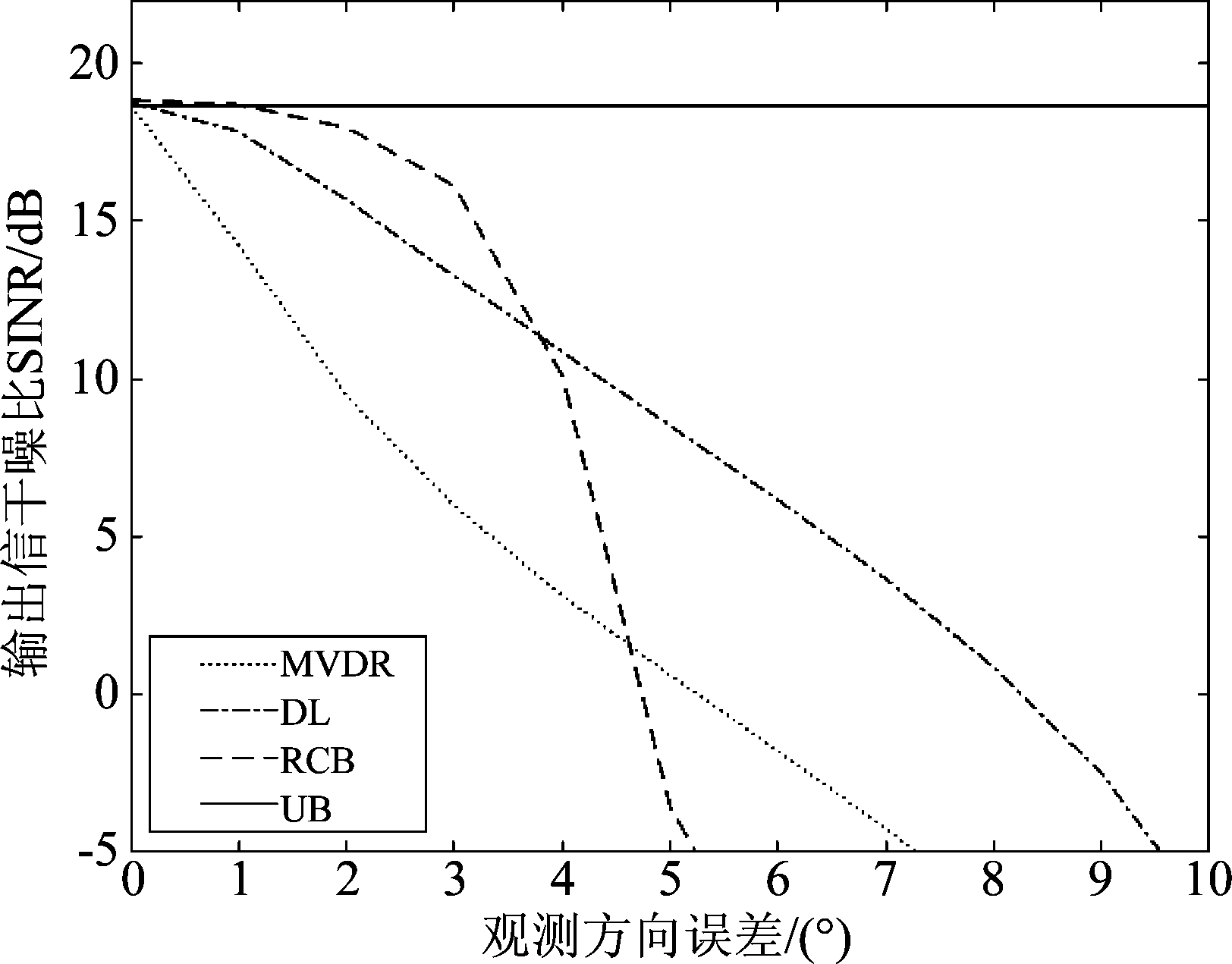
图3 输出信干噪比SINR随观测方向误差的变化曲线
Fig.3 Output SINR along with the steering vector mismatch
由图3可以看出,在输入信噪比为10 dB和快拍数为300的情况下,MVDR自适应波束形成方法对观测误差没有宽容性,DL自适应波束形成方法的输出信干噪比SINR在观测误差大于1°时急剧下降,同样对观测误差没有宽容性。当观测方向误差为大于3°时,RCB自适应波束形成方法的输出信干噪比SINR开始急剧下降,而本文的基于均匀分布的Bayesian波束自适应方法的输出信干噪比SINR完全不受观测误差的影响,保持较高的恒定值。这是因为本文方法在计算权矢量的过程中,没有直接利用期望信号的到达方向,而是假设期望信号的到达方向在一个区间内服从均匀先验分布,然后利用基于这个均匀分布的阵列接收数据和Bayesian后验分布来估计期望信号的到达方向,最后计算权矢量。这样就避免了观测方向误差对权矢量值的干扰,从而使得本文的方法对观测方向误差有着较好的稳健性。
4.3 输入信噪比对输出信干噪比的影响
仿真模型:假设10元均匀线列阵,目标信号从0°方向入射,观测方向误差Δ=4°,两个干扰信号分别从-40°和50°方向入射,干噪比均为30 dB,阵元间距为半波长,快拍数为300,输入信噪比SNR从-5 dB变化到25 dB,每个输入信噪比下做100次Monte-Carlo仿真取平均值。各方法的输出信干噪比SINR随输入信噪比SNR的变化情况如图4所示。
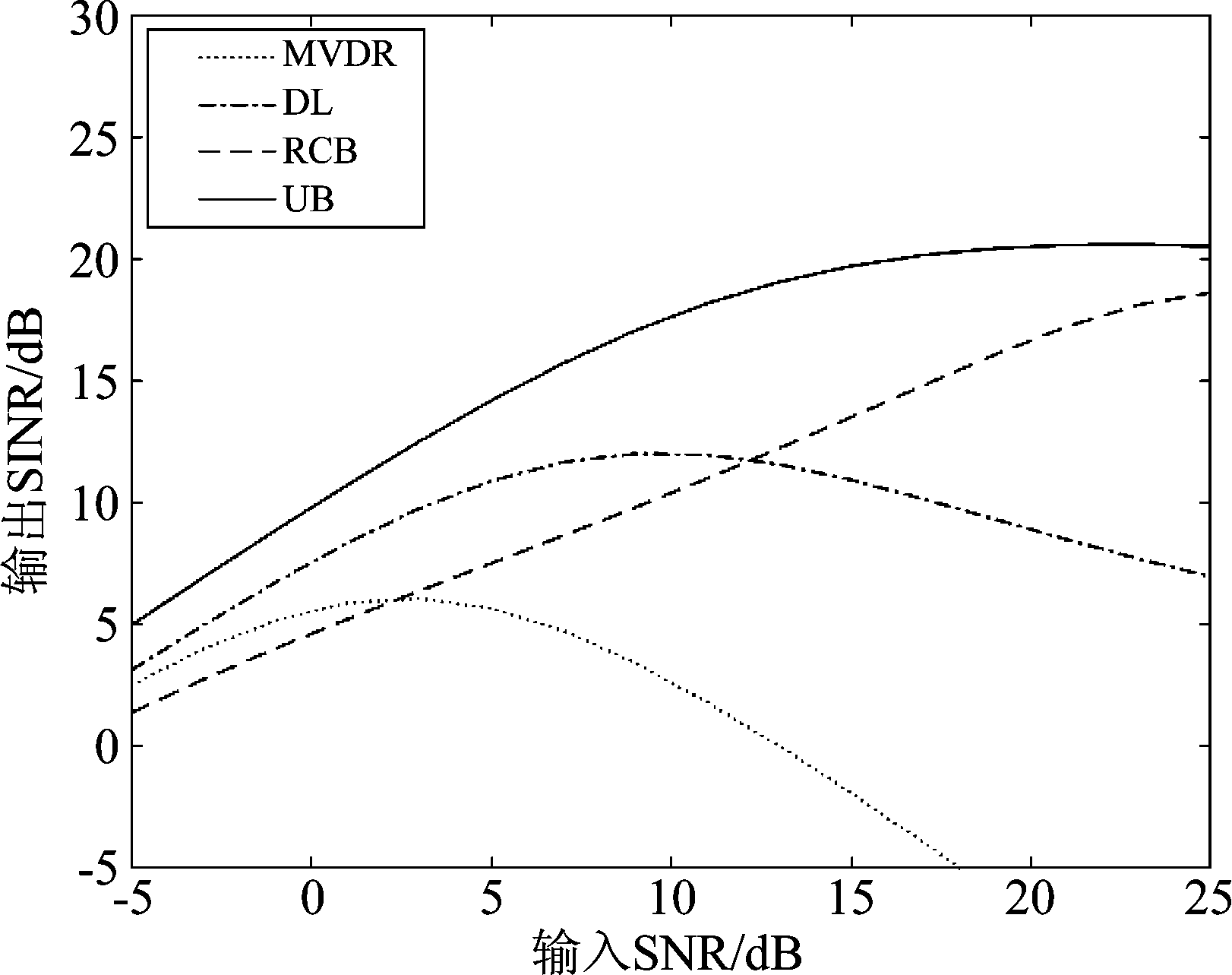
图4 输出信干噪比SINR随输入信噪比SNR的变化曲线
Fig.4 Output SINR along with input SNR
由图4可以看出,有限快拍数时,MVDR自适应波束形成方法和DL波束形成方法由于对观测误差不具有宽容性,随着输入信噪比SNR的增加会产生不同程度的目标信号对消,其输出信干噪比SINR随着输入信噪比的增加而有相应程度的降低。而RCB自适应波束形成方法和本文基于均匀分布的Bayesian自适应波束形成方法的SINR都随着输入信噪比SNR的增加而稳定增加,由第4.1节的仿真结果,本文方法的主波束对目标的实际到达方向指向最准确,因此在高输入信噪比时仍然具有较高的输出信干噪比SINR。
4.4 快拍数对输出信噪干扰比的影响
仿真模型:假设10元均匀线列阵,目标信号从0°方向入射,输入信噪比SNR为10 dB,观测方向误差Δ=4°,两个干扰信号分别从-40°和50°方向入射,干噪比均为30 dB,阵元间距为半波长,快拍数从1变化到600,每个快拍数下做100次Monte-Carlo仿真取平均值。各方法的输出信干噪比SINR随快拍数变化情况如图5所示。
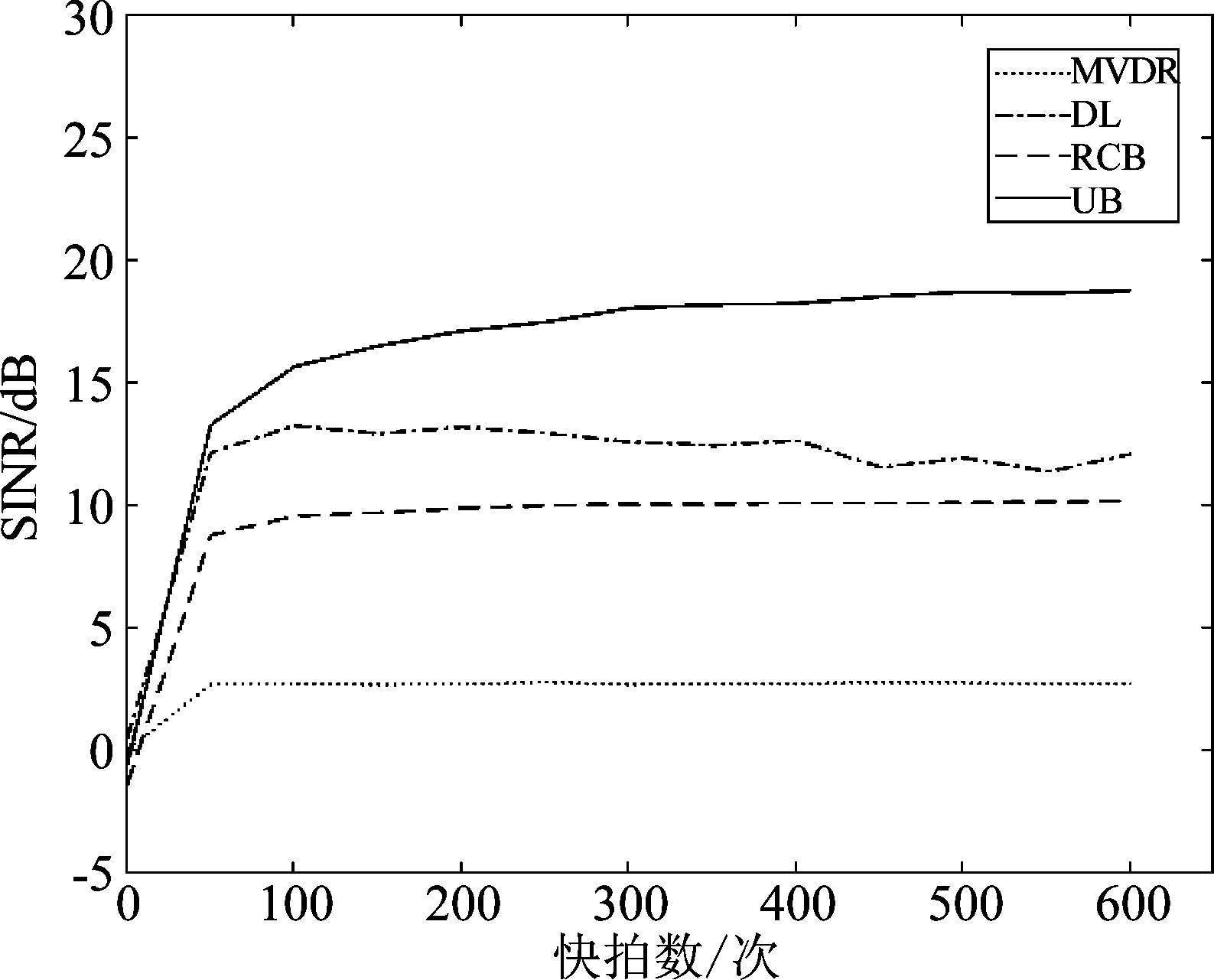
图5 输出信干噪比SINR随快拍数的变化曲线
Fig.5 Output SINR along with the snapshot number
由图5可以看出,DL自适应波束形成方法和MVDR自适应波束形成方法的输出信干噪比SINR没有随着快拍数的增加而增加,这是因为这两种方法对信号观测方向有误差的情况不具有宽容性,RCB自适应波束形成方法和本文基于均匀分布的Bayesian自适应波束形成方法的SINR都随着快拍数的增加而增加,尤以本文方法的输出信干噪比SINR最高。
通过以上阵列方向图比较以及观测方向误差、输入信噪比和快拍数对输出信干噪比影响的仿真分析,可以看出本文的方法有以下优点:(1)提取期望信号的同时有效抑制干扰。(2)对观测方向的误差具有稳健性。(3)输出信干噪比随着输入信噪比和快拍数的增加而稳定增加。
5 结论
本文针对水下航行器复杂的工作环境以及实际应用中出现的观测信号方向有误差的情况,考虑自适应波束形成的最小均方误差准则,假设期望信号的到达方向在一个区间内服从均匀先验分布,这样对期望信号的估计就变为一个Bayesian后验分布和条件最小均方误差估计的组合问题,其中最小均方误差估计是给定均匀先验分布时阵列接收数据的条件均值,然后利用基于这个均匀分布的阵列接收数据和Bayesian后验分布来估计期望信号的到达方向,最后计算权矢量。这样就避免了观测方向误差对权矢量值的干扰,从而使得本文的方法对观测方向误差有着较好的稳健性。并通过一系列计算机仿真分析了各相关方法性能,得到以下结论:
(1)当观测信号方向无误差时,CBF方法只能提取信号而不能抑制干扰;MVDR自适应波束形成方法提取信号的同时有效抑制干扰,但方法的旁瓣受有限快拍数的影响而过高;DL自适应波束形成方法提取信号的同时有效抑制干扰。
(2)当观测信号方向有误差时,RCB、MVDR和DL和本文的UB自适应波束形成方法均能有效抑制干扰,但MVDR自适应波束形成方法和DL自适应波束形成方法的主波束都偏离了期望信号方向,RCB自适应波束形成方法的主波束基本对准了期望信号的来向,从而适用于观测误差不大的情况。本文的UB自适应波束形成方法对观测方向的误差具有稳健性,输出信干噪比随着输入信噪比和快拍数的增加而稳定增加,随着观测方向误差的增大而保持稳定的恒定值,阵列方向图的主波束不受观测方向误差的影响,始终对准信号的到达方向。
[1] 黄磊. 非理想条件下的自适应波束形成算法研究[D]. [博士论文]. 中国科学技术大学, 2016.
Huang Lei. Adaptive beamforming algorithms under nonideal conditions[D]. [Dissertation of doctor]. University of Science and Technology of China, 2016.(in Chinese)
[2] Hang Ruan, Rodrigo C. de Lamare. Robust Adaptive beamforming based on Low-Rank and Cross-Correlation technique[J]. IEEE Transactions on Signal Processing, 2016, 64(15): 3919-3932.
[3] Nguyen T. Nghia, Hoang D. Tuan, Trung Q. Duong, et al. MIMO beamforming for secure and Energy-Efficient wireless communication[J]. IEEE Signal Processing Letters, 2017, 24(2): 236-239.
[4] Min Li, Lin Bai, Quan Yu, et al. Optimal beamforming for Dual-Hop MIMO AF relay networks with cochannel interferences[J]. IEEE Transactions on Signal Processing, 2017, 65(7): 1825-1840.
[5] Bell K L, Ephraim Y, Van Trees H L. Bayesian approach to robust adaptive beamforming[J]. IEEE Transaction Signal Processing, 2000, 48(2): 386-398.
[6] Biguesh M, Valaee S, Champagne B. A new beamforming algorithm based on signal subspace eignvectors[C]∥In Proceedings of IEEE Workshop on Statistical Signal and Array Processing, 2000: 444- 447.
[7] 杨益新, 孙超. 任意结构阵列宽带恒定束宽波束形成新方法[J]. 声学学报, 2001, 26(1): 55-58. doi:10.15949/j.cnki.0371- 0025.2001.01.010
Yang Yixin, Sun Chao. A new method of broadband constant beamwidth beamforming for arbitrary geometry arrays[J]. Acta Acustica, 2001, 26(1): 55-58. doi:10.15949/j.cnki.0371- 0025.2001.01.010.(in Chinese)
[8] Johnson D H, Dudgeon D E. Array signal processing-concepts and techniques[C]∥Prentice-Hall, Englewood Cliffs, NJ, 1993.
[9] 刘力, 杨小鹏. 稳健的相干干扰抑制算法[J]. 信号处理, 2017, 33(12):1555-1561.
Liu Li, Yang Xiaopeng. Robust Algorithm to Suppress Coherent Jamming [J].Journal of Signal Processing,2017,33(12):1555-1561.(in Chinese)
[10] Chunwei J L, Andrew C S. Bayesian beamforming for DOA uncertainty: theory and implementation[J]. IEEE Transaction on Signal Processing, 2006, 54(11): 4435- 4445.
[11] Jinwoo Kim, Wan Choi, Hyuncheol Park. Beamform-ing for full-duplex multiuser MIMO systems[J]. IEEE Transactions on Vehicular Technology, 2017, 66(3): 2423-2432.
