1 引言
D2D通信是5G移动通信系统中的一项关键技术,能提高频谱效率和能量效率,并降低传输延迟。从物理层安全角度考虑,还可以适当地控制D2D用户对蜂窝用户带来的干扰同时使窃听链路恶化,从而提高蜂窝用户的安全可达速率[1- 4]。由于频繁传输隐私信息以及有限的功率存储和计算能力,D2D用户本身比蜂窝用户更容易被窃听,但是D2D通信的物理层安全问题却较少得到关注。因此,本论文研究在保证蜂窝用户传输性能的前提下,如何提高D2D用户的物理层安全性能。
物理层安全问题通常是在被动窃听的情况下研究的。如果窃听者变得更加智能和主动,例如,可以选择性地采用窃听或主动干扰的攻击方式,这比在单纯的被动窃听下更难保证通信的安全性和可靠性。根据主动窃听者的双工方式,可以分为半双工主动窃听和全双工主动窃听。在半双工主动窃听下,主动窃听者在同一时刻只能选择被动窃听或者主动干扰,而全双工主动窃听者可以同时进行被动窃听和主动干扰的攻击。一些文献考虑了主动窃听下合法用户通过联合中继选择、友好干扰和功率分配[5- 8]等方法来提升物理层安全性能。如在文献[5]中,研究了在半双工主动窃听情况下,合法用户如何对抗被动窃听或主动干扰攻击,提高合法用户的平均安全可达速率。在文献[8]中,研究了全双工主动窃听情况下,蜂窝用户和D2D用户的协作,以及合法用户和全双工主动窃听者之间的对抗。考虑到主动窃听者能量消耗的约束和隐蔽性的要求,其可以依概率采用不同的攻击方式。因此,本文研究更为实际的依概率主动窃听下的蜂窝网络中D2D用户的安全可靠通信问题。
考虑到蜂窝用户和D2D用户不同的优化目标,可以通过博弈论来分析蜂窝用户和D2D用户的竞争或合作。此外,D2D用户需要在满足一定的干扰条件下才能接入蜂窝链路,因此蜂窝用户与D2D用户之间存在一种天然的分层结构,分层(斯坦伯格)博弈适合于建模它们之间的交互关系[9-12]。本文假设在依概率主动窃听下,蜂窝用户想要最大限度地提高其传输速率,而所有的D2D用户都想要最大化其安全吞吐量。首先,考虑到蜂窝用户与D2D用户之间的共用信道干扰,引入干扰代价机制,D2D用户通过对蜂窝用户支付合理的干扰代价,提高其安全性能。其次,针对依概率主动窃听者攻击模式的动态变化,在分层博弈的框架下设计合法用户的期望效用。最后,提出一种分层稳健的离散功率控制算法。
本论文的主要贡献总结如下:
本文考虑的主动窃听下物理层安全问题与现有大多数研究不同,研究的是更为实际的依概率主动窃听场景,即主动窃听者能量受限,以一定的概率选择被动窃听或主动干扰。
在一个领导者-多个追随者的斯坦伯格博弈框架中研究了蜂窝用户和D2D用户的竞争与合作交互关系,并对其在依概率主动窃听下的平均效用进行了优化,证明了该博弈中斯坦伯格均衡的存在性。
提出了一种稳健协同的D2D离散功率控制算法,该算法收敛于斯坦伯格均衡。数值结果表明,该算法的性能优于随机功率控制算法和D2D自私离散功率控制算法。
2 系统模型和问题描述
本文考虑的是一个蜂窝小区,其中存在一个基站,一个蜂窝用户,N个D2D用户和一个主动窃听者。假设D2D用户是以underlay的方式与蜂窝用户共享上行信道进行通信的。基站、蜂窝用户、主动窃听者和第i个D2D用户分别标记为0、C、A和
所有节点间的信道增益记为hij,其中
特别地,h00是基站和蜂窝用户之间的信道增益,
是D2D用户发射机到D2D用户接收机之间的信道增益。
假设主动窃听者以概率PE窃听D2D链路,以概率PJ=1-PE干扰所有链路。当窃听者选择被动窃听时(sA=E),合法用户的可达速率和窃听者的窃听速率为
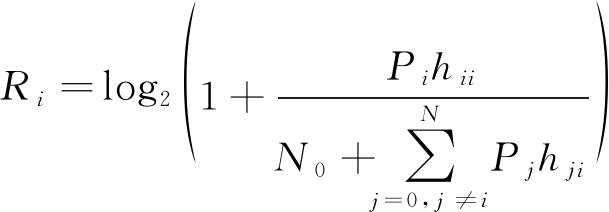
(1)
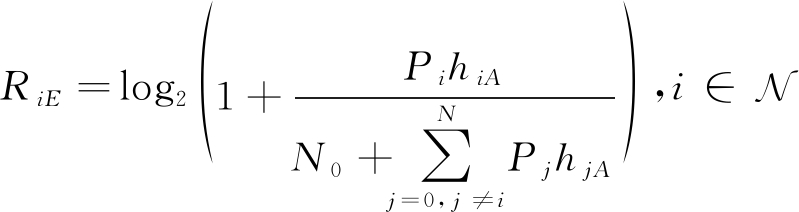
(2)
其中P0和Pi是蜂窝用户和第i个D2D用户的发射功率,N0是背景的加性高斯白噪声。
在被动窃听下,第i个D2D用户的安全可达速率为
(3)
当窃听者选择主动干扰时(sA=J),合法用户的可达速率为
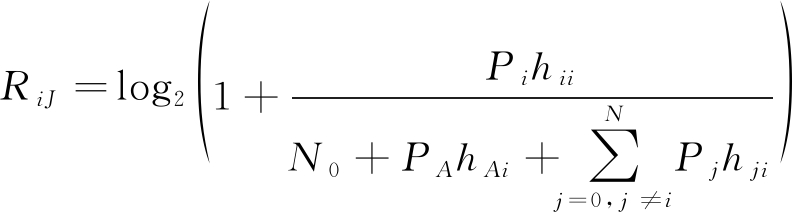
(4)
其中PA是窃听者的干扰功率。
在不同攻击模式下考虑蜂窝用户的传输速率和D2D用户的安全可达速率,蜂窝用户和第i个D2D用户的平均效用为
u0=pER0+pJR0J
ui=pERiS+pJRiJ
(5)
此外,考虑干扰代价因子以及所有D2D用户的发射功率损耗后,蜂窝用户和第i个D2D用户的效用函数设计为
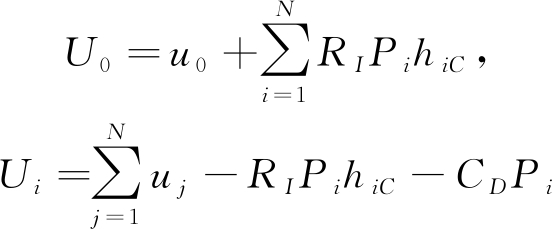
(6)
其中RI是由基站确定的干扰代价因子,CD是D2D用户的发射功率损耗因子。
假设蜂窝用户可以调整的策略是干扰代价因子,D2D用户可以调整的策略是离散的发射功率。首先,蜂窝用户选择干扰代价因子,D2D用户据此调整发射功率,使得他们在向蜂窝用户支付干扰代价的同时,总的平均效用最大并且单个用户的发射功率损耗最小。蜂窝用户通过调整干扰代价因子可以影响D2D用户的发射功率等级从而间接地提升自己的传输速率。基于以上分析,本文蜂窝用户和D2D用户的优化问题分别表述如下
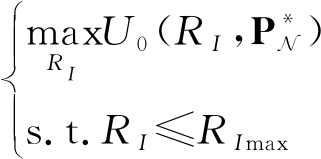
(7)
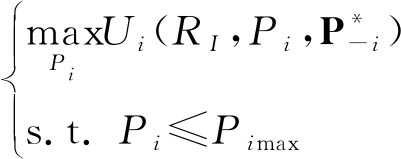
(8)
其中
和P-i分别是所有D2D用户和除第i个D2D用户外的N-1个D2D用户的功率选择,RImax是最大的干扰代价因子,Pimax是第i个D2D用户最大的发射功率。
3 稳健博弈建立和算法分析
3.1 斯坦伯格博弈和均衡分析
我们发现上面的优化问题是一个分层优化问题,很适合用斯坦伯格博弈来进行建模。因此,我们将蜂窝用户和D2D用户之间的相互作用建模为一个斯坦伯格博弈,即
其中博弈的参与者是蜂窝用户和所有的D2D用户,
和
分别为干扰代价因子和离散功率选择集合,U0是蜂窝用户的效用函数,
是所有D2D用户的效用函数集合。现在讨论如何求解这个斯坦伯格博弈,即斯坦伯格均衡(Stackelberg equilibrium, SE)。
定义1 所提博弈模型的斯坦伯格均衡(SE)满足下式:
(9)
(10)
其含义就是通过分层博弈,上层的蜂窝用户和下层所有的D2D用户都不能通过单方面地调整策略获得各自的效用提升,即达到一个平衡状态。
从优化问题的公式(7)中,我们发现所提分层博弈的斯坦伯格均衡受到下层所有D2D用户组成的子博弈的影响。因此我们首先讨论下层子博弈中纳什均衡的存在性。作为领导者,蜂窝用户决定了干扰代价因子,所有在底层的D2D用户之间的协作关系可以表示为一个子博弈
其中子博弈的参与者为所有的D2D用户,子博弈的策略集和效用函数集合是所有D2D用户的离散功率集合和效用函数集合。
定义2 所提子博弈的纯策略纳什均衡(Nash equilibrium, NE)满足下式:
(11)
在给定蜂窝用户的干扰代价因子的条件下所有D2D用户的稳健功率选择策略组合
是所提子博弈的纯策略纳什均衡,即在这种均衡情况下任何D2D用户都无法通过单方面调整其离散功率策略而提高其效用函数。
为了证明所提子博弈的纯策略纳什均衡的存在性,我们引入精确势能博弈[13](exact potential game)的概念。
定义3 如果存在势能函数φ满足
(12)
则
是一个精确势能博弈, 其中
是第i个博弈者的策略,a-i是其他N-1个博弈者的策略。也就是说,只要找到一个满足条件(12)的势能函数,就可以证明一个博弈是精确势能博弈。
定理1 本文所提出的子博弈存在至少一个纯策略的纳什均衡。
证明 首先定义所有D2D用户的总效用和总的干扰代价和功率损耗的折中函数为
并且
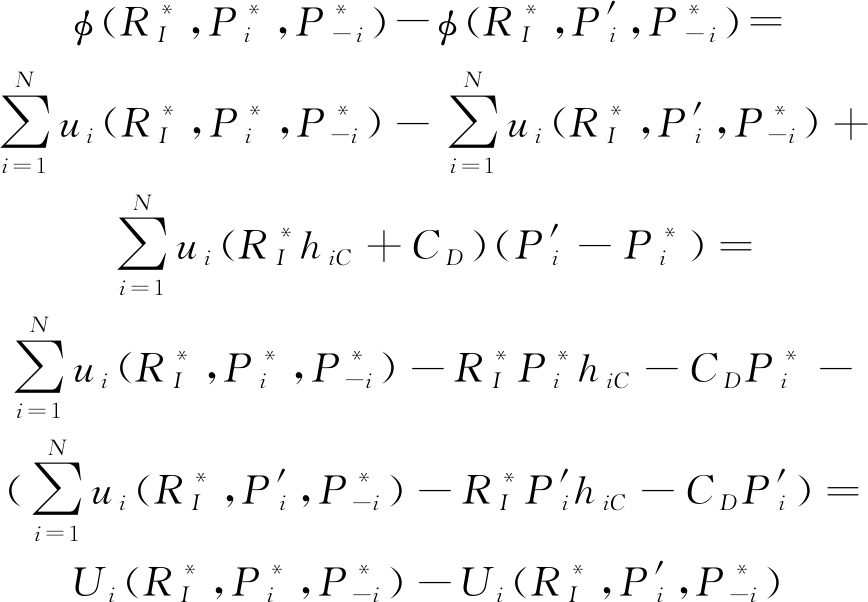
(13)
通过推导发现其满足公式(12),也就是说我们设计的这个折中函数是一个势能函数,因此我们提出的子博弈也是一种精确势能博弈。根据参考文献[13]和[14]可知,精确势能博弈至少存在一个纯策略的纳什均衡,因此本文提出的底层子博弈也至少存在一个纯策略的纳什均衡。
定理2 本文所提出的分层博弈存在至少一个纯策略的斯坦伯格均衡。
证明 斯坦伯格博弈通常是通过逆向推导来求解其斯坦伯格均衡。通过以上的分析,我们发现子博弈是一个精确势能函数,其存在至少一个纯策略的纳什均衡。根据公式(9)～(10),我们发现在底层子博弈达到纯策略纳什均衡后,上层的领导者总能在此基础上做出最佳决策,因此在此分层博弈中至少存在一个纯策略的斯坦伯格均衡。
3.2 稳健功率控制算法描述
考虑攻击模式的不确定性和动态变化,我们提出了一个基于随机学习自动机(stochastic learning automata, SLA)的D2D稳健功率控制算法,能够在动态环境下收敛到子博弈的纯策略纳什均衡[15]。通过必要的信息交互,基站使用基于更佳响应(better response, BR)的算法更新其干扰代价因子策略,最终所提的分层算法可以收敛到所提博弈的纯策略斯坦伯格均衡。假设所有的D2D用户有L个等级的离散发射功率,用pil(t)表示第i个D2D用户在时刻t选择第l个离散功率等级的概率,pi(t)=[pi1(t),...,pil(t)]表示第i个D2D用户在时刻t的混合策略。所有的D2D用户根据下面的公式来更新其混合策略
pil(t+1)=pil(t)+bri(t)(1-pil(t)),ai(t)=l
(14)
pil(t+1)=pil(t)-bri(t)pil(t),ai(t)≠l
(15)
其中b表示学习速率,
表示第t个时隙第i个D2D用户归一化效用。
据此,D2D用户稳健协同功率控制算法总结如下。
表1 D2D用户稳健功率控制算法
Tab.1 Robust D2D power control algorithm
算法1 D2D用户稳健功率控制算法1. 初始化: 基站的干扰代价因子和D2D用户功率集合ɢI和ɢ;2. 每个D2D用户选择不同功率等级的概率pil(0)←1/L;3. 基站随机选择一个RI,并且外层循环k=1;4. 基站将RI广播给所有的D2D用户;5. 迭代次数t=1;6. Repeat7. 每个D2D用户根据功率选择概率选择其功率值;8. 所有的D2D用户监测主动窃听者的攻击模式,估计各自的效用函数,并根据公式(13)或(14)更新各自的混合策略;9. t=t+1;10. Until t=Tmax或者pil(t)接近于1,比如0.99;11. 蜂窝用户基于攻击模式和基站的反馈来估算自己的效用函数U0(RI);
续表1
12. 基站随机选择另一个干扰代价因子R'I;13. Repeat 5～10;14. If U0(R'I)≥U0(RI);15. RI(k+1)←R'I(k);16. End if17. k=k+1;18. Repeat 4～17;19. Until k=Kmax。
一方面,当基于随机学习自动机算法的学习速率足够小时,本文提出的稳健功率控制算法可以在随机变化的攻击模式下收敛到底层精确势能博弈的一个纯策略纳什均衡,从而斯坦伯格博弈通过相应更佳响应算法达到其斯坦伯格均衡。另一方面,本文所提出的功率控制算法适用于不同的D2D用户数目,不同数量级的干扰代价因子以及不同的攻击概率,因此本文所提出的功率控制算法是稳健的,下一部分通过仿真结果进行验证。
4 数值结果与讨论
假设一个1 km×1 km的蜂窝小区,存在一个基站,处在小区中心,一个蜂窝用户,3个D2D通信对和一个主动窃听者随机分布其中。假设大尺度路径损耗因子n=3。假设基站的发射功率PB=1 W,主动窃听者的干扰功率PA=1 W。每个D2D用户的离散功率值集合为
W,基站的干扰代价因子集合
首先我们验证算法的收敛性。在一次仿真中一个D2D用户的离散功率选择概率的变化如图1所示。我们可以发现这个D2D用户在大约600次迭代后以概率1选择0.8 W的发射功率。并且从图2我们发现3个D2D用户在此算法下使他们的功率分别收敛到0.2 W、0.6 W、和0.8 W。
接着,本文通过1万次的蒙特卡洛仿真,估计该稳健协同算法的平均性能,并且与D2D用户的自私功率控制算法和随机功率控制算法进行比较。在稳健协同算法中,所有的D2D用户共享平均安全吞吐量并且考虑个人的干扰代价和功耗。在D2D自私功率控制算法中,每个D2D用户都想最大化其个人的平均效用而不关心其他D2D用户的安全性能。在随机功率控制算法中,所有D2D用户随机地选择功率。
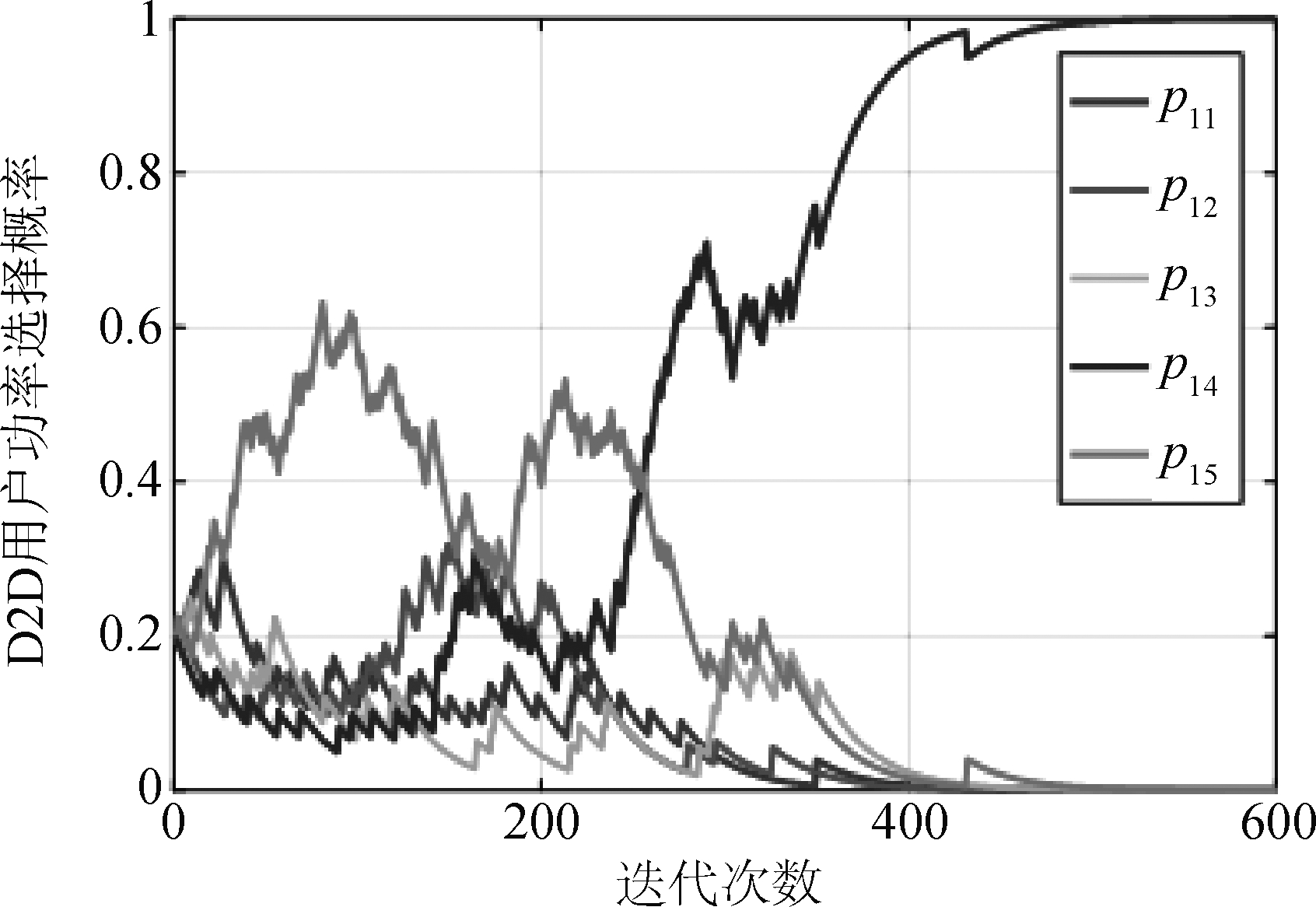
图1 D2D用户功率选择概率收敛曲线
Fig.1 Convergence of power selection probability
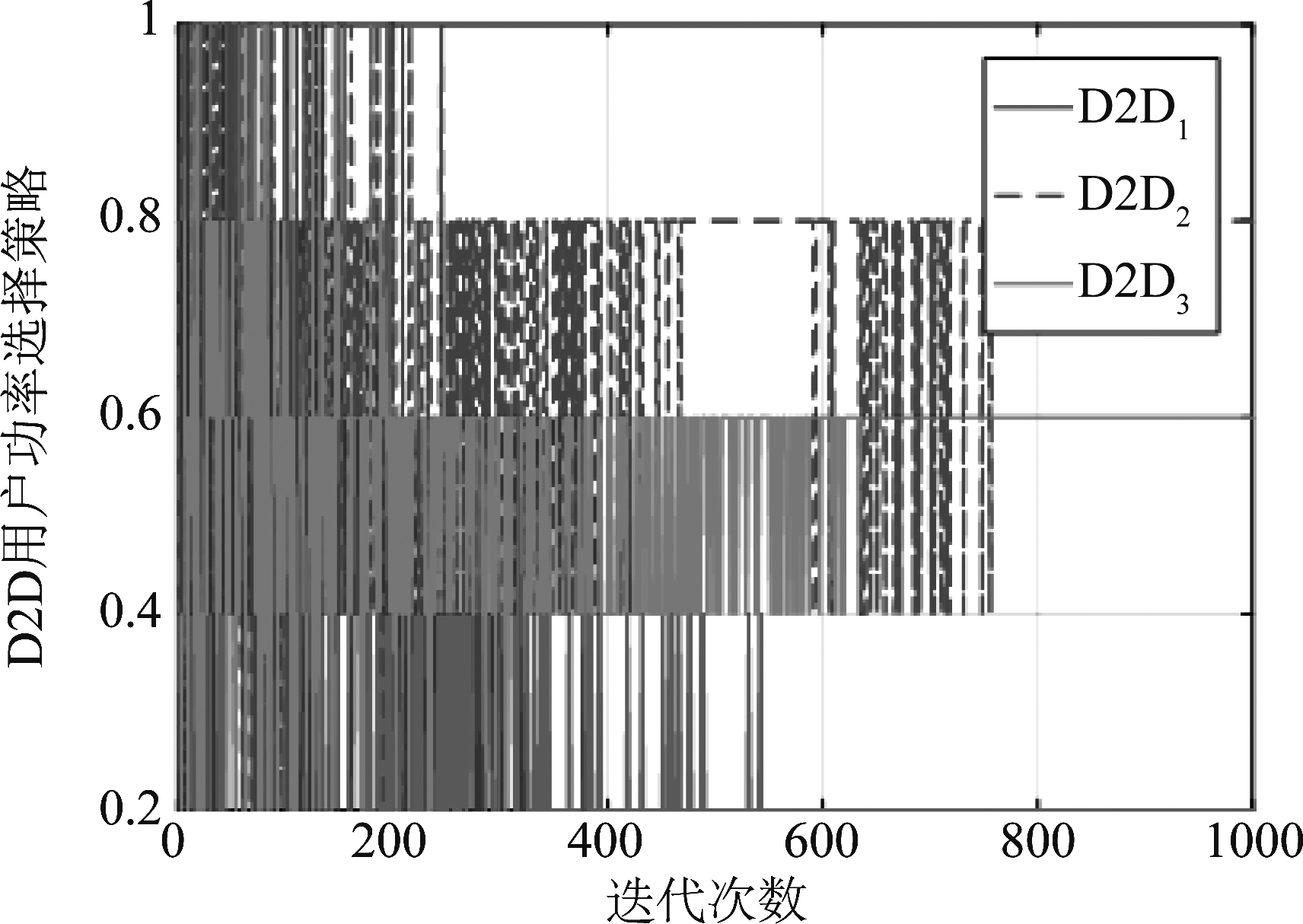
图2 D2D用户功率选择策略收敛曲线
Fig.2 Convergence of power selection strategies for all D2D users
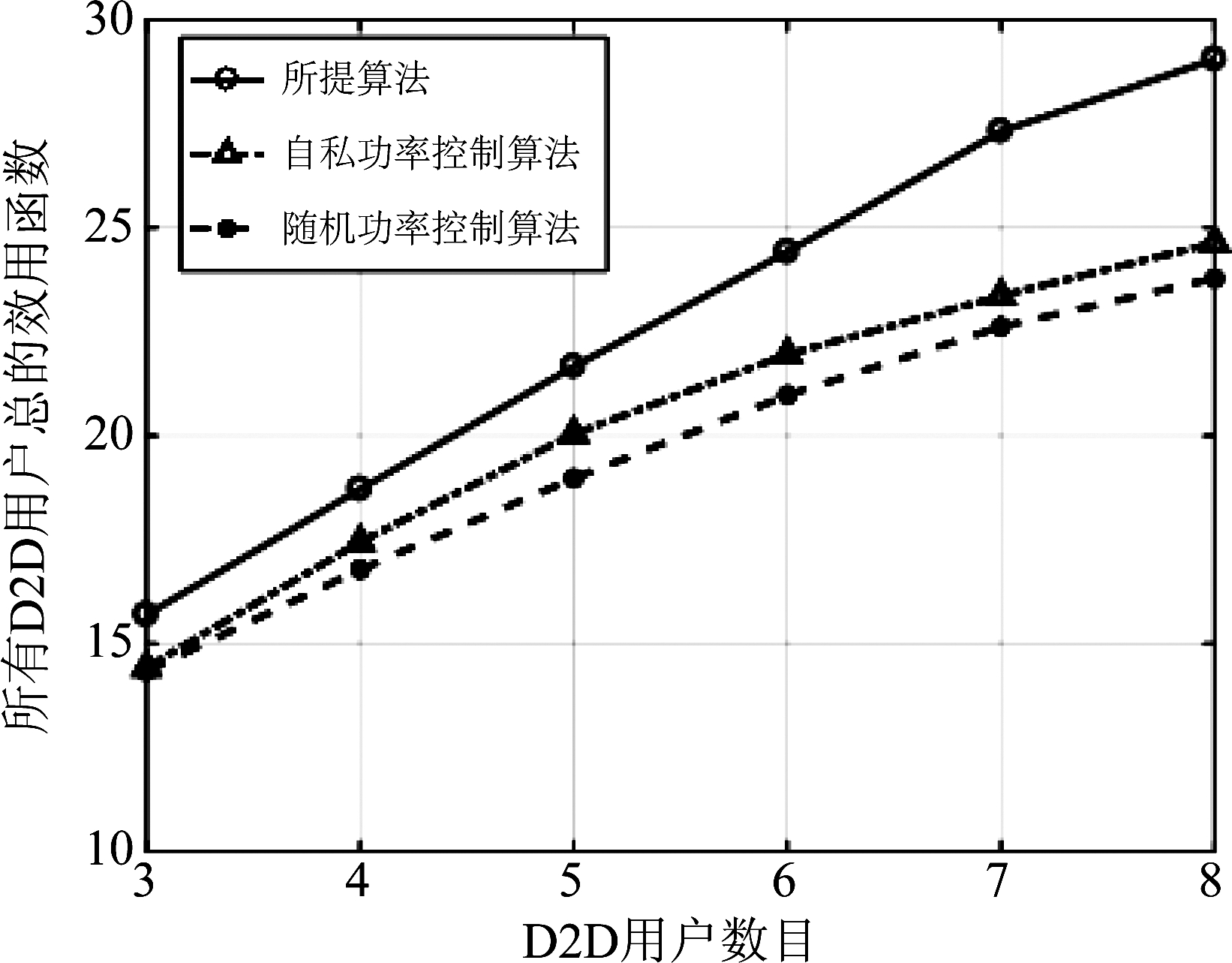
图3 D2D用户总的效用随其数目变化曲线
Fig.3 Sum utility of D2D users versus number of all D2D users
在图3和图4中,我们研究依概率主动窃听者的攻击概率和D2D用户的数量对合法用户的总效用和D2D用户的总效用的影响。在图3中,我们发现所有D2D用户的总效用随着D2D用户数量的增加而增加。相反,在图4中,主动窃听者的主动干扰概率越大,总的效用越小。这是因为,D2D用户越多,他们的平均安全吞吐量越大,而主动窃听者选择主动干扰的概率越大,它带来的外部干扰越多,D2D用户的平均传输速率越低。图5仿真了不同的干扰代价因子对D2D用户效用函数的影响,从图中可以看出,随着干扰代价因子的增大,D2D用户总的效用函数会逐渐减小。
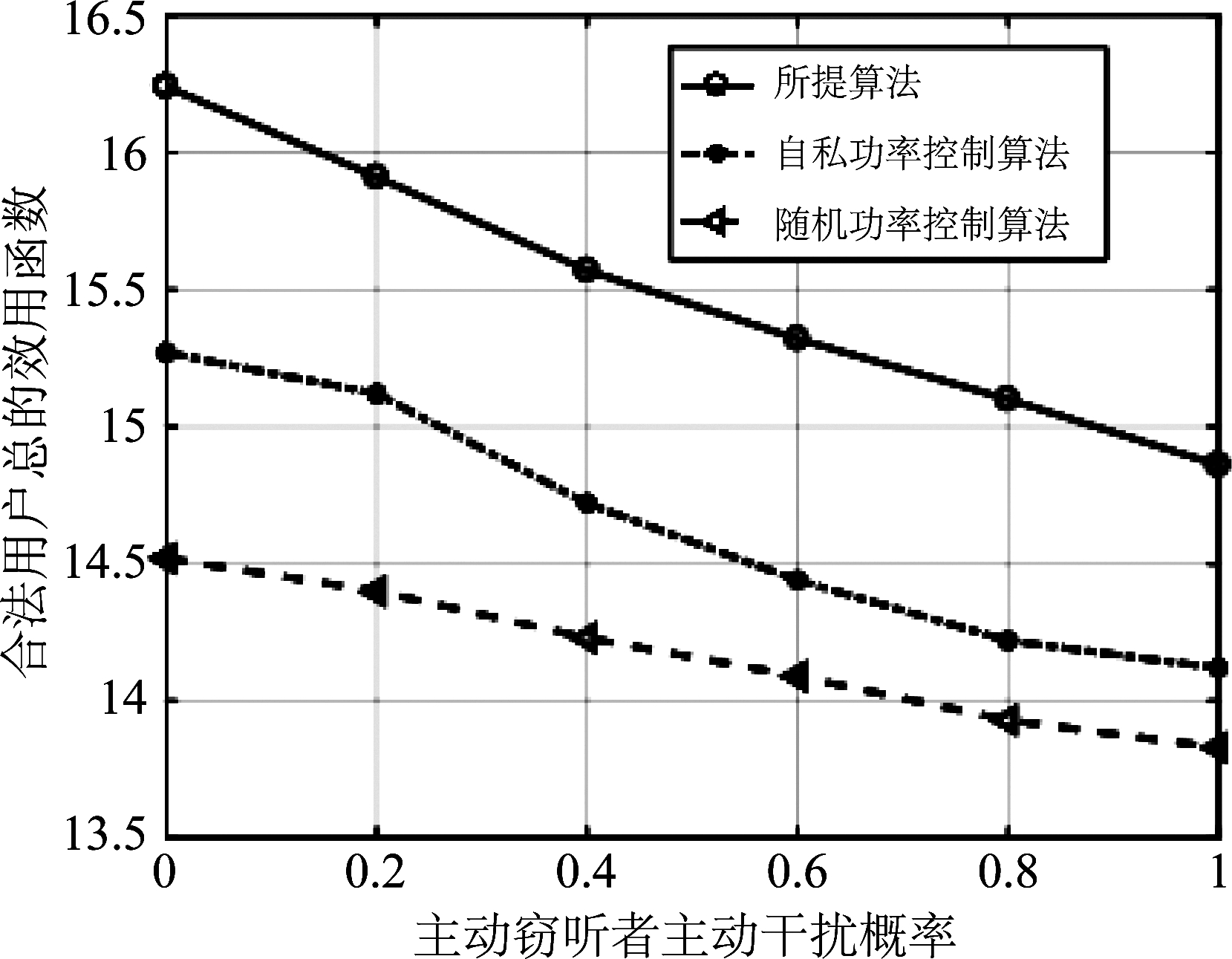
图4 合法用户总效用随着主动窃听者主动干扰概率变化曲线
Fig.4 Sum utility of legitimate users versus the active jamming probability of the active eavesdropper
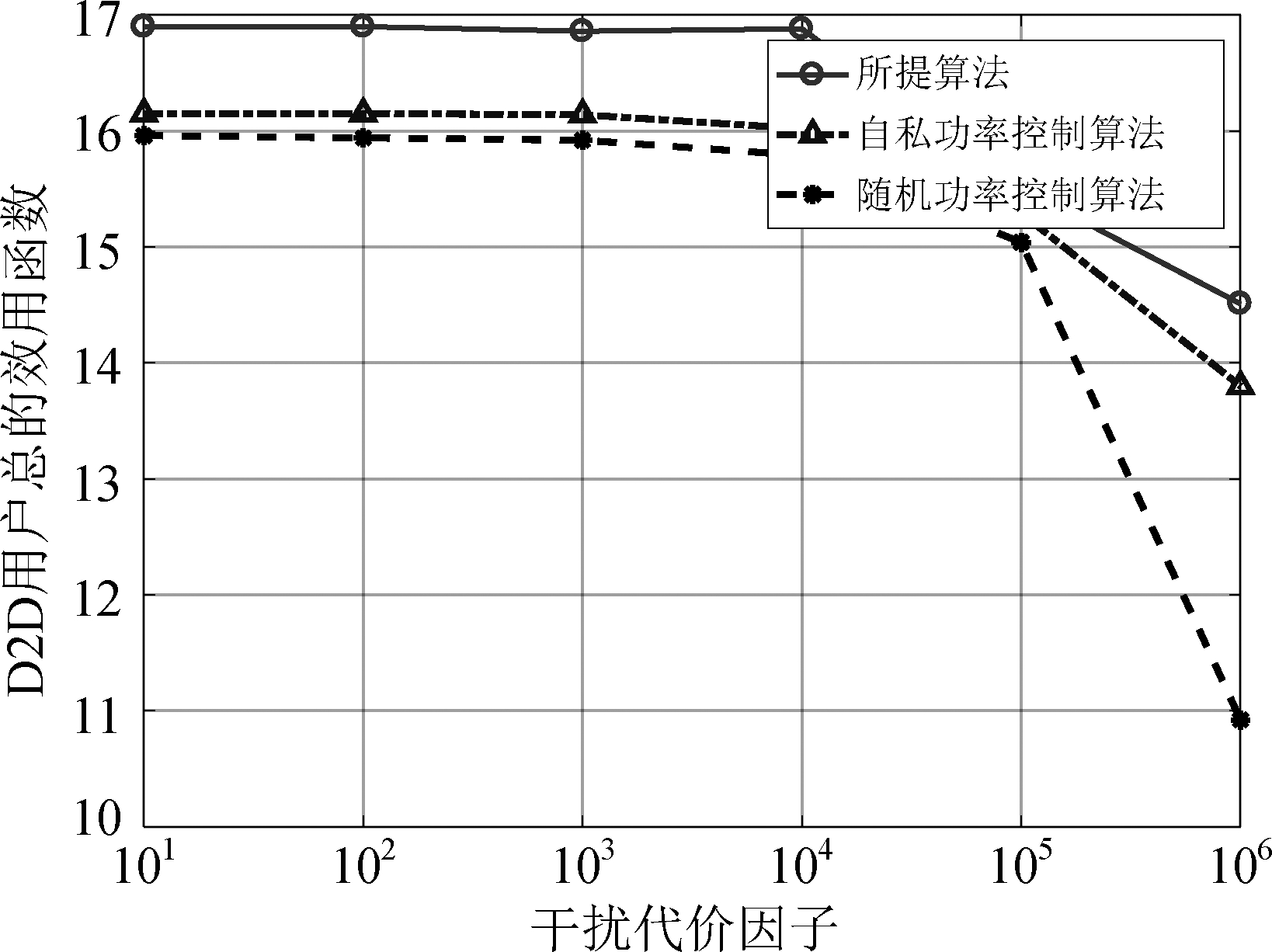
图5 D2D用户总的效用随干扰代价因子变化曲线
Fig.5 Sum utility of all D2D users versus interference cost factor
从图1和图2我们可以看出,所提算法在主动窃听者攻击方式动态变化的情况下仍然可以收敛到确定的功率策略;从图3到图5,我们发现不管是蜂窝用户的干扰代价因子、D2D用户的数目,或者主动窃听者的干扰概率发生变化,本文所提算法都优于其他两种对比算法。因此我们提出的功率控制算法是是稳健的,并具有较好的物理层安全性能。
5 结论
本文分析了面向依概率主动窃听者分层博弈框架下的蜂窝用户与多个D2D用户之间的分层交互作用。我们考虑了D2D用户的接入对蜂窝网络传输能力的影响,引入了一种蜂窝用户与D2D用户之间的干扰代价机制。建立了D2D用户之间的精确势能子博弈,分析了所提博弈的均衡问题。提出了一种稳健、协同的D2D功率控制算法,提高了合法用户的平均抗干扰和防窃听性能。
[1] Yue Jianting, Ma Chuan, Yu Hui, et al. Secrecy-Based access control for device-to-device communication underlaying cellular networks[J]. IEEE Communication Letter, 2013, 17(11): 2068-2071.
[2] Lee K S, Hong J P. Power control for energy efficient D2D communication in heterogeneous networks with eavesdropper[J]. IEEE Communication Letter, 2017, 21(11): 2536-2539.
[3] Wang Wei, Teh K C, Li K H. Enhanced physical layer security in D2D spectrum sharing networks[J]. IEEE Wireless Communication Letter, 2017, 6(1): 106-109.
[4] Alavi F, Mokari N, Javan M R, et al. Limited feedback scheme for device-to-device communications in 5G cellular networks with reliability and cellular secrecy outage constraints[J]. IEEE Transactions on Vehicular Technology, 2017, 66(9): 8072- 8085.
[5] 罗屹洁, 崔丽, 杨旸. D2D使能蜂窝网络中存在主动窃听者的物理层安全研究[J]. 信号处理, 2018, 34(1): 119-125.
Luo Yijie, Cui Li, Yang Yang. Research on physical layer security in D2D enabled cellular networks with an active eavesdropper[J]. Journal of Signal Processing, 2018, 34(1): 119-125.(in Chinese)
[6] Wang Wei, Teh K C, Li K H, et al. On the impact of adaptive eavesdroppers in multi-antenna cellular networks[J]. IEEE Transactions on Information Forensics and Security, 2018, 13(2): 269-279.
[7] Do Q V, Hoan T K, Koo I. Optimal power allocation for energy-efficient data transmission against full-duplex active eavesdroppers in wireless sensor networks[J]. IEEE Sensors Journal, 2019, 19(13): 5333-5346.
[8] Abedi M R, Mokari N, Saeedi H, et al. Robust resource allocation to enhance physical layer security in systems with full-duplex receivers: active adversary[J]. IEEE Transactions on Wireless Communications, 2017, 16(2): 885- 899.
[9] Chu Zheng, Nguyen H X, Le T A, et al. Game theory based secure wireless powered D2D communications with cooperative jamming[J]. IEEE Wireless Days Conference, 2017: 95-98.
[10] Zhang Ning, Cheng Nan, Lu Ning, et al. Partner selection and incentive mechanism for physical layer security[J]. IEEE Transactions on Wireless Communications, 2015, 14(8): 4265- 4276.
[11] Fang He, Xu Li, Zou Yulong, et al. Three-stage Stackelberg game for defending against full-duplex active eavesdropping attacks in cooperative communication[J]. IEEE Transactions on Vehicular Technology, 2018, 67(11): 10788-10799.
[12] Kun Z, Ekram H. Joint mode selection and spectrum partitioning for device-to-device communication: A dynamic Stackelberg game[J]. IEEE Transactions on Wireless Communications, 2015, 14(3): 1406-1420.
[13] Monderer, Shapley. Potential games[J]. Games Economic Behavior, 1996, 14(1): 124-143.
[14] La Q D, Chew Y H, Soong B H. Potential game theory applications in radio resource allocation[M]. Switzerland: Springer, Cham, 2016, 2: 24- 69.
[15] Xu Yuhua, Wu Qihui, Wang Jinlong, et al, Robust multiuser sequential channel sensing and access in dynamic cognitive radio networks: potential games and stochastic learning[J]. IEEE Transactions on Vehicle Technology, 2015, 64(8): 3594-3607.
