1 引言
气象雷达是气象探测的重要手段[1],机载气象雷达(WXR)的基本功用是探测飞机前方航路上的雷暴雨、冰雹、湍流、风切变等恶劣气象区域,其性能直接影响飞行的舒适性和安全性[2]。晴空湍流、干性低空风切变等不伴随可见气象,雷达回波信噪比很低,常规机载气象雷达尚无法有效检测,因此这些危害天气对飞行安全存在较大的威胁[3]。
机载气象雷达目标检测的本质是回波谱矩估计,气象目标类型和雷达回波的谱矩参数(平均多普勒频率和多普勒谱宽)密切相关[4]。低空风切变的检测依据风速(平均多普勒频率)随距离的变化特性,湍流检测依据一定区域内风速的变化剧烈程度(多普勒谱宽)。常规的谱矩估计方法是脉冲对法(Pulse Pair Processing,PPP)[5],该方法计算简单,在现有雷达中广泛应用。但PPP法仅适用于高信噪比的场景[6],针对晴空湍流、干性低空风切变的检测[7- 8],由于回波信噪比很低,PPP法估计误差太大[9]。针对此问题,目前学者们开展了一些理论研究,一般利用回波服从高斯谱[10]的性质通过建立频谱和协方差矩阵的参数化模型[11],构建代价函数进行估计。文献[12]提出了一种简单化的方法-随机最大似然法,该方法采用最大似然函数并采用迭代的思想求解;文献[13]提出了一种参数化的广义Capon谱矩估计方法,该方法构建代价函数时选择是在保证信号无失真的情况下让输出功率最小;文献[14]提出了一种利用协方差矩阵拟合湍流谱宽估计方法,该方法将湍流回波信号的协方差矩阵与参数化模型进行拟合,然后通过搜索代价函数来实现对湍流回波谱宽的准确估计;文献[15]提出了一种基于RELAX的气象雷达回波参数化谱矩估计方法,该方法采用RELAX的思想估计多个高斯谱信号混合时的谱矩参数。上述参数化方法虽然在低信噪比时性能较好,但是在求解代价函数时都涉及对谱矩的二维搜索,且每次搜索都需要对协方差矩阵进行求逆计算,运算复杂度大,实际应用受限。
本文在分析协方差矩阵参数化模型的基础上,得出其具有范德蒙结构[16]的形式,进而提出了基于傅里叶变换(DFT)的代价函数计算方法,避免了谱矩估计时的二维搜索,降低了运算复杂度。本文安排如下:第2部分给出了利用范德蒙特性质得出变换后的协方差矩阵,第3部分给出了基于DFT的谱矩估计,第4部分比较了传统方法和本文方法的复杂度,然后通过仿真实验验证了本文方法的有效性,最后给出结论。
2 回波协方差矩阵的范德蒙特性
气象目标和地面都由大量的散射粒子组成,属于分布式目标,因此其雷达回波频谱服从高斯分布。气象雷达在探测时,回波信号包括目标信号,地杂波以及噪声。
s(t)=r(t)+c(t)+n(t)
(1)
其中,r(t),c(t),n(t)分别为气象目标信号,地杂波和噪声。
气象雷达回波信号服从高斯分布,则其频谱的参数化模型为
(2)
其中
为噪声功率,N为高斯谱的个数,Si( f )可表示为
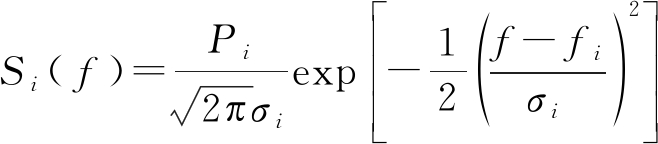
(3)
其中Pi, fi,σi分别为其中某一个目标回波的功率、平均多普勒频率和多普勒谱宽。通过功率谱可以得到信号的自相关函数,其参数化模型为
(4)
则推出雷达回波信号的协方差矩阵参数化模型可以写成
(5)
其中
R(f0,σf)=PA(a(f0))D(σf)AH(a(f0))
(6)
(7)
(8)
(9)
其中f0,σf为归一化的平均多普勒频率和多普勒谱宽,K为协方差矩阵的维数,H表示共轭转置,A(a(f0))为a( f )对角化处理矩阵。
通过对雷达回波信号的协方差矩阵进行分析,可以将其中a( f )分解为两个矩阵的乘积,则可写为如下形式:
a( f )=Tv( f )
(10)
可以得到具有范德蒙结构矩阵的形式
其中W为v( f )的维数,则T为W*K维的采样矩阵。根据气象雷达的回波信号服从高斯分布,变换后的协方差矩阵可表示为
(11)
其中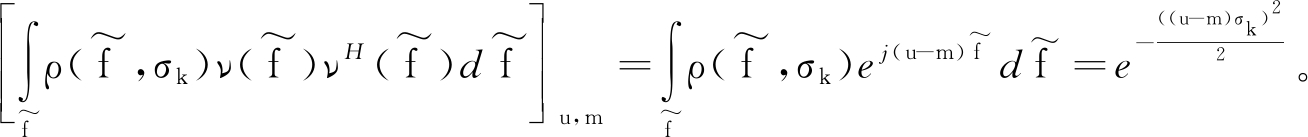
根据上述模型写成闭合解的协方差矩阵的参数化形式为
(12)
通过上述分析得出一种闭合解的协方差矩阵的参数化模型,不同于一般采用的在谱宽值不大的假设下的近似模型[17]。该模型可以在谱宽值较大时仍能保持适用性;且该模型具有范德蒙结构形式,可在估计代价函数时利用傅里叶变换(DFT)来计算,详见下述内容。
3 基于DFT的谱矩估计方法
3.1 估计代价函数
传统的子空间法利用信号子空间与噪声子空间具有正交性的特性,求解代价函数的同时估计谱矩参数,该方法首先对信号协方差矩阵的进行特征值分解,可以得到
(13)
其中
和
分别为目标回波信号和噪声的特征向量,Λs=
和
分别为目标回波信号和噪声的特征值,且λ1≥λ2≥…≥λK,r为信号子空间矩阵的维数。则基于子空间的代价函数可表示为
P(f0,σf)=||ξ1/2R(f0,σf)
=Tr{R(f0,σf)ξR(f0,σf)}
(14)
其中
表示矩阵的迹。
估计代价函数求得雷达回波的谱矩,可表示为
(15)
从上述分析过程可以看出子空间法在求解代价函数时涉及二维搜索,且精细化的搜索网格是提高估计精度的重要手段,会使运算量进一步增加。针对这一代价函数的计算,下面提出一种无需搜索的快速代价函数计算方法,具体过程如下。
前述提到,回波协方差矩阵可以表示为
(16)
其中,ρ为概率密度函数可表示为:
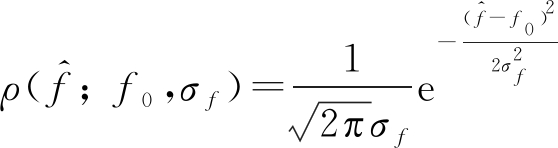
(17)
将a( f )分解后带入式(16)中得到的协方差矩阵写为如下形式:
(18)
将具有范德蒙结构特性的协方差矩阵模型带入式(14)中,则代价函数可表示为如下的积分形式,并计算下式中积分的黎曼和。
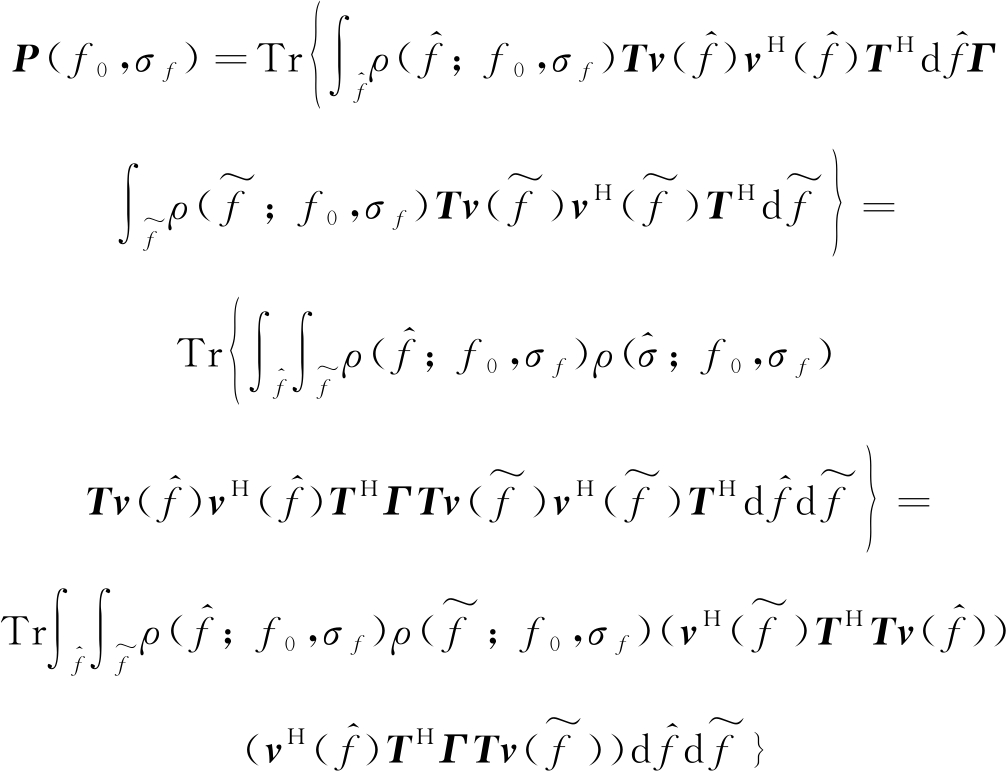
(19)
对上述代价函数进行分析,由于Tr(AB)=Tr(BA),则可以看出:
和
只需要进行一次计算,极大程度上降低了运算量。
和
的DFT形式可以写成如下形式
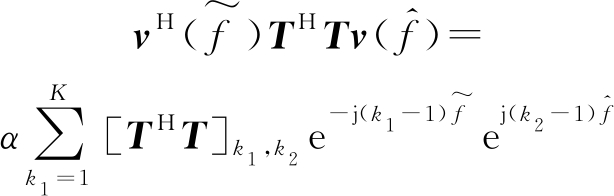
(20)
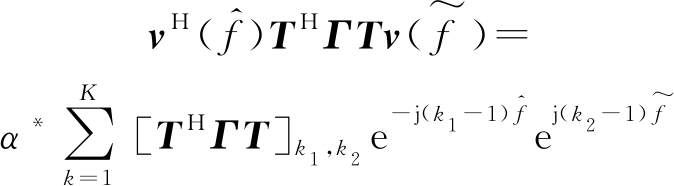
(21)
其中
则αα*=1,由公式分析可得,计算
和
时可对THT(和THΓT)的每一列的进行FFT,然后对所得结果每一行再进行IFFT计算。
通过上述分析,因为
具有范德蒙结构,则矩阵THT和THΓ T可利用FFT和IFFT进行计算,具体表示为如下的两个矩阵的形式,即:
M1=QF-T{FT{THT}}
(22)
M2=QF-1{FT{THΓ T}}
(23)
其中Q为计算FFT和IFFT的次数,F-1{·}表示对矩阵的每一列进行逆FFT(IFFT)计算,FT{·}和F-T{·}表示对矩阵每一列进行FFT和IFFT后,再对所得矩阵进行转置。然后计算M1和M2的Schur-Hadamard积得到矩阵M3为:
M3=Re{M1⊙M2}
(24)
其中Re代表矩阵的实数部分,⊙为Schur-Hadamard积。
由于M3是一个实对称矩阵,且厄米特矩阵的虚部(即M1⊙M2)总和为0,则仅需要对实数部分进行计算,并且由于气象目标雷达回波频谱服从高斯分布,则对代价函数进行变换可以写为如下形式:
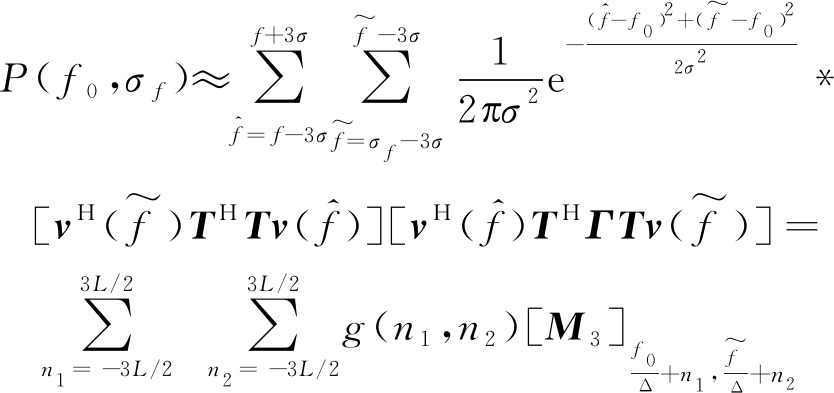
(25)
其中
表示二维离散高斯核函数,归一化谱宽为[-σ,σ],Δ=2σ/L为搜索间隔。在计算时仅需计算[f-3σ, f+3σ]区间范围内的值,因为高斯分布中该区间占函数总面积的99%以上,可在降低运算量的同时保证结果的准确性。
3.2 方法流程
由上述分析可得,本文给出的雷达回波谱矩的快速估计算法步骤如下:
步骤1 通过利用雷达回波协方差矩阵的范德蒙结构特性进行分解,得到变换后的协方差矩阵;
步骤2 利用变换后的协方差矩阵,对代价函数进行变换,可根据其范德蒙结构特性进行DFT计算,并根据式(22)、(23)、(24)计算矩阵M3;
步骤3 对M3的主对角线上从(f1, f1)到(f2, f2)的元素进行高斯加权滑窗,得到如式(25)所示的代价函数;
步骤4 估计代价函数,得到目标信号的平均多普勒频率和多普勒谱宽的值。
4 算法性能分析
4.1 算法复杂度分析
采用传统的子空间法[18]对平均多普勒频率和多普勒谱宽进行估计时,根据需要估计的精度,要在平均多普勒频率和多普勒谱宽坐标轴上选取多个点进行计算,且每一次计算都需要对信号协方差矩阵进行一次求逆运算,且在计算代价函数时需要进行二维搜索计算,计算复杂且运算量大。有效计算代价函数是降低复杂度的关键。本文算法复杂度主要集中在估计代价函数的过程,其中归一化平均多普勒频率和多普勒谱宽设为[f1, f2]和[σ1,σ2],设
因雷达回波频谱服从高斯分布,则τ=3。在计算M1时,因为只进行了一次计算,则其复杂度为O(1),在计算M2中THΓ T时需要O(4KK2+2K2K)=O(6K3),则在计算M3时复杂度为O(2JcJr)。如表1所示,比较了与传统的子空间法的运算量,设在平均多普勒频率搜索点数为J,多普勒谱宽搜索点数为S,可以看出本文方法的运算量要低于子空间法。
表1 子空间法和本文方法运算量对比
Tab.1 Complexity comparison of subspace-based and the proposed method
算法运算量子空间法O(3SJ(K4+1))本文方法O(6QK3+1+2JcJr+SJ)
由上述子空间法与本文方法对比分析中可得,如图1所示,将归一化多普勒频率设为-0.5～0.5,归一化谱宽设定为0～0.2, K为协方差矩阵的维数,可以更加直观的看出本文方法运算量要低于传统子空间法。
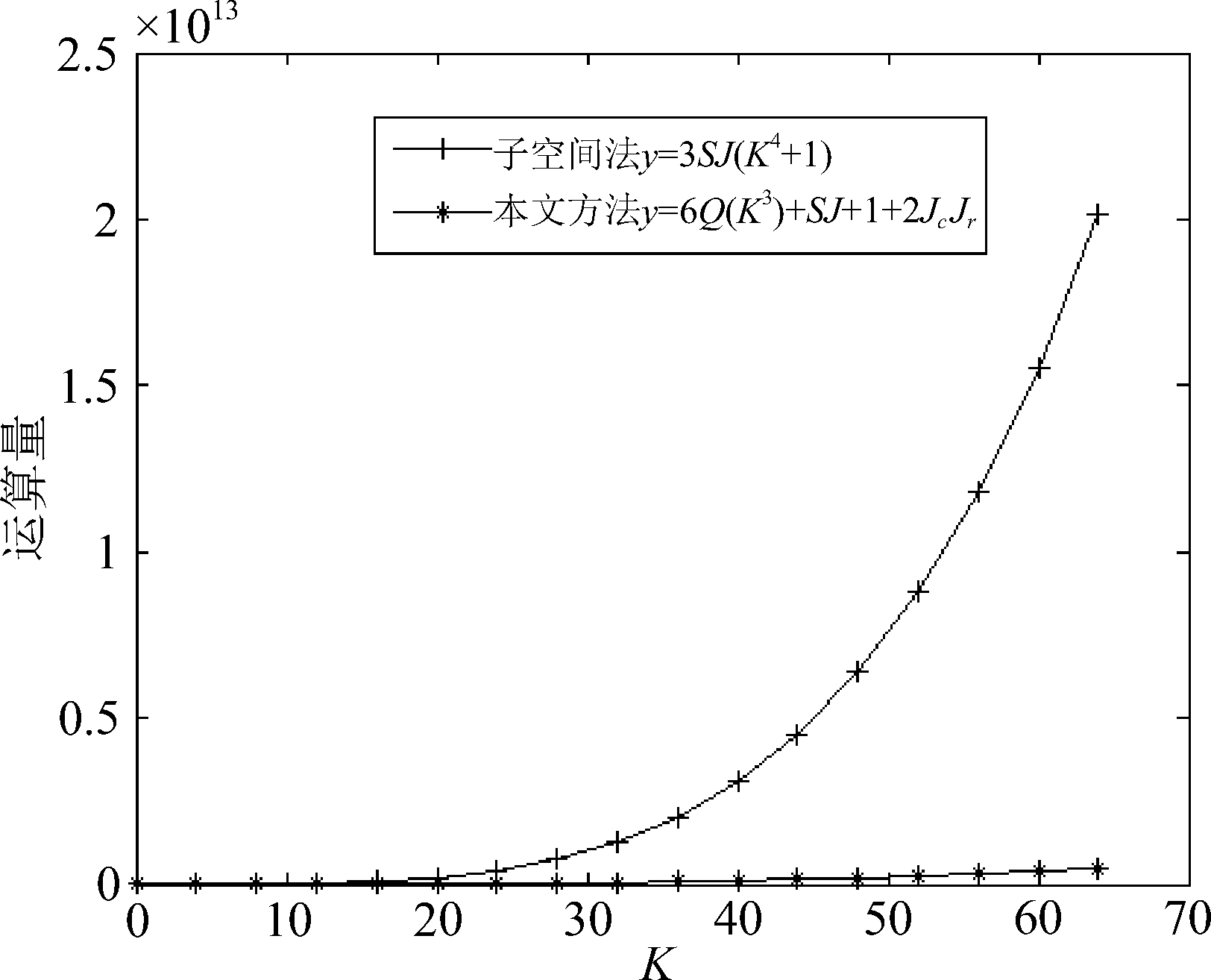
图1 子空间法和本文方法运算量对比
Fig.1 Comparison of the calculation volume of the subspace method and the method of this paper
4.2 仿真性能分析
4.2.1 代价函数分析
在对谱宽结果进行估计时,通过构建参数化模型,设定相应的多普勒谱宽值和平均多普勒频率值,令f0=0.2;σf=0.07,通过上述实验分析,如图2所示,图(a)为代价函数的三维分布图,图(b)为俯视图,可以看出在理论值处,所估计的代价函数达到最大值。
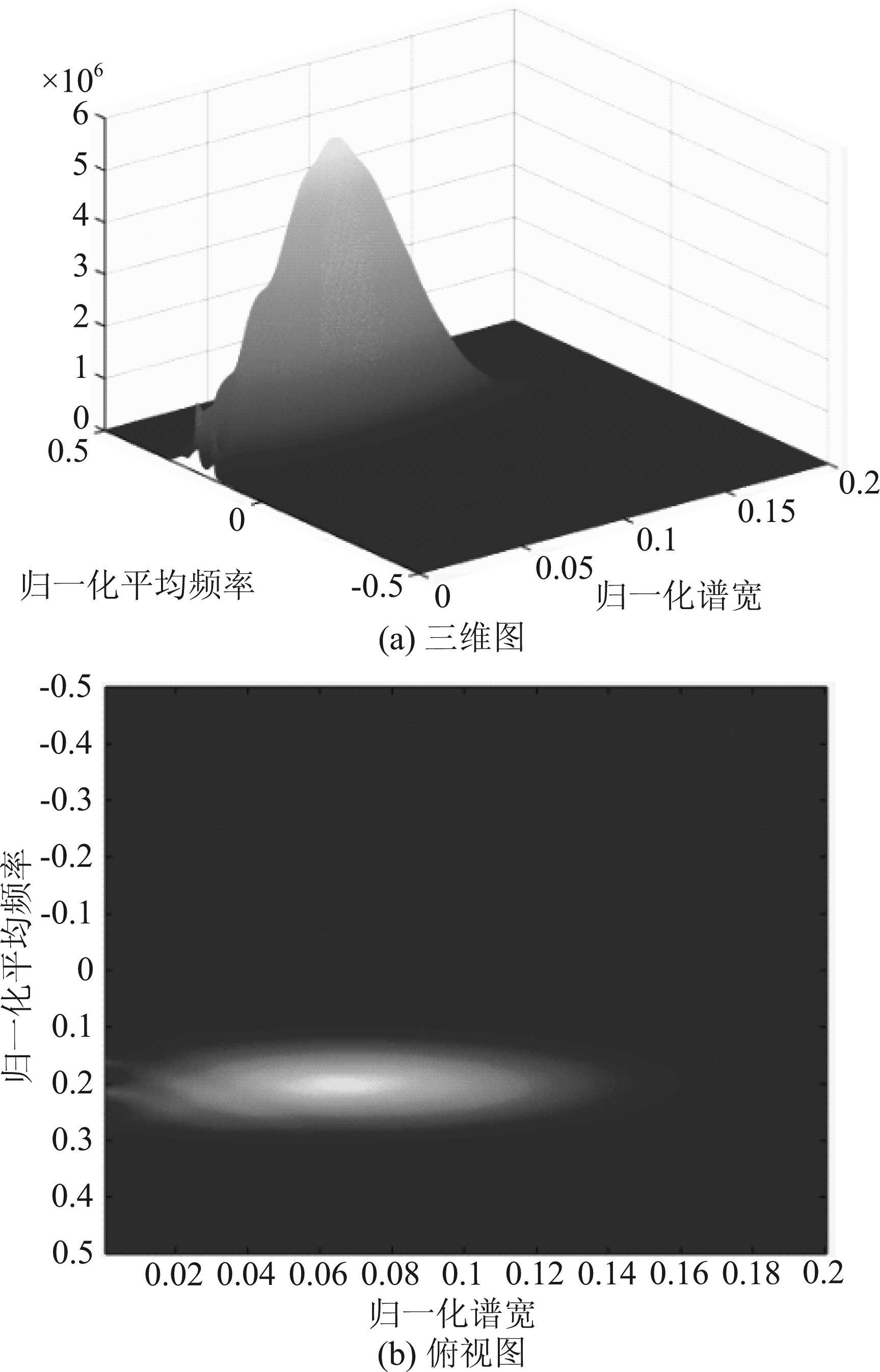
图2 本文方法的代价函数分布图
Fig.2 The cost function
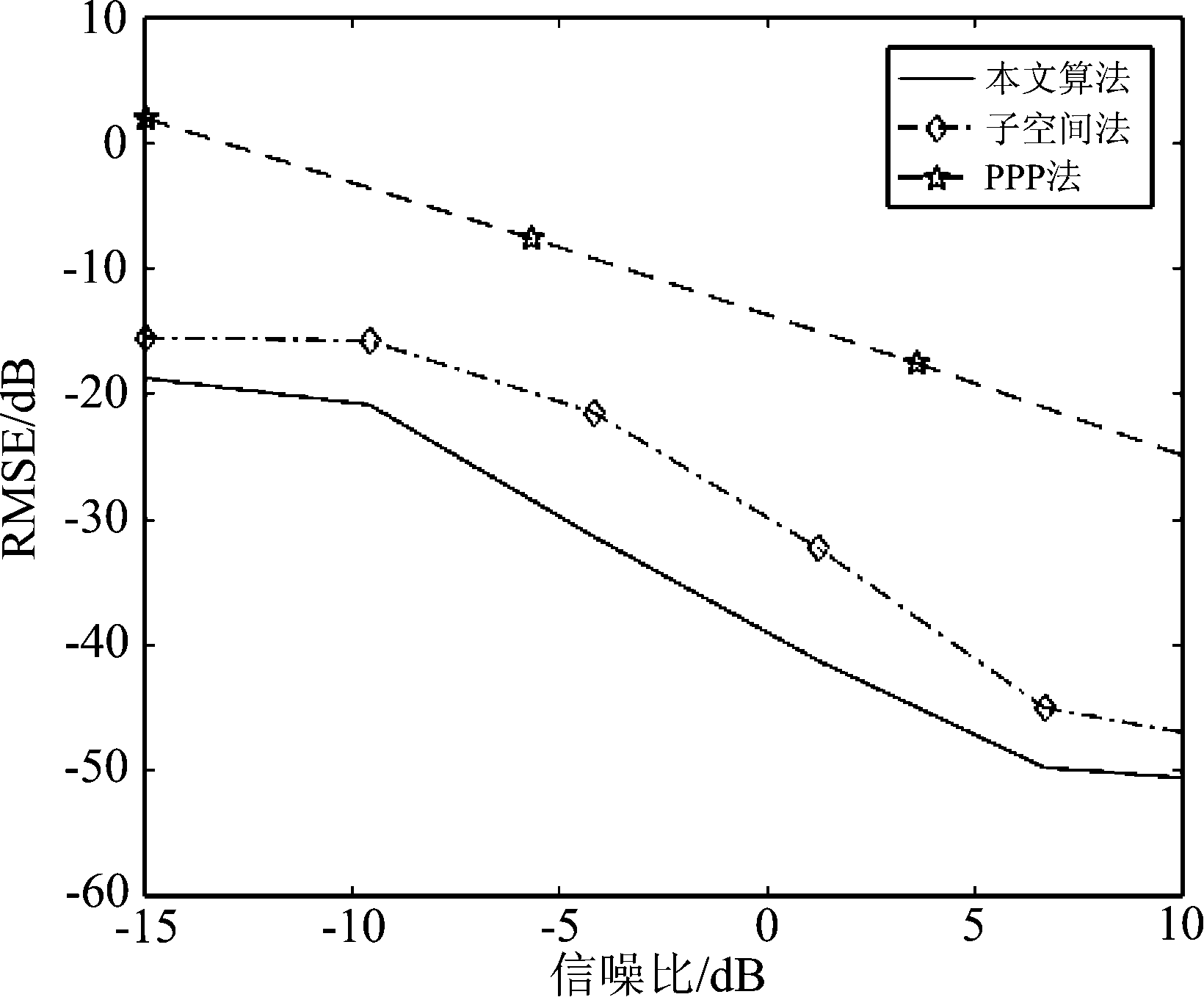
图3 不同算法的谱宽估计结果
Fig.3 Spectrum width estimation of different algorithms
4.2.2 不同信噪比下的性能
本部分通过仿真实验分析本文方法在低信噪比时的谱矩估计性能。如图3所示,选取固定平均多普勒频率(f0=0.2)和多普勒谱宽(σf=0.05),选取等间隔不断改变信噪比,对其结果进行100次蒙特卡洛实验,并求解均方误差。实验结果通过与子空间法和PPP法进行对比,表明该方法在低信噪比较低的情况下可较准确估计雷达回波谱矩,且性能优于子空间法,而PPP法在低信噪比时误差太大。
4.2.3 不同谱宽值的性能分析
本部分通过仿真实验分析本文方法在不同谱宽值时的谱矩估计性能。如图4所示,选取固定的平均多普勒频率(f0=0.2)和信噪比(SNR=5 dB),改变多普勒谱宽,并进行100次蒙特卡洛实验,求解均方误差。实验结果表明,本文方法在谱宽值较大时仍有较好的估计性能,进一步验证了前述理论分析时得出的结论。
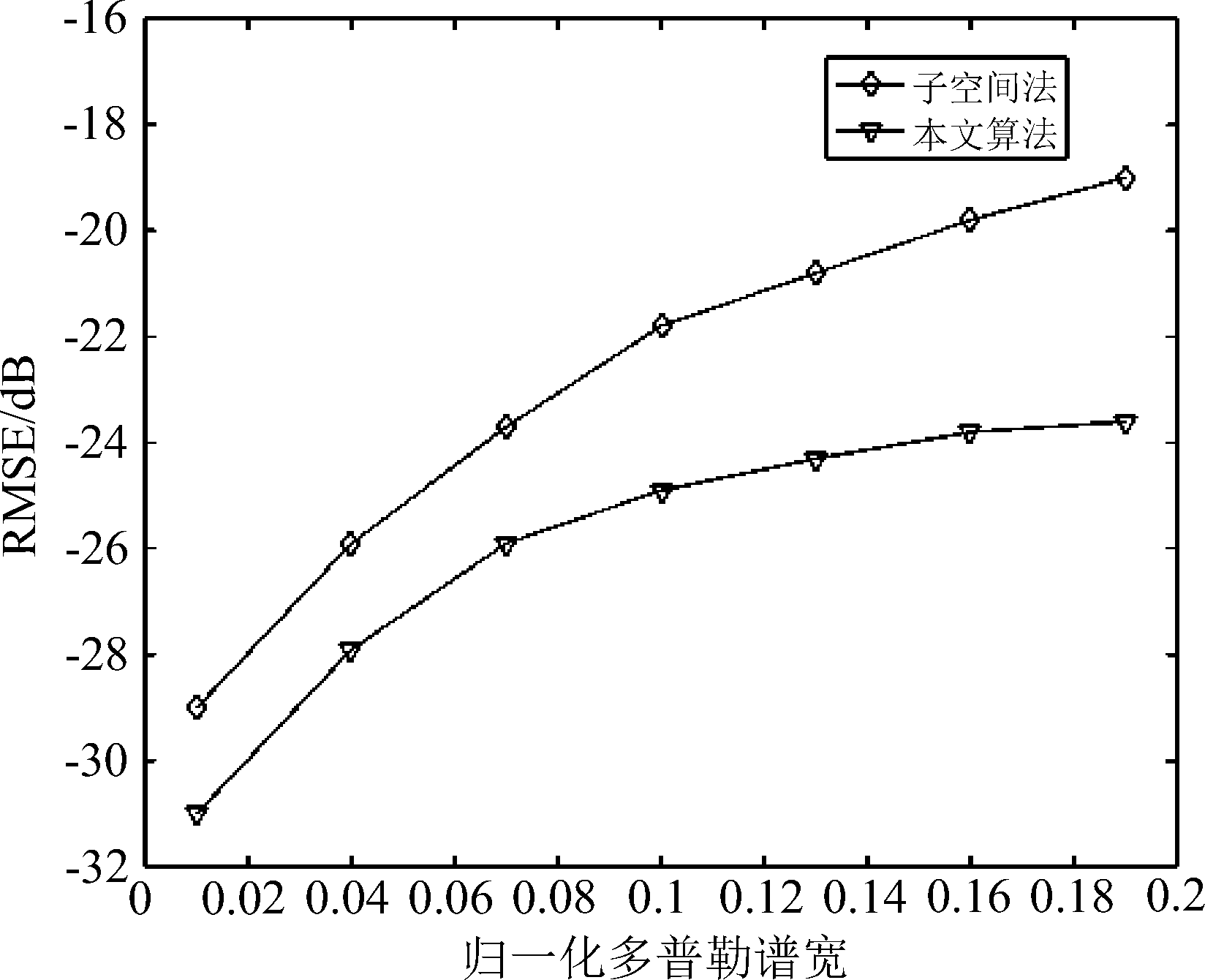
图4 改变谱宽对比本文方法和子空间法性能
Fig.4 Comparing the performance of this method and the subspace method by changing the spectral width
5 结论
本文提出了一种基于参数化的雷达回波谱矩快速估计的方法,可适用于低信噪比和谱宽值较大的情况。该方法通过对雷达回波的协方差矩阵进行分解,得出变换后具有范德蒙结构特性的一种闭合式协方差矩阵,因为该模型没有采用近似结构,故在谱宽值较大时仍保持较好的估计性能。再利用范德蒙结构具有的特性进而得出基于DFT的无需搜索的代价函数计算流程,该方法在估计代价函数时不需要进行频率分割,采用全部数据进行计算,降低了运算量的同时提高了估计性能。
[1] 石海杰, 李京华, 岳露. 机载气象雷达巡航阶段目标探测方法及仿真[J]. 系统工程与电子技术, 2018, 40(2): 280-286.
Shi Haijie, Li Jinghua, Yue Lu. Meteorological target detection method and simulation of airborne weather radar in cruise stage[J]. Systems Engineering and Electronics, 2018, 40(2): 280-286.(in Chinese)
[2] 张三爱. 机载气象雷达系统原理及常见故障定位排查分析[J]. 测控技术, 2018, 37(S2): 236-239.
Zhang San-ai. Airborne Meteorological Radar System Principle and Location Troubleshooting Analysis of Common Faults[J]. Measurement and Control Technology, 2018, 37(S2): 236-239.(in Chinese)
[3] 徐婷, 段炼, 顾雷, 等. 近5年冬季我国晴空颠簸的分布及气象要素特征[J]. 中国民用航空, 2017(1): 38- 40.
Xu Ting, Duan Lian, Gu Lei, et al. The distribution and meteorological characteristics of clear air turbulence in winter in recent 5 years in China[J]. China Civil Aviation, 2017(1): 38- 40.(in Chinese)
[4] Rambukkange M P, Verlinde J. Using Doppler Spectra to Separate Hydrometeor Populations and Analyze Ice Precipitation in Multilayered Mixed-Phase Clouds, IEEE Geoscience and Remote Sensing Letters, 2011, 8(1): 108-112.
[5] Warde D A, Torres S M. Improved spectrum width estimators for Doppler weather radars[C]∥Proc. 8th Eur. Conf. Radar Meteorol. Hydrol.(ERAD). 2014: 8.
[6] 卢晓光, 范源丹, 李海, 等. 利用RR-MWF的低信噪比下机载气象雷达回波谱矩估计方法[J]. 信号处理 2019, 35(7): 1125-1132.
Lu Xiaoguang, Fan Yuandan, Li Hai, et al. A RR-MWF Based Spectral Moments Estimation Algorithm for Airborne Weather Radar Echoes with Low SNR[J]. Journal of Signal Processing, 2019, 35(7): 1125-1132.(in Chinese)
[7] Kim J H, Chun H Y. A numerical simulation of convectively induced turbulence above deep convection[J]. Journal of Applied Meteorology Climatology, 2012 51(6): 1180-1200
[8] Chan P W, Lee Y F. Application of short-rang lidar in windshear alerting[J]. Journal of Atmospheric and Oceanic Technology, 2012, 29(2): 207-220.
[9] Yanovsky F J, Lekhovytskiy D I, Atamanskiy D V. Advanced algorithm of velocity measurement for modern meteorological radar[C]∥Radar Conference (EuRAD), 2012 9th European. IEEE, 2012: 134-137.
[10] 丁留贯. 气象雷达脉冲压缩技术研究[D]. 南京: 南京信息工程大学, 2007.
Ding Liuguan. The techniques of pulse compression for weather radar[D]. Nanjing: Nanjing University of Information Science and Technology, 2007.(in Chinese)
[11] Ligthart L P, Yanovsky F J, Prokopenko I G. Adaptive algorithms for radar detection of turbulent zones in clouds and precipitation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(1): 357-367.
[12] Boyer E, Petitdidier M, Lazarbal P. Stokastic Maximum Likelihood parametric estimation of overlapped doppler echoes[J]. Annales Geophysice, 2004, 22(11): 3983-3993.
[13] 卢晓光. 基于Capon的机载气象雷达回波谱矩估计[J]. 中国民航大学学报, 2014, 32(3): 27-30.
Lu XiaoGuang. Spectral moments estimation of airborne weather radar based on Capon[J]. Journal of Civil Aviation University of China, 2014, 32(3): 27-30.(in Chinese)
[14] 李海, 湛蕾, 吴仁彪. 基于空时协方差矩阵拟合的湍流谱宽估计方法[J]. 中国民航大学学报, 2018, 36(1): 23-27.
Li Hai, Zhan Lei, Wu Renbiao. Turbulence spectral width estimation method based on space-time covariance matrix fitting [J]. Journal of Civil Aviation University of China, 2018, 36(1): 23-27.(in Chinese)
[15] 卢晓光, 吴仁彪. 基于RELAX的气象雷达回波参数化谱矩估计方法[J]. 信号处理, 2011, 27(8): 1250-1253.
Lu Xiaoguang, Wu Renbiao. A Parametric Spectral Moments Estimation Algorithm for Weather Radar Echoes Employing RELAX[J]. Signal Processing, 2011, 27(8): 1250-1253.(in Chinese)
[16] Kurpjuhn T R, Ivrlac M T, Nossek J A. Vandermonde invariance transformation[C]∥Acoustics, Speech, and Signal Processing, 2001. Proceedings. (ICASSP'01). 2001 IEEE International Conference on. IEEE, 2001.
[17] Pinsky M, Jordi F I V, Otto T, et al. Application of a Simple Adaptive Estimator for an Atmospheric Doppler Radar[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(1): 115-127.
[18] 卢晓光. 机载气象雷达信号处理若干关键技术研究[D]. 天津: 天津大学, 2014.
Lu Xiaoguang. Research on Key Techniques of Signal Processing for Airborne Weather Radar[D]. Tianjin: Tianjin University, 2014.(in Chinese)
