1 引言
在现代通信系统中,二进制偏移载波(binary offset carrier, BOC)通过加入副载波调制将原信号频谱搬移到中心频点两侧,改善了卫星导航信号之间相互干扰以及频段拥挤的问题[1-2]。同时包括交替二进制偏移载波(alternate binary offset carrier, AltBOC)信号在内的其他衍生信号相继被提出。恒包络AltBOC信号是在标准AltBOC信号基础上加入互调分量并引用复数形式的重建副载波,使其在卫星导航系统经过射频功率放大器时避免非线性失真的发生。AltBOC信号与传统BOC信号相比具有测距精度高、抗干扰能力强与较好的码跟踪等性能[3],在卫星导航领域中具有广阔的应用前景。对该信号进行研究对今后在我国“北斗”系统中应用具有重要理论参考价值。而估计信号序列的伪码周期、副载波速率、载频以及组合码序列作为实现信号解扩频调制以及完成信号捕获跟踪的基础,是一个非常值得研究的课题。
AltBOC(15,10)信号已被Galileo系统的E5a与E5b频段所采用,是目前全球卫星导航系统(global navigation satellite system, GNSS)中最复杂的信号,国内外关于其研究主要集中在调制方式分析[3- 4]、功率谱的推导[5- 6]以及捕获跟踪[7- 8]上,针对其码序列估计文献相对较少。已有的关于BOC信号组合码序列以及DSSS信号伪码序列盲估计方法,如文献[9]针对BOC信号组合码估计提出一种消除酉模糊现象的改进SVD算法;文献[10]将长码直扩信号构造成含有缺失数据的信号模型,再利用最小二乘投影算法对其扩频序列进行盲估计;文献[11]针对SVD算法估计CBOC组合码序列计算量和存储量大的问题,提出一种无监督NN的自适应主分量神经网络算法对CBOC信号组合码序列进行盲估计;而AltBOC信号使用的互调分量和复数形式的四值副载波调制机制极为复杂,文献[9-11]采用的各种算法已不再适用于对其组合码序列进行估计。针对这一问题,参考无监督学习中的K-means聚类算法[12],通过寻找数据内部存在的分布结构对数据集进行划分以达到聚类的效果,文献[13]将该算法运用到多序列直扩信号的盲解扩中,但是所采用的随机选取聚类初始均值向量会导致聚类效果较差,从而会降低信号伪码序列估计的正确概率。
本文对AltBOC(15,10)信号调制方式进行分析,并根据信号特点采用改进的K-means算法对其进行组合码序列盲估计,首先对信号取实部(该复杂信号实部包含传输信号的全部信息),并将其分段成单倍组合码周期窗长的不重叠观测数据矩阵,然后采用K-means算法对数据矩阵进行组合码序列盲估计,并通过得到的组合码合作解扩信息码。本文与文献[13]算法不同的是通过相似性原理[14]提前选取初始聚类均值向量,提高组合码序列估计的准确性。仿真实验表明利用K-means聚类算法能够在信噪比-15 dB下估计组合码序列的错误概率小于0.1。
2 AltBOC(15,10)调制信号模型
2.1 AltBOC信号调制方式分析
AltBOC(15,10)调制同时传输四路信号,在中心频率为1176.45 MHz的E5a子频段与中心频率为1207.14 MHz的E5b子频段分别传输一路数据信号与一路导频信号,基带AltBOC(15,10)调制信号可以表示为:
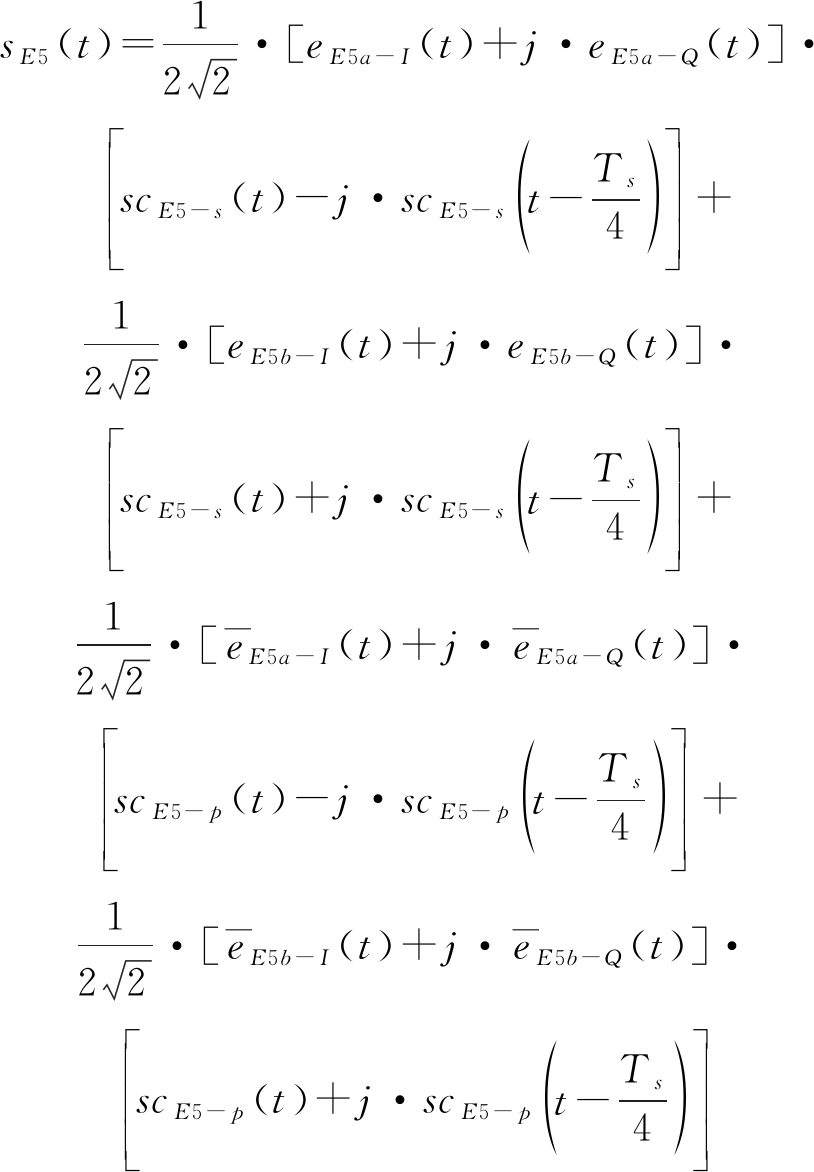
(1)
其中
表示互调分量,其作用是使调制结果不具有零振幅,表达式为:
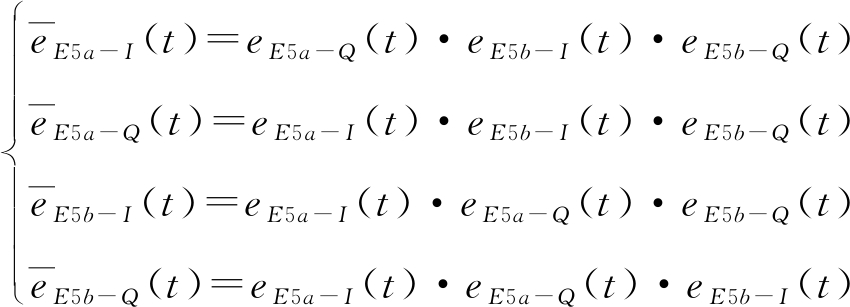
(2)
式中eE5a-I(t)、eE5b-I(t)分别表示E5a与E5b传输的数据信道信号经伪码调制获得的扩频序列,eE5a-Q(t)、eE5b-Q(t)则是E5a与E5b传输的导频信道信号。scE5-s(t)、scE5-p(t)为四电平副载波,其中scE5-s(t)表示单信号副载波,scE5-p(t)表示积信号副载波,其一周期波形如图1所示,表达式为:
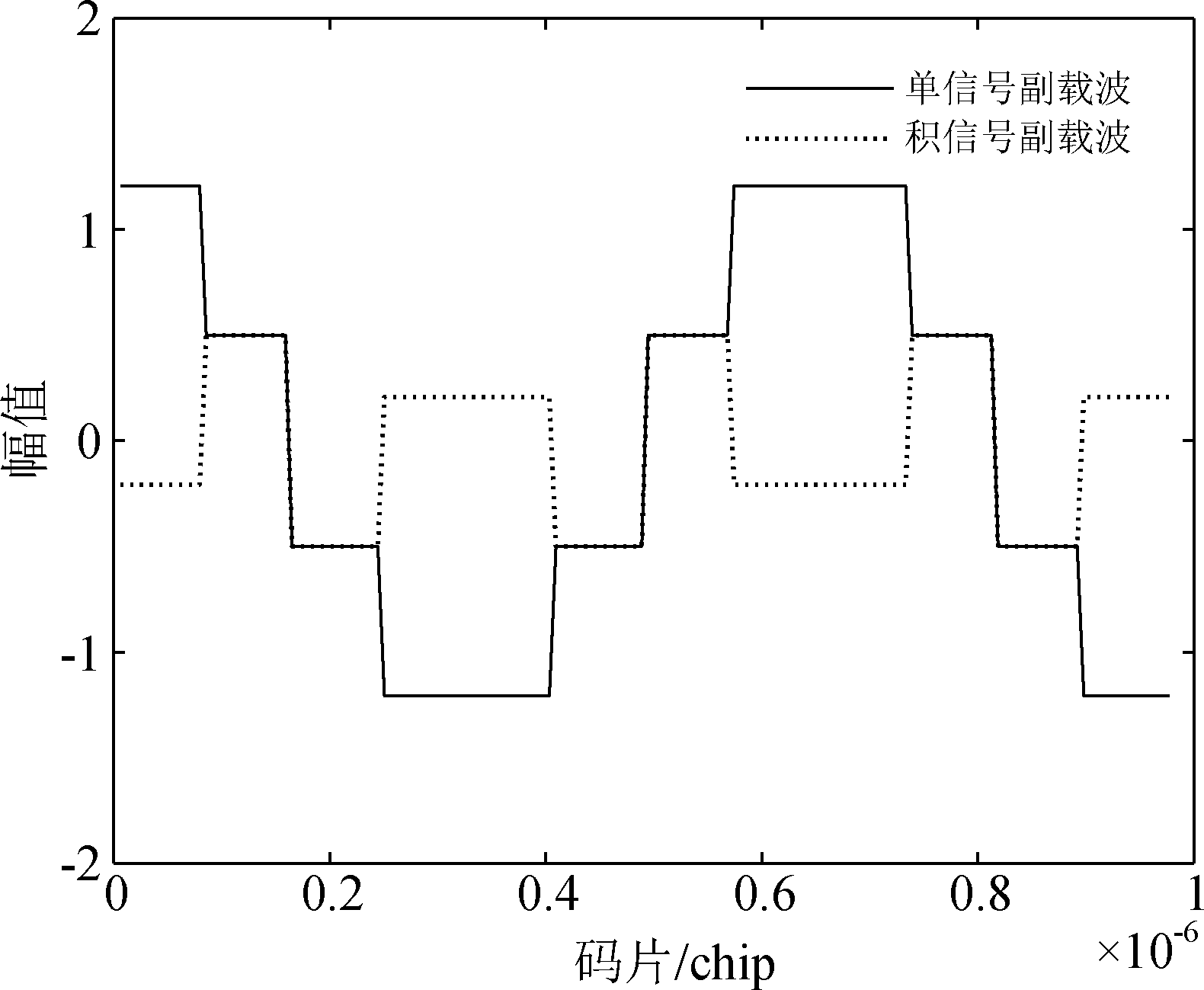
图1 恒包络AltBOC(15,10)信号的副载波
Fig.1 The subcarrier of the constant-enveloped AltBOC(15,10) signal
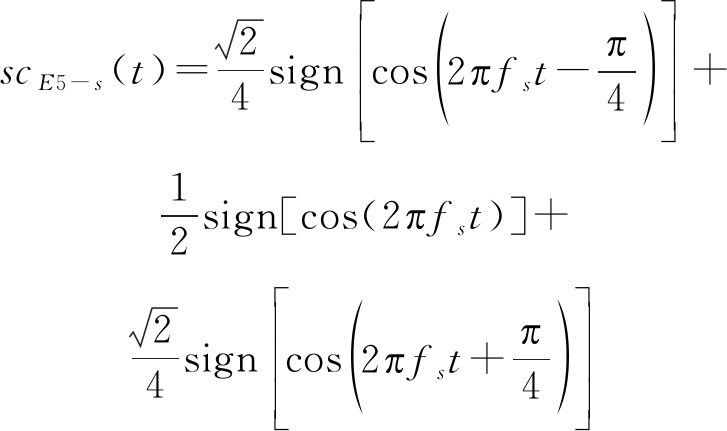
(3)
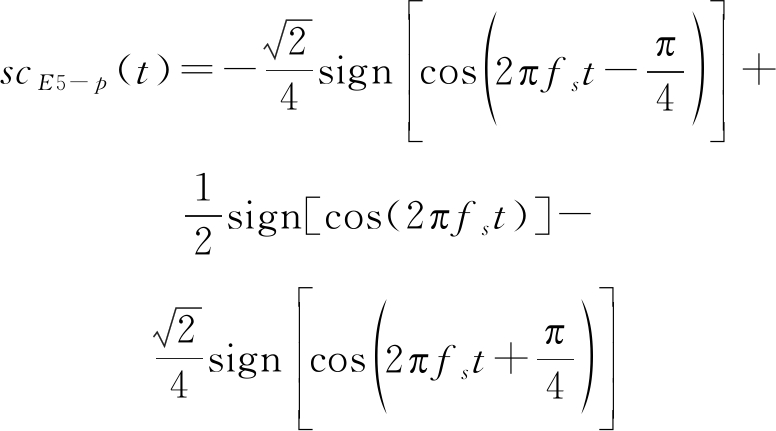
(4)
对AltBOC(15,10)信号取实部可以得到式(5):
s(t)=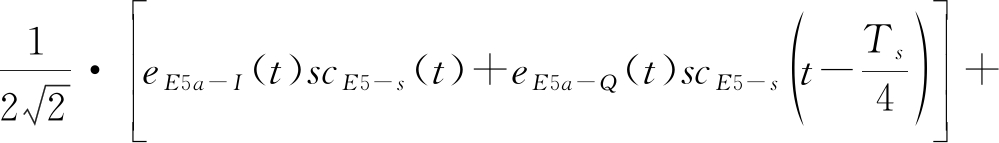
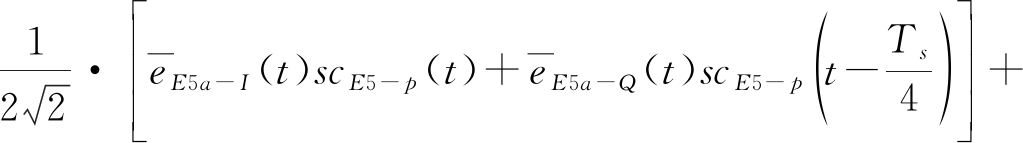
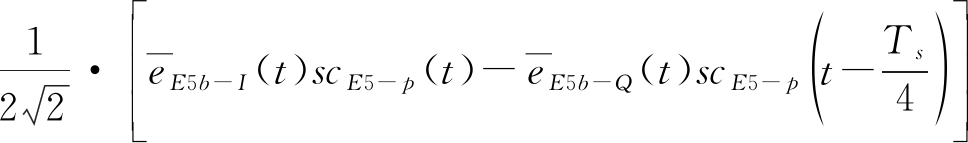
(5)
为方便信号组合码估计,将AltBOC(15,10)信号的信息序列与组合码分开进行表示,构造2.2节信号模型。
2.2 估计组合码相应的AltBOC(15,10)信号模型
根据2.1节对恒包络AltBOC信号的调制方式分析,可将其构建如下信号模型:将传输的信息码bn(t)经过串/并变换转换为2比特并行数据分别在不同的数据通道进行传输,即将每2比特信息码分为一组,这时每组信息码可能存在四组不同状态,根据每组信息码状态的不同来选取相应的组合码序列(这里将不同数组所对应的输出数据称为组合码)。经过串/并变换后的信息码可表示为:
(6)
式中
表示对传输的信息码元进行分组,dl表示每组内信息码元,hd(t)为归一化矩形脉冲函数,Td为每位信息码元的周期,T0=2Td表示每组信息码元的周期。
设p=[0,1,2,3]表示每传输一组信息码所对应的4种组合码序列编号。根据式(5)可将AltBOC信号组合码看作8路副载波调制伪码序列之和,可以表示为:
(7)
式中, j=0,1,2,3,Nc为伪码序列长度,cj,i,n∈{±1}表示第j条组合码的第i条子组合码序列的第n个伪码码元,Ns为副载波序列长度,ψi,n,m表示第i条子组合码序列的第n个伪码码元调制的第m位副载波幅值,uTs是幅度为1且持续时间为Ts的矩形脉冲,Tc和Ts分别表示伪码码片宽度和副载波码片宽度,且有T0=2Td=NcTc=NcNsTs。扩展后的组合码序列可表示为:
(8)
AltBOC(15,10)信号经过理想的加性高斯白噪声信道后可以表示为:
x(t)=Axs(t-τ)+ν(t)
(9)
式中,Ax表示信号幅值,τ为传输时延,ν(t)表示零均值、方差为
的理想高斯白噪声,且ν(t)和s(t)互不相关。假设AltBOC(15,10)信号的组合码周期和码片速率已知,通过组合码码片速率对上式进行采样,可以得到采样后的离散基带AltBOC(15,10)信号模型为:
x(n)=Axs(t-τ)+ν(t)|t=nTs=s(n-τ)+ν(n)
(10)
然后按AltBOC(15,10)信号组合码序列周期NcNsTs对采样后的离散信号序列x(n)进行分段,这时每段信号含NcNs-1个采样点,有:
xm=[x(mNcNs-NcNs) x(mNcNs-NcNs+1)… x(mNcNs-1)]
(11)
式中,m=1,2,…,M表示第m个信号分段,M表示总的分段数,从而采样后的矩阵表达式为:X=[x1 x2 … xM]T。
3 改进K-means聚类算法对AltBOC(15,10)信号组合码序列盲估计
根据AltBOC(15,10)信号调制方式的特性提出一种无监督聚类算法中较为经典的K-means算法对其组合码序列进行盲估计,首先选取各聚类初始均值向量,通过逐一计算每一数据到聚类均值向量的距离划分成若干簇,并不断更新各簇的均值向量直到其收敛。聚类完成后,同一聚类之间的数据相似性较高,不同聚类间的数据相似性较低,以此达到分类的效果。通过这种方法可以有效地对AltBOC(15,10)信号组合码进行估计,但是随机选取聚类初始均值向量会影响数据估计的准确性,并有可能造成局部最优的情况[15-16]。不失一般性,下文将聚类数k值一般化,根据相似性法则对初始均值向量进行选取。
3.1 K-means算法初始均值向量的确定
通过相似性原理选取观测数据中距离较远的样本作为各聚类的初始均值向量。根据2.2节可将AltBOC(15,10)信号表示为矩阵形式:
X=[x1 … xi … xM]T, i=1,2,…,M
(12)
式中,xi=(xi1 xi2 … xiN)表示第i个分段的数据向量,N表示单倍组合码周期长度,两数据向量xi与xj之间的相似度可表示为:
(13)
当聚类数为任意k值时,可首先求观测数据集中任两个样本之间的距离,选取满足
的两个u1和u2作为该数据集合的前两个初始均值向量,在剩余的(M-2)个数据段中,找到满足
的第3个聚类的初始均值向量u3,依次类推,选取到k个初始均值向量。
3.2 AltBOC(15,10)信号组合码和信息码的盲估计
对于K-means算法,求每一数据样本与其聚类均值向量的平方误差,并将其最小化,可以表示为:
(14)
式中
表示x所属簇的均值向量,E的意义在于描述了每一簇内数据的紧密程度,取值越小各簇内数据越紧密。
取式(14)最小值需要考察观测数据集划分为簇的每一种情况,并不容易进行计算,因此K-means算法通过迭代优化该平方误差求其近似解,并对所得聚类进行提取,完成AltBOC(15,10)信号组合码序列的估计,具体的算法步骤如下:
步骤1 初始化τ=0,迭代次数α=0,构建接收信号的数据集X,令聚类数k=4,初始化聚类所得簇C={C1 C2 C3 C4}=∅。
步骤2 通过3.1节最大距离检测的方法,对聚类的初始均值向量进行选取,可以表示为:
Uk=[u1,u2,…,uk]
(15)
步骤3 令α=α+1,依次计算数据集X中的数据与各聚类内均值向量ui的距离并将其划分到距离最近的聚类中,公式表达如下:
dji=||xj-ui||2
(16)
式中,xj表示第j个数据样本,ui表示第i个簇的均值向量。
步骤4 根据
更新各聚类样本的均值向量。
步骤5 判断步骤4是否达到收敛要求
满足,保持当前均值向量不变,不满足则返回步骤3。
步骤6 当各簇内均值向量均未再更新,结束循环,完成聚类。
步骤7 对估计到的k个簇中心样本进行提取并设置分类阀值(副载波为四值副载波,导致组合码也为四值)对AltBOC(15,10)信号组合码进行估计,并通过估计到的组合码完成信号盲解扩。
改进K-means算法对AltBOC(15,10)信号组合码以及信息码序列估计的基本流程如图2所示。
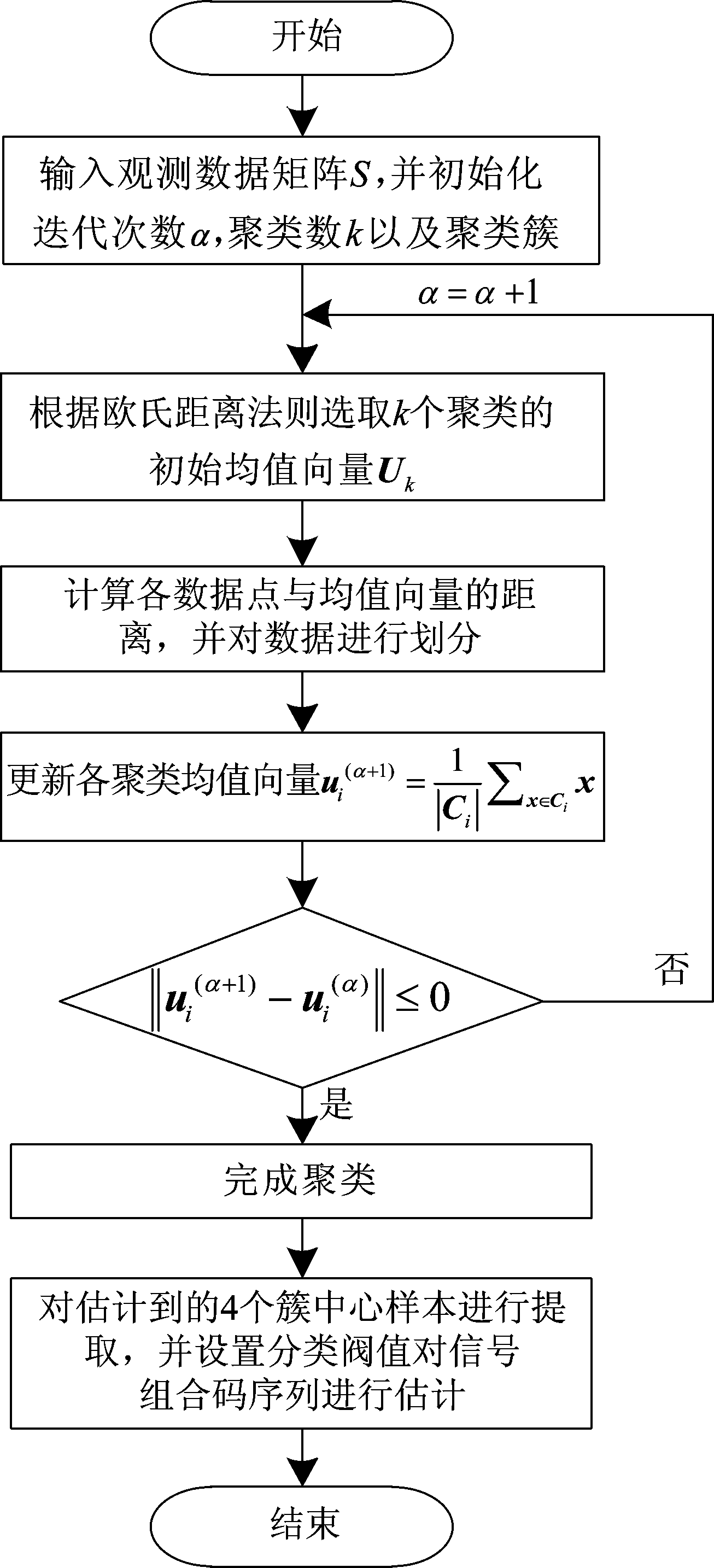
图2 本文算法的基本流程
Fig.2 The basic flow of the algorithm in this paper
4 仿真实验与结果分析
(1)组合码序列错误概率的计算:
(17)
即对进行蒙特卡洛实验中出现估计错误的码元数目与码元总数的比值取平均。
(2)信噪比的公式表达:
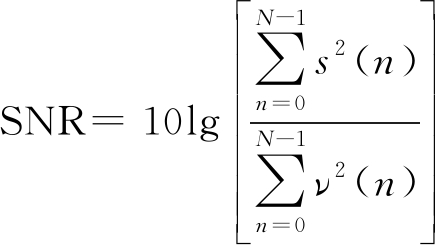
(18)
式中
和
分别表示信息码元的能量以及噪声能量。
(3)在实验2到实验5中,均设置信噪比SNR=-25～0 dB,且在每一SNR下进行300次蒙特卡洛仿真。
实验1 通过估计AltBOC(15,10)信号组合码序列与真实值相对比来验证本文算法的有效性,设置在信噪比SNR=5 dB的情况下,取伪码序列长度Nc=127,即组合码序列长度N=127×12=1524,判值电平取
实验结果如图3、图4所示(仅截取一部分码值)。
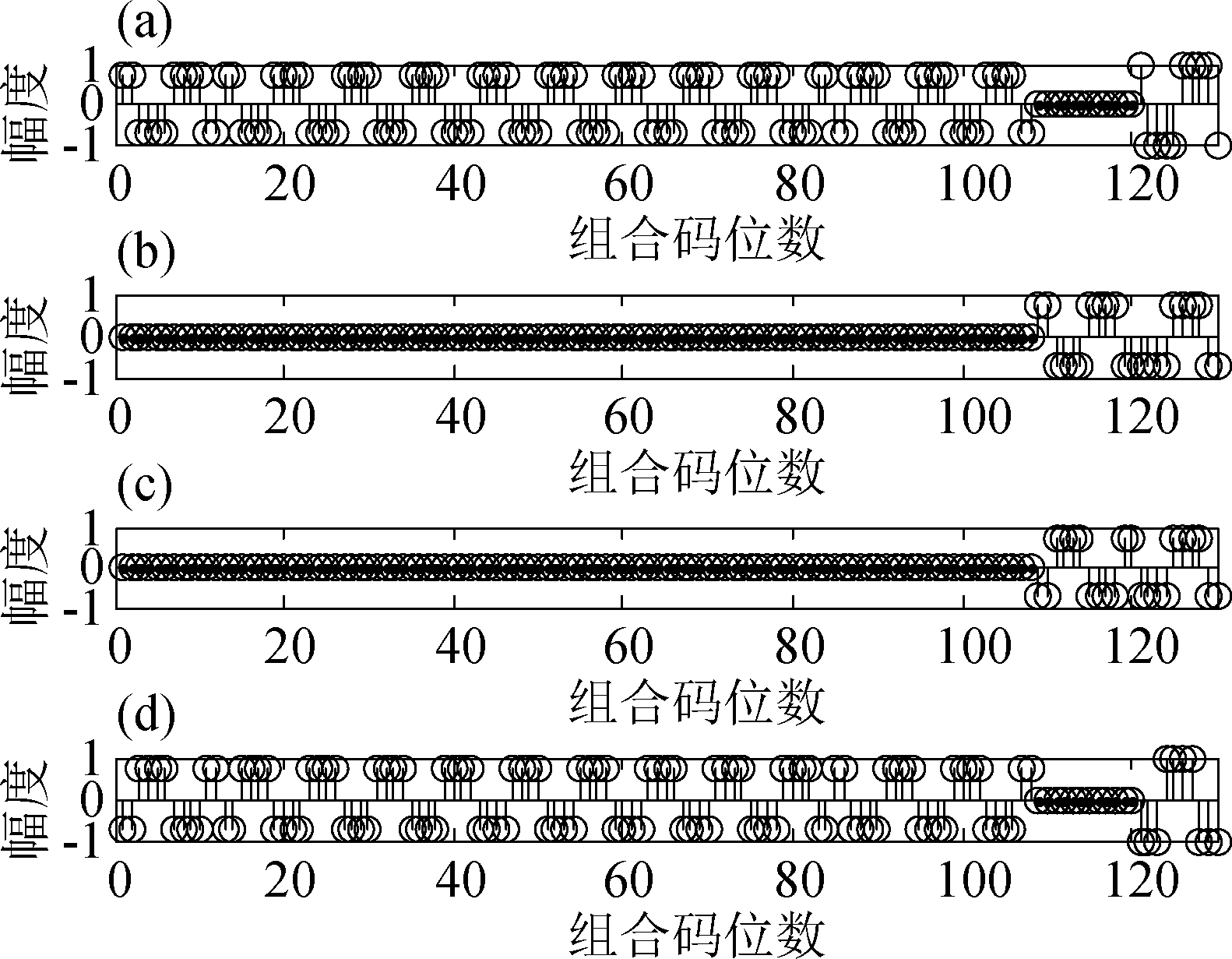
图3 AltBOC(15,10)信号组合码序列真实值((a)、(b)、(c)、(d)分别表示4组组合码序列真实值)
Fig.3 True value of AltBOC(15,10) signal combination code sequence ((a)、(b)、(c) and (d) represent the real values of the four combined code sequences respectively)
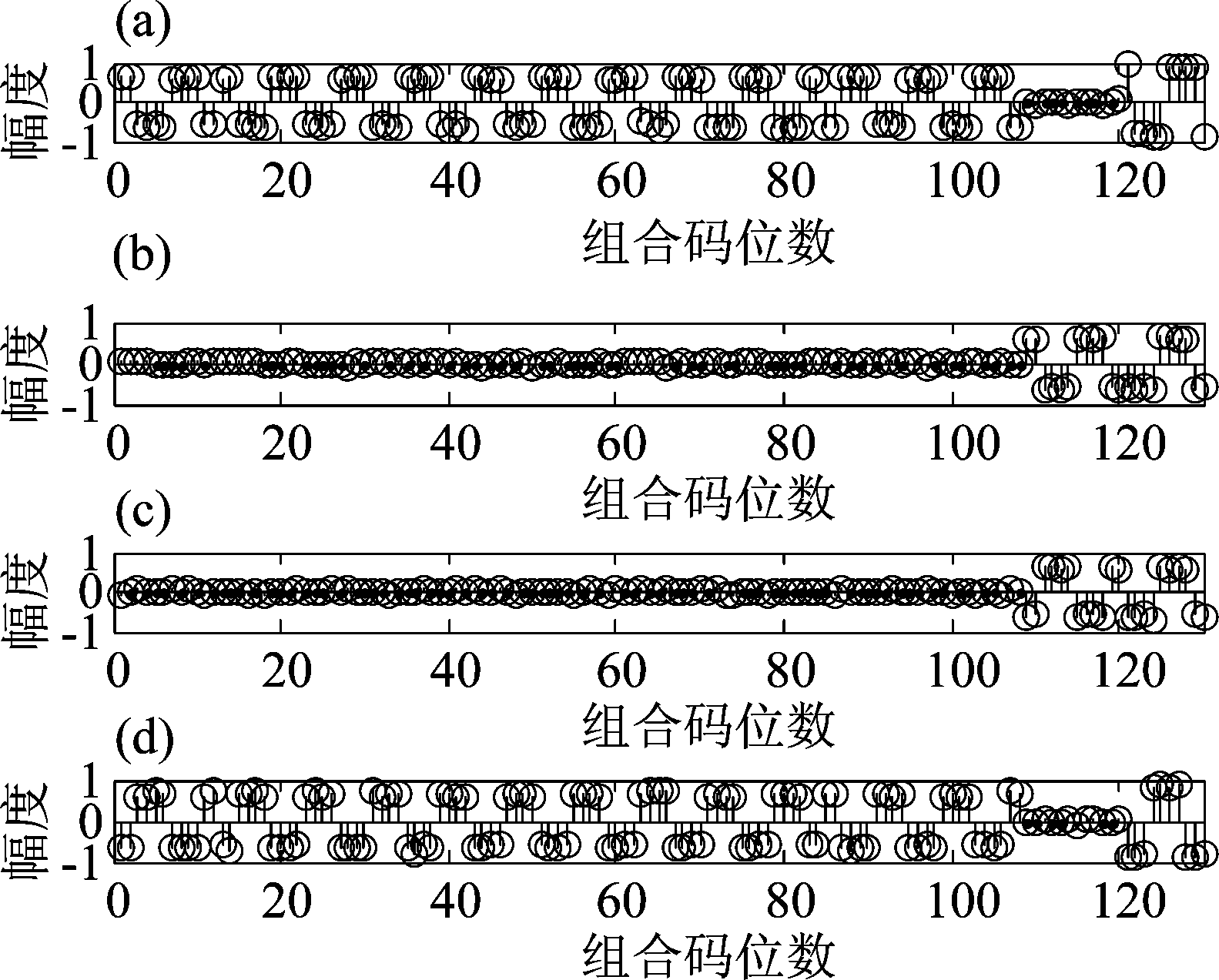
图4 AltBOC(15,10)信号组合码序列估计值((a)、(b)、(c)、(d)分别表示4组组合码序列真实值所对应的估计值)
Fig.4 Estimated value of AltBOC(15,10) signal combination code sequence ((a)、(b)、(c) and (d) represent the estimated values corresponding to the true values of the four groups of combination code sequences)
从图3、图4可以看出,AltBOC(15,10)信号组合码的幅值具有四个电平,在信噪比5 dB的情况下,估计的组合码序列与真实值完全对应(对估计得到的组合码进行阀值判决处理),因此,本文所提算法能够有效估计出AltBOC(15,10)信号组合码序列。
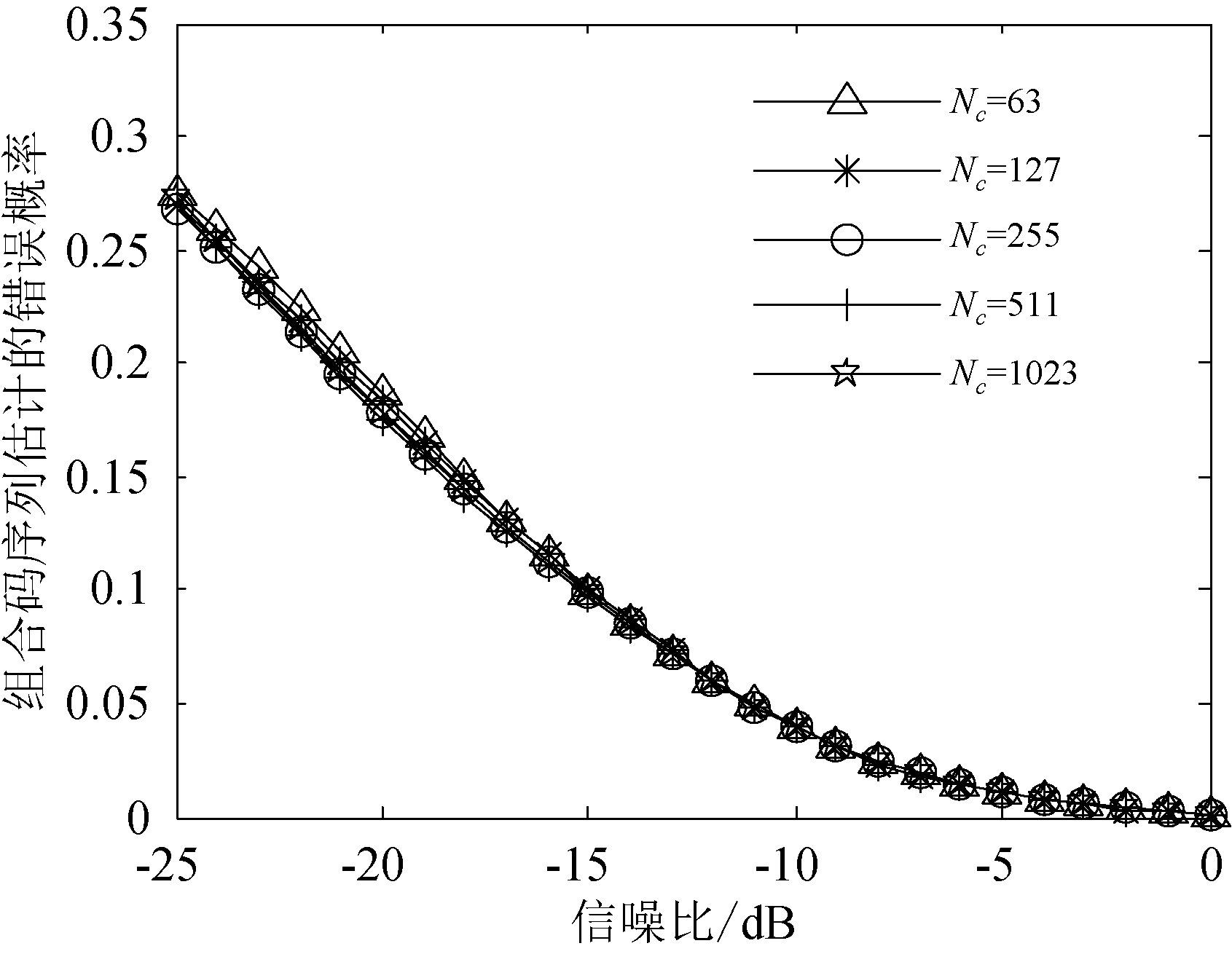
图5 不同伪码序列长度下组合码序列估计的错误概率
Fig.5 Error probability estimation of composite code sequences with different pseudo-code sequence lengths
实验2 在本实验中,通过比较不同伪码序列长度下本文算法估计组合码序列的误码率来验证伪码长度对算法性能的影响,分别取Nc=63 chips,127 chips,255 chips,511 chips,1023 chips,信息码组数M=1000组,所得仿真结果如图5所示。
由图5可知,不同伪码序列长度下本文算法估计组合码序列的误码率皆随着SNR的增加而降低,且当SNR固定为某一值时,不同组合码序列长度下估计的错误概率变化不大,这是因为组合码序列越长,信号的扩频处理性能也会相对增强,但由于其副载波四值性质,使得其抗噪声能力变差,所以综合来看变化不大。
实验3 比较本文算法在不同的信息码组数下估计AltBOC(15,10)信号组合码序列的错误概率,设置伪码序列长度为Nc=127 chips,信息码组数取M=300,500,1000,2000,所得仿真结果如图6所示。
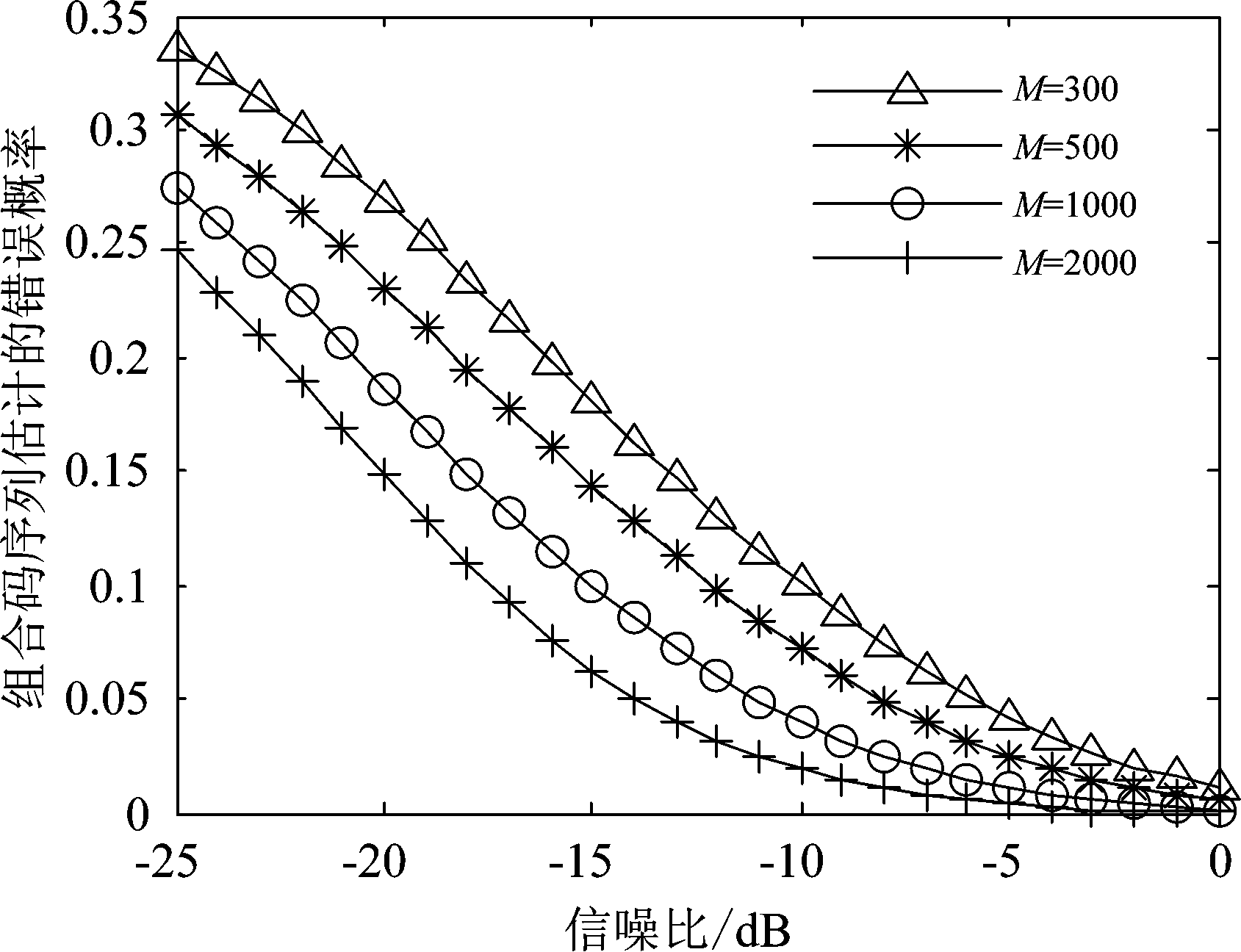
图6 不同信息码长度下组合码序列估计的错误概率
Fig.6 Error probability of combination code sequence estimation at different information code lengths
由图6可知,本文算法在不同的信息码组数下估计组合码序列的错误概率皆随着信噪比的增加呈现逐渐减小的趋势,并且当信噪比固定时,估计组合码序列的错误概率随着信息码长度的增加而减少,在信息码组数分别取300、500、1000、2000,组合码序列估计的错误概率达到0.1以下分别在信噪比为-10 dB、-12 dB、-15 dB、-17 dB,这是因为信息码越长,观测数据越多,为组合码估计所提供的有用信息越多,从而估计组合码序列的正确概率越大。通过实验得出可以通过增加信息码长度来提高组合码序列估计的正确概率。
实验4 比较本文方法与文献[13]算法估计组合码序列的错误概率对比,取信息码序列组数M=1000,伪码序列长度设置为Nc=127 chips,所得仿真结果如图7所示。
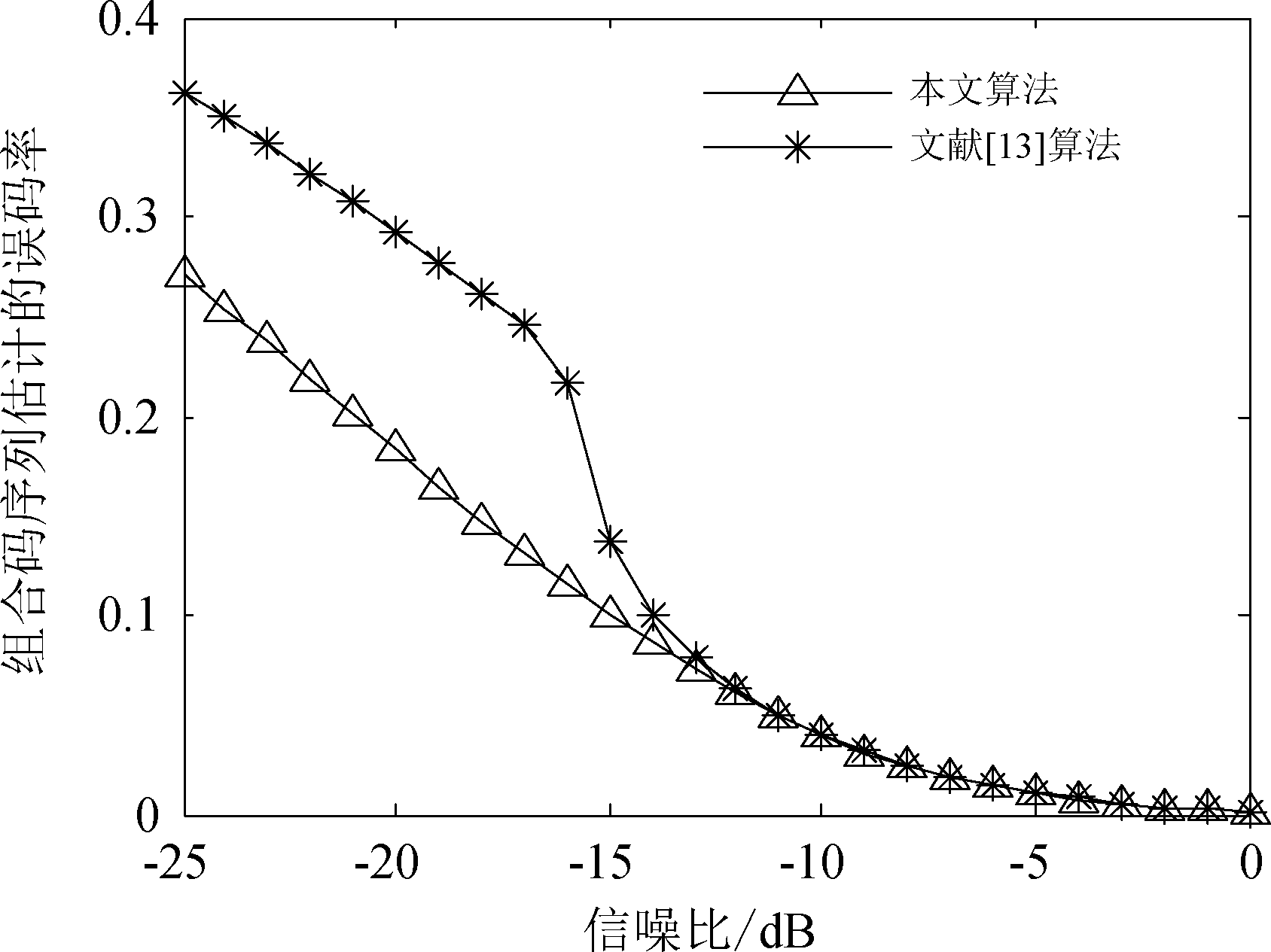
图7 不同算法对组合码序列估计性能对比
Fig.7 Comparison of estimation performation of combination code sequence by different algorithms
由图7可知两种算法对AltBOC信号组合码序列估计的错误概率随着信噪比的增加呈现递减的趋势,且在一定SNR下,本文算法估计组合码序列出错概率明显低于文献[13]算法,本文算法在信噪比-21 dB估计组合码序列出现错误的概率在0.2以下,而文献[13]算法在信噪比-16 dB出现错误的概率已经达到0.2以上,这说明本文利用最大距离法则选取聚类初始均值向量的方法相比较文献算法对组合码序列的估计效果更佳。
实验5 比较本文改进的K-means算法,合作解扩方法以及文献[13]算法对正确估计信息码序列的影响,设置AltBOC信号伪码序列长度为Nc=127 chips,信息码序列组数M=1000,仿真结果如图8所示。
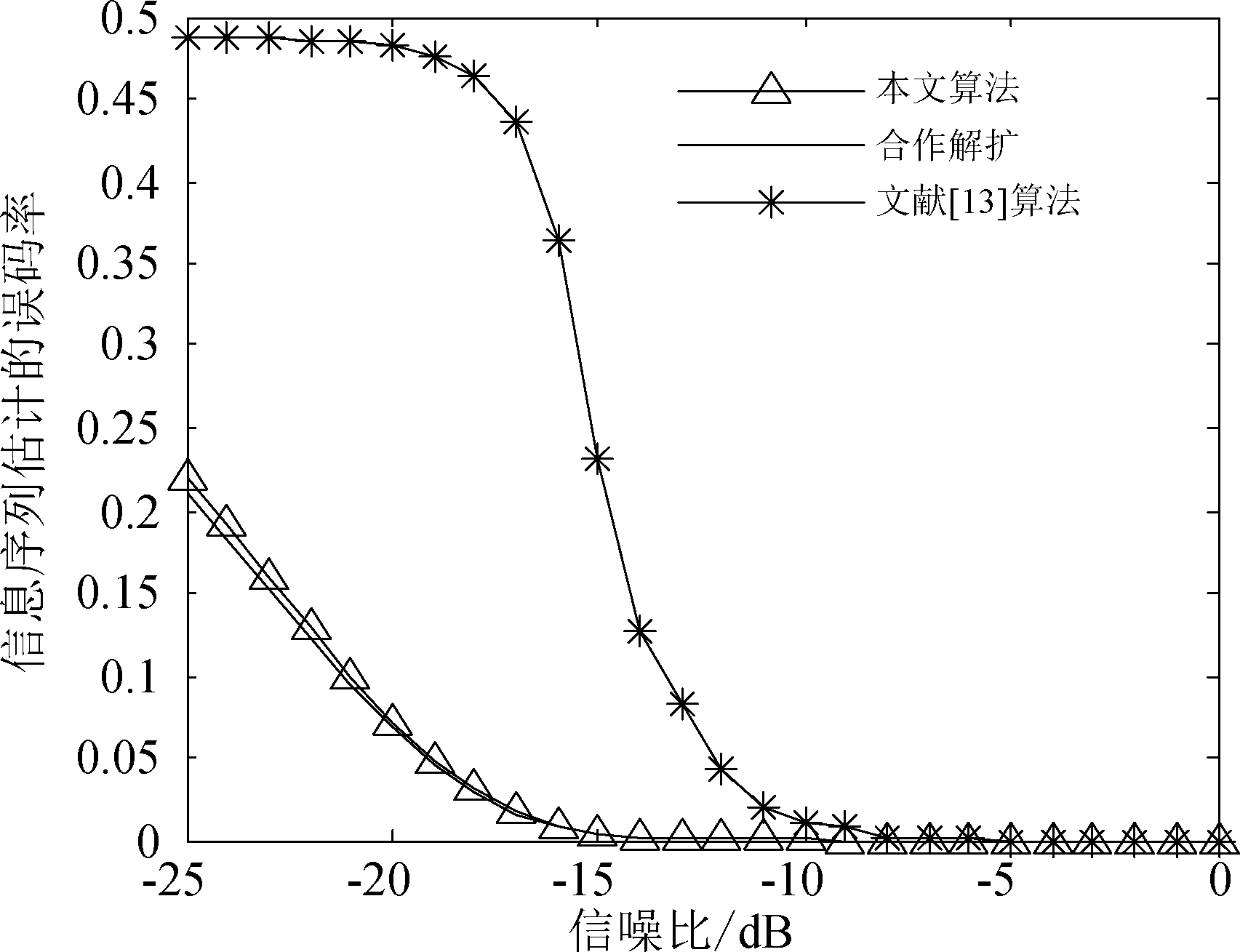
图8 不同算法对信号盲解扩性能对比
Fig.8 Comparison of performance of blind demodulation of signals by different algorithms
由图8可知三种方法对AltBOC信号信息码序列估计的错误概率随着信噪比的增加呈现递减的趋势,当信噪比一定时,本文方法对组合码序列盲解扩性能明显优于文献[13]未改进方法且与合作解扩信息码性能相接近,在信噪比为-21 dB时,文献[13]估计信息码序列的错误概率已达到0.48以上,而本文算法解扩信息码序列的误码率在0.1左右,这说明本文算法盲解扩性能优于文献[13]未改进算法。
5 结论
对于AltBOC信号组合码与信息序列难以估计的问题,本文首先对其信号模型进行分析,再利用K-means算法对AltBOC信号组合码进行聚类,利用相似性原则对各聚类的初始均值向量进行选取,避免了原K-means算法可能出现估计不稳定的情况。仿真结果表明,在对组合码以及信息码序列的估计上,本文算法性能明显优于未改进算法。随着信息序列的增加,本文所提的改进K-means聚类算法可以在信噪比-15 dB情况下估计组合码序列的错误概率小于0.1,对信息码序列盲解扩的错误概率小于0.01,与在相同信噪比下通过正确的组合码合作解扩信息码估计的错误概率相差不大,并且可以通过增加信息码组数来逼近合作解扩的正确性。
[1] Tian Feng, Zhang Kai, Cheng Liang. Unambiguous tracking of BOC signals using coherent combination of dual sidebands[J]. IEEE Communications Litters, 2016, 20(8): 1555-1558.
[2] Benedetto F, Giunta G, Lohan E S, et al. A fast unambiguous acquisition algorithm for BOC modulation signals[J]. IEEE Transactions on Vehicular Technology, 2013, 62(3): 1350-1355.
[3] 周艳玲, 罗雪姣, 温小青, 等. 卫星导航信号AltBOC调制方式分析[J]. 湖北大学学报: 自然科学版, 2015, 37(4): 334-339.
Zhou Yanling, Luo Xuejiao, Wen Xiaoqing, et al. Analysis of satellite navigation signal alternate binary offset carrier modulation[J]. Journal of Hubei University: Natural Science, 2015, 37(4): 334-339.(in Chinese)
[4] Qin Changlu, lv Jing, Li Yangzhi, et al. Research of AltBOC Modulation[C]∥International Conference on Communication Technology, 2010: 925-929.
[5] Emilie Rebeyrol, Christophe Macabiau, Laurent Lestarquit, et al. BOC power spectrum densities[C]∥Proceeding of the 2005 National Technical Meeting of the Institute of Navigation, San Diego, California, 2005: 769-778.
[6] 田野, 徐启炳, 张立新. 导航发射信道对双频复用信号质量的影响[J]. 电讯技术, 2018, 58(1): 18-24.
Tian Ye, Xu Qibing, Zhang Lixin. Effect of Navigation Transmission Channel on Dual-frequency Multiplexing Signal Quality[J]. Telecommunication Engineering, 2018, 58(1): 18-24.(in Chinese)
[7] 杨建雷, 金天, 黄智刚, 等. 补0的TD-AltBOC多信号分量联合捕获方法[J]. 哈尔滨工程大学学报, 2014, 35(11): 1427-1433.
Yang Jianlei, Jin Tian, Huang Zhigang, et al. Multi-signal components combining acquisition method based on padding zero for TD-AltBOC[J]. Journal of Harbin Engineering University, 2014, 35(11): 1427-1433.(in Chinese)
[8] 刘明凯. “北斗”B2频段导航信号伪码跟踪性能分析[J]. 电讯技术, 2018, 58(1): 25-29.
Liu Mingkai. Pseudo Noise Code Tracking Performance Analysis of Beidou B2 Frequency Band Navigation Signal[J]. Telecommunication Engineering, 2018, 58(1): 25-29.(in Chinese)
[9] 张天骐, 刘董华, 袁帅, 等. 改进的SVD算法对BOC信号组合码与信息序列盲估计[J]. 系统工程与电子技术, 2019, 41(1): 194-202.
Zhang Tianqi, Liu Donghua, Yuan Shuai, et al. Blind estimation of the combination code and the information sequences for BOC signal with improved SVD algorithm[J]. Systems Engineering and Electronics, 2019, 41(1): 194-202.(in Chinese)
[10] 张花国, 魏平. 同步多用户长码直扩信号的盲解扩[J]. 电子与信息学报, 2011, 33(7): 1748-1751.
Zhang H G, Wei P. Blind dispreading of synchronous multi-user long-code DS-SS signals[J]. Journal of Electronics & Information Technology, 2011, 33(7): 1748-1751.(in Chinese)
[11] 张天骐, 赵军桃, 江晓磊. 基于多主分量神经网络的同步DS-CDMA伪码盲估计[J]. 系统工程与电子技术, 2016, 38(11): 2638-2647. doi:10.3969/j.issn.1001-506X.2016.11.27.
Zhang Tianqi, Zhao Juntao, Jiang Xiaolei. PN code sequence blind estimate of synchronous DS-CDMA based on multi-principal component neural network[J]. Systems Engineering and Electronics, 2016, 38(11): 2638-2647.doi:10.3969/j.issn.1001-506X.2016.11.27.(in Chinese)
[12] 李峰, 张明祥, 张宇敬. 局部迭代的快速K-means聚类算法[J]. 计算机工程与应用, 2019.
Li Feng, Zhang Mingxiang, Zhang Yujing. Partial iterative fast K-means clustering algorithm[J]. Computer Engineering and Applications, 2019.(in Chinese)
[13] 王航, 郭静波, 王赞基. 基于聚类的软扩频信号盲解扩方法[J]. 电子与信息学报, 2009, 31(2): 422- 425.
Wang Hang, Guo Jingbo, Wang Zanji. Clustering based blind despread method of tamed direct sequence spread spectrum signals[J]. Journal of Electronics & Information Technology, 2009, 31(2): 422- 425.(in Chinese)
[14] 阴爱英, 吴运兵, 朱敏琛, 等. 基于MapReduce框架下K-means的改进算法[J]. 计算机应用研究, 2018, 35(8): 2295-2298.
Yin Aiying, Wu Yunbing, Zhu Minchen, et al. Improved K-means algorithm based on MapReduce framework[J]. Application Research of Computers, 2018, 35(8): 2295-2298.(in Chinese)
[15] 翟东海, 鱼江, 高飞, 等. 最大距离法选取初始聚类中心的K-means文本聚类算法的研究[J]. 计算机应用研究, 2014, 31(3): 713-715.
Zhai Donghai, Yu Jiang, Gao Fei, et al. K-means text clustering algorithm based on centers selection according to maximum distance[J]. Application Research of Computers, 2014, 31(3): 713-715.(in Chinese)
[16] 冯勇, 张学理, 王嶸冰, 等. 融入密度和距离的K-means初始簇中心优选方法研究[J]. 小型微型计算机系统, 2018, 49(8): 1805-1808.
Feng Yong, Zhang Xueli, Wang Rongbing, et al. Research of K-means initial Cluster Center Optimization Selection Based on Density and Distance[J]. Journal of Chinese Computer Systems, 2018, 49(8): 1805-1808.(in Chinese)
