1 引言
ADS-B作为一种应用于空中交通管理的监视技术,其机载ADS-B通信设备在同一频段以随机广播的方式向外发送飞机的ID代号、位置等信息,使地面站可以对其进行监视。因此,ADS-B系统应用于民用航空可以有效追踪飞机的多种飞行状态参数。然而由于ADS-B信号具有随机广播发送的特点,不同ADS-B信号之间会不可避免的产生信号交织问题。如果没有有效的交织信号分离算法,交织问题将会导致解码错误和监视信息丢失,从而造成ADS-B系统监视性能的显著下降。
信号解交织问题可以分为时域解交织与空域解交织,空域解交织利用阵列天线所具有的空间分辨能力来分离交织信号[1]。目前基于阵列天线的信号分离方法可以分为两类,其中一类是利用波达方向(Direction of Arrival, DOA)估计方法分离不同来向的信号,如文献[2]中利用最大似然估计的方法进行信号解交织,但该方法需要阵列校准。另一类则利用盲源分离算法,如快速独立主成分分析(Fast Independent Component Analysis, FastICA)[3- 4]、曼彻斯特解码(Manchester Decoding Algorithm, MDA)[5]、正交投影算法(Project Algorithm,PA)[6]等。由于以上几种算法均存在不足,很多学者提出了改进算法。如文献[7]基于PA算法提出了一种高增益的稳健PA算法,文献[8]提出了改进的MDA算法。
相比于阵列天线接收机,单天线ADS-B接收机更加普遍并且成本低、维护方便,因此本文考虑利用MVDR算法解决单通道接收机ADS-B信号交织问题。文献[9]中提出了单通道ICA信号分离算法,当信号的频谱不相交,并且信号之间相互独立时可以分离交织信号。但是该算法的分离效果取决于初始值并且运算量较大;文献[10]中针对语音信号的特点提出利用线性时变滤波器分离交织信号;文献[11]提出了基于高斯混合模型(Gaussian Mixture Models,GMM)的单通道交织信号分离算法同样也不适用于ADS-B信号模型;文献[12]针对单通道ADS-B信号交织问题,提出一种基于累加分类判决的解交织算法,该算法在信号之间存在一定的功率差时能够保持良好性能。近年来,不少学者利用虚拟多通道构建的思想将单通道接收数据转化为虚拟多通道数据模型,从而利用多通道中的信号分离算法进行信号解交织[13-14]。例如文献[15]从二次雷达信号的编码特点出发,首先将单通道接收数据转化为虚拟多通道数据模型,从而利用MDA算法分离交织信号,但该方法在信号相对时延较大时性能变差并且需要比较复杂的联合对角化计算;文献[16]提出运用单天线投影算法(Project Antenna Single Antenna,PASA)分离二次雷达交织信号,同样是利用虚拟多通道的思想,首先构建了一个虚拟均匀线阵模型,然后再利用PA算法分离二次雷达交织信号。由于ADS-B信号与S模式二次雷达信号模型相近,PASA算法同样可以应用于ADS-B信号解交织。但是该算法的缺点在于将单天线接收到的交织信号进行虚拟多通道模型构建之后,如果想要准确估计其中一条信号的虚拟导向矢量,要求信号之间的相对时延大于10 μs。
在阵列信号处理中,统计最优波束形成问题是在某一准则下寻求最优权矢量,这些准则包括最小均方误差准则、最大信干噪比准则、最小噪声方差准则。其中最小噪声方差准则表示为当期望信号方向已知时,使输出功率最小可以保证信号的良好接收,得到的最优波束形成器即为MVDR波束形成器,也称为Capon波束形成器[17]。该准则的意义为:当期望信号的方向已知,其构成的导向矢量便为已知,并且在对该导向矢量的增益为常数的条件下,输出功率最小。而当单天线接收数据模型转化为虚拟均匀线阵模型后,期望信号的虚拟导向矢量可以由信号的频率得出。因此,本文提出一种新的单天线ADS-B信号解交织方法,即如果能够准确估计出信号的频率便可以得到信号的虚拟导向矢量,通过结合MVDR算法可以得到信号对应的权矢量,从而有效分离交织信号。然而由于信号频率估计通常利用FFT,在采样频率和采样点数固定的情况下会产生较大的误差,因此将细化快速傅里叶变换(Zoom-FFT)[18]应用于ADS-B信号频率的准确估计,改善由频率估计误差引起的ADS-B信号解交织效果变差的问题。并针对信号最优权矢量公式中的矩阵求逆问题,通过利用ADS-B接收数据的协方差矩阵为Hermite矩阵的特点进行矩阵的快速求逆运算[19]。除此之外,本文提出的解交织方法对信号之间的相对时延问题不敏感。
2 信号模型
1090ES数据链格式下的ADS-B信号载波频率为1090 MHz,可允许的频率偏差范围为±1 MHz。每帧ADS-B基带信号由8比特的前导脉冲和112比特的数据块脉冲组成,且每一比特符号都使用曼彻斯特编码方式进行编码,即‘0’编码为‘01’,‘1’编码为‘10’,随后通过脉冲位置调制(PPM)获得基带PPM信号[20]:
(1)
其中,bν表示第ν个二进制符号,p(t)表示一个脉冲宽度为Ts=0.5 μs的矩形脉冲。
图1为经过PPM调制后的ADS-B基带信号。
在给定的信号采样频率下,单通道接收到的信号可以表示为:
xr=s+n
(2)
其中,s=[s1 … sm … sM]T表示ADS-B信号,n表示加性高斯白噪声,sm可以表示为:
(3)
其中,M为全部采样点数, f0表示接收机的中频频率, fs表示信号采样频率,I代表ADS-B信号交织个数。对于第i条ADS-B信号, fi来自于接收机频差和多普勒频移,τi表示从观测时间开始的相对时延。pi、Di(m)和φi分别表示第i条信号的功率、编码二进制符号和初始相位。为了便于描述,令公式(3)中的I=2,即对两条信号交织问题进行分析。
3 单天线ADS-B交织信号分离
3.1 虚拟多通道模型的构建
为了方便推导信号的虚拟导向矢量,此时令公式(3)中的I=1,即针对一条信号进行分析。此时只取一个脉冲持续时间(0.5 μs)内的数据按照如下公式进行矩阵重构:
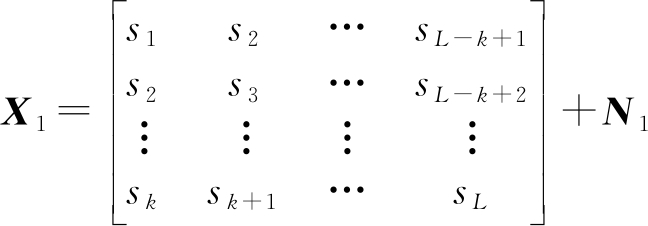
(4)
其中,k称作重构因子,其取值范围为:2≤k≤L,L表示一个脉冲持续时间内的样本数量,N1为对应的噪声矩阵。
将公式(3)带入公式(4)中,通过整理可以得到矩阵X1的另外一种表示方法:
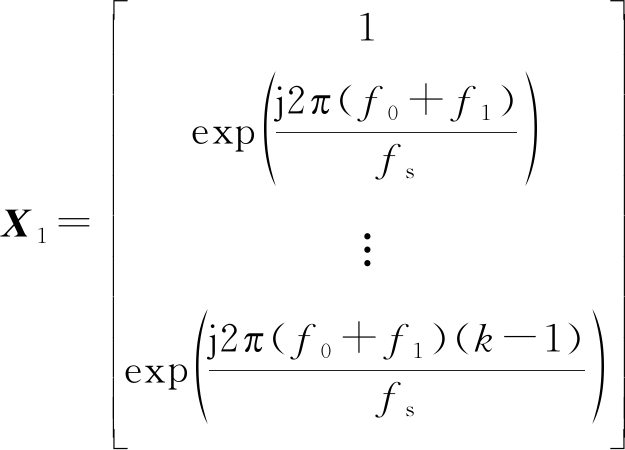
[s1 s2 … sL-k+1]+N1
(5)
则信号的虚拟导向矢量可以表示为:
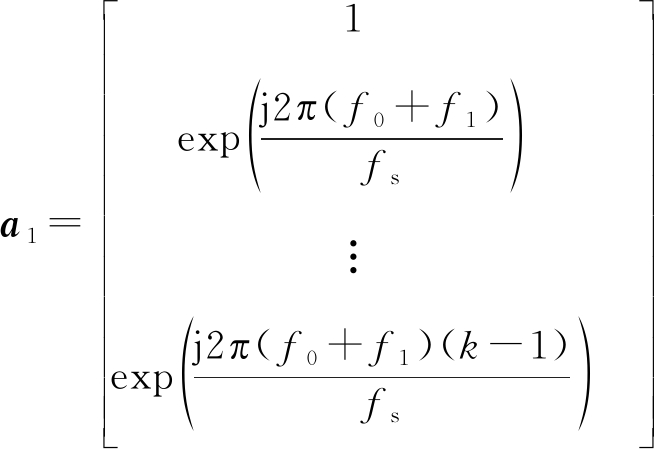
(6)
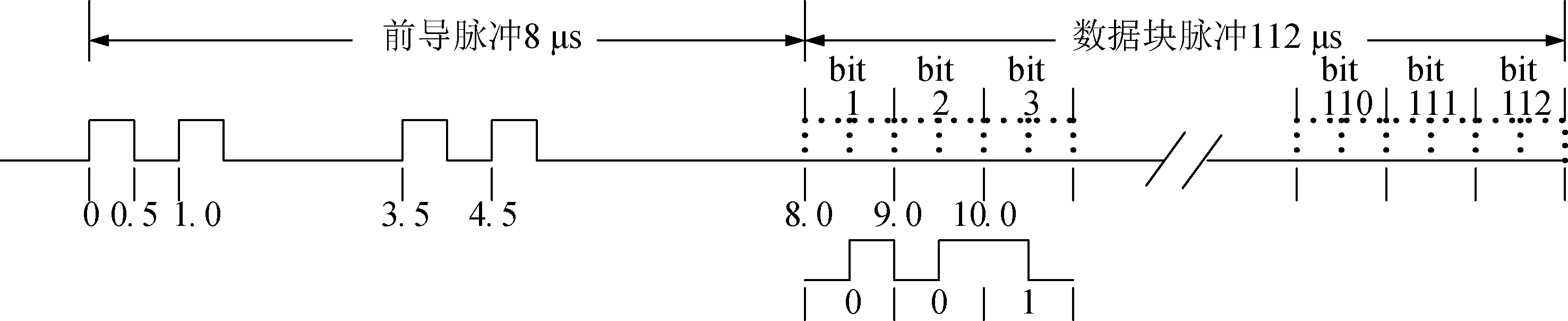
图1 ADS-B基带信号
Fig.1 ADS-B baseband signal
根据公式(6)同样可以得另外一条信号对应的虚拟导向矢量。因此从单天线接收机接收到的第一个信号数据开始,将每0.5 μs时间内的样本数据按照公式(4)的构造方法得到矩阵Yi,最终可以得到一个完整的虚拟多通道数据模型:
Y=[Y1 … Yi … Yl]k×N
(7)
其中,l=
,N为快拍数。
3.2 基于MVDR算法的信号解交织
当信号的虚拟导向矢量已知,计算最优权矢量使输出功率最小,需要满足的约束优化条件表达式为:
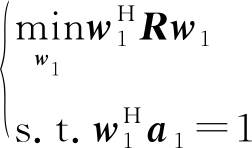
(8)
其中
由公式(6)得出。
用拉格朗日乘子法求解公式(8)可以得到:
(9)
则可以得到解交织的一条信号:
(10)
同理,另一条解交织信号也可以用相同方法得到。
由公式(6)和(9)可以得出,如果能够准确估计出一条信号的频率,则该条信号对应的最优权矢量也可以得出,从而利用公式(10)可以达到分离交织信号的目的。
因此对单天线接收信号FFT,利用频谱图便可以得到信号的频率。但是由于FFT的结果在频域是离散的,则信号的频率有可能会落在两条谱线之间,即产生了所谓的栅栏效应,因此对信号的频率估计将会产生误差,从而影响信号最优权矢量的生成,最终导致信号解交织效果变差甚至无法分离交织信号。
由于两条相邻谱线之间的频率间隔与采样频率和采样点数有关,而Zoom-FFT在不改变采样频率和采样点数的情况下,通过对信号的频率进行局部细化放大,使感兴趣的频带获得较高的频率分辨率,从而减小由栅栏效应产生的频率估计误差。该方法的基本思想是通过频移、低通滤波和降低采样率来提高分辨率,具体步骤如下:1)将感兴趣的频带的下限频率移至原来的零频率位置,相当于将感兴趣频段放大到整个频率显示范围上。通过乘以单位旋转因子exp(-j2πfkt)对信号进行频率调制,将频率原点由0处移到所需要细化的频率fk处。2)用低通数字滤波器对频移后的数据进行滤波,去除目标频带范围之外的频率。3)对低通滤波后的数据进行重采样,即每隔D-1个点取一个数据来使采样频率变为原频率的
倍。4)对重采样后的数据进行相同采样点数的FFT计算。5)对FFT计算结果重新排序,获得精确估计的信号频谱图,从而得到信号的频率估计值。将Zoom-FFT得到的信号频率估计值带入信号的虚拟导向矢量中,利用得到的最优权矢量便可以有效分离交织信号。
又由公式(9)可以得知,信号最优权矢量的生成需要对样本协方差矩阵求逆,而对于一个k阶方阵R,只计算乘加次数,运用常规矩阵求逆所需的总运算量为:
T1(k)≈k4-2k3+2k2-1
(11)
因此当k比较大的时候,利用常规矩阵求逆所带来的运算量是非常巨大的。为了减少运算量,对矩阵R按照如下方式进行分块:
(12)
当m和n最接近时计算效率最高,R的逆矩阵分块如下:
(13)
根据矩阵分块求逆原理有
(14)
其中,I代表单位矩阵。
通过计算可以得出矩阵R进行一次分块求逆的总运算量为:
T2(k)≈6mn2+8nm2-5mn+2m3
(15)
由于ADS-B信号构成的样本协方差矩阵R为Hermite矩阵,利用Hermite矩阵的对称性质可以得出:
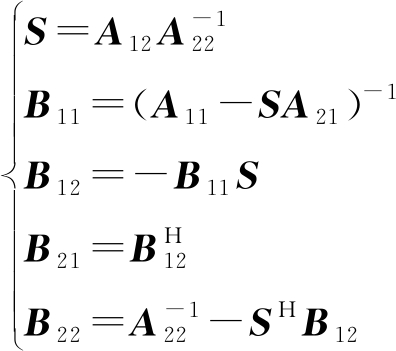
(16)
通过计算可以得出利用Hermite对称性质的矩阵分块求逆运算所需运算量为:
T3(k)≈4mn2+4nm2-2mn
(17)
又由于Matlab函数库中使用的矩阵求逆利用的是LU分解求逆方法,其所需的运算量约为:
T4(k)≈k3+k2
(18)
由于常规矩阵求逆的运算复杂度约为O(k4),因此只画出后三种矩阵求逆方法的运算量与重构因子k的关系曲线,此时令公式(15)和(17)中的
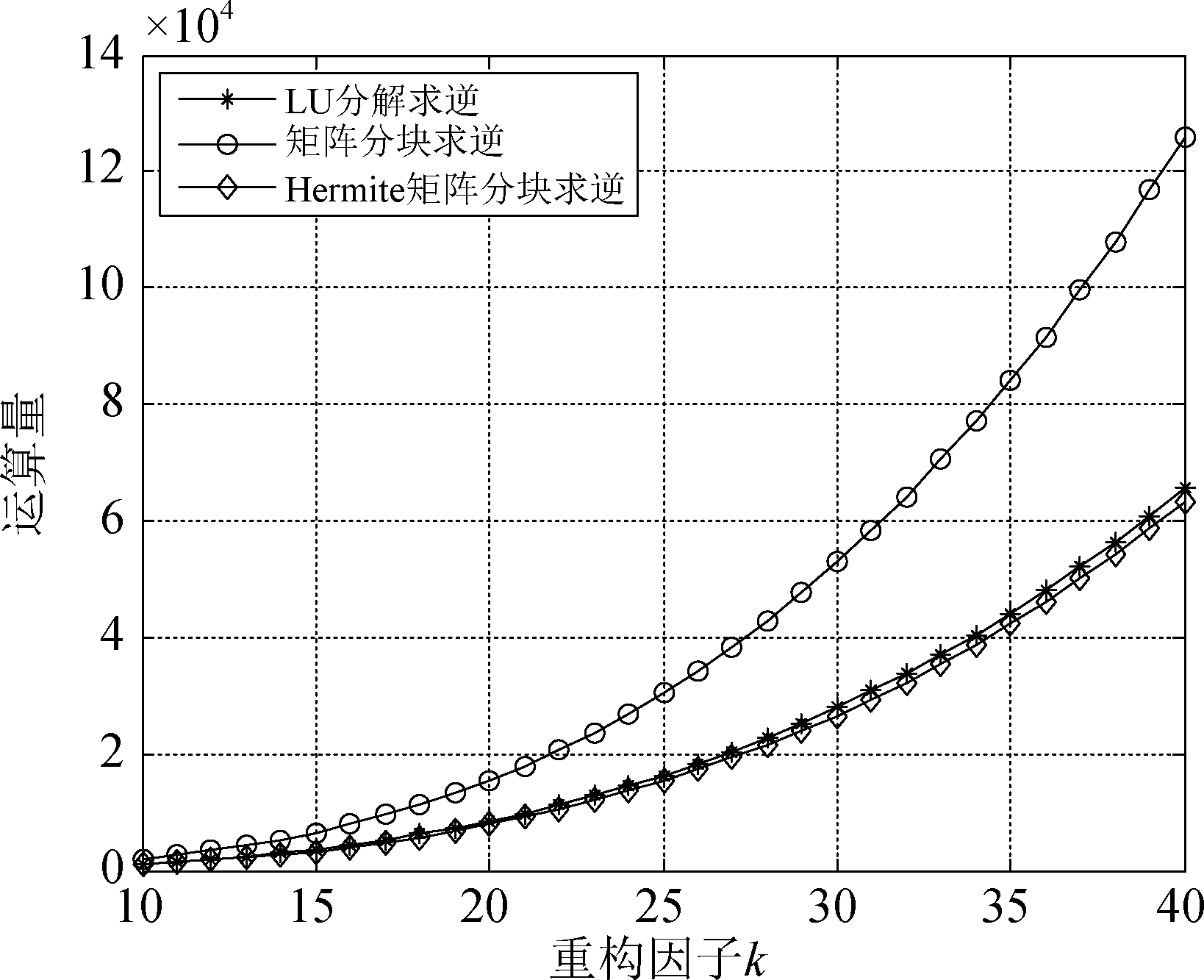
图2 运算量与重构因子关系曲线
Fig.2 Relationship between computational complexity and reconstruction factor
由图2可以得出,对公式(9)中的样本协方差矩阵利用基于Hermite特性的矩阵分块方法进行求逆,可以降低运算量。
至此,基于MVDR算法的信号解交织步骤如下:1)选择合理的k值,按照公式(4)的矩阵重构方式构造虚拟多通道数据模型Y。2)利用Zoom-FFT估计出两条信号对应的频偏f1与f2,并带入公式(6)中构造信号的虚拟导向矢量a1与a2。3)将信号的虚拟导向矢量带入公式(9)中,并利用公式(16)的矩阵求逆方法获得信号的最优权矢量w1和w2。4)利用最优权矢量得到解交织信号:
4 实验结果及分析
仿真实验参数设置:采样频率80 MHz,中频频率10 MHz。仿真生成两条信号,其信噪比均为15 dB,其中信号1的数据位信息为:飞机号780AAA,高度33150 ft,经纬度(117.5°,37.5°);信号2的数据位信息为:飞机号780ABC,高度33350 ft,经纬度(110.5°,31.5°)。两条信号相对时延为50 μs,信号之间的频偏为0.4 MHz,即信号1频率为fs1=9.8 MHz,信号2频率为fs2=10.2 MHz,初始相位随机。图3为两条信号交织的时域波形图。
图3 交织信号时域波形图
Fig.3 Overlapping signal in time domain
为了能够同时获得两条信号的频率,选取单天线接收信号的交织部分进行采样点数为N=512点的Zoom-FFT与FFT变换,此时的采样率仍为80 MHz, Zoom-FFT的细化倍数为D=8,获得的部分频谱图如图4所示。由图4可以看出,当采样率和采样点数固定的情况下,传统FFT由于频谱泄露和栅栏效应而对两条信号的频率估计产生了较大的误差,而Zoom-FFT通过对特定频段的细化而提高了该频段的频谱分辨率,降低了对两条信号的频率估计误差。
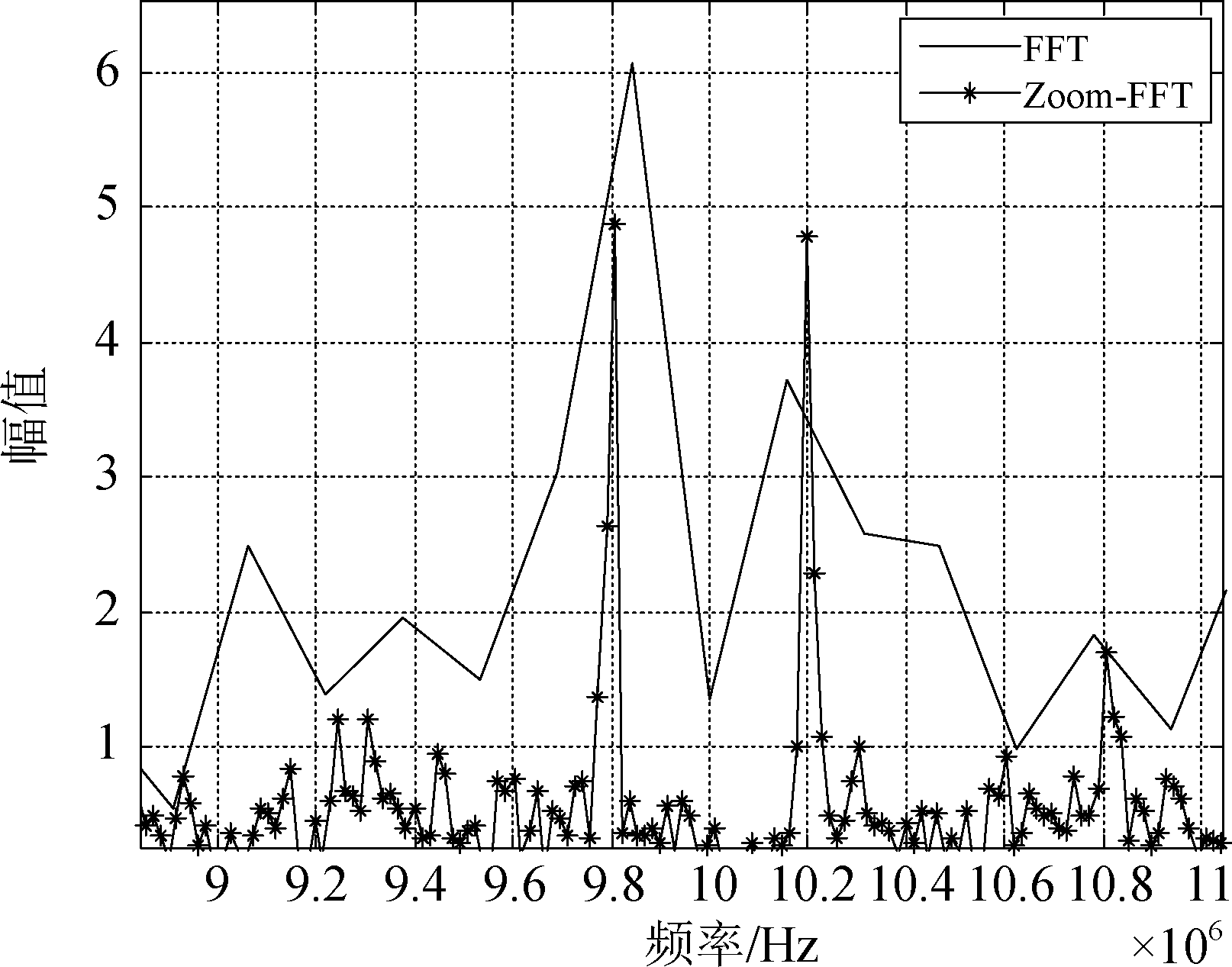
图4 ADS-B信号频谱
Fig.4 Spectrum of ADS-B signal
利用Zoom-FFT和FFT估计得到的信号1的频率可以获得信号1的最优权矢量,图5为利用最优权矢量生成的一个完整周期内的波束图。对图5中10 MHz信号中频频率附近的波束图进行放大可以得到如图6所示结果。可以看出,在频率为10.23 MHz和10.28 MHz附近产生了一个较深的零陷,但由于信号2的频率为10.2 MHz,两种频率估计方法相对于信号2频率的误差分别为ΔfZoom-FFT=30 kHz、ΔfFFT=80 kHz,将误差分别带入公式(6)中可以得到其对应的角度误差为:
即Zoom-FFT相比于FFT,由于估计得到的信号频率误差更小,从而造成的角度误差也更小,因此对信号的解交织效果好于FFT。这里需要指出的是,当采样率为80 MHz,如果想要使角度误差控制在0.5°范围内,通过计算可以求出相应的频率误差应小于111 kHz。
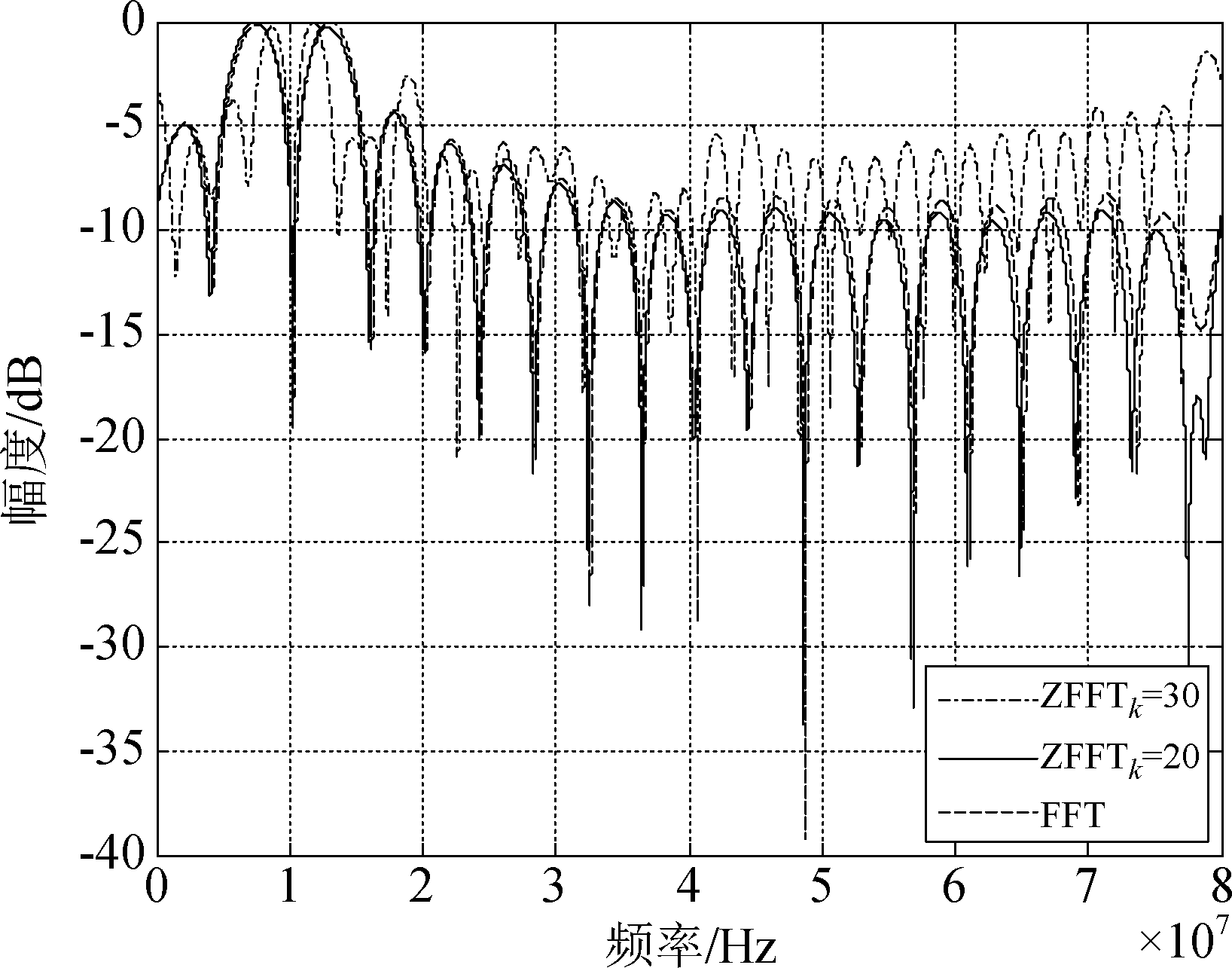
图5 利用信号1的最优权矢量生成的波束图
Fig.5 The beamforming pattern generated by utilizing the optimal weight vector of signal 1
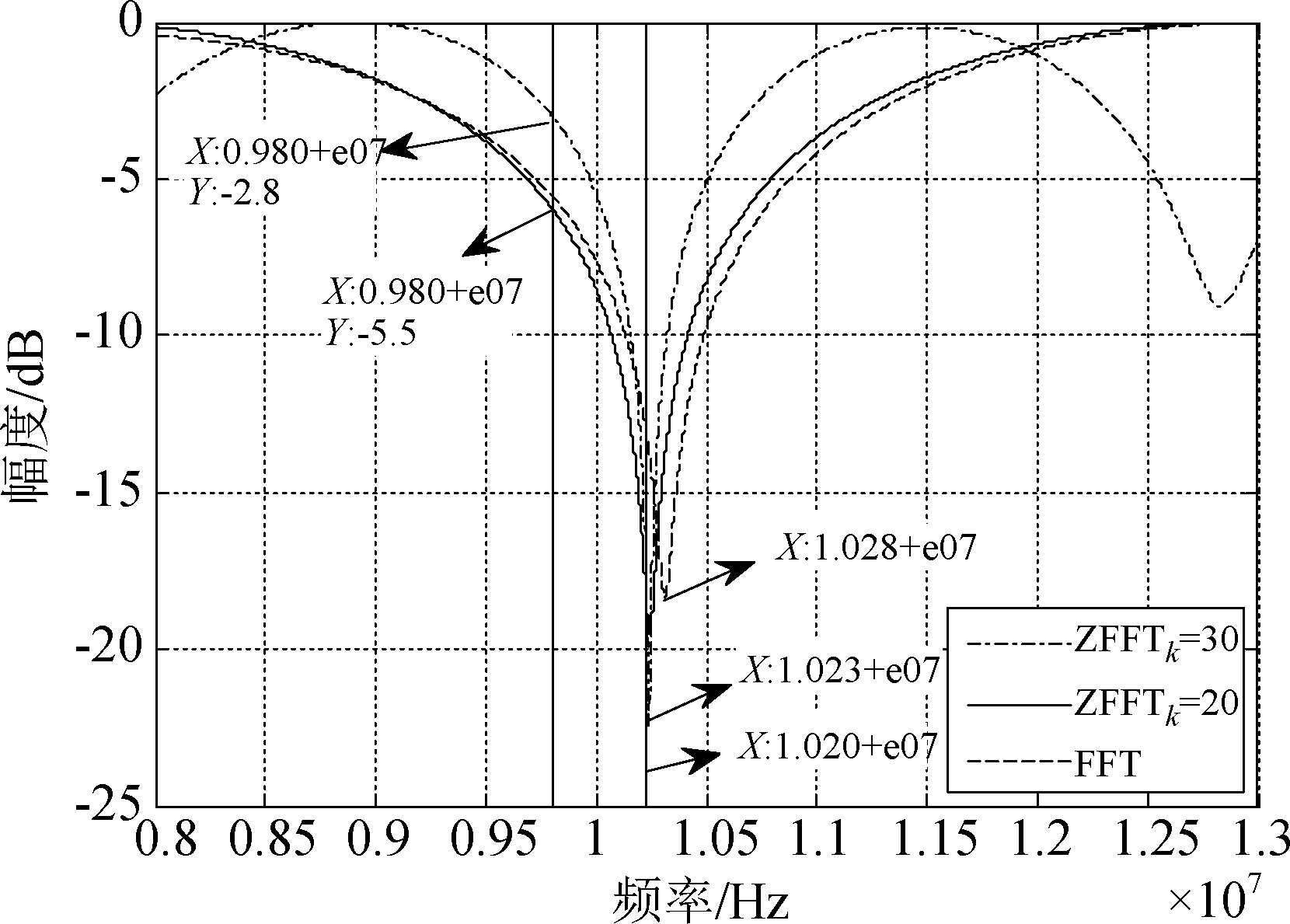
图6 利用信号1的最优权矢量生成波束图的局部放大
Fig.6 The local amplification of beamforming pattern generated by utilizing the optimal weight vector of signal 1
利用Zoom-FFT估计得到的信号频率构造两条信号的最优权矢量并进行交织信号分离,此时重构因子k=20,图7所示为源信号与利用最优权矢量得到的解交织信号对比图。由图7可以看出，解交织后的信号幅度相比与原始信号的幅度发生了降低，原因是因为MVDR算法用于单天线ADS-B信号解交织的效果受信号频率估计准确性的影响，而Zoom-FFT虽然可以降低信号频率估计误差，但是无法完全消除误差，所以对期望信号的输出不为1，即存在抑制效果。除此之外，该方法的解交织效果同样受到噪声的影响。
为了进一步验证本文所提算法的分离结果,将解交织信号分别送入软件接收机解码,解码结果如表1所示。
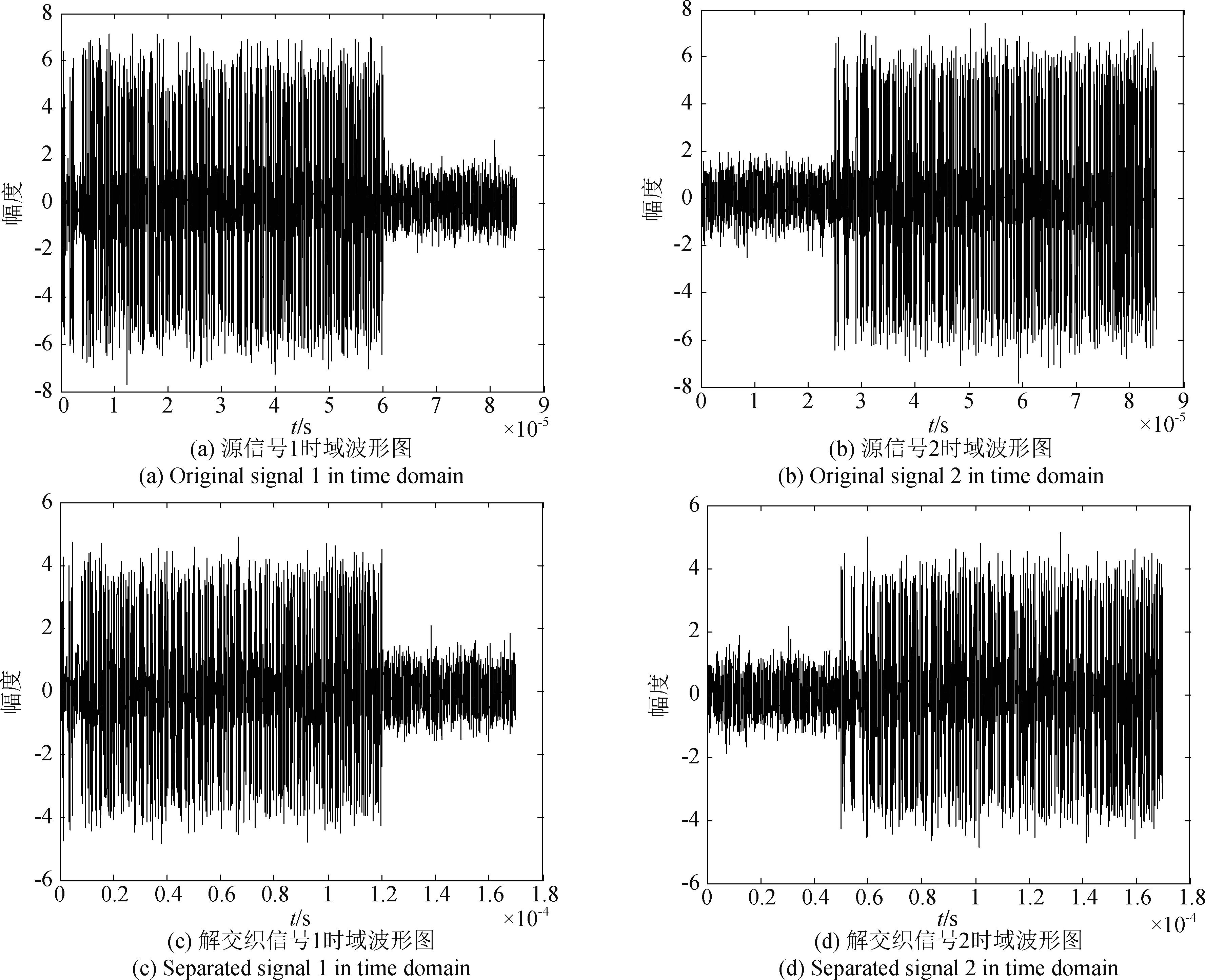
图7 源信号与解交织信号时域波形图对比
Fig.7 Comparison figure of original signals and separated signals with Zoom-FFT in time domain
表1 接收机解码结果
Tab.1 Decoding result of receiver
AADF消息类型高度/ft经度/(°) 纬度/(°)信号1780AAA17空中位置消息33150117.537.5信号2780ABC17空中位置消息33350110.531.5
为了验证本文所用算法相比于文献[16]提出的PASA算法对信号相对时延要求不敏感,在接下来的仿真实验中,令信号频偏为0.4 MHz,两条信号的相对时延从0.5 μs开始逐渐增加到15 μs,进行200次蒙特卡洛实验。图8比较了相对时延对两种算法输出信噪比的影响,从仿真结果可以看出,本文所用算法对信号相对时延问题不敏感,而PASA算法在两条信号完全交织时失效。随着信号之间相对时延的逐渐增加,PASA算法由于拥有足够多的数据用于准确估计信号导向矢量,其解码正确率才能与本文所用方法保持一致。
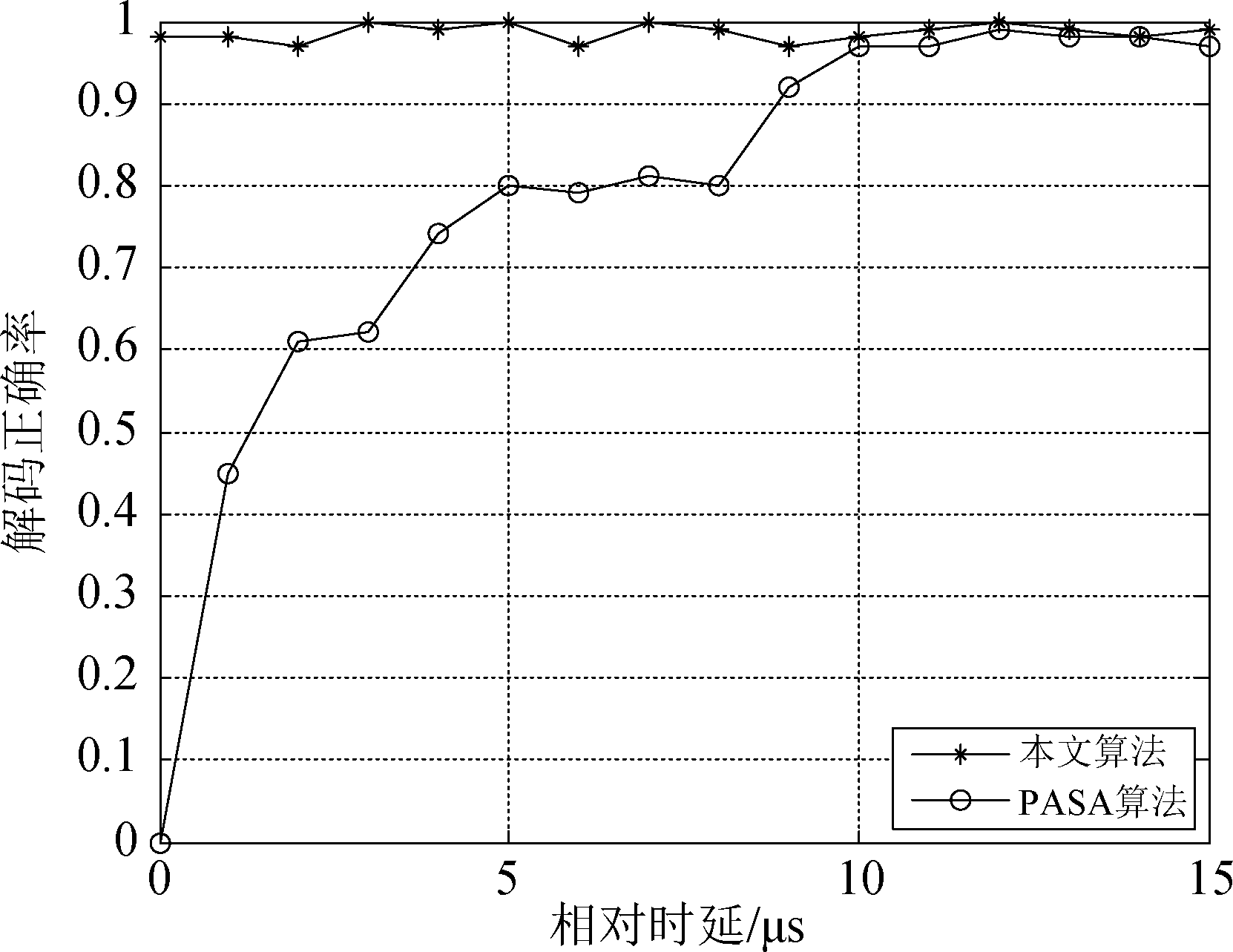
图8 解码正确率与相对时延关系曲线
Fig.8 Decoding correctly rate comparison for different relative time delays
为了进一步验证本文所提算法的准确性,在接下来的仿真实验中,改变信号的输入信噪比,假设两条信号的相对时延仅为0.5 μs,频偏为0.4 MHz,其他实验仿真参数不变,图9比较了输入信噪比对两种算法解码正确率的影响。由图可以得出:本文所用方法性能优于PASA算法,只有当两条信号的信噪比大于20 dB时,两种算法的解码正确率才都为100%。
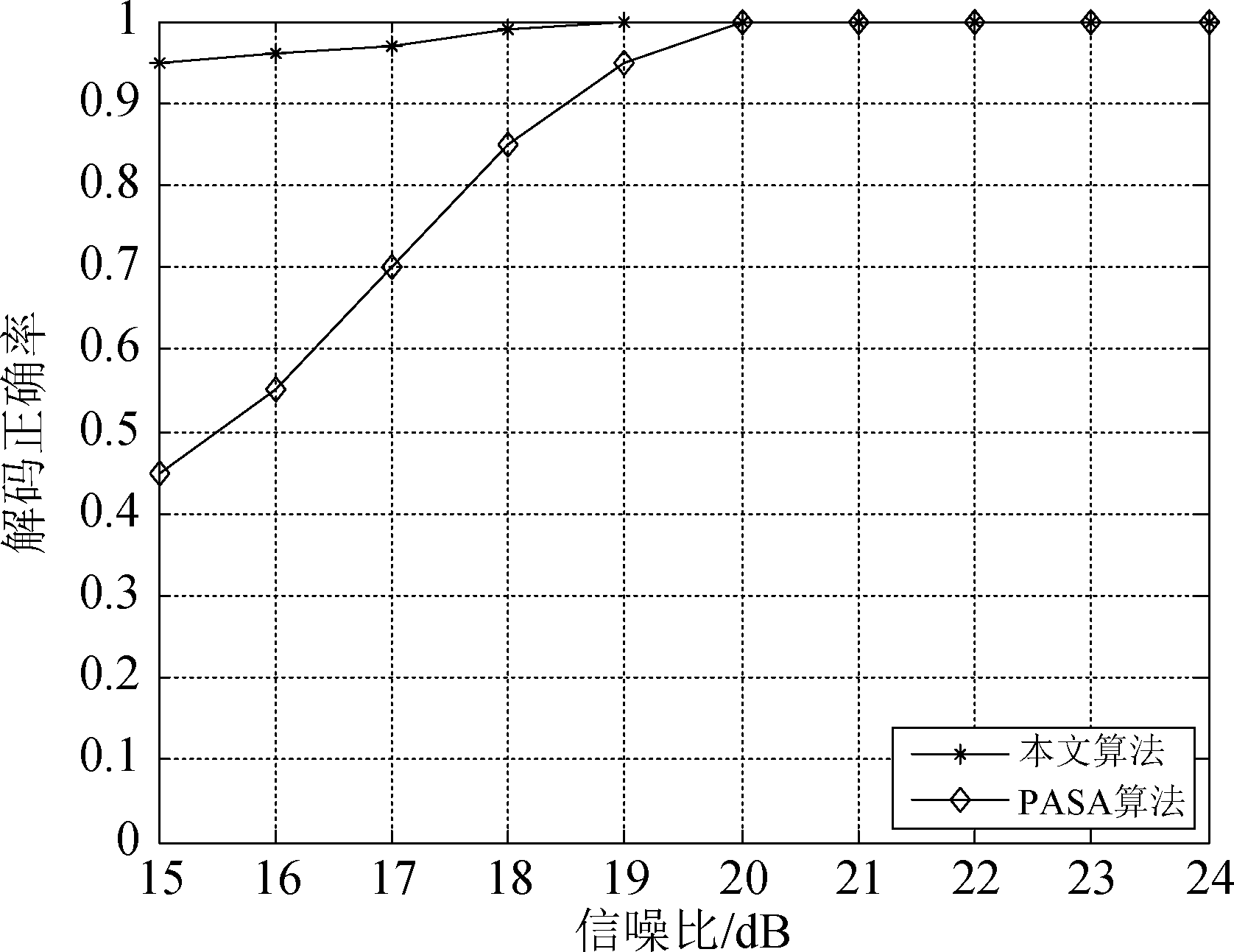
图9 解码正确率与输入信噪比关系曲线
Fig.9 Decoding correctly rate comparison for different input signal to noise ratio
通过以上全部仿真实验可以得出本文所提算法在能够准确估计信号频率的前提下可以有效分离交织信号并且对信号相对时延问题不敏感。
5 结论
本文针对单天线ADS-B信号交织问题,提出一种新的矩阵重构方法将单天线模型转化为虚拟均匀线阵模型,从而将阵列信号处理中的MVDR算法用于信号解交织。在能够准确估计信号频率的前提下,可以利用信号的虚拟导向矢量构造最优权矢量来达到分离交织信号的目的。仿真实验表明该方法在信噪比大于15 dB时可以有效分离交织信号并且对信号之间的相对时延问题不敏感。
[1] 张小飞, 汪飞. 阵列信号处理的理论与应用[M]. 第2版. 北京: 国防工业出版社, 2013: 1-7.
Zhang Xiaofei, Wang Fei. Theory and application of array signal processing[M]. Second edition. Beijing: National Defese Industry Press, 2013: 1-7.(in Chinese)
[2] 唐波, 程水英, 张浩. 基于多通道阵列处理的二次雷达混扰信号分选[J]. 电讯技术, 2014, 54(5): 534-540.
Tang Bo, Cheng Shuiying, Zhang Hao. Separation of garbled secondary surveillance radar signal based on multichannel array processing[J]. Telecommunication Engineering, 2014, 54(5): 534-540.(in Chinese)
[3] Novey M, Adali T. On extending the complex FastICA algorithm to noncircular sources[J]. IEEE Transactions on Signal Processing, 2008, 56(5): 2148-2154.
[4] 朱立娟, 赵风海. 一种改进的FastICA算法在语音信号盲源分离中的应用[J]. 电声技术, 2019, 43(5): 64- 68.
Zhu Lijuan, Zhao Fenghai. An improved FastICA algorithm for blind source separation of speech signals[J]. Audio Engineering, 2019, 43(5): 64- 68.(in Chinese)
[5] Petrochilos N, Van der veen A J. Algebraic algorithm to separate overlapping secondary surveillance radar replies[J]. IEEE Transactions on Signal Processing, 2007, 55(7): 3746-3759.
[6] Galati G, Petrochilos N, Piracci E G. Separation of SSR signals by array processing in multilateration systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(3): 965-982.
[7] 卢丹, 赵敏同. 用于ADS-B解交织的高增益稳健PA算法[J]. 信号处理, 2018, 34(9): 1060-1067.
Lu Dan, Zhao Mintong. A robust and high gain algorithm for separation overlapped ADS-B signal based on PA[J]. Journal of Signal Processing, 2018, 34(9): 1060-1067.(in Chinese)
[8] Petrochilos N, Piracci E G, Galati G. Improved MDA, a case for de-garbling SSR mode S replies[C]∥Tyrrhenian International Workshop on Digital Communication-Enhanced Surveillance of Aircraft and Vehicles, Rome, Italy, 2014: 87-91.
[9] Davies M E, James C J. Source separation using single channel ICA[J]. Signal Process, 2007, 87(8): 1819-1832.
[10] Hopgood J R, Rayner P J W. Single channel nonstationary stochastic signal separation using linear time-varying filters[J]. IEEE Transactions on Signal Processing, 2003, 51(7): 1739-1752.
[11] Todros K, Tabrikian J. Blind separation of independent sources using Gaussian mixture model[J]. IEEE Transactions on Signal Processing, 2007, 55(7): 3645-3658.
[12] 吴仁彪, 吴琛琛, 王文益. 基于累加分类的ADS-B交织信号处理方法[J]. 信号处理, 2017, 33(4): 572-576.
Wu Renbiao, Wu Chenchen, Wang Wenyi. A method of overlapped ADS-B signal processing based on accumulation and classification[J]. Journal of Signal Processing, 2017, 33(4): 572-576.(in Chinese)
[13] 付卫红, 周新彪, 农斌. 单通道盲源分离的研究现状与展望[J]. 北京邮电大学学报, 2017, 40(5): 1-11.
Fu Weihong, Zhou Xinbiao, Nong Bin. The research of SCBSS technology: survey and prospect[J]. Journal of Beijing University of Posts and Telecommunication, 2017, 40(5): 1-11.(in Chinese)
[14] 郭一娜. 单通道线性混合信号盲源分离算法研究[M]. 北京: 电子工业出版社, 2015: 13-17.
Guo Yina. Blind source separation algorithm for single channel linear mixed signal[M]. Beijing: Publishing House of Electronics Industry, 2015: 13-17.(in Chinese)
[15] 李丞, 张玉, 唐波. 基于曼彻斯特编码算法的单通道二次雷达信号重构方法[J]. 探测与控制学报, 2018, 40(3): 66- 69.
Li Cheng, Zhang Yu, Tang Bo. Secondary Surveillance Radar Replies Received in Single Channel Based On Manchester Decoding Algorithm[J]. Journal of Detection & Processing, 2018, 40(3): 66- 69.(in Chinese)
[16] Galati G, Petrochilos N, Piracci E G. Degarbling Mode S replies received in single channel stations with a digital incremental improvement[J]. IET Radar Sonar & Navigation 2015, 9(6): 681- 691.
[17] 王永良, 丁前军, 李荣锋. 自适应阵列处理[M]. 北京: 清华大学出版社, 2013: 30-34.
Wang Yongliang, Ding Qianjun, Li Rongfeng. Adaptive array processing[M]. Beijing: Tsinghua University Press, 2013: 30-34.(in Chinese)
[18] Proakis J G. Digital signal processing[M]. England: Pear-son Prentice Hall, 2009.
[19] 高飞, 王永良, 陈辉, 等. STAP中的矩阵求逆问题研究[J]. 雷达科学与技术, 2009, 6(3): 215-218.
Gao Fei, Wang Yongliang, Chen Hui, et al. Study on matrix inversion for STAP[J]. Radar Science and Technology, 2009, 6(3): 215-218.(in Chinese)
[20] Wang Wenyi, Wu Renbiao, Liang Junli. ADS-B signal separation based on blind adaptive beamforming[J]. IEEE Transactions on Vehicular Technology, 2019, 68(7): 6547- 6556.
