1 引言
过去十年以来,物联网、车联网等各种业务系统快速的发展,以及无线设备制造工艺的进步,促进了具有高速率、大连接和低延迟特点的5G移动通信系统研发与部署。通常,通过网络密实化的微蜂窝微小区、毫米波技术和大规模MIMO技术实现频谱效率的提升[1]。当前的低频段的频谱资源已无法满足人们生活中对于高速率数据传输的需求,无线通信技术的发展迫使研究者把毫米波频段纳入研究的范围。毫米波频率分布于30 GHz到300 GHz范围,其充裕的带宽成为学术界和工业界研究的热点,较短的波长使得不仅仅在基站端而且可以在移动端较小的物理空间内部署大量的天线。但是毫米波由于在空间传输过程中受到大气和雨水吸收严重,以及有限的传播路径数,导致其有效传播距离短的特点,非常适合覆盖范围小的高数据传输速率的微蜂窝微小区通信,通过提供充裕的阵列增益形成针状波束减轻干扰,而被视为5G的关键技术之一[2]。当在毫米波的发射端部署大量的天线,全数字预编码需要为每一根发送天线配备专用的射频链,具有天线数目的射频链(由数模转换器,混频器等组成)带来成本高昂以及能量消耗不可接受。因此,低维的基带数字预编码器和高维的射频模拟预编码器代替全数字预编码器的研究设计引起了极大的兴趣。在单用户通信系统中有通过最小化混合模拟和数字预编码与全数字预编码的欧几里得距离以提高频谱效率[3- 6],也有通过联合发送端模拟预编码器和接收端模拟组合器最大化频谱效率的研究[7-9]。在多用户通信系统中也研究了具有全连接结构的混合预编码[10-12],如文献[11]直接利用信道共轭转置的相位作为模拟预编码器,然后采用迫零(Zero Forcing, ZF)方式设计基带数字预编码器。文献[12]提出两阶段(Two-stage)的混合预编码,在设计模拟预编码时分别提取最大比变换(Maximum Ratio Transform, MRT)和迫零预编码得到的全数字预编码的相位,然后结合信道矩阵所得的等效矩阵通过迫零方式消除用户间干扰得到基带数字预编码,但这些基于全连接结构的混合预编码需要使用较多的射频链和高精度的相移器,导致昂贵的硬件费用和与精度成比例的功率消耗,阻碍了混合预编码结构在基站端与移动端具有严格尺寸和功率限制的毫米波蜂窝网系统中的部署。
为了降低硬件的使用数量和精度,进一步进行了部分连接结构混合预编码的研究[13-18]。文献[15]首次提出了基于机器学习自适应交叉熵的开关和反向器的混合预编码,文献[17]把基于机器学习自适应交叉熵应用于透镜阵列开关结构的混合预编码,文献[18]进一步分析了基于机器学习自适应交叉熵的重要参数对开关和反向器结构混合预编码的和速率及能量效率的影响。文献[19]则提出自适应连接结构的预编码,可以更好地实现波束增益,但仍需要较高精度的相移器(至少6比特精度)才能有接近最优全数字预编码的可达和速率性能,较低精度如1比特量化的自适应连接结构可达和速率性能严重下降。为了解决自适应连接结构1比特量化的相移器可达和速率性能较差问题,本文提出基于机器学习自适应交叉熵的1比特量化相移的自适应连接混合预编码(Adaptive Connection Network based Machine Learning Adaptive Cross-Entropy, ACN based MLACE)。通过最大化用户接收信号功率得到射频链与基站天线匹配关系的自适应连接结构,比固定子连接更加灵活。根据概率分布随机生成模拟预编码器,采用经典的ZF预编码得到相应的数字预编码器;根据可达和速率自适应地加权模拟预编码器。然后,通过减小交叉熵和加入常数平滑参数更新模拟预编码的概率分布,如此重复,最终得到可达和速率几乎最优的混合预编码器。
本文中,(·)T、(·)H、(·)-1和||·||F分别表示矩阵的转置、共轭转置、逆和Frobenius范数;|·|可以表示绝对值、求模运算符或集合的势;E(·)表示期望;
表示基站天线集合,∅表示空集;IK表示K×K的单位矩阵;⊗表示克罗内克积。
2 系统模型
如图1所示,考虑多用户下行链路的大规模MIMO系统[12],基站部署N根天线,NRF个射频链,同时服务K个具有单天线的非协作用户,通常,在大规模MIMO系统中满足K≤NRF≪N[10],本文中设为NRF=K。模拟预编码器FRF由少量射频链、自适应连接网络和大量的天线组成,假定发送到K个用户的符号s=[s1,s2,…,sK]T独立同分布,且均为服从零均值复高斯分布的符号,满足
为基站总的发射信号功率。K个用户接收的信号可以表示为:
y=HTFRFFBBs+n
(1)
其中,HT=[h1,h2,…,hK]T∈CK×N表示基站到所有用户的下行信道,hk∈CN×1表示基站到第k个用户的信道增益。
表示高维的只能调整信号相位的恒模模拟预编码器,
表示低维的既能调整信号幅度又能调整信号相位的数字预编码器。n表示K×1维矢量加性复高斯白噪声(Additive Gaussian White Noise, AWGN),满足E(nnH)=σ2IK,σ2表示加性高斯白噪声的功率。为了保证总的发送功率约束,在设计好模拟预编码矩阵FRF之后,相应的数字预编码矩阵FBB应满足功率约束||FRFFBB
=K。对于信道增益矢量,为了更好地描述毫米波信道极高的传播路径损失导致的有限空间选择和有限散射的特点,并且毫米波发射机大量的天线阵列导致很大程度的天线相关性[3],采用几何Saleh-Valenzuela信道模型,假设发射端是均匀线性阵列(Uniform Linear Array, ULA)天线,第k个用户的信道增益可以表示为[10]:
(2)
其中,N为基站均匀线性阵列天线的天线数。Lk表示第k个用户的传播路径数,
和
分别表示第k个用户的第l条路径的复增益和离开方位角度,a(φ)表示维数为N×1的发送阵列响应矢量,可以表示为:
(3)
这里,λ为毫米波的波长,d为均匀线性天线阵元之间的距离,通常设为半波长d=λ/2[2]。
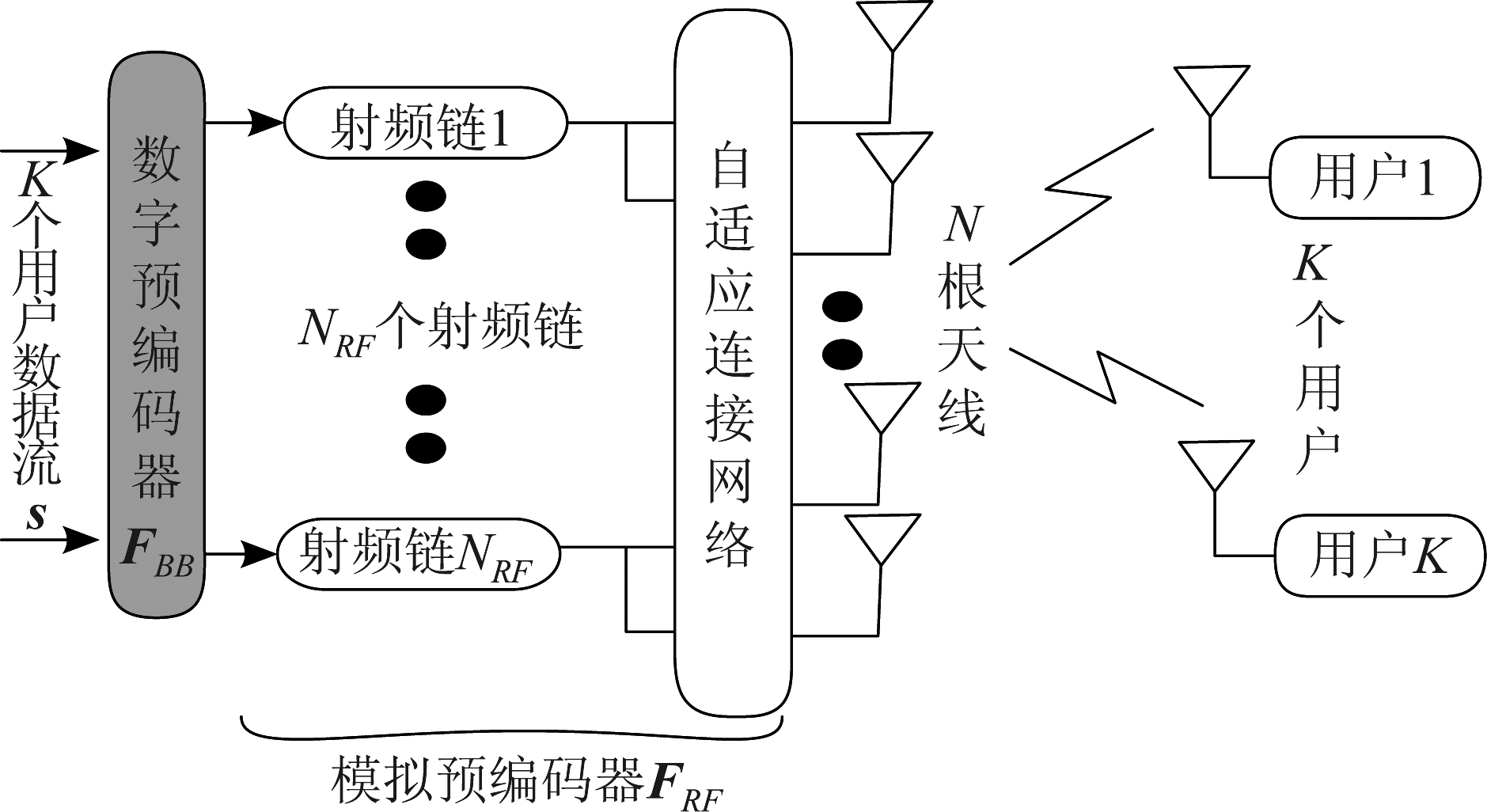
图1 多用户大规模系统自适应连接混合预编码
Fig.1 Multi-user large-scale system adaptive connection hybrid precoding
3 基于自适应交叉熵优化的自适应连接方案
传统的低精度相移器部分连接结构的模拟预编码常常不能很好的实现毫米波大维天线的阵列增益,受文献[19]中自适应连接结构模拟预编码的启发,本文模拟预编码器也采用自适应连接。应用自适应连接网络代替固定子连接的开关和反向器(相当于1比特量化的相移器)。和固定子连接结构相同,自适应连接仅仅需要相当于N个1比特量化的相移器,NRF个射频链,不需要加法器;和全连接的需要N×NRF个高精度相移器,NRF个射频链,N个加法器相比,极大地降低了硬件复杂度(费用及其能量消耗)。自适应连接网络可以更好地匹配下行链路改善用户的可达和速率,这种结构可以用低计算复杂度的芯片实现[19]。为了更好地利用自适应交叉熵优化应用于自适应连接结构,需要在特定信道状态信息下实现射频链与天线的匹配,也就是找到对应的模拟预编码矩阵FRF中非零元素的位置。
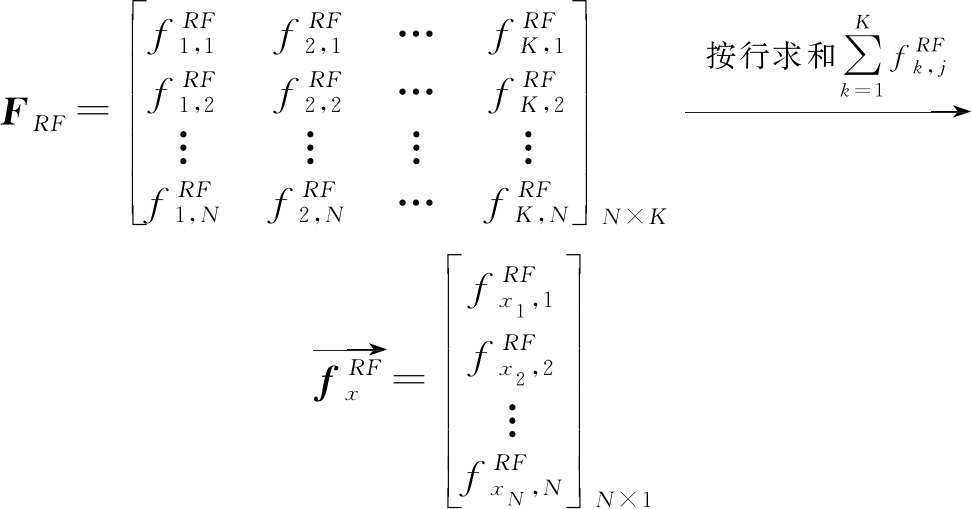
(4)
由于自适应连接的特殊结构和模拟预编码器中元素的常模约束,对应的模拟预编码FRF为稀疏矩阵,如式(4)所示,
表示其第j行第k列的元素,也即第k个射频链连接第j根基站天线,其元素
对FRF的每一行求和得到矢量
其第j个元素
因此,自适应连接结构模拟预编码有两个约束:
和
(5)
假设N/K=M为整数,把N根基站天线分割为互相独立的K个集合,用
表示第k个射频链连接基站天线的集合,
表示第k个射频链连接第j根基站天线,并有
所以式(5)还等价为:
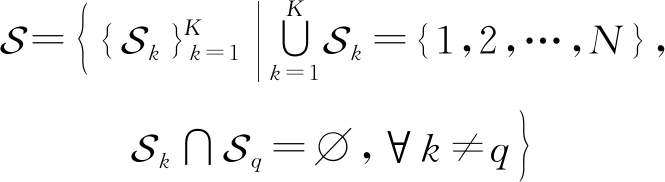
(6)
表示所有的射频链和基站全部天线的连接关系。
设计的模拟预编码FRF和数字预编码FBB要使服务的K个用户下行可达和速率最大:
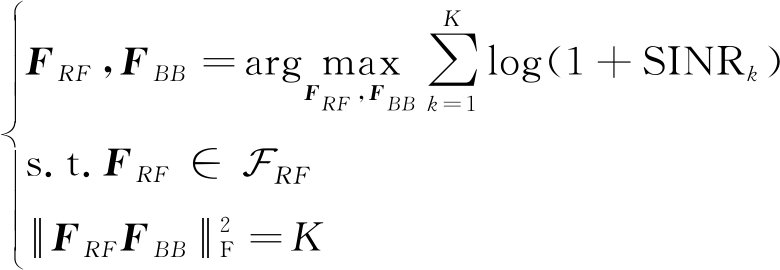
(7)
其中SINRk表示第k个用户的信干噪比(SINR),有:
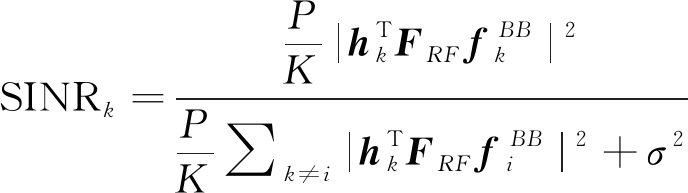
(8)
可以看到,式(7)在功率约束和自适应连接结构的约束下,是一个非凸优化问题。要使总的可达和速率最大,即要使各个用户接收符号的信干噪比最大,所以最大化第k个用户的接收信号功率,FRF的第k列
要满足:
约束(5)}
(9)
中仅有M个非零元素,需匹配信道hk元素模的前M个最大值,每次匹配一个元素并返回天线位置,存储于集合
(10)
约束
表示FRF的第j行还没有被取值或第j根天线还没有被匹配。
执行一次(10)便可匹配第k个射频链与一根基站天线,也即得到FRF中一个非零元素位置,为保证射频链的公平性,K个射频链轮流匹配,进行M次轮流,即可得到满足约束(5)的FRF的N个非零元素的位置,或者满足约束(6)的射频链与天线匹配关系的集合
在ACN based MLACE方案中,由于相移器被1比特量化,式(7)非凸优化问题已经转化为组合优化问题,怎样获取可达和速率最大的FRF和FBB？需要穷尽搜索找到N个确定位置上的非零元素值的2N个组合,涉及到极高的计算复杂度。对于毫米波大规模MIMO系统来说,N常常是大的,例如N=56,需要穷尽搜索256≈7.2×1016。另辟蹊径,用机器学习自适应交叉熵优化方法智能搜索最优的自适应连接模拟预编码[15,22],同著名的模拟退火算法、遗传算法等,属于随机搜索方法,并且交叉熵是基于概率模型的随机搜索算法[22],通过迭代求解组合优化问题。在每次迭代中,根据一个概率分布生成Z个N×1维的矢量,这些矢量按照每个射频链与基站天线的匹配关系集合
就可得到Z个候选模拟预编码矩阵FRF,每个候选模拟预编码矩阵FRF有对应的可达和速率,选择可达和速率最优的Zelite个FRF,通过最小化交叉熵和加入平滑参数更新概率分布,如此循环,将会以概率1得到可以生成接近最优候选模拟预编码矩阵中非零元素的概率分布[15]。
模拟预编码器中每一行非零元素组成的矢量
根据找到的匹配关系重构FRF,用p=[p1,p2,...,pN]T表示
中对应元素的概率,
的第j个元素
为伯努利随机变量[13],即
的概率为
的概率为1-pj。基于机器学习自适应交叉熵的自适应连接伪代码将在后面列出,下一步,详细地解释自适应交叉熵优化的几个重要步骤。
首先,通过初始化概率分布参数p(0)为
是全1矢量),根据概率分布
生成Z个候选矢量
样本,利用已经获得的确定匹配关系重构生成Z个候选模拟预编码
样本,然后根据等效信道
计算相应的Z个数字预编码
样本。在本文中,采用经典的数字ZF预编码消除用户间干扰方式得到相应的第z个数字预编码矩阵[10]:
(11)
对其进行功率约束:
之后,通过把
和
代入式(7)和式(8)获得可达和速率
在步骤13中降序排序Z个
为自适应地更新下一次的概率p(i+1),需要在步骤14中得到可达和速率最优的前Zelite个
定义最优的Zelite个模拟预编码可达和速率的平均值为T:
或
(12)
这里第z个模拟预编码矩阵是第z个矢量
根据射频链与基站天线匹配关系获得,因此
第z个模拟预编码矩阵对应的可达和速率的权重
根据当前的概率分布和权重自适应地更新下一次的概率:
(13)
同样有
其中:
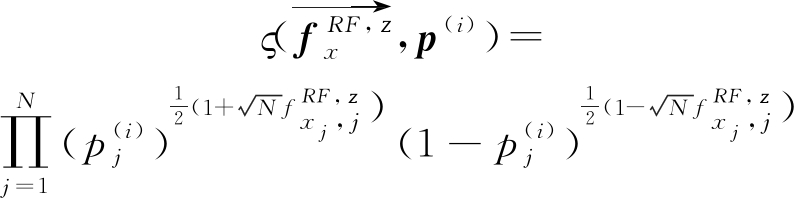
(14)
把式(14)代入式(13),然后式(13)对其第j个概率元素pj(i)求一阶导数,得到:
(15)
把式(15)设为等于零,就可得到下一次概率分布的第j个元素:
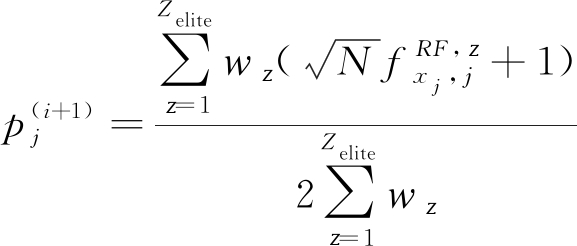
(16)
为了保证自适应交叉熵优化收敛到最优解避免局部收敛[21],可以在当前概率分布和下一次概率分布之间进一步地加上常数平滑参数α:
p(i+1)=αp(i+1)+(1-α)p(i)
(17)
这里0<α≤1,直到达到I次迭代结束,将会得到生成最优模拟预编码的概率分布p(I),选择第I次生成样本中最优的模拟预编码
和最优的数字预编码
这就是对应信道状态信息条件下几乎最优的自适应连接混合预编码。具体的算法如下所示:
基于机器学习自适应交叉熵的自适应连接混合预编码算法(ACN based MLACE)
输入:信道矩阵HT,迭代次数I,候选数Z,最优候选数Zelite,平滑参数α,初始化:基站天线集合 ={1,2,…,N},匹配关系 k=⌀,1≤k≤K,i=0, p(0)=12×1N×1。1.for m=1到M;2. for k=1到K;3. jopt=argmaxj∈ {hk,j}4. k=jopt5. = -jopt6. end for7. end for8.for i=1到I;9.根据萍(fRF,zx→,p(i))随机生成Z个候选矢量{fRF,zx→}Zz=1;
10.根据匹配关系集合{ k}Kk=1和{fRF,zx→}Zz=1重构Z个{FzRF}Zz=1,即: FzRF( 1, 2,…, K)=fRF,zx→;11. 根据式(11)计算数字预编码{FzBB}Zz=1;12.根据式(7)和(8)计算可达和速率{R(FzRF)}Zz=1;13.降序排序R(F1RF)≥R(F2RF),...,≥R(FZRF);14.选择前Zelite个R(F1RF),R(F2RF),...,R(FZeliteRF),获得{FzRF}Zelitez=1;15.计算前Zelite个加权系数{wz}Zelitez=1;16.根据{wz}Zelitez=1、{fRF,zx→}Zz=1和常数平滑参数α,利用式(16)和(17)更新p(i+1);17.end for输出:F1RF,F1BB。
接下来考虑所提ACN based MLACE方案计算复杂度。从上面的伪代码知道在搜索每个射频链与基站天线匹配关系集合时,其主要的复杂度在步骤3,所涉及的计算复杂度为
在利用自适应交叉熵优化智能搜索最优模拟预编码时,其主要的复杂度在步骤11,12,15和16。在步骤11中,需要根据等效信道
计算Z个数字预编码器,其复杂度为
在步骤12中,需要计算Z个混合预编码的可达和速率,这部分的计算复杂度为
在步骤15中需要计算Zelite个加权系数,涉及到的计算复杂度为
在步骤16中,更新概率分布p(i+1)所需的计算复杂度为
次迭代之后,自适应交叉熵智能搜索模拟预编码器所需的计算复杂度为
总之,第一个搜索匹配关系循环的计算复杂度与第二个交叉熵智能循环相比是相当小的,复杂度主要取决于第二个模拟预编码器的智能搜索循环,所以,基于机器学习自适应交叉熵的自适应连接混合预编码的计算复杂度为而基于机器学习的固定子连接混合预编码不需要进行射频链与基站天线的匹配集合搜索,仅仅进行模拟预编码器的智能搜索,因此,所提ACN based MLACE方案的计算复杂度稍微高于文献[15]基于机器学习固定子连接的混合预编码方案,是可以接受的。
4 仿真结果
自适应连接结构的混合预编码[19]、基于机器学习的固定子连接开关和反相器结构的混合预编码[15]和本文的基于机器学习的自适应连接结构混合预编码(ACN based MLACE)具有相同的较低硬件复杂度,省去了全连接混合结构所需要的NNRF个相移器和N个加法器,因此这里仅以和速率作为不同预编码方案性能的比较。仿真参数设置如下,均匀线性阵列(ULA)天线之间的距离设为毫米波半波长d=λ/2。根据式(2)获得第k个用户的信道增益矢量,设置每个用户的到达波束传播路径数都相等,即Lk=3,1≤k≤K。第k个用户的第l条路径的复增益服从复高斯分布,即
离开角服从均匀分布,
信噪比为P/σ2。
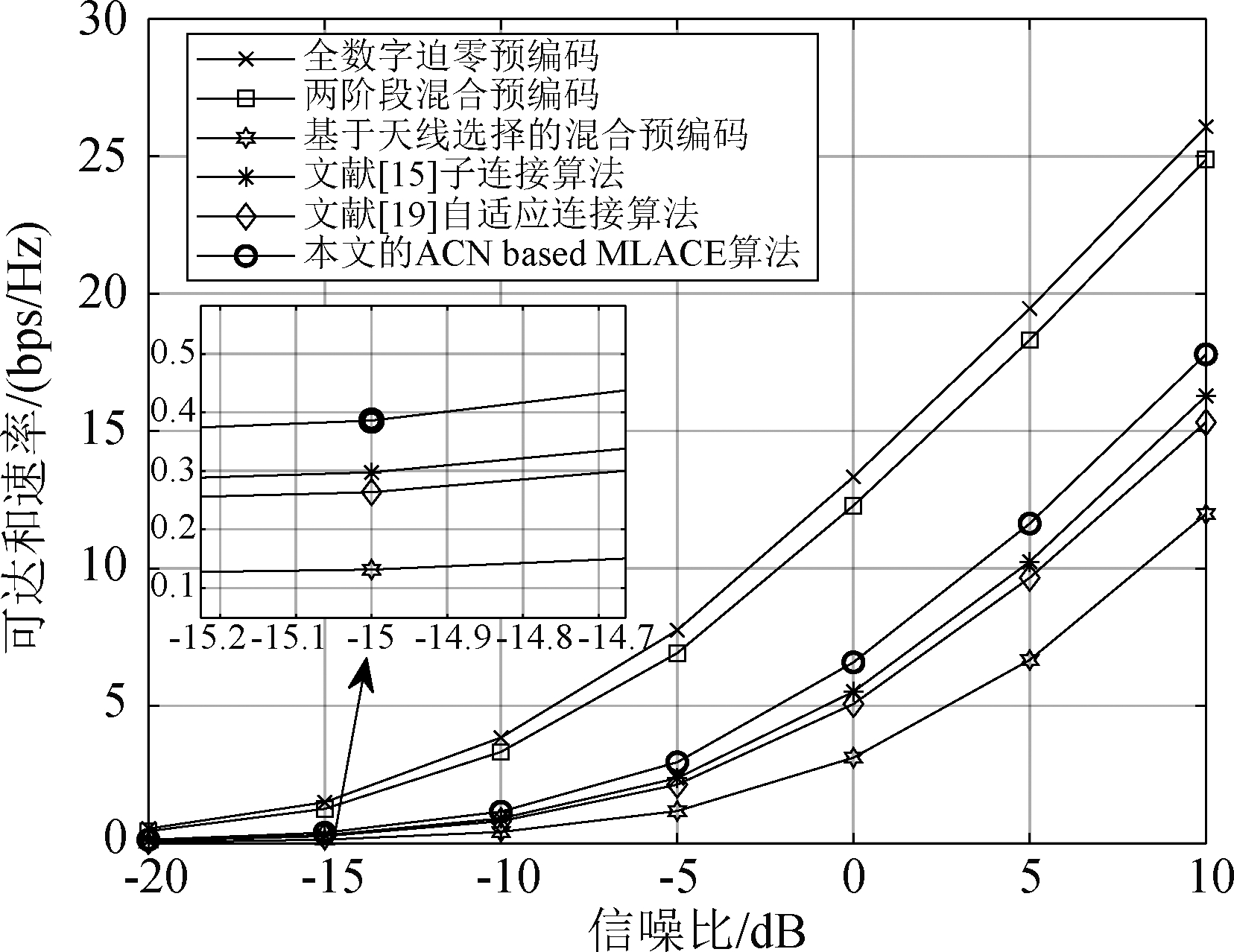
图2 可达和速率比较
Fig.2 The comparation of achievable sum-rate
图2显示了毫米波大规模MIMO系统不同混合预编码方案的可达和速率,通过1000次信道实现,天线数N=56,射频链数与用户数相等,NRF=K=4,模拟预编码候选可行解个数Z=200,候选样本中的最优样本个数Zelite=40,迭代次数I=20,常数平滑参数α=0.9,文献[15]固定子连接自适应交叉熵没有考虑常数平滑参数,为保证收敛[21],加上平滑参数进行可达和速率性能比较。在上述参数设置下,和在整个信噪比范围,本文所提的ACN based MLACE算法可达和速率大于文献[15]基于机器学习的固定子连接结构的可达和速率,后一种的可达和速率性能稍微优于文献[19]的自适应连接(1比特量化)的性能。基于机器学习自适应交叉熵优化辅助的固定子连接结构的可达和速率比只用自适应连接的可达和速率还高,说明仅仅用1比特量化的自适应连接结构不能很好地实现阵列增益,所以本文利用基于机器学习的自适应交叉熵优化方法改善1比特自适应连接结构可达和速率性能。在基于机器学习的自适应交叉熵优化方法的辅助下,其可达和速率性能较自适应连接结构的可达和速率性能提升不少,进一步验证了本文基于机器学习的自适应连接结构的可行性。在相同的低硬件开销情况下,所提方法更加接近全数字迫零预编码和4比特量化相移器的两阶段混合预编码[12]的可达和速率。
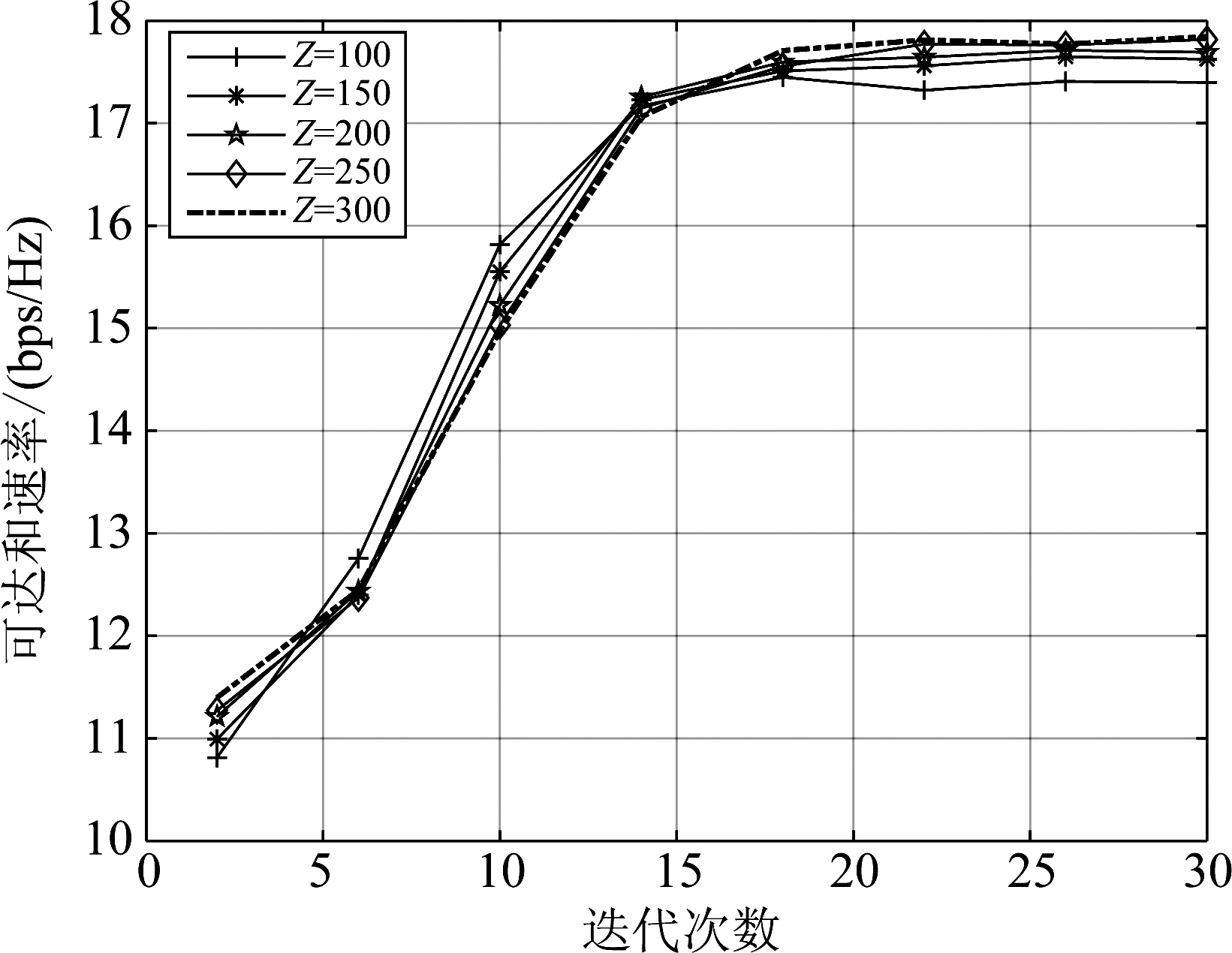
图3 可达和速率与Z和I的关系(SNR=10 dB)
Fig.3 Achievable sum-rate against Z and I (SNR=10 dB)
图3显示了基于机器学习的自适应连接混合预编码的可达和速率性能与候选个数Z和迭代次数I变化的关系。可以看到仿真信噪比SNR=10 dB,N=56,NRF=K=4,Zelite=40, α=0.9,和
时,所提ACN based MLACE方案可达和速率随着迭代次数的增加而增大,当迭代次数超过20次,可达和速率趋于缓和,说明迭代次数设为I=20是合适的。并且,迭代次数超过20次以后,Z=300可达和速率最高,Z=100可达和速率最低,考虑到计算复杂度,选择候选数Z=200是适中的。
图4显示了ACN based MLACE的可达和速率分别与迭代次数I和最优样本数与总样本数的比率
的关系。可以明显地看到SNR=10 dB,N=56,NRF=K=4,Zelite=40,Z=200和α=0.9时,rho=0.2 的可达和速率最高,说明rho=0.2是最好的选择,证明了图2中所提混合预编码方案参数选择的合理性。
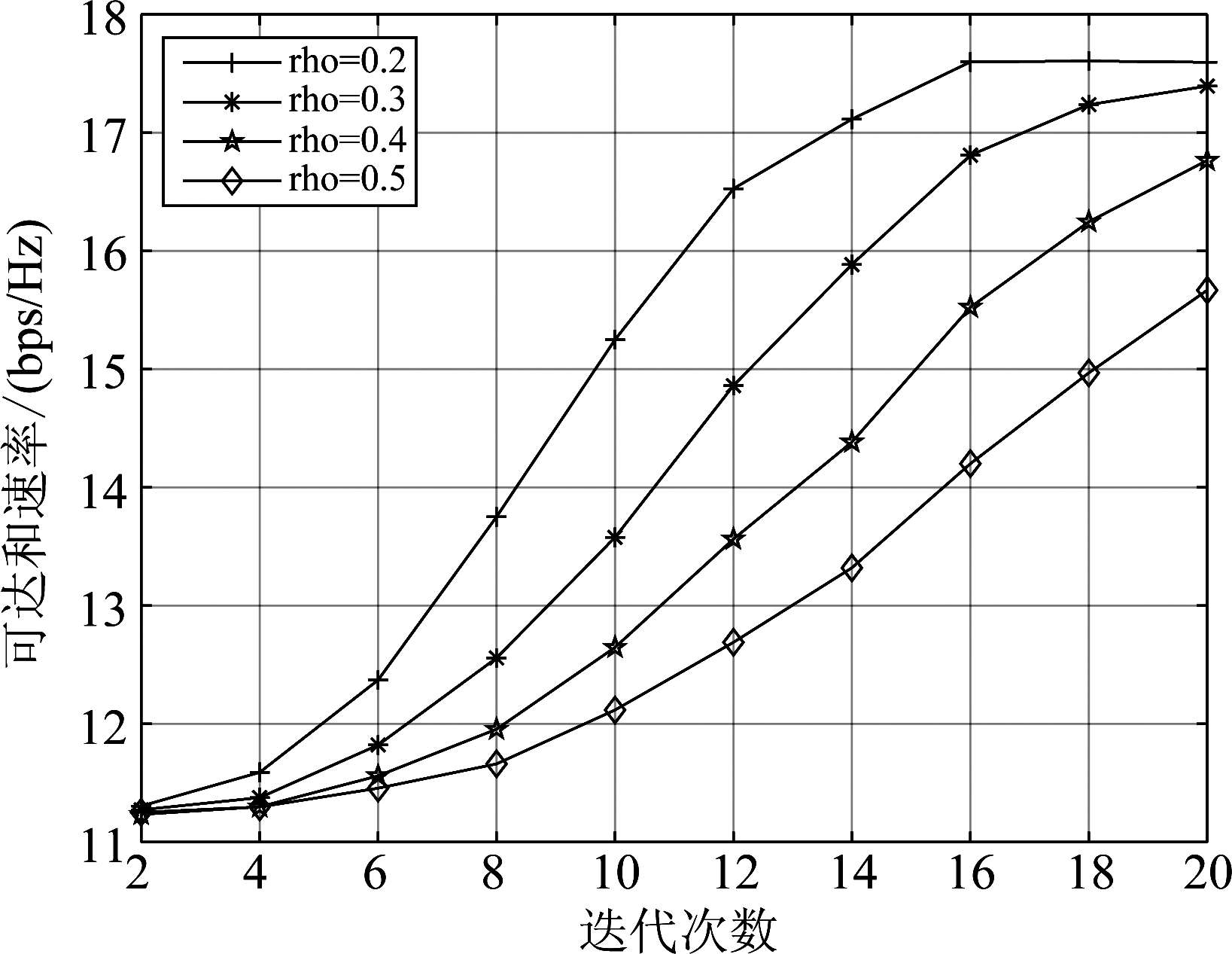
图4 可达和速率与rho和I的关系(SNR=10 dB)
Fig.4 Achievable sum-rate against rho and I (SNR=10 dB)
图5和图6显示了不同混合预编码方案的可达和速率与用户数变化的关系。射频链数与用户数相等NRF=K,信噪比SNR=10 dB,ACN based MLACE方案的其余仿真参数与图2仿真参数相同。全数字预编码和两阶段混合预编码虽然具有较高的可达和速率性能,但是全数字预编码需要与天线数目相同的N=56个高能量消耗射频链,两阶段混合预编码需要NNRF=224个4比特精度的高能耗相移器,其满意的天线阵列增益和消除多用户数据流之间相互干扰的能力是以极高的硬件复杂度为代价换取的。ACN based MLACE方案、基于机器学习的具有开关和反相器结构混合预编码、自适应连接结构混合预编码具有相同的较低的硬件复杂度,但本文的ACN based MLACE方案以轻微的计算复杂度增加为代价具有比它们更高的可达和速率。在所有的混合预编码方案中,基于天线选择开关结构的混合预编码的硬件复杂度最低,开关结构简单,能耗低,实现阵列增益的性能较差,所以其可达和速率也欠佳。图6的SNR=-10 dB,其余仿真参数与图5相同,可以看到,所提的ACN based MLACE方案在较差的信道条件较低的信噪比情况下仍然比基于机器学习的开关和反相器结构的混合预编码可达和速率高。总之,匹配射频链与基站天线关系集合导致计算复杂度轻微的增加,带来可达和速率的改善是值得的。
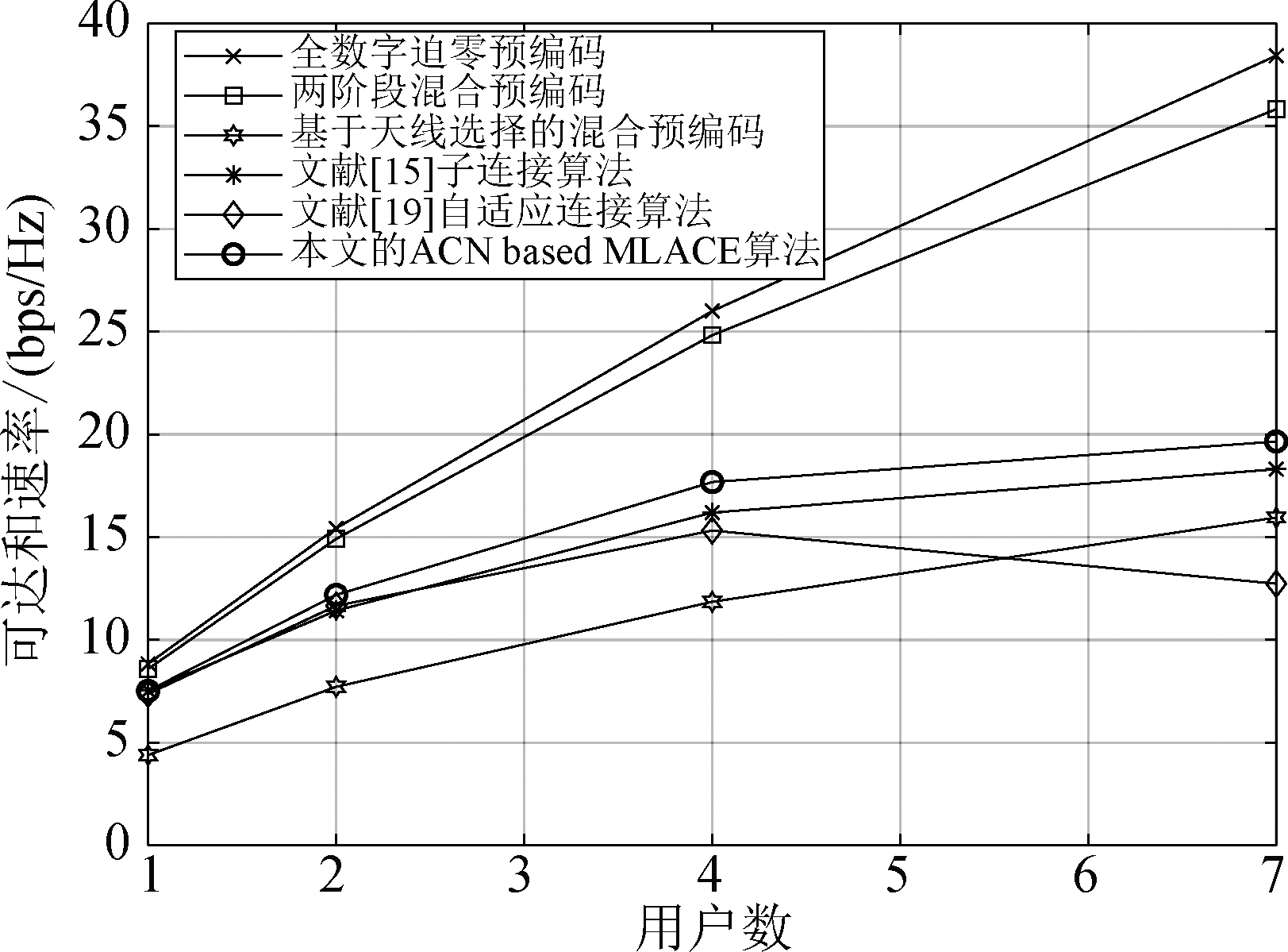
图5 可达和速率与用户数的关系(SNR=10 dB)
Fig.5 Achievable sum-rate against number of users (SNR=10 dB)
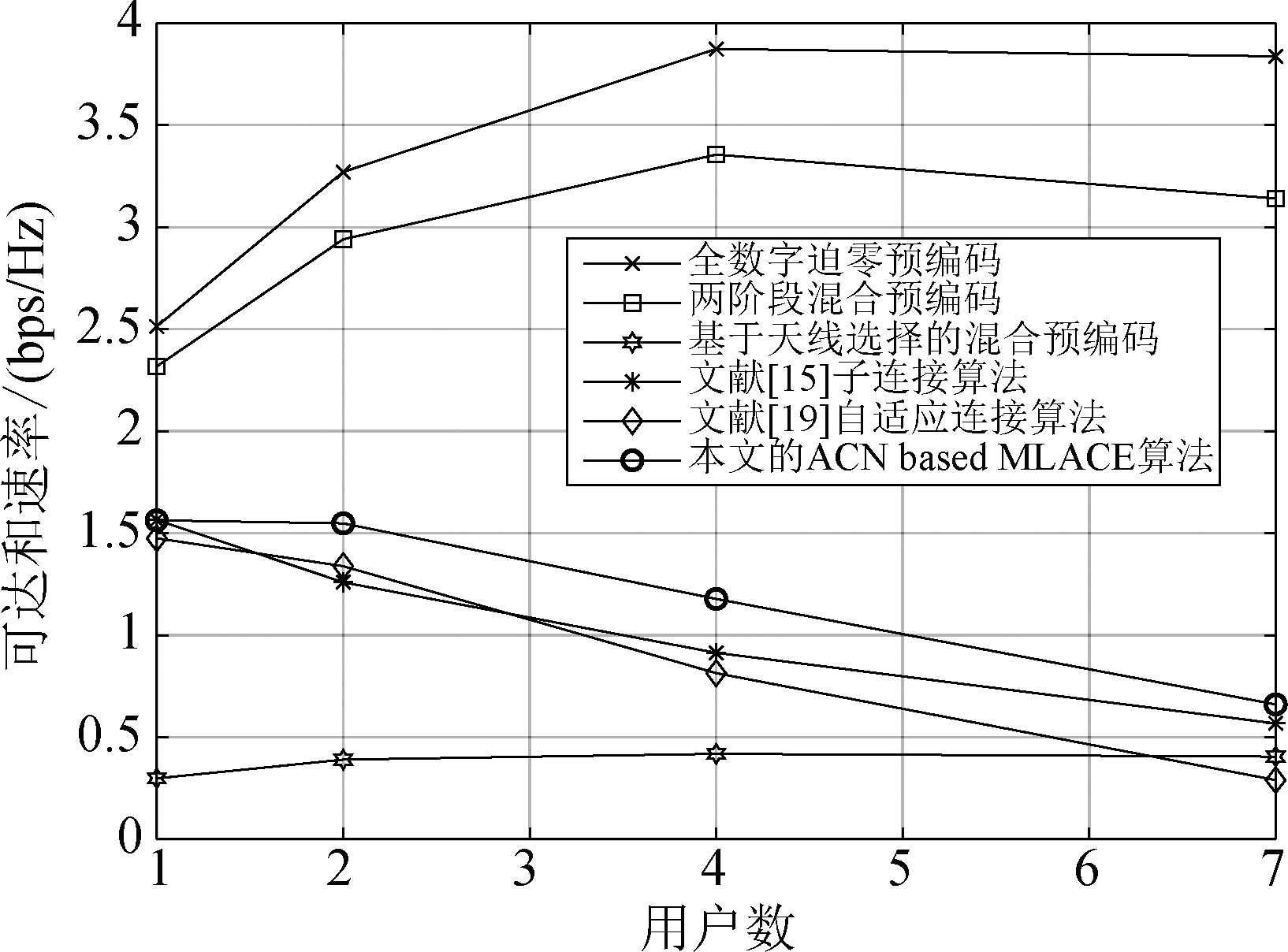
图6 可达和速率与用户数的关系(SNR=-10 dB)
Fig.6 Achievable sum-rate against number of users (SNR=-10 dB)
5 结论
本文提出了1比特量化的自适应连接网络的混合预编码,并把基于机器学习的自适交叉熵优化算法应用于自适应连接结构混合预编码中,改善了自适应连接结构1比特量化相移器的可达和速率性能。在相同的低硬件复杂度下,所提的方案以稍高的计算复杂度为代价具有比基于机器学习固定子连接的开关和反相器混合预编码和自适应连接结构的混合预编码更优异的可达和速率性能。最近已经有运行高效的深度学习方法应用于混合预编码[23],更低计算复杂度更优频谱效率的预编码值得进一步的研究。
[1] Zhou L, Wu D, Dong Z, et al. When Collaboration Hugs Intelligence: Content Delivery over Ultra-Dense Networks[J]. IEEE Communications Magazine, 2017, 55(12): 91-95.
[2] Han S, C. I, Xu Z, et al. Large-scale antenna systems with hybrid precoding analog and digital beamforming for millimeter wave 5G[J]. IEEE Communications Magazine, 2015, 53(1): 186-194.
[3] Ayach O E, Rajagopal S, Abu-Surra S, et al. Spatially Sparse Precoding in Millimeter Wave MIMO Systems[J]. IEEE Transactions on Wireless Communications, 2014, 13(3): 1499-1513.
[4] Méndez-Rial R, Rusu C, Gonz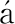
lez-Prelcic N, et al. Dictionary-free hybrid precoders and combiners for mmWave MIMO systems[C]∥2015 IEEE 16th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), 2015: 151-155.
[5] Wang Y, Zou W. Hybrid Digital and Analog Precoding Algorithm for Millimeter Wave MIMO Systems[C]∥2019 IEEE Wireless Communications and Networking Conference Workshop (WCNCW), 2019: 1- 6.
[6] Ni W, Dong X, Lu W. Near-Optimal Hybrid Processing for Massive MIMO Systems via Matrix Decomposition[J]. IEEE Transactions on Signal Processing, 2017, 65(15): 3922-3933.
[7] Wang Z, Li M, Liu Q, et al. Hybrid Precoder and Combiner Design With Low-Resolution Phase Shifters in mmWave MIMO Systems[J]. IEEE Journal of Selected Topics in Signal Processing, 2018, 12(2): 256-269.
[8] Zhang R, Zou W, Wang Y et al. Hybrid precoder and combiner design with finite resolution PSs for mmWave MIMO systems. China Communications, 2019, 16(2): 95-104.
[9] Dong F, Wang W, Wei Z. Low-Complexity Hybrid Precoding for Multi-User MmWave Systems With Low-Resolution Phase Shifters[J]. IEEE Transactions on Vehicular Technology, 2019, 68(10): 9774-9784.
[10] Liang L, Xu W, Dong X. Low-Complexity Hybrid Precoding in Massive Multiuser MIMO Systems[J]. IEEE Wireless Communications Letters, 2014, 3(6): 653- 656.
[11] 王磊, 仲伟志, 顾勇, 等. 面向无人机小区覆盖的毫米波波束优化设计[J]. 信号处理, 2019, 35(7): 1152-1159.
Wang Lei, Zhong Weizhi, Gu Yong, et al. Optimum Design of Millimeter-Wave Beams for UAV Cellular Coverge[J]. Journal of Signal Processing, 2019, 35(7): 1152-1159.(in Chinese)
[12] Ren Y, Wang Y, Xu G. Two-stage hybrid precoding for massive MIMO systems[C]∥22nd International Conference on Telecommunications, 2015: 294-297.
[13] Méndez-Rial R, Rusu C, Alkhateeb A, et al. Channel estimation and hybrid combining for mmWave: Phase shifters or switches?[C]∥Information Theory and Applications Workshop, 2015: 90-97.
[14] 何雪云, 钱旸, 梁彦. 毫米波大规模MIMO系统中基于智能搜索的混合预编码算法[J]. 信号处理, 2019, 35(11): 1826-1834.
He Xueyun, Qian Yang, Liang Yan. A Hybrid Precoding Algorithm Based on Intelligent Search in Millimeter Wave Massive MIMO Systems[J]. Journal of Signal Processing, 2019, 35(11): 1826-1834.(in Chinese)
[15] Gao X, Dai L, Sun Y, et al. Machine learning inspired energy-efficient hybrid precoding for mmWave massive MIMO systems[C]∥IEEE International Conference on Communications, 2017: 1- 6.
[16] 刘斌, 任欢, 李立欣. 基于机器学习的毫米波大规模MIMO混合预编码技术[J]. 移动通信, 2019, 43(8): 8-13.
Liu Bin, Ren Huan, Li Lixin. Machine Learning-based mmWave Massive MIMO Hybrid Precoding[J]. Journal of Mobile Communications, 2019, 43(8): 8-13.(in Chinese)
[17] Ding T, Zhao Y, Li L, et al. Hybrid Precoding for Beamspace MIMO Systems With Sub-Connected Switches: A Machine Learning Approach[J]. IEEE Access, 2019, 7: 143273-143281.
[18] Tian M, Zhang J, Zhao Y, et al. Switch and Inverter Based Hybrid Precoding Algorithm for mmWave Massive MIMO System: Analysis on Sum-Rate and Energy-Efficiency[J]. IEEE Access, 2019, 7: 49448- 49455.
[19] Zhu X, Wang Z, Dai L. Adaptive Hybrid Precoding for Multiuser Massive MIMO[J]. IEEE Communications Letters, 2016, 20(4): 776-779.
[20] Zerovnik J. The cross-entropy method: A unified approach to combinatorial optimization, Monte-Carlo simulation and machine learning[J]. Journal of The Operational Research Society, 2006, 57(12): 1503-1503.
[21] Costa A, Jones O D, Kroese D. Convergence properties of the cross-entropy method for discrete optimization[J]. Oper. Res. Lett., 2007, 35(5): 573-580.
[22] Wu Z, Kolonko M. Asymptotic Properties of a Generalized Cross-Entropy Optimization Algorithm[J]. IEEE Transactions on Evolutionary Computation, 2014, 18(5): 658- 673.
[23] Elbir A M, Papazafeiropoulos A K. Hybrid Precoding for Multiuser Millimeter Wave Massive MIMO Systems: A Deep Learning Approach[J]. IEEE Transactions on Vehicular Technology, 2020, 69(1): 552-563.
