1 引言
随着通信和存储等领域的快速发展,对信息传输的可靠性要求越来越高。但受深衰落,强干扰等因素的影响,信息传输过程中不仅存在随机错误,还经常产生连续的突发删除,严重破坏了通信或存储的质量。对于这种具有多种错误类型的信道,单一的纠错编码方法不能保证信息的可靠传输。因此,急需找到一种可高效纠正该混合错误的编码方案,提高信息系统的可靠性。
乘积码作为一种将差错控制和交织技术相结合的信道编码机制,为纠正多种混合信道错误提供了可能[1-4]。低密度奇偶校验(Low-Density Parity-Check,LDPC)码由于其逼近香农极限的优越性能而被广泛用于构造乘积码[5-7]。里德-所罗门(Reed-Solomon,RS)码是在Galois域 GF(q=2m)上定义的最大距离可分码,因其较强的纠正突发删除的能力被多数乘积码方案采用[8-10]。文[11]采用LDPC码和RS码组成的乘积编码器有效地纠正了比特错误,并基于错误估计提出了一种新的乘积码优化方案,但其主要针对图像传输的应用场景。文[12]给出了RS-LDPC乘积码在高信噪比(Signal to Noise Ratio,SNR)下的应用,利用比特翻转法来改进乘积码的性能,但该方案只适用于信噪比较高的信道条件,未针对纠正随机错误和长突发错误的能力进行优化设计。针对LDPC-RS 二维乘积码,文[13]提出了类“turbo”混合迭代译码,改进了低信噪比下的乘积码性能,随着迭代次数的增加,纠错能力有明显改进,但迭代次数的增大也使得方案的复杂度成倍增加。上述乘积码方案均由二进制LDPC码组成,二进制LDPC码是基于比特的编码机制,且译码后的残留错误比特分布较为随机,将其转换为符号后,分散的比特错误也会使得对应符号错误的数量较多,造成更多的外码译码失败。因此,二进制LDPC码与基于符号纠错的RS码进行级联,未能充分挖掘RS码基于符号纠错的特性,存在性能损失,即二进制LDPC码无法与定义在Galois域中的RS码实现更好地错误匹配。因此,本文设计了采用RS码与多进制LDPC码组成的级联码。
多进制LDPC(Non-Binary LDPC code,NB-LDPC)码是由Davey和Mackay首次提出,将LDPC 码扩展到了Galois域 GF(q)(q为整数且满足q>2)[14-16]。通过对多进制LDPC码的残留删除和错误特性的分析可知,与二进制LDPC码相比,NB-LDPC码有较强的纠正随机错误的能力,且一个错误符号中包含多个错误比特[17-20]。因此,本文提出了一种纠正随机错误和长突发删除的多进制乘积码方案。采用在同一个Galois域GF(q=2m,m>1)中定义的NB-LDPC码和高码率RS码来构造乘积码,从而实现乘积码内码与外码之间更有效的错误匹配;同时,对于存在长突发删除的信道,采用交织的方法将其分散到不同的NB-LDPC码码字中。为进一步优化多进制乘积码的性能,本文提出了一种新的选择迭代译码方案,该方案通过修正比特概率信息进而优化符号概率来实现,可以有效地减少信息传输中的错误;由于只有部分码字需进行再次译码,因此,该方案所带来的额外复杂度也是较低的。
2 乘积码中NB-LDPC码残留的错误和删除分布
本节首先给出了乘积码的结构,然后分析了乘积码中NB-LDPC码在加性高斯白噪声(Additive White Gaussian Noise,AWGN)信道下的残留错误分布情况,同时也分析了存在长突发删除的AWGN信道下的残留删除分布情况。
2.1 乘积码结构
乘积码是一种可以同时纠正多种错误类型的编码机制,因此,对于同时存在随机错误和连续删除错误类型的信道,构造乘积码可以有效地纠正该信道下的错误。
乘积码是一种由多个短线性分组码构造长码的编码技术,一般常用的主要是二维、三维乘积码[21]。本文以有限域符号(非二进制比特)构造的二维乘积码为例进行研究。其中多进制RS码作为外码,多进制LDPC码作为内码。假设两个线性分组码分别为C1(n1,k1)和C2(n2,k2),其中n1 (n2)为RS码(LDPC码)符号长度,k1 (k2)为RS码(LDPC码)信息符号长度。构造乘积码主要包括下述三个步骤:
(1) 将信息符号按顺序排列成k1行k2列的矩阵;
(2) 纵向取k1个符号进行外码编码,生成纵向符号的校验信息,得到n1×k2符号矩阵;
(3) 将每行k2个符号作为内码的信息码字进行内码编码,最终编码生成n1×n2符号矩阵。
经上述内码和外码多进制编码生成的乘积码结构如图1所示,信息位所在的每一列符号组成了一个RS码码字,每一行符号组成了一个NB-LDPC码码字。对应图1,图中信息位,行校验位,列校验位以及行校验位的列校验位四部分相应矩阵大小分别为k1×k2,k1×(n2-k2),(n1-k1)×k2,(n2-k2)×(n1-k1)。
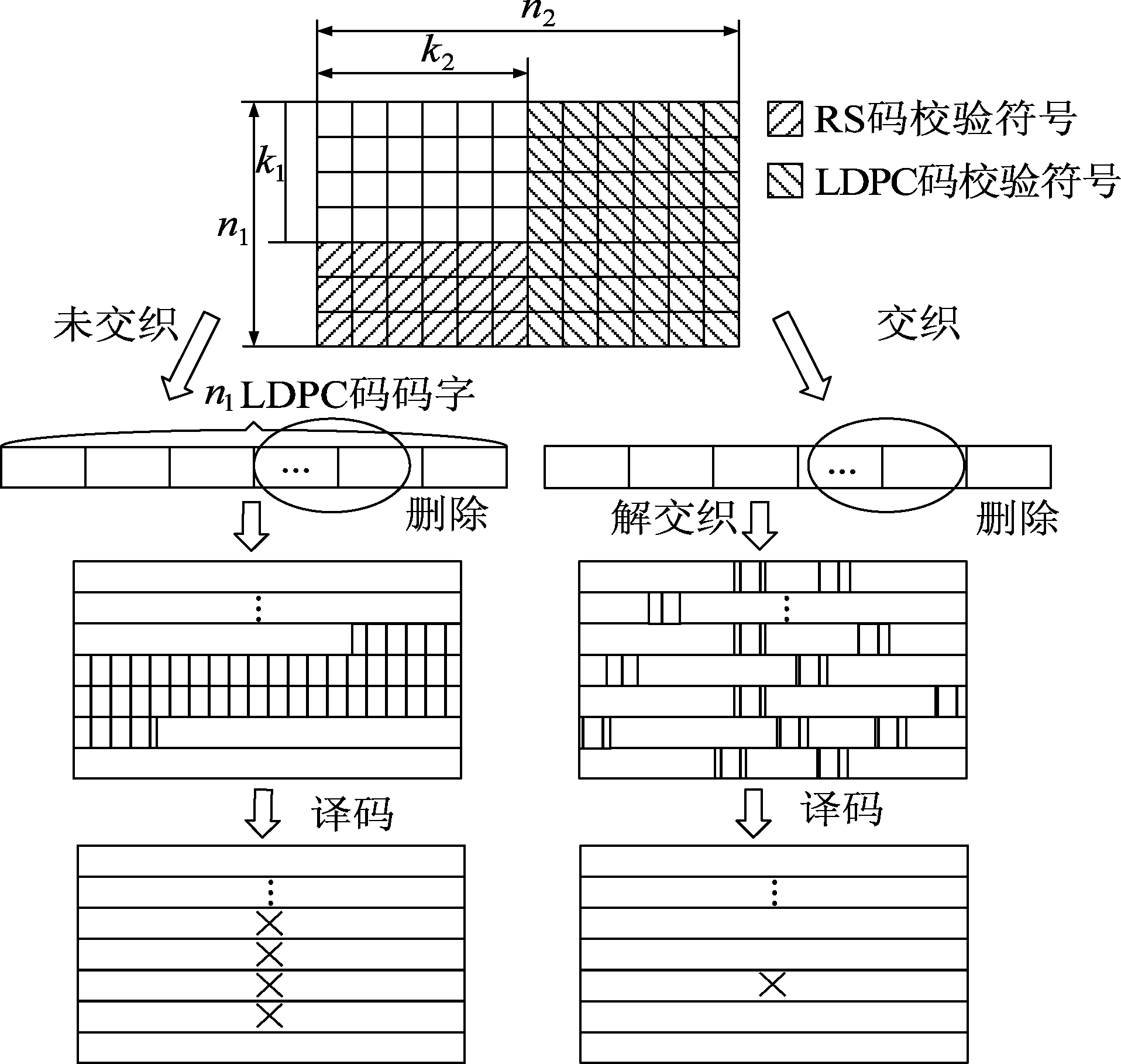
图1 乘积码结构
Fig.1 The structure of product code
2.2 存在长突发删除信道下的NB-LDPC码残留错误分布
该部分给出了包含长连续突发删除信道下的NB-LDPC码的残留错误分布。如图1所示,交织可有效将突发删除分散到各个NB-LDPC码码字中,从而使得NB-LDPC码码字成功译码的概率增加。当突发删除长度较短时,即删除错误集中在数量非常少的码字时,内码译码后的残留错误仍然在外码的纠错能力之内,此时是否采用交织并不影响乘积码的性能。而当突发删除长度较长时,如果集中在若干LDPC码字处理,则会造成较多的LDPC码译码失败,从而造成外码也译码失败。若采用交织方案,则LDPC码的码字错误率会降低,适合纠错能力有限的外码充分发挥其纠错能力。因此,与传统的乘积码方案不同,本文采取的系统模型在信息传送到信道前需执行交织,相似地,在进行乘积码译码前需先进行解交织。
本文以Galois域GF(256)上的NB-LDPC(72,36)码为例进行分析,其中NB-LDPC码基矩阵的行重为4,列重为2,非零元素的选取采用文[22]提出的方法。与多进制LDPC码相同,RS码也是基于符号的多进制编码方法,选择相同Galois域上定义的NB-LDPC码与RS码构造乘积码可以在编译码时直接进行符号的传递,减少符号的映射复杂度。另外,也可使得NB-LDPC译码后的残留错误尽可能集中在RS码的单个符号内;而RS码是基于符号的纠错码,即使单个符号内存在多个比特错误也不影响RS码的译码结果,只有错误符号的个数是决定RS码是否能译码成功的关键。因此,相同有限域上的RS码与多进制LDPC码能实现最佳的匹配。综上,本文采用相同域上的RS码作为外码来构造乘积码,即此处n1=255。对NB-LDPC码采用基于快速傅里叶变换(Fast Fourier Transform,FFT)的置信传播(Belief Propagation,BP)译码算法[23]。
为了更直观地观察交织与未交织的差异,该部分对两种情况下残留的错误NB-LDPC码码字的数量进行了统计,仿真在AWGN信道下进行,采用二进制相移键控(Binary Phase Shift Keying,BPSK)调制方法。连续的n1=255个NB-LDPC码码字作为一组,同时随机连续选取2%的信息作为删除去分析删除信道下的残留错误情况。不同信噪比下的错误码字统计结果如图2所示,交织后残留的错误NB-LDPC码码字明显少于未交织的情况,当Eb/N0为2.4 dB时,未交织的残留错误码字数量大约是交织后的3倍。
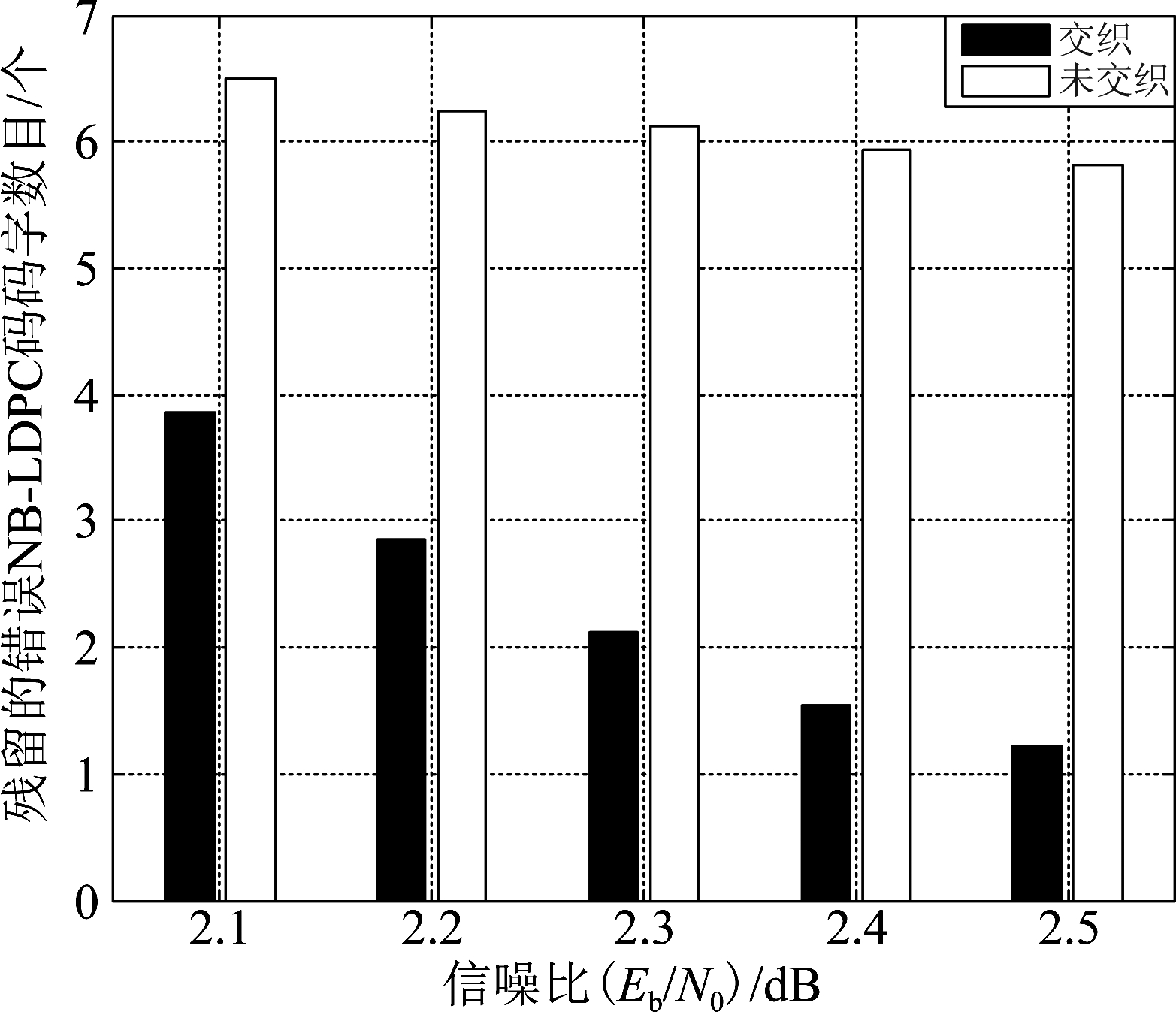
图2 包含2%删除错误的AWGN信道下残留的错误NB-LDPC码码字数目
Fig.2 The residual number of error non-binary LDPC codewords under the AWGN channel with 2% erasures
2.3 AWGN信道下的NB-LDPC码残留错误分布
基于上述乘积码结构,本部分对NB-LDPC码的残留错误进行分析,从而根据错误分布选择合适的构造方案。详细地,对NB-LDPC码和二进制LDPC码的错误比特位置分布进行了分析,进一步通过连续仿真n1=255个LDPC码码字,对同一位置发生错误的符号数目及其对应概率进行了统计[24]。采用的NB-LDPC码参数与2.2节相同,均采用GF(256)下的NB-LDPC码,其中一个符号对应8个比特。与NB-LDPC码的码长码率一致,本文选取IEEE 802.16e标准下的码长为576比特,码率为1/2的二进制LDPC码来进行下述比较分析[25]。仿真在AWGN信道下进行,采用BPSK调制方法。
首先,对NB-LDPC码和二进制LDPC码的错误比特位置进行了分析。二进制LDPC码和NB-LDPC码之间最大的差别是其构成单元,NB-LDPC码以符号为单位,而二进制LDPC码以比特为单位。NB-LDPC以符号为单位进行译码,则一个符号译码错误,对应得到的比特矢量也是错误的,一个错误符号中包含多个错误比特。例如,GF(2m)域下的一个NB-LDPC码码字译码后的矢量表示为{s1,s2,s3,…,sx},相同码长码率的二进制LDPC码码字译码后的矢量表示为{b1,b2,b3,…,bx′}。假设NB-LDPC码译码后只有t个错误符号
而二进制有t′个错误比特
错误位置均为随机,NB-LDPC码的错误符号可对应映射成t×m个比特,少数c个比特映射正确,从而使得该情况下的NB-LDPC码与二进制LDPC码有的错误比特数目相似,即t×m-c≈t′。但
比特位置并不相邻,映射后的位置包含在了更多的符号中。
本文采用信噪比为1.8 dB下的多进制LDPC码的错误码字和信噪比为2.2 dB下的二进制LDPC码的错误码字来进行验证。为了更清晰地可视化分布结果,随机选取了多组具有相同比特错误的NB-LDPC码码字和二进制LDPC码码字作为一组进行分析,对每个错误的NB-LDPC码码字和二进制LDPC码码字的错误符号个数进行了统计。统计结果如图3所示,其中横坐标为每组码字的错误比特数目,纵坐标为每组码字的错误符号数目。可明显看出,NB-LDPC码码字的错误符号数目明显小于具有相同错误比特数目的二进制LDPC码码字,详细地,对于存在18个比特错误的NB-LDPC码码字和二进制LDPC码码字,NB-LDPC码码字只有6个错误符号,而同时二进制LDPC码码字有15个错误符号。与二进制LDPC码的残留错误分布相比,NB-LDPC码的错误比特分布更加集中,多个错误比特分布在同一个符号中。因此,采用相同域下的NB-LDPC码与RS码构造乘积码可高效实现错误模式的匹配。
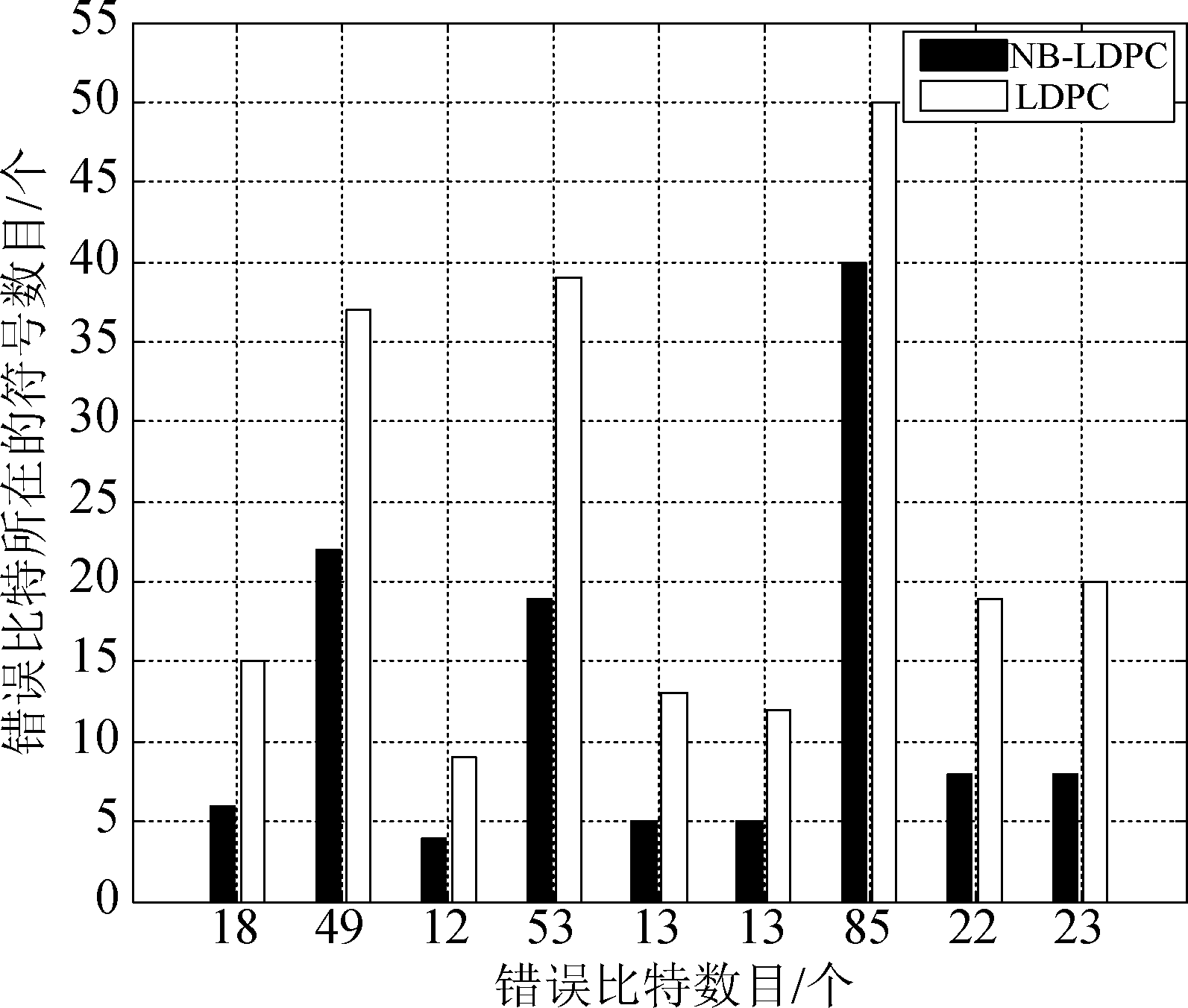
图3 相同比特错误数目的NB-LDPC码和二进制LDPC码码字的错误符号个数统计结果
Fig.3 The number of error symbols in an NB-LDPC codeword and a binary LDPC codeword under the same number of error bits
然后,在连续的255个LDPC码码字中,本文对同一位置出现的错误符号个数进行了概率统计。LDPC码包括多进制LDPC码译码失败后的残留错误,与码字结构以及译码算法均有关系,残留错误多出现在一些容易出错的易错子结构,例如陷阱集、停止集或者小环等位置[26-27]。但是这些陷阱集等易错结构与LDPC码的结构(或者Tanner图)的关系较为复杂,且在每个码字传输不同的噪声分布下,存在错误的组合结构出现的位置是随机的。不同的传输噪声下,最后收敛的易错子结构的位置往往是不相同的。针对该问题,本文采用统计的方法,分析连续传输的255个码字的相同位置的错误分布情况,为设计乘积码提供依据。
在不同的信噪比下,GF(256)域上NB-LDPC(72,36)码的错误符号的分布情况如图4所示,其中se表示LDPC码译码后的码字在同一位置残留的错误符号个数,p(se)表示对应残留错误个数所发生的概率。从图中可以看出,随着错误符号数量的增加,发生的概率逐渐降低;随着信噪比的增加,概率降低的速度越来越快。同时也可看出NB-LDPC码发生的错误符号个数多数小于3,在相同的信噪比下,多进制LDPC码的残留错误符号明显小于二进制LDPC码错误符号的个数。对于码长为n个符号,码率为k /n的RS码,硬判决译码算法可纠正(n-k)个删除或(n-k)/2个错误。因此,对于外码,本文采用纠错能力低的,码率较高的码字就可以实现对多数NB-LDPC码残留错误的纠正,尽可能将码率损失降到最低。
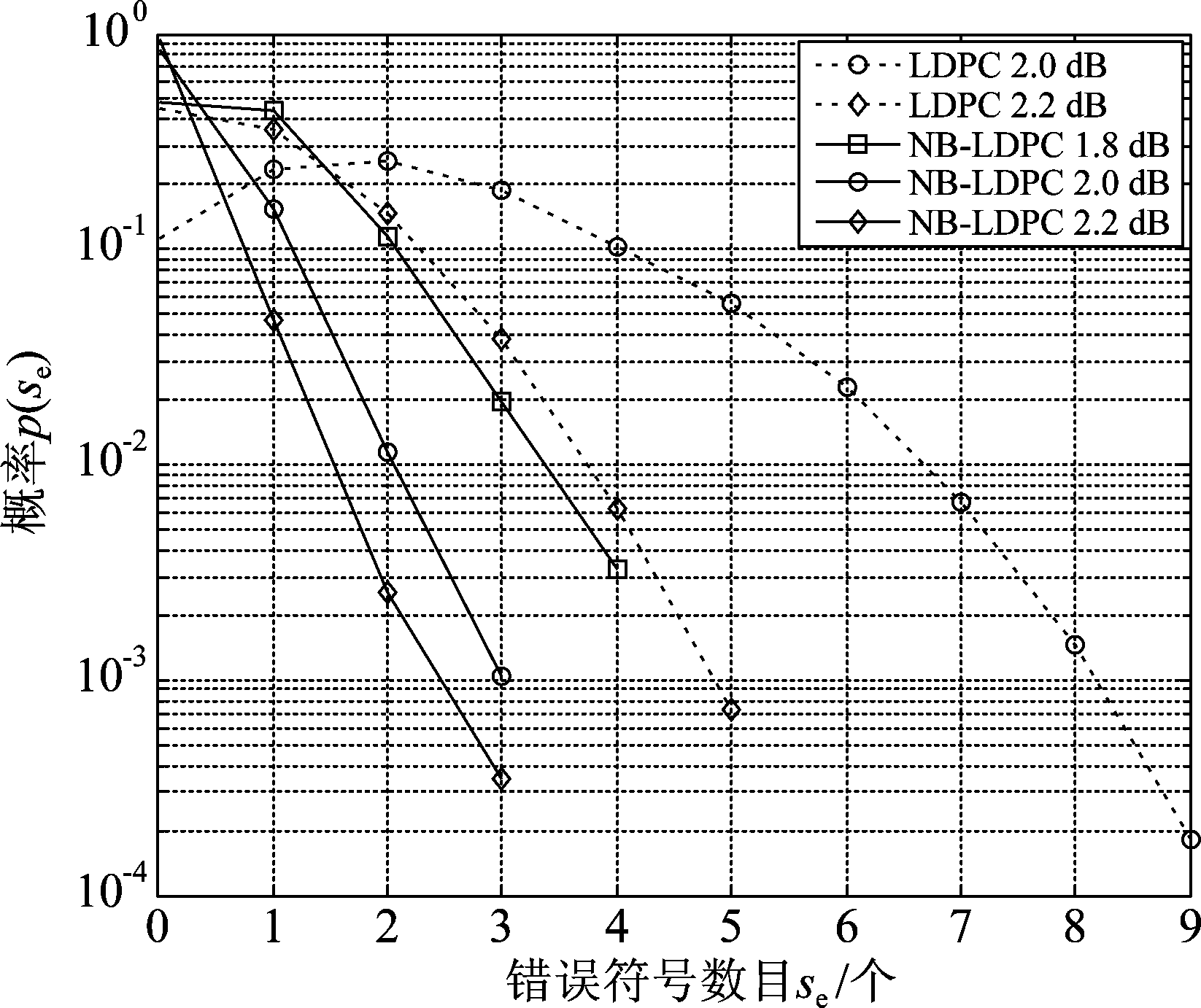
图4 不同信噪比下同一位置错误符号个数分布情况
Fig.4 Distribution of the number of error symbols in the same position under different SNRs
3 多进制LDPC-RS乘积码的迭代译码
3.1 乘积码的迭代译码方案
下面给出多进制LDPC-RS乘积码的译码算法,主要包括初始化,NB-LDPC译码,RS译码,以及更新先验信息等四个步骤,具体步骤如下:
首先,在译码之前需先进行译码状态的初始化标记,用ldpc_mark表示LDPC码码字的状态,rs_mark表示RS码码字的状态,Iter表示迭代的次数。LDPC码的标记维度为n1,RS码的标记维度为k2,对于所有的ldpc_mark和rs_mark标记为0,对应公式表达为:
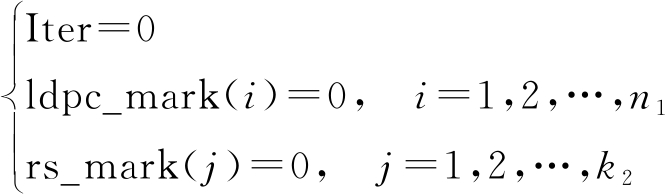
(1)
然后,计算n1×n2个符号概率及其初始的符号判决结果c。对于乘积码码字中第i行第j列符号,用
表示。根据信道观测值,可以得到比特初始概率信息,用Pinit表示。对于Galois域GF(256)中的符号,每个符号可以被表示为8比特的矢量,因此,根据比特概率信息,可以计算得到每个符号的256个概率值。对于第k个接收到的符号,及其比特矢量表示中的第j个比特分别用yk和
表示。在噪声方差为σ2的AWGN信道下,比特为1或0的初始概率分别计算为:
(2)
其中,
表示第k个符号对应比特矢量的第j个比特为b(b∈{0,1})的概率。对应每个符号的初始概率信息计算为:
(3)
其中a∈GF(2m),aj是符号a对应比特矢量中第j个比特值(0或1),
为第k个符号是a的概率。根据得到的符号概率大小,得到符号初始判决结果c,判决方法为找到2m个符号概率的最大值,最大值所对应的符号即为该符号判决结果。
基于上述得到的概率信息,选择相应的码字执行NB-LDPC码译码。需先对判决结果c按行进行校验,即计算
的值,在这里的计算是Galois域内的加法和乘法。若校验结果为矢量0,则不执行NB-LDPC码译码,c即为译码结果,并将对应码字的状态ldpc_mark更新为1;否则进行NB-LDPC内码译码,译码算法采用通用的FFT-BP译码算法,从而得到n1×n2个符号内码译码结果,用yLDPC表示。对应乘积码矩阵中第i个LDPC码码字的第j个符号表示为
对得到的译码结果
进行校验,即计算H·(yLDPC-i)T,可以得到n1个LDPC码码字的校验值,同时根据校验结果更新ldpc_mark,第i个LDPC码的更新方法如下式:
(4)
在外码RS译码过程中,需先计算校正子s,并据此更新rs_mark的值,第j个RS码码字的状态更新如下:
(5)
若rs_mark标记为1,则对该码字不译码,否则执行RS码译码。本文采用RS码的硬判决译码方法对NB-LDPC译码后的残留错误进行纠正,从而得到外码译码结果yRS。yRS的维度大小为n1×k2,第j个码字的第i个符号的表示为
使用公式(5),并根据得到的译码结果重新计算校正子并更新rs_mark。
最后,根据内外码符号译码结果ydec去更新NB-LDPC码译码的先验信息实现迭代。乘积码译码结果可被描述为下述公式:
(6)
为了进一步优化多进制乘积码的性能,充分利用内外码之间可回馈的信息,本文提出了一种新的迭代译码方法,通过前一次迭代的译码结果不断修正NB-LDPC码译码的比特初始概率信息,进而优化符号概率,从而提高多进制乘积码的性能。详细的更新迭代方案在算法1中给出。在更新比特的初始概率信息时,只需对译码正确的LDPC码码字和RS码码字所包含的比特位置进行更新,且更新只需要用到比特的译码结果信息。将计算得到的新的先验概率信息返回进行NB-LDPC码译码,从而实现迭代。需要注意的是,当迭代次数达到设置的最大迭代次数,或者在某次迭代后的译码结果均满足乘积码码字的行校验值均为0,即所有的LDPC码标记ldpc_mark均为true,则停止迭代。
算法1 多进制乘积码的迭代更新方案
Algorithm 1 The probability updating scheme of non-binary product code iterative decoding
算法1 多进制乘积码的迭代更新方案输入:前一次迭代的RS码码字标记rs_mark;前一次迭代的LDPC码码字标记ldpc_mark;前一次迭代的符号译码结果ydec;初始的先验概率信息Pinit;输出:信息更新l次后的先验概率信息P(l)new;新的符号判决结果c。1) 在乘积码中,根据ydec按行计算n1个NB-LDPC码码字的校验值,第i个NB-LDPC码码字计算为H·(ydec-i)T,将校验为0的码字ldpc_mark标记为1,否则,对应的ldpc_mark保持不变。2) 根据ydec按列计算k2个RS码码字的同步校正子s,如果码字校验为0,则rs_mark标记为1,否则,对应码字的rs_mark值保持不变。3) 基于Galois域GF(2m)上的符号与比特之间的映射关系,将符号译码结果ydec进行映射得到m·dim(ydec)维度大小的比特译码结果,用ybitdec表示。4) 更新迭代次数Iter=Iter+1,l=Iter,对应(未迭代)初次译码时的译码结果的Iter状态值为1。5) 如果比特所在码字的ldpc_mark或者rs_mark标记值为1,则更新对应LDPC码码字或RS码码字所在比特的先验信息,新的先验信息计算公式如下:P(l)new(ybitdec)=1/[1+exp(-2×1-2ybitdec)], rs_mark=1 or ldpc_mark=1Pinit, others 对应更新后的该比特为 !ybitdec的概率为1-P(l)new(ybitdec)。6) 根据新的比特概率信息计算新的符号概率信息,如公式(3)所示,并根据得到的符号概率进行判决,得到新的判决结果c。7) 返回c和P(l)new去执行NB-LDPC码译码。
3.2 复杂度分析
在复杂度方面,首先,针对NB-LDPC码采取了复杂度较低的FFT-BP译码方法,将校验节点更新的步骤转化到频域上执行,使用快速傅里叶变换把计算复杂的卷积过程进行转换,从而简化了乘法的计算;同时,研究证明了FFT-BP译码算法在降低复杂度的条件下,与BP译码算法相比,性能依旧优良,且没有损失[28]。除此之外,本文采用的是相同Galois域上定义的内外码,因此,两者信息传递时,不需要进行符号转换,从而减少了所需的计算。
表1 多进制LDPC码与二进制LDPC码译码复杂度比较
Tab.1 Comparison of decoding complexity of NB-LDPC codes and binary LDPC codes
算法加法乘法NB-LDPC码译码(FFT-BP)变量节点更新0n2wcq校验节点更新(n2-k2)(wr+1)qlog2q(n2-k2)(wr-2)q二进制LDPC译码(BP)变量节点更新02n'2wc校验节点更新2(n'2-k'2)(wr-1)2(n'2-k'2)(2wr-3)
与二进制LDPC-RS乘积码方案相比,本文所提出的多进制乘积码方案的复杂度主要来源于NB-LDPC译码复杂度和迭代译码两个方面,而LDPC码译码复杂度主要来源于变量节点和校验节点的信息更新。NB-LDPC码译码采用FFT-BP译码算法和二进制LDPC码采用BP译码算法时校验节点和变量节点更新一次所需的加法和乘法数量分别如表1所示。其中wr表示LDPC码校验矩阵的行重,wc表示LDPC码校验矩阵的列重,q为多进制LDPC码所在的Galois域的阶数。从表中可以看出,NB-LDPC码的译码复杂度与所在Galois域的阶数有直接的联系,随着阶数的增长,复杂度也成倍增加。对于码长为n2符号,码率为k2/n2的NB-LDPC码译码,其需存储n2q个初始概率信息,而码长为
比特,码率为
的二进制LDPC码需存储
个概率信息。在相同的码长条件下,即
时,对于高阶域上的NB-LDPC码,NB-LDPC码所需存储的信息量明显多于二进制LDPC码。综上,NB-LDPC码译码加法运算量大约是二进制LDPC码译码的q/2倍,乘法运算量及初始信息存储量大约是二进制LDPC码的q/(2log2q)倍。
其次,所提出的迭代译码方案为条件选择性译码,在后续的迭代过程中,并不是对所有LDPC码码字和RS码码字均需要进行译码。假设LDPC码第l次迭代所需译码的比例大小为
码第l次迭代所需译码的比例大小为
一个NB-LDPC码码字译码的复杂度为CLDPC,一个RS码码字的译码复杂度为CRS,第l次更新先验信息的复杂度表示为
则对于GF(256)域上的NB-LDPC(72,36)和RS码所构成的多进制乘积码,其迭代译码复杂度可表示为
其中max_Iter为最大迭代次数。由于
因此更新先验信息的复杂度相较于NB-LDPC码译码来说可忽略不计,即迭代译码复杂度可重写为
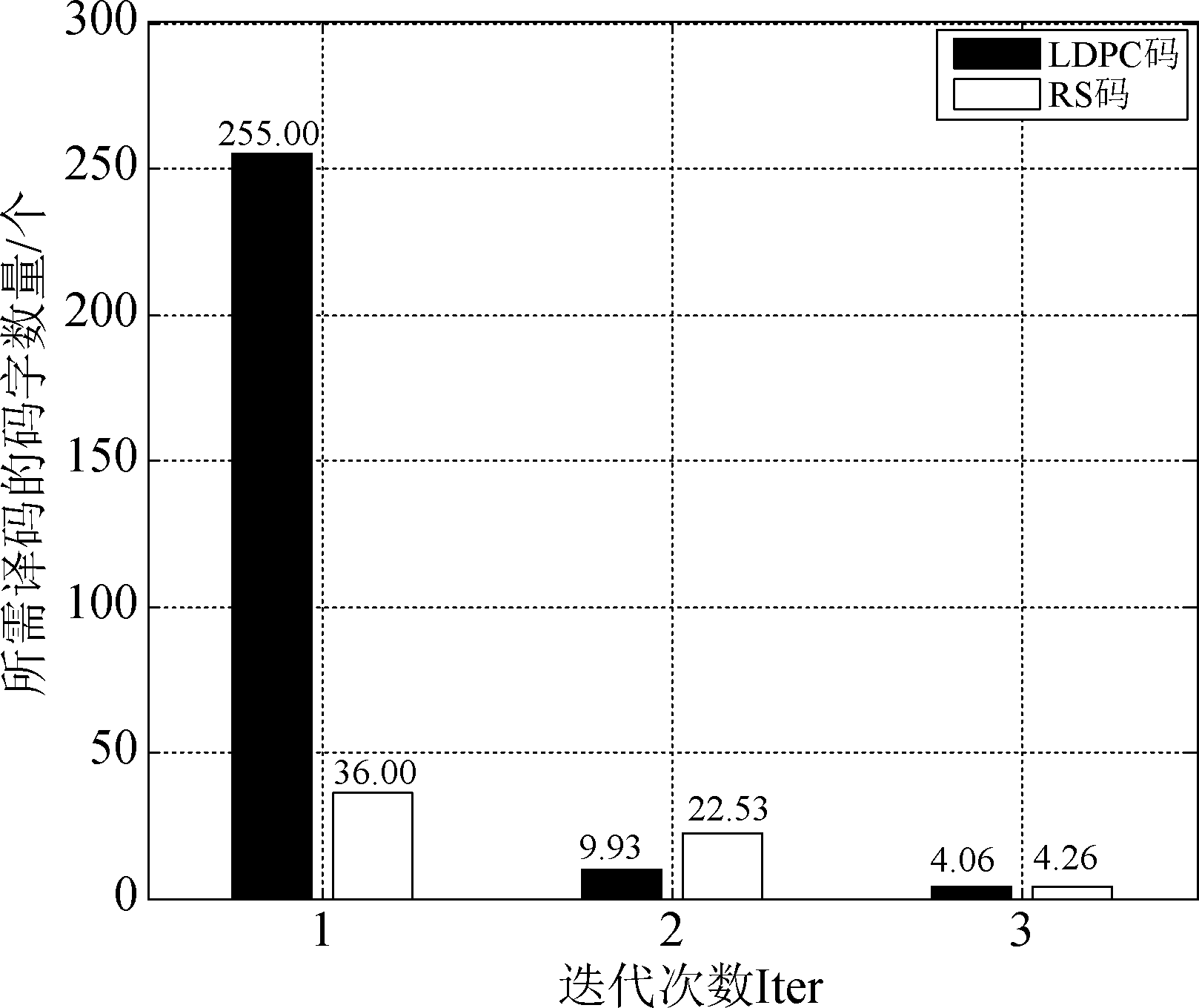
图5 Eb/N0 为 1.6 dB时迭代译码过程中所需译码的平均码字数量
Fig.5 The number of average additional codewords required for decoding in the iteration rounds when Eb/N0 is 1.6 dB
另外,如图5所示,经过一次迭代后(Iter=2),乘积码中所需译码的码字数量急剧下降。例如Eb/N0为1.6 dB时,多进制LDPC(72,36)-RS(255,251)乘积码迭代一次后只有3%的码字需要执行NB-LDPC码译码,且随着迭代次数的增加,比例逐渐降低,因此,对于NB-LDPC码来说,迭代带来的复杂度是可忽略的。同时,由上述分析可知RS码迭代一次后所需译码的比例不能忽略,但后续迭代的码字数可忽略不计,因此,本文提出的多进制乘积码迭代译码方案复杂度可更新为
不难看出,迭代所带来的额外复杂度是较小的。
综上,本文所提出的迭代译码的复杂度主要来自于NB-LDPC码译码以及RS码译码所带来的复杂度。与现有多进制LDPC码方案相比,提出的多进制乘积码方案的复杂度主要来源于外码RS码译码所增加的复杂度。RS码译码复杂度与其纠错纠删能力有着直接的联系,本文所采取的是高码率RS码,因此,RS码译码的复杂度也相对较低。与二进制LDPC码和RS码构成的乘积码相比,复杂度的增加主要来源于NB-LDPC码译码,对于GF(256)域上的NB-LDPC码,其乘法运算量是二进制LDPC译码运算量的16倍左右。虽然NB-LDPC-RS乘积码的复杂度有倍数的增长,但对错误和删除的纠正能力也有较大的提升。
4 仿真与性能分析
本部分对提出的多进制乘积码性能进行了仿真测试,仿真在AWGN信道下进行,采用的调制方式为BPSK。本文所采用的NB-LDPC码和RS码均是基于Galois域GF(256),即每8个比特构成了一个符号[29]。与上文参数相同,本文采用码长为72符号(576比特),码率为1/2的NB-LDPC码作为内码,对应Galois域上码长为255符号的高码率RS码作为外码来进行性能的验证,并与相同码长码率的IEEE 802.16e标准下的二进制LDPC(576,288)码构成的乘积码进行了比较。
4.1 AWGN信道下的性能验证
首先,对多进制乘积码的性能验证,与相同码长码率的二进制LDPC-RS乘积码进行了比较。NB-LDPC-RS乘积码错误比特分布的集中特性使得乘积码纵向统计的错误符号的个数明显降低,从而增加了纵向错误个数在高码率的RS码纠正能力之内的概率,使得RS码充分发挥了其纠错能力,提高了乘积码的性能。仿真结果如图6所示,其中Nb为NB-LDPC码的比特长度,在误比特率(Bit Error Rate,BER)为10-5时,与二进制LDPC码相比,多进制LDPC码有0.35 dB左右的性能增益。同时,在BER为10-5时,与多进制LDPC码相比,多进制LDPC码与RS(255,253)码构造的乘积码有0.35 dB左右的性能增益,而与RS(255,251)码构造的乘积码有0.5 dB左右的性能增益,而在相同误比特率的条件下,与二进制LDPC码相比,二进制LDPC码和高码率的RS码构成的乘积码只有0.25 dB/0.4 dB左右的性能增益。进一步验证了多进制LDPC码可与RS码形成更好的错误模式匹配。
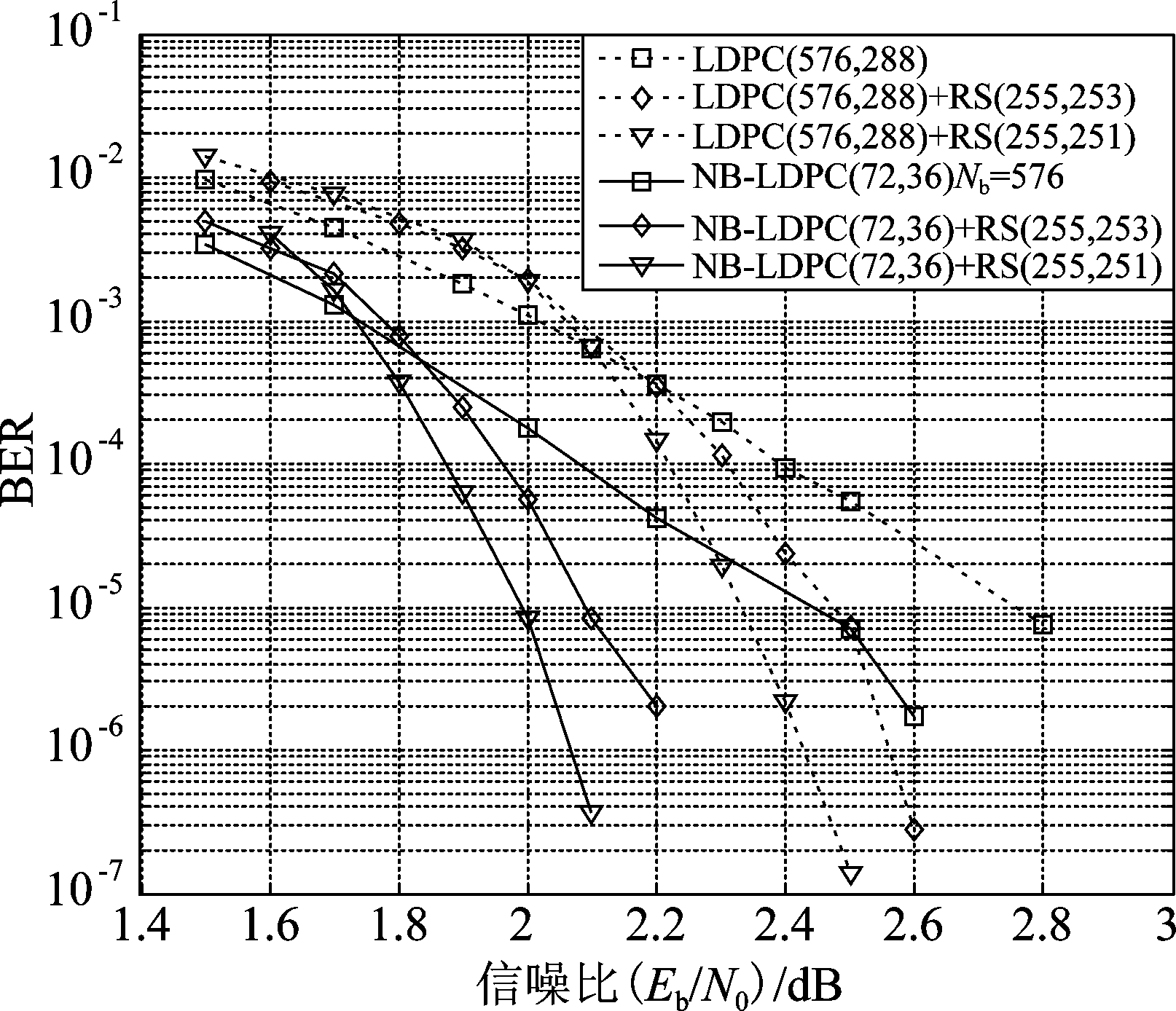
图6 多进制LDPC-RS乘积码与二进制LDPC-RS乘积码性能比较
Fig.6 Performance comparison between non-binary LDPC-RS product code and binary LDPC-RS product code
然后,对算法1所提出的多进制迭代译码方案的性能进行了验证。仿真结果如图7所示,其中Iter表示迭代的次数,未迭代时的Iter=1。仿真验证同样采用的是LDPC(72,36)码和RS(255,253)/RS(255,251)码构成的乘积码,从图中可以看出,采用所提出的修正比特符号概率的迭代译码方案,有明显的性能增益。根据算法1中的更新公式可知,初次译码正确的码字相应位置比特的先验信息被更新后会使得在下一次迭代时部分比特的先验信息更加准确,比特对应译码结果的概率得到修正。采用更新后的先验信息进行译码会使得前一次译码不正确的码字在迭代译码后可以被相应纠正,从而减少译码的残留错误,对于多进制LDPC-RS乘积码,可以有效提高其可靠性。对于NB-LDPC(72,36)-RS(255,251)乘积码,在信噪比Eb/N0为1.75 dB时,与未迭代的性能相比,迭代一次后,即Iter=2时的误比特率降低了两个数量级。
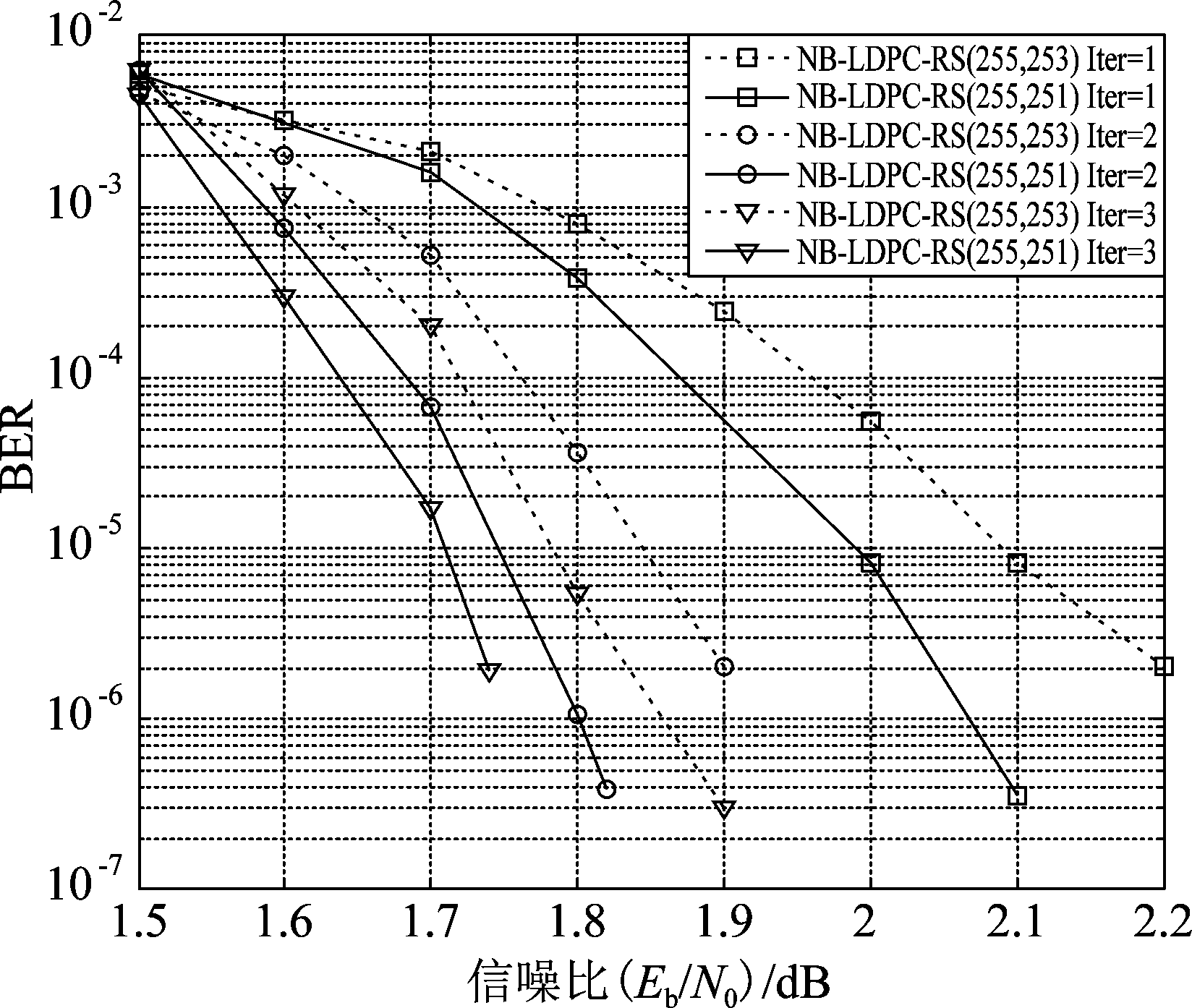
图7 不同迭代次数下的乘积码性能
Fig.7 The performance of non-binary product code under different iterations
整体而言,与同码率二进制LDPC-RS乘积码相比,在信噪比Eb/N0为1.75 dB时,在Iter=3时,本文提出的多进制乘积码迭代方案的BER下降了约四个数量级,而复杂度只增加了大约两个数量级,以较小的额外复杂度代价换取了性能的有效改善。
4.2 存在长突发删除AWGN信道下的性能验证
该部分验证了提出的多进制乘积码迭代方案在同时包含长突发删除和随机错误信道下的高可靠性。首先,在包含1%长连续突发删除的AWGN信道条件下进行了仿真,仿真结果如图8所示,从图中可看出,与未交织的性能相比,进行交织操作后的性能有较大的优势。对于NB-LDPC-RS(255,253)乘积码,随着信噪比的增加,未交织方案的性能几乎没有优化,但采用交织方案后的BER明显下降。然而,对于二进制LDPC-RS(255,253)乘积码,交织后的性能与未交织的NB-LDPC-RS(255,251)的性能较为接近,即使采用了交织,性能仍有较大的提升空间。在BER为10-5时,与二进制LDPC-RS(255,253)乘积码相比,NB-LDPC-RS(255,253)乘积码性能有0.3 dB的性能增益,提出的多进制乘积码方案有更优异的性能。在误比特率为10-5时,与未迭代的性能相比,迭代一次后的性能有0.2 dB的性能增益,提出的多进制乘积码迭代译码方案对存在删除的信道下的性能仍有较大提高。
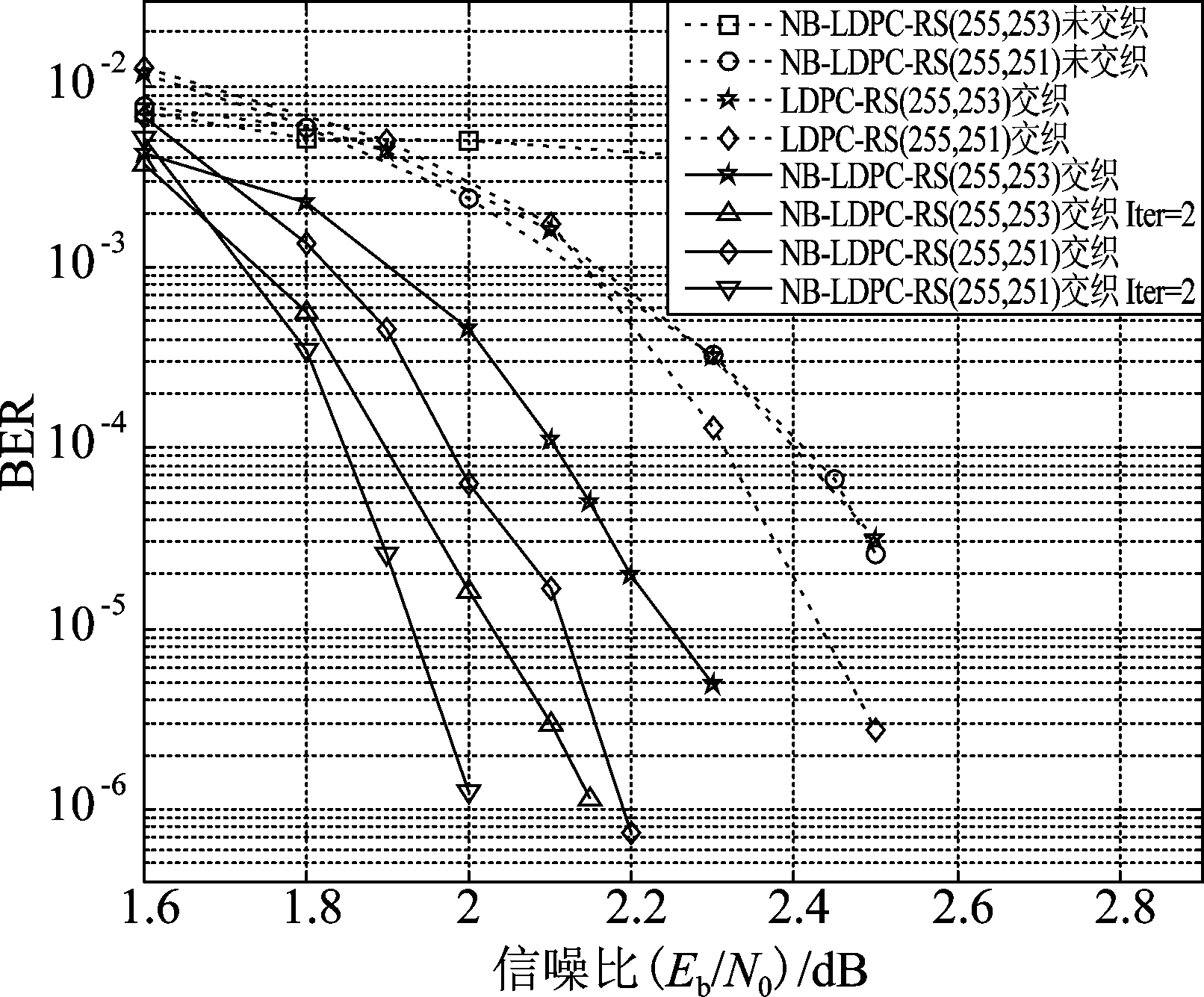
图8 包含1%删除的AWGN信道条件下的多进制乘积码性能
Fig.8 The performance of non-binary product code under AWGN with channel 1% erasures
进一步,改变突发删除发生的参数至2%进行性能的验证,仿真结果如图9所示。从图中可明显看出,是否交织对存在连续删除的信道的性能有明显影响,同时,采用本文提出的迭代译码方案,可以进一步优化多进制乘积码的性能。与二进制LDPC-RS乘积码相比,提出的多进制乘积码方案有明显的性能增益,在相同的码率条件下,信噪比为2.3 dB时,NB-LDPC-RS乘积码的误比特率降低了大约两个数量级。在BER为10-5时,与未迭代的性能相比,NB-LDPC-RS(255,251)乘积码迭代一次后的性能有0.35 dB左右的增益。对于存在长连续删除的信道,提出的多进制乘积码方案仍可以有效地纠正该信道条件下的错误,并通过提出的迭代译码方案可进一步优化性能,减少信息传输中的错误。
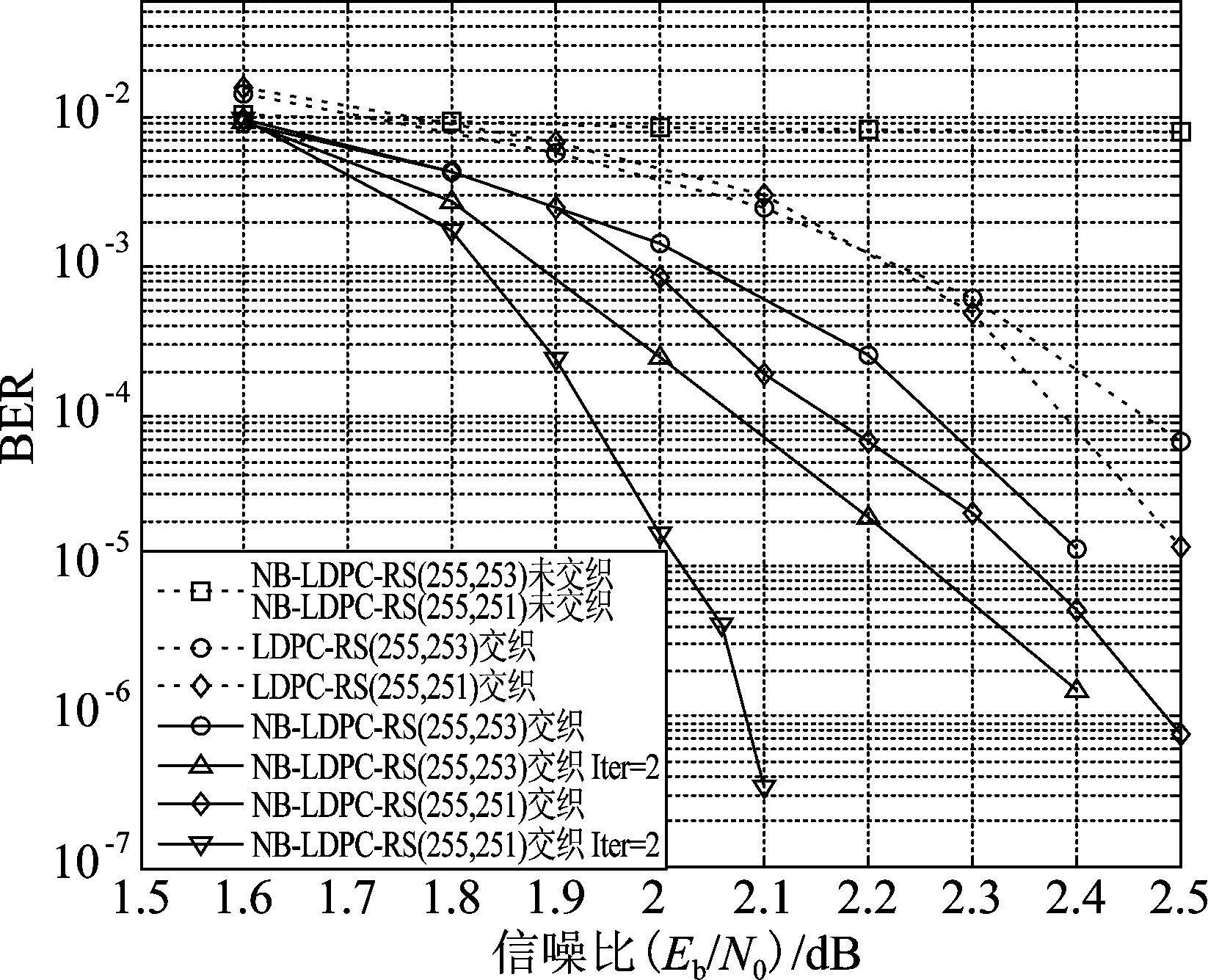
图9 包含2%删除的AWGN信道条件下的多进制乘积码性能
Fig.9 The performance of non-binary product code under AWGN with channel 2% erasures
综上,对于包含长突发删除的AWGN信道,采用交织可有效分散错误,减少残留在同一个码字中的删除数量,使得绝大多数码字的错误数目在其可纠正的范围之内,增强了NB-LDPC码译码成功的概率,进而可充分利用RS码的纠错能力。但对于二进制LDPC与RS码构造的乘积码方案,采用交织后的性能仍有大量错误,RS码的纠错能力未能得到充分发挥。而本文所提出的多进制乘积码的迭代译码方案可以更有效地纠正随机错误和长突发删除,降低信息传输的误比特率。
5 结论
基于对NB-LDPC码的残留错误和删除特性的分析,本文采用相同Galois域下的NB-LDPC码与高码率RS码构造多进制乘积码,实现了较好的符号错误特性的匹配。进一步,根据译码结果不断修正内码译码所需的比特概率信息进行选择性迭代译码,从而使得多进制乘积码译码后的错误不断减少,用较低的额外复杂度换取了较大的性能增益。仿真结果验证了本文所提出的多进制乘积码方案的优越性,与二进制LDPC码构造的乘积码相比,多进制乘积码方案的BER性能更为突出,且通过迭代进一步改善了其性能,可有效纠正信道中的随机错误和长突发删除,减少信息传输的错误。综上,本文所提供的多进制乘积码方案有着较高的可靠性,在高可靠信息系统有着广阔的应用前景。
[1] Elias P. Error-free coding[J]. IRE Transactions on Information Theory, 1954, 4(4): 29-37.
[2] Cideciyan R D, Furrer S, Lantz M A. Product codes for data storage on magnetic tape[J]. IEEE Transactions on Magnetics, 2017, 53(2): 1-10.
[3] Häger C, Pfister H D, Graell i Amat A, et al. Density evolution for deterministic generalized product codes on the binary erasure channel at high rates[J]. IEEE Transactions on Information Theory, 2017, 63(7): 4357- 4378.
[4] Van Overveld W. Multiple-burst error-correcting cyclic product codes (Corresp)[J]. IEEE Transactions on Information Theory, 1987, 33(6): 919-923.
[5] Zhan Ming, Pang Zhibo, Dzung D, et al. Channel coding for high performance wireless control in critical applications: survey and analysis[J]. IEEE Access, 2018, 6: 29648-29664.
[6] Djordjevic I B. On advanced FEC and coded modulation for ultra-high-speed optical transmission[J]. IEEE Communications Surveys & Tutorials, 2016, 18(3): 1920-1951.
[7] Tzimpragos G, Kachris C, Djordjevic I B, et al. A survey on FEC codes for 100G and beyond optical networks[J]. IEEE Communications Surveys & Tutorials, 2016, 18(1): 209-221.
[8] Oh J, Ha J, Park H, et al. RS-LDPC concatenated coding for the modern tape storage channel[J]. IEEE Transactions on Communications, 2016, 64(1): 59- 69.
[9] Park S I, Wu Y, Kim H M, et al. LDPC-RS two dimensional code for the next generation cloud transmission system[C]∥In Proc. IEEE International Symposium on Broadband Multimedia Systems and Broadcasting. Beijing, China: IEEE Press, 2014: 1-2.
[10] Liu Bo, Li Yaqi, Rong Bo, et al. LDPC-RS product codes for digital terrestrial broadcasting transmission system[J]. IEEE Transactions on Broadcasting, 2014, 60(1): 38- 49.
[11] Thomos N, Boulgouris N V, Strintzis M G. Product code optimization for determinate state LDPC decoding in robust image transmission[J]. IEEE Transactions on Image Processing, 2006, 15(8): 2113-2119.
[12] Shah D, Padia Y, Jadawala H. RS-LDPC product code for high snr applications[C]∥In Proc. 2nd International Conference on Signal Processing and Integrated Networks. Noida, India: IEEE Press, 2015: 280-284.
[13] 李雅琪. 二维乘积码在下一代数字电视广播中的应用[D]. 上海: 上海交通大学, 2014.
Li Yaqi. Application of 2D product codes in next generation digital television broadcasting[D]. Shanghai: Shanghai Jiao Tong University, 2014.(in Chinese)
[14] Xu Hengzhou, Li Huaan, Xu Mengmeng, et al. Two classes of QC-LDPC cycle codes approaching Gallager lower bound[J]. Sciece China Information Sciences, 2019, 62(10): 209305: 1-209305: 3.
[15] Babu J C, Reddy C C, Prasad M N G, et al. Generation and decoding of non-binary LDPC codes using MSA decoding algorithm[C]∥In Proc. 2nd International Conference on Micro-Electronics, Electromagnetics and Telecommunications. Singapore: Springer, 2018: 583-591.
[16] 宿晨庚, 黄勤, 刘旭楠. 北斗卫星导航系统多进制LDPC编码性能评估[J]. 国防科技大学学报, 2019, 2019(4): 121-128.
Su Chengeng, Huang Qin, Liu Xunan. Performance evaluation of BDS M-ary LDPC encoding[J]. Journal of National University of Defense Technology, 2019, 2019(4): 121-128.(in Chinese)
[17] Huang Qin, Song Liyuan, Wang Zulin. Set message-passing decoding algorithms for regular non-binary LDPC codes[J]. IEEE Transactions on Communications, 2017, 65(12): 5110-5122.
[18] Sunghye C, Kyungwhoon C, Kyeongcheol Y. Design of nonbinary LDPC codes based on message-passing algorithms[J]. IEEE Transactions on Communications, 2018, 66(11): 5028-5040.
[19] Nhan N Q, Rostaing P, Amis K, et al. Precoded MIMO systems with non-binary LDPC codes and many-to-one mapping[J]. IEEE Transactions on Vehicular Technology, 2018, 67(4): 3186-3194.
[20] Cedric M, Emmanuel B, Hassan H, et al. Hybrid check node architectures for NB-LDPC decoders[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2019, 66(2): 869- 880.
[21] 黄英, 雷菁. 基于多维乘积码的编码协作方案研究[J]. 信号处理, 2010, 26(2): 170-174.
Huang Ying, Lei Jing. Research of coded cooperation scheme based on multidimensional product code[J]. Signal Processing, 2010, 26(2): 170-174.(in Chinese)
[22] Poulliat C, Fossorier M, Declercq D. Design of regular (2, dc)-LDPC codes over GF(q) using their binary images[J]. IEEE Transactions on Communications, 2008, 56(10): 1626-1635.
[23] Wang Ziyong, Meng Jiahui, Deng Zhibin, et al. FPGA implementation scheme of mixed logarithmic domain FFT-BP decoding algorithm based on non-binary LDPC codes[C]∥In Proc. the 37th Chinese Control Conference. Wuhan, China: IEEE Press, 2018: 8459- 8464.
[24] Chen Weigang, Dong Tongxin. Low complexity product codes with LDPC codes achieving ultra low BER[C]∥In Proc. IEEE International Conference on Communication Technology. Chengdu, China: IEEE Press, 2012: 1312-1316.
[25] IEEE Std 802.16e-2005, IEEE standard for local and metropolitan area networks part 16[S]. New York, USA: IEEE Computer Society and the IEEE Microwave Theory and Techniques Society, 2006.
[26] 陈为刚, 殷柳国, 陆建华. 低密度奇偶校验码迭代译码算法的误码平台特性[J]. 清华大学学报:自然科学版, 2009, 49(1): 61- 64.
Chen Weigang, Yin Liuguo, Lu Jianhua. Error floor properties of low-density parity-check codes using iterative decoding algorithms[J]. Journal of Tsinghua University: Science and Technology, 2009, 49(1): 61- 64.(in Chinese)
[27] Kyung G B, Wang C. Finding the exhaustive list of small fully absorbing sets and designing the corresponding low error-floor decoder[J]. IEEE Transactions on Communication, 2012, 60(6): 1487-1498.
[28] Barnault L, Declercq D. Fast decoding algorithm for LDPC codes over GF(2q)[C]∥In Proc. IEEE Information Theory Workshop. Paris, France: IEEE Press, 2003: 70-73.
[29] 史治平. 多元LDPC码及其在无线通信中的应用[M]. 北京: 国防工业出版社, 2011: 25-27.
Shi Zhiping. Nonbinary low-density parity-check codes and their applications in wireless communications[M]. Beijing: National Defense Industry Press, 2011: 25-27.(in Chinese)
