1 引言
空间微动目标指除质心平动以外,还存在如自旋、振动和锥旋等微动[1]的目标。相较于单基雷达三维成像[2- 4]仅能获得目标在雷达径向上的信息、以及双/多基雷达三维成像[5- 6]联合处理复杂困难,用单部三天线雷达系统对空间微动目标进行干涉式三维成像[7-9],可以获得目标真实的三维坐标信息,且系统实现简单,因此近年来得到了国内外学者的广泛关注。
在窄带雷达系统中,为了能将各散射点的子回波分开来,同时保留各散射点的干涉相位,通常采用线性类时频分析方法,如短时傅里叶变换(STFT)、Gabor变换等,将回波转换到时频域上分析,在时频图像上可以看到各散射点对应的微动曲线,曲线上则蕴含着散射点用于干涉处理的相位信息。但是,当微动曲线交叉时,干涉相位值会遭到破坏,重构出错误的坐标,所以在进行干涉成像前,需要找到曲线的交叉位置,将这些交叉位置处的干涉相位信息剔除掉,确保用于干涉处理的数据有效。文献[10]中没有介绍如何对交叉位置进行剔除;文献[11]中,对出现曲线交叉情况的时刻上的数据均予以剔除,当有多个散射点时,这些时刻上未交叉的曲线数据也被剔除掉,会损失散射点很多有效信息。文献[12]利用微动曲线方程找到曲线的交叉点,对交叉点时刻的数据进行剔除,然而由于窗函数的影响,曲线交叉位置不仅仅占据一个时间采样单元,往往跨越多个时间采样单元,所以用这种方法对破坏了的干涉相位值剔除不干净,并且,当微动曲线方程无法获得的时候,交叉点也无法找到。
本文提出了基于Harris角点检测与聚类算法的空间自旋目标干涉成像方法,利用Harris角点检测方法对时频图像中的微多普勒曲线进行检测,找出交叉区域的大致位置,并利用聚类算法对角点进行分类并计算各类的中心点,然后利用一门限对交叉区域进行限定,剔除掉交叉区域内错误的干涉相位信息。再利用各散射点有效的干涉相位信息重构出了两基线方向上的坐标,最后根据目标在空间中的圆轨迹与两基线平面内的椭圆轨迹之间的几何关系,实现对空间微动目标的干涉三维成像。所提方法能准确找到交叉位置,避免了很多有效干涉相位信息的损失,并且对交叉区域剔除较干净。仿真结果验证了所提方法的有效性。
2 窄带雷达微动目标干涉成像模型
L型三天线自旋目标干涉成像系统如图1所示。以天线A为坐标原点构成雷达坐标系(X,Y,Z),天线B和C分别位于(L,0,0)和(0,0,L),即AB、AC组成一对正交基线,基线长度为L,其中,A为收发一体天线,B和C为接收天线。以目标质心O为原点有两个坐标系:坐标系(u,ν,w)为本地坐标系,随着目标在空间中的运动而运动;坐标系(U,V,W)为参考坐标系,坐标轴分别与雷达坐标系的坐标轴平行,随目标质心的平动而整体平动。坐标系(u,ν,w)和(U,V,W)间的关系由欧拉旋转矩阵Rinit[13]确定。
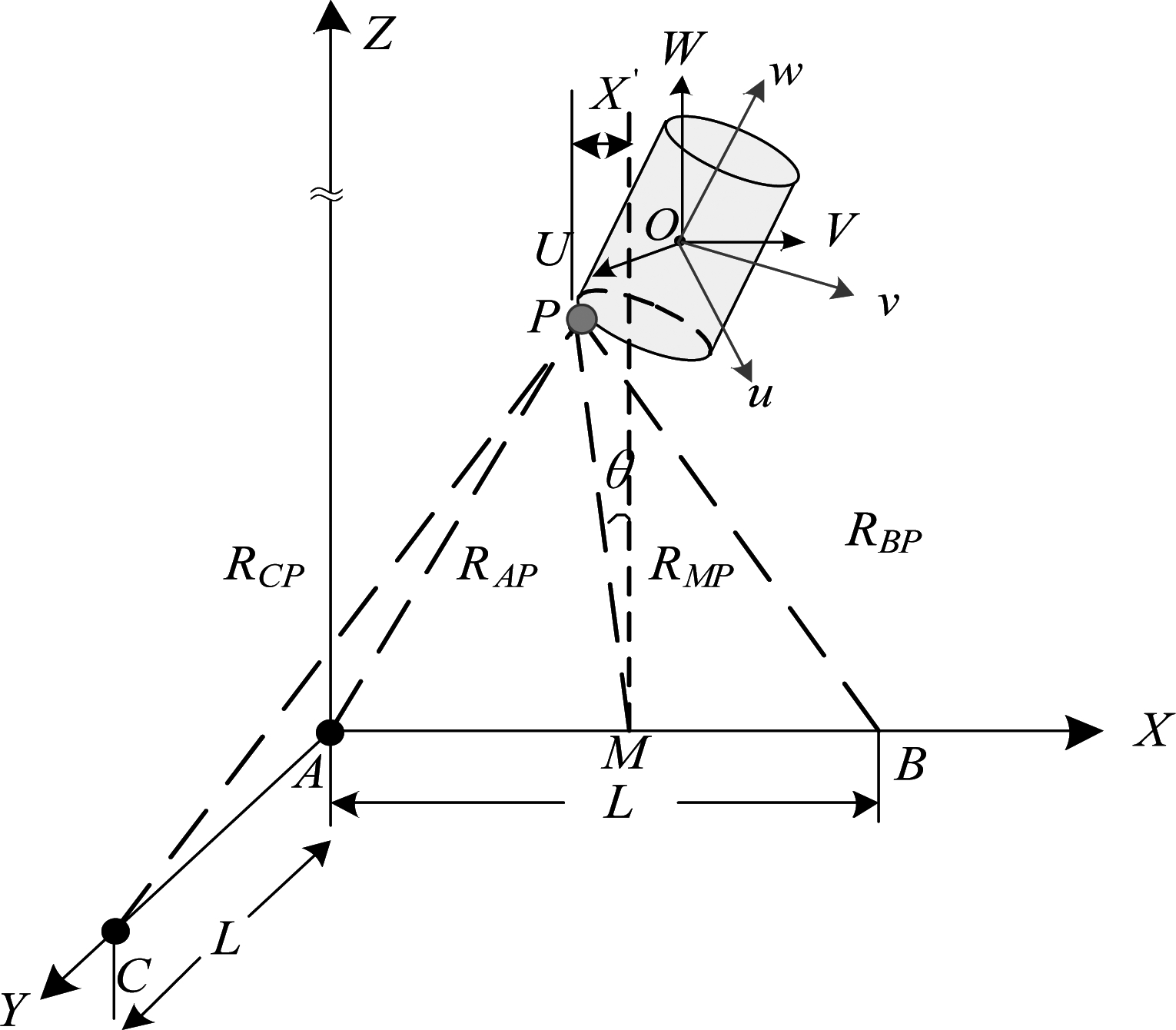
图1 空间自旋目标干涉三维成像模型
Fig.1 3D interferometric imaging model of spatial spinning targets
假设目标位于雷达远场且天线电轴附近,目标上一散射点P,不仅随目标平动,同时还绕本地坐标系的u轴、ν轴和w轴作自旋运动。
设M为天线AB的中点。P点到天线A、B、C的距离分别为RAP、RBP和RCP,到M点的距离为RMP。假设雷达发射单频连续波信号,载频为fc,即
p(t)=exp(j 2πfct)
(1)
则天线接收到的散射点P的基带回波信号分别为
(2)
![]()
σexp(jΦBP(tm))
(3)
![]()
σexp(jΦCP(tm))
(4)
式中:tm表示时间,σ为P点的散射系数,![]() 为波长,c为光速,ΦAP(tm)、ΦBP(tm)、ΦCP(tm)分别为天线A、B、C基带回波信号的相位。
为波长,c为光速,ΦAP(tm)、ΦBP(tm)、ΦCP(tm)分别为天线A、B、C基带回波信号的相位。
假设平动分量已补偿,对每个时刻回波信号分别进行干涉处理,得到干涉相位差为
ΔφAB(tm)=angle[sAP(tm)*sBP(tm)]=
ΦAP(tm)*ΦBP(tm)=2π![]()
(5)
ΔφAC(tm)=angle[sAP(tm)*sCP(tm)]=
ΦAP(tm)*ΦCP(tm)=2π![]()
(6)
式中:“angle”为提取复数的相角;“*”代表共轭。
干涉相位差需满足相位不模糊条件:|ΔφAB(tm)|≤π、|ΔφAC(tm)|≤π。在远场条件下,有以下几何关系成立:
(7)
因此,联立(5)、(7)可得该时刻P沿基线AB方向的坐标为:
(8)
同理可得tm时刻散射点P沿基线AC方向的坐标为:
(9)
由此,可以通过干涉处理计算出散射点P沿两基线的坐标。
由目标在空间作自旋运动这一先验条件,利用目标上散射点在空间中的圆轨迹与其在X-Y平面上投影的几何关系,可实现各散射点的空间三维圆轨迹重构,从而得到自旋目标的干涉三维成像。这一过程在文献[16]中有具体介绍,本文不再赘述。
由于窄带雷达系统中各散射点回波均在距离-慢时间平面的某一距离单元里,为了将各散射点回波分开,且保留信号的相位信息,用于后续的干涉处理,需借助线性类时频分析工具将回波信号转换到时频面上进行分析,其中最常用的是短时傅里叶变换(STFT)。每个旋转散射点的回波在时频图像上对应着一条微动曲线,曲线上各点是该时刻散射点时频能量峰值,蕴含着各散射点的相位信息。将各散射点微动曲线对应位置进行干涉处理,即
ΔφAB(tm)=angle[sAPSTFT(tm, f)*sBPSTFT(tm, f)]
(10)
ΔφAC(tm)=angle[sAPSTFT(tm, f)*sCPSTFT(tm, f)]
(11)
得到各个时刻的干涉相位差,通过(8)、(9)即可计算出每个时刻散射点的X、Y轴坐标。
但是当空间中有多个散射点时,微动曲线会存在交叉现象,交叉位置处的相位信息是两个散射点相位信息的叠加,导致这两个散射点用来重构坐标的相位信息均被破坏,所以必须剔除。由于STFT用到窗函数,窗函数主瓣和旁瓣的存在会影响干涉相位的精度。为了方便描述,把某时刻两散射点峰值重合点称为交叉点,在交叉点时刻前后,两散射点的相位信息早已互相影响,用来重构坐标误差较大,把这些位置称为交叉区域。为了保证坐标重构的准确性,需将交叉区域内的干涉相位信息剔除。
3 基于Harris角点检测和聚类算法的交叉区域剔除
角点是指图像上梯度值和梯度方向的变化速率都很高的点,时频图像上的交叉区域的点可被认为是角点,所以本文借助Harris角点检测方法寻找图像中的交叉区域。
3.1 Harris角点检测算法
Harris角点检测原理是利用一个固定大小的模板在图像中沿任意方向滑动,计算窗口中的像素值滑动前后的灰度变换值[14-15],若在任意方向上都有着较大灰度变化的点认为是角点。用数学方法刻画如下所述。
已知一幅图像I(x,y)以及一个以像素点(x,y)为中心的高斯模板q(x,y),将模板沿x、y方向分别平移i, j个单位,模板内因平移产生的灰度变化量表示为
(12)
当移动距离较小时,有以下一阶泰勒级数展开式近似:
[I(x+i,y+j)-I(x,y)]≈I(x,y)+iIx+jIy
(13)
式中,Ix,Iy分别是图像I在x,y方向上的梯度。
将(13)代入(12)中得
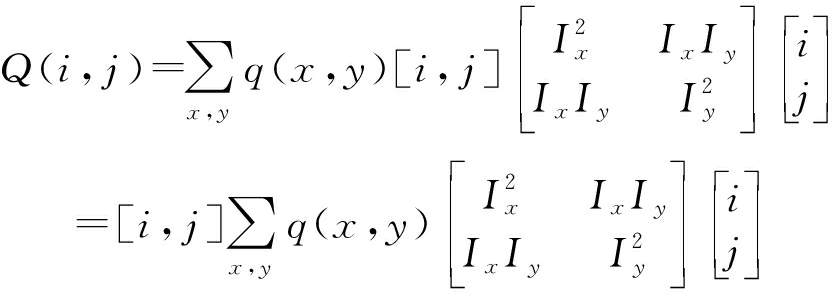
(14)
令矩阵
(15)
由(15)可知M是一个对称矩阵,用λ1、λ2表示它的特征值,特征值的大小与检测到的图像特征(角点、平面、线)有三种对应关系:1)当λ1≈λ2,且值都较大时,模板内含有角点;2)当λ1≈λ2,但值较小时,模板检测到的是平坦区域,即平面;3)当λ1≫λ2,或者λ1≪λ2时,则检测到的是直线。
Harris角点检测并非通过计算M的两个特征值的具体值来确定角点,而是通过关于M的函数——角点响应函数R判定,R的表达式为:
R(M)=det(Μ)-C·trace2(Μ)
(16)
式中,det(Μ)=λ1λ2,trace(Μ)=λ1+λ2, C是常量,通常取值为0.04~0.06,只是用来调节函数的形状。对R进行阈值判定,当R大于给定的阈值时,则判定为角点。
利用Harris角点检测算法对时频图像进行搜索,得到的是一系列分布在各交叉点附近的角点簇,还需借助聚类算法对检测到的角点进行分类,并找到各簇中心,即交叉点大概位置。
3.2 聚类算法
聚类算法,顾名思义,就是对样本数据进行挖掘,按照某个相似度准则把样本数据分成不同的类,类间相似度低,类中相似度高[14]。
本文采用的是简单有效的K-means聚类算法,算法思想就是以K为参数,在本文中K为时频图像中交叉区域的个数,初始时刻,随机选取K个点作为质心,再将每个点指派到距离最近的质心,形成K个类,最后重新计算每个类或簇的质心,直到K个类不再发生变化停止迭代。最终得到的K个质心即认为是散射点微动曲线的交叉点。
3.3 交叉区域剔除
由于微动目标回波信号为正弦调频信号,用固定窗长对信号做时频分析,不同时间段内,信号的频率变化程度不同,所以加窗后的频谱各有差异,因此,采用以下方法对交叉区域进行剔除:分别计算横、纵两个方向上各个类中角点与质心的最大距离,然后以最大距离为门限,将时频平面上两个门限所限制的矩形区域内的干涉相位信息予以剔除。
4 基于Harris角点检测和聚类算法的空间自旋目标干涉三维成像步骤
从3.1节分析可知,Harris角点检测方法是一种图像检测方法,而时频分析中窗长的选择直接影响时频图像的效果,有学者对窗函数的窗长问题进行了分析,并以使时频图像熵最小的窗长作为干涉成像时的窗长,此时得到的图像时频聚集性最佳,本文采用该方法确定窗长,并对得到的时频图像进行角点检测。检测过程中阈值的大小将直接影响检测的结果,当阈值过大时,检测到的角点数会很少,导致最终错误相位的剔除不干净,当阈值过小时,检测到的结果将不止交叉位置处,而且此时容易受噪声影响,所以,对阈值的大小要根据具体情况有效折中。
综上所述,基于Harris角点检测与聚类算法的窄带雷达空间自旋目标干涉成像具体步骤为:
Step 1 接收三天线回波,采用STFT将回波信号转换到时频平面上;
Step 2 用Harris角点检测与聚类算法对A天线时频图像进行处理,找到交叉区域;
Step 3 对时频平面上的回波进行干涉处理,得到两个干涉相位差矩阵,并剔除交叉区域中的干涉相位差值;
Step 4 采用Hough变换提取时频图像中各散射点微动曲线,在干涉相位差矩阵中提取曲线上的干涉相位信息;
Step 5 根据公式(8)、(9),计算各个时刻散射点的X、Y维坐标,用正弦类曲线拟合函数拟合坐标曲线,获得各散射点完整的坐标曲线;
Step 6 采用椭圆拟合方法,根据几何关系,最终实现目标的干涉三维成像。
5 仿真实验
5.1 算法有效性验证
仿真参数设置如下,天线之间的基线长度L=50 m,雷达发射载频fc=6 GHz,照射目标时间为0.5 s,脉冲重复频率为3200 Hz。目标的旋转速度为(4π,4π,4π) rad/s,质心在雷达坐标系中的位置为(0.02,0,100)km,目标上有三个散射点,在参考坐标系中的坐标分别为(1.5,2.0,0.8),(2.8,0.8,1.0),(0.5,1.0,2.0),各散射点散射系数均为1。信号中加入30 dB 的高斯白噪声。图2给出了各个步骤的仿真结果图。
图2(a)为A天线回波做STFT得到的时频图像。图2(b)为用Harris角点算法检测出的角点,可以看到,它是一系列的角点簇,这些角点簇的位置与图(a)中交叉区域的位置相对应。根据聚类算法,对角点进行分类,并计算出各类的质心,得到结果如图2(c)所示,图中黑色圆圈代表各类的质心,其与交叉点的位置基本相同。图2(d)中矩形区域即为3.3节所述三天线回波时频图像需剔除的交叉区域,与分析一致,由于频率为正弦调频这一特性,每一交叉区域需剔除的范围不尽相同。图2(e)、( f )给出了交叉区域剔除前各散射点的X、Y维坐标曲线,可以看出,在微多普勒曲线交叉处坐标值出现明显错误。从图2(g)、(h)中可以看到错误的坐标值被剔除干净,并且,同一时刻没有出现交叉现象的散射点坐标值没有被剔除,图2(i)、(j)给出了用正弦类曲线拟合后的散射点坐标与理论坐标曲线,重构出来的坐标与理论坐标几乎完全一致,最后根据散射点在空间中的圆轨迹与其投影在X-Y平面内的椭圆轨迹之间的几何关系,重构出各散射点在空间中的三维运动轨迹,如图2(k)所示,重构出的轨迹与理论轨迹契合。
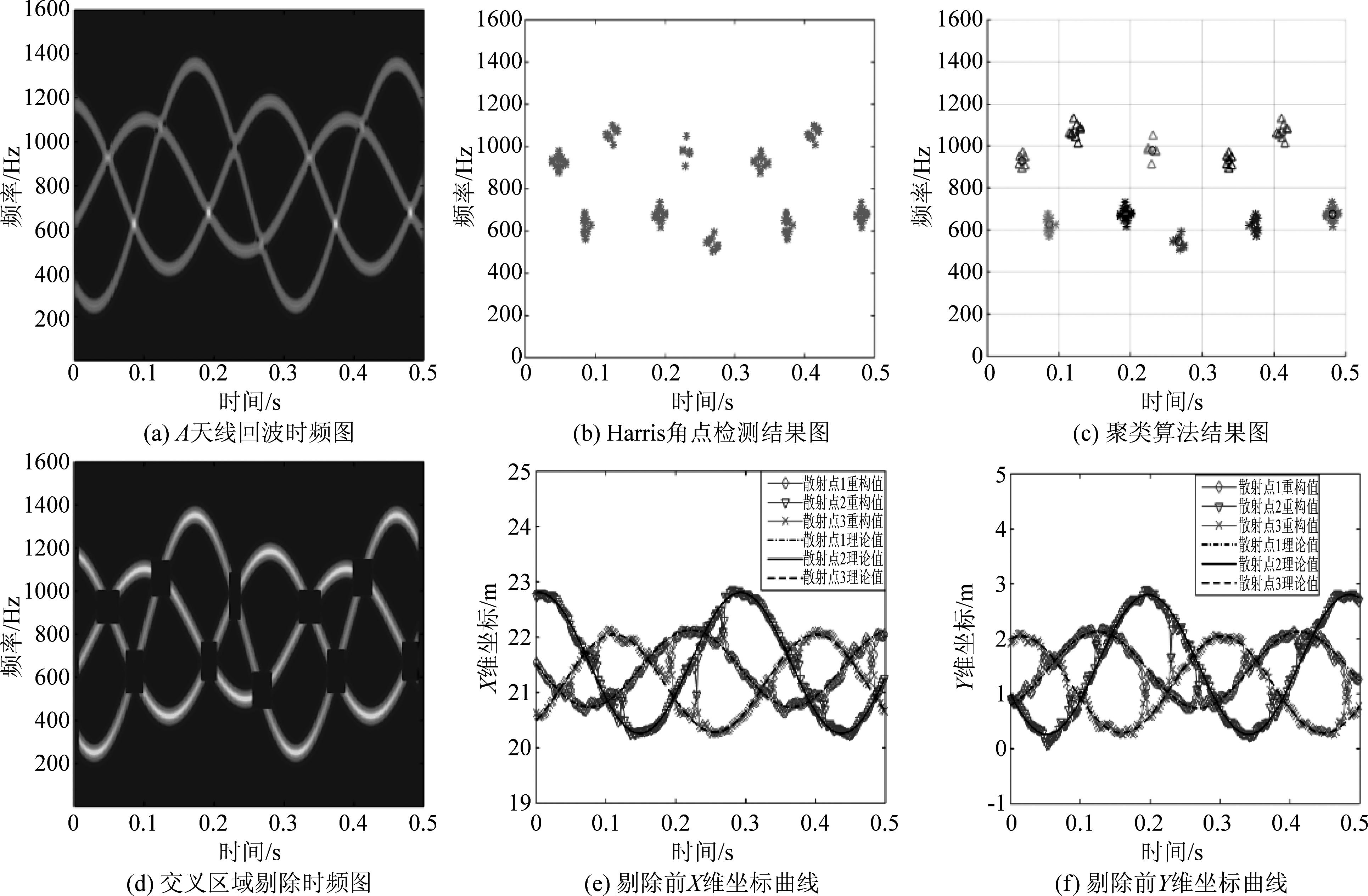
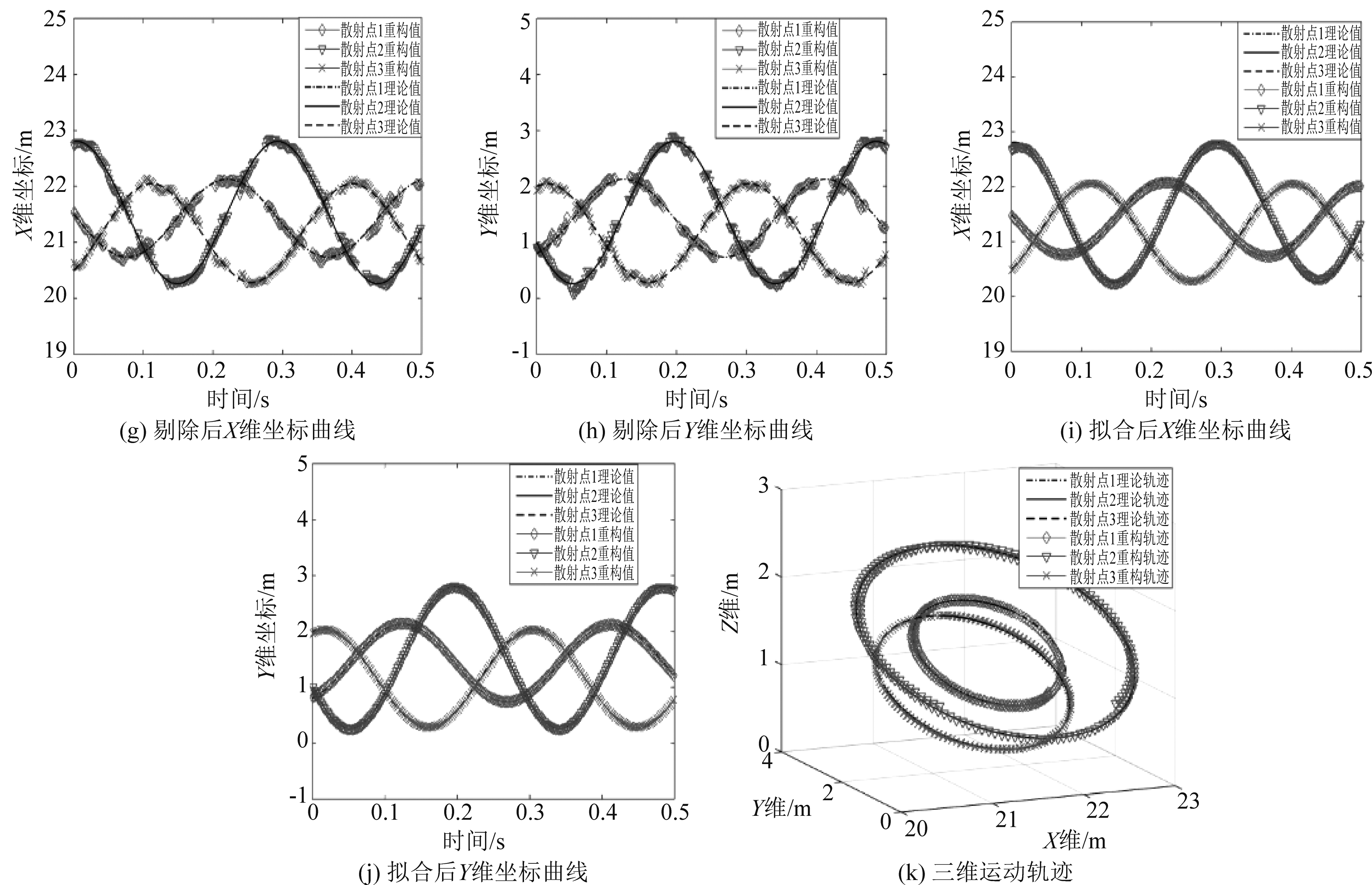
图2 仿真结果图
Fig.2 Simulation diagrams
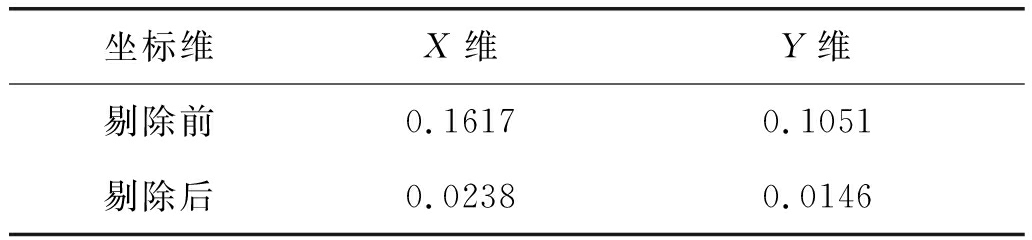
为了进一步说明本文所提方法的有效性及分析的正确性,下面从数值上进行对比分析,表1给出了剔除错误干涉相位信息前后经曲线拟合后得到重构坐标值与理论坐标值的绝对误差。可以看出,利用本文所提方法剔除交叉区域后,拟合的坐标曲线更贴近理论曲线,所以成像精度得到了一定的提高,三维成像质量得以提升。
表1 交叉区域剔除前后坐标重构值与理论值绝对误差
Tab.1 Absolute errors between reconstruction value and theoretical value of coordinate before and after elimination of cross region m
坐标维X维Y维剔除前0.16170.1051剔除后0.02380.0146
5.2 算法鲁棒性分析
(1)噪声污染
其他参数不变,在信号中加入不同信噪比的高斯白噪声,分析Harris角点检测算法的抗噪性能。图3给出了信噪比为5~20 dB下利用Harris角点检测算法检测出来的结果图。
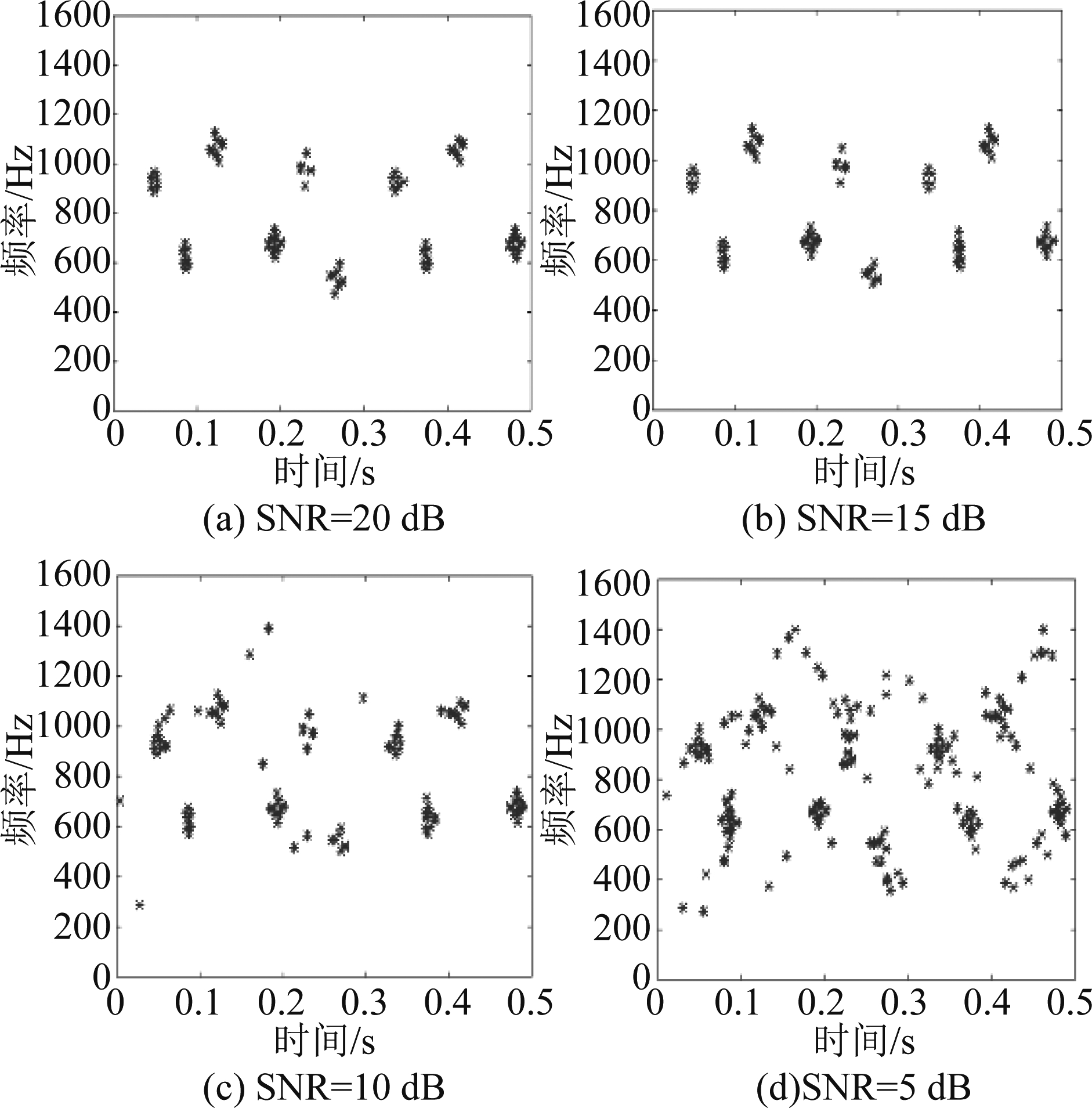
图3 不同信噪比下角点检测结果图
Fig.3 Results of corner point detection in different SNR
从图中可以看出,信噪比越低,算法受噪声影响越大,检测出来的角点位置不仅仅是交叉区域位置,还有噪声点位置。但当信噪比不低于15 dB时,用Harris角点检测算法检测出的角点均为微多普勒曲线交叉区域位置。而在窄带雷达空间微动目标干涉三维成像中,干涉相位对噪声非常敏感,当信噪比低于20 dB时,相位信息被噪声严重破坏,重构出来的坐标值与理论坐标值误差非常大。所以说,在干涉相位信息不被破坏,能准确重构各散射点沿基线方向坐标的前提下,利用Harris角点检测方法能有效的检测出微多普勒曲线交叉区域的位置。
(2)时变散射系数
实际中,散射点散射系数不是一成不变的,随着观测视角等因素的变化,散射点散射强度会时刻变化,下面分析散射点时变散射系数对算法带来的影响。
假设其他参数不变,散射点散射系数强度变为
σ(t)=Esin(Ωt+ξ)+F, E+F=1, E≥0, F≥0
(17)
式中,Ω为目标旋转角速度,ξ为随机初相,则散射点强度范围为[F-E,1]。
假设三个散射点的散射系数分别为
σ1(t)=0.45sin(Ωt+π/6)+0.55
(18)
σ2(t)=0.45sin(Ωt+π/2)+0.55
(19)
σ3(t)=0.45sin(Ωt+π)+0.55
(20)
图4(a)为此时A天线回波时频图像,用Harris角点检测算法得到的交叉区域如图4(b)所示,可以发现,当散射点强度较小时,算法对交叉点的检测能力弱,这样会导致剔除错误干涉相位不干净,影响最终成像效果。
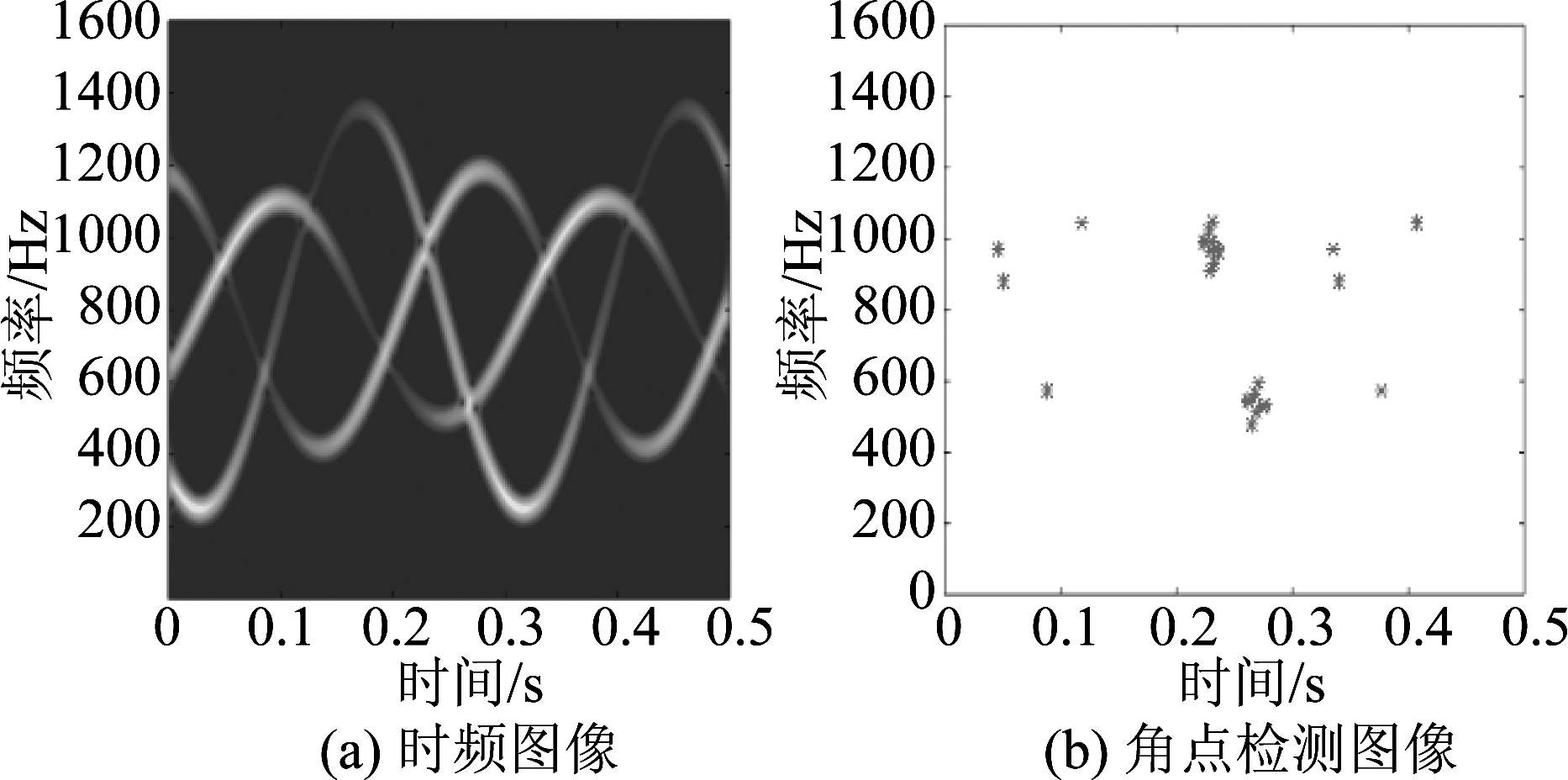
图4 散射系数时变仿真结果图
Fig.4 Simulation diagrams when scattering coefficients vary with time
表2给出了不同的散射系数强度变化即不同的F-E情况下,重构的散射点1 X、Y坐标的绝对误差值。
表2 不同散射系数强度变化下坐标重构值与理论值绝对误差
Tab.2 Absolute errors between reconstruction value and theoretical value of coordinate under different scattering coefficients intensity m

F-EX维Y维0.10.15070.09480.20.11350.08070.30.40.50.60.70.80.90.08640.04280.02400.02390.02380.02380.02380.06260.03410.01850.01480.01460.01460.0146
从表中可以分析出,当散射点散射系数强度大于0.5时,微多普勒曲线的交叉区域能被较好的检测出来,基于此对错误的干涉相位信息进行剔除,最终得到的坐标曲线与理论结果基本一致。
6 结论
本文提出了基于Harris角点检测与聚类算法的微多普勒曲线交叉区域剔除方法,所提方法无需知道各散射点的微动方程,直接在图像上找到交叉位置,且对于交叉区域的剔除能剔除干净,最终成像精度高。本文方法不仅对自旋目标有效,对振动、进动等微动目标进行干涉成像时,均能利用本文方法进行错误干涉相位信息的剔除。
[1] 李靖卿, 冯存前, 贺思三, 等. 利用微动信息矩阵的弹道目标特征提取算法[J]. 信号处理, 2016, 32(4): 488- 495.
Li Jingqing, Feng Cunqian, He Sisan, et al. Employing Micro-motion Information Matrix for Feature Extraction of Ballistic Targets[J]. Journal of Signal Processing, 2016, 32(4): 488- 495.(in Chinese)
[2] Xing M, Qi W, Wang G, et al. A Matched-Filter-Bank-Based 3-D Imaging Algorithm for Rapidly Spinning Targets[J]. IEEE Transactions on Geoscience & Remote Sensing, 2009, 47(7): 2106-2113.
[3] Qi W, Xing M, Lu G, et al. High-Resolution Three-Dimensional Radar Imaging for Rapidly Spinning Targets[J]. IEEE Transactions on Geoscience & Remote Sensing, 2007, 46(1): 22-30.
[4] Mo D, Wang N, Li G, et al. 3-D Inverse Synthetic Aperture Ladar Imaging and Scaling of Space Debris Based on the Fractional Fourier Transform[J]. IEEE Geoscience and Remote Sensing Letters, 2019, 16(2): 1-5.
[5] Wang R, Deng B, Qin Y, et al. Bistatic Terahertz Radar Azimuth-Elevation Imaging Based on Compressed Sensing[J]. IEEE Transactions on Terahertz Science & Technology, 2017, 4(6): 702-713.
[6] Bai X, Feng Z, Xing M, et al. Scaling the 3-D Image of Spinning Space Debris via Bistatic Inverse Synthetic Aperture Radar[J]. IEEE Geoscience & Remote Sensing Letters, 2010, 7(3): 430- 434.
[7] Chen Q, Gang X, Lei Z, et al. Three-dimensional interferometric inverse synthetic aperture radar imaging with limited pulses by exploiting joint sparsity[J]. Radar Sonar & Navigation Iet, 2015, 9(6): 692-701.
[8] 刘承兰, 高勋章, 黎湘. 干涉式逆合成孔径雷达成像技术综述[J]. 信号处理, 2011, 27(5): 737-748.
Liu Chenglan, Gao Xunzhang, Li Xiang. Review of Interferometric ISAR Imaging[J]. Signal Processing, 2011, 27(5): 737-748.(in Chinese)
[9] Li L , Li D , Pan Z . Compressed sensing application in interferometric synthetic aperture radar[J]. Science China Information Sciences, 2017, 60(10):187-203.
[10] Sun Y, Luo Y, Zhang Q, et al. Time-varying three-dimensional interferometric imaging for space rotating targets with stepped-frequency chirp signal[J].Iet Radar Sonar & Navigation, 2017, 11(9):1397-1405.
[11] 陈永安, 罗迎, 王恺, 等. 多天线干涉处理的窄带雷达空间旋转目标三维成像[J]. 空军工程大学学报: 自然科学版, 2016, 17(4): 46-51.
Chen Yongan, Luo Ying, Wang Kai, et al. Three Dimensional Imaging for Spinning Space Target Based on Multi-antenna Interferometric Processing[J]. Journal of Air Force Engineering University: Natural Science Edition, 2016, 17(4): 46-51.(in Chinese)
[12] 梁婷, 罗迎, 王聃, 等. 基于稀疏字典分解的窄带雷达自旋目标干涉三维成像[J]. 空军工程大学学报: 自然科学版, 2019, 20(1): 40- 46.
Liang Ting, Luo Ying, Wang Dan, et al. Three-dimensional Interferometric Imaging of Spinning Space Target Based on Sparse Dictionary Decomposition in Low-resolution Radar[J]. Journal of Air Force Engineering University: Natural Science Edition, 2019, 20(1): 40- 46.(in Chinese)
[13] 章鹏飞, 李刚, 霍超颖, 等. 基于双雷达微动特征融合的无人机分类识别[J]. 雷达学报, 2018, 7(5): 557-564.
Zhang Pengfei, Li Gang, Huo Chaoying, et al. Classification of Drones Based on Micro-Doppler Radar Signatures Using Dual Radar Sensors[J]. Journal of Radars, 2018, 7(5): 557-564.(in Chinese)
[14] 陈典典, 程培培, 马军山. 基于Harris角点检测和聚类算法的掌纹图像ROI提取方法[J]. 光学仪器, 2018, 40(5): 31-38.
Chen Diandian, Cheng Peipei, Ma Junshan. ROI extraction method of palmprint based on the Harris point detection and clustering algorithm[J]. Optical Instruments, 2018, 40(5): 31-38.(in Chinese)
[15] 蒙倩颜. 基于Harris算法的SAR图像配准研究[J]. 电子世界, 2019(3): 88- 89.
Meng Qianyan. Research on SAR image registration based on Harris algorithm [J]. Electronics World, 2019(3): 88- 89.(in Chinese)
[16] 胡健, 罗迎, 张群, 等. 空间旋转目标窄带雷达干涉式三维成像与微动特征提取[J]. 电子与信息学报, 2019, 41(2): 270-276.
Hu Jian, Luo Ying, Zhang Qun, et al. Three-dimensional Interferometric Imaging and Micro-motion Feature Extraction of Rotating Space Targets Based on Narrowband Radar[J]. Journal of Electronics & Information Technology, 2019, 41(2): 270-276.(in Chinese)




