1 引言
广播式自动相关监视技术依靠数据链通信技术以完成空中飞行器间及飞行器与地面的通信。该技术已被国际民航组织(ICAO)视为空中监视管理的新技术,并将该技术进行推广,目前许多国家和地区纷纷引进并使用该技术。ADS-B技术的应用可提供空域信息,加强对空中交通信息的监视。除此之外,该技术的应用可降低空管系统对多重雷达覆盖的要求,从而降低费用。该系统可为使用者提供飞机的航班号、速度、位置等信息,机组可在飞行中了解周围的飞行情况,地面可通过该系统对飞行器进行监视,因此该系统的使用可增加飞行时的安全性。但由于ADS-B技术的广泛应用,空中的信号交织问题也日益严重,而两条信号的交织现象最为普遍[1-3]。
空中同时发送ADS-B信号的飞机数量越多,则ADS-B信号的交织概率越高。据统计,当同时发送信号的飞机数量为121架时,空中ADS-B信号交织概率为5%,如果使用解交织技术将交织信号分离,则在该交织概率下空域同时发送信号的飞机数量可增加至2284架[4]。由此可见,若能将交织信号解交织,则可大大提高空中飞机的数量[5]。
单天线ADS-B接收机在使用中成本低且维护方便[6],因此得到广泛应用,故单天线解交织算法需要得到进一步的发展。目前多天线解交织技术日趋成熟,但关于单天线解交织技术的文献数量较少,基于公开的文献,目前典型的单天线解交织算法是PASA(Projection Algorithm Single Antenna)算法[7]。单天线交织位置检测技术的成熟能为单天线方面的其他工作带来便利,目前国内外已有的交织位置检测方法有:报头检测法,通过对报头四脉冲[8]进行交叠测试,以判断信号报头是否交织,但该方法不能准确检测到交织的位置;文献[9]中的相对时延估计法,利用信号的总长度与标准信号长度作差得出交织位置,该法在两条信号交织情况下有效,当交织信号数多于两条时,此法失效。由于报头检测法与时延估计法的局限性,在检测信号交织位置时,目前一般使用奇异值分解法[10],该法依据信号协方差矩阵的特征值判断交织位置,但这种方法计算量较大且并没有精准的找到交织的位置。
本文提出了一种ADS-B信号交织位置检测方法:依据信号交织时时域波形可能出现的异常:报头脉冲数量的增加及位置偏移、脉冲宽度及幅度改变[11]来检测信号的交织位置。本文算法克服了其他交织检测算法的缺点,能以较快的速度精准的检测到多条信号交织时的交织位置。
2 信号模型
1090ES数据链是ADS-B系统中应用最为广泛的数据链,载频为1090 MHz,采用ASK(Amplitude Shift Keying)调制。如图1所示,ADS-B信号时长120 μs,包含8 μs的报头和112 μs的数据域,一个比特位的码元包含两个码片,每个码片持续时间为0.5 μs,若宽度为0.5 μs的脉冲(以下简称脉冲)位于前置码片,则该码元表示比特1,若脉冲位于后置码片,则该码元表示比特0。在112 bit的数据域内,不同的消息字段分别包含了如位置、高度、速度等信息[12]。
单天线在时刻t接收到的信号可以表示为:
(1)
其中L表示信源的个数,Pi、fi、φi、τi分别表示:第i条信号的功率、载波频率、载波初相、相对时延;n(t)为加性高斯白噪声;Di(t)是第i条ADS-B信号在相对时延为τi下的基带信号,其表达式为:

图1 ADS-B信号格式
Fig.1 ADS-B signal format
![]()
(2)
p(t)为周期T是0.5 μs的矩形脉冲,d(n)是第n个码片处的取值,其取值1或0以表示该码片处脉冲的有无。
3 交织位置检测算法
3.1 交织分类
120 μs的ADS-B信号由报头和数据域两部分组成,报头8 μs信号格式固定,在0、1.0 μs、3.5 μs、4.5 μs处有4个脉冲,每个脉冲持续时间为0.5 μs,其余部分没有脉冲;数据域112 μs服从曼彻斯特编码规则,每个比特的码元中有且仅有0.5 μs脉冲。两条信号交织时,交织位置一定是后达信号报头首脉冲与先达信号交织产生的。将交织位置分为两大类:一类在先达信号报头如图2所示,后达信号报头与先达信号报头交织产生;另一类是在先达信号数据域如图3所示,后达信号报头与先达信号数据域交织产生。交织位置在报头时,将破坏报头原有固定格式,在检测交织位置时,只需找出报头中与固定格式相异的首个脉冲起始位置,该位置即为交织位置;交织位置在数据域时,则需要对数据域每个脉冲按序进行检测,直至找出交织位置。
3.2 交织检测算法
接收到交织信号x(t)后,对该信号作Hilbert变换:
(3)
其复信号为:
z(t)=x(t)+jy(t)
(4)
进而得到该信号的瞬时包络:
(5)
首先对信号报头进行交织检测,由于报头首脉冲即发生交织的概率较小,故可将其幅度均值A作为参考幅值。假设接收机中的噪声是方差为σ2的高斯白噪声,依据参考幅值得出该信号的信噪比S1(dB):
(6)
以该信噪比生成8 μs标准信号报头,取交织信号报头与标准报头进行作差,检测作差信号有无脉冲,首脉冲的起点位置即为信号的交织位置,若无脉冲,则对数据域进行检测。
单天线接收到两条交织信号时,即L=2时,接收到的信号为:
(7)
对于重叠脉冲,数据域的每个码片处可能出现以下四种交织情况:
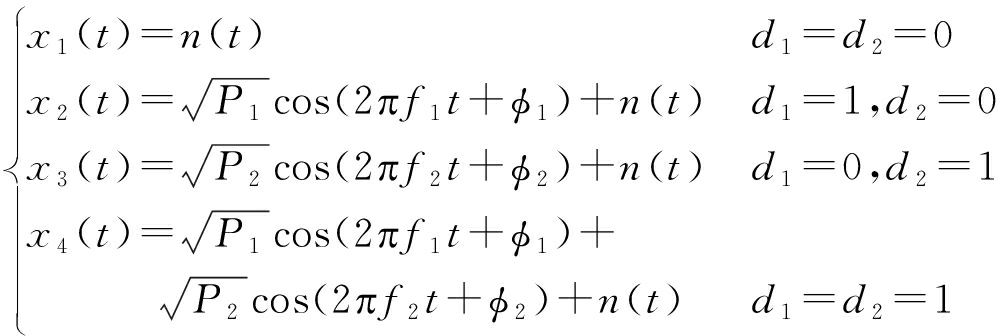
(8)

图2 交织位置在报头
Fig.2 Overlapped position in the preamble

图3 交织位置在数据域
Fig.3 Overlapped position in the data block
t∈[t0,t0+0.5],t0为码片的起始位置,φ1、φ2为两叠加信号的初相,假设每条ADS-B信号产生时其初相已为定值,故初相对信号幅值的影响并非时变的。但x4(t)中的载波相位与时间成正比,叠加后信号幅值将随时间改变且先达信号幅值将被增强或削弱,在忽略噪声条件下,该脉冲处信号幅度范围为![]()
由上所述,考虑两码片的相对时延,将每个码片处的交织情况主要归为两类如表1所示:脉冲的不完全重叠,此情况概率较大,由于脉冲叠加处信号幅度为![]() 范围内时变的值,叠加后脉冲宽度变化从而与标准脉宽不符,因此可以通过检测脉冲宽度和幅值来判断此处是否有交织;后达信号脉冲与先达信号低电平处交叠时,信号脉冲个数将增加,对于数据域,脉冲个数的增加使该位置码元与相邻位置码元不符合曼彻斯特编码规则。
范围内时变的值,叠加后脉冲宽度变化从而与标准脉宽不符,因此可以通过检测脉冲宽度和幅值来判断此处是否有交织;后达信号脉冲与先达信号低电平处交叠时,信号脉冲个数将增加,对于数据域,脉冲个数的增加使该位置码元与相邻位置码元不符合曼彻斯特编码规则。
表1 每个码片处脉冲交织位置分类
Tab.1 Classification of pulse overlapped positions at each chip
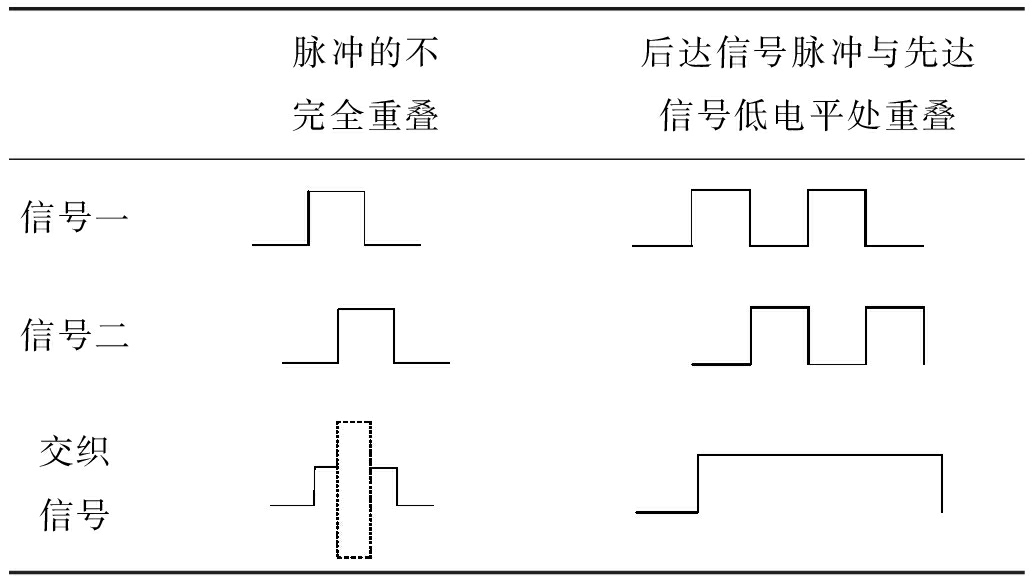
脉冲的不完全重叠后达信号脉冲与先达信号低电平处重叠信号一信号二交织信号
对数据域进行交织检测时,依据脉冲波形的上升沿与下降沿位置计算脉宽并求其幅度均值。在无交织情况下,脉冲宽度为0.5 μs,叠加相消时脉冲宽度小于0.5 μs且大于给定阈值(考虑噪声波形宽度的影响);叠加增强时,脉宽为大于0.5 μs且不包含1 μs的数值。脉宽为1 μs时,无交织情况下,由数据域两相邻比特编码分别为“0”与“1”所产生;交织情况下,需两脉冲码片位置紧连,故交织产生1 μs脉宽概率较小,本文中将1 μs宽的脉冲均视为无交织脉冲。根据ICAO规定,S模式下脉冲的平坦度应该在1~2 dB以内,信号交织情况下,当脉冲幅度均值与参考幅值相差2 dB以上时,认为在该脉冲处有交织。
本文所提的交织位置检测算法步骤如下:
(1)找到交织信号的起始位置;并由起始首脉冲获得参考幅值。
(2)判断信号报头有无交织,即对信号的前8 μs作交织检测:
由步骤(1)的参考幅值生成标准8 μs报头,取待检测信号报头与标准报头作差得作差信号,检测作差信号中首个宽度大于给定阈值的脉冲,该脉冲起点即为交织位置处。
(3)检测数据域有无交织,对8~120 μs作交织检测:
计算数据域每个脉冲的宽度及其幅度均值,脉冲宽度非正常脉宽或脉冲的幅值与参考幅值差值大于给定阈值,取此脉冲的起点为交织位置处。
(4)若检测无交织,则此信号为无交织信号。
本文所提的单天线下交织位置检测算法流程如图4所示。
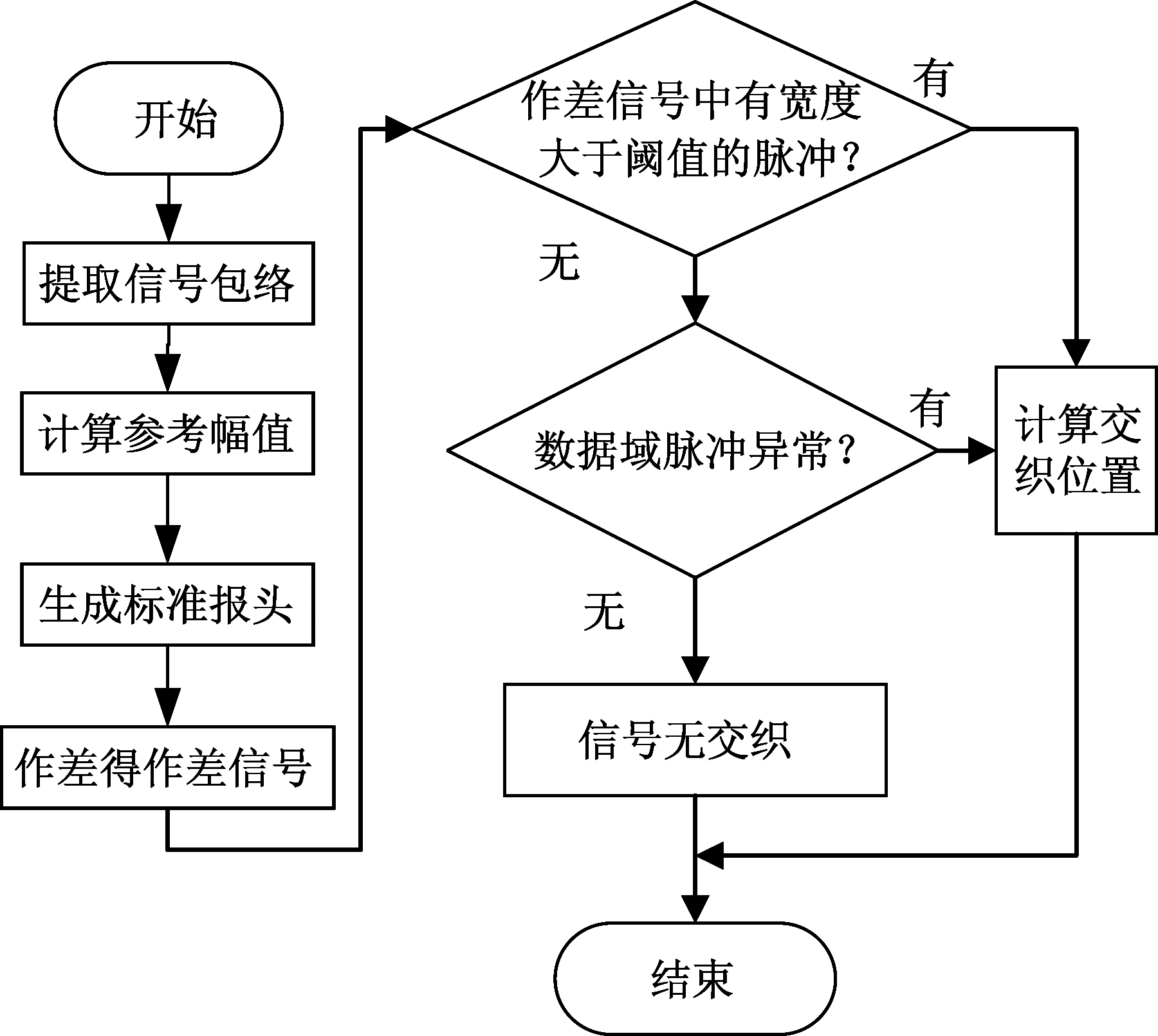
图4 算法流程图
Fig.4 The algorithm flow chart
以上是对两条信号交织时的交织位置检测,当信源数多于两条时,由于两条信号完全重叠的概率极小,且两信号之间存在明显的到达时间差,故可先将所有的后达信号当作整体,检测出该整体与先达信号的交织位置,也即信号的首个交织位置。同理可再使用该算法找出其余交织位置。
3.3 算法运算量分析
假设t(1)、t(2)分别为信号一、信号二的到达时间,则两信号相对时延为τ(μs),且τ=t(2)-t(1),采样频率为f(MHz),则该交织信号共有N个采样点,且N=(120+τ)f。以下分别对SVD分解法及交织检测法的运算量进行分析和对比[13]。如图5所示为两信号交织示意图。
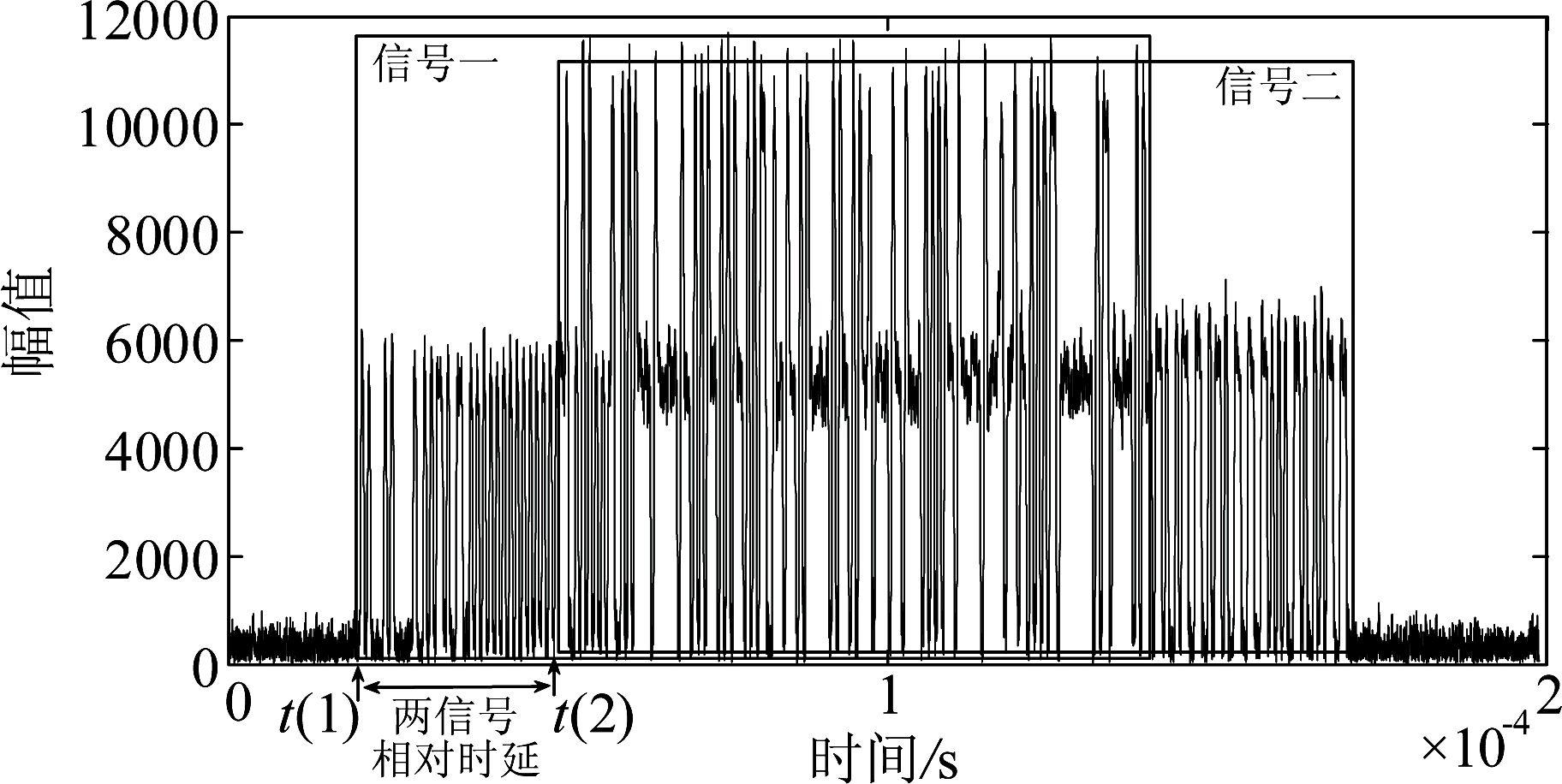
图5 两信号交织示意图
Fig.5 The waveform of the two overlapped signals
对于文献[7]中的SVD分解法,设接收到的N个采样点存储在矩阵X1×N中,对该矩阵进行变形时,设采用m(m≪N,为方便一般取m=1/2fTb,Tb为码元的周期1 μs)行存储该N个数据,对每s(μs)(s≥4 μs且为整数,一般取值为4 μs)时长的信号作一次SVD分解,当检测到交织位置时至少需进行τ/s(此处假设τ为s 的整数倍,在实际需对该值进行向上取整)次分解,设在s(μs)时间的矩阵内有l列(l=sf/m)。对于每次作SVD分解的矩阵Am×l,依据奇异值分解定理:
(9)
则进行一次SVD分解需作l2(l+m)次乘运算及20l3次加运算。在对所有的矩阵进行分解后的乘运算量为:
(10)
加运算量为:
(11)
代入l值后,乘运算量为:
(12)
加运算量为:
(13)
本文算法中,由于报头检测与数据域检测方法不同,故当0<τ<8时,在生成报头参考幅值时,需乘运算0.5f次,加运算0.5f-1次,作差信号计算需8f次加运算。故报头检测时共需乘次数:0.5f次,加次数:8.5f-1次。当τ≥8时,首先需要进行报头检测,其次检测数据域脉冲时,由于脉冲为曼彻斯特编码方式,故最多需对数据域(τ-8)f/2个点进行脉冲检测:上升沿与下降沿检测需进行20(τ-8)f/2次加运算,脉宽检测最多需2(τ-8)次加运算,脉冲均值检测的乘运算与加运算次数分别为:(τ-8)f/2、(τ-8)(0.5f-1)/2。故数据域检测最多需乘次数:(τ-7)f/2,加次数为:10.25fτ+1.5τ-73.5f-13。
SVD分解法与本文算法的乘加运算量在表2中列出。当两信号相对时延为0~120 μs时,两种算法检测运行时间范围在表2中列出,可以看出,本文所提的交织位置检测算法降低了运算的复杂度,同时减少了检测时间。
表2 运算量与检测时间范围比较
Tab.2 Comparison of calculation amount and detection time range

交织位置在报头(0<迈<8)乘次数加次数交织位置在数据域(迈≥8)乘次数加次数运行时间范围/sSVD分解法(s2f3m3+sf2m)迈20s2f3迈m3(s2f3m3+sf2m)迈20s2f3迈m3[0.314,0.782]本文所提算法0.5f8.5f-1(迈-7)f/210.25f迈+1.5迈-73.5f-13[0.008,0.093]
4 仿真实验结果
仿真实验采用单天线接收ADS-B信号,采样频率为80 MHz。本实验对两条ADS-B信号的交织情况进行仿真,其中一条信号的多普勒频移为0.2 MHz;另一条信号的多普勒频移为-0.2 MHz,两信号信噪比均为18 dB。
取先达信号起始位置100 μs,后达信号起始位置105 μs,两信号的相对时延为5 μs,此时交织位置在先达信号报头。图6是信号报头包络,该信号报头与标准报头格式不符,图7中作差信号的首个0.5 μs脉冲起始位置也即信号交织位置,经检测105.025 μs处为交织位置。
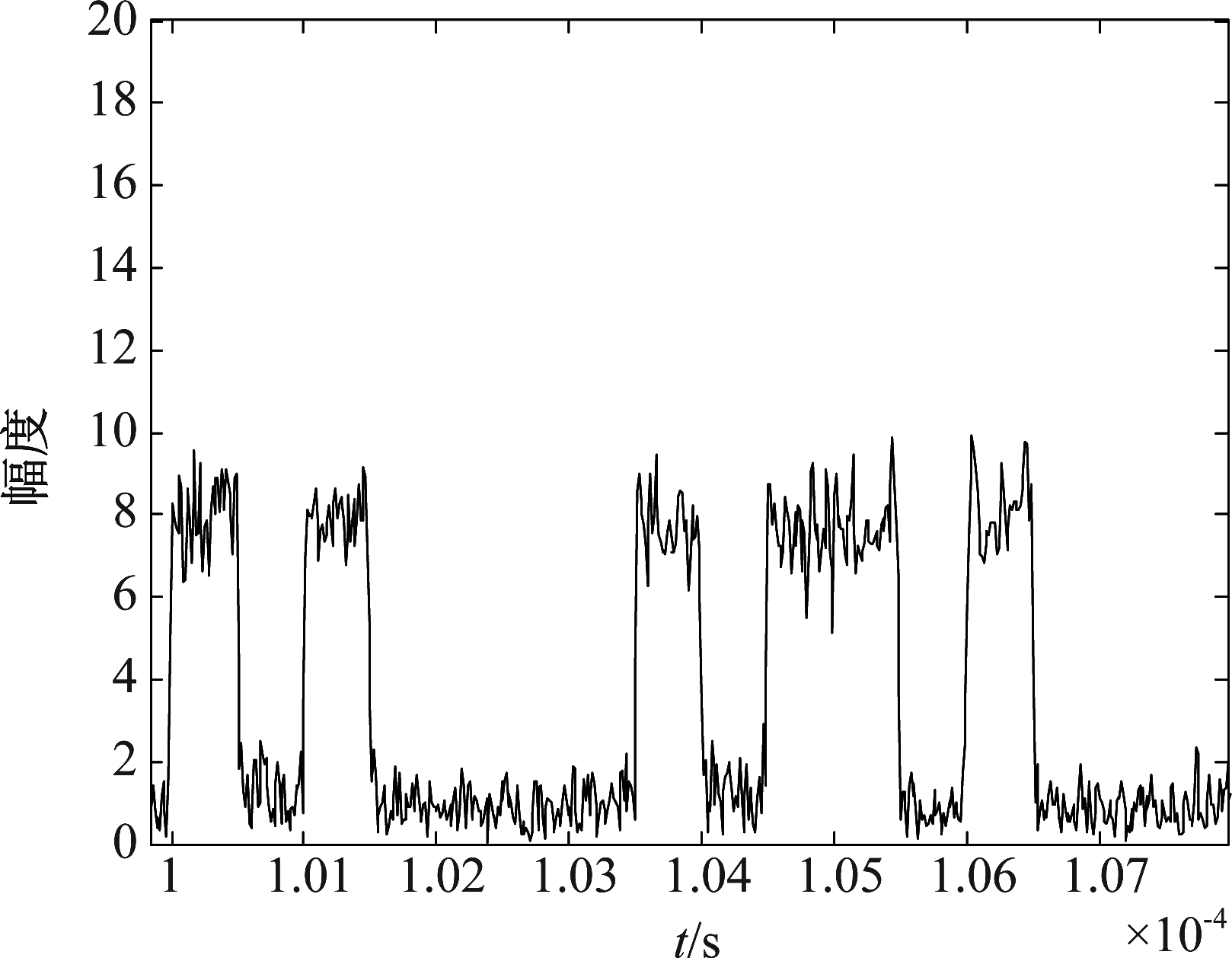
图6 信号报头包络
Fig.6 The envelope of the signal preamble
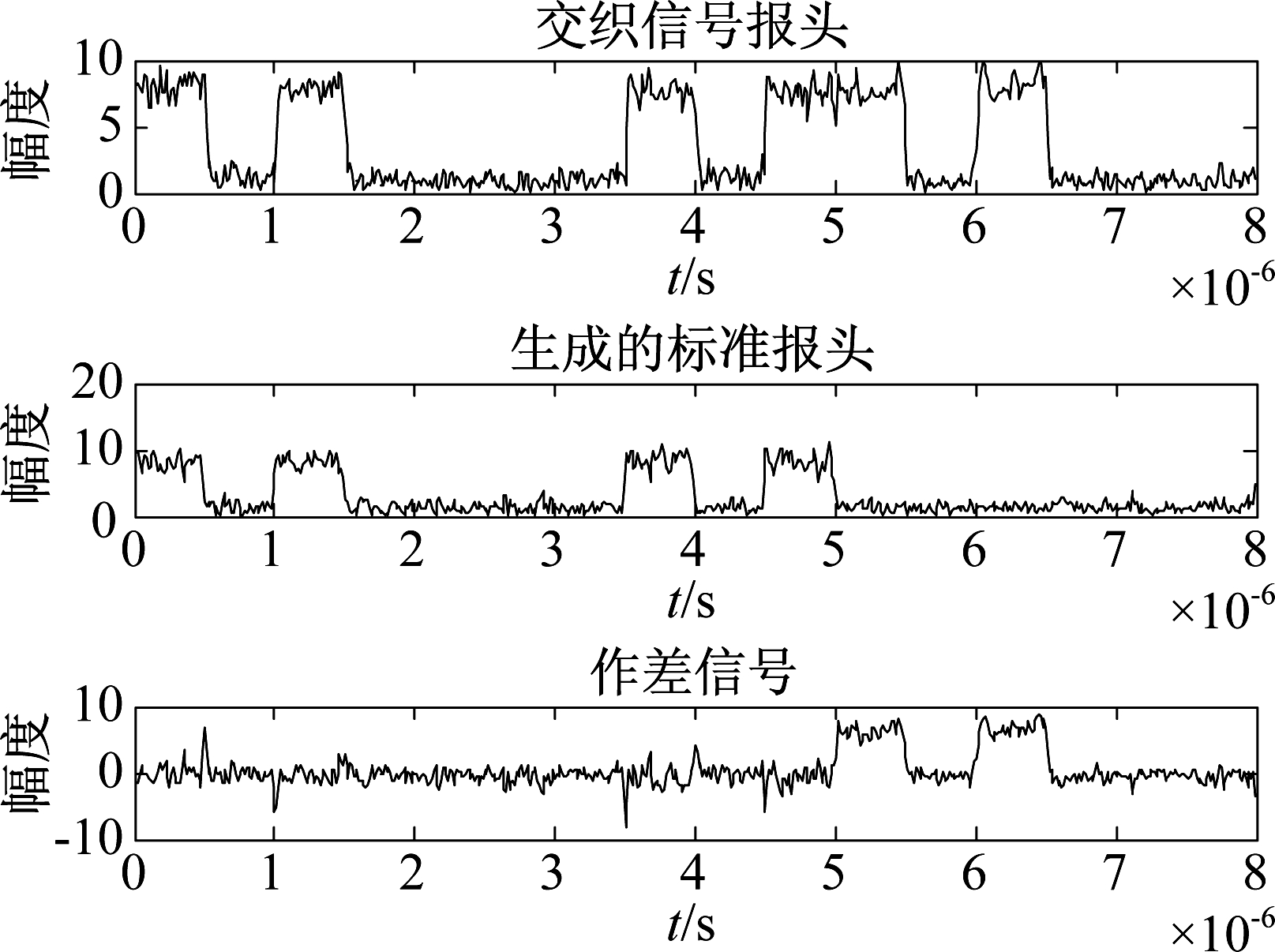
图7 报头脉冲比较
Fig.7 Preamble pulses comparison
固定先达信号的起始位置,改变后达信号起始位置并设置在150 μs处,也即两信号的相对时延是50 μs,图8是该信号的瞬时包络。
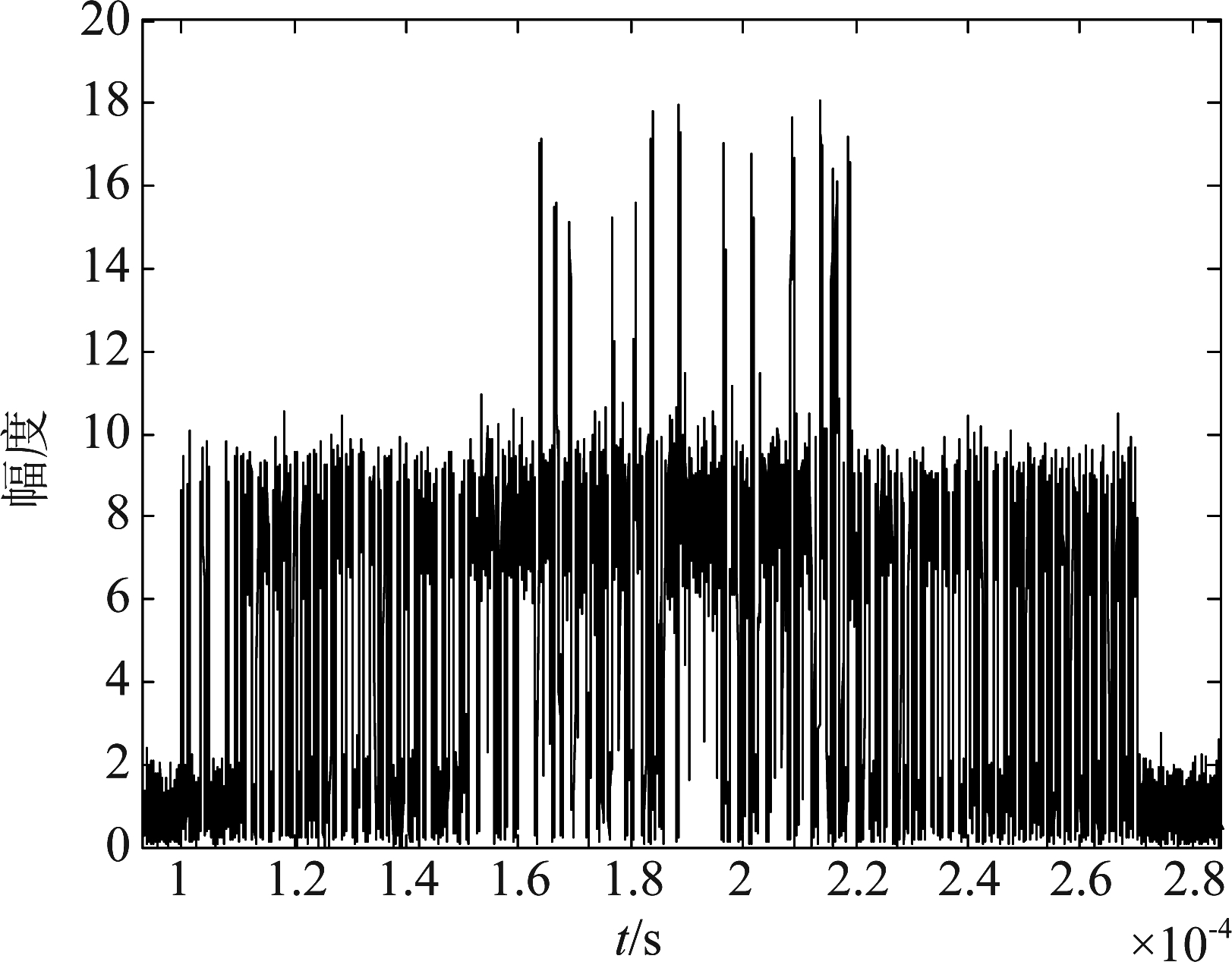
图8 交织信号瞬时包络
Fig.8 The envelope of overlapped signals
信号起始位置检测后,对信号报头作交织检测:由起始脉冲幅值求取参考幅值及信噪比,以该信噪比生成标准8 μs ADS-B报头信号,对生成的标准报头作希尔伯特变换、取模等信号处理,提取信号包络,并对两信号包络进行相应位置作差得到作差信号,三种信号波形如图9所示,可以看出,作差信号中虽有些尖脉冲,但由于其宽度未大于阈值0.2 μs,算法视为作差信号中无脉冲,也即在前8 μs的报头无交织。
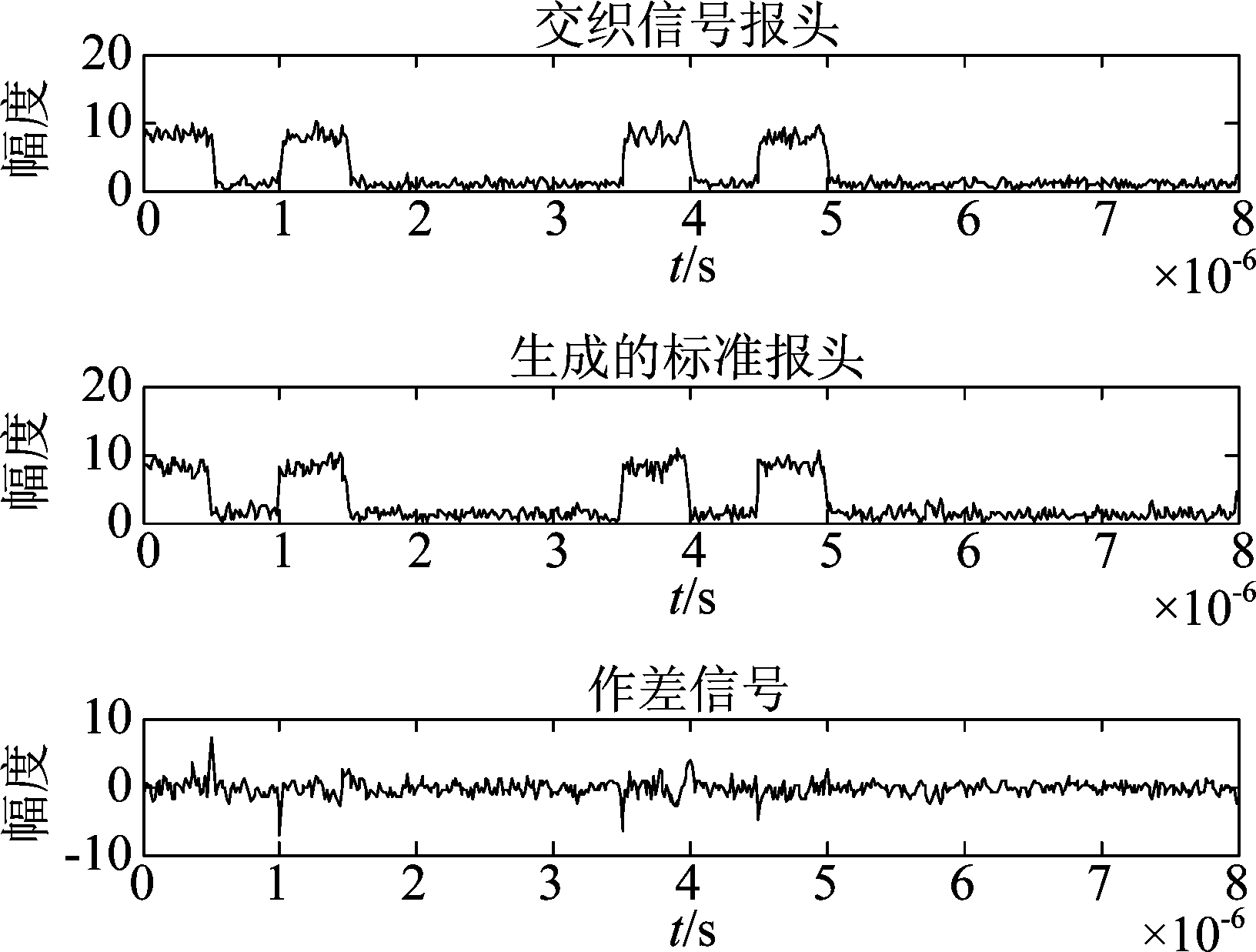
图9 报头脉冲比较
Fig.9 Preamble pulse comparison
然后对数据域进行交织检测,按序找出脉冲的上升沿与下降沿,并判断该脉冲是否正常,即是否满足脉宽为0.5 μs或1 μs且该脉冲的幅度与参考幅度的差值在2 dB内。在此实验中,检测到有脉冲均值与参考幅值相差2 dB以上,如图10所示为信号交织位置处的信号包络,经算法检测150.175 μs处为信号的交织位置。
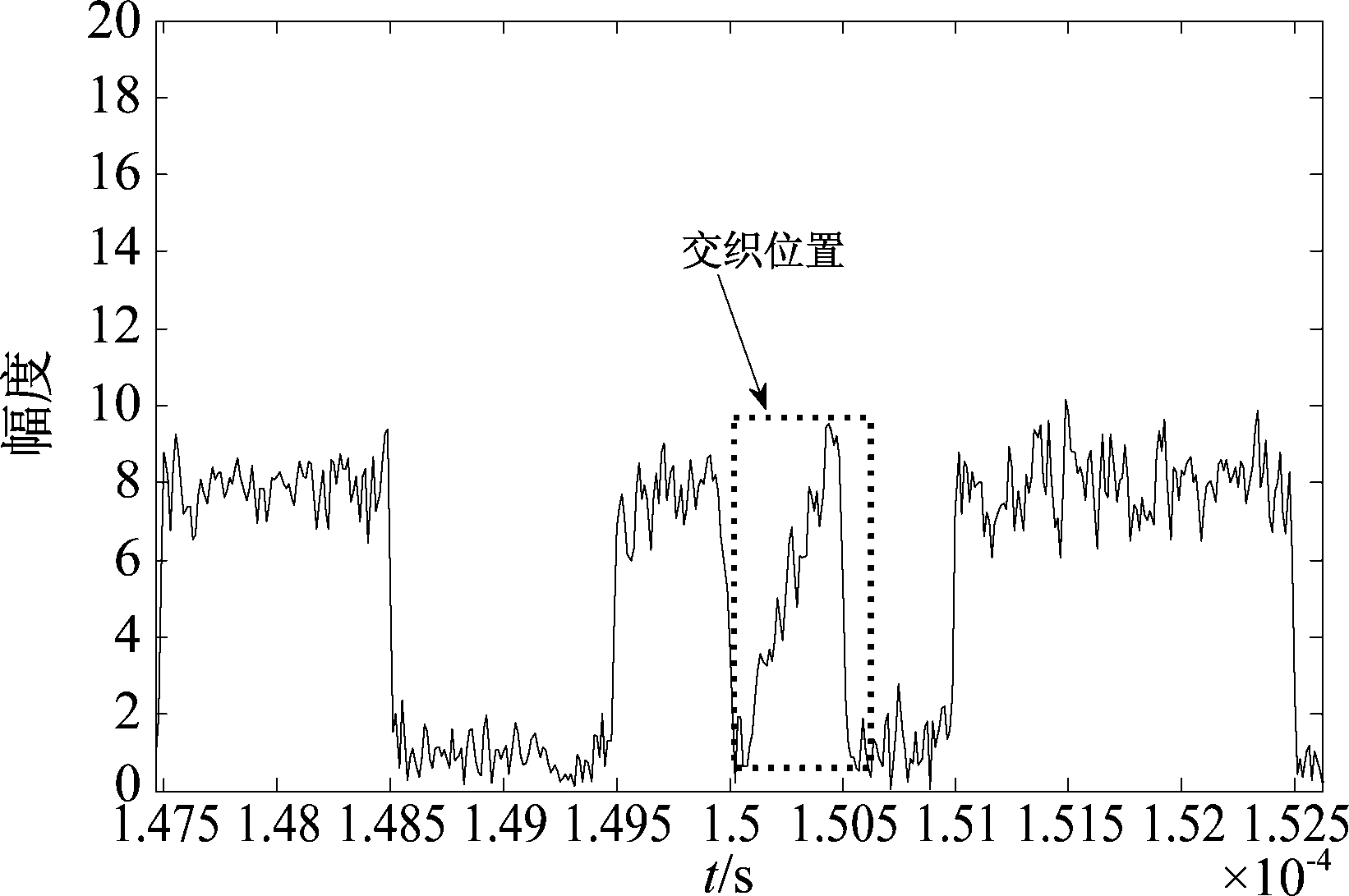
图10 信号首个交织位置时域波形图
Fig.10 Time domain waveform of first overlapped position
在该实验条件下,为验证在不同时延条件下的算法性能,取两信号的相对时延遍历1~119 μs之间的整数,如图11所示为实验结果。图(a)显示,估计时延与真实时延的关系;从图(b)中可以看出在不同时延下,估计误差基本在[- 0.5,0.2]范围内,可在得出交织位置后向前取以保证该位置确无信号交织。当时延取29 μs、49 μs、74 μs时,后达信号的报头首脉冲与先达信号叠加生成1 μs宽的脉冲,算法检测到交织信号的第二个非标准脉冲,并将该脉冲起始位置作为交织位置,故在该处存在最大误差,而在SVD算法中误差最大为奇异值分解窗的宽度,故本文算法最大误差小于SVD法。本文算法中,若将在[- 0.5,0.2]误差范围内的误差视为时延估计正确,则不同时延下的正确率分布曲线图如图12所示。
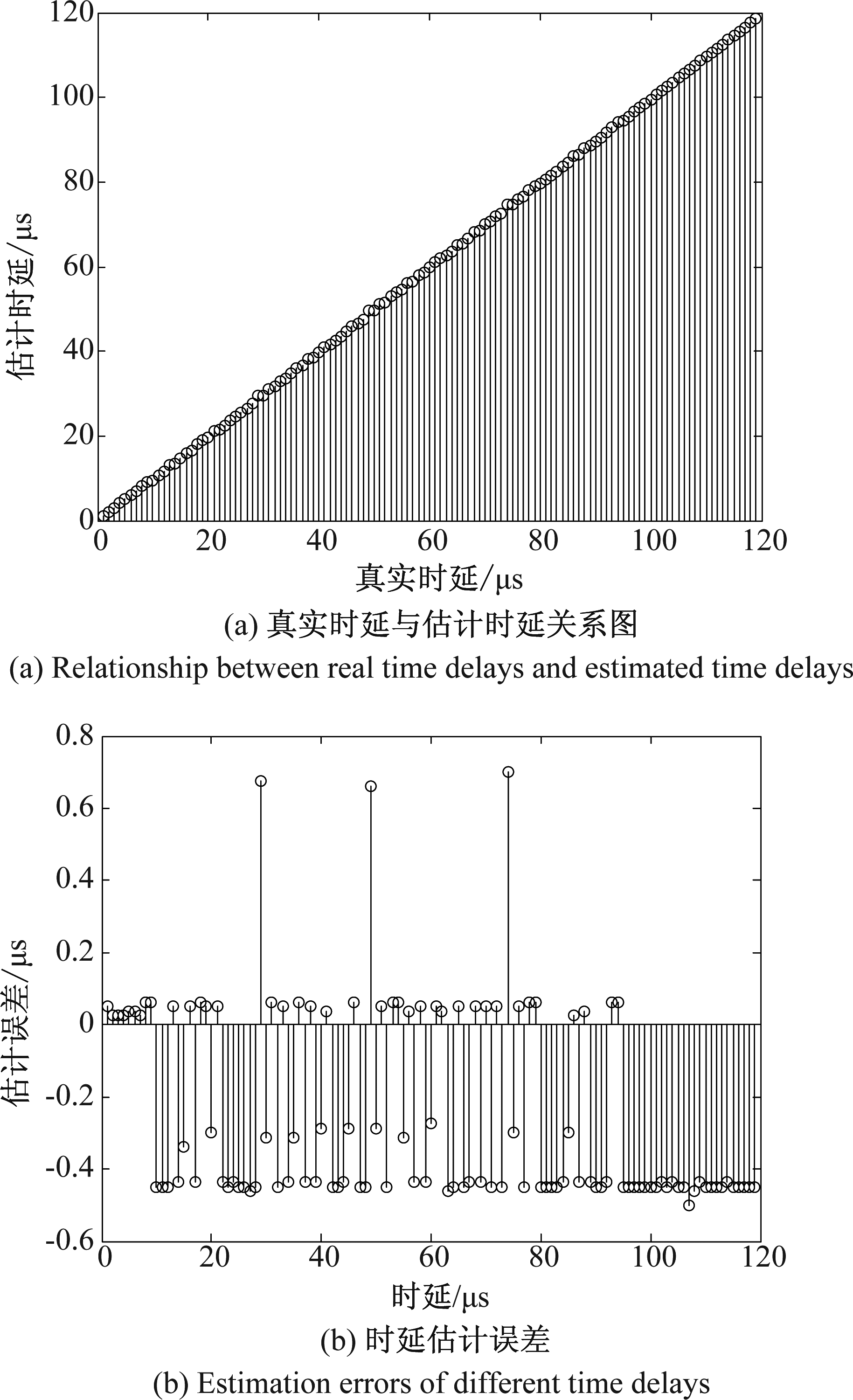
图11 信号时延估计误差
Fig.11 The estimation error among different signal delays
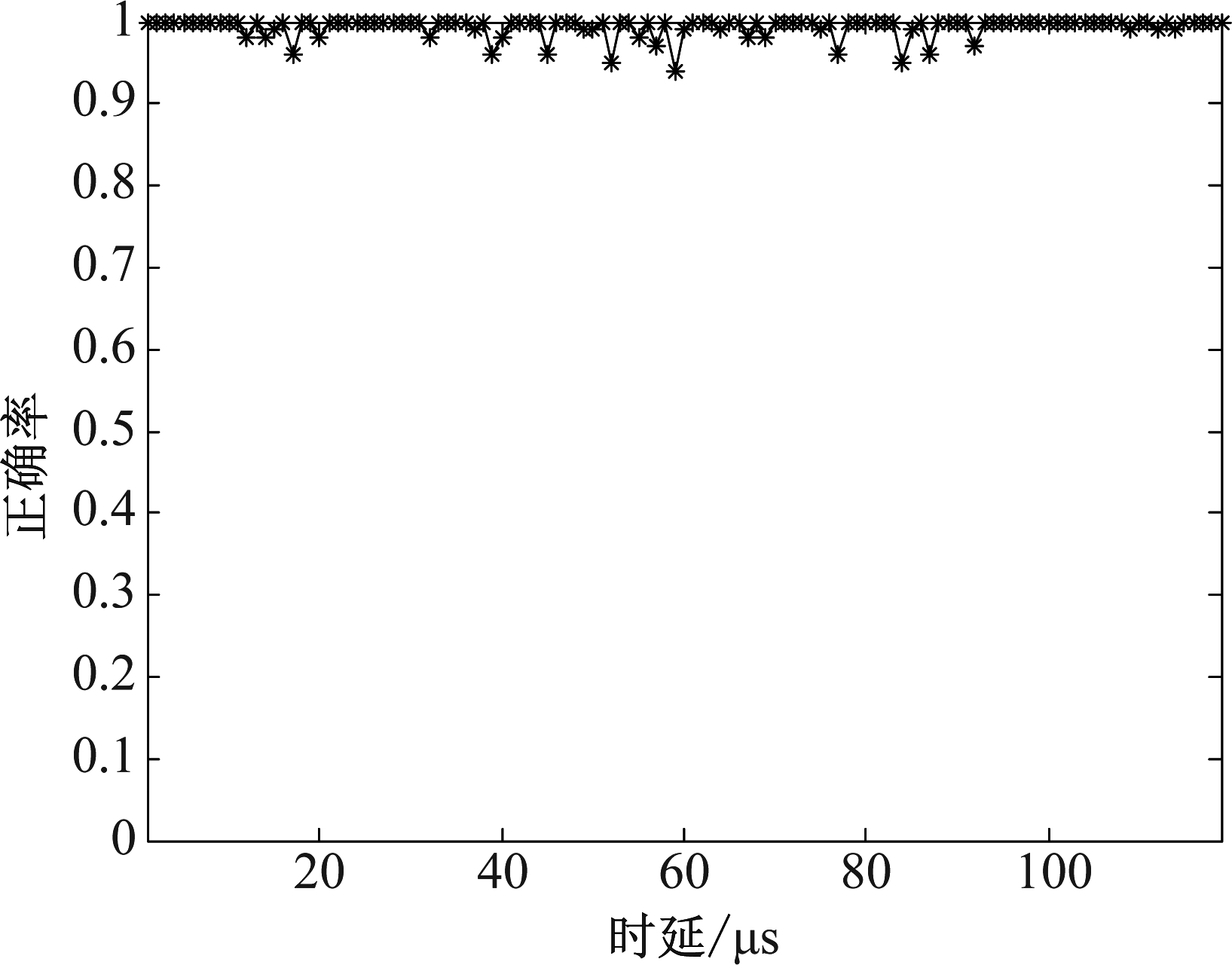
图12 不同时延下的检测正确率
Fig.12 Detection accuracies under different delays
为验证该算法在不同环境中的性能,研究了较易影响信号的两个主要因素:信号的信噪比及多普勒频移,并分析对本算法检测正确率的影响。如图13所示为第二条信号信噪比的改变对检测正确率影响的关系曲线图,当信噪比较低时,其幅值不易被检测,故此时正确率较低。图14中,两信号的信噪比为定值,改变两信号的多普勒频移差值大小,以得到检测正确率的关系曲线图,可以看出,算法对两信号多普勒频差不敏感。为验证程序的复杂度,对比了本文所提算法与SVD分解法的复乘与复加运算量之和。依据表2,在SVD分解法中,取s=4 μs,m=40,得到图15所示关系图,可见本文提出算法复杂度低于SVD分解法。
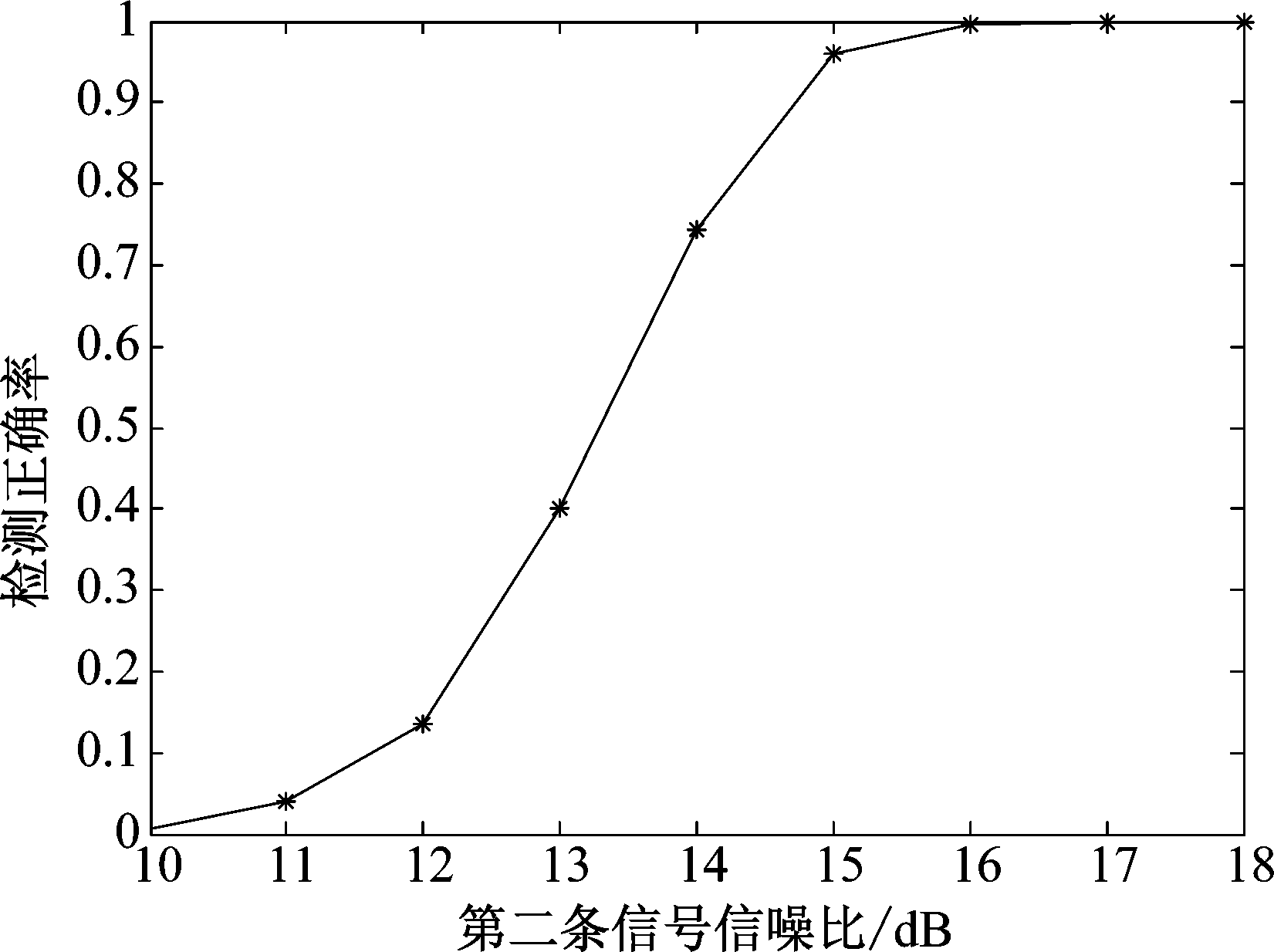
图13 不同信噪比下正确率
Fig.13 Correct rate under different SNR
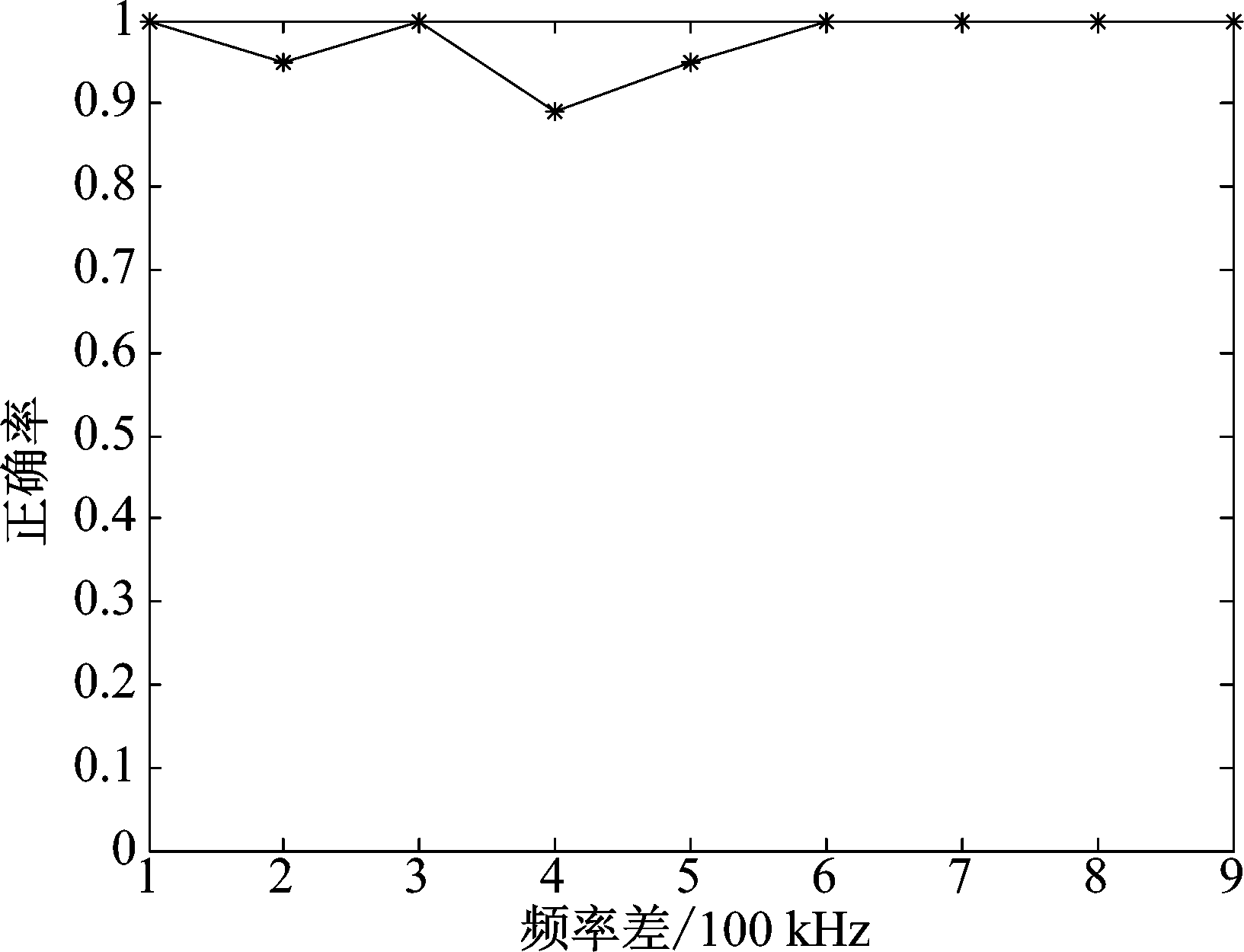
图14 正确率随频差变化关系图
Fig.14 Accuracies and frequency differences
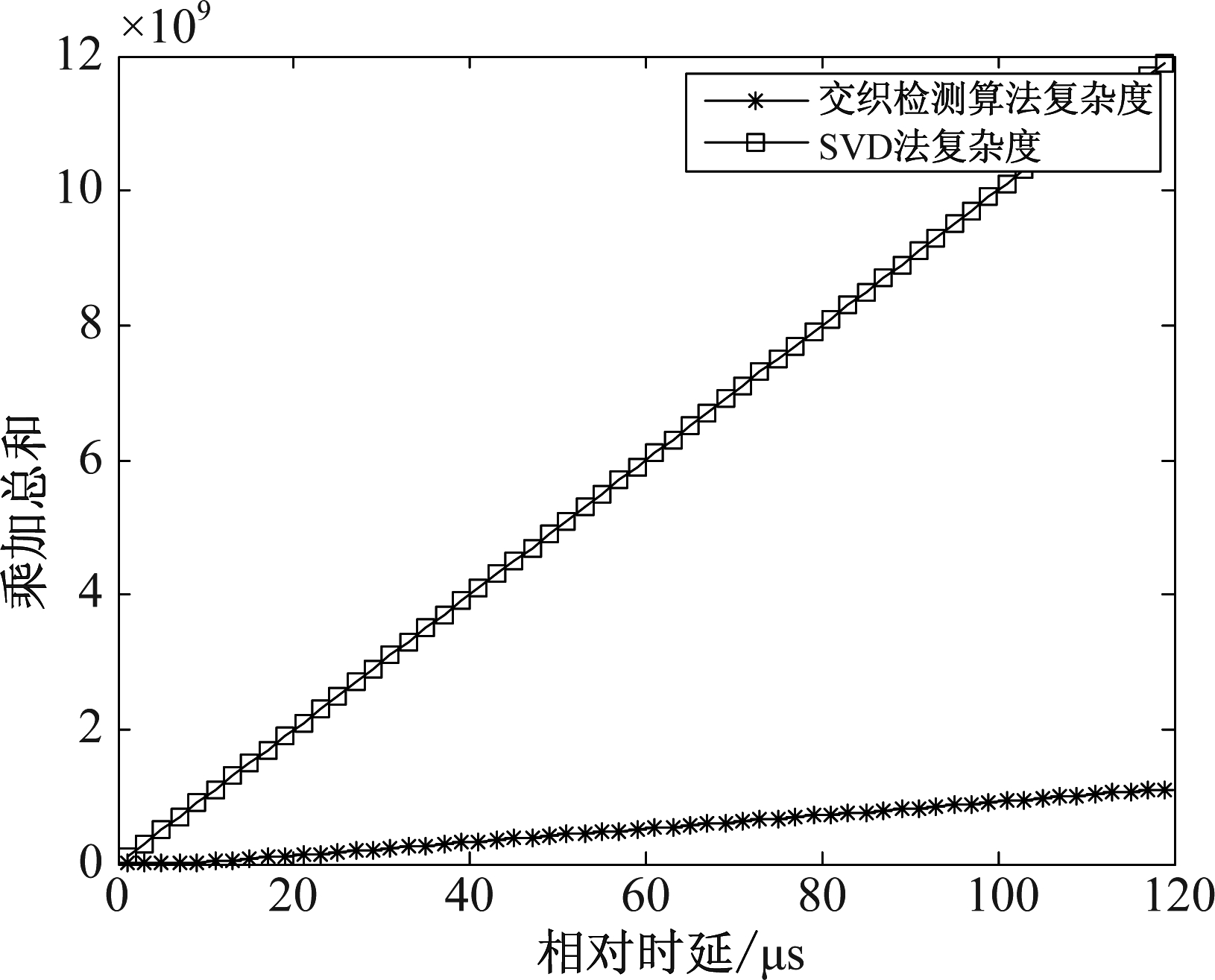
图15 相对时延与计算量关系图
Fig.15 Relationship between time delays and calculations
5 实采数据验证
为进一步验证算法的有效性,我们用十字阵列的实采数据对所提算法进行了验证,取两条时间间隔为50 μs的ADS-B信号进行人为的交织并发送该信号,采集的信号来源如图16所示,选取1号天线所接收的交织信号数据进行实验验证。信号采样频率为80 MHz,交织信号瞬时包络如图17所示。

图16 天线实物图
Fig.16 Antenna physical diagram
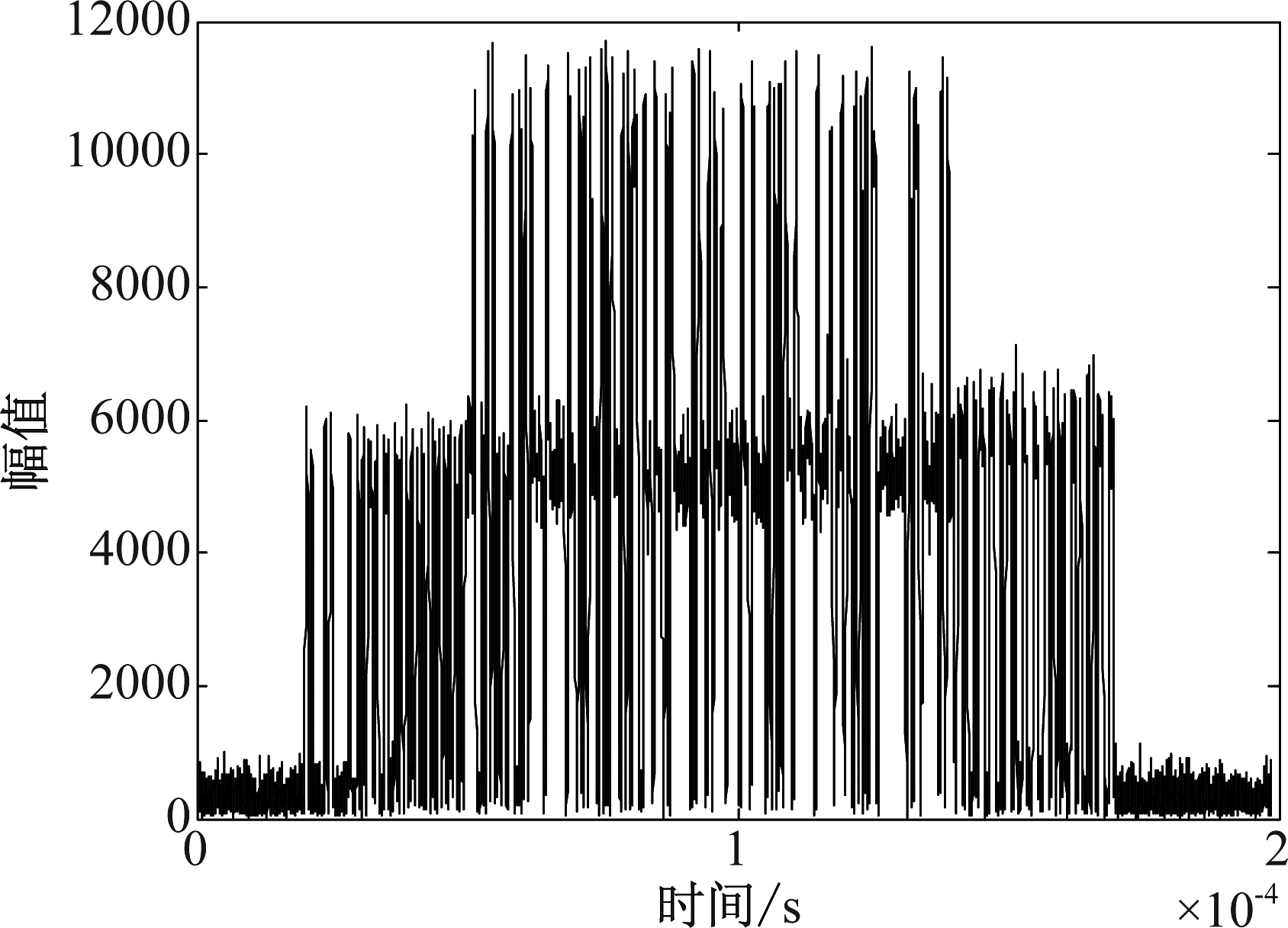
图17 交织信号瞬时包络波形图
Fig.17 The envelope of overlapped signals
该交织信号经由本文算法检测到首个交织位置处的波形图,如图18所示,经算法检测两信号的交织位置为49.625 μs。再根据文献[7]使用SVD分解法对同一条交织信号进行交织检测,得到如图19的特征值分布图,在该算法中所取快拍数为160,交织位置在第12个快拍处,计算得交织位置为48 μs。本实验中,所提算法与真实值误差为0.375 μs,而特征值分解法误差为2 μs,所以提出的算法能够更准确地检测到信号交织位置。
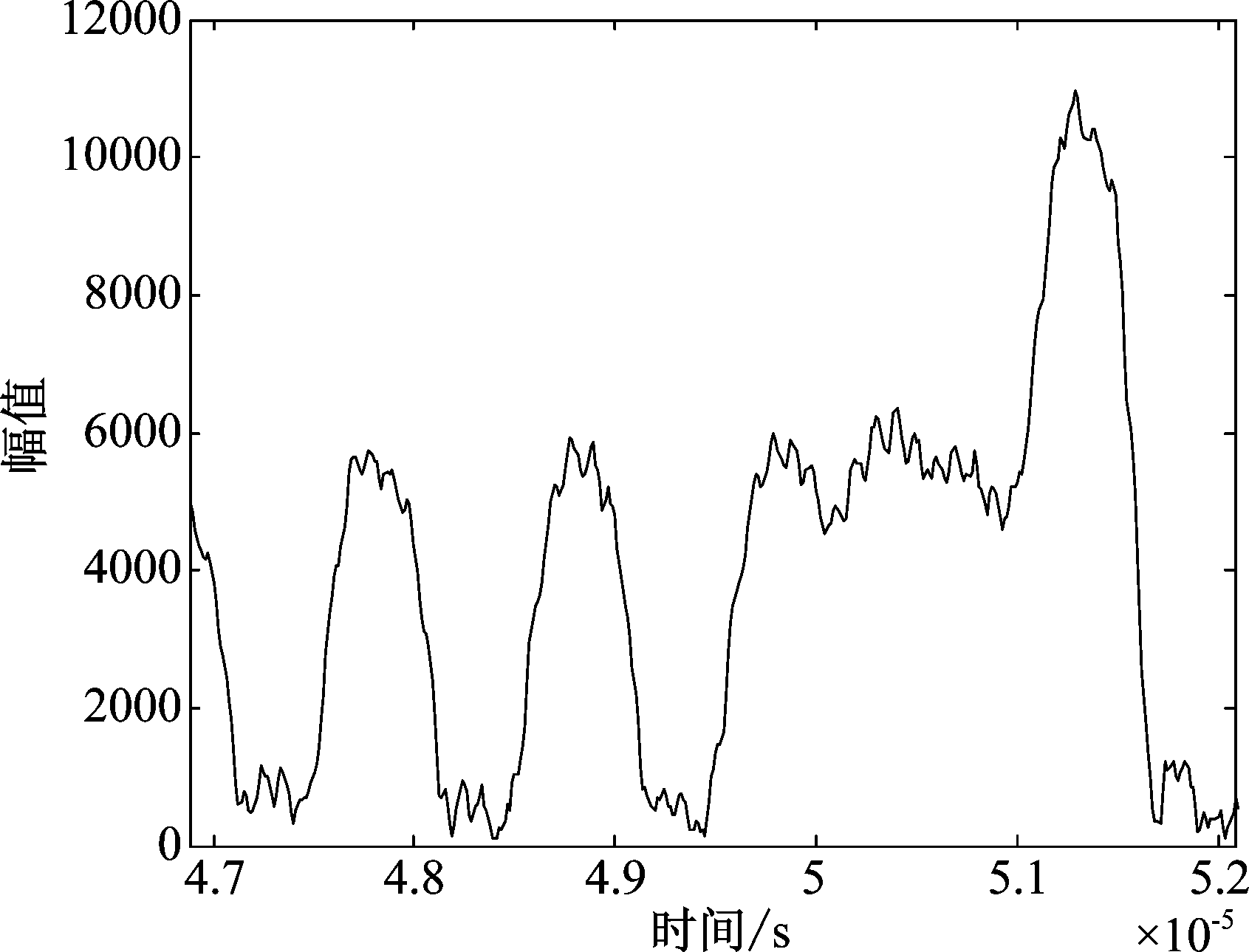
图18 非正常脉冲波形
Fig.18 Abnormal pulse waveform
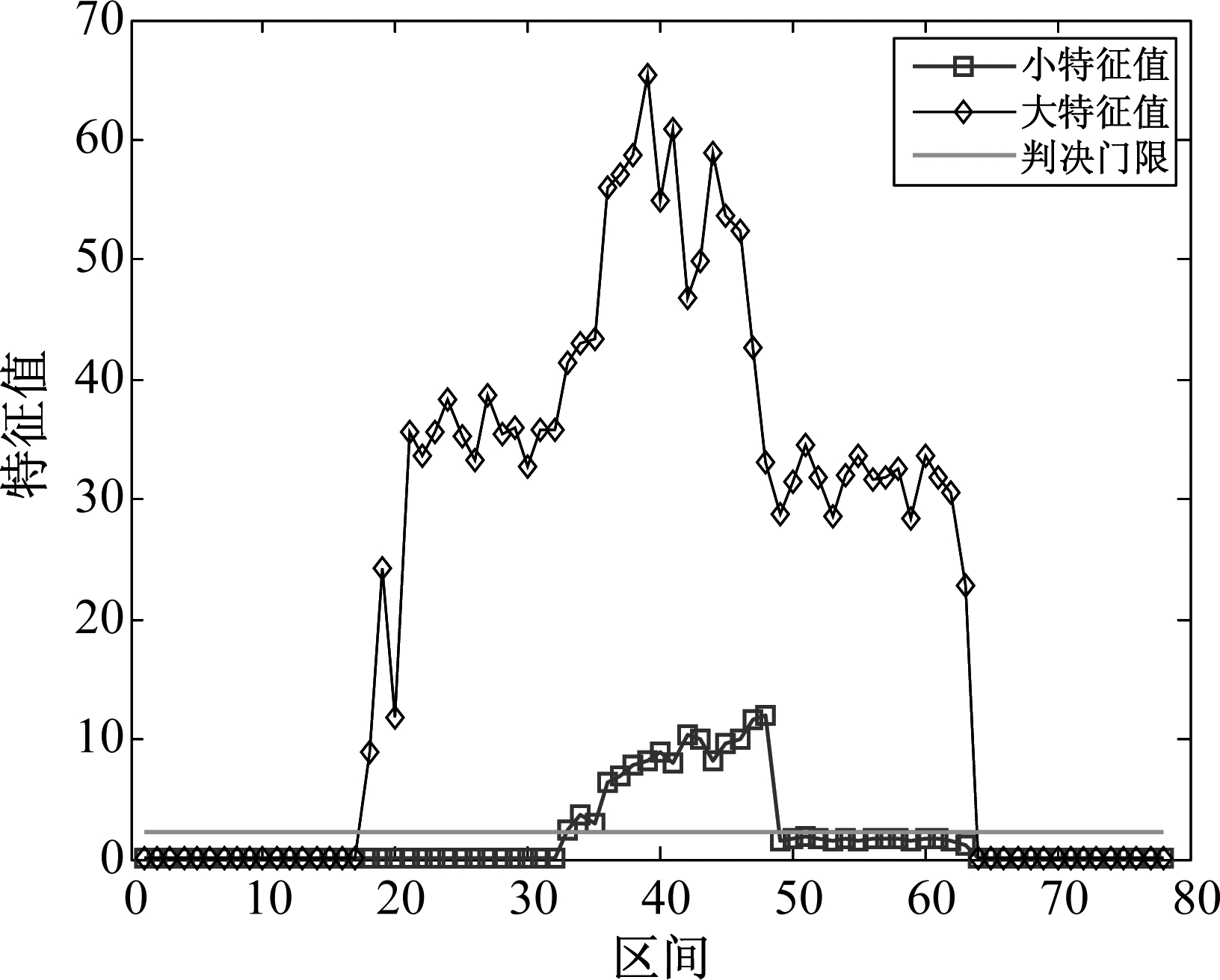
图19 特征值分布图
Fig.19 Eigenvalue distribution curve
6 结论
针对检测信号交织位置的问题,本文提出一种低复杂度的交织位置检测方法,首先通过Hilbert变换和取模等提取信号的瞬时包络,以信号报头的首脉冲幅值作为参考幅值生成标准报头,提取信号报头包络与标准报头包络作差得到作差信号,检测作差信号中首个脉冲的起始位置,进而检测信号报头交织情况,结合ICAO标准文件对脉冲的宽度及幅值的相关标准,在对数据域进行检测时,当检测到数据域首个非正常脉冲即为数据域的交织位置。本文基于单天线ADS-B标准时域波形与信号交织时时域波形图差异,提出一种可对多条交织信号进行交织位置检测的方法。通过仿真和实采实验表明:本文所提算法不仅能更加精确的找出交织位置,算法复杂度低、检测速度快,且对多普勒频移的变化不敏感,降低了算法对信号的频率的要求,能更好的为解交织算法带来便利。
[1] Petrochilos N, Galati G, Mene L. Separation of multiple secondary surveillance radar sources in a real environment by a novel projection algorithm[C]∥IEEE International Symposium on Signal Processing and Information Technology, 2005: 125-130.
[2] Petrochilos N, Piracci E, Galati G. Separation of multiple secondary surveillance radar sources in a real environment for the near-far case[C]∥Antennas and Propagation Society International Symposium. Honolulu: IEEE, 2007: 3988-3991.
[3] Massa G, Costanzo S, Borgia A, et al. Multiple sources discrimination by array processing[C]∥European Conference on Antennas and Propagation. Rome: IEEE, 2011: 620- 622.
[4] Petrochilos N, Galati G, Piracci E. Separation of SSR signals by array processing in multilateration systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(3): 965-982.
[5] Petrochilos N, Galati G, Piracci E. Projection Techniques for Separation of Multiple Secondary Surveillance Radar Sources in a Real Environment[C]∥IEEE Workshop on Sensor Array and Multichannel Processing, 2006: 344-348.
[6] 呼延帅斌. ADS-B技术分析和应用[J]. 数字技术与应用, 2019, 37(4): 109,111.
Huyan Shuaibin. Analysis and Application of ADS-B Technology[J]. Digital Technology and Application, 2019, 37(4): 109, 111.(in Chinese)
[7] Gaspare G, Nicolas P, Emilio G, et al. Degarbling Mode S replies received in single channel stations with a digital incremental improvement[J]. IET Radar Sonar and Navigation, 2015, 9(6): 681- 691.
[8] ICAO. Manual on the secondary surveillance radar system[S]. Montreal: 2004.
[9] 吴仁彪, 吴琛琛, 王文益. 基于累加分类的ADS-B交织信号处理方法[J]. 信号处理, 2017, 33(4): 572-576.
Wu Renbiao, Wu Chenchen, Wang Wenyi. A Method of Overlapped ADS-B Signal Processing Based on Accumulation and Classification[J]. Journal of Signal Processing, 2017, 33(4): 572-576.(in Chinese)
[10] 张凯院, 徐仲. 矩阵论[M]. 西安: 西北工业大学出版社, 2017: 159-165.
Zhang Kaiyuan, Xu Zhong. Matrix Theory[M]. Xi’an: Northwest University of Technology Press, 2017: 159-165.(in Chinese)
[11] 吴杰, 郭建华, 蒋凯, 等. ADS-B二重交织信号时域分离算法[J]. 通信技术, 2017, 50(10): 2184-2189.
Wu Jie, Guo Jianhua, Jiang Kai, et al. ADS-B Double Intertwined Signal Separation Algorithm in Time Domain[J]. Communication Technology, 2017, 50(10): 2184-2189.(in Chinese)
[12] Minimum Operational Performance Standard for ADS-B and TIS-B[S]. RTCADO-260A: 1090.2006.
[13] Mark Allen Weiss. 数据结构与算法分析[M]. 张怀勇,译.北京: 人民邮电出版社, 2007: 25- 80.
Mark Allen Weiss. Data Structure and Algorithm Analysis[M]. Zhang Huaiyong,translate.Beijing: People’s Posts and Telecommunications Press, 2007: 25- 80.(in Chinese)

