1 引言
近年来,随着人们各种需求的不断增加,卫星数目也在不断增多。随着而来的就有一些问题的存在,比如干扰。随着信号处理技术的发展,干扰检测在众多领域中发挥着重要的作用。但是干扰检测仍旧存在的诸多问题待解决。比如在众多信号和背景噪声起伏变化比较复杂的情况下,干扰检测就存在一些困难。因此,找寻新的干扰检测方法就显得很重要。
在干扰检测领域,门限的设置一直是干扰检测效果的一项非常重要的工作。门限设置过低可以得到较好的检测效果,但是虚警点数也会大大增加;同时复杂的背景噪声导致待检测频谱不够平滑,从而给干扰检测带来了很多的不便。近些年,许多学者已经对各种各样的通信系统中的干扰检测做了非常深入的研究[1- 8]。文献[4]介绍的方法是采用多次测量噪声功率的情况下,然后设置干扰检测的门限值,但是此方法在底噪信号起伏较大的情况下,不能适用于各类场景。文献[5]应用了形态学进行预处理对复杂背景噪声进行滤除,从而估计噪底,进一步通过排序计算得到门限值,由于计算过程中存在很多的排序运算增大了算法复杂度。文献[6]采用形态学梯度的方法,通过判断梯度值正负确定干扰所在的位置,实现窄带干扰的检测与定位但存在背景噪声复杂的情况下梯度值较多无法正确定位的现象。文献[7]通过形态学的方法很好的获得该段信号的噪声基底估计,并通过双门限的方法对干扰进行检测得到很好的检测效果,但是由于只有结构元素的长度大于窄带干扰的长度时才能将干扰滤除,在实际的应用中我们无法预知干扰的宽度如何,因此不适用于任何频谱带宽的干扰的情况。
本文将数字形态学引入卫星信号干扰检测的预处理过程中,然后根据预处理后功率谱分布情况,根据不同的分布选择门限值实现门限自适应,对检测不同占用有用信号带宽的大小的窄带干扰提供了方法。此外,本文还针对形态学中的结构元素长度的不同选取对检测效果进行仿真和分析,仿真结果得出当结构元素的长度为25时,可以达到很好的检测效果。
2 形态学基本原理
形态学最早是出现在图像处理中的,在图像中处理的是二维信号,当形态学应用于一维数字信号中时,也同样具有同在二维信号中的效果,可用于提取信号的形态特征,并与背景分离,有效抑制噪声干扰[8]。
2.1 数字形态学基本运算
数字形态学在一维信号处理的过程中,将待处理的信号当成一个集合,通过结构元素去找到信号中与结构元素相关的部分,然后通过信号与结构元素之间的关系,从而提取出有用的信息以及特征。
在数字处理过程中,设f(n)和g(n)分别为定义在F={1,2,…,N}、G={1,2,…,M}上的一维离散函数,且M<N,这里f(n)为输入信号序列,g(n)为结构元素,则f(n)关于g(n)腐蚀定义为:
(fΘg)(n)=min{f(n+m)-g(m)}
(n=0,1,…,N-M)
(1)
根据定义,腐蚀处理的实现过程是将接收到得信号f向左平移m个单位,其中m在结构元素的定义域内,然后再对每次移动后的信号值减去结构元素g(m),这样对于每次移动的信号值都得到了一组相对应的与结构元素相减的信号值,最后求出对应同一变量所有信号的最小值,便可得到腐蚀的结果。
f(n)关于g(n)膨胀定义为:
(f⊕g)(n)=max{g(n-m)+f(m)}
(n=0,1,…,N+M-2)
(2)
根据定义,膨胀处理的实现过程是将接收到得信号f向右平移m个单位,其中m在结构元素的区间内,然后再对每次移动后的信号值加上结构元素g(m),这样对于每次移动的信号值都得到了一组相对应的与结构元素相加的信号值,最后求出对应同一变量所有信号的最大值,便可得到膨胀的结果。
通常情况下,膨胀运算可以达到增大信号的峰值并且平滑峰值的目的同时也可以加宽信号值;而腐蚀运算与膨胀有近似相反的过程,腐蚀减小信号的峰值使谷值也可以平滑,同时也减小了信号的宽度。式子(3)(4)定义了f(n)对g(n)的开运算和闭运算:
f∘g=[(fΘg)⊕g](n)
(3)
f·g=[(f⊕g)Θg](n)
(4)
2.2 形态学结构元素
结构元素在形态学运算中的作用就类似于一般信号处理时的滤波窗口或者参考的模板。它的选取直接影响了最终的滤波效果,如果想要达到想要的滤波效果,必须要选择合适的结构元素。结构元素的选择涉及到形状、长度和幅值等要素[9]。
2.2.1 结构元素的形状
常见几种结构元素的形状有以下几种,如图1所示。
从已有的研究分析[8-11],在不同的信号处理中,需要选择与要提取波形相似的结构元素。通常情况下,一般选用几何形状(比如三角形、圆等)简单或扁平结构元素。其中扁平结构元素是指一种在所在的定义域上取常数的结构元素。因此在一维信号处理中通常选取扁平结构元素且在其定义域上幅值设为零[7]。
2.2.2 结构元素的长度
结构元素的长度的选取决定了运算过程中的运算速度以及对噪声的处理能力。结构元素的长度越长,则运算量越大,计算所需要的时间越长,去除噪声的能力越强,但是对干扰信号的边缘检测比较粗糙模糊;反之,结构元素的长度越短,则运算量越小,计算需要的时间越短,去除噪声的能力越弱[9]。
3 连续均值去除算法(CME)干扰检测算法
CME算法[12]是基于频率域算法,是在能量检测的基础上改进得来的。它的基本思想是将整个集合中的点分成两部分,分别是未受到干扰的频点集合与受到干扰的频点集合,首先将所有的频点认为是没有受到干扰的频点,从而得到一个门限值,将集合中所有频点对应的幅度值与此门限值进行比较, 大于门限值的频点归到受到干扰的频点集合,反之则归到未受到干扰的频点集合,下一次迭代,讨论的对象仅仅是上一次迭代中未受到干扰的频点集合,以次类推,反复迭代,从未受到干扰的频点集合中不断的剔除大于门限值得频点,加到受到干扰的频点集合中,直至没有频点被剔除或者达到最大迭代次数为止。
CME干扰检测算法的具体流程为:
第一步:初始化m=1,Im={1,2,…,N},Jm={},假设均值![]()
第二步:接下来需要根据门限值来计算集合Im+1和Jm+1,计算的准则如下:
(5)
第三步: 计算集合Jm+1的长度P;
第四步: 当P=0或者达到设定的最大迭代次数时,跳转到第九步执行;
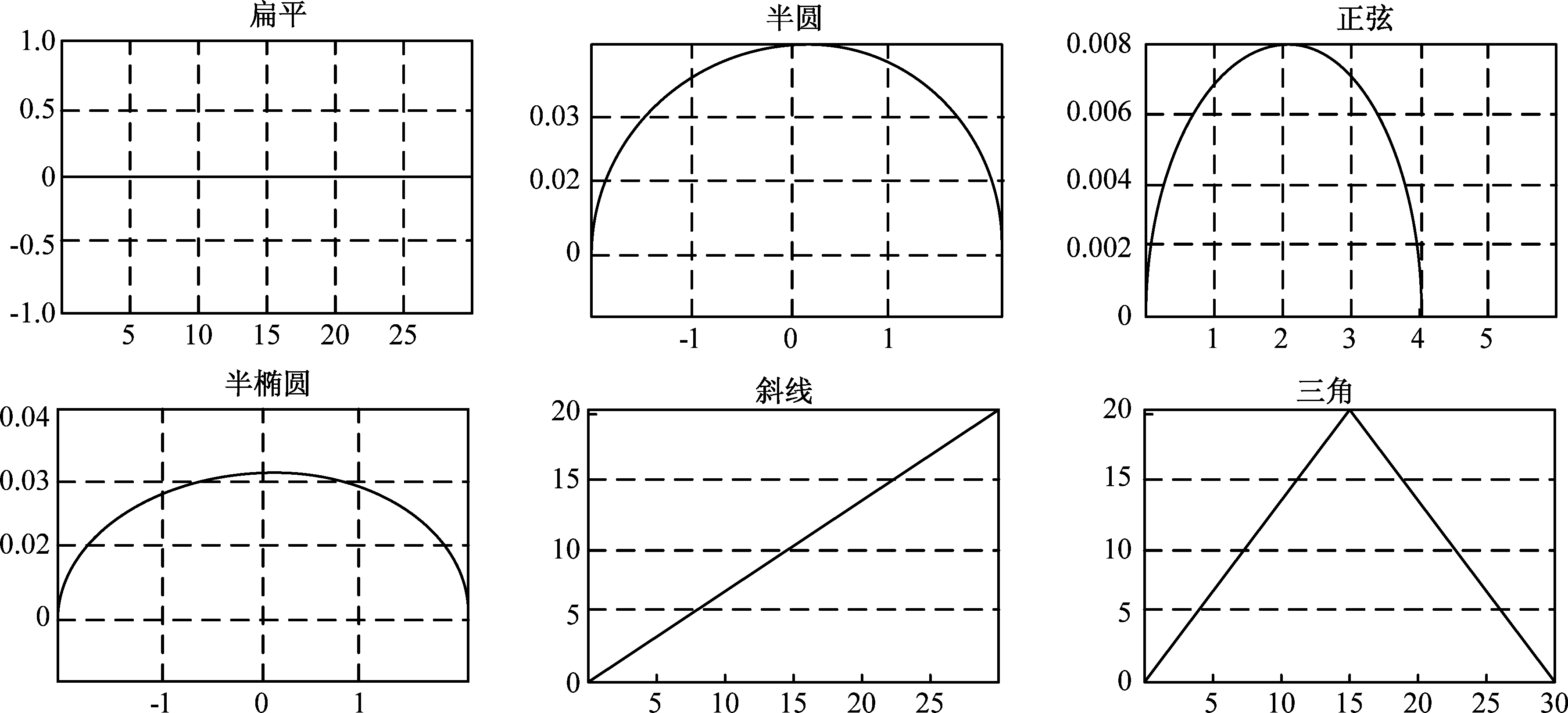
图1 不同类型的结构元素
Fig.1 Different types of structural elements
第五步: 存储集合Jm+1;
第六步: 更新![]()
第七步: 更新N,Nm+1=Nm-P;
第八步:m=m+1,跳转到第一步,继续进行迭代;
第九步:最终,干扰信号的集合可以表示为J=J1∪J2…Jm,进行IFFT前,将干扰信号集合J中的所有元素置零,即R(k)={0|k∈J}。
该算法存在的问题,当干扰功率较小时,有可能遗漏干扰,漏检概率较大,且对80%以上宽带干扰失效。因此提出本文的形态学自适应干扰检测算法。
4 形态学自适应门限检测算法
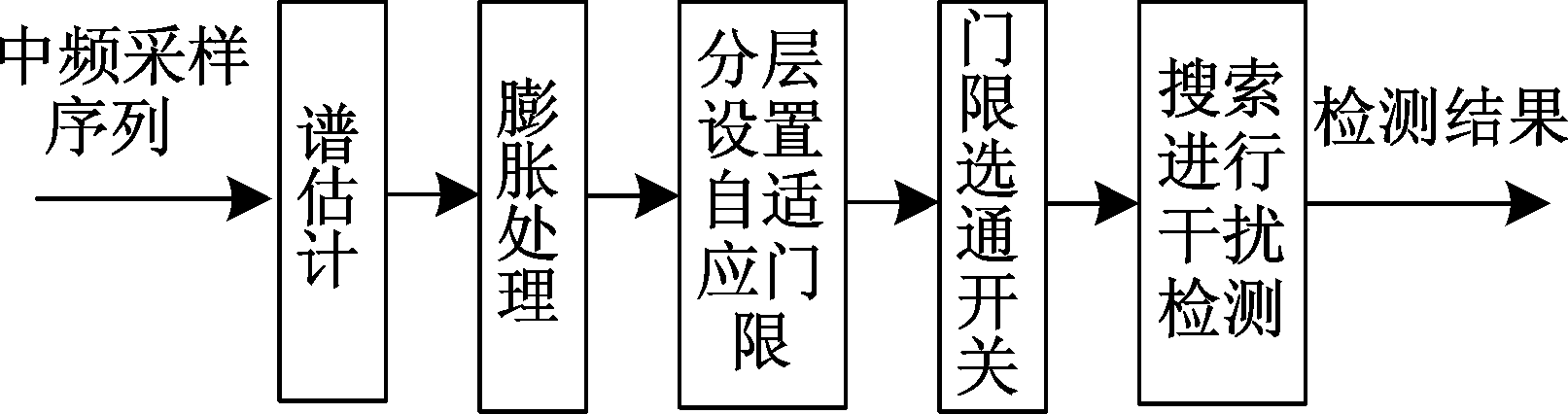
图2 算法流程图
Fig.2 Algorithm flowchart
算法具体实现步骤:
4.1 谱估计
Welch算法作为周期图法的改进算法,在不严重影响信号分辨率的情况下,对信号进行分段和加窗,能够很有效的对频谱进行估计,是一种有效的谱估计方法[13]。设采样数据为
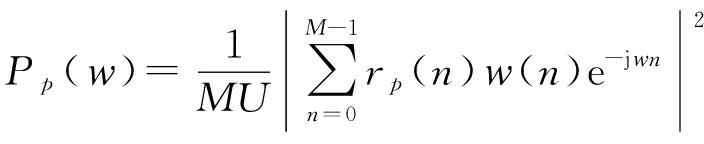
(6)
其中![]() 为归一化因子,w(n)为窗函数,rp(n)为第p段数据,p=0,1,2,…,L-1。
为归一化因子,w(n)为窗函数,rp(n)为第p段数据,p=0,1,2,…,L-1。
4.2 形态学处理
该文采用的预处理的方法是膨胀处理。如图3所示,原始信号f长度为200,采用半圆形结构元素g长度20,通过式子(2)进行膨胀处理。在做干扰检测的过程中,随着干扰幅值的增大检测效果会得到提升。仿真发现,膨胀处理后原始信号f的峰值增大,并且尖峰变得也得到了展宽。
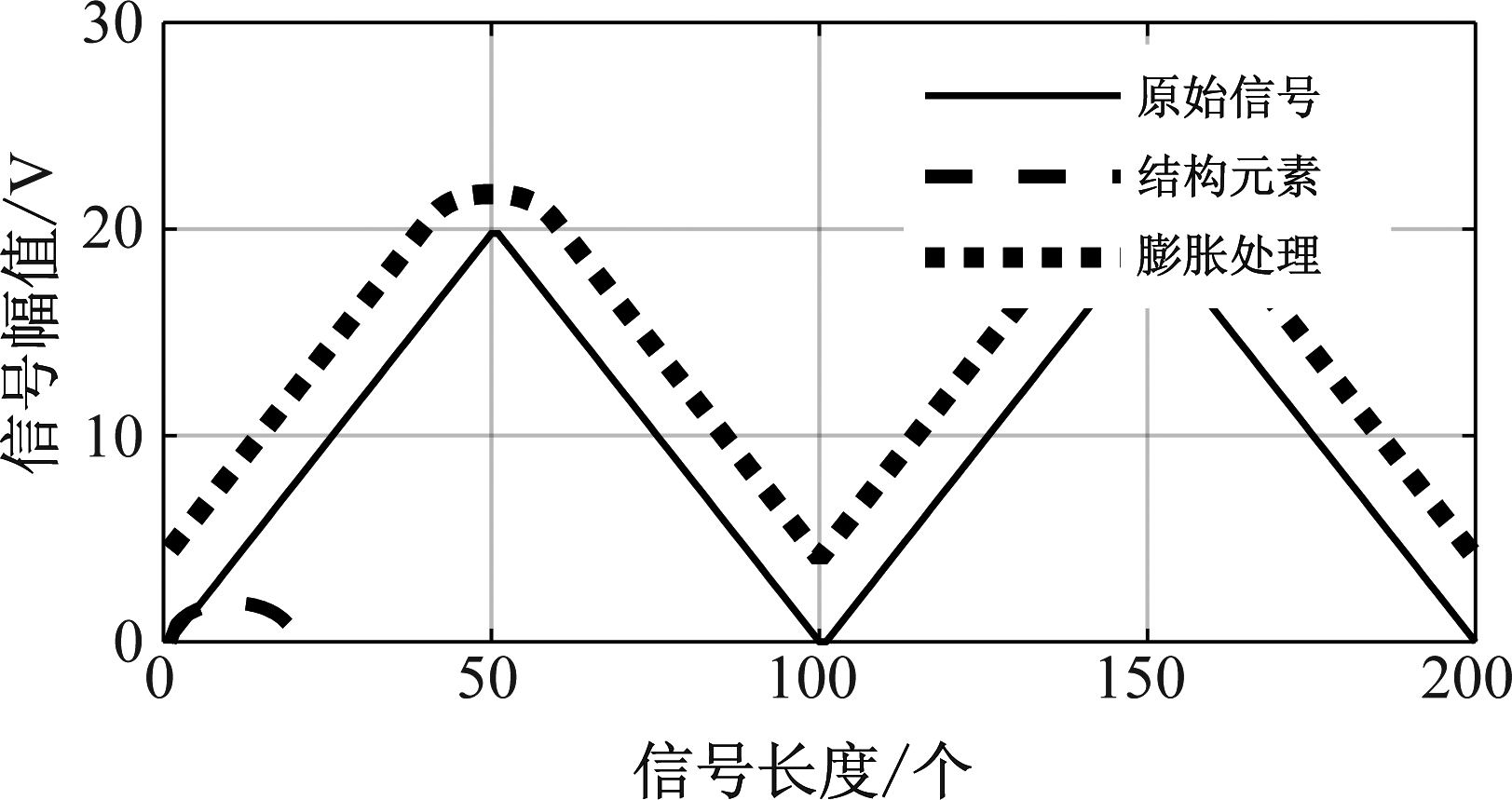
图3 膨胀运算的结果图
Fig.3 The graph of the result of the expansion operation
4.3 信号幅值分层,选通门限值
在仿真过程中我们发现,根据功率谱的幅值我们可以粗略的将信号分成噪声区、不确定区(噪声或者干扰)、干扰区,在仿真过程中,发现分的区域越多则仿真得到的效果越好,但是门限值的设置就越复杂。该文采用的分为4段,如图4所示。
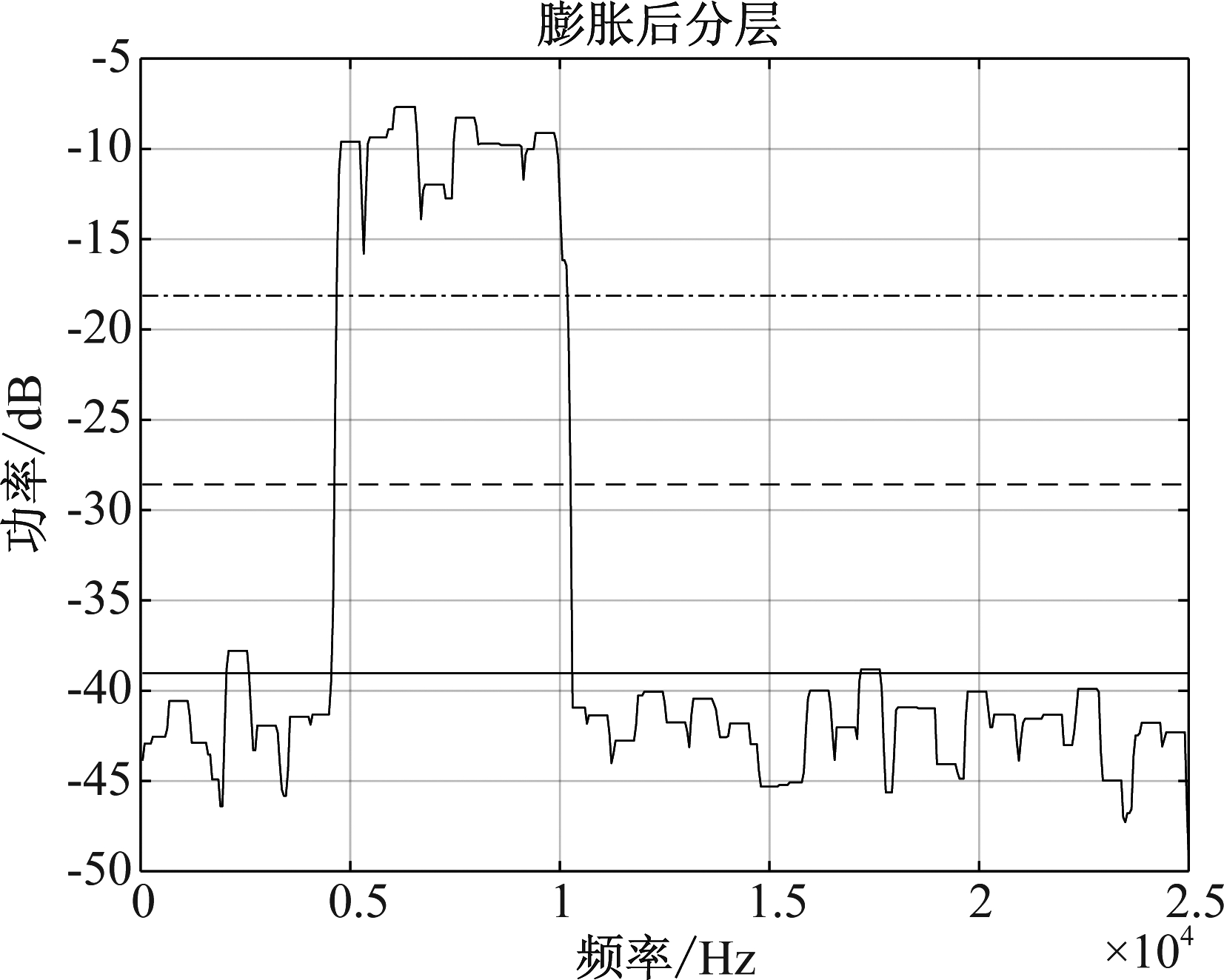
图4 膨胀后的功率谱分层处理
Fig.4 Delamination of power spectrum after expansion
具体实施过程[14]:
4.3.1 均分功率谱有效区间
有效区间指的就是功率谱从最小值到最大值的范围,通过式子(7)和(8)可得:
A=max(Pp(w))
(7)
B=min(Pp(w))
(8)
将此区间均分为4等份,每份的取值为![]()
4.3.2 求第i个区间点集
由下向上,各层范围区间可表示为[B,B+C),[B+C,B+2*C),[B+2*C,B+3*C),[B+3*C,A]。由此定义处于每个区间内的功率谱的值的频数分别为p1,p2,p3,p4。得到每个区间内的频率为d1=p1/(p1+p2+p3+p4)、d2=p2/(p1+p2+p3+p4)、d3=p3/(p1+p2+p3+p4)、d4=p4/(p1+p2+p3+p4),将频谱中所有的频点对应到不同的区间后,为自适应门限的设置提供条件。
4.4 门限选通开关设置
在仿真的过程中我们可以发现,我们通过不断地尝试,并参考一些文章[3,5],文献[3]中去除信号频段波形时的门限值:
t=a+(Fmax-Fmin)*0.2
(9)
(10)
通过计算频谱数据的极差然后乘以0.2再加上a得到门限值。其中,Mi表示频谱数据F中的前30%的频点幅值,a是对整个频谱数据F中前30%频点的平均值,Fmax为频谱数据F的最大值,Fmin为频谱数据F的最小值。
文献[5]门限值的计算方法:
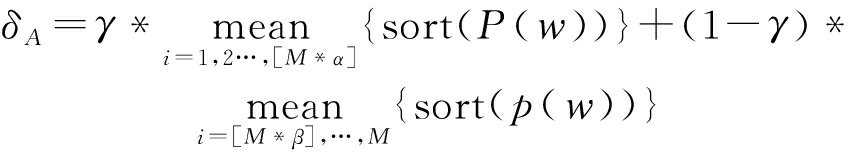
(11)
其中,0<α,β,γ<1为比例因子,sort(·)表示升序排列,符号[·]表示向下取整,mean(·)表示取均值。
因此得出门限值的设置是与功率谱的均值与极差是有联系的。设置门限的计算公式为
th=average+(Pp(w)max-Pp(w)min)*a
(12)
diff=Pp(w)max-Pp(w)min
(13)
其中,th表示最后的门限值,average表示的是所有功率谱的均值,Pp(w)max表示功率谱信号的最大值,Pp(w)min表示功率谱信号的最小值。a表示修正系数,可正可负。利用模型进行解释。
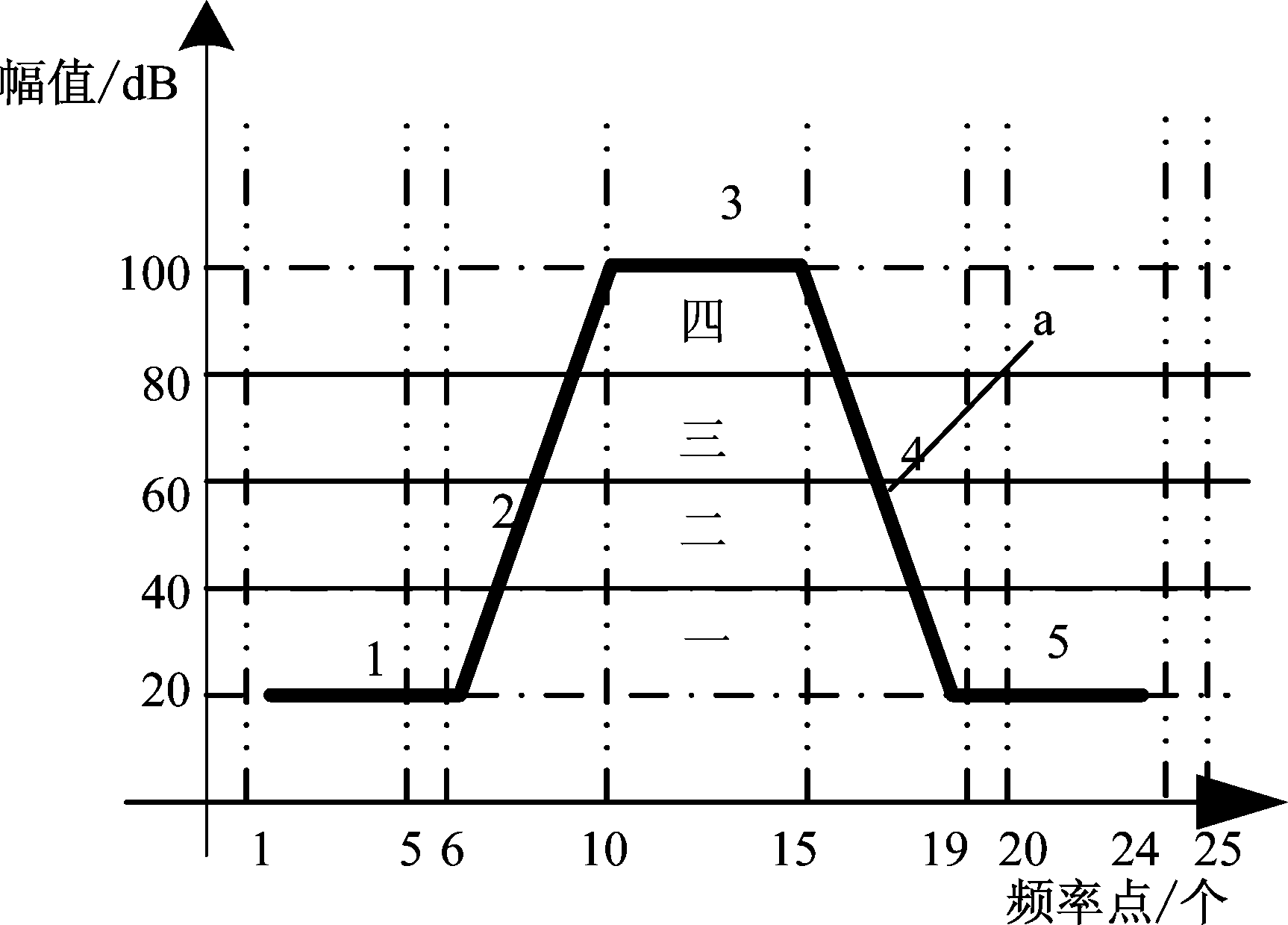
图5 预处理后信号模型
Fig.5 Post-preprocessing signal model
如图5,假设折线a近似代表膨胀滤波后的功率谱图,a有2300个数据点,极差diff为100-20=80,第1段的点数为![]() 同理第2段的点数为400且平均值为60,第3段的点数为500,第4段的点数为400且平均值为60,第5段的点数为500。因此可以计算出整个数据点的均值average为
同理第2段的点数为400且平均值为60,第3段的点数为500,第4段的点数为400且平均值为60,第5段的点数为500。因此可以计算出整个数据点的均值average为
(20*500+60*400+100*500+60*400+20*500)/2300=51.30
处于第2段和第4段的数据点分别被分成了四层,且每一层均匀分布100个点。因此,第一层有500+100+100+500=1200个点占总点数的52.17%,第二层有100+100=200个点,占总点数的8.7%,第三层有100+100=200个点,占总点数的8.7%,第四层有100+500+100=700个点,占总点数的30.4%。
为了最终不产生或者尽量少的产生虚警点数,设置的门限值选在70附近,因此采用极差diff来修正结果,
th=average+diff*a
(14)
那么a=(70-51.3)/80=0.234,由于在仿真的过程中生成的信号肯定没有模型完美,可以调整a的值更新门限。仿真过程中发现,如果diff的值大于某个值的情况下,门限值直接取一个固定值即可。
进一步分析:
d4的值近似反映了干扰的带宽大小。如果比较大说明干扰的带宽比较大并且干扰的功率比较大或者干扰数目比较多,如果比较小说明干扰的带宽比较小或者干扰数目较少,可以通过搜索确定干扰的位置。d3比较大的情况下,说明信号的毛刺比较多信号还不是很平稳。d2的值比较小的时候说明底噪的起伏不是很大或者干扰的带宽较小,信号还是在干噪比比较小的情况下,如果d2的值比较大时说明底噪起伏很大。d1越大说明底噪信号占据的频段越宽或者干扰信号不存在。
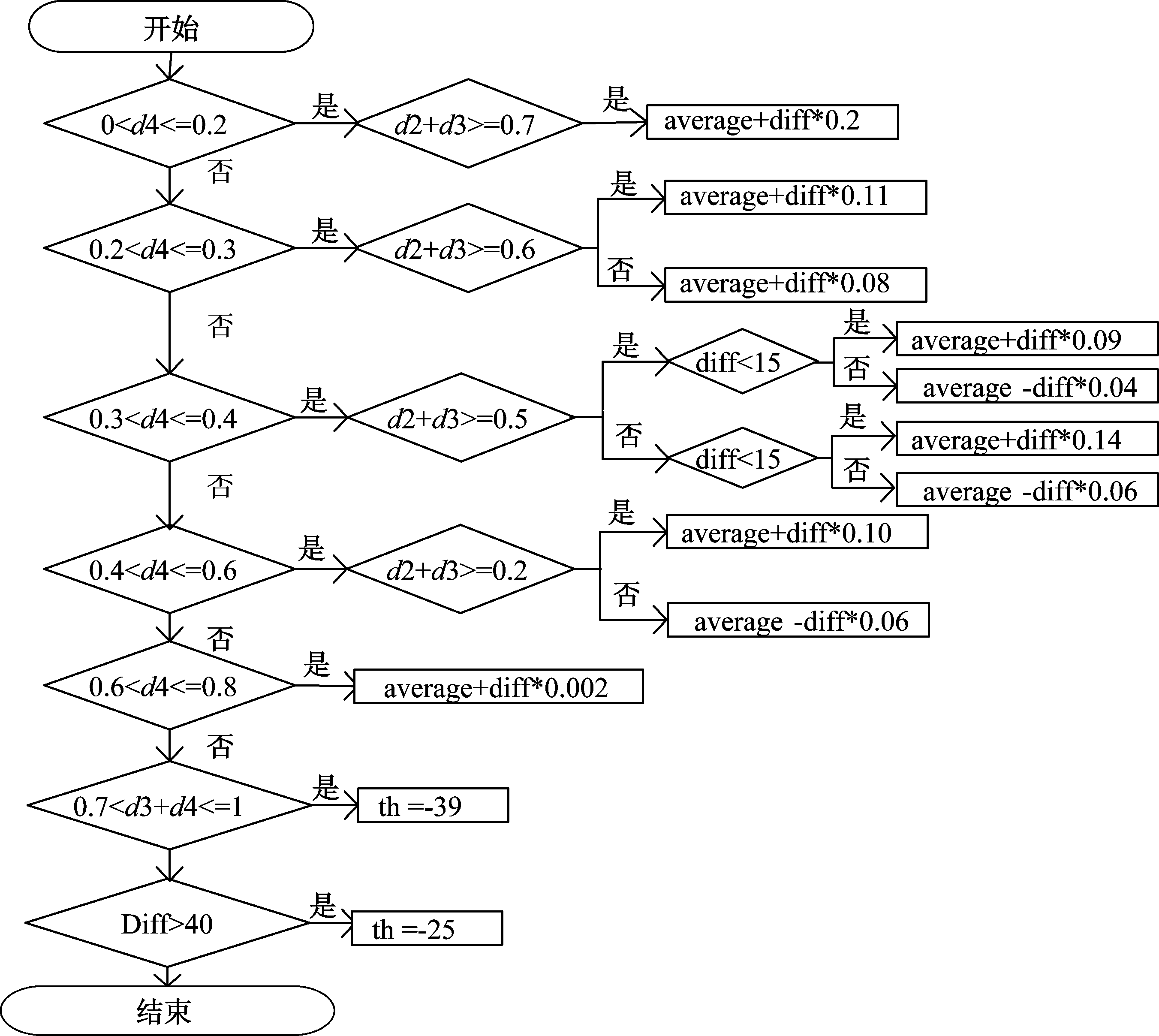
图6 门限选择的流程图
Fig.6 Flowchart of threshold selection
结合d3+d4的值分析,当d3+d4的值比较大的情况下可以大概得到干扰信号的频带宽度大,信号的均值还是很大的,如果直接采用均值作为门限值的话,可能会出现漏警的情况。再结合d2+d3的值,当d2+d3的值也比较大(此时说明干扰信号的干噪比比较小,频谱还不是很稳定),同时还要考虑d1、d4的大小,如果d1大于d4说明功率谱值还是比较集中在中间的两个区间,均值大小一般,如果选择均值作为门限,那么就会出现较多的虚警;如果d1小于d4,均值会整体比之前上移,但是也可能存在虚警或漏警的情况。
结论:要充分考虑到d1、d2、d3、d4的值的大小以及d3+d4、d2+d3、d2+d1的关系最终确定门限的值。
门限选通的流程图如图6所示。
5 性能仿真及分析
仿真的整个频段带宽为25 kHz,分别加入不同占有用信号带宽大小的窄带干扰信号。针对不同占有用信号带宽大小的窄带干扰相关公式定义,Nr为蒙特卡洛的总次数,Nd为此次干扰信号被检测出来的次数,Nf为某次检测出来虚警点数。由于信号在求功率谱的时候会出现频谱泄露,因此我们在干扰信号存在的范围左右分别增加500 Hz,即如果在这些频段检测到干扰存在,并且检测到的干扰的点数除以原本的干扰点的个数大于等于80%,我们就认为是检测成功记为1。虚警点数就是原本不是干扰但是检测为干扰的点数。
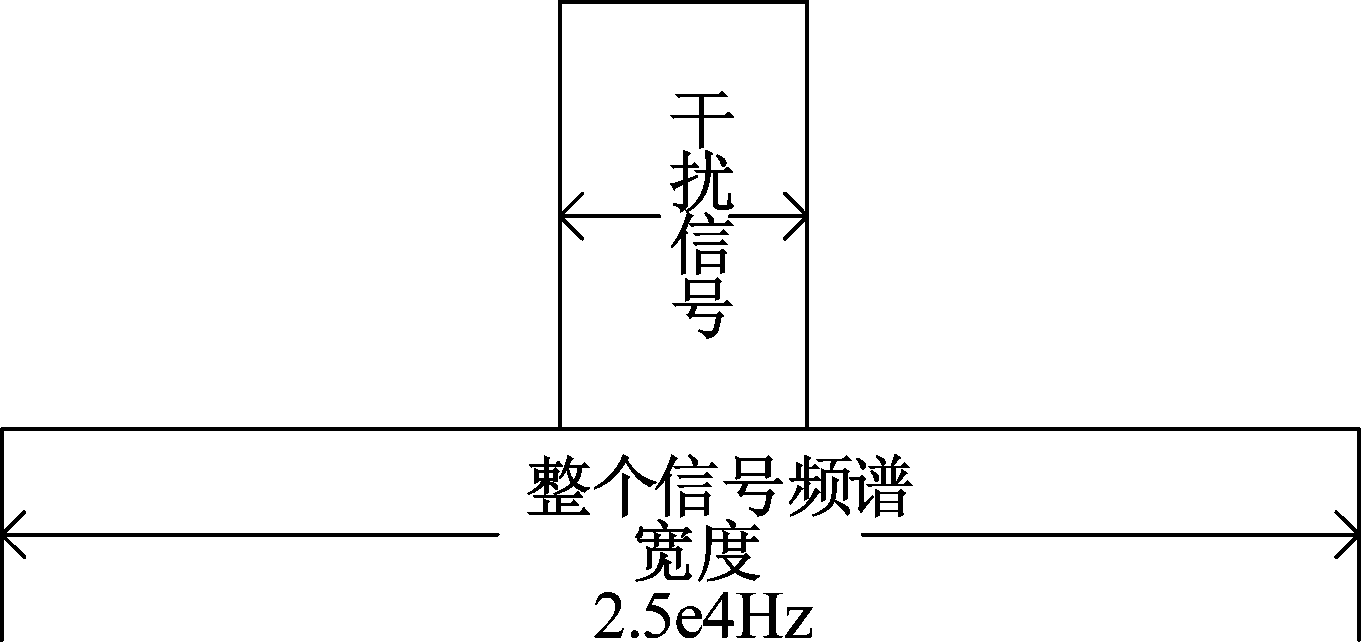
图7 干扰信号模型
Fig.7 Interference signal model
检测概率Pd的定义如下:
(15)
虚警点数Nf的定义如下:
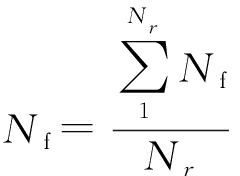
(16)
表示每次蒙特卡洛检测出来的干扰点数和除以蒙特卡洛的总次数。
5.1 针对不同长度的结构元素进行仿真分析
从文献[8-10]得知,扁平型结构元素在信号处理中得到更加广泛的应用,并且为了计算方便,采用幅度为0的扁平型结构元素对信号进行处理。图8、图9分别仿真了不同长度的结构元素在不同干噪比的情况下的检测概率与虚警点数。

图8 不同干噪比情况下不同长度结构元素的检测概率
Fig.8 Detection probability of structural elements with different length under different JNR
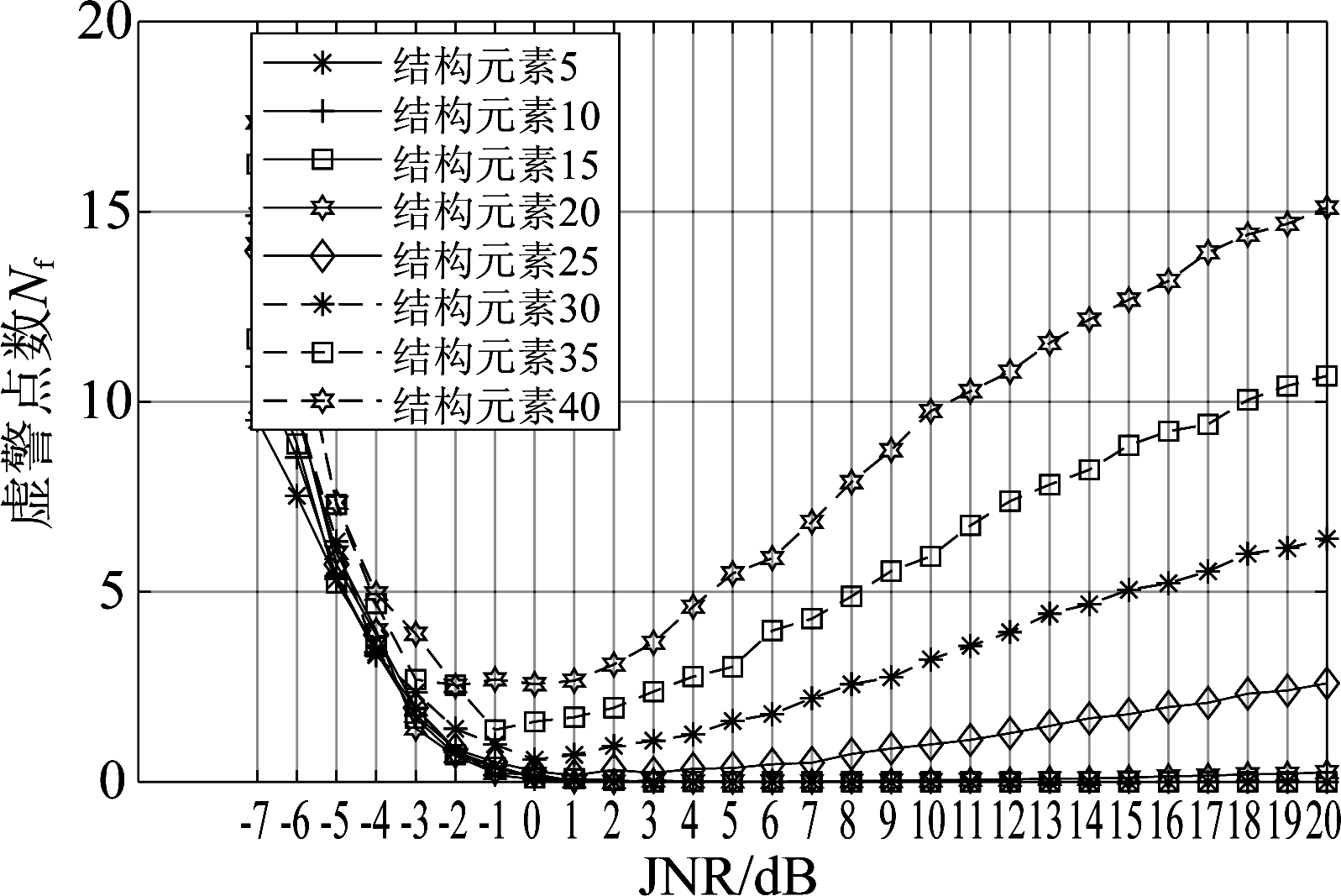
图9 不同干噪比情况下不同长度结构元素的平均虚警点数
Fig.9 Mean false alarm points of structural elements with different length under different JNR
图8可以得出,随着结构元素的长度不断地增加,检测概率也在不断地增加,呈现出更好地检测效果,结构元素长度为40时检测概率最好,而结构元素长度为5检测概率最低。
图9却得出与图8相反的结果,随着结构元素的不断增加,虚警点数也在不断地增加,特别是当结构元素的长度为40、35、30时,虚警点数大于4个。结合检测概率和虚警概率分析,结构元素长度选取25作为该文的分析。
5.2 针对不同窄带干扰的仿真分析
经过蒙特卡洛实验后,针对CME算法[12]和该文提出的自适应进行仿真对比,得到占有用信号带宽30%、50%、70%的窄带干扰的检测概率、平均虚警点数如图10和表1所示。
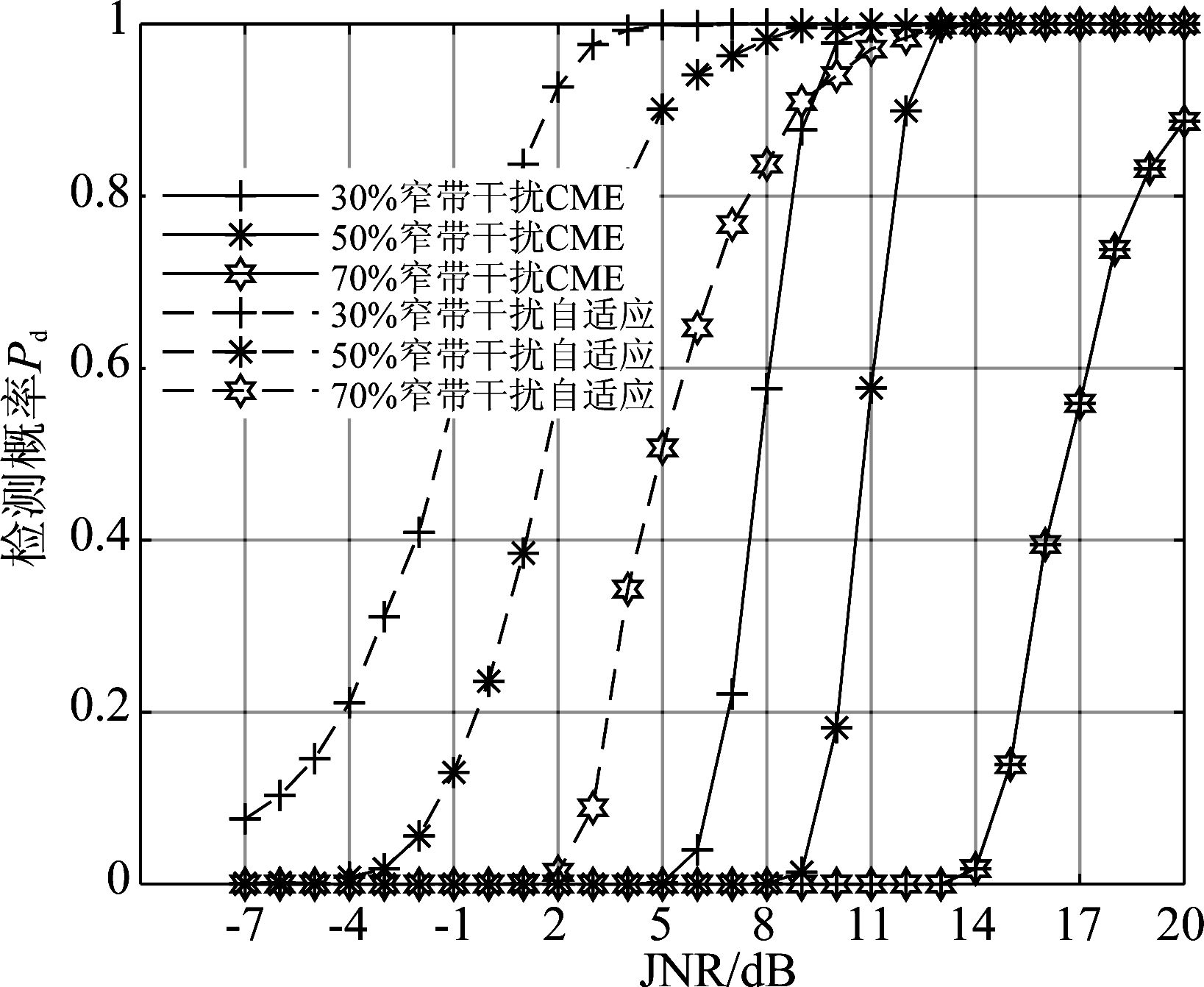
图10 不同窄带干扰分别使用CME、自适应算法的检测概率曲线
Fig.10 The detection probability curves of CME and adaptive algorithm were used for different narrowband interferences
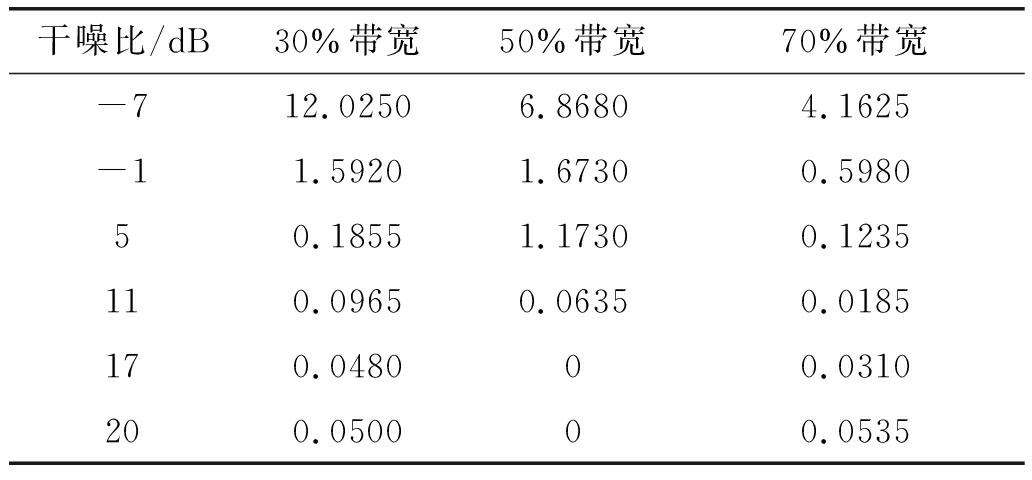
表1 不同占有用信号带宽大小的窄带干扰使用自适应门限的平均虚警点数
Tab.1 Statistics of average false alarm points under different relative bandwidth interference
干噪比/dB30%带宽50%带宽70%带宽-712.02506.86804.1625-11.59201.67300.598050.18551.17300.1235110.09650.06350.0185170.048000.0310200.050000.0535
从检测概率图和平均虚警概率点数表来看,干扰门限的设置与均值和极差两个量是有很大的关系的。
图10分别仿真了30%、50%、70%不同占有用信号带宽大小的窄带干扰,干噪比从-7 dB到20 dB的情况。从图上很容易看出,该文提出的自适应门限的检测效果相对于CME算法有明显的提高。其中占用有用信号30%带宽的窄带干扰自适应门限要比CME提高6 dB, 占用有用信号50%带宽的窄带干扰自适应门限要比CME提高4 dB,在占用有用信号70%带宽的窄带干扰的检测中,其中CME在干噪比达到20 dB时检测概率还未达到90%,而该文提出的自适应门限在干噪比达到8 dB时检测概率就达到100%。
表1不同干扰的平均虚警点数可以看出,随着干噪比的不断增加,不同占有用信号带宽大小的窄带干扰的平均虚警点数也不断减少,其中在干噪比为-1 dB时,不同窄带干扰的平均虚警点数就小于2个,本算法体现出了很好的性能。
6 结论
本文采用的应用形态学的通信信号自适应门限的干扰检测方法,首先通过对接收的信号进行功率谱计算,通过形态学中的膨胀处理,然后根据信号功率谱的分布情况,划分成4个不同的区间,根据每个区间的点数的分布,选通不同的门限值,实现门限的自适应,对检测不同带宽的干扰提供了方法。仿真结果表明对于不同占有用信号带宽大小的窄带干扰、不同干噪比下的干扰检测概率、虚警点数情况,在低复杂度的条件下,对噪底复杂、带宽不断变化的干扰具有很好的检测效果。
[1] Appleton S. Proceedings of the first international workshop on Technology and policy for accessing spectrum[C]∥International Workshop on Technology & Policy for Accessing Spectrum. ACM, 2006.
[2] Deshmukh M V, Oza S. Spectrum Sensing based on Energy Detection for Cognitive Radio using FPGA[J]. International Journal of Engineering Research and Technology, 2019, 8(5): 37-39.
[3] 白晓东. 基于底噪拟合的Ku频段卫星频谱信号检测方法[J]. 南京邮电大学学报: 自然科学版, 2019, 39(3): 51-57.
Bai Xiaodong. Noise based on bottom fitting Ku band satellite frequency spectrum signal detection method[J]. Journal of Nanjing University of Posts and Telecommunications: Natural Science Edition, 2019, 39(3): 51-57.(in Chinese)
[4] 刘阿娜, 李琳, 于宏毅, 等. 一种基于路由信息能量有效的无线传感器网MAC协议[J]. 电子与信息学报, 2008, 30(1): 29-32.
Liu Ana, Li Lin, Yu Hongyi, et al. An effective MAC protocol based on routing information energy for wireless sensor networks[J]. Journal of Electronics and Information, 2008, 30(1): 29-32.(in Chinese)
[5] 王登超, 江桦, 裴立业. 基于形态学的通信信号搜索预处理方法[J]. 通信技术, 2017, 50(3): 416-420.
Wang Dengchao, Jiang Hua, Pei Liye. A preprocessing method of communication signal search based on morphology[J]. Communication Technology, 2017, 50(3): 416-420.(in Chinese)
[6] 胡婧, 边东明, 谢智东, 等. 应用形态学滤波的卫星通信窄带干扰检测新方法[J]. 计算机科学, 2016, 43(10): 120-124.
Hu Jing, Bian Dongming, Xie Zhidong, et al. A new method for narrowband interference detection of satellite communication using morphological filtering[J]. Computer Science, 2016, 43(10): 120-124.(in Chinese)
[7] 李敏乐, 毕大平, 韩佳辉. 基于形态学运算的子带频谱检测算法[J]. 探测与控制学报, 2017,39(4):49-53.
Li Minle, Bi Daping, Han Jiahui. Subband spectrum detection algorithm based on morphological operation[J]. Chinese Journal of Detection and Control, 2017,39(4):49-53.(in Chinese)
[8] 刘姝. 数字形态学在信号处理方面的应用研究[D]. 大连: 大连理工大学, 2006.
Liu Shu. Application of digital morphology in signal processing[D]. Dalian: Dalian University of Technology, 2006.(in Chinese)
[9] 李伟. 分布式微机母线保护的研究[D]. 成都: 西南交通大学, 2008.
Li Wei. Research on distributed microcomputer bus protection[D]. Chengdu: Southwest Jiaotong University, 2008.(in Chinese)
[10] 郭晓鑫, 刘立, 冯志鹏. 数学形态学在信号处理中的应用综述[C]∥全国虚拟仪器大会, 2009.
Guo Xiaoxin, Liu Li, Feng Zhipeng. Application of mathematical morphology in signal processing[C]∥National Virtual Instrument Congress, 2009.(in Chinese)
[11] 张杰. 基于数学形态学的故障行波测距方法研究[D]. 昆明: 昆明理工大学, 2005.
Zhang Jie. Study on fault traveling wave ranging method based on mathematical morphology[D]. Kunming: Kunming University of Science and Technology, 2005.(in Chinese)
[12] Henttu P, Aromaa S. Consecutive mean excision algorithm[C]∥IEEE Seventh International Symposium on Spread Spectrum Techniques & Applications, 2002: 450- 454.
[13] 张峰, 石现峰, 张学智. Welch功率谱估计算法仿真及分析[J]. 西安工业大学学报, 2009, 29(4): 353-356.
Zhang Feng, Shi Xianfeng, Zhang Xuezhi. Welch power spectrum estimation algorithm simulation and analysis[J]. Journal of Xi’an Polytechnic University, 2009, 29(4): 353-356.(in Chinese)
[14] 张玉龙, 张更新, 胡婧, 等. 一种基于统计直方图的信号检测算法[J]. 军事通信技术, 2017(1): 28-32, 36.
Zhang Yulong, Zhang Gengxin, Hu Jing, et al. A signal detection algorithm based on statistical histogram[J]. Military Communication Technology, 2017(1): 28-32, 36.(in Chinese)




