1 引 言
图像融合技术可将某一场景多种不同传感器获得的两幅或多幅图像集成并有机的融合成一幅图像,融合后的图像能够综合每幅输入图像间的互补信息,同时减少和降低图像之间的冗余信息,从而实现对场景更加全面和准确的描述,便于人眼和机器的理解和感知[1]。红外和可见光图像融合是图像融合的一个重要分支,现阶段被大量的应用到军事武器装备研发和我们的日常生活中[2]。比如:目标探测,侦察,情报收集和视频监控等。红外图像呈现的是场景中所有物体的热辐射值,对场景中一些目标的边缘和轮廓特征刻画较为明显,且不易受光照、烟雾、遮挡等条件的影响,但是红外图像空间分辨率较低、图像对比度差、细节和纹理信息不丰富;可见光图像是场景在自然光条件下的反射图像,包含了场景的边缘、纹理等细节信息,但是受场景照明、环境等影响较大。因此,红外与可见光图像进行融合,是充分利用了这两种图像间信息的互补性[3],全面和准确地对场景中的环境和目标信息进行描述。
现有的红外和可见光图像融合算法有很多种,其中,稀疏表示的图像融合方法在这些年来因模型灵活多变和字典构建多样化而受到很多学者的青睐[4]。稀疏表示的思想是一个信号在进行处理时,可利用少量的字典原子进行线性组合展开和表示。Li等在论文[5]中首先提出在图像融合领域使用稀疏表示的方法,之后,许多学者也进行了尝试,提出了多种利用稀疏表示的融合方法,使融合结果的精度进一步提升。但是,许多稀疏表示的算法通常是利用图像块为单位,将图像分成小图像块并进行融合,容易造成结果出现很多孤立的块状模糊区域。还有一些算法在采样的过程中,采用滑动窗工具[6-7],减少融合后所出现的局部模糊和孤立效应,但会造成融合后的图像对比度有所下降,丢失相关细节信息,同时使融合方法的计算复杂度大幅度增加。
本文提出利用结构化和一致性约束的稀疏表示模型,进行红外和可见光图像融合算法,该算法将所有源图像的图像块进行联合并采用主成分分析(PCA)算法[1]进行学习得到字典,然后构建结构化稀疏表示模型,对源图像进行结构化稀疏表示,使图像分解为背景和显著性(误差)信息,再分别设计融合规则,对背景信息和显著性信息分别进行融合并利用字典重构出融合图像,较大程度上提高了融合结果的可靠性。这其中,为了降低局部模糊,减少信息丢失,本文首先对源图像块采用特征相似性和空间位置关系进行了结构化划分,本着处于相同结构层的图像块具有相似的稀疏特性的原理,以结构树的形式对处于同层之间及层与层之间的图像块综合进行稀疏表示,并在稀疏模型中引用了拉普拉斯一致性约束项,利用该约束项对结构化稀疏表示后得到的显著性信息施加约束,使显著性信息能够整体的保留在融合图像中,从而进一步提取并凸显输入图像中的显著特征。
2 基本理论
2.1 稀疏表示与鲁棒稀疏表示模型
稀疏表示是以小波理论为基础而提出的[8],对信号表示时,可以利用过完备字典中的原子根据信号本身的特点进行重构,因为字典是冗余的,所以重构系数是稀疏的,该系数的稀疏度越强,表示效果越好。多年来,因高效的信息表示和提取能力,稀疏表示得到了大量的应用。稀疏表示是基于信号可利用少量的字典原子进行线性组合表示[9]。给定信号x∈Rn,和过完备字典D=[d1,…,di,…,dK]∈Rn×K,K为字典D的原子个数,di∈Rn是字典中的第i个原子,存在系数z∈RK,可利用少数字典D中原子线性组合来近似重构原始信号y的,即x≈Dz,z为稀疏表示系数。其数学表示公式如下:
(1)
其中,||z||0为l0范数,表示向量z中所包含的非零元素个数,ε为容许误差因子,控制重构精度。
在图像融合中,为了能够对图像进行完全重构,同时突出细节信息,Zhang等人在[10]中将容许误差转换为稀疏重构误差,并进行编码计算,得出图像中的背景信息和显著性信息,其模型如公式(2)所示:
(2)
其中,Z是X基于字典表示的系数矩阵,Z具有稀疏特性,式中对Z进行了稀疏约束。E是稀疏的误差,||·||2,0为l2,0范数,是对E施加列稀疏约束。稀疏表示后,原始图像数据被分解为两部分,其中一部分为稀疏的背景,另一部分为稀疏的显著性(误差)信息[10]。显著性信息E包含较为丰富的结构和边缘信息,从而能够较好的提取图像中的显著性信息,本文也将E称为显著性信息矩阵。
公式(2)的优化问题是一个NP难问题,通常可利用凸松弛算法[11]进行求解,即在满足一定的条件时,公式(2)中l0范数可通过凸优化转化为l1范数进行求解,即:
(3)
2.2 基于图论的一致性约束
在图论中,可以利用顶点和临近关系对数据集的几何结构进行建模[12-13]。在图像处理中,给定一个数据集X=[x1,…,xi,…,xN]∈Rn×N,包含N个图像子块,每个子块可以当作顶点,可构建出该数据集的加权图G={X,W},其中,
为权重矩阵,wij为第i个点与第j个点的权重值,该权重描述的是加权图G中任意两个顶点的临近度或相似程度,利用拉普拉斯进行相似性映射时[12],一般假设,若数据X中的两个数据点xi和xj,是相互“邻近”的,则该数据点在利用相同的字典基表示的过程中,其分解结果也是“邻近”的。可利用最小化差值的方式进行映射和实现:
(4)
||xi-xj
表示xi和xj之间的欧式距离,可用来衡量xi和xj之间的“临近性”,wij为权重值,定义为:
(5)
上式中,t为离散参数,即高斯核,在实验中,本文将t设置为1。
利用式(5)建立权重,将公式(4)可映射到稀疏表示结果中,使相似的图像区域,其表示误差也具有相似性,即通过映射和矩阵变换,转换为:
Tr(ECET)-Tr(EWET)=Tr(ELET)
(6)
其中,E=[ε1,ε2,…,εN]∈RK×N在为X系数分解误差,Tr(·)表示对矩阵求取迹,即矩阵对角线之和。L∈RN×N为拉普拉斯约束因子,L=C-W,W∈RN×N是对称矩阵,通过数据点之间的权重值进行构建,即为:W(i, j)=wij,C∈RN×N,是对角矩阵,可利用权重矩阵进行计算,即:
对公式(6)进行最小化约束,可使两个具有相似特征的数据点,其系数误差也能够具有一定的相似性,将数据集的相似性传递到表示结果中,因此,公式(6)通常称为一致性约束项[13]。
3 融合算法
3.1 算法框架
本文算法是利用结构化和一致性约束的稀疏表示模型进行红外和可见光图像融合,过程包括:源图像分块和向量化,字典的构建,树形结构与拉普拉斯矩阵的建立,模型的构建与编码,构造融合规则并进行融合图像的重构等过程,算法整个框架如图1。
3.2 构建源图像对应的向量化矩阵
源图像首先被划分为N个相互无重叠的图像子块[14]。划分时,选用大小为n×n的一个窗口,采用步长n,从左至右,由上到下,对输入图像IA和IB进行的遍历和复制,对每幅源图像获取N个图像块,再将这些子图像块垂直排列成向量的形式,并组合成矩阵XA和XB,其中
表示源图像第i个图像块所对应的向量,为该矩阵的第i列,
的大小是根据图像大小、计算能力和图像结构信息综合进行选取的,如果选取的n值太小时,组合成的图像矩阵维数较多,会增加计算量,同时,图像块较小时,将图像中一些边缘或显著性信息分散到不同的图像块中,在进行分解提取之后,会造成融合结果丢失一些重要的结构信息。若选取的n值太大,各图像块在分解后提取信息时,均匀性较差,融合图像中块与块之间信息会出现不连续性,造成大面积模糊和信息的丢失。根据以往已发表的文献以及相关实验[3,6,10],在图像大小适中(128×128～512×512之间)时,图像块边长选择3～9之间,可达到较好的效果。为了提高计算效率,同时能够较好的提取出图像中的结构信息,保证算法的高效性,本论文根据实验,选取n=7。
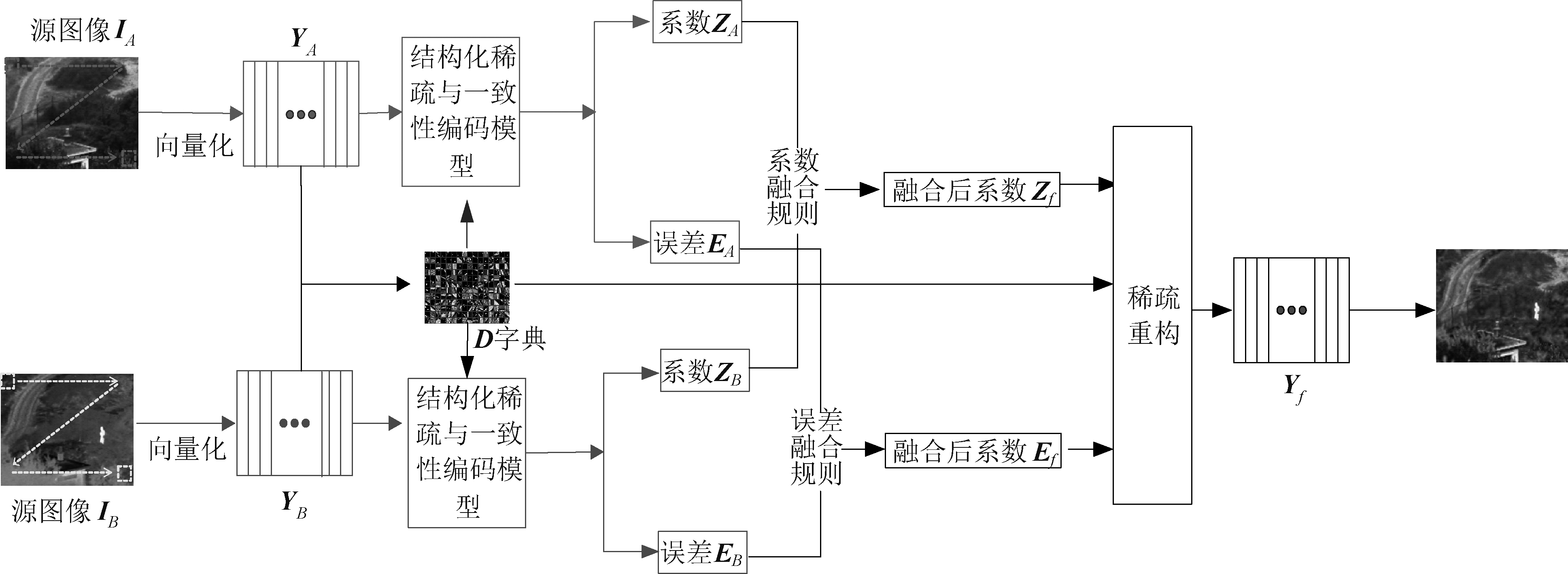
图1 融合算法框架
Fig.1 The framework of fusion algorithms
3.3 构建稀疏表示字典
一个紧凑并且结构丰富的字典,不仅拥有较好的表示能力,同时能够大幅度的降低运算复杂度。最早一些学者采用固定基(离散余弦变换DCT[5]、离散小波变换DWT等)作为字典进行图像表示,虽然简单易行,但字典的表示能力较差。之后一些算法,通过对自然图像或原图像利用K-SVD[15]、MOD[16]等算法学习得到的,虽然具有较好的表示能力,但字典冗余度较高,大幅度增加了计算量。为了提高字典表示能力并降低冗余度,本文采用一种跨模态联合的方式进行字典的构建,将两种模态图像联合起来,进行降维并生成字典。同一场景的多模态图像包含了融合图像所有的结构信息,但是他们并不均匀的分布在各个原图像上,因此,本文选用两幅原图像作为模板资源进行字典学习,提高了字典的自适应性。将两幅原图像分解为若干个子图像块,然后对所有的子图像块采用K均值算法进行聚类,使得结构信息相似的图像块聚为一类;再对每一图像块类采用主成分分析(PCA)提取出主要的能量较高的信息,丢弃一些冗余的,不重要的信息,从而保留了丰富的结构信息,并且大幅度压缩了数据量;最后再将所有类利用PCA算法得到的矢量数据进行组合,建立了稀疏表示字典。因为进行了聚类,并且利用PCA算法进行了降维和信息提取,因此,本文方法构建的字典原子个数较少且结构更丰富。
图2 利用K-SVD建立的字典和本文提出方法建立的字典比较:(a)传统K-SVD算法所建立的字典,(b)本文字典
Fig.2 Comparison between the dictionaries constructed by K-SVD algorithm and the method proposed in this paper:
(a) is the dictionary constructed by K-SVD algorithm,
(b) is dictionary constructed by the method proposed above
图2为传统字典学习与本文采用的字典学习方法得到的字典进行直观的对比,图2(a)为传统的利用K-SVD对原图像进行的字典学习得到的过完备字典直观表示图,图2(b)是本文所采用的跨模态联合聚类方法所得到的字典,从图中可以看出,本文采用的字典构建方法得到的字典原子个数较少,同时结构更丰富。
3.4 模型的构建和编码
为了缓解“块效应”,提高融合精度,本文在鲁棒稀疏表示模型的基础上结合了结构化[17]先验和一致性约束项[14]。结构化先验是利用特征相似性构建出一个树形结构索引,在进行编码时对稀疏表示系数按索引树进行结构化联合编码,处于同一层次的图像块,因其特征具有相似性,且空间位置相近,在利用字典进行重构的过程中,较大程度上具有相似的稀疏特性,即表示结果具有一致性。同时,本文利用鲁棒稀疏表示模型将源图像分解为背景信息和显著性信息E,若原图像某些“子块”特征相似,其显著性信息E也具有一定的相似性,因此,本文根据图像块的特征相似性构建了拉普拉斯一致性约束项[13],对相似区域的显著性信息加以约束。
3.4.1 树形结构的构建
索引树T的构建[17]同样是基于图论的思想,其中,整幅图像看作是图,对图像进行块划分后,每一个子图像块看作是一个节点,利用节点之间的相似度进行分割和合并。对于空间相邻的一对子图像块(pi,pj),其相似度权重计算如下:
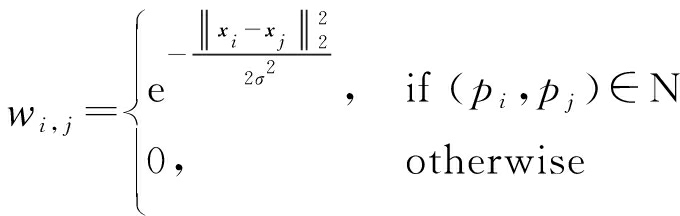
(7)
其中,xi和xj为子图像块pi和pj构成的列向量。N代表(pi,pj)空间相邻。根据子图像块之间的权重,采用基于图论的图像分割算法[18]。对每个结构层,设置一个区域融合的阈值θ,得到不同尺度上图像分割与相互组合的结果,下一层的分割将当前层分割结果作为基础。最终,得到一个多层的从精细到粗糙的结构化分割结果,称之为图像的树形结构划分。如图3所示。
图3中,
表示结构化分割中,第i层的第j个节点,上层节点是下层结点的双亲,同一层节点之间是互斥的,不重叠。
3.4.2 权重矩阵的构建
某一图像块中包含的显著性信息,和其他具有相似特征的图像块,较大可能具有相似性。即当某些图像块特征相似时,这些图像很可能具有相似的显著性信息,而这些显著性信息是多模态图像中所包含的较为重要的信息,应尽可能的保留在融合图像中,因此,在模型求解时,对显著性信息进行一致性约束,对最终的融合质量具有至关重要的作用。为了建立一致性约束,首先需要特征较为相似的图像块聚为一类,本文以树形结构的第二层作为聚类结果,然后利用图论的方式来约束这种相似性,即利用2.2节中提到的方法构建出一致性约束项。以图像块为图的顶点,建立出相似性权重矩阵:
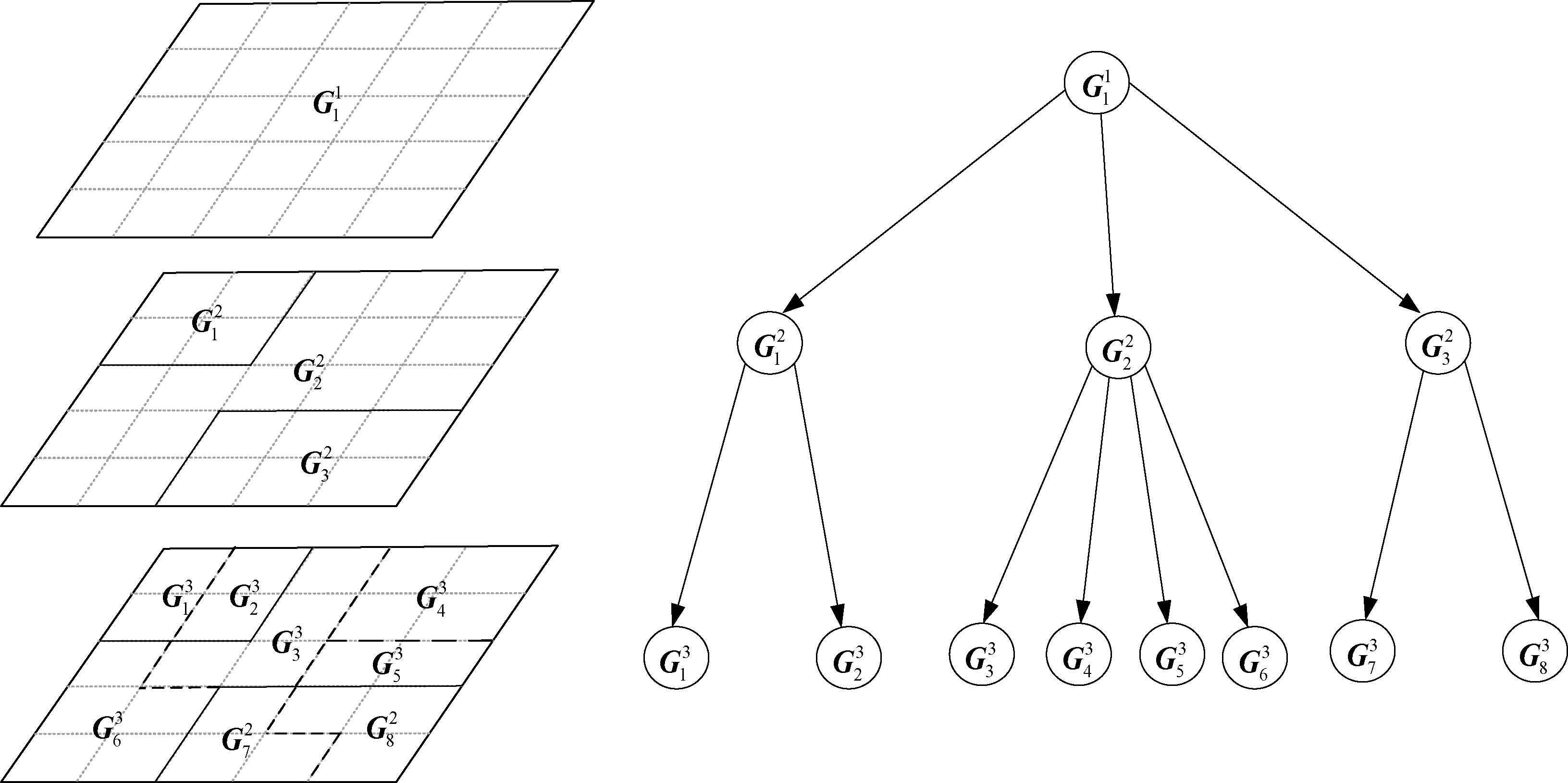
图3 结构化索引树的构建过程
Fig.3 Construction of structured index tree
(8)
3.4.3 结构化稀疏表示与一致性约束模型
为了进一步增强模型的表示能力,提高融合结果的准确性,本文在传统鲁棒稀疏表示的基础上,增加了结构化先验和一致性约束项,得到结构化稀疏表示模型,将源图像分解为背景信息和显著性信息(误差)。如公式(9)所示:
s.t.X=DZ+E
(9)
其中,X为输入的源图像向量化后得到的矩阵,D为构建的字典,Z表示为系数矩阵,E为误差矩阵,也称为显著性信息矩阵,
为子矩阵
的l1范数,能够约束子矩阵
的稀疏特性。
表示在每一个尺度下,处于相同子区域的图像块,在表示时,其系数有相似的稀疏特性。||E||2,1是对E进行l2,1范数约束,表示对E进行列稀疏约束,L为拉普拉斯矩阵,由公式(6)进行构建。
3.4.4 模型的优化和求解
公式(9)可以采用线性迭代方向法[19](LADMAP)进行求解,引入变量J,能够转化成如下等价优化模型:
s.t.X=DZ+E Z=J
(10)
该模型优化可通过增广拉格朗日乘子法进行求解,即最小化下式:
〈Y1,X-DZ-E〉+〈Y2,Z-J〉+
(11)
其中,Y1,Y2是拉格朗日乘子,μ>0是惩罚因子,〈A,B〉表示矩阵A和B内积。优化时,通过固定其余变量,每次更新其中某一个变量,该拉格朗日函数求解过程可转换为以下求解优化问题:
(1)更新变量J
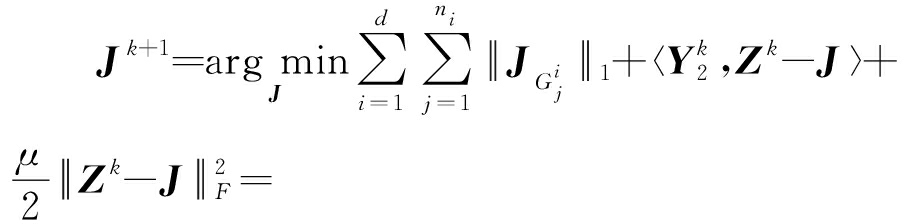
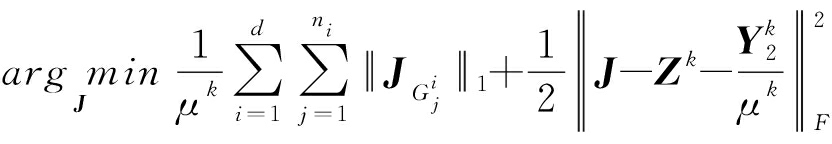
(12)
在对树形结构求解时,将第i层的第j组采用公式表示,如下:
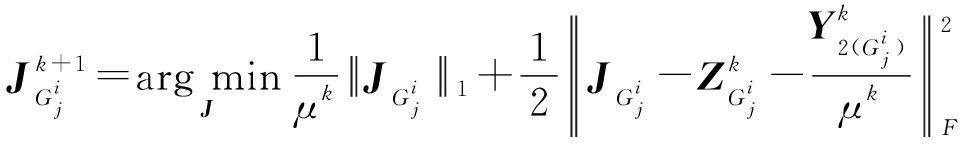
(13)
为了求解J,定义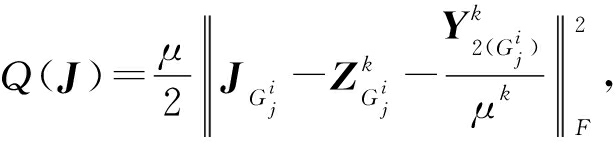
并将Q(J)在J的上次迭代结果处进行一阶泰勒展开得到(为简单表示,在此省略下标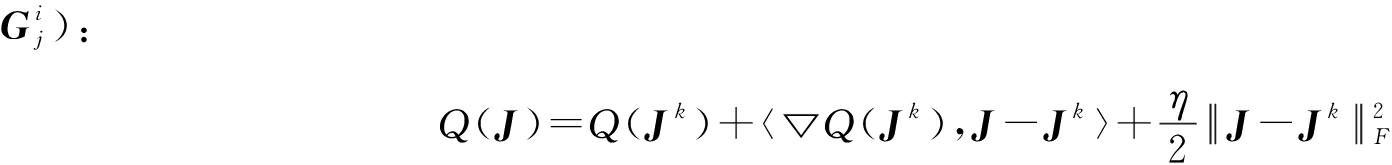
(14)
公式(14)的优化问题转化为公式(15)的优化问题:
〈▽JQ(Jk),J-Jk〉=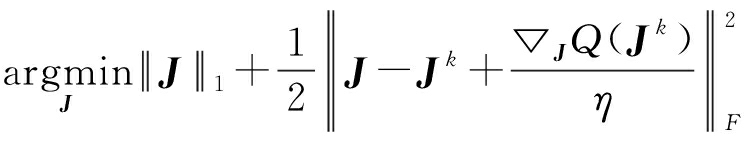
(15)
其中,
表示Q(J)关于J的导数,〈A,B〉表示矩阵A和B的内积,η=(2*||Y2||F+μ)*1.02,公式(15)的优化问题存在如下最优解[10]:
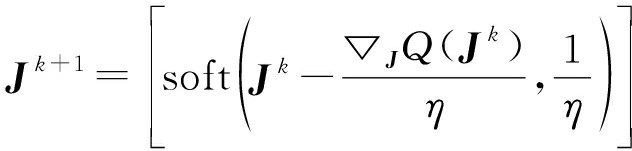
(16)
soft(G,δ)表示软阈值函数,定义方式和公式如下:
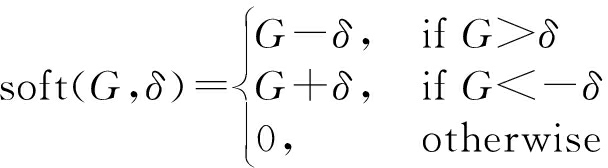
(17)
(2)更新变量Z
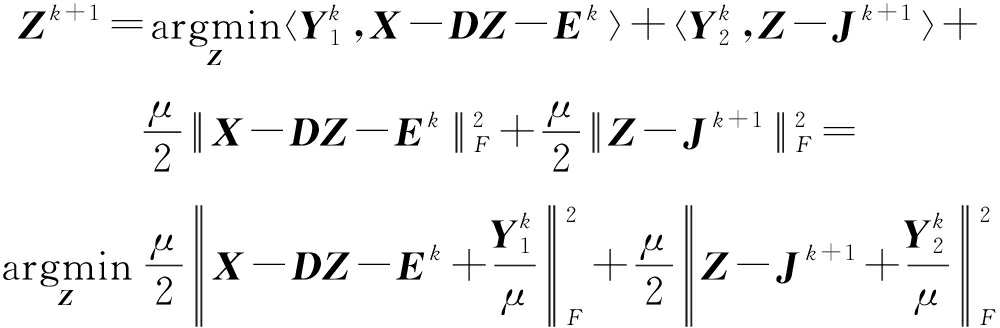
(18)
该式为严格的凸函数,对齐求导并变换可得:
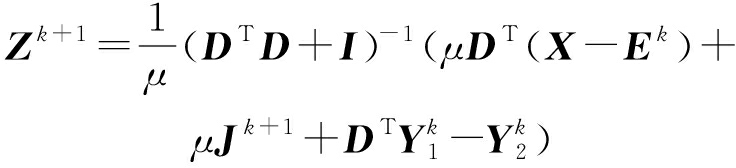
(19)
(3)更新变量E
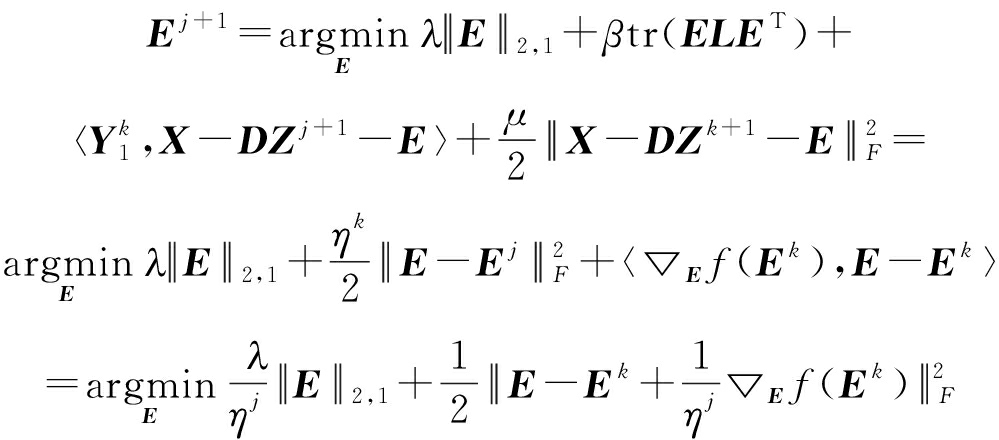
(20)
其中,
是f(E)对E求偏导。
该子优化问题存在闭式解[20]:
Ej+1(:,i)=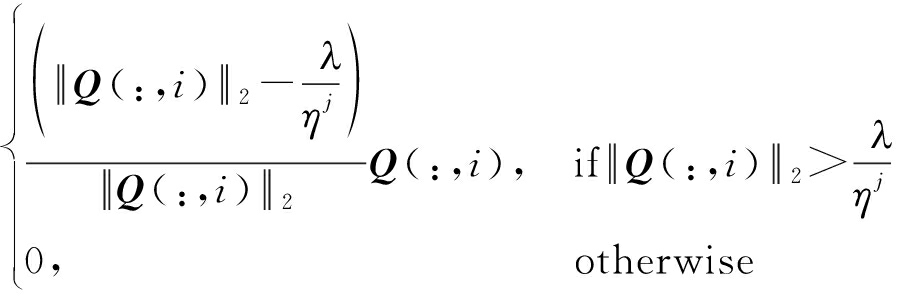
(21)
其中,
和Q(:,i)分别代表E和Q的第i列。
上述模型,在求解后,其编码计算过程见算法1。
算法1:结构化和一致性约束的稀疏表示模型输入:(a)向量化数据集X,表示字典D,参数迚和β,树形索引T={Gji},最大迭代次数itermax以及全局的容许误差ε。(b) 算法初始化:Z0=J0=0,E0=0,Y01=0,Y02=0,μ=10-6,ϕ=1.1,μmax=106,ε=10-8,itermax=103。迭代步骤:(1) 固定其他变量,更新J:Jk+1=soft Jk-▽JQ(Jk)η,1η (2) 固定其他变量,更新Z:Zk+1=1μ(DTD+I)-1(μDT(X-Ek)+μJk+1+DTYk1-Yk2)(3) 固定其他变量,更新E:Ej+1(:,i)=(Q(:,i)2-迚ηj)Q(:,i)2Q(:,i), ifQ(:,i)2>迚ηj0, otherwise(4) 更新拉格朗日乘子Y1和Y2:Yk+11=Yk1+μk(X-DZk+1-Ek+1),Yk+12=Yk2+μk(Zk+1-Jk+1)(5) 更新μ:μk+1=min(μkϕ,μmax)(6) 检查是否满足收敛条件maxX-DZk+1-Ek+1∞<ε andmaxZk+1-Jk+1∞<ε·∞代表矩阵的无穷范数,满足式(6)给出的收敛条件,迭代结束;否则,继续执行步骤1～6。输出:稀疏表示系数Z和误差E。
3.5 融合规则的选取
利用模型对源图像结构化稀疏求解之后,DZ项描述多模态(红外和可见光)图像背景信息,E描述的是图像的结构(显著性)信息。背景信息包含了红外和可见光图像的纹理特征,而显著性信息中包含了图像的结构和边缘特征。两部分都包含了图像的一些本质信息,因此,需要对背景信息和显著性信息分别进行融合规则的选定。DZ是背景信息,D为字典,包含了各种单元结构信息,其中,Z越大,代表背景结构信息越丰富,因此,本算法中,采用系数Z的l2范数取大作为背景部分的融合规则。如公式(22)所示。其中,A和B分别代表两幅源图像。
(22)
在图像融合中,显著性信息代表图像所表达的重要信息,为了防止信息丢失并突出部分细节信息,进行显著性信息融合时,本算法将两部分信息进行叠加,得到最终融合图像的显著性信息部分,如公式(23)所示。
Ef=EA+EB
(23)
最终,我们利用稀疏表示系数Zf,字典D和叠加后的显著性信息Ef反重构得到最终的融合后图像子图像块的向量化矩阵Yf。
Yf=DfZf+Ef
(24)
对矩阵Yf进行块状重构并按图像块索引进行重构,得到最终的融合图像。
4 实验与分析
本节在Matlab2016a环境下,通过一系列仿真实验,验证本文提出算法的有效性。首先是进行字典的有效性测试,通过不同方式构建字典,对选取的五组红外和可见光图像进行融合,从客观上对本文字典的有效性进行测试。其次,通过与现有的一些算法进行比较,主要包括:非负稀疏表示算法(NNSR)[21]、自适应稀疏表示算法(ASR)[22]、引导滤波(GFF)[23]和隐式低秩表示算法(LatLRR)[24]和稀疏表示算法(SR)[5],对同一组红外和可见光图像进行融合,从主观上验证本文算法高效的信息提取和保持能力。最后利用这些算法同时对五组红外和可见光图像进行融合,从主观和客观上综合对融合结果做了分析和比较。客观比较时,主要选用五种指标进行定量比较,包括:结构信息保留度QAB/F[25]、边缘结构信息相似性Qy[26]、归一化互信息NMI[27]、人类视觉感知特征QCB[28]和时间Ts。这五种指标能够描述出融合图像与源图像之间的结构和边缘的一致性、信息提取和保持程度以及感官视觉效果。
本文选取的红外和可见光图像均来自多模态图像融合的公开数据库,具有通用性和普遍性。
4.1 字典性能的测试
为了讨论不同字典对融合结果的影响,同时对字典的有效性进行验证,本文进行了对比实验。实验中,利用不同方法构建了两种字典,并采用本文的融合算法,分别使用构建的两种字典对数据库中的五组红外和可见光图像进行融合,如图4所示,该五组图像其中三组源图像大小为512×512,两组源图像大小为240×320。融合后,对融合结果利用客观指标进行了度量和比较。其中,第一个字典为利用传统K-SVD算法对源图像进行学习得到字典,表示为DK-SVD,第二个字典为本文所采用的字典,即利用多模态图像块进行聚类,采用PCA进行学习得到的字典,记为DPCA,其融合结果客观指标值如表1所示。
图4 五组红外和可见光图像
Fig.4 Five pairs of infrared and visible images
从表1可以看出,利用这两种字典都能够达到较好的融合性能,其融合结果较为相似。但是,利用传统字典DK-SVD,因其冗余度较高,字典结构信息较为欠缺,因此,比起本文采用的字典DPCA,其具有较高的运算复杂度,计算时间较长。而本文采用的字典,不但融合性能具有一定的优势,且大幅度的提高了计算效率,节省了融合时间。
表1 对五组红外和可见光图像使用不同字典融合得到的客观评价指标平均值对比
Tab.1 Objective evaluation by using different dictionaries, scores for the 5 image pairs are averaged
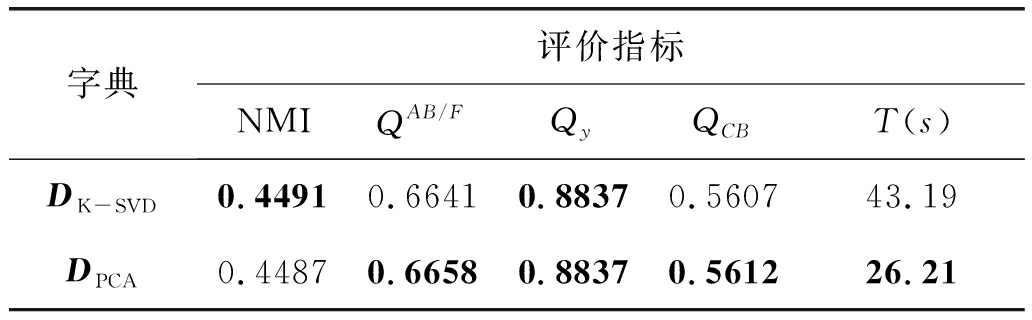
字典评价指标NMIQAB/FQyQCBT(s)DK-SVD0.44910.66410.88370.560743.19DPCA0.44870.66580.88370.561226.21
4.2 算法的有效性验证
为了从主观上验证本文算法的高效性,本文利用现有的五种算法对数据库中选取的一组红外和可见光图像进行了测试,并对测试结果进行主观上的对比。如图5所示。
图5中IA和IB分别为场景的可见光图像和红外图像,IB图中的虚线圆圈内有一白色噪点,不应该保留到最终的融合图像中,NNSR、ASR、LatLRR和SR算法都将其当作高频信息,并引入了结果中。同时,在NNSR、ASR、LatLRR算法融合图像的虚线方框中,可看到在过渡边缘和结构丰富的区域没能够有效的保留源图像中的高频结构信息,引入较多的低频信息,造成信息干扰,影响图像视觉效果。在LatLRR、GFF和SR算法结果的椭圆中出现了大量孤立的块状模糊和局部形变,造成融合图像质量的下降。GFF算法图像白色圆形区域甚至丢失了红外图像的高频目标信息。而本文算法充分考虑了图像的局部信息、相似信息和整体像信息之间联系和层次关系,采用树性结构进行划分并建立权重矩阵,不但较好的去除源图像中的噪声和错误信息,增强了算法的鲁棒性,还能准确高效的提取源图像中的结构和目标信息,并去除冗余信息,使融合结果信息丰富且清晰自然。同时,本文算法在稀疏表示的基础上引入了结构化和一致性约束项,充分利用了图像块之间的联系,保证了相似或位置相近的图像块之间的一致性,有效缓解了一些融合算法中存在的局部形变和孤立的块状模糊,提高了融合结果的准确性。
图5 不同算法对同一组图像的融合结果的主观图
Fig.5 Subjective results of fusion for the same set of images by different algorithms
为了将本文算法与现有算法从主观上和客观上进行综合对比,本文利用这些算法对图4选取的五组源图像分别进行了融合,得出每个算法所对应的融合图像,并对这些算法的融合结果利用几种客观指标进行了定量的比较。图6是五组图像采取不同的方法所得到的融合效果图。对比该实验结果可以看出,现有的几种红外和可见光图像融合算法得到的融合结果中都包含有一些昏暗的模糊区域。例如图6中,采用NNSR算法得到的融合结果,在第四幅虚线椭圆区域内,融合图像中丢失了可见光图像中的纹理信息,使得可见光图像中树叶的纹理信息几乎全部丢失,椭圆区域内只能看到一些模糊的灰度信息,造成该对该区域的分辨较为困难。同样在LatLRR算法、GFF算法所得到的融合图像中的虚线椭圆区域也存在此种情况,出现融合图像纹理信息的丢失,造成区分性不强,影响了融合图像的质量。而本文提出的方法构建的融合图像能够较大程度保留源图像所表达的一些纹理和细节信息,相比较其他四种方法具有较大的优势,减少了局部模糊的情况,其准确度较高。其次,在实线圆形区域中,可以明显判别出其他四种算法,比起本文算法,其对比度较低,遗失了部分信息,造成清晰度降低。同时,如图6中各种算法得到的融合结果中红色矩形框里所示,对于不同模态图像中显著性的目标信息(如矩形框中的人物信息),这些融合算法都能较好的将其保留在融合图像中,但GFF、ASR和LatLRR这三种算法所得到的融合图像中,目标信息不够突出,引入了一些干扰和冗余信息,造成对比度下降,目标灰度变暗等现象(人物信息来自红外图像,但却未能较完整的将目标信息保留在融合图像中,其较为昏暗)。相比而言,NNSR、GFF算法和本文所提出的算法能够较好的保持目标的对比度信息,但前两者算法丢失了目标的一些边缘信息,造成目标与其他区域之间的过渡区域出现细节信息的丢失,而本文的算法引入了结构化的稀疏约束,同时对图像块施加了拉普拉斯一致性约束项,将源图像分解成背景信息和显著性信息,同时将显著性信息采用叠加的融合规则并保留到融合图像中,使得融合结果不仅没有造成信息的丢失,还对细节信息一定程度上进行了增强,突出了目标信息,保留目标的边缘和强度特征,使得融合图像对目标的表达更完整、更准确,同时具有较好的视觉效果。
图6 不同算法对五组图像融合结果的主观图
Fig.6 Subjective results of fusion for five sets of images by different algorithms
通过该实验,充分的从主观上验证了本文提出的算法其融合结果的有效性。为了对不同算法从客观上进行评价,本文统计了上述实验得到的结果,其客观指标评价的平均值进行了比较,结果如表2所示。
表2 五组红外和可见光图像采用不同融合算法的客观评价指标平均值对比
Tab.2 Objective evaluation by different methods, scores for the 5 image pairs are averaged
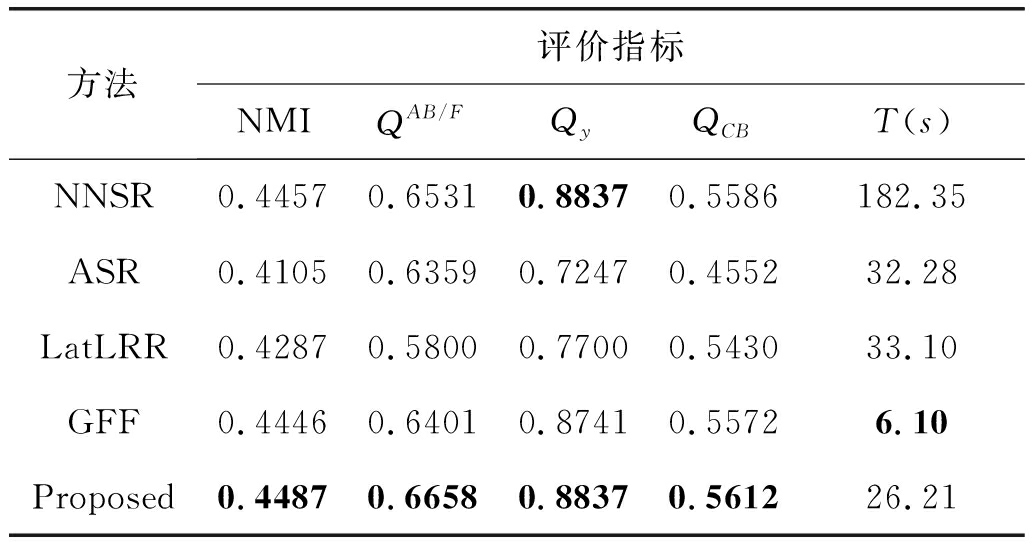
方法评价指标NMIQAB/FQyQCBT(s)NNSR0.44570.65310.88370.5586182.35ASR0.41050.63590.72470.455232.28LatLRR0.42870.58000.77000.543033.10GFF0.44460.64010.87410.55726.10Proposed0.44870.66580.88370.561226.21
表2中客观数据表明:相比现有的其他几种算法,本文算法客观指标具有较为明显的优势,表格中GFF算法虽然时间上具有更高的融合效率,然而比较GFF算法与本文提出的算法可发现,本文算法的几种客观评价指标值,明显较GFF算法的高。由此可推断,本文提出的利用结构化和一致性约束的稀疏表示模型进行红外和可见光图像融合算法在进行融合时,能够获得更高质量的图像。
5 结论
本文提出了一种新的利用结构化和一致性约束的稀疏表示模型进行红外和可见光图像融合的算法,该算法在原始鲁棒稀疏表示的基础上增加了结构化稀疏约束和拉普拉斯一致性约束。结构化约束首先是将图像块采用空间位置关系和特征相似性进行多层次的划分,其中,处于相同层次的图像块,其位置相近,同时特征具有相似性,因此,其具有相似的稀疏特性。基于该原理,本文将生成的结构树应用到稀疏表示中,进行同层之间、层与层之间的结构化稀疏约束,充分利用了图像区域的局部相似性,提高了稀疏表示之后背景系数对细节和纹理信息的表示能力。为突出源图像中的显著性信息,并减少信息丢失,本文对稀疏表示的显著性信息部分采用了一致性拉普拉斯约束,将特征相似的显著性信息共同提取出来,保证了融合图像信息的最终的完整性和准确性。该模型在使用时,对源图像分别进行了稀疏表示,并对表示结果的背景信息和显著性信息分别采取不同的融合规则进行融合,再进行稀疏重构得到了最终的融合图像。该算法不但能够保留图像的显著性信息,同时较好的保持了源图像中的细节和纹理信息,通过与现有的几种多聚焦图像融合算法进行了比较实验,验证结果表明,本文算法无论从主观上还是客观上,明显优于现有的一些算法。
[1] Kim M, Han D K, Ko H. Joint patch clustering-based dictionary learning for multimodal image fusion[J]. Information Fusion, 2016, 27: 198-214.
[2] Liu C H, Qi Y, Ding W R. Infread and visible image fusion method based on saliency detection in sparse domain[J]. Infrared Physics & Technology, 2017, 83: 94-102.
[3] 余南南, 邱天爽. 压缩传感条件下红外和可见光图像融合技术的研究[J]. 信号处理, 2012, 28(5): 692- 698.
Yu N N, Qiu T S. Fusion Technology of Infrared and Visible Images in Compressive Sensing[J]. Signal Processing, 2012, 28(5): 692- 698.(in Chinese)
[4] Li S, Kang X, Fang L, et al. Pixel-level image fusion: A survey of the state of the art[J]. Information Fusion, 2017, 33: 100-112.
[5] Yang B, Li S. Multifocus image fusion and restoration with sparse representation[J]. IEEE Transactions on Instrumentation and Measurement, 2010, 59(4): 884- 892.
[6] Liu Y, Liu Y, Liu S, et al. A general framework for image fusion based on multi-scale transform and sparse representation[J]. Information Fusion, 2015, 24: 147-164.
[7] Yin H, Li Y, Chai Y, et al. A novel sparse-representation-based multi-focus image fusion approach[J]. Neurocomputing, 2016, 216: 216-229.
[8] Mallat S G, Zhang Z. Matching pursuits with time-frequency dictionaries[J]. IEEE Transactions on Signal Processing, 1993, 42(12): 3397-3415.
[9] Zhang Q, Liu Y, Blum R S, et al. Sparse representation based multi-sensor image fusion for multi-focus and multi-modality images: a review[J]. Information Fusion, 2018, 40: 57-75.
[10] Zhang Q, Levine M. Robust multi-focus image fusion using multi-task sparse representation and spatial context[J]. IEEE Transaction on Image Processing, 2016, 25(5): 2045-2058.
[11] Liu G, Lin Z, Yan S, et al. Robust recovery of subspace structures by low-rank representation[J]. IEEE Transaction on Pattern Analysis and Machine Intelligence, 2013. 35(1): 171-184.
[12] Chung F R K. Spectral graph theory[M]. American Mathematical Society, 1997.
[13] Belkin M, Niyogi P. Laplacian eigenmaps and spectral techniques for embedding and clustering[C]∥Advances in neural information processing systems, 2002: 585-591.
[14] Zhang Q, Shi T, Wang F, et al. Robust sparse representation based multi-focus image fusion with dictionary construction and local spatial consistency[J]. Pattern Recognition, 2018, 83: 299-313.
[15] Aharon M, Elad M, Bruckstein A. K-SVD: an algorithm for designing over-complete dictionaries for sparse representation[J]. IEEE Transaction on Signal Processing, 2006, 54(11): 4311- 4322.
[16] Engan K, Aase S O, Hus
y J H. Multi-frame compression: Theory and design[J]. Signal Processing, 2000, 80(10): 2121-2140.
[17] Peng H, Li B, Ling H, et al. Salient Object Detection via Structured Matrix Decomposition[J]. IEEE Transaction on Pattern Analysis and Machine Intelligence, 2017, 39(4): 818- 832.
[18] Felzenszwalb F P, Huttenlocher D P. Efficient graph-based image segmentation[M]. Kluwer Academic Publishers, 2004.
[19] Lin Z C, Liu R S, Su Z X. Linearized alternating direction method with adaptive penalty for low-rank representation[C]∥Advances in neural information processing systems, 2011: 612- 620.
[20] Zhang Q, Liu Y, Zhu S, et al. Salient object detection based on super-pixel clustering and unified low-rank representation[J]. Computer Vision and Image Understanding, 2017, 000: 1-14.
[21] Wang J, Peng J, Feng X, et al. Fusion method for infrared and visible images by using non-negative sparse representation[J]. Infrared Physics & Technology, 2014, 67: 477- 489.
[22] Liu Y, Wang Z F. Simultaneous image fusion and denoising with adaptive sparse representation[J]. IET Image Processing, 2015, 9(5): 347-357.
[23] Li S, Kang X, Hu J. Image fusion with guided filtering[J]. IEEE Transaction on Image Processing, 2013, 22(7): 2864-2874.
[24] Cheng B, Jin L, Li G. General fusion method for infrared and visual images via latent low-rank representation and local non-subsampled shearlet transform[J]. Infrared Physics & Technology, 2018, 92: 68-77.
[25] Xydeas C, Petrovic V. Objective image fusion performance measure[J]. Electronics Letters, 2000, 36(4): 308-309.
[26] Yang C, Wang J, Wang X, et al. A novel similarity based quality metric for image fusion[J]. Information Fusion, 2008, 9(2): 156-160.
[27] Hossny M, Nahavandi S, Creighton D. Comments on ‘Information measure for performance of image fusion’[J]. Electronics Letters, 2008, 44(18): 1066-1067.
[28] Chen Y, Blum R. A new automated quality assessment algorithm for image fusion[J]. Image and Vision Computing, 2009, 27(10): 1421-1432.
