1 引言
指静脉为近十几年来新兴的生物特征,与指纹、掌纹等传统生物特征相比,静脉特征位于手指皮下组织中,属于内部特征,具有活体性、唯一性、防伪性等优点[1]。由于存在位置的特殊性,在图像采集过程中,光源模糊、手指姿态变化等都会对识别的准确率造成影响[2-3],因此,探索稳定性和鲁棒性更强的特征表达方法,对指静脉识别技术的发展至关重要。
近几年,相关学者提出基于图模型的全局生物特征表达并取得了较好的效果。图是一种结构化数据,具有对局部噪声不敏感、对图像描述效率高等特点,将结构图模型与数字图像处理相结合,可以弥补成像条件和算法有效性对图像的影响[4]。与生物特征局部图的研究相比,构建全局生物特征图的研究还相对较少。Arakala等人[5]将视网膜、掌静脉、指静脉的一个血管生物特征样本表示成一个空间图,选择细节点作为图的节点,血管连接作为边集,表明使用简单的图结构可以减少匹配时间。然而图像的细节点不稳定,图像增强也可能会产生虚假的节点。Ye Ziyun等人[6]提出了一种基于特征相似度构建加权三角剖分图的手指静脉识别方法,验证了该加权图能够较好的描述指静脉网络结构,并且具有良好的识别性能。然而上述方法都是基于传统算法提取的手工特征作为生物特征图的特征,需要经过一系列复杂的预处理,虽然在特定场景的数据库下能够取得较好的效果,但这些特征整体上缺乏强大的表征和泛化能力,并且匹配效率受图模型的大小影响。
针对上述问题,本文提出通过超像素分割算法构建指静脉的加权图模型,改进GCNs提取指静脉加权图的图级特征作为图像最终特征进行匹配。超像素是由一系列位置相邻且颜色、灰度、纹理等特征相似的像素点组成的区域,其保留了原始图像的有效信息,在超像素上表示图,计算效率较高,并且超像素含有更多的感知信息[7]。
图为非欧几里得域的不规则结构化数据,卷积神经网络(Convolution Neural Network, CNN)无法进行操作。2013年,在图信号处理的基础上,Bruna首次提出基于频域的图卷积网络Spectral CNN[8],定义了图卷积核和滤波器,但该模型没有局部信息。2016年,Defferrard等人提出ChebyNet[9],其Cheby图卷积层使用切比雪夫多项式来拟合卷积核,引入了K-hop局部感受野,运算量相比Spectral CNN降低,但卷积网络参数量仍较大。除了图卷积,图的下采样也是重要构建块。ChebyNet提出一种快速图池化操作,其通过使用Graclus聚类算法[10]聚类相似节点得到粗化图后,添加虚假节点并进行排序构建平衡二叉树实现图池化,然而该粗化方法需要对节点进行手动排序,不能自适应的实现节点池化,并且存在虚假节点。2019年,Gao Hongyang等人提出了gPool池化操作[11],其使用一个可训练的投影向量p将所有节点特征投影到一维然后执行k-max实现自适应地图池化。
针对以上问题,本文首先通过SLIC超像素分割算法[12]生成指静脉超像素图,将一个超像素块构成指静脉加权图的一个节点,节点特征为像素强度值和质心坐标,根据超像素质心之间的空间距离得到图的权值;其次通过简化归一化拉普拉斯矩阵特征分解后的特征值减小图卷积运算的复杂度,简化后的图卷积层称为SCheby,并对卷积核尺寸、滤波器数、卷积层数等进行调整;针对于ChebyNet中快速池化操作不能自适应地实现节点池化的问题,提出应用gPool池化层,并将gPool层中的单层投影改进为多层来训练投影向量,使池化后的图保留原始图更多有效的信息,改进后的池化层称为MgPool;由于层级池化网络结构可能会导致池化后的重构图中出现不连通的节点影响下一图卷积层特征提取效果,因此本文提出构建全局池化的网络结构,并在池化层后增加读出层提取图级特征,最终改进后的GCN网络模型称为SCheby-MgPool。在训练中应用数据增强策略构建指静脉加权图并输入到网络中,测试时提取网络读出的图级特征,通过度量指静脉图级特征之间相似度的方法进行匹配。
2 指静脉加权图的构建
一个N个节点的加权图可以表示为G=(V, E, A),V={ν1,ν2,…,νN}是节点集,E={eij}为边集,其中eij=(νi,νj)(i≠j),无向图中eij=eji,A∈RN×N为图的权值邻接矩阵,wij∈A表示边eij上的权值。定义图上的信号为x,图的节点特征矩阵用X∈RN×C表示,定义xi∈RC为第i个节点的特征向量,C为节点特征的维度大小。构建指静脉集加权图模型的操作包括节点集的构建、节点特征的计算、边集的构建以及权值的计算。
2.1 节点集的构建、节点特征的计算
SLIC基于改进的K均值聚类生成超像素,输入一幅指静脉原始图像,给定分割数k,算法首先将图像转换到CIELAB颜色空间,并将每个像素的亮度、颜色值(L, a, b)和空间坐标(x, y)组成一个五维向量(L, a, b, x, y),在图像内设置k个初始聚类中心Ci=[li,ai,bi,xi,yi]T,然后在间隔![]() 个像素的网格上采样,N为总像素数,为了避免聚类中心落在梯度较大的轮廓边界,将聚类中心移动到3×3邻域内梯度最小的位置,在聚类中心搜索邻域内为每个像素点分配标签。和标准的K均值聚类在整张图中搜索不同,SLIC的搜索范围限制为2S×2S,减少了距离计算,从而能加速算法的收敛。对搜索到的每个像素点分别计算它和聚类中心的颜色距离dc和空间距离ds并归一化得到最终的距离度量D′:
个像素的网格上采样,N为总像素数,为了避免聚类中心落在梯度较大的轮廓边界,将聚类中心移动到3×3邻域内梯度最小的位置,在聚类中心搜索邻域内为每个像素点分配标签。和标准的K均值聚类在整张图中搜索不同,SLIC的搜索范围限制为2S×2S,减少了距离计算,从而能加速算法的收敛。对搜索到的每个像素点分别计算它和聚类中心的颜色距离dc和空间距离ds并归一化得到最终的距离度量D′:
(1)
(2)
(3)
式中Ns=S为类内最大空间距离,Nc为最大颜色距离,一般在[1,40]区间内取一个固定的常数值m,权衡颜色相似性和空间邻近度之间的相对重要性。不断迭代上述步骤直到误差收敛,最后使用连通分量算法将不连续的、尺寸过小的超像素重新分配给邻近的超像素区域。
通过SLIC算法得到指静脉超像素图后,将一个超像素块构成加权图的一个节点。由于不同手指个体的表皮和皮下组织厚度不同,对应指静脉成像中灰度特征不同,同一静脉图像中静脉与非静脉部分区域的灰度也存在差异,并且每块超像素具有不同的空间位置特征,因此通过计算每个超像素块的像素强度值![]() 和质心坐标Csp=(xi,yi)/Smax得到节点的灰度特征和空间特征,其中Ni表示第i个超像素内像素的总数,pn为每个像素的像素值,Smax是图像尺寸的最大值。由于两特征尺度不同,进行z-score(zero-mean)标准化处理得到最终指静脉加权图的节点特征xi=[Msp,Csp],所有节点特征构成特征矩阵X。图1所示为k取100,即超像素分割数为100,m取10时,经过高斯平滑、归一化后的指静脉ROI图像通过SLIC算法构建节点集的示意图。
和质心坐标Csp=(xi,yi)/Smax得到节点的灰度特征和空间特征,其中Ni表示第i个超像素内像素的总数,pn为每个像素的像素值,Smax是图像尺寸的最大值。由于两特征尺度不同,进行z-score(zero-mean)标准化处理得到最终指静脉加权图的节点特征xi=[Msp,Csp],所有节点特征构成特征矩阵X。图1所示为k取100,即超像素分割数为100,m取10时,经过高斯平滑、归一化后的指静脉ROI图像通过SLIC算法构建节点集的示意图。
2.2 边集的构建、权值的计算
图的边描述的是节点之间的连接关系,边上的权值则描述了节点之间连接关系的强弱。
典型的边集表示构成的图有区域邻接图,K近邻图和三角剖分图等[4],这些都是局部连接的图结构,构成的图高度稀疏,图卷积提取的感知信息较少,因而本文提出构建无向完全图,每对不同的顶点之间都只存在一条边,如图2所示。

图1 节点集的构建
Fig.1 Generation of node-set
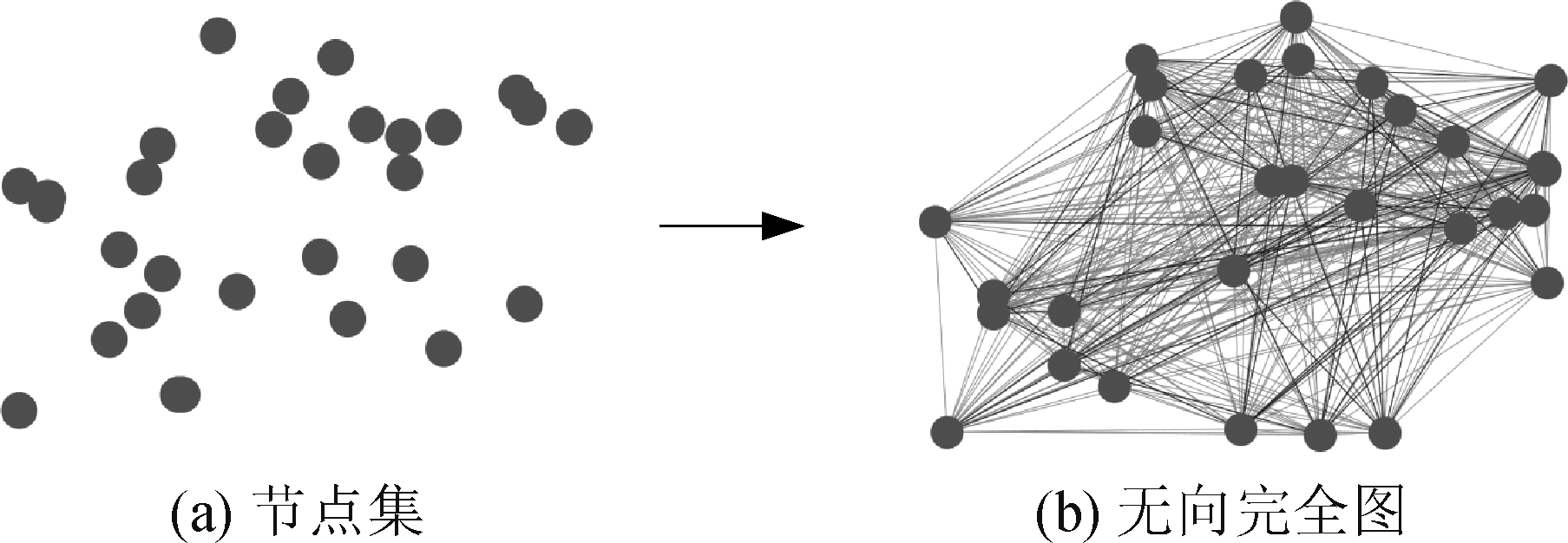
图2 边集的构建
Fig.2 Generation of edge-set
定义加权图节点之间的权值为节点之间的空间亲密度,由超像素质心坐标的空间距离计算得到,权值越小,表示两超像素质心之间距离越大,则对应节点之间的空间亲密度越小,连接关系越弱。权值计算公式为:
wij=exp(-||(xi,yi)-(xj,yj)![]() /σ2)
/σ2)
(4)
其中(xi,yi)和(xj,yj)为两超像素块的质心坐标,σ为取值[0, 1]的常数值,实验中取0.1×π时能够获得较好的权值分布。
3 图卷积神经网络
GCNs可分为基于频域和基于空域两类[13]。基于频域的方法从图信号处理的角度引入滤波器来定义图卷积算子,借助图谱的理论来实现拓扑图上的卷积操作,而空域图卷积定义聚合函数聚合节点及其一阶邻域特征信息。本文构建的指静脉加权图为非稀疏图,相比空域图卷积的一阶信息聚合和层数堆叠,频谱图卷积的卷积核感受野可扩展,能提取图中更高阶的信息。
基于频域图卷积的方法首先根据图傅里叶变换将图信号转换到傅里叶域,图上傅里叶变换的定义依赖于图拉普拉斯矩阵分解后的特征向量和特征值,然后根据卷积定理对谱空间的信号做乘法运算,再利用傅里叶逆变换将信号转换到原始空间定义卷积算子。对于一个N节点的图G=(V, E, A),其归一化拉普拉斯矩阵的定义为L=IN-D-1/2AD-1/2,其中D∈RN×N为度矩阵,Dii∈∑jAij,IN为单位矩阵。拉普拉斯矩阵是对称矩阵,进行特征分解L∈UΛUT,得到一组正交的特征向量U=[u0,…,uN-1]∈RN×N,对应的特征值为Λ=[λ0,…,λN-1]∈RN×N。对于图信号x的傅里叶变换及逆变换定义为:![]() 有了图的傅里叶变换定义后,可以定义图G上的卷积操作为:
有了图的傅里叶变换定义后,可以定义图G上的卷积操作为:
(x*gθ)G=Ugθ(Λ)UT=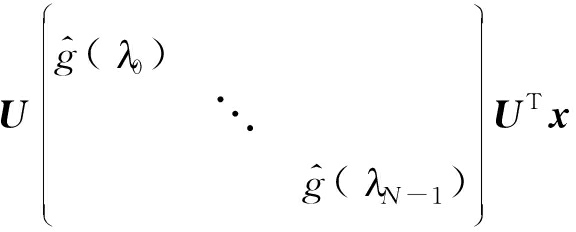
(5)
其中gθ(Λ)为可学习的卷积核。
3.1 ChebyNet
上述定义的卷积核gθ(Λ)为无参滤波器,图卷积操作没有局部信息,每次卷积都是所有的节点全部参与运算,计算复杂度很大。ChebyNet中图卷积层Cheby通过定义特征向量对角矩阵的切比雪夫多项式为滤波器对卷积核进行参数化,可以捕捉图的局部特征。切比雪夫多项式递归定义为:T0(x)=1,T1(x)=x,Tk(x)=2xTk-1(x)-Tk-2(x),使用切比雪夫多项式拟合卷积核,得到Cheby图卷积定义:
(6)
式中定义拉普拉斯矩阵为![]() 为缩放后的特征向量矩阵,缩放是为了满足切比雪夫多项式Kth阶截断的条件:自变量范围需在[-1,+1]之间。
为缩放后的特征向量矩阵,缩放是为了满足切比雪夫多项式Kth阶截断的条件:自变量范围需在[-1,+1]之间。
ChebyNet还提出了一种图的快速池化操作Coarse Pool,其对卷积后的图首先通过Graclus聚类算法进行粗化,然后添加虚假节点将粗化后的图转换为一个平衡二叉树,在最粗的层次上对节点任意地排序,再将这个排序传递到平衡二叉树的较低层次,最后会在最细的层次上产生一个节点的规则排序得到池化后的图,网络结构为两层图卷积图池化的层级结构,池化后的图经过全连接层后通过softmax进行分类,图3展示了ChebyNet模型结构效果图。
3.2 SCheby-MgPool
Cheby定义的图卷积操作虽然引入了K-hop局部感受野,实现了GCNs网络的局部性和加速计算,然而其卷积运算复杂度仍较高,并且增大切比雪夫滤波器局部感受野即卷积核尺寸K,会大大增加训练参数的总数,如果K等于节点数目时,滤波器的感受野则是整个图。由于指静脉数据集样本普遍较少,并且本文构建的指静脉加权图规模相对较小,每层都使用较大的卷积核造成网络参数量较大,从而可能导致模型过拟合,为了抑制参数数量防止过拟合,模型中构建了三层图卷积,在第一层图卷积层中设置局部感受野即卷积核大小K>2,所有节点获得来自高阶邻域的加权聚合,设置32个卷积核;在获得K阶图权后,图中所有节点状态更新;第二、三层图卷积层中,固定卷积核大小为2,卷积核数分别为64,128,仅聚合邻近节点的特征信息,并令Cheby滤波器中归一化拉普拉斯矩阵特征分解后的最大特征值λmax为2,得到简化后的归一化拉普拉斯矩阵定义,进一步简化运算量,简化后的图卷积层称为SCheby。

图3 ChebyNet模型结构效果图
Fig.3 ChebyNet model structure renderings
L=IN-D-1/2AD-1/2
(7)
(8)
(9)
ChebyNet利用完全二叉树实现图的池化操作,池化过程中需通过增加虚假节点保证二叉树的构建,并且经过Graclus聚类算法得到的粗化图中的节点是无规则排列的,需要重新排序才能进行有效的池化,不能实现自适应的选择节点。对此,本文提出在模型中应用能够实现自适应图池化操作的gPool,其主要通过定义一个可训练的投影向量p,将所有节点特征投影到一维后执行top k操作实现自适应地选择节点子集。对于N个节点的图G,输入到网络中的信息可以用邻接矩阵Al和特征矩阵Xl表示,l表示当前的层数,给定一个节点i及其特征向量xi,其在p上的标量投影为yi=xi/||p||Xl。gPool图池化层分层传播规则为:
y=Xlpl/||pl||
(10)
idx=rank(y,k)
(11)
(12)
(13)
Al+1=Al(idx,idx)
(14)
(15)
式中k为新图中选择的节点数,定义池化率为r=(1-k/N)×100%。y为Xl在pl上的标量投影,y=[y1,…,yN]T∈RN,rank(y,k)是节点排序的操作,返回y中k个最大值的索引。y(idx)通过索引idx提取y中的值然后进行sigmoid函数激活。Xl(idx,:)和Al(idx,idx)执行池化后重构图的节点特征矩阵和邻接矩阵操作,最后使用![]() 和
和![]() 的点积来控制所选节点的信息,实现门控操作,从而使投影向量p可以通过反向传播进行训练。
的点积来控制所选节点的信息,实现门控操作,从而使投影向量p可以通过反向传播进行训练。
yi测量的是将节点i投影到p的方向上,可以保留多少节点i 的信息,对图节点进行下采样操作,为了使池化后的图保留原始图更多有效的信息,本文提出将gPool层中的单层投影改进为使用三层线性层训练投影向量,每层神经元数分别为32,16,1,每层之间使用Relu函数激活,参数传播过程为:
W3Relu(W2Relu(pX)+b2)+b3
(16)
投影向量p为第一层线性层的可训练权重,第一层不学习偏置,改进后的池化层称为MgPool,后续实验表明,与单层投影的gPool相比,MgPool具有更好的性能。图4展示了MgPool层对一个具有5个节点,每个节点特征维度为3的图执行池化操作的过程,池化率设置为40%,即新图中选择的节点数为k=3。
在生成所有更新后的节点特征之后,直接使用所有节点特征作为指静脉最终特征在存储时占用空间大,并且匹配耗时长,因此本模型加入了一层读出(Readout)层[13],其输入是所有节点表示,该层将所有节点特征聚合起来,形成一个固定大小的表示,称为图级特征。目前,全局池化是实现图的下采样最原始也是最有效的方法,本文读出层采用Global max池化获得图级特征,即指静脉图像的最终特征表达:
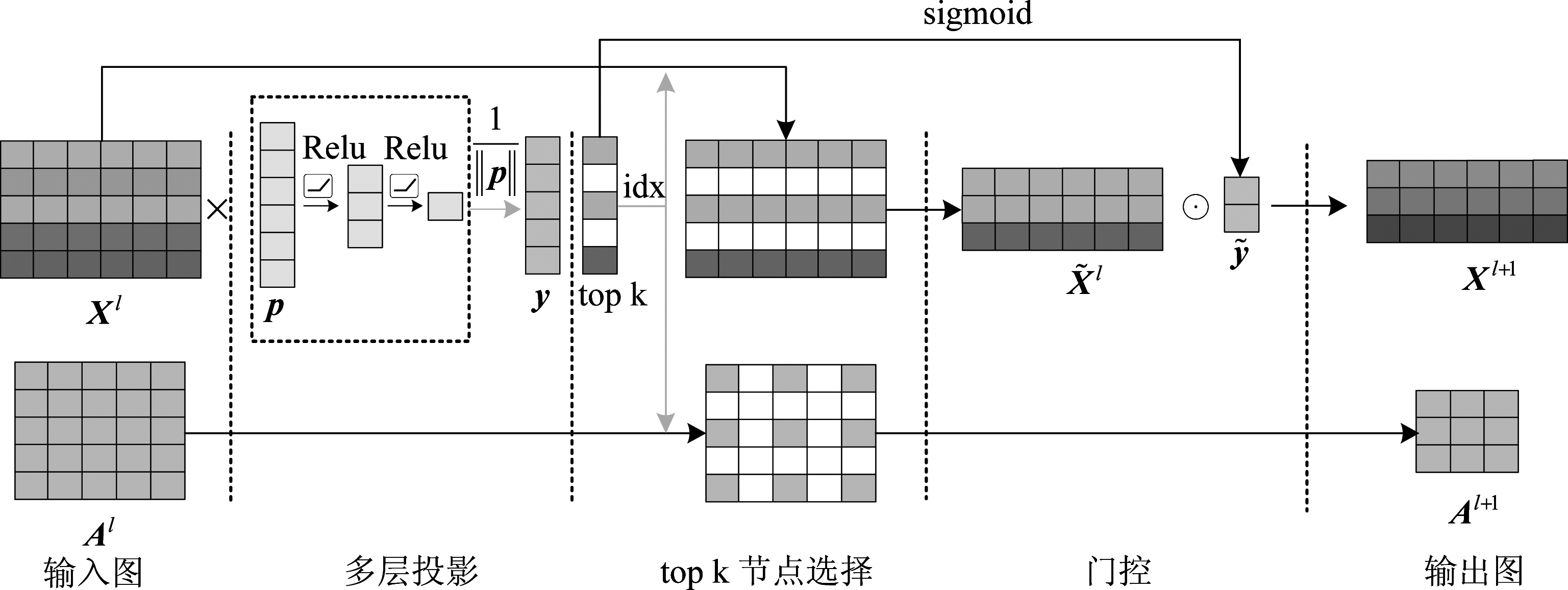
图4 k=3时,MgPool示意图
Fig.4 An illustration of the MgPool layer with k=3
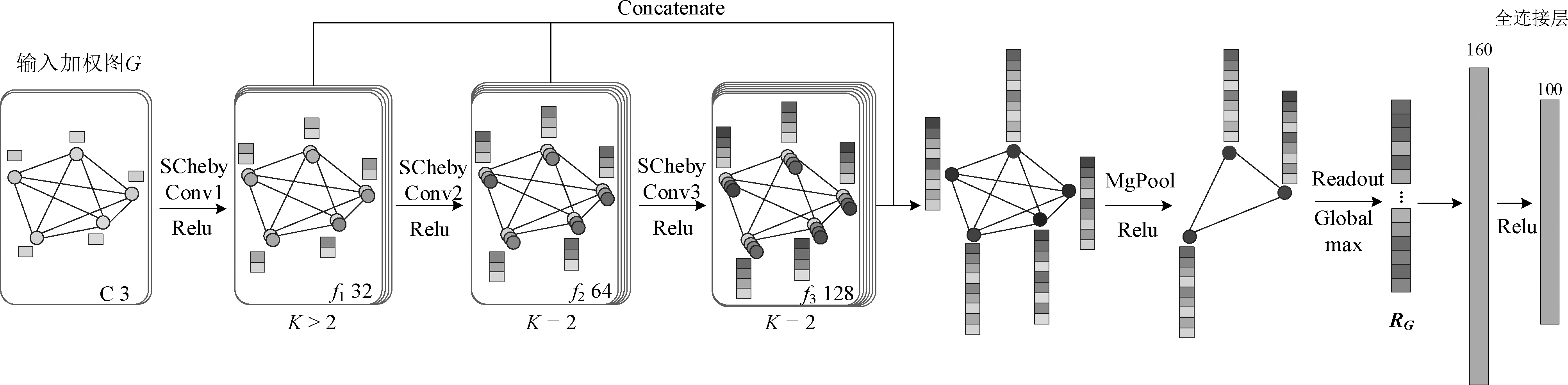
图5 SCheby-MgPool模型结构效果图
Fig.5 SCheby-MgPool model structure renderings
(17)
在MgPool层对图节点的池化操作中,池化节点的同时也池化了相关的边,而构建层级池化结构可能会导致池化后的重构图中出现不连通的节点,因此本模型构建了全局池化网络结构[14]的SCheby-MgPool模型。图5为本文提出的图卷积神经网络结构示意图,网络由三层图卷积层组成,每层的输出连接起来,节点特征在池化层之后的读出层中聚合得到加权的图的图级特征,最后经过两层全连接层。
在得到指静脉的图级特征后,采用度量不同指静脉加权图的图级特征相似度的方法实现手指静脉的匹配[6],其定义如式(11)所示:
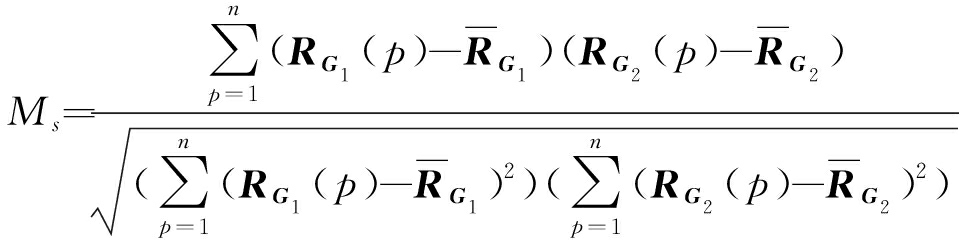
(18)
其中RG1和RG2分别表示待匹配的两幅指静脉图像的图级特征向量,![]() 和
和![]() 为对应的均值,n为特征向量的维数。
为对应的均值,n为特征向量的维数。
4 实验结果分析
4.1 实验环境及数据集
本算法实验环境使用Ubuntu64位操作系统,CPU为Inter(R) Core(TM) i5- 8300H CPU, 主频率为2.30 GHz,内存为8 GB;GPU为NVIDIA GeForce GTX 1050 Ti,编程语言使用Python3.5,深度学习框架为Pytorch1.1.0。
实验中使用了两个数据集对本文提出的指静脉特征表达方法的性能进行分析和评估,分别是实验室自制数据集以及公开的指静脉数据集FV-USM[15]。实验室自制指静脉数据库共585类,每类10个指静脉样本;FV-USM指静脉数据库共123类,分两期采集,每期中一类采集了6张样本。实验中,从两数据库中各随机选取100类,并提取ROI图像作为实验数据集,分别记为Data-1和Data-2,ROI定位后的图像尺寸分别91×200和100×300。实验中两数据集均被划分为训练集和测试集两部分,比例分别为7∶3和4∶2。
4.2 实验参数设置
对于数据库一类样本数量较少以及为了进一步提升模型的鲁棒性和泛化能力,在网络训练前,使用python中的opencv模块对指静脉图像通过随机亮度调整、旋转变换和局部放大操作进行数据扩充,扩充后的Data-1和Data-2训练集样本数量分别为2800和1600。本实验中两数据集中采用的训练块(Batch)分别为28和16,均进行30步(Epoch)的迭代训练,使用Adam优化器,学习率为0.001,为了进一步避免网络训练中的过拟合现象,采用dropout正则化方法,该方法在训练中随机丢弃一部分网络节点,dropout率均为0.5。实验中使用交叉熵损失函数进行反向传播:
loss(x,class)=-x[class]+log(∑jexp(x[j]))
(19)
x为模型最后一层的预测输出。
4.3 加权图参数及图卷积核对识别结果影响
本节设计了三个实验详细研究影响识别结果的几个因素:1.实验(1)分析了基于不同超像素分割数构建的加权图对识别结果的影响;2.实验(2)探究了模型中第一个图卷积层局部感受野K的大小对识别结果的影响;3.实验(3)对比了不同图结构构建的指静脉加权图的识别性能。
实验(1)中对Data-1和Data-2数据库指静脉图像设置超像素分割数在[100,600]区间内间隔100取值,超像素分割数不同时,分割效果不同,构建的指静脉加权图的大小也不同,图卷积提取的特征存在差异。图6给出了从两个数据库中各取一个样本得到的不同超像素分割数下指静脉分割示例图。

图6 不同超像素数下的指静脉分割示例图
Fig.6 Sample images of finger-vein segmentation with different superpixel numbers
从上图可以看出,随着超像素分割数的增多,分割后的指静脉超像素块形状变得规则,同时构建的指静脉加权图的节点数增多,图的规模变大。对不同超像素分割数下的指静脉超像素图构建加权图并输入到网络中,设置第一层图卷积核大小为6,Mgpool池化率为30%,识别ROC曲线如图7所示,识别等误率(EER)如表1所示。
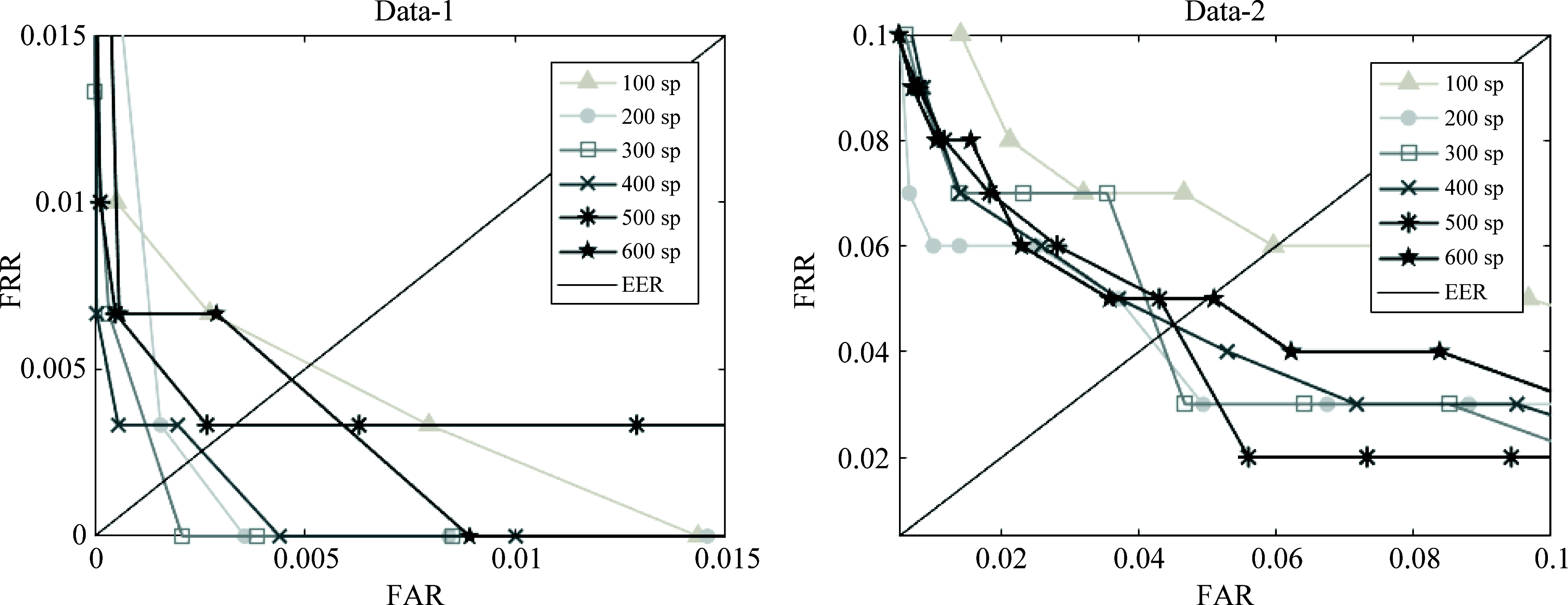
图7 不同超像素数下的ROC曲线
Fig.7 ROC curves for different numbers of superpixel
表1 不同超像素数下的等误率
Tab.1 EER of different numbers of superpixel
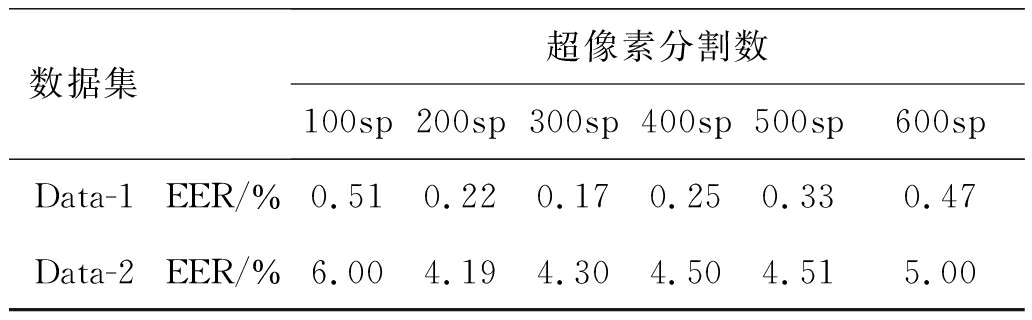
数据集超像素分割数100sp 200sp300sp400sp500sp600spData-1EER/%0.510.220.170.250.330.47Data-2EER/%6.004.194.304.504.515.00
根据实验结果可知,由于两数据库ROI定位后图像的尺寸、灰度不同,不同分割数对识别结果的影响也不同。在Data-1和Data-2中,超像素分割数分别为300sp和200sp时,指静脉特征识别性能较好,当分割数过少时,其对于细节区域的处理不够精细,容易将一些背景区域划分为静脉区域,从而造成识别结果下降;当超像素分割数较大时,指静脉图像分割的过细,容易受到一些噪声的干扰,并且构建的指静脉加权图节点数较多,图的规模较大,同时造成网络计算复杂度增大。
实验结果中Data-1的等误率较低,这是因为实验室自制数据库相比FV-USM数据库采集的指静脉图像成像质量较好,受光照和手指运动变化较小。
本文提出的模型中,设置第一层图卷积层的局部感受野即卷积核K>2,第二、三层为2,因此实验(2)中探究了模型中第一个图卷积层的局部感受野对识别结果的影响。实验中取不同K值得到的识别结果及训练时间变化曲线如图8所示。
如图所示,当第一层图卷积核K取9时,Data-1和Data-2的识别结果最好,等误率分别为0.09%,3.41%,而当K取值过小时,K-hop局部感受野较小,图卷积提取的感知信息少,特征表达不充分;当K取值较大时,图卷积计算复杂,造成网络参数量大,不仅增加训练时长,还会出现过拟合现象,从而造成识别效果变差,后续实验中第一层图卷积核尺寸均设置为9。
为了验证本文构建的完全图的有效性,实验(3)中对比了不同图结构下指静脉加权图的识别性能。首先使用SLIC算法生成指静脉超像素图,其次,分别构建了完全图、三角剖分图、8NN图以及区域邻接图结构的指静脉加权图,输入到网络中训练、测试识别,得到的识别ROC曲线如图9所示,识别等误率以及训练所用时间如表2所示。
表2 不同图结构下的识别结果和训练时长
Tab.2 Recognition results and training time under different graph structures
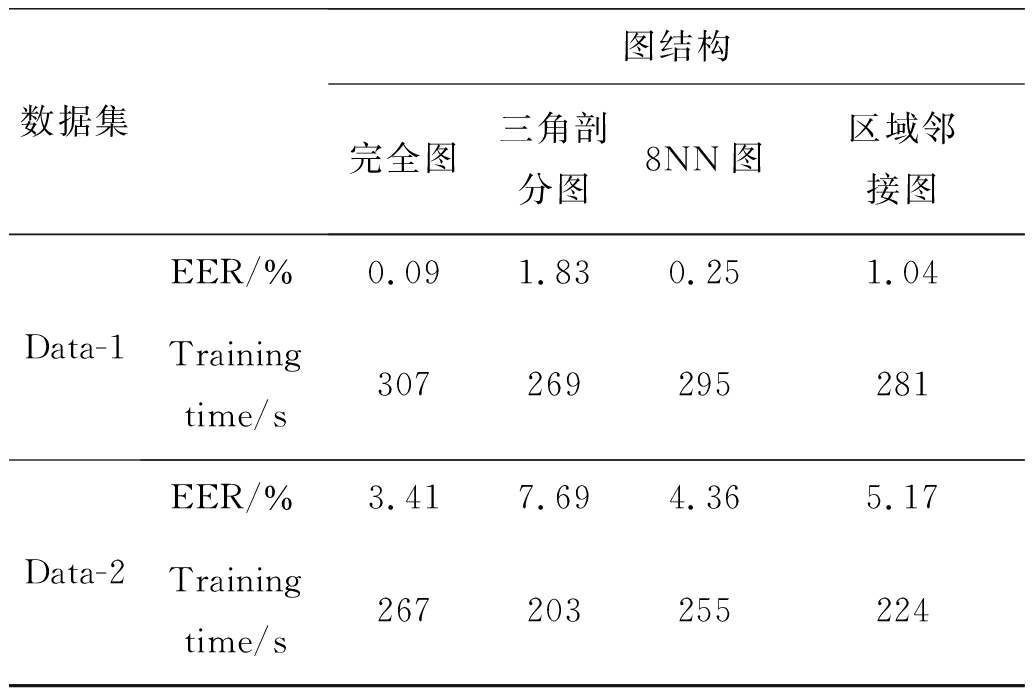
数据集图结构完全图 三角剖分图8NN图区域邻接图Data-1EER/%0.091.830.251.04Training time/s307269295281Data-2EER/%3.417.694.365.17Training time/s267203255224
根据实验结果可知,本文构建的完全图结构的指静脉加权图与其他图结构相比具有更好的识别性能,训练所用时间与其他图结构相差较小,这是因为与其他局部图结构的边集数相比,虽然完全图
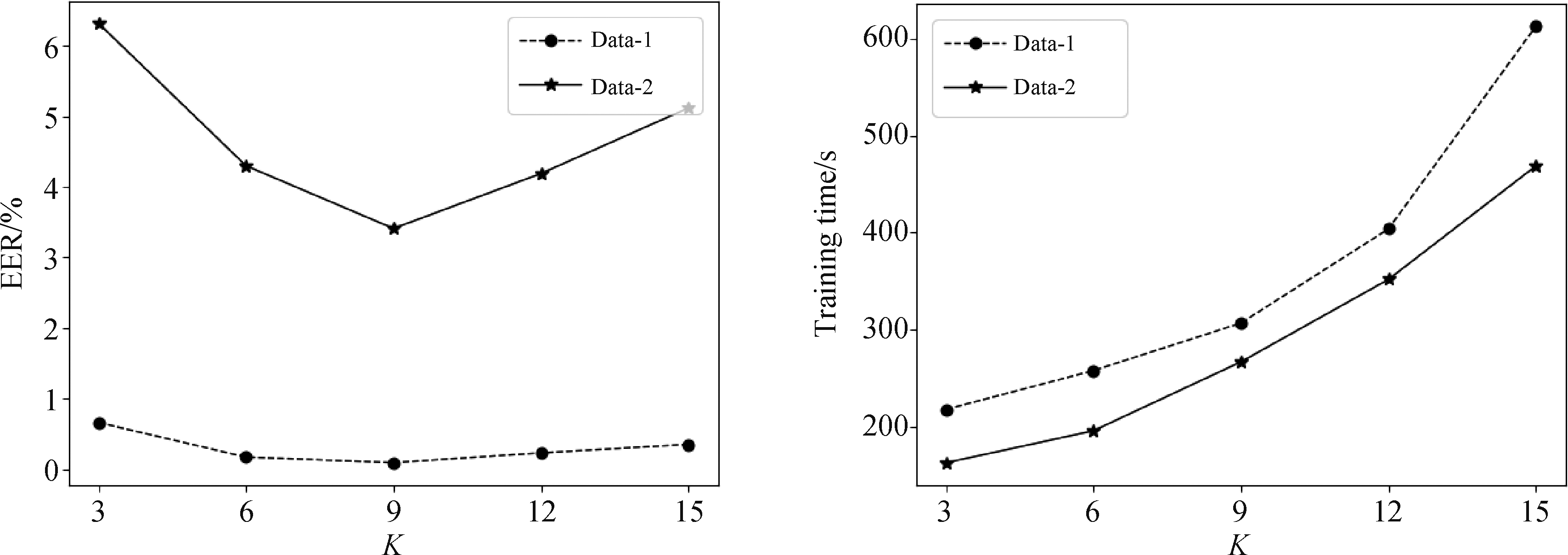
图8 不同K值下的识别结果和训练时间
Fig.8 Recognition results and training time at different K values
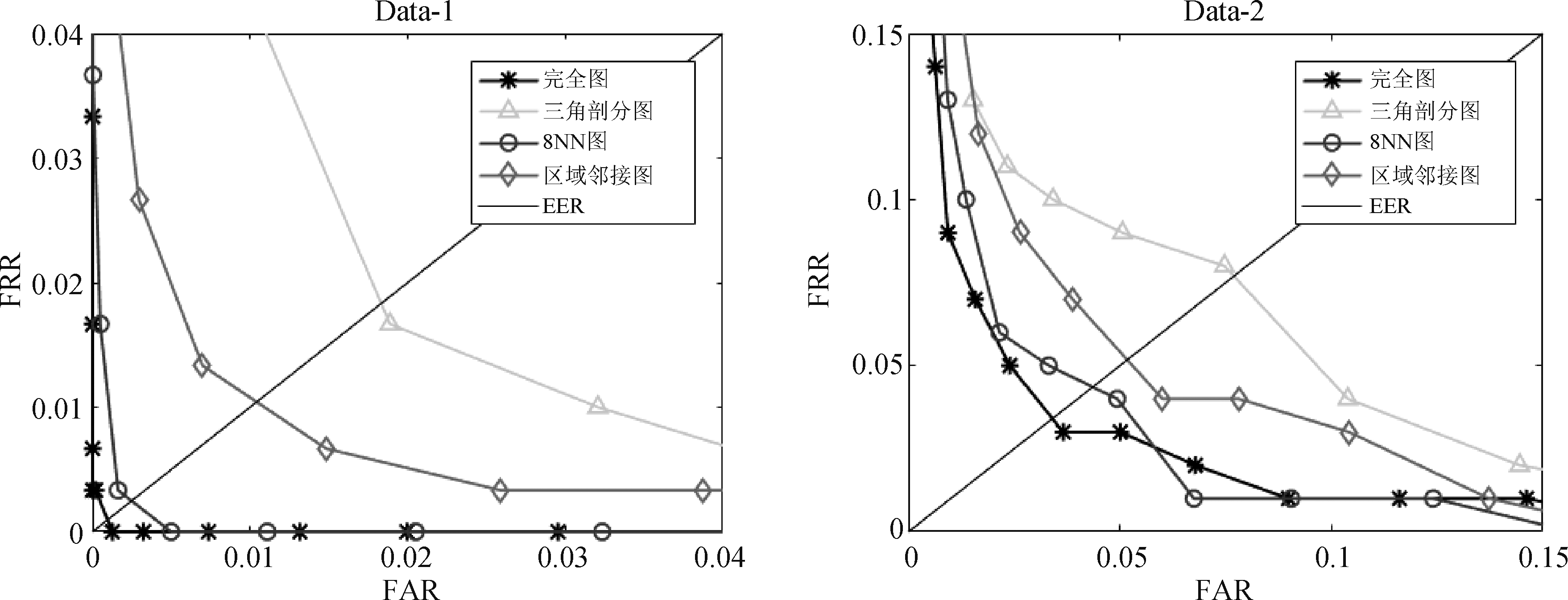
图9 不同图结构的ROC曲线
Fig.9 ROC curves of different graph structures
的边集较多,但其边集权值是归一化的,度量的是节点空间距离的远近,许多连接关系较弱的边,权值极小,从而不会造成计算过于复杂。
4.4 对比实验
为了进一步评估本模型的识别性能,本节设计了三个对比实验。实验(1)将提出的SCheby-MgPool图卷积神经网络与其他GCNs模型进行对比;实验(2)中与其他基于加权图的指静脉识别方法相对比,验证本文提出的方法在识别精度和时间上的有效性;实验(3)中将本模型与经典的卷积神经网络模型进行对比。
实验(1)对比了Cheby[9],ChebyGIN[16],GCN[17],GIN[18]四种图卷积和gPool[11],Coarse Pool[9],SAGpool[19]三种池化层。Cheby和Coarse Pool为ChebyNet中的图卷积层和池化层。GCN和GIN为基于空域的方法提出的图卷积方法,其定义的聚合函数每次卷积只能聚合来自一节邻域节点的信息,为保证不同图卷积方法卷积运算的感受野相同,设置SCheby,Cheby,ChebyGIN中卷积核的大小均为2,并设置相同的池化率50%,实验结果如表3所示。
由实验结果可知,在Data-1和Data-2数据库中,与GCN,GIN和ChebyGIN图卷积构建的模型相比SCheby识别等误率最低,与Cheby相比识别等误率分别高了0.30%,1.01%,但训练所用时间分别缩短了38.9%和46.6%,这说明SCheby网络参数较小,当增大图卷积核时,模型不容易过拟合。本文提出的MgPool池化方法与表中其他池化方法相比识别等误率最低,其中在两数据库中相比于gPool分别降低了0.52%,1.62%,说明提出的基于多层投影的池化方法对节点的选择更准确,进一步提高了特征的区分度。
表3 不同GCNs模型的识别结果和训练时长
Tab.3 Recognition results and training time of different GCNs models
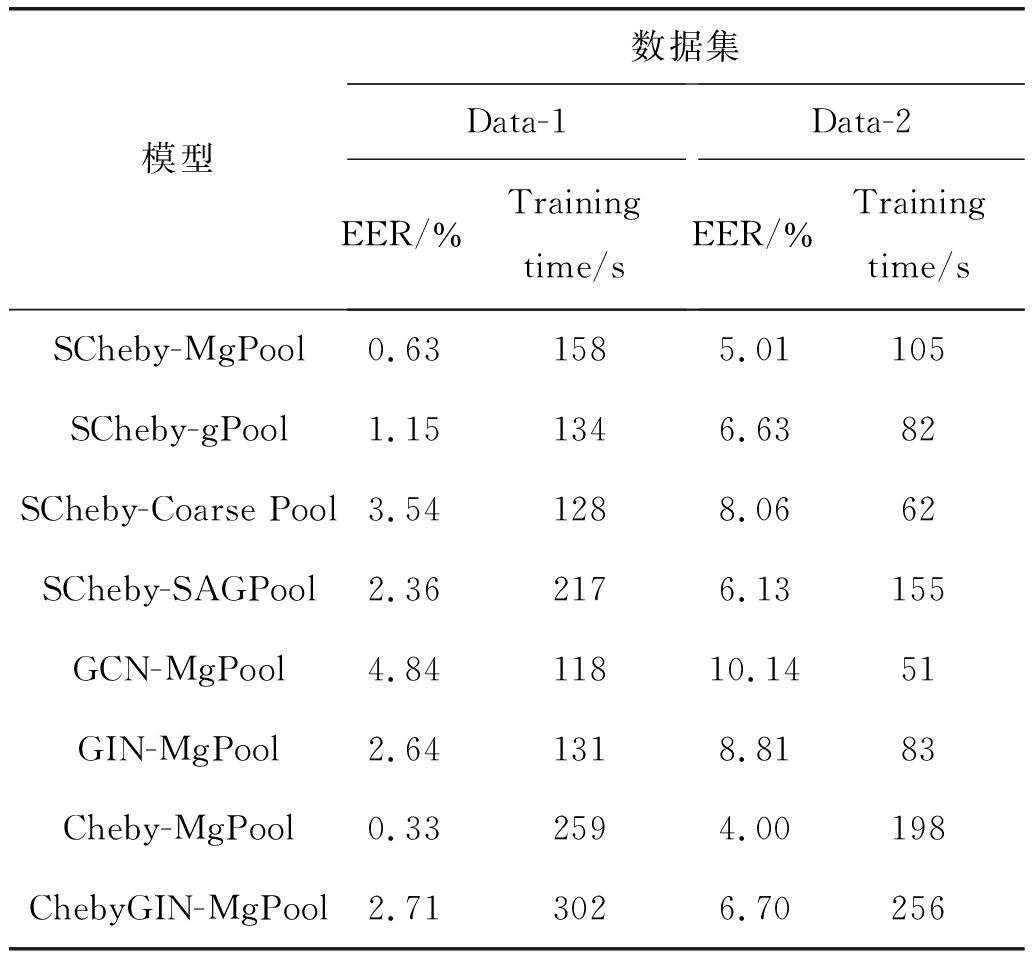
模型数据集Data-1 EER/%Training time/sData-2 EER/%Training time/sSCheby-MgPool0.631585.01105SCheby-gPool1.151346.6382SCheby-Coarse Pool3.541288.0662SCheby-SAGPool2.362176.13155GCN-MgPool4.8411810.1451GIN-MgPool2.641318.8183Cheby-MgPool0.332594.00198ChebyGIN-MgPool2.713026.70256
为了更好的评估本文提出的指静脉加权图特征的表征能力和识别效率,实验(2)中将本文方法与文献[6]提出的基于一种加权图的指静脉识别方法进行对比,其利用图块划分构建指静脉加权图的节点集,使用三角剖分构建边集,基于方向可调滤波器提取图块的方向能量分布特征并计算所连接节
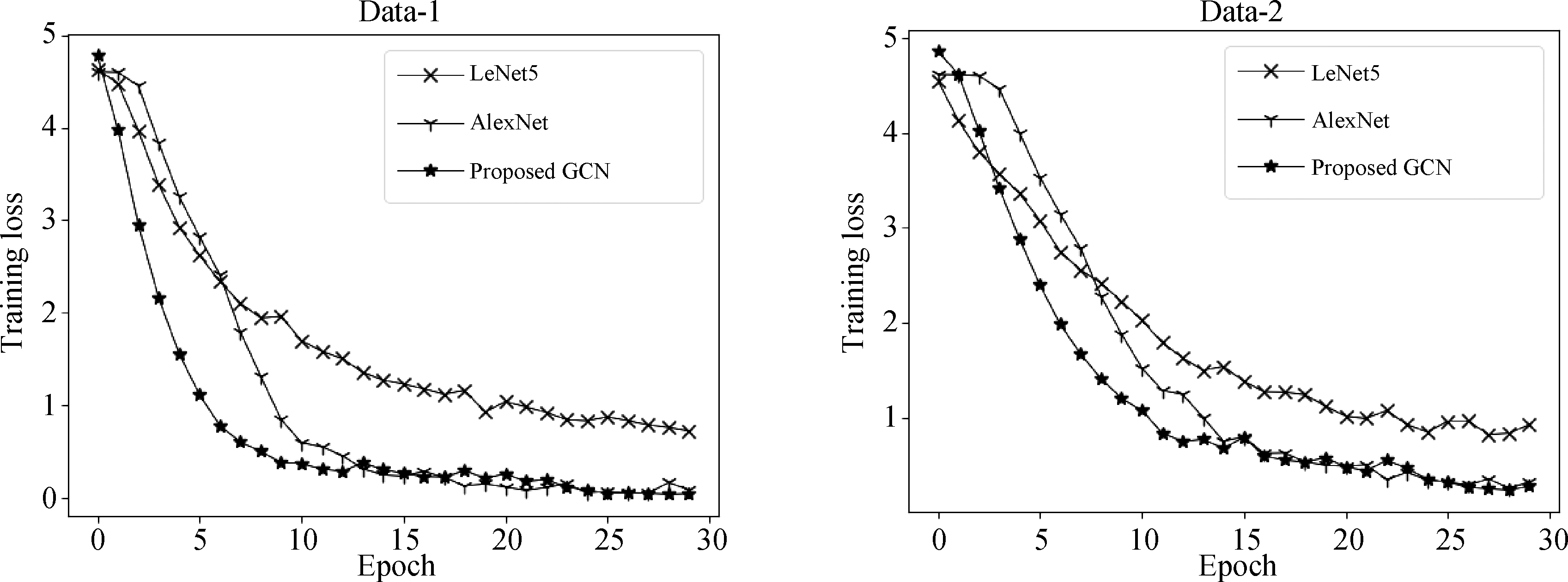
图10 训练损失变化曲线
Fig.10 Training loss curvs
点的特征相似度作为权值,通过度量邻接矩阵相似度进行图的识别。文献方法中,采用尺寸9×9和15×15的图块划分图像,在Data-1数据库中得到节点数为525和180的指静脉加权图,在Data-2中得到节点数为300和750的加权图,本文方法中构建节点数相同的指静脉加权图,实验结果如表4所示。
表4 对比实验结果
Tab.4 Compare experimental results
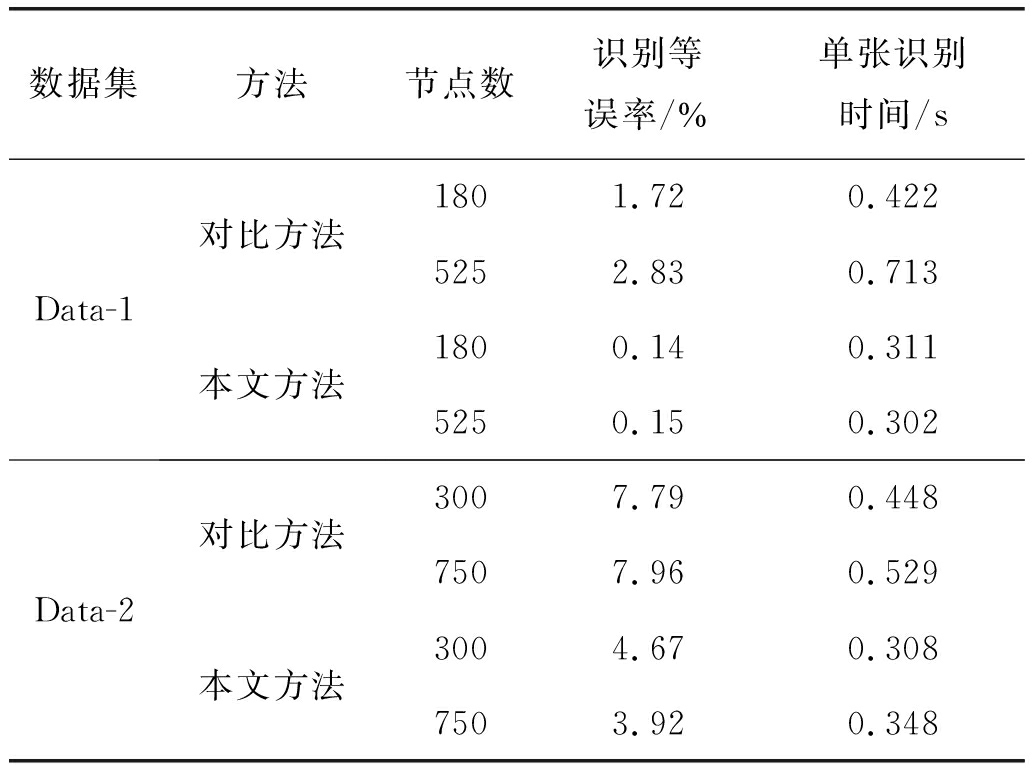
数据集方法节点数识别等误率/%单张识别时间/sData-1对比方法本文方法1801.720.4225252.830.7131800.140.3115250.150.302Data-2对比方法本文方法3007.790.4487507.960.5293004.670.3087503.920.348
由表4可知,本文提出的基于超像素构建指静脉图模型的特征表达方法识别精度较高,并且识别时间不随构建的图模型大小而有较大的改变,单张识别效率较高,这是说明模型提取的指静脉图级特征维度更小并且表征能力更好。
实验(3)中将本文提出的GCN模型与其他CNN模型(LeNet5[20]和AlexNet[21])进行对比,实验环境设置相同。Data-1和Data-2经过三种网络训练后,训练集损失变化曲线如图10所示。测试时提取所有网络输出的特征,本文方法中提取读出层图级特征,其他两种CNN网络中提取其第一层全连接层整合的一维特征,实验记录了所有网络训练时间、单张测试时间及识别等误率,如表5所示。
表5 不同模型的识别性能
Tab.5 Recognition performance of different models
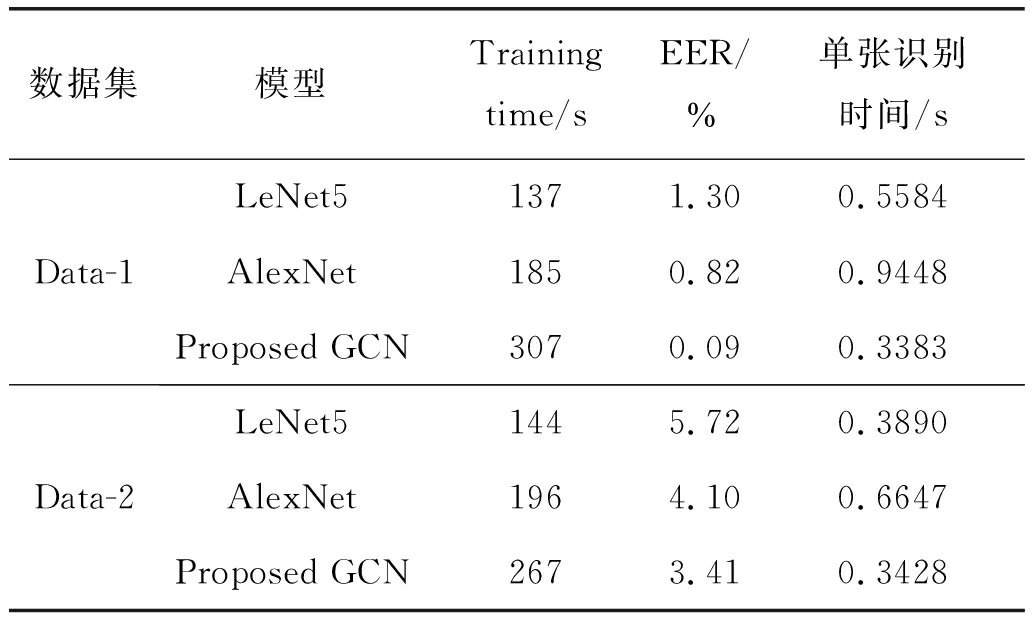
数据集模型Training time/sEER/%单张识别时间/sData-1LeNet51371.300.5584AlexNet1850.820.9448Proposed GCN3070.090.3383Data-2LeNet51445.720.3890AlexNet1964.100.6647Proposed GCN2673.410.3428
根据实验结果可知,虽然在训练时间上提出的GCN模型不具有一定的优势,但其收敛速度更快,在两数据集中均能取得更低的损失和识别等误率,并且其提取的特征单张识别时间较短,这是因为提出的GCN模型中读出操作能够提取图的低维高层的图级特征,该特征不仅维度更小并且特征区分度较高。
5 结论
本文提出了一种基于超像素构建指静脉加权图并改进GCNs网络提取图级特征的指静脉特征表达方法,首先通过SLIC超像素分割算法构建了一种完全图结构的加权图,选取超像素块灰度特征和空间特征作为节点特征,超像素块之间的空间亲密度作为权值;其次对于ChebyNet中的图卷积层Cheby利用特征分解最大特征值的简化得到简化后的SCheby,本文还提出应用可实现自适应池化节点的图池化方法gPool替代ChebyNet中的快速池化,并将gPool中的单层投影训练改进为多层投影训练的MgPool,本文还在网络中增加了基于最大池化的读出层,最终构建了全局池化结构的SCheby-MgPool模型。实验详细研究了影响模型的几个因素,并与文中引用的不同卷积层与池化层构建的GCNs模型对比,改进后的模型在识别效果和训练时间上都具有较好的性能;将本文提出方法与基于传统特征构建的指静脉加权图进行对比,实验证实本文方法提取的指静脉特征表征能力更强,并且匹配时间不受加权图大小的影响;与经典的CNN模型相对比本文提出的模型识别效果更好。
本文提出的方法仍有提升的空间:需进一步提高模型对光照和姿态的鲁棒性并在用户数量更大的数据库中验证本模型的可靠性。
[1] Yang Jinfeng, Shi Yihua. Towards finger-vein image restoration and enhancement for finger-vein recognition[J]. Information Sciences, 2014, 268(6): 33-52.
[2] 李振娟, 贾桂敏, 杨金锋, 等. 手指静脉图像血管网分形修复方法[J]. 信号处理, 2019, 35(8): 1334-1342.
Li Zhenjuan, Jia Guimin, Yang Jinfeng, et al. Vascular Networks Restoration Method for Finger-vein Images Based on Fractal[J]. Journal of Signal Processing, 2019, 35(8): 1334-1342.(in Chinese)
[3] 贾桂敏, 李树一, 杨金锋, 等. 指静脉红外图像特征不变性编码新方法[J]. 红外与激光工程, 2018, 47(9): 410- 416.
Jia Guimin, Li Shuyi, Yang Jinfeng, et al. Novel invariant feature encoding method for finger-vein IR images[J]. Infrared and Laser Engineering, 2018, 47(9): 410- 416.(in Chinese)
[4] 江波, 汤进, 罗斌. 计算机视觉中的图匹配方法研究综述[J]. 安徽大学学报: 自然科学版, 2017, 41(1): 29-36.
Jiang Bo, Tang Jin, Luo Bin. A survey on graph matching algorithms in computer vision[J]. Journal of Anhui University: Natural Science Edition, 2017, 41(1): 29-36.(in Chinese)
[5] Arakala A, Davis S A, Hao H, et al. Value of Graph Topology in Vascular Biometrics[J]. IET Biometrics, 2017, 6(2): 117-125.
[6] Ye Ziyun, Yang Jinfeng, Palancar J H. Weighted Graph Based Description for Finger-Vein Recognition[C]∥Chinese Conference on Biometric Recognition(CCBR). Springer, 2017: 370-379.
[7] 王春瑶, 陈俊周, 李炜. 超像素分割算法研究综述[J]. 计算机应用研究, 2014, 31(1): 6-12.
Wang Chunyao, Chen Junzhou, Li Wei. Review on superpixel segmentation algorithms[J]. Application Research of Computers, 2014, 31(1): 6-12.(in Chinese)
[8] Bruna J, Zaremba W, Szlam A, et al. Spectral networks and locally connected networks on graphs[J]. arXiv preprint arXiv: 1312.6203, 2014.
[9] Defferrard M, Bresson X, Vandergheynst P. Convolutional neural networks on graphs with fast localized spectral filtering[C]∥Proceedings of the Advances in Neural Information Processing Systems. Barcelona, Spain, 2016: 3844-3852.
[10] Dhillon I S, Guan Y, Kulis B. Weighted Graph Cuts Without Eigenvectors: A Multilevel Approach[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence (PAMI), 2007, 29(11): 1944-1957.
[11] Gao Hongyang, Ji Shuiwang. Graph U-Nets[J]. arXiv preprint arXiv: 1905.05178, 2019.
[12] Achanta R, Shaji A, Smith K, et al. SLIC Superpixels Compared to State-of-the-Art Superpixel Methods[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(11): 2274-2282.
[13] Si Zhang, Hanghang Tong, Jiejun Xu, et al. Graph convolutional networks: a comprehensive review[J]. Computational Social Networks, 2019, 6(1): 1-23.
[14] Zhang Muhan, Cui Zhicheng, Neumann M, et al. An End-to-End deep learning architecture for graph classification[C]∥AAAI Conference on Artificial Inteligence. New Orleans, 2018: 4438- 4445.
[15] Mohd Asaari M S, Suandi S A, Rosdi B A. Fusion of band limited phase only correlation and width centroid contour distance for finger based biometrics[J]. Expert Systems with Applications, 2014, 41(7): 3367-3382.
[16] Knyazev B, Taylor G W, Amer M R. Understanding attention in graph neural networks[C]∥Proceedings of the International Conference on Learning Representations(ICLR), Workshop on Representation Learning on Graphs and Manifolds, 2019.
[17] Kipf T N, Welling M. Semi-supervised classification with graph convolutional networks[J]. arXiv preprint arXiv: 1609.02907, 2017.
[18] Xu Keyulu, Hu Weihua, Leskovec J, et al. How Powerful are Graph Neural Networks?[C]∥Proceedings of the International Conference on Learning Representations(ICLR), 2019.
[19] Junhyun L, Inyeop L, JaeWoo K. Self-Attention Graph Pooling[C]∥Proceedings of the 36th International Conference on Machine Learning(ICML), 2019.
[20] Yann L, Leon B, Yoshua B, et al. Gradient Based Learning Applied to Document[J]. IEEE, 1998, 86(11): 2278-2324.
[21] Krizhevsky A, Sutskever I, Hinton G. ImageNet classification with deep convolutional neural networks[C]∥Advances in Neural Information Processing Systems, 2012: 1097-1105.



