1 引言
合成孔径雷达具有全天时,全天候,高分辨和不受云雾影响等优点,被广泛地应用于农业,水洋,军事等领域[1-2]。SAR对静止目标的成像技术已经趋于成熟,许多SAR处理器设计也是基于假设在合成孔径时间内目标是静止的,因此,经典的SAR成像技术无法得到静态场景运动目标的高分辨率图像。而在实际情况中,雷达探测的目标往往处于运动状态,因而实现SAR对运动目标高分辨率成像受到越来越多的关注[3- 4],在过去的几十年间,SAR对运动目标的成像算法主要集中在运动参数估计方面[5-7]。
ISAR孔径合成原理不同于SAR,ISAR正是利用目标的运动产生其对雷达的相对旋转来合成孔径。基于SAR,ISAR各自的优缺点,NJ Proter提出基于混合式的SAR/ISAR成像方法[8]。此后许多国内外学者在此领域展开研究,A.Aprile等人提出平动和转动补偿(Translational and Rotational Motion Compensation,TRMC)处理链用于SAR/ISAR混合成像[9],文献[10]中采用时频分析方法代替FFT得到目标的图像,此外,周鹏等人提出针对海面舰艇的SAR/ISAR混合成像算法[11-13]。SAR图像中存在多个运动目标,难以采用统一的相位补偿项获得高质量图像,M. Martorella等人提出了一种对SAR图像中运动目标的识别和重聚焦系统[14-16],首先检测SAR图像中运动目标,然后反向投影到回波域并重新作为ISAR处理的原始数据,该系统利用ISAR算法实现对SAR图像中运动目标的重聚焦。以上算法集中在对目标运动参数的估计以及时频分析方法得到目标的图像,在实际情况中,场景及目标的运动形态的复杂多变,运动目标不仅存在平动还存在三维运动,在这种情况下对目标的运动很难做出准确的估计。时频分析方法建立在非线性处理基础上,引入的交叉项也会对成像造成影响。
三维运动导致了目标的多普勒频率呈时变特性,难以得到高分辨率的目标图像。为了提高成像质量,需要选择等效转动的角速度较大且平稳的数据段。自适应时间窗是一种基于图像对比度的筛选方法[17],该方法以图像对比度为标准交替迭代成像时刻与时段来获得最优的数据段。ICBA是一种计算量相对较小的自聚焦算法,在ISAR成像中得到了成功的应用[18-19]。该算法以图像对比度为聚焦准则迭代搜索估计值,当对比度函数达到最大值时,ICBA的估计值最逼近真实值,并以此估计值补偿误差相位得到目标聚焦图像。
近年来,相位恢复算法在多个领域得到了广泛的应用[20-21]。该算法根据信号在某个变换域的幅度信息利用数字迭代算法恢复原始信号[22]。史洪印等人提出改进的相位恢复算法[23-24],充分利用传统成像方法得到的模糊图像信息作为迭代过程的先验条件以提高算法的收敛速度,对平移运动目标取得可靠、准确的重建结果。但当目标的旋转增大时,相位恢复算法无法对旋转运动引起的多普勒频移校正。
针对上述问题,本文提出一种基于相位恢复原理和ISAR算法的运动目标相位误差校正方法。首先,对SAR图像中模糊的运动目标提取,利用反演算法得到回波域数据;然后利用自适应时间窗算法和ICBA算法实现对运动目标的运动参数估计并粗补偿;最后利用相位恢复算法实现对误差相位的精确补偿。该方法充分利用粗补偿得到的模糊图像信息作为相位恢复算法的先验条件,提高了算法的收敛性,理论分析与仿真实验进一步验证了本文所提方法的有效性。
2 运动目标成像模型
相对于静止目标成像模型,当成像场景中有运动目标时,由于雷达与目标同时发生运动,因此两者之间相对运动的距离不再符合可预测的双曲线模型,而会由于动目标的速度、加速度和旋转的不同产生不同的成像结果。本文所研究的目标模型为海面上的船只,其拥有更复杂的运动形态(侧摆,俯仰,偏航),假设SAR处于正侧视工作状态,雷达与目标船只的几何位置关系如图1所示。定义T=(X,Y,Z)为固定参考坐标系,T′=(X′,Y′,Z′)为运动坐标系,随船只运动而运动。方位向时间为t,雷达的方位向速度为V,t=0时,目标位于(x0,y0)处,目标中心O′到雷达接收机的距离为R0,场景中动目标的方位向速度为νx,距离向速度为νy。三维转动的角度分别为:侧摆θr,俯仰θp,偏航θy,θp,r,y(t)=Ωp,r,y(t)t+φp,r,y,Ω(t)表示三维转动的瞬时角速度,φp,r,y表示三维转动初相。
t时刻目标到雷达平台的瞬时距离为:
(1)
将(1)改写成如下形式:
(2)
其中R(t)为目标的运动引起目标到雷达距离的改变量。
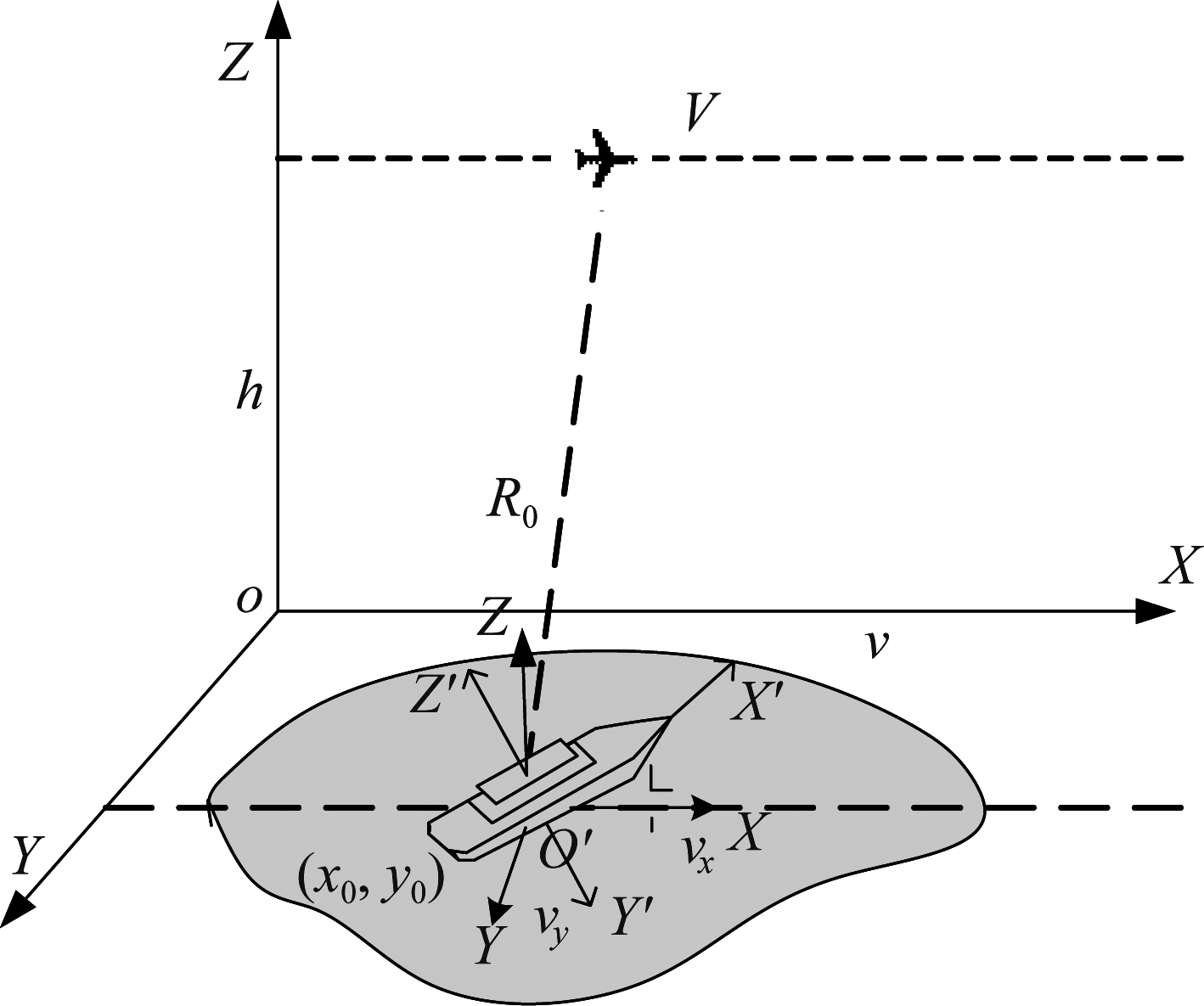
图1 SAR运动目标空间几何模型
Fig.1 SAR geometric model of moving target
假设雷达在合成孔径时间内发射M组步进频脉冲串,每个脉冲串含N个子脉冲,则第m组第n个子脉冲信号可以表示为:
sT(τm,n)=ωm,n(τ)cos(-j 2πfm,nτm,n)
(3)
其中ω(τ)为矩形窗函数,τ为距离向时间, fm,n为第m组第n个子脉冲的中心频率,设步进频率间隔Δf不变,起始频率为f0,则fm,n=f0+(mN+n)Δf。
假设目标由Q个散射点组成,那么,雷达接收到的回波信号可近似表示为:
(4)
其中Aq表示第q个散射点的散射强度振幅。
回波信号中包含雷达平台运动及目标的运动,直接对回波信号运用成像算法难以得到聚焦的图像,本文提出一种对SAR场景中运动目标重新聚焦方法,其重聚焦过程如图2所示。
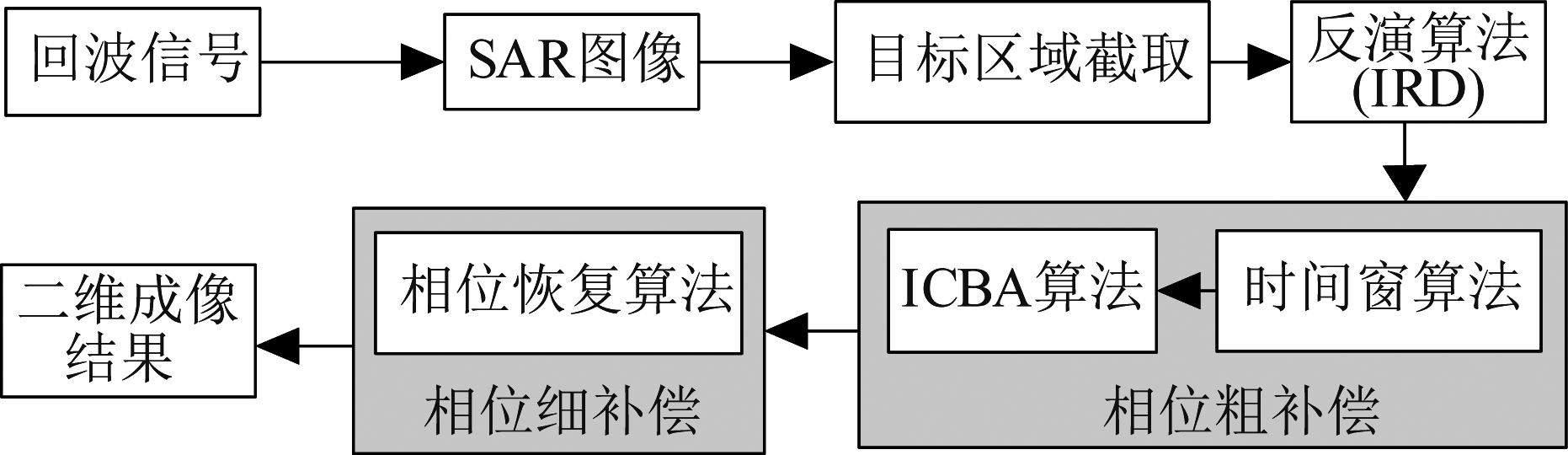
图2 SAR场景中运动目标重聚焦流程图
Fig.2 Refocusing flow chart of moving targets in SAR scenarios
3 SAR图像运动目标提取
SAR通过处理大量的数据来获得SAR图像,数据可以包含多个目标,每个目标拥有不同的运动形态,因此不能使用形成SAR图像的原始回波数据作为ISAR处理阶段的输入数据,需要对SAR图像中运动目标提取,得到只包含单一目标及少量杂波的回波数据。本文采用经典的RD成像算法得到SAR场景图像,逆RD算法通常通过二维快速傅里叶逆变换(IFFT)实现,在反演过程中不需要进行逆运动补偿的处理,平台的运动在SAR聚焦成像过程中已经补偿,可视为雷达静止,这与ISAR成像系统相似,因此,经平台运动补偿和IRD算法处理后信号可以近似表示为:
(5)
其中Rq(t)表示t时刻第q个散射点到雷达平台的剩余距离,此距离并非实际散射点到雷达的距离,而是由于运动引起的目标到雷达相对于静止场景中心到雷达的距离偏差。ISAR处理过程正是要移除这一项,当目标的尺寸远小于雷达到目标的距离时可以近似得到:
(6)
其中R0(t)表示目标平动引起的剩余距离量,
为用于标识目标上散射点的列向量,iLOS为雷达视线方向,在观测时间内R0(t)可二阶近似展开为:
(7)
其中νr,ar分别表示目标的径向速度和径向加速度。
因此式(5)可以表示为:
exp(-jχn(fm,n,t))
(8)
其中
(9)
4 基于ISAR算法的运动目标重聚焦
4.1 基于自适应时间窗算法的旋转补偿
当目标的旋转角度变化增大时,由角度变化引起的多普勒频率时变将不可忽略,如果仅通过目标的平移运动来选择时间帧,得到的图像将会很模糊,因此需要引入自适应时间窗,图3是ISAR成像模型。
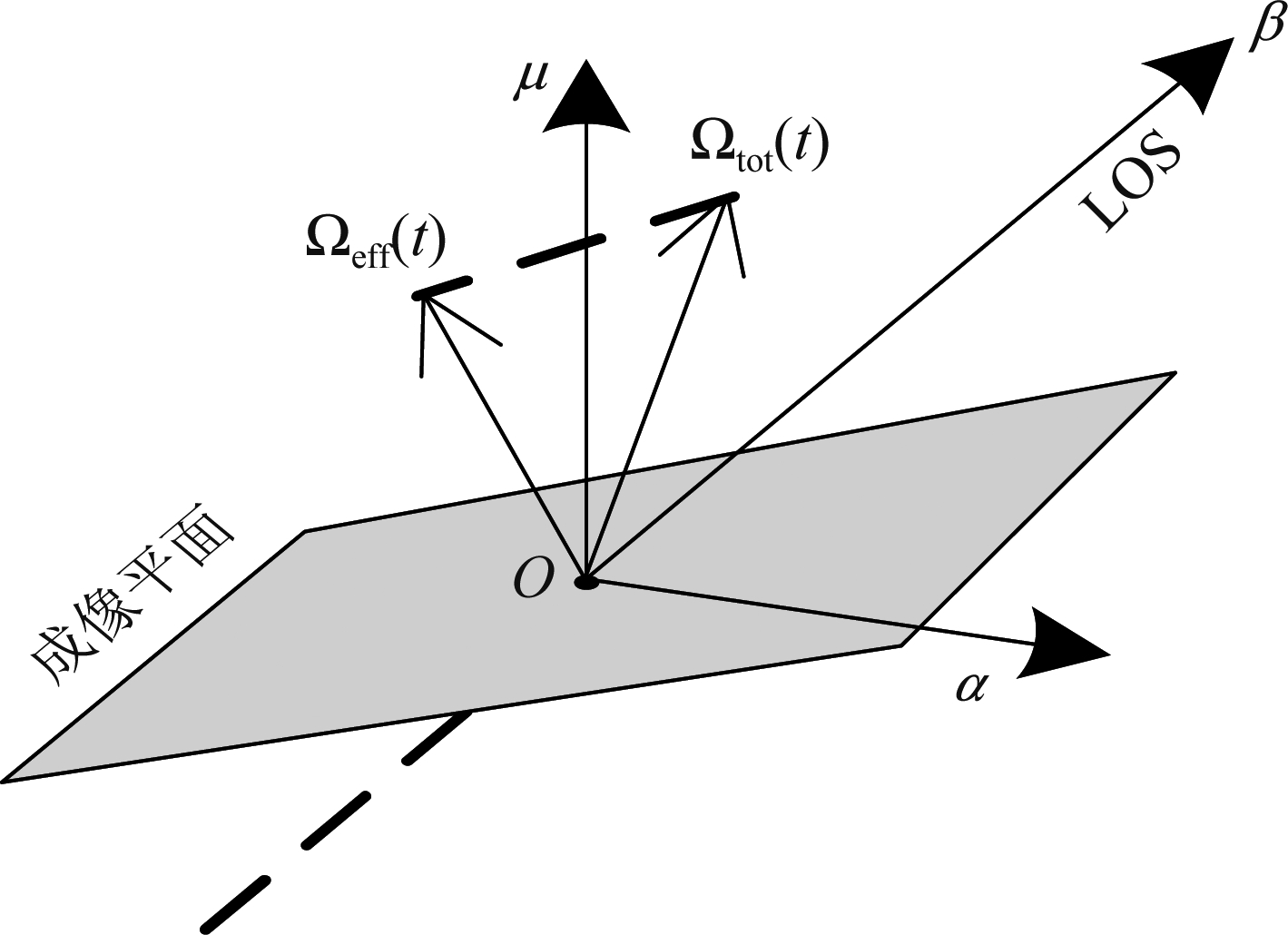
图3 ISAR成像模型
Fig.3 ISAR imaging model
β与雷达视线方向重合,
表示目标的旋转矢量,是通过投影得到的有效旋转矢量,图像平面正交于有效旋转矢量。多普勒频率
可以看出当目标经历复杂的角运动时,多普勒频率取决于角运动和散射体位置,并且对时间的依赖性很强,多普勒频率-时间关系是一条起伏的曲线,在曲线的波峰,波谷多普勒频率可以认为是不变的,并且发现在该点有较高的IC值,因此本文采用自适应时间窗来解决这一问题,通过最优化图像对比度得到合适的窗中心时间和窗口宽度Topt,ΔTopt,即解决以下优化问题:
(Topt,ΔTopt)=arg(max[IC(T,ΔT)])
(10)
其中
(11)
其中I(T,ΔT)=|2DFT[sR(fm,n,t)]|2表示图像强度,A{·}表示图像空间的均值。
经时间窗处理后在ΔTopt内可以认为目标的旋转矢量近似不变,即
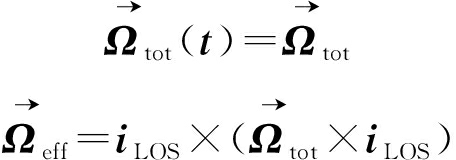
(12)
当目标的旋转矢量不变时,ISAR的图像平面也是确定不变的,所有散射点在图像平面中的位置可以用距离向,方位向坐标系(y1,y2)表示,则公式(9)可改写为:
(13)
将式(13)二阶泰勒展开近似得到:
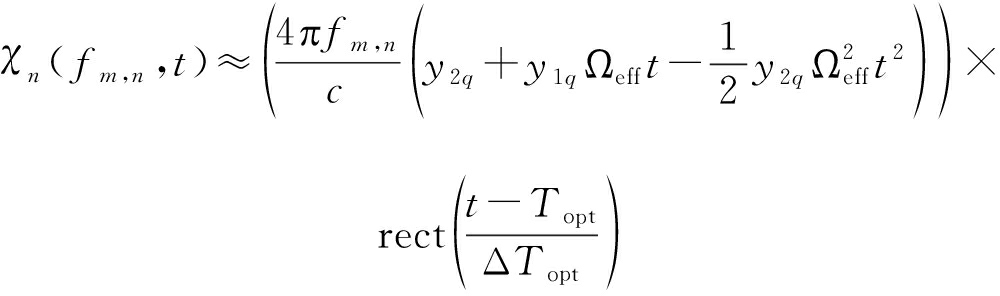
(14)
在ΔTopt内目标的多普勒fd不变,因此第三项可忽略不计,将式(14)带入式(8)得:
sR(fm,n,t,Topt,ΔTopt)=TW[sR(fm,n,t)]≈
(15)
4.2 基于ICBA的平动粗补偿
ICBA是基于图像对比度的参数估计方法,运用RT(radon transform)变换和半穷举搜索(semi-exhaustive search)对运动参数预估计,然后解决最优问题,找到使图像对比度最大的值即为最终的估计值,ICBA算法的实现框图如图4所示。
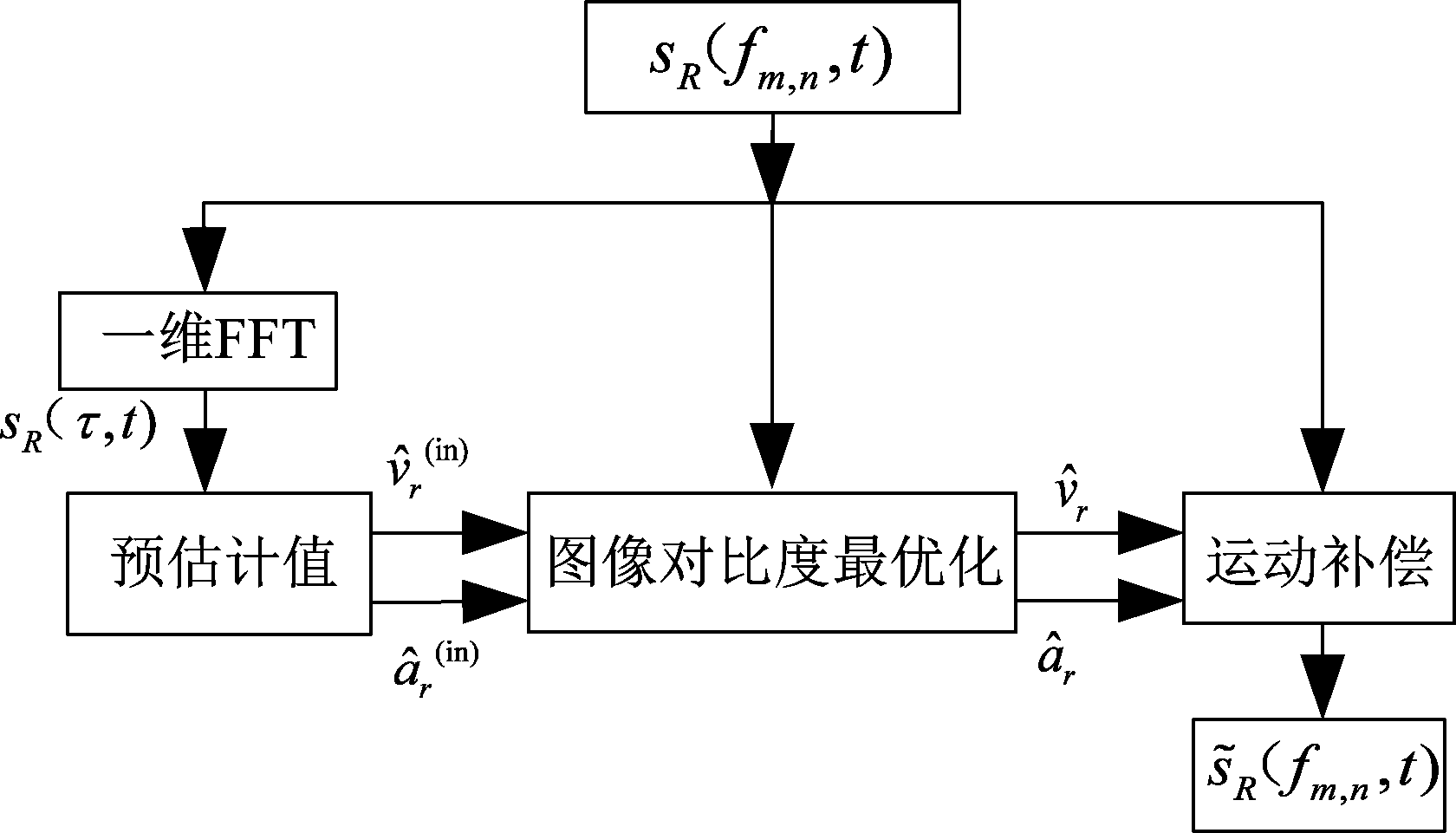
图4 ICBA算法流程图
Fig.4 ICBA algorithm flow chart
将sR(τ,t)写成采样形式sR(τ,kTr),Tr为脉冲持续时间,k=-K/2,-K/2+1,…,K/2-1,K为采样数,为了得到距离坐标r,假设:
(1)散射点距离轨迹近似满足线性关系,即
(2)聚焦点R0(kTr)同样近似满足线性关系,即
如果上述(1),(2)大致满足,则预估计值
便可通过计算距离轨迹的平均斜率得到
为距离轨迹与时间轴的夹角,
其中RTsR(r,φ)表示对sR(τ,kTr)进行RT变换。
(16)
预估计值
通过在区间[amin,amax]内进行线性搜索使图像对比度最大得到,即:
(17)
解决全局最优化问题得到最终估计值
(18)
本文中只考虑目标存在径向速度,设ar=0,则经ICBA算法补偿后的信号可以表示为:
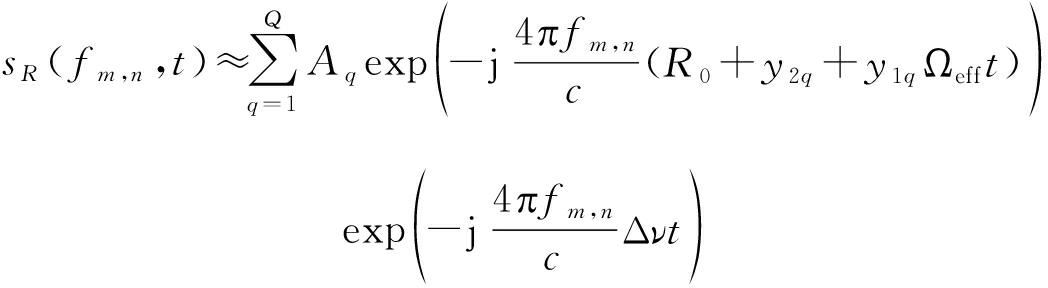
(19)
其中
表示估计误差。
对公式(19)取模值得:
|sR(fm,n,t,Topt,ΔTopt)|=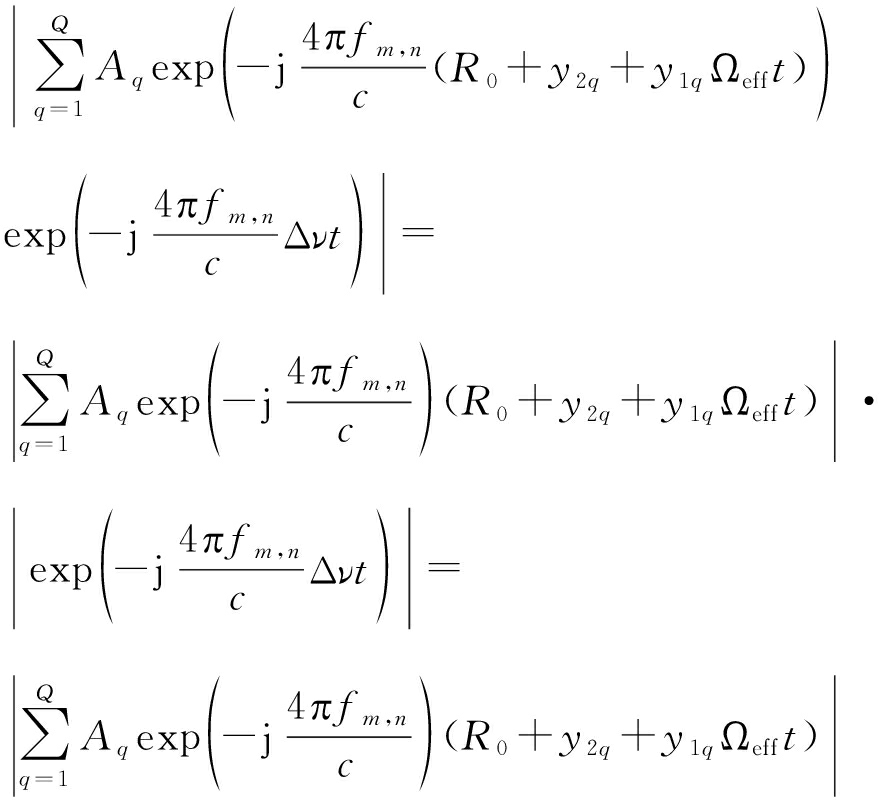
(20)
可以看出,经ICBA算法和自适应时间窗处理后信号的模值不受剩余速度分量Δν的影响,因此,可以应用相位恢复算法对剩余的多普勒分量补偿。
5 基于相位恢复算法的运动细补偿
现有的测量仪器只能获取信号的幅度信息而无法获取信号相位信息,如何根据已有的信号幅度信息去恢复相位信息,从而重构原始信号就是相位恢复问题。本文采用的是改进的OSS相位恢复算法[23],传统的OSS相位恢复算法由于可以利用的先验信息只有幅度信息,无法保证结果的唯一性,改进的OSS相位恢复算法利用传统成像算法得到的模糊图像对时域支撑域进行约束以及模糊成像的误差相位信息代替OSS算法中的初始随机输入信号,这样就避免了从一个完全随机的噪声开始进行迭代,同时利用平滑高斯滤波器,来滤除支撑域外的干扰信息,保留支撑域内部的信息,减小对迭代过程的影响,提高迭代过程的收敛速度,以降低陷入局部最小值的概率。
输入复信号表示为:
f(x,y)=|f(x,y)|·exp[jφ(x,y)]
(21)
f(x,y)傅里叶变换的输出为:
g(u,ν)=F[f(x,y)]
=|g(u,ν)|·exp[jφ(u,ν)]
(22)
其中|f(x,y)|和φ(x,y)分别表示图像域中的幅度信息与相位信息,|g(u,ν)|和φ(u,ν)分别表示傅里叶域中的幅度信息和相位信息,F为傅里叶变换。相位恢复OSS算法通过图像域和频域中对信号的幅度信息和相位信息进行交替迭代,最终得到信号的相位信息和原始复信号。
本算法中将式(19)所得复信号作为相位恢复OSS算法的输入信号,其误差相位:
(23)
式(23)作为迭代的相位初始值,经过相位恢复OSS算法迭代求解后得到输出信号为:
(24)
相位恢复算法消除因剩余径向速度引起的多普勒频移项,得到多普勒频率时不变的输出信号,实现对相位的精确补偿。
6 实验结果与分析
我们进行了两组仿真实验验证本文所提方法的有效性,实验所用雷达参数如表1所示,图5(a)为模拟的散射点小船模型,本节的仿真成像中都是应用此模拟图,图5(b)为时间窗处理后信号幅度谱。
表1 雷达参数
Tab.1 Radar parameters
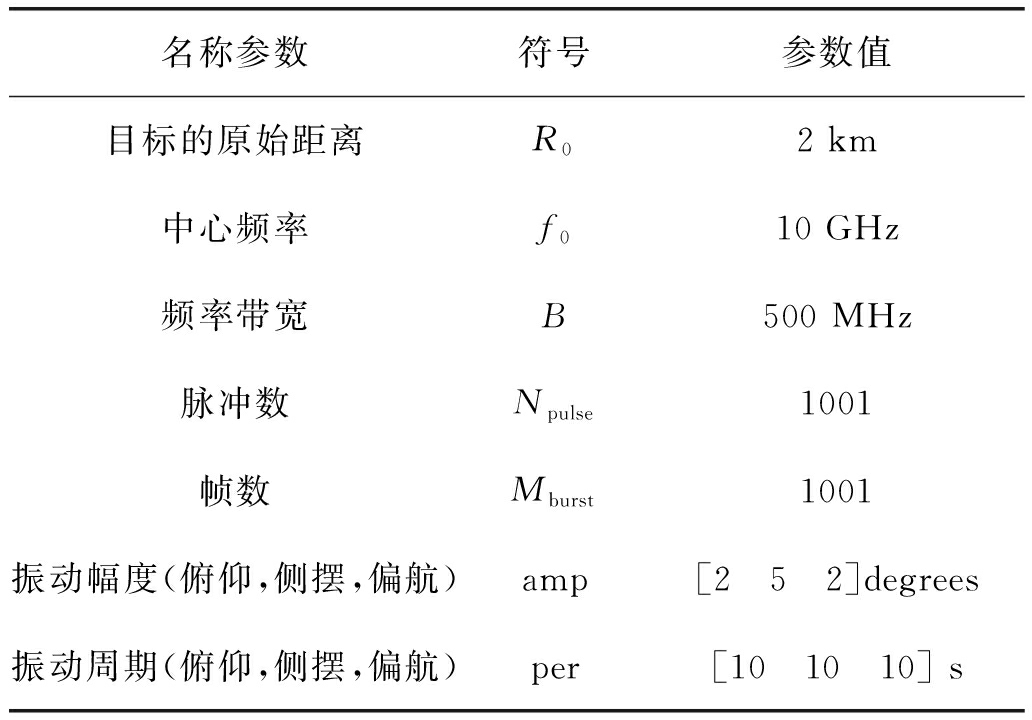
名称参数符号参数值目标的原始距离R02 km中心频率f010 GHz频率带宽B500 MHz脉冲数Npulse1001帧数Mburst1001振动幅度(俯仰,侧摆,偏航)amp[2 5 2]degrees振动周期(俯仰,侧摆,偏航)per[10 10 10] s
6.1 仿真实验一
当小船速度V=30 km/h时,小船在杂波背景下的SAR场景如图6(a)所示,截取后的子图像如图6(b)所示,OSS算法迭代次数为200次,支撑域大小设置为50×100。从图6(c)成像结果可以看出,由于目标速度的存在,成像结果呈现出明显散焦现象,图6(d)为本文算法恢复结果,对比两图可以看出本文算法对运动目标进行了精确的重聚焦。选取四个散射点进行剖面图分析,图中分别用p1,p2,p3,p4标出,图6(e)和图6( f )为p1,p3点方位向和距离向剖面图,图6(g)和图6(h)为p2,p4点方位向和距离向剖面图,可以看出,在ICBA算法及自适应时间窗算法下,方位向和距离向回波旁瓣峰值略高,而相位恢复对旁瓣抑制性能大幅度提高,聚焦更好。
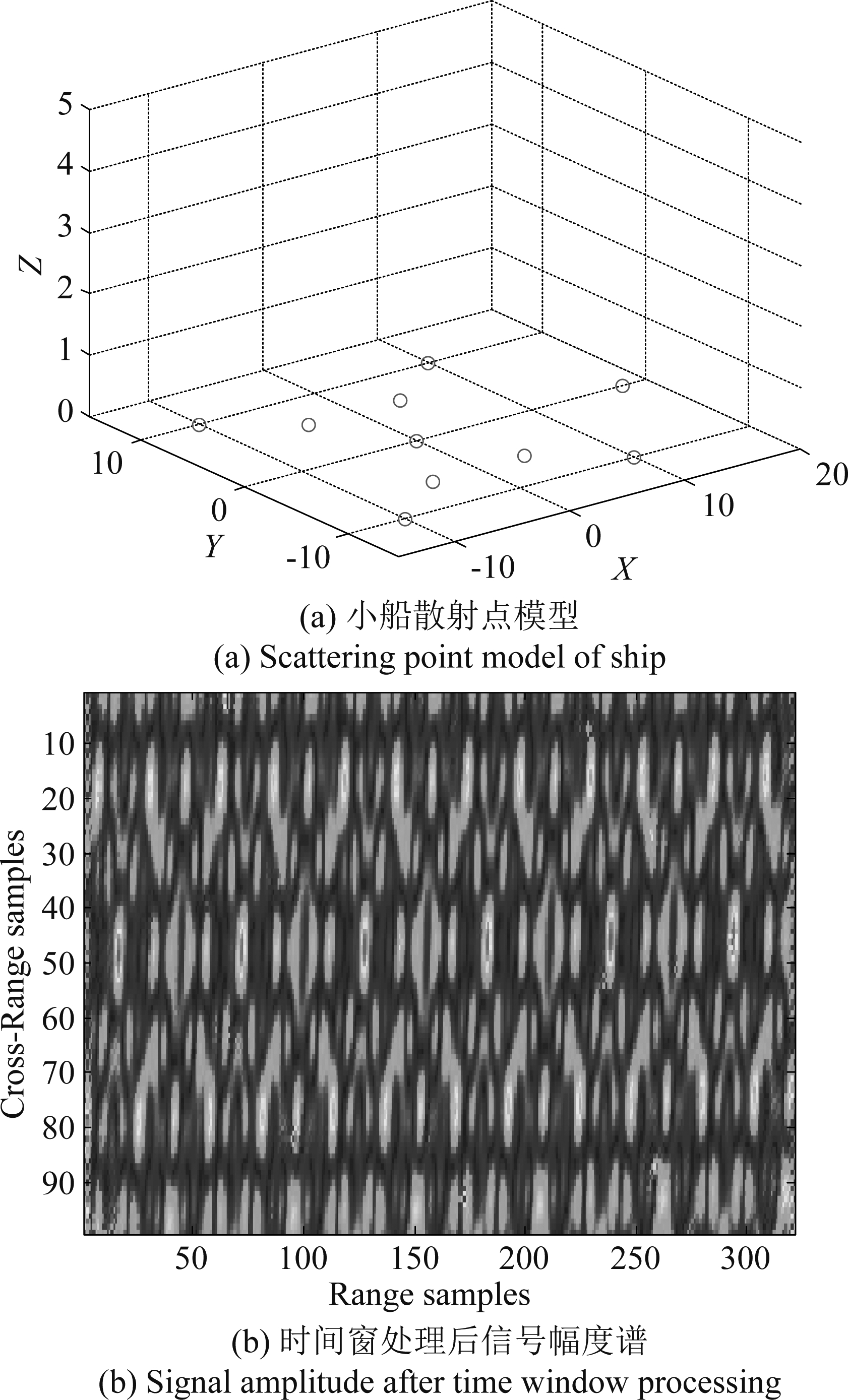
图5 散射点模型与时间窗处理后信号幅度谱
Fig.5 Scattering point model and signal amplitude after time window processing
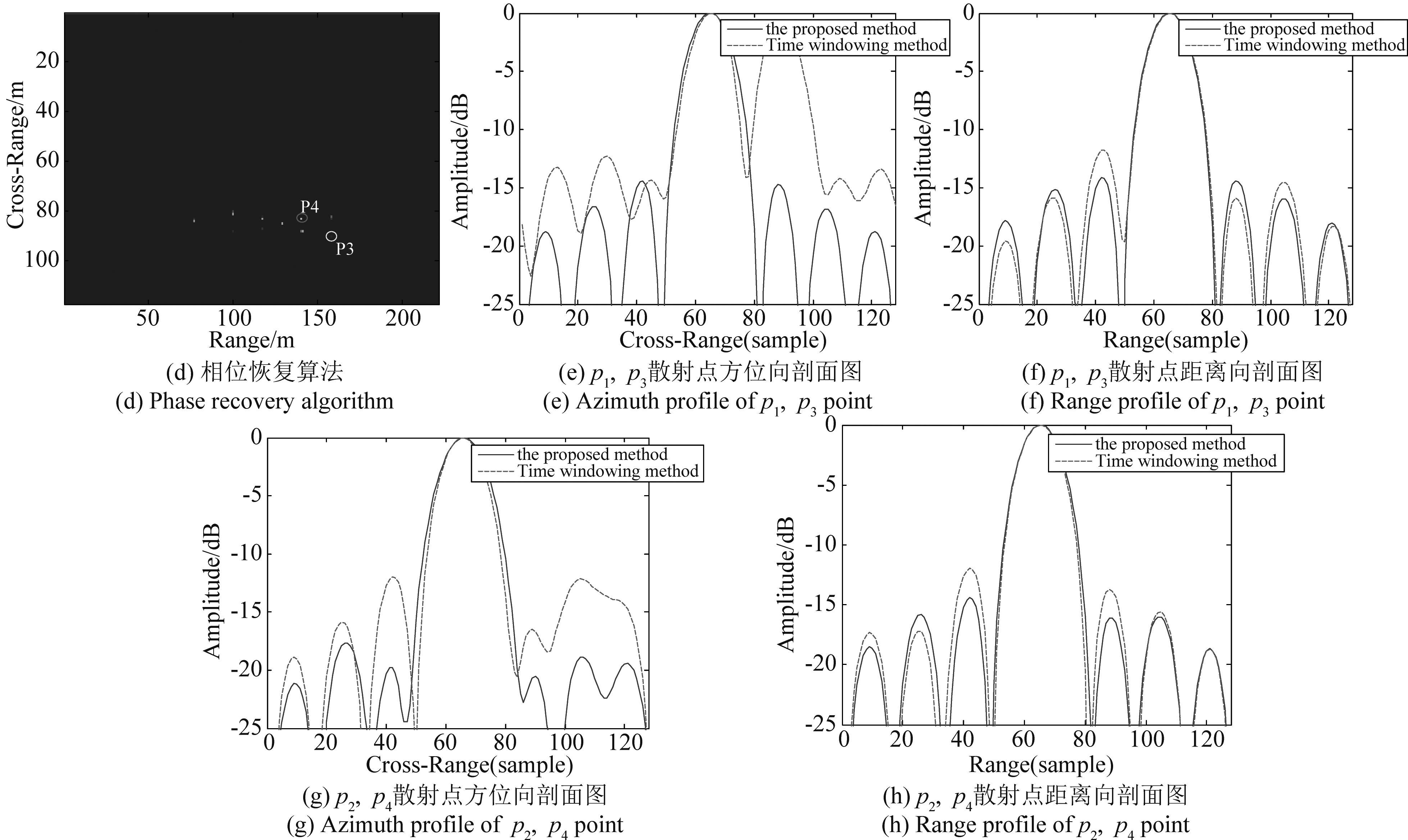
图6 V=30 km/h成像结果图
Fig.6 Imaging results of V=30 km/h
6.2 仿真实验二
当小船速度增加到50 km/h,对比图6(b),图7(b)可以看出目标速度增大,SAR图像散焦程度变大,图7(c)所示的ICBA算法及自适应时间窗算法成像结果对比于图6(c)散焦程度更严重,图7(e)和图7( f )分别为p5,p7点在方位向和距离向剖面图,图7(g)和图7(h)分别为p6,p8点在方位向和距离向剖面图,对比于图6(e)、图6(f)和图6(g)、图6(h)可以看出旁瓣幅度增大,说明速度越大目标的散焦越严重,图7(d)为本文算法恢复结果,对比7(d),6(d)两图可以看出本文算法均解决了运动目标成像散焦的问题。
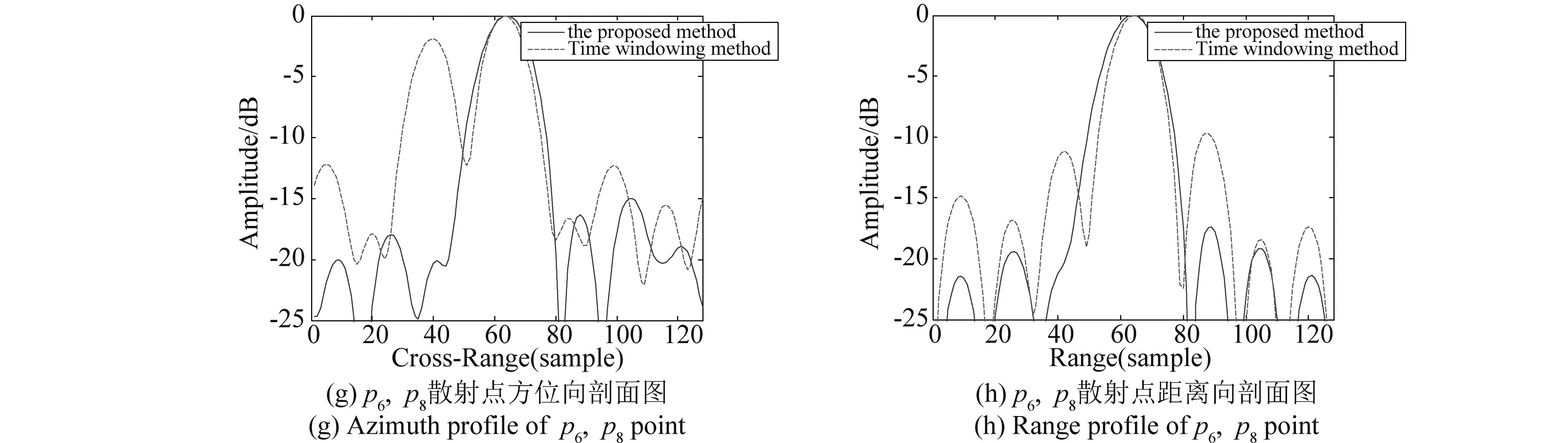
图7 V=50 km/h成像结果图
Fig.7 Imaging results of V=50 km/h
通过以上仿真实验结果及分析可以看出,本文提出的方法有效的补偿了目标的剩余平动问题,实现了运动目标的高分辨率成像。
7 结论
针对SAR图像中运动目标由于运动引起的成像模糊问题,本文提出一种基于相位恢复原理和ISAR算法的运动目标相位误差校正方法,该方法消除了目标运动引起的多普勒频移,得到了清晰的图像。首先提取和恢复SAR图像中选定的运动目标回波域数据作为ISAR处理原始数据;然后运用ISAR算法对误差相位粗补偿得到模糊图像;最后利用相位恢复算法对估计剩余的多普勒分量补偿实现对运动目标的重聚焦,充分利用粗补偿得到的模糊图像信息作为相位恢复算法的先验条件,提高算法的收敛性。本文模拟海面稀疏场景中船只同时存在平移运动及三维转动进行仿真实验,最终成像结果证明了该方法的有效性。
[1] 汪玲, 岳怡然, 熊倩. 利用多普勒分辨率的FMCW SAR成像算法[J]. 信号处理, 2017, 33(7): 961- 969.
Wang Ling, Yue Yiran, Xiong Qian. A FMCW SAR Imaging Algorithm Capable of Exploiting Doppler Resolution[J]. Journal of Signal Processing, 2017, 33(7): 961- 969.(in Chinese)
[2] 欧建平, 李伟, 张军. 低飞平台大斜视SAR的 ω-k 成像算法实现[J]. 信号处理, 2014, 30(1): 1- 6.
Ou Jianping, Li Wei, Zhang Jun. ω-k Imaging Algorithm for SAR with Low Height and Large Squint Angle[J]. Journal of Signal Processing, 2014, 30(1): 1- 6.(in Chinese)
[3] Li Z Y, Wu J J, Liu Z T, et al. An Optimal 2-D Spectrum Matching Method for SAR Ground Moving Target Imaging[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(10): 5961-5974.
[4] Baumgartner S V, Krieger G. Simultaneous High-Resolution Wide-Swath SAR Imaging and Ground Moving Target Indication: Processing Approaches and System Concepts[J]. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2017, 8(11): 5015-5029.
[5] Noviellp C, Fomaro G, Martorella M. Focused SAR image formation of moving targets based on Doppler parameter estimation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(6): 3460-3470.
[6] Wang X Y, Wang R, Li N, et al. A method of estimating the velocity of moving targets for use in high-resolution wide-swath SAR imaging[J]. Remote Sensing Letters, 2018, 9(4): 305-313.
[7] 杨娟娟, 贺亚鹏, 张选民, 等. 机载高分辨滑动聚束SAR成像处理方法[J]. 信号处理, 2016, 32(4): 479- 487.
Yang Juanjuan, He Yapeng, Zhang Xuanmin, et al. The Method of Imaging for Air-borne Sliding Spotlight SAR[J]. Journal of Signal Processing, 2016, 32(4): 479- 487.(in Chinese)
[8] Porter N J, Tough R J A. Processing Schemes for Hybrid SAR/ISAR Imagery of Ships[C]∥IEEE Colloquium on Radar and Microwave Imaging, 1994: 5/1-5/5.
[9] Aprile A, Mscri Pellizzeri T, Mauri A, et al. Application of the TRMC processing chain to SAR/ISAR imaging[C]∥Proceedings of the 6th Europe Radar Conference, 2009: 429- 432.
[10] Cai Y N, Chong J S. The Study of SAR-ISAR Ship Imaging Based on Time-Frequency Analysis[C]∥IEEE Youth Conference on Information, Computing and Telecommunication, 2009: 158-161.
[11] Chen Y M, Zhou P, Dai Y S. Application of an existing approach to refocusing maritime moving targets on Radarsat-2 SLC images[C]∥2015 IEEE 5th Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), 2015: 502-506.
[12] 周鹏, 陈艳梅, 刘希红, 等. 海上船只目标多角度成像技术[J]. 中国海洋大学学报(自然科学版), 2017, 47(2): 62- 69.
Zhou Peng, Chen Yanmei, Liu Xihong et al. Imaging techniques from different squint angles for marine ships[J]. Periodical of Ocean University of China, 2017, 47(2): 62- 69.(in Chinese)
[13] Jiang Y, Wang H. Hybrid SAR/ISAR imaging of ship targets based on parameter estimation[J]. Remote Sensing Letters, 2017, 8(7): 657- 666.
[14] Martorella M, Pastina D, Berizzi F, et al. Spaceborne Radar Imaging of Maritime Moving Targets With the Cosmo-SkyMed SAR System[J]. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2014, 7(7): 2797-2810.
[15] Preiss M, Gray D. A, Stacy N. J. S. Detecting scene changes using synthetic aperture Radar interferometry [J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(8): 2041-2054.
[16] Martorella M, Giusti E, Beizzi F, et al. ISAR based technique for refocusing non-cooperative targets in SAR images[J]. IET Radar. Sonar, Navigation, 2012, 6(5): 332-340.
[17] Martorella M, Beizzi F. Time windowing for highly focused ISAR image reconstruction[J]. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(3): 992-1007.
[18] Berizzi, F, Cosini G. Autofocusing of Inverse Synthetic Aperture Radar Images Using Contrast Optimization[J] IEEE Transactions on Aerospace and Electronic Systems, 1996, 32(3): 1185-1197.
[19] Martorella M, Beizzi F, Haywood B. A contrast maximization based technique for 2D ISAR autofocusing[J]. IEEE Proceedings-Radar, Sonar and Navigation, 2005, 152(4): 253-262.
[20] Netrapalli P, Jain P, Sanghavi S. Phase Retrieval Using Alternating Minimization[J]. IEEE Transactions on Signal Processing, 2015, 63(18): 4814- 4826.
[21] Shenoy B A, Mulleti S, Seelamantula C S. Exact Phase Retrieval in Principal Shift-Invariant Spaces[J]. IEEE Transactions on Signal Processing, 2016, 64(2): 406- 416.
[22] Rodriguez J A, Xu R, Chen C C, et al. Oversampling smoothness: an effective algorithm for phase retrieval of noisy diffraction intensities[J]. Journal of Applied Crystallography, 2013, 46(2): 312-318.
[23] Shi H Y, Xia S X, Tian Y. ISAR imaging based on improved phase retrieval algorithm[J]. Journal of Systems Engineering and Electronics, 2018, 29(2): 278-285.
[24] Shi H Y, Yang T, Qiao Z J. ISAR autofocus imaging algorithm for maneuvering targets based on phase retrieval and Gabor wavelet transform [J]. Remote Sensing, 2018, 10(11): 1810.
