1 引言
直方图均衡算法因其简单、快速、有效,已在图像增强中得到广泛的应用[1]。传统直方图均衡算法根据直方图数据生成的映射表调整图像灰度级,由于其数据的不加选择性,导致结果图中常出现过度增强、细节丢失和均值漂移等问题。为改善以上缺点,出现了众多的直方图均衡改进算法。这些算法可按不同属性进行分类,其他划分方法可参考综述文献[2- 4]。本文在此根据是否具有亮度保持属性进行简单阐述。
传统直方图均衡(THE)存在亮度均值漂移的缺陷,导致图像亮度发生明显变化。影视图像的艺术效果需要在特定的背景环境下拍摄。比如对于夜晚的拍摄画面的增强不能亮如白昼。视频传输中若前后两帧图片的亮度变化明显,会引起人眼的眩晕感。因此部分改进的直方图均衡(HE)算法通过保护图像的亮度来实现亮度保持性。Kim最早于1997年提出的BBHE[5](Brightness preserving Bi-Histogram Equalization)根据图像亮度均值分割直方图,并确定子直方图的动态范围,因而使BBHE具有一定的亮度保持性能。此后基于BBHE的改进算法[6-11]不断被提出,如使用亮度中值和OTSU分割点代替亮度均值分割点的BHEMHB[6]和TOHE[7]。Milos等人在2016年采用递归的思想确定子直方图动态范围,并提出了DRSIHE[12](Dynamic Recursive Sub-image Histogram Equalization)。
亮度保持类算法虽然可以在一定程度上保持图像的亮度不变。但是在工业和军事应用中如工业测量和安防布控等,需要改变图像亮度以获取清楚的图像前景或背景信息。因此,有学者在保持THE的亮度不保持特性下,针对THE所导致的过度增强、细节丢失等问题,提出一系列的直方图修正方法。Wang等人使用映射函数,在2007年提出了WTHE[13](Weighted Threshold Histogram Equalization),实现提升直方图小数据并抑制尖峰的功能。Kuldeep等人于2014年提出了ESIHE[14](Exposure based Sub Image Histogram Equalization),它先按阈值钳位直方图,再按取亮度均值反向分割直方图,最后进行子直方图均衡。Shih-Chia等人在2016年提出了AGCWD[15](Adaptive Gamma Correction with Weighting Distribution),算法先后对直方图的概率密度和灰度级进行两次Gamma校正。S. lee等人于2018年提出RDST[16](Ramp Distribution-Based Contrast Enhancement Techniques and Over-Contrast Measure),算法使用斜分布函数对全局升序直方图进行修正,进而自适应的确定直方图的钳位阈值。Chen引入对比度和信息熵两种客观指标,在2019年提出了EPMP[17](Image Contrast Enhancement and Image Entropy Preservation),它将恒等映射结合直方图均衡映射曲线,加权求和得到映射曲线。但算法对于动态范围较小的图像增强效果不足。
为了进一步提升亮度不保持算法的细节提升能力,有学者提出了二维直方图均衡算法[18-19]。Kim等人在2016年提出了TDHE[20](2D Histogram Equalization),算法对于具有相同灰度差区域中的暗区分配更多权重,以提升图像细节。
以上算法均为全局处理,为改善图像过度增强问题,有学者提出局部增强算法。Pizer 等人在1990年首次提出CLAHE[21](Contrast Limited Adaptive Histogram Equalization),对分块图像进行均衡和插值处理,实现了对比度限制的功能。Yakun Chang等人在2018年对CLAHE进行了改进,提出ACLAHE[22](Automatic Contrast Limited Adaptive Histogram Equalization with Dual Gamma Correction),它使用纹理性自适应地设置直方图的钳位值,再使用双伽玛校正。
此外,在大数据、数字化社会和神经网络算法的高速发展的背景下,基于深度学习的图像增强算法[23]逐渐受到研究人员的关注。
为拓展应用面,提升直方图均衡算法的通用性,本文提出一种非亮度保持算法。首先介绍图像质量渐变模型,该模型输出得到图像序列,并统计每张图像的信息熵和对比度值;其次本文设计一种基于信息熵与对比度的混合优化模型来求解序列图像的统计参数,确定序列中最佳图像;最后本文提出了一种可提升主观感受、保护图像细节的直方图后处理方法。
2 图像渐变模型
CLAHE[21]将图像的直方图按固定阈值(直方图数组的均值)钳位后,再将被钳位部分的像素总数平均分配到全部灰度范围上。
本文受CLAHE[21]的钳位再分配方法的启发,设计一种图像质量渐变模型。在遍历钳位阈值的过程中,阈值从小到大变化,输出图像的质量也随之变化,即输出为原图到经典HE的动态变化序列图。渐变序列图如下图所示:

图1 质量渐变序列图
Fig.1 Quality gradient sequence images
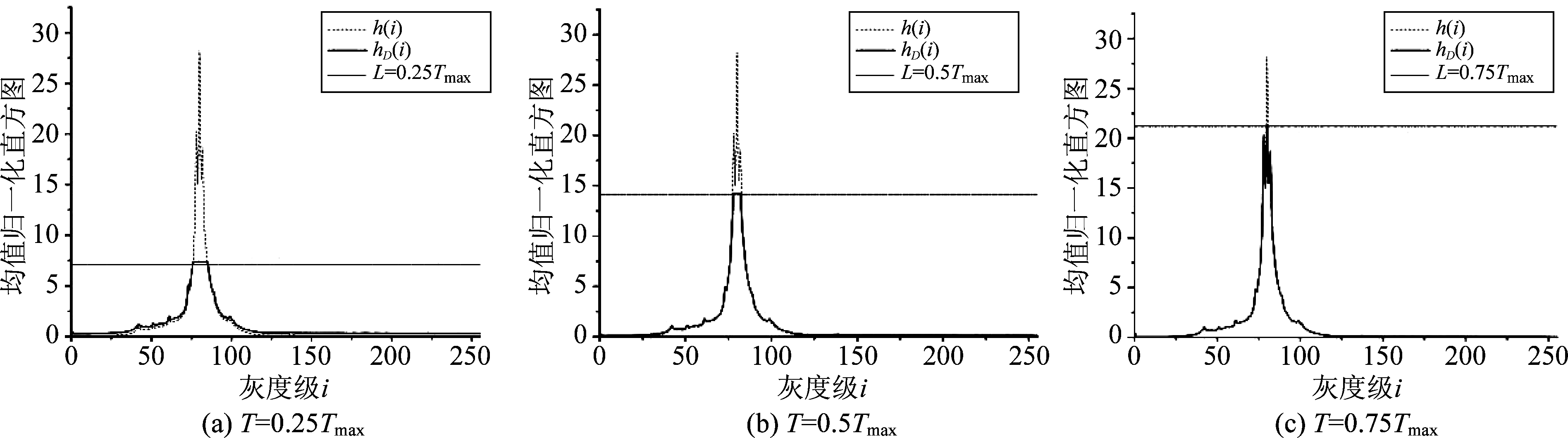
图2 直方图渐变示意图
Fig.2 Histogram gradient illustration
图像渐变模型描述如下:
(1)
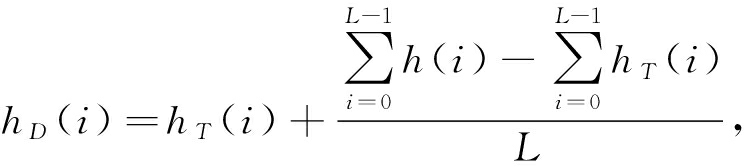
i∈[0,L-1]
(2)
其中,T为钳位阈值,L为灰度级的动态范围,h(i)表示原图直方图,hT(i)表示按阈值钳位后的直方图,hD(i)表示将截断区域平均分配后形成的钳位直方图。分别取截断阈值T=0.25Tmax,0.5Tmax,0.75Tmax,描述直方图渐变过程,如图2所示。
3 混合优化模型
在图像处理中,增强效果好的图像具有较佳自然度和确定性。自然度要求在遵循图像本身的特点下,图像在亮度、饱和度等方面强度适中,满足人眼的视觉要求。确定性是指在保持人眼视觉舒适度的前提下,图像尽可能的呈现更多图像细节的性能。
图像渐变模型所输出的由原图向HE过渡的序列图像,其自然度和确定性也在变化。为使图像具有较好的自然度和确定性,本文选取客观指标信息熵和对比度,以衡量图像的自然度和确定性,并设计一种混合优化模型。
3.1 信息熵与对比度
1948年香农在其所著《通信的数学原理》中指出:“信息是用来消除随机不确定性的东西”,并提出了用来量化信息的信息熵[24]:
(3)
其中Pi表示直方图中i灰度级的的概率密度。一幅图像中,图像像素值的概率分布越均匀,其信息熵越大,但在直方图均衡的过程中会导致小的直方图数据合并,它会减少(最多保持)图像的熵[25]。因此信息熵可以在一定程度上度量图像的细节丢失程度。许多算法利用此特性进行图像增强,如TPEM[26]和EDSHE[27],将信息熵作为一种指标求取各种限制条件下的参数,以达到增强目的。图像质量渐变模型中,输出序列图的信息熵整体呈变小的趋势。
对比度是指一幅图像中明暗区域最亮的白与最暗的黑之间不同亮度层级的测量[28]。对比度越大,图像越清晰醒目,色彩也越鲜明艳丽[29]。本文采用Wu[30]于2011年提出的对比度公式:
C(p)=p0(x1-x0)+∑1≤k≤Kpk-1(xk-1-xk-2)
(4)
其中,x0~xk-1表示图直方图中的非零灰度级,p0~pk-1是非零灰度级所对应的概率。根据对比度定义,对于灰度级连续的自然图像,对比度为1;对于8 bit的二值图像,对比度为255。在上述的图像质量渐变模型中,对比度整体呈变大的趋势。
在图像质量渐变过程中,信息熵整体在逐渐变小而对比度逐渐变大。而人眼主观感知效果,出现先逐渐上升后逐渐下降的相反趋势。因此,如何综合以上两种评测指标求取人眼感知效果最好的某个中间状态,是下一小节所研究的重点。
3.2 混合优化模型
图像质量渐变过程中,信息熵整体呈下降趋势、对比度整体呈上升趋势。图像的自然度和确定性要求,图像应具有适中的的信息熵和对比度强度。因此,本文采用混合优化模型选取最优控制参数,过程描述如下:
(5)
Tbest=arg max(EC(T)),T∈[0,Tmax]
(6)
其中,E(T)和C(T)分别表示钳位阈值为T时均衡后的图像熵和对比度,并对信息熵和对比度做归一化处理。Tmax表示直方图中的最大值。Tbest表示混合优化模型寻优得到的最佳钳位阈值。对于公式(5)有:
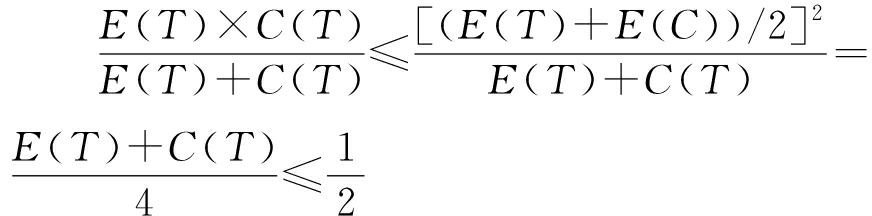
(7)
公式(7)中,E(T) (0,1],C(T)
(0,1],C(T) (0,1],当E(T)=C(T)=1时等号成立,即公式(5)存在理论上界。因此公式(6)理论上一定存在最大值。
(0,1],当E(T)=C(T)=1时等号成立,即公式(5)存在理论上界。因此公式(6)理论上一定存在最大值。
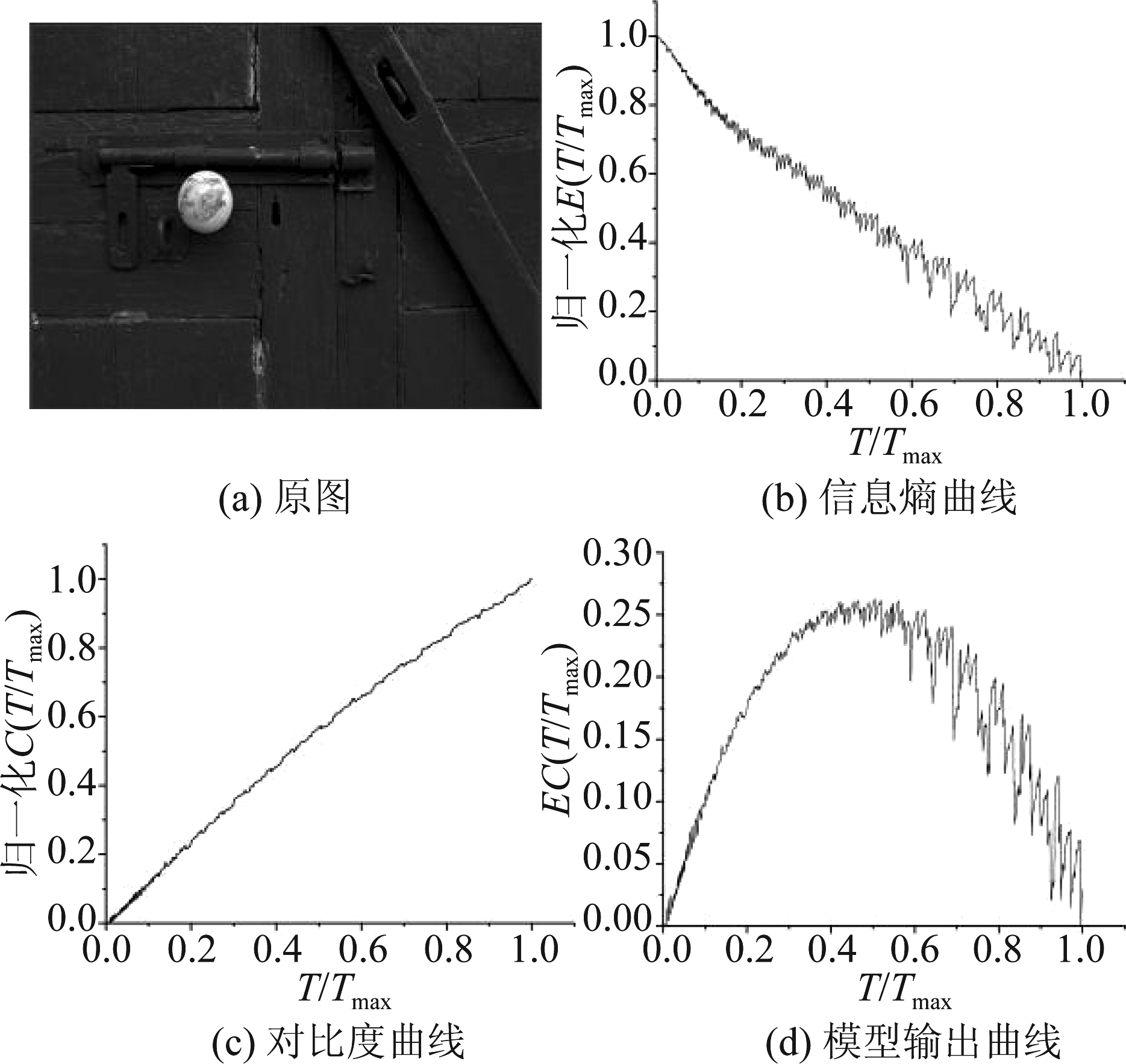
图3 混合优化模型指标的变化曲线
Fig.3 Change curve of hybrid optimization model indicators
质量渐变模型中对比度和信息熵曲线分别如图3(a)和3(b)所示,本节所述模型结果如图3(d)。(为方便绘图,横坐标做归一化处理)。
4 基于图像序列分析的全局直方图均衡算法
本节描述基于图像序列分析的全局直方图均衡算法。首先,利用混合优化模型遍历直方图,确定最佳钳位阈值;然后用最佳阈值对直方图进行钳位再分配处理;模型中采用的是平均分配法,即将截下的数据平均分配到整个灰度范围内。但是在对大量图片测试的过程中,发现部分图像,存在由于分配的数据过大,直方图出现拉伸不开、增强效果不足等现象。
为改善上述问题,本文提出一种直方图后处理方案,具体步骤为:
(1)直方图均值归一化处理:先归一化直方图,再乘以灰度级有效动态范围,使新直方图数组的均值为1。
(2)伽马校正替代原来的平均分配法:仅对均值归一化直方图中小于1的数值,进行伽马校正,以提升直方图小数据所对应的细节部分。
平均分配法和伽马校正法如图4所示。后处理测试对比图如图5所示。
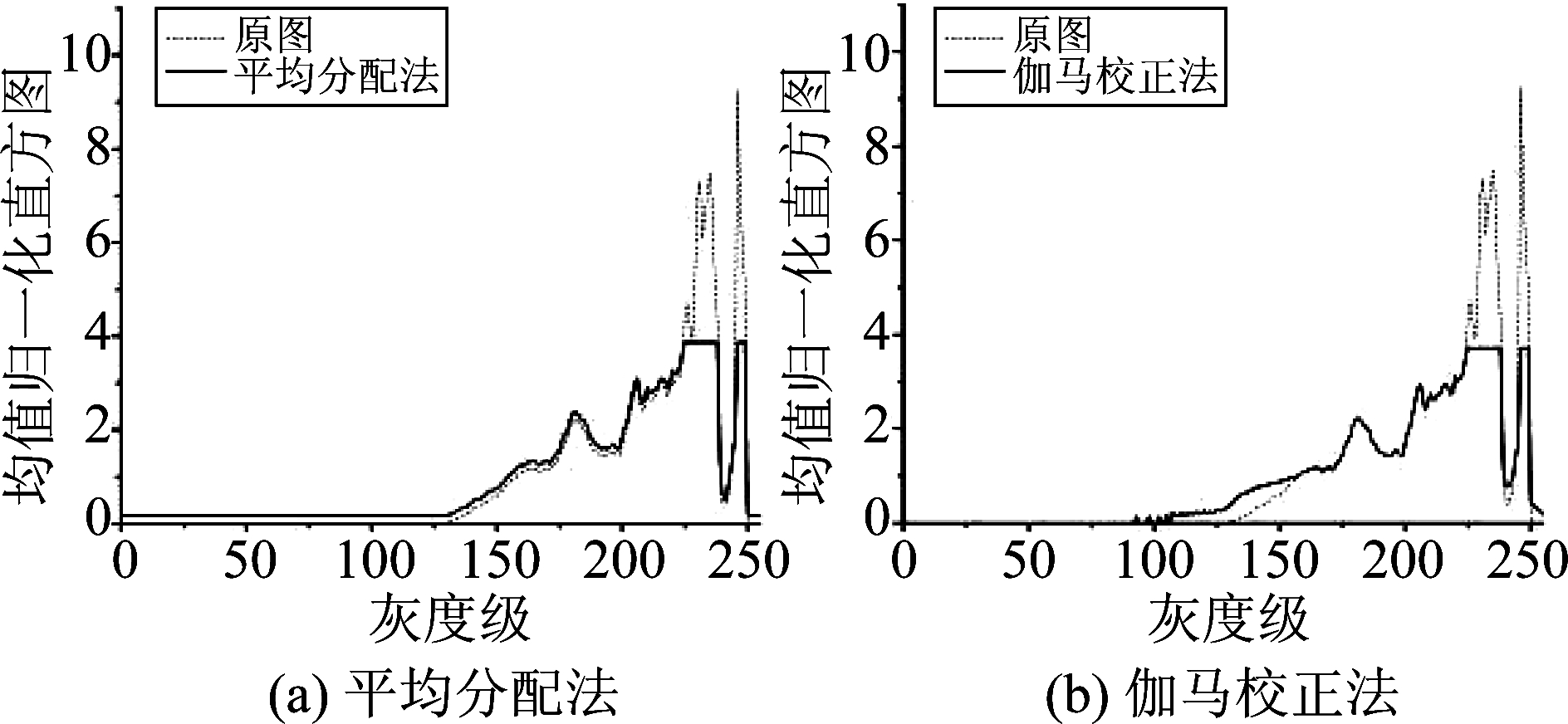
图4 平均分配法和伽马校正法
Fig.4 Equal distribution and Gamma correction

图5 后处理测试对比
Fig.5 Post-processing test comparison
图5中,按平均分配法处理的图片的整体对比度过大,而伽马校正图整体对比度适中,细节提升明显。并且从图中羽毛的细节放大图可看出,采取新方法后,羽毛部分细节保持效果比平均分配法效果好。
经过上述处理后,对调整后的直方图进行传统直方图均衡,输出结果。至此,本文算法的完整步骤如下所示:

本文算法流程1. Begin2. 获得彩色图像的亮度通道。3. 获得亮度通道直方图h(i)。4. for T=0 to Tmax5. 将T作为钳位阈值,对直方图进行钳位和再分配。6. 根据当前参数T对图像进行处理、计算熵和对比度。7. end for8. 将熵和对比度数组代入混合优化模型中得到Tbest。9. 根据最优化参数对直方图进行钳位及后处理操作。10. 进行传统直方图均衡操作。11. 进行彩色图像变换,输出彩色图像增强结果。12. End
5 实验结果与分析
本实验在CPU为Intel i5- 8300H @ 2.30GHz(2304 MHz),内存8G,Windows10操作系统,利用MATLAB 9.0软件进行实验。其中本文算法采用的参数为:Gamma=0.125,TL=10-6。采用HE、WTHE、AGCWD等不保持亮度的算法以及ESIHE、DRSIHE、TDHE等能够保持亮度的算法作为对比算法。实验中AGCWD对概率密度函数进行Gamma校正的参数值为文章中实验部分的取值为0.75;WTHE的参数采用的是其文章实验部分给出的参数:ν为0.5,r为0.5。
5.1 主观评价
算法测试了多个图像数据库(USC-SIPI[31],CSIQ[32],Kodak[33],tid2008[34],BSR Berke-ley[35]等)。选取不同亮度类型的图像进行算法的对比,实验结果如图6所示。
从图6可以看出,对于低照度图像(a)的增强,AGCWD对于图片房梁部分增强效果不足;RDST对于图中右下方的消防标志及其地面投影的增强过曝。ESIHE图整体增强效果适中,但对于消防标志及左下方的拖把的增强略曝。
对于中等亮度图像(b)的增强,RDST图地面的对比度虽有所提升,但其飞机机身部分处理效果不好,机身变黑;EPMP图则对于地面的细节增强不足。本文方法相比于其他算法,图片的地面细节增强适中,飞机机翼与飞机阴影部分层次分明且过渡自然。
对于高亮图像(c)的增强,DRISHE的图片整体对比度较低;EPMP对图中兔子以及雪地细节均未得到有效增强。本文方法和ESIHE的效果相同,图片背景部分细节有所增强,图片左上角区域变暗但没有下溢,整体主观感觉较好。
在处理彩色图像时,本文采用了亮色分离的YCbCr色彩空间,且仅对亮度分量进行处理。从图(d)可以看出,WTHE图在房屋细节没有进行有效的保护;ESIHE图的整体对比度略微偏低,RDST图整体亮度有所提升,但在图中黄色房屋部分亮度提升过多导致细节丢失。而本文所述方法在对图像的对比度进行有效增强的同时,房屋细节也得到了有效的保留。

图6 实验结果
Fig.6 Experimental result
综上所述,本文方法相较于其他的全局直方图均衡算法,具有对比度提升适中,视觉效果自然的特点。本文利用混合优化模型自适应寻找最佳钳位阈值,实验表明对于各类图像都能取得有效的增强效果。
5.2 客观评价
为了定量描述本文方法的处理效果,经过对比后本文选用NIQE[36]以及MCMA[37]两种客观评价指标进行比较。
两种客观评价指标的介绍如下:
(1)NIQE(Naturalness Image Quality Evaluator)是Mittal等人在2013年提出对图像视觉感知自然度的定量描述的无参考图像质量评价算法。它先对显著图像块的进行特征提取,然后根据提取的特征得到MVG模型的均值和方差矩阵,MVG的模型公式如下:
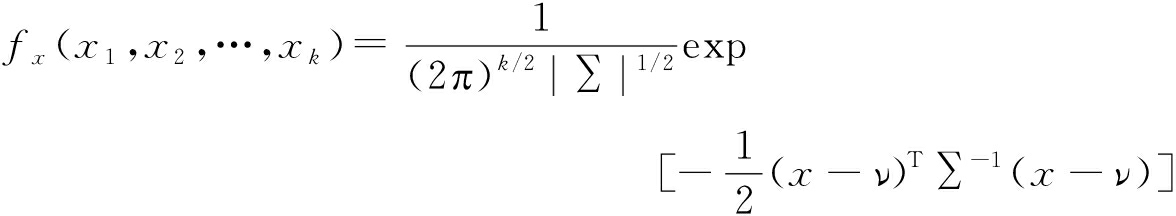
(8)
最后根据待评价图像特征模型参数与预先建立的模型参数之间的距离来评价图像质量[38]。具体的计算公式如下:
D(ν1,ν2,…∑1,∑2)=![]()
(9)
其中ν1,ν2以及∑1,∑2分别为自然图像和失真图像的MVG模型均值和方差矩阵,NIQE算法评价值与人眼感知结果具有较好的一致性,并且NIQE数值越小,图像质量越好。
(2)MCMA(Maximizing Contrast with Minimum Artefact)是Mohsen在2019年提出的一种基于直方图以及像素域的无参考图像质量评价指标,它着重于对图像失真和对比度的综合度量。该指标结合了图像的动态范围、图像直方图相似度以及图像局部像素丰富度对图像进行评估。其计算公式为:
MCMA=0.71×(0.4×PDRO-0.3×PHSD-
0.7×PPU+1)
(10)
其中PDRO、PHSD、PPU分别为图像的动态范围,图像全局直方图相似度和图像的局部像素丰富度,其MCMA指标越大越好。表1至表2为评价指标的测试结果,采用的部分测试图像如图7所示。

图7 部分测试图像
Fig.7 Part of the test image
表1 NIQE评价指标
Tab.1 Evaluation index of NIQE
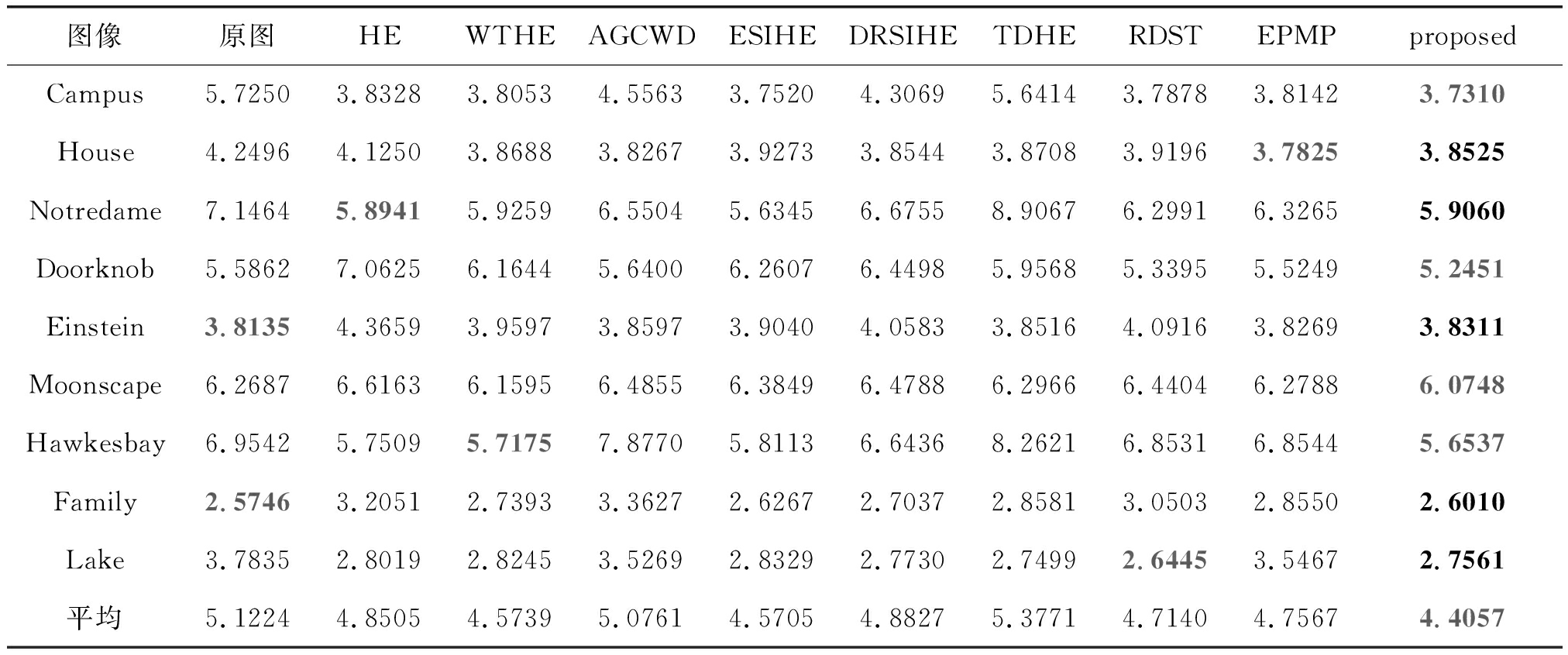
图像原图HEWTHEAGCWDESIHEDRSIHETDHERDSTEPMPproposedCampus5.72503.83283.80534.55633.75204.30695.64143.78783.81423.7310House4.24964.12503.86883.82673.92733.85443.87083.91963.78253.8525Notredame7.14645.89415.92596.55045.63456.67558.90676.29916.32655.9060Doorknob5.58627.06256.16445.64006.26076.44985.95685.33955.52495.2451Einstein3.81354.36593.95973.85973.90404.05833.85164.09163.82693.8311Moonscape6.26876.61636.15956.48556.38496.47886.29666.44046.27886.0748Hawkesbay6.95425.75095.71757.87705.81136.64368.26216.85316.85445.6537Family2.57463.20512.73933.36272.62672.70372.85813.05032.85502.6010Lake3.78352.80192.82453.52692.83292.77302.74992.64453.54672.7561平均5.12244.85054.57395.07614.57054.88275.37714.71404.75674.4057
表2 MCMA评价指标
Tab.2 Evaluation index of MCMA
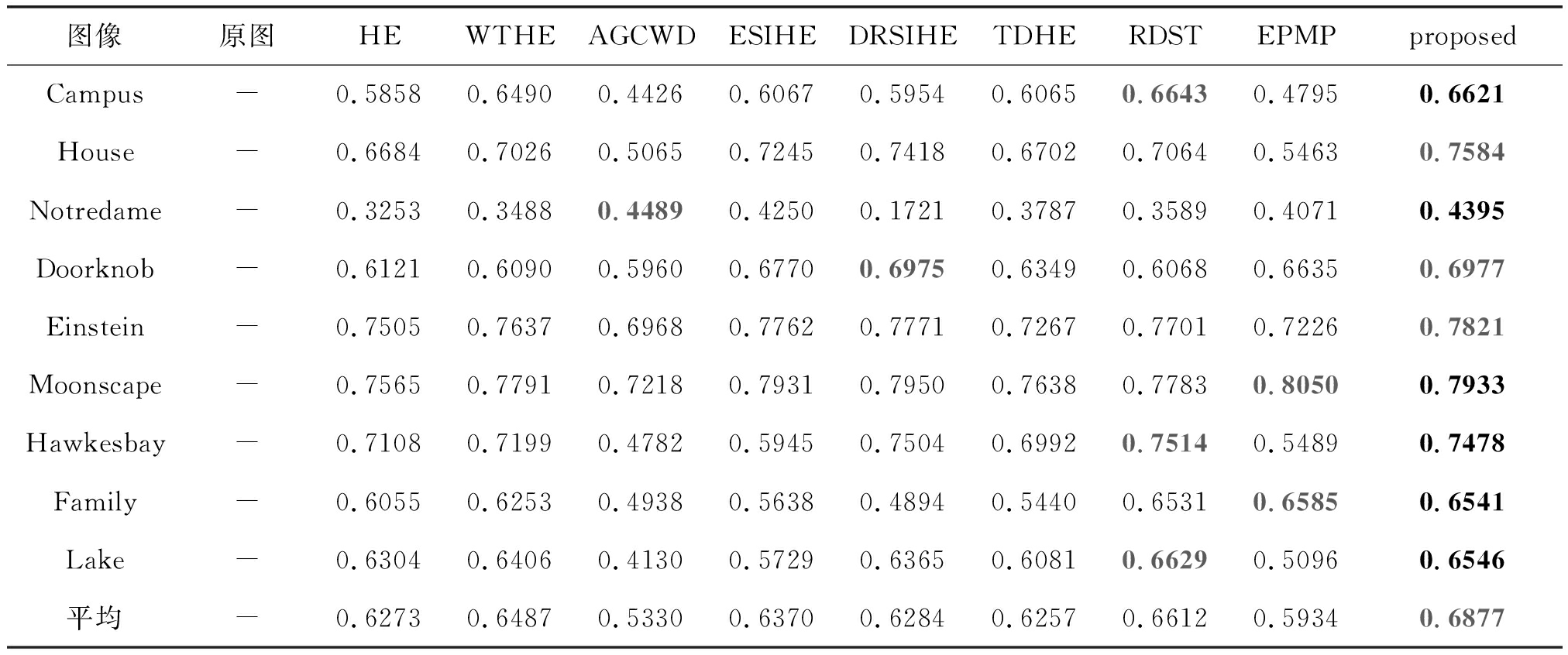
图像原图HEWTHEAGCWDESIHEDRSIHETDHERDSTEPMPproposedCampus-0.58580.64900.44260.60670.59540.60650.66430.47950.6621House-0.66840.70260.50650.72450.74180.67020.70640.54630.7584Notredame-0.32530.34880.44890.42500.17210.37870.35890.40710.4395Doorknob-0.61210.60900.59600.67700.69750.63490.60680.66350.6977Einstein-0.75050.76370.69680.77620.77710.72670.77010.72260.7821Moonscape-0.75650.77910.72180.79310.79500.76380.77830.80500.7933Hawkesbay-0.71080.71990.47820.59450.75040.69920.75140.54890.7478Family-0.60550.62530.49380.56380.48940.54400.65310.65850.6541Lake-0.63040.64060.41300.57290.63650.60810.66290.50960.6546平均-0.62730.64870.53300.63700.62840.62570.66120.59340.6877
表1和表2中,理论最优值为红色加粗的数据。其中,NIQE越小、MCMA越大,越符合人眼视觉特性。
从表1可以看出,本文方法的NIQE值总体偏小,在其不为最小值时也与最小值相差不多,对于处理各种类型的图像的客观评测结果较好。从表2可以看出,本文方法的MCMA评测值总体偏大,对于图像的细节实现了有效的保留。
综上所述,相比于其他算法,本文方法能够保持更多的细节、对比度提升适中,且客观指标与HVS的主观感知结果相符。
5.3 计算复杂度分析
本文算法虽涉及图像的迭代循环操作,从算法流程看整体计算量是其他非循环算法的N倍(设N为循环次数)。实际上,每次循环时并不需要先计算得到中间图像,而只需要对直方图数据计算进行操作即可。因此,在确定最优参数后,只需要进行一次图像数据的查表操作。
6 结论
受直方图钳位再分配的对比度限制策略启发,本文提出了基于图像序列分析的全局直方图均衡算法。首先设计出图像渐变模型,输入单张图片输出图像质量渐变的序列图,并统计序列图中每个图像的信息熵和对比度等统计参数,然后输入本文所提的混合优化模型,求解得到最佳参数,算法最后还提出一种有效的后处理方案,用来进一步保护图像细节,提升主观感知舒适性。
实验表明,本文方法对于不同类型的图片均具有较好的效果,从主观和客观两方面表明其优于其他对比算法。且本文算法保持了HE算法计算复杂度低的优点,因此本文算法除具有一定的理论研究价值外,还具有广泛的实用性。
[1] 邢世宏, 杨晓东, 姜璐, 等. 薄雾条件下退化图像的直方图均衡模型[J]. 计算机工程与应用, 2016, 52(3): 211-214.
Xing Shihong, Yang Xiaodong, Jiang Lu, et al. Mathematical Model of Histogram Equalization for Degraded Images in Mist[J]. Computer Engineering and Applications, 2016, 52(3): 211-214.(in Chinese)
[2] Tan S F, Isa N A M. Exposure Based Multi-Histogram Equalization Contrast Enhancement for Non-Uniform Illumination Images[J]. IEEE Access, 2019, 7: 70842-70861.
[3] Parihar A S, Verma O P. Contrast Enhancement Using Entropy-based Dynamic Sub-histograme Equalization[J]. IET Image Processing, 2016, 10(11): 799- 808.
[4] Park S, Shin Y, Ko S. Contrast Enhancement Using Sensitivity Model-Based Sigmoid Function[J]. IEEE Access, 2019, 7: 161573-161583.
[5] Kim Y T. Contrast Enhancement Using Brightness Preserving Bi-histogram Equalization[J]. IEEE Transactions on Consumer Electronics, 1997, 43(1): 0- 8.
[6] Tang J R, Mat Isa N A. Bi-histogram equalization using modified histogram bins[J]. Applied Soft Computing, 2017, 55: 31- 43.
[7] Shanmugavadivu P, Balasubramanian K. Thresholded and Optimized Histogram Equalization for contrast enhancement of images[J]. Computers and Electrical Engineering,2014,40(3).
[8] Yao Zhijun, Lai Zhongyuan, Wang Chun. Brightness preserving and non-parametric modified bi-histogram equalization for image enhancement[C]∥ 2016 12th International Conference on Natural Computation and 13th Fuzzy Systems and Knowledge Discovery (ICNC-FSKD). IEEE, 2016.
[9] Chen Soong-Der, Ramli Abd Rahman. Minimum mean brightness error Bi-histogram equalization in contrast enhancement[J]. IEEE Transactions on Consumer Electronics, 2003, 49(4): 1310-1319.
[10] Wang Yu, Chen Qian, Zhang Baeomin. Image enhancement based on equal area dualistic sub-image histogram equalization method[J]. IEEE Transactions on Consumer Electronics, 1999,45(1):0-75.
[11] Chao Zuo, Chen Qian , Sui Xiubao. Range Limited Bi-Histogram Equalization for image contrast enhancement[J]. Optik-International Journal for Light and Electron Optics, 2013, 124(5): 425- 431.
[12] Jordanski M, Arsic A, Tuba M. Dynamic Recursive Subimage Histogram Equalization Algorithm for Image Contrast Enhancement[C]∥2015 23rd Telecommunications Forum Telfor(TELFOR). IEEE, 2015.
[13] Wang Q, Ward R K. Fast Image/Video Contrast Enhancement Based on Weighted Thresholded Histogram Equalization[J]. Consumer Electronics IEEE Transactions on, 2007, 53(2): 757-764.
[14] Singh K, Kapoor R. Image Enhancement Using Exposure Based Sub Image Histogram Equalization[M]. Elsevier Science Inc, 2014.
[15] Huang Shih-Chia,Cheng Fan-Chieh,Chiu Yi-Sheng. Efficient Contrast Enhancement Using Adaptive Gamma Correction with Weighting Distribution[J]. IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society, 2013, 22(3): 1032-1041.
[16] Lee S Y, Kim D, Kim C. Ramp Distribution-Based Image Enhancement Techniques for Infrared Images[J]. IEEE Signal Processing Letters, 2018, PP(99): 1-1.
[17] Chen B H, Wu Y L, Shi L F. A Fast Image Contrast Enhancement Algorithm Using Entropy-Preserving Mapping Prior[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2019, PP(99): 1-1.
[18] Celik T, Tjahjadi T. Contextual and Variational Contrast Enhancement[J]. IEEE Transactions on Image Processing, 2011, 20(12): 3431-3441.
[19] Celik Turgay,Tjahjadi Tardi. Automatic image equalization and contrast enhancement using Gaussian mixture modeling[J]. IEEE Transactions on Image Processing : a Publication of the IEEE Signal Processing Society,2012,21(1).
[20] Kim S W, Park W J, Ko S J, et al. 2D Histogram Equalisation Based on the Human Visual System[J]. Electronics Letters, 2016, 52(6): 443- 445.
[21] Pizer S M, Johnston R E, Ericksen J P, et al. Contrast-Limited Adaptive Histogram Equalization: Speed and Effectiveness[C]∥Conference on Visualization in Biomedical Computing, 1990.
[22] Chang Y, Jung C, Ke P, et al. Automatic Contrast Limited Adaptive Histogram Equalization with Dual Gamma Correction[J]. IEEE Access, 2018, PP(99): 1-1.
[23] Gharbi, Micha⊇l, Chen J , Barron J T , et al. Deep Bilateral Learning for Real-Time Image En-hancement[J]. Acm Transactions on Graphics, 2017, 36(4):1-12.
[24] Shannon C E. A Mathematical Theory of Communication[J]. The Bell System Technical Journal, 1948, 27: 379- 423 & 623- 656.
[25] Wang C, Ye Z. Brightness Preserving Histogram Equalization with Maximum Entropy: A Variational Perspective[J]. IEEE Transactions on Consumer Electronics, 2005, 51(4): 1326-1334.
[26] Niu Y, Wu X, Shi G. Image Enhancement by Entropy Maximization and Quantization Resolution Upconversion[J]. IEEE Transactions on Image Processing, 2016, 25(10): 4815- 4828.
[27] Parihar A S, Verma O P. Contrast enhancement using entropy-based dynamic sub-histogram equalisation[J]. Iet Image Processing, 2016, 10(11): 799- 808.
[28] 葛彬, 周宁宁. 基于MMTD的保留灰度值的直方图均衡化[J]. 计算机技术与发展, 2012(12): 69-72.
Ge Bin, Zhou Ningning. A Gray Value Retention Histogram Equalization Based on MMTD[J]. Computer Technology and Development, 2012(12): 69-72.(in Chinese)
[29] 方吉米, 王克鸿, 黄勇. 基于透红外视觉传感的GMA-AM熔池图像质量评价[J]. 焊接学报, 2018, 39(12): 93-98, 136-137.
Fang Jimi, Wang Kehong, Huang Yong. Weld Pool Image Quality Evaluation of Gas Metal Arccditive Manufacturing Based on Infrared Visual Sending[J]. Transactions of the China Welding Institution, 2018, 39(12): 93-98, 136-137.(in Chinese)
[30] Wu X. A Linear Programming Approach for Optimal Contrast-Tone Mapping[J]. IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society, 2011, 20(5): 1262-1272.
[31] Allan Weber. The USC-SIPI Image Data-base[DB/OL]. http:∥sipi.usc.edu/database/, 1977.
[32] Larson E C, Chandler D M. CSIQ Image Quality Database[DB/OL]. http:∥vision.eng.shizuoka.ac.jp/mod/page/view.php?id=23, 2016- 04-29.
[33] Rich Franzen. Kodak Lossless True Color Image Suite[DB/OL]. http:∥r0k.us/graphics/kodak/, 2013- 01-27.
[34] Ponomarenko N, Lukin V, Zelensky A, et al. Tampere Image Database2008[DB/OL]. http:∥www.ponomarenko.info/tid2008.htm, 2010- 02-22.
[35] Pablo Arbelaez, Charless Fowlkes, David Martin. The Berkeley Segmentation Dataset and Benchmark[EB/OL]. https:∥www2.eecs.berkeley.edu/Research/Projects/CS/vision/bsds/, 2007- 06.
[36] Mittal A, Soundararajan R, Bovik A C. Making a “Completely Blind”Image Quality Analyzer[J]. IEEE Signal Processing Letters, 2013, 20(3): 209-212.
[37] Abdoli M, Nasiri F, Brault P, et al. Quality Assessment Tool for Performance Measurement of Image Contrast Enhancement Methods[J]. IET Image Processing, 2019, 13(5): 833- 842.
[38] 戴声奎, 钟峥, 黄正暐. 基于最大熵模型的双直方图均衡算法[J]. 电子学报, 2019, 47(3): 678- 685.
Dai Shengkui, Zhong Zheng, Huang Zhengwei. Maximum Entropy Model Based Bi-histogram Equalization Algorithm[J]. Acta Electronica Sinica, 2019, 47(3): 678- 685.(in Chinese)


