1 引言
近年来,电子设备和多媒体信息广泛传播,盗版、数字伪造和未经授权使用的现象屡禁不止,使得数据信息的安全极具挑战性。数字水印[1]在信息安全以及知识产权保护上起到了重要作用,目前数字水印技术种类大致可分为三种:图像水印[2-3]、音频水印[4]和视频水印[5- 6]。本文研究的是图像水印技术。已有的大多数图像水印技术能够很好的抵抗诸如噪声、滤波等常规信号的攻击,但对于几何攻击,尤其是平移、缩放、旋转、剪切等依然缺乏鲁棒性。这是因为遭受几何攻击后的图像破坏了原来图像与水印之间的同步性,即使图像中包含有水印信息,但由于同步误差的影响,提取出的水印图像必然是扭曲的或者被恶意修改过的。因此,如何采用可靠高效的方法抗几何攻击是近年来的热点话题。
现阶段在对抗几何攻击的水印算法中,图像归一化[7- 8]已被广泛研究。文献[7- 8]提出了变换域结合图像归一化的算法,但当归一化应用到整个图像当中,图像很容易受到局部失真和裁剪的影响。在Radon变换[9],极谐波变换[10]以及Zernike矩技术[11]等不变域方法中,由于不变域引起的内插和由矩引起的离散化增加了同步误差,使得水印嵌入和检测未对准,因此图像易遭受剪切的影响。文献[12]采用了模板校正结合支持向量机(support vector machines, SVM)的算法,由于图像嵌入了同步模板,因此降低了水印的嵌入容量,只能抵抗简单的几何攻击,对旋转以及其组合攻击的鲁棒性不强。基于图像特征点诸如Harris检测[13],Harris-Laplace检测[14],尺度不变特征变换[15](scale invariance feature transform, SIFT),仿射尺度不变特征变换[16](affine-scale invariance feature transform, ASIFT),快速鲁棒局部特征[17](speeded up robust features, SURF)的水印算法使得水印在执行检测时不容易出现同步错误,因而具有更好的鲁棒性。文献[13]利用Harris角点提取稳定的特征点并构造圆形特征区域,利用Contourlet-Zernike完成水印嵌入和提取。由于Harris角点提取的稳定特征点较多且区域固定,图像对缩放攻击十分敏感,因此这种方法对缩放攻击存在局限性。文献[15]利用图像特征点结合机器学习算法,通过使用遗传算法(Genetic algorithm, GA), 粒子群优化(Particle swarm optimization, PSO)以及其他基于群体的优化算法改善图像SIFT特征点的尺度因子来增强水印的鲁棒性,并利用BP和RBF两种级联神经网络模型生成用于嵌入数字水印的动态模式从而提高水印的抗几何攻击能力,该算法不足之处在于对高斯白噪声以及剪切攻击的抵抗力显得相对弱势。文献[16]利用ASIFT获得离散余弦变换后的低频子带的特征点,然后利用水印图像和接收图像之间的获取点特征来实现重新同步,由于图像进行了ASIFT特征点匹配,因此该算法对于大多数几何攻击表现出较强抵抗力,但仍受限于剪切及其各种不同组合攻击。文献[17]利用SURF提取图像特征区域并通过量化的方式将水印信息嵌入到每一个归一化圆形区域当中,该方法对旋转、缩放攻击的鲁棒性不强。
本文结合了图像特征和图像归一化两种抗几何攻击类型,提出了一种Blob-Harris特征区域结合Contourlet变换以及奇异值分解的鲁棒图像水印算法,首先利用Blob-Harris提取原始图像Contourlet变换域的低频分量的特征区域,然后将其四周补零后进行归一化操作,利用小波变换提取出低频水印图像并进行奇异值分解得到水印信息,最后将水印信息重复嵌入到每一个归一化区域的圆内接正四边形中。仿真实验结果表明,该算法不仅对一些常规信号有很强的抵抗力,而且对几何攻击诸如平移、缩放、剪切攻击也有相对较强的鲁棒性。
2 Contourlet变换
轮廓波(Contourlet)变换[18]也称塔型方向滤波器组(Pyramid directional filter bank, PDFB),是一种多尺度、多分辨率、多方向的几何性变换。Contourlet变换由两个步骤实现:拉普拉斯金字塔(Laplacian pyramid, LP)分解和方向滤波器组(Directional filter bank, DFB)滤波,PDFB先进行LP变换实现多尺度分析,使用DFB捕获方向信息,得到多方向子带,即高频子带。图1(a)是Contourlet分解流程图,图1(b)是Contourlet方向分布图。
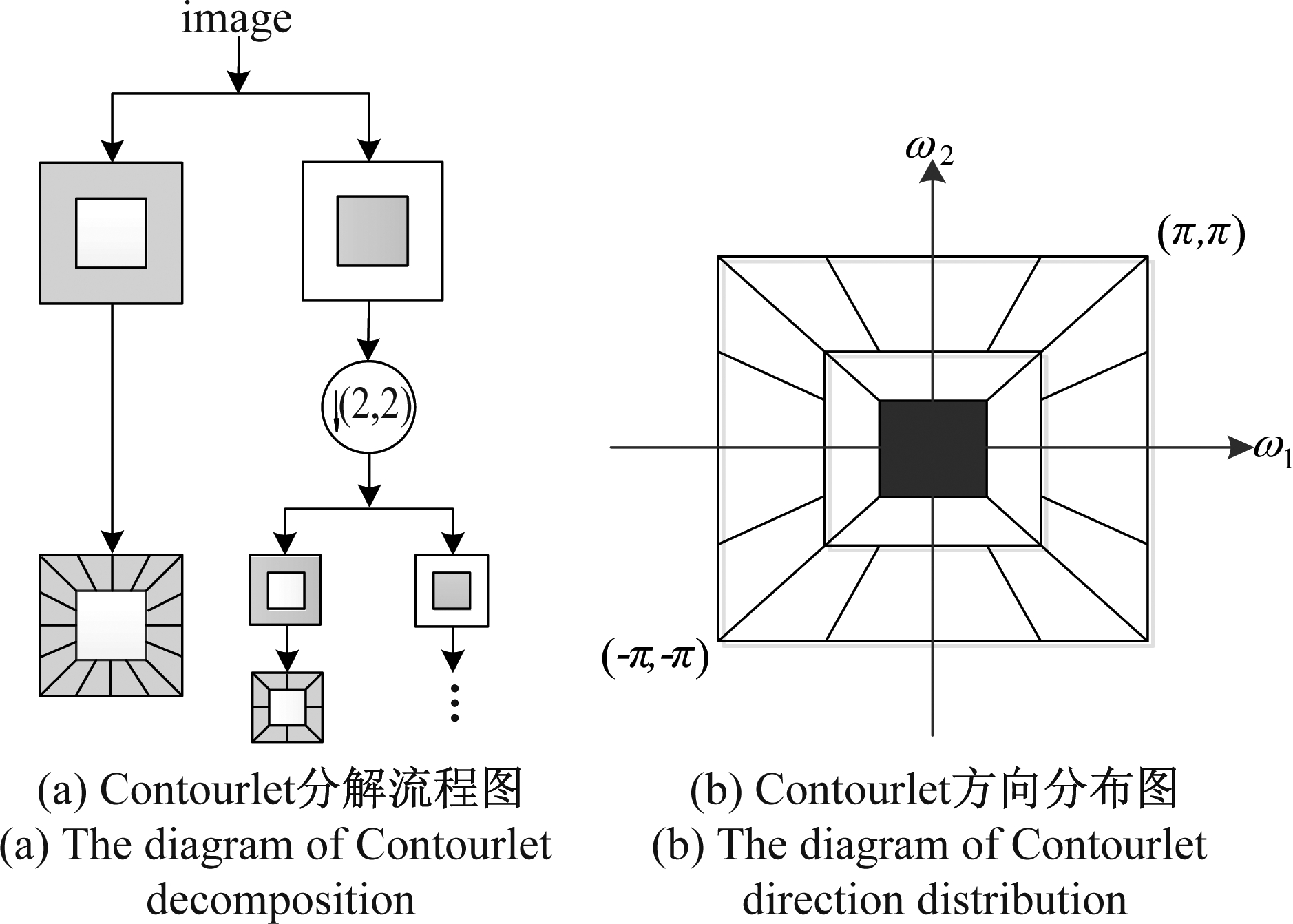
图1 Contourlet变换
Fig.1 Contourlet transform
以256×256的Lena灰度图像I为例,对其进行两层Contourlet分解,得到一个64×64的低频分量IJ、4个和8个细节方向上的高频子带
其中j表示第j级LP分解,lj表示DFB分解层数,k表示由lj级DFB分解得到的第k个精细子带。
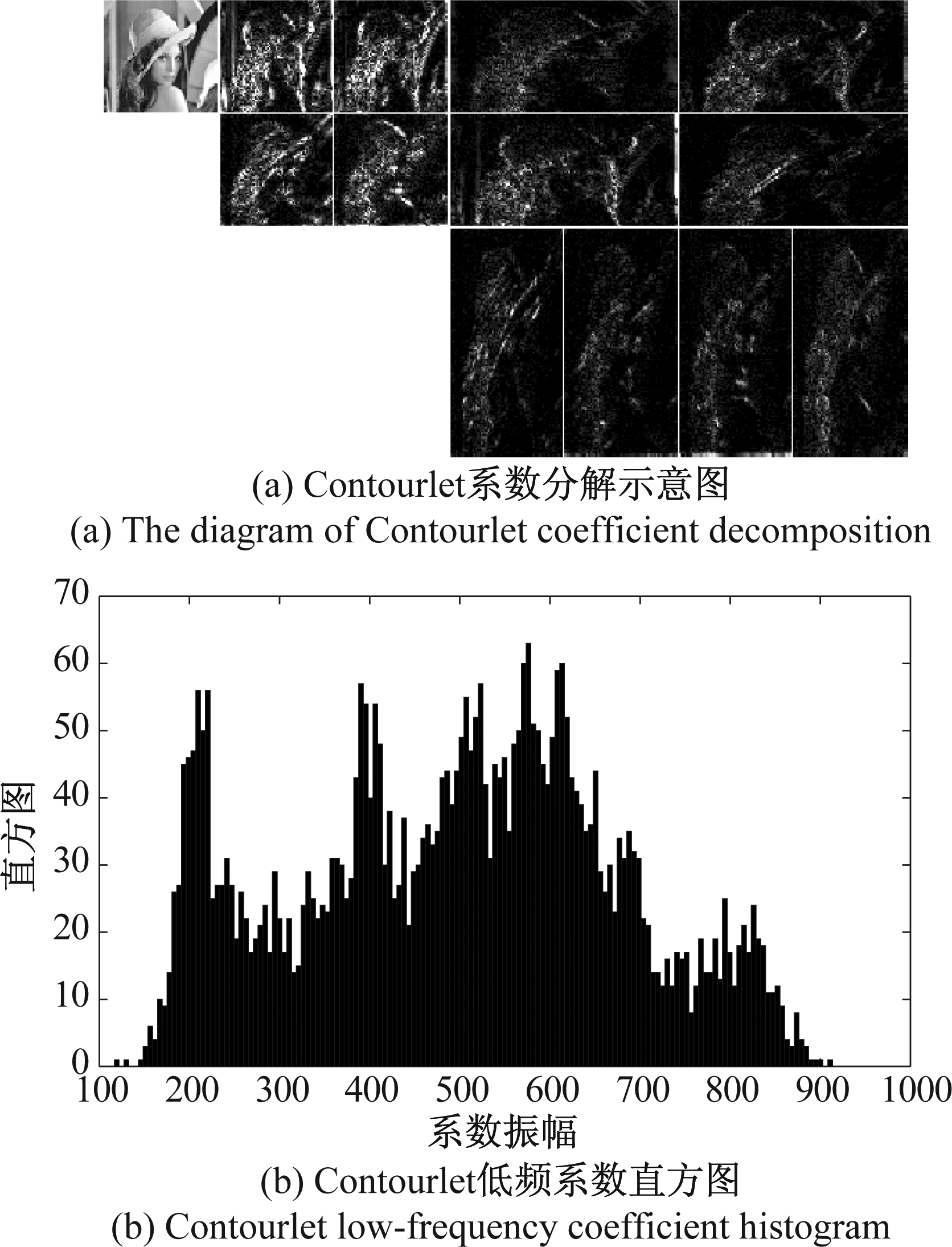
图2 Contourlet分解
Fig.2 Contourlet decomposition
图2(a)显示了原始图像经过两层Contourlet分解系数示意图。图2(b)显示的是低频系数直方图,低频子带图像是原始载体图像的逼近图像,因此在水印嵌入到低频图像中有相对较强的鲁棒性。图像的大部分像素信息都集中在低频上,低频图像包含重要载体信息,为了避免图像在视觉效果上达不到理想画质,在满足视觉感知的条件下通过调节水印的嵌入强度平衡鲁棒性与不可见性之间的关系。
3 水印嵌入区域的形成
3.1 Blob-Harris特征区域的形成
Blob-Harris特征点检测是基于尺度空间理论,具体步骤如下:
步骤1 生成高斯滤波器的拉普拉斯算子(Laplacian of Gaussian, LoG)[19]。对于一幅图像f(x,y),将尺度为σ的高斯函数定义为:
(1)
由于拉普拉斯变换是对图像二阶求导的一种近似,因此LoG函数可以表示为:
2g(x,y,σ)=gxx(x,y,σ)+gyy(x,y,σ)
(2)
其中,2为二阶求导,2g(x,y,σ)表示高斯函数的Laplacian变换,gxx(x,y,σ)和gyy(x,y,σ)分别表示高斯函数在x方向和y方向上的二阶偏导数。
步骤2 建立一个n级别的尺度空间。尺度空间的建立从初始尺度σ0开始,在当前尺度σ上使用规范化的拉普拉斯算子滤波图像,将求得的拉普拉斯响应的平方保存为当前级别的尺度空间图像,以当前尺度的m倍作为新的尺度,然后对新的尺度进行n次迭代后得到n个级别的Laplacian尺度空间。
算子的响应值很大程度上取决于图像域中斑点结构的大小和高斯函数之间的关系,为了自动捕获图像域中不同尺度σ大小的斑点,因此需要考虑规范化的LoG函数为:
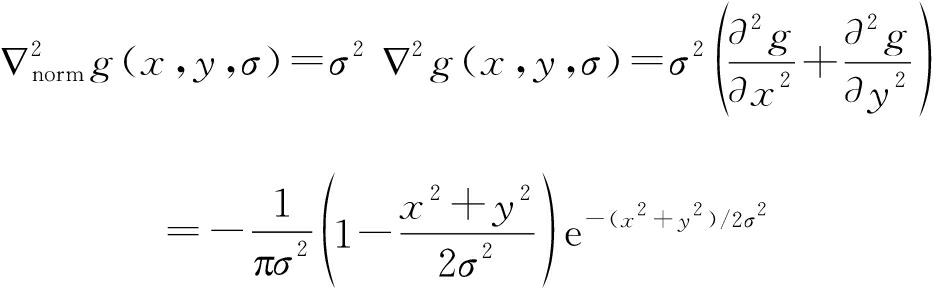
(3)
Laplacian算子能够检测图像的局部极值点,但是对噪声的抵抗能力很差,因此需要用一个高斯低通滤波将图像中的噪声点去除。高斯滤波后的图像为图像f(x,y)与高斯函数卷积后的结果,即:
L(x,y,σ)=g(x,y,σ)*f(x,y)
(4)
然后对高斯滤波后的图像进行Laplacian变换:
2L(x,y,σ)=2[g(x,y,σ)*f(x,y)]
=2[g(x,y,σ)]*f(x,y)
(5)
由式(3)可知,规范化的高斯滤波图像进行Laplacian变换得:
2L(x,y,σ)
=σ22[g(x,y,σ)]*f(x,y)
(6)
为了检测
在尺度空间的局部最大值或最小值,需要求出规范化的LoG函数的最大值或最小值。规范化的LoG函数的极值点由式(7)得到:
(7)
对式(7)进行求解:
(8)
其中,∂(·)表示求LoG函数的偏导,r表示Blob区域半径,满足公式x2+y2=r2。
因此,对于图像中的白色或者黑色Blob区域,当
时,LoG函数响应值达到最大或最小,特征尺度为LoG函数响应值达到峰值时的σ值。计算出图像在不同σ下的LoG响应值,依次检查尺度空间中的每个点,如果该点的LoG响应值都大于或小于其他26个(9+8+9)空间领域的值,那么该点就是被检测到的图像斑点。
图3展示了14个级别不同尺度下的拉普拉斯尺度空间。首先将初始尺度σ0设为2.0,拉普拉斯响应的平方作为当前级别的尺度空间图像,然后以当前尺度的1.2倍作为新的尺度,进行14次迭代后得到14个级别的拉普拉斯尺度空间图像。图3(a)表示的是尺度2.0下的第1级尺度空间,图3(b)表示的是尺度为2.4的第2级尺度空间,以此类推,可以得到不同尺度下的14个级别的尺度空间。
步骤3 在尺度空间中执行非最大值抑制。拉普拉斯算子不仅在斑点处而且在边缘处都具有强烈的响应,但由于边缘处存在不稳定因素,为了避免得到不稳定的特征区域,因此需要计算每个检测到的拉普拉斯区域的Harris响应,将仅具有一个主要梯度方向的区域(即沿边缘的区域)去除。首先计算每一层尺度图像各像素点的相关矩阵M:
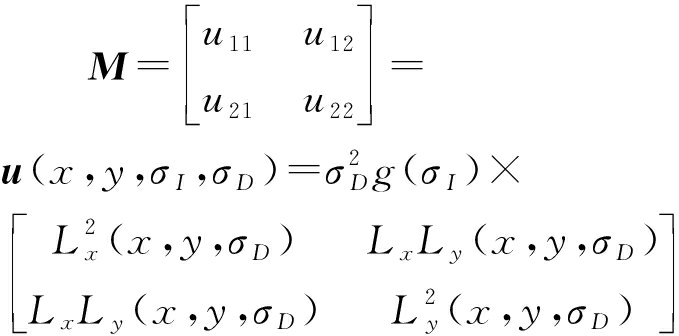
(9)
图3 不同尺度σ下的尺度空间
Fig.3 Scale space at different scales
其中,u为Harris矩阵,σI表示积分尺度,σD表示微分尺度,且满足关系σI=lnσ0,σD=sσI,n为尺度级数,l为尺度因子,一般可以取值为
为初始图像的尺度,本文算法将初始图像尺度设为2.0,s为常数,Lx(x,y,σD)、Ly(x,y,σD)分别表示高斯滤波图像在x, y上的一阶偏导,LxLy(x,y,σD)表示高斯滤波图像同时在x和y方向上的二阶导。
根据式(9)计算每一层尺度图像上各像素点的Harris角点量:
C=det[u(x,y,σI,σD)]-β×trace2[u(x,y,σI,σD)]
(10)
其中,det表示矩阵u的行列式,trace为矩阵u的迹,β为常量,一般情况下取0.04～0.06。根据角点量C提取每一层尺度图像上的角点,当C大于某特定阈值,且在矩阵C中为尺度空间极值点时,则提取该点为Harris特征点。
步骤4 根据特征尺度的大小显示结果圆,显示的圆形区域就是所要求的Blob-Harris特征区域。
图4显示的是检测到的Blob-Harris特征点以及特征区域,图中显示的圆形区域有34个,检测到的图像斑点对应的特征尺度大小为2.0, 2.4, 2.9, 3.5, 5.0, 6.0, 8.6。根据式(8)求得Blob区域半径大小为2.828, 3.394, 4.073, 4.887, 7.038, 8.446, 12.161,对应圆形区域个数分别为21, 1, 4, 5, 1, 1, 1。
图4 Blob-Harris特征点以及特征区域
Fig.4 Blob-Harris feature points and feature regions
3.2 水印嵌入区域的选取
为了保证提取的Blob-Harris特征点在对抗几何攻击时具有良好的稳定性,需要选择优质的特征点作为水印嵌入点。设由Blob-Harris提取的特征点集合为P,取某一个以特征点O,(x0,y0)为圆心,半径为r的圆形区域ro,即:
(11)
由图4可知,通过式(11)选择的某一个圆形区域ro内可能包含其他特征点,因此容易造成区域混叠的现象。本文采用冗余嵌入的方法,将水印重复嵌入到每一个区域当中,由于区域混叠会产生水印叠加嵌入的后果,严重破坏了图像水印的像素信息,因此为了避免水印叠加嵌入带来的影响,可通过特征点所在位置及大小优化筛选出稳定的互不重叠的特征点。首先根据特征尺度σs将这些圆形区域从小到大依次排列,小的特征尺度对应的特征点具有较低的稳定性[20],特征尺度大的特征点稳定性高,但由于其特征区域覆盖面积大容易造成区域混叠,因此选择适中的σs对应的特征点作为候选水印嵌入点,本文选择的σs范围在(2.8, 6.0)之间。
图5展示了局部特征区域的形成。图5(a)显示的是特征点在中间特征尺度范围内形成的特征区域,根据圆心位置去除图像重叠区域对应的特征点,设候选的水印嵌入点集合为P′,优先选择P′中σ最大的特征点
在
形成的特征区域内删除重叠区域对应的特征点,然后再对P′内剩下的特征点继续判断,直到P′内所有的特征点判断完毕为止,最终得到水印嵌入点集合为P″,P″中的特征点稳定且形成的特征区域两两互不重叠,如图5(b)所示。图5(c)为选取的局部特征区域。
图5 局部特征区域的形成
Fig.5 Formation of local feature regions
图6(a)为选取的某一局部特征区域,由于图像的归一化实质上是基于矩的归一化,因此图像在进行归一化之前需要将选取的圆形水印区域四周补零,使其成为2r×2r的矩形区域(图6(b)),然后对矩形区域进行归一化操作(图6(c)),归一化的过程[8]主要为图像的中心化、x-shearing变换、缩放变换、旋转变换。水印的嵌入是以特征区域的奇异值矩阵为基础,为了将水印信息更加充分完整的嵌入到特征区域当中并且成功提取出来,需要划分出归一化特征区域的圆内接正四边形作为最终水印嵌入区(图6(d))。
图6 水印嵌入区域
Fig.6 Watermark embedding area
4 Blob-Harris特征区域的水印算法实现
4.1 水印的嵌入
图7展示了水印的嵌入过程,具体的操作过程如下:
1)将一副N×N的灰度图像W作为水印图像,将经过小波变换的水印提取低频分量WLL,并对其进行SVD变换:
(12)
其中,ULL,VLL是酉矩阵,SLL是水印嵌入的一部分,diag(SLL)=(σ1,σ2,σ3,…,σk,…,σm),σ1≥σ2≥σ3≥…≥σk且σk+1=…=σm=0。σ1,σ2,σ3,…,σk是低频分量WLL的k个正实数奇异值。
2)对原始图像I作Contourlet 变换。用Blob-Harris算子从CT的低频图像ILL中提取出特征点,设特征点的集合为P={pi,i=1,2,…,n}。
3)确定水印嵌入区域。从低频图像中划分出一系列互不重叠的稳定特征区域R={ri,i=1,…,m},将局部特征区域R四周“补零”并对其进行归一化操作得到方形区域Sq={si,i=1,…,m},水印图像W嵌入到归一化特征区域圆内接正四边形当中,最终的水印嵌入区域为Z={zi,i=1,…,m}。
4) 为了保证水印信息能够成功嵌入,需要调整Z的大小。首先提取出Z中某一区域z1,将z1放大至和低频水印图像WLL同样大小,然后再对z1进行奇异值分解:
z1=U·S·VT
(13)
5)把SLL加入到z1的奇异值矩阵S中,得到嵌入水印后的奇异值矩阵S′。嵌入规则为:
S′=S+∂·SLL
(14)
其中,SLL表示低频水印图像的奇异值矩阵,∂表示水印嵌入强度,本文将∂设置为0.2。
6) 局部特征区域重构。重构的图像由两部分组成,一部分是由没有进行奇异值分解的归一化区域s1rem生成,即:
s1rem=s1-z1
(15)
另一部分是经过嵌入修改后的某一水印嵌入区域z1′,z1′满足式(16)
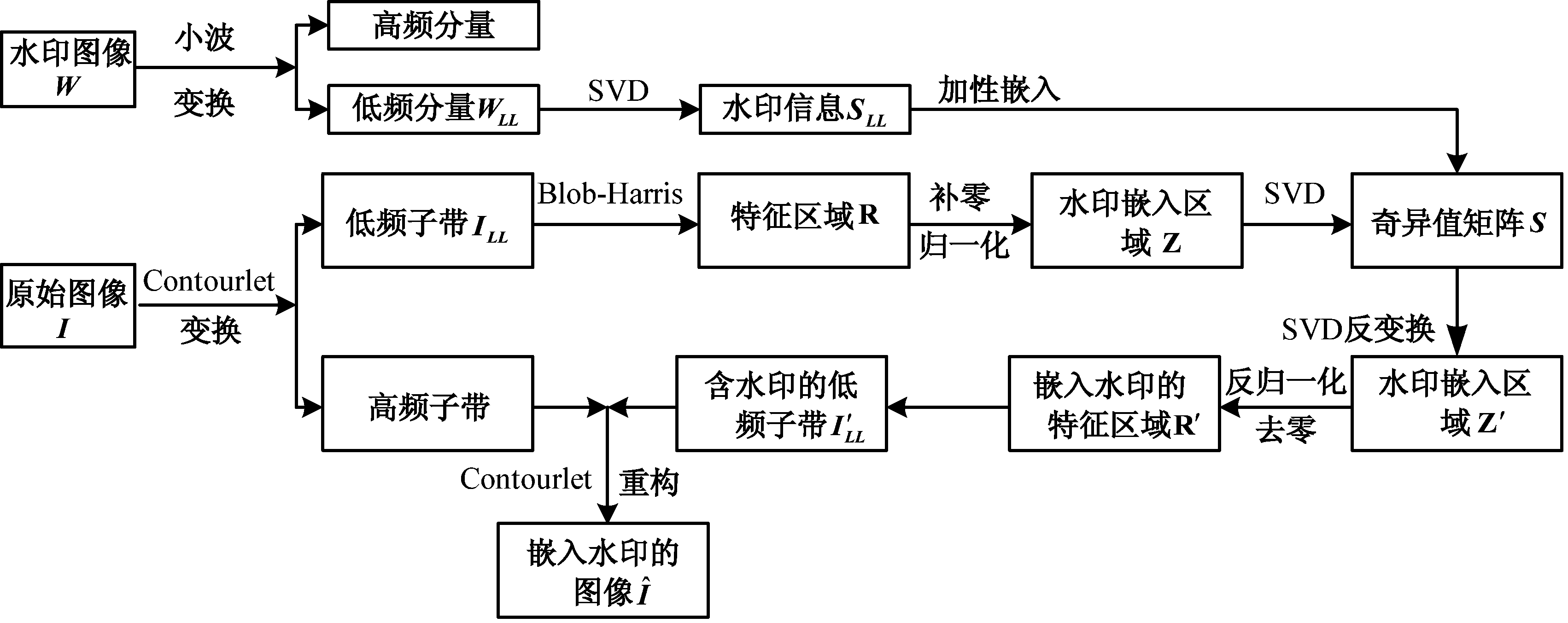
图7 嵌入过程框图
Fig.7 Diagram of embedded process
z′1=U·S′·VT
(16)
因此重构的某一方形区域
可以表示为:
(17)
将其进行反归一化并将四周的零元素去除,得到重构的某一局部特征区域。
7)低频子带图像重建。对水印嵌入区域Z重复上述操作(4)～(6),直到Z中的局部区域都处理完毕,得到重构之后的局部特征区域R′=(r′i,i=1,2,…,m)。低频重建图像也由两部分组成,一部分是没有被选定为局部特征区域的图像:
ILLrem=ILL-R
(18)
另一部分是修改后的局部特征区域R′,因此含水印信息的Contourlet低频子带图像
可以表示为:
(19)
8)将重建后的低频子带图像和原始图像的高频分量重构得到嵌入水印的图像
4.2 水印的提取
图8展示了水印的提取过程,具体的操作过程如下:
(1)水印图像跟嵌入时的水印图像相同,水印图像W经过小波变换得到其低频分量WLL,对其进行SVD变换
(20)
(2)对待检测的含水印图像
作Contourlet 变换。用Blob-Harris算子从CT低频图像
中提取出特征点,设特征点的集合为
(3)从
中划分出一系列两两互不重叠的稳定特征区域
对
四周补零后进行归一化处理得到方形区域
取归一化特征区域圆内接正四边形作为水印提取区域,最终的水印提取区域为
4)调整
中各区域的大小,然后对原始图像I经过Contourlet变换后的低频图像ILL和水印提取区域分别做SVD得到U1、S1、V1以及
即:
(21)
(22)
5)按照式(23)进行水印的提取,得到的
是W低频分量的重要信息:
(23)
6) 式(24)得到提取的W的低频分量
(24)
7)对获得的低频分量与W高频分量进行小波逆变换从而提取出的新的水印图像W′。
5 仿真实验
为了验证水印算法的高效性和可靠性,分别进行了不可见性测试、水印的鲁棒性测试包括对一些常规信号处理及抗几何攻击的测试,并将本文算法与文献[16]、文献[21]中的算法进行对比。本实验的实验环境为Matlab2016a,操作系统是windows 7。本文所选用的原始图像分别为256×256标准灰度图像Lena以及Peppers。水印图像为32×32的含有“邮电大学”字样的灰度图像。仿真实验中,Contourlet变换采用的LP类型为 “9-7”,DFB采用“pkva”方向滤波器。
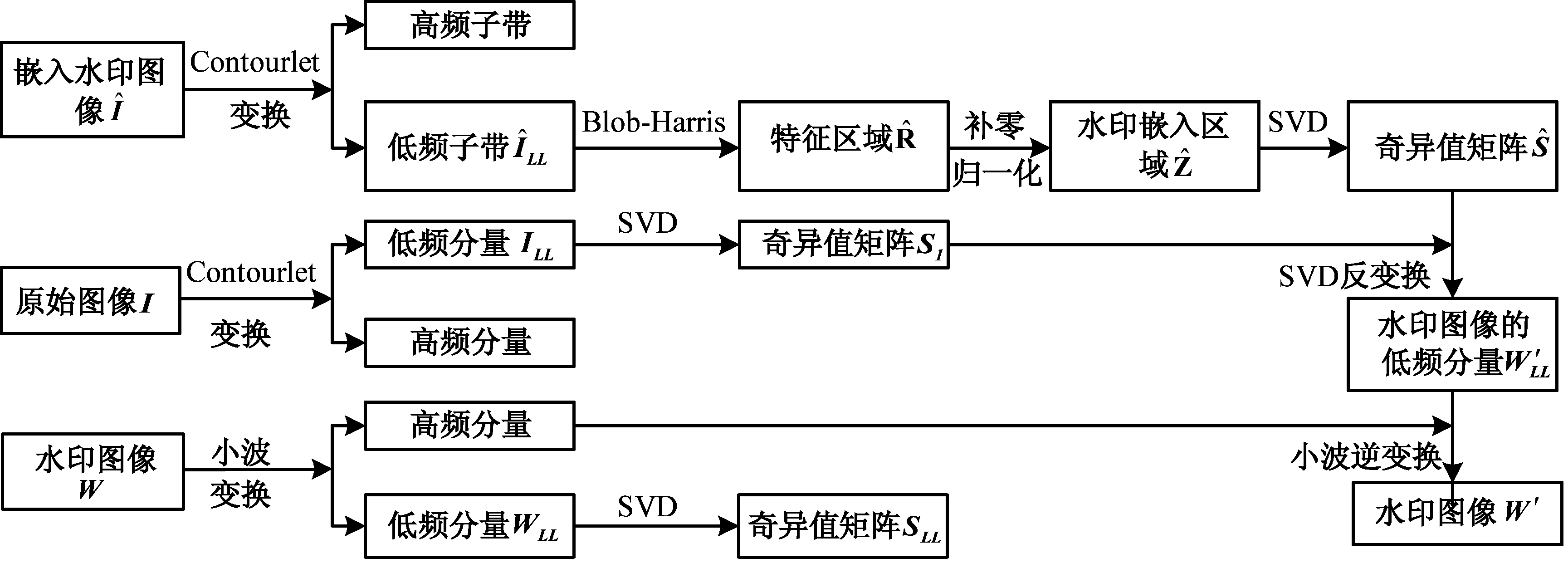
图8 提取过程框图
Fig.8 Extraction process diagram
5.1 不可见性测试
不可见性的评价标准要同时满足主观和客观要求,主观上人眼要不可察觉图像的失真和畸变。客观评价采用峰值信噪比(Peak-signal-to-noise-ratio,PSNR)作为算法的不可见性指标。
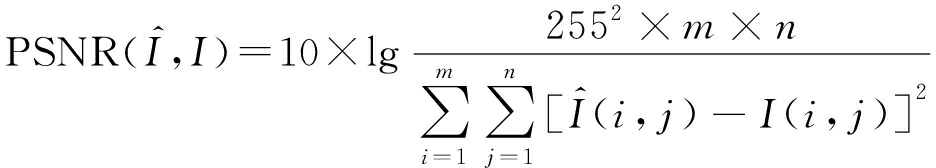
(25)
其中,m×n为图像大小,I(i, j)为原始图像第(i, j)个像素点的值,
为嵌入水印后的图像第(i, j)个像素点的值。
图9为Lena原始图像(图9(a))、Peppers原始图像(图9(b))以及水印图像(图9(c)),Lena和Peppers嵌入水印效果图分别如图10(a)、图10(c)所示。利用本文算法得到的Lena和Peppers嵌入水印图像的PSNR值分别为43.4538以及41.6191。Peppers图像的PSNR值略低于Lena图像,主要原因在于,Peppers图像获得了较多的稳定特征区域(10个),在不引起视觉感知的情况下获得了更大强度的水印信息,而Lena图像获得的稳定特征区域有7个,由于嵌入的水印强度较小,因此获得较大的PSNR值。
图9 原始图像
Fig.9 Original image
图10 未受攻击时水印嵌入和提取
Fig.10 Not attacked watermark embedding and extraction
归一化相关系数(normalized correlation, NC)是水印算法中鲁棒性评价标准之一。当水印没有受到攻击时,提取的NC值越趋近于1,说明该算法性能越好,能够比较完整的提取出所嵌入的水印图像。图10(b)、图10(d)分别为嵌入水印的Lena和Peppers图像在未受攻击时提取出的水印,NC值达到了0.999以上,提取水印的质量良好,与原始水印几乎无差别,说明本文算法具有良好的不可见性。
5.2 鲁棒性测试
为了验证算法抗几何攻击的鲁棒性,本次实验选取PSNR值较大的Lena图像进行部分常规攻击和几何攻击测试。用提取的最大NC值来衡量鲁棒性的强弱。在本文算法中,当NC值达到0.5以上时,说明提取出的水印是有效的。实验结果如表1、表2所示。
表1 图像水印对常规信号的鲁棒性
Tab.1 Image watermark resistance to conventional signals
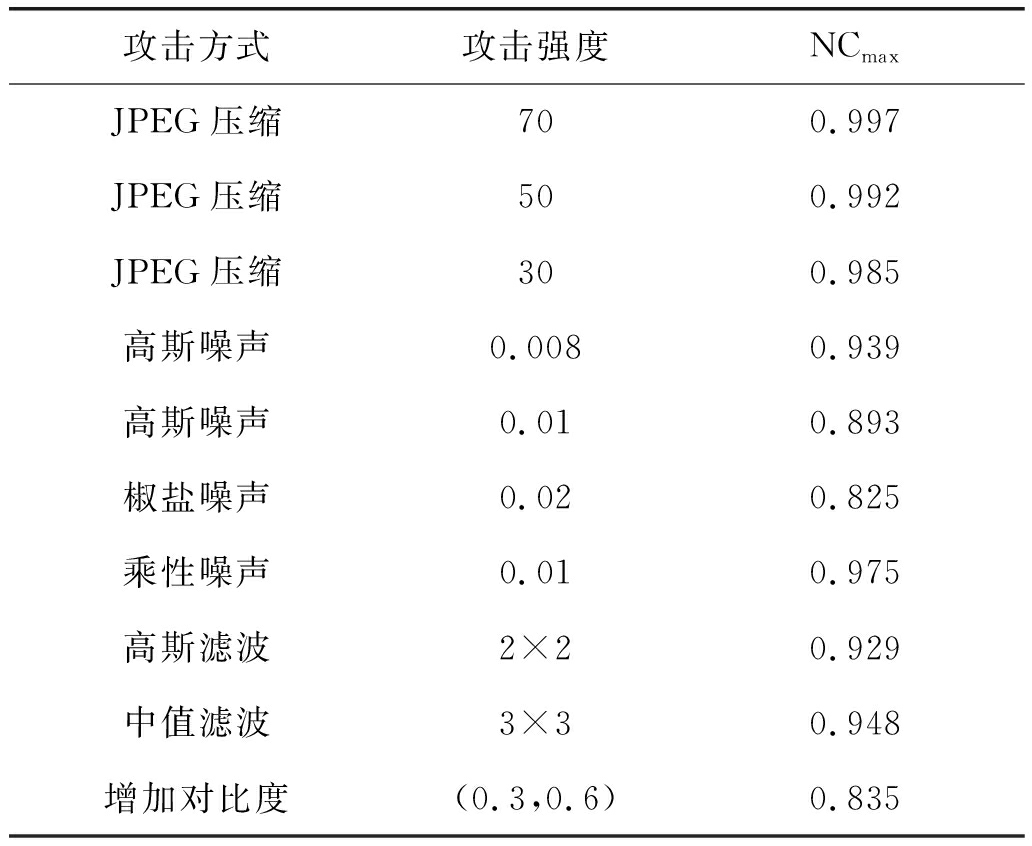
攻击方式攻击强度NCmaxJPEG压缩700.997JPEG压缩500.992JPEG压缩300.985高斯噪声0.0080.939高斯噪声0.010.893椒盐噪声0.020.825乘性噪声0.010.975高斯滤波2×20.929中值滤波3×30.948增加对比度(0.3,0.6)0.835
图11 攻击图像及提取水印
Fig.11 Attack image and extracted watermark image
表2 图像水印对几何攻击及其组合攻击的鲁棒性
Tab.2 Image watermark resistance to geometric attacks and combined attacks
攻击方式攻击强度NCmax旋转10°0.892旋转20°0.840旋转30°0.793平移(x=20, y=-40)0.995平移(x=-20, y=20)0.984平移(x=-30, y=30)0.973平移(x=-70, y=-60)0.946缩放0.80.996缩放1.20.997剪切1/100.970旋转+平移10°+(x=-10, y=20)0.890旋转+平移20°+(x=10, y=10)0.813缩放+平移0.6+(x=50, y=-40)0.974缩放+平移1.2+(x=-30, y=20)0.982旋转+剪切15°+(3/25)0.875旋转+缩放30°+0.80.790剪切+平移(1/16)+(x=-30,y=20)0.972
由表1可知,本文算法能够有效抵抗一些常规信号诸如JPEG压缩、噪声、滤波、增加对比度的攻击。
图11是部分几何攻击的效果图以及提取水印图像,分别对Lena图像进行平移(图11(a))、旋转(图11(c))、缩放(图11(e))、剪切(图11(g))、剪切+平移(图11(i))以及缩放+平移攻击(图11(k))。提取出的水印图像分别为图11(b)、图11(d)、图11(f)、图11(h)、图11(j)、图11(l)。由图11可以看出,本文算法能够很好的抵抗缩放、平移、剪切等几何攻击,对旋转也有较好的抵抗力,说明本文算法对几何攻击有相对较强的鲁棒性。
由表2可以看出,本文算法对平移、缩放、剪切及其组合攻击具有很强的抵抗力,最大NC值均达到0.94以上,对旋转攻击及其组合攻击的抵抗力较强。
为了进一步验证水印对几何攻击的鲁棒性,将本文算法与文献[16]、文献[21]进行对比,为提高对比结果的准确性,本文将原始Lena图和水印改成与文献[16]、文献[21]相同大小的图像,原始图像大小改为512×512,水印大小改成64×64。对比结果如表3所示。
表3 提取水印NC值对比
Tab.3 Comparison table of extracted watermark NC value
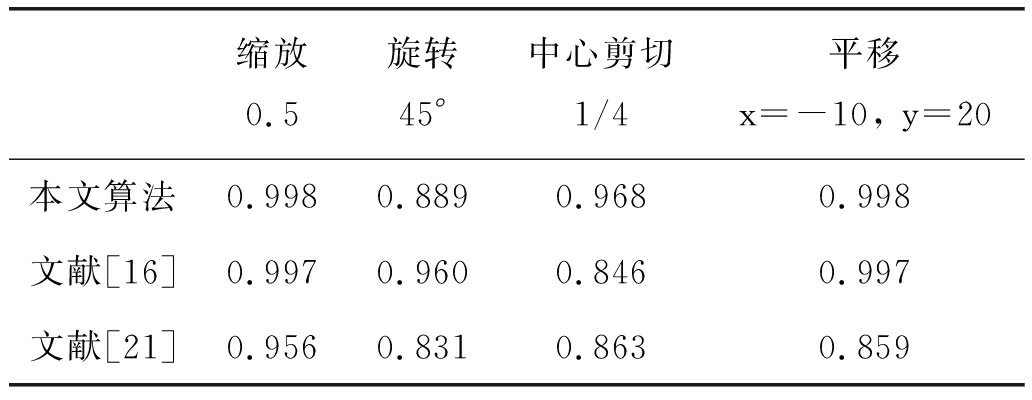
缩放0.5旋转45°中心剪切1/4平移x=-10, y=20本文算法0.9980.8890.9680.998文献[16]0.9970.9600.8460.997文献[21]0.9560.8310.8630.859
表3的结果表明,文献[16]对几何攻击具有较强的鲁棒性,在对抗旋转攻击时NC值达到0.96,明显优于本文算法,但文献[16]对剪切攻击的鲁棒性有待提高。文献[21]能够较好地抵抗几何攻击,其中对剪切的抵抗力优于文献[16],但本文算法在抗缩放、旋转、剪切、平移攻击的鲁棒性均强于文献[21]。因此本文算法在对抗几何攻击综合能力方面上优于文献[16]和文献[21]。由以上分析可知,本文算法在抵抗几何攻击诸如缩放、平移、剪切方面都有相对较强的鲁棒性。
6 结论
本文采用了图像特征结合归一化抗几何攻击水印的思想。利用Contourlet变换和SVD的优势,提出了一种Blob-Harris特征区域结合CT-SVD的鲁棒图像水印算法。该算法首先用Blob-Harris算子从原始图像Contourlet分解后的低频图像中提取特征点,然后根据各个特征点的特征尺度确定特征区域,从中选择适中的互不重叠的圆形特征区域将其四周补零后进行归一化处理,利用SVD把水印嵌入到归一化特征区域的圆内接正四边形当中。实验结果表明,峰值信噪比PSNR达到40 dB以上时,本文算法除了对一些常规攻击有很好的抵抗力之外,对几何攻击也有相对较强的鲁棒性,特别是平移、缩放、剪切攻击以及其两两组合攻击,最大NC值能够达到0.94以上。
[1] Amini M, Ahmad M O, Swamy M N S. Digital watermark extraction in wavelet domain using hidden Markov model[J]. Multimedia Tools and Applications, 2017, 76(3): 3731-3749.
[2] 肖红, 李盼池, 李滨旭. 改进的量子图像水印算法[J]. 信号处理, 2017, 33(2): 135-143.
Xiao Hong, Li Panchi, Li Binxu. Improved Quantum Image Watermarking Algorithm[J]. Journal of Signal Processing, 2017, 33(2): 135-143.(in Chinese)
[3] Abdelhakim A M, Saad M H, Sayed M, et al. Optimized SVD-based robust watermarking in the fractional Fourier domain[J]. Multimedia Tools and Applications, 2018, 77(21): 27895-27917.
[4] 张涛, 张彩霞, 高新意, 等. 自适应的混合域音频水印新算法[J]. 信号处理, 2017, 33(6): 828- 835.
Zhang Tao, Zhang Caixia, Gao Xinyi, et al. Adaptive Audio Watermarking Algorithm in the Hybrid Domain[J]. Journal of Signal Processing, 2017, 33(6): 828- 835.(in Chinese)
[5] Imen N, Nouredine Aa, Sarra B. A Novel Blind and Robust Video Watermarking Technique in Fast Motion Frames Based on SVD and MR-SVD[J]. Security and Communication Networks, 2018, 2018(10): 1-17.
[6] 陈雪贞, 冯国瑞, 王朔中. 抵抗共谋攻击的运动一致性空域视频水印[J]. 信号处理, 2011, 27(2): 298-303.
Chen Xuezhen, Feng Guorui, Wang Shuozhong. Spatial Domain Video Watermarking with Motion Coherence against Collusion Attacks[J]. Signal Processing, 2011, 27(2): 298-303.(in Chinese)
[7] Wang Weiwei, Yuan Zhihua, Zhao Wenqiang, et al. Strong robust zero watermarking algorithm based on NSCT transform and image normalization[C]∥Advanced Information Technology, Electronic and Automation Control Conference. Chongqing, China: IEEE, 2018: 236-240.
[8] 朱丹丹, 吕鲤志. 基于归一化和非下采样Contourlet变换的数字水印方案[J]. 北京理工大学报, 2017, 37(4): 391-395.
Zhu Dandan, Lü Lizhi. A Watermarking Scheme Based on Normalization and Nonsubsampled Contourlet Transform[J]. Journal of Beijing Institute of Technology, 2017, 37(4): 391-395.(in Chinese)
[9] Kozachok A V, Kopylov S A, Mescheriakov R V, et al. An approach to a robust watermark extraction from images containing text[J]. Trudy SPIIRAN, 2018, 60(5): 128-155.
[10] Wang X, Xu H, Zhang S, et al. A Color Image Watermarking Approach Based on Synchronization Correction[J]. Fundamenta Informaticae, 2018, 158(4): 385- 407.
[11] Munib S, Khan A. Robust image watermarking technique using triangular regions and Zernike moments for quantization based embedding[J]. Multimedia Tools and Applications, 2017, 76(6): 8695- 8710.
[12] Islam M, Laskar R H. Robust image watermarking technique using support vector regression for blind geometric distortion correction in lifting wavelet transform and singular value decomposition domain[J]. Journal of Electronic Imaging, 2018, 27(5): 053008- 053026.
[13] Zhu D, Lv L. A New Image Watermarking Algorithm Using the Contourlet Transform and the Harris Detector[C]∥CCF Chinese Conference on Computer Vision. Springer, Berlin, Heidelberg, 2015: 439- 447.
[14] Chih Yu Yen, Kuo Lung Hung. Watermarking Technique Based on Harris-Laplace Feature Point Detector Capable of Resisting Geometric Attacks[C]∥Asia Joint Conference on Information Securit. Kobe, Japan: IEEE, 2019: 119-126.
[15] Parmalik K, Sharma A K. Optimized Features of SIFT Transform Function for Digital Image Watermarking using Hybrid Swarm Intelligence and Neural Network[J]. International Journal of Recent Technology and Engineering, 2019, 8(3): 2179-2190.
[16] Wang C, Zhang Y, Zhou X. Robust image watermarking algorithm based on ASIFT against geometric attacks[J]. Applied Sciences, 2018, 8(3): 410- 428.
[17] 侯翔, 闵连权. 基于SURF特征区域的鲁棒水印算法[J]. 武汉大学学报: 信息科学版, 2017, 42(3): 421- 426.
Hou Xiang, Min Lianquan. A Robust Watermarking Algorithm Using SURF Feature Regions[J]. Journal of Wuhan University: Information Science Edition, 2017, 42(3): 421- 426.(in Chinese)
[18] Liu H, Xiao G F, Tan Y L, et al. Multi-source remote sensing image registration based on contourlet transform and multiple feature fusion[J]. International Journal of Automation and Computing, 2019, 16(5): 575-588.
[19] Xu H, Lu C, Berendt R, et al. Automatic nuclei detection based on generalized laplacian of gaussian filters[J]. Biomedical and Health Informatics, 2016, 21(3): 826- 837.
[20] 邓成, 李洁, 高新波. 基于仿射协变区域的抗几何攻击图像水印算法[J]. 自动化学报, 2010, 36(2): 221-228.
Deng Cheng, Li Jie, Gao Xinbo. Geometric Attacks Resistant Image Watermarking in Affine Covariant Regions[J]. Journal of Automation, 2010, 36(2): 221-228.(in Chinese)
[21] Muhammad I, Bruce A H, Muhammad A, et al. A block-based secure and robust watermarking scheme for color images based on multi-resolution decomposition and de-correlation[J]. Frontiers of Information Technology & Electronic Engineering, 2019, 20(7): 946-963.
