是相同的,并推导得到AM和MQAM的通用公式。然后,利用归一化四阶累积量切片特征参数检测噪声中通信信号,利用占用带宽特征参数将信号分为扩频信号和常规调制通信信号两类;最后利用瞬时特征参数和高阶累积量特征参数,分别识别扩频信号和5种常规调制通信信号。仿真结果表明,当信噪比高于1 dB时,该算法对上述7种信号的正确识别率可达到100%。摘 要： 由于直扩信号(Direct Sequence Spread Spectrum, DSSS)通常淹没在噪声中,为了有效地识别直扩信号、跳频信号(Frequency Hopping Spread Spectrum, FHSS)和常规调制信号,提出基于瞬时特征和高阶累积量的识别算法。首先推导证明了FM、MFSK、MPSK、DSSS、FHSS信号的归一化四阶累积量切片是相同的,并推导得到AM和MQAM的通用公式。然后,利用归一化四阶累积量切片特征参数检测噪声中通信信号,利用占用带宽特征参数将信号分为扩频信号和常规调制通信信号两类;最后利用瞬时特征参数和高阶累积量特征参数,分别识别扩频信号和5种常规调制通信信号。仿真结果表明,当信噪比高于1 dB时,该算法对上述7种信号的正确识别率可达到100%。
通信信号识别是通信信号参数估计与解调的重要技术之一,它可以判断未知信号的调制方式,并估计出某些调制参数,为信号解调提供参数依据,从而得到有用信息。目前,基于特征提取的模式识别算法中,由于高阶累积量抗噪性能好,基于高阶累积量特征参数的数字调制信号识别算法引起众多研究者关注。文献[1]利用四阶和六阶累积量构成的特征参数对MQAM(Multiple Quadrature Amplitude Modulation)信号进行类内识别,对相位噪声和载波频率偏移具有鲁棒性。文献[2]利用单输入多输出模型,提出一种基于异步四阶累积量的调制信号分类器,计算所有子信道上四阶累积量平均。该识别算法在瑞利和莱斯衰落信道有较好的识别性能。文献[3]利用二、四、六、八阶累积量构造的五个特征参数,识别2ASK(2 Amplitude Shift Keying)、MPSK(Multiple Phase Shift Keying)、MQAM和MAPSK(Multiple Amplitude and Phase Shift Keying)等8种信号,当信噪比大于-3 dB时,信号识别率达到90%以上。文献[4]利用四阶和六阶累积量构成的特征参数识别16QAM、32QAM、16APSK和32APSK信号,当信噪比大于10 dB时,信号识别率达到96%。瞬时特征参数多用于模拟和数字调制信号的综合识别。文献[5]利用四阶和六阶累积量构成的三个特征参数, 识别OFDM(Orthogonal Frequency Division Multiplexing)、MASK、MPSK、MFSK(Multiple Frequency Shift Keying)和MQAM等12种信号,并引入深度学习网络结构表征微弱特征。该算法对相位和频率偏移具有很好的鲁棒性。文献[6]提出了带宽占用比特征参数,该参数对噪声和调制类型不敏感。文献[7]改进9种常用瞬时特征参数,并用于14种常规模拟和数字调制信号的分类识别,实验表明改进后信号识别率明显提高。文献[8]结合信号瞬时信息和功率谱信息识别AM(Amplitude Modulation)、2ASK、BPSK、QPSK、2FSK、MSK(Minimum Frequency Shift Keying)信号,当信噪比大于5 dB时,识别率达到92%以上。
以上文献都是对常规调制信号进行识别,对扩频信号和常规调制信号识别的研究成果较少。目前,扩频信号调制识别方法基本上都是对信号进行时频分析,然后利用得到的时频域特征实现信号调制识别。文献[9]通过判断信号的频率变化周期性来识别跳频信号,利用信号时域自相关曲线峰值位置间隔是否近似相等,来区分直扩信号和常规调制信号;当信噪比大于-3 dB时,扩频信号识别率达到90%以上,但该算法比较复杂,需要的样本数目多。本文结合瞬时特征参数和高阶累积量特征参数,研究直扩信号DSSS、跳频信号FHSS和常规调制信号AM、FM(Frequency Modulation)、BFSK、QPSK及16QAM的识别算法,并给出了仿真实验结果。
为了识别扩频信号和AM、FM、BFSK、QPSK及16QAM信号,利用信号特点本节研究特征参数选取。
2.1.1 高阶矩和高阶累积量公式
令x(t)为零均值平稳随机信号,根据高阶累积量理论,得到二阶和四阶累积量公式如下[10]:
c2x(τ)=m2x(τ)=E{x(n)x(n+τ)}=Rx(τ)
(1)
m4x(τ1,τ2,τ3)=E{x(n)x(n+τ1)x(n+τ2)x(n+τ3)}
(2)
c4x(τ1,τ2,τ3)=E{x(n)x(n+τ1)x(n+τ2)x(n+τ3)}-
E{x(n)x(n+τ1)}E{x(n+τ2)x(n+τ3)}-
E{x(n)x(n+τ2)}E{x(n+τ1)x(n+τ3)}-
E{x(n)x(n+τ3)}E{x(n+τ1)x(n+τ2)}=
m4x(τ1,τ2,τ3)-c2x(τ1)c2x(τ3-τ2)-
c2x(τ2)c2x(τ1-τ3)-c2x(τ3)c2x(τ2-τ1)
(3)
当τ1=τ2=τ3=0时,得到:
c4x(0,0,0)=m4x(0,0,0)-3m2x(0)m2x(0)
(4)
进行归一化,得到信号x(t)的归一化四阶累积量切片
为:
(5)
2.1.2 信号归一化四阶累积量切片
(1)调制信号归一化四阶累积量切片
调制信号可表示为:s(t)=a(t)cos(2πfct+φ+φ(t)),其中a(t)是信号幅度, fc是载波频率,φ是在[0,2π)内均匀分布的随机变量,φ(t)为瞬时相位偏移。可推导得到调制信号的二阶和四阶累积量分别为:
m2s(0)=E[s(t)s(t)]=
m4s(0,0,0)=E[s(t)s(t)s(t)s(t)]=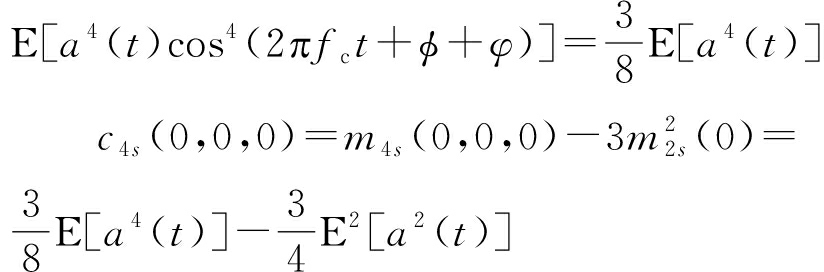
得到归一化四阶累积量切片为:
(6)
下表分别给出了常规调制信号AM、FM、BFSK、QPSK以及QPSK直扩信号和BFSK跳频信号的幅度a(t)和相位偏移φ(t),其中,A为常数。
表1 调制信号的部分瞬时值
Tab.1 Partial instantaneous value of the modulated signal
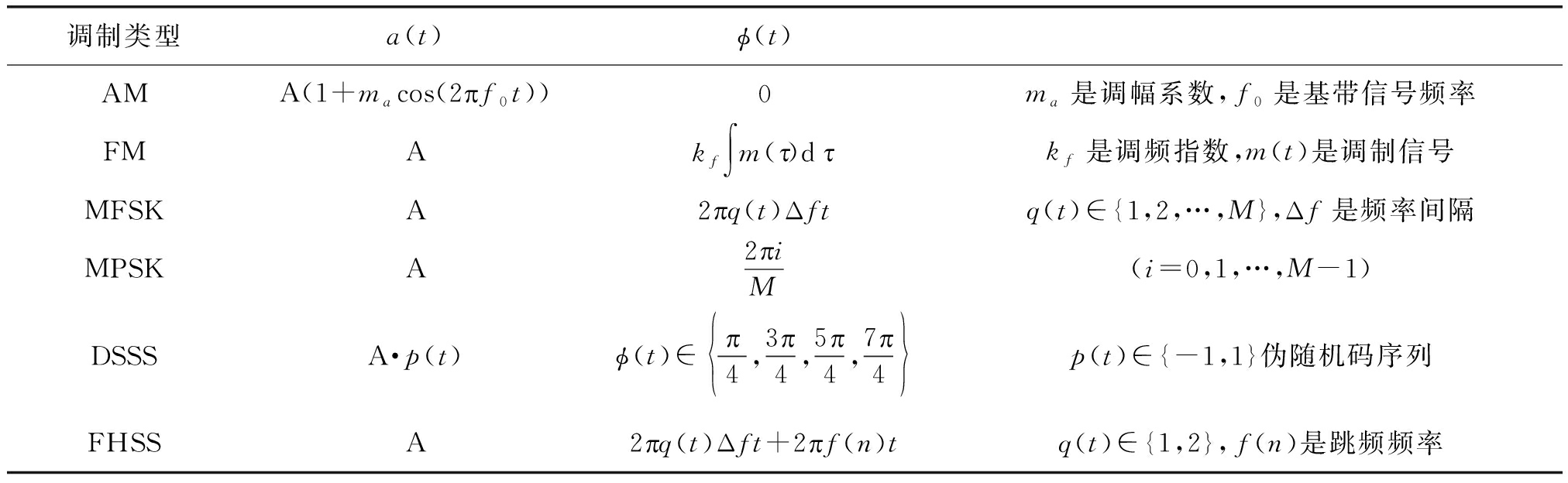
调制类型a(t)ϕ(t)AMA(1+macos(2葩f0t))0ma是调幅系数,f0是基带信号频率FMAkf∫m(葳)d葳kf是调频指数,m(t)是调制信号MFSKA2葩q(t)Δftq(t)∈{1,2,…,M},Δf是频率间隔MPSKA2葩iM(i=0,1,…,M-1)DSSSA·p(t)ϕ(t)∈ 葩4,3葩4,5葩4,7葩4 p(t)∈{-1,1}伪随机码序列FHSSA2葩q(t)Δft+2葩f(n)tq(t)∈{1,2},f(n)是跳频频率
根据上表可推导得到FM、MFSK、MPSK、DSSS、FHSS的E[a2(t)]=A2,E[a4(t)]=A4,代入式(6),得到归一化四阶累积量切片为:
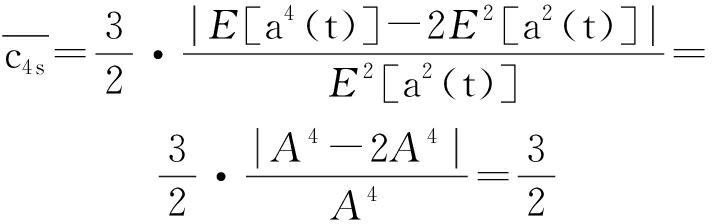
(7)
对于AM信号,推导得到
代入式(6),得到归一化四阶累积量切片为:
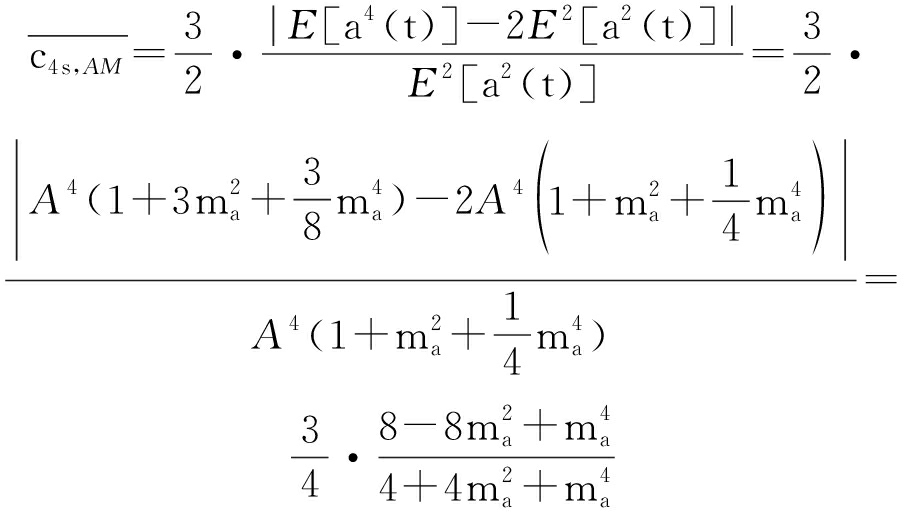
(8)
对于MQAM信号,可表示为
其中
根据高阶累积量理论,MQAM信号的二阶矩和四阶矩分别为:
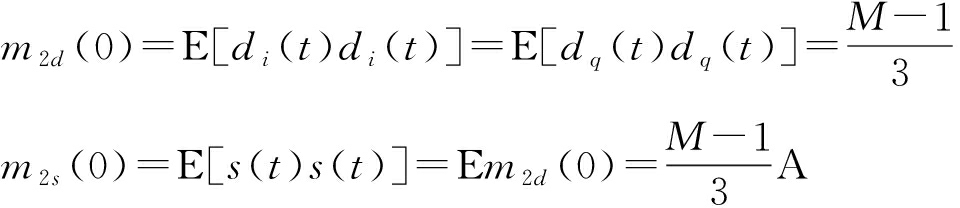
m4d(0,0,0)=E[di(t)di(t)di(t)di(t)]=
m4s(0,0,0)=E[s(t)s(t)s(t)s(t)]=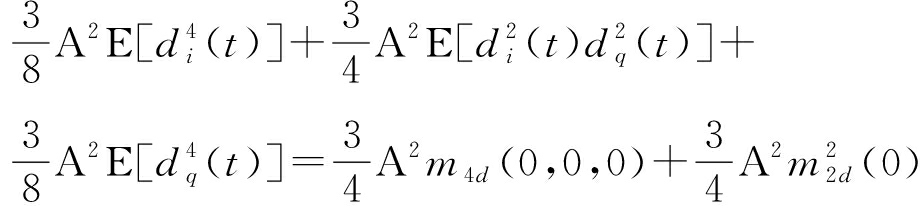
由式(4)可得MQAM信号的四阶累积量切片c4s(0,0,0)为:
因此可得归一化四阶累积量切片
为:
(9)
(2)接收信号归一化四阶累积量切片
由于受到噪声影响,接收信号可表示为x(t)=s(t)+n(t),其中,s(t)是有用信号,n(t)是噪声。假设n(t)是与s(t)统计独立的高斯白噪声,其均值为零,方差为
可推导得到接收信号的二阶和四阶累积量为:
c4x(0,0,0)=c4s(0,0,0)
由于高斯白噪声的
得到的归一化四阶累积量切片为:
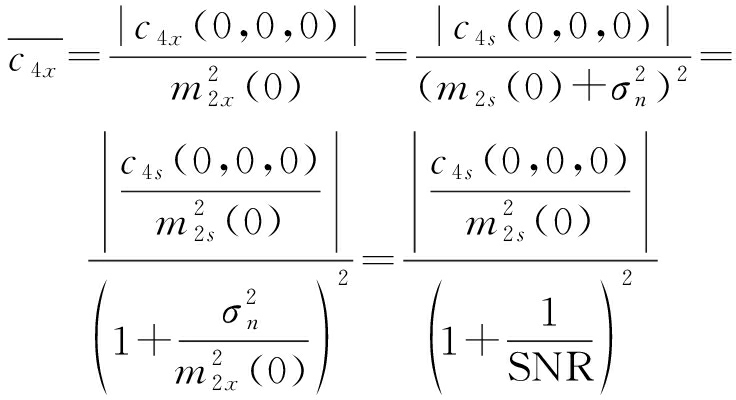
(10)
因此,AM、MQAM和其他调制信号的归一化四阶累积量切片分别为:
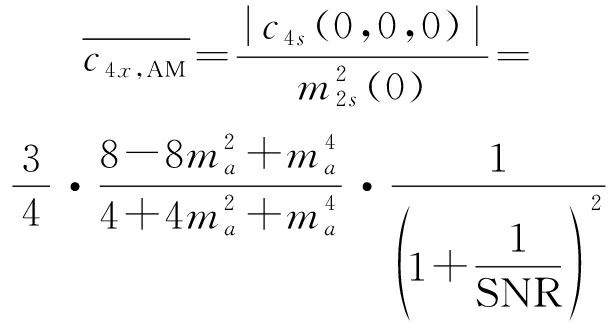
(11)
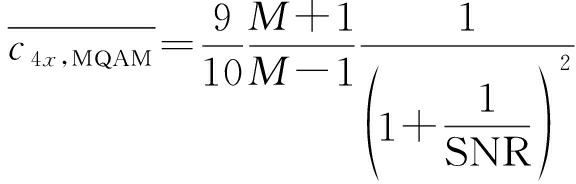
(12)
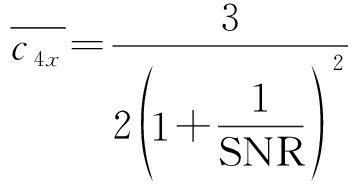
(13)
零中心归一化瞬时幅度谱的最大值[11]γmax表征了信号瞬时幅度的变化情况,可以反映调制信号包络的变化特性,可以用来区分无包络起伏的跳频信号与包络微弱起伏的直扩信号,其定义如下:
γmax=max|DFT(Acn(i))|2/N
(14)
其中,N为采样点数,Acn(i)为零中心归一化瞬时幅度,由下式计算:
Acn(i)=An(i)-1
其中,An(i)=A(i)/ma,而
为瞬时幅度A(i)的平均值。
特征参数占用带宽是指:在接收信号的幅度谱上,占幅度谱总功率的99%的宽带,即在占用带宽频率下限之下或频率上限之上的功率各等于总功率的0.5%。可以用来区分宽带调制信号(即扩频信号)与窄带调制信号(即常规调制信号)。
峰度又称峰态系数,表征概率密度分布曲线在平均值处峰值高低的特征数,其定义如下:
(15)
其中,P是输入信号作FFT变换后的幅度谱。可以用来区分峰度较低的QPSK、16QAM调制信号和其他信号。
利用高阶累积量理论,可计算得到QPSK和16QAM信号的|C40|和|C80|,分别如表1所示,从而构造特征参数F为:
(16)
计算得到的F理论值如表2所示。由于QPSK和16QAM信号的F值不同,因此可以通过F区分之。
表2 QPSK与16QAM信号的高阶累积量理论值
Tab.2 Higher order cumulant theoretical values for QPSK and 16QAM signals
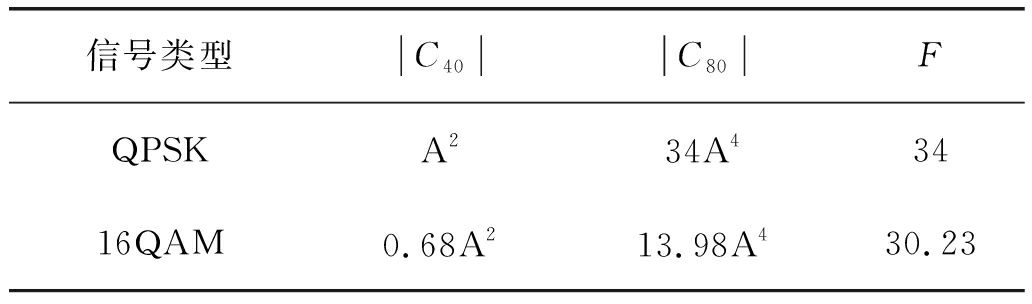
信号类型C40C80FQPSKA234A43416QAM0.68A213.98A430.23
理论上,FM信号谱峰个数为1,BFSK信号谱峰个数为2,因此可以用信号幅度谱峰值个数Pn区分这两种信号。
利用上述六种特征参数,可对常规调制信号{AM、FM、BFSK、QPSK、16QAM}和扩频信号{ DSSS、FHSS },通过决策树分类器进行分类识别。首先利用接收信号的归一化高阶累积量切片及其门限TC,在噪声中将通信信号检测到;其次利用功率谱密度的占用带宽B及其门限TB,将接收信号分为扩频信号类{DSSS、FHSS}和常规调制信号类{AM、FM、BFSK、QPSK、16QAM};接着利用零中心归一化瞬时幅度谱密度最大值γmax及其门限Tm1,将信号类{DSSS、FHSS}区分为DSSS和FHSS;并利用功率谱密度的峰度K及其门限TK,将信号类{AM、FM、BFSK、QPSK、16QAM}区分为类{AM、FM、BFSK}和类{QPSK、16QAM};再者利用零中心归一化瞬时幅度谱密度最大值γmax及其门限Tm2,将类{AM、FM、BFSK}区分为AM和类{FM、BFSK};然后利用功率谱密度的峰值个数Pn及其门限TP,区分BFSK和FM;最后利用高阶累积量特征参数F及其门限TF,识别QPSK和16QAM。因此可得本文AM、FM、BFSK、QPSK、16QAM、DSSS、FHSS信号识别算法的流程图如图1所示。
七种待识别信号AM、FM、BFSK、QPSK、16QAM、DSSS和FHSS的码元速率为50 kHz,载波频率为1.55 MHz,采样频率为62 MHz,通信带宽为31 MHz。直扩信号和跳频信号采用的伪随机码序列是长度为127的m序列,伪随机码速率为635 kHz,直扩信号调制方式为QPSK,跳频频率最小间隔为310 kHz,跳频频率个数为64,跳频信号调制方式为BFSK。噪声是均值为0,方差为1的高斯白噪声,信噪比从-10 dB到10 dB。
3.2.1 特征参数有效性及门限确定
图2是特征参数归一化高阶累积量切片随信噪比变化的曲线。由图可见,高斯噪声的值接近理论值0,而带噪声的通信信号的值大于0,且随信噪比增大而增大,这与式(11)至(13)所表示的相符,因此可利用参数检测通信信号。高斯噪声功率为1时,1000次仿真得到噪声的最大值为0.0081,因此下文仿真中取门限TC=0.0081。
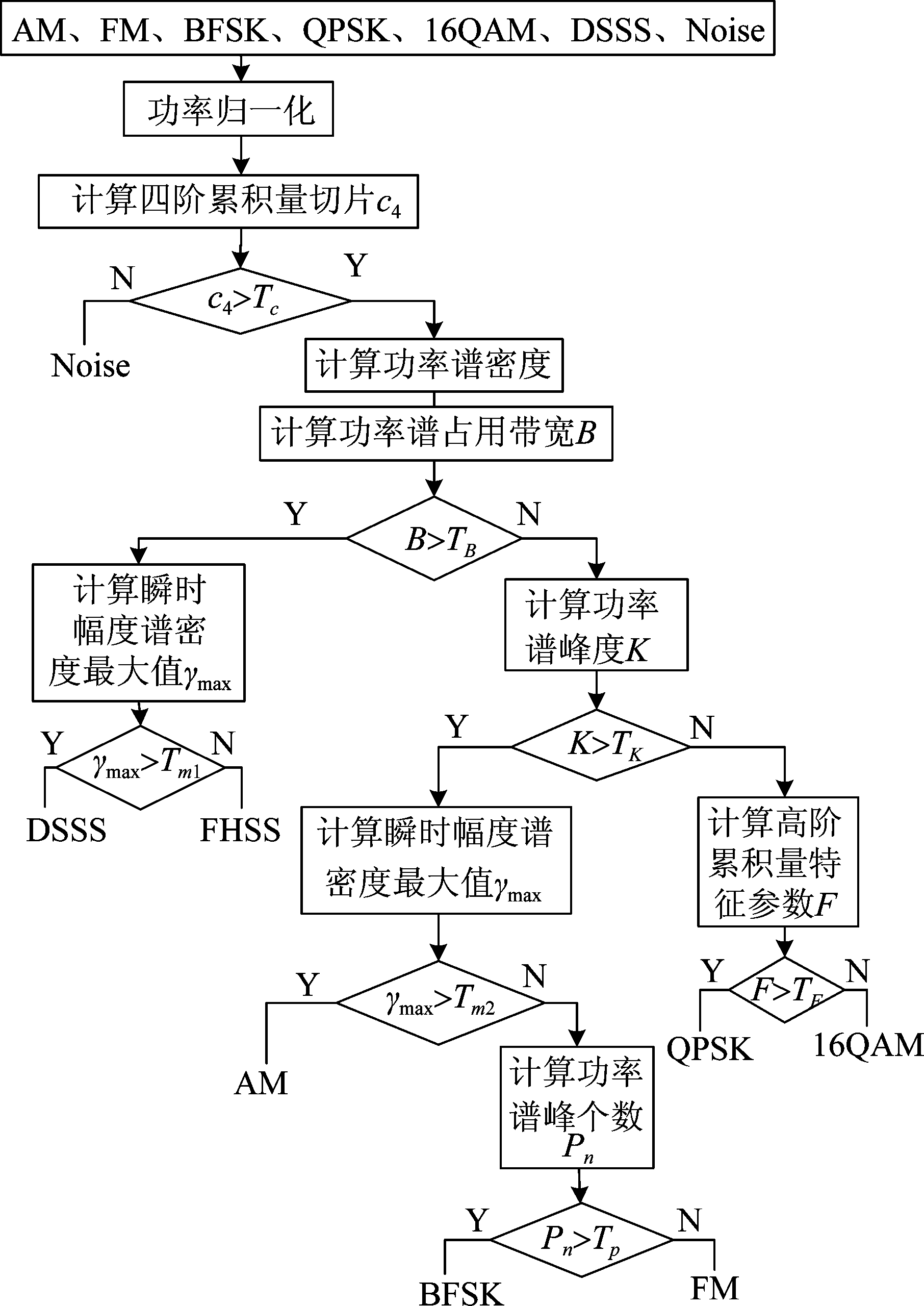
图1 算法流程图
Fig.1 Algorithm flowchart
图2 归一化高阶累积量切片随信噪比变化曲线
Fig.2 Normalized high-order cumulant slice with signal-to-noise ratio curve
图3是信号功率谱密度的占用带宽B随信噪比变化的情况。从图中可以看出,在信噪比大于2 dB时,曲线都趋于平稳,且两种扩频信号的占用带宽大于常规调制信号,因此,参数占用带宽可以区分扩频信号和常规调制通信信号。由图中得到:在信噪比-10 dB时,常规信号中QPSK和16QAM信号的占用带宽值最大为0.79,扩频信号的占用带宽最小为0.91,下文仿真中取这两值的中值为门限值,即TB=0.85。
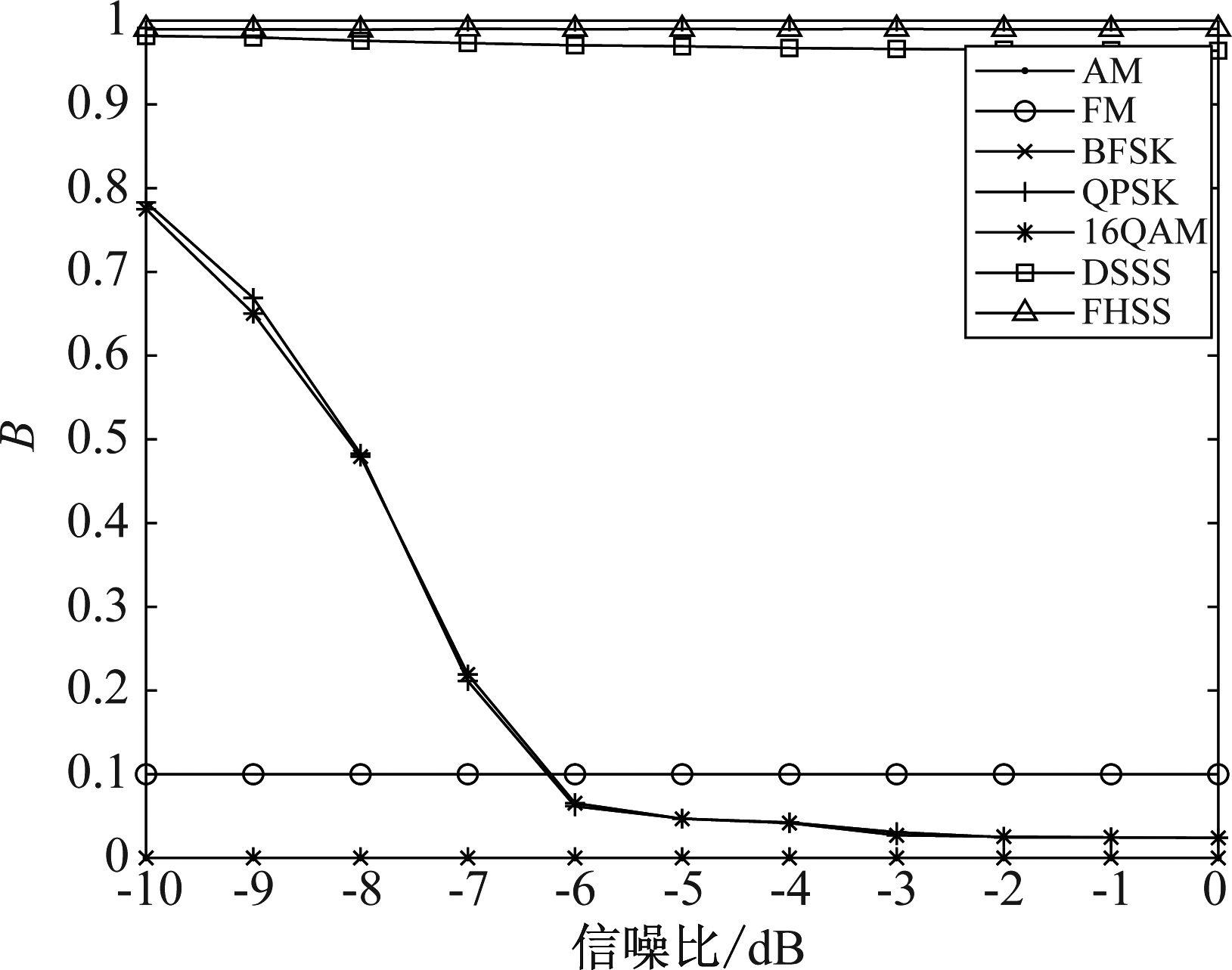
图3 占用带宽随信噪比变化曲线
Fig.3 Occupied bandwidth with signal-to-noise ratio curve
图4是零中心归一化瞬时幅度谱密度最大值γmax随信噪比变化曲线。由图(a)可以看出,AM信号的γmax值远大于其他信号,由图(b)可以看出,DSSS信号的γmax值大于FHSS信号的γmax值。因此,参数γmax可以区分出AM信号与其他信号,以及区分开DSSS信号和FHSS信号。通过图(b)得到:DSSS信号γmax值最小为346.2,FHSS信号的γmax值最大为31.4,下文仿真中这两特征值的中值为门限值,即Tm1=188.8;通过图(a)得到:AM信号γmax值最小为2143,{FM、BFSK}的γmax值最大为838,下文仿真中这两特征值的中值为门限值,即Tm2=1490.5。
图5是信号功率谱密度的峰度K随信噪比变化的情况。从图中可以看出,AM、FM和BFSK信号的峰度值远大于其他几种常规调制通信信号,因此,峰度可以将常规调制通信信号区分为{AM,FM,BFSK}和{QPSK,16QAM}两类。从图5中得到{AM,FM,BFSK}的峰值最小为105200,{QPSK,16QAM}的峰值最大为4135,下文仿真中取这两值的中值为门限值,即TK=54667.5。
图6是功率谱密度的峰值个数随信噪比改变的情况。可以看出,峰值个数不随信噪比变化而变化,因此利用峰值个数可以很好的识别BFSK信号。下文仿真中取门限TP=2。
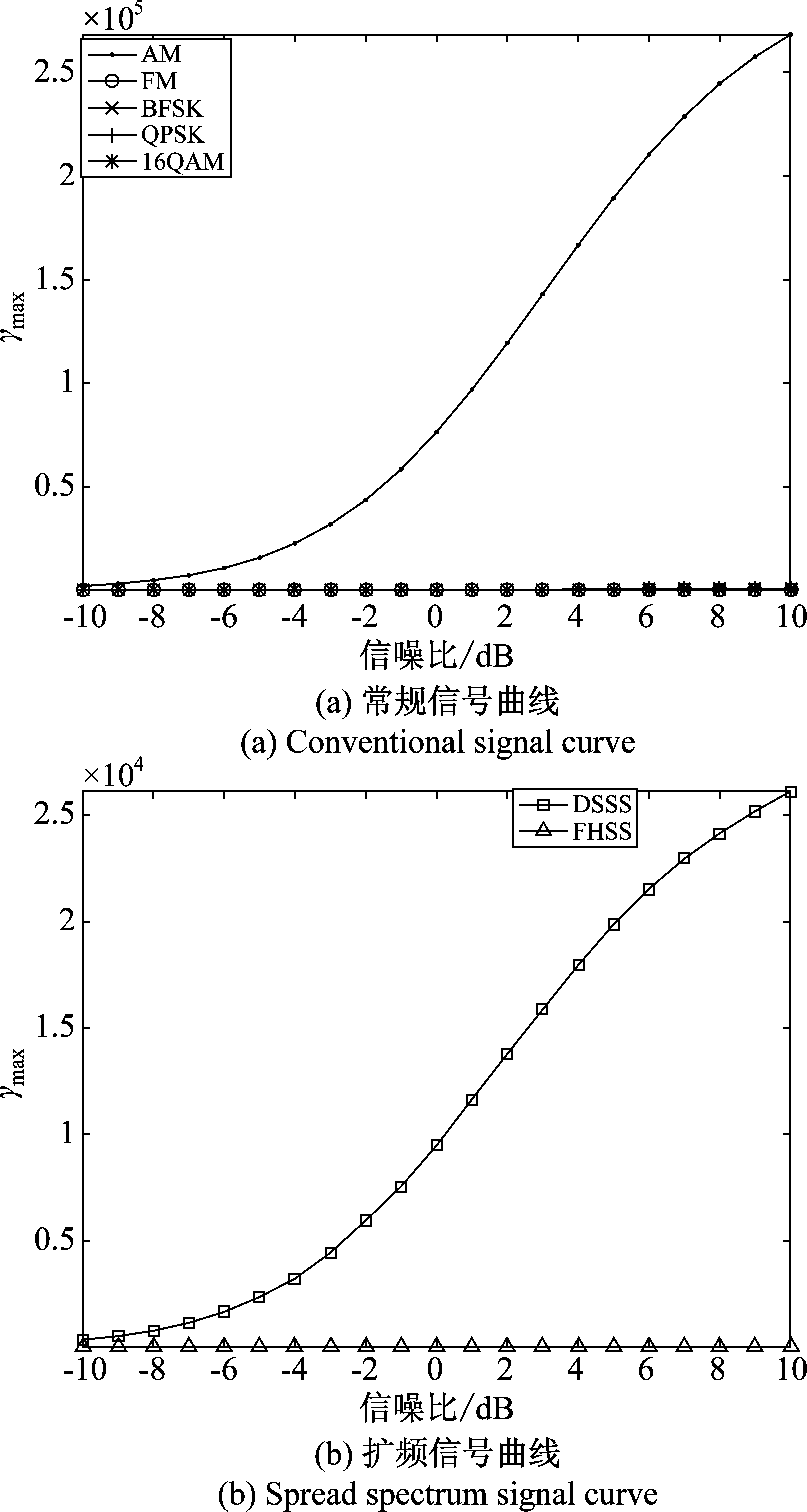
图4 零中心归一化瞬时幅度谱密度最大值随信噪比变化曲线
Fig.4 Zero center normalized instantaneous amplitude spectral density maximum with signal-to-noise ratio curve
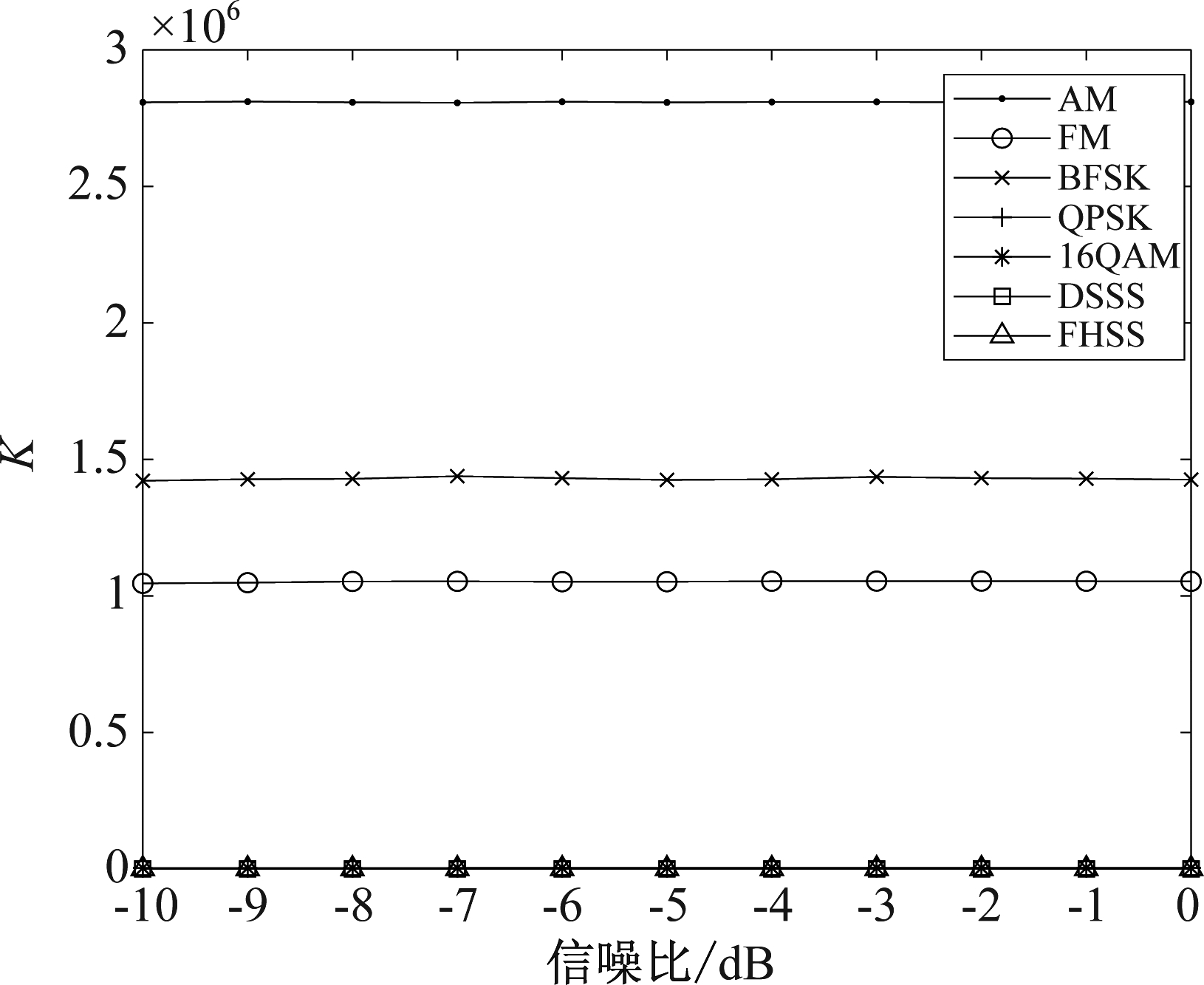
图5 信号功率谱密度的峰度随信噪比变化曲线
Fig.5 Peak power of signal power spectral density with signal-to-noise ratio curve
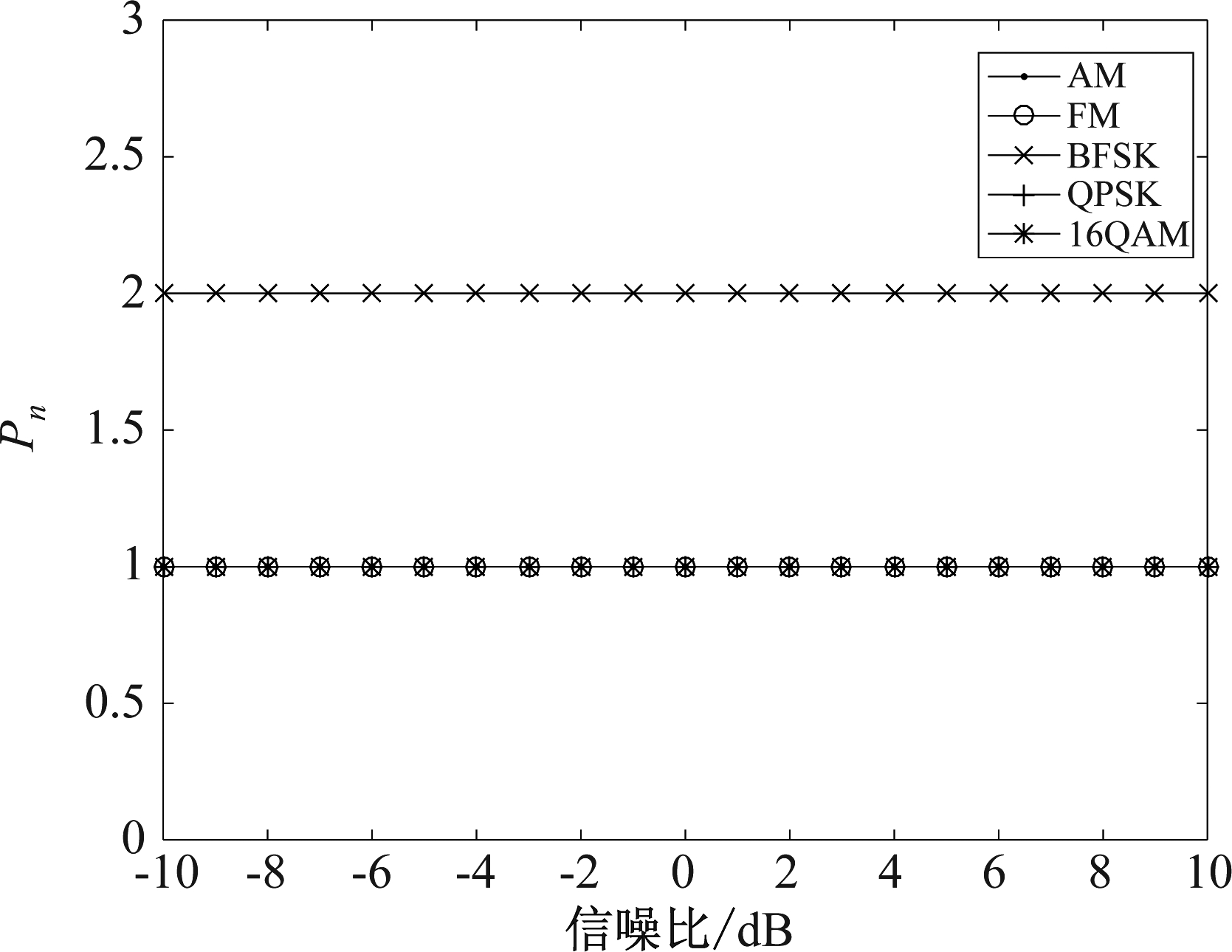
图6 功率谱密度的峰值个数随信噪比变化曲线
Fig.6 Peak number of power spectral density with signal-to-noise ratio curve
图7是高阶累积量特征参数F随信噪比变化曲线。当信噪比小于-2 dB时,由于噪声影响,高阶累积量计算误差大,偏离理论值。当信噪比大于-2 dB时,F值稳定且接近理论值,因此,可以通过F对QPSK与16QAM信号进行识别。下文仿真中取门限为两种信号F值的中值,即TF=32.115。
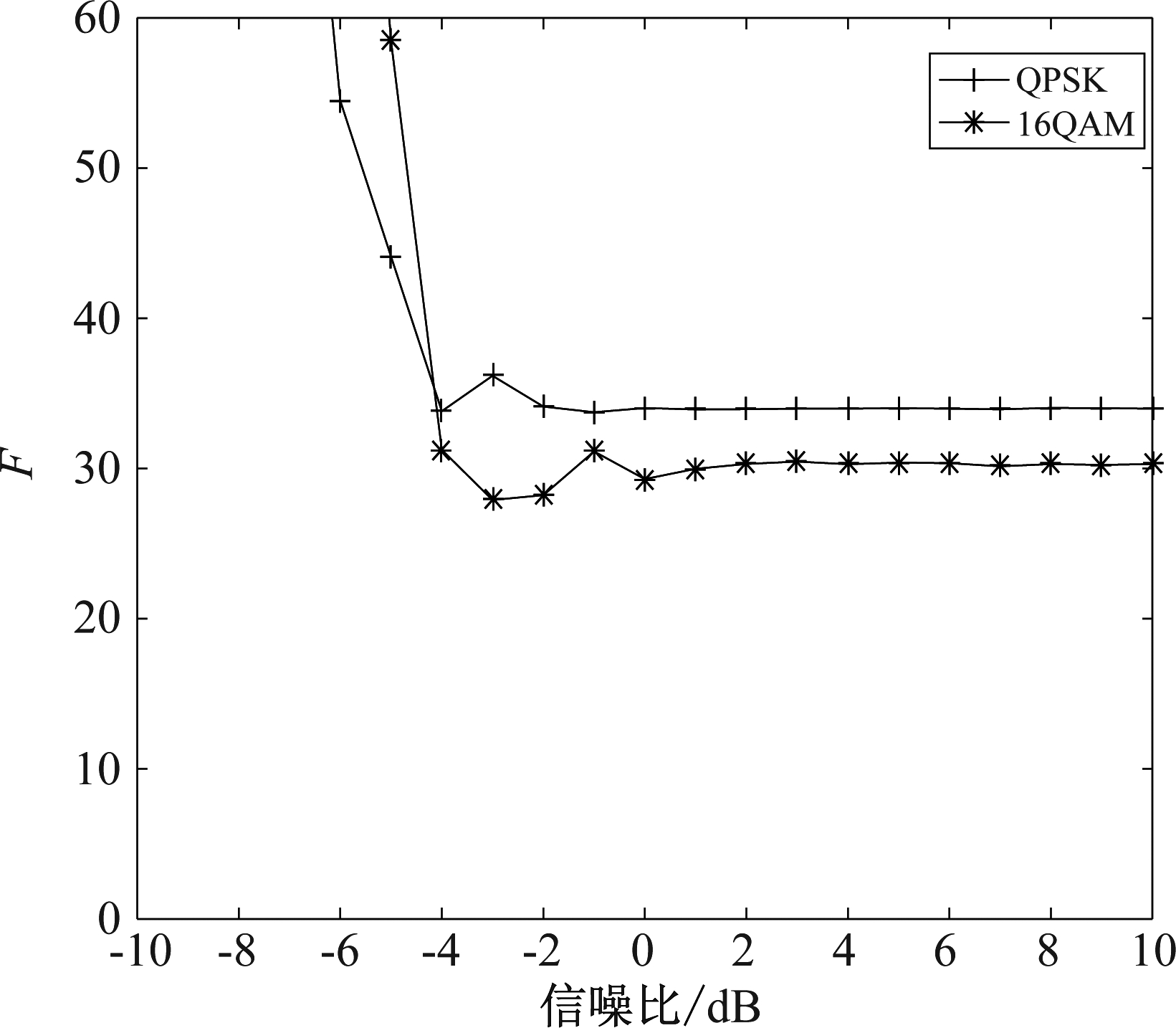
图7 高阶累积量特征参数随信噪比变化曲线
Fig.7 Higher order cumulant characteristic parameter with signal-to-noise ratio curve
3.2.2 性能分析
每种信号在不同信噪比下分别独立进行了100次的测试,得到本文算法对七种信号的正确识别率如图8所示。
仿真结果表明,当信噪比大于1 dB时,各种信号正确识别率达到100%,当信噪比小于-5 dB时, QPSK和16QAM两种信号正确识别性能较差,这与特征参数F受噪声影响大有关。当信噪比为5 dB时,本文算法对信号BFSK、QPSK、16QAM信号识别率高于文献[5];在信噪比为0 dB时,本文算法对信号AM、FM、BFSK、QPSK信号识别率高于文献[6- 8]。
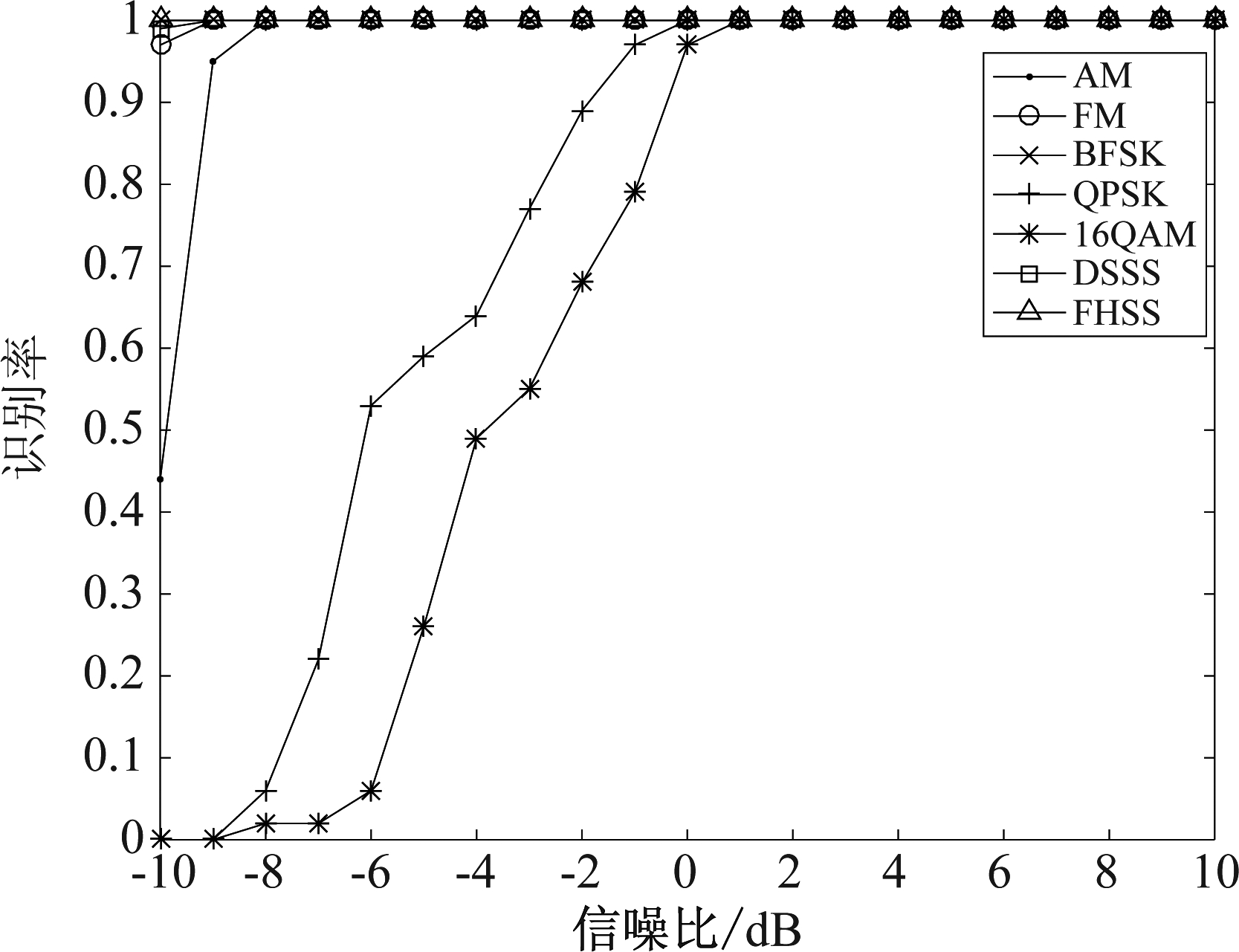
图8 信号正确识别率随信噪比变化曲线
Fig.8 Correct recognition rate of signal with SNR curve
为验证本文算法识别不同扩频码序列的直扩信号,以及不同跳频频率数目的跳频信号的有效性,进行了仿真验证实验。当信噪比为0 dB时,直扩信号扩频码长度与信号正确识别率的关系如图9所示,跳频信号频率数目与信号正确识别率的关系如图10所示。
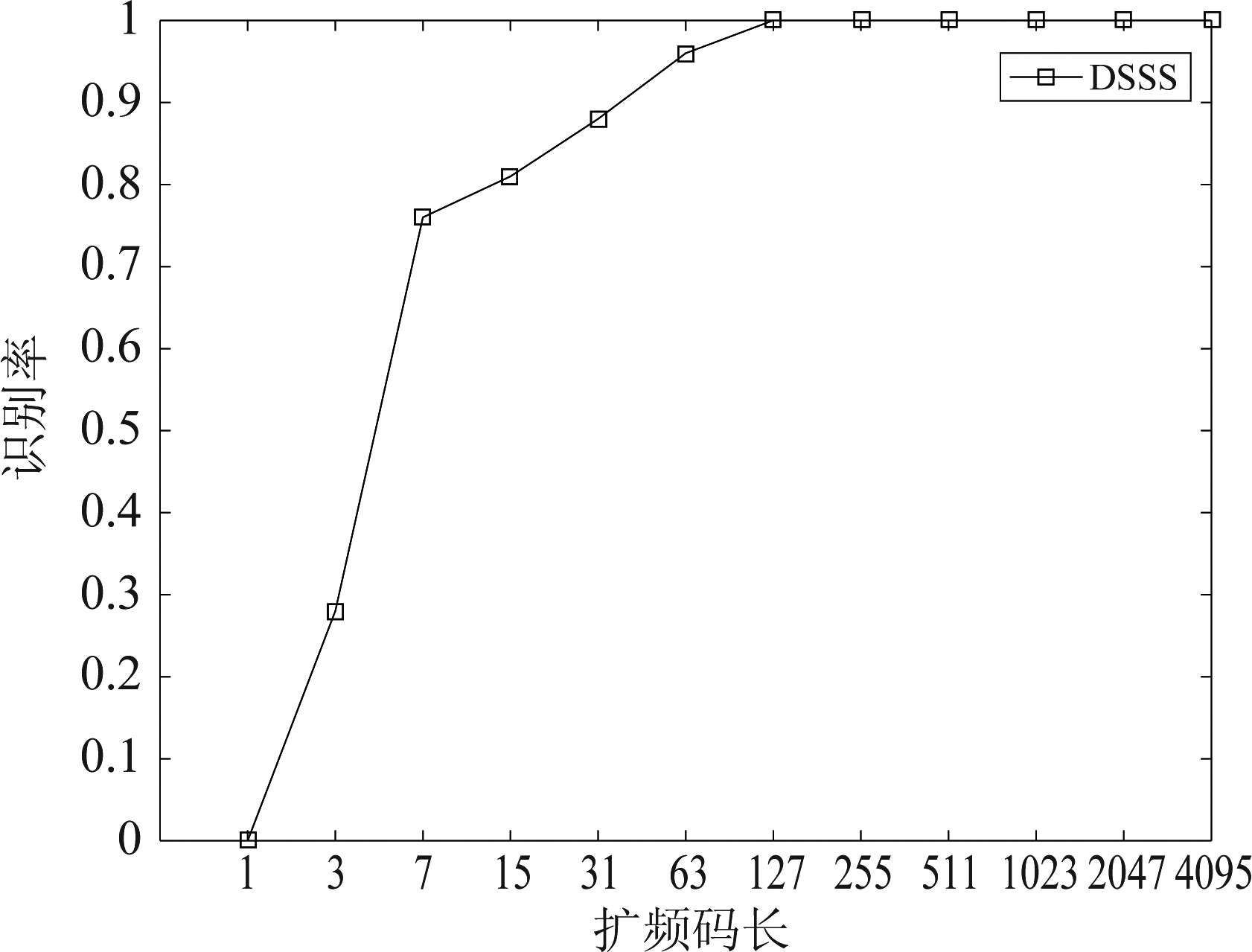
图9 直扩信号识别率随扩频码长度变化曲线
Fig.9 Curve of DSSS signal recognition rate as a function of spreading code length
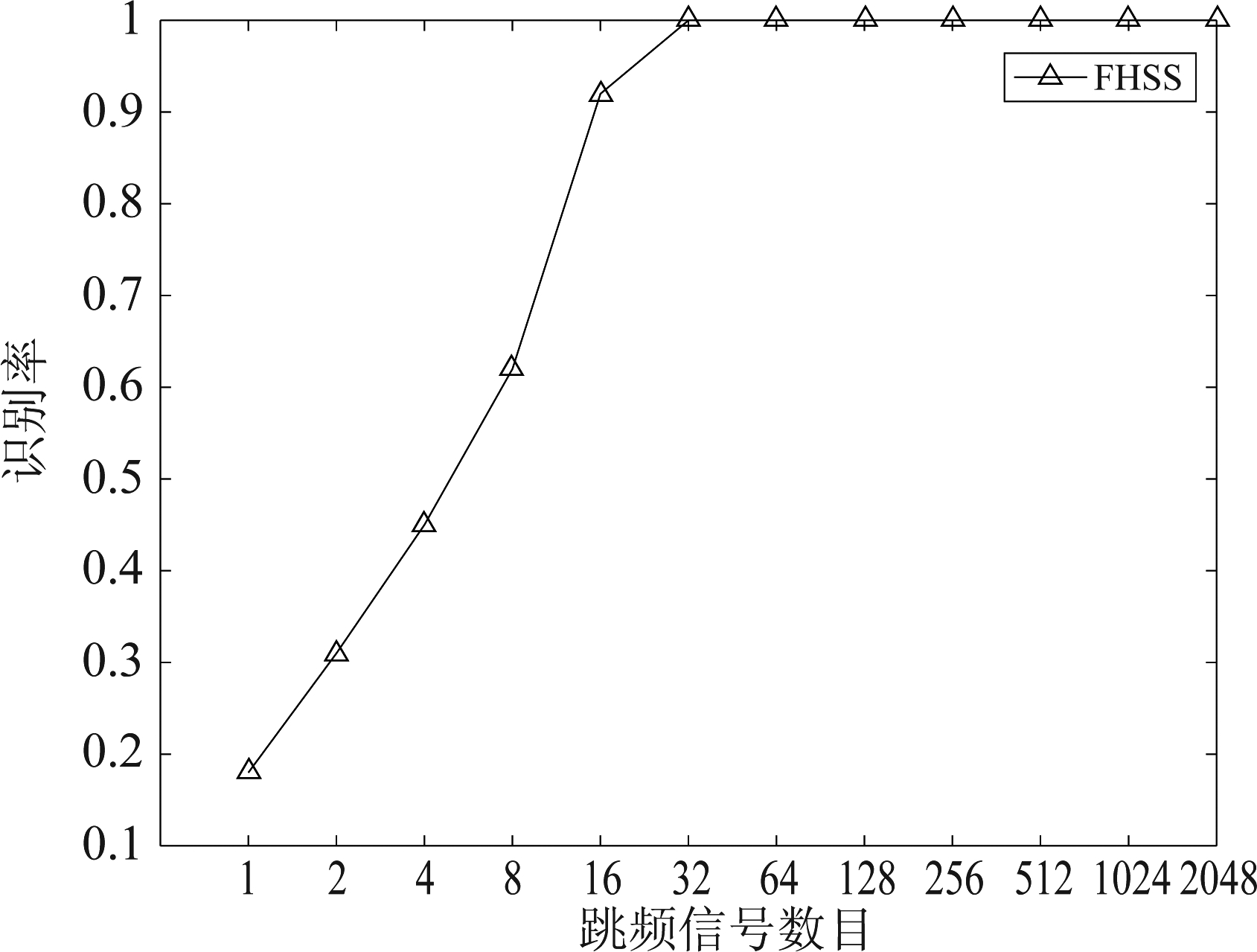
图10 跳频信号识别率随跳频频率数目变化曲线
Fig.10 Frequency hopping signal recognition rate as number of frequency hopping frequencies
从上两图中得到:信号正确识别率随着扩频码长度或跳频频率数目增大而增大,当扩频码长度大于127时,直扩信号识别率达到100%;跳频信号频率数目大于32时,跳频信号识别率达到100%。这是因为识别扩频信号的三个主要特征参数:归一化高阶累积量切片不随扩频序列长度变化;特征参数占用带宽会随着扩频码长度增加而增大到一定范围,就不再变化。直扩信号的零中心归一化瞬时幅度谱密度最大值会随扩频序列长度增加而增大,跳频信号由于变化的是频率个数,不会影响幅度,因此跳频信号的零中心归一化瞬时幅度谱密度最大值不会改变。从而随着扩频序列长度增加,这两个信号更容易区分。因此,本文算法能对长扩频序列的扩频信号进行有效识别。
本文算法与文献[9]的识别算法对DSSS信号和FHSS信号的识别如图11所示。
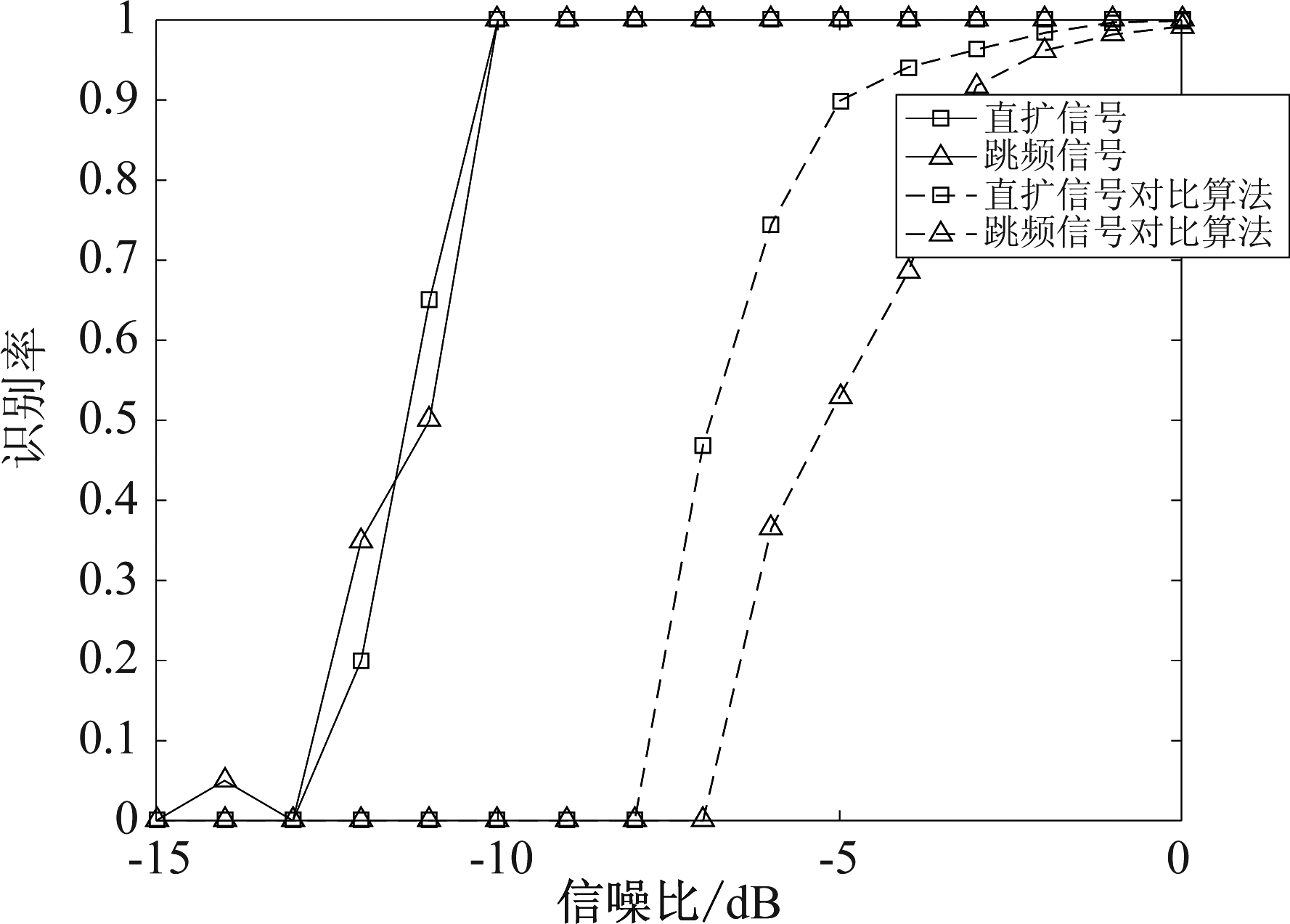
图11 算法性能比较
Fig.11 Algorithm performance comparison
从图中可以看到,本文算法对直扩信号和跳频信号的识别效果比文献[9]算法更好。并且文献[9]需要对信号进行分段FFT,得到信号的时频信号,再通过分析时域自相关曲线的峰值位置来识别直扩信号,通过分析信号的频率变化周期性来识别跳频信号,这就要求信号长度至少包括两个跳频频率周期才能有效识别扩频信号和常规信号。该算法的特征提取较为繁琐,且信号长度过长也就导致算法实时性差。而本文算法利用的是瞬时特征和高阶累积量特征,对信号长度没有那么高的要求,并且特征提取简单。因此本文算法复杂度更低,便于实现。
为了识别常规调制信号AM、FM、BFSK、QPSK和16QAM与扩频信号DSSS和FHSS,本文研究了基于信号瞬时特征和高阶累积量的6种特征参数。仿真结果表明,当信噪比大于1 dB时,各种信号正确识别率达到100%。该算法识别率高,便于硬件实现,具有一定的应用价值。
[1] Jayatunga E H , Dobre O A . A robust higher-order cyclic cumulants feature-based vector for QAM classification[A]. 2014 9th International Symposium on Communication Systems, Networks & Digital Sign (CSNDSP)[C]∥Manchester, 2014:417- 421.
[2] Liu P , Ji X, Zhao G. Asynchronous classification of digital modulations in multipath flat-fading channel using fourth-order cumulant[A]. 2016 IEEE 13th International Conference on Signal Processing (ICSP)[C]∥Chengdu, 2016:1435-1439.
[3] 李跃, 郭兴吉, 赵欣. 基于高阶累积量的调制方式识别研究[J]. 西南科技大学学报, 2018, 33(3): 64- 68.
Li Yue, Guo Xinji, Zhao Xin. Research on Modulation Recognition Based on Higher Order Cumulants[J]. Journal of Southwest University of Science and Technology, 2018, 33(3): 64- 68.(in Chinese)
[4] 解辉, 姚智刚, 马俊涛, 等. 一种基于高阶累积量的复杂调制样式识别方法[J]. 电讯技术, 2019, 59(8): 925-929.
Xie Hui, Yao Zhigang, Ma Juntao, et al. A Complex Modulation Pattern Recognition Method Based on Higher Order Cumulants[J]. Telecommunications Technology, 2019, 59(8): 925-929.(in Chinese)
[5] 袁莉芬, 宁暑光, 何怡刚, 等. 基于高阶累积量特征学习的调制识别方法[J]. 系统工程与电子技术, 2019, 41(9): 2122-2131.
Yuan Lifen, Ning Shuguang, He Yigang, et al. Modulation Recognition Method Based on Higher Order Cumulant Feature Learning[J]. Systems Engineering and Electronics, 2019, 41(9): 2122-2131.(in Chinese)
[6] Park C S, Kim D Y. A novel robust feature of modulation classification for reconfigurable software radio[J]. IEEE on Consumer Electronics Transactions, 2006, 52(4): 1193-1200.
[7] 卢璐. 通信信号调制分类识别与参数提取技术研究[D]. 西安: 西安电子科技大学, 2010.
Lu Lu. Research on classification and identification of communication signal modulation and parameter extraction technology[D]. Xi’an: Xidian University, 2010.(in Chinese)
[8] 李齐超. 低频通信信号检测技术研究与实现[D]. 哈尔滨: 哈尔滨工程大学, 2019.
Li Qichao. Research and implementation of low frequency communication signal detection technology[D]. Harbin: Harbin Engineering University, 2019.(in Chinese)
[9] 鲍杰. 扩频信号检测、分类与参数估计研究[D]. 南京: 南京理工大学, 2016.
Bao Jie. Research on Spread Spectrum Signal Detection, Classification and Parameter Estimation[D]. Nanjing: Nanjing University of Science and Technology, 2016.(in Chinese)
[10] Wang A, Li R. Research on Digital Signal Recognition Based on Higher Order Cumulants[A]. 2019 International Conference on Intelligent Transportation, Big Data & Smart City (ICITBS)[C]∥Changsha, China, 2019:586-588.
[11] 杨杰. 通信信号调制识别: 原理与算法[M]. 北京: 人民邮电出版社, 2014.
Yang Jie. Communication Signal Modulation Recognition: Principles and Algorithms[M]. Beijing: People’s Posts and Telecommunications Press, 2014.(in Chinese)
Abstract: Since the direct sequence spread spectrum is usually submerged in noise, in order to effectively recognize the direct spread sequence signal, the frequency hopping spread spectrum and the conventional modulated signals, an identification algorithm based on instantaneous characteristics and high-order cumulants is proposed. Firstly, the normalized fourth-order cumulant slice parameters 
is used to detect the communication signals in the noise. And then the occupied bandwidth characteristic parameter is used to divide the signal into two types: spread spectrum signals and conventional modulation communication signals. Finally, the parameters of instantaneous characteristic and high-order cumulants characteristics are utilized, which identify the spread spectrum signals and the five conventional modulated communication signals, respectively. The simulation results show that when the signal-to-noise ratio is higher than 1 dB, the correct recognition rate of the above seven kinds of signals can reach 100%.
Reference format: Zhan Jinmin, Zhao Zhijin. Modulation Identification Algorithm for Conventional Modulation Signals and Spread Spectrum Signals[J]. Journal of Signal Processing, 2020, 36(4): 511-519. DOI: 10.16798/j.issn.1003- 0530.2020.04.005.
占锦敏 女, 1995年生, 江西上饶人。杭州电子科技大学硕士研究生, 主要研究方向为通信信号识别。
E-mail: 122956262@qq.com
赵知劲 女, 1959年生, 浙江宁波人。西安电子科技大学博士, 杭州电子科技大学教授, 博士生导师, 研究方向为通信信号处理、认知无线电、自适应信号处理等。
E-mail: zhaozj03@hdu.edu.cn