1 引言
低空风切变一般出现在距地面高度为600 m以下,在飞机起飞或者降落阶段,由于高度低,空速小,这样的情况下遭遇低空风切变,短时间内高度、姿态变化大,飞行员没有足够时间和空间修正动作从而造成危险[1],由于其不易探测特性,人们常把低空风切变称为“隐形杀手”。由于飞机正处于降落状态,飞行高度较低,当飞机遭遇风切变时,飞行员没有足够的时间来调整飞机姿态,很可能造成空难,这对民用航空的飞行安全尤其具有威胁性[2]。所以对低空风切变的探测和预警俨然成为当下民航界重点研究课题之一。
在飞机起飞或着落时,由于高度较低,下视探测风切变时,由于地杂波的影响,微弱的风切变信号必然会被强大的地杂波信号掩盖,对地杂波信号滤除不干净时,则会给随后的风速估计带来困难。空时自适应处理技术(STAP),是广泛运用在相控阵体制雷达中的一种信号处理技术,相控阵体制雷达接受回波信号包含空域信息[3],故在信号处理时,可以联合空时域二维信息进行杂波抑制、信号匹配[4]。目前,针对低空风切变的风速估计方法主要有基于广义相邻多波束空时自适应处理的低空风切变风速估计[5]、多通道联合自适应处理的低空风切变风速估计[6]、基于空时自适应处理的低空风切变风速估计[7]和基于压缩感知的机载相控阵雷达低空风切变风速估计[8]等。上述文章虽然给出了低空风切变风速估计方法,但是均没有考虑存在幅相误差下的情况,当存在幅相误差时,不仅导致空时二维谱展宽,而且杂波自由度也相应增大[9],从而使上述算法性能出现恶化,从而导致杂波抑制不完全和风速估计结果失准。因此,对存在幅相误差下低空风切变风速估计的研究具有重大意义。
基于此,针对存在幅相误差情况下,本文提出一种基于CMCAP-JDL低空风切变风速估计方法。该方法通过对空时域进行加权,同时增加多个局域处理单元参与联合处理的方式计算降维变换矩阵构造降维处理器。该处理器不仅降低了由于幅相误差引入的旁瓣杂波的影响,而且提高了空时域自由度,补偿由于幅相误差导致的杂波谱向空域扩展的问题。
2 信号模型
图1所示的是机载前视阵雷达模型,雷达天线固定在机头,垂直于飞机飞行方向上,即前视方向放置,天线为均匀面阵,信号处理时,通常将面阵通过微波合成等效为一个阵元数为N等距均匀线阵,X轴表示飞机飞行方向,λ为电磁波波长,V为载机飞行速度,H为载机高度, fr为脉冲重复频率,阵元间距为d=λ/2,在一次相干处理时间(CPI)有K个脉冲,其中,杂波块的俯仰角和方位角是φ、θ,风切变信号的俯仰角和方位角是φl、θ0。第l个距离单元的雷达回波数据为Xl,表示为:
Xl=Γ·Sl+Γ·Cl+Nl
(1)
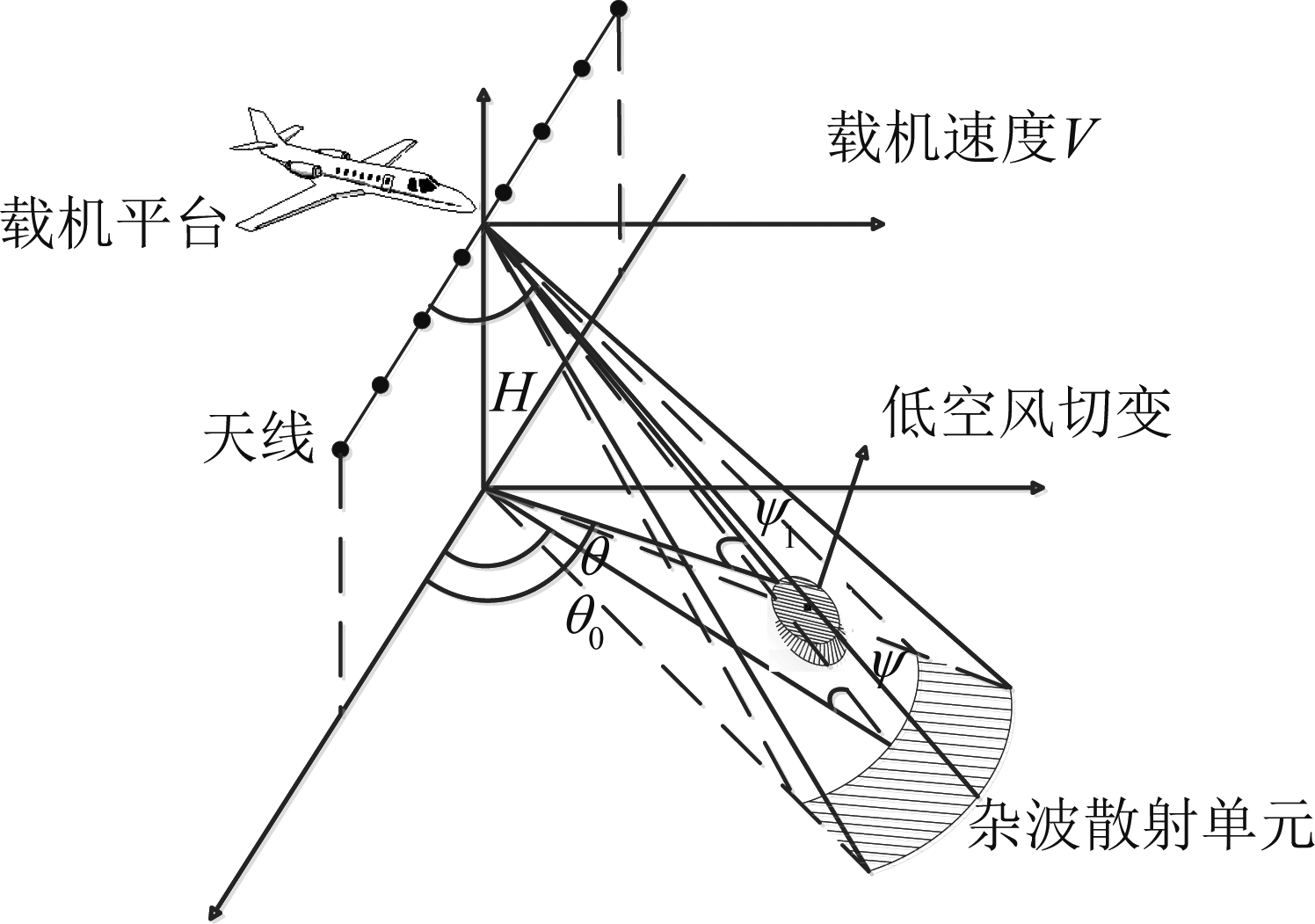
图1 机载前视阵示意图
Fig.1 Schematic diagram of airborne forward looking array
当存在幅相误差时,定义σa=[γ1ejε1,γ2ejε2,…,γNejεN]T为误差矩阵,γn和εn是第n个阵元的幅度、相位误差,Γ=IK⊗(diag(σa)),IK是K*K的单位阵;Nl是加性高斯白噪声,Cl是第l个距离单元地杂波信号的回波数据,Sl为第l个距离单元低空风切变信号的回波数据,表示为:
Sl=βd·Al(fd,ψ0)=βd·(At(fd)⊗As(ψ0))
(2)
At(fd)=at(fd)⊙g(σf)
(3)
As(ψ0)=as(ψ0)⊙g(ψ0)
(4)
其中,符号⊗是kronecker积;⊙为Hadamard积;βd表示第l个距离单元的低空风切变的回波振幅;fd表示第l个距离单元的低空风切变的中心多普勒频率;ψ0表示风切变的空间锥角,且cosψ0=cos θ0cos φ0;由于风切变信号属于分布式目标,所以单个距离单元的空时导向矢量在空间和时间上都会出现一定的扩展,At(fd)和As(ψ0)分别表示扩展后的低空风切变的时间导向矢量和空间导向矢量,at(fd)=[1,ej2πfd,…,ej(K-1)2π fd]T表示该距离单元中多普勒中心频率为fd的点目标的时域导向矢量,
表示的是风切变信号频率扩展函数;as(ψ0)=[1,ej2πdcos ψ0/λ,…,ej(N-1)πdcos ψ0/λ]T表示的是该距离单元风场方位为ψ0的点目标的空间导向矢量,g(ψ0)=[1,e(2πd/λ)2Δ/2,…,e(2π(N-1)d/λ)2Δ/2]T表示的是风切变信号的角度扩展函数,其中,
方向扩展系数为σφ,θ0方向上的扩展系数为σθ [10]。
3 基于CMCAP-JDL风速估计
首先对杂波进行距离依赖性矫正[11-12],并对待测距离单元的杂波协方差矩阵进行估计,然后采用基于CMCAP-JDL空时自适应处理的方法来抑制地杂波和估计风速。
图2表示该方法的原理图,该方法主要分为两部分,第一部分是计算降维变换矩阵,第二部分是通过空时自适应处理进行风速估计。其中降维变换矩阵的计算分为三个步骤,分别是波束形成、多普勒滤波和选取局域处理单元进行联合处理。下文分别就这两个部分展开论述。
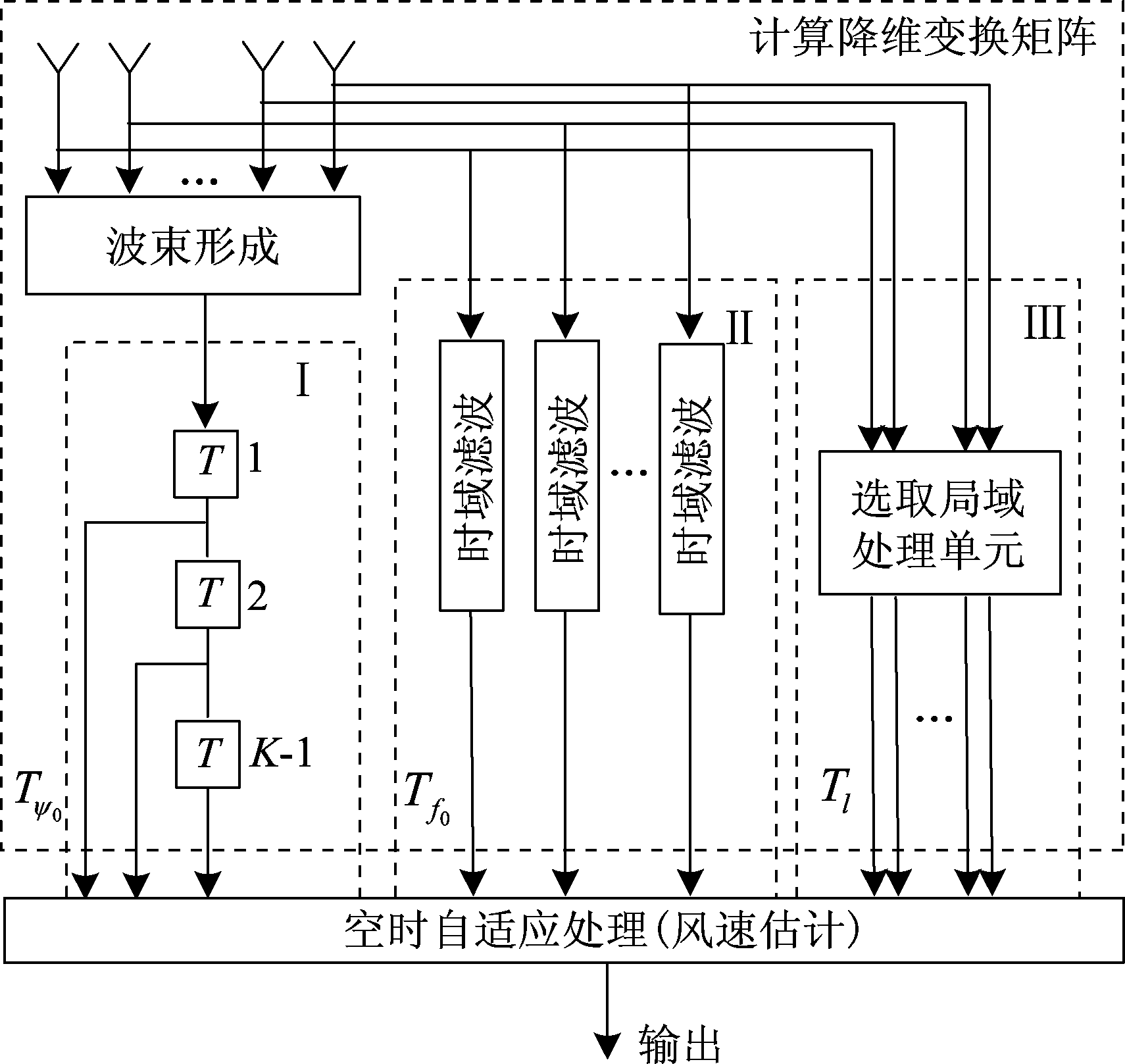
图2 CMCAP_JDL自适应处理器结构图
Fig.2 CMCAP-JDL adaptive processor architecture
3.1 求解降维变换矩阵
首先计算波束形成和多普勒滤波系数,当风场信号方位已知时,对第l个距离单元,分别以风场方位ψ0为空域主波束和第q(q=1,2,…,K)个多普勒通道的归一化多普勒频率flq(flq∈[-1,1])为时域主通道定义如下两个二维导向矢量集合:
Aψ={a(ψ0, f), f∈[-1,1]}
(5)
Af={a(ψ, flq),ψ∈[0,π]}
(6)
Aψ和Af分别表示所有沿着ψ=ψ0和f=flq的加权导向矢量的集合,其中Aψ中的任何向量都可以表示为:
a(ψ0, f)=bt( f )⊗bs(ψ0)=
bt( f )[Ik⊗bs(ψ0)]=bt( f )Tψ0
(7)
上式Tψ0=Ik⊗bs(ψ0)为一个NK*K的矩阵,代表了波束形成系数,经过Tψ0变换后的数据对应各个脉冲的空域波束输出;Ik为K*K的单位阵;bt( f )={At( f ), f∈[-1,1]}为归一化多普勒频域内所有时间导向矢量的集合;bs(ψ0)为空域波束形成的导向矢量,可以表示为:
bs(ψ0)=Qs⊙As(ψ0)=Qs⊙as(ψ0)⊙g(ψ0)
(8)
Qs=[qs1,qs2,…,qsN]T表示空域的切比雪夫权矢量。
同理,求解出Af中所有的向量
a(ψ, flq)=bt(flq)⊗bs(ψ)=
[bt(flq)⊗IN]bs(ψ)=Tf(flq)bs(ψ)
(9)
上式Tf(flq)=bt(flq)⊗IN为一个NK*N的矩阵,代表了时域多普勒滤波系数,经过Tf(flq)变换后的数据对应于多普勒滤波后的各个阵元的输出;IN为N*N的单位阵。bs(ψ)={As(ψ),ψ∈[0,π]}为空域范围所有空间导向矢量的集合;bt(flq)为时域多普勒导向矢量,可以表示为:
bt(flq)=Qt⊙At(flq)=Qt⊙at(flq)⊙g(σf)
(10)
Qt=[qt1,qt2,…,qtK]T表示时域的切比雪夫权矢量。
为了降低幅相误差的影响,接下来选取局域处理单元参与联合处理,在风场方位ψ0上将角度-多普勒单元分成L组,每组称为一个局域处理单元(LPR),定义了每个局域处理单元分别具有ηa=3个角度单元、ηd=3个多普勒单元,示意图如3所示,让LPR参与联合处理,有效的增加空时域自由度,从而提高系统的稳定性。
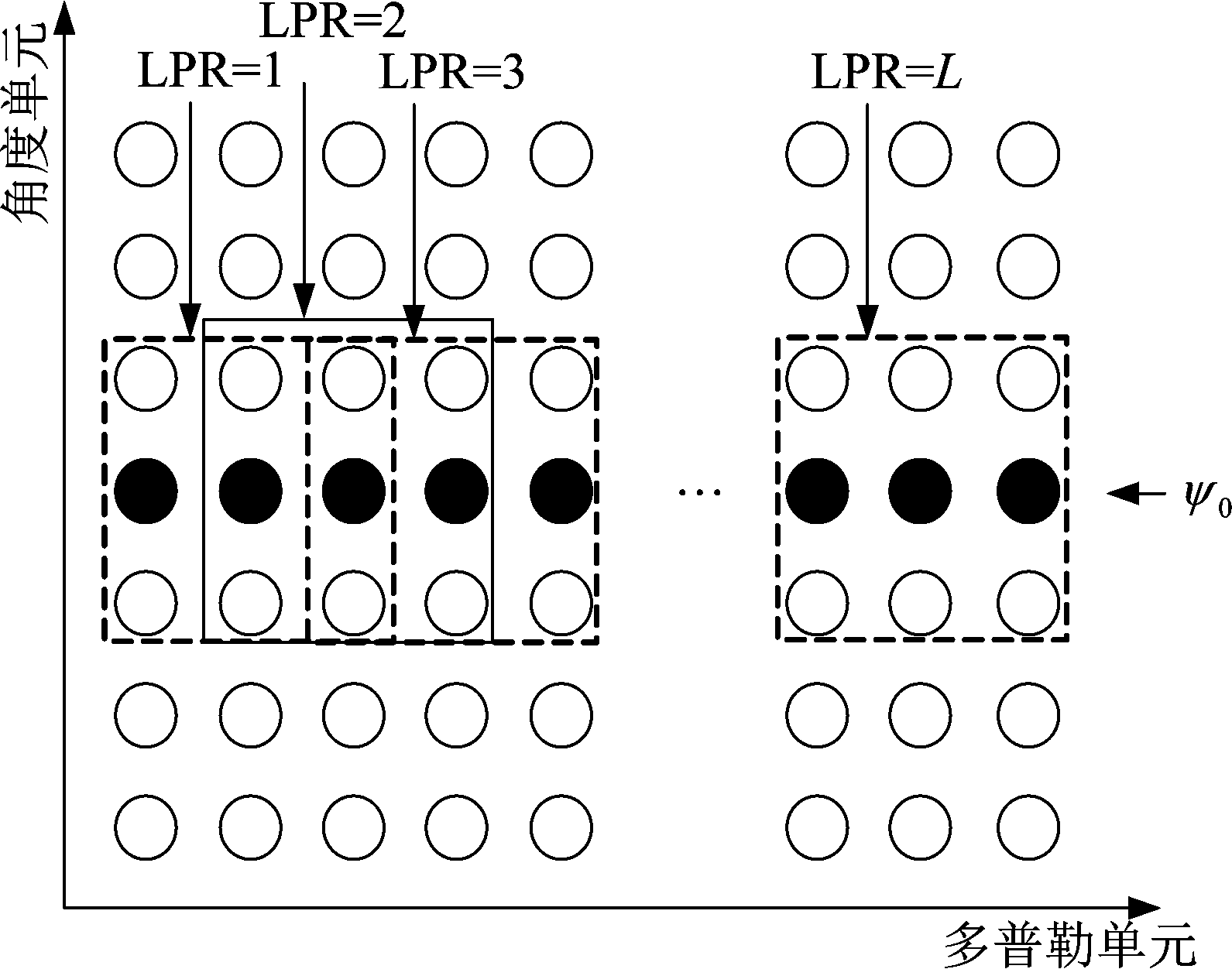
图3 选取局域处理单元
Fig.3 Select local processing unit
局域处理单元中的角度单元选取的原则是,固定空域主波束ψ0方位,选择
为间隔的相邻两列,表示为
多普勒单元的选取,以多普勒频率flq(flq∈[-1,1],q=1,2,…,K)为中心,
接下来以时域主通道flq(flq∈[-1,1],q=1,2,…,K)相邻三列在整个多普勒域进行扫描,利用所选的三行角度单元与三列多普勒单元与选取的做kronecker积,可以得到Tl(flq):
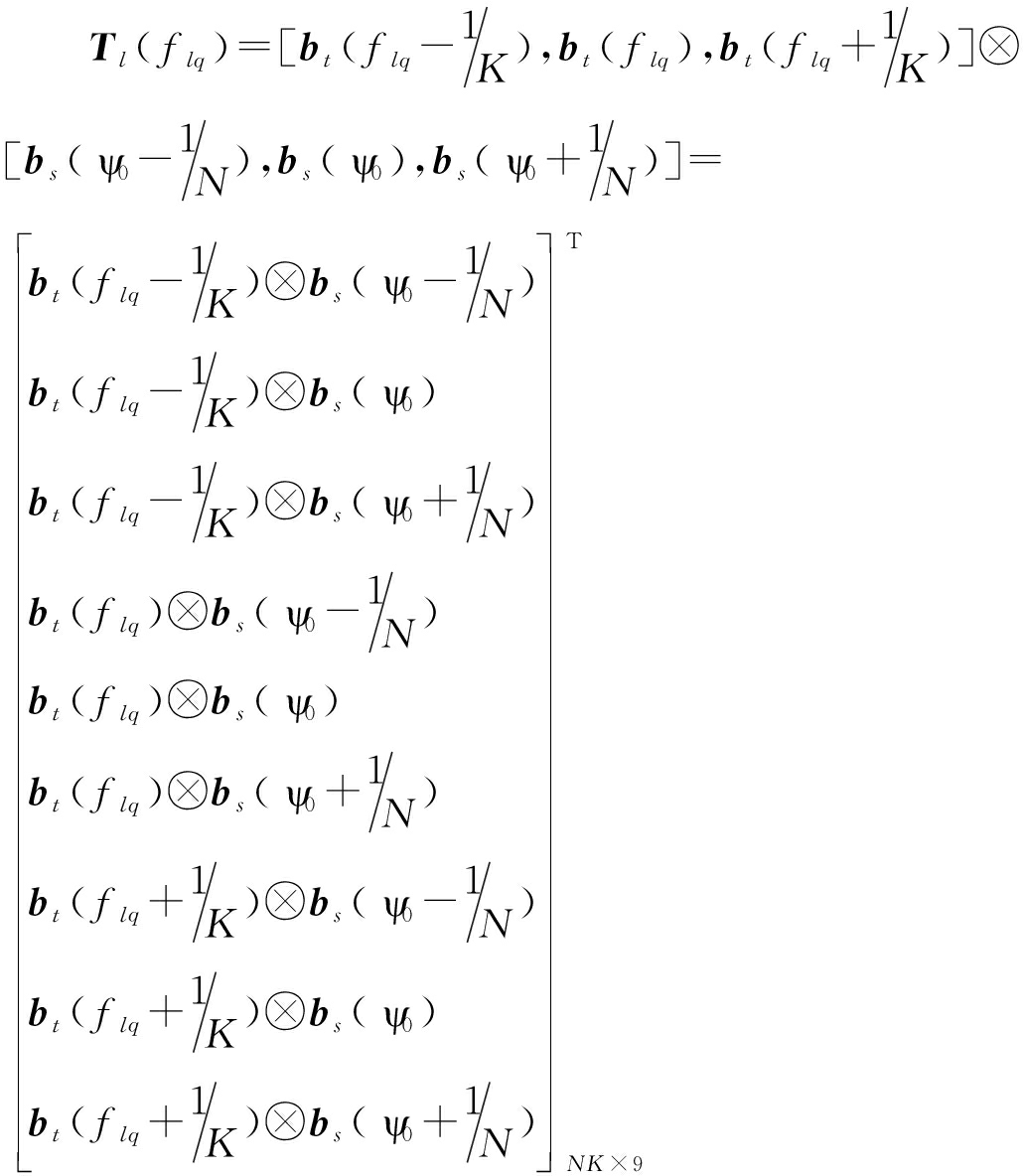
(11)
上述通过波束形成、多普勒滤波及选取局域处理单元参与联合处理计算出的降维变换矩阵为:
(12)
由文献[13]可知,
表示对Tf(flq)前N-1个天线做多普勒滤波。
3.2 低空风切变风速估计
由LCMV准则,求解第l个待测距离单元中第q个多普勒通道的最优权矢量Wlq,可用以下数学优化问题描述:
(13)
其中,Rl(flq)=T(flq)HRT(flq)是第l个待测距离单元内降维杂波协方差矩阵,R是第l个待测距离单元估计得到的杂波协方差矩阵,blq是第l个待测距离单元内降维变换后的低空风切变的空时导向矢量,表示为:
blq=T(flq)Hb(flq,ψ0)=T(flq)Hbt(flq)⊗bs(ψ0)
(14)
b(flq,ψ0)为构造空时导向矢量。第l个待测距离单元内第q个多普勒通道的最优权矢量Wlq为:
(15)
雷达回波数据通过组合空时主通道-局域联合自适应降维处理器后,可以实现杂波抑制及风切变信号的匹配。此时,可以通过下式作为代价函数来对第l个待测距离单元内风切变信号的多普勒频率进行估计
(16)
当代价函数为最大值时,即得到参数估计结果。其中,XlT为第l个距离单元的降维后数据,XlT=T(flq)HXl,因此,对第l个距离单元风切变风速估计值为:
(17)
4 方法流程
基于CMCAP-JDL的低空风切变风速估计方法流程图如图4所示。其关键步骤如下:
图4 基于CMCAP-JDL的低空风切变风速估计方法流程图
Fig.4 Flow chart of low altitude wind shear wind speed estimation method based on CMCAP-JDL
步骤1 利用先验信息,对由于载机平台运动而导致的多普勒频偏进行补偿,Xl=xle-jΩ,其中,Xl表示经过速度补偿后的第l个待测距离单元雷达回波数据;xl表示原始雷达回波数据,Ω=4πVcos θ0cos φl/λ fr;
步骤2 首先对杂波进行距离依赖性矫正,然后对待测距离单元的杂波协方差矩阵进行估计。
为估计得到的第l号距离单元的杂波协方差矩阵,其中,γm=Qm,lXm,(1≤m≤L,m≠l)是第m号距离单元经过矫正距离依赖性后的数据,Xm为第m号距离单元接收的雷达回波数据,Qm,l为杂波配准补偿矩阵;
步骤3 构建降维变换矩阵,并对待测距离单元的雷达回波数据进行降维处理;
步骤4 根据LCMV准则,求解自适应处理器的最优权矢量;
步骤5 利用最优权矢量对雷达回波数据进行自适应滤波处理;
步骤6 找出多普勒检测通道的多普勒频率,使得自适应处理器输出功率最大,进而估算出该距离单元的风场速度。
5 实验结果及分析
5.1 算法仿真条件
表1是系统仿真参数的设置,风切变信号在载机8.5 km～16.5 km处,仿真采用微波合成,将面阵等效为均匀线阵来处理。方位角为90°,俯仰角为0°。定义通道幅相误差矩阵σa=[(1+ε1)ejϑ1,(1+ε2)ejϑ2,…,(1+εN)ejϑN]T,其中,N是阵元数;εi(i=1,2,…,N)表示通道幅度误差,服从正态分布,即
其中
为正态分布的方差,取值范围在0.01～0.05之间,记作1%～5%;ϑi(i=1,2,…,N)表示通道相位误差,服从均匀分布,即εi～U(-Δθ,Δθ),Δθ的取值范围在1°～5°之间。
表1 系统仿真参数设置
Tab.1 Model parameters of real blade
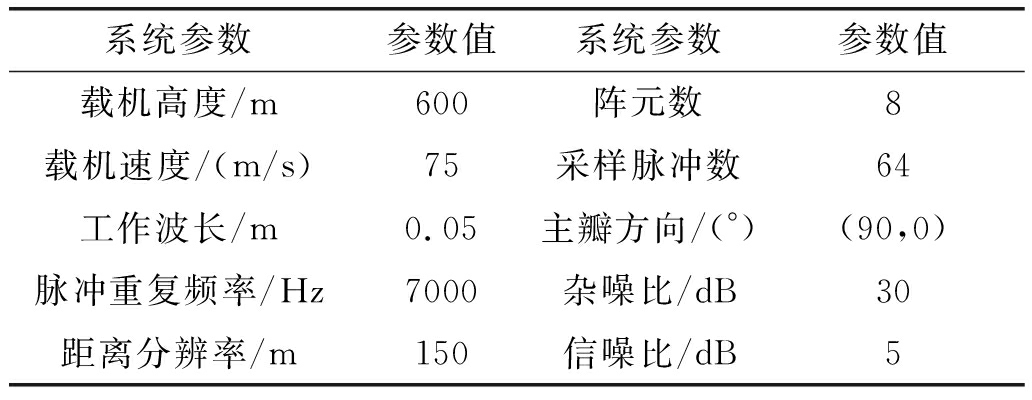
系统参数参数值系统参数参数值载机高度/m600阵元数8载机速度/(m/s)75采样脉冲数64工作波长/m0.05主瓣方向/(°)(90,0)脉冲重复频率/Hz7000杂噪比/dB30距离分辨率/m150信噪比/dB5
本文空时域的加权量的大小采用实验的方法给出,仿真中,采用的是Dolph-Chebshev加权,将误差的大小固定,空时域加权量的大小从5 dB到100 dB之间,步进量为5 dB,计算不同权值下风速估计结果的均方根误差,其均方根误差最小时即为所对应的权值。空时域加权深度与幅相误差之间的定量关系如表2所示。
表2 不同幅相误差时权值大小
Tab.2 Weights at different amplitude and phase errors
幅相误差加权值/dB1%602%553%904%605%50
5.2 仿真结果分析
首先仿真了机载雷达回波数据的空时二维谱,仿真对比分析了有误差和无误差的两种情形,图5是前视阵地杂波信号和风切变信号的空时二维谱,图中呈现半圆形状的是地杂波信号的空时二维谱;图中呈现为一条窄带形状的是低空风切变信号,其功率远远小于杂波,所以在雷达回波数据中,风切变信号被杂波完全淹没,这给低空风切变的探测和参数估计带来困难。图6是误差5%时空时二维谱,对比没有误差情况下,误差的存在使杂波产生扰动,杂波自由度增大,引起杂波谱出现展宽,并且引入大量的旁瓣杂波,为后面的杂波滤除带来困难。
图5 回波信号空时二维谱
Fig.5 Space-time two-dimensional spectrum of echo signal
图6 误差回波信号空时二维谱
Fig.6 Space-time two-dimensional spectrum of error echo signal
图7是在误差为1%-1°,3%-3°,5%-5°下,第82号距离单元自适应处理器的频响图,该自适应处理器在归一化多普勒频率为零处形成凹口,可以实现地杂波的滤除。对比了图8是存在5%-5°误差情况下的改善因子,从实验结果可以看出,本方法在主杂波区凹口明显变窄,在误差情况下,本文所提方法在性能上有2.70 dB的提升,说明了本方法的性能优于CMCAP。
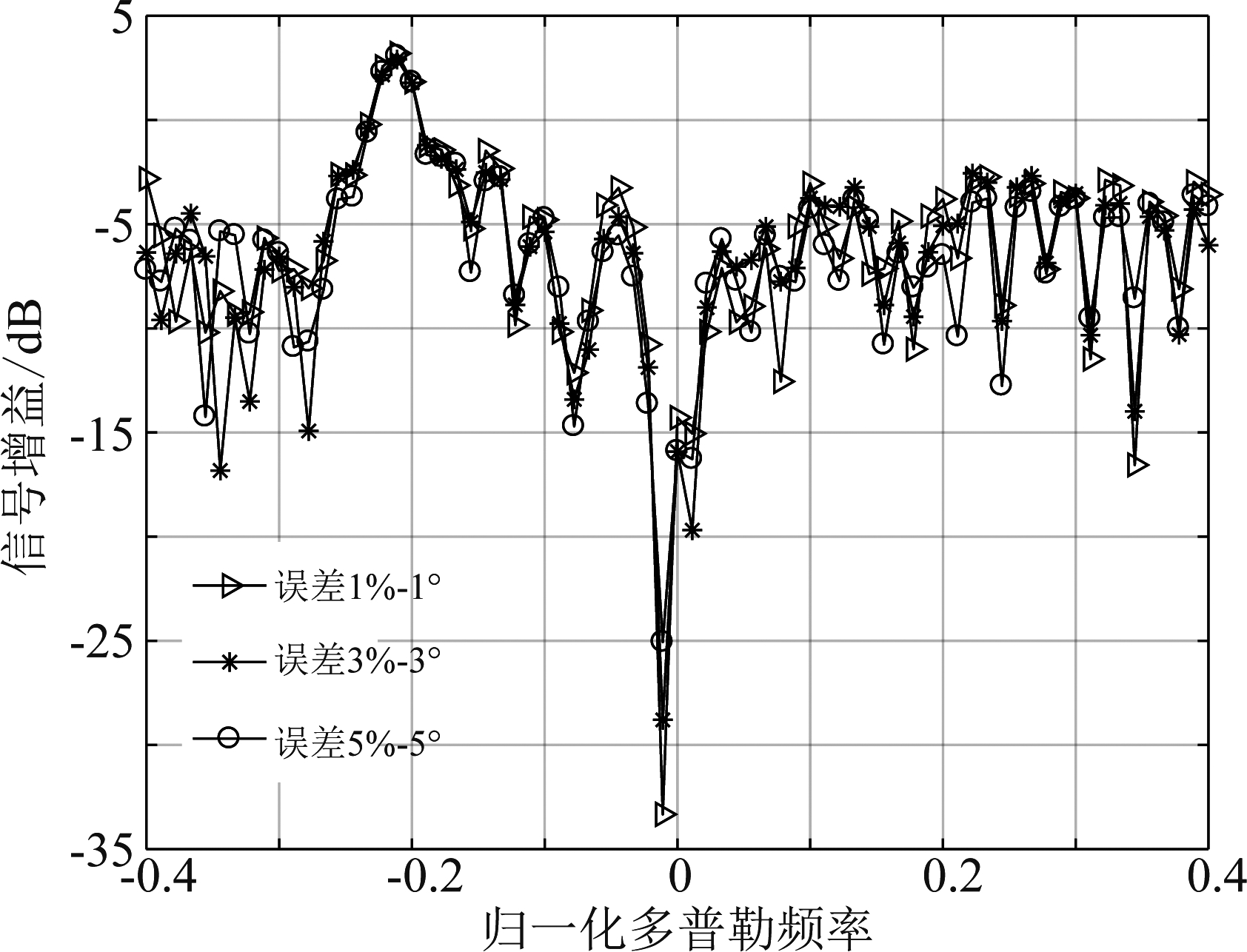
图7 82号距离单元自适应处理器频响图
Fig.7 Frequency response diagram of 82 distance unit adaptive processor
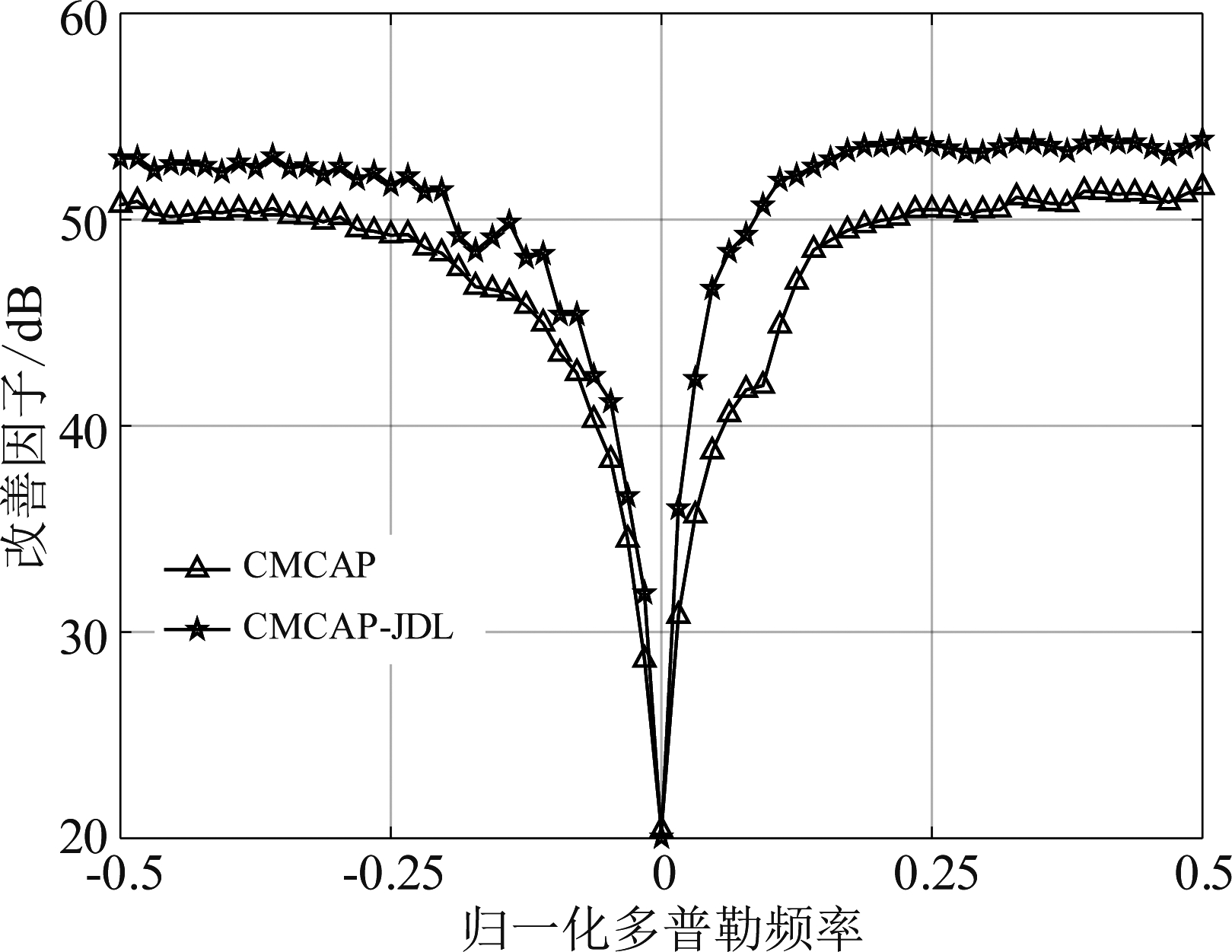
图8 误差下改善因子对比图
Fig.8 Comparison of improvement factors under error
图9、图10及图11是幅相误差分别为1%-1°、3%-3°、5%-5°时,风场位于60°、90°及120°时的风速估计结果。通过所提方法得到的风切变风速估计结果对比可以看出,风场速度随着距离的变化呈现反“S”形状,这也是风切变风场最为突出的特点。并且随着幅相误差增大,所提方法仍能够准确的对风场速度进行估计。幅相误差导致杂波自由度增大,本文方法在对空时域进行深加权的同时增加多个局域处理区域参与联合处理,能够更好在幅相误差下实现杂波的抑制。
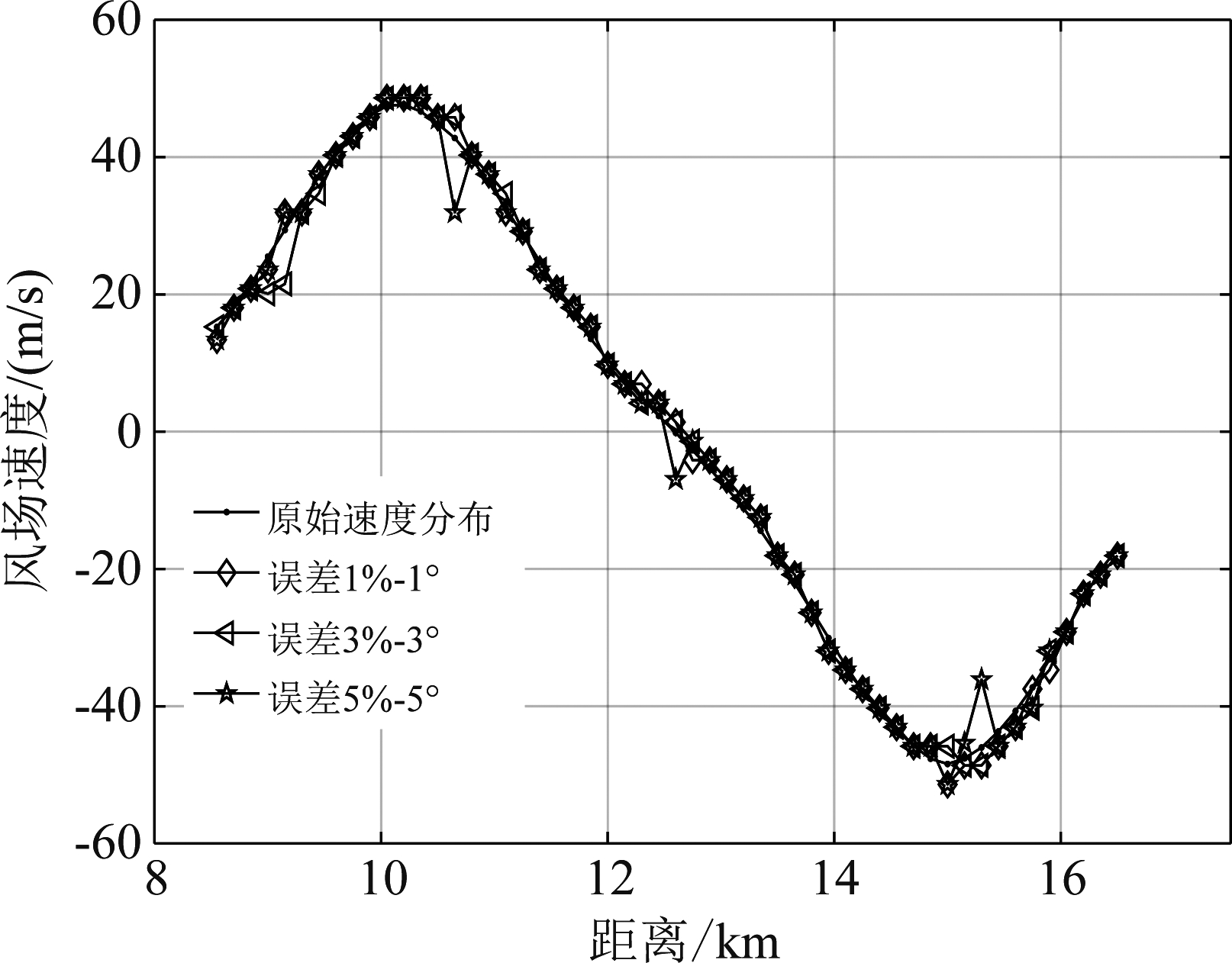
图9 风场方位60°时风速估计结果
Fig.9 Wind speed estimation results at 60 ° wind field bearing
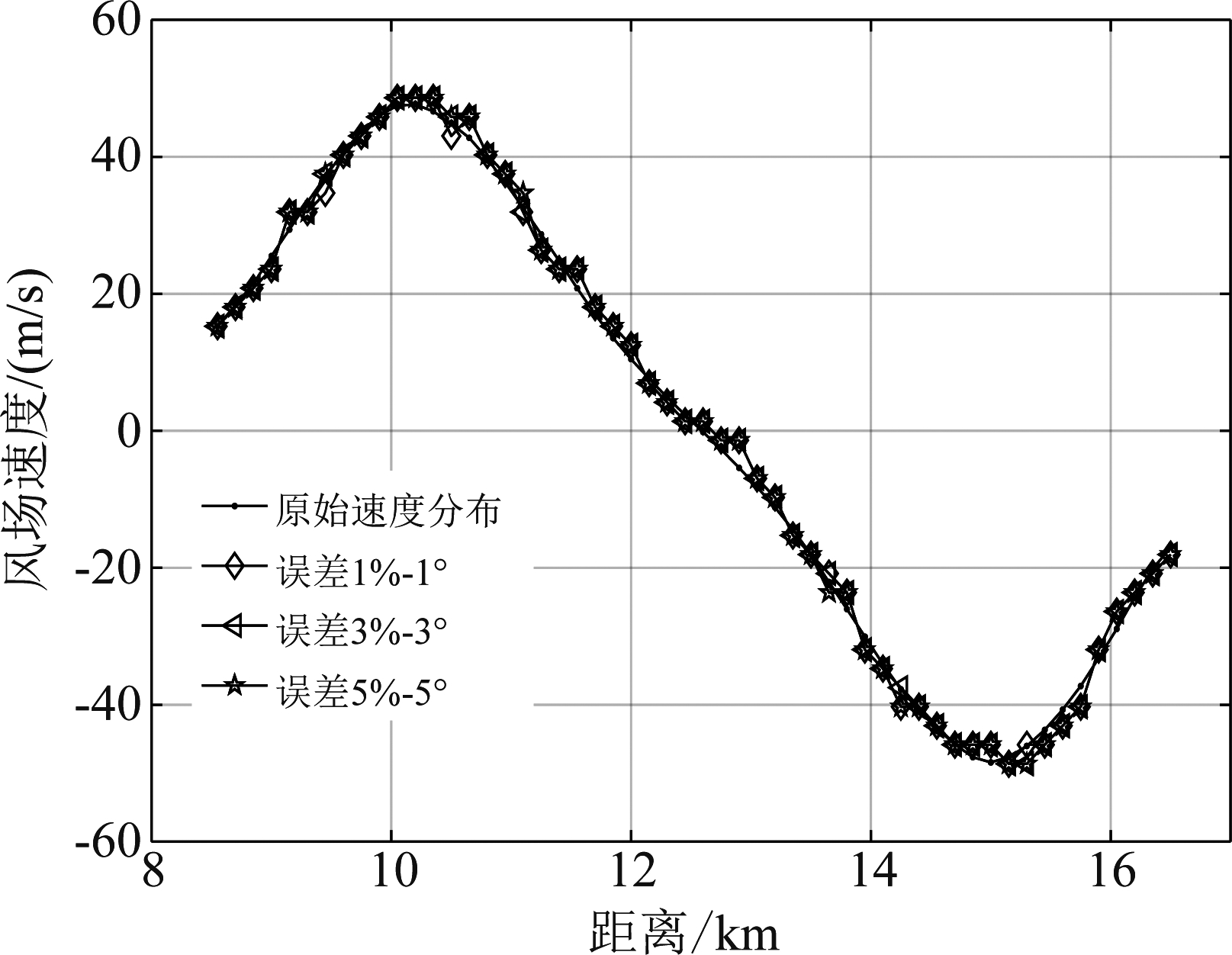
图10 风场方位90°时风速估计结果
Fig.10 Wind speed estimation results at 90 ° wind field bearing
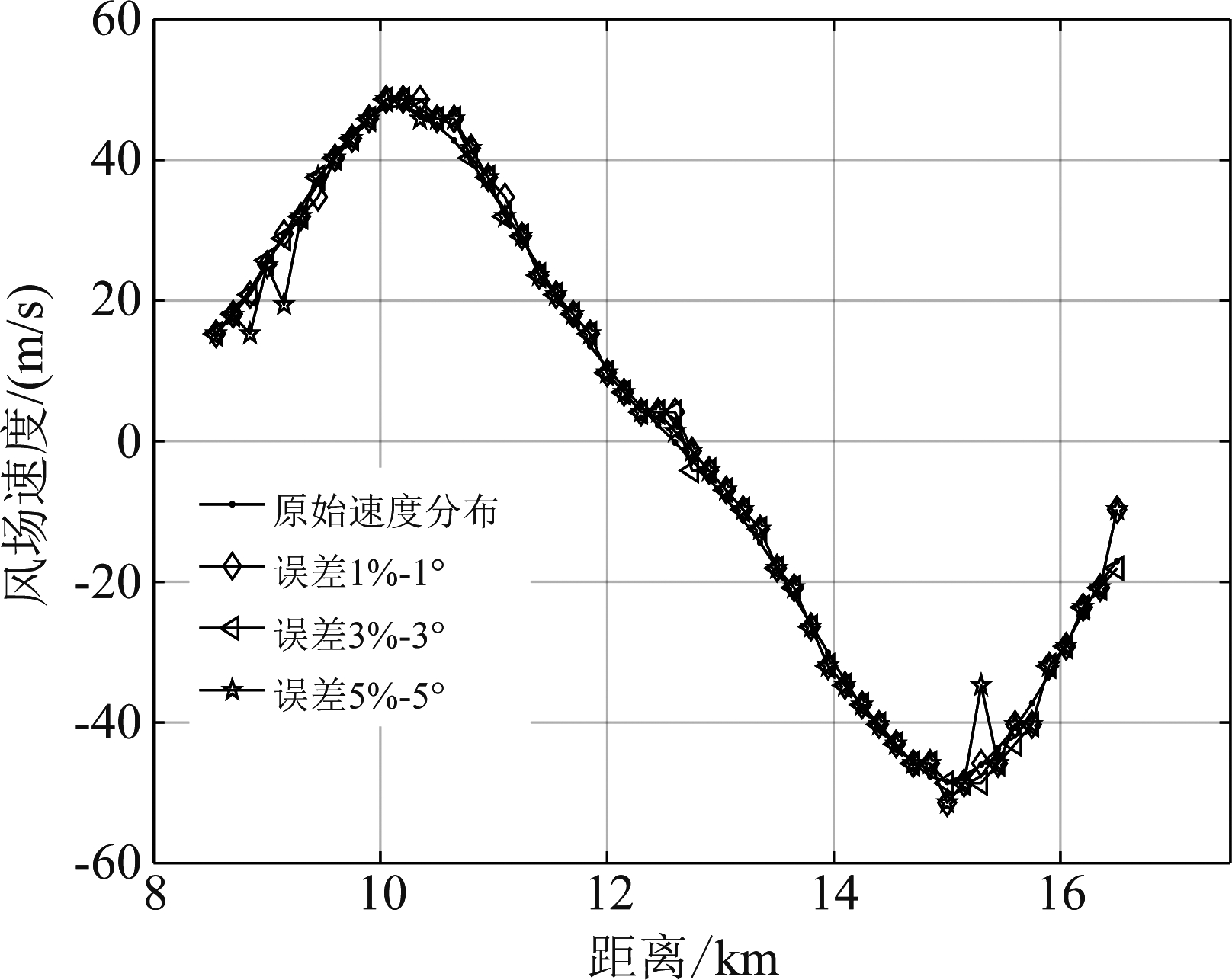
图11 风场方位120°时风速估计结果
Fig.11 Wind speed estimation results at 120 ° wind field bearing
图12是本文方法与3DT、JDL法在误差下的性能对比图,由图12改善因子可知,相比于3DT和JDL方法,本方法在主杂波区凹口明显变窄,有更好的杂波抑制性能,以及由图13的风速估计结果可知,故所提方法可以有效的抑制杂波并且可以准确的实现风速估计。
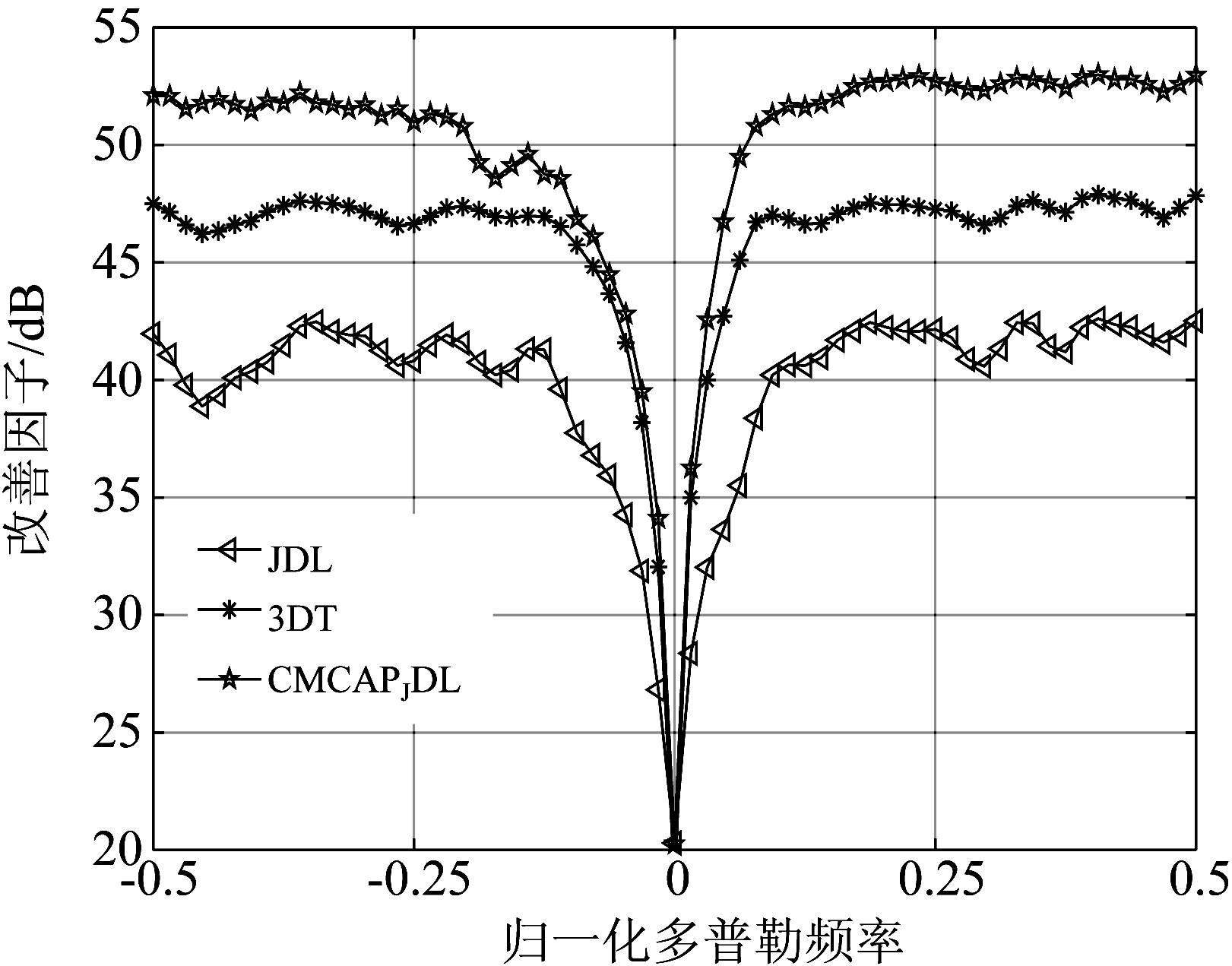
图12 误差下不同方法间改善因子对比图
Fig.12 Comparison of improvement factors between different methods under error
图13中的(a)、(b)、(c)分别是在误差为1%-1°,3%-3°,5%-5°时,所提方法与3DT及JDL风速估计结果对比图。由图13可以看出,同时存在不同幅度和相位误差时,杂波谱展宽,但本方法依然可以较准确的得到整体的风速估计结果,并且随着幅相误差的增大,本文所提方法优势更加突出。由表3可以得出,所提方法的风速估计结果精度较高,远远好于JDL和3DT的风速估计结果,因此本文所提方法应该能够满足低空风切变风速工程应用精度。
表3 不同风速估计方法的均方根误差
Tab.3 Root mean square error of different wind speed estimation methods
风速估计方法均方根误差/(m/s)JDL16.383DT12.36本文方法2.32
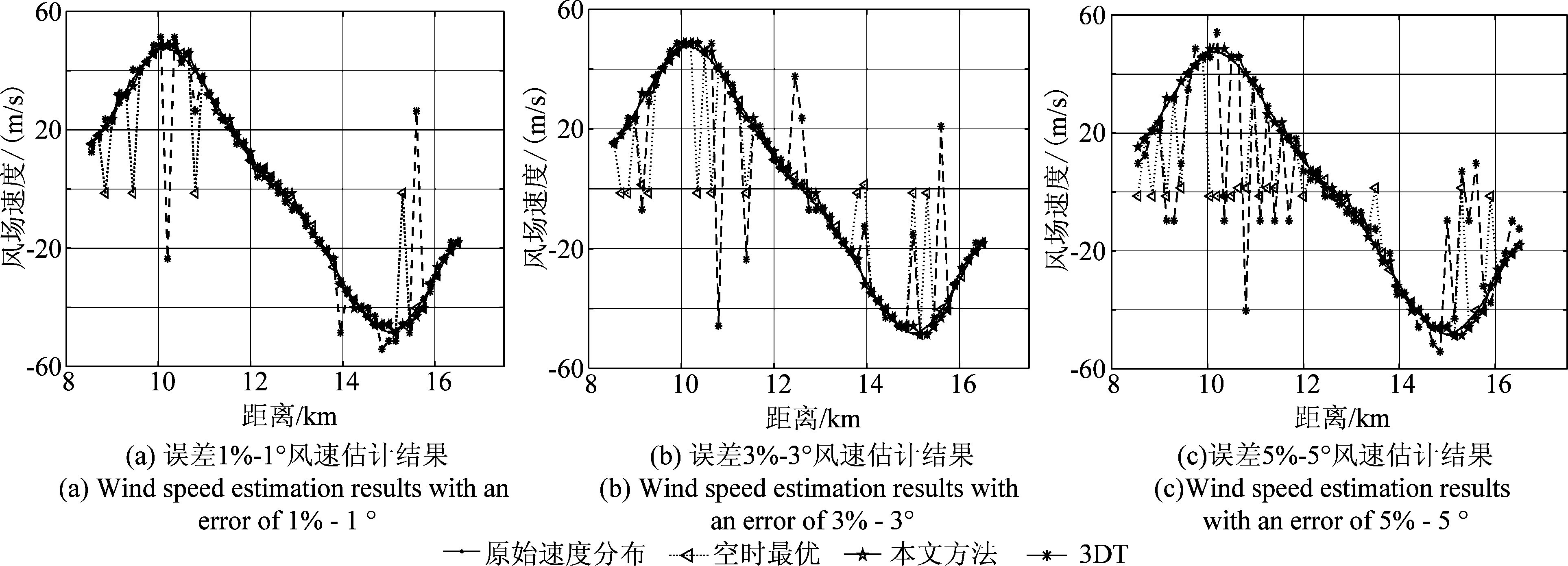
图13 误差下三种算法风速估计结果
Fig.13 Wind speed estimation results of three algorithms under error
6 结论
针对幅相误差引起的低空风切变风速估计不准确的问题,本文提出了一种基于组合空时主通道-局域联合空时自适应处理的低空风切变风速估计方法。该方法对空时域的深加权,形成的空域主波束和时域主通道,降低由于幅相误差引入的旁瓣杂波的影响,同时再增加多个局域处理区域参与联合处理,提高了空时域自由度,很好补偿了由于幅相误差导致的杂波谱向空域扩展的问题,消减误差对处理器的影响。仿真结果表明,在存在幅相误差情况下,该方法能够实现低空风切变风场速度的准确估计。
[1] Falconi M T, Marzano F S. Weather Radar Data Processing and Atmospheric Applications: An overview of tools for Monitoring Clouds and Detecting Wind Shear[J]. IEEE Signal Processing Magazine, 2019, 36(4): 85-97.
[2] Sinha S, Sarma T V C, Regeena M L. Estimation of Doppler Profile Using Multiparameter Cost Function Method[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(2): 932-942.
[3] Klemm R. Principles of Space-Time Adaptive Processing[M]. Third Edition. London: Institution of Engineering & Technolog, 2006: 672.
[4] Riedl M, Potter L C. Multimodel Shrinkage for Knowledge-Aided Space-Time Adaptive Processing[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(5): 2601-2610.
[5] Li Yijing, Li Hai, Wu Renbiao. Wind Speed Estimation of Low-Altitude Wind-Shear Based on Generalized Adjacent Multi-Beam Space-Time Adaptive Processing under Aircraft Yawing[C]∥14th IEEE International Conference on Speech and Signal Processing. Beijing: IEEE, 2018: 220-223.
[6] Li Hai, Zhou Meng, Wu Renbiao, et al. Wind Speed Estimation of Low-Altitude Wind-Shear Based on Multiple Doppler Channels Joint Adaptive Processing[C]∥IEEE International Conference on Acoustics, Speech and Signal Processing. Shanghai: IEEE, 2016: 3116-3120.
[7] Wu Renbiao, Zhang Biao, Li Hai, et al. Wind Speed Estimation for Low-Attitude Wind-shear Based on Space-Time Adaptive Processing[J]. Journal of Electronics & Information Technology, 2015, 37(3): 631- 636.
[8] Li Hai, Zhou Meng, Guo Qinghua, et al. Compressive Sensing-Based Wind Speed Estimation for Low-Altitude Wind-Shear with Airborne Phased Array Radar[J]. Multidimensional Systems & Signal Processing, 2018, 29(2): 719-732.
[9] 刘洋, 张永顺, 刘汉伟, 等. 一种稀疏恢复的稳健配准补偿方法[J]. 西安电子科技大学学报, 2017, 44(5): 165-170, 183.
Liu Yang, Zhang Yongshun, Liu Hanwei, et al. Robust Registration Based Compensation Method Based on Sparse Recovery[J]. Journal of Xidian University, 2017, 44(5): 165-170, 183.(in Chinese)
[10] 姚晖. 分布式信号源参数估计技术研究[D]. 郑州: 解放军信息工程大学, 2013.
Yao H. Research on Parameter Estimation Method for Distributed Sources [D]. Zhengzhou: PLA Information Engineering University, 2013.(in Chinese)
[11] 贾逢德, 何子述, 李军, 等. 机载雷达平面阵前视杂波距离依赖性补偿[J]. 现代雷达, 2018, 40(7): 36- 40.
Jia Fengde, He Zishu, Li Jun, et al. Forward-looking Clutter Range-Dependence Compensation in Planar Array for Airborne Radar[J]. Modern Radar, 2018, 40(7): 36- 40.(in Chinese)
[12] 王娟, 王彤, 吴建新. 非正侧阵机载雷达杂波谱迭代自适应配准方法[J]. 系统工程与电子技术, 2017, 39(4): 742-747.
Wang Juan, Wang Tong, Wu Jianxin. Registration-Based Compensation Using Iterative Adaptive Approach in Non-Side-Looking Airborne Radar[J]. Systems Engineering and Electronics, 2017, 39(4): 742-747.(in Chinese)
[13] 刘青光, 彭应宁. 机载雷达自适应杂波抑制的联合通道变换方法[J]. 电子学报, 1994, 22(6): 1-9.
Liu Qingguang, Peng Yingning. Adaptive Clutter Suppression in Airborne Radar by A Combined Channel Transformation Approach[J]. Acta Electronica Sinica, 1994, 22(6): 1-9.(in Chinese)
