1 引言
基于数字射频存储装置(Digital Radio Frequency Memory, DRFM)的频谱弥散干扰[1](SMeared SPectrum jamming,SMSP)由多个线性调频(Linear Frequency Modulation, LFM)子信号时域拼接而成,用以对抗LFM脉冲压缩体制雷达。自卫式干扰条件下,干扰信号与真实回波时、频域重叠,信号分离难度大。围绕SMSP干扰抑制,文献[2]以双谱盒维数、信息维数为特征参数,利用支持向量机分类器进行回波类型识别,但自卫式干扰条件下,回波信号中包含真实回波,即使识别出回波类型,仍需要做进一步抑制处理。为抑制回波中SMSP干扰,文献[3]将真实回波与干扰信号视为独立源信号,利用盲源分离算法进行信号分离,算法虽然通过改进复值非高斯最大算法以提高抗噪性能,但仍要求可分离信噪比大于10 dB,且算法仅适用于多通道雷达接收模型。为提高算法适用范围,文献[4-5]通过估计SMSP干扰子信号个数、幅度、相位等全部参数重构干扰信号,将回波信号减去重构信号,实现干扰抑制。文献[4-5]基于干扰重构、回波对消的干扰抑制方法为对抗SMSP干扰提供了新的思路,但干扰全参数估计实现较为困难,理论上估计部分干扰参数,利用信号处理工具同样可重构干扰信号。分数阶傅里叶变换(Fractional Fourier Transform, FRFT)以其处理LFM信号方面的优势[6- 8],在有源干扰识别抑制领域应用广泛,但SMSP干扰子信号调频斜率对应阶次下的FRFT为多个辛格函数,为重构干扰信号需要进行多次滤波处理。利用估计的部分干扰参数,设计参考信号,将回波中的SMSP干扰调制成一个LFM信号,能够避免该问题。
基于上述思路,本文以自卫式干扰条件下LFM脉冲压缩雷达抗SMSP干扰为背景,联合时频重排(Time-Frequency Reassignment)和双正交傅里叶变换(Biorthogonal Fourier Transform,BFT),提出一种基于部分干扰参数估计、单次滤波解调重构和干扰对消的SMSP干扰抑制算法。文中分析了SMSP干扰时频特征,阐述了干扰抑制原理和具体实现,仿真分析验证算法可行性。
2 干扰时频特征
不考虑回波时延因素[2- 4],自卫式干扰条件下,真实回波复数形式可表示为:
(1)
式中,σ为目标反射系数,Tp为脉冲宽度,k=B/Tp为调频斜率,B为信号带宽。根据SMSP干扰产生方法,第1个LFM子信号为:
(2)
式中,Aj为子信号幅度,N为子信号个数,kj=Nk为调频斜率,将j1(t)复制N-1次,时域拼接得到SMSP干扰:
(3)
取SMSP干扰相位:
(4)
相位求导得到SMSP干扰瞬时频率:
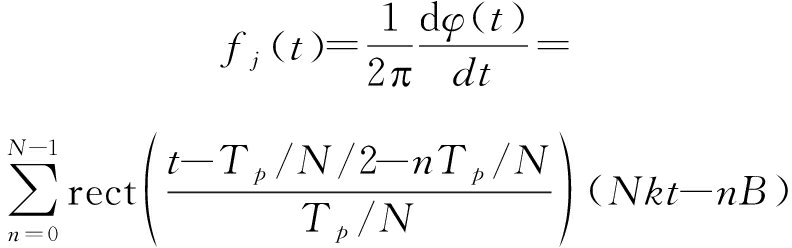
(5)
式(5)可以看出,SMSP干扰瞬时频率由N条相同斜率、不同截距的直线线段组成,每条线段时域宽度为Tp/N,斜率为Nk,截距为-nB。
3 干扰抑制原理
为方便分析,暂不考虑噪声因素,自卫式干扰条件下受干扰回波信号为:
x(t)=sr(t)+j(t)
(6)
回波信号瞬时频率为:
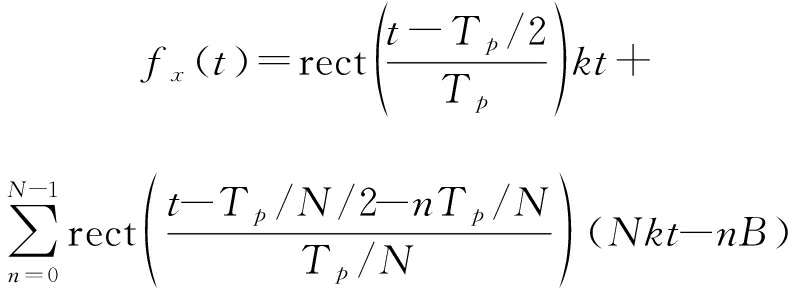
(7)
设参考信号瞬时频率为:
(8)
对应的时域信号为:
(9)
利用参考信号调制回波,令fx(t)加上fcoef(t)得到调制后回波瞬时频率为:
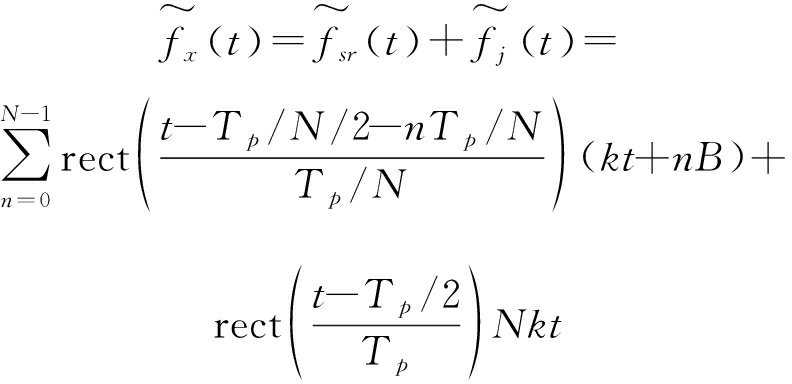
(10)
式中,
分别为调制后真实回波和SMSP干扰瞬时频率。调制后真实回波和SMSP干扰时域形式分别为:
(11)
(12)
综合式(11)～(12)可以看出,调制后的真实回波为N个相同调频斜率的LFM信号,每个LFM信号时宽Tp/N,带宽B/N,最大瞬时频率为(N-1)B+B/N。调制后SMSP干扰为1个LFM信号,时宽Tp,调频斜率Nk,带宽NB。为直观显示,图1给出了N=5时SMSP干扰调制前后瞬时频率示意图。
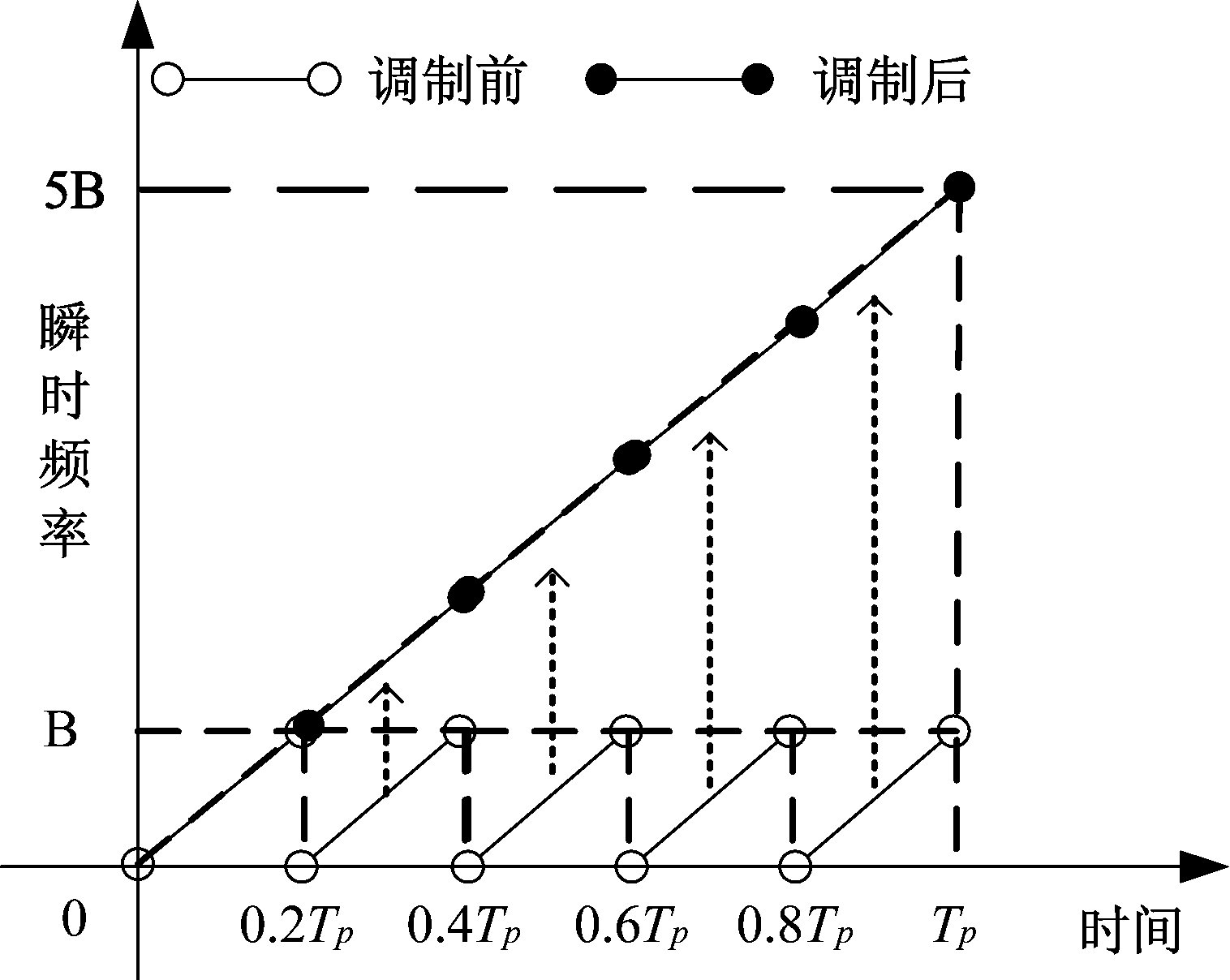
图1 SMSP干扰调制前后瞬时频率示意图
Fig.1 The instantaneous frequency sketch map of SMSP jamming before and after modulation
文献[9]通过对信号采用双正交函数展开设计提出双正交傅里叶变换,零初频LFM信号BFT斜率谱为一辛格函数,峰值位置对应调频斜率,峰值滤波可重构LFM信号,本文利用BFT从调制后回波信号中重构SMSP干扰。连续信号f(t)的BFT定义为:
F(ω2)=2
f(t)te-iπω2t2dt
BFT[f(t)]
(13)
对于调制后的回波信号
(14)
式中,
为调制后的噪声。考虑到SMSP干扰是一个与雷达匹配滤波器适配的干扰信号,干扰功率通常远大于真实回波和基底噪声,则调制后回波信号BFT可近似表示为:
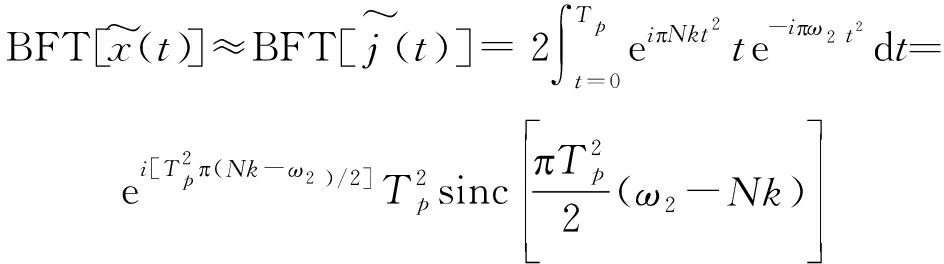
(15)
式(15)可知,调制后的回波信号BFT近似为一辛格函数,斜率谱峰值对应调频斜率Nk。对
进行峰值滤波,解调重构干扰信号:
(16)
式中,Win(ω2)为BFT斜率谱矩形滤波窗,IBFT为BFT逆变换,则干扰对消后的回波信号为:
(17)
需要注意的是,调制后的SMSP干扰信号
带宽为原SMSP干扰带宽的N倍,根据采样定理,BFT处理前,需要对原始回波信号进行插值,将采样率提升N-1倍,同时对于重构信号
干扰对消前需进行N倍抽取,调整回原始采样频率。
4 实现方法
4.1 基于时频重排的干扰参数估计
第2节分析可知,SMSP干扰瞬时频率由N条相同斜率、不同截距的直线线段组成,对受干扰回波时频矩阵进行直线检测,可估计干扰子信号个数。很明显,回波时频矩阵聚焦性越好,估计效果也越好。魏格纳分布(Wigner-Vill Distribution, WVD)和短时傅里叶变换(Short Time Fourier Transform, STFT)是常用的时频分析手段,但分别受交叉项[10]和时频分辨率[11]影响,通过WVD和STFT得到的时频矩阵并不理想,基于STFT的时频重排[12-13]能够显著提高时频聚焦性,且不存在交叉项。时频重排的基本思想是根据时频质心对原始时频矩阵进行重新排列,一种有效的质心计算方法为:
(18)
(19)
式中,
为信号f在窗g下的
为信号f在窗tg下的
为信号f在窗g′下的STFT,g′为g的导数,Re(·)表示取实部,Im(·)表示取虚部。第2节分析可知,SMSP干扰瞬时频率由多条直线段组成,斜率相同,而真实回波瞬时频率为一条直线段,调频斜率为干扰子信号的1/N,利用radon变换将时频矩阵变换至参数空间[14-15],根据上述特点即可鉴别SMSP干扰与真实回波,进而估计干扰子信号个数。
4.2 BFT斜率谱滤波窗宽度选取
公式(16)可知,重构SMSP干扰需设计斜率谱滤波窗Win(ω2)。对于调制后SMSP干扰
设插值后的采样频率
为原采样频率fs的N倍,且fs=2B,根据文献[11]可得
离散BFT斜率谱分辨率为:
(20)
式中,D=TpB为雷达发射信号时宽带宽积。最大斜率Ω2为:
(21)
公式(15)中辛格函数第一级零点宽度为4πk/D,因此为有效重构SMSP干扰,BFT斜率谱滤波窗宽度应不小于2Δω2,即两个离散斜率谱采样点。综上分析,设计SMSP干扰抑制流程如图2所示。
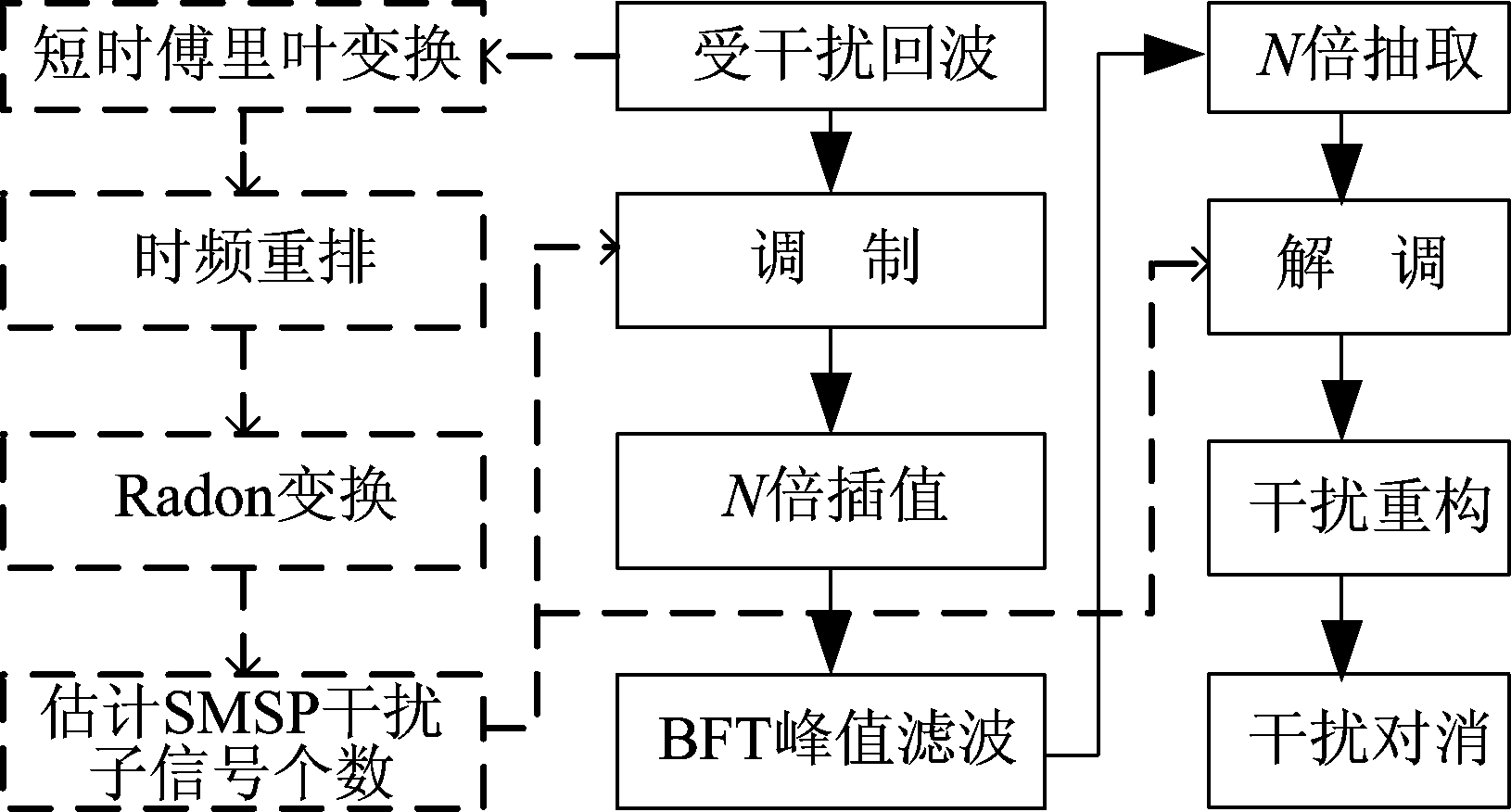
图2 SMSP干扰抑制流程
Fig.2 SMSP jamming suppression process
5 仿真结果
5.1 参数设置和SMSP干扰时频特性
设雷达发射信号为LFM脉冲信号,脉宽50 μs,带宽4 MHz,采样频率16 MHz,调频斜率80 GHz/s,真实目标为点目标,幅度为1 V,SMSP干扰脉冲宽度50 μs,子信号个数为5,调频斜率400 GHz/s。图3对比真实回波给出了SMSP干扰时域波形。可以看出,不同于真实回波,SMSP干扰由5个LFM子信号时域拼接而成。利用短时傅里叶变换(汉明窗,窗长64,交叠60,DFT点数64)得到SMSP干扰谱图如图4所示。可以看出,SMSP干扰时频矩阵上存在5条相同斜率、不同截距的直线段,线段较宽,时频聚焦性较差。
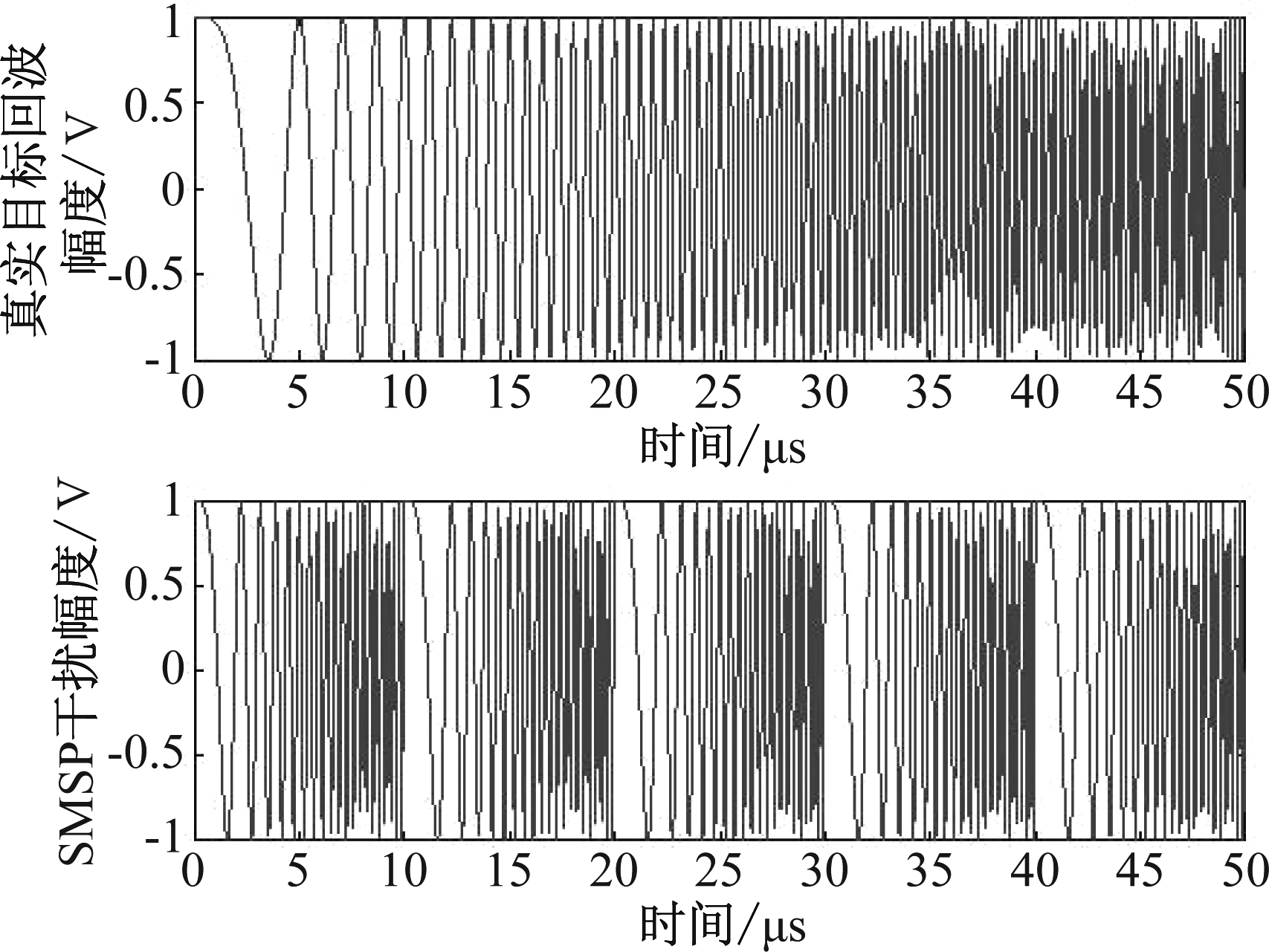
图3 真实回波、SMSP干扰波形
Fig.3 The waveform of target echo and SMSP jamming
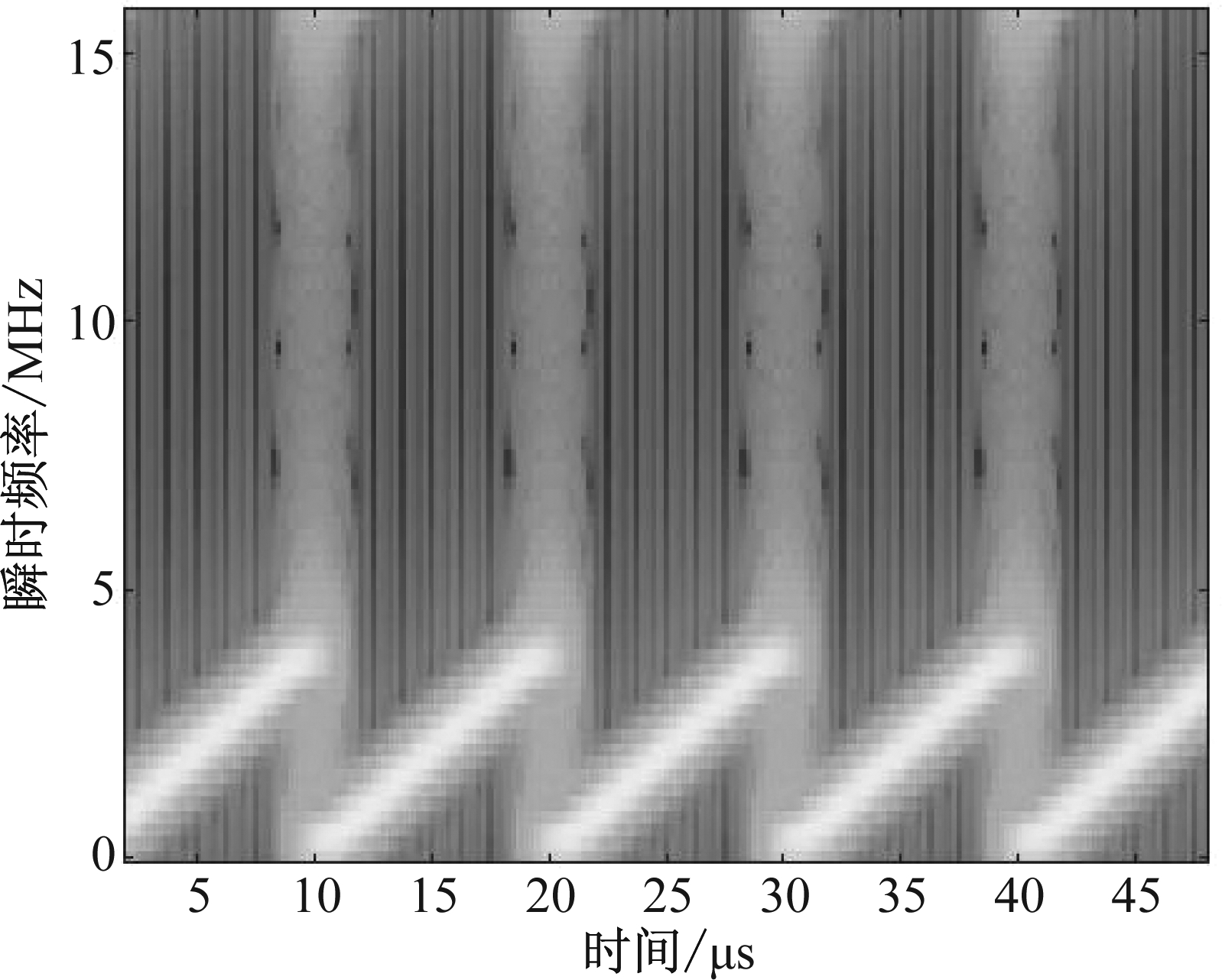
图4 SMSP干扰谱图
Fig.4 The spectrogram of SMSP jamming
5.2 抑制算法可行性分析
根据图2所示干扰抑制流程,分析算法可行性。设信噪比(Signal to Noise Ratio, SNR)为-5 dB,干信比(Jamming to Signal Ratio, JSR)为20 dB,图5给出了受干扰回波STFT时频重排结果。对比图4可以看出,重排后回波时频矩阵聚焦性明显提高。对重排矩阵进行Radon变换,结果如图6所示,估计得到SMSP干扰子信号个数为5,与仿真使用参数一致。对受干扰回波信号进行3倍插值(仿真参数中设采样频率为雷达发射信号带宽的4倍),根据公式(9)构造参考信号,调制后回波时频重排结果如图7所示,回波中SMSP干扰被调制成一个LFM信号。对调制后回波进行BFT处理,结果如图8所示。设斜率谱矩形滤波窗宽度为20 GHz/s,经BFT峰值滤波、解调、3倍抽取得到干扰重构信号,时域波形如图9所示,重构信号与真实干扰高度相似。从回波中减去重构信号,图10给出了干扰抑制前后回波脉冲压缩结果,可以看出,SMSP干扰生成的虚假目标幅度整体下降约15 dB,真实目标得到有效检测。
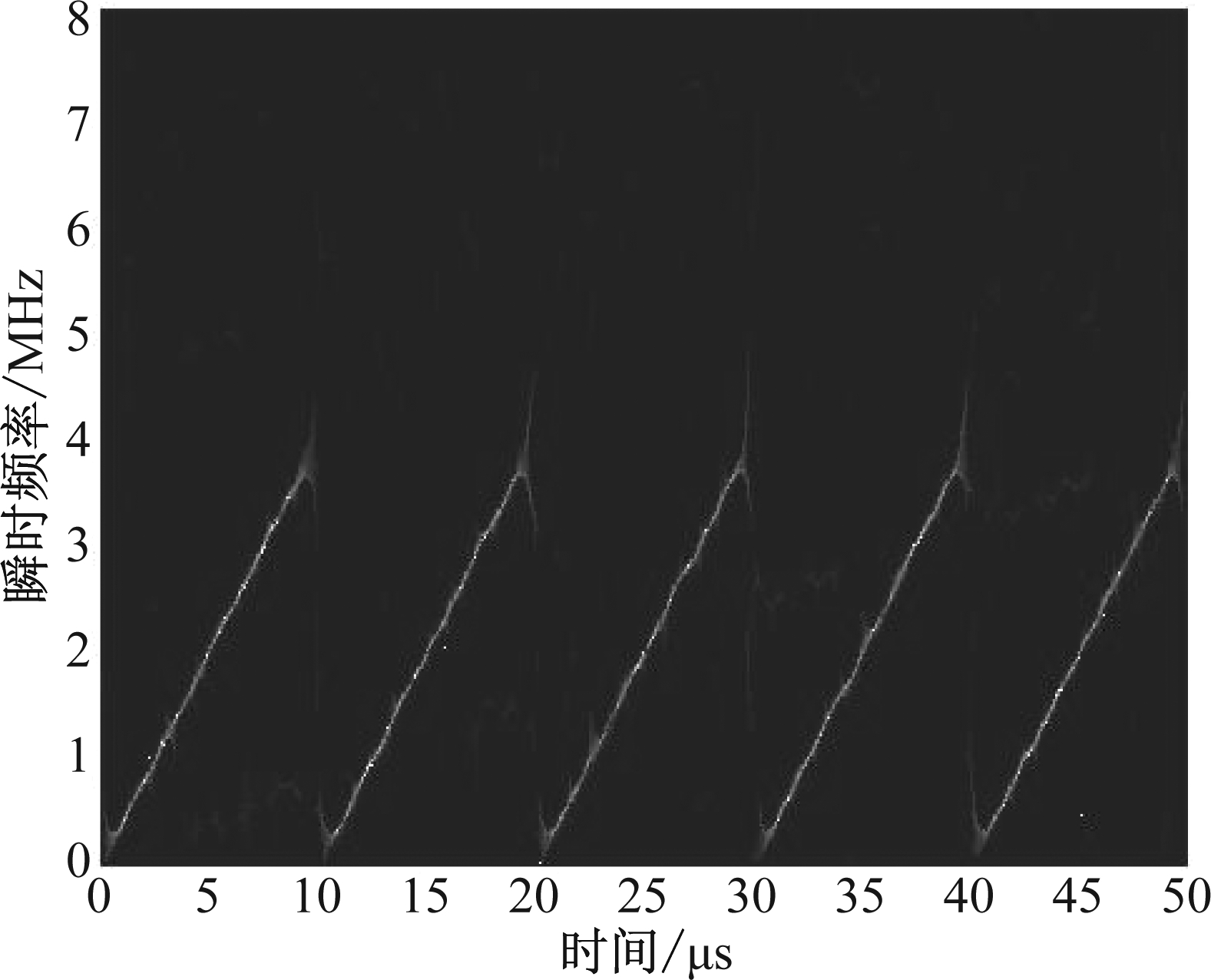
图5 回波信号时频重排结果
Fig.5 The time-frequency reassignment result of echo
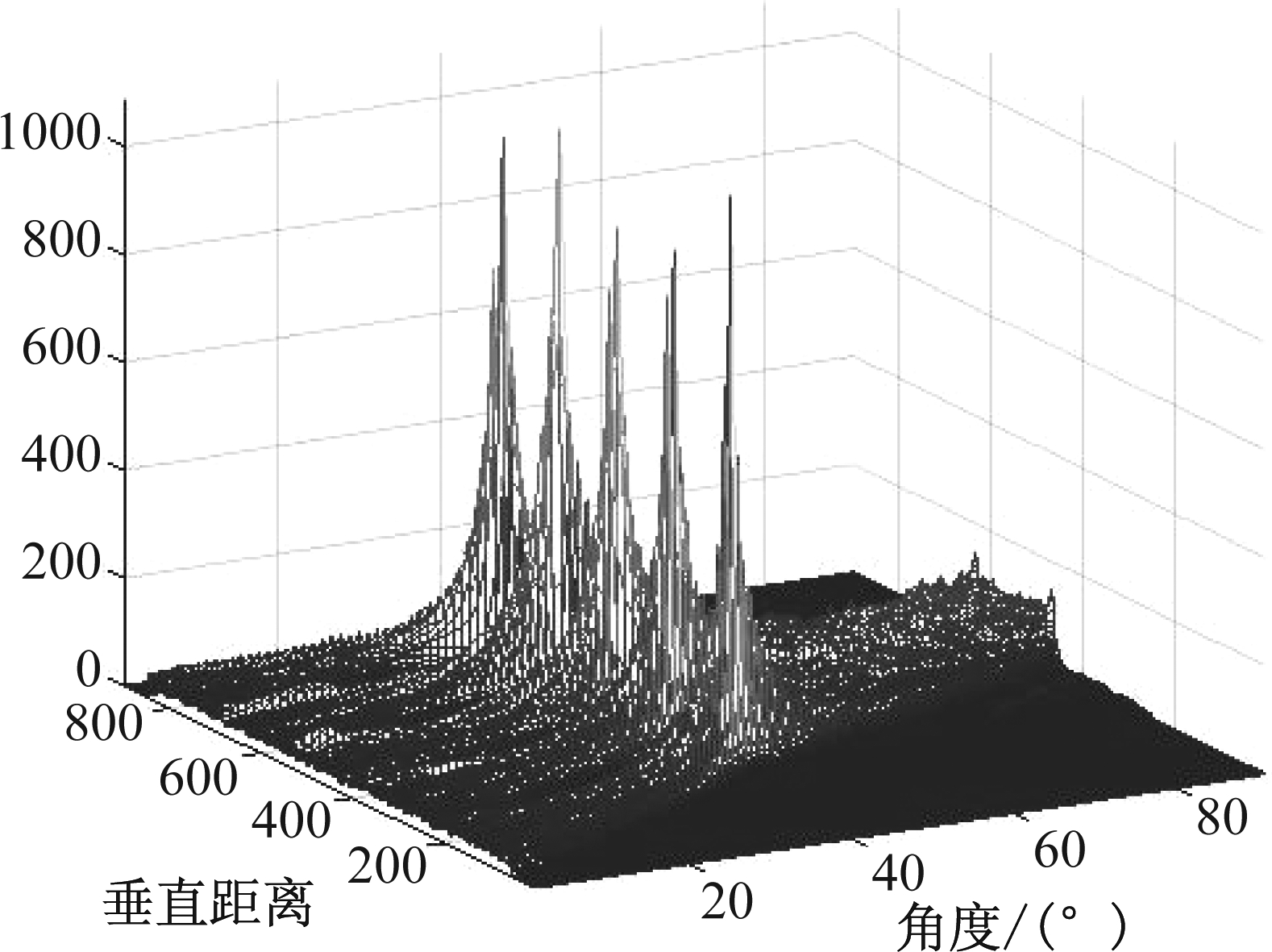
图6 直线检测结果
Fig.6 Lines detection result
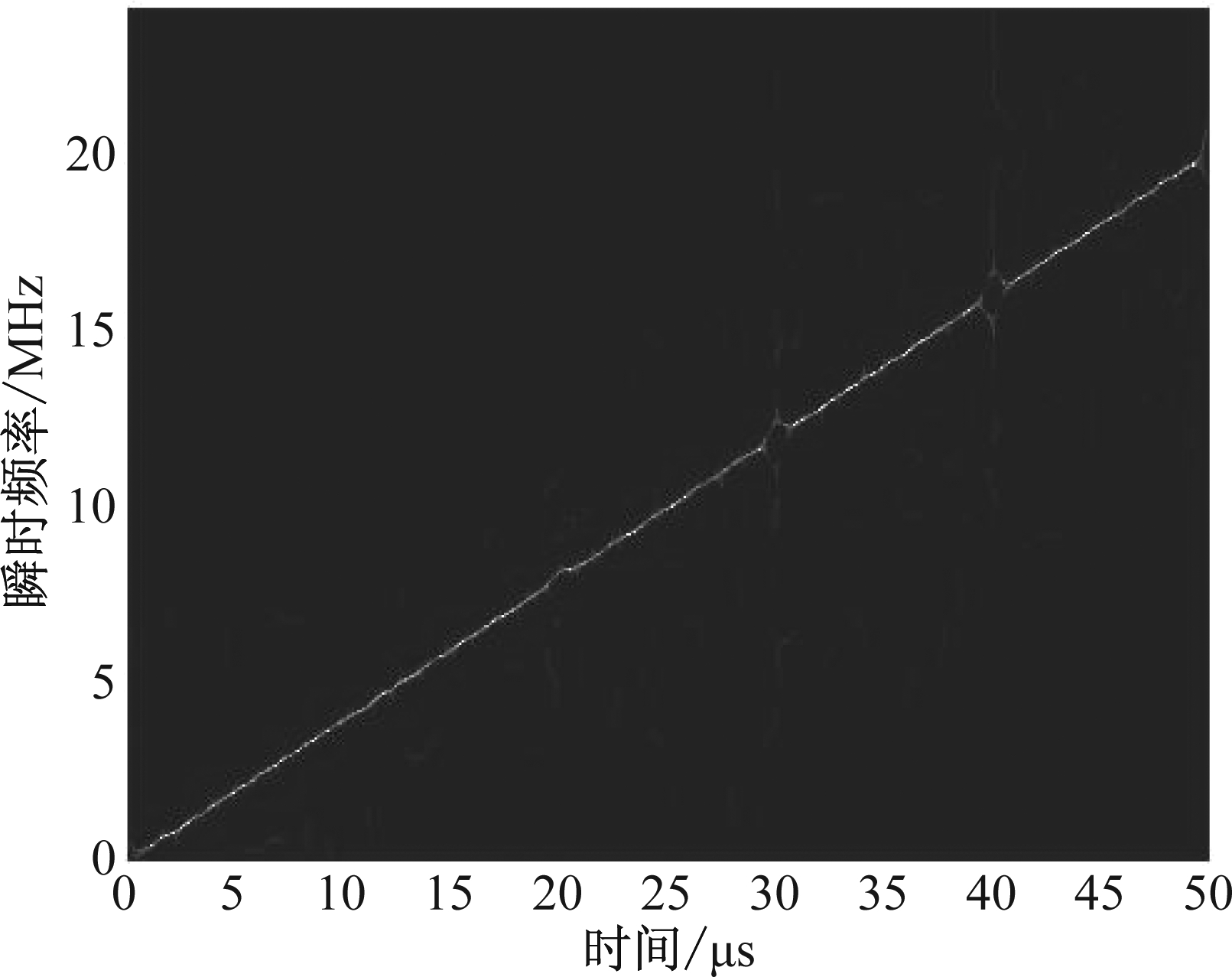
图7 调制后回波时频重排结果
Fig.7 The time-frequency reassignment result of modulated echo
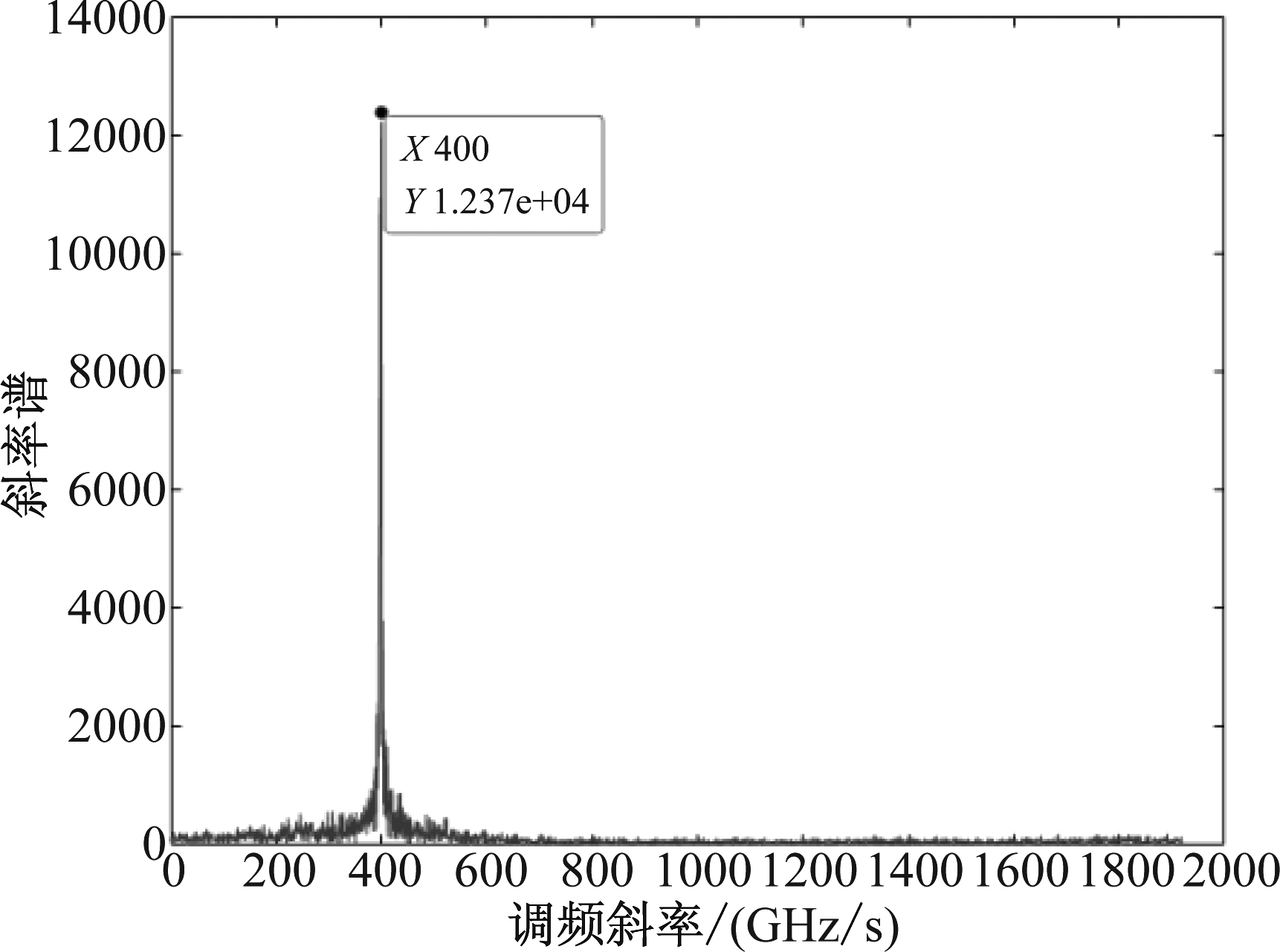
图8 调制后回波BFT结果
Fig.8 The BFT result of modulated echo
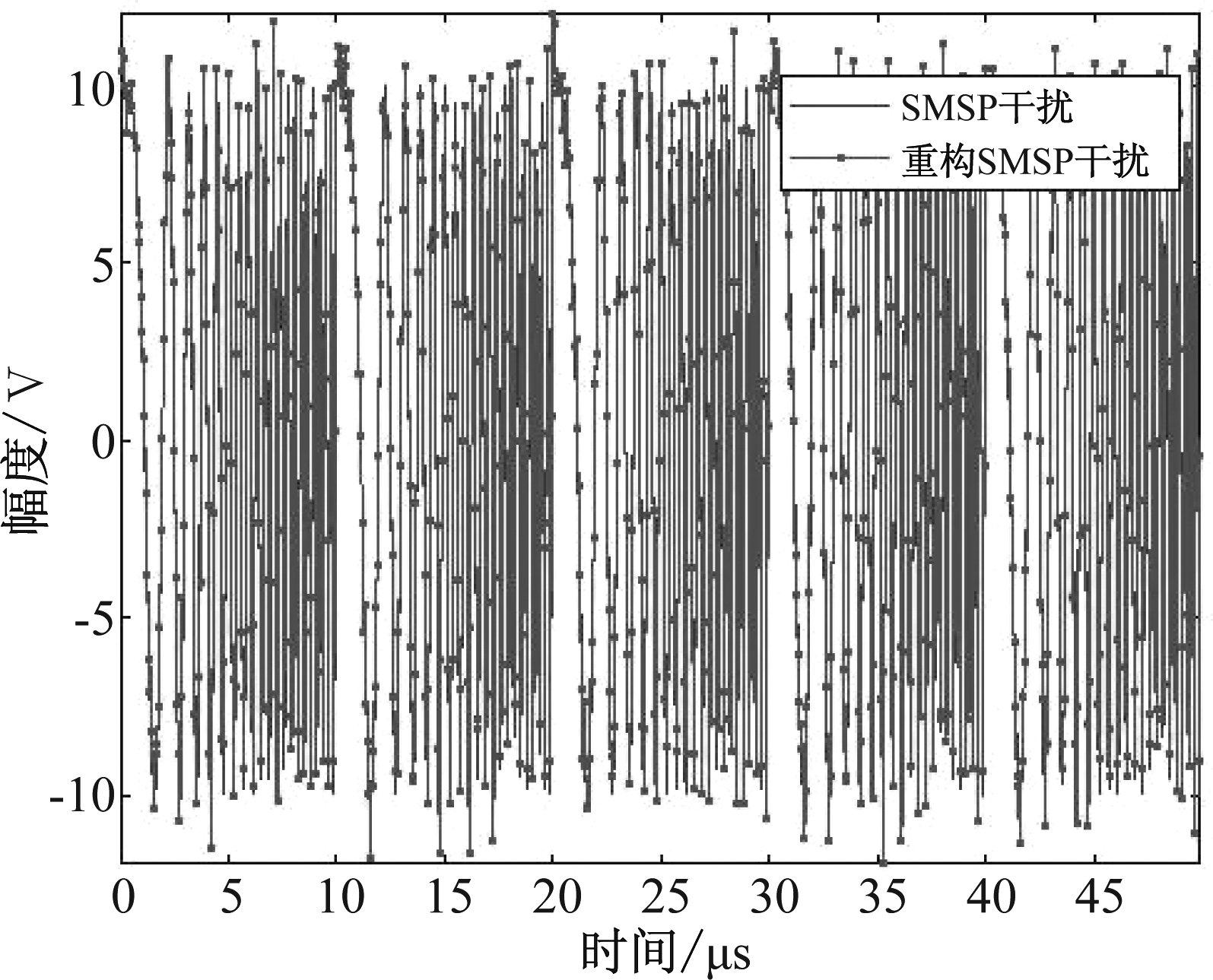
图9 SMSP干扰重构信号波形
Fig.9 The waveform of reconstructed SMSP jamming
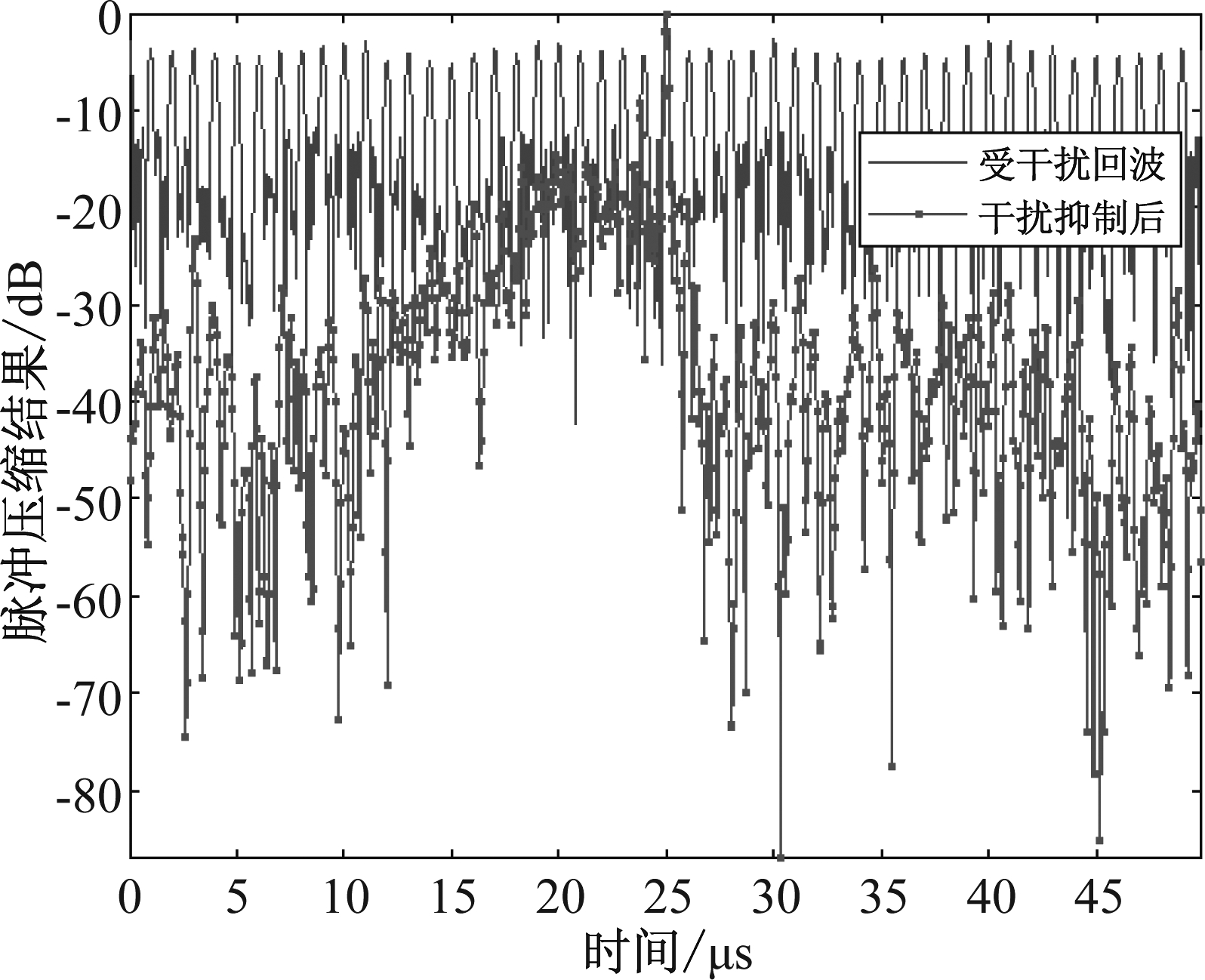
图10 干扰抑制前后回波脉冲压缩结果
Fig.10 The pulse compression result before and after jamming suppression
6 结论
基于DRFM的SMSP干扰,单个干扰信号经雷达匹配滤波器即可生成高密度假目标群,对雷达系统达成压制兼欺骗干扰效果。本文结合通信领域常用的调制解调技术,以自卫式干扰条件下LFM脉冲压缩体制雷达抗SMSP干扰为背景,联合时频重排和双正交傅里叶变换提出一种干扰重构、干扰对消的SMSP干扰抑制算法。算法通过估计干扰子信号个数,设计参考信号,将回波中SMSP干扰调制成一个LFM信号,单次BFT峰值滤波、解调即可准确重构干扰信号。仿真结果验证了所提算法的可行性。
[1] Sparrow M J, Cikalo J. ECM techniques to counter pulse compression radar[P]. United States Patent, 7081846, 2006.
[2] 杨少奇, 田波, 周瑞钊. 应用双谱分析和分形维数的雷达欺骗干扰识别[J]. 西安交通大学学报, 2016, 50(12): 128-135.
Yang Shaoqi, Tian Bo, Zhou Ruizhao. A jamming identification method against radar deception based on Bispectrum analysis and fractal dimension[J]. Journal of Xi’an Jiaotong University, 2016, 50(12): 128-135.(in Chinese)
[3] 尹洪伟, 李国林, 路翠华. 一种基于复值盲分离的欺骗干扰抑制算法[J]. 上海交通大学学报, 2015, 49(10): 1564-1569.
Yin Hongwei, Li Guolin, Lu Cuihua. An algorithm of deception jamming suppression based on complex value blind source separation[J]. Journal of Shanghai Jiaotong University, 2015, 49(10): 1564-1569.(in Chinese)
[4] 李欣, 王春阳, 原慧, 等. 基于干扰重构和峭度最大化的SMSP干扰抑制方法[J]. 北京航空航天大学学报, 2018, 44(6): 1176-1184.
Li Xin, Wang Chunyang, Yuan Hui, et al. SMSP jamming suppression method based on jamming reconstruction and kurtosis maximum[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(6): 1176-1184.(in Chinese)
[5] 原慧, 王春阳, 安磊, 等. 基于信号重构的频谱弥散干扰抑制方法[J]. 系统工程与电子技术, 2017, 39(5): 961-967.
Yuan Hui, Wang Chunyang, An Lei, et al. Smeared spectrum jamming suppression method based on signal reconstruction[J]. Systems Engineering and Electronics, 2017, 39(5): 961-967.(in Chinese)
[6] Bultheel A, Martinez S H. Recent developments in the theory of the Fractional Fourier Transform and Linear Fractional Transforms[J]. Bulletin of the Belgian Mathematical Society Simon Stevin, 2006, 13(5): 1336-1336.
[7] Serbes A. On the estimation of LFM signal parameters: analytical formulation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 4(54): 848- 860.
[8] 陈艳丽, 郭良浩, 宫在晓. 简明分数阶傅里叶变换及其对线性调频信号的检测和参数估计[J]. 声学学报, 2015, 40(6): 762-771.
Chen Yanli, Guo Lianghao, Gong Zaixiao. The concise Fractional Fourier Transform and its application in detection and parameter estimation of the linear frequency-modulated signal[J]. Chinese Journal of Acoustics, 2015, 40(6): 762-771.(in Chinese)
[9] 王本庆, 李兴国. LFM信号调频斜率的双正交Fourier变换分析算法[J]. 电子与信息学报, 2009, 31(7): 1620-1623.
Wang Benqing, Li Xingguo. Analysis algorithm to frequency rate of LFM signal based on Biorthogonal Fourier Transform[J]. Journal of Electronics & Information Technology, 2009, 31(7): 1620-1623.(in Chinese)
[10] Li Xiukun, Wu Yushuang. Cross-term removal of Wigner-Ville distribution for multi-component LFM signal[J]. Acta Electronica Sinica, 2017, 11(6): 657- 662.
[11] Simeunovic M, Popovic B V, Djurovic I. The STFT-based estimator of Micro-Doppler parameters[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 5(53): 1273-1283.
[12] Auger F, Flandrin P, Lin Y T, et al. Time-frequency reassignment and synchrosqueezing: An overview[J]. IEEE Signal Processing Magazine, 2013, 30(60): 32- 41.
[13] Auger F, Flandrin P. Improving the readability of time-frequency and time-scale representations by the reassignment method[J]. IEEE Transactions on Signal Processing, 1995, 43(5): 1068-1089.
[14] 邹红星, 周小波, 李衍达. 基于Radon-STFT变换的含噪LFM信号子空间分解[J]. 电子学报, 1999, 27(12): 4- 8.
Zou Hongxing, Zhou Xiaobo, Li Yanda. Subspace decomposition for noisy LFM signal using Radon-STFT transform[J]. Acta Electronica Sinica, 1999, 27(12): 4- 8.(in Chinese)
[15] 陶然, 耿鹏飞. 基于Radon-STFT的DSSS系统线性调频干扰抑制[J]. 北京理工大学学报, 2005, 25(10): 900-904.
Tao Ran, Geng Pengfei. Linear frequency modulation interference detection and suppression based on Radon-STFT in direct sequence spread spectrum system[J]. Transactions of Beijing Institute of Technology, 2005, 25(10): 900-904.(in Chinese)
