1 引言
机器学习是人工智能一个重要学科分支。作为机器学习中最火热的一个分支,深度学习在过去的几年里更是在学术界和工业界持续升温,在计算机视觉、语音处理和文本处理等复杂任务上陆续取得重要的突破,在某些领域已经达到甚至超越了人类的表现。然而,尽管这些模型在很多预测任务上达到了令人印象深刻的正确率,但是其多层嵌套的非线性结构使得模型高度不透明,内部工作机制对于研究者来说仍然是未解之谜[1]。以计算机视觉领域中广泛使用的卷积神经网络(convolutional neural network, CNN)为例。目前,CNN在行人检测[2]和人脸识别[3]等领域得到广泛的使用,在图像处理领域[4]取得了巨大的成功,但是该模型仍然存在一些关键问题亟待解决[5- 6]。有研究指出,通过对原始图像人为添加一些微小的扰动会使模型进行误判,而这些扰动并不影响人类做出正确的判断,这使得人们对深度神经网络的有效性产生了质疑[7- 8]。另一方面,表现优异的深度神经网络的层数往往达到了上百层甚至更深,这使得模型的训练变得异常繁琐,且整个调参过程需要丰富的经验和技巧,消耗大量的时间试错。这些问题的解决离不开对神经网络作用机制的探索。
对于探究神经网络的原理,一种方案是直接对其进行数学机理上的探究[9],但是该方法相对复杂且存在一定的局限性;另一种相对直观的方式是借助可视化的手段帮助我们理解神经网络的作用机理,这也是当前神经网络领域的研究热点之一。当前可视化方法主要包含两类:一是针对神经网络学到的特征进行可视化[10-11],用人类能理解的图片或文字解释网络的功能;二是基于热力图[12]或显著图[13]的可视化方法,将输入数据中支持模型分类决策的像素部分进行高亮显示,从而突出其主要的分类依据。这些研究对于帮助我们理解神经网络的工作机制做出了重要的贡献,但是其研究对象主要局限于计算机视觉领域常用的卷积神经网络,且可视化的对象绝大多数是局限于样本层面。对于基本的全连接网络(Fully-Connected Neural Network,FCNN),也出现了像Tensorflow Playground(1)1网址:http:∥playground.tensorflow.org/和ConvNetJS(2)2网址:https:∥cs.stanford.edu/people/karpathy/convnetjs/demo/classify2d.html这样的可视化工具,二者分别从神经元对原始特征空间的剖分和隐层对特征空间的变换的角度对网络的内部工作机制进行了展示,但是其各自出发点都相对片面。
全连接神经网络作为一种基础的网络模型,对其分类原理的探究对于我们理解神经网络的工作原理具有重要意义。因此,本文以一个简单的全连接神经网络为例,从特征变换、剖分、编码三个角度对网络的分类过程进行分析和可视化,试图打开神经网络分类过程的黑盒。
本文第2节介绍了本文所使用的实验数据和网络结构,并对后文中出现重要的概念进行了定义和举例说明。在第3节,通过“特征变换”、“特征空间剖分”、“激活编码”3个小节,从不同的角度分析了全连接网络的分类过程。然后,借助编码这一工具,讨论了网络在分类过程中出现的“压缩”与“自正则”现象,并通过实验分析了自正则、胞腔数量以及网络学习能力之间的联系。最后进行了总结和展望。
2 网络结构
2.1 实验数据与网络
为了探究全连接神经网络在分类过程中对特征空间的作用,我们生成了如图1所示的“同心圆”模拟数据。该数据包含两个维度,其中内圆的点为“正类”样本,外圆的点为“负类”样本。使用含有两个隐层的全连接网络对该数据进行训练,网络结构如图2所示,第一个隐层设置3个隐节点,第二个隐层设置2个隐节点,除输出节点的激活函数为sigmoid函数外,其余节点的激活函数均设置为ReLU函数[14]。为方便描述,约定四个网络层分别为L1、L2、L3和L4,各个节点的编号详见图2。网络训练完成后,训练精度达到99.7%(3)3本文所使用实验数据与代码已上传至:https:∥github.com/JiChaoInBNU/Visualization-and-Coding-of-Original-Feature-Space-Partitioning-Process。将整个特征空间离散化成若干的特征点,得到每个特征点预测为正类的概率,如图3所示。
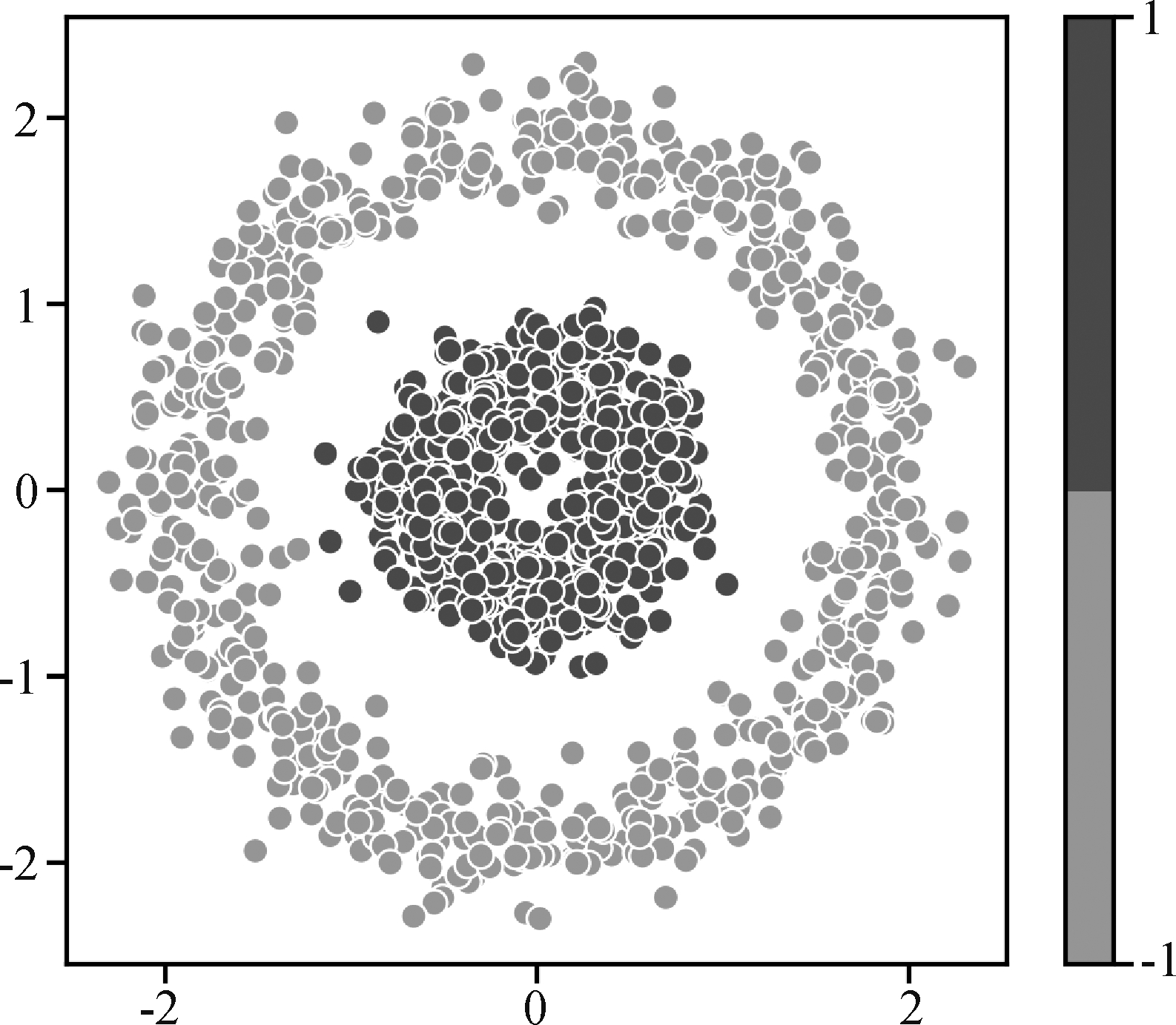
图1 “同心圆”模拟数据示意图
Fig.1 Schematic diagram of “concentric circle” simulation data
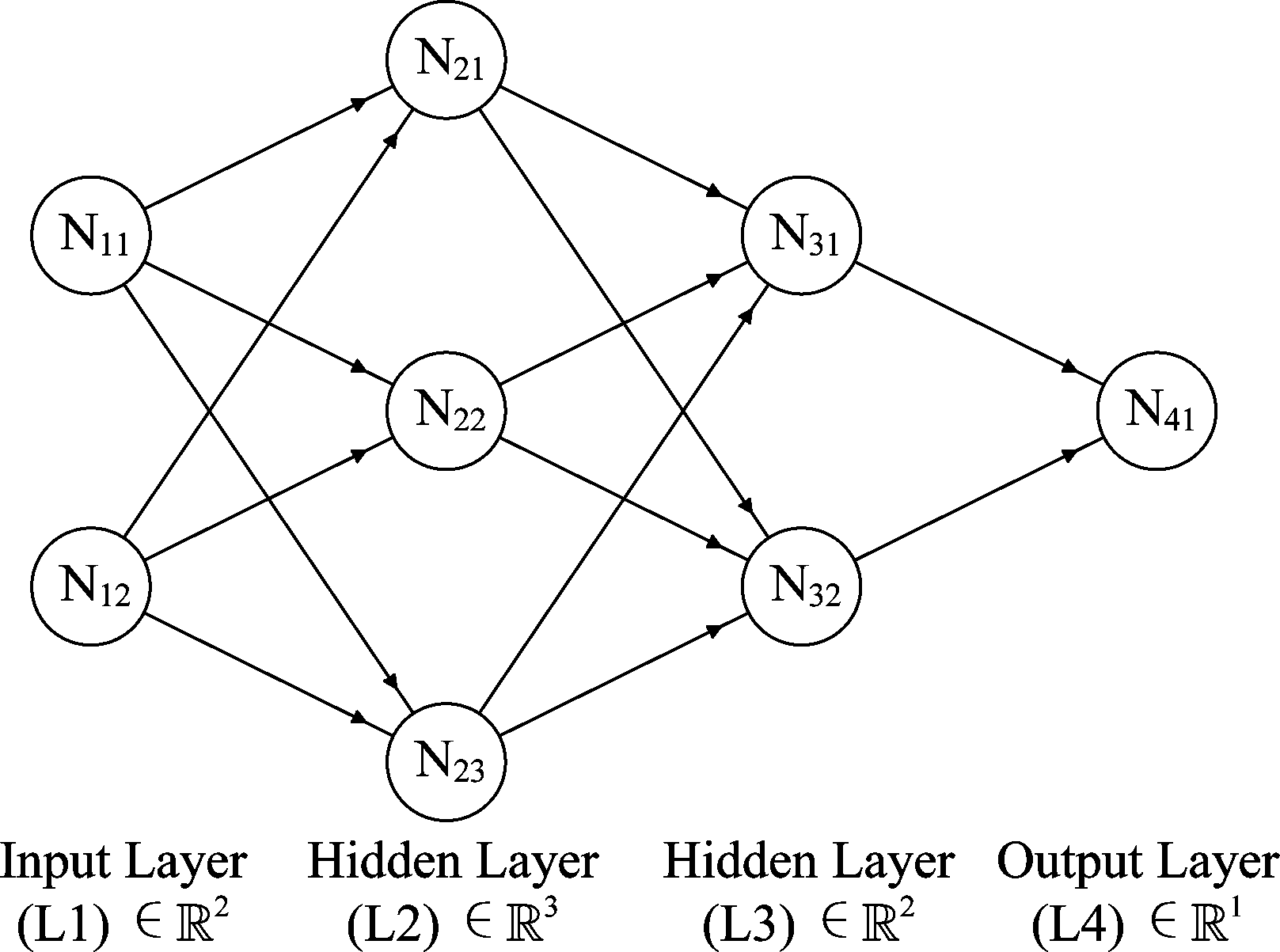
图2 网络结构示意图
Fig.2 Network structure diagram

图3 特征空间的分类结果
Fig.3 Classification results of feature space
2.2 特征变换
全连接神经网络的神经元模型可以表示成如下形式:
(1)
其中xi是前一层神经元的激活值,wi 为其对应的权重系数,θ为阈值, f为激活函数,一般为非线性函数,a为该神经元的激活值。对于网络中除了输出节点之外的每一个神经元,均将其激活值作为下一层所有神经元的输入值。对于给定输入样本,按照上述规则由浅层到深层逐层计算即可实现全连接网络的前向计算过程。
若wl,bl分别表示网络第l-1层(m个节点)与第l层(n个节点)之间的权重矩阵和偏置向量,al表示第l层各神经元的激活值向量, f表示非线性函数,则该过程可以表示为矩阵乘法的形式:
al=f(wlal-1+bl)
(2)
该式表示第l层对由第l-1层的激活值构成的空间先后进行了仿射变换与非线性变换,将m维空间中的点映射到了n维空间,实现了隐层的特征变换[15]。以L2为例,其接受L1输出的2维向量,先后进行了仿射变换与非线性变换,将特征空间从2维映射到3维,实现了特征空间的变换,该过程如图4所示。
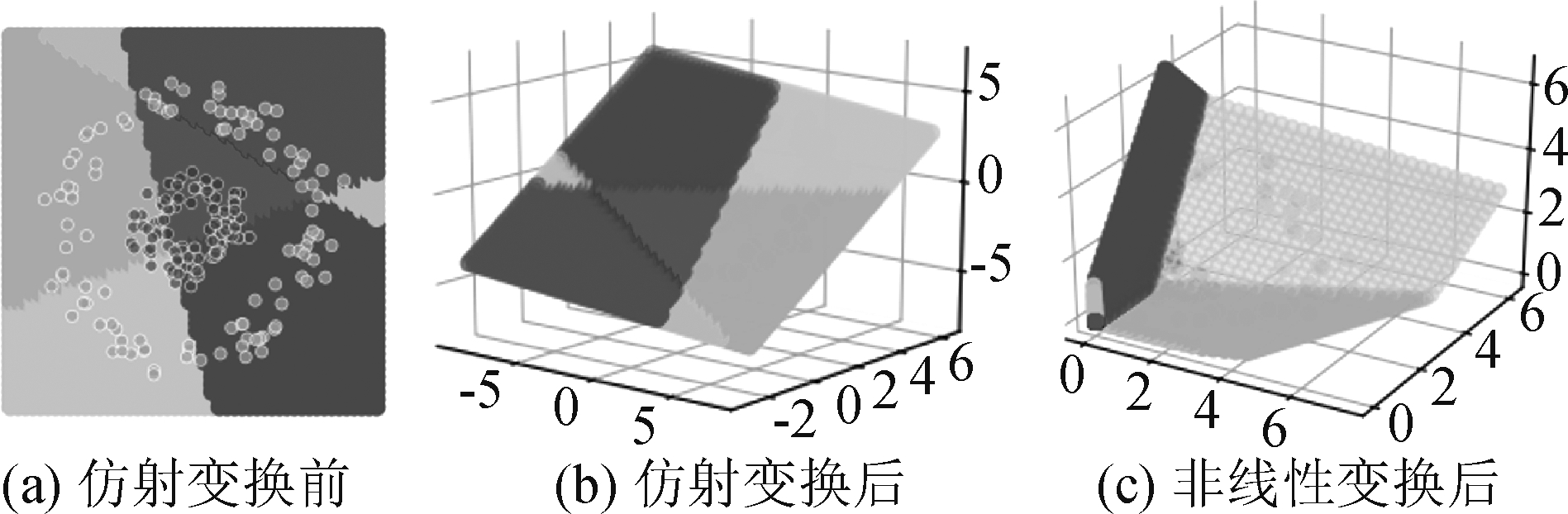
图4 L2对特征空间的变换
(其中通过不同颜色进行区分的区域即后文将要介绍的“胞腔”)
Fig.4 The transformation of L2 to feature space
2.3 特征空间的剖分
对于公式(1),令
(3)
显然,神经元模型可以看成两个函数f和g复合而成。令其中的一个函数g(X)=0,这个方程表示n维空间中的一个超平面。 该超平面将特征空间剖分成两个子空间,即实现了神经元节点对特征空间的剖分。以L2各节点为例,如图5所示,其输入空间为2维空间,各节点在其输入空间中形成了一个超平面将该2维空间分别剖分为两个子空间。
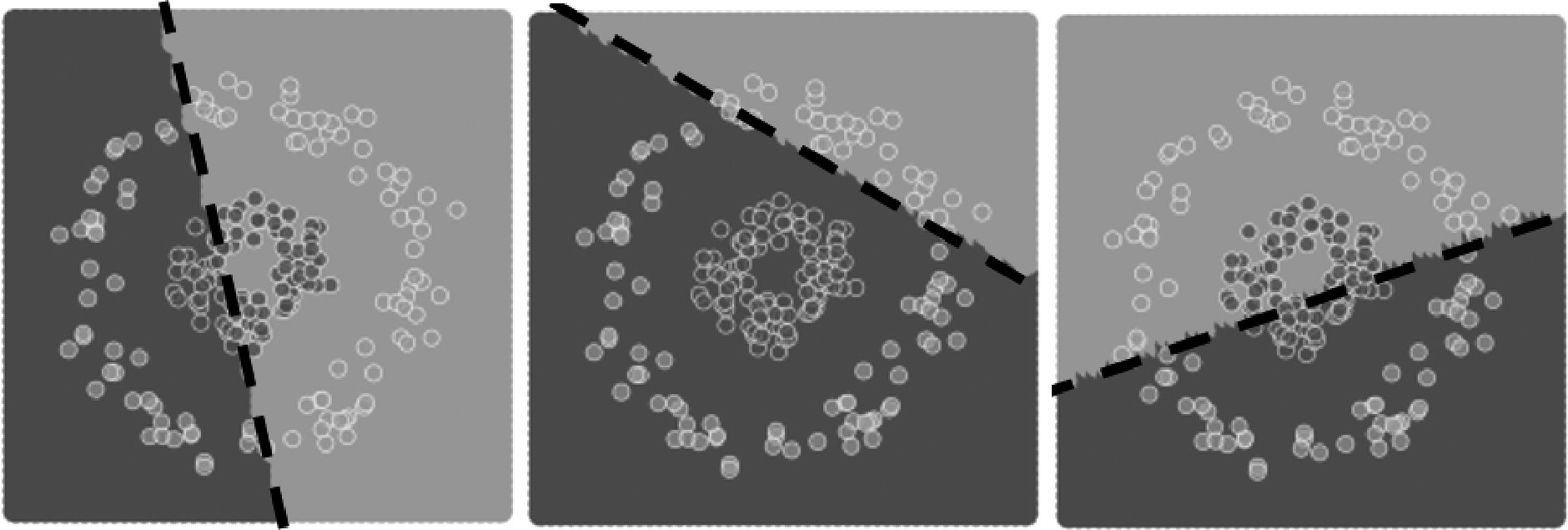
图5 L2各节点对特征空间的剖分结果
(从左到右分别为节点N21、N22、N23的对L1特征空间的剖分结果)
Fig.5 The result of each node to the feature space
2.4 激活编码
当g(X)>0时,X落在超平面的正半空间,神经元对其输入X呈现激活状态,用编码“1”表示;当g(X)<0时,神经元对X呈现抑制状态,用编码“0”表示。将这种用二进制编码方式表示神经元对其输入的激活状态的表示方式称为“激活编码”。以节点N31为例,如图6所示,该节点将特征空间剖分为两个子空间,对于正半空间的特征点,N31对其呈现激活状态,用编码“1”表示;对于负半空间的特征点,N31对其呈现抑制状态,用编码“0”表示。

图6 N31对特征空间的编码
(以超平面为分界面,超平面一侧的特征点全部被编码为“0”,另一侧特征点全部被编码为“1”)
Fig.6 Coding of N31 to the feature space
将特征空间中拥有相同激活编码的特征点所构成的集合称为“胞腔”(cell)[16]。对于一胞腔,若其在某一隐层的激活编码均为“0”,则称该隐层对该胞腔进行了“压缩”。对于某一节点,若特征空间中的所有特征点在该节点的编码均为“0”,则称该节点为“真哑节点”;若特征空间中的所有特征点在该节点的编码均为“1”,则称该节点为“伪哑节点”。真哑节点与伪哑节点均不对特征空间进行剖分,这类节点统称为“哑节点”,将出现哑节点的情况称为“自正则”[17]。
3 分类过程可视化
3.1 特征变换
对于单个样本,网络按照前向计算的规则逐层进行计算,最终得到该样本的类别归属,这一过程并没有明显的几何意义。而从样本的集合,即特征空间的角度来看,前向计算的过程就是逐层对特征空间进行变换的过程。如图7所示,左列展示的是各层经过仿射变换后的分布,右列展示的是各层经过非线性变换后的分布。对于每一个隐层,该隐层都对来自上一层输出的特征空间先后进行仿射变换与非线性变换,再将变换后的空间传递给下一隐层作为输入。经过逐层的特征变换,在原始特征空间中的线性不可分问题可以逐渐转换为线性可分的问题。
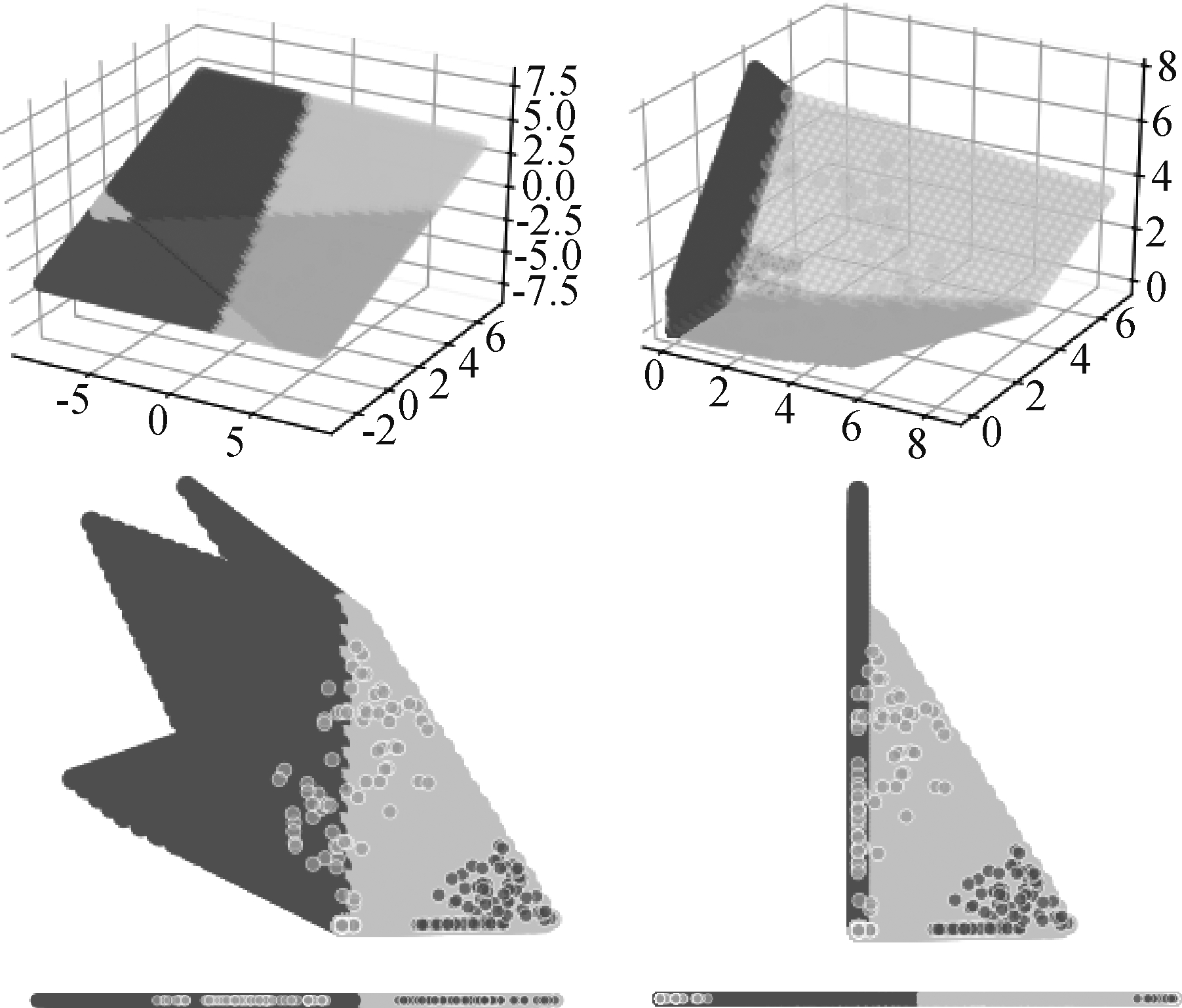
图7 网络特征变换示意图
(三行分别展示的是L2、L3、L4的变换情况,左列展示的是各层经过仿射变换后的分布,右列展示的是各层经过非线性变换后的分布)
Fig.7 Schematic diagram of network feature transformation
3.2 特征空间剖分
从特征变换的角度出发分析网络的分类过程,使我们对于网络前向计算的过程有了更形象的认识。但是特征变换的可视化对于我们理解网络的原理和作用所带来的帮助仍然有限,在本节我们将从剖分的角度出发,进一步理解网络在分类过程中的作用。
节点对特征空间剖分的定义已在第2节中给出,而将某一隐层各个节点的剖分进行叠加即可得到该隐层对特征空间的剖分。如图8所示,L2将特征空间剖分成7个互不重叠的小区域,即胞腔。
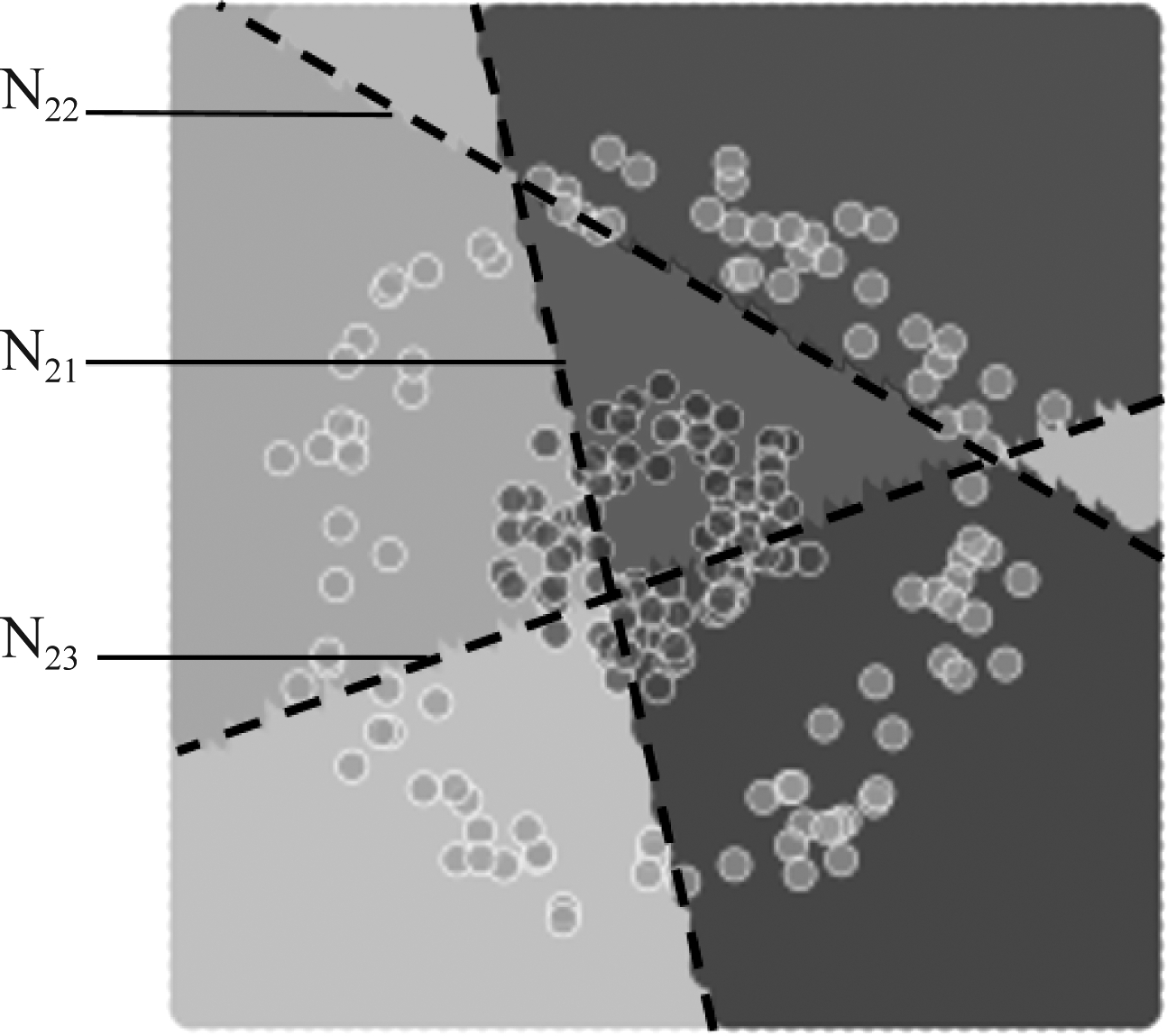
图8 L2对特征空间的剖分
Fig.8 The partition of L2 to feature space
由于L2的输入空间即为原始特征空间,L2的三个节点的剖分在原始特征空间形成的边界均为直线。但对于L3,其节点对输入空间仍然进行线性的剖分,但是由于L2的传递作用,剖分结果在原始特征空间形成了非线性的边界,如图9所示。同时,由于特征点全部位于N32所形成的超平面的正半空间,如图11所示,N32对特征空间并没有直接起到剖分作用,对这一现象的讨论将在第3节进行。
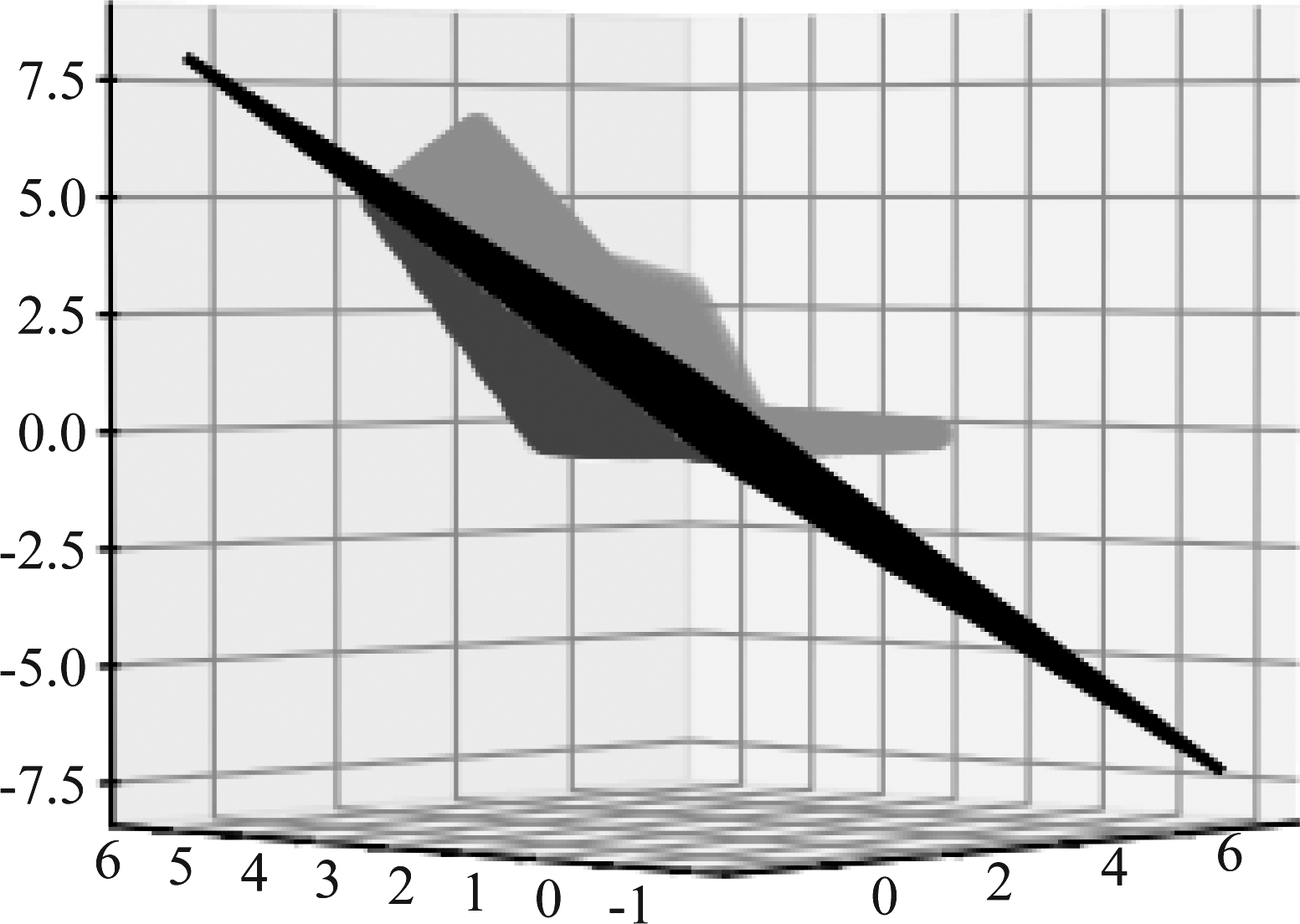
图9 N31对特征空间的剖分
Fig.9 The partition of N31 to feature space

图10 N31对原始特征空间的剖分
Fig.10 The partition of N31 to original feature space
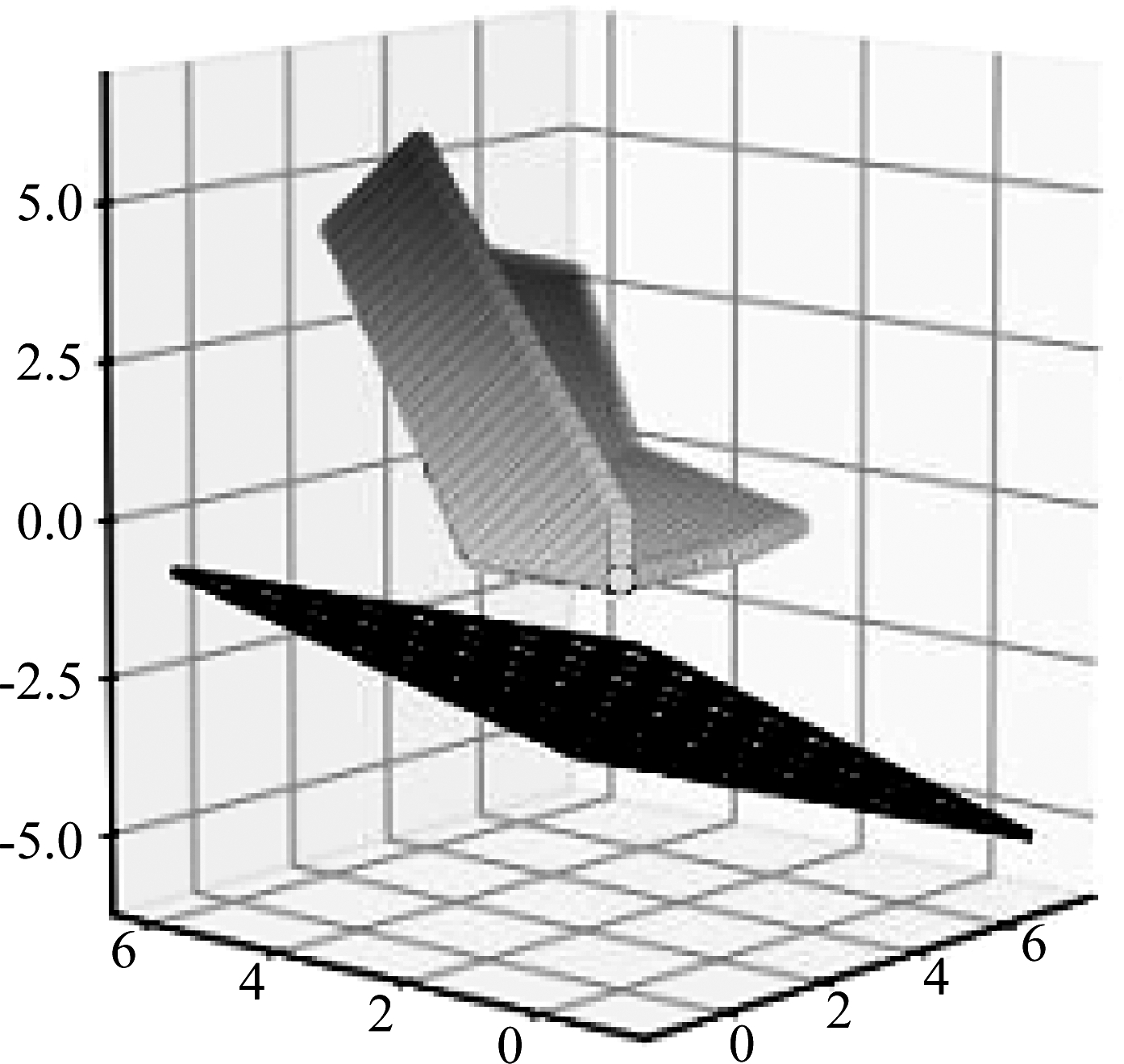
图11 N32对特征空间的剖分
Fig.11 The partition of N32 to feature space
经过L3的剖分,L2所形成的部分胞腔分别被剖分成了两个子胞腔,从而使特征空间被进一步剖分,如图12所示。将网络所有节点的剖分进行叠加得到网络对于原始特征空间的剖分,如图13所示。此时同一个胞腔内的所有特征点将被划分为相同的类别,此时的胞腔成为网络进行类别划分的最小单元。

图12 L2与L3剖分的叠加
Fig.12 The superposition of the partition of L2 and L3

图13 网络对特征空间的剖分
Fig.13 The partition of the network to feature space
3.3 激活编码
通过上一节的分析,展示了网络在分类过程中对原始特征空间的剖分过程,并对这一过程进行了可视化。在特征空间维数较低时,可以通过可视化的方式直观的了解特征空间的剖分情况。但是在特征空间的维数较高时,这一工作将难以进行。通过本文提出的“激活编码”的方式,可以部分地窥视网络在原始特征空间的剖分结果。
节点激活编码的定义已在第2节中给出。对于某一网络层,将该层所有节点的激活编码按照节点序号从小到大的顺序进行排列即得到该层的激活编码,如图14所示。将网络各个层的激活编码按照层的序号从小到大进行排列即得到了该网络的激活编码,如图15所示。
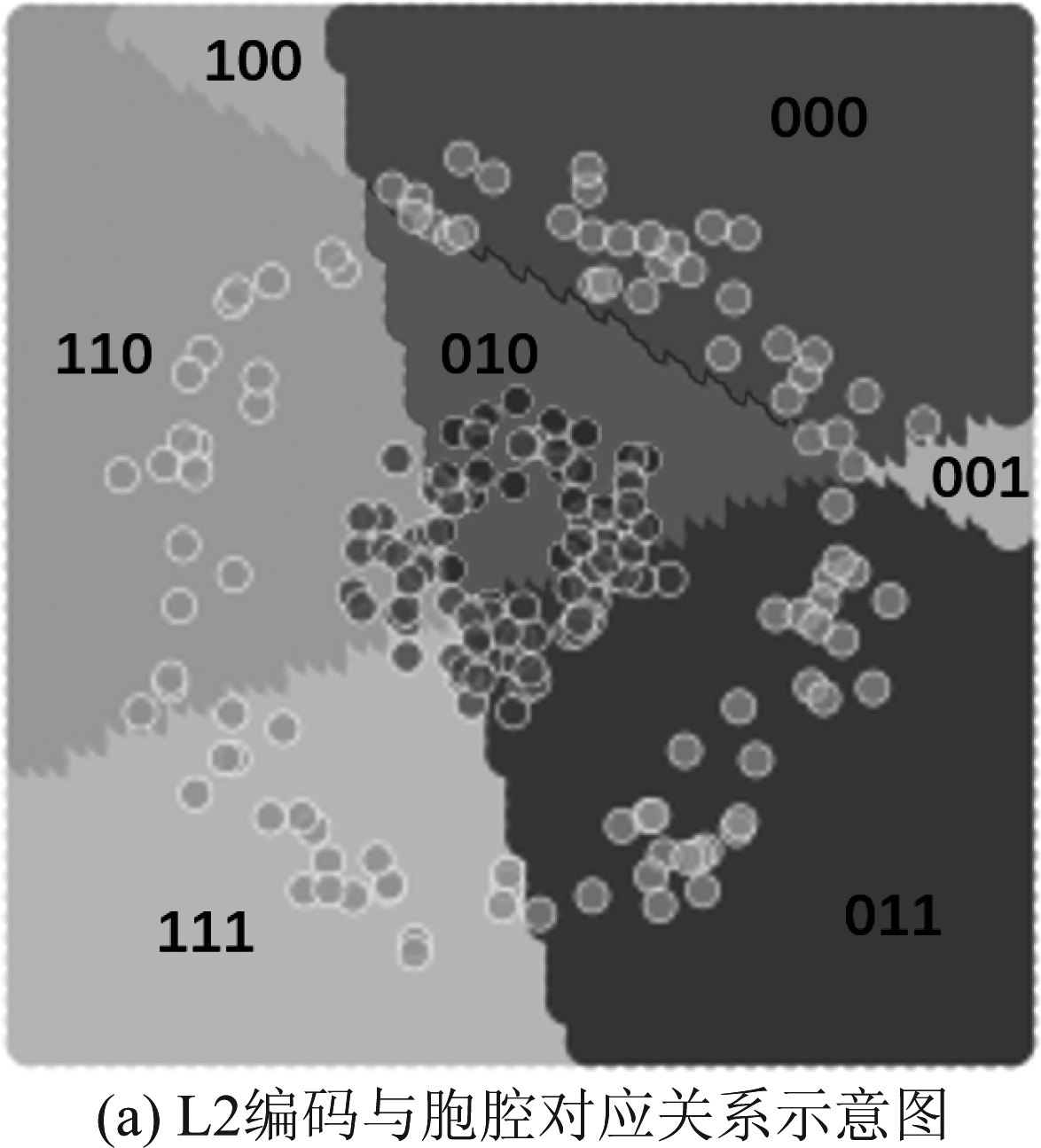
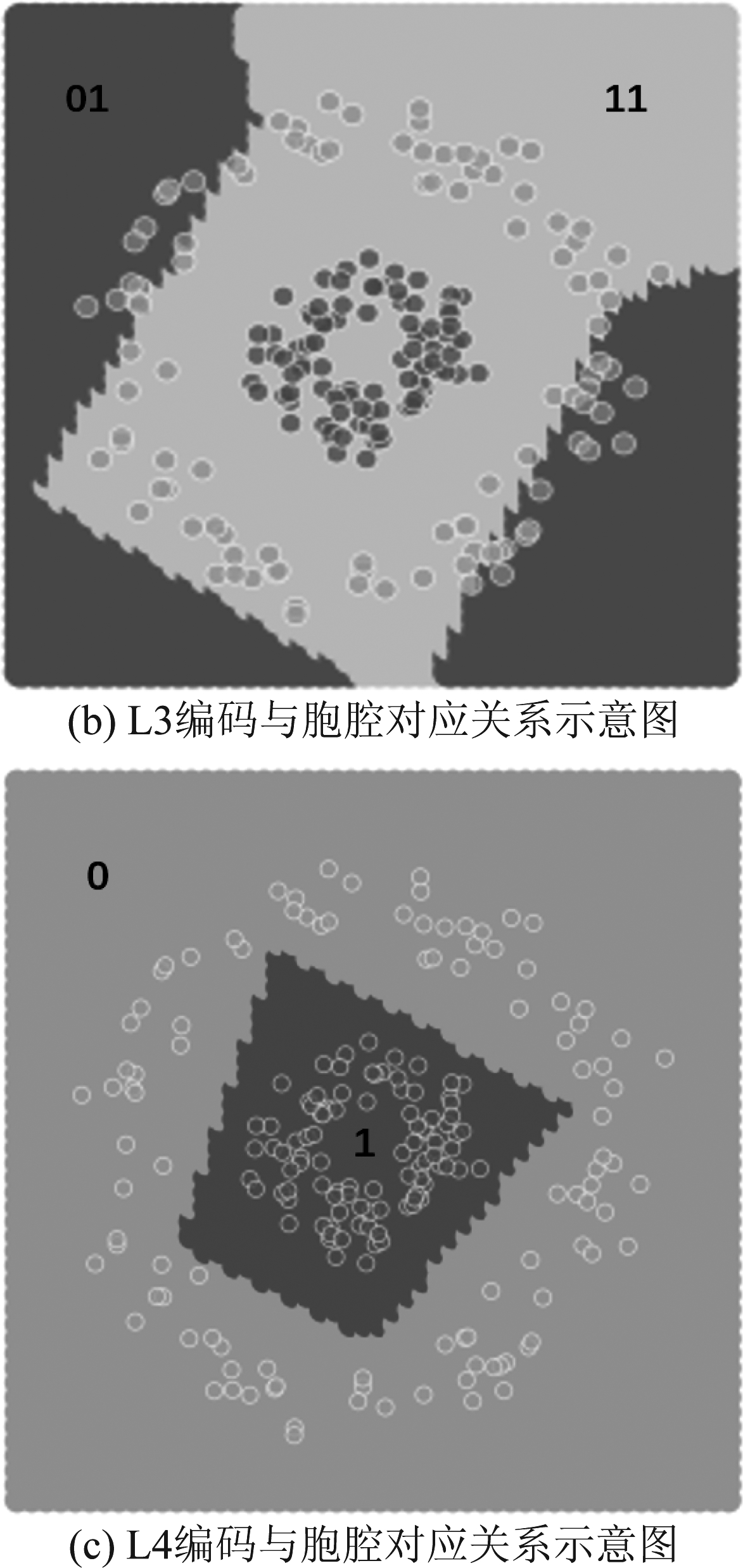
图14 L2、L3、L4的编码情况
Fig.14 The coding situations of L2,L3,L4

图15 编码与胞腔的对应关系示意图
(其中,被框包围的3位的编码来自L2,2位的编码来自L3,1位的编码来自L4)
Fig.15 Schematic diagram of correspondence between coding and cells
网络的激活编码与胞腔是一一对应的关系,不同胞腔对应着不同的激活编码。同一胞腔内的所有的特征点拥有相同的激活编码,它们被同一组神经元所激活或抑制,最终划分为同一类别。编码的每一位与隐层神经元一一对应,编码的值指示了该神经元对于该胞腔特征点的激活状态,最后一位编码则指示了该胞腔的类别划分。当特征空间的维度较高时,胞腔的剖分情况将难以进行可视化,而由于编码与胞腔一一对应的性质,我们可以借助编码的方式对网络对特征空间的剖分情况进行分析,从而对网络的工作情况进行评估。
4 讨论
4.1 压缩
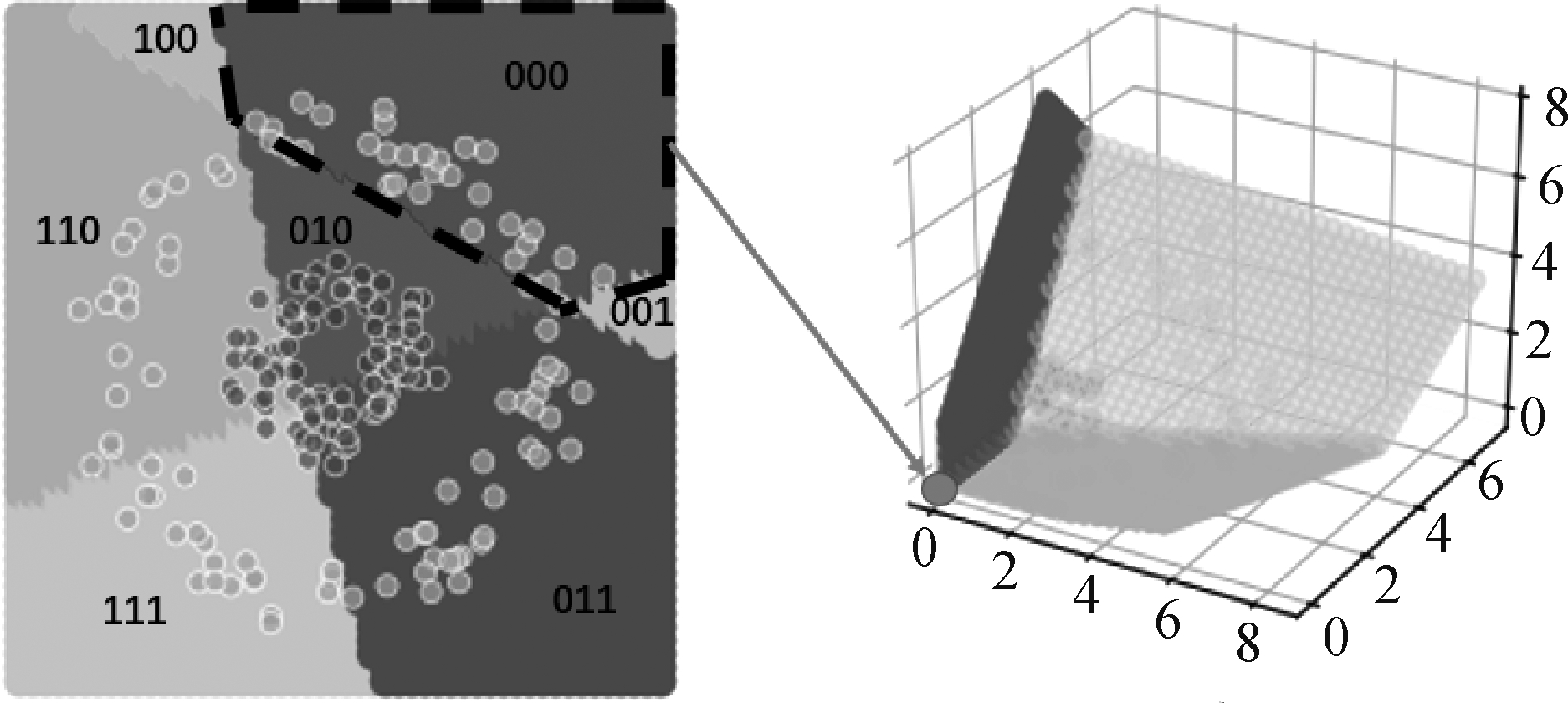
图16 压缩示意图
Fig.16 Schematic diagram of compression
压缩是网络执行分类功能的重要手段。如图16所示,特征空间中虚线指示的胞腔在L2的激活编码为“000”,即该胞腔内的所有特征点在经过L2各个节点时被该层所有节点抑制。在经过特征变换后,该胞腔内所有特征点均被映射到输出空间的坐标原点,在后续的剖分过程中,该胞腔将不再继续细分,最终该胞腔中所有特征点将被分配同样的类别。
通过逐层的压缩,网络实现了类内距离的缩小,减小了后层特征空间的分类难度,帮助网络将线性不可分的问题转化为线性可分问题。
4.2 自正则
自正则的定义已在第2节中给出。对于真哑节点,其输出的激活值始终为“0”。显然,即使在原有的网络结构中去掉真哑节点,保持其他节点的参数不变,网络的功能不发生改变。
相应地,当网络中某一节点对特征空间中的所有特征点均激活,此时该节点为伪哑节点。如图11所示,此时该节点对于特征空间没有进行剖分,对于其输入空间仅做仿射变换而没有非线性变换,这类似于残差网络(ResNet)[18]中的跳跃连接(skip connection)结构。由于该节点没有起到剖分作用,我们推测该节点可能是冗余的。因此我们进行了如下实验:使用第2节中介绍的实验数据与网络结构进行10000次训练,每次训练开始时均随机初始化权重,每次训练至损失曲线收敛或训练达到10000轮即停止。仅讨论精度在90%以上的情况,在10000次实验中,精度在90%以上的有2837次,其中出现自正则的情况有649次,自正则的情况均是在L3出现一个哑节点。因此,去掉L3的一个节点,此时两个隐层分别为3个节点和1个节点,按照同样的方法进行10000次实验,精度在90%以上的有1352次。作为对比,在原始网络结构的基础上去掉L2的一个节点,此时两个隐层均为两个节点,按照同样的方法进行10000次实验,没有出现精度在90%以上的情况。该实验结果一定程度上印证了我们的推测,同时说明根据自正则的情况对网络进行剪枝具有一定的合理性。
为了进一步探索自正则对网络学习能力的影响,同时验证本文提出方法的推广性和实用性,我们使用全连接网络在模拟数据上进行了三组实验。训练数据和测试数据使用“同心圆”和“螺旋线”两种模式的数据,如图17所示。同一组实验中训练数据和测试数据来自相同模式下的采样,且两者样本数量比为1∶1。实验一和实验三使用“螺旋线”数据,实验二使用“同心圆”数据;实验一和实验二网络为10个隐层,实验三为5个隐层,三组实验中网络的每个隐层均为10个节点。三组实验都进行100000次训练,每次训练开始时均随机初始化权重,每次训练至损失曲线收敛或训练达到10000轮即停止。实验统计结果如图18所示,三列图分别展示了实验一、实验二和实验三的情况,第一行图展示的是100000次训练中,每次训练结束后的胞腔数量(横轴)和该胞腔数量下多次实验的平均精度(纵轴),其中蓝色曲线表示训练精度,橙色曲线表示测试精度。第二行展示的是100000次训练中每次训练结束后的胞腔数量(横轴)与其出现频数(纵轴)的关系。第三行展示的是100000次训练中每次训练结束后哑节点数量(横轴)与多次实验的平均胞腔数量(纵轴)的关系。
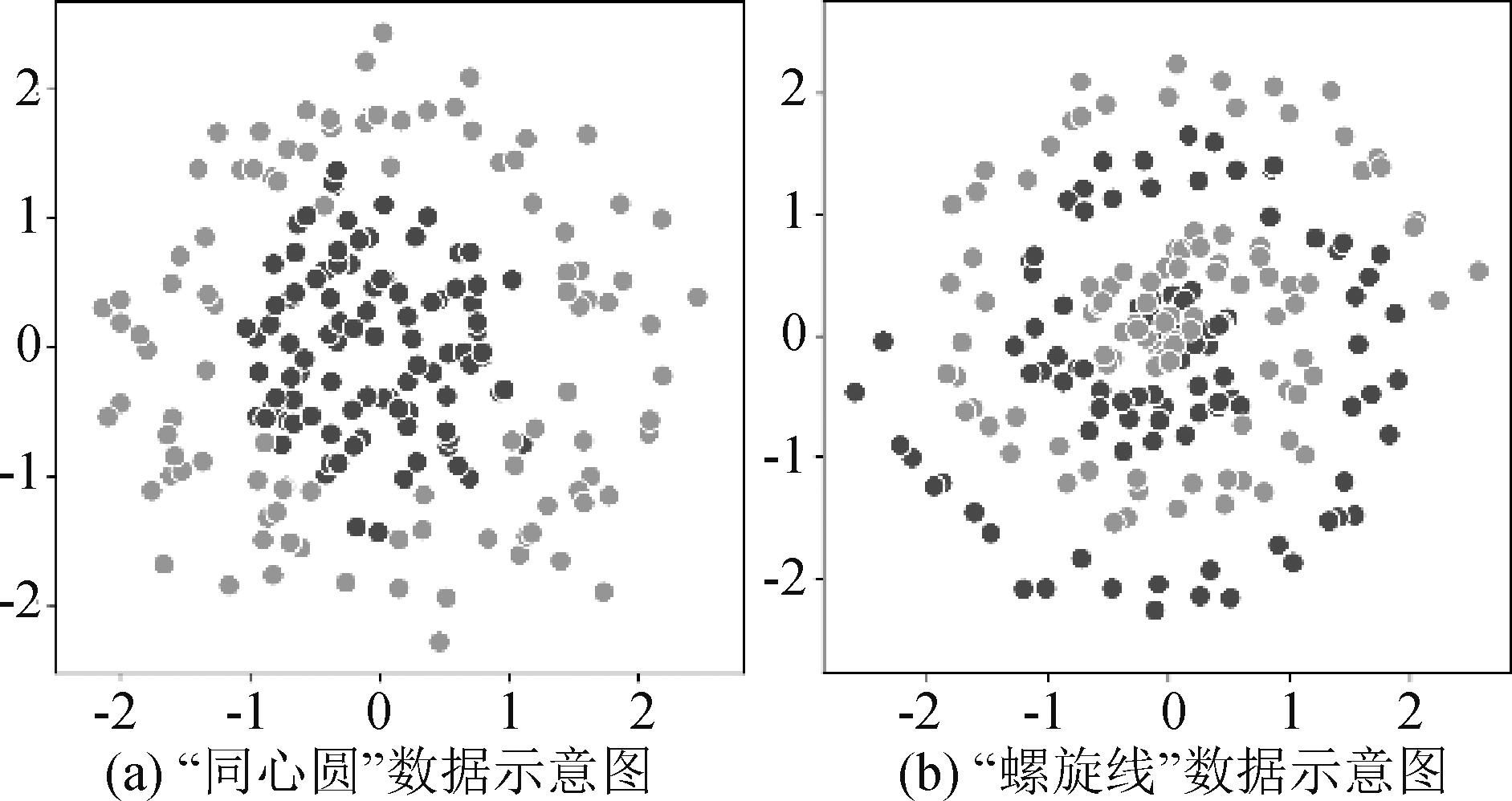
图17 模拟数据示意图
Fig.17 Schematic diagram of simulation data
从第一行图中可以看到,在一定范围内,随着胞腔数量的增加,网络的分类精度也呈现逐渐增长的趋势,这说明胞腔数量可能是影响网络学习能力的因素之一,且两者基本呈现正相关关系。需要指出的是,胞腔数量一定程度上刻画了网络对特征空间的剖分能力,但剖分能力并不等价于学习能力。对比第一行第一列和第三列可以看到,实验一在产生600个胞腔时平均训练精度约为70%,而实验三在产生600个胞腔时平均训练精度在90%以上,这说明在剖分能力相近时,网络学习能力却可能产生较大差异。同时,从第一行第二列中可以看到,随着胞腔数量的不断增加,胞腔达到一定数量后测试精度存在逐渐减小的趋势,说明过多的胞腔可能导致网络出现过拟合。从第二行可以看到,对于给定的网络结构,即使经过充分训练,网络也并非总是形成尽可能多的胞腔以充分利用其复杂度,而是以较大的概率得到一个复杂度适中的模型。同时,对比第二行第一列和第二列可以看到,在同样的网络结构下,网络在更简单的数据集上倾向于产生更少的胞腔。这种机制可能有利于保证模型的泛化能力。从第三行可以看到,随着哑节点数量的增加,胞腔数量呈现下降的趋势。因此,哑节点的出现有助于限制胞腔的数量,从而对网络的学习能力进行调节。
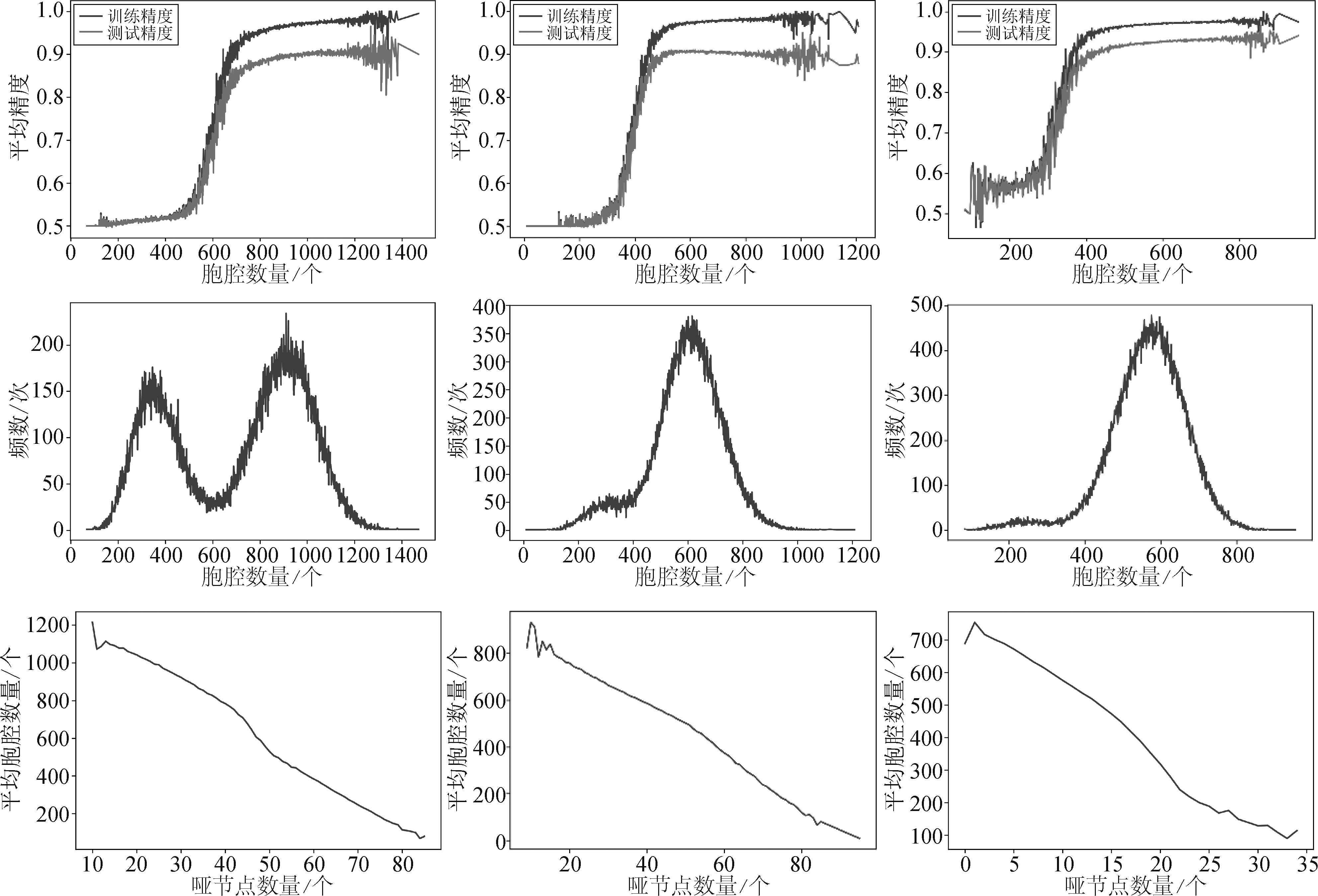
图18 三组实验统计结果
Fig.18 Statistical results of three groups of experiments
5 结论
本文通过在模拟数据上的实验,从特征变换、剖分、编码三个角度分析了一个简单的全连接网络在分类过程中各个节点与各隐层的作用,并对其进行了可视化。需要指出的是,根据本文第2节给出的相关定义,网络对特征空间的变换、剖分以及编码结果均由学习过程完成时网络的权值直接决定。在给定网络结构下,在不同的训练数据、训练过程中网络的初始化权重、优化算法、训练停止条件等因素影响下网络一般会学习到不同的权值,进而使得特征空间的变换、剖分以及编码产生不同的结果。本文着眼于从原始特征空间进行分析,对网络最小的分类单元——胞腔形成和分解的过程进行了分析和可视化。借助本文提出的激活编码的方式,对“压缩”与“自正则”两种现象进行了定义与讨论。在对“自正则”的讨论中,通过分析相同训练数据下不同网络结构的表现以及相同网络结构在不同训练数据上的表现,揭示了自正则、胞腔数量以及网络学习能力之间的联系。
通过编码的方式,可以不必通过可视化的方式对网络的胞腔分解情况进行了解,从而快速实现对网络隐层及其节点工作情况的评估。除了本文已经完成的工作,还有许多问题值得进一步探索。如:哑节点的位置和不同类型的哑节点对胞腔的形成以及网络的性能有何影响?是否可以借助编码这一工具帮助我们加深对全连接神经网络学习过程以及卷积神经网络分类原理的理解?这将是本文工作进一步拓展的研究方向。
[1] Zintgraf L M, Cohen T S, Welling M. A new method to visualize deep neural networks[J]. arXiv preprint arXiv:1603.02518, 2016.
[2] Cao J, Pang Y, Li X. Pedestrian Detection Inspired by Appearance Constancy and Shape Symmetry[J]. IEEE Trans Image Process, 2016, 25(12): 5538-5551.
[3] Ding C, Tao D. Trunk-Branch Ensemble Convolutional Neural Networks for Video-based Face Recognition[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2018, PP(99): 1-1.
[4] Schwartz E, Giryes R, Bronstein A M. DeepISP: Towards Learning an End-to-End Image Processing Pipeline[J]. IEEE Transactions on Image Processing, 2018, PP(99): 1-1.
[5] Ball J E, Anderson D T, Chan C S. Comprehensive survey of deep learning in remote sensing: theories, tools, and challenges for the community[J]. Journal of Applied Remote Sensing, 2017, 11(4): 042609.
[6] Razzak M I, Naz S, Zaib A. Deep learning for medical image processing: Overview, challenges and the future[M]. Classification in BioApps. Springer, Cham, 2018: 323-350.
[7] Xu W, Evans D, Qi Y. Feature squeezing: Detecting adversarial examples in deep neural networks[J]. arXiv preprint arXiv:1704.01155, 2017.
[8] Carlini N, Wagner D. Adversarial examples are not easily detected: Bypassing ten detection methods[C]∥Proceedings of the 10th ACM Workshop on Artificial Intelligence and Security. 2017: 3-14.
[9] Vidal R, Bruna J, Giryes R, et al. Mathematics of deep learning[J]. arXiv preprint arXiv:1712.04741, 2017.
[10] Yosinski J, Clune J, Bengio Y, et al. How transferable are features in deep neural networks?[C]∥Advances in Neural Information Processing Systems, 2014: 3320-3328.
[11] Nguyen A, Yosinski J, Clune J. Multifaceted feature visualization: Uncovering the different types of features learned by each neuron in deep neural networks[J]. arXiv preprint arXiv: 1602.03616, 2016.
[12] Ribeiro M T, Singh S, Guestrin C. " Why should i trust you?" Explaining the predictions of any classifier[C]∥Proceedings of the 22nd ACM SIGKDD international conference on knowledge discovery and data mining, 2016: 1135-1144.
[13] Simonyan K, Vedaldi A, Zisserman A. Deep inside convolutional networks: Visualising image classification models and saliency maps[J]. arXiv preprint arXiv: 1312. 6034, 2013.
[14] Nair V, Hinton G E. Rectified linear units improve restricted boltzmann machines[C]∥International Conference on International Conference on Machine Learning, 2010.
[15] Kim K J. Artificial neural networks with feature transformation based on domain knowledge for the prediction of stock index futures[J]. Intelligent Systems in Accounting, Finance & Management: International Journal, 2004, 12(3): 167-176.
[16] Lei N, An D, Guo Y, et al. A Geometric Understanding of Deep Learning. Engineering,https:∥doi.org/10.1016/j.eng.2019.09.010.
[17] Tian Y, Jiang T, Gong Q, et al. Luck Matters: Understanding Training Dynamics of Deep ReLU Networks[J]. arXiv preprint arXiv: 1905.13405, 2019.
[18] He K, Zhang X, Ren S, et al. Deep residual learning for image recognition[C]∥Proceedings of the IEEE conference on computer vision and pattern recognition, 2016: 770-778.

