1 引言
阵列信号处理[1-2]作为现代信号处理领域中的一个重要分支,在雷达、声呐、无线通信等多个领域具有广泛的应用。其基本原理是将一组传感器按照特定方式进行布局,构成传感器阵列,之后再对空间中的信号进行采样,最后通过对获取的采样数据进行处理来获得目标信号的参数信息。理论上,阵元数为M-1的阵列的自由度为M-1,即最多能够分辨M-1个信号。随着当前环境下空域中信号的数量日益增多,为了获得更高的分辨力,增加物理阵元的方法虽然易于实现,但这对传感器阵列的工作环境会有更高的要求,并且还需要付出高昂的硬件成本和维护成本。因此,如何使用较少的阵元获得高于阵元个数的自由度,是阵列信号处理领域里富有实际意义的热点问题之一。
通过研究发现,传统的均匀线阵中存在大量的冗余阵元。通过调整布阵方式,能够达到减小阵元冗余,提高阵列自由度的目的[3],稀疏阵列由此开始成为研究热点。最小冗余阵列[4]是目前已知的冗余度最小的稀疏阵列。但最小冗余阵列的阵列结构无解析表示,尽管目前有学者通过穷尽的搜索程序和模拟退火等智能优化算法得到了部分阵元数下的最小冗余阵列结构[5],但这种阵列结构的适用性仍然很低。P.Pal在文献[6]中首次提出差协同阵列,将物理阵元的位置差与一个假想的虚拟域阵列相对应,将阵列实际接收数据转换到该虚拟阵列上进行处理,能够有效的提高阵列自由度。在此基础上,P.Pal等人于2010年提出了嵌套阵列[7],于2011年提出了互质阵列[8]。这两种稀疏阵都是由传统均匀线阵组合构成,存在阵列结构的解析表示,适用范围较广。在此基础上,又有许多改进的扩展阵列结构被相继提出[9-11]。
针对稀疏阵列的研究目前主要集中在利用扩展的自由度进行DOA 估计,对于波束形成的研究较少。大致分为以下两种思路:一种是将稀疏阵列视为多个均匀线阵的组合,由各子阵分别进行波束形成后再进行综合;干鹏等人在文献[12]中提出基于互质思想的分子阵布阵方法,获得了更低的旁瓣级;K. Adhikari在文献[13]中提出一种半互质阵列,将其视为三个均匀线阵的组合叠加,分别实现波束形成后进行性能上的融合,在阵列自由度上取得显著提升;另一种是将稀疏阵列转化至虚拟域阵列,在虚拟域阵列中进行波束形成加权值的等效求解。Lei Yu等人在文献[14-15]提出了基于稀疏阵列的自适应波束形成方法,周成伟等人在文献[16]中针对互质阵中的波束形成进行了研究,在传统MVDR算法的基础上,对干扰噪声协方差矩阵进行重构,取得了更优的波束形成器性能。但通过进一步的分析发现,其稳健性较差,特别是在高干噪比和阵元数较多的情况下,对方位和功率的估计性能会有明显下降。
针对稀疏阵列中的波束形成问题,本文将压缩感知模型引入稀疏阵列波束形成算法中,在虚拟域阵列上通过压缩感知算法对信源和干扰的方位和功率进行估计,从理论上证明了该方法的可行性,进而对干扰噪声协方差矩阵进行重构,对传统MVDR波束形成算法进行优化,通过仿真证明该方法能够将压缩感知算法与稀疏阵列的优势相结合,在提高自由度的同时,实现性能良好的波束形成器设计。
2 稀疏阵列信号处理
2.1 差协同阵列
假设阵列有M个阵元,qi代表阵列第i个阵元的位置,i=1,2,…,M,阵元位置集合为Q=[q1,q2,…,qM],差协同阵列定义为:
QΔ={qm-qn,∀qm,qn∈Q}
(1)
可知,针对M个阵元的物理域阵列,任意选取两个阵元的组合共有
种情况,由于两者作差的对称性,加上可重复选取同一阵元的情况,可得到理想情况下,差协同阵列的最大自由度为:
DOFmax=M(M-1)+1
(2)
此时得到的差协同阵列为阵元位置对称的均匀直线阵列。
实际上,差协同阵列仅在阵元数为某些值的情况下,可以达到最大自由度,多数情况下虚拟域中的阵元位置会存在冗余;但我们可以选择其中具有最多连续阵元的部分作为虚拟域阵列进行分析,仍然可以获得相较于物理域阵列更高的自由度。
2.2 两级嵌套阵列
两级嵌套阵列是一种典型的稀疏阵列结构,其具有易于解析表示,虚拟域阵列孔洞少,可扩展自由度高等优点。
两级嵌套阵列是将两个均匀线阵拼接而成的一种稀疏阵列结构,分别称为内层线阵和外层线阵。内层阵元数为M1,阵元间距为d1;外层阵元数为M2,阵元间距d2=(M1+1)d1。两个子阵之间的间距为d1;阵列结构如图1。
图1 两级嵌套阵列结构
Fig.1 Two-level nested array structure
阵元位置分别为:
Qin={md1,m=1,2,…,M1}
(3)
Qout={n(M1+1)d1,n=1,2,…,M2}
(4)
将两级嵌套阵列对应的差协同阵列记为QNA,从中去除冗余阵元后,得到的连续虚拟域阵列为:
(5)
其自由度为2M2(M1+1)-1,通常大于物理域阵元数M1+M2。因此,若能将原物理域阵列接收数据合理转换至虚拟域阵列上,则可在更高自由度下,达到更高的阵列信号处理的算法性能。
2.3 稀疏阵列数据接收模型
假设任意稀疏阵列含有M个阵元,阵元位置为:
Q=[qi,q2,…,qM]·d
(6)
其中qi为整数,d通常取半波长。
有K个远场窄带信号入射到该稀疏阵列,入射信号之间相互独立,入射角为[θ1,θ2,…,θK],则在方位θk处的阵列流形向量可表示为:
a(θk)=[e-jq1φk,e-jq2φk,…,e-jqMφk],φk=2πdsin θk/λ
(7)
稀疏阵列接收信号可以表示为:
x(n)=As(n)+ν(n)
(8)
其中,阵列流形矩阵A=[a(θ1),a(θ2),…,a(θK)],是一个Vandermonde矩阵。当接收数据共有n个快拍时,阵列接收信号表示为:
X=AS+N
(9)
其中X=[x(1),x(2),…,x(n)]∈CM×n,信号矩阵S=[s1(n),s2(n),…,sK(n)]T∈CK×n,噪声矩阵N=[ν(1),ν(2),…,ν(n)]∈CM×n。
假设信号功率为
噪声为均值为0,方差为
的高斯白噪声,信号与噪声满足相互独立,则接收数据协方差矩阵为:
(10)
RXX中的第m行第n列的元素可以表示为:
(11)
其中,δm,n为Kronecker delta函数,当m=n时为1,当m≠n时为0。
从上式中可以看出,原物理域阵列的协方差矩阵中的每一个元素都可看作其对应的差协同阵列中的某一阵元接收的单快拍数据,因此通过将原始的协方差矩阵RXX向量化,即可将阵列接收数据模型从物理域转化至虚拟域。
向量化RXX得:
(12)
其中vec为向量化符号,⊙表示Khatri-Rao积,(A*⊙A)表示如下:
A*⊙A=[a*(θ1)⊗a(θ1),a*(θ2)⊗a(θ2),
…，a*(θK)⊗a(θK)]∈CM2×K
(13)
其中⊗表示Kronecker积,信号功率向量p=
噪声向量
∈CM2×1,列向量ei中仅有第i个元素为1,其余元素都为0。
为便于表示,记AΔ=A*⊙A,上式表示为:
(14)
将式(14)与物理域阵列接收模型(8)对比,可以看出,两者具有十分相似的表达形式,差协同阵列的接收数据模型可以视为K个单快拍功率信号入射到均匀直线阵列的情况,XΔ为各个虚拟阵元接收到的数据,AΔ为差协同阵列的阵列流形向量。
由于差协同阵列可能存在孔洞以及阵元冗余,且虚拟阵元的位置排列并不是按均匀阵列的顺序排列。因此XΔ中的数据,并不全是有效数据,还需要对虚拟接收数据进行筛选,去冗余以及重排处理。
前文中已经推导了两级嵌套阵列对应的连续虚拟域阵列表示,据此可筛选出虚拟域阵列对应的接收数据并完成重排处理,伴随阵元冗余产生的接收数据冗余,即同一虚拟阵元对应的多个接收数据,我们可以取所有对应数据的均值作为该虚拟阵元接收到的数据:
(15)
l为满足qm-qn=i的(m,n)组合个数。
相应的,差协同阵列的阵列流形矩阵AΔ也需进行同样的修正处理,将经过筛选,去冗余和重排后的接收数据记为
阵列流形矩阵记为
则模型改写为:
(16)
至此,物理域阵列接收数据模型已经转化为虚拟域阵列接收模型,原波束形成问题等效为阵元数增加后的入射信号为单快拍信号下的波束形成问题。相当于以时域数据快拍数为代价,换取更高的自由度。
针对信号为单快拍的情况,所得协方差矩阵必然是亏秩的。因此可将其视作信源为相干信号的情况,在处理之前对采样数据进行解相干处理。通常可采用空间平滑算法[18]、Toeplitz矩阵重构法[28]等方法实现,但解相干的过程中阵列的自由度会受到一定的损失,文献[7]中给出的空间平滑子阵阵元数为连续虚拟域阵元数的一半,对于两级嵌套阵列,最终虚拟域阵列的阵元位置为:
(17)
实际自由度为DOF=M2(M1+1)。
3 压缩感知实现虚拟域阵列DOA估计
针对非相干信号入射到稀疏阵列的问题,将接收数据变换到虚拟域后,本质上都转化成为对单快拍接收信号的处理,而压缩感知算法[17]在处理快拍数较少时的DOA估计问题上,相比于其他算法具有明显优势。并且压缩感知方法具有天然的解相干能力,因此能够更好的利用稀疏阵列提高的自由度,提高 DOA 估计性能。
3.1 稀疏阵列中的压缩感知模型建立
信号稀疏的数学定义为:假设存在一个信号x,若信号在某个域中只有少量非零值,那么它在该域稀疏,该域也被称为信号的稀疏域。信号在某个域内是稀疏的,意味着在稀疏域中存在一组基向量Ψ=[φ1,φ2,…],原信号x可表达为:
x=Ψw
(18)
其中,w为原信号x在稀疏域中的表达,称为稀疏系数,w中仅有少量值为非零值。
在虚拟域阵列接收模型中,
仅包含信源方位对应的阵列流形向量,相对应的,p中仅含有对应方位的单快拍功率信号。显然,单快拍功率信号p在空域中是稀疏的,不再需要对其稀疏化,对应到压缩感知模型中,相当于稀疏基矩阵为单位阵的情况,即Ψ=I。但在表达式中的p仅包含若干个有效的稀疏系数,并非完整的稀疏信号。因此,我们需要对信号以及阵列流形矩阵进行扩展。
将空域范围进行离散化,均匀划分为D份,D≫K,则整个空间可表示为[θ1,θ2,…,θD],原阵列流形矩阵扩充为一个完备的字典集
为:
a(θ2),…，a*(θD)⊗a(θD)]
(19)
对进行去冗余和重排后,记新的阵列流形矩阵为
同理,将空域变换系数扩充为一个完整的空域稀疏信号:
w=[p(θ1),p(θ2),…,p(θD)]
(20)
w中仅有K个非零值,出现在对应的信源方位上。因此,原数据接收模型改写为:
(21)
为了形式上的统一,记
式(21)重写为:
(22)
以上过程实现了基于压缩感知理论的虚拟域阵列接收数据模型的建立,扩展字典集
等效于压缩感知模型中的感知矩阵。根据压缩感知理论,由于稀疏基矩阵为单位阵,所以也可视作是对空域稀疏信号的测量矩阵。
3.2 感知矩阵的有效性证明
压缩感知理论指出,感知矩阵必须满足RIP准则[27],RIP准则定义为:对于由K个信号组成的稀疏度为K信号矢量x和一个矩阵Φ,若存在常数ε,且ε∈(0,1),使得如下不等式成立:
(1-ε)‖x‖2≤‖Φx‖2≤‖x‖2
(23)
则称矩阵Φ满足RIP准则,其中ε为限制等容常数。
文献[19]证明,RIP准则的等价准则如下:对于一个稀疏度为K的信号,当满足感知矩阵任意2K列线性无关时,能够保证把任意一个2K稀疏信号映射为唯一的测量信号。
当信号经过稀疏表示且矩阵Φ满足 RIP 准则时,测量信号可以视作稀疏信号经压缩采样后的结果。因此,下面对字典集作为感知矩阵的合理性,即满足RIP条件进行证明:
在选取任意2K列之前,需要明确的是,感知矩阵并非一个方阵,记的维度为r×q,由前文对稀疏阵列的分析,可知的行数r为虚拟域阵列的阵元个数,即:
r=2M2(M1+1)-1
(24)
由于的秩
所以当2K>r时,矩阵的秩不可能超过r,即不存在任意2K列都线性无关的情况。因此,上述结论证明需要满足以下前提:
2K≤r
(25)
即重构信号的稀疏度不大于虚拟域阵元个数的一半,这与前文所提到的针对单快拍数据解相干的一系列算法的结论是一致的,在虚拟域中扩充的自由度并不能完全得以利用。
在满足上述条件后,从字典集中任意选取2K列,有以下两种情况:
(1)2K列全部来自于的前D列时,根据阵列信号数据模型可知,由前D列构成的矩阵为Vandermonde矩阵,其中任意2K列必然满足线性无关。
(2)2K列中包含最后一列时,对于以下等式:
α1(a*(θm1)⊗a(θm1))+α2(a*(θm2)⊗a(θm2))+
(26)
其中
中仅有M个非零行。要证明2K列满足线性无关,即证明式(26)中:
α1=α2=…α2K=0
(27)
对于
中为零的每一行,式(26)的左边求和中最后一项为0,仅剩前2K-1列,而前2K-1列全部来自前D列构成的矩阵为Vandermonde矩阵,因此满足线性无关,所以有:
α1=α2=…α2K-1=0
(28)
将结果代入式(26)后,前2K-1项求和为0,等式仅剩最后一项
又因为中存在非零行,所以必有α2K=0。因此,所有的系数都为0,线性无关条件得证。对于字典集中任意2K列都满足线性无关,满足RIP条件。
因此,将虚拟域阵列接收数据视作对空域稀疏信号经压缩采样后的结果是可行的。
3.3 稀疏信号重构
根据以上分析可知,虚拟域阵列接收模型满足稀疏重构压缩感知算法的使用条件,下一步将要实现对空域稀疏系数
的重构。Candes等人提出了基于最小l0范数问题的稀疏重构求解方法,此方法可以通过以下数学模型加以表示:
(29)
其中,
为稀疏系数
的l0范数,表示系数向量中非零元素的个数,即系数向量中非零元素的个数要求最少。这是一个NP-hard问题,难以求解。
文献[19]中证明,在测量矩阵满足严格等距特性条件下,最小l0范数优化问题与最小l1范数优化问题具有相同的解,在一定意义上是等价的。而针对观测信号包含噪声的情况,通常将等式约束优化问题松弛为包含误差扰动的不等式约束l1范数最小化问题[23]:
(30)
其中ε是设定的误差值,表示可容许的噪声大小。
为了便于求解,通常利用拉格朗日乘子法,将不等式约束l1范数最小化问题变型为:
(31)
实际上,式(31)即为求解线性回归的最小绝对收缩与选择(LASSO)算法的数学模型。其中,λ为正则化参数。
凸优化算法具有估计精度高,计算量大的特点,工程上常采用已经开发的凸优化计算工具箱进行求解,如Sedumi,CVX等。利用工具箱求解得到
中最后一个位置处的值为的估计值。中真正有信号入射的方位对应较大值,而没有信号入射的方位,值很小或几乎为0。由于虚拟域阵列所对应的接收信号恰好为单快拍功率信号,因此由前文中定义
可知,从中除去后得到的w即为方位谱图。谱峰所在位置就是信号入射的方向,峰值大小对应的就是估计信号的功率,具有极高的估计精度。
4 干扰噪声协方差矩阵重构
传统的MVDR波束形成器优化函数如下:
(32)
当存在干扰信号时,上式中的噪声可理解为包含干扰的广义噪声,即:
(33)
在实际应用中,上式中的Ri+n通常是难以直接得到的,因此常用接收数据协方差矩阵RX进行代替,而当期望信号包含于阵列数据中时,利用协方差矩阵代替干扰噪声协方差矩阵,常常会出现信号“自消”现象,导致自适应波束形成器性能的急剧下降[1]。因此,要得到更为准确的波束形成器,可利用方位估计得到的干扰方位和功率,对干扰噪声协方差矩阵进行重构。
上述要求决定了高分辨DOA估计算法中的一系列子空间类算法在这里并不适用,原因在于该类算法所得到的方位谱是伪谱,从中仅能获取干扰的方位信息,缺乏准确的功率信息;而前文中已经证明,采用压缩感知算法在虚拟域阵列进行方位估计,能够得到信源的方位以及功率信息,因此可采用估计得到的信源方位和功率重构干扰噪声协方差矩阵。
设经过稀疏信号重构得到的信源方位估计值为
功率估计值为
当估计得到的信源中包含波束指向的信源目标时,将其余信源视为干扰,假设波束指向方位为θs,该方向信源功率为
则有:
干扰噪声协方差矩阵:
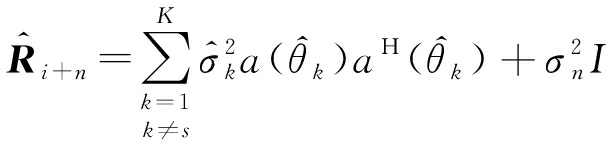
(34)
代入式(34)中的目标函数,采用拉格朗日极值法求得最优加权值:
(35)
至此,采用压缩感知算法对嵌套阵列的波束形成进行优化的过程全部完成。现将步骤总结如下:
(1)根据式(12)将稀疏阵列接收数据转换至虚拟阵元域,并通过式(19)～(22)得到基于压缩感知理论的单快拍功率信号接收模型。
(2)将式(22)表示的稀疏信号恢复问题变型为式(31)的优化问题,采用凸优化工具箱进行求解,得到信源方位的估计值
和功率的估计值
(3)由估计信源中干扰信号的方位和功率值构造干扰噪声协方差矩阵
(4)在虚拟阵元域上采用MVDR算法求得最优阵元加权值,并得到波束形成输出。
5 仿真示例
针对由稀疏阵列导出的虚拟域单快拍数据模型,文献[16]中采用Toeplitz矩阵重构法[28]进行协方差矩阵重构,进而采用Capon算法得到信源的方位和功率的估计值,文献[14]针对重构的协方差矩阵补充了对角加载的过程,取得了更高的稳健性。
以下对嵌套阵列中的Capon(NA-Capon)[16],对角加载Capon(NA-DL-Capon)[14],本文采取的压缩感知算法(NA-CS),以及等效均匀直线阵中的Capon算法(ULA-Capon)分别进行DOA估计,进行多次仿真实验后分析四种估计算法的方位估计均方根误差,功率估计均方根误差随着输入信噪比,阵元数量的变化关系;并基于DOA估计的结果重构干扰噪声协方差矩阵,分析所得波束形成器的输出信干噪比随着输入信噪比,阵元数量的变化关系。
方位估计均方根误差和功率估计均方根误差分别定义如下:
(36)
(37)
其中,K为估计信源个数,N为仿真实验次数,
为信源方位估计值,θk为信源方位真实值。
为信源功率估计值,
为信源功率真实值。
输出信干噪比作为衡量波束形成器的重要参数:定义如下:
(38)
其中,wMVDR为最优加权值,
为干扰噪声协方差矩阵,Rs为目标信源协方差矩阵。
5.1 不同输入信噪比下算法性能仿真分析
5.1.1 平均方位误差、平均功率误差与输入信噪比的关系
仿真条件:
入射信号个数K=11,入射角度以10°为间隔,分别位于(-50°,-10°)和(10°,60°)之间,其中10°方向的信号为目标信号,其余方向视作干扰。目标与干扰,干扰与干扰之间统计独立,信噪比和干噪比在0～30 dB之间变化,快拍数为10000。嵌套阵列的阵元数为M=10,内层和外层的阵元数为M1=5,M2=5。等效均匀直线阵阵元数为M2(M1+1)=30,阵元间距为半波长,仿真次数50次。仿真结果如图2～图3。
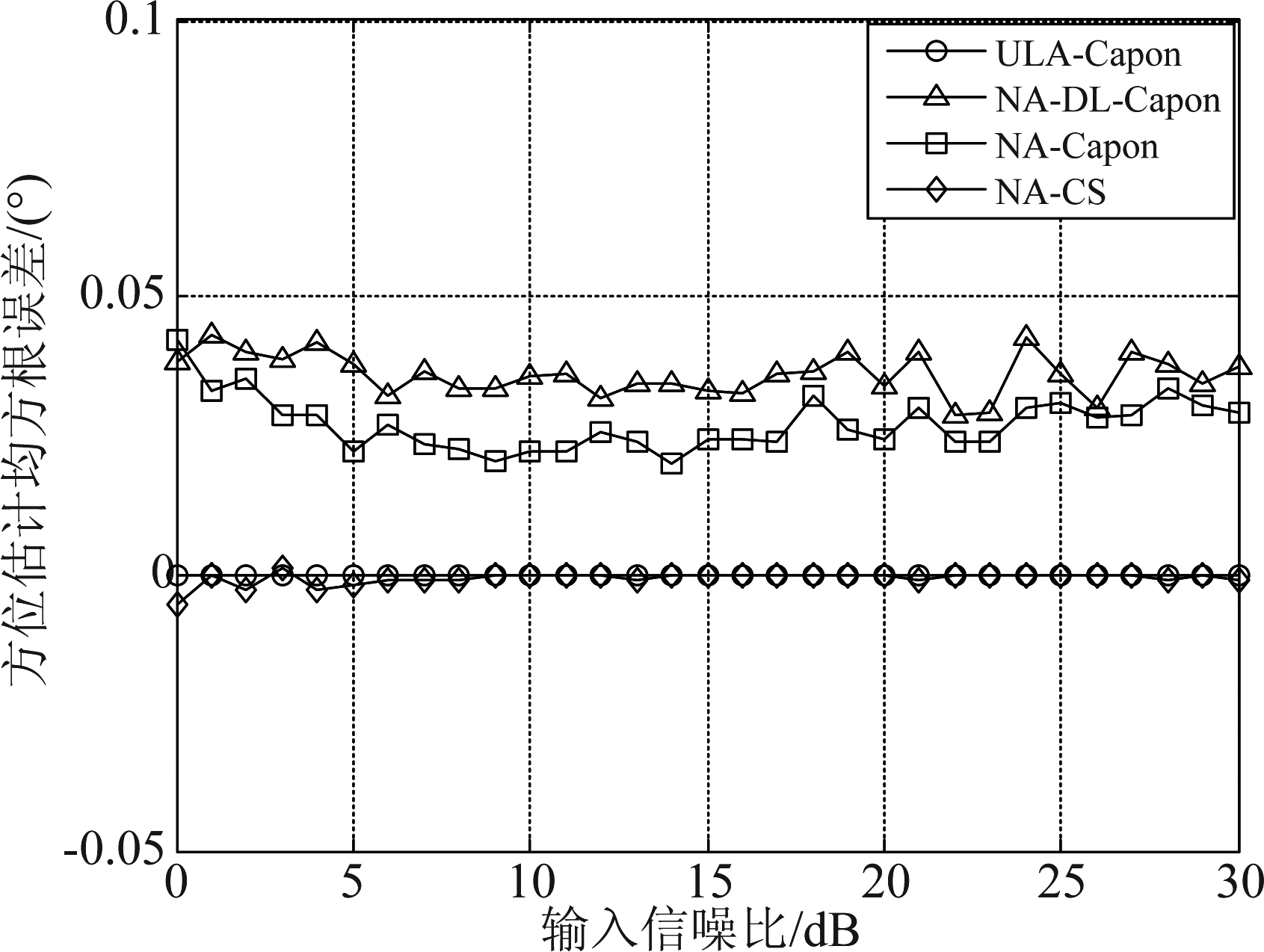
图2 方位估计均方根误差与输入信噪比的关系
Fig.2 Relationship between RMSE of DOA and the input signal-to-noise ratio
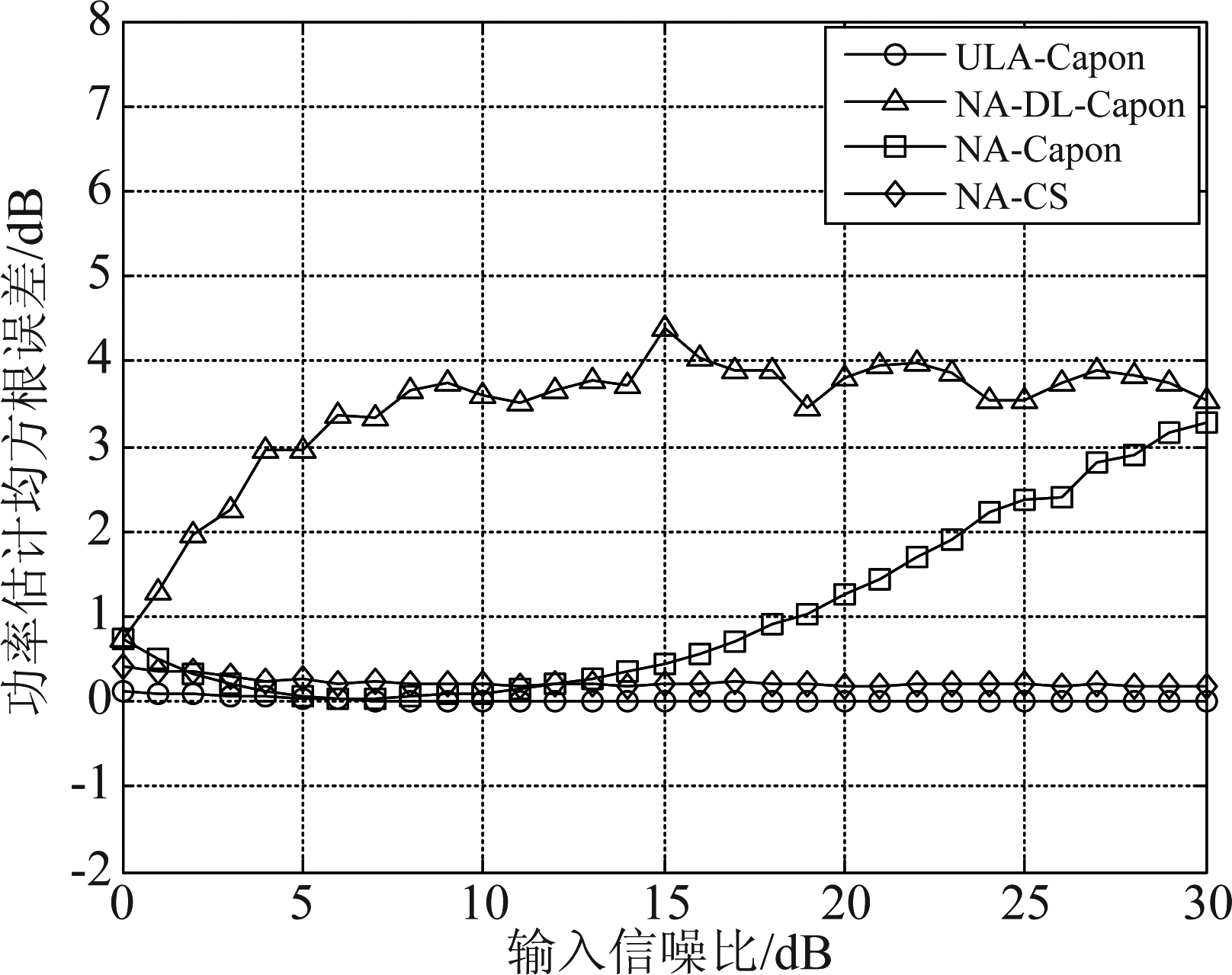
图3 功率估计均方根误差与输入信噪比的关系
Fig.3 Relationship between RMSE of power estimation and input signal-to-noise ratio
从仿真结果中可以看出,对于稀疏阵列,采用Capon算法的方位估计均方根误差最高,经过对角加载后误差有所减小,采用本文提出的稀疏阵列压缩感知算法的估计误差进一步减小,与等效均匀直线阵列的估计误差基本一致;在功率估计方面,随着输入信噪比的增加,采用Capon算法的功率估计均方根误差逐渐增大,经过对角加载后,在信噪比处于12 dB以内时,可以有效减小误差,但调节能力十分有限,随着信噪比继续增大,仍然无法避免功率误差逐渐增大的问题;采用稀疏阵列压缩感知算法的功率估计均方根误差与等效均匀直线阵的估计结果基本一致,误差一直被控制在较低的水平。
5.1.2 输出信干噪比与输入信噪比的关系
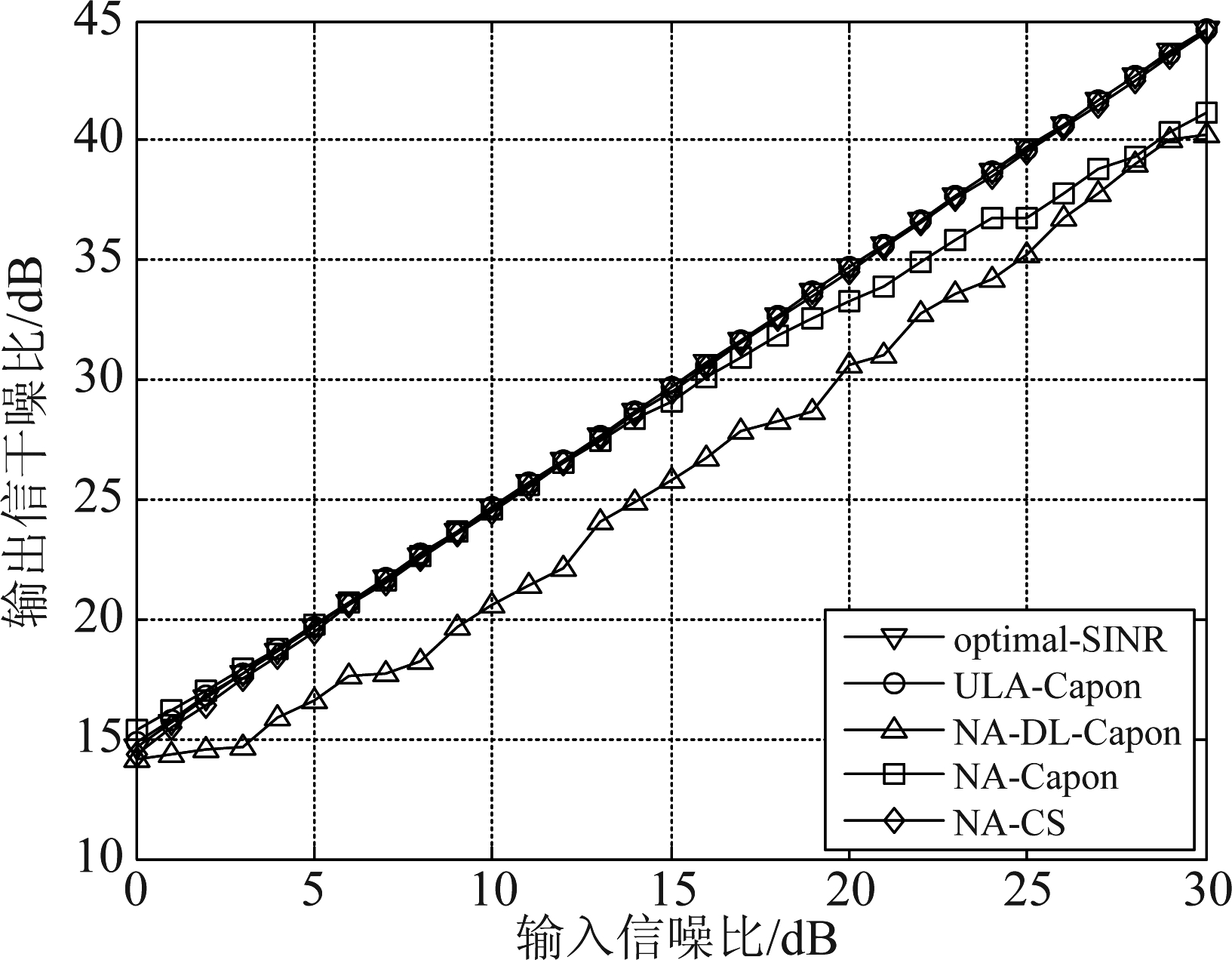
图4 输出信干噪比与输入信噪比的关系
Fig.4 Relationship between output signal-to-interference and noise ratio and input signal-to-noise ratio
从仿真结果中可以看出,随着输入信噪比的增加,对于稀疏阵列,采用Capon算法得到的输出信干噪比始终低于等效均匀直线阵列,大约相差5 dB,经过对角加载后,信噪比处于12 dB以内时,输出信干噪比可以达到理想水平,随着输入信噪比继续增大,输出信干噪比的损失开始增加;而采用稀疏阵列压缩感知算法,输出信干噪比的变化曲线与等效均匀直线阵列基本重合,达到了在提高自由度的同时,不损失波束形成器性能的理想效果。
5.2 不同稀疏阵元数下算法性能仿真分析
5.2.1 平均方位误差、平均功率误差与稀疏阵列阵元数的关系
仿真条件:
入射信号个数K=11,入射角度以10°为间隔,分别位于(-50°,-10°)和(10°,60°)之间,其中10°方向的信号为目标信号,其余方向视作干扰。目标与干扰,干扰与干扰之间统计独立,信噪比和干噪比为10 dB,快拍数为10000。嵌套阵列的内层和外层的阵元数相等,每层子阵阵元数在4～12之间变化,阵元间距为半波长。仿真次数50次。仿真结果如图5～图6。
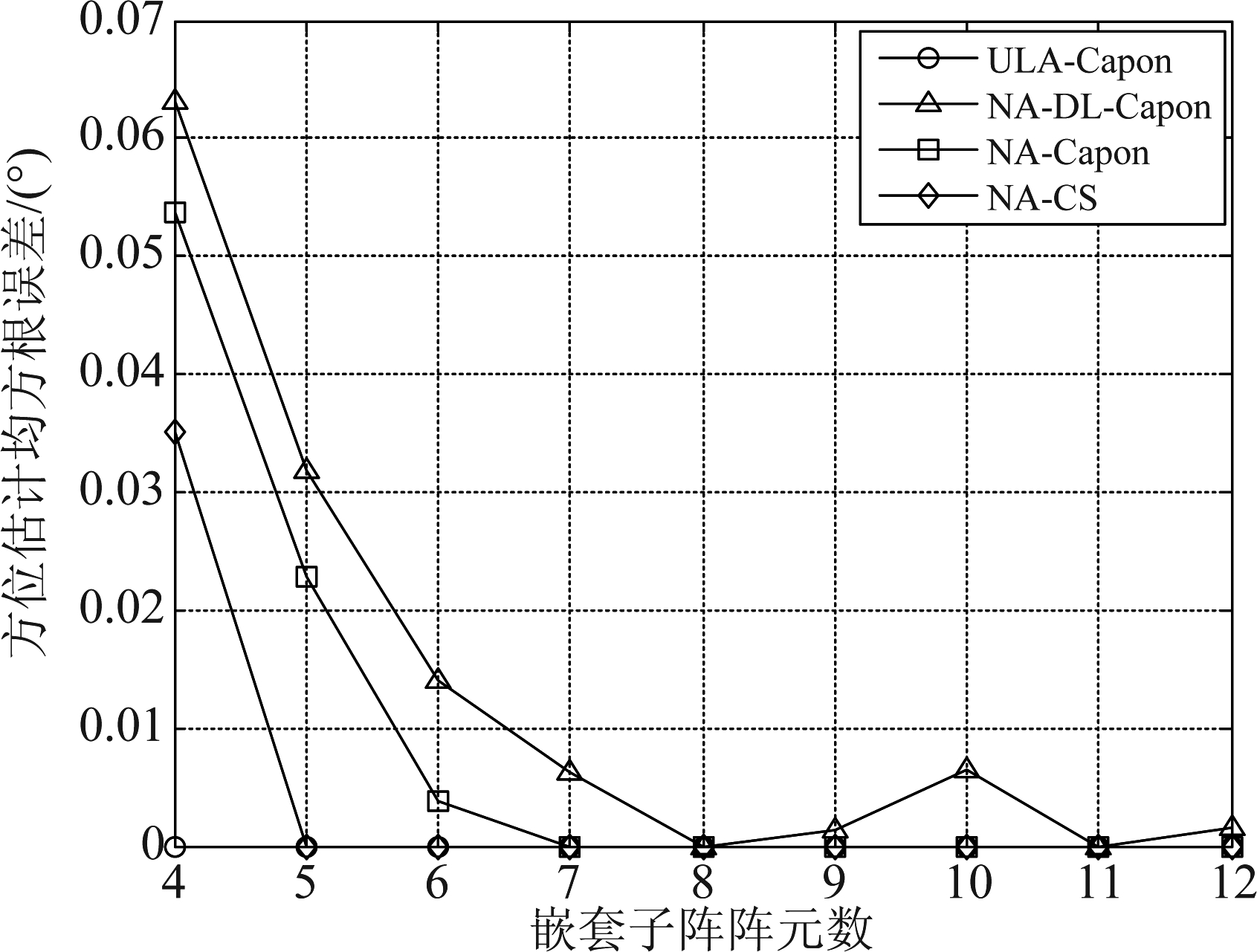
图5 方位估计均方根误差与嵌套子阵阵元数的关系
Fig.5 Relationship between the RMSE of DOA and the number of nested sub-array elements
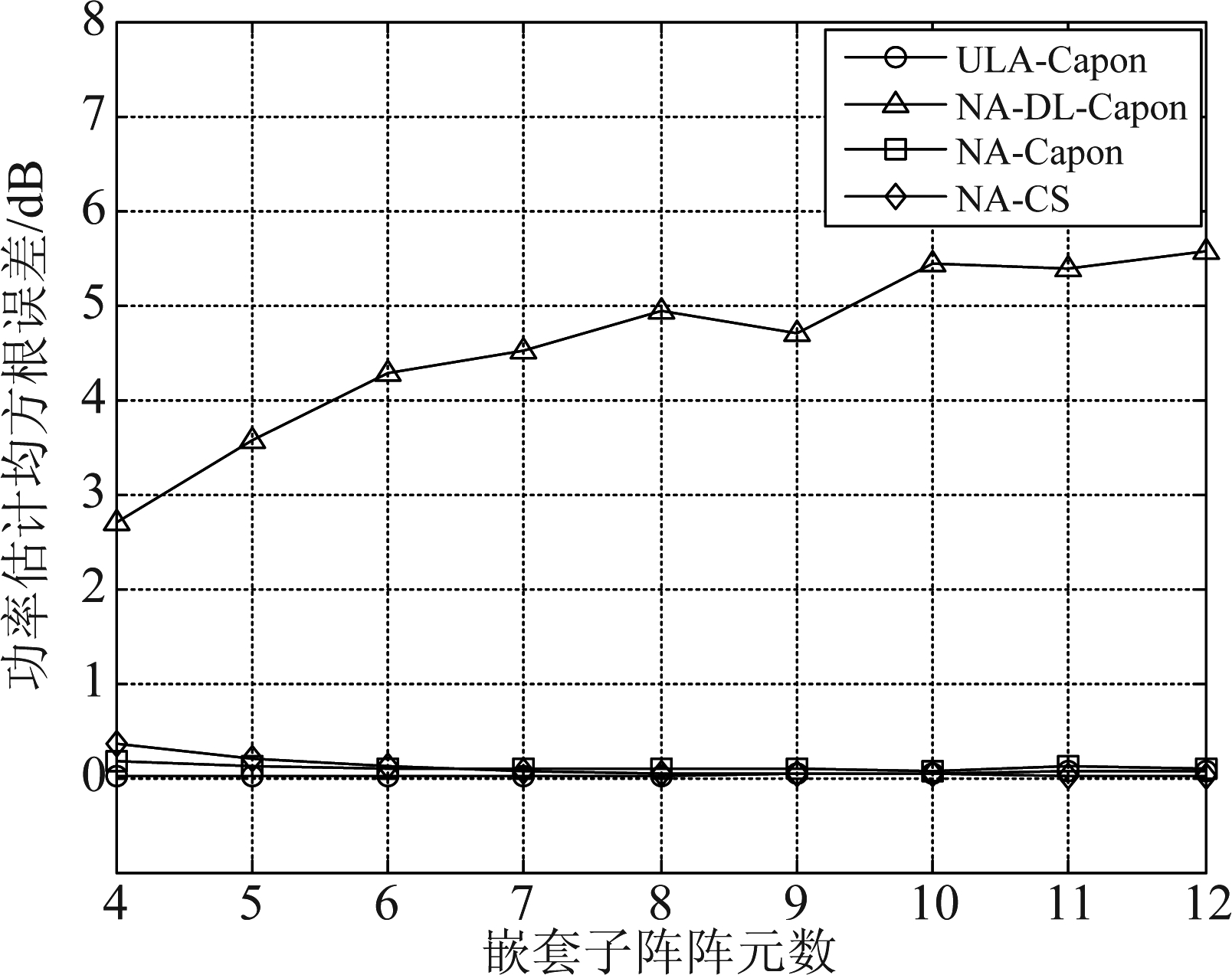
图6 功率估计均方根误差与嵌套子阵阵元数的关系
Fig.6 Relationship between RMSE of power estimation and the number of nested sub-array elements
从仿真结果中可以看出,随着阵元数增加,对于稀疏阵列,采用Capon算法的方位估计误差最高,经过对角加载后误差有所减小,采用稀疏阵列压缩感知算法的估计误差最小,与等效均匀直线阵基本一致;在功率估计方面,采用Capon算法的功率估计均方根误差随着嵌套子阵阵元数的增加而逐渐增大,而对角加载Capon算法和稀疏阵列压缩感知算法的估计误差基本与等效均匀直线阵保持一致,维持在较低的水平。
这一现象的主要原因在于,在快拍数有限的条件下,在物理域阵列得到的接收数据协方差矩阵存在失配,阵元数越多,失配越严重,相应的虚拟域阵列的单快拍数据模型的误差也会越来越大,而在采用Capon算法进行方位估计的过程中,还需对该单快拍数据进行协方差矩阵重构,例如文献[15]中采用的Toeplitz重构法。这种方法本质上可视为一种空间平滑[28],其稳健性并不高,因此误差将被进一步放大;对角加载是提高算法稳健性的一种有效方法,而压缩感知算法仅需要对数据在空域中进行扩展,没有后续的数据处理过程,也能够避免误差的累积。
5.2.2 输出信干噪比与稀疏阵列阵元数的关系
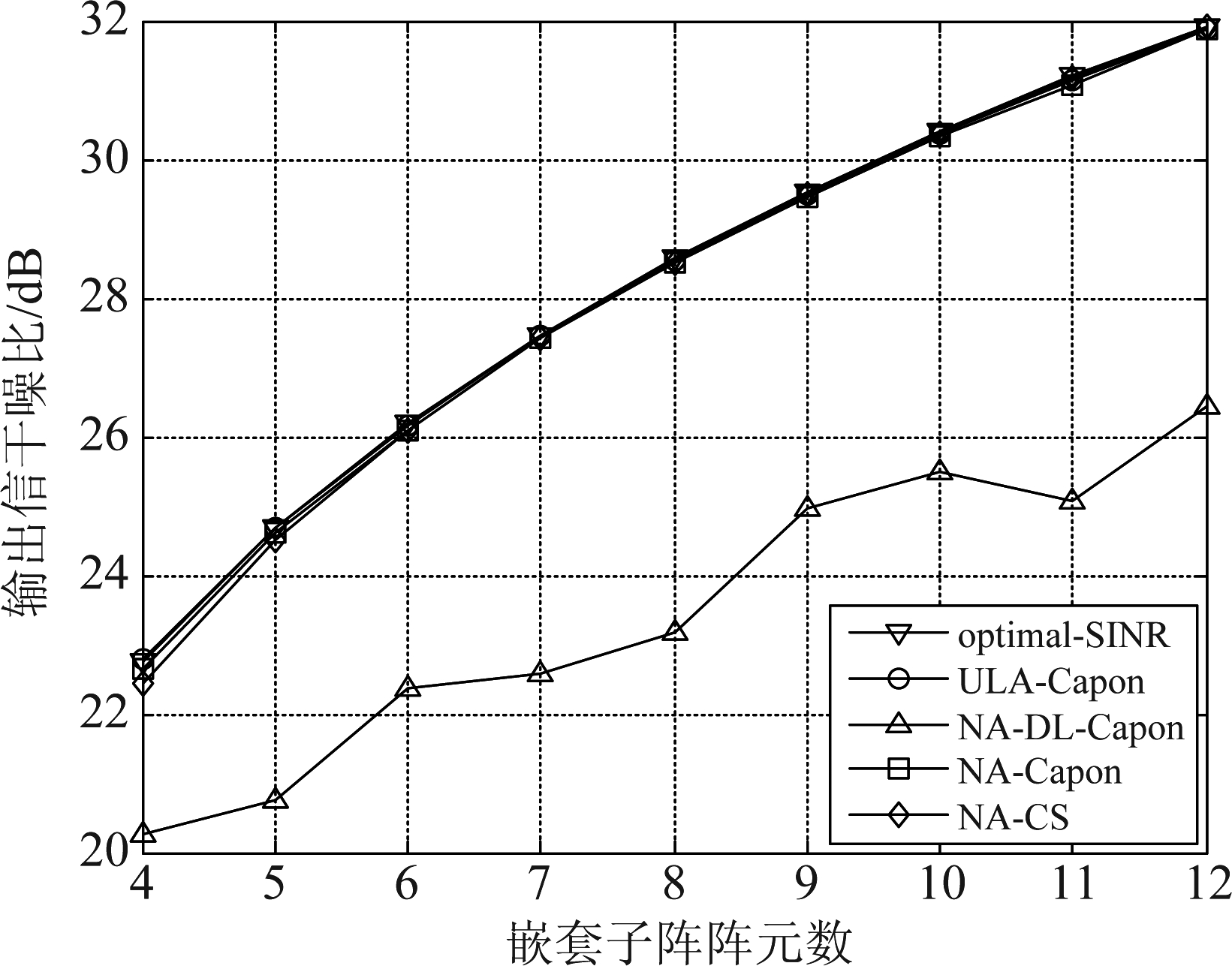
图7 输出信干噪比与嵌套子阵阵元数的关系
Fig.7 Relationship between output signal-to-interference and noise ratio and the number of nested sub-array elements
从仿真结果中可以看出,随着子阵阵元数的增加,采用Capon算法得到的输出信干噪比相较于等效均匀阵列有明显降低,误差较大。而采用对角加载Capon算法和压缩感知算法的结果与等效均匀阵列基本一致。
综合以上两组仿真可知,针对稀疏阵列转换至虚拟域阵列的阵列接收模型,采用传统的Capon算法进行方位估计,不仅在估计方位上存在误差,更大的缺陷体现在对信源功率的估计上。对角加载的方法可以在一定程度上减小误差,但改善能力有限。与之相比,稀疏阵列压缩感知算法在方位和功率的估计上都有着更高的准确度。
5.3 波束图性能仿真分析
仿真条件:
入射信号个数K=11,入射角度以10°为间隔,分别位于(-50°,-10°)和(10°,60°)之间,其中10°方向的信号为目标信号,其余方向视作干扰。目标与干扰,干扰与干扰之间统计独立,信噪比和干噪比为10 dB,快拍数为10000。嵌套阵列的内层和外层的阵元数相等,M1=M2=5。阵元总数为10。等效均匀线阵阵元数为M1(M2+1)=30,阵元间距为半波长。仿真次数50次。仿真结果如图8～图11。
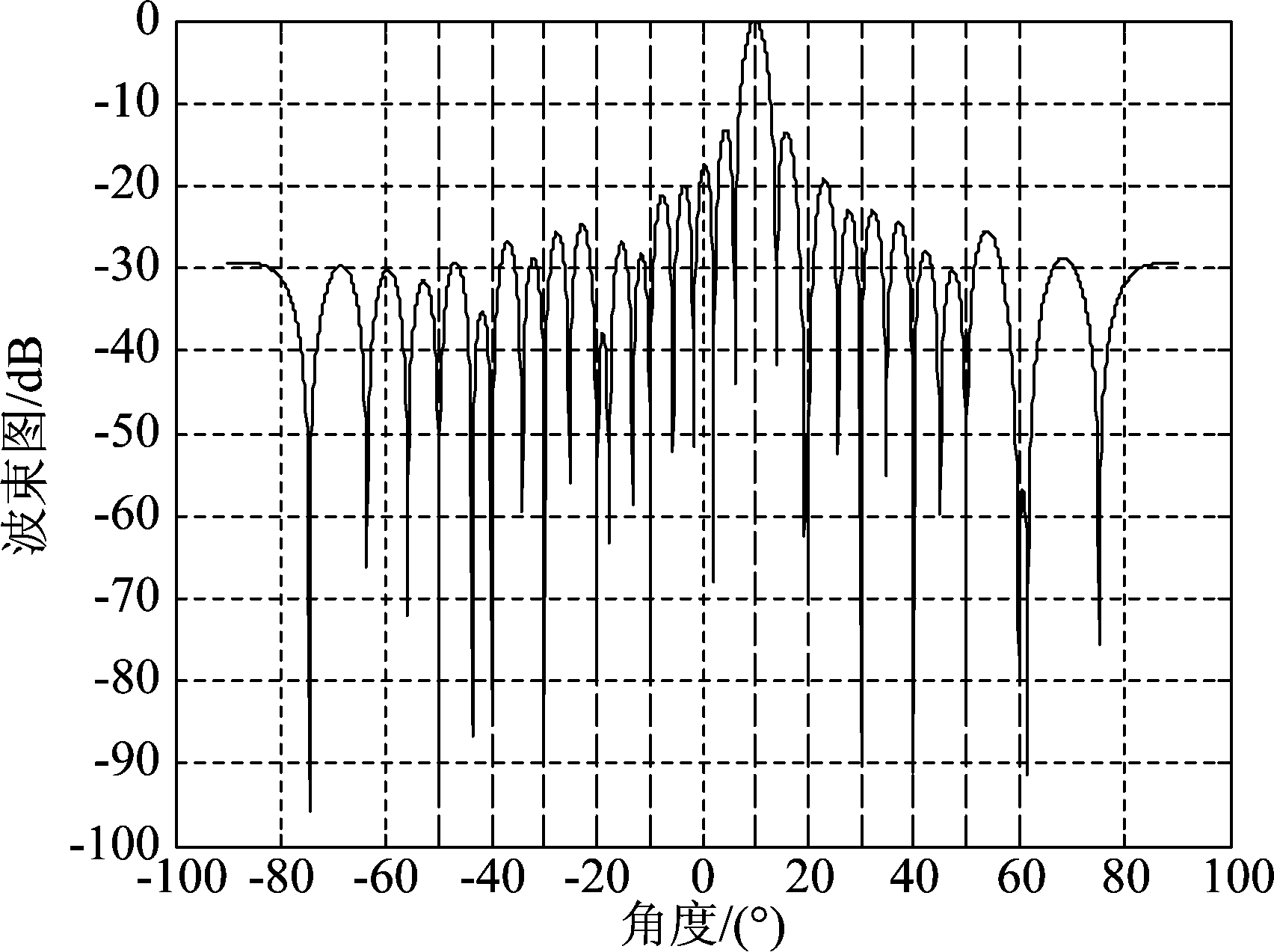
图8 ULA-Capon波束图
Fig.8 ULA-Capon beam pattern
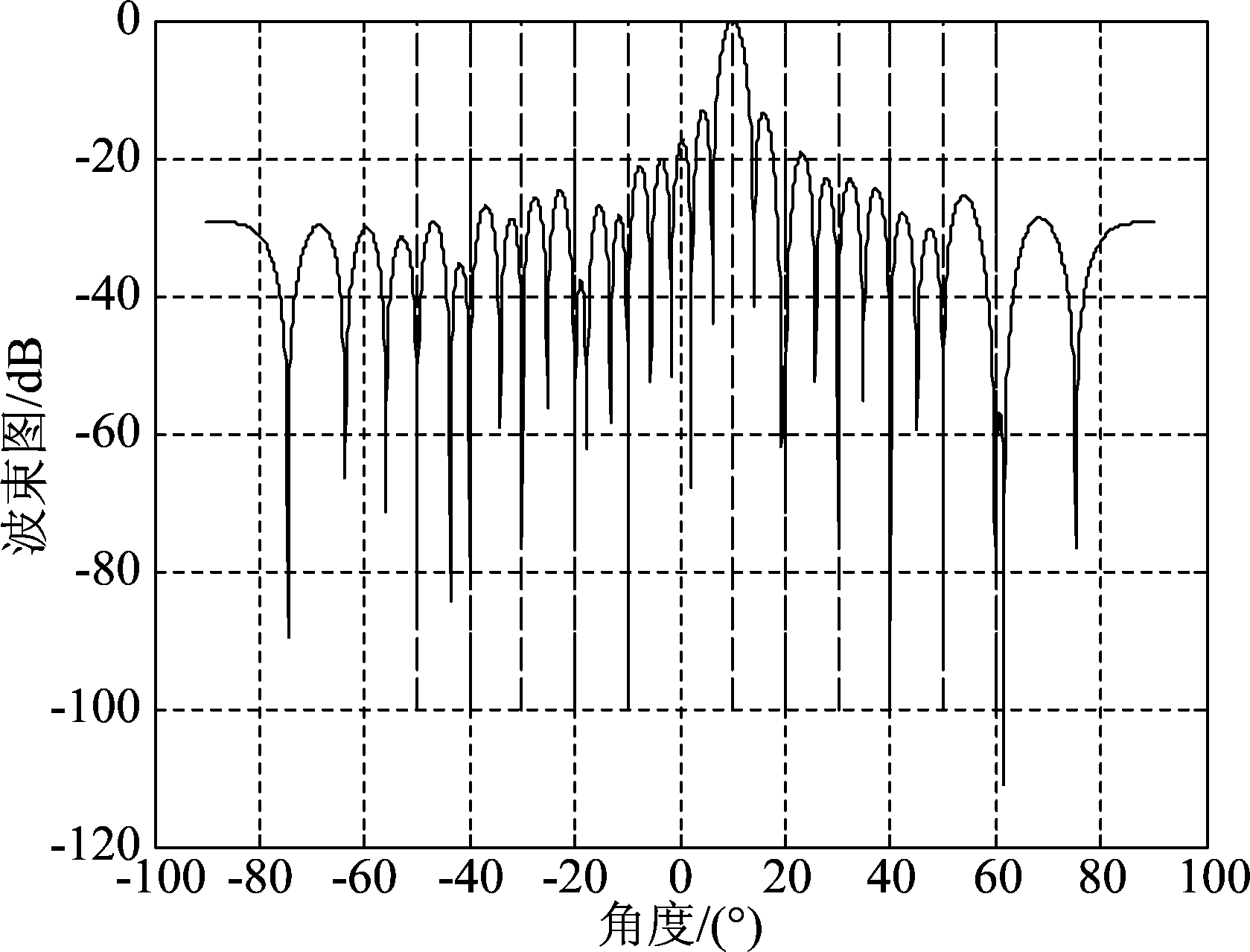
图9 NA-DL-Capon波束图
Fig.9 NA-DL-Capon beam pattern
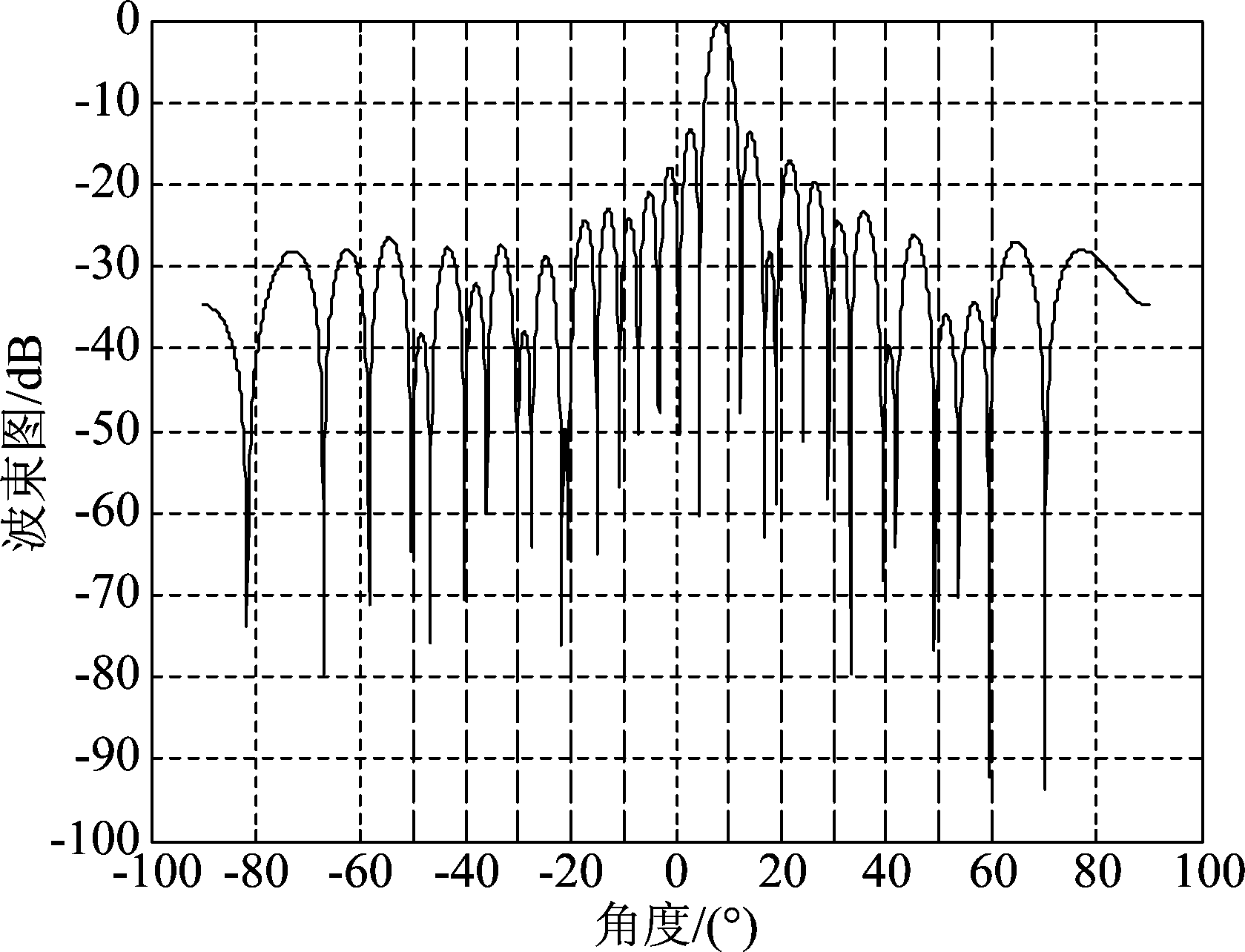
图10 NA-Capon波束图
Fig.10 NA-Capon beam pattern
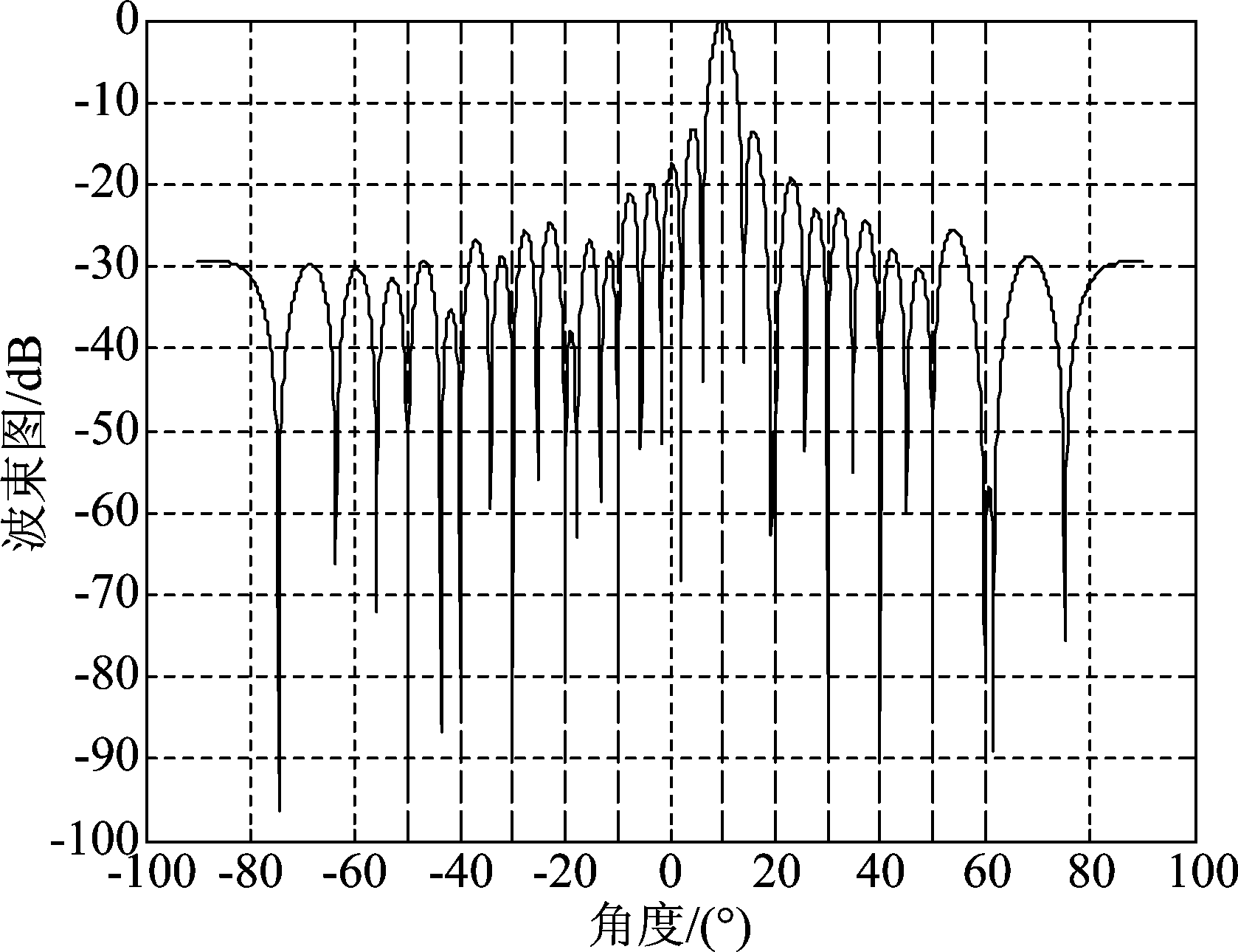
图11 NA-CS波束图
Fig.11 NA-CS beam pattern
从上述仿真结果可以看出,采用传统的Capon算法得到的波束图,主瓣方向存在一定的偏差,另外,在部分干扰出现的方位上并未出现零陷,可见效果并不理想;而经过对角加载后的Capon算法和压缩感知算法得到的波束图与等效均匀线阵的波束图基本重合,在目标方位形成了较窄的主瓣,干扰方位全部形成零陷,以阵元数较少的稀疏阵列达到了更高自由度下的波束形成器性能。
6 结论
本文将压缩感知算法应用于稀疏阵列中的方位估计,进而重构干扰噪声协方差矩阵,得到最优权向量。从理论上证明了压缩感知算法能够应用于稀疏阵列,并且能够较为准确地对空域信号的方位和功率进行估计。仿真结果表明,相较于其他方位估计算法,压缩感知算法具有更高的精确性和稳健性,设计得到的波束形成器性能也更为理想。针对toeplitz矩阵重构后得到的接收数据协方差矩阵存在误差的情况,尽管可以采用对角加载算法进行修正,但调节能力十分有限,并且还需要确定合适的对角加载因子,在算法步骤上相比压缩感知算法也更为繁琐。
[1] 鄢社锋. 优化阵列信号处理[M]. 北京: 科学出版社, 2018.
Yan Shefeng. Optimizing Array Signal Processing[M]. Beijing: Science Press, 2018.(in Chinese)
[2] 赵拥军, 李冬海, 赵闯, 等. 宽带阵列信号波达方向估计理论与方法[M]. 北京: 国防工业出版社, 2013: 1-2.
Zhao Yongjun, Li Donghai, Zhao Chuang, et al. Wideband Array Signal Direction of Arrive Estimation Theory and Methods[M]. Beijing: National Defence Industry Press, 2013: 1-2.(in Chinese)
[3] 干鹏. 非均匀阵列的信号处理算法研究[D]. 成都: 电子科技大学, 2018.
Gan Peng. Research on signal processing algorithms for non-uniform arrays[D]. Chengdu: University of Electronic Science and Technology of China, 2018.(in Chinese)
[4] Moffet A. Minimum-redundancy linear arrays[J]. IEEE Transactions on Antennas and Propagation, 1968, 16(2): 172-175.
[5] 李道京, 侯颖妮, 滕秀敏, 等. 稀疏阵列天线雷达技术及其应用[M]. 北京: 科学出版社, 2014: 12-13.
Li Daojing, Hou Yingni, Teng Xiumin, et al. Sparse array antenna radar technology and its application[M]. Beijing: Science Press, 2014: 12-13.(in Chinese)
[6] Pal P. New Directions In Sparse Sampling and Estimation For Underdetermined Systems[D]. Pasadena, California: California Institute of Technology, 2013.
[7] Pal P, Vaidyanathan P P. Nested arrays: a novel approach to array processing with enhanced degrees of freedom[J]. IEEE Transactions on Signal Processing, 2010, 58(8): 4167- 4181.
[8] Vaidyanathan P P, Pal P. Sparse Sensing With Co-prime Samplers and Arrays[J]. IEEE Transactions on Signal Processing, 2011, 59(2): 573-586.
[9] Qin S, Zhang Y D, Amin M. Generalized Coprime Array Configurations for Direction-of Arrival Estimation[J]. IEEE Transactions on Signal Processing, 2015, 63(6): 1377-1390.
[10] Yang M, Sun L, Yuan X, et al. Improved nested array with hole-free DCA and more degrees of freedom[J]. Electronics Letters, 2016, 52(25): 2068-2070.
[11] Liu C L, Vaidyanathan P P. Super Nested Arrays: Linear Sparse Arrays With Reduced Mutual Coupling—Part I: Fundamentals[J]. IEEE Transactions on Signal Processing, 2016, 64(15): 3997- 4012.
[12] 干鹏, 谢菊兰, 何子述. 基于互质思想的分子阵布阵方法[C]∥全国雷达学术年会, 成都, 2017.
Gan Peng, Xie Julan, He Zishu. Molecular array array method based on mutual quality thought[C]∥National Radar Academic Annual Meeting, Chengdu, 2017.(in Chinese)
[13] Adhikari K. Beamforming with semi-coprime arrays[J]. Journal of the Acoustical Society of America, 2019, 145: 2841-2850.
[14] Yu L, Wei Y, Liu W. A Novel Adaptive Beamforming Technique for Large-Scale Arrays[C]∥IEEE International Symposium on Signal Processing and Information Technology (ISSPIT), 2015.
[15] Yu L, Wei Y, Liu W. Adaptive Beamforming based on nonuniform linear arrays with enhanced degrees of freedom[C]∥IEEE Region 10 Conference, 2015.
[16] Zhou C, Shi Z, Gu Y. Coprime array adaptive beamforming with enhanced degrees-of freedom capability[C]∥In Proceeding of IEEE Radar Conference, 2017.
[17] Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.
[18] 王永良, 陈辉, 彭应宁, 等. 空间谱估计理论与算法[M]. 北京: 清华大学出版社, 2004: 99-105.
Wang Yongliang, Chen Hui, Peng Yingning, et al. Theory and Algorithm of Spatial Spectrum Estimation[M]. Beijing: Tsinghua University Press, 2004: 99-105.(in Chinese)
[19] CAND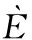
S E J, Emmanuel J. The restricted isometry property and its implications for compressed sensing[J]. Comptes Rendus Mathematique, 2008, 346(9-10): 589-592.
[20] Bilik I. Spatial compressive sensing for direction-of-arrival estimation of multiple sources Using dynamic sensor arrays[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(3): 1754-1769.
[21] Donoho D L, Elad M. Optimally sparse representation in general (nonorthogonal) dictionaries via l1 minimization[J]. Proceedings of the National Academy of Sciences, 2003, 100(5): 2197-2202.
[22] Gurbuz A C, Cevher V, McClellan J H. Bearing estimation via spatial sparsity using compressive sensing[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(2): 1358-1369.
[23] 包颜颜. 压缩感知重构问题的凸优化算法研究[D]. 西安: 西安电子科技大学, 2017.
Bao Yanyan. Research on convex optimization algorithm for compressed sensing reconstruction problem[D]. Xi’an: Xidian University, 2017.(in Chinese)
[24] Malioutov D, Çetin M, Willsky A S. A sparse signal reconstruction perspective for source localization with sensor arrays[J]. IEEE Transactions on Signal Processing, 2005, 53(8): 3010-3022.
[25] Zheng C, Li G, Zhang H, et al. An approach of DOA estimation using noise subspace weighted minimization[C]∥Acoustics, Speech and Signal Processing (ICASSP), 2011 IEEE International Conference on. IEEE, 2011: 2856-2859.
[26] Xu X, Wei X, Ye Z. DOA Estimation Based on Sparse Signal Recovery Utilizing Weighted l-Norm Penalty[J]. IEEE Signal Processing Letters, 2012, 19(3): 155-158.
[27] CANDS E J, TAO T. Near-optimal signal recovery from random projections: universal encoding strategies[J]. IEEE Transactions on Information Theory, 2006, Theory, 2006, 52(12): 5406-5425.
[28] Liu C L, Vaidyanathan P P. Remarks on the Spatial Smoothing Step in Coarray MUSIC[J]. IEEE Signal Processing Letters, 2015, 22(9): 1438-1442.
