1 引言
合成孔径雷达 (Synthetic Aperture Radar,SAR),是一种利用合成孔径原理的主动式微波成像传感器[1]。其成像具备全天时、全天候、高分辨、大幅宽等多种特点,有一定的地表穿透能力,在灾害监测、环境监测、海洋监测、资源勘查、农作物估产、测绘和军事等方面的应用上具有独特的优势,因此越来越受到世界各国的重视。但是,由于SAR图像的成像原理,相干斑的形成是它的固有特征,相干斑的存在严重地影响了SAR图像的能解译度,进而影响了后续的图像处理和应用[2]。
研究表明,相干斑噪声的特性是SAR图像固有的乘性噪声[3]。目前相干斑的抑制主要的方法有三大类,第一类是基于空域的方法,以Lee算法,Kuan算法和Frost算法以及各种增强算法为代表[4-5];第二类是基于变换域的方法,如基于小波变换的滤波算法和基于轮廓变换的滤波算法等[6-10];第三类是基于稀疏表示的方法,如基于超完备字典的K-SVD算法等[11]。这些算法大部分都能一定程度地滤除相干斑噪声,并能相对保留边缘和目标特征,但是传统的这些方案也各有其缺点。例如Lee及其增强算法主要通过边缘检测再对像素进行处理,因此仅对有边缘存在的区域滤波效果明显。Kuan及其增强算法在非平稳均值和非平稳方差图像模型上及加性噪声的图像上运用良好。Frost算法及其增强算法则是在假设SAR图像是平稳过程的基础上导出的具有最小均方误差的滤波算法,因此边缘保持能力较差。基于小波变换的阈值去噪算法其抑制噪声能力则主要取决于阈值函数以及噪声估计,另外相对边缘和细节保持能力较差。基于非下采样轮廓波变换的阈值去噪算法虽然克服了小波变换的缺点,对边缘信息和纹理信息的捕捉能力增强,却会导致伪边缘和块效应的出现。K-SVD算法明确指出了信号的稀疏性,但是却忽略了图像的非局部信息。
近几年,低秩矩阵表示(Low-Rank Matrix Representation,LRR)被广泛地用于图像处理,例如图像修复,超分辨率恢复,以及运动目标检测等[12-15]。一副自然清晰的图像其数据往往是低秩的或者是近似低秩的,如果秩比较高,往往说明图像中的噪声比较严重。即一幅含噪图像可以分解为低秩部分和稀疏部分,而图像中的大部分噪声包含在其稀疏部分。利用低秩稀疏分解可以将含噪图像分解为低秩恢复部分以及稀疏噪声部分[16]。在图像分解之后,需对图像的稀疏噪声部分采用合适的去噪方法。通常的图像去噪方法仅考虑图像的局部灰度分布,忽略了图像的结构分布,易导致图像边缘的过平滑问题[17]。而基于图像块的非局部均值滤波则能改善上述过平滑问题,它通过计算基于图像块之间结构相似性的权重系数,引入较多有效像素参与系数估计,建立加权均值模型,以避免平均加权造成的过平滑现象。但传统的非局部均值滤波选择固定的衰减因子,其值的过大或者过小都会影响图像的去噪效果。有学者提出利用图像的变差系数(Coefficient Variation,CV)自适应生成衰减因子,取得了一定的效果[18]。变差系数的优势在于不需要考虑数据的平均值,利用数据的标准差和平均值的比值来衡量数据的离散程度,从而选择不同的衰减程度,缺点在于当数据平均值较小时,微小的扰动也会对变差系数产生巨大影响,数据均值较大时,大变差系数会引起小衰减因子,因此对低灰度区域去噪性能不稳定,对高灰度区域则可能噪声残留严重。相比之下,结构张量(Structure Tensor, ST)模型能更准确地刻画图像边缘、特征结构和平滑区域,可以利用图像的方向场信息和局部几何结构,进行图像结构和细节特征描述。
在进行低秩稀疏分解之后,可以很好的将噪声分离出来,此时利用基于结构张量的非局部平均算法能充分考虑图像的方向场特征和局部几何结构,在抑制噪声的同时能够较好地保持边缘及其他重要特征,因此本文提出了基于低秩分解和改进的非局部平均的SAR图像相干斑抑制方法。
2 基于低秩分解和改进的非局部平均的SAR图像相干斑抑制原理
算法首先对输入含相干斑噪声的SAR图像进行对数处理,使得乘性噪声转换为加性噪声;接着基于增广拉格朗日准则将对数图像进行低秩稀疏分解;然后利用非局部平均滤波(NLM,Non-Local Means)对分解出的稀疏部分进行处理,保留图像的残留成分;结合低秩部分和滤波后的稀疏部分,恢复图像。算法框架如图1所示。
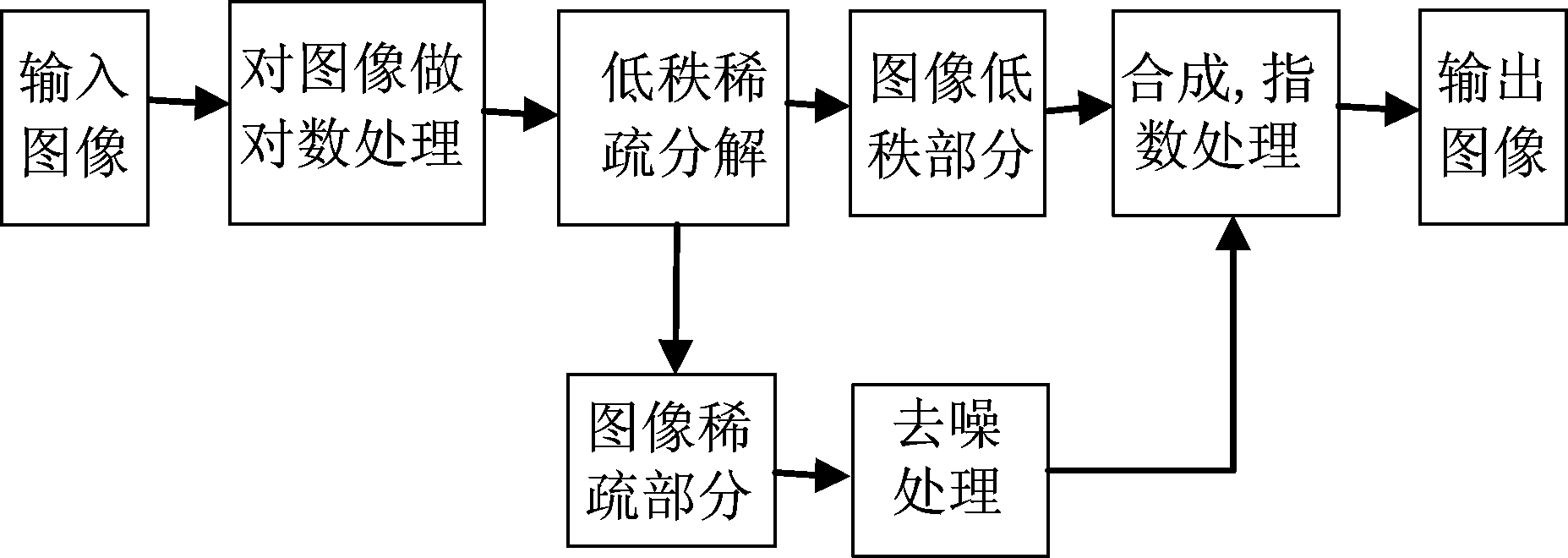
图1 算法框架
Fig.1 Algorithm framework
2.1 低秩稀疏分解原理
设Y表示原始SAR图像,由其成像原理决定SAR图像的相干斑噪声是乘性噪声,即有Y=N·I,其中N表示为乘性噪声,I为不含噪图像。首先对图像进行对数运算,lnY=lnN+lnI,将乘性噪声转换为加性噪声。
图像的低秩分解问题,设取对数的图像为M=lnY,将M分解为低秩部分A和稀疏部分E,即M=A+E,其中M∈Rm×n,低秩部分A∈Rm×n,rank(A)≤min (m,n),稀疏部分E∈Rm×n,其优化问题描述为:
(1)
其中,![]() 表示E矩阵的零范数,即E矩阵中非零元素的个数,λ是平衡因子,用来平衡矩阵的低秩性和稀疏性,这是个NP-hard问题,可以转换为如下凸优化问题的求解:
表示E矩阵的零范数,即E矩阵中非零元素的个数,λ是平衡因子,用来平衡矩阵的低秩性和稀疏性,这是个NP-hard问题,可以转换为如下凸优化问题的求解:
(2)
其中,![]() 表示E矩阵的1范数,即E矩阵的列元素绝对值之和,
表示E矩阵的1范数,即E矩阵的列元素绝对值之和,![]() 则表示A矩阵的核范数,即矩阵奇异值之和。
则表示A矩阵的核范数,即矩阵奇异值之和。
这个问题可以表示为增广拉格朗日问题:
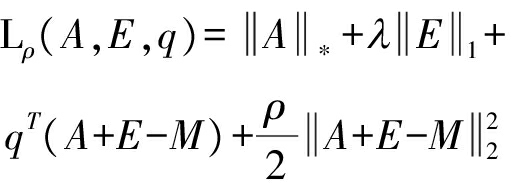
(3)
其中q为对偶变量,即将原来的约束求解min问题,转换为求对偶问题:![]()
求解这类问题的有效的方法是交替方向乘子法(Alternating Direction Method of Multipliers,ADMM)[19],该方法通过结合乘子法的弱条件的收敛性以及对偶上升法的可分解性对上述问题进行求解,固定其中两个变量,更新其中一个变量。
Step 3 qk+1=qk+ρ(Ak+1+Ek+1-M)。
其优化条件和停止准则:
原始残差:rk+1=Ak+1+Ek+1-M<∈primal;
对偶残差:sk+1=ρ(Ek+1-Ek)<∈dual。
经过低秩稀疏分解后,原始SAR图像被分解为低秩部分和稀疏部分,如图2所示。其中,原始图像像素为128*128,秩为97,经分解后,低秩图像部分秩为37,稀疏图像部分的零元素的个数为7390。

图2 对原始SAR图像进行低秩稀疏分解
Fig.2 Low-rank sparse decomposition of the SAR image
2.2 经典非局部平均滤波原理
非局部平均滤波由Baudes提出[20],通过估计非局部搜索窗内每个像素与中心像素在相似窗内的相似程度,以此作为权值对每个像素进行加权平均得到去噪后的图像。经过低秩稀疏分解后,大部分图像的冗余信息落在图像的稀疏成分,即噪声主要在图像的稀疏部分,利用非局部均值滤波对稀疏部分进行滤波处理。
假设一幅含噪图像表示为N={N(i)|i∈I},I表示整个图像范围,则对像素i,其输出值为:
No(i)=∑j∈Q(i)w(i, j)n(j)
(4)
其中,Q(i)表示以像素i为中心的大尺度搜索区域,w(i, j)为权重系数,它取决于像素i和像素j的相似程度。权重系数w(i, j)的定义为:
(5)
式中,![]() 为高斯加权欧氏距离,σ为高斯核标准差,h为滤波衰减参数,Z(i)为正则化因子,可以表示为:
为高斯加权欧氏距离,σ为高斯核标准差,h为滤波衰减参数,Z(i)为正则化因子,可以表示为:
(6)
其中,Pi和Pj分别表示以i和j为中心的小尺度相似窗,ν(Pi)和ν(Pj)则表示在相似窗内的图像观测值向量。
经典NLM算法因为采用了大尺度搜索窗来进行加权滤波,在噪声处理中,引入了较多有效像素参与权重系数的估计和平滑处理,从而达到了更好的噪声抑制和细节保留的效果。但是注意到,其采用常数h来控制负指数函数下降的速率,也因此控制图像滤波程度,当h过小时,可能导致残留的噪声严重,而h过大又会大量地损失边缘和纹理细节。
文献[18]提出了基于变差系数的NLM算法,则将h由变差系数CV自适应生成。文献中令自适应衰减因子为:![]() 其中h为指定常数,CVm、CVs和CVj分别表示图像的最大变差系数,最小变差系数以及对应j像素的变差系数,对去噪图像的边缘保留起到了较好的效果,但是在图像内部相似区域,会有较明显的噪声残留。
其中h为指定常数,CVm、CVs和CVj分别表示图像的最大变差系数,最小变差系数以及对应j像素的变差系数,对去噪图像的边缘保留起到了较好的效果,但是在图像内部相似区域,会有较明显的噪声残留。
为了在去除噪声的同时,能更好的保持边缘和纹理细节等特征,需要一个能更准确、精细地刻画图像边缘、特征结构和平坦区域的描述模型。结构张量模型能很好的解决这一问题,它能用来估计图像的方向场和分析图像的内部几何结构,结合其能量和特征的情况可以区分图像的不同结构,如边缘,纹理细节和平坦区域。因此,本文提出了NL-EST算法,即基于图像结构张量的能量(Energy of Structure Tensor,EST)的非局部平均的抑制相干斑算法。
2.3 改进的非局部平均滤波原理
对含噪图像N={N(i)|i∈I}中的每一个像素i,构建其结构张量矩阵:
(7)
其中,Nx和Ny分别代表像素i在x方向和y方向上的梯度。
结构张量的本质是把原来图像的梯度关系映射为新的结构关系,图像中的每个点都对应着一个张量矩阵。结构张量矩阵的迹表示结构的能量,而矩阵的两个特征值的差则代表了方向的一致性。如图3所示,(a)为图2中 SAR图像的稀疏图像部分的结构张量矩阵的能量图像,(b)、(c)和(d)则表示根据能量图像得到的图像的平坦部分、边缘纹理部分和角点部分的二值图像,其中图(b)、图(c)和图(d)中的灰度1分别代表图像的平坦部分、边缘和纹理部分和角点部分。

图3 结构张量的能量图以及分解
Fig.3 Energy image of structure tensor and decomposition images
令:
JE(i)=tr(J(i))
(8)
当JE(i)较小时,代表了图像的内部平坦区域,此时需要取较大的h来去除噪声。当JE(i)较大时,假设结构张量矩阵的特征根分别为λi1和λi2,且λi1≫λi2或者λi1≪λi2时,表示一个方向上图像灰度变化率较大,另一个方向则比较小,表明图像有明显的边缘和纹理结构特征。当JE(i)较大时,且λi1和λi2均比较大且近似相等时,表示图像在两个互相垂直的方向上灰度值都有较快的变化,表明在这个位置为图像的角点。在图像边缘纹理以及角点位置均需要取较小的h来保持边缘和细节部分。因此取自适应的衰减系数h为:
h=μ/JE(i)
(9)
式中μ为调节因子,由图像的均值确定。
本文的滤波过程算法如下:
Step 1 对于稀疏图像E中的任意像素i,选取以像素i为中心的搜索窗集合Q(i);
Step 2 选取Q(i)内像素i与其他像素j的小尺度相似窗Pi和Pj,计算权重系数w(i, j);
Step 3 对稀疏图像E的每个像素构造结构张量矩阵,得到其张量矩阵的能量图像,估计衰减因子h;
Step 4 根据各像素灰度值和对应加权系数,得到像素i的滤波估计值No(i)。
3 实验结果
为了客观评价本文算法的有效性,选取了两个真实的SAR图像进行实验比较,如图4所示,左侧图像是一幅MiniSar海湾图像的一部分,右侧图像来自MSTAR数据库。实验过程分别采用BM3D算法,经典NLM算法,NL-CV算法、NL-EST算法、LR-NL-CV算法、LR-NL-EST和本文算法,实验结果如图5所示。从视觉效果和参数评价来判别噪声抑制的性能优劣,评价参数采用SAR图像相干斑噪声的常规评价参数:等效视数(Equivalent Number of Looks,ENL)和边缘保持指数(Edge Preservation Index,EPI),其中等效视数表示相干斑的去除能力,其值越大表示相干斑抑制程度越好,而边缘保持指数则表示图像的边缘和细节保持能力,取值在[0,1]之间,其值越大表示边缘和细节的保持能力越好。

图4 原始真实SAR图像
Fig.4 Two real SAR images
实验中,对两幅图像进行噪声处理时,均多次实验采用最好的去噪性能参数。从各算法抑制噪声的结果对比,BM3D算法的抑制噪声效果较好,但在去噪图像中出现了振铃现象;经典NLM算法去噪效果较好,但细节保持不佳,去噪后的图像中出现了部分块状区域;NL-CV算法在相似图像区域会出现部分虚假细节;NL-EST算法则较NL-CV算法相比虚假细节相对较少;LR-NL-CV算法则相比NL-CV算法在相似区域有了改善;而经本文算法去噪后的图像不仅保持了低灰度相似区域的细节特征,同时图像内部去噪更加彻底,边缘细节保持更好,虚假细节也更少。
表1中ENL为等效视数,EPI_H,EPI_V分别表示水平边缘保持指数和垂直边缘保持指数。观察实验结果数据,比较各算法的等效视数数据,本文算法得到的结果最大,即相干斑噪声抑制效果最好;比较边缘保持指数数据,本文算法也体现了良好的参数特性,因此,本文算法对SAR图像的相干斑噪声抑制在视觉效果上和参数指标上均优于实验中的其余算法。

图5 六种算法对图4两幅真实SAR图像的噪声抑制效果对比
Fig.5 Comparison of despeckling effects of six algorithms on two real SAR images
表1 不同方法的评价指标比较表
Tab.1 Comparison of evaluation indexes
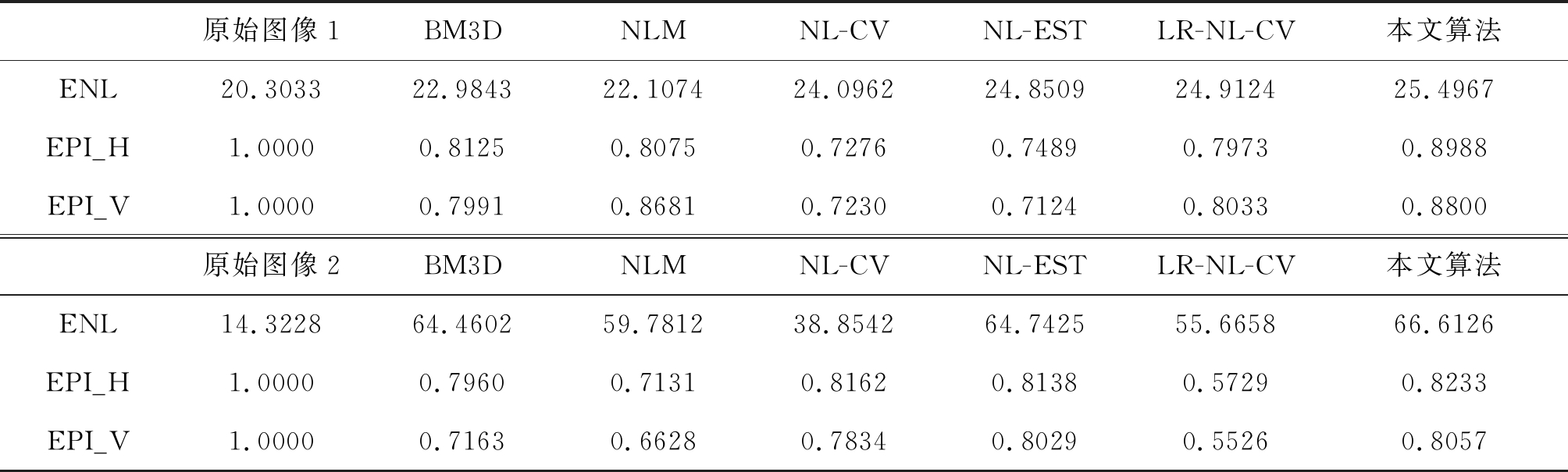
原始图像1BM3DNLMNL-CVNL-ESTLR-NL-CV本文算法ENL20.303322.984322.107424.096224.850924.912425.4967EPI_H1.00000.81250.80750.72760.74890.79730.8988EPI_V1.00000.79910.86810.72300.71240.80330.8800原始图像2BM3DNLMNL-CVNL-ESTLR-NL-CV本文算法ENL14.322864.460259.7812 38.854264.742555.665866.6126EPI_H1.00000.79600.71310.81620.81380.57290.8233EPI_V1.00000.71630.66280.78340.80290.55260.8057
4 结论
本文将低秩分解和基于结构张量能量的NLM滤波算法用于SAR图像的相干斑噪声的抑制,首先充分利用低秩分解时低秩矩阵部分对图像清晰信息的保留和稀疏矩阵部分持有噪声的特征,对含噪图像进行信噪分离。然后,利用结构张量的能量对图像平坦区域和边缘纹理等细节的精细的区分能力建立NLM滤波的自适应衰减因子,用改进的NLM滤波算法对图像进行相干斑噪声抑制。实验结果表明,该算法能在提高等效视数的同时保持和提高边缘保持指数,即该算法具有既能较好的抑制噪声和保护了边缘纹理等细节信息的能力。
[1] 邢相薇. SAR图像舰船目标检测方法研究[D]. 长沙: 国防科技大学, 2009.
Xing Xiangwei. Study on The Methods of Ship Detection in SAR Image[D]. ChangSha: National University of Defense Technology, 2009.(in Chinese)
[2] Gao F, Xue X, Sun J, et al. A SAR Image Despeckling Method Based on Two-dimensional S Transform Shrinkage[J]. IEEE Transactions on Geoscience & Remote Sensing, 2016, 54(5): 3025-3034.
[3] Wang Y, Ainsworth T L, Lee J. On Characterizing High-Resolution SAR Imagery Using Kernel-Based Mixture Speckle Models[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(5): 968-972.
[4] 曲长文, 李智, 周强, 等. 基于改进Frost滤波的SAR图像斑噪抑制算法[J]. 火力与智慧控制, 2018, 43(11): 1962-1965.
Qu Changwen, Li Zhi, Zhou Qiang, et al. SAR Image Noise Suppression Based on Improved Frost Filtering Algorithm[J]. Fire Power and Intelligent Control, 2018, 43(11): 1962-1965.(in Chinese)
[5] 金凤来, 钟何平. 一种改进的合成孔径声呐图像 Lee 滤波算法[J]. 舰船电子工程, 2017, 37(3): 95-99.
Jin Fenglai, Zhong Heping. An Improved Lee Filter Algorithm For Synthetic Aperture Sonar[J]. Ship Electronics Engineering, 2017, 37(3): 95-99.(in Chinese)
[6] 丁海勇, 郭瑞瑞, 罗海滨. 顾及纹理信息的遥感图像NSCT域自适应阈值去噪[J]. 遥感技术与应用, 2017, 32(3): 435- 442.
Ding Haiyong, Guo Ruirui, Luo Haibin. Denoising of Remote Sensing Images Using Adaptive Threshold in NSCT Domain By Concerning Texture Information[J]. Remote Sensing Technology and Application, 2017, 32(3): 435- 442.(in Chinese)
[7] 武晓玥, 郭宝龙, 李雷达. 一种新的基于非下采样Contourlet变换的图像去噪方法[J]. 光电子·激光, 2009, 5(5): 657- 661.
Wu Xiaoyue, Guo Baolong, Li Leida. A New Image Denoising Method Based on the Nonsubsampled Contourlet Transform[J]. Journal of Optoelectronics·Laser, 2009, 5(5): 657- 661.(in Chinese)
[8] 吴良斌. SAR图像处理与目标识别[M]. 北京: 航空工业出版社, 2013: 193-231.
Wu Liangbin. SAR Image Processing and Target Recognition[M]. Beijing: Aviation Industry Press, 2013: 193-231.(in Chinese)
[9] 李艺珠, 沈汀. 非下采样小波域的四阶偏微分SAR 图像去噪[J]. 遥感信息, 2016, 31(6): 95-99.
Li Yizhu, Shen Ting. SAR Image Denoising Using Fourth-Order PDE Based on NSWT[J]. Remote Sensing Information, 2016, 31(6): 95-99.(in Chinese)
[10]Xu B, Cui Y, Li Z H, et al. Patch Ordering Based SAR Image Despeckling Via Transform-Domain Filtering[J]. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2015, 8(4): 1682-1695.
[11]让-吕克-斯塔克, 菲昂-穆尔塔格, 贾拉勒-法蒂里. 稀疏图像与信号处理: 小波, 曲波, 形态多样性[M]. 肖亮,张军,刘鹏飞,译.北京: 国防工业出版社, 2015: 147-177.
Jean-Luc Starck, Fionn Murtagh, Jalal M Fadili. Sparse Images and Signal Processing: Wavelet, Curvelets, Morphological Diversity[M]. Xiao Liang, Zhang Jun, Liu Pengfei, translate.Beijing: National Defense Industry Press, 2015: 147-177.(in Chinese)
[12]戴琼海. 多维信号处理: 快速变换、稀疏表示与低秩分析[M]. 北京: 清华大学出版社, 2016: 104-113.
Dai Qionghai. Multidimensional Signal Processing: Fast Transform, Sparse Representation, and Low Rank Analysis[M]. Beijing: Tsinghua University Press, 2016: 104-113.(in Chinese)
[13]庞姣, 张世琪, 刘帅奇. 基于非局部自适应字典的SAR图像迭代去噪算法[J]. 河北大学学报: 自然科学版, 2018, 38(3): 309-314.
Pang Jiao, Zhang Shiqi, Liu Shuaiqi. SAR Image Iterative Denoising Algorithm Based on Non-local Adaptive Dictionary[J]. Journal of Hebei University: Natural Science Edition, 2018, 38(3): 309-314.(in Chinese)
[14]刘春辉, 齐越, 丁文锐. 基于聚类字典学习和稀疏表示的SAR图像抑斑方法[J]. 系统工程与电子技术, 2017, 39(8): 1709-1715.
Liu Chunhui, Qi Yue, Ding Wenrui. SAR Despeckling Based on Clustering Dictionary Learning and Sparse Representation[J]. Systems Engineering and Electronic Technology, 2017, 39(8): 1709-1715.(in Chinese)
[15]张禹涵, 符颖, 杨智鹏, 等. 基于无噪图像块先验的MRI低秩分解去噪算法研究[J]. 成都信息工程大学学报, 2019, 34(3): 246-250.
Zhang Yuhan, Fu Ying, Yang Zhipeng, et al. Low Rank Decomposition For MRI Denoising Based on Noise-Free Image Patch Prior[J]. Journal of Cheng Du University of Information Engineering, 2019, 34(3): 246-250.(in Chinese)
[16]王辉, 孙洪. 低秩稀疏分解下多尺度积的运动目标检测方法[J]. 信号处理, 2016, 32(12): 1425-1433.
Wang Hui, Sun Hong. A Method of Low-rank Decomposition With Multi-scale Product For Moving Object Detection[J]. Journal of Signal Processing, 2016, 32(12): 1425-1433.(in Chinese)
[17]龙云淋, 吴一全, 周杨. 结合NSST和快速非局部均值滤波的刀具图像去噪[J]. 信号处理, 2017, 33(11): 1505-1514.
Long Yunlin, Wu Yiquan, Zhou Yang. Cutting Tool Image Denoising Based on NSST and Fast Non-Local Means Filter[J]. Journal of Signal Processing, 2017, 33(11): 1505-1514.(in Chinese)
[18]Chen S B, Hou J H, Zhang H, et al. Despeckling Method Based on Non-Local Means and Coefficient Variation of SAR Image[J]. Electronics Letters, 2014, 50(18): 1314-1316.
[19]Davidson M M, Marco T V, Tiziano T, et al. Simulation of Pollutant Dispersion in the Atmosphere by the Laplace Transform: The ADMM Approach[J]. Water Air and Soil Pollution, 2006, 4(4): 411- 439.
[20]Buades A, Coll B, Morel J M. A Non-Local Algorithm For Image Denoising[C]∥Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Piscataway, NJ, USA: IEEE, 2005: 60- 65.


