1 引言
空时自适应处理(Space-Time Adaptive Processing,STAP)技术同时利用空域和时域信息进行自适应处理,可有效抑制机载雷达面临的强地、海杂波,显著提高机载雷达在复杂地貌环境下的运动目标探测性能[1- 4]。经过四十多年的发展,STAP技术面临的非平稳、非均匀等问题已经得到了一定程度的解决[5-10],且已从理论研究走向实际工程应用,美国新型E-2D预警机雷达即采用了多通道STAP技术。但是,STAP技术应用的前提是雷达具有多个接收通道,同时雷达平台必须是运动的。以上两方面因素导致STAP技术应用于实际工程时,不可避免地会遇到各种空时误差的影响。空时误差一方面会导致机载雷达杂波回波信号的空时去相关,即杂波自由度增大;另一方面会导致STAP滤波器预设的目标空时导向矢量与真实的目标空时导向矢量失配。以上两方面因素使得STAP方法的杂波抑制性能存在一定程度的下降。因此,系统研究各种空时误差的特性及其对STAP方法性能的影响具有重要的工程应用意义。
文献[1]给出了时域误差的信号模型,并分析了其对杂波特征谱的影响;文献[2]通过计算机仿真分析了天线阵列误差对STAP方法杂波抑制性能的影响;文献[3]初步分析了角度无关的通道失配和角度相关的通道失配,并研究了空域误差对杂波秩的影响。目前,仅有的少量关于机载雷达空时误差的研究文献主要存在以下不足:(1)所建立的误差数学模型仅是针对某一特定类型的误差,缺乏系统性;(2)未对误差对杂波自由度影响的机理进行深入分析;(3)未研究目标导向矢量失配对STAP性能的影响。
针对上述问题,本文首先给出了各种空时误差的数学模型,并通过数学推导从理论上详细分析了误差对STAP方法性能影响的内在机理,然后以信杂噪比(Signal to Clutter plus Noise Ratio,SCNR)损失为指标分析了不同误差对STAP性能的影响,最后通过仿真实验进行了有效性验证。
2 空域误差信号模型
空域误差可根据是否与方位角相关分为与角度无关的误差和与角度相关的误差,其中前者主要是由天线阵元之后的通道间失配引起的,后者主要是由阵元位置误差、宽带色散和近场散射等因素引起的。一般情况下,空域误差均与脉冲数无关。
2.1 与角度无关的误差
波束形成天线阵列通道包含高频放大器、混频器、中频放大器等模拟器件以及A/D数模转换器件。以上器件的构成电路存在加工误差,即相同功能的模拟器件所构成的电路不可能做得完全相同,使得每个阵元的通道幅相特性较之于理想情况出现固定的偏差。此外,阵列天线单元之间存在互耦,不但影响天线的增益、波束宽度等参数,而且还会影响阵列接收信号的幅度和相位,加之模拟电路的状态不断变化,导致通道幅相特性也发生随机变化。以上通道不一致性可统一用幅相误差来描述,且可分为通道间固定的幅相误差和通道间随机的幅相误差。
本文中假设天线阵为正侧视均匀线阵,当不存在目标且无空时误差时某一距离环对应的空时回波信号可表示为
x=xc+xn
(1)
其中,
表示杂波信号,xn表示噪声信号,ai和si分别表示第i个杂波块的回波幅度和导向矢量,Nc表示该距离环包含的杂波块的数目。
与角度无关的幅相误差在脉冲间是固定不变的,因此误差矢量可表示为
e=et⊗es
(2)
其中,
(3)
es=(es,1,es,2,…,es,N)T
(4)
es的第n(n∈{1,2,…,N})个元素可表示为
es,n=(1+εn)ejφn
(5)
其中,εn和φn分别表示幅度误差和相位误差。
需要注意的是对于通道间固定的幅相误差,es不随距离而变化,且通常假设幅度误差服从高斯分布,相位误差服从均匀分布,即εn～N(0,ξ2),φn～U(-ζ,ζ)。而对于通道间随机的幅相误差,es随距离而变化,且εn～U(-ξ,ξ)。
存在误差时空时回波信号可表示为
(6)
对应的空时协方差矩阵可表示为
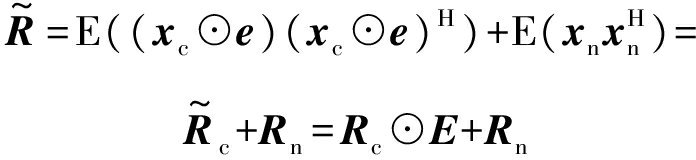
(7)
其中,Rc表示无误差时的杂波协方差矩阵,E=E(eeH)表示误差协方差矩阵。
因为通道间固定的幅相误差在距离间是固定不变的,所以E=E(eeH)=eeH,由此可知E的秩为1。而对于通道间随机的幅相误差,误差协方差矩阵可作如下分解
E=E(eeH)=E((et⊗es)(et⊗es)H) 
(8)
将
和
分别记为Et和Es,由于该误差与脉冲数无关,则上式可表示为
E=Et⊗Es=1K⊗Es
(9)
其中,1K是K维全1方阵,因此只需讨论Es的具体形式。根据εn和φn的分布模型可推得
的值为
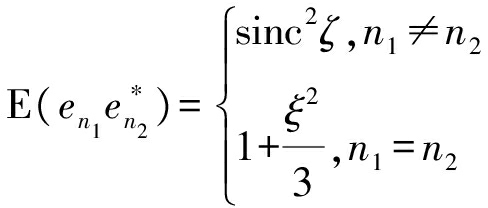
(10)
由上式可得
Es=A1N+BIN
(11)
其中,
表示N维全1方阵,IN表示N维单位矩阵。
由式(9)可得
E=1K⊗(A1N+BIN)
(12)
2.2 与角度相关的误差
阵元位置误差是一种典型的与角度相关的误差,由于阵元安装精度有限、天线热胀冷缩和机身机械抖动等因素,阵元位置误差是无法避免的。本节以该误差为例展开讨论。
阵元位置误差如图1所示,假设y轴为天线轴向。将不存在阵元位置误差时第n个阵元的位置记为(0,yn),则存在阵元位置误差时,第n个阵元的位置可记为
其中,
和Δyn分别表示第n个阵元的位置误差,且通常假设Δxn,Δyn～N(0,ξ2)。此时,第i个杂波块对应的空域导向矢量可表示为
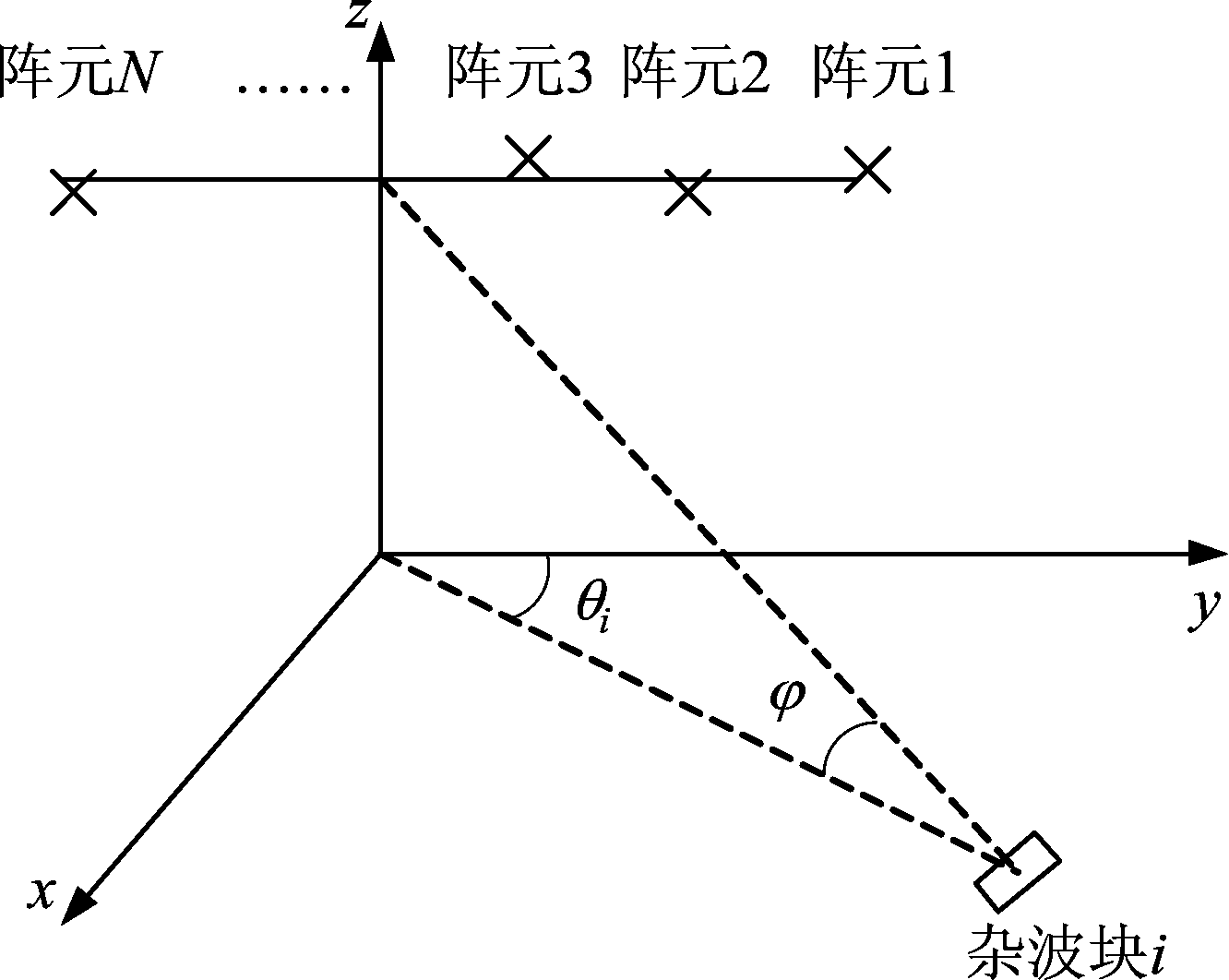
图1 阵元位置误差示意图
Fig.1 Schematic diagram of element position errors
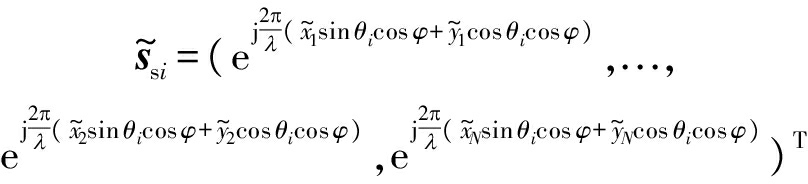
(13)
其中,θi和φ分别表示第i个杂波块对应的方位角和俯视角。设不存在阵元位置误差时的阵元间距为d,则yn=y1-(n-1)d,因此上式可变换为
(14)
其中,
(15)
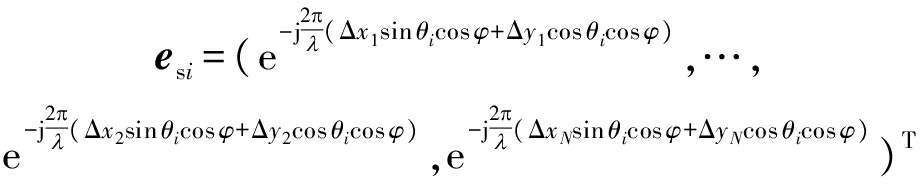
(16)
分别表示不存在阵元位置误差时的空域导向矢量和存在阵元位置误差时的空域位置误差矢量。
由于阵元位置误差与脉冲无关,因此根据式(16)可得空时位置误差矢量为
(17)
存在阵元位置误差时空时回波信号可表示为
(18)
其中,
和
分别表示存在阵元位置误差时第i个杂波块的回波幅度和空时导向矢量,si表示不存在阵元位置误差时第i个杂波块的空时导向矢量。
存在阵元位置误差时空时协方差矩阵可表示为
(19)
3 时域误差信号模型
时域误差主要来源于杂波内部运动,诸如植被和海浪等的随风运动。第i个杂波块对应的杂波内部运动矢量可表示为
(20)
其中,
eti=(eti,1,eti,2,…,eti,K)T
(21)
存在杂波内部运动时空时回波信号可表示为
(22)
对应的空时协方差矩阵可表示为
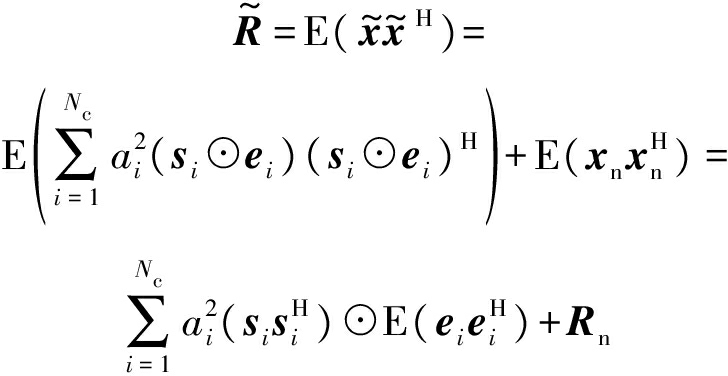
(23)
假设杂波内部运动在方位向是均匀的(即与杂波块无关),且不随距离而变化,则
可记为E。此时,上式可变换为
(24)
误差协方差矩阵E可作如下分解:
E=Et⊗1N
(25)
通常假设存在内部运动时的杂波频谱服从高斯分布。此时,Et(k1,k2)(k1,k2∈{1,2,…,K})的值可由下式给出
(26)
其中,σv表示杂波内部运动速度,Tr表示脉冲重复周期。由上式可以看出,Et是一个对称的Toeplitz矩阵。
4 误差影响分析
本节采用SCNR损失作为性能指标来分析误差对STAP性能的影响。为了便于分析,本节不考虑样本数对协方差矩阵估计的影响,即认为估计值为无偏估计,则SCNR损失可表示为
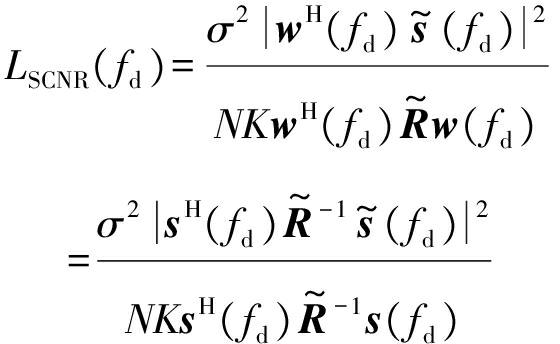
(27)
其中,σ2表示噪声功率,
和
分别表示存在误差时的目标空时导向矢量和杂波噪声协方差矩阵,
表示STAP权矢量,s(fd)表示预设的理想情况下的目标空时导向矢量。
由式(27)可知,误差导致的SCNR损失主要来源于两个方面:一方面是真实的目标导向矢量
与预设的目标导向矢量s(fd)之间的失配;另一方面是空时协方差矩阵特征空间(包括杂波子空间与噪声子空间)相对于理想的空时协方差矩阵特征空间的变化,主要表现为杂波特征值幅度的变化和杂波自由度的增大。
4.1 通道间固定的幅相误差
(1)目标导向矢量失配的影响
存在误差时的目标导向矢量
与不存在误差时的目标导向矢量s(fd)不一致,这种失配会增大SCNR损失。以清晰区为例,此时
其中,INK表示NK维单位矩阵。因此,式(27)可变换为
(28)
因为
所以LSCNR(fd)≤1。通常误差水平较小,目标导向矢量失配程度较小,即有
因此由目标导向矢量失配导致的SCNR损失也较小。
对于通道间随机的幅相误差和阵元位置误差,其由目标导向矢量失配导致的SCNR损失与通道间固定的幅相误差类似,因此后续不再进行讨论。
(2)杂波自由度增大的影响
首先讨论通道间固定的幅相误差对杂波秩,即杂波自由度的影响。对于任意相同维度的方阵A和方阵B,根据Hadamard乘积的性质可知rank(A⊙B)≤rank(A)rank(B),因此,
≤rank(Rc)rank(E)=rank(Rc)
(29)
由上式可知,通道间固定的幅相误差不会增加杂波自由度。
其次讨论通道间固定的幅相误差对杂波特征值幅度的影响。对于只存在相位误差的情况,即
es,n=ejφn
(30)
此时,空时协方差矩阵可分解为
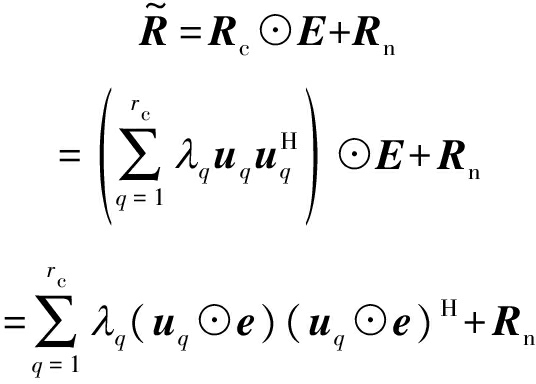
(31)
其中,rc表示杂波秩。因为特征矢量集{uq}中的矢量两两正交,且对于任意的q1,q2∈{1,2,…,rc}有
(uq1⊙e)H(uq2⊙e)= 
(32)
所以矢量集{uq⊙e}中的矢量也两两正交。由此可知,存在误差时的空时协方差矩阵和无误差时的空时协方差矩阵具有相同的特征值,且前者的特征矢量是后者的特征矢量与误差矢量的点乘。
对于同时存在幅度误差和相位误差的情况。此时,由于
式(32)不再成立。但实际上误差水平通常不大于5%,因此
此时的特征值和特征矢量相较于仅存在相位误差的情况会有轻微的变化。
根据上述分析,对于通道间固定的幅相误差,目标导向矢量失配程度较小,杂波自由度不变,杂波特征值变化幅度较小,因此,由其导致的SCNR损失较小。
4.2 通道间随机的幅相误差
存在通道间随机的幅相误差时,阵列接收到的第i个杂波块的回波信号可以表示为
(33)
其中,
=sti⊗(ssi⊙es)
(34)
时域导向矢量sti和空域导向矢量ssi可分别表示为
sti=(1,ejωti,…,ej(K-1)ωti)T
(35)
ssi=(1,ejωsi,…,ej(N-1)ωsi)T
(36)
其中,
(37)
(38)
分别表示时域角频率和空域角频率。
记
当α=1时,有ωti=ωsi,并将其简记为ωi。根据式(34)、式(35)和式(36)可得
(39)
其中,
U= 
(40)
V=(1,ejωi,ej 2ωi,…,ej(N+K-2)ωi)T
(41)
由上式可知,对于任意的
都可以由矩阵U的列矢量的线性组合来表示。为叙述方便,将与矩阵U同型的矩阵称为杂波基矩阵。如果e不随距离变化,则不同训练单元对应的杂波基矩阵是一致的。此时,不同训练单元不同方位的杂波信号均可由矩阵U的列矢量的线性组合来表示。矩阵U显然是列满秩的,因此可推得
=rank(U)=N+K-1
(42)
其中,
表示估计杂波协方差矩阵采用的第l个训练单元,L表示训练单元数。如果e随距离而变化,则不同训练单元对应的杂波基矩阵是不一致的。记第l个训练单元对应的杂波基矩阵为Ul,则不同训练单元不同方位的杂波信号均可由矩阵U1,U2,…,UL的所有列矢量的线性组合来表示。将由矩阵U1,U2,…,UL的所有线性无关列矢量组成的矩阵记为
则显然有
(43)
实际上,等号成立的概率近似为零。当α>1时,可用同样的方法进行分析,此处不再赘述。
根据上述分析可知,通道间随机的幅相误差会增加杂波自由度和杂波谱宽,在主瓣杂波区及其附近区域会导致明显的SCNR损失,而清晰区的SCNR损失主要来源于目标导向矢量失配,损失幅度较小。
4.3 阵元位置误差
阵元位置误差与其他误差不同的地方在于能够影响发射方向图,即能够改变发射信号功率在空间方位的分布。如果不考虑阵列加权,则存在阵元位置误差时的阵列发射方向图可表示为
(44)
其中,θ0和φ0分别表示主瓣方位角和俯视角。阵元位置误差会导致发射方向图出现起伏,主瓣指向随之会发生一定变化。实际上,阵元位置误差对发射方向图的影响最终表现为对杂波特征值幅度的影响。
至于阵元位置误差对杂波自由度的影响,同样可用4.2节的方法进行分析,需要注意的是此时的空域误差变成了阵元位置误差esi。esi与方位角有关,但不随距离变化,因此不同训练单元对应的杂波基矩阵是一致的。
根据上述分析可知,阵元位置误差不会增加杂波自由度和杂波谱宽,在主瓣杂波区及其附近区域会导致一定程度的SCNR损失。
4.4 杂波内部运动
对于杂波内部运动对杂波自由度的影响,依然可用4.2节的方法进行分析,杂波内部运动随距离变化,因此不同训练单元对应的杂波基矩阵是不一致的。记第l个训练单元对应的杂波基矩阵为Ul,则Ul可表示为
Ul=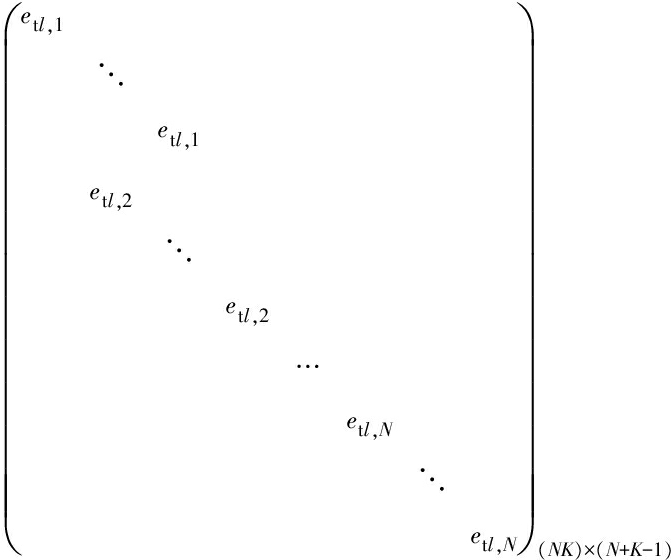 
(45)
不同训练单元不同方位的杂波信号可由矩阵U1,U1,…,UL的所有列矢量的线性组合来表示。将由矩阵U1,U1,…,UL的所有线性无关列矢量组成的矩阵记为
依然可推得式(43)。
根据上述分析可知,杂波内部运动会增加杂波自由度和杂波谱宽,在主瓣杂波区及其附近区域会导致明显的SCNR损失。杂波内部运动不会增大噪声功率,也不会导致目标导向矢量失配,因此,清晰区SCNR无损失。
5 仿真实验
仿真实验中设定杂波环的距离为150 km,阵元方向图为余弦方向图,合成子阵数为16,背面衰减系数为-10 dB。其他参数由表1给出。由给定的参数计算可得α=2,这意味着杂波占据了一半的脉冲重复频率范围,即存在清晰区。
表1 仿真参数
Tab.1 Simulation parameters
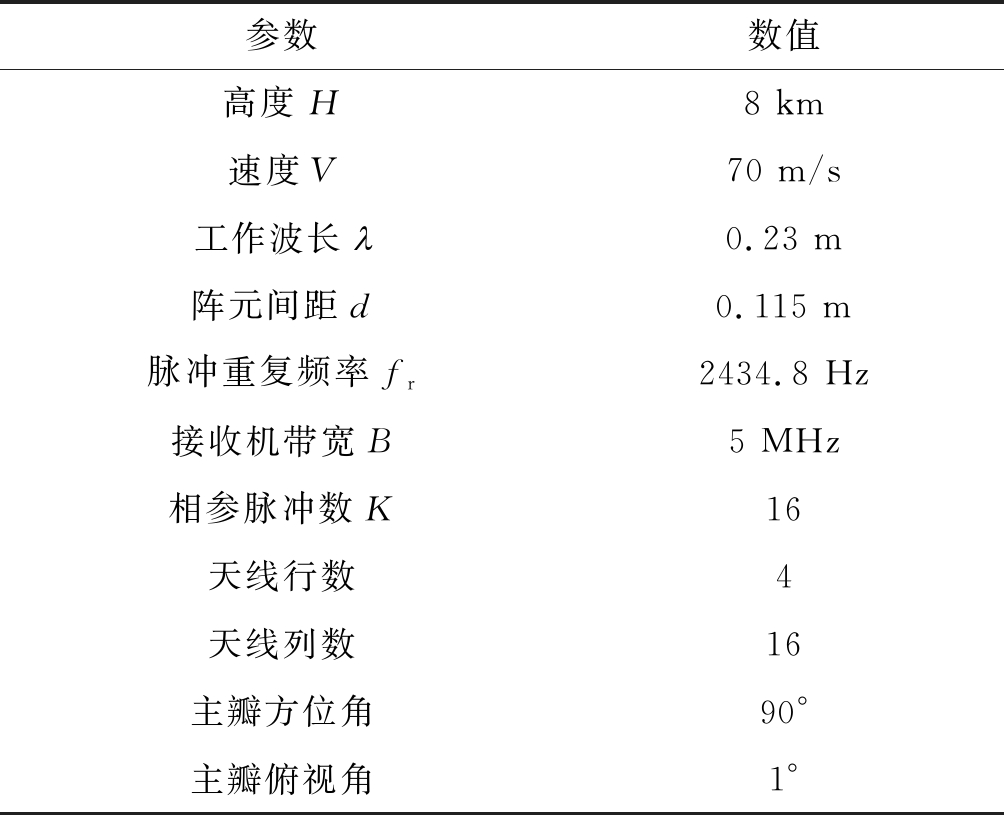
参数数值高度H8 km速度V70 m/s工作波长葜0.23 m阵元间距d0.115 m脉冲重复频率fr2434.8 Hz接收机带宽B5 MHz相参脉冲数K16天线行数4天线列数16主瓣方位角90°主瓣俯视角1°
由图2可以看出:(1)随着误差水平的升高,大特征值数不变,仅大特征值相对幅度有轻微变化,而小特征值无变化;(2)SCNR损失随着误差水平的升高而增大,但损失程度较小。例如当ξ=6%,ζ=3%时,清晰区(虚线内部区域为杂波区,两侧区域为清晰区)和副瓣杂波区的SCNR损失均小于2 dB。因此,通道间固定的幅相误差导致的SCNR损失程度较小。
由图3可以看出:(1)随着误差水平的升高,大特征值数明显增多;(2)SCNR损失随着误差水平的升高而增大,且清晰区和副瓣杂波区的损失程度均较大。例如当ξ=6%,ζ=3%, fd=±0.25时,副瓣杂波区的SCNR损失超过5 dB。因此,通道间随机的幅相误差导致的副瓣杂波区SCNR损失程度较大。
由图4可以看出:(1)随着误差水平的升高,大特征值数和小特征值相对幅度均没有明显变化;(2)SCNR损失随着误差水平的升高而增大,但损失程度较小。例如当ξ=6%时,清晰区和副瓣杂波区的SCNR损失均小于2 dB。因此,阵元位置误差导致的SCNR损失程度较小。
由图5可以看出:(1)随着误差水平的升高,大特征值数明显增多,小特征值相对幅度不变;(2)SCNR损失随着误差水平的升高而增大,损失程度较大,且主要局限于主瓣杂波区及其附近区域,而清晰区几乎无损失。此外,图3(b)和5(b)的仿真结果也反映了通道间随机的幅相误差和杂波内部运动会导致杂波谱在频域上存在一定程度的展宽。
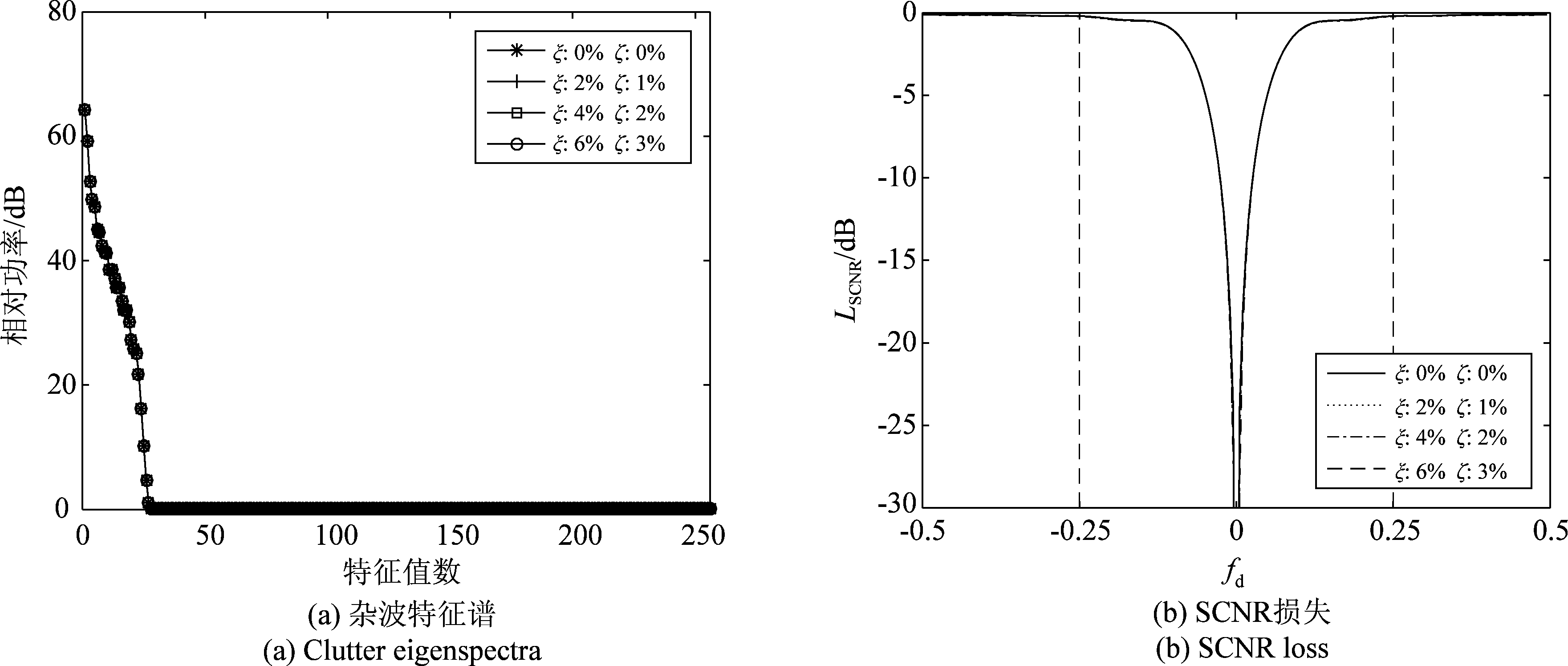
图2 通道间固定的幅相误差
Fig.2 Fixed amplitude and phase errors between channels
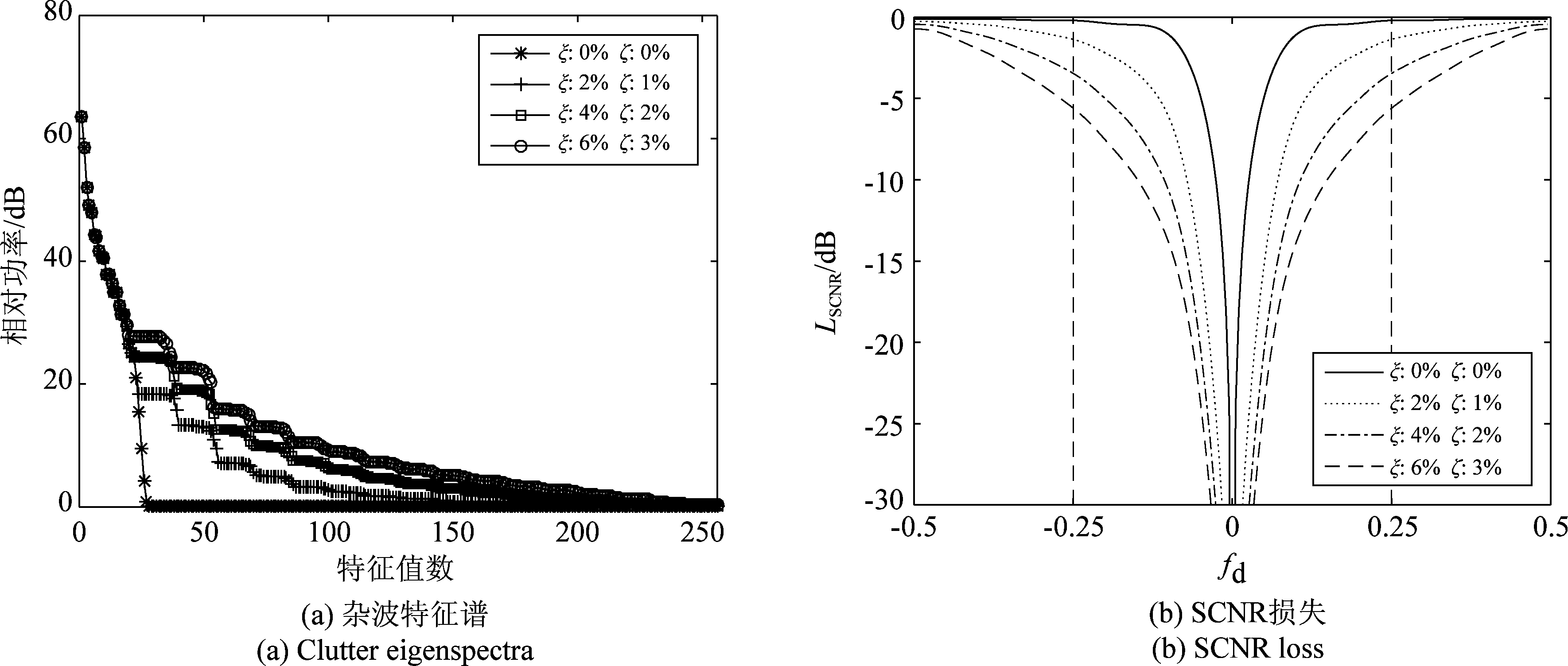
图3 通道间随机的幅相误差
Fig.3 Random amplitude and phase errors between channels
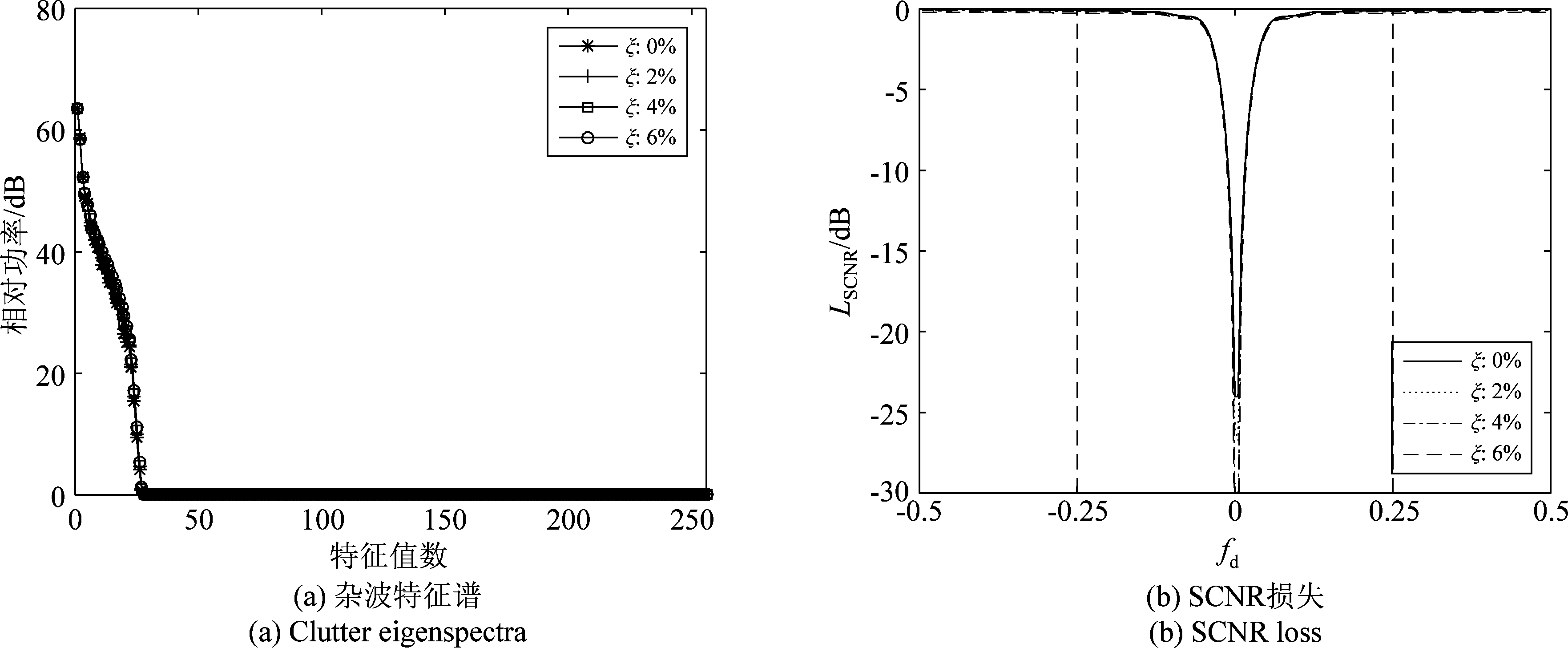
图4 阵元位置误差
Fig.4 Element position errors
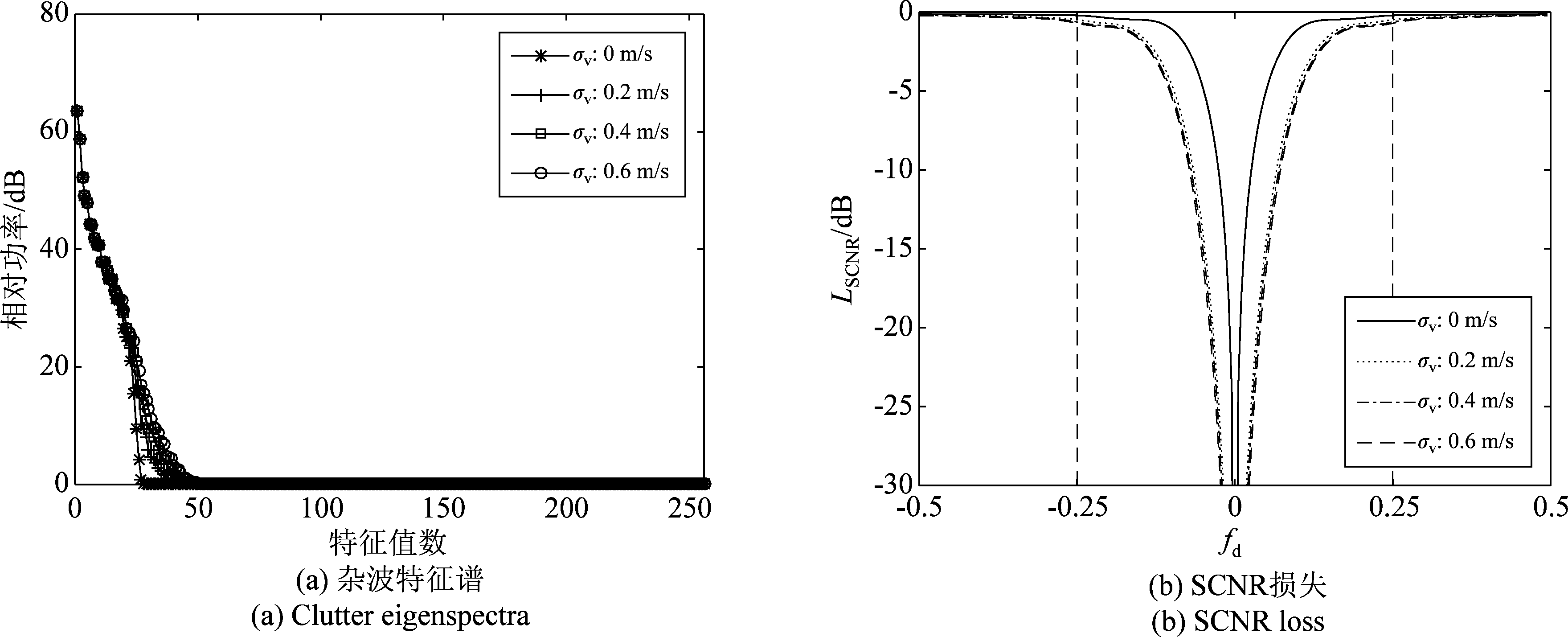
图5 杂波内部运动
Fig.5 Intrinsic clutter motion
表2 平均SCNR损失
Tab.2 Average SCNR loss
杂波分区通道间固定的幅相误差ξ=6%,ζ=3%通道间随机的幅相误差ξ=6%,ζ=3%阵元位置误差ξ=6%杂波内部运动σv=0.6 m/s清晰区0.25≤fd≤0.5-0.12 dB-2.64 dB-0.32 dB-0.34 dB副瓣杂波区0.15≤fd<0.25-0.33 dB-7.53 dB-0.54 dB-0.98 dB主瓣杂波区0.05≤fd<0.15-1.52 dB-14.51 dB-1.72 dB-6.2 dB
表3 误差影响总结Tab.3 Summary of error influences
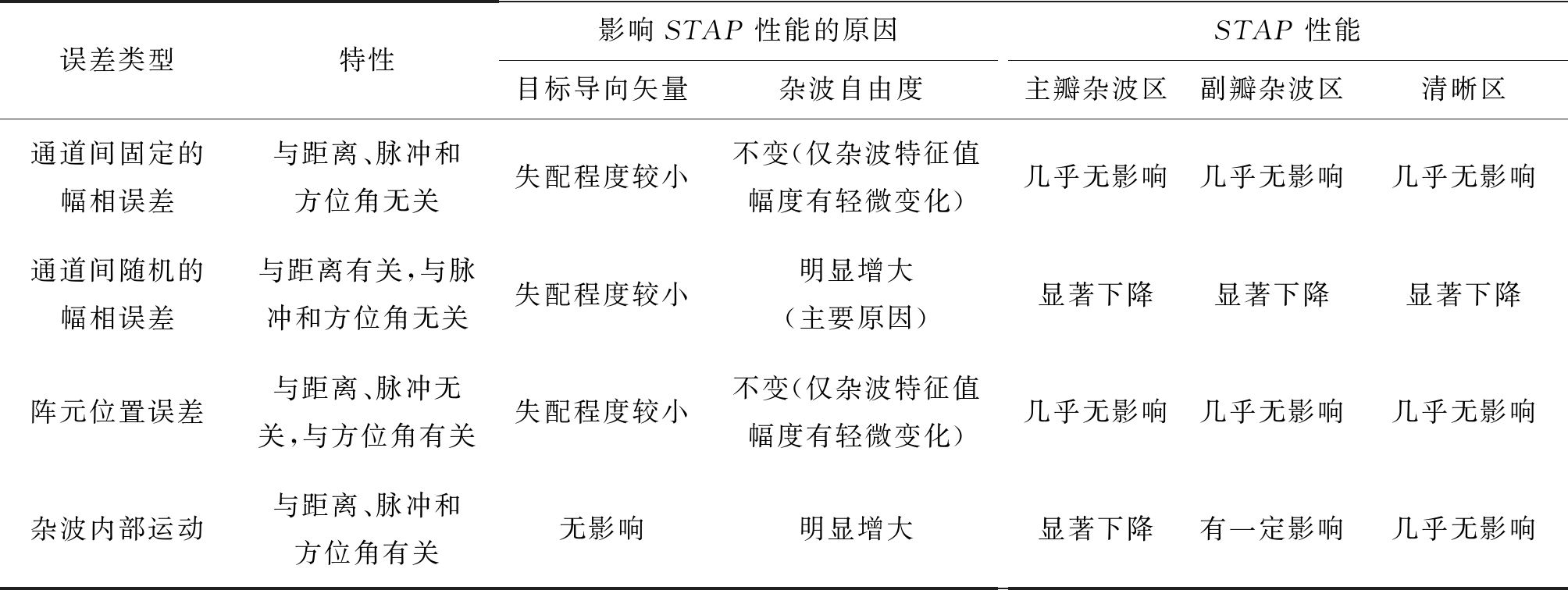
误差类型特性影响STAP性能的原因目标导向矢量杂波自由度STAP性能主瓣杂波区副瓣杂波区清晰区通道间固定的幅相误差与距离、脉冲和方位角无关失配程度较小不变(仅杂波特征值幅度有轻微变化)几乎无影响几乎无影响几乎无影响通道间随机的幅相误差与距离有关,与脉冲和方位角无关失配程度较小明显增大(主要原因)显著下降显著下降显著下降阵元位置误差与距离、脉冲无关,与方位角有关失配程度较小不变(仅杂波特征值幅度有轻微变化)几乎无影响几乎无影响几乎无影响杂波内部运动与距离、脉冲和方位角有关无影响明显增大显著下降有一定影响几乎无影响
综上所述,本节仿真结果与第4节理论分析结果一致。表2和表3对各种空时误差的特性及其对STAP杂波抑制性能的影响进行了总结。
下面给出解决误差问题的具体措施。(1)对于通道间固定的幅相误差和位置误差,可通过定期天线误差校正予以补偿;(2)对于通道间随机的幅相误差,可考虑利用不同距离门的回波数据重构杂波协方差矩阵,并通过距离向的平均弱化其影响;(3)对于杂波内部运动,其误差协方差矩阵仅与σv有关,如果可以重构其误差协方差矩阵,则利用重构的误差协方差矩阵点除估计的空时协方差矩阵即可减弱其对STAP的影响。σv的实际取值是未知的,但容易确定其取值范围,因此可通过设计某种具体方法从设定的取值范围中选取一个最优值作为σv的估计值,据此重构出误差协方差矩阵。该部分内容将是作者下一阶段的研究重点。
6 结论
在实际工程应用中各种不可避免的空时误差严重影响着STAP的性能。本文给出了各种误差的数学模型,并根据相关模型详细研究了不同误差的特性,同时从目标导向矢量失配和杂波自由度的增大两方面分析了空时误差影响STAP性能的内部机理。研究结果表明:(1)通道间固定的幅相误差和阵元位置误差导致的SCNR损失较小;(2)通道间随机的幅相误差导致的副瓣杂波区SCNR损失最大,同时导致了杂波谱的严重展宽;(3)杂波内部运动在主瓣杂波区及其附近区域会导致一定程度的SCNR损失和杂波谱展宽。通过本文工作,可以看出在机载雷达信号处理方案设计过程中应重点考虑对通道间随机的幅相误差和杂波内部运动稳健的STAP方法。
[1] Ward J. Space-time Adaptive Processing for Airborne Radar[R]. Lexington, MA: MIT Lincoln Laboratory, 1994: 1-5.
[2] Klemm R. Principles of Space-Time Adaptive Processing[M]. Third edition. London: The Institution of Electrical Engineers, 2002: 88-91.
[3] Guerci J R. Space-Time Adaptive Processing for Radar[M]. Boston London: Artech House, 2003: 67- 80.
[4] Melvin W L, Davis M E. Adaptive Cancellation Method for Geometry-Induced Non-Stationary Bistatic Clutter Environments[J]. IEEE Trans. Aerosp. Electron. Syst., 2007, 43(2): 651- 672.
[5] Sakar T K, Wang H, Park S, et al. A Deterministic Least Squares Approach to Space-Time Adaptive Processing[J]. IEEE Trans. on Antenna and Propagation, 2001, 49(16): 91-103.
[6] 魏民, 李小波, 黄中瑞, 等. 改进的最佳子集降维STAP方法[J]. 信号处理, 2016, 32(12): 1406-1411.
Wei Min, Li Xiaobo, Haung Zhongrui. An Improved Optimal Subset Reduced-rank Method[J]. Journal of Signal Processing, 2016, 32(12): 1406-1411.(in Chinese)
[7] Duan K, Xie W, Wang Y, et al. A Deterministic Auto-Regressive STAP Approach for Nonhomogenerous Clutter Suppression[J]. Multidim Syst. Sign. Process, 2016, 27: 105-119.
[8] 洪玺, 王文杰, 殷勤业. 基于多级维纳滤波器的空时自适应信号处理及其在无线通信系统中的应用[J]. 信号处理, 2017, 33(3): 430- 436.
Hong Xi, Wang Wenjie, Yin Qinye. Multistage Wiener Filter Based Space and Time Adaptive Signal Processing and Its Application in Wireless Communication Systems[J]. Journal of Signal Processing, 2017, 33(3): 430- 436.(in Chinese)
[9] Sun G, He Z, Tong J, et al. Knowledge-Aided Covariance Matrix Estimation via Kronecker Product Expansions for Airborne STAP[J]. IEEE Geosci. Remote Sens. Lett., 2018, 15(4): 527-531.
[10]Yang Z, Lamare R C. Enhanced Knowledge-Aided Space-Time Adaptive Processing Exploiting Inaccurate Prior Knowledge of the Array Manifold[J]. Digital Signal Process., 2017, 60: 262-276.
