1 引言
2.4 kbit/s及以下速率的低速率语音编码被广泛应用于数字对讲、卫星通信、短波和超短波通信等领域。低速率语音编码大多采用线性预测模型,提取线性预测系数、基音周期、能量、清浊音等人发声模型特征参数。The Mixed Excitation Linear Prediction (MELP)[1]编码器是其中较为成功和流行的一种。它在LPC10-e的基础上,采用多带混合激励,较好地克服了二元激励源模型的缺点,大大提高了合成语音的质量,被美国国防部定为数字保密通信的标准算法。在此基础了,提出的2.4/1.2 kbit/s MELPe被定为北大西洋公约组织标准算法。
在干净语音输入条件下,MELP可以合成出较高质量的语音。但是,输入语音存在失真条件下,失真语音不再吻合理想的人发声模型,会导致模型参数提取失真,编码语音质量下降。这也是没有编码的语音失真后听觉感知不明显,编码后却明显感觉存在失真的原因。
常见的失真包括背景噪声和截幅失真[2]。针对背景噪声对语音编码的影响,研究人员进行了详细的分析[3],并大多提出采用语音增强预处理减小噪声对语音编码的影响[4-7],语音增强性能的好坏极大程度影响语音编码的性能。目前,研究人员提出了多种截幅修复方法[8-15],但还没有人研究截幅对语音编码的影响,截幅修复方法也没有直接以提高语音编码质量为目标。其中的一些截幅修复算法也难以为编码性能带来提高。因此,首先详细分析了截幅失真对低速语音编码的影响,选取了能够对语音编码带来性能提高的方法。然后,针对高截幅条件下性能的进一步提升,提出采用两种改进型截幅修复方法对截幅语音进行预处理。最后,与原有方法进行比较,研究了改进型截幅修复方法对低速语音编码的影响。
本文其余章节安排如下:第2节介绍了MELP编码器的编码过程及编码参数;第3节对四种常用的截幅修复算法和两种改进型截幅修复算法进行简要介绍;第4节介绍了使用的评价指标以及对实验结果进行分析;第5节得出结论。
2 MELP编码器
MELP编码器是在传统LPC模型的基础上,采用混合激励、非周期脉冲、自适应谱增强、脉冲散布滤波、傅里叶级数等方法来提高其性能。MELP编码器在编码过程中把语音信号分解成激励参数和声道参数两个部分,激励参数用基音周期、带通强度、非周期性标志、傅里叶幅度和增益表示,声道参数用LPC表示。MELP编码器的编码流程框图如图1所示[15]。
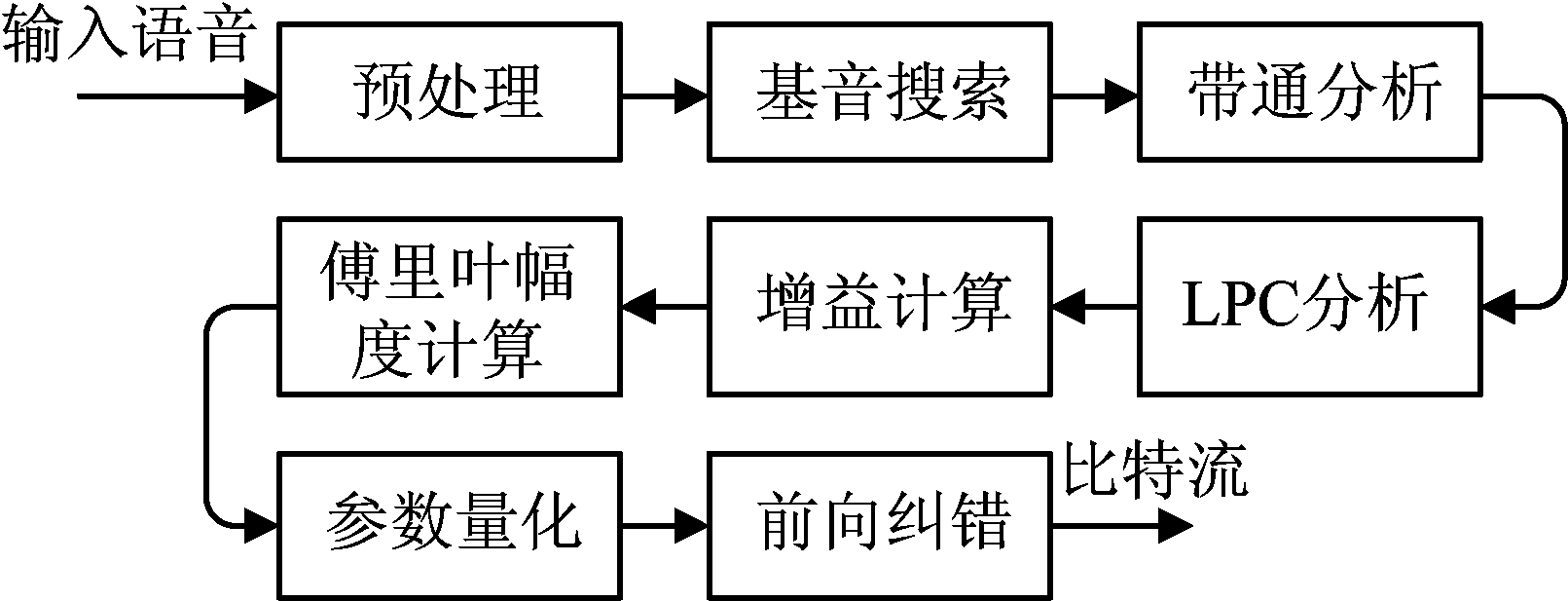
图1 MELP编码器的编码流程框图
Fig.1 Block diagram of the encoding process of the MELP
2.1 编码参数
低速语音编码器能否准确地提取基音周期、清浊音判决参数和LPC直接影响解码端合成语音的质量。因此,在实验阶段,我们选择基音周期、清浊音判决参数和LPC这三个参数来研究有截幅修复预处理和无截幅修复预处理对MELP编码器编码性能的影响,并使用基音估计准确率、清浊音判决错误率、LPC谱失真测度和合成语音的PESQ打分值对实验结果进行评估。
2.1.1 基音周期
MELP编码器首先使用1 kHz的巴特沃斯低通滤波器对输入语音进行滤波,利用归一化互相关法进行基音粗估得到整数基音值。然后进行分数基音分析,采用内插方法,求得分数基音估计的小数部分,此时分数基音值为整数基音与分数基音小数部分之和。最后采用6阶巴特沃斯带通滤波器把一帧语音分为五个子带,利用[0,500 Hz]子带信号与残差信号在分数基音值前后5个样点进行精细基音搜索,从而得到精确基音值。
2.1.2 清浊音判决
MELP编码器使用五个6阶巴特沃斯滤波器,将输入语音信号的频域分为5个子带。利用LPC系数确定的预测滤波器对输入语音信号进行逆滤波,得到残差信号,取残差信号的160个样点计算峰值,如果峰值大于门限值,则置最低频带的语音声强为1,如果峰值大于另一门限值,则置最低三个频带的语音声强为1。与传统的LPC编码算法不同,MELP对每个子带进行清浊音判决,以获得更好的解码性能。
2.1.3 LPC
LPC携带着声道的信息,低速语音编码能否对LPC进行准确的估计直接影响合成语音的质量和可懂度。LPC系数的计算采用Levinson-Durbin递归算法,计算时使用汉明窗对输入语音信号加窗,窗长为180个样本点(22.5 ms),窗的中心点位于当前帧的最后一个样本点。此外,对于求得的10阶LPC系数都乘以带宽扩展系数。
3 截幅修复算法
截幅失真作为一种常见的失真类型,可以看作是动态范围压缩的一种特例,是当语音信号的幅值超出设备允许的最大幅值时产生的一种失真现象。如图2所示,当样本点的幅值大于允许的最大幅值时,该样本点将会被截幅。截幅失真通过影响语音信号的波形,从而降低语音信号的可懂度,这将会对MELP的编码性能造成负面影响。
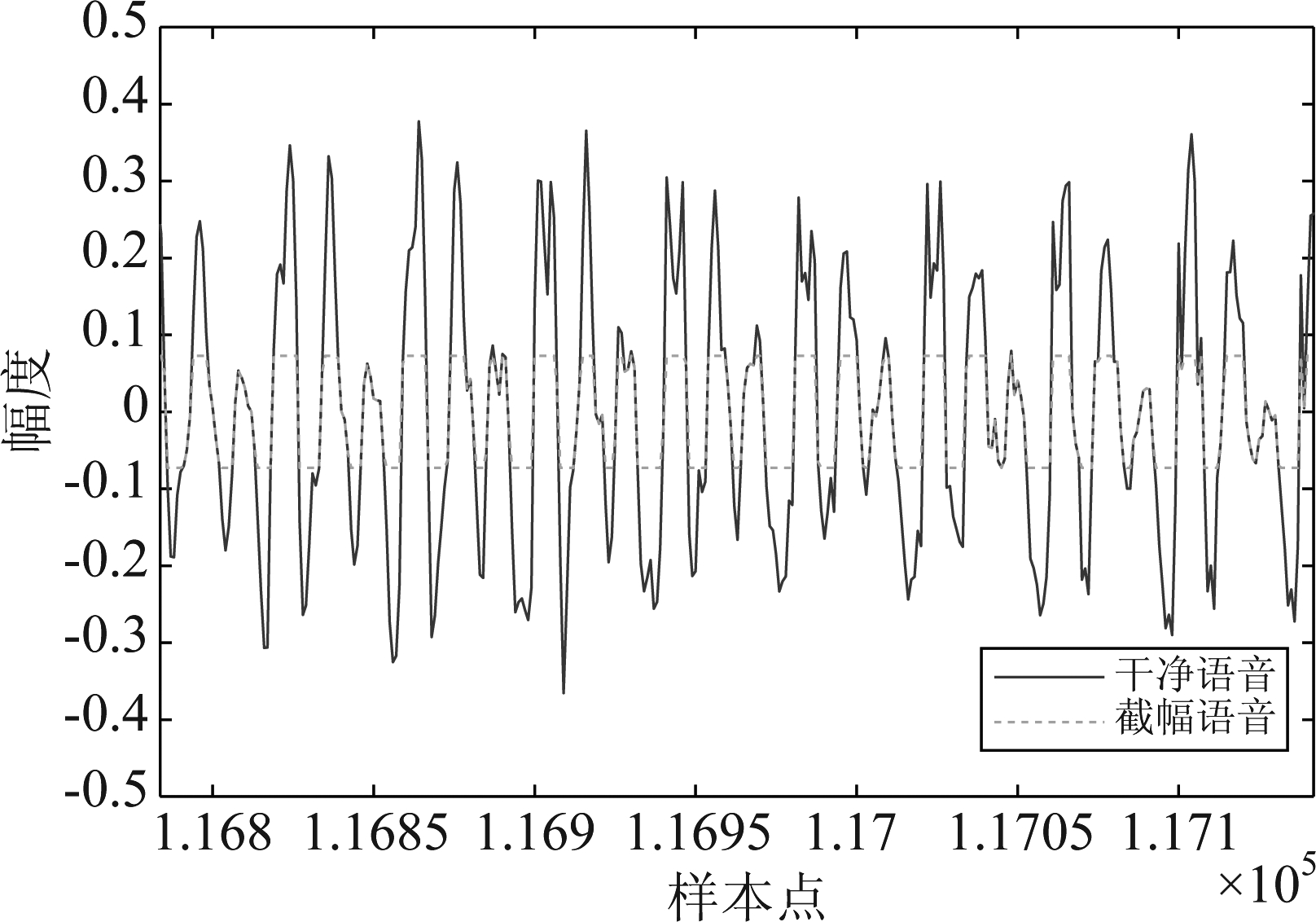
图2 截幅失真
Fig.2 Clipping of speech
令x∈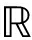
N为干净语音信号,y∈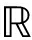N为受到截幅的语音信号,因此可以将y表示为:
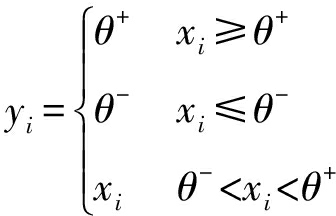
(1)
其中,θ+,θ-分别为正截幅门限和负截幅门限,xi为干净语音样本点,N为样本点总个数。因此y可以表示为:
y=MΩrx+θ+MΩc+1+θ-MΩc-1
(2)
其中,MΩr,MΩc+,MΩc-∈{0,1}N×N为掩蔽矩阵。Ωr={i=[N]:θ-<xi<θ+}为可靠样本点的索引,Ωc+={i=[N]:xi>θ+}为受到正截幅样本点的索引,Ωc-={i=[N]:xi<θ-}为受到负截幅样本点的索引。因此,当i∈S时,[MS]i,i=1;当i∉S时,[MS]i,i=0。而1∈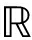N是元素全为1的向量。
目前,针对截幅语音信号修复的方法包括:自回归模型和贝叶斯估计等。自回归模型是利用语音样点间的相关性,通过线性预测分析对截幅样点进行插值以达到修复的目的。但是,当语音受到截幅失真的样本点较多时,该方法的修复效果不明显。贝叶斯估计是利用贝叶斯定理对截幅样本点的真实值进行估计,但该方法实现的前提是必须要有语音样点分布的先验信息,具有一定的局限性。近年来,基于稀疏表示的语音信号修复技术引起了广泛关注。这类方法的基本思想在于语音信号可以用字典进行稀疏表示,在截幅修复上展现出较好的性能。
在实验阶段,本文使用四种常见的截幅修复方法:正交匹配追踪算法(Orthogonal Matching Pursuit,OMP)[8]、约束正交匹配追踪算法(Constraint Orthogonal Matching Pursuit,COMP)[8]、一致字典学习算法(Consistent Dictionary Learning, CDL)[12]、一致迭代硬阈值算法(Consistent Iterative Hard Thresholding, CIHT)[13],和两种改进型方法:自适应一致字典学习算法(Adaptive Consistent Dictionary Learning, ACDL)[14]、自适应一致硬阈值算法(Adaptive Consistent Iteration Hard Threshold, ACIHT)[15]对截幅语音进行预处理。
3.1 常用截幅修复方法3.1.1 正交匹配追踪算法
Adler等人将截幅失真的修复看成简单的信号修复问题,通过丢弃受到截幅的样点并解决可靠样本上的稀疏分解问题,得到如下目标优化函数:
(3)
其中,D为过完备字典,
为稀疏表示系数。正交匹配追踪算法的流程框图如图3所示。
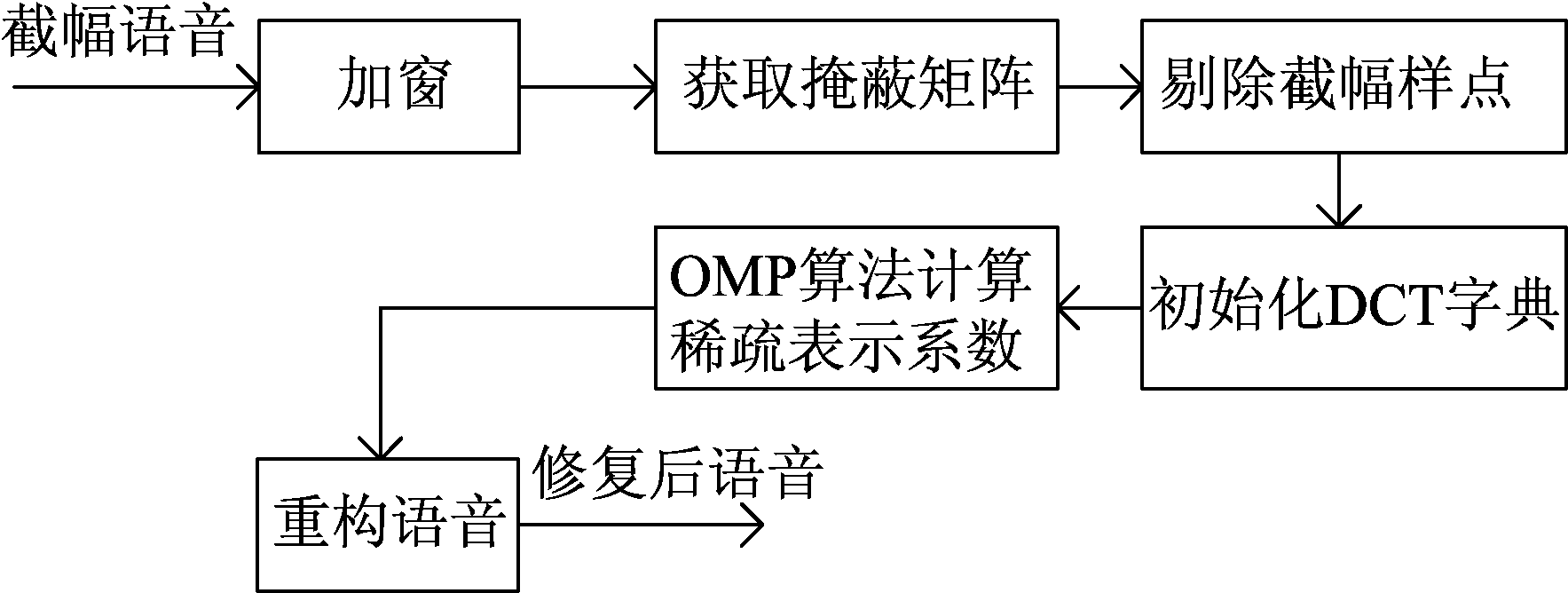
图3 正交匹配追踪算法流程框图
Fig.3 Block diagram of orthogonal matching pursuit
该方法首先获取截幅语音的掩蔽矩阵,并利用掩蔽矩阵剔除截幅样本点,然后使用正交匹配追踪算法在过完备离散余弦变换(Discrete Cosine Transform, DCT)字典上对可靠样点进行稀疏分解,最后利用过完备DCT字典和稀疏表示系数重构语音。由于正交匹配追踪算法在进行稀疏分解的过程中,需要不断遍历字典中的原子,因此正交匹配追踪算法需要较长的运算时间。
3.1.2 约束正交匹配追踪算法
截幅失真的存在会导致截幅样点的幅度小于原始幅度。因此,约束正交匹配追踪算法是在正交匹配追踪算法的基础上,通过添加截幅样点的约束条件来保证修复后语音幅值的绝对值大于截幅门限,从而提高修复效果,即考虑以下目标优化函数:
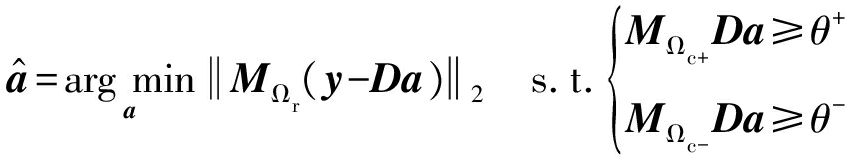
(4)
约束正交匹配追踪算法的流程框图如图4所示。
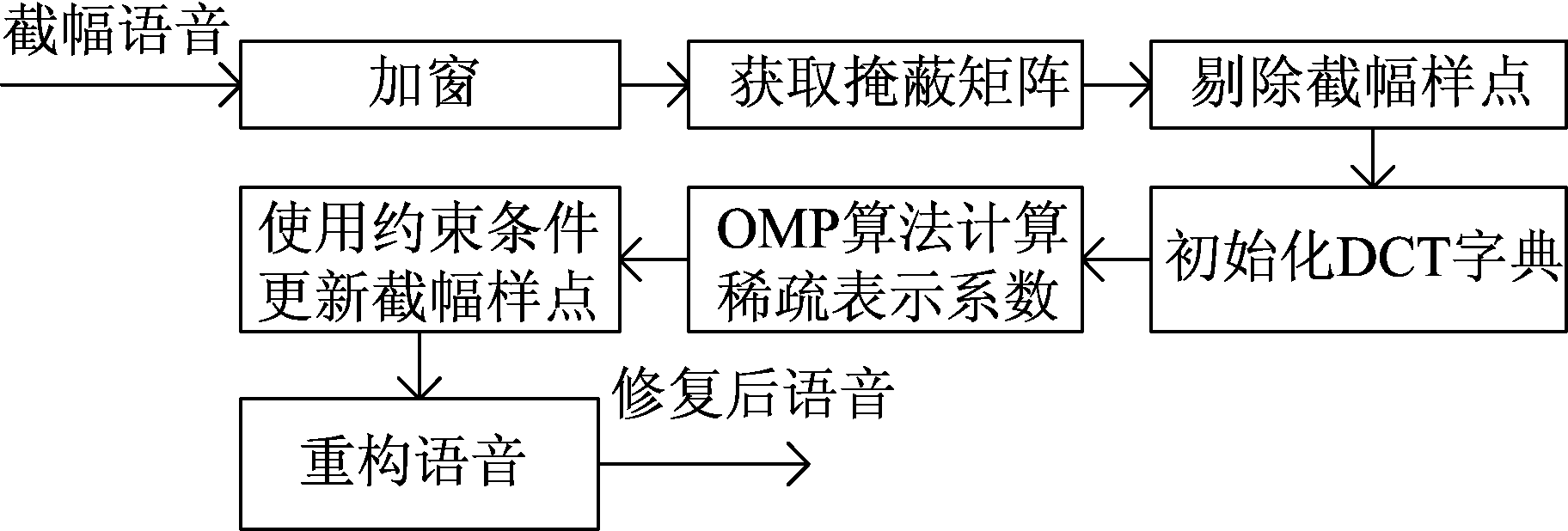
图4 约束正交匹配追踪算法流程框图
Fig.4 Block diagram of constraint orthogonal matching pursuit
约束正交匹配追踪算法首先利用正交匹配追踪算法计算可靠样点的稀疏表示系数
然后通过添加幅度约束条件使得截幅样点的幅值经过重构后会大于截幅门限或小于负截幅门限。约束正交匹配追踪算法在使用正交匹配追踪算法求得稀疏表示系数后,使用约束条件对截幅样点的幅值进行更新。因此,相比于正交匹配追踪算法,约束正交匹配追踪算法需要更长的运算时间。
3.1.3 一致迭代硬阈值算法
一致迭代硬阈值算法是在迭代硬阈值算法的基础上,使用两个正则项代替截幅约束条件,构造出一个统一的目标函数:
||MΩc-(θ-1-Da)-||2 s.t.||a||0≤K
(5)
其中,(u)+=max(0,u),(u)-=min(0,u)。K为稀疏度约束常数,||a||0≤K表示向量a中非零元素的个数小于等于K。公式(5)中的第二项和第三项蕴含了截幅语音的约束条件信息,使用梯度下降的方法可求解
一致迭代硬阈值算法的流程框图如图5所示。
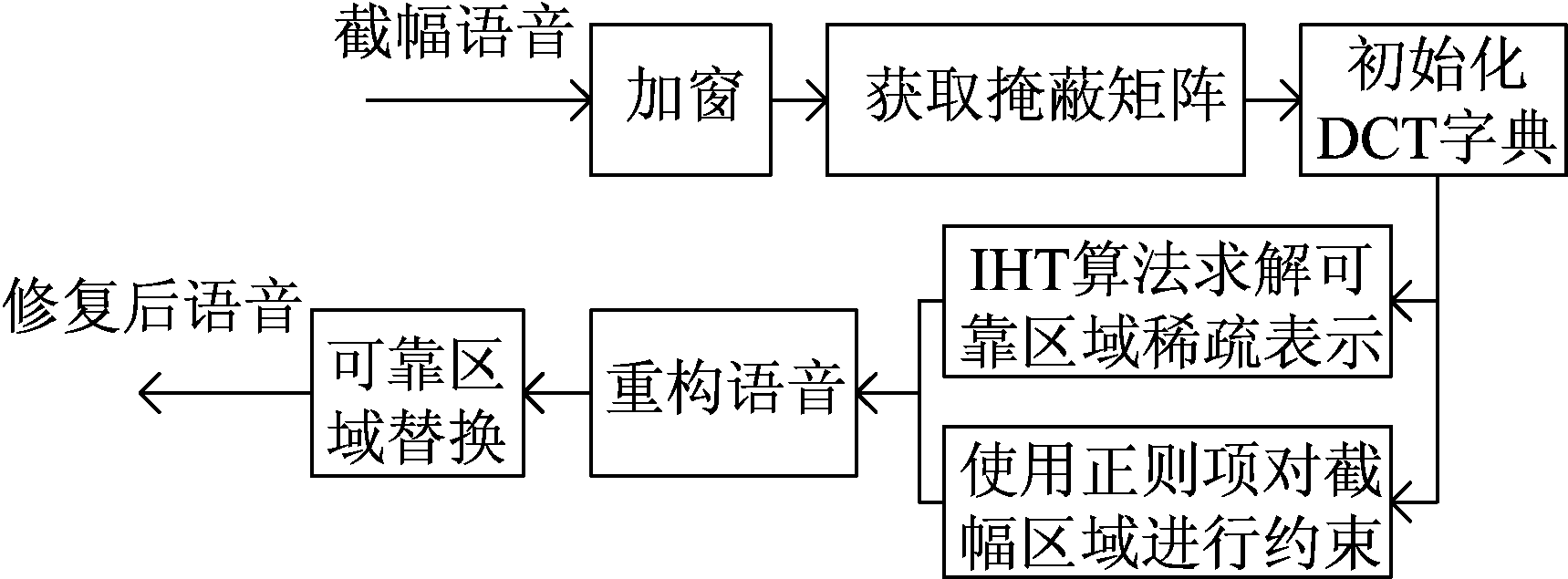
图5 一致迭代硬阈值算法流程框图
Fig.5 Block diagram of consistent iterative hard thresholding
一致迭代硬阈值算法通过在目标函数中使用两个正则项代替截幅样点的约束条件,并使用梯度下降的方法求解。因此一致迭代硬阈值算法不需要遍历字典中的所有原子,且在求解完稀疏表示系数后不需要对截幅样点进行更新,这使之拥有较快的运算速度。
3.1.4 一致字典学习算法
一致迭代硬阈值算法是在固定字典上对截幅语音进行稀疏分解,而固定字典对不同语音信号的适应能力较差。因此,一致字典学习算法在使用一致迭代硬阈值算法求解稀疏表示系数的过程中,对字典进行训练,从而获得拥有较强适应能力的字典。一致字典学习算法考虑如下目标优化函数:
+||Mc-(θ-1-Dat)-||2) s.t.||at||0≤K
(6)
其中,下标t代表第t帧语音。一致字典学习算法的流程框图如图6所示。
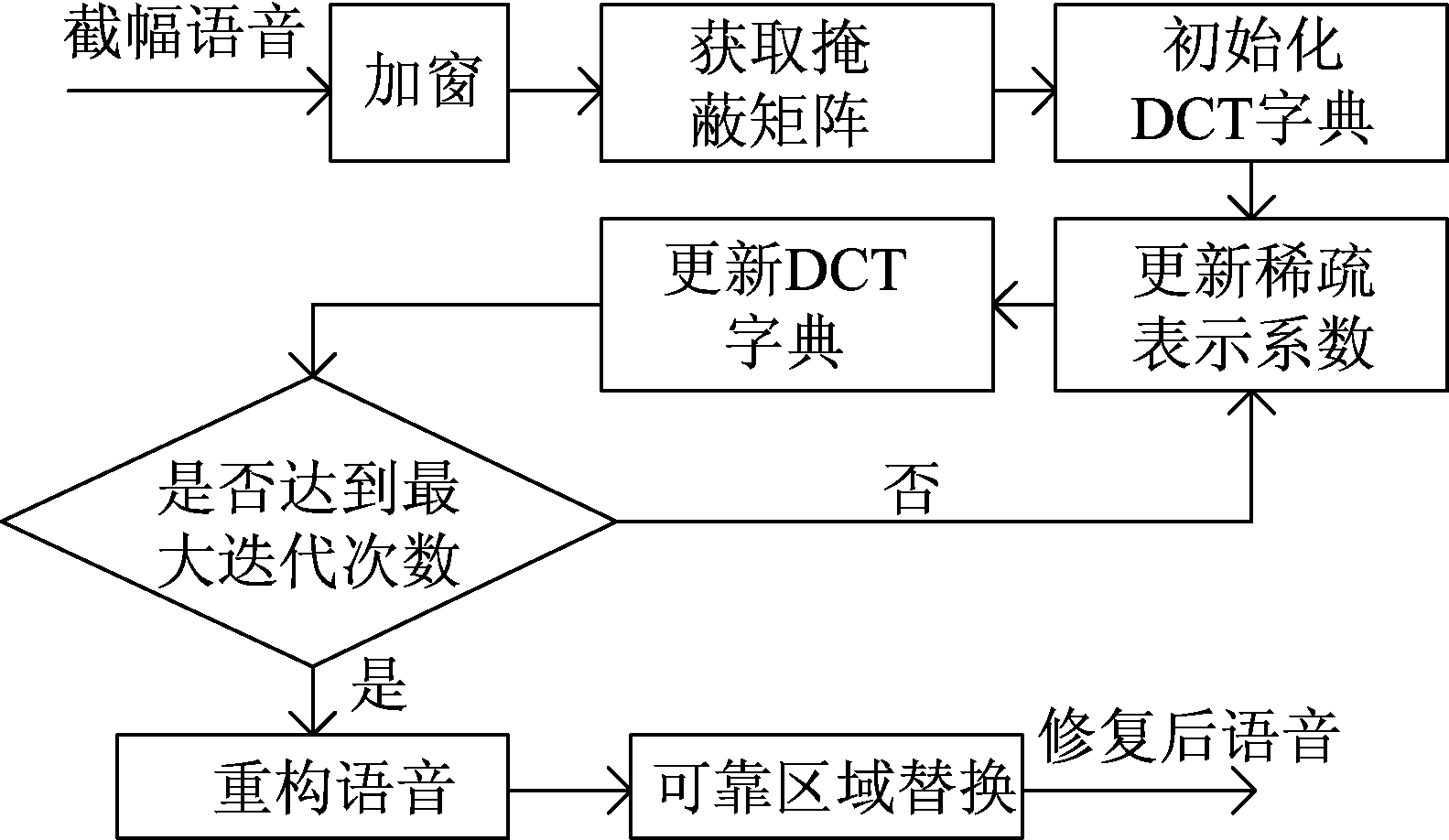
图6 一致字典学习算法流程框图
Fig.6 Block diagram of consistent dictionary learning
一致字典学习算法首先利用一致迭代硬阈值算法,在过完备DCT字典上对截幅语音信号进行稀疏分解,得到稀疏表示系数。然后固定稀疏表示系数对字典进行更新,迭代若干次后得到一个训练字典和稀疏表示系数,最后利用训练字典和稀疏表示系数重构语音信号。相比于一致迭代硬阈值算法,一致字典学习算法需要在求解稀疏表示系数阶段和字典更新阶段进行交替迭代。因此,一致字典学习算法需要较长的运算时间。
3.2 改进型截幅修复方法
现在大多数针对截幅修复的方法在截幅程度不大时有较好的修复效果,但对于截幅程度较大的语音信号,修复效果并不明显。截幅失真的程度往往是不可预知的,截幅修复方法对不同截幅程度的适应力差将无法为语音编码性能带来满意的提高。自适应一致迭代硬阈值算法和自适应一致字典学习算法是在一致迭代硬阈值算法和一致字典学习算法上进行改进得到的。自适应一致迭代硬阈值算法和自适应一致字典学习算法考虑到截幅程度越大,受到截幅失真影响的样本点就越多,原始信号样本点的振幅与截幅门限的差值就越大。因此,自适应一致迭代硬阈值算法和自适应一致字典学习算法通过计算截幅程度因子,把截幅程度信息添加到截幅修复中,提高算法对不同截幅程度的适应能力,从而提高语音编码的性能。
3.2.1 自适应一致迭代硬阈值算法
自适应一致迭代硬阈值算法是在一致迭代硬阈值算法上改进的方法,该方法通过加入截幅程度因子η(k)对公式(5)的一致性进行加强,于是考虑以下模型:
||MΩc+[η(k)(θ+1-Da)]+||2+ ||MΩc-[η(k)(θ-1-Da)]-||2 s.t.||a||0≤K
(7)
其中,β(k)=exp(2.279×exp(0.3815×lnk)),η(k)=[β(k)]ρ,ρ=1/(1+e-2000×(k-0.02))。k为截幅比Nc/N,Nc为受到截幅的样本点个数,N为总样本点个数。β(k)是利用干净语音信号进行不同程度的人为截幅,然后针对不同截幅程度的语音信号,选择有最优修复效果的β值进行拟合得到的。而ρ的作用是避免在截幅程度较小时,出现截幅样本点的幅值在经过重构后会大于原始样本点幅值,从而产生新失真的情况[15]。自适应一致迭代硬阈值算法的流程框图如图7所示。
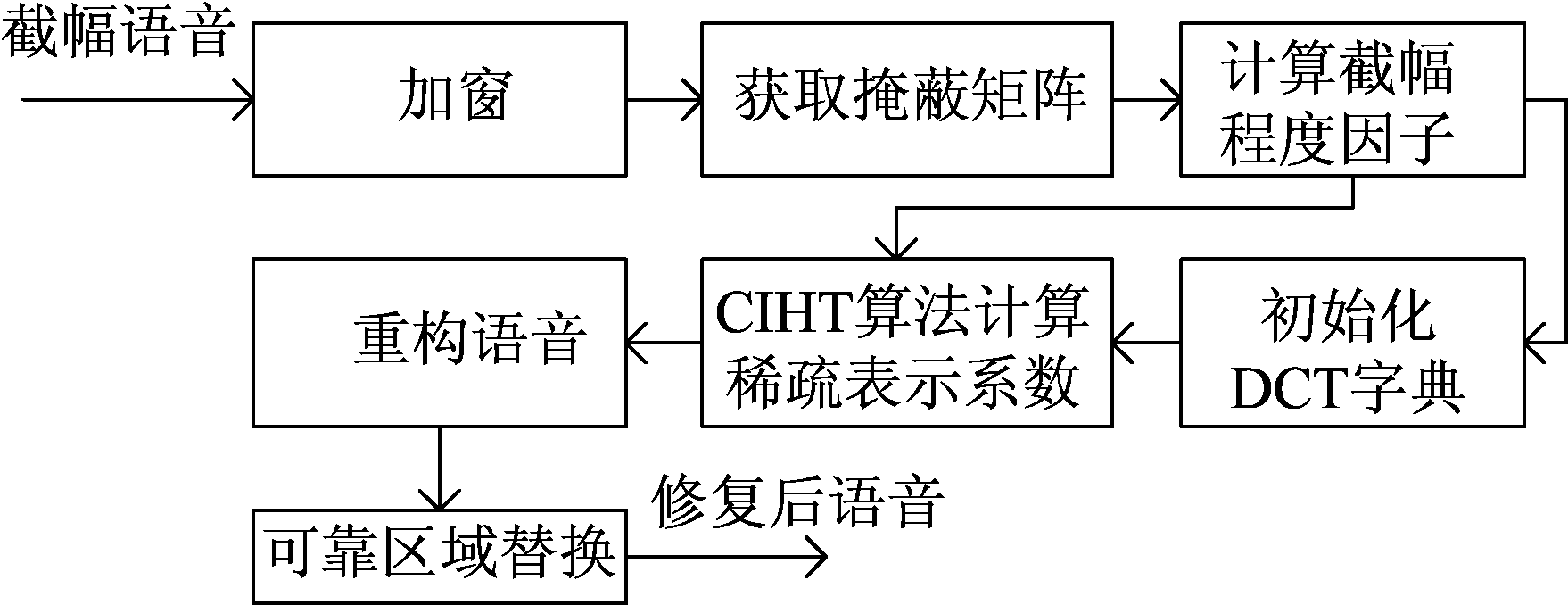
图7 自适应一致迭代硬阈值算法流程框图
Fig.7 Block diagram of adaptive consistent iteration hard threshold
自适应一致硬阈值算法自动估计语音信号的截幅程度,根据截幅程度信息,自适应调整算法中的截幅程度因子,对约束条件进行加强,从而达到在截幅程度较大时能有较好的修复效果。
3.2.2 自适应一致字典学习算法
自适应一致字典学习算法是在一致字典学习算法上改进的方法。与自适应一致迭代硬阈值算法相似,自适应一致字典学习算法通过加入截幅程度因子γ(k)对公式(6)的一致性进行加强,于是考虑以下模型:
||Mc+[γ(k)(θ+1-Dat)]+||2+ ||Mc-[γ(k)(θ-1-Dat)]-||2) s.t.||at||0≤K
(8)
其中,γ(k)=exp(2.13×exp(0.4254×lnk))。自适应一致字典学习算法的流程框图如图8所示。
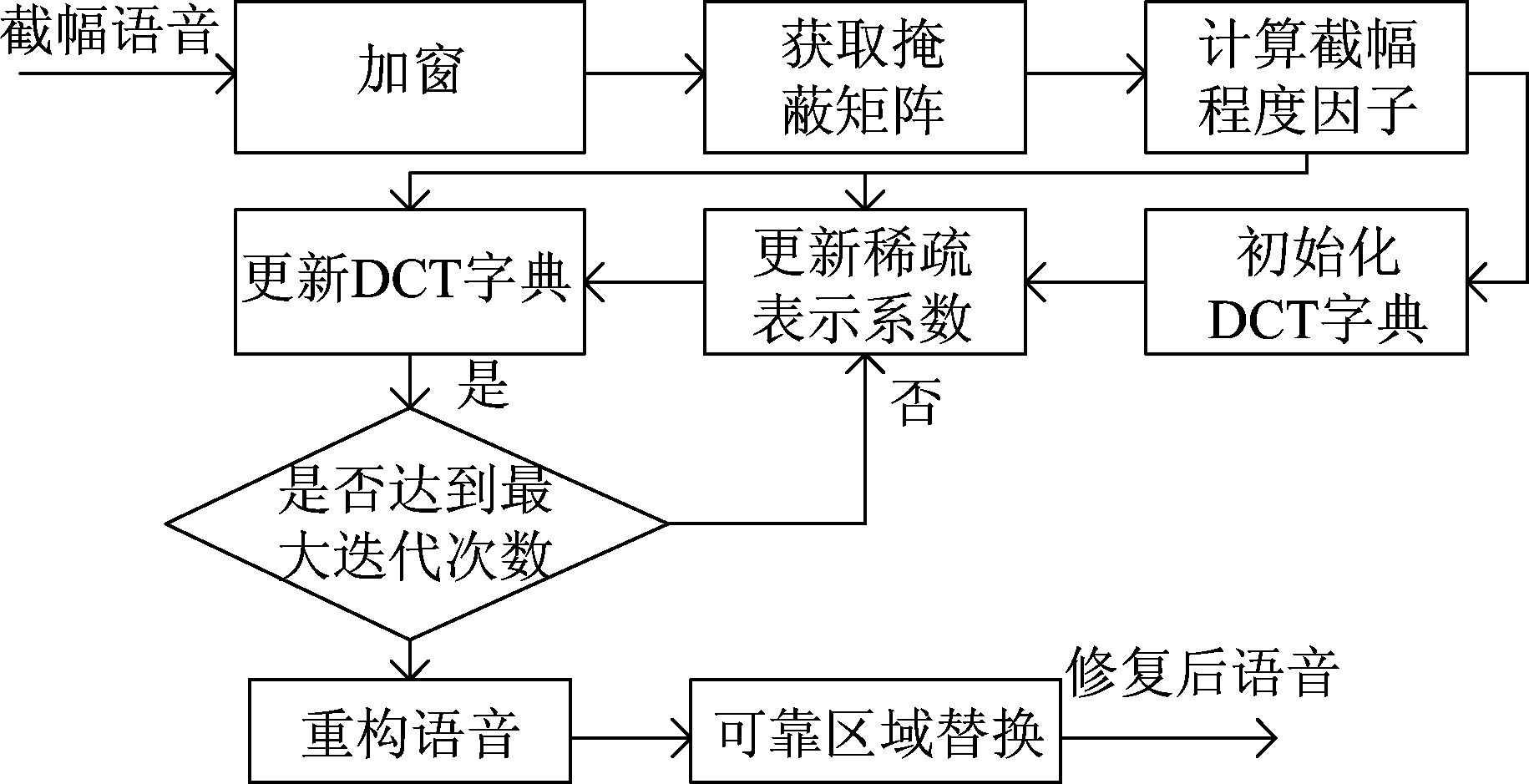
图8 一致字典学习算法流程框图
Fig.8 Block diagram of adaptive consistent dictionary learning
自适应一致字典学习算法能根据截幅程度信息,自适应地调整算法中的截幅程度因子,达到在截幅程度较大时也有较好的修复效果的目的。
4 实验结果及分析
实验测试语音来自TIMIT数据集[17]。在TIMIT数据库中,选择不同口音的5位男性和5位女性说话者共10个语句,并将其拼接成一个语句作为干净语音。截幅语音是通过对干净语音进行不同程度的人为截幅得到的,截幅程度用截幅百分比k=NC/NALL×100%来表示,其中NC为受到截幅失真的样点数,NALL为样点总个数。因此,截幅百分比越大代表截幅程度就越大。实验阶段使用六个不同程度的截幅比,分别为:5%,10%,15%,20%,25%和30%。当截幅比为5%时,截幅失真也会给语音带来较大的失真。为了客观地评估截幅修复预处理对MELP参数编码性能的影响,分别在干净语音、截幅语音和修复后语音中计算了基音估计准确率、清浊音判决准确率和LPC谱失真测度,并对合成语音进行PESQ打分。其中,利用MELP编码器从干净语音信号提取的参数作为参考标准值。在最后,测试了六种截幅修复算法修复截幅语音的运算成本。
4.1 截幅失真对编码参数的影响4.1.1 截幅失真对基音估计准确率的影响
基音估计准确率只在受到截幅失真影响的浊音帧上进行计算。当基音估计值不大于(或小于)参考标准值的百分之五时,则认为基音估计结果时正确的。基音估计准确率可以定义为:
(9)
其中,Ncorrect为基音估计正确的帧数,NCV为语音受到截幅失真影响的浊音帧数。
图9描述了在不同截幅程度下,截幅语音的基音估计准确率。从图9可以看出基音估计准确率随着截幅程度的增大而将低。
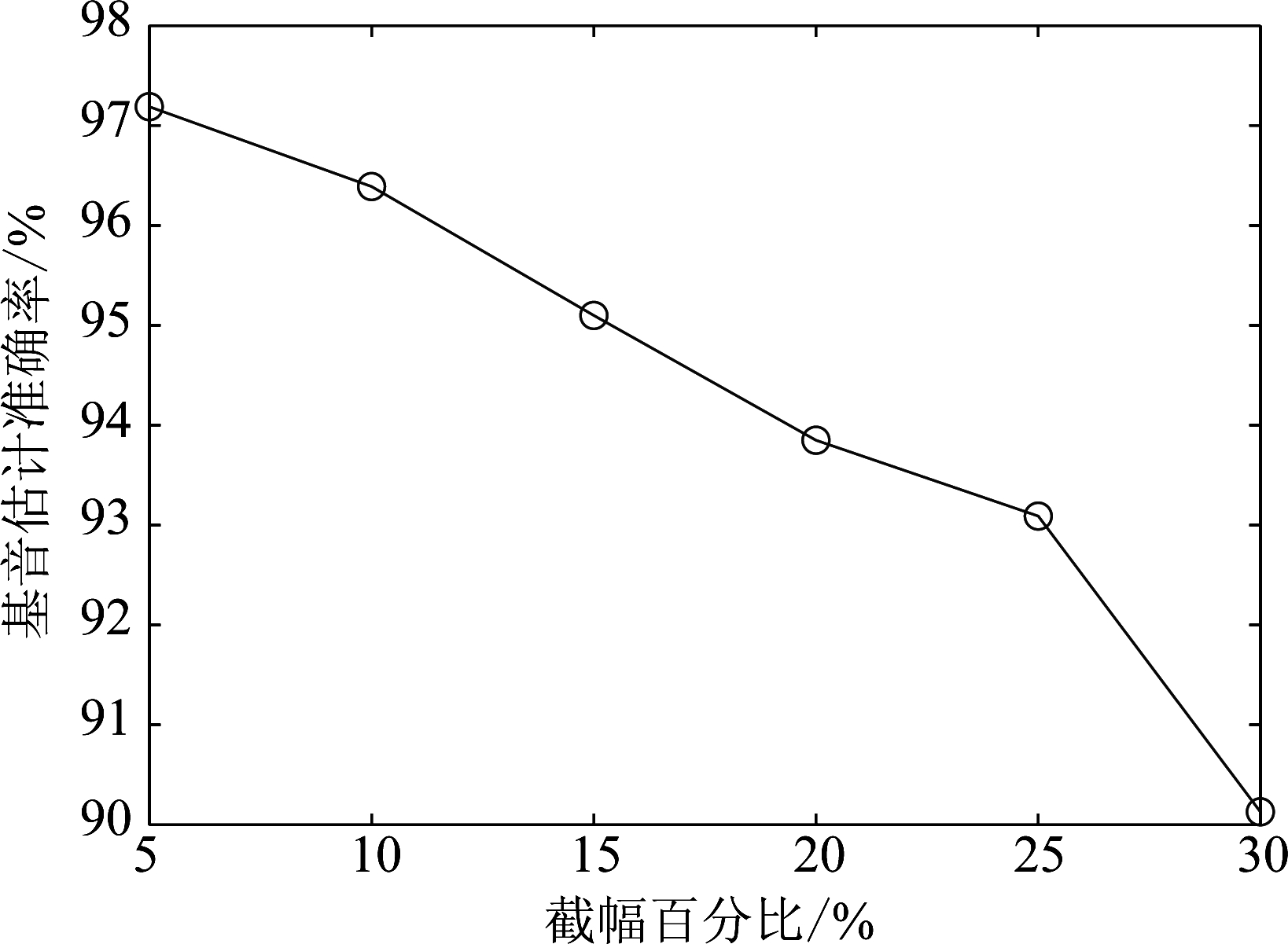
图9 截幅语音基音估计准确率
Fig.9 Pitch estimation accuracy rate of clipped speech at different clipping degrees
为了研究截幅失真对不同基音周期的具体影响,我们把基音周期分为2.5 ms～ 7.5 ms,7.5 ms～12.5 ms和大于12.5 ms三个范围,并得到实验结果如图10所示。随着截幅程度的增大,受到截幅失真影响的帧数越多。由图10(a)可见,相比于基音周期较大的帧,基音周期较小的帧更容易受到截幅失真的影响。这是由于基音周期较小的帧有着较大的能量,并且在数量上占绝大部分,因此,相比于基音周期较大的帧,基音周期较小的帧更容易受到截幅失真。从图10(b)可以发现,虽然截幅失真更容易对基音周期较小的帧造成影响,但随着截幅程度的增大,基音周期较小的帧也能保持较高的基音估计准确率。
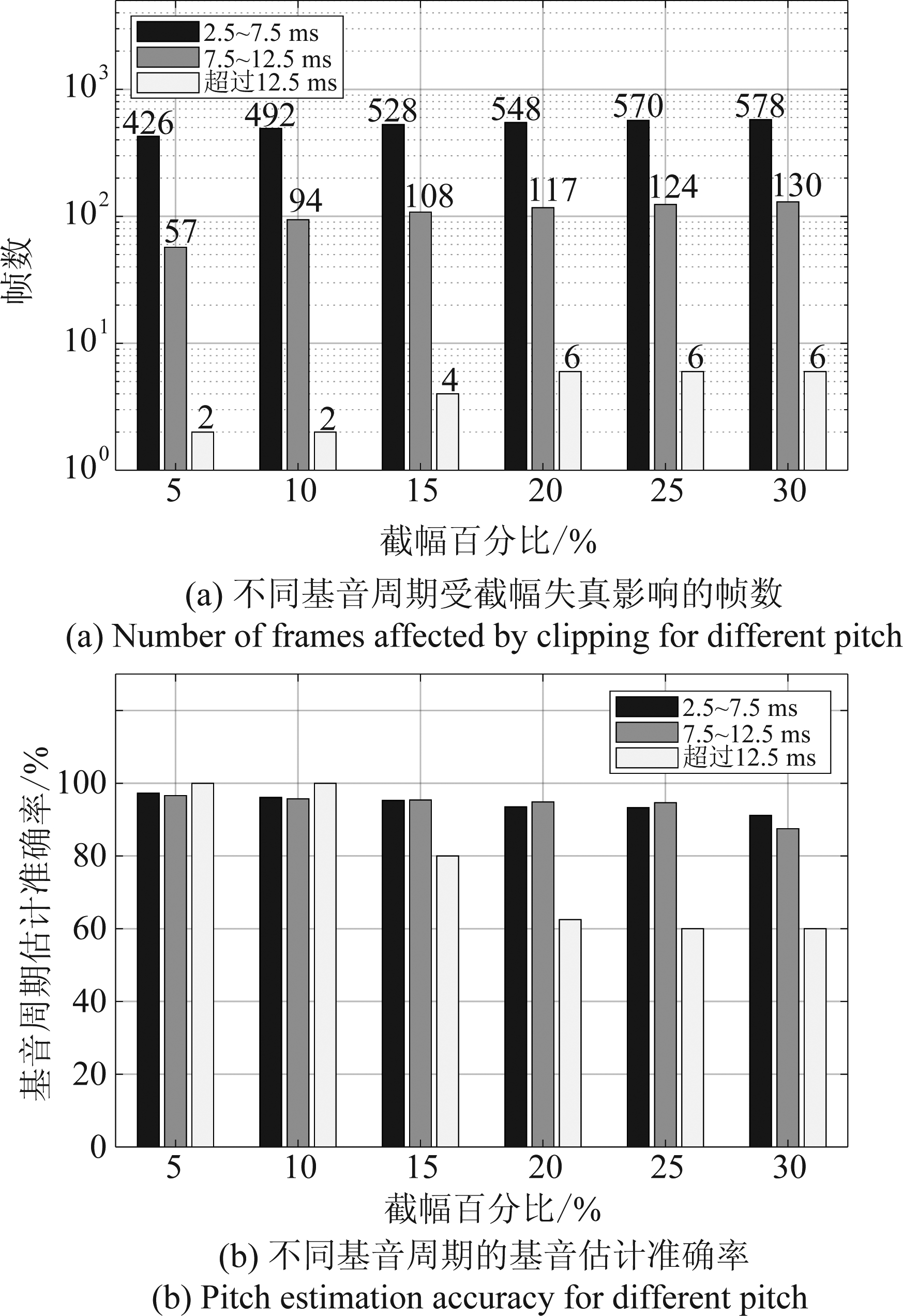
图10 不同基音周期受截幅失真影响的帧数 数量和对应的基音估计准确率
Fig.10 The number of frames affected by the clipping for different pitch and the corresponding pitch estimation accuracy
4.1.2 截幅失真对清浊音判决准确率的影响
清浊音判决只在有声帧上进行。清浊音判决准确率定义为:
(10)
其中,Nu→v为将清音误判为浊音的帧数,Nv→u为将浊音误判为清音的帧数,NC为语音受到截幅失真的帧数。
图11展示了在不同截幅程度下,截幅语音的清浊音判决准确率。由图11可见,截幅失真的存在会影响语音的清浊音判决准确率,且截幅程度越大,语音的清浊音判决准确率就越低。虽然截幅失真能对清浊音判决准确率造成影响,但在较大的截幅程度下,清浊音判决准确率也能保持在94%以上。
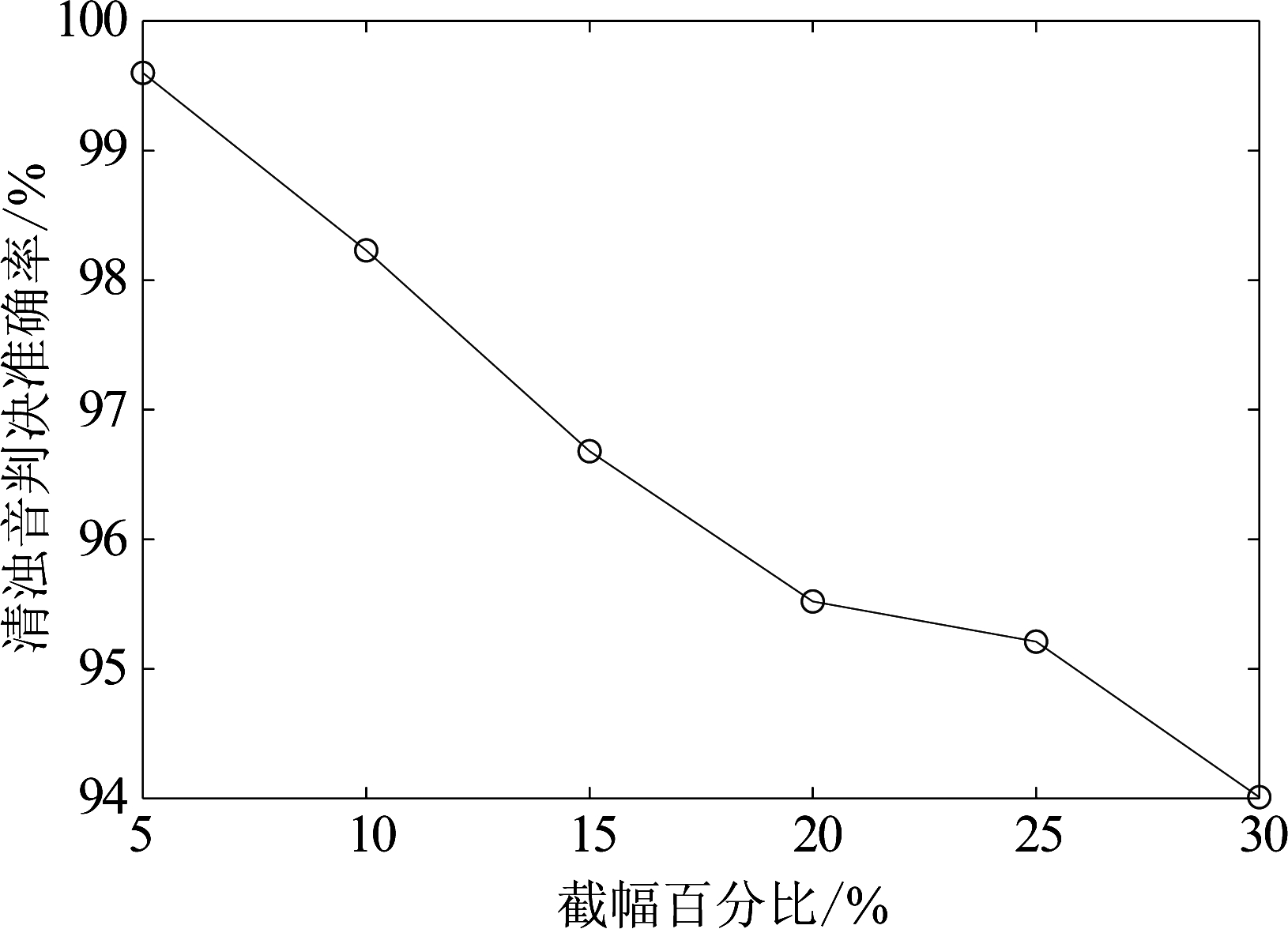
图11 截幅语音清浊音判决准确率
Fig.11 Voicing decision correct rate accuracy rate of clipped speech at different clipping degrees
4.1.3 截幅失真对LPC谱失真测度的影响
评价MELP编码器提取线性预测系数性能的方法有很多,较为常见的有对数谱距离、坂仓距离和谱失真测度(SD)[18]。本文使用LPC谱失真测度作为评价指标,且谱失真测度只在受到截幅失真的语音帧上计算,最后取平均值。第i帧语音的失真度Di定义如下:
(11)
(12)
其中,F为语音采样率,Pi( f )为截幅语音第i帧的LPC功率谱,
为截幅修复后语音第i帧的LPC功率谱。而Ai和
分别表示截幅语音和截幅修复后语音的LPC系数。因此,平均谱失真测度为:
SD=average(Di)
(13)
图12描述了在不同截幅程度下,截幅失真对LPC谱失真的影响。截幅失真的存在会降低MELP编码器提取线性预测系数的性能,随着截幅程度的增大,LPC谱失真值随之增大。
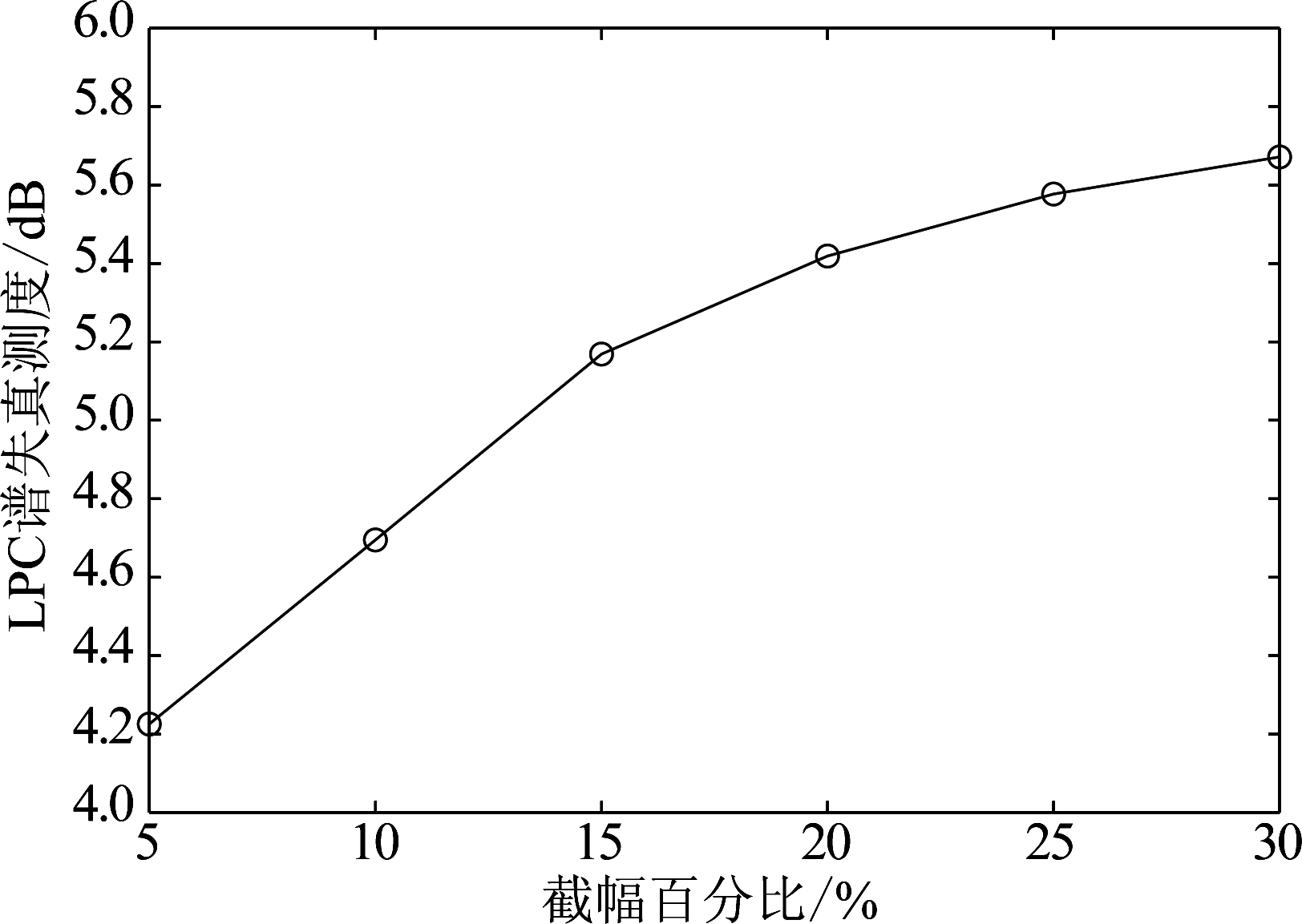
图12 截幅语音谱失真测度
Fig.12 Spectral distortion of clipped speech at different clipped percentage
4.2 常见修复方法对编码参数的影响4.2.1 常见修复方法对基音估计准确率的影响
图13描述了在不同截幅程度下,四种常见的截幅修复预处理对基音估计准确率的影响。由图13(a)可见,相比于未进行预处理的截幅语音,经过CIHT算法和CDL算法修复后的语音有着更高的基音估计准确率。CIHT算法和CDL算法是利用两个门限函数把可靠样点的稀疏分解问题和截幅样点的稀疏分解问题统一成同一个优化问题,然后在可靠样点的稀疏分解过程中对截幅样点的值进行重新估计,最后使用截幅语音可靠样点替换重构语音可靠样点以避免在重构过程中带入新的噪声。因此,CIHT算法和CDL算法能保证在修复截幅失真的过程中不会给截幅语音的可靠部分带入新的失真,从而达到较好的截幅修复效果。
由图13(b)可以发现,OMP算法和COMP算法只有在截幅程度较小时(截幅百分比为5%),才能提高修复后语音的基音估计准确率,当截幅程度较大时,使用OMP算法或COMP算法对截幅语音进行预处理后,反而会使基音估计准确率严重下降。图14给出了使用OMP算法和COMP算法在不同截幅程度下对截幅语音波形的修复结果。
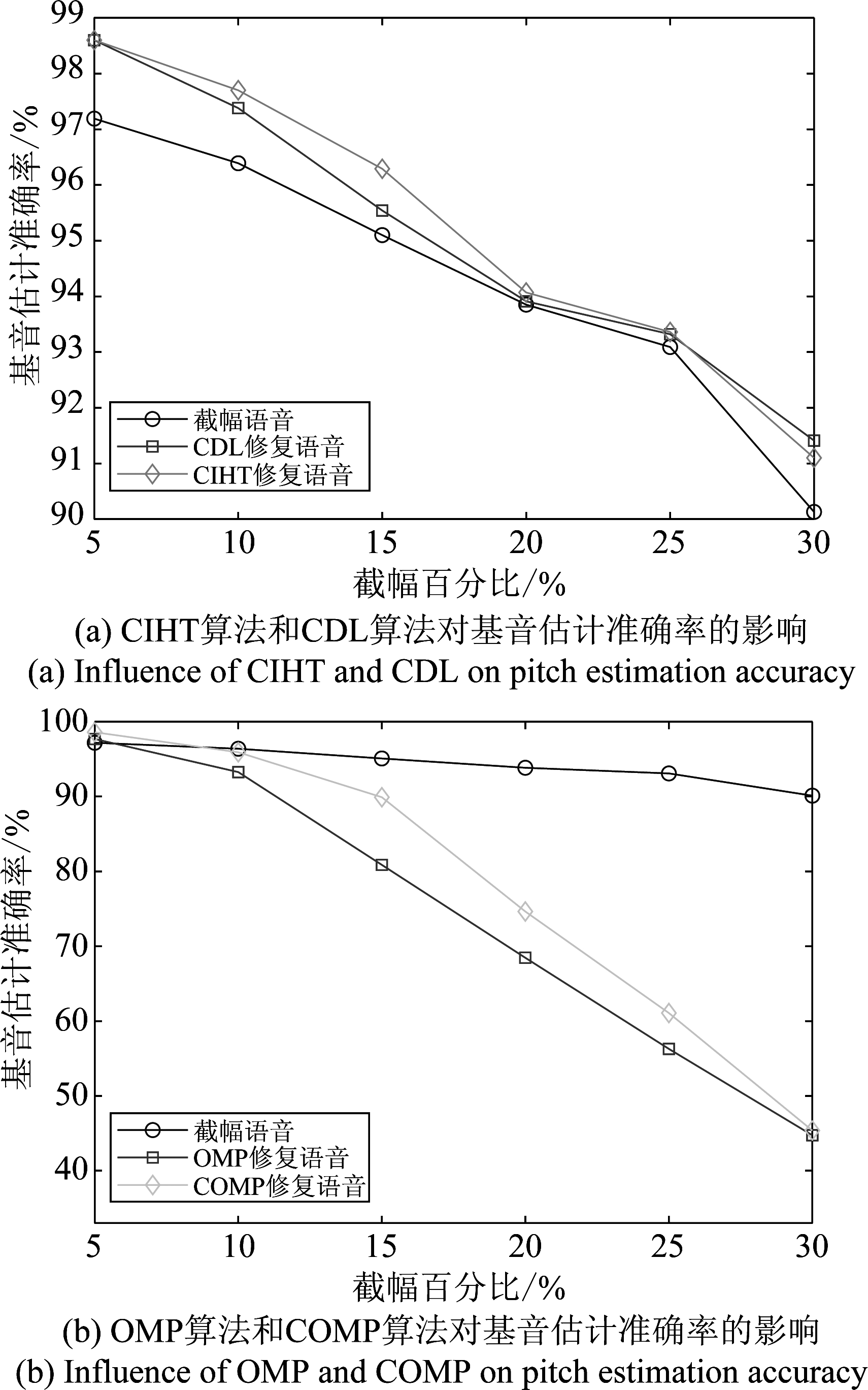
图13 基音估计准确率对比图
Fig.13 The comparison of pitch estimation accuracy
由图14(a)可见,当截幅程度较小时,OMP算法和COMP算法能起到修复波形的效果。当截幅程度较小时,截幅语音的可靠样点较多,使用OMP算法和COMP算法对可靠样点进行稀疏分解后得到的稀疏表示系数里携带了干净语音的大部分信息,因此,利用稀疏表示系数重构语音能达到修复截幅语音波形的目的。由图14(b)可见,当截幅程度较大时,使用OMP算法和COMP算法无法达到修复波形的效果。当截幅程度较大时,由于可靠样点数量少,使用OMP算法对可靠样点进行稀疏分解后得到的稀疏表示系数不足以表征干净语音的信息,因此OMP算法在截幅程度较大时无法起到修复截幅失真的作用,甚至会使得修复后语音的质量不如截幅语音。COMP算法是在OMP算法的基础上对截幅样点添加幅度约束条件来提高修复效果。但是,当截幅程度较大时,在OMP算法无法取得较好的修复效果的前提下,通过添加约束条件也无法找到一组能表征干净语音的稀疏表示系数,导致不能取得较好的修复效果。
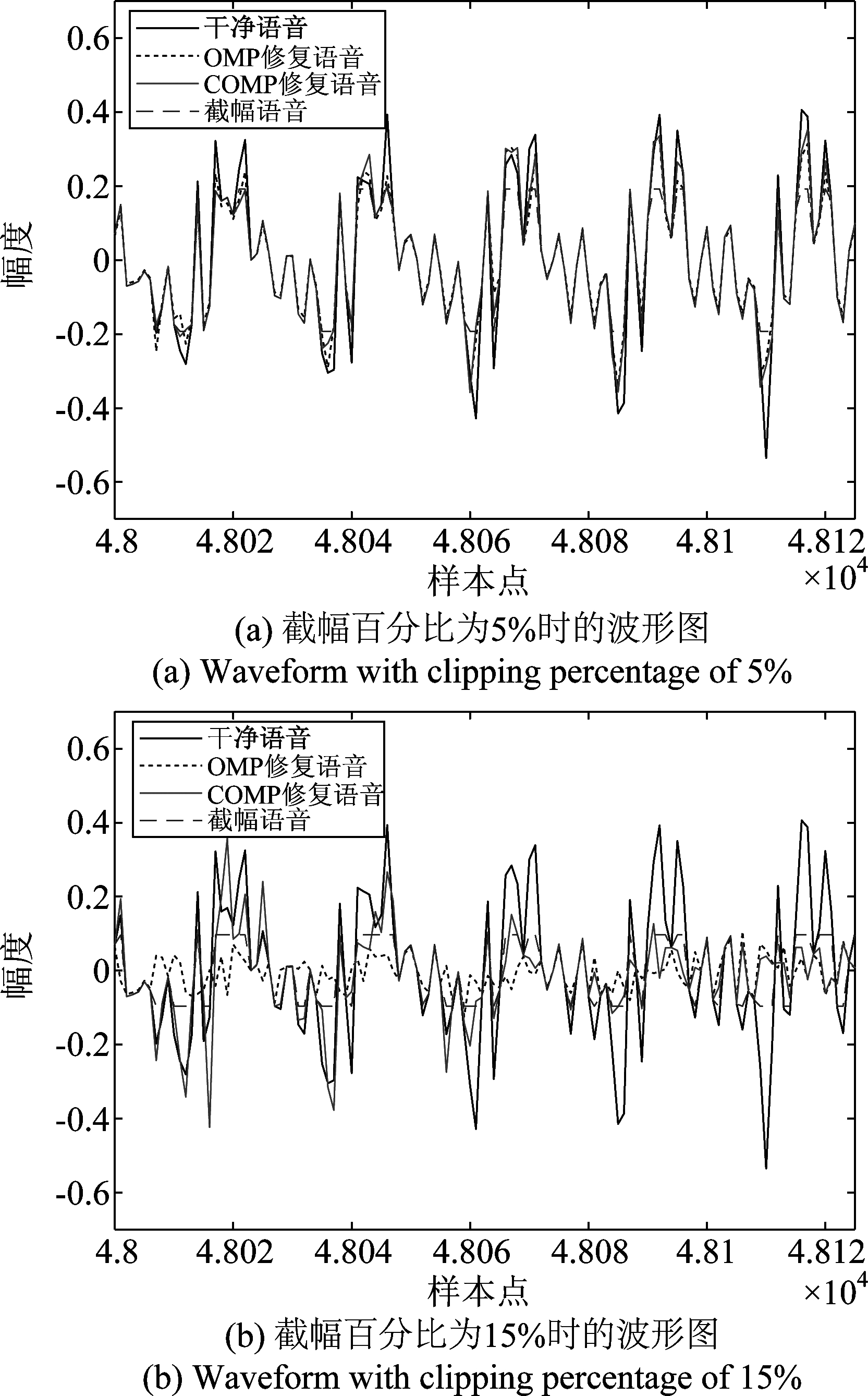
图14 OMP算法和COMP算法修复波形对比图
Fig.14 Comparison of the waveform reconstructed by OMP and the waveform reconstructed by COMP
4.2.2 常见修复方法对清浊音判决准确率的影响
图15给出了在不同截幅程度下,截幅修复预处理对清浊音判决的影响。由图15(a)可见,CIHT算法和CDL算法都能有效提高清浊音判决的准确率。其中CDL算法对清浊音判决准确率的提高更加明显。图15(b)展示了OMP算法和COMP算法对清浊音判决的影响。由于OMP算法和COMP算法在截幅程度较大时无法利用可靠部分对截幅语音波形进行修复,甚至使得波形失真更加严重,导致截幅语音携带的有用信息丢失,最终使得MELP编码器无法对语音进行正确的清浊音判决。
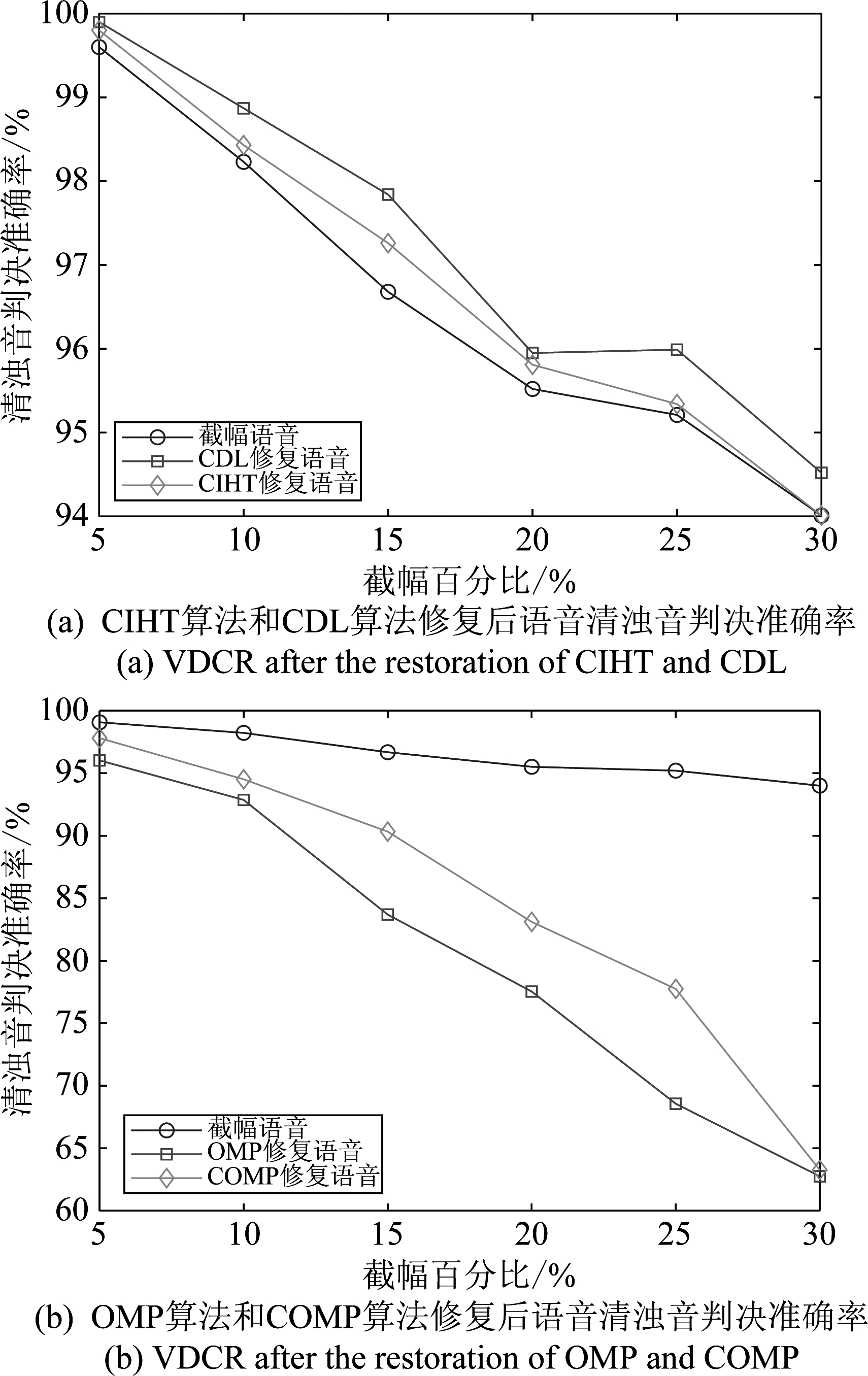
图15 清浊音判决准确率
Fig.15 Voicing decision correct rate
4.2.3 常见修复方法对LPC谱失真测度的影响
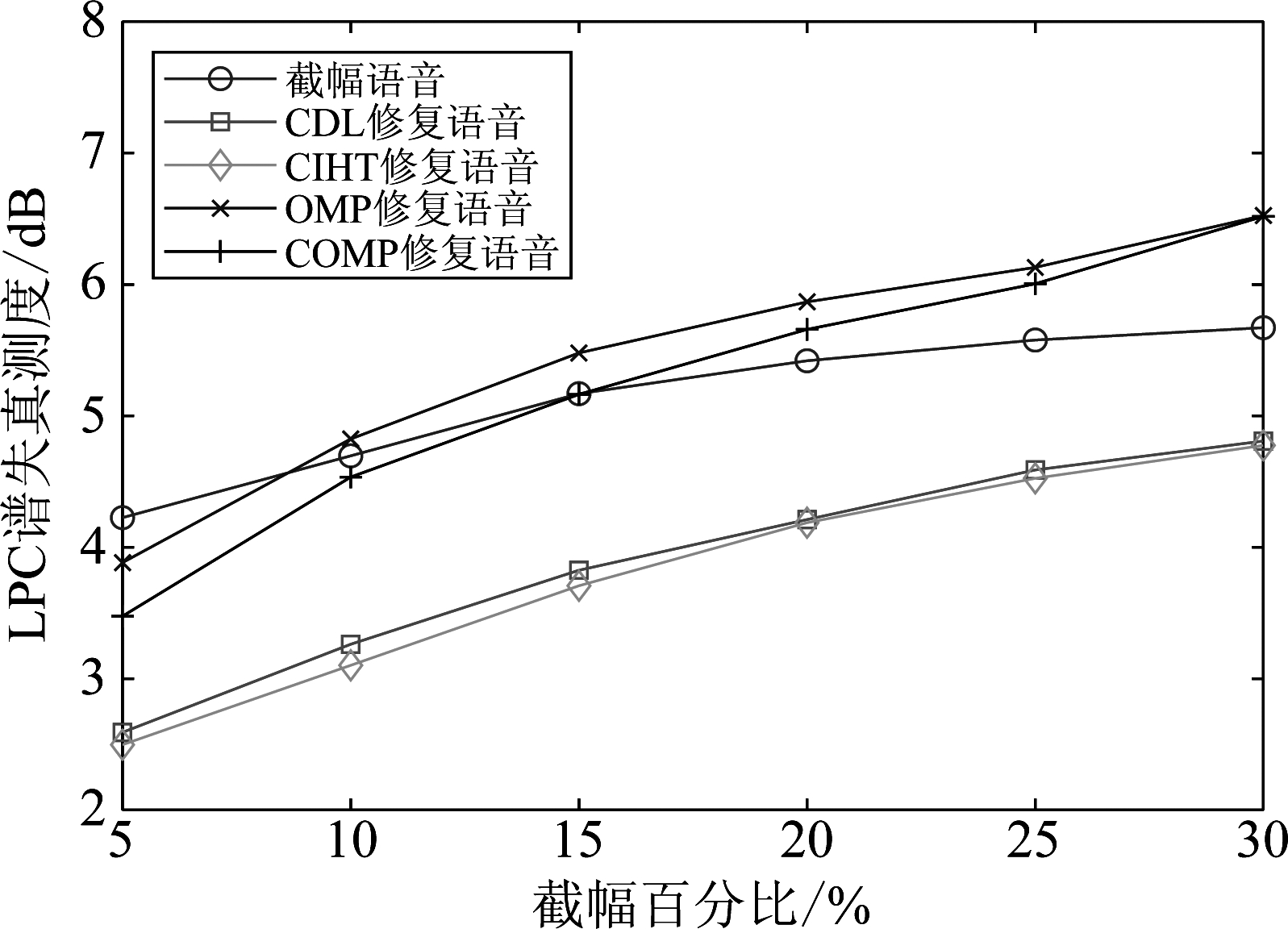
图16 谱失真测度
Fig.16 Spectral distortion at different clipped percentage
图16描述了在不同截幅程度下,截幅修复预处理对LPC谱失真的影响。由图可见,使用CIHT算法和CDL算法对截幅语音进行预处理能有效降低LPC谱失真值。而利用OMP修复算法和COMP修复算法只有在截幅程度较小时,才能降低LPC谱失真值。当截幅程度较大时,使用OMP算法和COMP算法对截幅语音进行修复后反而导致LPC谱失真值的上升。
图17展示了在截幅程度为15%的情况下,截幅修复预处理对LPC谱包络的影响。由图17可见,截幅失真的存在会使共振峰的位置发生明显的移位,从而导致MELP编码器无法准确地提取语音的LPC参数。截幅失真可以看作对语音波形的一次整形,当语音受到截幅失真的影响时,语音样本点之间的短时相关性受到了破坏,从而导致共振峰的移位。由图17(a)可知,使用CIHT算法和CDL算法对截幅语音进行预处理后,共振峰的位置与干净语音共振峰的位置更加接近。由图17(b)可见,使用COMP算法对截幅语音进行预处理后,虽然能使共振峰的位置与干净语音共振峰的位置更加接近,但LPC谱包络的形状与干净语音的LPC谱包络形状还有较大的差距。而使用OMP算法对截幅语音进行预处理并不能给截幅语音的LPC谱包络带来较好的改善。
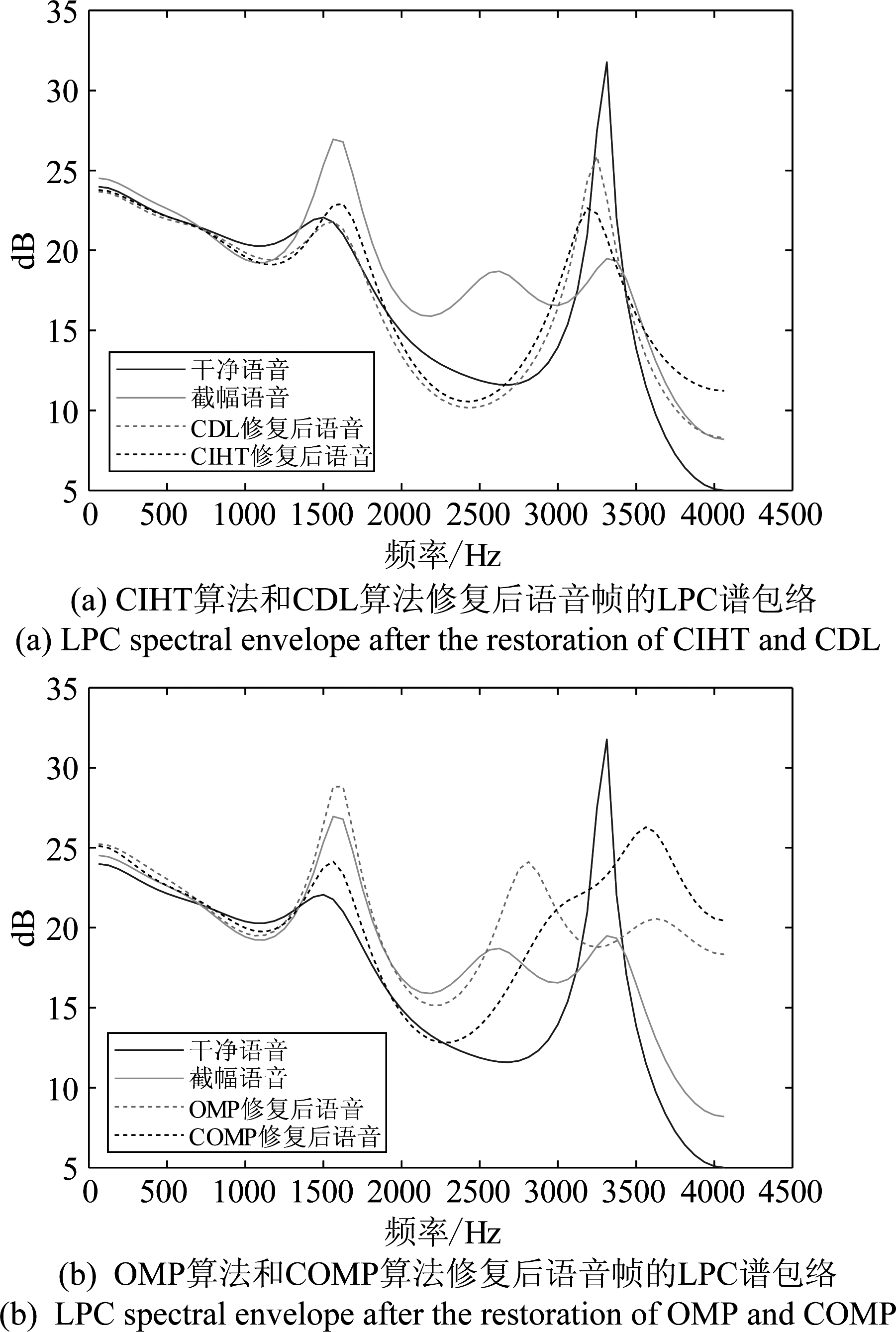
图17 LPC谱包络
Fig.17 LPC spectral envelope
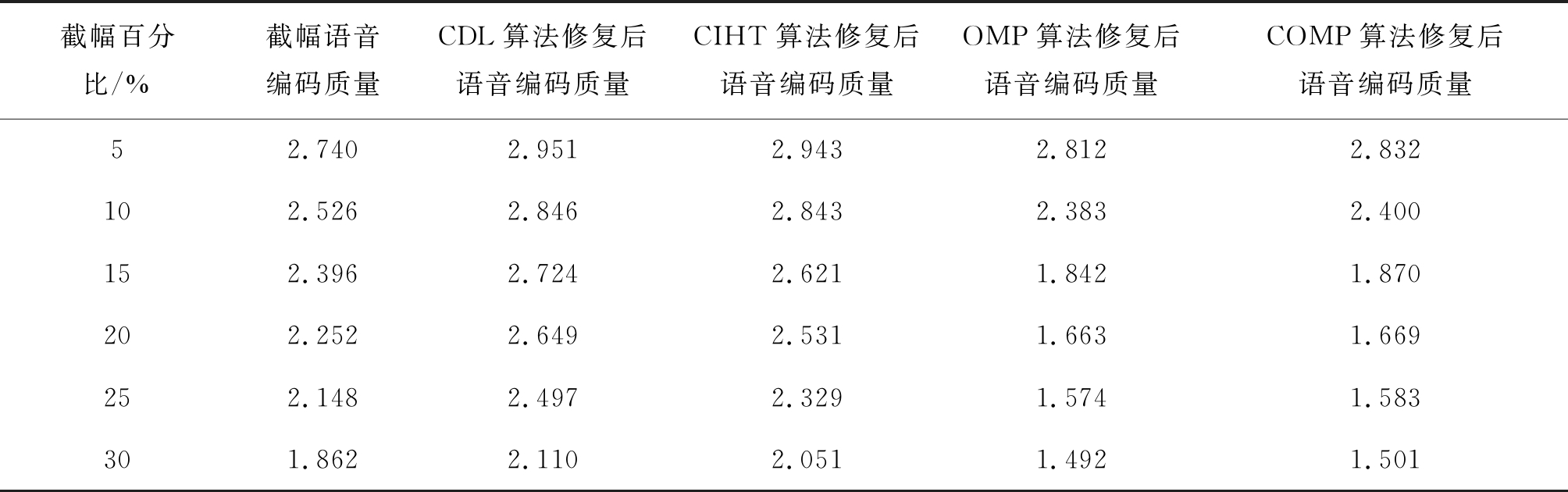
表1 合成语音PESQ打分对比表
Tab.1 PESQ score for synthetic speech
截幅百分比/%截幅语音编码质量CDL算法修复后语音编码质量CIHT算法修复后语音编码质量OMP算法修复后语音编码质量COMP算法修复后语音编码质量52.7402.9512.9432.8122.832102.5262.8462.8432.3832.400152.3962.7242.6211.8421.870202.2522.6492.5311.6631.669252.1482.4972.3291.5741.583301.8622.1102.0511.4921.501
4.2.4 常见修复方法对合成语音PESQ值的影响
本文使用MELP编码器在不同截幅程度下对截幅语音、CDL算法修复后语音、CIHT算法修复后语音、OMP算法修复后语音和COMP修复后语音进行编码和解码后得到合成语音。然后对合成语音进行PESQ打分,最后得到PESQ值如表1所示。
由表1可见,使用CIHT算法和CDL算法对截幅语音进行预处理能给合成语音的PESQ打分值带来0.2～0.4的提高。由于OMP修复算法和COMP修复算法在截幅程度较大时无法对截幅语音进行有效的修复,因此,当截幅百分比为5%时,使用OMP修复算法和COMP修复算法对截幅语音进行预处理能提高合成语音的PESQ值。但是,当截幅程度增大时,使用OMP算法和COMP算法无法提高合成语音的PESQ值,甚至使得合成语音的PESQ值低于截幅语音的PESQ值。
4.3 改进型修复方法对编码参数的影响
由4.2节可知,使用CIHT算法和CDL算法对截幅语音进行预处理能有效提高语音的编码质量。但是,CIHT算法和CDL算法在截幅程度较大时,截幅修复性能下降严重,算法对不同截幅程度的适应能力差[15]。为了克服此项缺点,本文采用ACIHT算法和ACDL算法两种改进型算法对语音进行预处理,并与CIHT算法和CDL算法进行对比,研究了改进型算法对低速语音编码性能的改善情况。
4.3.1 改进型修复方法对基音估计准确率的影响
图18描述了在不同截幅程度下,CIHT算法、CDL算法、ACIHT算法和ACDL算法对基音估计准确率的影响。相比于使用CIHT算法和CDL算法修复后的语音,经过ACIHT算法和ACDL算法修复后的语音有着更高的基音估计准确率。由图18可以发现,当截幅程度较大时,ACIHT算法和ACDL算法对基音估计准确率的提高优于CIHT算法和CDL算法。但是当截幅百分比为5%时,CIHT算法和CDL算法对基音估计准确率的提高优于ACIHT算法和ACDL算法。这是由于ACIHT算法和ACDL算法使用语音截幅程度的信息对约束条件进行加强,从而达到在截幅程度较大时有较好的修复效果。但是当截幅程度较小的时候,引入截幅程度信息对约束条件进行加强后,会导致修复后的截幅样点幅值大于干净语音的幅值,从而给语音带入新的失真,最终导致基音估计准确率的下降。
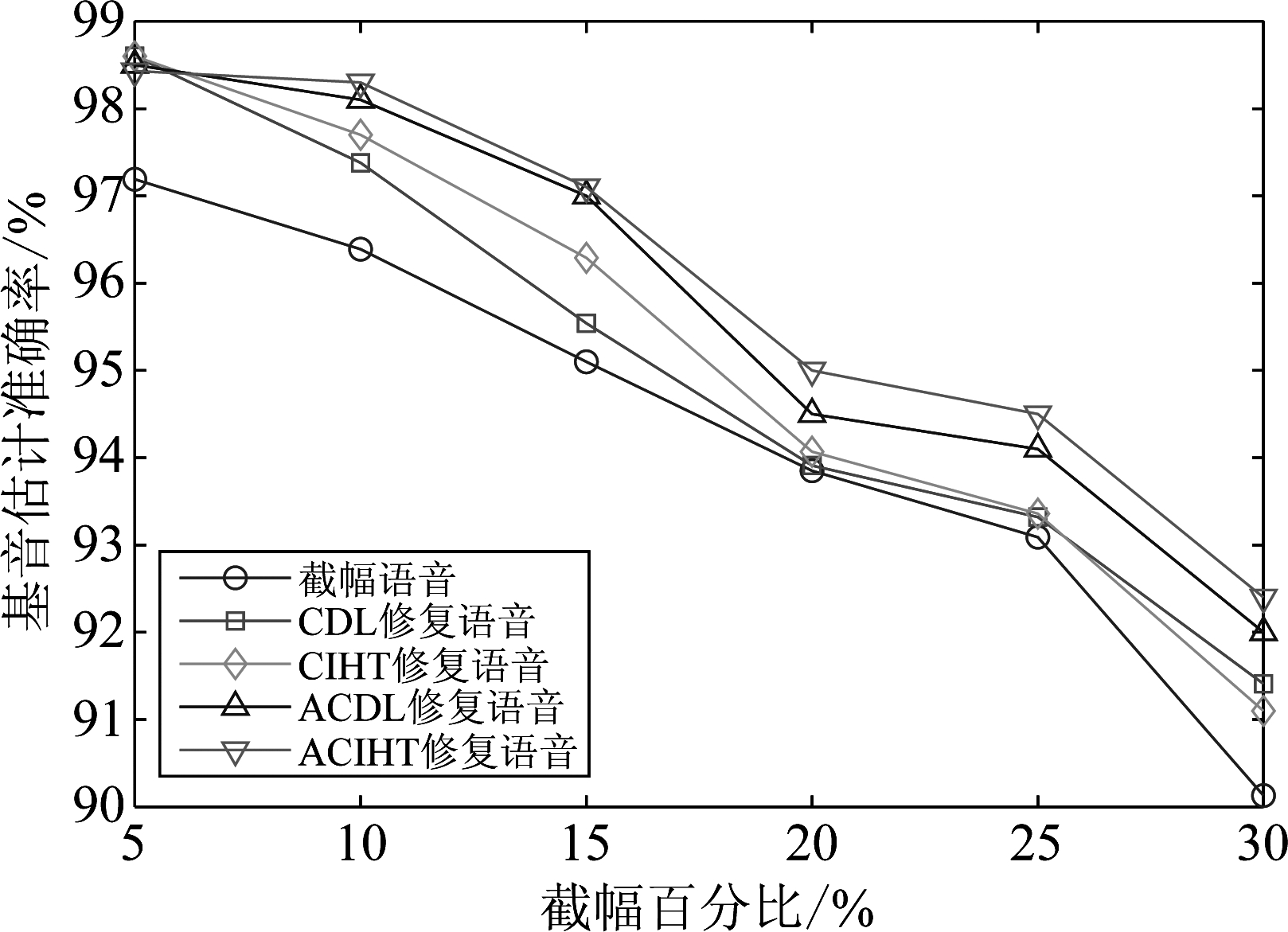
图18 CIHT算法、CDL算法、ACIHT算法和ACDL算法 修复后语音的基音估计准确率的影响
Fig.18 Pitch estimation accuracy after the restoration of CIHT, CDL, ACIHT and ACDL
4.3.2 改进型修复方法对清浊音判决准确率的影响
图19给出了在不同截幅程度下,截幅修复预处理对清浊音判决的影响。由图19可见,在截幅程度较大时,两种改进型截幅修复方法为清浊音判决准确率带来的提高更加明显。但是,在截幅程度为5%的情况下,由于ACIHT算法和ACDL使用截幅程度对约束条件进行加强后有可能导致新的失真产生,从而导致清浊音判决准确率提升不明显。
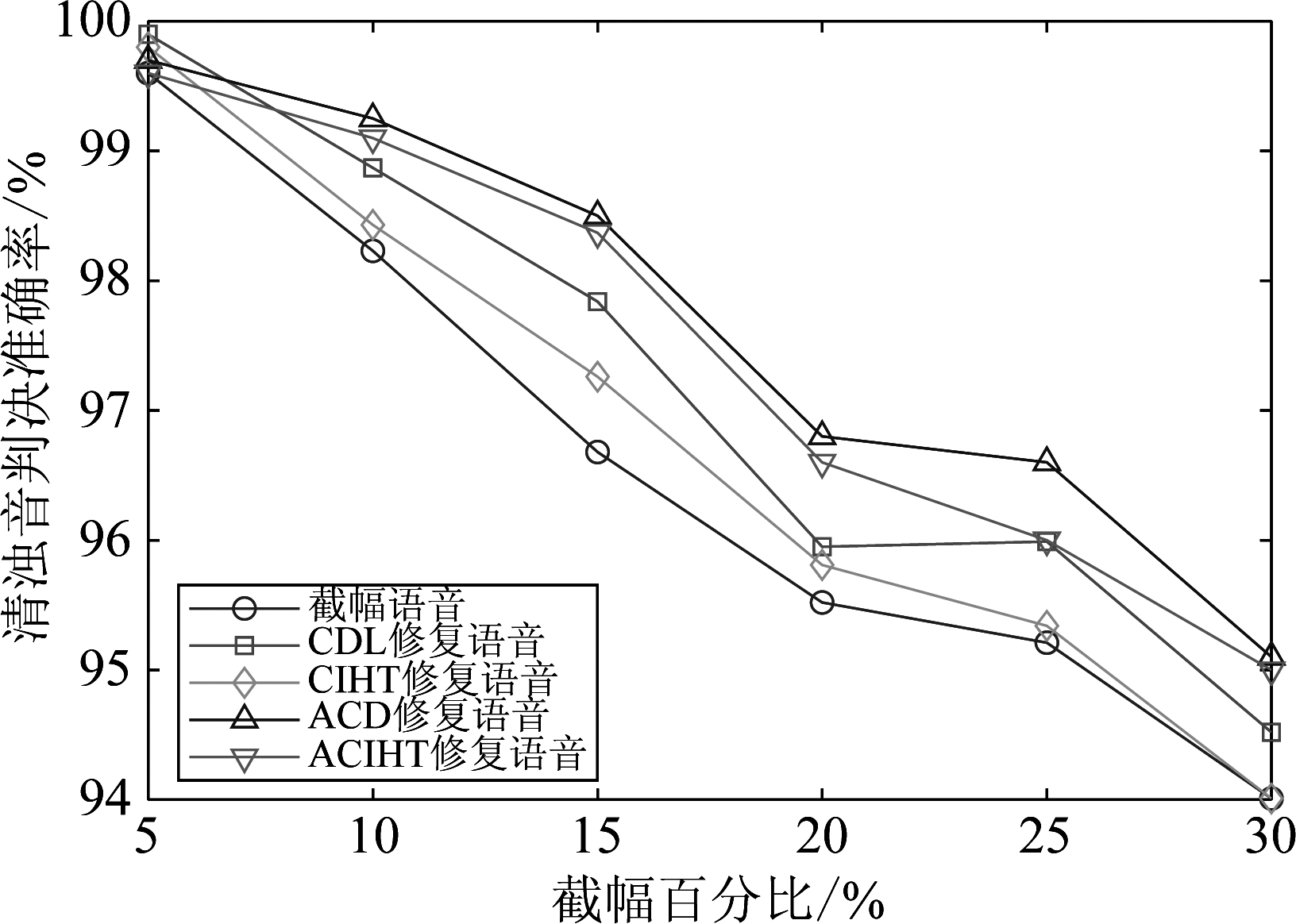
图19 CIHT算法、CDL算法、ACIHT算法和ACDL算法 修复后语音的清浊音判决准确率
Fig.19 VDCR after the restoration of CIHT, CDL, ACIHT and ACDL
4.3.3 改进型修复方法对LPC谱失真测度的影响
图20描述了在不同截幅程度下,使用CIHT算法、CDL算法、ACIHT算法和ACDL算法对截幅语音进行预处理后语音的谱失真测度。使用四种截幅修复算法对截幅语音进行预处理都能降低LPC谱失真值。相比于CIHT算法和CDL算法,ACIHT算法和ACDL算法为LPC谱失真值带来的降低更加明显。其中CIHT算法和CDL算法能给LPC谱失真值带来0.9dB～1.7dB的降低,而两种改进型方法能给LPC谱失真值带来1.1dB～2.1dB的降低。
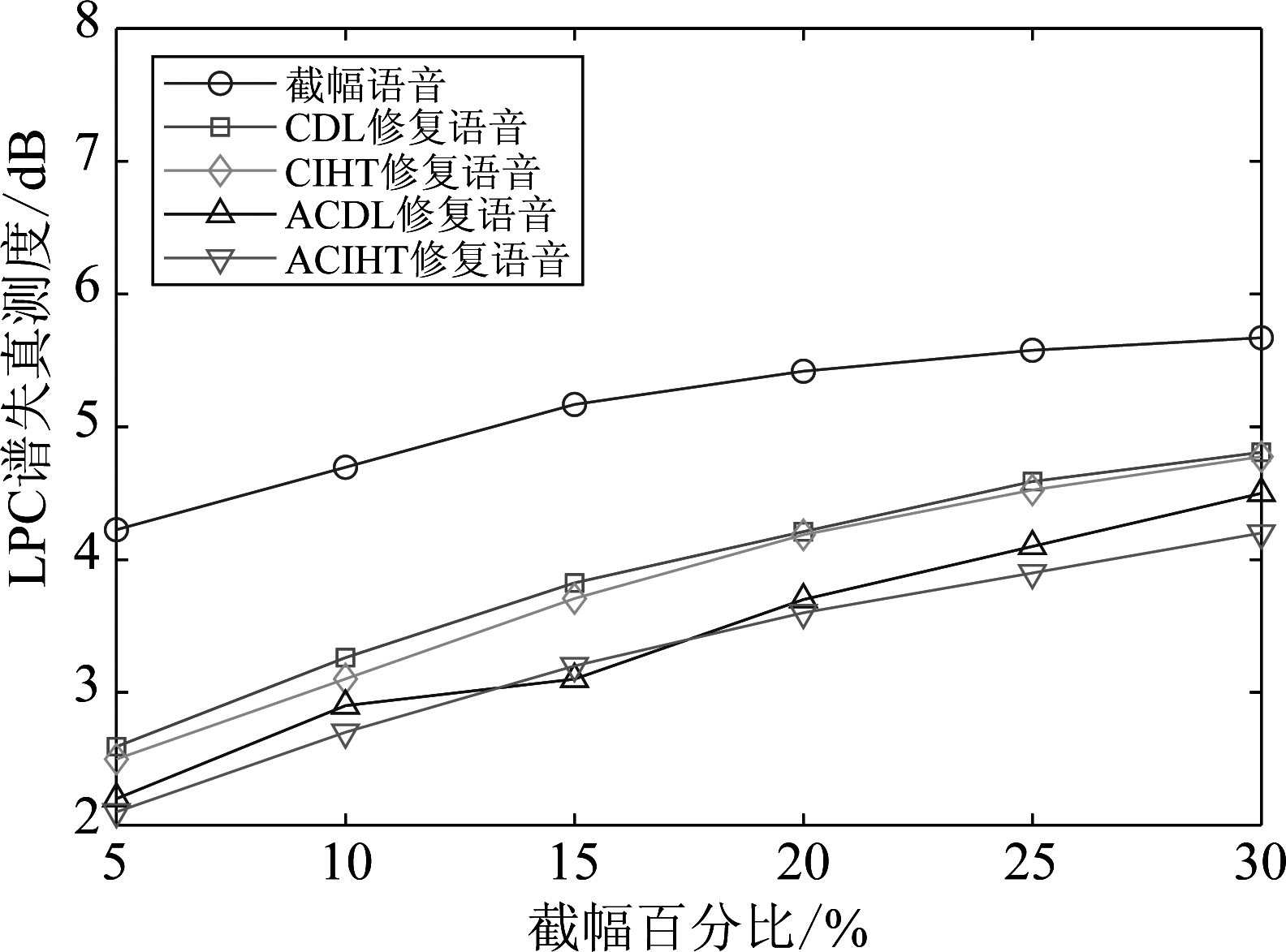
图20 CIHT算法、CDL算法、ACIHT算法和ACDL 算法修复后的谱失真测度
Fig.20 Spectral distortion at different clipped percentage
图21给出了在截幅程度为15%的情况下,CIHT算法、CDL算法、ACIHT算法和ACDL算法对LPC谱包络的影响。相比于CIHT算法和CDL算法,使用ACIHT算法和ACDL算法进行预处理能使共振峰位置与干净共振峰位置更接近,且LPC谱包络的形状与干净语音谱包络形状更相似。其中,使用ACIHT算法进行预处理后的LPC谱包络与干净语音最为相似。
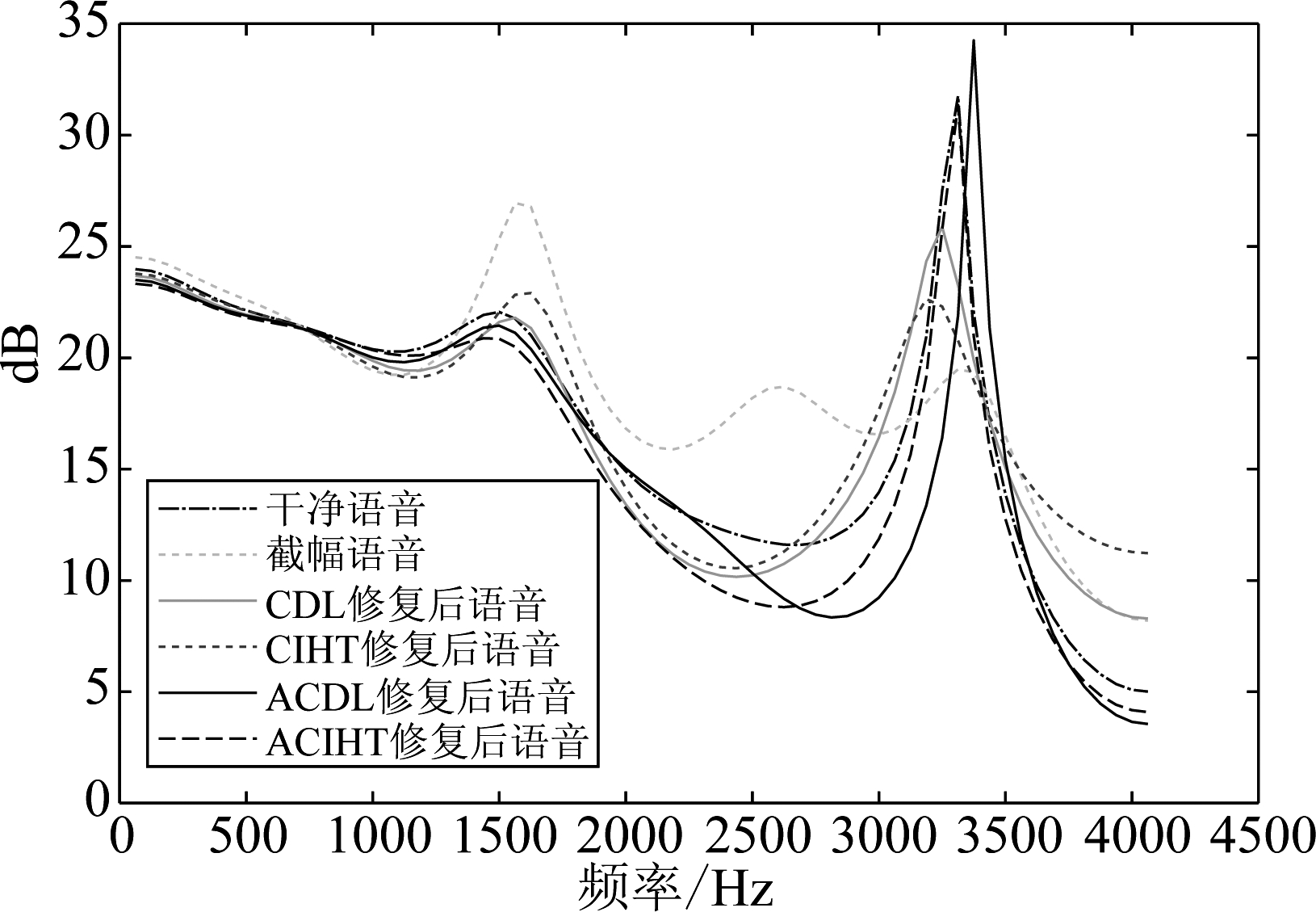
图21 LPC谱包络
Fig.21 LPC spectral envelope
4.3.4 改进型修复方法对合成语音PESQ值的影响
与4.2.4节相似,使用MELP编码器在不同截幅程度下对ACDL算法修复后语音和ACIHT算法修复后语音进行编码和解码得到合成语音。然后对合成语音进行PESQ打分,并与CIHT算法和CDL算法修复后合成语音的PESQ值进行对比,得到合成语音PESQ打分对比表如表2所示。
由表2可以看出,相比于CIHT算法和CDL算法,两种改进型算法对合成语音PESQ值的提高更加明显。在截幅程度较大时,ACIHT算法和ACDL算法也能给合成语音的PESQ值带来0.3～0.5的提高。
表2 合成语音PESQ打分对比表
Tab.2 PESQ score for synthetic speech
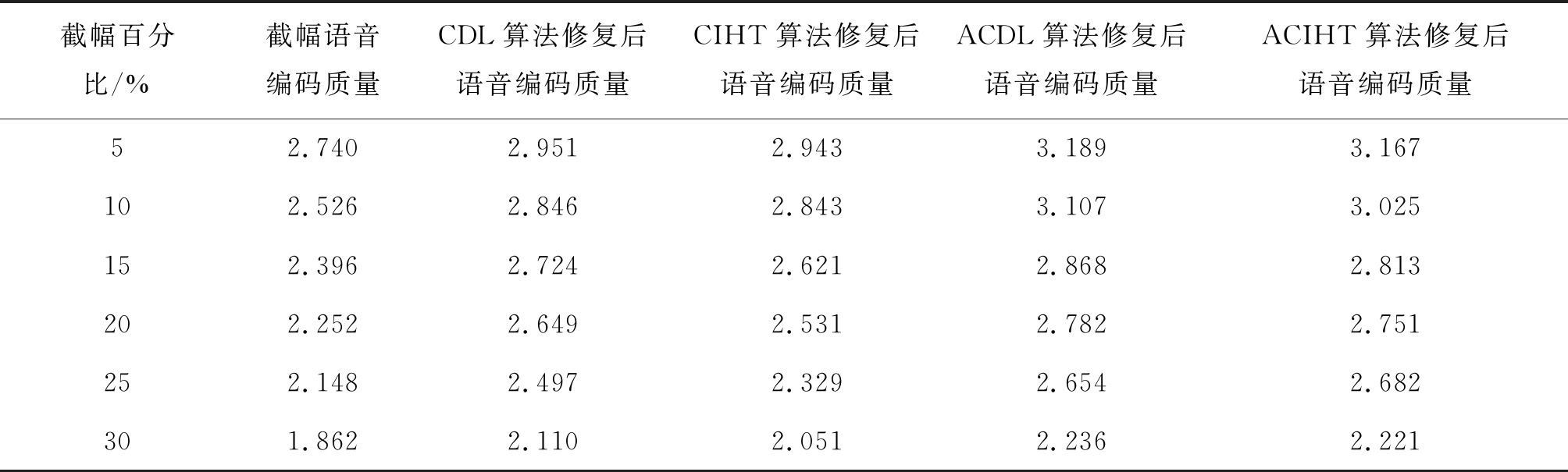
截幅百分比/%截幅语音编码质量CDL算法修复后语音编码质量CIHT算法修复后语音编码质量ACDL算法修复后语音编码质量ACIHT算法修复后语音编码质量52.7402.9512.9433.1893.167102.5262.8462.8433.1073.025152.3962.7242.6212.8682.813202.2522.6492.5312.7822.751252.1482.4972.3292.6542.682301.8622.1102.0512.2362.221
4.4 截幅修复算法计算成本对比
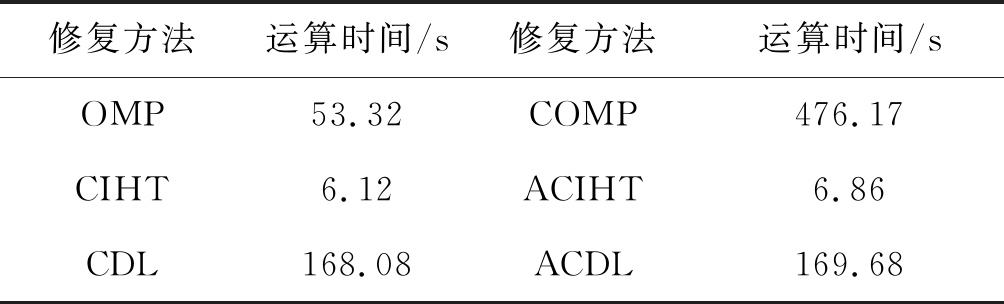
本文在运行环境为Intel(R) Core(TM) i5- 8250U的条件下,对六种不同截幅修复算法的运算成本进行测试,得到不同截幅修复算法的运算时间如表3所示。其中,测试语音的截幅比为15%,长度为34.38 s。
表3 不同截幅修复算法运算时间对比表
Tab.3 Computation time of different declipping algorithms
修复方法运算时间/s修复方法运算时间/sOMP53.32COMP476.17CIHT6.12ACIHT6.86CDL168.08ACDL169.68
由表3可见,CIHT算法和ACIHT算法拥有较快的运算速度。这是由于CIHT算法和ACIHT算法是使用梯度下降的方法求解稀疏表示系数,也没有字典更新的阶段,因此CIHT算法和ACIHT算法拥有较快的运算速度。相比于OMP算法,COMP算法在利用OMP算法求解稀疏表示系数后,需要使用约束条件对截幅样点的幅值进行更新,因此会大幅地增加算法的运算时间。而两种改进型算法的运算时间与原有算法相近,没有大幅增加算法的运算成本。
5 结论
对于低速语音编码器而言,基音周期、清浊音判决参数和线性预测系数的准确提取是十分重要的,这直接决定了解码端合成语音的质量。截幅失真的存在会直接影响低速语音编码器提取语音参数的性能,选择良好的截幅修复方法对截幅失真进行修复能有效提高低速语音编码器的编码性能,从而提升解码端合成语音的质量。在不同截幅程度下,本文使用基音估计准确率、清浊音判决准确率和LPC谱失真测度等评价指标分析了截幅失真对低速语音编码器参数提取性能的影响,然后使用常见截幅修复方法对截幅语音进行预处理,研究了截幅预处理对低速语音编码性能的影响,最后提出采用两种改进型截幅修复方法对截幅语音进行修复,并与原有方法进行对比,验证了改进型截幅方法在提升低速语音编码性能上的优越性。该研究对于设计特定的截幅修复算法或对低速语音编码器的各项参数使用最优截幅修复算法具有一定的指导意义。
[1] Supplee L, Cohn R, Collura J, et al. MELP: the new federal standard at 2400 Bps[C]∥IEEE International Conference on Acoustics., Speech, and Signal Processing. Germany: IEEE, 1997: 1591-1594.
[2] Defraene B, Mansour N, Steven H, et al. Declipping of Audio Signals Using Perceptual Compressed Sensing[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2013, 21(12): 2627-2637.
[3] Shi W H, Zhang X W, Zou X, et al. An experimental study of noise on the performance of a low bit rate parametric speech coder[C]∥IEEE International Workshop on Acoustic Signal Enhancement. China: IEEE, 2016: 1- 4.
[4] Guilmin G, Jeannes R, Gournay P. Study of the influence of noise preprocessing on the performance of a low bit rate parametric speech coder[C]∥European Conference on Speech Communication and Technology. Budapest, Hungary, 1999: 2367-2370.
[5] Agarwal T, Kabal P. Pre-processing of noisy speech for voice coders[C]∥Proc IEEE Workshop on Speech Coding. Japan: IEEE, 2002: 169-171.
[6] Guilmin G, Jeanne R. On the optimisation of noise pre-processing for a low bit rate parametric speech coder[C]∥Workshop on Friendly Exchanging through the Net March. Bordeaux, France, 2000: 22-24.
[7] Shi W H, Zhang X W, Zou X, et al. Experimental study on noise pre-processing for a low bit rate speech coder[C]∥International Conference on Wireless Communications & Signal Processing. China: IEEE, 2016: 1-5.
[8] Adler A, Emiya V, Jafari M G, et al. Audio inpainting[J]. IEEE Transactions on Audio Speech and Language Processing, 2012, 20(3): 922-932.
[9] Defraene B, Mansour N, Steven H, et al. Declipping of audio signals using perceptual compressed sensing[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2013, 21(12): 2627-2637.
[10]Ozerov A, Pilen C, Perez P. Multichannel audio declipping[C]∥IEEE International Conference on Acoustics, Speech, and Signal Processing. China: IEEE, 2016: 659- 663.
[11]Siedenburg K, Kowalski M, Monika D. Audio declipping with social sparsity[C]∥IEEE International Conference on Acoustics, Speech and Signal Processing. Italy: IEEE, 2014: 1577-1578.
[12]Rencker L, Bach F, Wang W W, et al. Consistent dictionary learning for signal declipping[C]∥International Conference on Latent Variable Analysis and Signal Separation. Guildford, UK: Springer, 2018: 446- 455.
[13]Kitic S, Jacques L, Madhu N. Consistent iterative hard thresholding for signal declipping[C]∥IEEE International Conference on Acoustics, Speech, and Signal Processing. Canada: IEEE, 2013: 5939-5943.
[14]Wu P L, Zou X, Sun M, et al. Adaptive Consistent Dictionary Learning for Audio Declipping[C]∥Proceedings of the 6th Conference on Sound and Music Technology. Springer, Singapore, 2019: 73- 83.
[15]邹霞, 吴彭龙, 孙蒙, 等. 一种用于截幅音频修复中的自适应一致迭代硬阈值算法[J]. 电子与信息学报, 2019, 41(4): 925-931.
Zou X, Wu P L, Sun M, et al. An adaptive consistent iterative hard thresholding algorithm for audio declipping[J]. Journal of Electronics & Information Technology, 2019, 41(4): 925-931.(in Chinese)
[16]Duta L, Gheorghe L, Tapus N. Real time implementation of melp speech compression algorithm using blackfin processors[C]∥International Symposium on Image and Signal Processing and Analysis. Croatia: IEEE, 2015, 25(4): 250-255.
[17]Zue V, Seneff S, Glass J. Speech database development at MIT: TIMIT and beyond[J]. Speech Communication, 1990, 9(4): 351-356.
[18]Gray A, Markel J. Distance measures for speech processing[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1976, 24(5): 380-391.
