1 引言
现代战争中对抗性和杀伤性不断升级,电子对抗和电子侦察逐渐成为“不开火”时的排头兵,地位逐渐崛起。雷达作为现代战争的千里眼,在战争中起着至关重要的作用。主动雷达面对具有低空突防和隐身等特性的高速飞行器,往往无法实现准确的探测,此时可利用被动探测技术,即电子侦察。在被动探测技术领域,电子侦察中的无源定位是指设备本身不辐射电磁波,通过接收辐射源目标辐射的电磁信号,并进行信号检测、单站测向或多站联合测向,求解目标辐射源坐标位置。在多站联合定位技术中,通过无人机集群实现对战场多目标同时定位具有先天优势。无人机平台上可以装载体积更小的测量设备(如干涉仪等),且无人机一般体积较小更加能够提高无源探测的隐蔽性和机动性,从而获取更多的战场信息。
在单目标的定位中,测向定位方法(angles of arrival, AOA)仅利用观测站观测到的角度信息对目标进行定位,引进的测量参数较少,且特殊环境下,其他传感器不能有效地进行测量,只能获得角度信息,所以测向定位有着非常重要的研究意义。但是在需要对多个目标进行定位的场景中,每个观测站的测量设备会获得所有目标的观测信息,如何对多个混合来波信号进行角度估计,并在三维空间中将双机角度与同一目标进行对应,是数量和维度增加所产生的新问题。因此,如何将双机信息进行匹配从而得到目标真实的角度估计,是多目标定位中最重要的问题。
文献[1]给出了多信号分类(multiple signal classification, MUSIC)算法,关注于多目标发射器(辐射源)的问题。MUSIC算法提供了1)存在的入射波前数的渐进无偏估计,2)信号的到达方向(direction of arrival, DOA),3)到达波之间的强度和相关关系,4)噪声干扰强度。算法从阵列信号的角度出发,利用特征分解得出信号子空间和噪声子空间,并通过谱搜索得出各个信号对应的来波方向,给后续的多目标信号处理做出了奠基性的研究。而传统MUSIC算法计算量非常大,文献[2]利用均匀圆阵列提出方位角和俯仰角的求解方法,其计算量小复杂度低且可以进行实数域的特征值分解,并能够提供方差估计。文献[3]略过测量的信息需要匹配同一目标的问题,提出一种直接位置确定(direct position determination, DPD)的方法,在二维空间中对所有源进行搜索。文献[4]给出了一种面向DOA测量的多目标位置信息场定位法。文献[5]使用正交投影矩阵方案,采用伪逆矩阵运算,改进了传统MUSIC算法计算量大的缺点。文献[6]提出了一种传感器分离算法来解决DOA系统的多目标信息匹配问题,无须额外的目标识别,将多目标问题变成多个单目标问题进行求解。文献[7]提出一个两阶段过程,首先以粗略间隔评估目标函数并确定峰值,第二阶段基于GSU最小化找出准确峰值,通过精细分辨率的迭代步骤找出缺失的峰。文献[8]提出了一种空间分离技术,用于估计来波的方位角和俯仰角,可以应用于同时确定多个有源目标或无源目标的到达方向。文献[9]给出了单站单目标的克拉美罗界推导过程。实现对目标的成功定位后,进而研究不同场景下目标跟踪的问题[10-11]。
在现有的多站对多目标定位算法中,传统MUSIC估计算法使用均匀线阵列(uniform linear arrays, ULA),计算量大[1]。而本文采用RB-MUSIC[2]算法,即利用均匀圆阵列(uniform circular arrays, UCA),减小了计算量。并且,大部分方法的思路是先对不同观测站观测到的同一目标的信息进行匹配[12],进行信息匹配的前提是需要知道辐射源的数量,因此,往往还要增加一个辐射源数量估计算法。这种方法的缺点是忽略了同一辐射源在不同观测站的接收信号的内在联系,在一定程度上损失了信息量,没有完全利用上所有的观测信息,导致观测精度下降。本文提出了一种联合双机MUSIC匹配测角算法,将两观测站的接收信号结合在同一矩阵中进行估计,通过一起处理观测数据,得出直接匹配相同目标的测向角度解算。并在此基础上,针对高维计算量大的问题,提出一种降维投影的双站联合MUSIC角度估计算法,大大减少了谱函数和谱峰搜索的计算量,且有着良好的测角精度和直接匹配同一目标测向线的优点。在仿真实验中,利用匹配测向法与双机联合MUSIC匹配测角算法进行测角,二者均利用最小二乘算法对目标进行定位解算[13]。并对二者进行了精度对比,仿真结果显示,利用双机联合MUSIC匹配测角算法在方位角的定位精度上有着明显的提升。
2 基于双机信号匹配的AOA定位算法
通过双机分别接收的信号求出对空间所有辐射源的角度估计后,此时所有测向线在空间中混叠,并不能将对应同一目标的双机测向线进行匹配,这样就无法在模型中对目标位置进行准确求解。因此,若想准确求出多个目标的位置,首先需要对双机观测到的信号进行匹配,将属于同一目标的信息联合起来,再对其位置进行解算,这样就可以将多目标问题转化为多个单目标问题[6]。
图1 基于双机信号匹配算法流程
Fig.1 Matching algorithm flow based on dual aircraft signal
为了将信号和噪声从接收数据中分离,对R进行特征分解可得
(1)
一般情况下,接收数据中噪声的能量小于其中信号的能量,所以在进行特征分解后,大特征值对应信号子空间,而小特征值对应噪声子空间。根据此种方法,就可以实现辐射源数量的估计。
然后,在实现辐射源数目估计基础上,需要对双机信息进行匹配。利用异面直线法,选定一个观测站中的一条测向线,计算与另一站中所有测向线的空间距离,选择最小距离所对应的一对测向线,作为两观测站对同一目标的测向角度[12],这样就可得出所有匹配的测向线。
最后,将匹配到同一目标的信息输入到AOA定位模型中,就可以解算出多个目标的位置[14]。在这种先利用空间位置关系对信号进行匹配再利用干涉仪测角的方法中,均是从两观测站对各自的接收信号信息分别独立处理。这样无疑是忽略了同一辐射源在不同观测站的接收信号的内在联系,在一定程度上损失了信息量,没有完全利用所有的观测信息,导致定位精度降低。
3 联合双机MUSIC匹配测角算法
AOA定位模型在定位精度上有着良好的表现[14]。模型重要的输入参量为辐射源来波信号的角度信息(θ,φ),所以如何获得更高精度的角度估计对于获得更高的定位精度起到关键作用。本文采用基于均匀圆阵列UCA的MUSIC算法对来波信号进行角度估计。本节首先介绍利用均匀圆阵列的MUSIC算法测角的原理,进而将其推广到双机定位中,可以直接得到匹配同一目标的角度信息。最后提出一种降维投影的方法对谱峰进行搜索,根据双机观测到的数据得到多个辐射源来波的角度估计。
3.1 基于MUSIC的多目标UCA阵列信号分析
在对圆阵的MUSIC算法研究前,首先对信号的参数和场景做一些简化和约束:(1)UCA中有N个天线,均匀分布在XOY平面;(2)各目标信号之间互不相关且为窄带信号,信号源的个数为Q且符合信源数小于天线数Q<N的前提;(3)接收阵元存在与信号互不相关,均值为0,方差为σ2的高斯白噪声。
设第n个阵元和圆阵中心参考处的由波程差导致的信号延迟为τn0,对窄带信号来说仅考虑在相位上的变化,并考虑存在随机噪声,则两站输出形式为
xn(t)=s(t-τn0)+nn(t)
(2)
由变换后表达可看出,第n个阵元和中心参考处仅有一个相位的变化e-jωτn0,而其中的相位差则是与阵元的几何位置构型直接相关。对于N个天线的均匀圆形阵列,假设第一个阵元位于X轴上,则第n阵元在平面中的角度为2πn/N,第q个信号在阵列中产生的相移为
(3)
对于N个阵元,Q个信源的N*Q方向导向矩阵为
A(θ,φ)=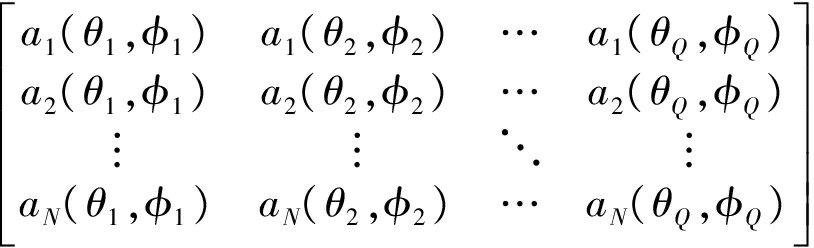 
(4)
则阵列输出信号的矩阵形式为
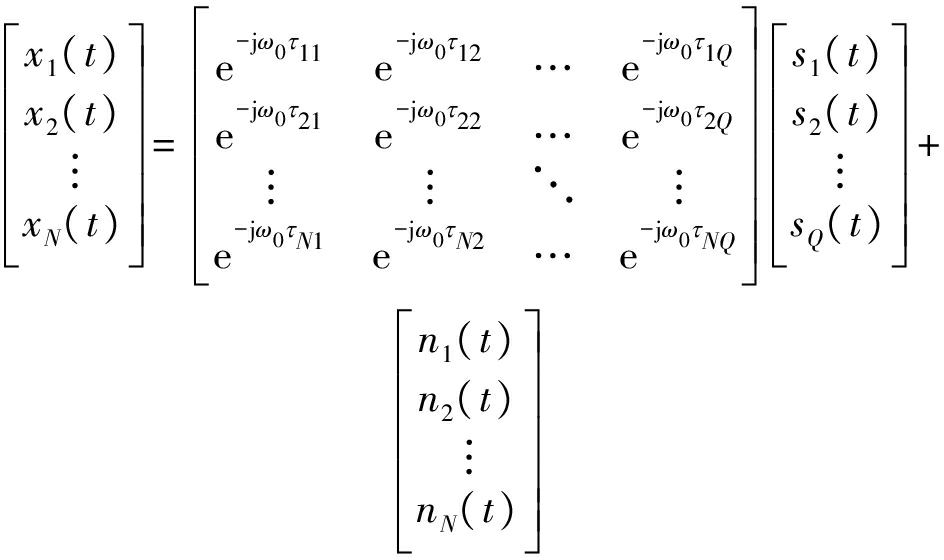
(5)
可进一步简写成
X(t)=A(θ,φ)S(t)+N(t)
(6)
其中,S(t)=[s1(t),s2(t),…,sM(t)]为信号向量,N(t)=[n1(t),n2(t),…,nN(t)]是叠加的噪声向量。可以看出,接收信号主要受阵列流形和噪声影响,首先对时间序列X(t)求协方差矩阵可得
R=E[XXH]=AE[SSH]AH+σ2I=ARSAH+σ2I
(7)
理想条件下,空间中目标信号和加性噪声之间是相互独立的,如上式中R能够划分为由信号和噪声两块组成,其中RS=E[SSH]为信号的自相关矩阵,RN=σ2I为噪声的自相关矩阵,σ2为噪声的功率值。
经典的MUSIC是在元素空间进行的计算,计算逐步过程复杂,且导向向量矩阵结构的局限性使得很多ULA中优秀的算法不能够在均匀圆阵中得到应用。UCA-RB-MUSIC将元素空间转换到了波束空间,通过相位模式激励的波束形成,使得比元素空间有了更多优点如大大减少计算量,可通过实数的特征值分解得到子空间估计,变换后矩阵的范德蒙结构可以利用前后向平均等等优点[15]。
对于均匀圆形阵列来说,第n个元素位置与x轴夹角为γn=2πn/N,此处的位置向量为
考虑到窄带平面波的波数为k0=2π/λ,入射方向为
方位角和俯仰角分别为θ和φ,方向单位向量为
第n元素与中心参考点的相位差为
则元素空间的导向流形向量可表示为
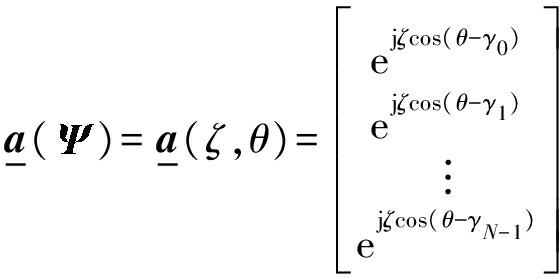
(8)
其中,俯仰角参数由ζ=k0rUcos φ来决定,且用向量
=(ζ,θ)来表示源信号的到达角方向。
对阵列的激励函数进行归一化得出向量
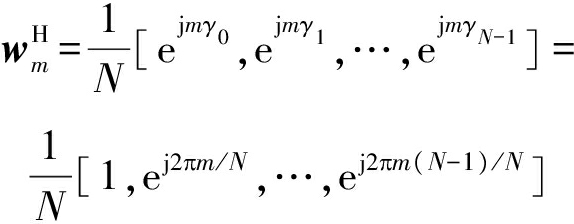
(9)
产生的阵列图案
(10)
为了减少传统MUSIC算法的计算量,减小噪声的影响,UCA-RB-MUSIC算法利用
来将元素空间变换到波束空间,并能够仅计算实值。波束空间变换
)=b()将(8)中的流形向量
)映射到波束空间中b()。波束空间流形b()在整个到达角度空间上=(ζ,θ)=(k0rcos φ,θ)都是实值,并且这使得UCA-RB仅需要实矩阵运算。
首先介绍波束形成器
基于相模激励的原理。这个波束形成器合成波束空间流形矩阵
)=ae(),下面给出各个变量的定义
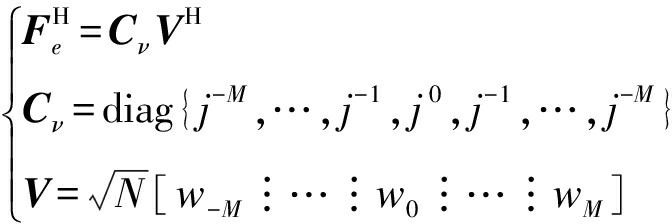
(11)
其中,
在前已给出定义形式,在m相位模式下激励UCA,得到阵列的方向图。其中j|m|被矩阵Cν中相应的j-|m|项抵消,ae()下标e代表偶数。因此合成的波束空间流形
ae(
(12)
其中,ae()的方位角变化通过向量表现
v(θ)=[e-jMθ,…,e-jθ,ej0,ejθ,…,ejMθ]T
(13)
这和ULA的流形向量十分相似。俯仰角的变化通过贝塞尔函数矩阵呈现对称的锥形振幅分布
Jζ=diag[JM(ζ),…,J1(ζ),J0(ζ),J1(ζ),…,JM(ζ)]
(14)
旨在反映Jζ的对角元素在中心元素周围均匀。下面给出和b()的定义:
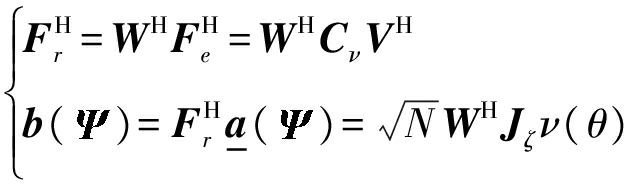
(15)
任何满足
的矩阵都将产生实值波束空间流形b()。除了方位角的旋转之外,构造W使每一列合成相同实值的方向图,也就是说,合成M′=2M+1个角度旋转波束f(ζ,θ-αi),其中f(ζ,θ)是基本波束方向图。这里αi=2πi/M′,i∈[-M,M]是方位角旋转角度。旋转角度的选择以W是为单位,所以是正交的波束形成器。所以有:
⋮…⋮v(α0)⋮…⋮v(αM)]
(16)
其中,v(α)在前定义过。通过W,基础的波束方向图就是ae()中元素之和;因此
合成了维度为M′=2M+1的实值波束空间流形b():
b()=[f(ζ,φ-α-M),…, f(ζ,φ-α-1), f(ζ,φ), f(ζ,φ-α1),…, f(ζ,φ-αM)]T
(17)
在波束空间中求出噪声的特征向量集G,并给出UCA-RB的谱函数
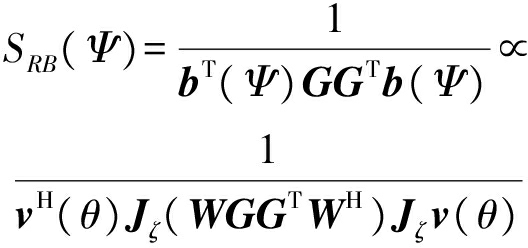
(18)
根据信号的到达方向在i=(θi,φi)处有峰值,因此到达角的估计可通过在2D平面中UCA-RB-MUSIC波谱搜索Q个波峰,根据波峰出现的位置坐标来取到达波的角度估计值。
由以上介绍可知,RB-MUSIC算法主要的优点是仅需要实值特征值分解,而普通MUSIC算法则需要复值特征值分解,这在一定程度上也对噪声进行了抑制,并且降低了算法的复杂度,提高了定位精度。
3.2 双机MUSIC算法模型的建立
对于两观测站A、B,阵列接收信号分别为
(19)
式中,AA,AB分别为两站的阵列导向流形矩阵,S(t)为辐射源信号,NA(t),NB(t)分别为两站接收阵列存在的均值为零,方差为σA,σB高斯白噪声。
对于观测站B接收信号,其阵列输出信号的矩阵形式为
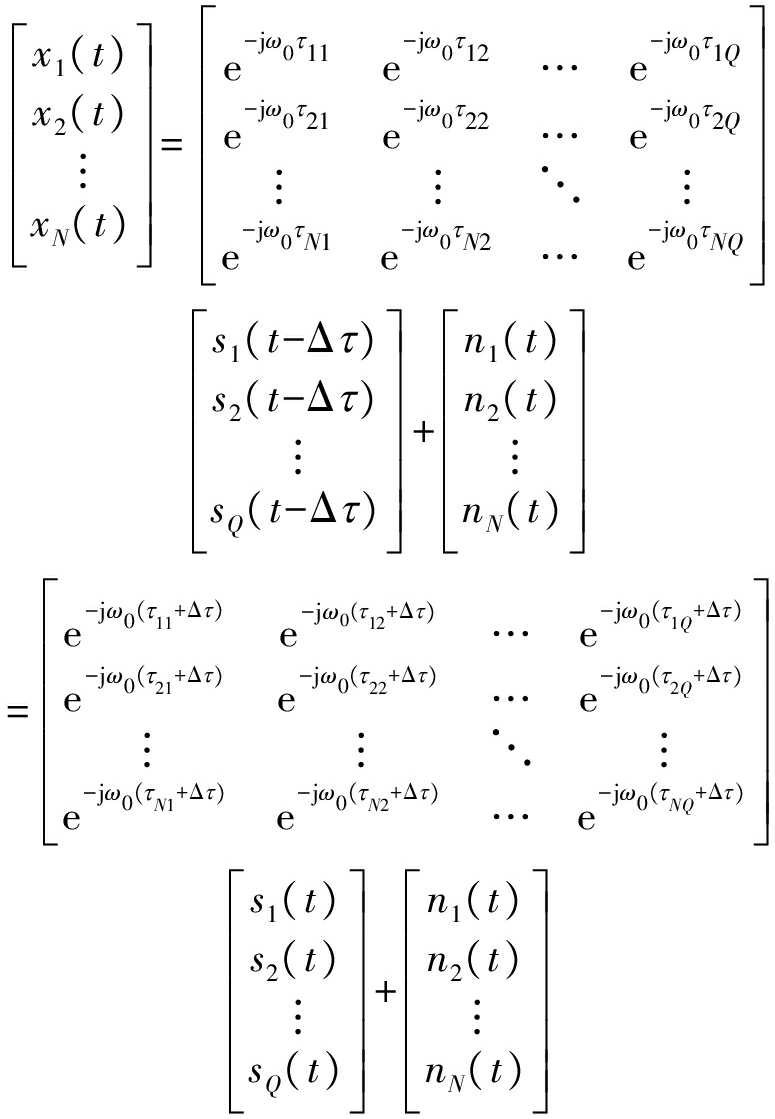
(20)
观测站B阵列接收信号可重新简写为
(21)
其中,
为考虑双站时延差的阵列导向流形矩阵,为了表述方便,后续统一写成AB。
将两站的接收信号放置一起构成新的统一接收信号XAB(t)
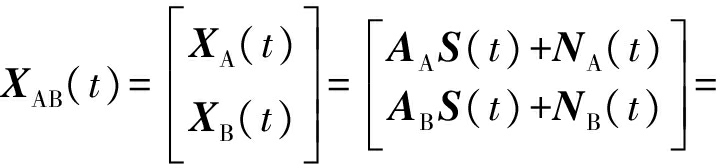
AABS(t)+NAB(t)
(22)
对XAB(t)求协方差矩阵RAB
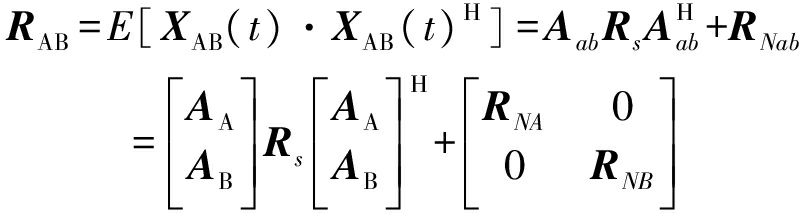
(23)
其中,假设噪声NA(t),NB(t)之间相互独立,且与信号S(t)独立。Rs为S(t)的协方差矩阵,
将上式进一步化简写成最终的分块矩阵形式
(24)
对RAB进行特征值分解,假设对第i个噪声特征值和向量,满足关系
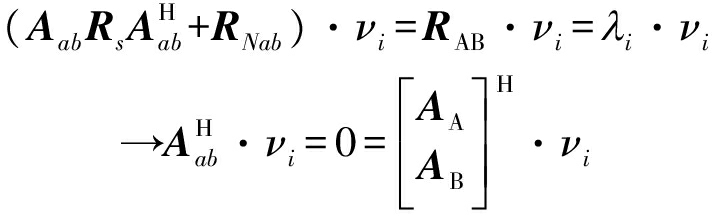
(25)
其中,由于是双站联合观测,
是由两观测站的阵列导向流形向量共同组成的,噪声子空间UNAB是由所有的噪声特征向量νi构成,利用MUSIC构造谱函数的原则得出
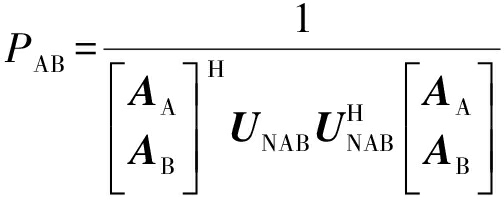
(26)
对得出的谱函数进行谱峰搜索,对应角度坐标位置即为两站对应同一目标的测向匹配角度。
3.3 基于降维投影的谱峰搜索
对于PAB,是受到A站方位角、俯仰角,B站方位角、俯仰角四个角度参数共同影响的谱函数,则需要在一定的步长精度下,在四维参数遍历得出的谱函数分布结果。进行谱峰搜索时若步长较大,可能会导致未能将所有的峰值都找出;若步长较小,则所需循环数较多。对于四维参数的遍历情况,首先在谱函数的生成上就是一件计算量十分巨大的任务,再进行四维谱峰搜索也十分困难,这些在编程实现的过程中都是在循环中完成,计算量和耗时成为了主要问题。同时在存在多个目标的情况下,会出现多个谱峰值。高维空间数据没办法直接进行可视化显示,对找出的峰值也很难进行直观地验证。
根据高维计算量巨大的问题,本文给出一种降维投影的方法,解决谱函数的生成和谱峰搜索的问题,在减小计算量的同时增加测角精度。首先针对辐射源目标一般都出现在远场条件下,较大的距离差使得俯仰角很小,于是可以先合理假设俯仰角φa,φb为0,在谱函数PAB中对方位角θa,θb进行二维遍历,从而完成了数据降维。因为在计算阵列导向流形中的公式为
(27)
即俯仰角的余弦项在整体变量中作为乘积,且当俯仰角接近0时对函数值的影响不大,所以预设为0是合理的。按照图2中的降维投影过程对角度进行估计。
首先,对方位角进行粗略估计。将φa,φb=0代入图2的谱峰搜索过程中,设置步长为1°,θ 的范围为[0,360°],得到了由θa,θb遍历的PAB(θ)1谱函数,是二维离散曲面分布。根据不同角度的视图可以发现,对PAB(θ)1进行侧视图投影,即可将谱峰峰值投影到一维向量的分布中,从而可以更好地分辨峰值位置,进而找出角度。记由第一次谱函数PAB(θ)1找出的方位角度估计为
第二步是将
作为已知量代入谱峰搜索过程中,对φa,φb进行二维遍历,从而找出俯仰角的准确估计。将带入阵列导向流形
中进行预设,对俯仰角参数φa,φb在[-10°,0°]范围内,以步长为0.1°进行遍历,得出谱函数PAB(φ)2。同样将PAB(φ)2分别在φa,φb方向上投影,进行一维的峰值搜索,并根据峰值大小对角度对应,得出俯仰角的准确估计
第三步是将
代入谱峰搜索过程中,求解方位角的准确估计。将带入阵列导向流形中进行预设,对方位角参数设置在
范围内,以步长为0.1°进行遍历,得出谱函数PAB(θ)2。同样将PAB(θ)2分别在θa,θb方向上投影,进行一维的峰值搜索,并根据峰值大小对角度对应,得出俯仰角的准确估计
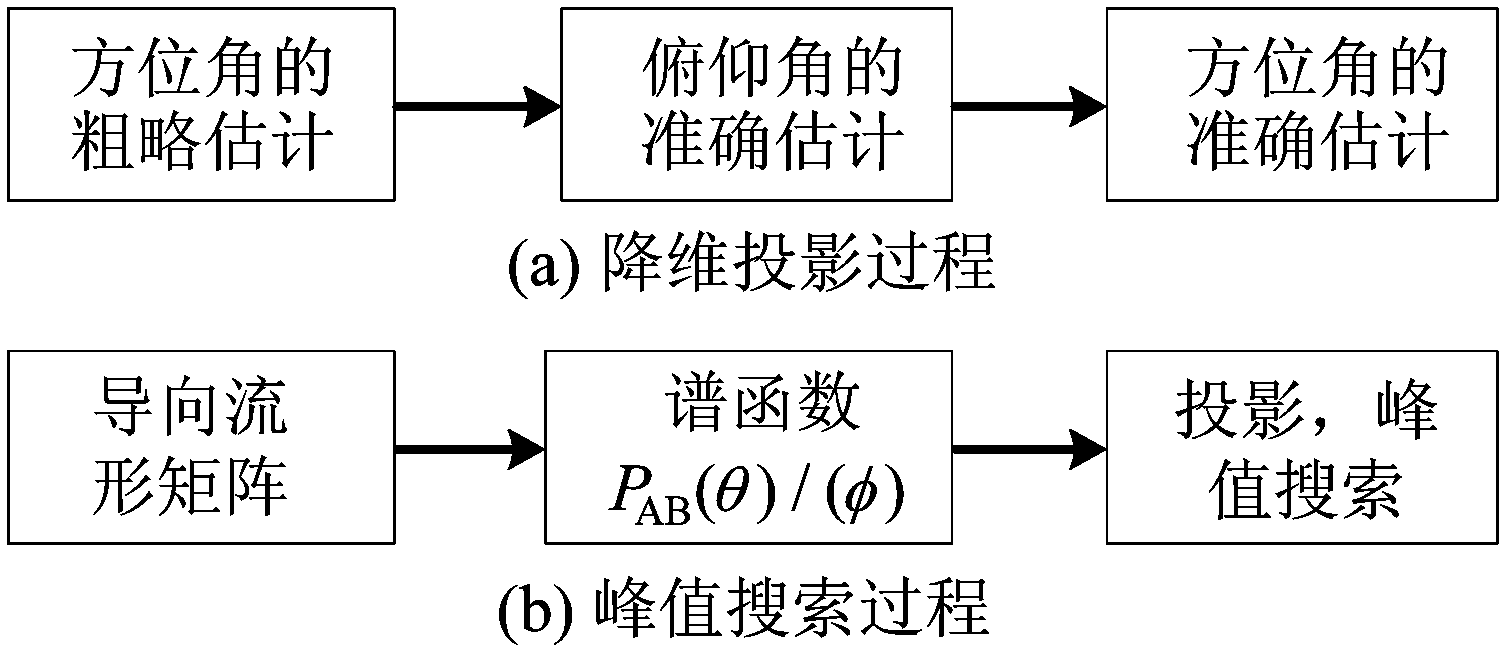
图2 降维投影角度估计步骤
Fig.2 Dimensional reduction projection angle estimation step
综上,通过图2中三次的降维投影、一维峰值搜索,即可获得双站方位角和俯仰角的准确估计,在循环次数上约是以1°步长的四维遍历的1/104,大大的减少了联合匹配测角的计算量,且在最终精准搜索时步长为0.1°,得出的结果还具有更高的测角精度。
3.4 双站联合MUSIC定位的克拉美罗界
双站联合MUSIC定位利用了两个移动站对目标信号的方位信息进行的无偏估计,其定位精度存在一个性能最优边界,即定位精度存在克拉美罗下界(Cramér-Rao lower bound, CRLB),根据经典文献[16]的推导,双站联合MUSIC定位方位角的CRLB可表示为
(28)
其中,
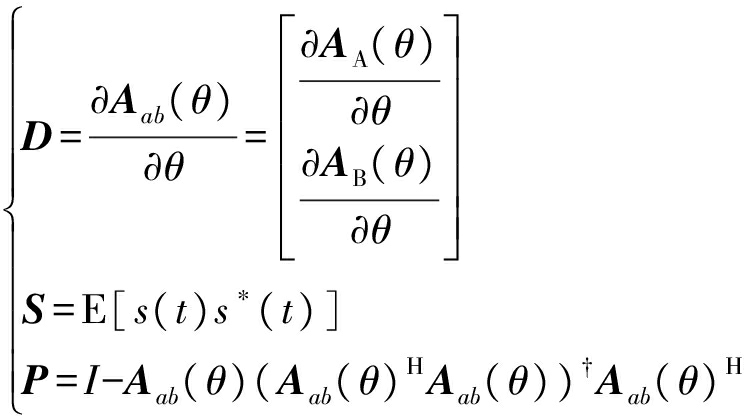
(29)
其中,AA,AB分别为A、B两站的阵列流形。
4 仿真实验
仿真实验条件为:两观测站坐标为(-50,0,10)T,(50,0,10)T,空间辐射源数为2,坐标为(20,100,0)T,(40,-80,0)T,两目标的在两站方位角俯仰角真值分别为θ1=(55.0079°,-41.6334°),φ1=(-4.6834°,-4.7473°),θ2=(-73.3006°,-82.8748°),φ2=(-5.4712°,-7.0705°),接收信号信噪比SNR=10 dB。误差采用均方误差(mean-square error, MSE)作为衡量定位精度的标准。
图3中(a)为预设两站俯仰角为零,将四维角度对应的谱函数PMUSIC(θA,θB,φA,φB)降至两方位角对应的谱函数PMUSIC(θA,θB)1空间分布情况,θA,θB∈[-180°,180°]。由算法原理和公式推导可知,谱峰出现的坐标即对应两站测得的方位角附近。此时由于第一步设定了俯仰角为零,所以是方位角的粗略估计;图(b)为图(a)的俯视图,图中的高亮点即谱峰出现的位置;图(c)、(d)分别是在A、B站方位角方向的侧视图,这样就可以将二维参数的空间谱搜索转化为一维向量分布。
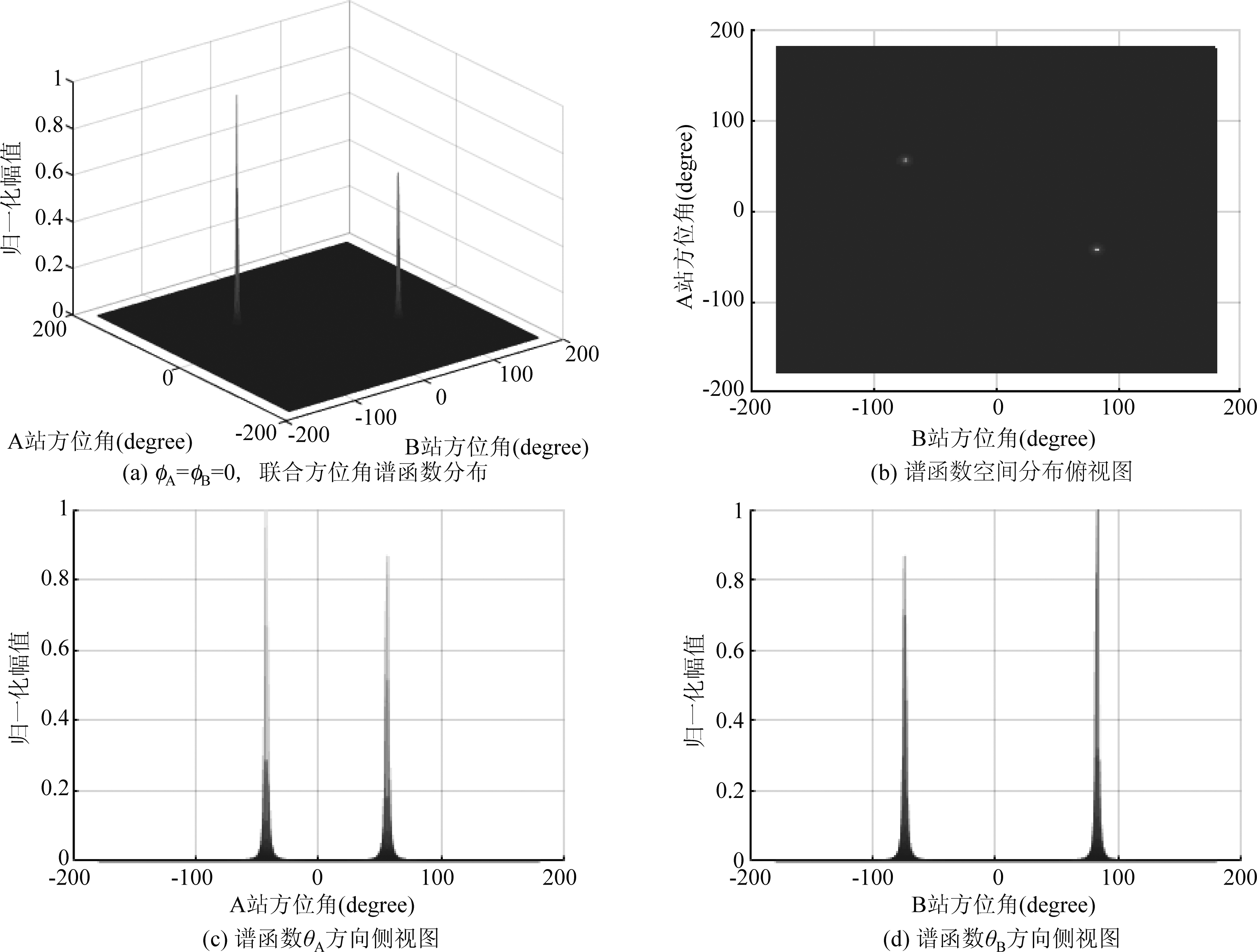
图3 双站联合MUSIC的方位角谱分布及三视图
Fig.3 Azimuth spectrum distribution and three views of dual station combined MUSIC
对PMUSIC(θA,θB)1向两方位角方向投影,分别得出两个一维向量的谱峰分布情况,找出峰值位置并其函数值对角度进行匹配对应,如图4所示。
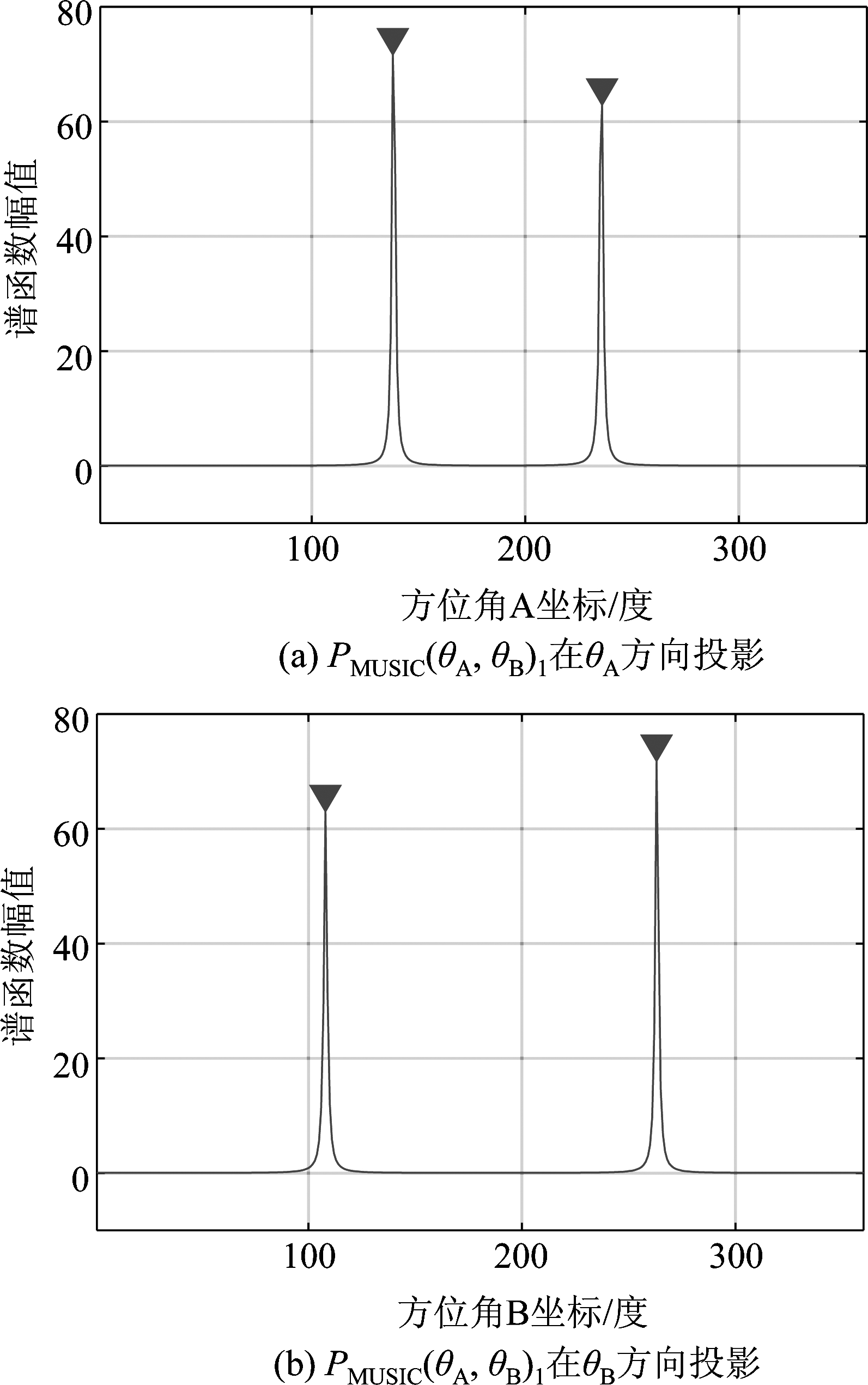
图4 谱函数在不同方位角方向降维投影
Fig.4 Dimensionality reduction projection of spectral functions in different azimuthal directions
图(a)、(b)中两个一维的谱峰进行搜索即可得出两站对同一目标的方位角粗估计
第二步是利用
进行预设,得出PMUSIC(φA,φB)2关于两站俯仰角的分布,如图5所示。同样通过降维投影,此步可得到俯仰角的精确估计
第三步利用
进行预设,重复过程求得方位角的精确估计
最后两步均可根据确定的目标数和匹配的角度,对每一位置进行单一的峰值确定,从而完成多目标的角度匹配估计。
如图6所示,在不同条件下方位角受影响较小,其精度约能控制在0.6°以内,具有良好的仿真表现;俯仰角则有稍明显变化,在信噪比较低时误差偏大,主要是由于UCA阵列为面阵,在Z轴方向上没有阵元分布,所以对俯仰角的测量误差难以消除。
本文提出的双机MUSIC算法在估计方位角方向上有较大优势,因此,仅对方位角进行CRLB的对比。将图6(a)中的平均角度误差换成均方误差,绘
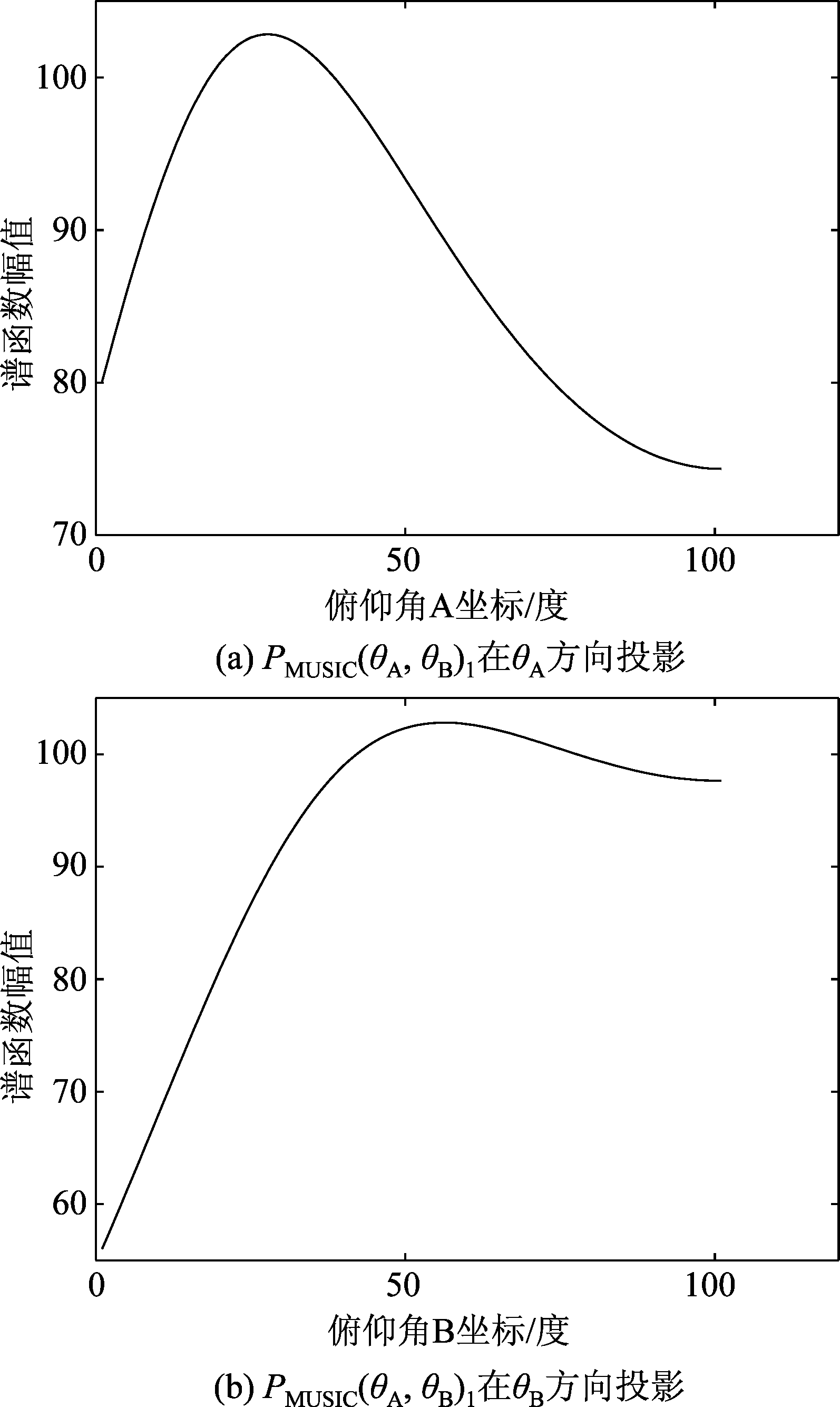
图5 谱函数在不同俯仰角方向降维投影
Fig.5 Dimensionality reduction projection of spectral functions in different elevation angles
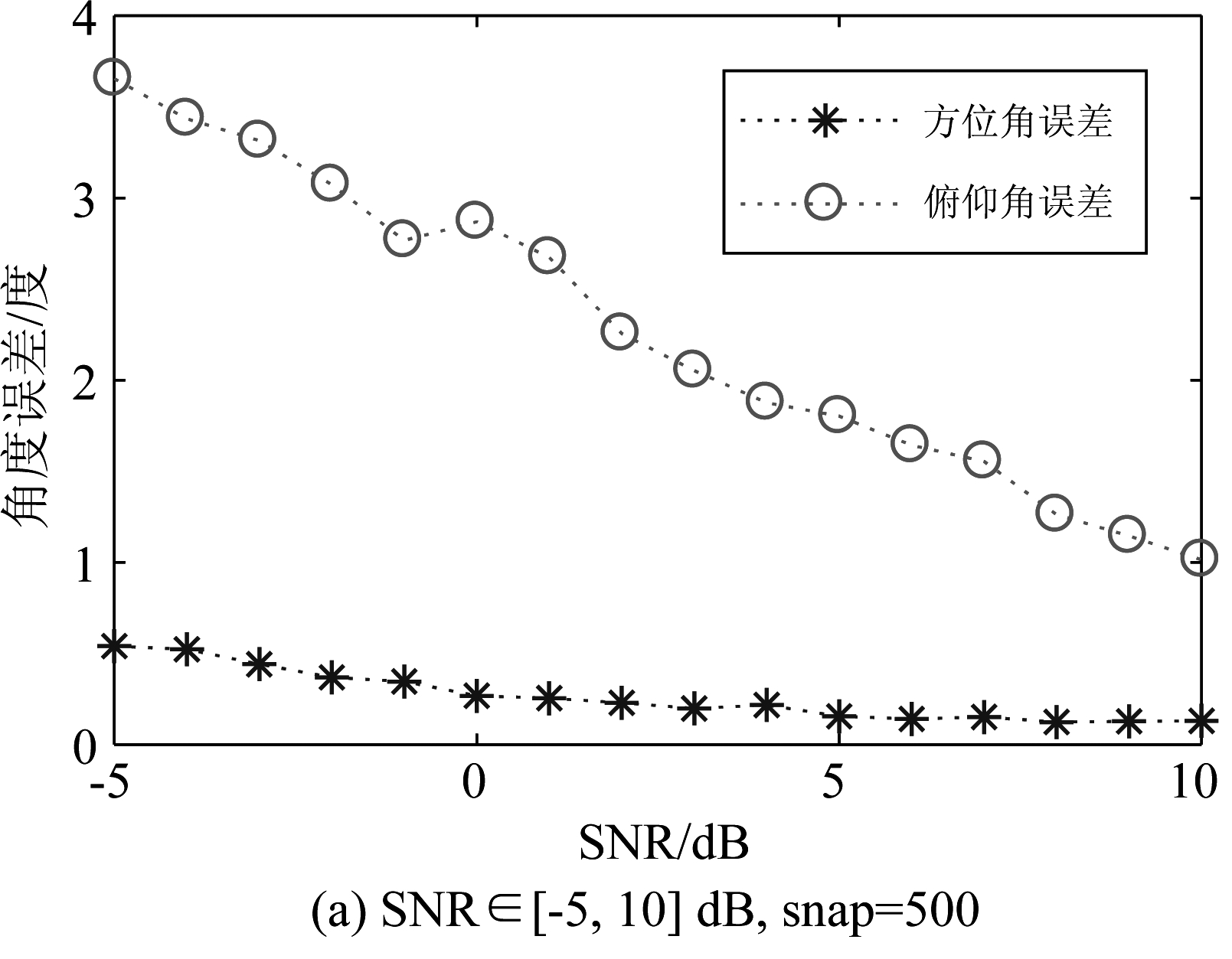
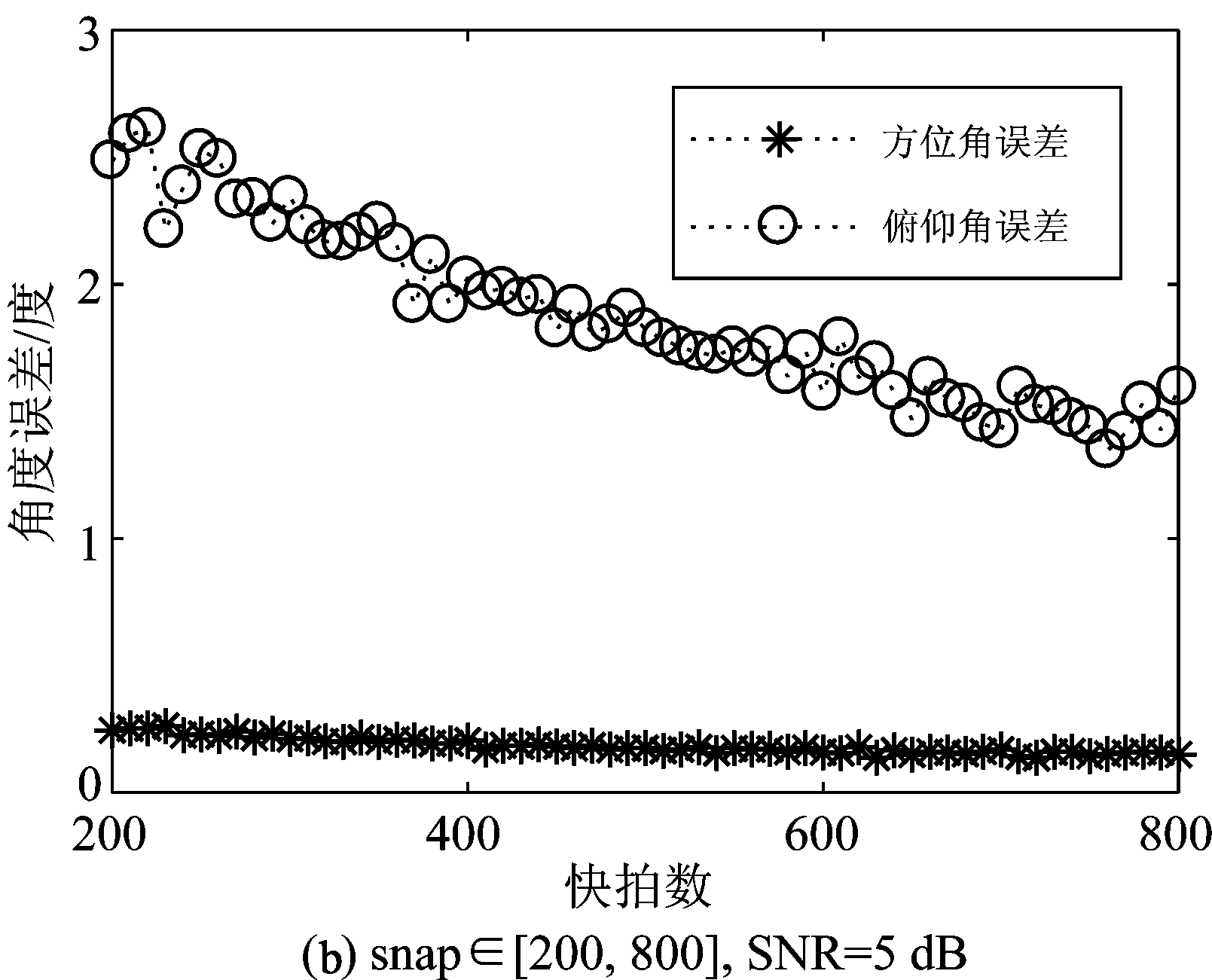
图6 不同SNR和snap条件下,联合降维-投影法 的角度平均误差
Fig.6 Angle error of joint dimensionality reduction-projection method under different SNR and snap conditions
制出与CRLB曲线对比如图 7所示。从仿真结果可以看出,随着信噪比增大,降维投影方法角度的均方误差逐渐趋近于CRLB,收敛性良好。
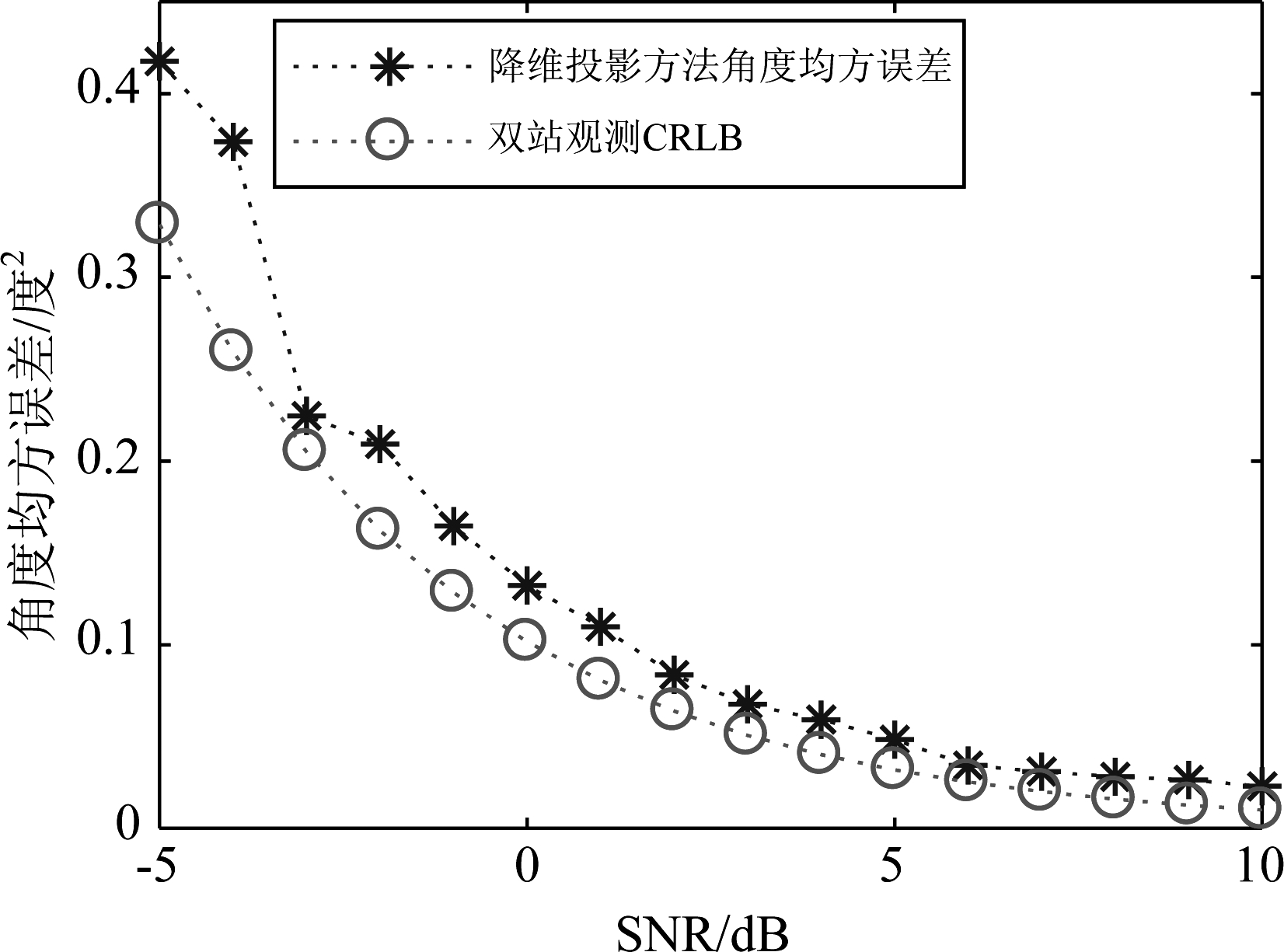
图7 不同信噪比下降维投影方法与CRLB误差曲线对比图
Fig.7 Comparision of different SNR down-dimensional projection methods and CRLB error curves
如图8所示,在空间中存在三个目标时,给出了10个估计点的分布情况,因为在俯仰角上的估计误差稍大,所以估计点主要分布在目标的Z轴方向上。在目标的位置解算过程,采用最小二乘算法[13]。
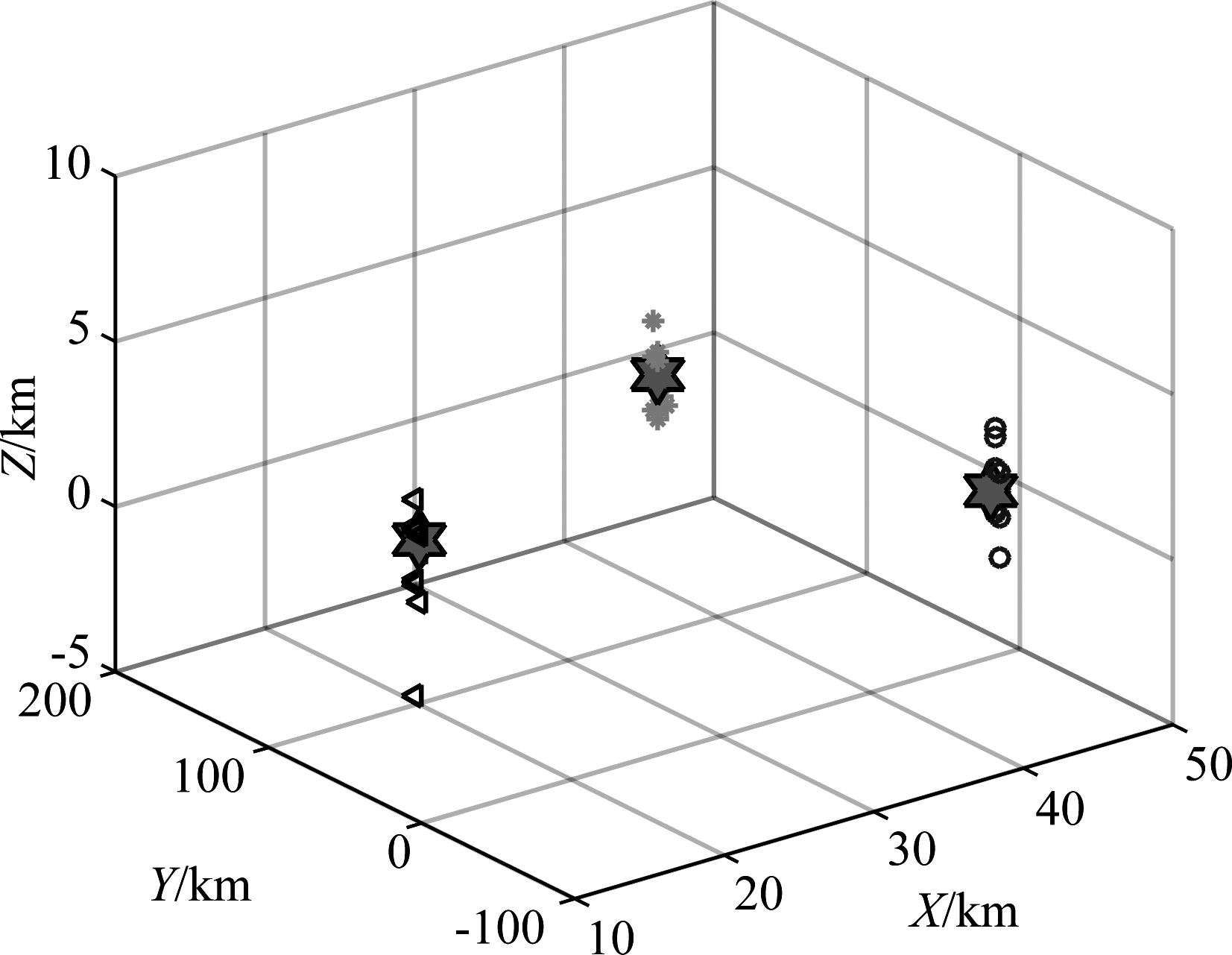
图8 空间中多目标定位示意图
Fig.8 Schematic diagram of multi-target positioning in space
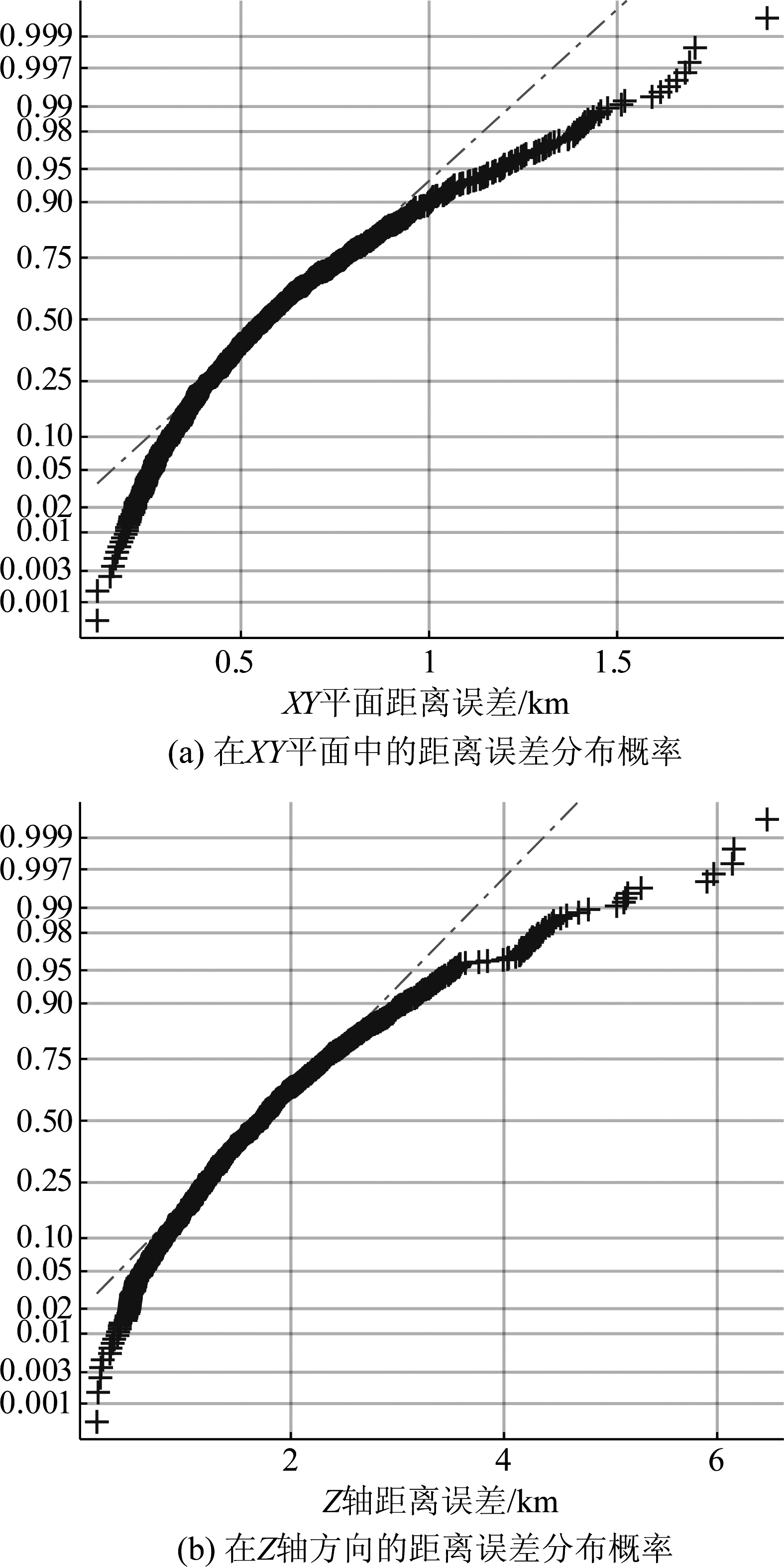
图9 在不同方向上距离误差
Fig.9 Distance error in different directions
如图9所示,由于方位和俯仰角的误差不同,则在不同方向上进行多目标定位误差分析。在XY平面中的距离误差90%以上都小于1 km,1000次定位误差均值为0.62 km;在Z轴方向90%以上都小于3 km,误差均值为1.86 km。图9中十字点表示距离误差可控制在一定范围内的概率,点划线为十字点拟合的分布直线。本文的定位场景主要针对地面的静止目标,所以对于定位精度来说在XOY平面的误差则显得格外重要,同时对于定位海上目标等场景也同样成立。
如图10所示,是在XOY平面和Z轴方向上不同信噪比下误差分布图,受噪声影响下误差均值、中位数和标准差的分布情况,在瞬时定位中有着较好的精度表现。图10中,正方形代表误差分布的中位数,十字代表误差均值,竖线代表误差的分布范围。
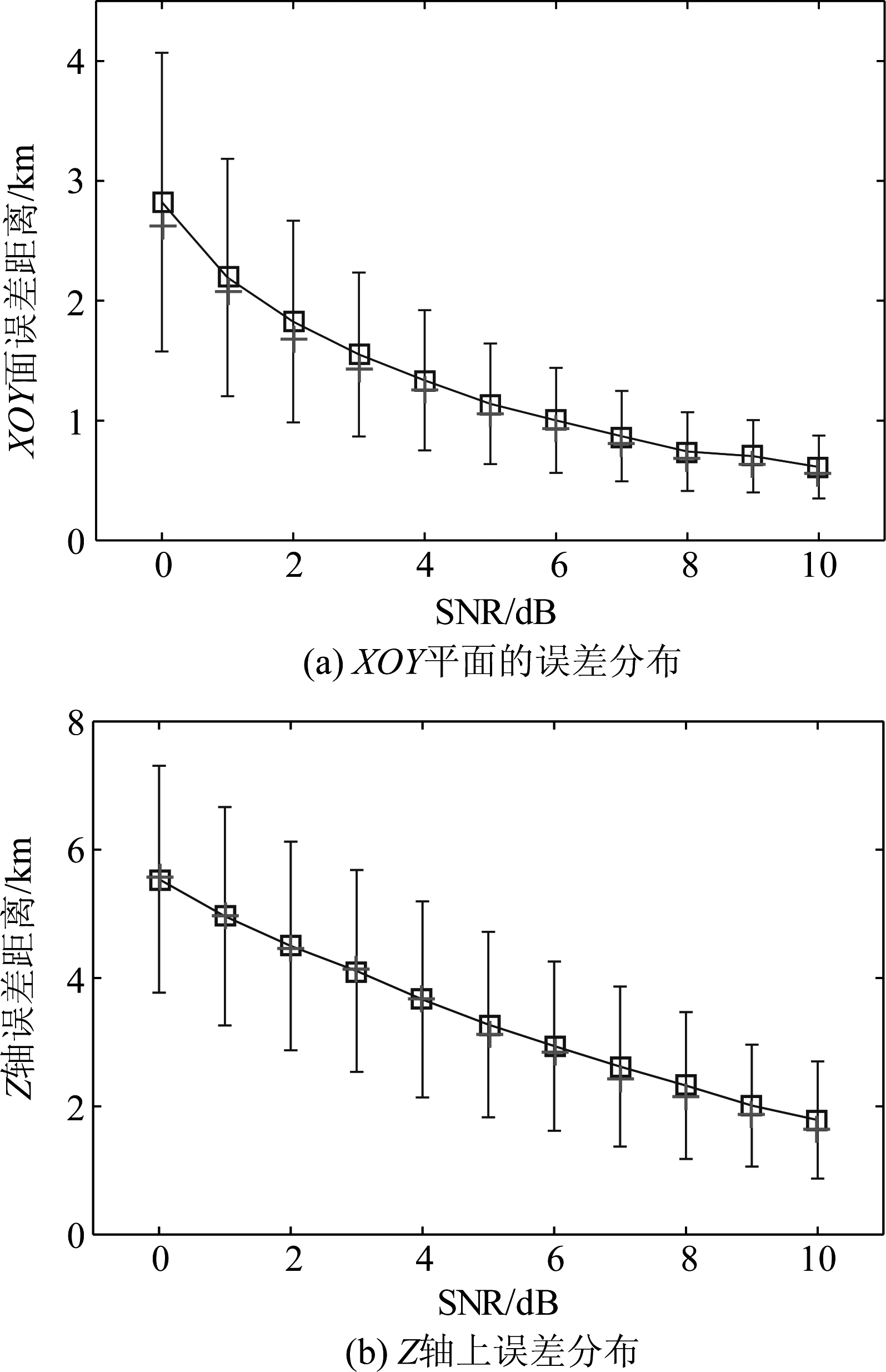
图10 [0,10]dB条件下的误差分布
Fig.10 Error bars at [0,10]dB
最后,对双机联合MUSIC匹配测角算法与单独利用双机信息进行匹配的算法进行精度对比,在信噪比SNR=10 dB的条件下,可得如表1所示误差对比结果。
表1 两种定位误差对比
Tab.1 Comparison of location error using two positioning algorithms
RMSE_xy/kmRMSE_z/kmRMSE/km匹配定位法[12]2.48120.99622.7078双机MUSIC定位法0.58661.91702.0284
综上,本文利用联合双机的MUSIC测角算法,将双机观测到的信息联合起来。提出了一种降维投影的方法对角度进行估计,最后利用最小二乘算法对目标位置进行解算。根据仿真结果显示,在xy维(水平方向,经纬度信息)度上,双机联合MUSIC算法的精度有着较大优势,但是在z维(垂直方向,高度信息)度上精度略差。在利用两种方法测角并利用最小二乘法解算中,双机联合MUSIC方法的最终解算结果在空间几何距离上,精度有着明显提高,并且经纬度信息对于战场信息获取意义更大。
5 结论
在双机协同的基于角度信息的多目标定位问题中,两个观测站会获得所有目标的角度信息。针对如何利用双机观测到的角度信息对多个目标都实现精准定位的问题,本文提出了一种双机联合MUSIC匹配测角算法,并利用降维投影的办法对角度进行估计,最后利用最小二乘算法求解目标的真实位置。在仿真实验中,基于降维投影的双机联合MUSIC算法在估计方位角并利用最小二乘法进行定位解算时,RMSE误差为0.5866 km,而利用匹配测向法定位的RMSE误差为2.4812 km,可以看出,双机联合MUSIC测角算法在估计方位角时有着巨大的优势。在总的定位精度上,利用双机联合MUSIC测角算法定位的RMSE精度为2.0284 km,而利用匹配测向法测角并定位的精度为2.7078 km,因此得出结论,这种双机联合MUSIC测角算法在定位中精度,尤其是在水平维度上,有了较大提升。
[1] Schmidt R O. Multiple Emitter Location and Signal Parameter-Estimation[J]. Ieee T Antenn Propag, 1986, 34(3): 276-280.
[2] Belloni F, Koivunen V. Unitary root-MUSIC technique for uniform circular array[J]. Proceedings of the 3rd Ieee International Symposium on Signal Processing and Information Technology, 2003: 451- 454.
[3] Amar A, Weiss A J. Direct position determination of multiple radio signals[J]. Int Conf Acoust Spee, 2004: 81- 84.
[4] 马贤同, 罗景青, 张奎. 面向DOA测量的多目标位置信息场定位法[J]. 信号处理, 2013, 29(1): 121-126.
Ma Xiantong,Luo Jingqing,Zhang Kui.A Location Method for Multi-target by Position Information Field Based on DOA[J].Journal of Signal Processing,2013,29(1):121-126.(in Chinese)
[5] Chang K, Chen K, Ma W, et al. An Enhanced MUSIC DoA Scanning Scheme for Array Radar Sensing in Autonomous Movers[C]∥ 2019 IEEE International Conference on Artificial Intelligence Circuits and Systems (AICAS), 2019: 152-153.
[6] Cheng M, Aziz M R K, Matsumoto T. A DOA-Based Factor Graph Technique for 3D Multi-Target Geolocation[J]. IEEE Access, 2019, 7: 94630-94641.
[7] Rangarao K V, Venkatanarasimhan S. gold-MUSIC: A Variation on MUSIC to Accurately Determine Peaks of the Spectrum[J]. Ieee T Antenn Propag, 2013, 61(4): 2263-2268.
[8] Berry P E, Kodituwakku S, Venkataraman K. Generalised phase monopulse for multi-target DoA estimation and extended target spatial imaging[C]∥ International Conference on Radar Systems (Radar 2017), 2017: 1- 6.
[9] Stoica P, Larsson E G, Gershman A B. The stochastic CRB for array processing: A textbook derivation[J]. Ieee Signal Processing Letters, 2001, 8(5): 148-150.
[10]Subedi S, Zhang Y M D, Amin M G, et al. Group Sparsity Based Multi-Target Tracking in Passive Multi-Static Radar Systems Using Doppler-Only Measurements[J]. Ieee T Signal Proces, 2016, 64(14): 3619-3634.
[11]Xiong Z, Xu K, Chen Y, et al. Research on multi-target bearings-only tracking method based on passive sonar systems[C]. 2017 IEEE 2nd Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), 2017: 1326-1330.
[12]Ruonan Z, Jiawei L, Xiaojiang D, et al. AOA-Based Three-Dimensional Multi-Target Localization in Industrial WSNs for LOS Conditions[J]. Sensors (Basel, Switzerland), 2018, 18(8).
[13]Jia T Y, Wang H Y, Shen X H, et al. An Accurate TDOA-AOA Localization Method Using Structured Total Least Squares[J]. Oceans-Ieee, 2017.
[14]Hejazi F, Norouzi Y, Nayebi M M. Lower Bound of Error in AOA Based Passive Source Localization Using Single Moving Platform[J]. Proceedings of Ieee East-West Design & Test Symposium (Ewdts 2013), 2013.
[15]Mathews C P, Zoltowski M D. Eigenstructure Techniques for 2-D Angle Estimation with Uniform Circular Arrays[J]. Ieee T Signal Proces, 1994, 42(9): 2395-2407.
[16]Stoica P, Nehorai A. Music, Maximum-Likelihood, and Cramer-Rao Bound[J]. Ieee Transactions on Acoustics Speech and Signal Processing, 1989, 37(5): 720-741.
