1 引言
随着无线通信技术的发展,人们对高数据速率等性能有着日益增长的需求。为此,考虑到毫米波与异构网络(heterogeneous networks, HetNets)的结合,可以让蜂窝网络的容量再提升[1]。
毫米波通信拥有丰富的频谱资源,可以提供高数据速率[2]。尽管在频谱方面潜力巨大,但毫米波频段的近场路径损耗严重。通过部署高方向性天线,利用旁瓣支持极小干扰的即时通信,可以实现更低的链路中断概率、更高的数据速率和更大的网络容量[3- 4]。文献[5]介绍了网络致密化可提高网络性能。通过部署大量的小型基站(Base Station,BS)构成HetNets。所有小小区、微微小区和毫微微小区与现有宏小区的重叠,提高了频率复用效率。因此,毫米波异构蜂窝网络具有很大的研究价值。
由于BS一般部署在用户设备(user equipment,UE)密集区域,不可避免的UE-BS耦合问题随之而来。在文献[6]的模型中,条件细化BS点过程以便目标用户更靠近其服务BS。然而,该模型仅限于单层网络,很难将其推广到多层网络。因此,为了有效地捕获UE-BS耦合问题和以UE对象为中心部署的特性,本文将热点区域中心建模为独立的泊松点过程(Poisson point process,PPP),其周围的BS和UE对象以不同的分布形式独立成簇。文献[7-17]介绍了基于簇模型的相关内容。文献[13-14]表明泊松簇过程(Poisson cluster process,PCP)更适合用来建模此类BS的位置。在宏小区区域内部署较小的BS,以便较小的BS成簇包围宏BS[15]。位于服务BS附近的UE对象避免了过多的路径损耗衰减,因此接收到的信号功率明显高于接收到的干扰。反之,接收到的干扰要高于接收到的信号功率,导致性能大大降低。因此,在每层BS作为独立的PCP分布的多层异构簇中,UE对象的性能不仅受到簇间(簇内)干扰的影响,而且受到层间(同层)干扰的影响[18]。为解决该问题,本文提出了基于簇UE对象分类的方案。每个簇划分为两个不相交的子区域,即簇中心区域和簇边缘区域。与之对应的UE称为簇中心用户设备(cluster-center user equipment,CCUE)和簇边缘用户设备(cluster-edge user equipment,CEUE),可用频带分为CCUE带和CEUE带,分别由与CCUE和CEUE相级联的微微基站(pico base station，PBS)所使用,毫微微基站(femto base station，FBS)通过接入因子η随机接入CCUE频带和CEUE频带,从而限制CCUE和CEUE受到的干扰,提升了网络性能。
综上所述,本文建立了基于独立PCP的现实框架。在由PBS和FBS组成的双层毫米波HetNets上,部署以UE对象为中心的多层BS。为解决干扰问题,将UE对象划分为CCUE或CEUE,推导出了所有可能级联场景的下行链路(downlink,DL)频谱效率。为了突出所提出的基于簇UE对象分类的优势,本文比较了其与无UE对象分类的DL频谱效率。此外,本文还研究了BS的传输功率和分类因子对DL频谱效率的影响。
2 系统模型和假设
2.1 系统模型
本文考虑了一个包含PBS和FBS的双层毫米波HetNets。它们的位置皆由托马斯簇过程(Thomas cluster process,TCP)建模,分别表示为
其中λC表示父PPP ΦC的密度,MH表示簇中的成员个数,簇中同时活动的成员个数被假定为一个平均值为
的泊松分布变量且H∈{P,F}。子过程
和
分布在同一个稳定的父PPP ΦC四周,PBS与FBS之间的异质性决定了MH和的值是有差别的。子过程和的密度分别为
和
以x为中心簇的PBS和FBS集合分别表示为
和
其中x∈ΦC。相应的,用
和
来表示活跃的PBS和FBS集合。假设随机选择的UE对象位于以0为原点、x0∈ΦC为中心的代表性簇中。图1给出了由PBS和FBS两种PCP组成的双层毫米波HetNets模型。
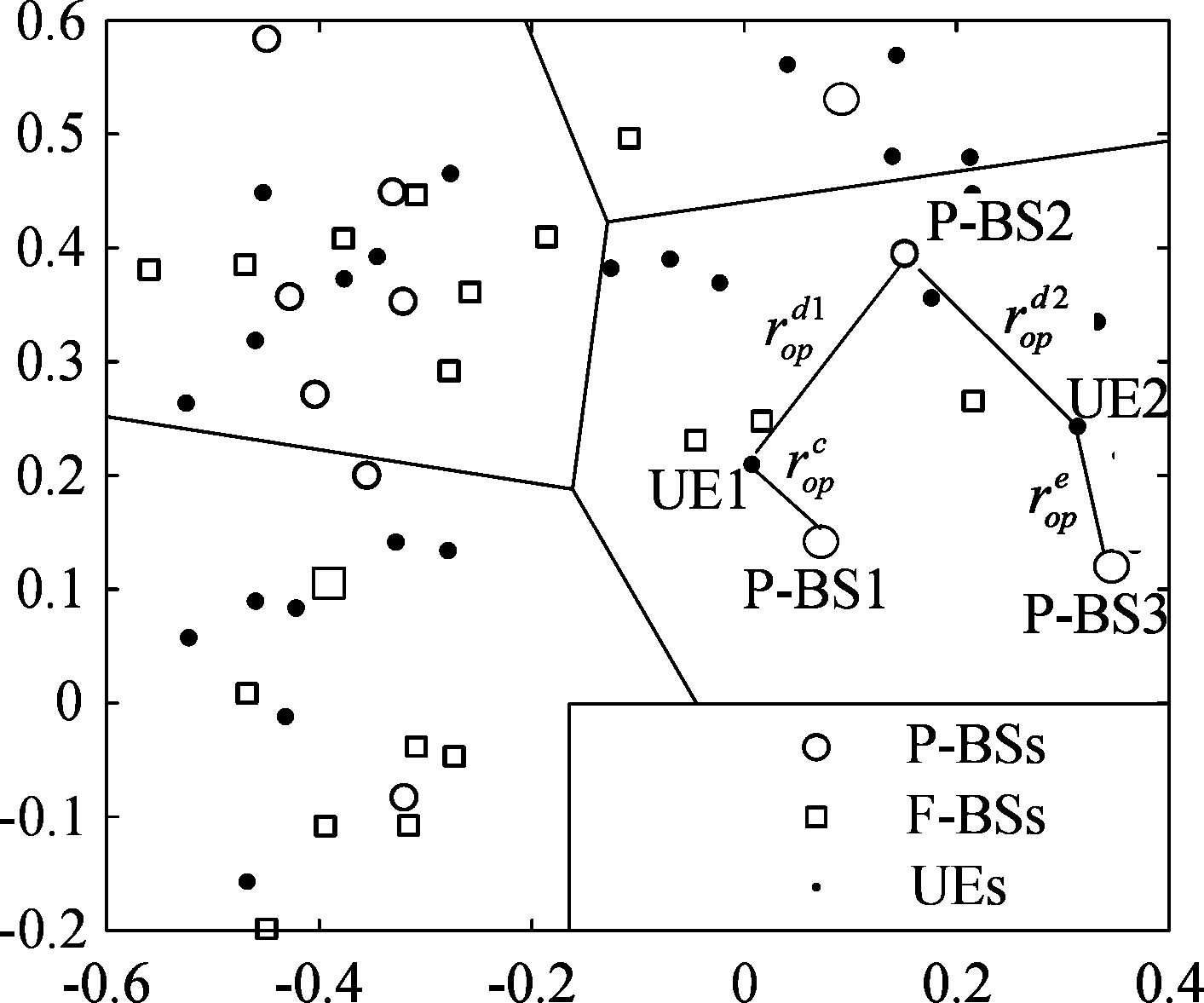
图1 双层毫米波异构网络模型图
Fig.1 2-tier millimeter wave HetNets model diagram
2.2 阻碍模型
假设在毫米波HetNets中,PBS、FBS和UE均配备多天线。为了方便分析问题,本文将实际的天线图案近似化为扇形模型。在该模型中,当偏离视轴的角度位于主瓣区域内时天线增益为常数M,位于旁瓣区域内时天线增益为常数m。由于毫米波的穿透能力较差,因此会产生视距与非视距链路。同时,视距链路和非视距链路的路径损耗因子不一样,所以信道衰落的参数也不同。本文提出了一种近似计算方法,即将视距范围等效于球形,其中球形半径为μ,定义为UE对象到附近阻塞的平均距离。当BS位于μ区域之内时,BS与UE对象之间的链路称为视距链路,反之则为非视距链路。借助于该模型,给出了距离为r的网络路径损耗定律:
L(r)=U(μ-r)CLr-αL+U(r-μ)CNr-αN
(1)
其中U(.)表示单位阶跃函数,Ck表示截距,αL和αN分别表示视距和非视距路径损耗指数,其大致范围分别为αL∈[1.9,2.5],αN∈[2.5,4.7][19-20]。
2.3 簇内和簇间距离的分布
通过以0为原点、x0∈ΦC为中心的代表簇里的UE对象来描述簇内距离的分布。假设从UE对象到代表簇中可能活跃的
的距离集合为
表示为
且
包含两种类型的距离,即从UE对象到服务BS的距离以及从UE对象到活跃的H-BS的簇内干扰距离。如图2所示,该UE对象与
且位于yd0的H-BS相级联。
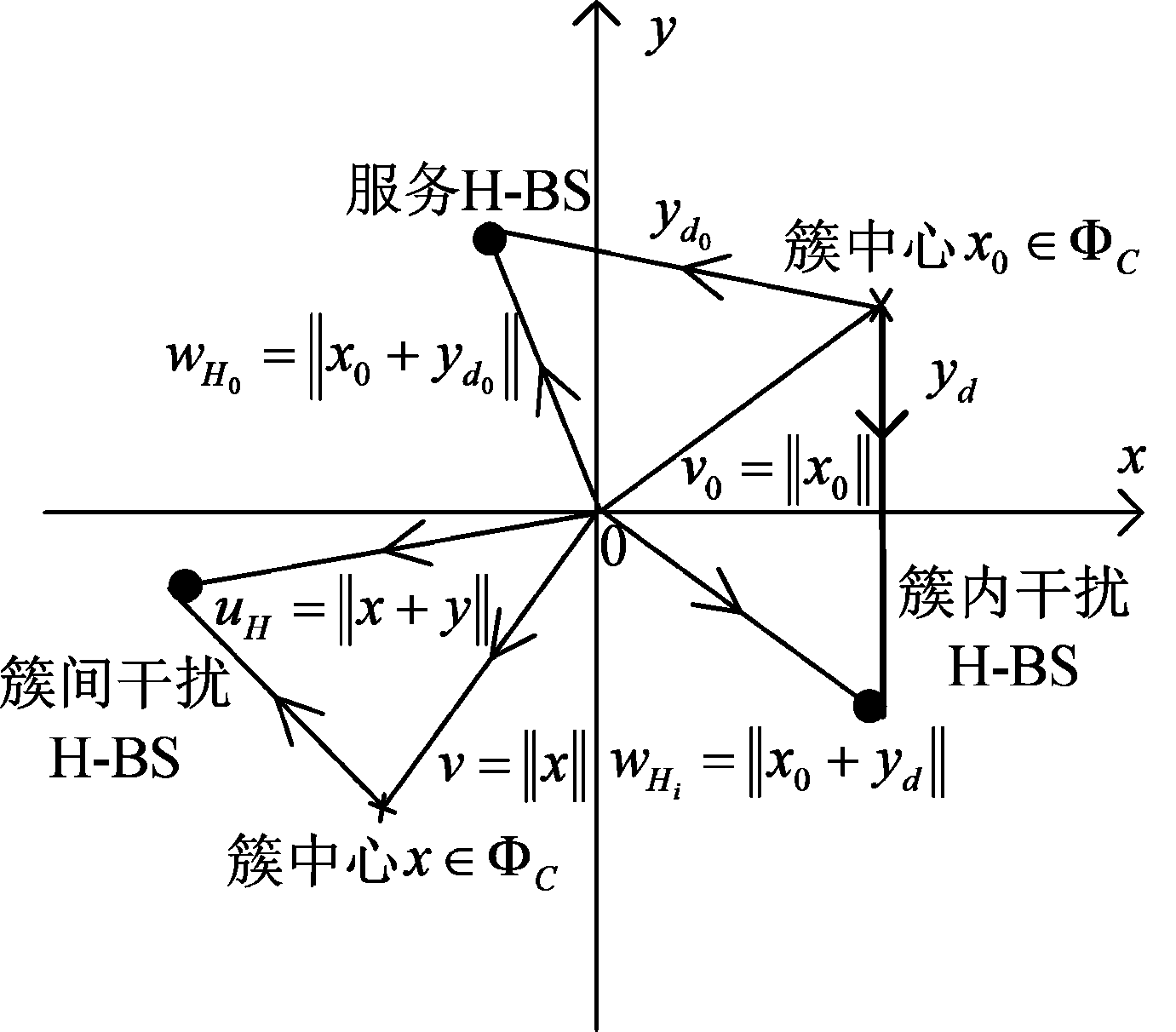
图2 簇内和簇间距离的分布
Fig.2 Distribution of intra-clusters and inter-clusters distances
图2中显示了从UE对象到服务BS的距离为wH0=||x0+yd0||,yd0表示簇中心x0∈ΦC到服务BS的距离。从UE对象到活跃的H-BS的簇内干扰距离为wHi=||x0+yd||,yd表示簇中心x0∈ΦC到HBS的距离。从准确分析的角度来看,由于存在公因子x0,簇内距离wH0和wHi的相关性很大。因此,根据[21]-[22]中的结果,在ν0=||x0||的条件下,wH0和wHi的莱斯概率密度函数(probabilities density function,PDF)分别写为:
fwH0(ω|||x0||)=PDF-Ri(w,ν0,σ2)
(2)
fwHi(ω|||x0||)=PDF-Ri(w,ν0,σ2)
(3)
然而,簇内距离之间的相关性非常弱,可以忽略不计[21-22]。因此,忽略条件ν0=||x0||将大大简化后续分析,并获得更清晰的见解。考虑到在wHi=||x0+yd||中,x0和yd是方差为σ2的高斯随机变量,x0+yd和x0+yd0是方差为2σ2的高斯随机变量。距离ωH0和ωHi的PDF和累积分布函数(cumulative distribution function,CDF)的近似表述为:
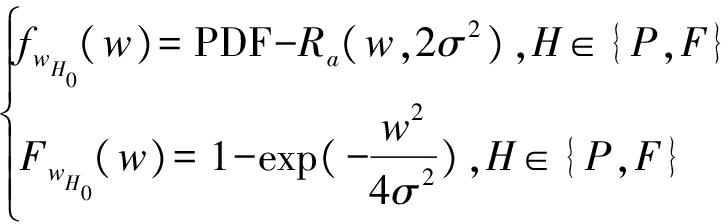
(4)
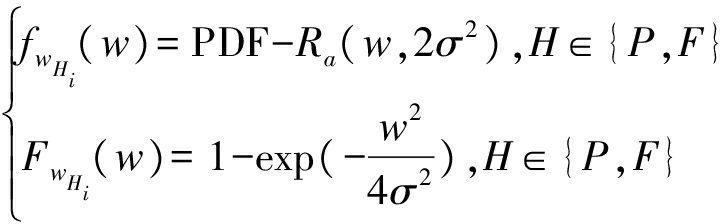
(5)
为了降低分析的复杂性,本文使用了近似模型(4)和(5)。
接下来给出了其他簇中的H-BS到UE对象的距离分布。类似地,假设UE对象和活跃的H-BS之间的距离集合
表示为
且
的实现用uHi来表示。
表示H-BS到簇中心x∈ΦC/x0的距离。删除uHi和UHi中的索引i,使用统一表达式uH=||x+y||来表示簇间距离。图2中展示了uH=||x+y||,x∈Φc/x0,H∈{P,F}。考虑到簇间干扰H-BS是随机选择的,簇间干扰距离uH的特征是在ν=||x||条件下的莱斯分布,UH的PDF表示为:
fUH(u|||x||)=PDF_Ri(u,ν,σ2)
(6)
3 UE分类的DL频谱效率
3.1 CCUE可实现的DL频谱效率
一般情况下,干扰的期望值可以通过干扰的拉普拉斯变换(Laplace Transform,LT)得到,利用该变换可以推导出所考虑的双层异构蜂窝网络的频谱效率和吞吐量。故而,针对簇过程
位于簇中心区域的情况,当UE对象通过接入距离
连接到PBS时,干扰
的LT为:
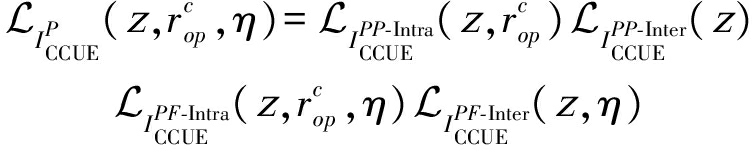
(7)
式中η表示接入因子。
同样的,当UE对象通过接入距离连接到FBS时,干扰
的LT为:
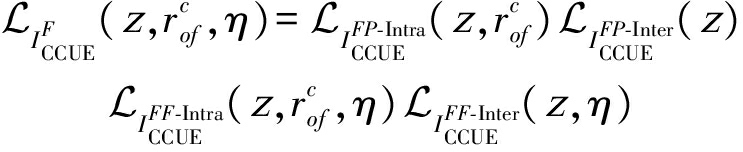
(8)
因此,当UE对象与最近的PBS相级联时,接收到的信号与干扰加噪声比(signal-to-interference plus noise ratio,SINR)计算为:
(9)
式中PP表示PBS的发射功率,MPt表示PBS层的主瓣增益,Mr表示主瓣增益,
表示距离为
的网络路径损耗,σu表示簇间干扰距离uH的方差。
当UE对象与最近的PBS相级联时,DL频谱效率计算为:
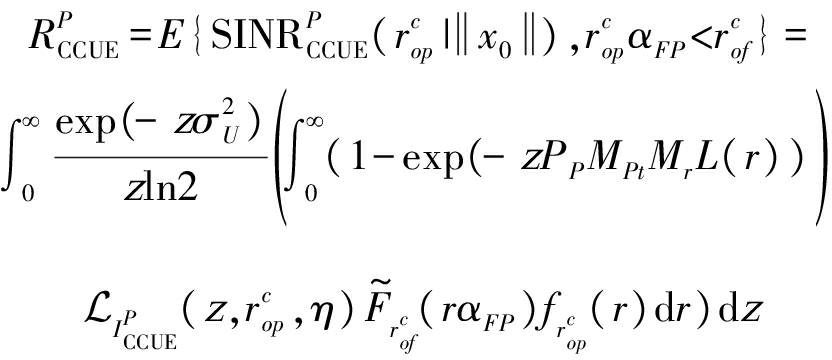
(10)
式中
由(7)给出,L(r)由(1)给出,
的互补CDF即
对象接入距离的PDF为:
(11)
其中
为分类因子。
当UE对象与最近的FBS相级联时,接收到的SINR计算为:
(12)
式中PF表示FBS的发射功率,MFt表示FBS层的主瓣增益,
表示距离为的网络路径损耗。
当UE对象与最近的FBS相级联时,DL频谱效率计算为:
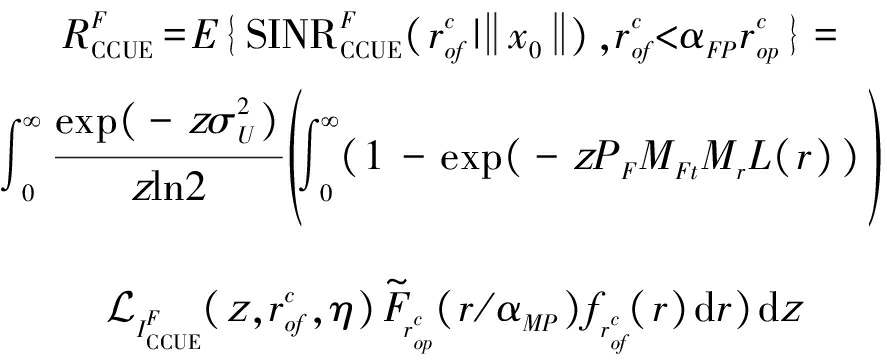
(13)
式中
由(8)给出,L(r)由(1)给出,的PDF即
对象接入距离互补的CDF为:
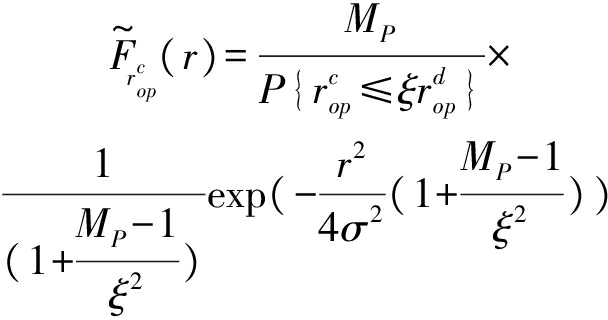
(14)
结合(10)和(13),有以下结论:在基于泊松簇的异构蜂窝网络中,为了限制严重的干扰,将UE对象划分为CCUE和CEUE。在这种情况下,CCUE的DL频谱效率为
3.2 CEUE可实现的DL频谱效率
类似于CCUE可实现的DL频谱效率,CEUE也分别考虑了两种级联场景下的DL频谱效率。针对簇过程位于簇边缘区域的情况,当UE对象通过接入距离
连接到PBS时,干扰
的LT为:
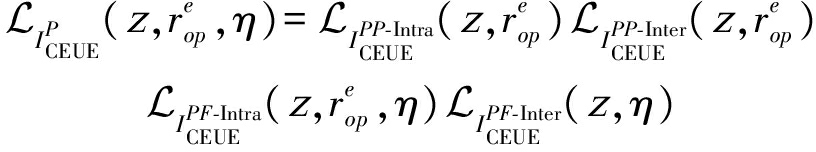
(15)
同样的,当UE对象通过接入距离
连接到FBS时,干扰
的LT为:
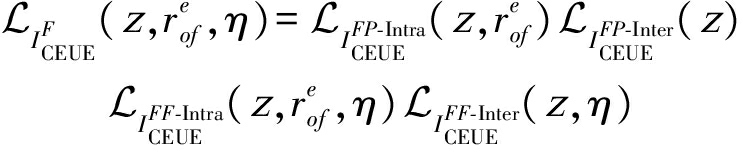
(16)
因此,当UE对象与最近的PBS相级联时,接收到的SINR计算为:
(17)
式中
表示距离为
的网络路径损耗。
当UE对象与最近的PBS相级联时,DL频谱效率计算为:
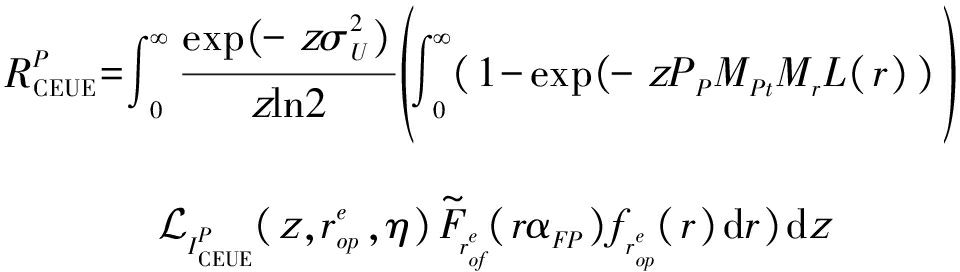
(18)
式中
由(15)给出,L(r)由(1)给出,
的互补CDF即
对象接入距离的PDF为:
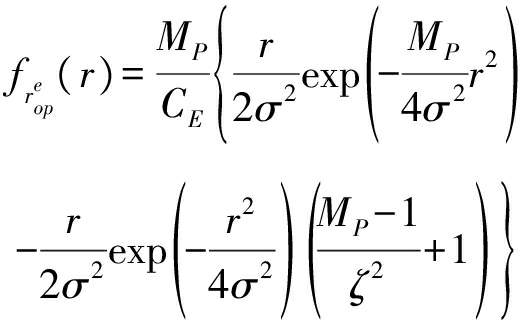
(19)
当UE对象与最近的FBS相级联时,接收到的SINR计算为:
(20)
式中
表示距离为的网络路径损耗。
当UE对象与最近的FBS相级联时,DL频谱效率计算为:
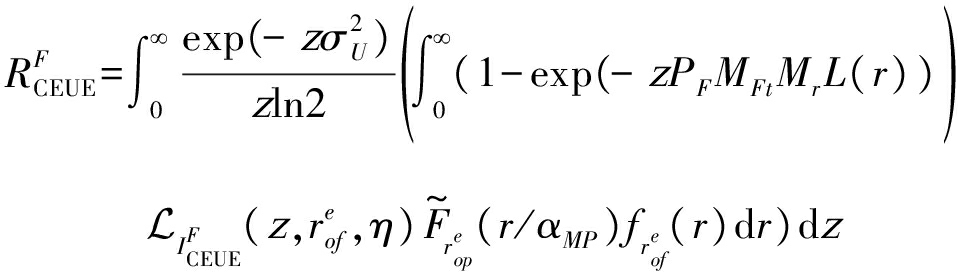
(21)
式中
由(16)给出,L(r)由(1)给出,的PDF即
对象接入距离互补的CDF为:
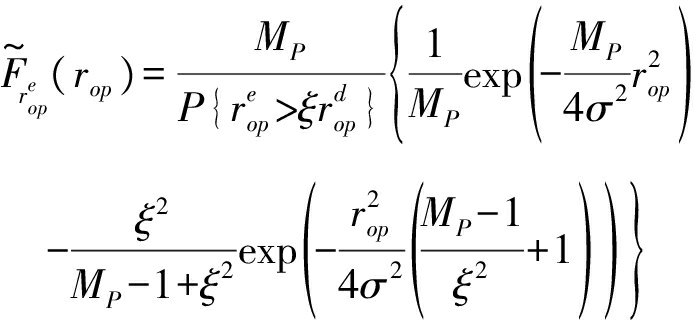
(22)
结合(18)和(21),有以下结论:在基于泊松簇的异构蜂窝网络中,为了限制严重的干扰,将UE对象划分为CCUE和CEUE。在这种情况下,CEUE的DL频谱效率为
因此,对于使用
和
部署的双层异构蜂窝网络,结合前两小节推导出的结论,可以很快推导出UE对象的DL总频谱效率RTot为RTot=CE×RCEUE+CC×RCCUE。
本节研究了UE对象的DL频谱效率。数值分析表明,一个UE对象可被分类为CCUE或CEUE且与PBS或FBS相级联,最终会有四种传输模式。
4 无UE分类的DL频谱效率
为了方便比较和突出基于UE分类的性能优化,本节将讨论无UE分类的DL频谱效率。当传统UE对象通过接入距离rop连接到PBS时,干扰
的LT为:
(23)
同样的,当传统UE对象通过接入距离rof连接到FBS时,干扰
的LT为:
(24)
因此,当传统UE对象与最近的PBS相级联时,接收到的SINR计算为:
(25)
式中L(rop)表示距离为rop的网络路径损耗。
当传统UE对象与最近的PBS相级联时,DL频谱效率计算为:
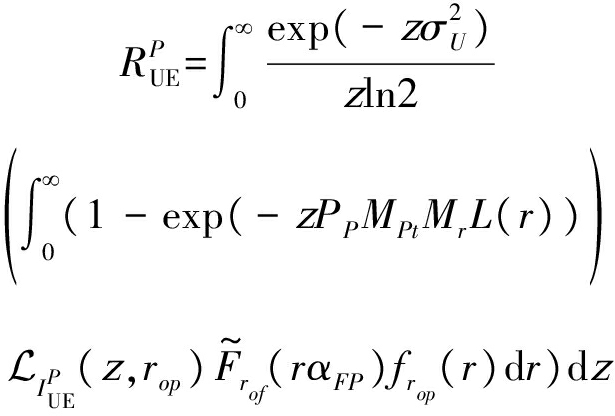
(26)
式中
由(23)给出,L(r)由(1)给出,rop的PDF即
对象接入距离rof的互补CDF即
当传统UE对象与最近的FBS相级联时,接收到的SINR计算为:
(27)
式中L(rof)表示距离为rof的网络路径损耗。
当传统UE对象与最近的FBS相级联时,DL频谱效率计算为:
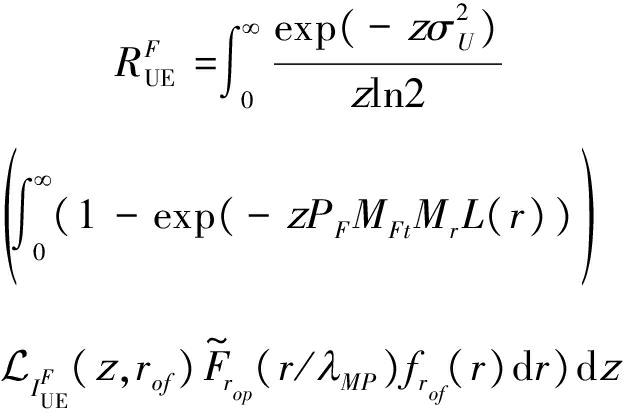
(28)
式中
由(24)给出,L(r)由(1)给出,rof的PDF即
对象接入距离rop的互补CDF即
结合(26)和(28),有以下结论:传统UE对象接收到的DL总频谱效率为
5 仿真与数值结果
本文构建了一个由PBS和FBS组成的双层异构蜂窝网络模型,仿真参数在表1中给出。
表1 仿真参数
Tab.1 Simulation parameters
参数取值参数取值S/km250×50αL2葜C 150αN4W/GHz1CN2fC/GHz 28CL3.3ξ{0.4,0.6}PP/dBm-10～45μ/m100PF/dBm0～35C-P1～20C-F1,5,10
基于上述参数,图3比较了CEUE和CCUE可实现PBS的DL频谱效率。同时,为了突出该方案的优点,给出了传统UE分类系统可实现PBS的DL频谱效率。图3表明,当发射功率PP较小时,CCUE和CEUE的DL频谱效率与传统UE的DL频谱效率的差别并不明显,随着发射功率PP的逐渐增大,UE分类对DL频谱效率的影响也逐渐扩大。采用簇UE分类提高了CCUE的DL频谱效率,同时也提高了CEUE的DL频谱效率。此外,UE的分类对CCUE的影响比CEUE更大,从而使CCUE获得更多的效率增益。
对比图3和图4,发现发射功率PP对PBS的DL频谱效率影响很大,但对FBS的DL频谱效率影响很小,特别是在PP较小的情况下。类似于图3,图4也表明,利用簇UE分类,FBS的DL频谱效率得到了提高。因此,使用簇UE分类可以提高整个网络的吞吐量。
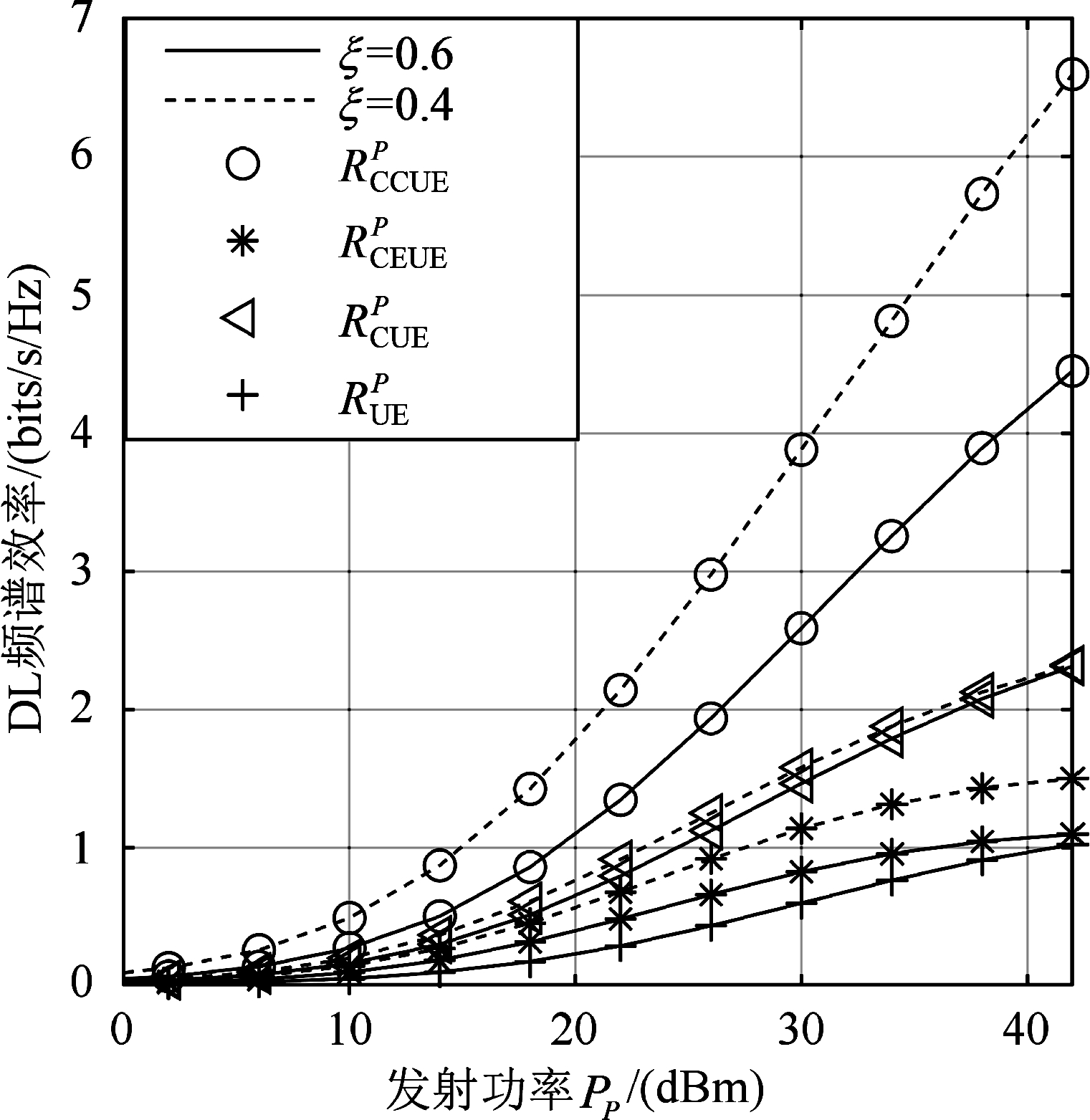
图3 基于PBS的DL频谱效率比较
Fig.3 Comparison of PBS DL spectral efficiency
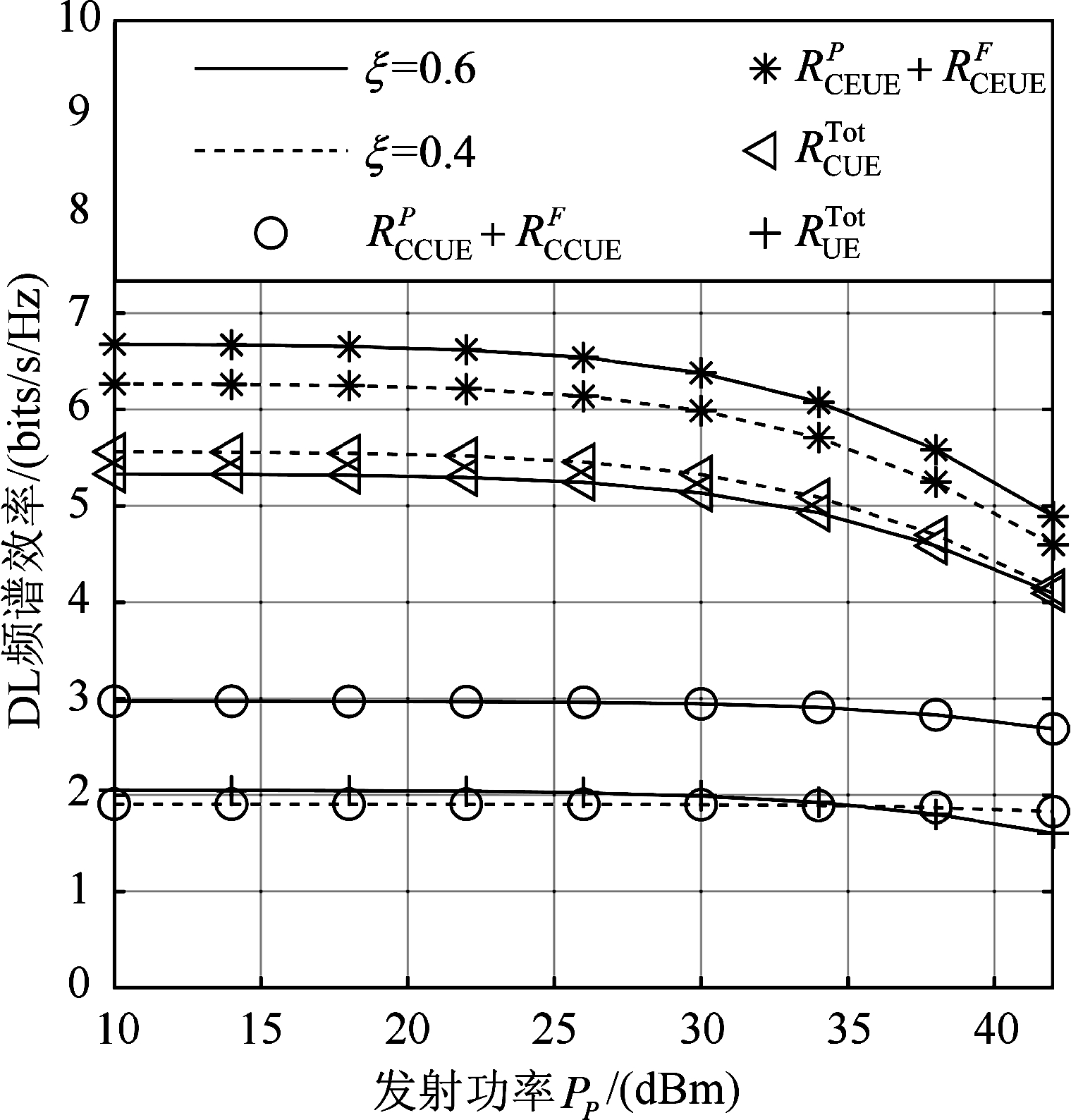
图4 基于FBS的DL频谱效率比较
Fig.4 Comparison of FBS DL spectral efficiency
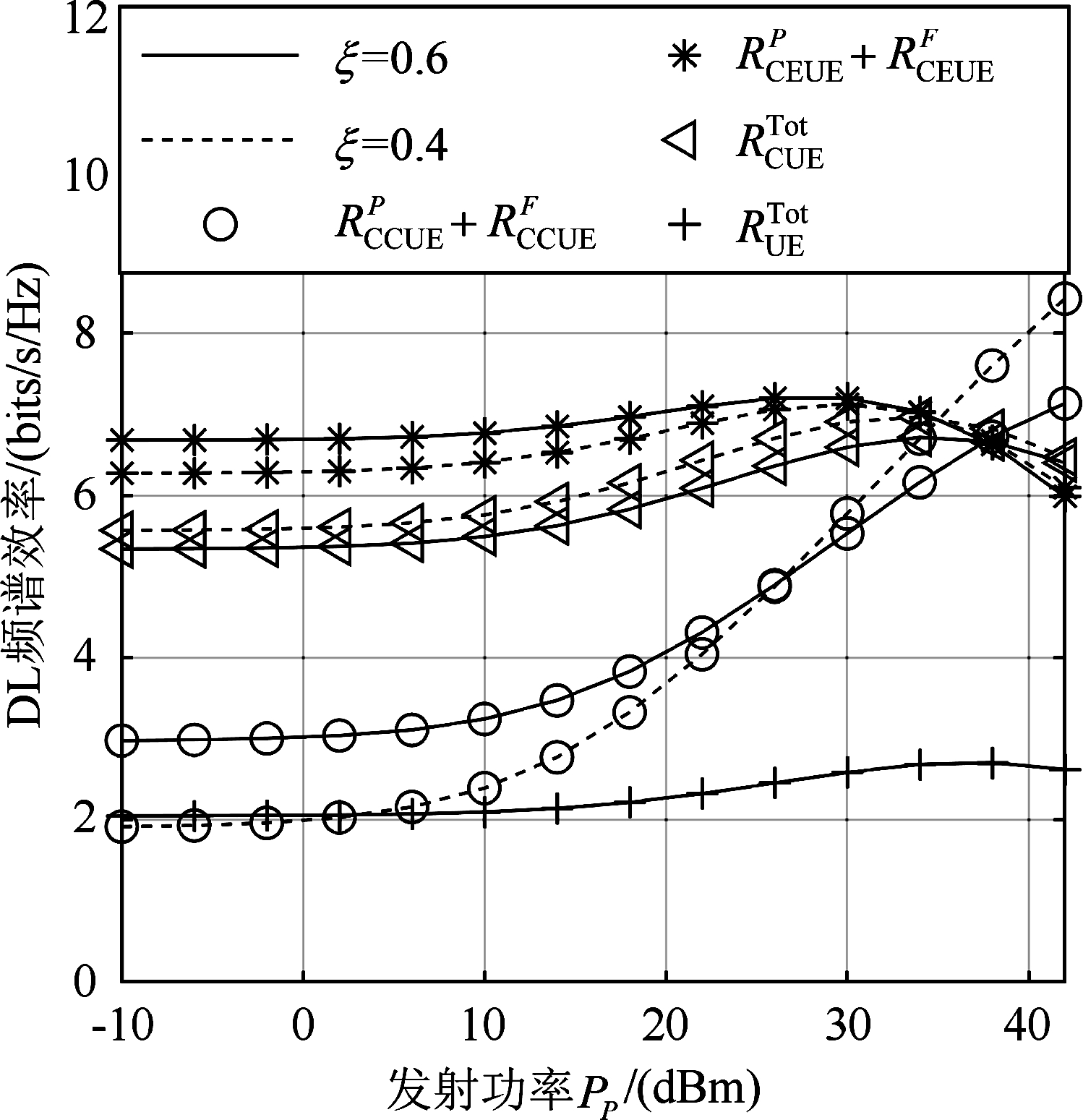
图5 DL总频谱效率比较
Fig.5 Comparison of total DL spectral efficiency
图5比较了DL总频谱效率。与图4相比,图5更清楚地说明了所提出的方案相对于传统的无UE分类方案的优势。结果表明,当发射功率PP较小时,CEUE的DL频谱效率大于CCUE的DL频谱效率。这一观察结果表明,簇用户的分类对CEUE更有效。然而,当发射功率PP较大时,CCUE的DL频谱效率大于CEUE的DL频谱效率。此外,图5研究了参数ξ对DL频谱效率的影响。当发射功率PP较小时,CEUE和CCUE的DL频谱效率随ξ的增加而增加。此外,随着发射功率PP的增加,频谱效率之间的差距减小。最后,当发射功率PP较高时,得到完全相反的结果。从DL频谱效率的角度来看,图5进一步显示了将簇UE分类为CCUE和CEUE能够改进整个网络吞吐量。
6 结论
本文提出了一种基于独立PCP的建模方案。为了限制严重的干扰和提高整个网络的吞吐量,将UE对象进行分类。根据视距球毫米波信号的传播模型,计算了所有可能的级联情况下CCUE和CEUE所受干扰的LT。进而在父PPP上推导出DL频谱效率并分析了相关参数对系统性能的影响。仿真结果表明,本文提出的方案能显著提高频谱效率和系统吞吐量。在未来的研究中,将进一步分析方案复杂度并对复杂度进行优化。
[1] 颉满刚, 贾向东, 周猛. 大规模MIMO蜂窝网与D2D混合网络物理层安全性能研究[J]. 重庆邮电大学学报: 自然科学版, 2017, 29(1): 19-28.
Xie Mangang, Jia Xiangdong, Zhou Meng. Study on physical layer security of hybrid networks with massive MIMO cellular and device-to-device networks[J]. Journal of Chongqing University of Posts and Telecommunications: Natural Science Edition, 2017, 29(1): 19-28.(in Chinese)
[2] Andrews J G, Bai T, Kulkarni M N, et al. Modeling and analyzing millimeter wave cellular systems[J]. IEEE Transactions on Communications, 2016, 65(1): 403- 430.
[3] Busari S A, Huq K M S, Mumtaz S, et al. Millimeter-wave massive MIMO communication for future wireless systems: A survey[J]. IEEE Communications Surveys & Tutorials, 2017, 20(2): 836- 869.
[4] Hemadeh I A, Satyanarayana K, El-Hajjar M, et al. Millimeter-wave communications: Physical channel models, design considerations, antenna constructions, and link-budget[J]. IEEE Communications Surveys & Tutorials, 2017, 20(2): 870-913.
[5] 徐文娟, 贾向东, 杨小蓉, 等. 多层异构网络第m阶用户级联方案[J]. 信号处理, 2019, 35(2): 275-284.
Xu Wenjuan, Jia Xiangdong, Yang Xiaorong, et al. A novel m-th best user association scheme for multi-tier heterogeneous networks[J]. Journal of Signal Processing, 2019, 35(2): 275-284.(in Chinese)
[6] Dhillon H S, Ganti R K, Andrews J G. Modeling non-uniform UE distributions in downlink cellular networks[J]. IEEE Wireless Communications Letters, 2013, 2(3): 339-342.
[7] Ying Q, Zhao Z, Zhou Y, et al. Characterizing spatial patterns of base stations in cellular networks[C]∥2014 IEEE/CIC International Conference on Communications in China (ICCC). Shanghai, China: IEEE, 2014: 490- 495.
[8] Saha C, Afshang M, Dhillon H S. Enriched K-tier HetNet model to enable the analysis of user-centric small cell deployments[J]. IEEE Transactions on Wireless Communications, 2017, 16(3): 1593-1608.
[9] Mankar P D, Das G, Pathak S S. Modeling and coverage analysis of BS-centric clustered users in a random wireless network[J]. IEEE Wireless Communications Letters, 2016, 5(2): 208-211.
[10]Saha C, Dhillon H S. Downlink coverage probability of K-tier HetNets with general non-uniform user distributions[C]∥2016 IEEE International Conference on Communications (ICC). Kuala Lumpur, Malaysia: IEEE, 2016: 1- 6.
[11]Turgut E, Gursoy M C. Downlink analysis in unmanned aerial vehicle (UAV) assisted cellular networks with clustered users[J]. IEEE Access, 2018, 6: 36313-36324.
[12]Tabassum H, Hossain E, Hossain J. Modeling and analysis of uplink non-orthogonal multiple access in large-scale cellular networks using Poisson cluster processes[J]. IEEE Transactions on Communications, 2017, 65(8): 3555-3570.
[13]Andrews J G, Ganti R K, Haenggi M, et al. A primer on spatial modeling and analysis in wireless networks[J]. IEEE Communications Magazine, 2010, 48(11): 156-163.
[14]Lee C H, Shih C Y, Chen Y S. Stochastic geometry based models for modeling cellular networks in urban areas[J]. Wireless Networks, 2013, 19(6): 1063-1072.
[15]李君, 王浩, 王秀敏, 等. 超密集异构网络中基于分簇的休眠优化策略[J]. 东南大学学报: 自然科学版, 2017, 47(5): 845- 849.
Li Jun, Wang Hao, Wang Xiumin, et al. Optimized clustering-based sleep strategy in hyperdense heterogeneous networks[J]. Journal of Southeast University: Natural Science Edition, 2017, 47(5): 845- 849.(in Chinese)
[16]Saha C, Dhillon H S, Miyoshi N, et al. Unified analysis of HetNets using Poisson cluster processes under max-power association[J]. IEEE Transactions on Wireless Communications, 2019, 18(8): 3797-3812.
[17]Afshang M, Dhillon H S. Poisson cluster process based analysis of HetNets with correlated user and base station locations[J]. IEEE Transactions on Wireless Communications, 2018, 17(4): 2417-2431.
[18]纪珊珊, 贾向东, 颉满刚, 等. 基于小区分割方案的异构网络覆盖性能研究[J]. 计算机工程, 2018, 44(8): 120-126.
Ji Shanshan, Jia Xiangdong, Xie Mangang, et al. Research on coverage performance for heterogeneous network based on cell split scheme[J]. Computer Engineering, 2018, 44(8): 120-126.(in Chinese)
[19]Rappaport T S, MacCartney G R, Samimi M K, et al. Wideband millimeter-wave propagation measurements and channel models for future wireless communication system design[J]. IEEE Transactions on Communications, 2015, 63(9): 3029-3056.
[20]Jia X, Xu W, Chen Y, et al. Hybrid Self-Backhaul and Cache Assisted Millimeter Wave Two-Tier Heterogeneous Networks With MIMO Equipped Backhaul Access Points[J]. IEEE Access, 2019, 7: 59963-59983.
[21]Yi W, Liu Y, Nallanathan A. Modeling and analysis of D2D millimeter-wave networks with Poisson cluster processes[J]. IEEE Transactions on Communications, 2017, 65(12): 5574-5588.
[22]Afshang M, Dhillon H S, Chong P H J. Modeling and performance analysis of clustered device-to-device networks[J]. IEEE Transactions on Wireless Communications, 2016, 15(7): 4957- 4972.
