1 引言
作为满足未来无线通信多样化需求的关键技术之一,近年来大规模多输入多输出(Multiple-Input Multiple-Output, MIMO)技术受到研究者广泛关注[1- 4]。大规模MIMO的增益依赖对阵列天线收发信号的相干处理,因此可靠信道估计成为决定系统性能的关键。
时分双工(Time Division Duplex, TDD)大规模MIMO系统中,基站阵列天线与用户之间的上行信道可以利用传统最小二乘(Least Square, LS)方法估计,所需导频开销较小(正比于用户个数[5])。下行信道可利用信道互易性得到,无需额外导频开销。频分双工(Frequency Division Duplex, FDD)模式下,信道互易性无法满足,此时基于LS的下行信道估计方案所需导频序列的长度正比于基站天线个数[5],基站配备大规模天线时将造成大量导频开销,降低系统频谱效率。实际场景中,基站通常部署在较高的位置,周围散射体稀少。因此,用户接收信号主要来自自身周围的散射作用,导致基站下行信号的离去角(Angle of Departure, AoD)扩展较窄。根据物理信道模型,此时基站与用户之间的下行信道可表示为角度域的等效稀疏向量[6-7]。在假设信道大尺度信息(如信道相关矩阵、AoD分布或用户位置)理想已知前提下,文献[6-7]表明,利用角度域信道的等效低维表示能够有效降低下行信道估计所需的导频开销。当缺少信道大尺度信息的先验认知时,上述方法难以直接应用。为解决这一问题,文献[8-11]将下行信道估计建模为稀疏恢复问题,并利用正交匹配追踪(Orthogonal Matching Pursuit, OMP)、稀疏贝叶斯学习(Sparse Bayesian Learning, SBL)等压缩感知方法实现稀疏信道的估计,此类方法无需信道大尺度信息,但估计性能有所下降。
另一方面,在用户高速移动场景,信道时变性使得相干时间大幅缩短,进一步降低了传统信道估计方法的效率。文献[12]提出基于经典Kalman滤波的时变信道估计方案,但是该方案无法有效利用信道稀疏特性,因此在FDD大规模MIMO下行信道估计中仍会引入高额导频开销。在假设用户位置信息理想已知前提下,文献[13]利用信道空时相关性与用户位置的关系,提出一种用户位置信息辅助的时变信道估计方案。文献[14]提出一种角度域信道系数和支撑基的联合估计/追踪方案,该方案无需已知信道大尺度信息,但仍要求用户在角度域是可分的。
针对上述问题,本文研究FDD大规模MIMO系统的下行时变信道估计方法。首先分析FDD大规模MIMO时变信道的空时稀疏特性,在此基础上,提出软结构先验模型驱动的稀疏贝叶斯信道估计(Soft-Structured Prior Model based Sparse Bayesian Estimation, SSPM-SBE)方案,针对方案涉及的复杂贝叶斯估计问题,给出基于变分优化的低复杂度求解方法。最后,给出方案估计性能的数值仿真,验证方案优越性。
符号定义:(·)T、(·)H和tr{·}分别表示矩阵的转置、共轭转置和迹,||·||表示欧几里德范数,[X]i, j表示矩阵的第i行第j列的元素, [·]表示统计期望,
[·]表示统计期望,![]()
![]() )表示向量x服从均值为μ、协方差矩阵为
)表示向量x服从均值为μ、协方差矩阵为![]() 的复高斯分布。
的复高斯分布。
2 系统模型
考虑一个基站与K个单天线用户组成的单小区系统,其中基站配备大规模天线阵列(天线数为N)。根据文献[14]给出的时变信道模型,时刻t基站与用户k之间的下行信道向量可表示为
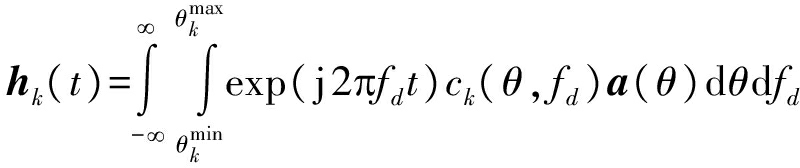
(1)
式中,![]() 表示基站发送信号的AoD区间。a(θ)表示阵列响应向量,即
表示基站发送信号的AoD区间。a(θ)表示阵列响应向量,即
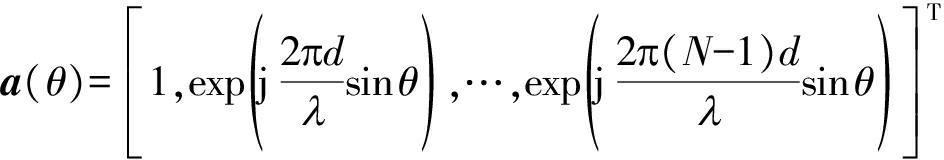
(2)
其中d表示天线间隔,λ表示载波波长。ck(θ, fd)表示AoD θ、多普勒频率fd对应的信道复增益。对于不同(θ, fd),假设ck(θ, fd)的取值互不相关[14],即

![]()
![]()
(3)
其中![]() 和
和![]() 分别表示角度和多普勒功率谱。
分别表示角度和多普勒功率谱。
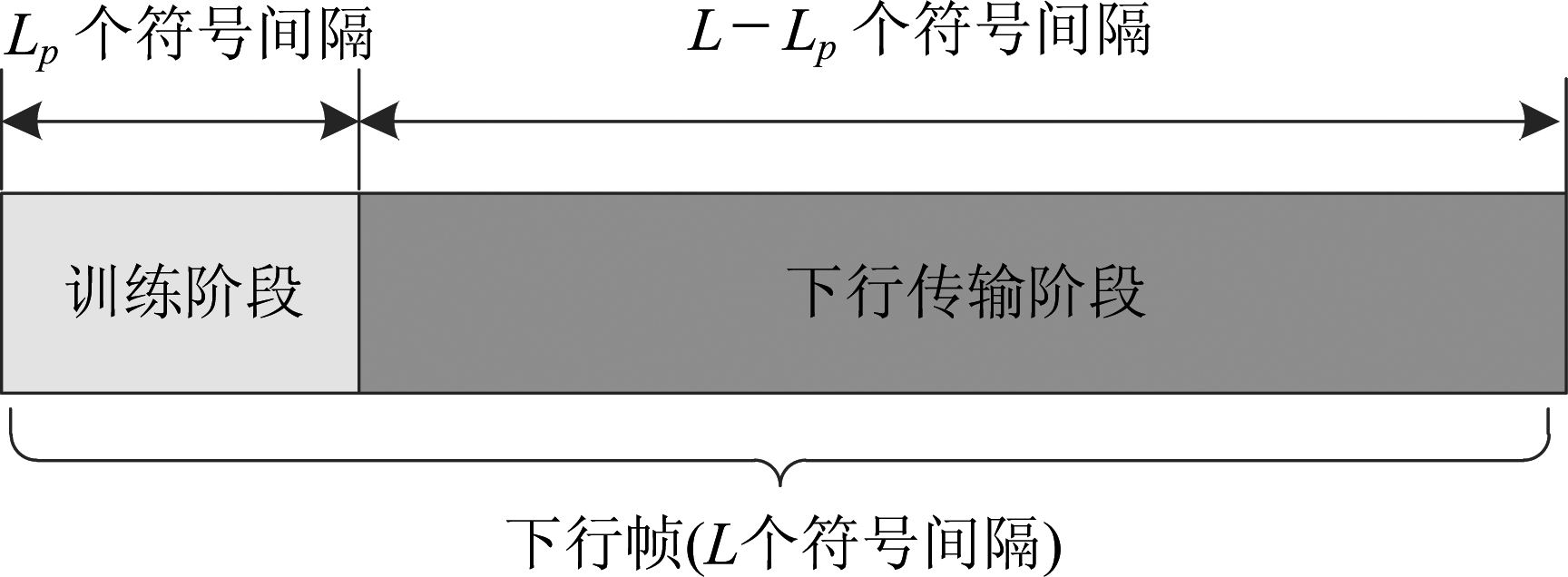
图1 下行帧结构示意
Fig.1 Illustration of downlink frame structure
如图1所示,每个下行帧由训练阶段(Lp个符号间隔)和下行传输阶段(L-Lp个符号间隔)组成。由于实际系统中Lp通常远小于L,因此近似认为训练阶段内信道的变化可忽略不计。需要注意的是,根据式(1)给出的模型,整个帧内信道是连续时变的。令T表示单个符号间隔的长度,则在第m个下行帧的训练阶段,基站与用户k之间的下行信道可表示为
hk,m=hk((m-1)LT+T)
(4)
在第m个下行帧的训练阶段,令![]() 表示连续Lp个符号间隔中基站广播的下行导频信号,则用户k的接收导频信号可表示为
表示连续Lp个符号间隔中基站广播的下行导频信号,则用户k的接收导频信号可表示为
(5)
其中nk,m为服从分布![]() 的加性高斯白噪声向量。
的加性高斯白噪声向量。
3 信道稀疏结构分析
考虑信道的等效角度域表示
(6)
式中F表示N维移位离散傅里叶矩阵,其第n列可表示为
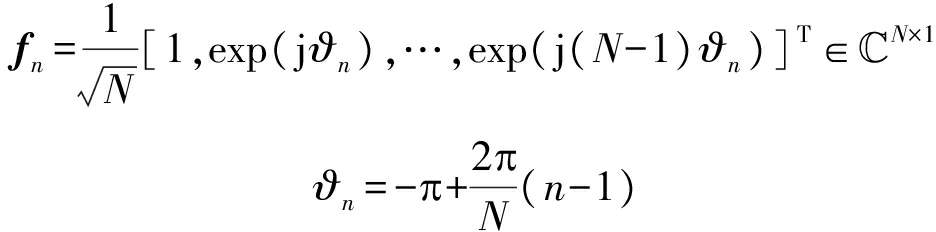
(7)
定义式(2)中的πsin θ为虚拟AoD,若将![]() 可看作区间[-π,π]内虚拟AoD的等间隔采样,角度域信道
可看作区间[-π,π]内虚拟AoD的等间隔采样,角度域信道![]() 可看作信道在虚拟AoD采用点
可看作信道在虚拟AoD采用点![]() 上的信道增益。
上的信道增益。
根据式(3)、(4)、(6),角度域信道的空时相关矩阵可以表示为
Ck(Δm)=
![]()
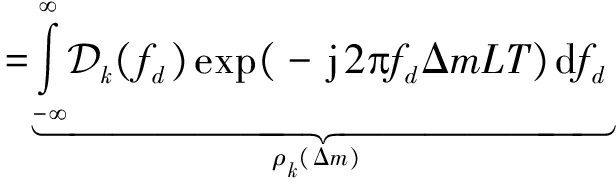

(8)
式中ρk(Δm)为时间相关系数,![]() 为空间相关矩阵。根据一阶自回归模型[15],相邻下行帧训练阶段信道之间的时变特性可以近似建模为
为空间相关矩阵。根据一阶自回归模型[15],相邻下行帧训练阶段信道之间的时变特性可以近似建模为
(9)
其中![]() 为模型误差。
为模型误差。
利用文献[5,7,14]中的多种分析方法,可以验证空间相关矩阵![]() 具有如下渐近性质。
具有如下渐近性质。
性质1 在大N区间,![]() 的非对角素趋于0,且仅当虚拟AoD采样ϑn满足
的非对角素趋于0,且仅当虚拟AoD采样ϑn满足![]() 的第n个对角元素具有显著幅度。
的第n个对角元素具有显著幅度。
如前文所述,由于用户接收信号主要来自自身周围的散射作用,导致下行发送信号的AoD区间或等价虚拟AoD区间(即![]() 较窄。同时,令
较窄。同时,令![]() 和ek,m,n分别表示
和ek,m,n分别表示![]() 和ek,m的第n个元素,由
和ek,m的第n个元素,由![]() 的定义可得
的定义可得
![]()

![]()
 [|ek,m,n|2]
[|ek,m,n|2]
因此,根据性质![]() 和ek,m中仅有少数元素有显著幅度。具体而言,
和ek,m中仅有少数元素有显著幅度。具体而言,![]() 和ek,m具有以下两种空时稀疏结构。
和ek,m具有以下两种空时稀疏结构。
时域共稀疏结构:由于空间相关矩阵可认为近似不变,![]() 和ek,m中显著元素的序号集(用
和ek,m中显著元素的序号集(用![]() 表示)在数个邻近下行帧内是相同的;
表示)在数个邻近下行帧内是相同的;
空域簇稀疏结构:由于![]() 可表示为
可表示为![]()
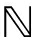
![]() 和ek,m中的显著元素成簇出现。
和ek,m中的显著元素成簇出现。
4 基于空时稀疏结构的信道估计方案
将式(6)代入(5),可将用户接收导频信号重写为
(10)
若已知角度域信道![]() 则原始信道hk,m可直接由基扩展模型
则原始信道hk,m可直接由基扩展模型![]() 给出,因此下文考虑角度域信道
给出,因此下文考虑角度域信道![]() 的估计。
的估计。
由于![]() 为稀疏向量,可采用典型SBL方法[16]进行估计。但典型SBL无法有效利用信道空时特性(如空时稀疏结构),导频资源受限情况下估计性能较差。本节给出一种SSPM-SBE方案来提升信道估计的可靠性。不失一般性,假设当前处于第M帧,为有效利用信道空时特性,SSPM-SBE方案联合利用当前接收导频信号yk,M和此前M-1帧的接收导频信号
为稀疏向量,可采用典型SBL方法[16]进行估计。但典型SBL无法有效利用信道空时特性(如空时稀疏结构),导频资源受限情况下估计性能较差。本节给出一种SSPM-SBE方案来提升信道估计的可靠性。不失一般性,假设当前处于第M帧,为有效利用信道空时特性,SSPM-SBE方案联合利用当前接收导频信号yk,M和此前M-1帧的接收导频信号![]() 估计当前信道
估计当前信道![]() 同时,为了促使算法输出具有第3节所述空时稀疏结构的估计结果,本文提出
同时,为了促使算法输出具有第3节所述空时稀疏结构的估计结果,本文提出![]() 和ek,m的软结构先验(Soft-Structured Prior, SSP)模型
和ek,m的软结构先验(Soft-Structured Prior, SSP)模型
(11)
(12)
其中αk=[αk,1,…,αk,N]T,η为大于0的标量参数。v=[νL,ν,νR]为指示向量,其取值在[1,0,0]、[0,1,0]和[0,0,1]之间等概率选择,因此v的概率分布可表示为
(13)
![]() 和ek,m的精度(Precision)矩阵(即ηAk和Ak)为对角矩阵,其对角元素由参数αk和v决定,即
和ek,m的精度(Precision)矩阵(即ηAk和Ak)为对角矩阵,其对角元素由参数αk和v决定,即
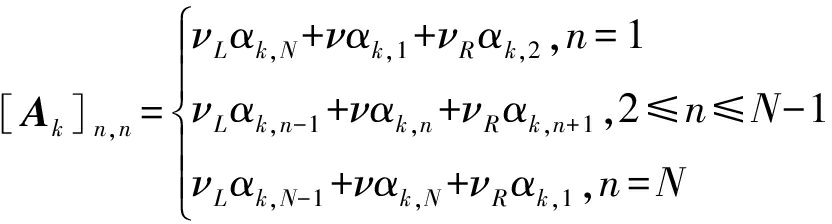
(14)
根据式(9)和![]() 与
与![]() 之间的转移概率,即给定
之间的转移概率,即给定![]() 条件下
条件下![]() 的条件分布可表示为
的条件分布可表示为
(15)
类比典型SBL方法,为了构建完全贝叶斯问题,引入αk的Gamma超先验(Hyperprior)模型
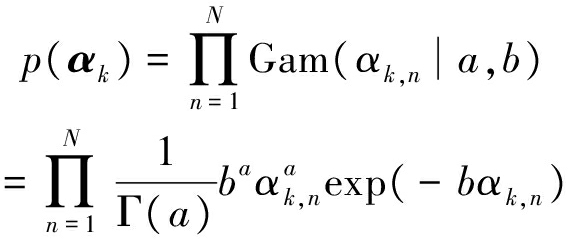
(16)
式中Γ(a)表示Gamma函数[17, 8.310.1],超参数a和b设置为较小的正数[16](如a=b=10-4)。
上述SSP模型能够鼓励估计算法输出具有两种空时稀疏结构的信道估计,具体原因如下:
首先,传统信道估计方案(如典型SBL)输出的某些次优解中,邻近帧角度域信道可能具有不同的稀疏结构(与第三节结论相悖),造成较大估计误差。由式(11)、(12)中的先验概率和式(15)中的转移概率表达式,SSP模型迫使![]() 的精度矩阵和给定
的精度矩阵和给定![]() 条件下
条件下![]() 的精度矩阵具有相同结构(区别仅在于标量系数η),从而可有效消除此类次优解的影响。
的精度矩阵具有相同结构(区别仅在于标量系数η),从而可有效消除此类次优解的影响。
其次,根据式(11)和![]() 中第n个元素的精度可表示为νLαk,n-1+ναk,n+νRαk,n+1(不失一般性,考虑2≤n≤N-1的情况)。若[νL,ν,νR]=[1,1,1],则SSP模型退化为文献[11]给出的结构先验模型。结构先验模型能够鼓励算法输出具有簇稀疏结构的估计,具体而言,模型中的共享参数αk,n不仅影响
中第n个元素的精度可表示为νLαk,n-1+ναk,n+νRαk,n+1(不失一般性,考虑2≤n≤N-1的情况)。若[νL,ν,νR]=[1,1,1],则SSP模型退化为文献[11]给出的结构先验模型。结构先验模型能够鼓励算法输出具有簇稀疏结构的估计,具体而言,模型中的共享参数αk,n不仅影响![]() 第n个元素的估计,同时影响相邻元素的估计。若算法输出较大的αk,n,则
第n个元素的估计,同时影响相邻元素的估计。若算法输出较大的αk,n,则![]() 的第n-1、n和n+1个元素将同时趋近于0,导致估计中0元素(或近似为0的元素)成簇出现。但结构先验模型的引入使得相应估计问题只能通过启发式算法近似求解[11],收敛性难以验证。相对而言,SSP模型在结构先验模型基础上增加了共享参数的随机指示系数[νL,ν,νR],不仅能促使算法输出具有所需稀疏结构的信道估计,而且使得后续算法在每个阶段都可精确求解,从而在理论上保证了算法的收敛性。
的第n-1、n和n+1个元素将同时趋近于0,导致估计中0元素(或近似为0的元素)成簇出现。但结构先验模型的引入使得相应估计问题只能通过启发式算法近似求解[11],收敛性难以验证。相对而言,SSP模型在结构先验模型基础上增加了共享参数的随机指示系数[νL,ν,νR],不仅能促使算法输出具有所需稀疏结构的信道估计,而且使得后续算法在每个阶段都可精确求解,从而在理论上保证了算法的收敛性。
4.1 SSPM-SBE方案的变分优化求解
为获得![]() 的最大后验(Maximum Posterior Probability, MAP)估计,需要求解最优参数αk、ρk(1)下
的最大后验(Maximum Posterior Probability, MAP)估计,需要求解最优参数αk、ρk(1)下![]() 的后验概率分布,本节利用变分优化求解这一问题。
的后验概率分布,本节利用变分优化求解这一问题。
变分优化方法的主要思想是,通过函数近似将多变量的联合分布分解为多个单变量分布的乘积,进而通过迭代优化得到目标变量后验分布的近似。根据[18, 10.1],接收导频信号Yk=[yk,1,…,yk,M]的对数边缘分布可表示为
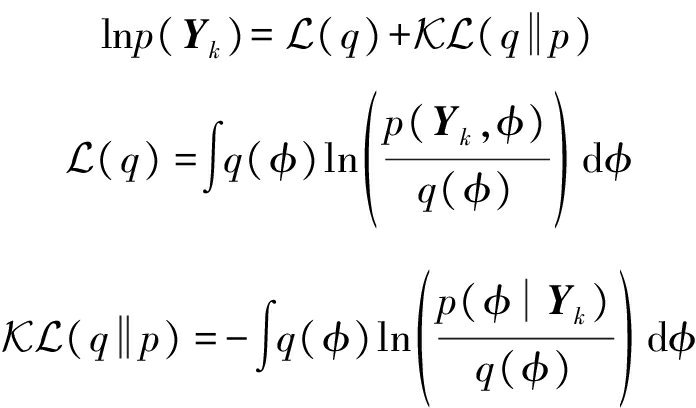
(17)
其中![]() 联合概率p(Yk,φ)由下式给出
联合概率p(Yk,φ)由下式给出
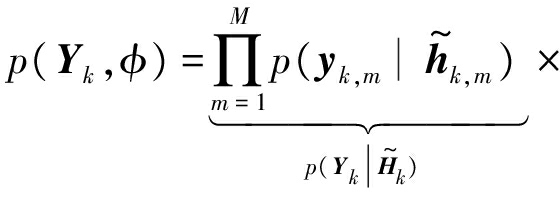
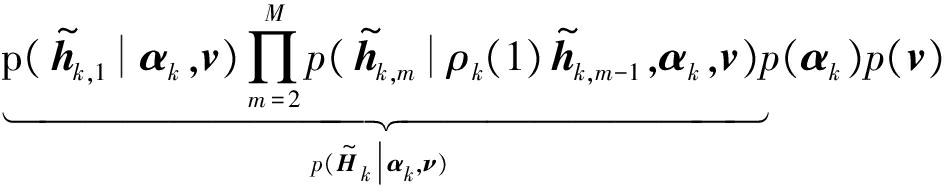
(18)
式(17)中,![]() 表示Kullback-Leibler散度,其取值表征实际后验分布p(φ|Yk)与其变分近似q(φ)之间的差异。由于
表示Kullback-Leibler散度,其取值表征实际后验分布p(φ|Yk)与其变分近似q(φ)之间的差异。由于![]() 的取值非负,函数
的取值非负,函数![]() 是lnp(Yk)的下界,通常称为变分下界。引入q(φ)的如下分解形式
是lnp(Yk)的下界,通常称为变分下界。引入q(φ)的如下分解形式
(19)
其中![]() 和q(v)分别为
和q(v)分别为![]() 的变分分布,即相应后验分布的近似。
的变分分布,即相应后验分布的近似。
变分优化方法对![]() 和参数ρk(1)、η进行迭代优化,以最小化
和参数ρk(1)、η进行迭代优化,以最小化![]() 或等价地最大化变分下界
或等价地最大化变分下界![]() 这里假设v为分布已知的参数,因此算法中直接令q(v)=p(v)。
这里假设v为分布已知的参数,因此算法中直接令q(v)=p(v)。
![]() 的更新:根据[18, 10.1],每次迭代中
的更新:根据[18, 10.1],每次迭代中![]() 按照如下规则更新
按照如下规则更新
![]()
 αk,v[lnp(Yk,φ)]+const.
αk,v[lnp(Yk,φ)]+const.
(20)
式中,const.表示与优化变量无关的常数, αk,v[·]表示针对变分分布q(αk)和q(v)的期望。将式(11)、(13)、(15)、(16)代入(17)、(20)并将
αk,v[·]表示针对变分分布q(αk)和q(v)的期望。将式(11)、(13)、(15)、(16)代入(17)、(20)并将![]() 的无关项并入const.可得
的无关项并入const.可得
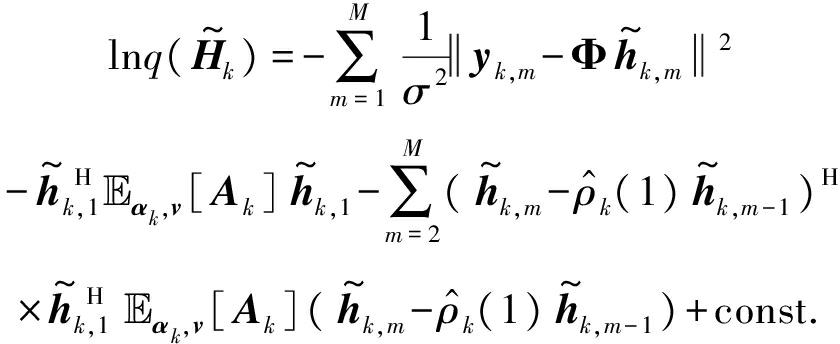
(21)
其中![]() 表示最近一次迭代中ρk(1)的估计,
表示最近一次迭代中ρk(1)的估计, αk,v[Ak]可由下文q(αk)更新过程中的方法计算。
αk,v[Ak]可由下文q(αk)更新过程中的方法计算。
可见在变分分布(21)下,![]() 构成一个线性动态系统,因此
构成一个线性动态系统,因此![]() 的变分分布可表示为[18, 13.3]
的变分分布可表示为[18, 13.3]
![]()
![]() k,m)
k,m)
(22)
其中μk,m和![]() k,m可看作是
k,m可看作是![]() 后验均值和协方差矩阵的近似,其取值可利用Kalman滤波和Kalman平滑公式[18, 13.3]计算,具体流程由算法1给出。此外
后验均值和协方差矩阵的近似,其取值可利用Kalman滤波和Kalman平滑公式[18, 13.3]计算,具体流程由算法1给出。此外![]() 与
与![]() 之间的相关矩阵可表示为[18, 13.3]
之间的相关矩阵可表示为[18, 13.3]
(23)
其中矩阵Jk,m-1由算法1给出。

算法1 利用Kalman滤波和Kalman平滑公式计算 μk,m和k,m1.初始化:令'k,m、″k,m和k,m分别表示给定{yk,i}m-1i=1、{yk,i}mi=1和{yk,i}Mi=1条件下h~k,m的后验协方差矩阵;令μ″k,m和μk,m分别表示给定{yk,i}mi=1和{yk,i}Mi=1条件下h~k,m的后验均值。2.Kalman滤波:For m=1,…,M计算'k,m,'k,m=( αk,v[Ak])-1,m=1ρ^2k(1)″k,m-1+( αk,v[Ak])-1,m≥2;

计算″k,m,″k,m= ('k,m)-1+1σ2ΦHΦ -1 令Kk,m='k,mΦH(Φ'k,mΦH+σ2ILp),计算 μ″k,m μ″k,m= Kk,myk,m,m=1ρ^k(1)μ″k,m-1+Kk,m(yk,m-ρ^k(1)Φμ″k,m-1),2≤m≤M 3.Kalman平滑:For m=M,…,1若m=M,令k,m=″k,m;否则令Jk,m=ρ^k(1)″k,m('k,m)-11)计算k,m,k,m=″k,m+Jk,m(k,m+1-'k,m+1)JHk,m;2)计算μk,m, μk,m=μ″k,m+Jk,m(μk,m+1-ρ^k(1) μ″k,m)。4.输出{k,m}Mm=1、 {μk,m}Mm=1和{Jk,m}Mm=1。
2)q(αk)的更新:每次迭代中q(αk)按照如下规则更新
![]()
![]()
![]()
(24)
其中![]() 表示针对变分分布
表示针对变分分布![]() 和q(v)的期望。将式(11)、(13)、(15)和(16)代入式(24),并将αk的无关项并入const.可得
和q(v)的期望。将式(11)、(13)、(15)和(16)代入式(24),并将αk的无关项并入const.可得
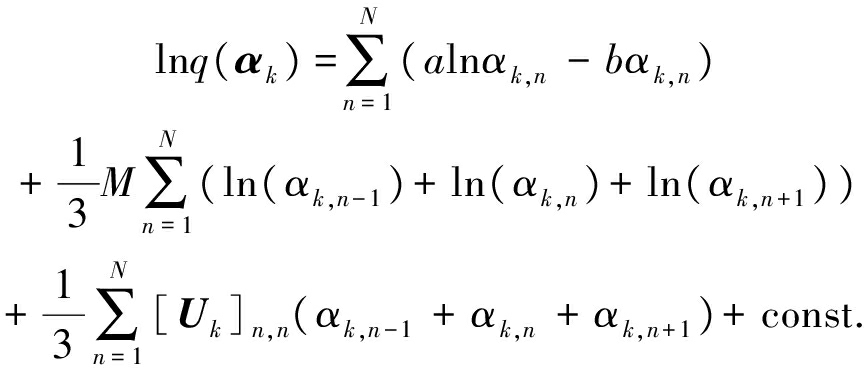
(25)
式中矩阵Uk由下式给出
![]()
![]()
![]()
(26)
其中,![]() 表示最近一次迭代中η的估计。整理式(25)可得
表示最近一次迭代中η的估计。整理式(25)可得
![]()
![]()
![]()
![]()
(27)
其中C为与αk无关的常数。利用式(27)给出的变分分布可对式(21)中的期望 αk,v[Ak]进行计算。由于
αk,v[Ak]进行计算。由于 αk,v[Ak]为对角矩阵,仅需考虑其对角元素。若x服从参数为(c1,c2)的Gamma分布,即x~Gam(x|c1,c2),则x的均值可表示为
αk,v[Ak]为对角矩阵,仅需考虑其对角元素。若x服从参数为(c1,c2)的Gamma分布,即x~Gam(x|c1,c2),则x的均值可表示为 [x]=c1/c2。利用这一性质和式(13)、(14)可得
[x]=c1/c2。利用这一性质和式(13)、(14)可得
[ αk,v[Ak]]n,n=
αk,v[Ak]]n,n= 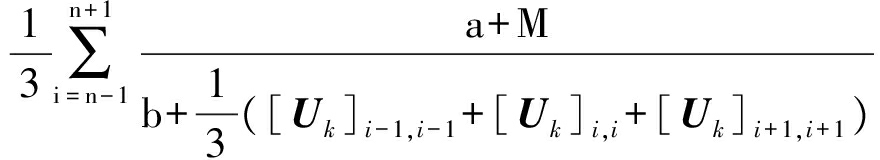
(28)
3)参数η的更新:将![]() 和q(αk)的表达式代入式(17),并将η的无关项并入const.,可将变分下界重写为
和q(αk)的表达式代入式(17),并将η的无关项并入const.,可将变分下界重写为
![]()
![]()
 αk,v[Ak])+const.
αk,v[Ak])+const.
(29)
其中,![]() 表示针对变分分布
表示针对变分分布![]() 和q(v)的期望,期望
和q(v)的期望,期望 αk,v[Ak]已由式(28)给出。令上式对η的一阶导数为零可得
αk,v[Ak]已由式(28)给出。令上式对η的一阶导数为零可得
(30)
4)参数ρk(1)的更新:将![]() 和q(αk)的表达式代入式(17),并将ρk(1)的无关项并入const.,可将变分下界重写为
和q(αk)的表达式代入式(17),并将ρk(1)的无关项并入const.,可将变分下界重写为
![]()
![]()
![]()
 αk,v[Ak]}+const.
αk,v[Ak]}+const.
(31)
其中期望 αk,v[Ak]已由式(28)给出。令上式对ρk(1)的一阶导数为零可得
αk,v[Ak]已由式(28)给出。令上式对ρk(1)的一阶导数为零可得
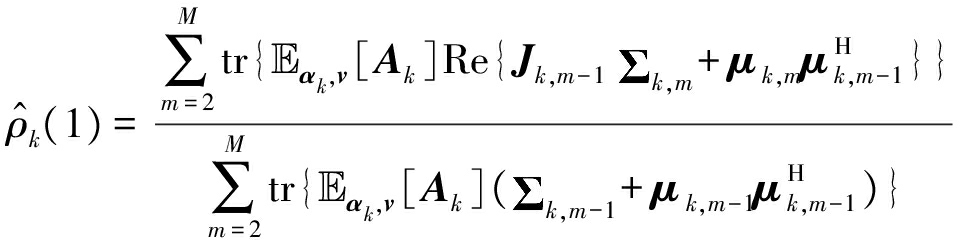
(32)
算法收敛后,![]() 的近似MAP估计即为其后验均值
的近似MAP估计即为其后验均值![]() 原始信道hk,M的估计可根据基扩展模型
原始信道hk,M的估计可根据基扩展模型![]() 计算。需要注意的是,
计算。需要注意的是,![]() 是对训练阶段信道的估计。在实际应用中,我们也将该估计值作为下行传输阶段信道的近似估计。由于整个帧内信道是连续时变的,因此估计的近似程度会随时间下降。
是对训练阶段信道的估计。在实际应用中,我们也将该估计值作为下行传输阶段信道的近似估计。由于整个帧内信道是连续时变的,因此估计的近似程度会随时间下降。
4.2 计算复杂度分析
SSPM-SBE方案的计算复杂度主要来源于算法1中的矩阵求逆。Kalman滤波阶段需要进行N维矩阵(![]() ′k,m)-1+σ-2ΦHΦ的求逆运算,利用矩阵求逆引理,所需计算复杂度可降低为
′k,m)-1+σ-2ΦHΦ的求逆运算,利用矩阵求逆引理,所需计算复杂度可降低为![]() 平滑阶段需要进行N维矩阵
平滑阶段需要进行N维矩阵![]() 的求逆运算,直接计算的复杂度较高
的求逆运算,直接计算的复杂度较高![]() 为解决这一问题,可采用文献[19,20]给出的一系列Neumann级数展开方法对求逆运算进行近似,所需计算复杂度可降低为
为解决这一问题,可采用文献[19,20]给出的一系列Neumann级数展开方法对求逆运算进行近似,所需计算复杂度可降低为![]() 综上所述,SSPM-SBE方案的总计算复杂度为
综上所述,SSPM-SBE方案的总计算复杂度为![]() 其中I为变分优化所需的迭代次数。
其中I为变分优化所需的迭代次数。
5 数值仿真
本节仿真所提信道估计方案的均方误差(Mean Square Error, MSE)性能,即
(33)
其中hk(lT)表示lT时刻基站与用户之间的下行信道,![]() 表示hk(lT)的估计。B表示连续下行帧的个数,在所有仿真中取B=200。第m个下行帧内,下行信道hk(lT)(l∈[(m-1)L+1,mL])的估计均为
表示hk(lT)的估计。B表示连续下行帧的个数,在所有仿真中取B=200。第m个下行帧内,下行信道hk(lT)(l∈[(m-1)L+1,mL])的估计均为![]() 为了便于对比,将大尺度衰落和噪声方差归一化为1。仿真中,根据公式(1)生成整个帧内连续时变的信道[21]。用户平均AoD,即
为了便于对比,将大尺度衰落和噪声方差归一化为1。仿真中,根据公式(1)生成整个帧内连续时变的信道[21]。用户平均AoD,即![]() 由区间[-π/2,π/2]内随机采样得到。角度功率谱
由区间[-π/2,π/2]内随机采样得到。角度功率谱![]() 建模为截断Laplace模型[22],多普勒功率谱建模为Jakes功率谱模型[23]。定义E/σ2为平均信噪比(Signal-to-Noise Ratio, SNR),其中E表示基站发送导频符号的功率,主要仿真参数由表1给出。为验证SSPM-SBE方案的优越性,仿真中同时给出典型SBL[16]、结构SBL[11]方案和Genie-aided LS[5,7]的MSE性能,其中Genie-aided LS方案假设信道大尺度信息(如信道相关矩阵、AoD分布或用户位置)理想已知,其性能为其他方案性能的上界。
建模为截断Laplace模型[22],多普勒功率谱建模为Jakes功率谱模型[23]。定义E/σ2为平均信噪比(Signal-to-Noise Ratio, SNR),其中E表示基站发送导频符号的功率,主要仿真参数由表1给出。为验证SSPM-SBE方案的优越性,仿真中同时给出典型SBL[16]、结构SBL[11]方案和Genie-aided LS[5,7]的MSE性能,其中Genie-aided LS方案假设信道大尺度信息(如信道相关矩阵、AoD分布或用户位置)理想已知,其性能为其他方案性能的上界。
表1 仿真参数
Tab.1 Simulation parameters
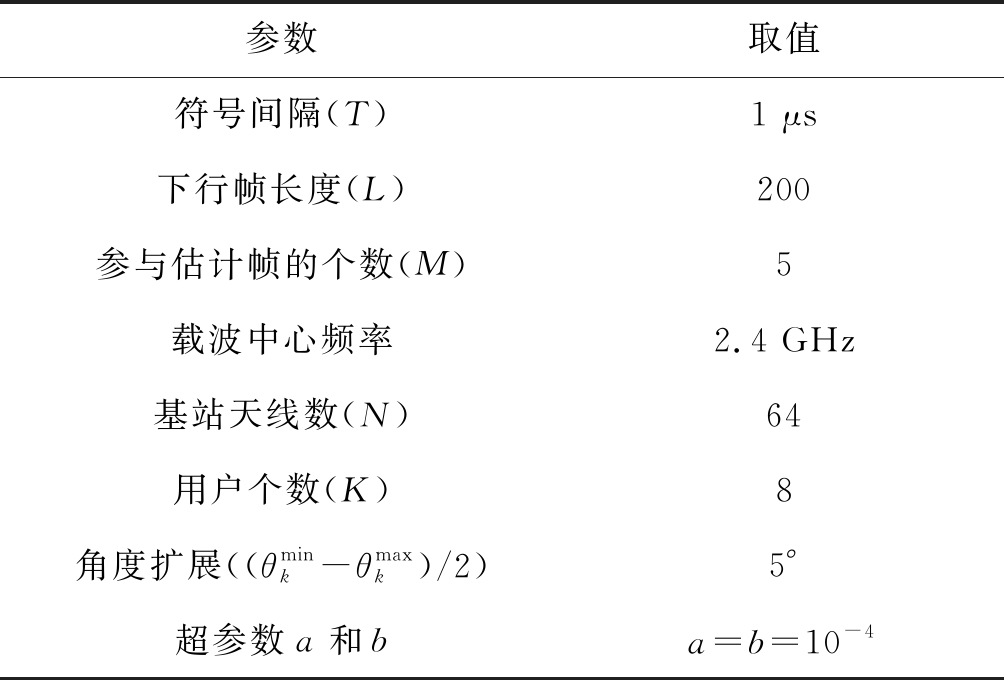
参数取值符号间隔(T)1 μs下行帧长度(L)200参与估计帧的个数(M)5载波中心频率2.4 GHz基站天线数(N)64用户个数(K)8角度扩展((θmink-θmaxk)/2)5°超参数a和ba=b=10-4
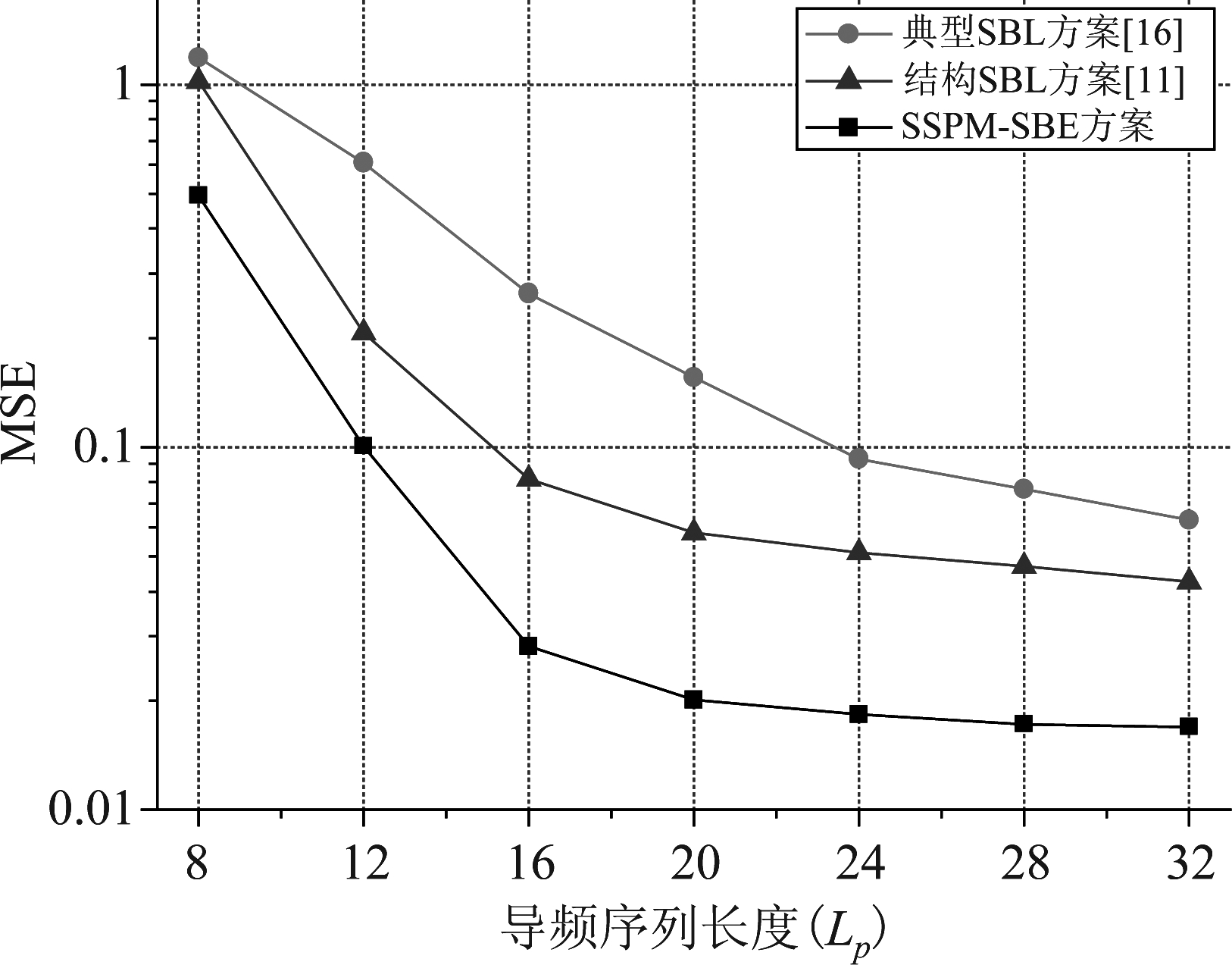
图2 MSE性能随导频序列长度变化趋势 (用户移动速度为50 km/h)
Fig.2 MSE performances for different lengths of pilot sequence (The user velocity is 50 km/h)
图2和图3仿真了SSPM-SBE、典型SBL和结构SBL方案的MSE性能随导频序列长度的变化趋势,其中用户移动速度分别为50 km/h(图1)和150 km/h(图2),平均SNR设为15 dB。如图所示,实现同等MSE条件下,SSPM-SBE方案所需的导频开销远小于两种对比方案,其原因是SSPM-SBE方案能够更加有效的利用信道空时稀疏结构。此外,随着导频序列长度增加,所有方案的MSE收敛于一定的性能平台,其原因是增加 Lp不能有效降低下行传输阶段信道时变造成的估计误差。
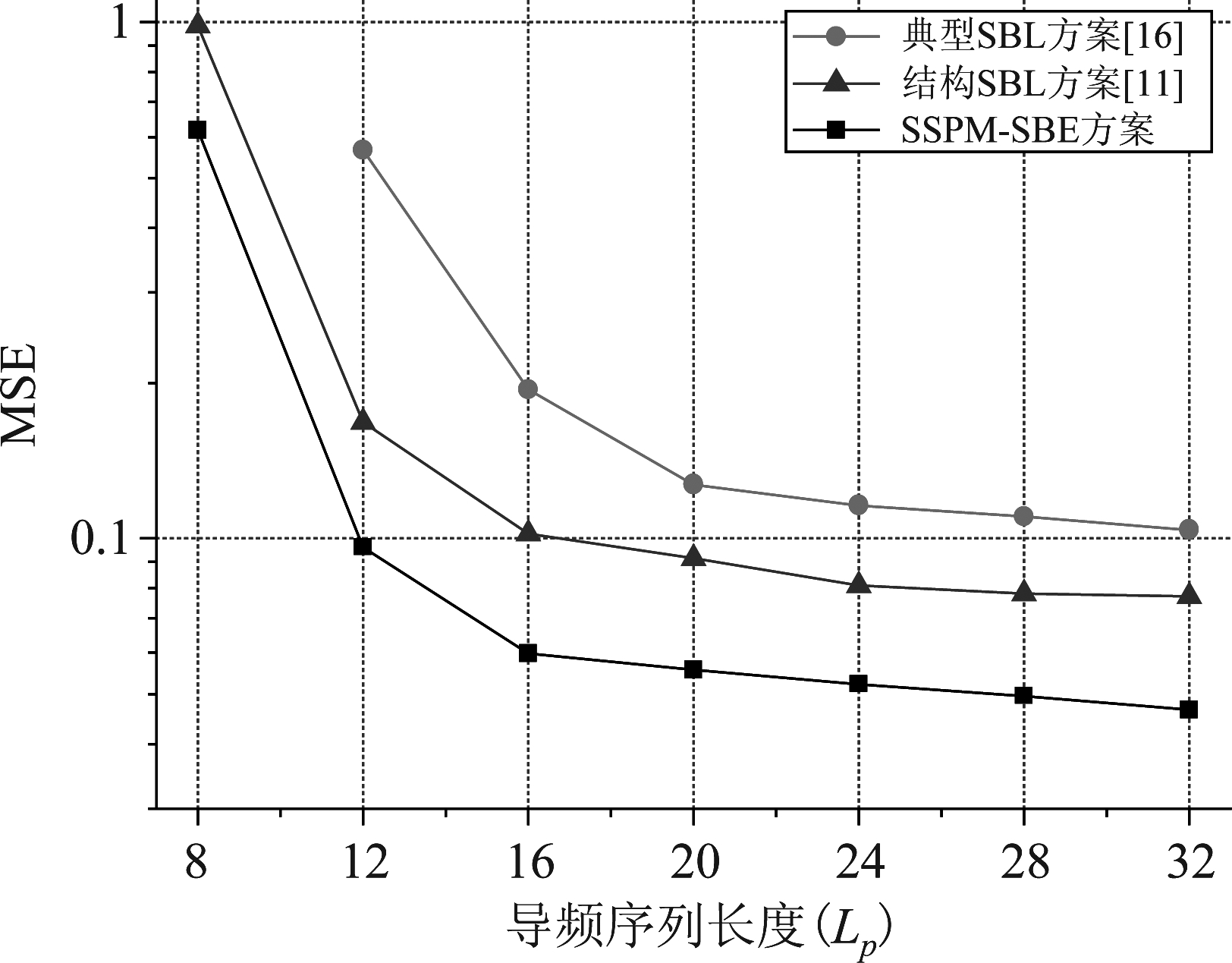
图3 MSE性能随导频序列长度变化趋势 (用户移动速度为150 km/h)
Fig.3 MSE performances for different lengths of pilot sequence (The user velocity is 150 km/h)

图4 MSE性能随平均SNR变化趋势 (用户移动速度为50 km/h)
Fig.4 MSE performances for different average SNRs (The user velocity is 50 km/h)
图4和图5仿真了SSPM-SBE、典型SBL和结构SBL方案的MSE性能随平均SNR的变化趋势,其中用户移动速度分别为50 km/h(图4)和150 km/h(图5),导频序列长度设为Lp=16。如图所示,在整个观察区间内SSPM-SBE方案具有最优性能。在高SNR区间,所有方案的MSE收敛于一定的性能平台,其原因是增加SNR不能有效降低下行传输阶段信道时变造成的估计误差。
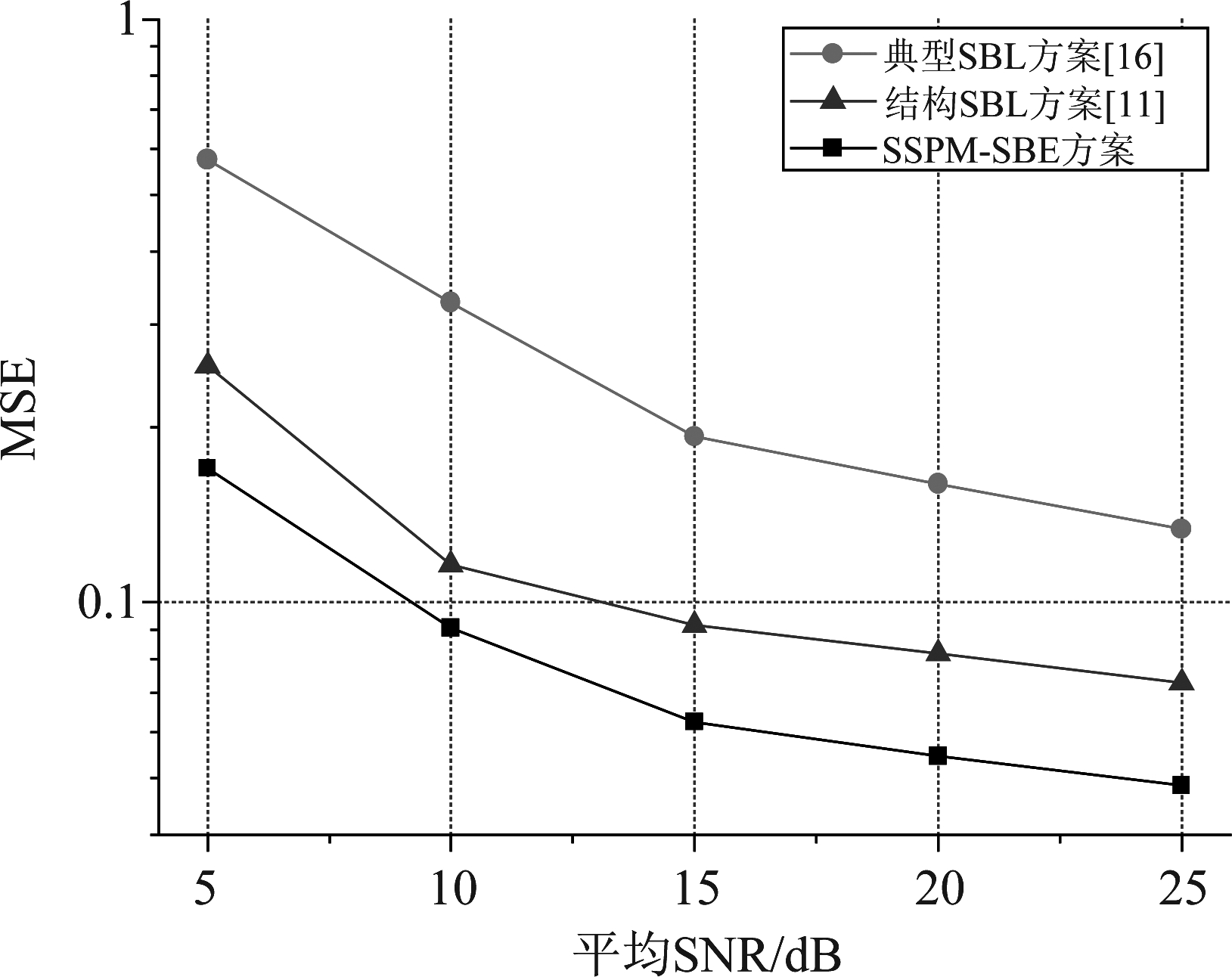
图5 MSE性能随平均SNR变化趋势 (用户移动速度为150 km/h)
Fig.5 MSE performances for different average SNRs (The user velocity is 150 km/h)
图6仿真了SSPM-SBE、典型SBL和结构SBL方案的MSE性能随用户移动速度的变化趋势,其中平均SNR为20 dB,导频序列长度为Lp=16,用户移动速度在25 km/h至200 km/h之间变化,对应的归一化频移如表2所示。如图所示,所提方案的性能增益随用户移动速度增加而降低,根据图2~图5所得结论,其原因是随着用户移动速度增加,下行传输阶段信道时变性的影响逐渐增强。尽管如此,当用户移动速度增至200 km/h时,SSPM-SBE方案仍能提供可观的性能提升。
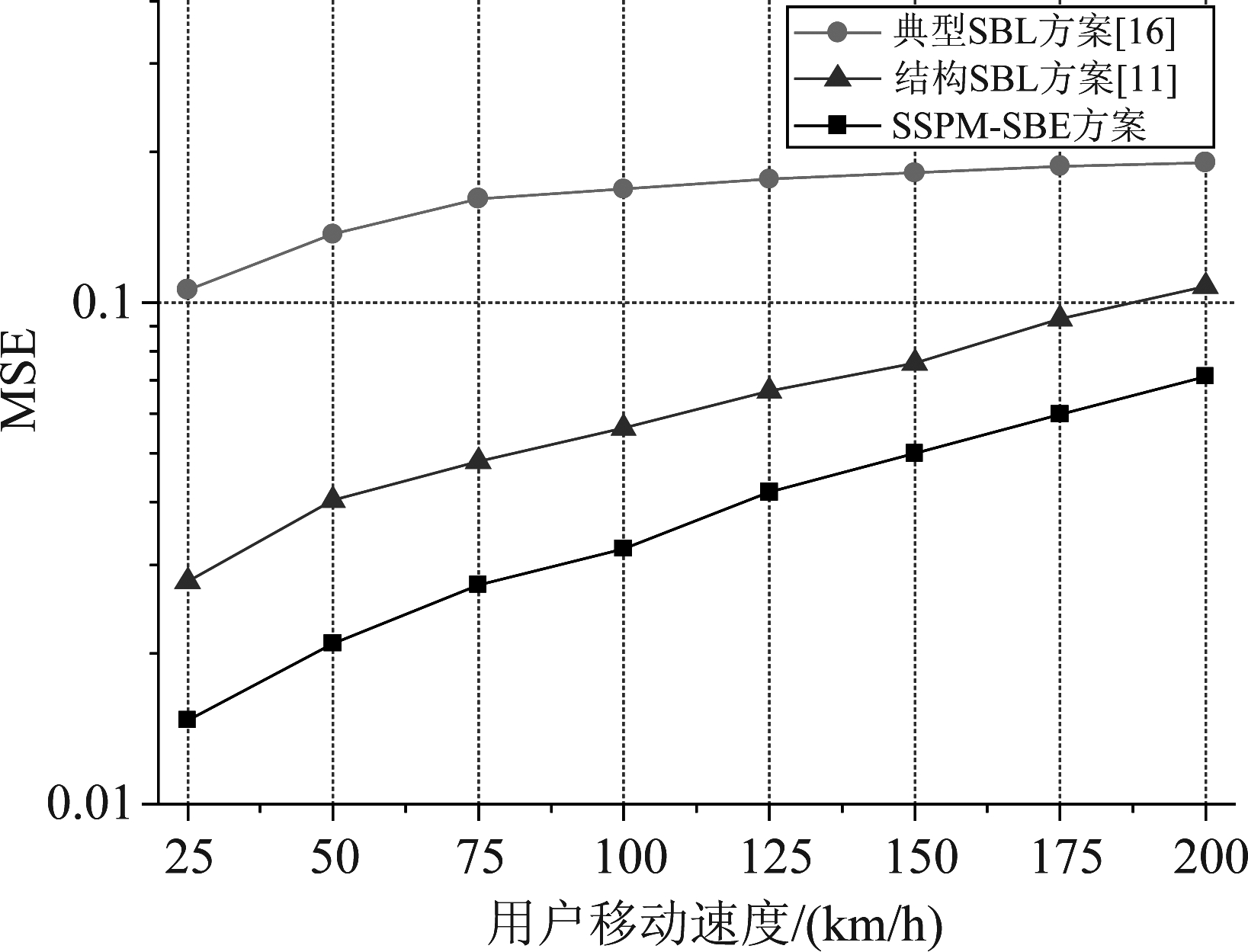
图6 MSE性能随用户移动速度变化趋势
Fig.6 MSE performances for different user velocities
表2 不同用户移动速率下的归一化多普勒频移
Tab.2 Normalized Doppler frequency for different user velocity

速度/km255075100125150175200归一化多普勒频移0.0110.0220.0330.0440.0560.0670.0780.089
6 结论
针对FDD大规模MIMO系统中的下行时变信道估计问题,提出了一种基于信道空时稀疏性的SSPM-SBE信道估计方案。通过引入角度域信道的软结构先验模型,SSPM-SBE方案可以促使算法输出符合空时稀疏结构特征的信道估计。仿真结果表明,SSPM-SBE方案能够有效降低信道估计所需的导频开销,或在相同导频开销下显著提升估计的可靠性。同时SSPM-SBE方案无需信道大尺度信息(如信道相关矩阵、AoD分布或用户位置)的先验认知,在实际系统中易于应用。
[1] Marzetta T L. Noncooperative cellular wireless with unlimited numbers of base station antennas[J]. IEEE Transactions on Wireless Communications, 2010, 9(11): 3590-3600.
[2] Sun C, Gao X, Jin S, et al. Beam division multiple access transmission for massive MIMO communications[J]. IEEE Transactions on Communications, 2015, 63(6): 2170-2184.
[3] Lin H, Gao F, Jin S, et al. A new view of multi-user hybrid massive MIMO: non-orthogonal angle division multiple access[J]. IEEE Journal on Selected Areas in Communications, 2017, 35(11): 2268-2280.
[4] 沈哲贤, 许魁, 王雨榕,等. 全双工大规模MIMO异构网络频谱效率分析及优化[J]. 信号处理, 2018, 34(4): 379-390.
Shen Z X, Xu K, Wang Y R, et al. Spectral Efficiency Analysis and Optimization for Full Duplex Heterogeneous Network with Massive MIMO[J]. Journal of Signal Processing, 2018, 34(4): 379-390.(in Chinese)
[5] Adhikary A, Nam J, Ahn J, et al. Joint spatial division and multiplexing: the large-scale array regime[J]. IEEE Transactions on Information Theory, 2013, 59(10): 6441- 6463.
[6] Xie H, Gao F, Zhang S, et al. A unified transmission strategy for TDD/FDD massive MIMO systems with spatial basis expansion model[J]. IEEE Transactions on Vehicular Technology, 2017, 66(4): 3170-3184.
[7] Xia X, Xu K, Zhang D, et al. Beam-domain full-duplex massive MIMO: realizing co-time co-frequency uplink and downlink transmission in cellular system[J]. IEEE Transactions on Vehicular Technology, 2017, 66(10): 8845- 8862.
[8] Lee J, Gil G, Lee Y. Channel estimation via orthogonal matching pursuit for hybrid MIMO systems in millimeter wave communications[J]. IEEE Transactions Communications, 2016, 64(6): 2370-2386.
[9] Cheng X, Sun J, Li S. Channel estimation for FDD multi-user massive MIMO: a variational bayesian inference-based approach[J]. IEEE Transactions Wireless Communications, 2017, 16(11): 7590-7602.
[10]Dai J, Liu A and Lau V. K. N. FDD massive MIMO channel estimation with arbitrary 2D-array geometry[J]. IEEE Transactions on Signal Processing, 2018, 66(10): 2584-2599.
[11]Wang Y, Liu A, Xia X, et al. Learning the structured sparsity: 3D massive MIMO channel estimation and adaptive spatial interpolation[J]. IEEE Transactions on Vehicular Technology, 2019, to appear, DOI: 10.1109/TVT.2019.2909392.
[12]Noh S, Zoltowski M. D, Sung Y. Optimal pilot beam pattern design for massive MIMO systems[C]∥ 2013 Asilomar Conference on Signals, Systems and Computers. Pacific Grove, CA, USA, 2013: 1- 6.
[13]Zhang C, Zhang J, Huang Y, et al. Location-aided channel tracking and downlink transmission for HST massive MIMO systems[J]. IET Communications, 2017, 11(3): 2082-2088.
[14]Ma J, Zhang S, Li H, et al. Sparse Bayesian learning for the time-varying massive MIMO channels: acquisition and tracking[J]. IEEE Transactions Communications, 2018, 67(3): 1925-1938.
[15]Chen B, Yang C, Liao W. Robust fast time-varying multipath fading channel estimation and equalization for MIMO-OFDM systems via a fuzzy method[J]. IEEE Transactions on Vehicular Technology, 2012, 61(4): 1599-1609.
[16]Ji S, Xue Y, Carin L. Bayesian compressive sensing[J]. IEEE Transactions on Signal Processing, 2008, 56(6): 2346-2356.
[17]Gradshteyn I S, Ryzhik I M. Table of Integrals, Series and Products[M]. 7th edition, Salt Lake City, USA: Academic Press, 2007.
[18]Bishop C M. Pattern recognition and machine learning[M]. New York, USA: Springer-Verlag, 2006.
[19]Zhu D, Li B, Liang P. On the matrix inversion approximation based on Neumann series in massive MIMO systems[C]∥ 2015 IEEE International Conference on Communications(ICC). London, UK, 2013: 1763-1769.
[20]Tang C, Liu C, Yuan L, et al. High precision low complexity matrix inversion based on newton iteration for data detection in the massive MIMO[J]. IEEE Communications Letters, 2016, 20(3): 490- 493.
[21]Fleury B H. First-and second-order characterization of direction dispersion and space selectivity in the radio channel[J]. IEEE Transactions on Information Theory, 2000, 46(6): 2027-2044.
[22]Xiong X, Jiang B, Gao X, et al. QoS-guaranteed user scheduling and pilot assignment for large-scale MIMO-OFDM systems[J]. IEEE Transactions on Vehicular Technology, 2016, 65(8): 6275- 6289.
[23]Jakes W C. Microwave Mobile Communications[M]. 2nd Edition. New York, USA: IEEE Press, 1994.


