1 引言
手指静脉识别近年来成为生物特征识别领域的一项热门研究,因其不易被伪造、不易被磨损、活体性强等突出优点,已经逐渐发展至实际应用当中,比如门禁系统等[1]。手指静脉血管的网络结构是指静脉的特征体现,因此对指静脉的研究,关键在于对血管网状结构特征的提取[2]。指静脉传统的特征提取方法主要是借鉴于其他生物特征提取方法,比如人脸识别和指纹识别,均以图像为研究对象进行指静脉的识别工作[3- 4]。
传统的特征提取方法如编码特征等,容易忽略图像特征间的结构关系。而图论中的“图”作为一种图像描述方式,能够描述图像局部特征以及区域间关联性,表达图像全局信息。由于其优异的特性,图论在图像检索、图像分割等领域都取得了很大进展[5]。Ye Ziyun等人提出把一幅手指静脉图像表示为一个加权图,在识别效率上较传统方法有所提升,但识别率有待提高[6]。为了提高识别率,Das Rig等人提出基于深度学习的手指静脉识别方法,但是在计算效率方面存在很大的提升空间[7]。
针对以上问题,本文提出一种基于轻量型图卷积网络(Graph Convolutional Network, GCN)的手指静脉识别方法。GCN由Joan Bruna等人于2014年提出,图数据各个顶点的相邻顶点数目不尽相同,是一种不规则的数据结构,称为非欧氏数据。而传统的离散卷积在这类数据上无法保持平移不变性,即不能用一个同样尺寸的卷积核进行卷积运算[8]。2019年,Zhongdao Wang等人针对人脸聚类的问题,通过图卷积网络获得节点信息从而判断节点的连接关系,进而达到较好的聚类效果[9]。图卷积网络自提出以来,在节点分类、疾病预测、网络安全等许多方面都取得很大进展。
本文首先对手指静脉图像构建加权图,利用划分图像块的方式对预处理之后图像进行降维,提取图块的方向能量特征作为顶点特征,对所有顶点构建k-NN图,然后根据相连顶点的特征相似性给边赋予权值。该图数据作为图卷积网络的输入,根据图结构建立基于切比雪夫多项式的图卷积公式,经过图粗化算法协助实现快速图池化过程,在全连接层通过Softmax分类器,进而完成手指静脉的识别任务。
2 构建加权图
加权图是由顶点集、边集和权值函数的三元关系组成的数据:顶点集V、边集E和边的权值w,加权图记为G(V,E,w)。
在构建手指静脉图像的加权图时,不能选择像素点作为图G的顶点,因为指静脉图像的像素点很多,得到的图维度非常大,会给后面的计算带来很大麻烦;也不能选取细节点作为图的顶点,指静脉图像采集机制等原因,成像细节点不稳定,且在图像预处理过程中会产生虚假细节点,所以把静脉图像的局部区域作为图结构的顶点[6]。
2.1 顶点特征表示
对于图G(V,E,w),设其顶点集记为{ν1,ν2,…,νn },其中n为顶点个数,也就是原图像分块得到的图块数。本研究使用滑动窗口的方式划分图块,图块之间存在部分重叠,使得顶点间特征的关联性更强,提高图像平移的鲁棒性。
根据所得图像块的纹理结构信息,使用基于Steerable滤波器的方向能量分布特征(Orientated Energy Distribution,OED)作为顶点特征。在进行特征提取之前,采用文献[10]和[11]中的方法对指静脉原图进行预处理。本文所用Steerable滤波器公式如下:
(1)
(2)
OED={E(1),E(2),…,E(θ),…,E(360)|I}
(3)
式(1)中,θ是Steerable滤波器的方向,k(θ)是插值函数,可调整θ旋转方向。fφj(x,y)为三角函数构成的基础滤波器组,用来构成方向滤波空间的一组基底,本文采用高斯函数的4阶倒数作为基础滤波。N为f(x,y)的数目。式(2)为方向滤波器能量计算公式,即图块I与滤波器hθ在某一方向θ上的能量,X,Y是滤波器和图块I的尺寸。式(3)将不同θ的方向能量组成一个向量,从而得到指静脉图块的方向能量分布特征。
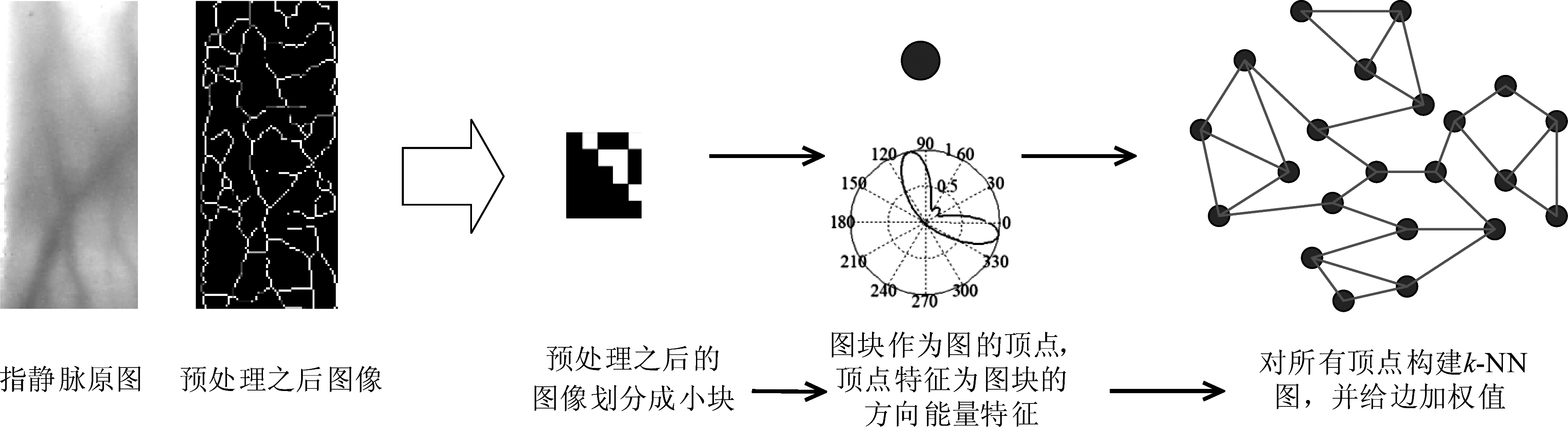
图1 构建加权图过程示意图
Fig.1 The process diagram of weighted graph constructing
2.2 边的加权
在完成特征提取之后,使用k-最近邻(k-Nearest Neighbor, k-NN)图建立边集,记作E={e12,e23,…,eij,…},其中eij为连接相邻顶点νi和νj的边。k-NN图表示距离最近的k个顶点有边连接,在图邻接矩阵中对应值为1,否则为0。然后计算相连顶点特征的相似性,给边赋予权值,加权公式如下:
(4)
其中, fi、 fj分别为顶点i、 j的方向特征向量,L为fi、 fj的长度。本文均采取无向加权图,即Wi, j=Wj,i。
3 图卷积网络
有两种方向构建图卷积网络,空间域和谱域。虽然可以考虑在空间域直接实现图卷积[12],但是每个顶点的邻域不同,且空间域卷积需要每个顶点聚合其所有邻居节点特征,使得计算处理必须针对每个顶点,计算复杂度很大,对处理器要求更高。在谱域的图变换拥有完整的定义过程,通过图谱理实现图数据上的卷积操作[13-14]。本文使用基于切比雪夫多项式的图卷积核,通过定义滤波器多项式的次数实现滤波的局部性,且计算复杂度较小。在池化层结合图粗化(Graph coarsening),构建标准平衡二叉树结构,实现快速池化。接着经过全连接层Softmax分类器实现手指静脉图像识别。图2为本文图卷积网络结构示意图。
3.1 图卷积滤波器
表示加权图G=(V,E,w)的矩阵叫做加权邻接矩阵,设为W。利用图谱理论定义图卷积公式,首先要得到图的拉普拉斯矩阵。对于图G,其拉普拉斯矩阵定义式为L=In-D-1/2WD-1/2,其中In为单位矩阵,D为W的度矩阵,Dii=∑jWij。从传统的傅里叶变换、卷积类比到图信号上的傅里叶变换和卷积得到如下的图卷积定义式:
y=Ugθ(Λ)UTx
(5)
其中,x是输入图信号,(UTx)是图信号x的傅里叶变换的矩阵形式,其中U是图拉普拉斯矩阵的特征向量,L=UΛUT,Λ=diag([λ0,…λn-1])∈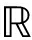
n×n。gθ(Λ)=diag(θ),θ∈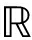n是一个傅里叶系数向量。此图卷积方式对整个图进行卷积,没有实现局部卷积滤波,且每一次前向传播,需计算U、gθ(Λ)和UT三项的乘积,导致计算复杂度非常高。
为了构建轻量型图卷积网络,减少图卷积核参数,利用切比雪夫多项式的递推关系设计图卷积滤波器。将gθ(Λ)这一项替换为切比雪夫多项式系数向量作为参数:
(6)
其中,参数θ∈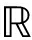K是一个切比雪夫系数组成的向量,
n×n是k次切比雪夫多项式的特征值对角阵
由L=UΛUT和矩阵性质推导得出基于切比雪夫多项式的图卷积滤波公式如下:
n
(7)
其中,xs,i是输入图结构s,ys, j是s的第j个输出特征图,θi, j为每一层的可训练参数。神经网络多个卷积层参数的训练使用反向传播算法完成:
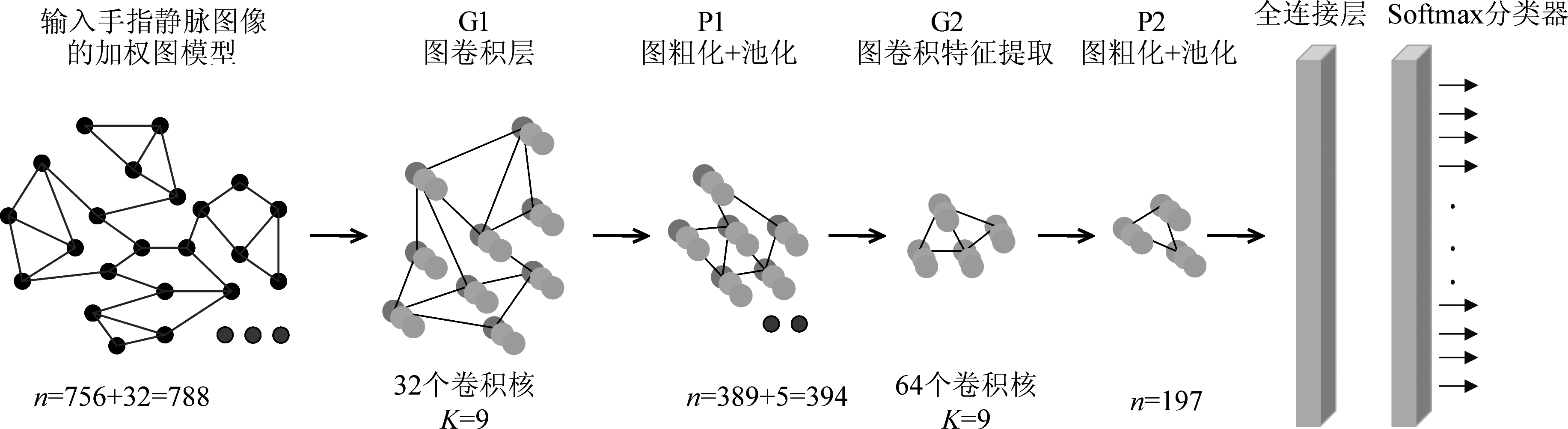
图2 图卷积网络结构图
Fig.2 Architecture of the GCN
(8)
(9)
其中,E是S个样本输入训练之后的能量损耗。
借助切比雪夫多项式构建图卷积核,可以通过定义多项式实现局部滤波,卷积核参数个数为K,一般K远小于n。根据矩阵变换性质得出的卷积公式(7),使用拉普拉斯矩阵L进行变换,在矩阵计算和参数计算方面都提升了整体图卷积网络模型的计算速度。
3.2 图池化过程
为了进一步提高网络的训练速度,本文使用一种快速图池化方法。首先对输入图进行粗化,在池化过程中加入虚假节点,使每个粗化层与上一层形成标准平衡二叉树结构,使得池化过程类似于一维信号的池化,从而使池化效率更高。
图的粗化采取Graclus多层次聚类算法(Graclus multilevel clustering algorithm)的粗化阶段[15]。因为图池化操作需要有关联的相邻节点在一起,也就是顶点的聚类。对各层不同尺寸的图来说,相当于保留局部图结构的多尺度聚类。多层聚类算法可以在每一层得到一个比原图结构分辨率低的粗化图。此外,该粗化算法可以精确的控制粗化图的尺寸大小。Graclus多层聚类算法的粗化阶段使用到贪心算法:在粗化层随机选择一个节点i,若在i的邻域内存在未标记的节点j,使得局部归一化剪切权值Wi, j(1/di+1/dj)最大化,则标记这两个节点,并将粗化的权值设置为这两个节点权值的和。按照上述方法,遍历所有节点,完成粗化层。
粗化之后的图节点是无规则排列的,不能进行有效的池化。图池化过程如图3举例说明:如果池化核的尺寸p是4,那么粗化的层数l就是l=log2p=2,得到粗化层G1和G2,G0是输入的原图结构,这些顶点是以任意方式排列的。在G0层,顶点数目n0=8,经过Graclus得到G1的顶点n1=5,第二个粗化层G2的顶点个数n2=3。为了构建平衡二叉树,所以节点数目需要设置成n0=12,n1=6,则在G0和G1层分别加入4个虚假节点和1个虚假节点。虚假节点的值设置为零,属于未连接的顶点,并不会对池化结果产生影响。实验过程表明每一层只会产生少量的虚假节点,所以不会增加网络计算复杂度。该过程快速有效实现了图池化。
4 实验与结果分析
本研究的实验过程使用到两个数据集。数据集1是本实验室自制的手指静脉数据集,该数据集中采集了585类手指静脉图片,每类10张,总共5850张图片。图4是该数据集原始采集图像和感兴趣区域(Region of Interest,ROI)图像,ROI像素为90×210。数据集2是由山东大学建立的指静脉数据库(SDUMLA-FV),该数据库采集了106人的左右手食指、中指和无名指,每根手指采集6张图片,采集像素为320×240,总共3816张图片[16]。图5是SDUMLA-FV的原始采集图像和ROI图像对比。
实验时,图卷积网络首先采用(卷积层+池化层)× 2的结构,池化核大小为2的最大池化,一层全连接层,分类器选择Softmax分类器。损失函数为交叉熵损失函数,优化策略选择Momentum,其冲量系数设置为0.9,学习率为0.1,一个训练批次为200个样本。
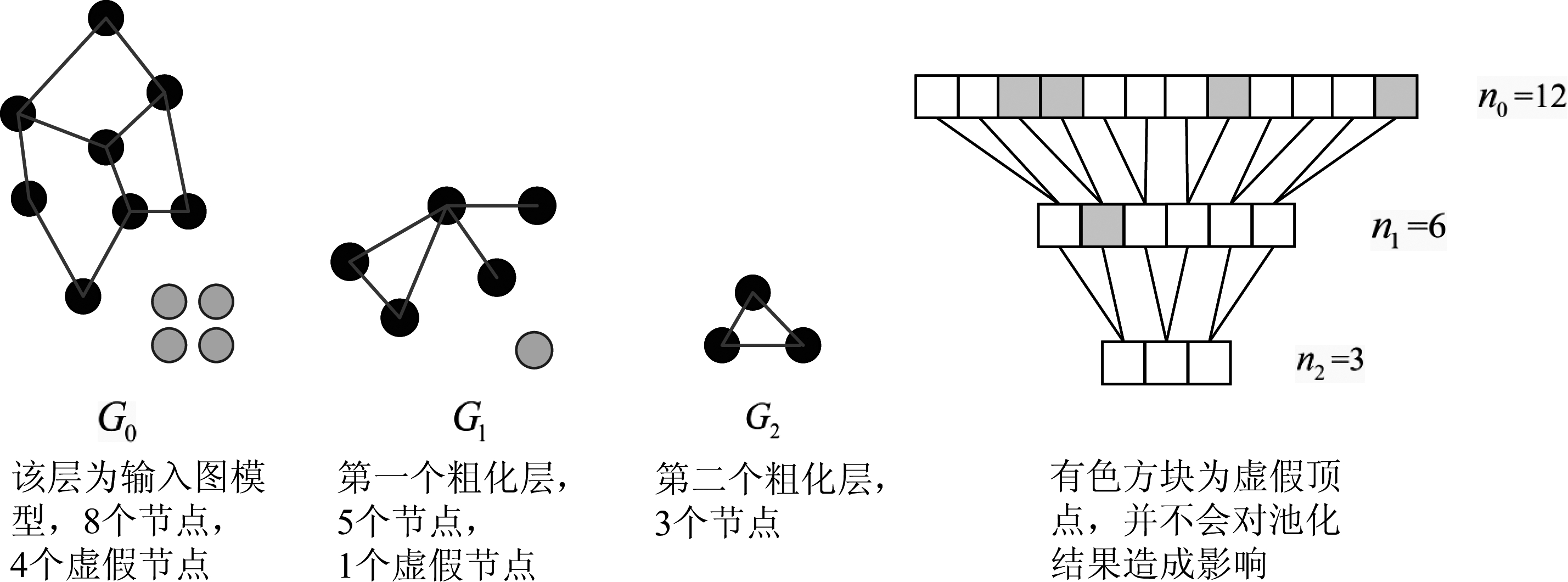
图3 图粗化和池化过程
Fig.3 The process of graph coarsening and pooling
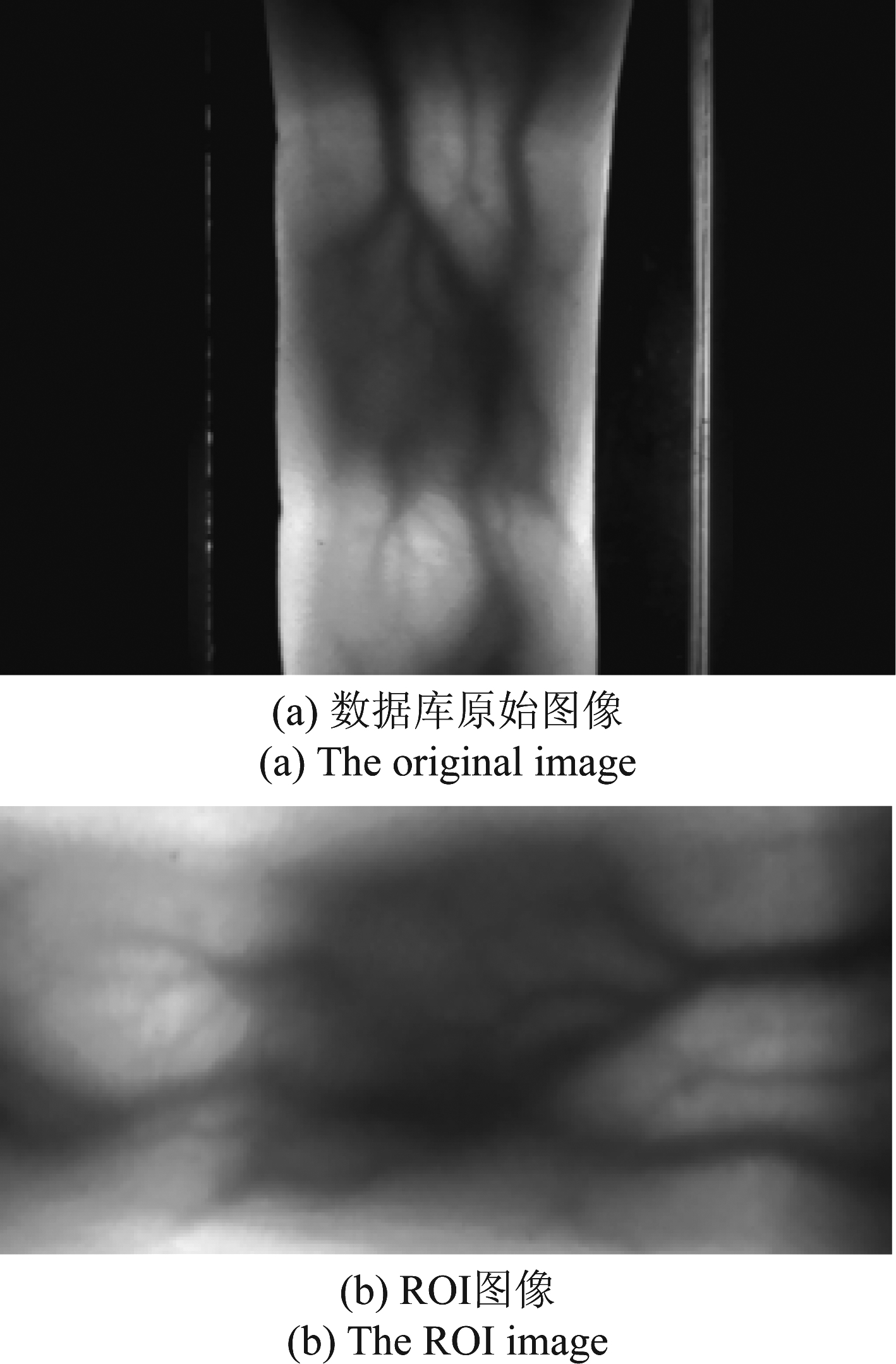
图4 实验室自制数据库采集图像和ROI图片
Fig.4 The original image and ROI image of our homemade database
图5 SDUMLA-FV采集图像和ROI图片
Fig.5 The original image and ROI image of SDUMLA-FV
4.1 图数据质量和图卷积核对识别结果的影响
在数据集1中随机选取4680张指静脉图像作为训练集,1170张作为验证集,训练集∶验证集=8∶2。本部分探究了两个方面实验:实验(1)探究图卷积核对识别结果的影响;实验(2)探究输入图的质量对识别结果的影响。
实验(1)改变切比雪夫次数K,即改变图卷积核的大小,探究识别结果变化。从图6的实验结果可以看出,当K=9=3×3时,识别率最高,且此时的识别效率较高。分析知当K越大,能学习到的顶点特征越多,但图卷积局部性越差,引入了更多噪声,导致识别率降低。当K越小时,网络需要训练的参数越少,计算代价更低,识别效率增高,但当K=1×1时,卷积核不再具有提升感受野的作用。综上,以下的实验均采取K=3×3。
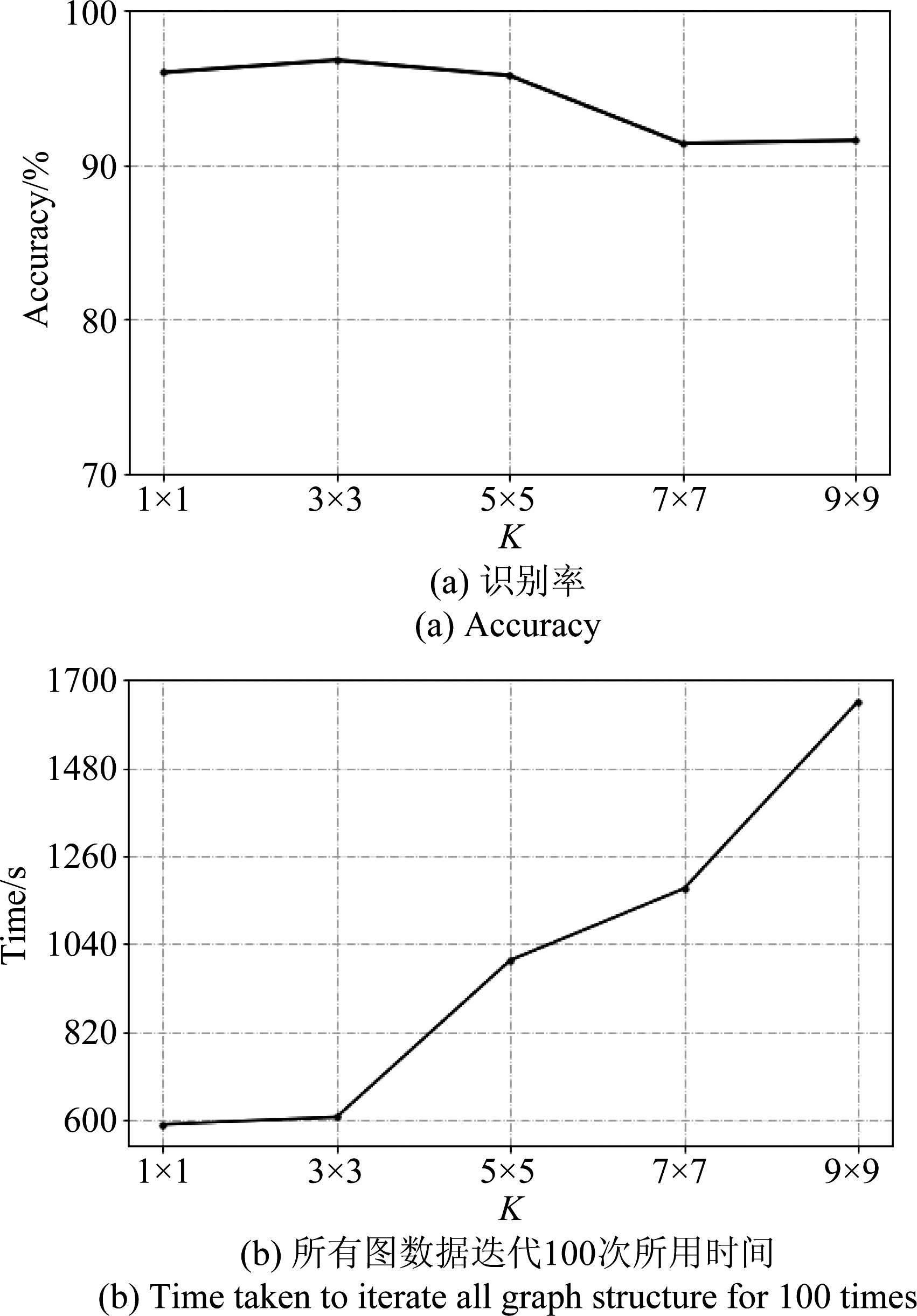
图6 不同K值对识别的影响
Fig.6 The results of different K
在探究图卷积合适层数时,2层图卷积加2层池化已经可以得到较为理想的识别率,更深的网络没有使识别率有显著的提升,反而计算代价非常大。所以实验均采取2层图卷积。
实验(2)从顶点和边两个方面探究图的质量。首先探索顶点对图质量的影响。增加图像块的重叠率,效果近似于减小了图像块的尺寸,都使顶点数目增加。通过改变图像块的尺寸和划分时图像块之间的重叠率得到以下几组不同数量的顶点。这里选择8-NN图建立边集。从图7可以看出,随着顶点数目的增多,识别率逐渐上升。结合图像块重叠率和尺寸大小分析,当重叠率越高使得顶点关联性越高,提高了图像平移的鲁棒性,对识别结果有利;当尺寸越小,图像块包含方向特征越单一,这样的图结构不仅表达指静脉的局部特征,还更好的表达了局部特征的关系。
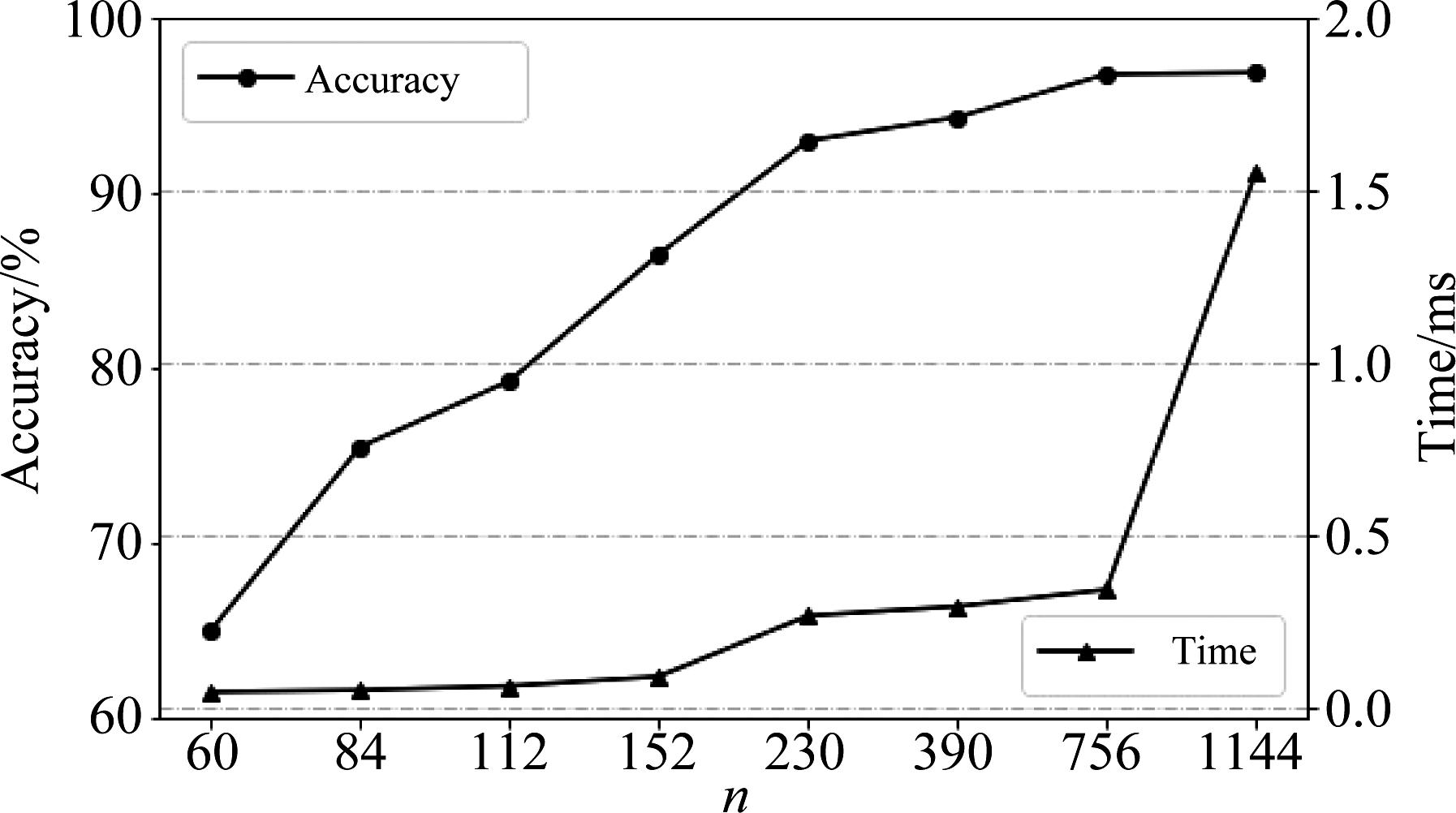
图7 顶点数目对识别的影响
Fig.7 The effect of the number of nodes on the recognition result
同样由图7可知,随着顶点数目增多,计算代价明显升高,单张图片识别所需时间随之上升。在同时兼顾识别率和识别效率的情况下,选择构建756个顶点的图结构进行下面各实验,此时图像块尺寸为15×15,重叠率为图像块的2/3。
为了探究顶点的连接方式对图质量的影响,选择k=4、k=8、k=16时的k-NN图,并与顶点的三角剖分连接以及顶点随机连接两种方式做出对比,其中随机图边的数量等于8-NN图结构中边的数量。根据表1实验结果分析可知,k的变化对实验结果没有很大影响,三角剖分连接方式的识别率与k-NN近似,而随机连接方式的识别率有明显下降。因为指静脉图像的局部关联性强,相邻顶点连接能够增强图结构对全局信息的描述能力,从而提高模型的识别率。
表1 不同顶点的连接方式结果对比
Tab.1 The comparison of different methods to link the nodes
4-NN8-NN16-NN三角剖分图随机图识别率/%95.9096.8096.1097.0094.30
4.2 对比实验
对比实验分两部分,实验(1)和(2)均在实验室自制指静脉数据库上进行,选取4680张指静脉图像作为训练集,1170张作为验证集。并根据以上实验,对所有数据构建756个顶点的8-NN图结构,建立图卷积核K=9的图卷积网络。
实验(1)与其他两组经典图卷积网络进行对比。本部分实验选取无参数图卷积滤波器[13]和文献[6]提出的卷积核半径等于图顶点数目的方法进行对比,分析对手指静脉识别结果的影响。以下三种图卷积网络的深度相同,图池化部分均借助Graclus多层次聚类算法的粗化过程。
图8的(a)、(b)分别显示了随着训练次数的增加,使用切比雪夫参数滤波器和另外两种图卷积滤波器的识别率和训练能量损耗变化曲线。表2分析了三种滤波器的计算效率。可以看出,切比雪夫参数设计的图卷积核局部性学习能力,识别率优于另外两种卷积,而且收敛速度明显比另外两种快。Spline卷积核需要n个参数,而无参数滤波需要计算整个图拉普拉斯算子,且局部学习性能不好,都具有较高的计算复杂度。
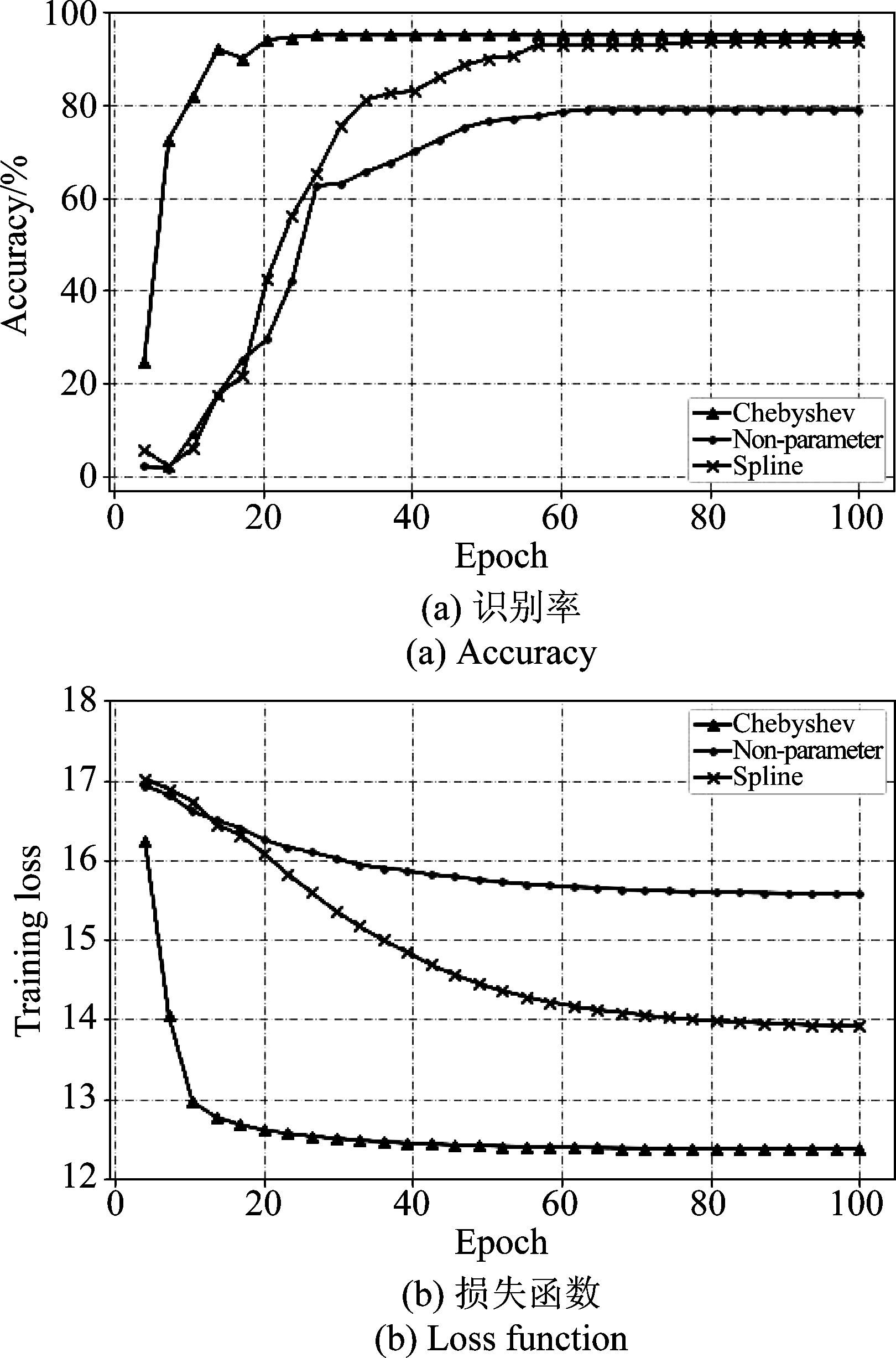
图8 三种不同图卷积滤波器的识别率和损失函数
Fig.8 Plots of validation accuracy and training loss for the first 100 epochs with different filter
表2 不同网络训练完成所用时间
Tab.2 Time to finish the training of different network
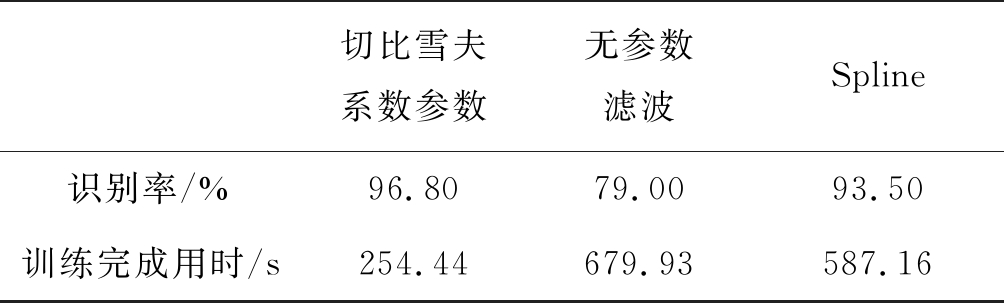
切比雪夫系数参数无参数滤波Spline识别率/%96.8079.0093.50训练完成用时/s254.44679.93587.16
实验(2)把本文提出的方法和传统的手指静脉识别方法进行对比,方法(1)基于卷积神经网路的手指静脉识别[17];方法(2)基于图邻接矩阵相似度的识别;方法(3)自适应Gabor卷积神经网络的手指静脉识别[18]。对比方法(1)和方法(3)在达到较理想的识别率时,均需要5层卷积结构,所以计算效率低。图9为对比不同模型的ROC(Receiver Operating Characteristic)曲线,表3为不同模型的单张图片识别时间,综合分析可以看出,本文提出的轻量型图卷积网络模型识别效率远高于其他对比方法,且识别性能与传统卷积神经网络相当。
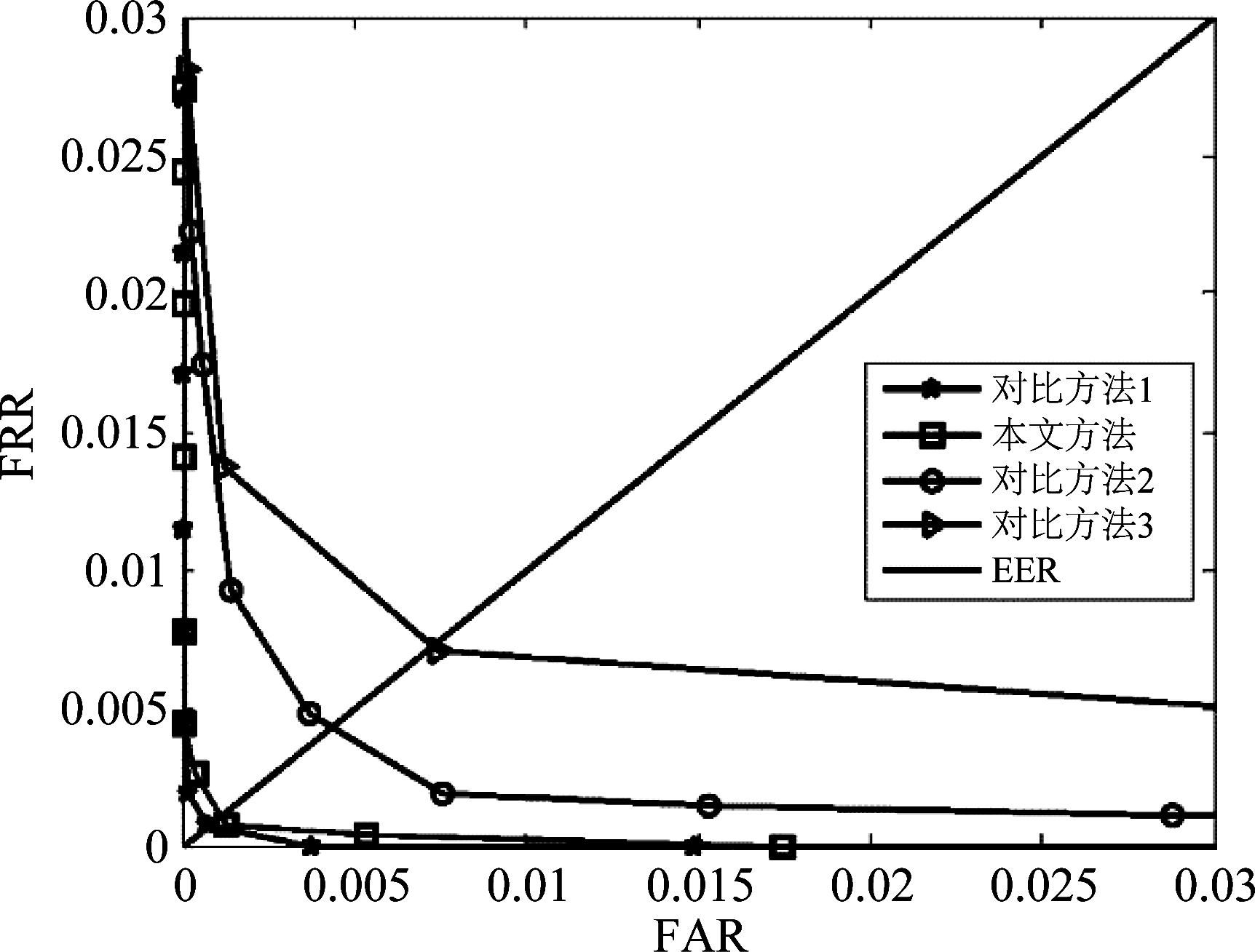
图9 与不同手指静脉识别方法的ROC对比
Fig.9 Comparison results of the ROC for different finger vein recognition methods
表3 与不同手指静脉识别方法的识别效率对比
Tab.3 Comparison with different methods of finger vein recognition efficiency
单张识别时间/ms本文方法0.3452对比方法(1)843.1564对比方法(2)173.7167对比方法(3)251.2106
4.3 模型的普适性
本部分实验验证了本文方法的普适性,在SDUMLA-FV数据库中随机选取2544张作为训练集,1272张作为验证集,训练集∶验证集=4∶2,为了构建规模相同的加权图,所有数据的ROI图像大小均为90×210,识别结果如下表所示。
表4 本方法在不同手指静脉数据库的识别率
Tab.4 The recognition accuracy in different finger-vein database
数据库实验室自制数据库SDUMLA-FV识别率/ %96.8090.33
根据表格信息可以看出,本文提出的基于图卷积网络的手指静脉识别方法在不同数据库上均有较好的识别效果。其中,在SDUMLA数据库的识别率要低于本实验室的数据库,分析原因是SDUMLA-FV数据集每类只有6张图片,没有足够的样本用来训练。且经过分析不同数据库的采集图像得出,实验室自制的指静脉图像类内光照变化及姿势变化角度比SDUMLA-FV数据库要小,成像更均匀,所以识别率更好。
5 结论
本文提出了一种基于图卷积网络的手指静脉识别方法,并研究了输入图和图卷积方式对识别结果的影响,然后针对不同数据库,验证了该方法的普适性。通过和其他识别方式的对比,得出本文方法的优势与不足之处。
本研究的不足之处体现在:虽然提出的识别方法在识别效率上具有很大优势,但是还需要进一步提高识别的精度;对于原指静脉图像的构图方式仍然不够简便,后续可以考虑在构建图方面做到不丢失顶点特征的前提下精简过程。
[1] 郑方, 艾斯卡尔·肉孜, 王仁宇, 等. 生物特征识别技术综述[J]. 信息安全研究, 2016, 2(1): 12-26.
Thomas Fang Zheng, Askar Rozi, Wang Renyu, et al. Overview of Biometric Recognition Technology[J]. Journal of Information Security Research, 2016, 2(1): 12-26.(in Chinese)
[2] 杨金锋, 石滨萌. 手指双模态特征图像感兴趣区域稳定定位方法研究[J]. 信号处理, 2019, 35(7): 1191-1200.
Yang Jinfeng, Shi Binmeng. Reliably Location ROIs of Dual-Modal Biometric Images of Human Fingers[J]. Journal of Signal Processing, 2019, 35(7): 1191-1200.(in Chinese)
[3] Meraoumia A, Korichi M, Chitroub S, et al. Finger-Knuckle-Print identification based on histogram of oriented gradients and SVM classifier[C]∥First International Conference on New Technologies of Information & Communication. IEEE, 2016.
[4] 温梦娜, 杨金锋. 手指静脉图像的概率分割方法研究[J]. 小型微型计算机系统, 2018, 39(7): 195-199.
Wen Mengna, Yang Jinfeng. Research on finger-vein Image Segmentation based on Probability Maps[J]. Journal of Chinese Computer Systems, 2018, 39(7): 195-199.(in Chinese)
[5] Shi Jianbo, Malik J. Normalized cuts and image segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(8): 888-905.
[6] Ye Ziyun, Yang Jinfeng, Palancar J H. Weighted Graph Based Description for Finger-Vein Recognition[C]∥Chinese Conference on Biometric Recognition. Springer, Cham, 2017.
[7] Das Rig, Piciucco Emanuela, Maiorana Emanuela, et al. Convolutional neural network for finger-vein-based biometric identification[J]. IEEE Transactions on Information Forensics and Security, 2018, 14(2): 360-373.
[8] Bruna J, Zaremba W, Szlam A, et al. Spectral networks and locally connected networks on graphs[J]. arXiv preprint arXiv: 1312.6203, 2013.
[9] Wang Zhongdao, Zheng Liang, Li Yali, et al. Linkage Based Face Clustering via Graph Convolution Network[C]∥arXiv: 1903.11306v3, 2019.
[10]Yu Chengbo, Qin Huafeng. Finger-vein image recognition combining modified Hausdorff distance with minutiae feature matching[J]. Interdisciplinary Sciences: Computational Life Sciences, 2009, 1(4): 280-289.
[11]Yang Jinfeng, Zhong Zhen, Jia Guimin, et al. Spatial Circular Granulation Method Based on Multimodal Finger Feature[J]. Journal of Electrical and Computer Engineering, 2016, 1(1): 1-7.
[12]Kipf T N, Welling M. Semi-supervised classification with graph convolutional networks[J]. arXiv preprint arXiv: 1609.02907, 2016.
[13]Defferrard M, Bresson X, Vandergheynst P. Convolutional neural networks on graphs with fast localized spectral filtering[C]∥Advances in neural information processing systems. 2016: 3844-3852.
[14]Shuman D I, Narang S K, Frossard P, et al. The emerging field of signal processing on graphs: Extending high-dimensional data analysis to networks and other irregular domains[J]. IEEE Signal Processing Magazine, 2013, 30(3): 83-98.
[15]Dhillon I S, Guan Y, Kulis B. Weighted Graph Cuts without Eigenvectors A Multilevel Approach[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007, 29(11): 1944-1957.
[16]Yin Yilong, Liu Lili, Sun Xiwei. SDUMLA-HMT: A Multimodal Biometric Database[M]. Biometric Recognition, 2011.
[17]Das R, Piciucco E, Maiorana E, et al. Convolutional neural network for finger-vein-based biometric identification[J]. IEEE Transactions on Information Forensics and Security, 2018, 14(2): 360-373.
[18]Zhang Yakun, Li Weijun, Zhang Liping, et al. Adaptive Gabor Convolutional Neural Networks for Finger-Vein Recognition[C]∥International Conference on High Performance Big Data and Intelligent Systems, 2019.
