1 引言
自古至今,在战争中抓住战场通信的主动权是决定战争胜负的关键,而通信协议分析则是军事通信领域不可或缺的重要部分,在非合作的军事对抗领域,协议分析是获取敌方通信信息和进行灵巧干扰的前提,通信时,发送方会选择将数据打包成帧后在物理层进行传输,接收机要理解接收到的数据的含义就必须与数据流的帧结构保持同步,为了确保收发端顺利传输信息,接收机需要帧同步码作为比特群划分的依据。根据协议类型的不同帧同步序列长度不定码型不定,通信合作方已知同步序列[1-5],可以通过比对处理对接收到的数据准确分组,完成信息的传送,作为非合作方缺少同步序列的先验信息,因此,非合作通信中的协议识别就面临着对帧同步盲识别的问题且难度较大,因此国内外许多学者开展了对帧同步识别[6-20]的研究。杨晓静[13]等人提出了基于偏三阶相关函数峰值特性的识别帧长和帧同步码,但该算法只对同步码是m-序列的数字序列有识别作用。白彧[14]等人提出基于相关滤波和哈达玛变换的帧同步识别技术识别帧同步。张玉[15]等人利用小区域检测来估计帧长,并在帧长识别的基础上通过相关滤波和模糊匹配的方法识别帧同步,但该方法是将同步码的码型作为先验信息进行匹配,只对码型确定的同步码识别率较高,对同步码码型不确定、码长不确定的数字信号识别率明显降低。郭凯丰[16]等人提出一种累积滤波算法,用来识别数据帧的帧头和数据部分,该算法在帧结构复杂或帧同步码长不确定的时候判决门限很难确定。王和洲[17]等人提出一种基于数据挖掘的帧切割算法,该方法利用了帧内序列的频繁性和序列间的关联规则将未知比特流按帧长切割。
纵观国内外对集中插入式帧同步盲识别算法的研究现状和发展趋势可以看出,除了个别只针对某一类同步码(如m-序列)的识别算法外,其他识别算法[14-18]都无法做到从极少量帧数据中准确识别出同步码,换言之,很少有算法既能适用于绝大多数同步码,又能无视数据量的限制,但是结合集中插入式帧同步在军事通信中的实际应用场景,我们可以发现,多数采用集中插入式帧同步方式的军事信号具有突发性,如武器制导数据链信号,传统的帧同步识别算法在对目标数据识别时需要积累一定的数据量,若想要提高对抗设备的反应时间就需要尽可能地缩短数据积累时间,就需要具备从极少量帧数据中识别出帧同步的能力,并且在全盲的条件下我们无法事先获取通信方同步码的类型,所以说只针对某一类同步码(如m序列)的识别算法在实际应用时存在着一定的局限性,为了克服上述两种问题,首次提出一种基于离散度分析的帧同步快速盲识别算法。
2 物理帧
2.1 基础知识
几乎所有的数字数据流都具有一定的帧结构,接收机要理解接收到的数据的含义就必须与数据流的帧结构保持同步。一般来说,接收机需要帧同步码作为比特群划分的依据。帧同步码的插入方法有两种:集中插入和分散插入。前者是将一段具有特殊性质的码组插入物理帧的前面,多用于对建立同步要求高或信息间断传输的通信,后者是将一种特殊的周期性同步码元分散插入信息码元序列中,多用于信息连续传输的通信。
图1 集中插入法
Fig.1 Concentratively inserted frame synchronization
多数军事信号具有的实时性、防抗截获性和隐蔽性等特点,而集中插入式帧同步方式实时性高、可间断传输等优点,因此集中插入式帧同步方式在军事通信领域应用广泛,因此本文研究的对象为集中插入式帧同步。发送端在每帧的开始插入一段特殊的码组作为同步序列,根据协议类型的不同,同步序列长度不定码型不定,同步序列部分用于帧同步,信息部分用来承载来自高层的传输块数。
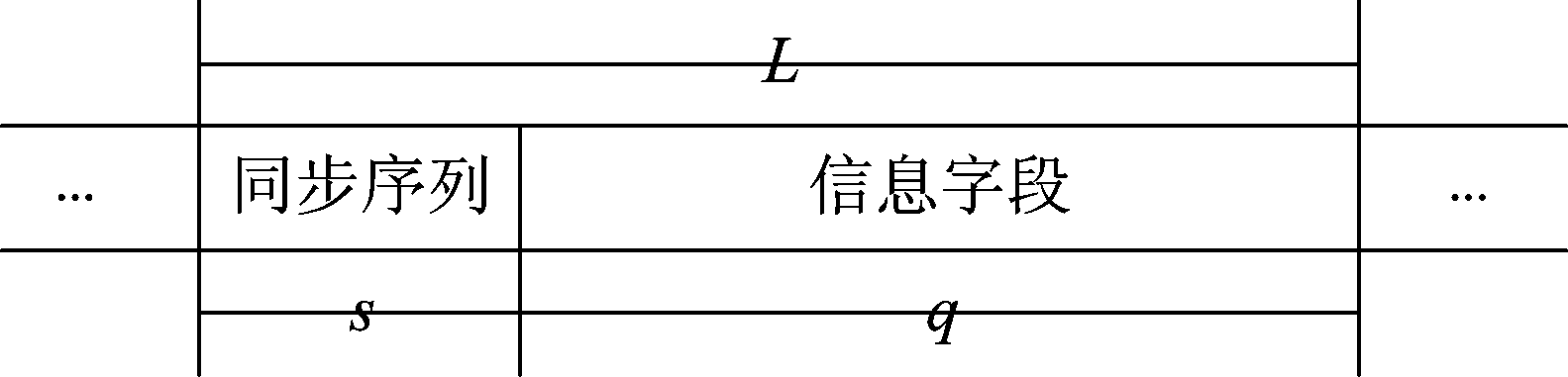
图2 物理帧结构
Fig.2 Physical frame structure
2.2 帧同步码的相关性
对于突发式传输的军事信号,要求快速获取帧同步,为了提高同步性能,要求同步码具有很强的自相关性,也就是说要求同步码的相关旁瓣的绝对值很小[21],相关旁瓣是指码字根自身时移后的码字的相关值。
设一组n位的帧同步码组为x=(x1,x2,…,xn),具有j个码元移位的相关旁瓣可由式(1)表示。
(1≤i≤n, j=整数)
(1)
其中xi的取值为±1的码元,同步码的相关函数满足式(2)关系
R(0)≫R(j)
(2)
即同步字段具有自相关值远大于相关旁瓣。最大相关旁瓣幅度为1的码字称为巴克码,巴克码序列如表1所示。
表1 巴克码序列
Tab.1 Barker code sequence
N巴克码序列11211或1-1311-14111-1或11-115111-116111-1-11-111111-1-1-11-1-11-11311111-1-111-11-11
以7位巴克码为例,它的自相关函数如式(3)所示。
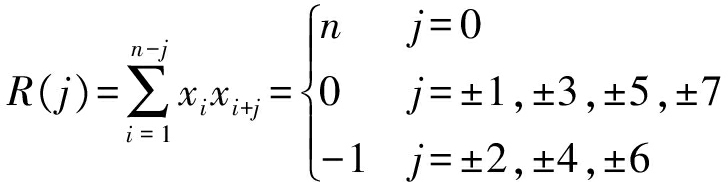
(3)
但巴克码受其长度的制约,作为长序列的同步码时性能并不理想,在巴克码之后一些学者又找到适用于帧同步的码组,如威拉德(Willard)码、N=30的毛瑞型(Maury-styles)码和N=40的林德(Linder)码等,另外伪随机序列也可以作为同步码的一种选择。
3 数据分析
对侦收到的集中插入式帧同步数据进行分析。
3.1 二元性
侦察截获得到的比特流数据具有二元性,即数据非0即1,下面对数据中0,1分布情况展开分析。
定义1[22] 若二进制序列中1的出现概率为p,则序列的有偏性是1/2-p,它反映了序列中0,1比特的分布情况。
假设输出的物理帧数据是y=(y1, y2,…,yL),其中同步字长度是s,有偏性是λ,信息段长度是q,有偏性是η,如图3所示。
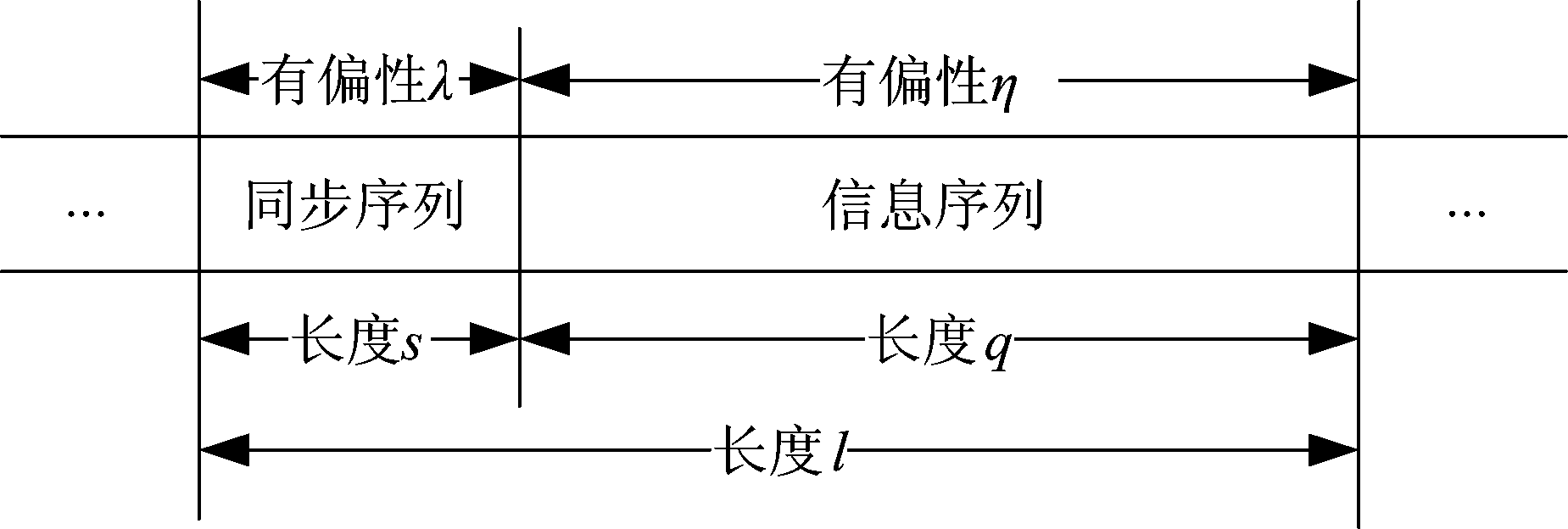
图3 物理帧信息
Fig.3 Physical frame information
同步码的有偏性为λ,所以同步码中1出现的概率如式(4)所示。
(4)
同理,信息序列中1出现的概率如式(5)所示
(5)
物理帧中1出现的概率如式(6)所示
i=1,2,…,l
(6)
由式(7)可知物理帧的有偏性为:
(7)
信息字段经过加密、加扰和交织等处理后呈现出随机性,即0、1出现的概率近似相等,因此η≈0。当同步码为伪随机序列时,其0、1出现的概率也近似相等,因此λ≈0,所以物理帧的有偏性φ≈0。
3.2 无界性
对于侦收到的物理帧数据,我们无法确定哪一个比特是一帧的开始和结束,也就是说我们无法确定帧同步码在数据中的位置,主要有以下三种可能性。
(1)数据起始位为同步码起始位
从侦察的角度,采取对信号全频段、全时段的控守,而同步码作为界定数据的标志一般出现在帧首部,因此截获到的数据的起始位有很大的可能性就是同步码的起始位。
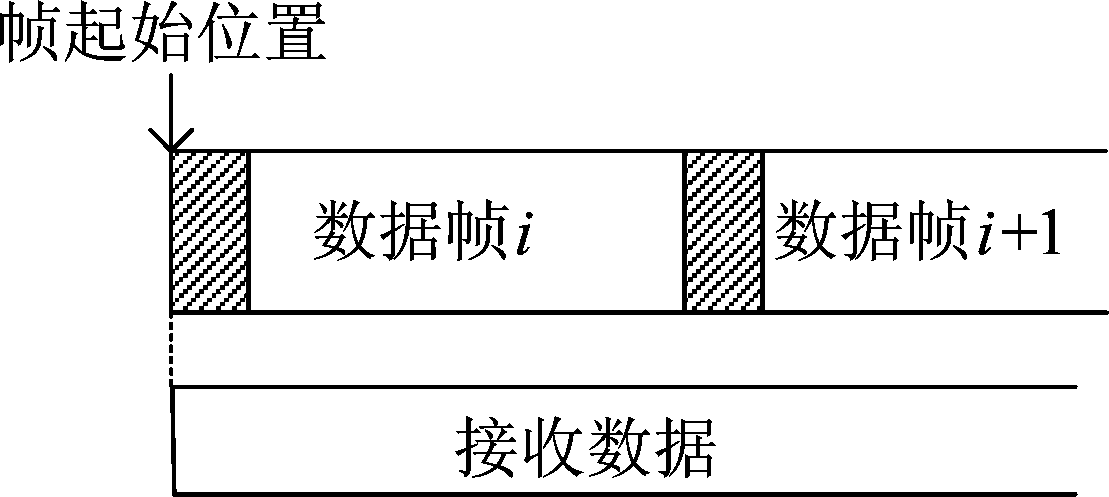
图4 数据起始位为同步码起始位
Fig.4 The starting bit of data is the starting bit of synchronization code
(2)数据起始位在信息字段
由于噪声或者信号强度弱等实际因素导致截获的数据的起始位在物理帧的信息段。
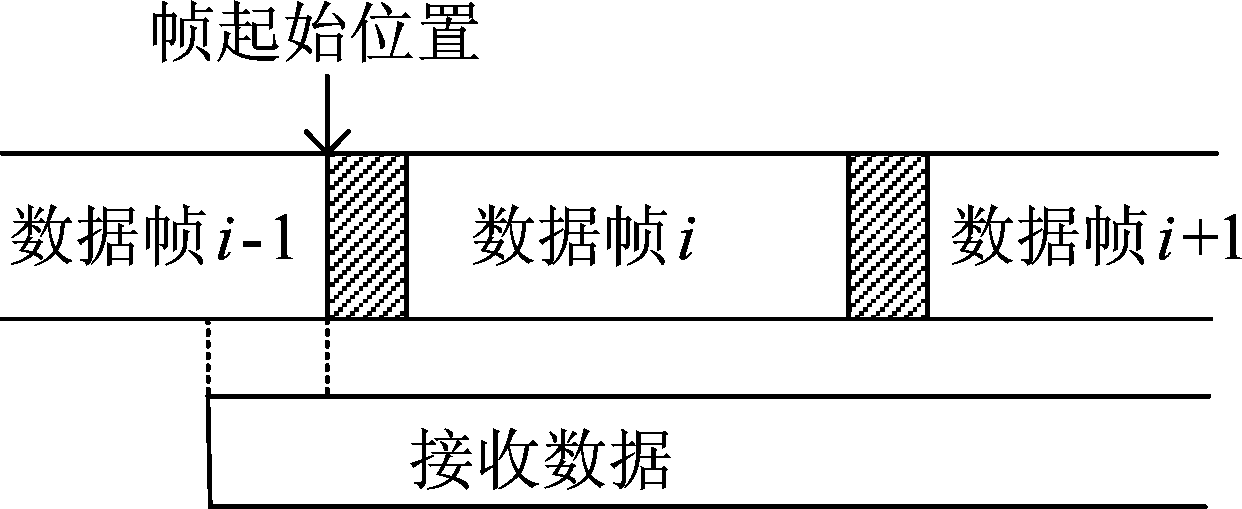
图5 数据起始位在信息字段
Fig.5 The data start bit is in the information field
(3)数据起始位在帧同步字段
假设待识别序列一帧中同步字长度是s,信息段长度是q,因此接收数据起始位在帧同步字段的概率如式(8)所示。
(8)
当q≫s时,式(8)的值取0,即信息段远长于同步字段时,数据起始位在帧同步字段的可能性很小。
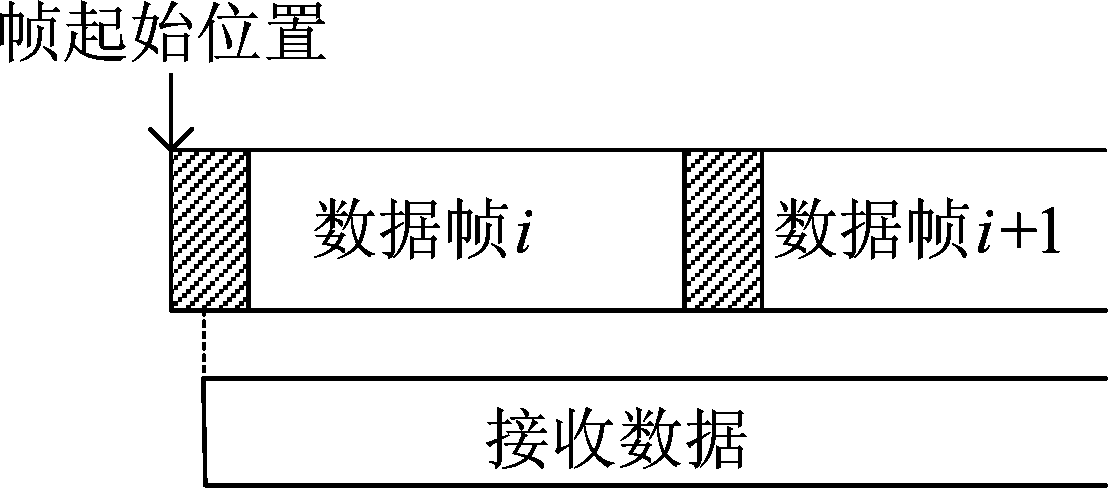
图6 数据起始位在帧同步字段
Fig.6 Data start bit in frame synchronization field
3.3 关联性
对于一个突发内的数据,其包含的物理帧数量非常少,甚至只有1帧数据,因此数据内特殊字段周期性出现的特征被弱化,很难挖掘出关联规则。
4 帧同步码识别
离散度分析法是统计学一项重要的方法,主要用来测度一组数据的分散程度。分散程度反映了一组数据远离其中心值的程度。对于一组数据变动趋势的分析,要从集中趋势和分散程度两个方面进行说明。
同步码的自相关函数值等于同步码长,互相关函数值始终在0值附近小范围内波动,而信息字段的相关旁瓣值相对要大的多,因此对待识别序列的相关函数的旁瓣进行离散度分析,通过离散度分析法可以得到各待识别序列相关旁瓣远离中心值的程度。若相关旁瓣的相对离散度值最小则该段序列为同步码或同步码的一部分。
在该处分析中,数字序列的值用±1,求待识别序列的相关函数R(j),
(1≤i≤n, j=整数)
(9)
对相关函数进行离散度分析。
(10)
式中σ表示关键字段互相关函数值相对0值的波动程度。但是σ只反映了除自相关值外的相关函数的波动程度,是数值的绝对量,无法反映相关函数的整体离散情况,因此引入相对离散度值
(11)
为防止噪声对识别结果产生的影响,在一定范围内取多个m值,重复上述过程,统计每个n值对应的多个相对离散度值,并对其取平均。
(12)
其中,
的值越小代表序列相关旁瓣在0附近的离散程度越小,对于待识别数据的所有子序列来说,只有同步序列的值最小。
对于一段包含多帧的待识别数据，本文提出利用循环切分的方法找到其中相对离散度值最小的子序列，该方法使得识别算法不受数据量的限制(即待识别数据为一帧或者多帧数据都可以完成识别)，下面给出具体实现方法。
对集中插入式帧同步码来说,其长度一般不会小于7 bit,一般来说同步码的长度与信息字段的长度成正比,传输数据量越大的物理帧其同步码也相对较长,在无需遍历起始位的情况下,我们按照设置的分割长度φ对识别数据进行分割,本算法可以有效保证分割过程向着完整切分同步码的方向收敛,下面对其进行分析。
因为所提算法只需要较短数据量就可以完成对帧同步的盲识别,所以我们不妨设假设待识别数据长L,L等于一个物理帧长度,待识别序列一帧中同步字长度是s,信息段长度是q,按照分割长度φ分割待识别数据,共产生
个分割段,包含同步码的分割段个数有
则包含信息段的分割段为⎣(s-Mφ+q)/φ」,因此包含同步码的分割段所占比例如式(13)所示。
(13)
化简式(13)得式(14)。
(14)
因为M=⎣s/φ」,s-φM>0,已知同步码在一帧中所占比例很小,即q≫s,则式(14)的值很小,对待识别数据进行切割是为了从中完整地提取出同步码,因此φ取值范围通常比L小很多。已知按照分割长度φ对识别数据进行切割会产生个分割段,分别计算每个分割段的相对离散度值(共有个),然后取其中最小相对离散度值。选取φ的取值区间为[a,b],然后在区间上对φ遍历取值,此时会产生b-a+1种切分方案,分别计算每个方案的最小相对离散度值(共有b-a+1个),进行对比,最小的相对离散度值对应分割长度φ近似等于同步码长s,此时相对离散度值最小的分割段为同步码或同步码的一部分。对于长度一定的物理帧数据的所有子序列,同步码相关旁瓣的绝对值是最小的。按照分割长度φ对待识别数据进行循环切分,通过计算分割段的相关旁瓣的相对离散度值,实现同步字的准确识别。基于离散度分析的帧同步快速盲识别算法的详细步骤见表2。
5 仿真实验及结果分析
实验选取5种集中插入式帧同步数据,物理帧1的同步码为13 bit的巴克码,物理帧2和物理帧3的同步码分别为127 bit和255 bit的m-序列,物理帧4和物理帧5的同步码选取的是作为应用在实际通信系统中的一种相关性好的同步序列,物理帧的信息段是由随机产生的0、1序列经过加扰、编码、交织后形成的。
表2 基于离散度分析的帧同步快速盲识别算法步骤
Tab.2 Step of frame synchronization fast blind recognition algorithm based on discrete degree analysis
基于离散度分析的帧同步快速盲识别算法1. 载入待识别序列y,确定分割长度φ的取值范围φ∈[a,b];2. For φ=a:b3. 按照设置的序列分割长度φ将长度为L的待识别序列y划分成Lφ行、φ列的矩阵Z;4. 将矩阵Z的每行数据作为一个待识别子序列,分别计算每个子序列的相对离散度值μn,并取其中最小的一个值μn;5. End For6. 经过循环得到b-a+1个最小的相对离散度值,并比较它们的大小,取其中最小的值;7. 最小的相对离散度值对应的分割长度φ近似等于同步码长s,该段子序列为同步码或同步码的一部分,此时完成同步码的识别。
表3 物理帧特征统计Tab.3 Physical frame feature statistics
物理帧同步码同步码长帧长物理帧1111110011010113269物理帧210000011001101010011100111101101000010101011111010010100011011100011111110000111011110010110010010000001000100110001011101011011271407物理帧31000000110010010011011100100000101011011010110010110000111110110111101011101000100001101100011110011100110001011010010001010010101001110111011001111011111101001100110101000110000011101010101111100101000010011111111000010111100011010000000100011100010010112551535物理帧4物理帧5000000010110001111010000111111110010000101001111101010101110000011000101011001100101111110111100110111011100101010010100010010110100011001110011110001101100001000101110101111011011111000011010011010110110101000001001110110010010011000000111010010001110001025613284352
5.1 不同码型的同步码识别
在无误码的条件下,分别仿真产生两帧上述物理帧数据,从第一帧第1位开始截取,对物理帧1分割长度的区间设为[7,50],对物理帧2- 4分割长度φ的区间设为[60,300],图7～图11分别展示了基于离散度分析的帧同步盲识别算法对表3中5种物理帧数据的识别结果,图中横坐标对应的为分割段的长度,图(a)展示了各分割段的离散度值,图(b)展示各分割段在比特流数据中的起始位置,图(b)表示离散度值最小的分割段在比特流数据中的位置为同步码起始位。
如图7所示为对物理帧1的同步码识别结果,可见当分割长度为13 bit时,相对离散度值最小,此分割段所在位置为1 bit～13 bit, 此处为物理帧1的同步码所在位置;如图8所示为对物理帧2的同步码识别结果,可见当分割长度为127 bit时,相对离散度值最小,此分割段所在位置为数据的1 bit～127 bit,此处为物理帧2的同步码所在位置;如图9所示为对物理帧3的同步码识别结果,可见当分割长度为255 bit时,相对离散度值最小,此分割段所在位置为数据的1 bit～255 bit,此处为物理帧3的同步码所在位置;如图10所示为对物理帧4的同步码识别结果,可见当分割长度为256 bit时,相对离散度值最小,此分割段所在位置为数据的1 bit～256 bit, 此处为物理帧4的同步码所在位置;由图7～图10可以看出,本文提出的帧同步盲识别算法对不同类型的集中插入式帧同步码都有很好的识别效果。如图11所示为对物理帧4的同步码识别结果,可见当分割长度为256 bit时,相对离散度值最小,此分割段所在位置为数据的1 bit～256 bit,此处为物理帧5的同步码所在位置,由图10～图11可以看出,本文提出的帧同步盲识别算法对同种同步码不同信息段的数据也有较好的识别效果。由图7～图11可以看出识别结果能够完全匹配正确同步码,达到了较高的识别准确性。
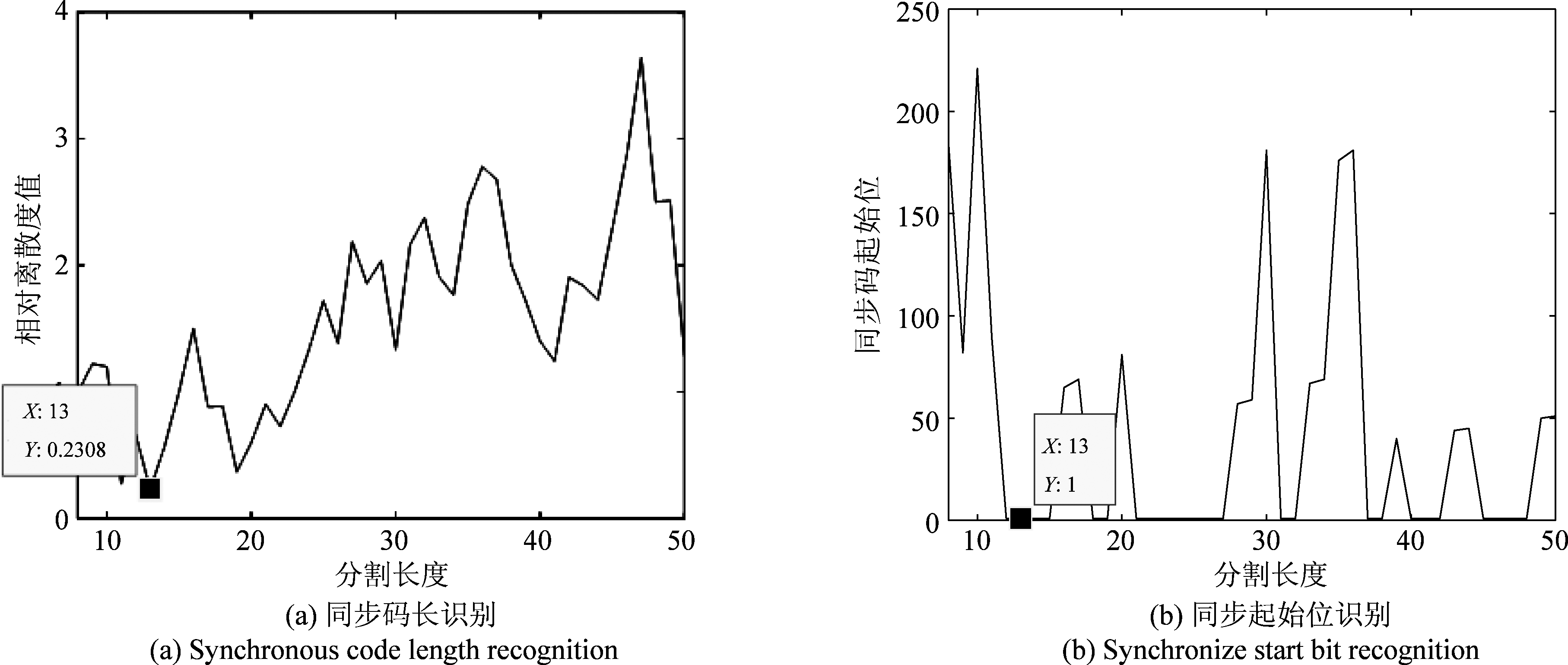
图7 物理帧1同步码识别结果
Fig.7 Synchronization code recognition result of physical frame 1
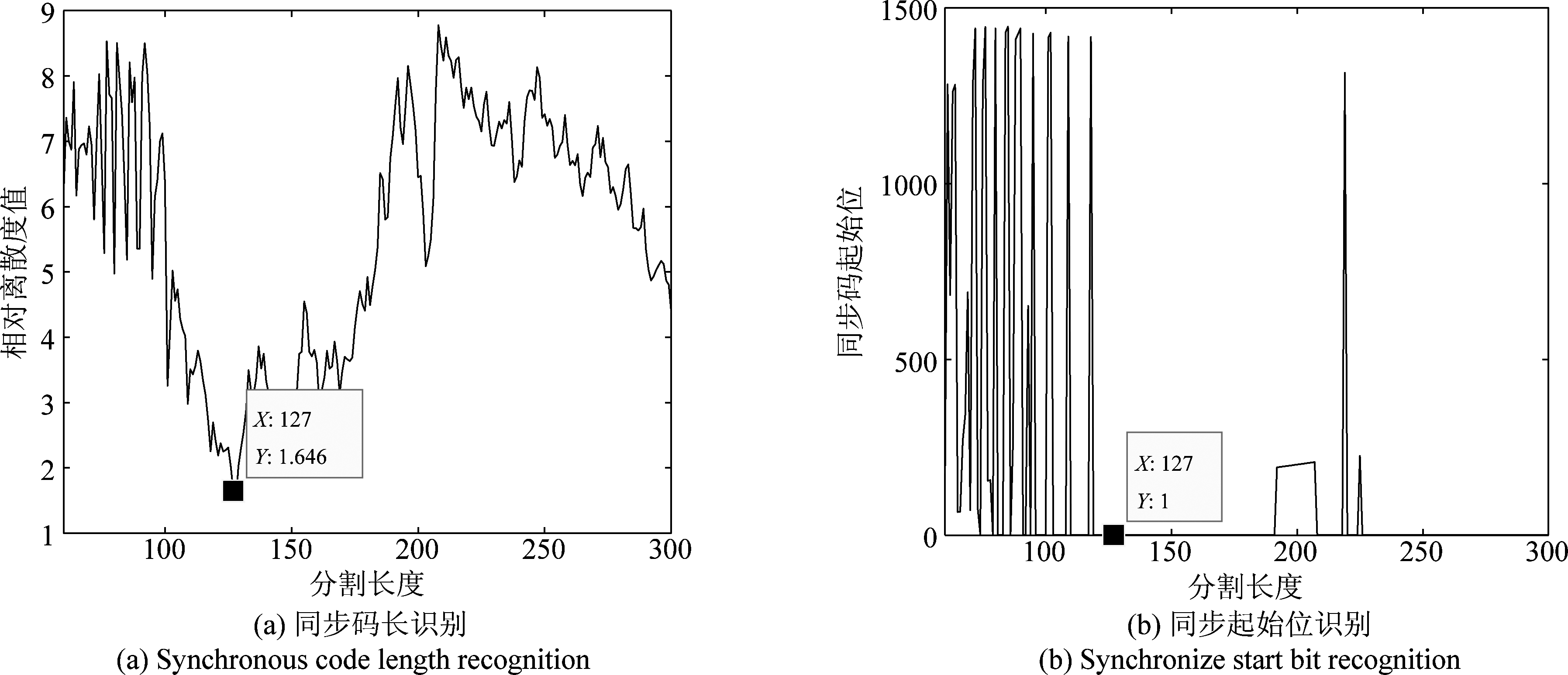
图8 物理帧2同步码识别结果
Fig.8 Synchronization code recognition result of physical frame 2
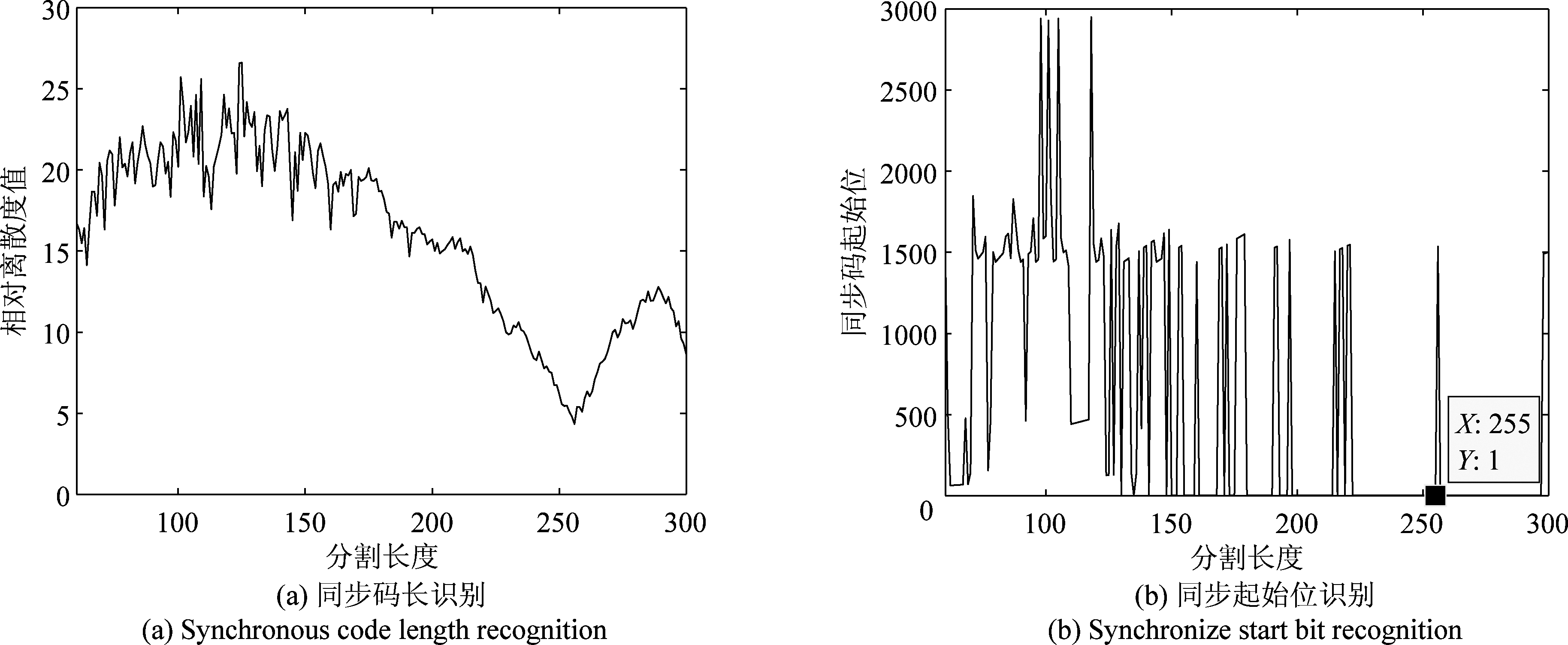
图9 物理帧3同步码识别结果
Fig.9 Synchronization code recognition result of physical frame 3
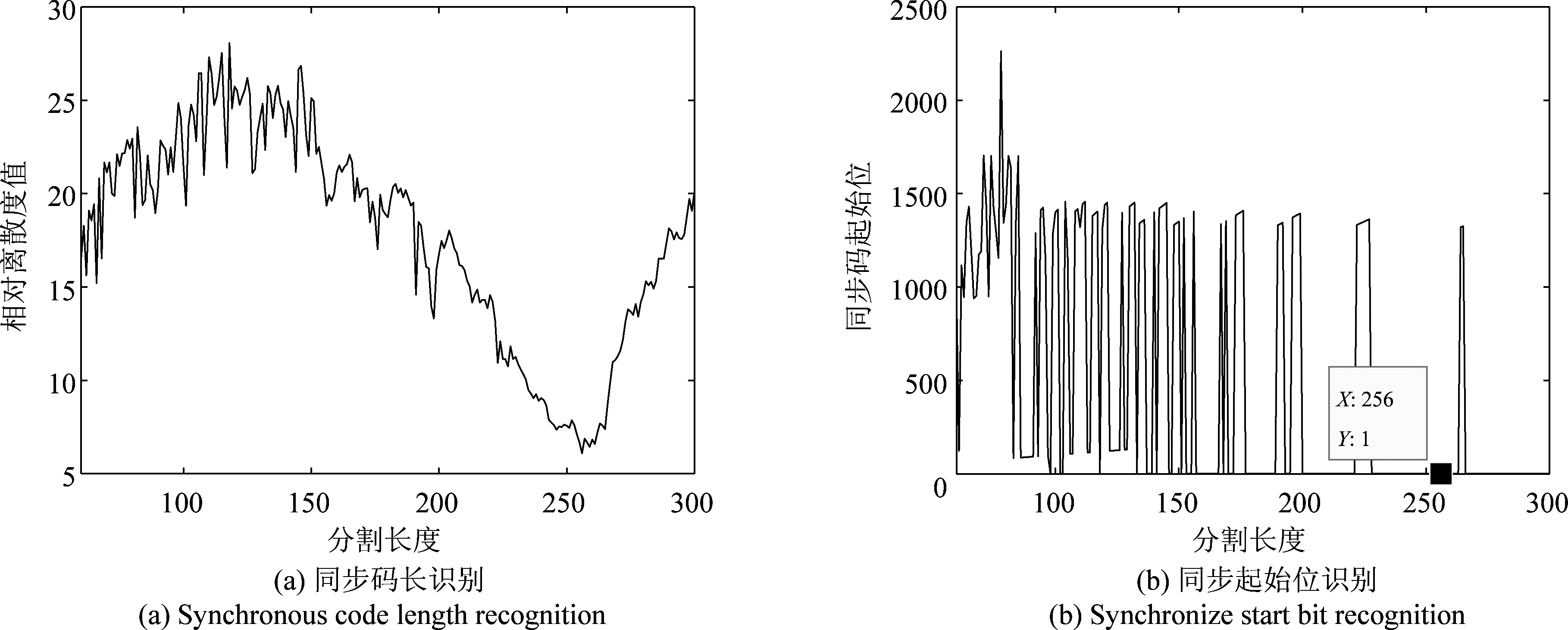
图10 物理帧4同步码识别结果
Fig.10 Synchronization code recognition result of physical frame 4
图11 物理帧5同步码识别结果
Fig.11 Synchronization code recognition result of physical frame 5
5.2 不同起始位的同步码识别
在无误码的条件下,分别仿真产生两帧物理帧4和物理帧5数据,从第561位开始截取物理帧4的数据,从第1793位开始截取物理帧5的数据,分割长度φ的区间设为[60,300]。
由图12可以看出从561位开始截取的物理帧4数据中同步码为769 bit～1024 bit,识别得到同步码所在的分割段为769 bit～1024 bit,分割段长度为256 bit,可见识别得到的分割段包含完整的同步码,识别结果能够完全匹配正确同步码;由图13可以看出,从1793位开始截取的物理帧5数据中同步码为2561 bit～2816 bit,识别得到同步码所在的分割段为2561 bit～2816 bit,分割段长度为256 bit,可见识别结果能够匹配正确同步码,达到了较高的识别准确性。
5.3 误码性能分析
在误码率是5%时分别仿真产生两帧物理帧3数据,从第一帧第1位开始截取,帧同步识别结果如图14所示,可以看出由于待识别数据中存在误码使图中切割长度对应的相对离散度值与图9中不同,但可以看出在分割长度为255 bit处仍为最小值,且就整体来看在逼近255 bit时相对离散度值下降趋势较明显,说明在一定误码率下,算法可以保证一定的同步码长识别率。图中同步码位置识别结果与实际情况完全吻合,说明在一定误码率下,算法可以保证一定的同步码位置识别率。
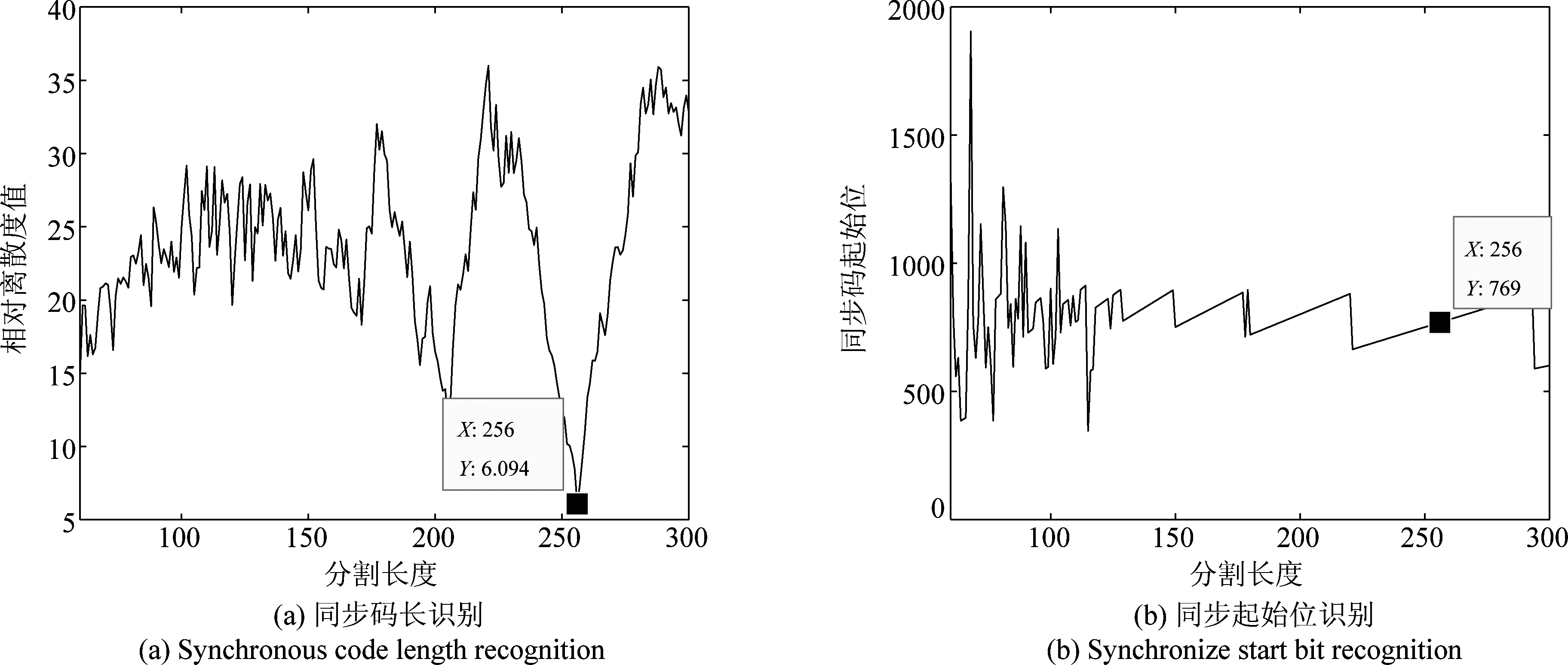
图12 随机起始位的物理帧4的同步码识别结果
Fig.12 Synchronization code identification results of physical frame 4 with random start bit
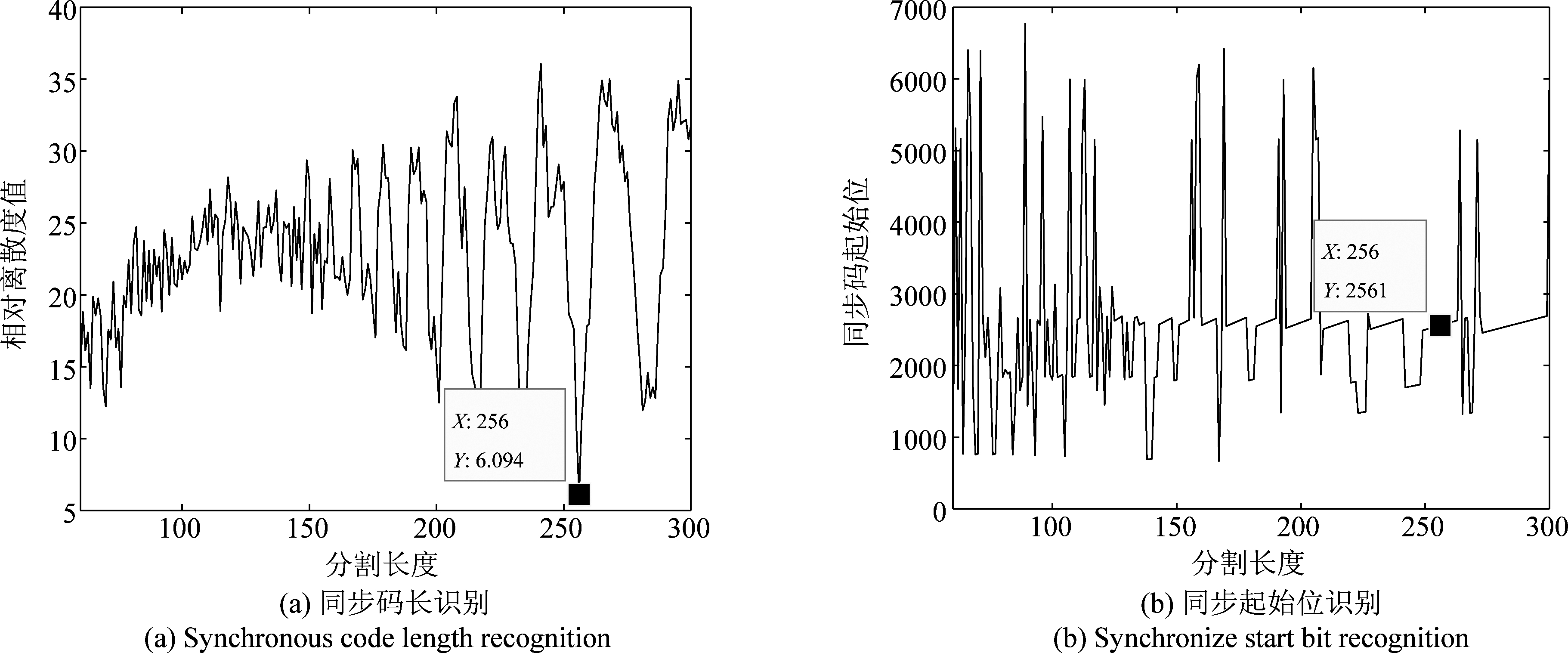
图13 随机起始位的物理帧5的同步码识别结果
Fig.13 Synchronization code identification results of physical frame 5 with random start bit
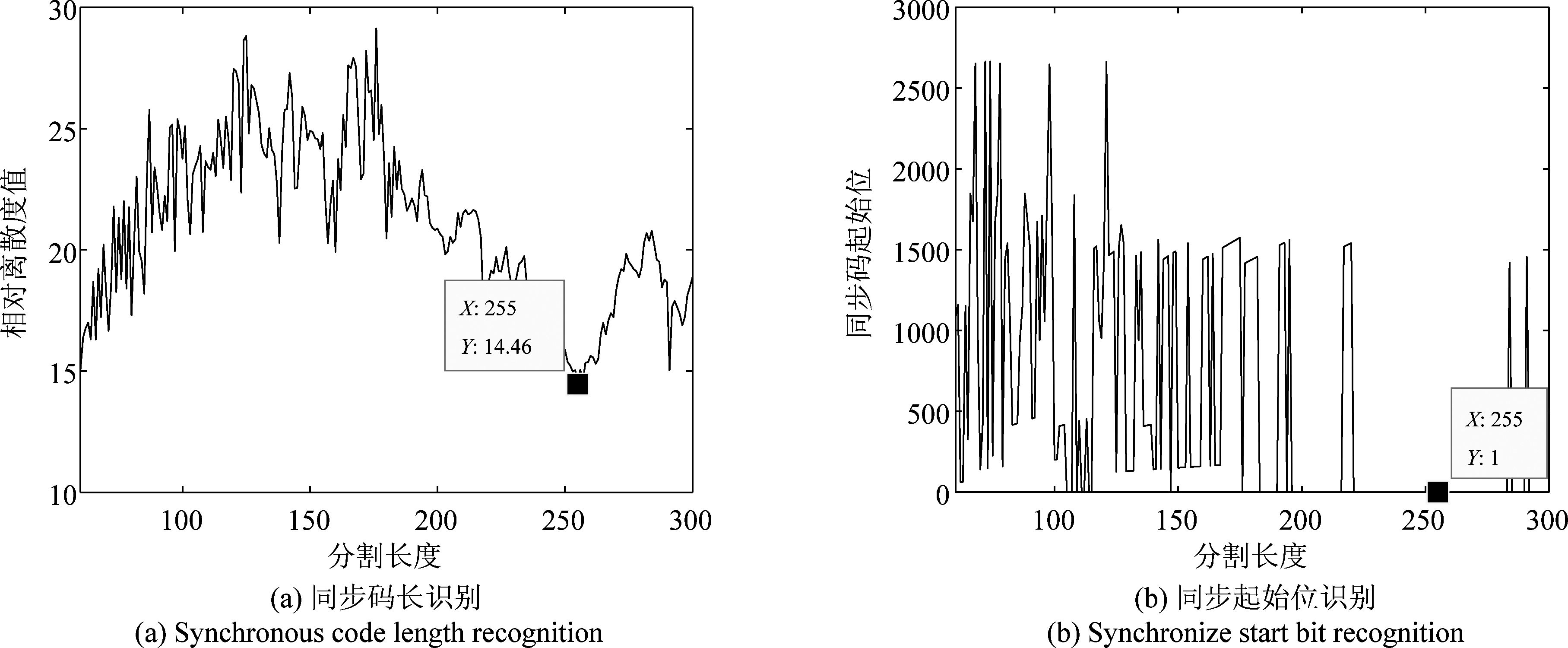
图14 误码率5%时物理帧3的同步码识别结果
Fig.14 Synchronization code identification results of physical frame 3 at 5% bit error rate
5.4 算法性能对比
将本文方法分别与文献[12]、文献[13]、文献[15]和文献[18]的方法进行性能对比,此处分别对四种算法进行简单介绍,文献[12]提出基于多重分形谱的帧同步字盲识别方法,该方法基于协议帧的有偏性小于同步字的基础,通过比较序列多重分形谱宽度对信息段进行删减,最后通过计算序列中固定长度字段浓度值分布,实现帧同步识别。文献[13]提出基于高阶统计处理技术的m-序列帧同步码识别方法,该方法利用m-序列采样后的偏三阶相关函数峰值相似度高的特性将同步码与信息段分开。文献[15]提出了模糊匹配帧同步识别算法,算法主要包括小区域检测寻找帧长、二次滤波寻找帧同步码起始位和模糊匹配三部分。文献[18]提出一种基于分层的矩阵秩帧同步识别方法,该方法首先建立分层模型并根据统计概率确定帧长值,在帧长识别的基础上利用滑窗搜索最小秩值的位置完成帧同步的识别。
可以看出当基于多重分形谱的帧同步字盲识别方法只适用于同步码和信息段有偏性不同的数据,也就是说该算法并不能识别是伪随机序列的同步码。基于高阶统计处理技术的m-序列帧同步码识别方法只适用于识别是m-序列的同步码,不能识别其他类型的同步码。而基于二次滤波和模糊匹配的帧同步码识别算法和基于分层的矩阵秩帧同步识别算法都需要具有多个集中插入式帧的数据,也就是说此类算法对帧数较少的数据无能为力。
选取20帧物理帧3作为实验数据,从第一帧第1位开始截取,分别用文献[12]、文献[13]、文献[15]、文献[18]中算法和本文算法在不同误码率条件下进行蒙特卡洛同步码长识别仿真实验,识别结果如图15所示,文献[12]提出基于多重分形谱的帧同步字盲识别方法不适用于m-序列帧同步码的识别。
图15 各算法同步码识别结果对比
Fig.15 Comparison of synchronization code recognition results of each algorithm
由图15可知,当误码率达到3%时,高阶统计处理技术的同步码识别率在60%左右,模糊匹配算法和基于分层的矩阵秩算法的同步识别率为80%左右,而本文算法的识别率保持在90%以上;误码率继续升高到6%,此时高阶统计处理技术的同步码识别率只有20%左右,模糊匹配算法的识别率为40%左右,基于分层的矩阵秩算法的识别率为50%左右,而本文算法的识别率保持在60%;误码率继续升高到10%,此时高阶统计处理技术、模糊匹配算法、基于分层的矩阵秩算法和本文算法的识别率都几乎为0,因此随着误码率的升高,本文算法的识别率要高于文献[13]、文献[15]和文献[18]所提算法,这是因为文献[15]和文献[18]所提算法同步识别性能与帧的数量有直接关系,而本文所提算法的识别性能不受帧数量的影响。
6 结论
本文针对协议类型未知条件下集中插入式帧同步的盲识别问题,首次提出了一种基于离散度分析的快速帧同步盲识别算法。在分析得出集中插入式同步码都具有相关旁瓣小的特点的基础上,根据离散度分析理论通过计算序列的相对离散度值分析序列的相关性,利用上述方法对待识别数据进行循环切分并计算每个切分段的相对离散度值,达到准确切分帧同步码的目的。最后,找到最小离散度值对应的子切分序列,实现同步码的准确识别。仿真试验验证了本文算法的有效性,表明识别算法不受同步码型和数据量的约束,并且算法的抗误码性能较好、识别速度较快,因此具有一定的工程应用价值。
[1] Chiani M, Martini M G. Practical Frame Synchronization for Data with Unknown Distribution on AWGN Channels[J]. Communications Letters IEEE, 2005, 9(5): 456- 458.
[2] Kopansky A, Bystrom M. Detection of Aperiodically Embedded Synchronization Patterns on Rayleigh Fading Channels[J]. IEEE Transactions on Communications, 2006, 54(11): 1928-1932.
[3] 甘华强, 王军, 周鹏, 等. 复杂多径信道下的OFDM抗干扰同步算法[J]. 信号处理, 2015, 31(11): 1461-1466.
Gan Huaqiang, Wang Jun, Zhou Peng, et al. OFDM Anti-interference Synchronization Algorithm in Complex Multipath Channels[J]. Journal of Signal Processing, 2015, 31(11): 1461-1466.(in Chinese)
[4] 吴艺彬, 邵高平, 汪洋. 定时同步与匹配滤波频域联合实现技术[J]. 信号处理, 2018, 34(9): 1105-1113.
Wu Yibin, Shao Gaoping, Wang Yang. Timing Synchronization and Matched Filtering Frequency Domain Joint Realization Technology[J]. Journal of Signal Processing, 2018, 34(9): 1105-1113.(in Chinese)
[5] 黎锁平, 陈伟儒, 湛兴祥, 等. 基于训练序列的OFDM系统定时同步改进算法[J]. 信号处理, 2011, 27(7): 1095-1099.
Li Suoping, Chen Weiru, Zhan Xingxiang, et al. Improved Timing Synchronization Algorithm of OFDM System based on Training Sequence[J]. Signal Processing, 2011, 27(7): 1095-1099.(in Chinese)
[6] 薛开平, 柳彬, 王劲松, 等. 面向链路比特流的未知帧关联分析[J]. 电子与信息学报, 2017, 39(2): 374-380.
Xue Kaiping, Liu Bin, Wang Jinsong, et al. Data Link Bit Stream Oriented Association Analysis on Unknown Frame[J]. Journal of Electrinics & Information Technology, 2017, 39(2): 374-380.(in Chinese)
[7] 曹成宏, 雷迎科, 徐一鸣. 面向链路层比特流数据频繁统计的AC-IM算法[J]. 小型微型计算机系统, 2018, 39(7): 1436-1440.
Cao Chenghong, Lei Yingke, Xu Yiming. AC-IM Algorithm Oriented Frequent Statistics of Link-layer Bit Stream Data[J]. Journal of Chinese Computer Systems, 2018, 39(7): 1436-1440.(in Chinese)
[8] 曹成宏, 雷迎科. 面向比特流的链路层未知帧分析技术综述[J]. 小型微型计算机系统, 2018, 39(2): 297-303.
Cao Chenghong, Lei Yingke. Survey of Bit-stream Oriented Link-layer Unknown Frame Analysis Techniques[J]. Journal of Chinese Computer Systems, 2018, 39(2): 297-303.(in Chinese)
[9] Mehrabi M, Lafond S, Wang L. Frame Synchronization of Live Video Streams using Visible Light Communication[C]∥2015 IEEE International Symposium on Multimedia (ISM). IEEE, 2015: 128-131.
[10]李歆昊, 张旻, 韩树楠. 基于多重分形谱的物理层帧结构检测算法研究[J]. 电子与信息学报, 2018, 40(2): 400- 407.
Li Xinhao, Zhang Min, Han Shunan. Study on Frame Structure Detection in Physical Layer Based on Multi-fractal Spectrum[J]. Journal of Electrinics & Information Technology, 2018, 40(2): 400- 407.(in Chinese)
[11]李歆昊, 张旻. 基于人工免疫的链路层协议帧同步字识别[J]. 电子与信息学报, 2017, 39(3): 561-567.
Li Xinhao, Zhang Min. Frame Synchronization Word Identification of Link Layer Protocol Based on Artificial Immune[J]. Journal of Electrinics & Information Technology, 2017, 39(3): 561-567.(in Chinese)
[12]李歆昊, 张旻, 韩树楠. 基于多重分形谱的链路层协议帧同步字盲识别[J]. 电子与信息学报, 2017, 39(7): 1666-1672.
Li Xinhao, Zhang Min, Han Shunan. Frame Synchronization Word Identification of Link Layer Protocol Based on Multi-fractal Spectrum[J]. Journal of Electrinics & Information Technology, 2017, 39(7): 1666-1672.(in Chinese)
[13]白彧, 杨晓静, 张玉. 基于高阶统计处理技术的m-序列帧同步码识别[J]. 电子与信息学报, 2012, 34(1): 33-37.
Bai Yu, Yang Xiaojing, Zhang Yu. A Recognition Method of m-sequence Synchronization Codes using Higher-order Statistical Processing[J]. Journal of Electrinics & Information Technology, 2012, 34(1): 33-37.(in Chinese)
[14]白彧, 杨晓静, 王懋. 基于相关滤波和哈达玛变换的帧同步码识别[J]. 探测与控制学报, 2011, 33(3): 69-72.
Bai Yu, Yang Xiaojing, Wang Mao. Recognition Method of Frame Synchronization Codes based on Relativity Filter and Hadamard Transformation Algorithm[J]. Journal of Detection and Control, 2011, 33(3): 69-72.(in Chinese)
[15]张玉, 杨晓静. 集中插入式帧同步识别方法[J]. 兵工学报, 2013, 34(5): 554-560.
Zhang Yu, Yang Xiaojing. Recognition Method of Concentratively Inserted Frame Synchronization[J]. Acta Armamentarii, 2013, 34(5): 554-560.(in Chinese)
[16]郭凯丰, 王萌. 基于等帧长信号的帧头检测方法研究[J]. 信号与信息处理, 2014, 44(6): 33-36.
Guo Kaifeng, Wang Meng. Research on Detection of Frame Head on Fixed Frame Length[J]. Journal of Signal and Information Processing, 2014, 44(6): 33-36.(in Chinese)
[17]王和洲, 薛开平, 洪佩琳, 等. 基于频繁统计和关联规则的未知链路协议比特流切割算法[J]. 中国科学技术大学学报, 2013, 43(7): 554-560.
Wang Hezhou, Xue Kaiping, Hong Peilin, et al. An Unknown Link Protocol Bit Stream Segmentation Algorithm based on Frequent Statistics and Association Rules[J]. Journal of University of Science and Technology of China, 2013, 43(7): 554-560.(in Chinese)
[18]陆凯, 张旻, 李歆昊. 一种有效的等帧长帧同步盲识别方法[J]. 火力与指挥控制, 2015(9): 68-71.
Lu Kai, Zhang Min, Li Xinhao. A Blind Recognition Method of Fixed Frame Length Frame Synchronization[J]. Fire Control & Command Control, 2015(9): 68-71.(in Chinese)
[19]Qin J, Huang Z, Liu C, et al. Novel Blind Recognition Algorithm of Frame Synchronization Words Based on Soft-Decision in Digital Communication Systems[J]. PloS one, 2015, 10(7): e0132114.
[20]Liang Y, Rajan D, Eliezer O E. Sequential Frame Synchronization based on Hypothesis Testing with Unknown Channel State Information[J]. IEEE Transactions on Communications, 2015, 63(8): 2972-2984.
[21]Sklar B. Digital Communications: Fundamentals and Applications[M]. Publishing House of Electronics Industry, 2006: 458- 497.
[22]Liu X B, Koh S N, Chui C C, et al. A Study on Reconstruction of Linear Scrambler using Dual Words of Channel Encoder[J]. IEEE Transactions on Information Forensics and Security, 2013, 8(3): 542-552.
