1 引言
近年来,混合多输入多输出(Multiple-Input Multiple-Output,MIMO)相控阵技术在雷达领域吸引了越来越多学者的关注,它是以相干MIMO雷达为基础,将发射阵列划分成若干子阵列,因此子阵列间的发射信号相互正交,子阵内部在相控阵模式下工作。从而使得混合MIMO相控阵雷达兼具相控阵雷达和MIMO雷达的特点,实现了发射相干处理增益和波形分集增益的结合[1-3]。
虽然混合MIMO相控阵雷达有着上述特点,但是作为性能折中的产物,相比于两种传统雷达,原有优势均受到了不同程度的削弱:相比于相控阵雷达,波束聚焦能力减弱,硬件成本增加;相比于MIMO雷达,由于正交信号的减少,使得雷达扩展虚拟孔径的能力减弱,进而带来阵列自由度(Degree of Freedom, DOF)的损失。对雷达检测目标的能力造成影响,降低了雷达整体性能的发挥[4-5]。
而对于如何提高阵列自由度的问题,前人也已经进行了大量的研究。最小冗余阵[6](Minimum Redundant Array,MRA)不仅可以减少阵元数量,而且扩展孔径的能力很强,但它的缺点在于没有闭合的表达式,进行最优化搜索所需要的大量计算阻碍了它的实际应用[7]。文献[8]中的互质阵与MRA相比,虽然在运算量上大幅降低,但是它做差异阵列后的虚拟阵列并不是密集排布的[9-10],即:不能形成一个均匀线阵,这对孔径扩展造成了一定程度的影响,仅能够利用M+P个阵元产生了O(MP)的自由度,扩展孔径的能力不强。为解决上述问题, Pal P等人提出的嵌套阵[11-12]以及后续Liu C L提出的超级嵌套阵[13-14],不但可以形成“无孔(均匀线阵)”的差异阵列,而且能够以Q个阵元实现O(Q2)的自由度。在低计算复杂度的基础上实现了高自由度,具有较好的应用意义。
由于嵌套阵在各方面表现优异,所以这种结构被广泛应用到MIMO雷达阵列设计中:文献[15]以孔径大小为标准,将嵌套阵划分为不同的子阵,设计了一个嵌套阵结构的发射子孔径的线阵MIMO雷达,在嵌套阵内部实现了混合MIMO相控阵的功能;文献[16]则在收发端共同设置嵌套的MIMO雷达,经过MIMO雷达虚拟孔径扩展和差异阵列扩展后,进一步增大了自由度;文献[17]在保证“无孔”的前提下,对嵌套阵位置进行调整所形成的平移嵌套阵进一步提高了稀疏率,有效降低了互耦效应;文献[18]则是在文献[1]的基础上,将嵌套阵作为接收阵列,以收发联合的方式将混合MIMO相控阵雷达和嵌套阵优势进行了结合。然而以上研究都是以线阵为基础,对于在实际应用中更有优势的面阵没有涉及。因此文献[19]在文献[18]的基础上将二维嵌套阵运用到混合MIMO相控阵雷达面阵的收发联合设计中,使得阵列的DOA估计的能力大幅提升,但是由于结构设计不够合理,导致阵元数目过多,增加了运算成本。因此,如何在不增加硬件成本且不减弱雷达的其他性能的基础上,使用较少阵元数目来实现更高的自由度,是混合MIMO相控阵雷达实用化过程中的重要问题。
所以我们以L形结构为基础,借助嵌套阵对混合MIMO相控阵雷达的收发阵列进行设计。这样既不损失混合MIMO相控阵雷达的优势,又实现了阵列虚拟的孔径扩展以及自由度的提高。而且通过垂直放置的发射阵和横向的接收阵,用阵元数目较少的L形布阵实现了二维混合MIMO相控阵雷达的结构。本文主要工作有:首先是提出了一种嵌套阵结构的L形收发阵列结构,该结构与常规混合MIMO相控阵雷达相比能够获得更大的孔径和更高的自由度;其次是推导出了阵列流形的矩阵形式,克服了最小冗余阵无闭合表达式的问题;最后通过计算机仿真实验,证明了与其他两种结构的混合MIMO相控阵雷达相比,我们这种结构的性能更优。
2 接收端一维嵌套阵列模型
对于嵌套阵来说,当它的级数大于二时,差异阵列[20]扩展后的虚拟阵列会变成“有孔”的,因此我们选用二级嵌套阵,二级嵌套阵可以看做一个密集阵列和一个稀疏阵列组合而成。若嵌套阵有N个阵元,xi代表阵列中第i个阵元位置,那么总体的差异阵列可以表示为:{xi-xj},i, j=1,2,…,N。
用卷积公式来表示,可以看出做差异阵列之后的阵元位置为:
γ=c[m]*○c[-m]
(1)
其中*○代表卷积运算,由上式可以看出,N元均匀线阵(Uniform Liner Array, ULA)产生的结果是一个2N-1元的ULA。进而对于一个二级嵌套线阵来说,假设密集阵元数为N1,阵元间距为d1;稀疏阵元数为N2,阵元间距为d2=(N1+1)d1,且满足N1+N2=N。对它进行卷积运算,我们就可以发现形成了长度为2N2(N1+1)-1的ULA。且所得到的扩展后的阵元位置可表示为:
md2,{m=-[N2(N1+1)-1],…,[N2(N1+1)-1]}
(2)
这也就是嵌套阵扩展自由度的根源。以图1中的4元嵌套线阵为例,仅仅利用四个阵元便实现了11的自由度:
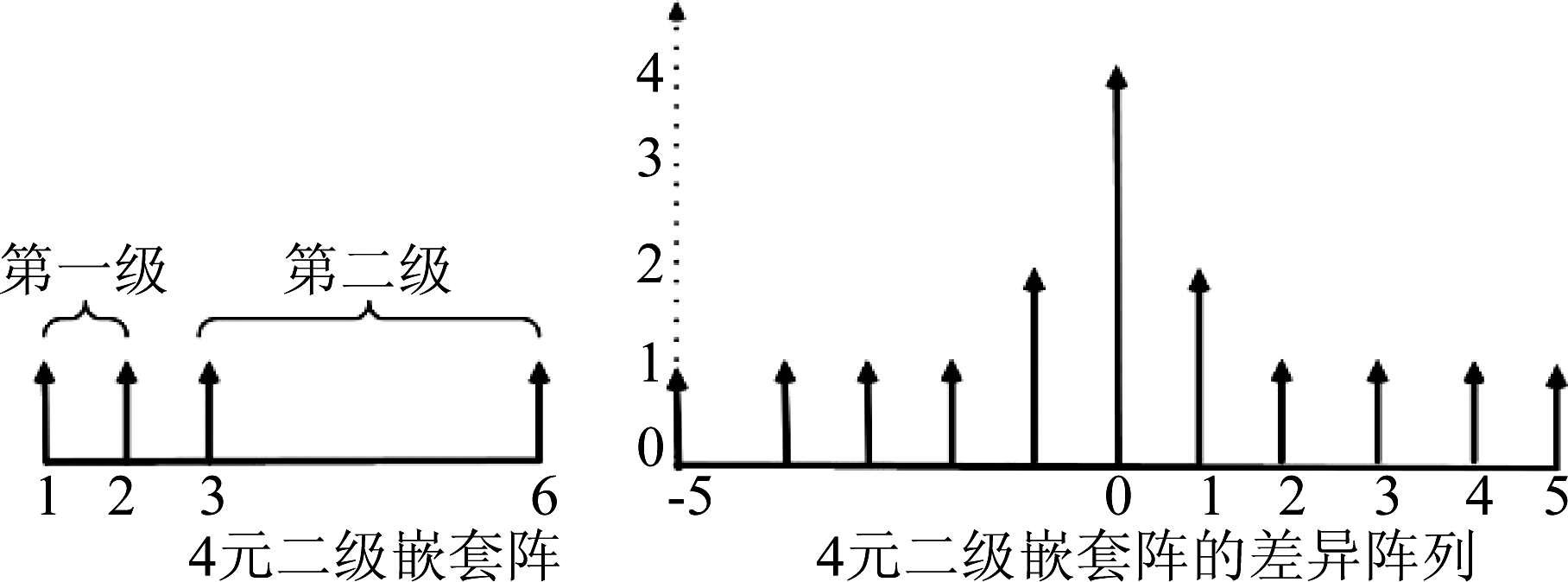
图1 四元嵌套阵及差异阵列示意图
Fig.1 Four elements nested array and difference coarray schematic
对于传统的N元均匀线阵,其自由度为N-1,即均匀线阵可识别的目标数目为N-1。但对N元的嵌套阵线阵而言,在做差异阵列扩展的同时会带来阵列自由度的扩展。若取N为奇数,则
是N元嵌套阵的自由度最大值。如果在实际阵元数目固定,嵌套阵相比于其他同类阵列,能够在较大程度上扩充阵元数目,获得O(N2)的阵列自由度。
3 二维混合MIMO相控阵雷达模型
混合MIMO相控阵雷达是以相干MIMO雷达为基础,将发射阵列划分成若干子阵列,从而子阵的内部在相控阵模式下工作、子阵之间仍工作在MIMO模式的混合系统。在本文设计中,虽然发射阵列是一个混合MIMIO相控线阵,但是考虑到做差异阵列之后二维目标的估计问题,我们在这里把一维的混合MIMO相控阵当作特殊的二维混合MIMO相控阵雷达来处理。
混合MIMO相控阵雷达由M×P个阵元的矩形面阵构成,其中M为纵向每一列的阵元数目,P为横向每一行的阵元数目,在本结构中P=1,横向或纵向阵元间距为半波长λ/2。将阵列均匀重叠地划分为K个子阵列,设Zk是由0、1构成的M×P矩阵,代表每个子阵列的阵元位置信息,那么第k个子阵列的发射导向矢量:
ak(θ,φ)=vec(Zk⊙[μ(θ,φ)υΤ(θ,φ)]) k=1,2,…,K
(3)
式中K≤MP,vec(·)为矩阵的向量化表示,⊙代表哈达玛乘积,(·)T为转置符号。设横向阵元间距为dm,纵向阵元间距为dp,方位角为φ,俯仰角为θ。
μ(θ,φ)=[1,ej2πdmsin(θ)cos(φ),…,ej2π(M-1)dmsin(θ)cos(φ)]T υ(θ,φ)=[1,ej2πdpsin(θ)sin(φ),…,ej2π(P-1)dpsin(θ)sin(φ)]T
(4)
设发端第k个子阵的发射阵列权值矩阵为wk,k=1,2,…,K,则相干处理增益定义为:
(5)
分集增益定义为:
d(θ,φ)=[e-jτ1(θ,φ),…,e-jτK(θ,φ)]T
(6)
τk(θ,φ)代表波束从第1个子阵的首阵元传播到第k个子阵的首阵元之间的时间差值,所以混合MIMO相控阵雷达的流形矩阵定义为:
u(θ,φ)=c(θ,φ)⊙d(θ,φ)⊗b(θ,φ)
(7)
其中b(θ,φ)为接收导向矢量,⊗是Kronecker积,K个发射信号定义为:φ(τ)=[φ1(t),φ2(t),…,φK(t)],
则目标反射信号以及接收阵列的信号为:
(8)
x(t)=r(t,θ,φ)b(θ,φ)+n(t)
(9)
n(t)为噪声信号,若雷达脉冲长度用T0表示,
则接收信号经过匹配滤波之后表示为:
(10)
4 L形收发阵列联合模型
4.1 收发阵列结构
混合MIMO相控阵雷达系统如图2所示。由于本文中发射端为纵向放置的M元线阵,所以P=1,把发射端分割为K个均匀重叠子阵,接收端为水平的4元嵌套阵。
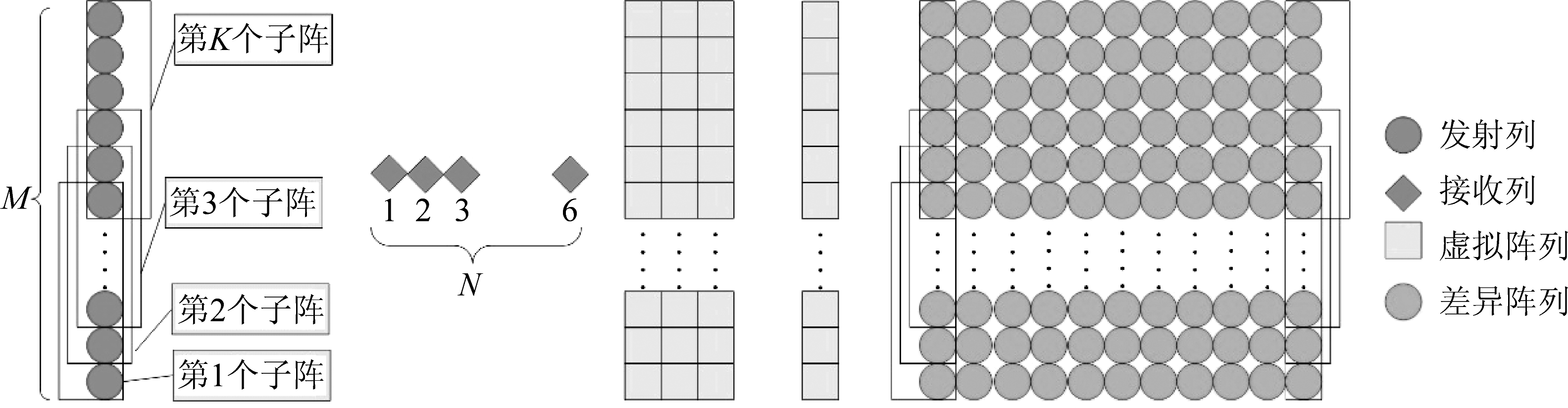
图2 系统结构图
Fig.2 System structure diagram
以N=4为例,则接收端是一个稀疏阵元和密集阵元数均为2的二级嵌套阵。首先,发射端和接收端经过虚拟阵列的扩展,形成了一个M×4的“有孔”平面阵;其次在横向上,各阵元互相做差得到对应的差异阵列,最终形成了一个M×11的“无孔”平面阵。相比于没有嵌套阵结构的设计方法,该结构的自由度大大提升,雷达性能得到进一步增强。
4.2 收发联合系统的阵列流形
接下来重点分析阵列流形在经过MIMO雷达虚拟孔径扩展和差异阵列扩展后的变化。即通过数学分析来证明雷达系统自由度扩展的原因。将式(10)写作如下形式:
(11)
式中,D是目标的数量,L=D+1为目标数目和干扰数目之和,对匹配滤波后的信号(11)变形,公式两端乘系数
(12)
U为虚拟阵列的流形矩阵,各空间目标的反射系数为:β=[β1(θ1,φ1),β2(θ2,φ2),…,βL(θL,φL)]T,记
根据文献[22],那么
的自相关矩阵可以写作:
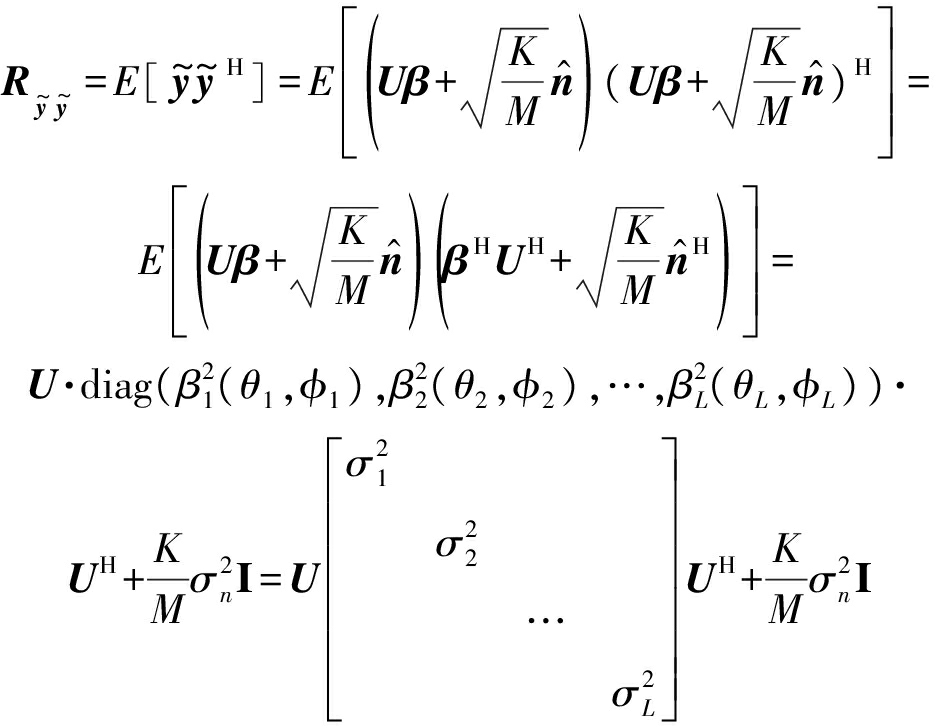
(13)
(·)H为共轭转置运算,
为噪声信号的方差,将
按列展开写成矢量形式:
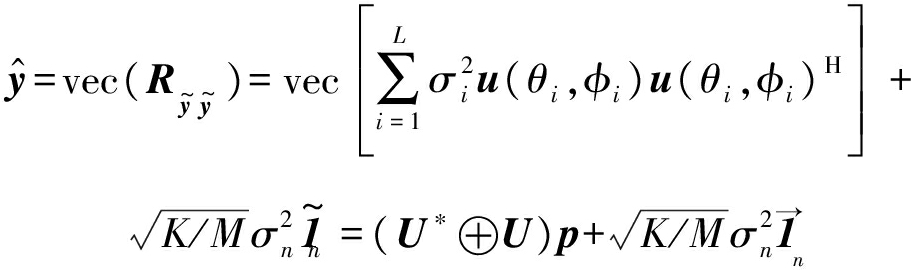
(14)
式中
为J个空间目标的功率集,
为单位向量构成的矩阵,在
中只有第i个元素值为1,其余为0,⊕为K-R积。而混合MIMO相控阵雷达均匀分割,所以能量也是均匀分配给每个子阵[23],因此发射波束形成权值定义为:
(15)
那么归一化的发射相干处理增益c(θk,φk)为公式(16)的形式:
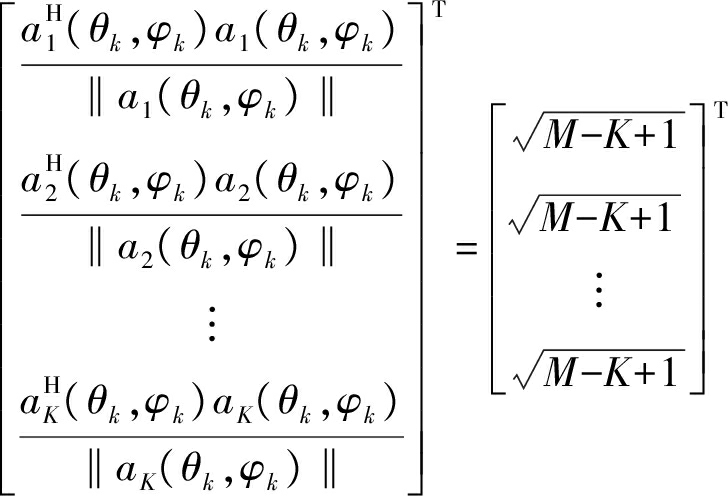
(16)
在这里我们使用矩阵NTk来代表第k个发射子阵的首阵元位置坐标,uk可以表示为uk=sin φk[cos θksin θk]T,则波形分集增益可写作:
(17)
接收增益为:
(18)
那么阵列的虚拟导向矢量表示为公式(19):
(19)
进而对应的阵列流形矩阵计算为式(20)的形式:
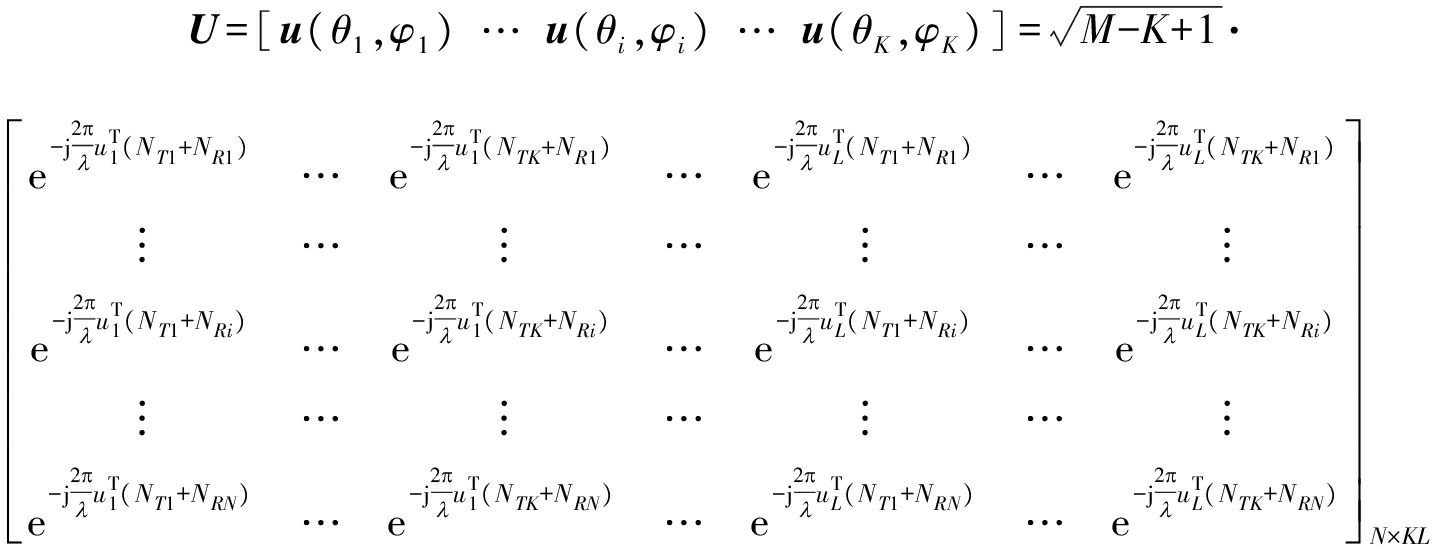
(20)
最后,新的虚拟阵列流形矩阵可以表示为定义A=U*⊕U,表示为式(21):
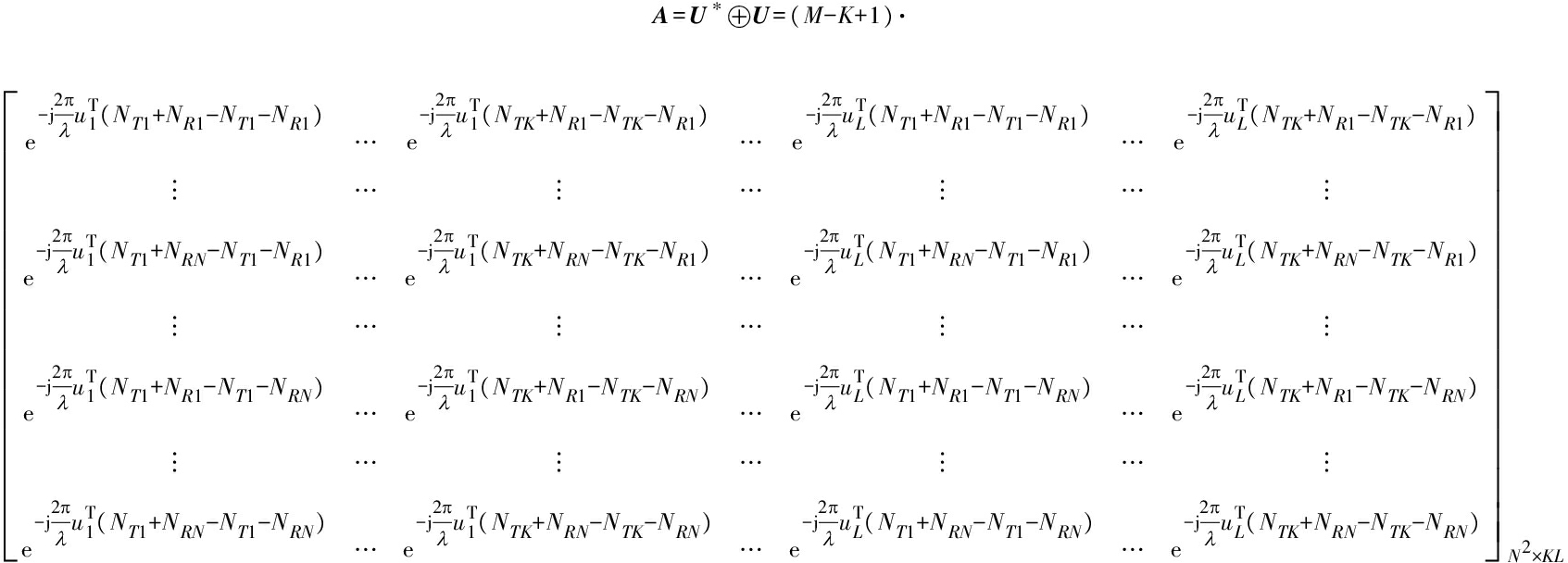
(21)
4.3 阵列流形矩阵的空间平滑处理
对旧的阵列流形矩阵进行K-R乘积形成新的流形矩阵,其本质是在嵌套阵中做差异阵列,对阵元坐标做差,此时新的流形矩阵维度为N2×KL,相比于原来的流形矩阵维度得到了可观的扩展,但差异阵列做差之后所得的虚拟阵元位置会有重合,因此在流形矩阵中也会有重复的信息,所以需要对矩阵A去冗余。若M是奇数,N是偶数,将去冗余后的新矩阵称为A1,w为去冗余运算后矩阵A1的行数,KL是矩阵A1的列数,那么新矩阵A1的大小为w·KL,那么对应的矩阵y可以写作y1:
(22)
由于接收噪声信号之间不相关且方差为
所以阵列经虚拟扩展后,观测噪声仍为白噪声。在式(22)中,
为在(w+1)/2点处值为1的单位向量,从y1也能看出矩阵维度的扩展,即自由度增加的本质。
下面进行空间平滑处理:按照混合MIMO相控阵雷达的分割方式,将矩阵A1划分为
个均匀重叠的子矩阵,每个子矩阵内部有
个值,第i个子阵在矩阵中的行数为:
{(-i+1+n),n=(w+1)/2,…,w}
(23)
即:第i个子阵在y1中对应的行数为从(w+1)/2-i+1到w-i+1。令半波长为d,Φ=diag(e-j(2π/λ)du1,e-j(2π/λ)du2,…,e-j(2π/λ)duL),取矩阵A1的(w+1)/2-i+1到w-i+1行并命名为
是i点值为1的单位向量。则[11]:
(24)
对y1i取期望:
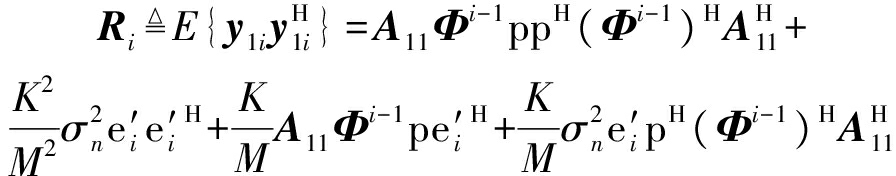
(25)
最后对所有子阵的Ri取平均,得到最终的协方差矩阵Rss:
(26)
协方差矩阵Rss便可以运用到MUSIC谱估计算法中了。
5 计算机仿真实验
如图1所示,我们分别对这种新型混合MIMO相控阵雷达的收发端进行设计:发射端为纵向放置的混合MIMO相控阵雷达线阵,接收端为横向放置的嵌套阵。作为对比,混合MIMO相控阵发射端与本文所提出的雷达结构相同,而接收端是横向放置的、阵元数目也为N的ULA。
我们参考文献[21]中的混合MIMO相控阵雷达子阵分割方法,将混合MIMO相控阵雷达发射端分割为K=(M/2)-1个子阵,每个子阵包含(M/2)+2个阵元。那么我们所提出的这种阵列排布方式,经过做虚拟阵列和差异阵列的双重扩展之后,形成了自由度为K×[N(N-1)+1]的“无孔”平面阵。而在相同的阵元个数,且接收端为4元ULA的情况下,经过虚拟阵列扩展后的阵列自由度仅为K×N。两种阵列结构的自由度对比如图3所示。
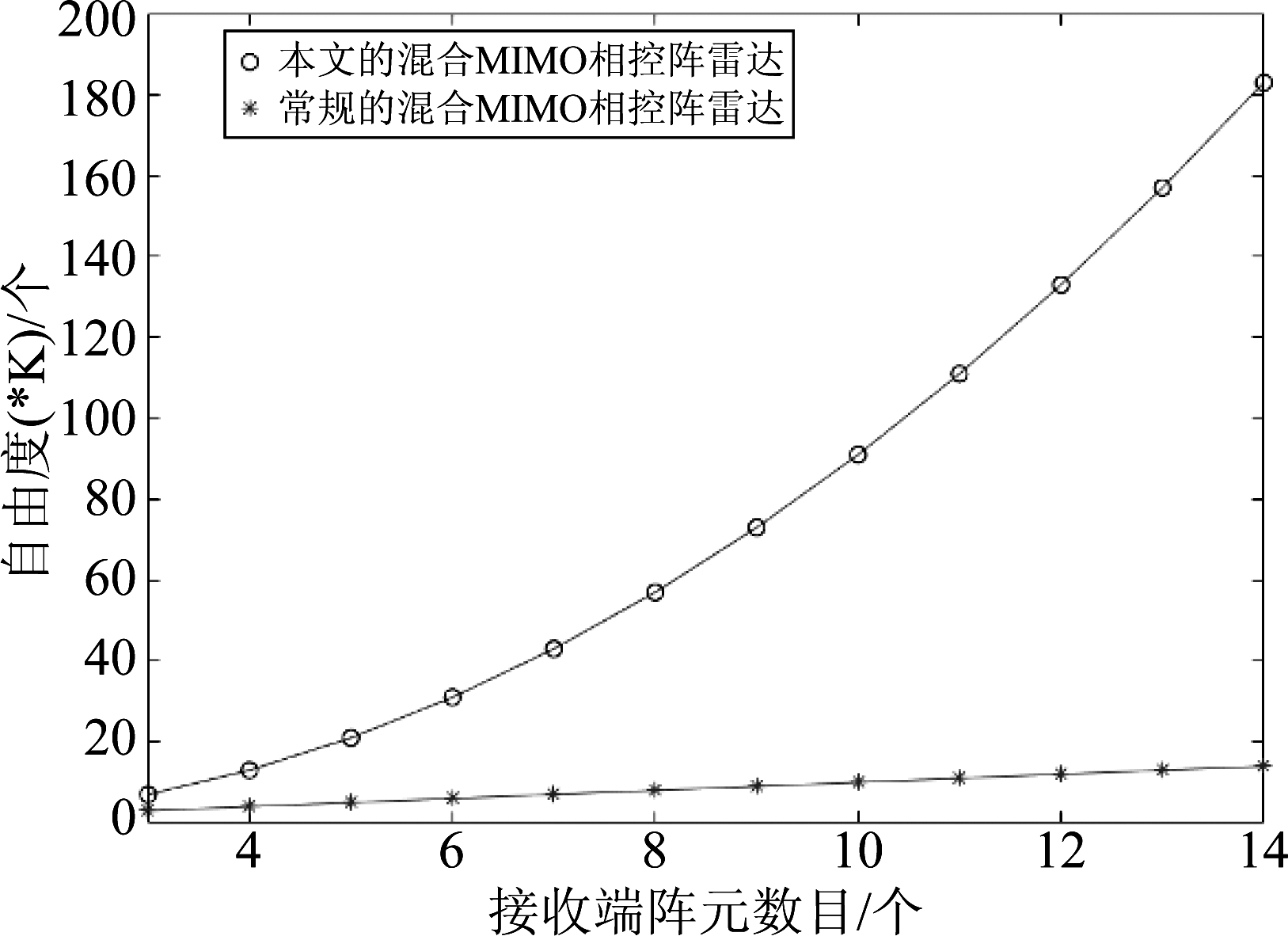
图3 自由度随接收端阵元数目变化的关系
Fig.3 DOF as a function of the number of elements at the receiving end
从图中可以看出,随着接收端阵元数目的增加,常规混合MIMO相控阵雷达的自由度是线性增长的,而我们提出的混合MIMO相控阵雷达的自由度是呈平方数增长的。这也是我们提出的混合MIMO相控阵雷达性能更优的直接原因。
我们在发射端取M=16,K=7,在接收端取N=4。在信噪比为0 dB的环境下,假设空间中存在16个非相干目标,排成一个正方形的样式,均匀散布在方位角和俯仰角均为20°～50°的方块内。使用常规的混合MIMO相控阵雷达以及本文提出的嵌套的混合MIMO相控阵雷达对它们进行二维目标MUSIC谱估计。估计效果如图4所示。
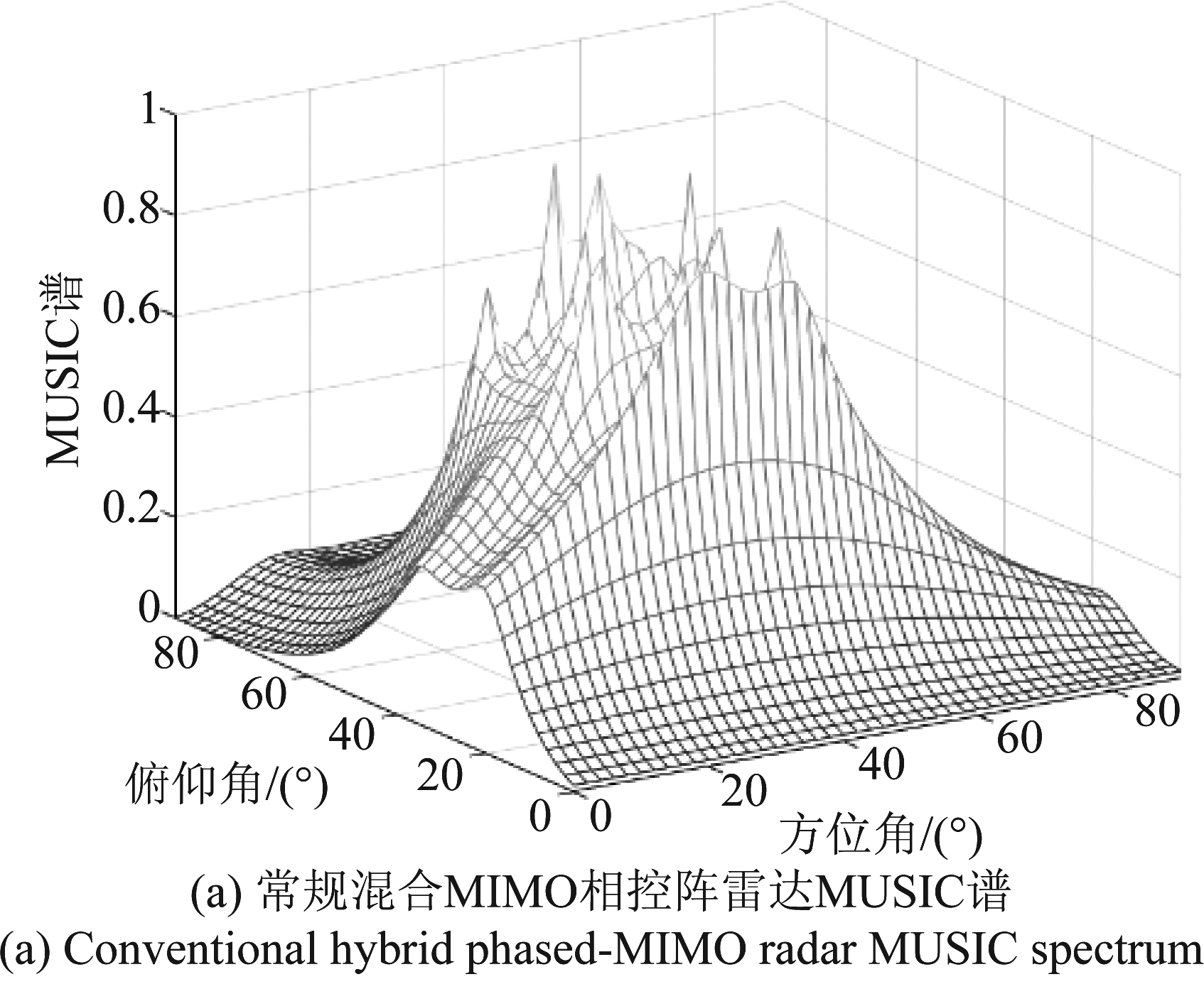
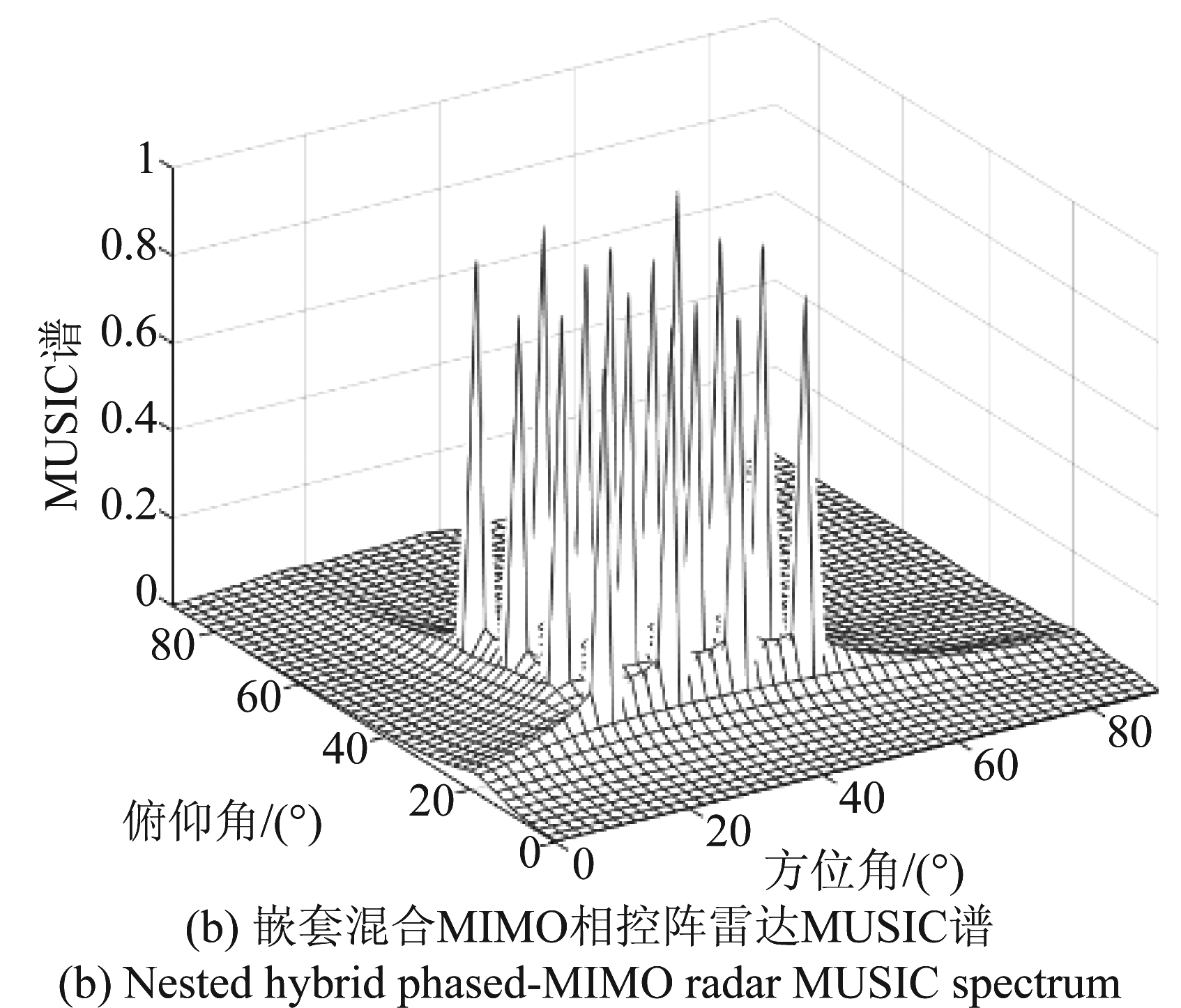
图4 对16个信源进行DOA估计的MUSIC谱图
Fig.4 MUSIC spectrum of DOA estimation for 16 sources
从MUSIC谱中已经可以看出,我们提出的二维混合MIMO相控阵雷达与传统的二维混合MIMO相控阵雷达的谱峰相比,更加清晰和准确。为了进一步验证本文所提方法的自由度扩展性能,我们继续增加信源数量,对均匀分布在方位角20°～60°,俯仰角20°～60°的正方形区域内的25个非相干目标,和均匀分布在方位角20°～70°,俯仰角20°～70°的正方形区域内的36个非相干目标进行估计。并在方位角40°的平面上,对所得的MUSIC谱做截面,如图5所示。
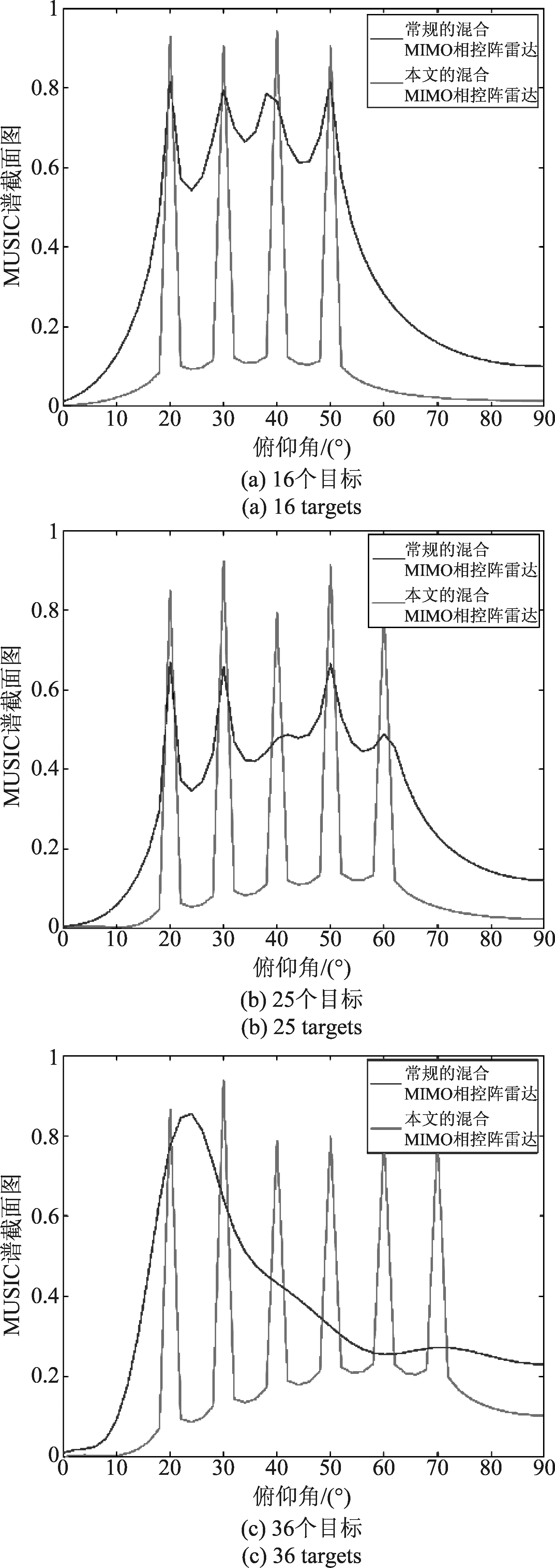
图5 不同目标个数下MUSIC谱截面图
Fig.5 MUSIC spectrum cross-section of different target numbers
结合谱估计的三维图和截面图可以清楚的看出:传统的二维混合MIMO相控阵雷达对应的谱峰较模糊,且出现了局部的混叠和失真,估计的结果不甚理想;与此相反,嵌套的二维混合MIMO相控阵雷达较为正确地估计出了所有的目标,估计结果的谱峰清晰完整,仅在谱峰底部也产生了轻微的混叠,这是由于经过流形矩阵的扩展后,虚拟通道之间噪声已不独立,对目标DOA估计精度会产生较小的影响。(在做MUSIC谱归一化处理时,谱峰最高点不一定在方位角40°的平面上,因此MUSIC谱的截面图最大值并非是1)。
为了更加精确地对比本文所提的嵌套混合MIMO相控阵雷达的估计精度,对空间16个目标进行DOA估计,并比较二者的DOA估计的均方根误差(root-mean-square error,RMSE),取蒙特卡洛数为100。结果如图6所示。
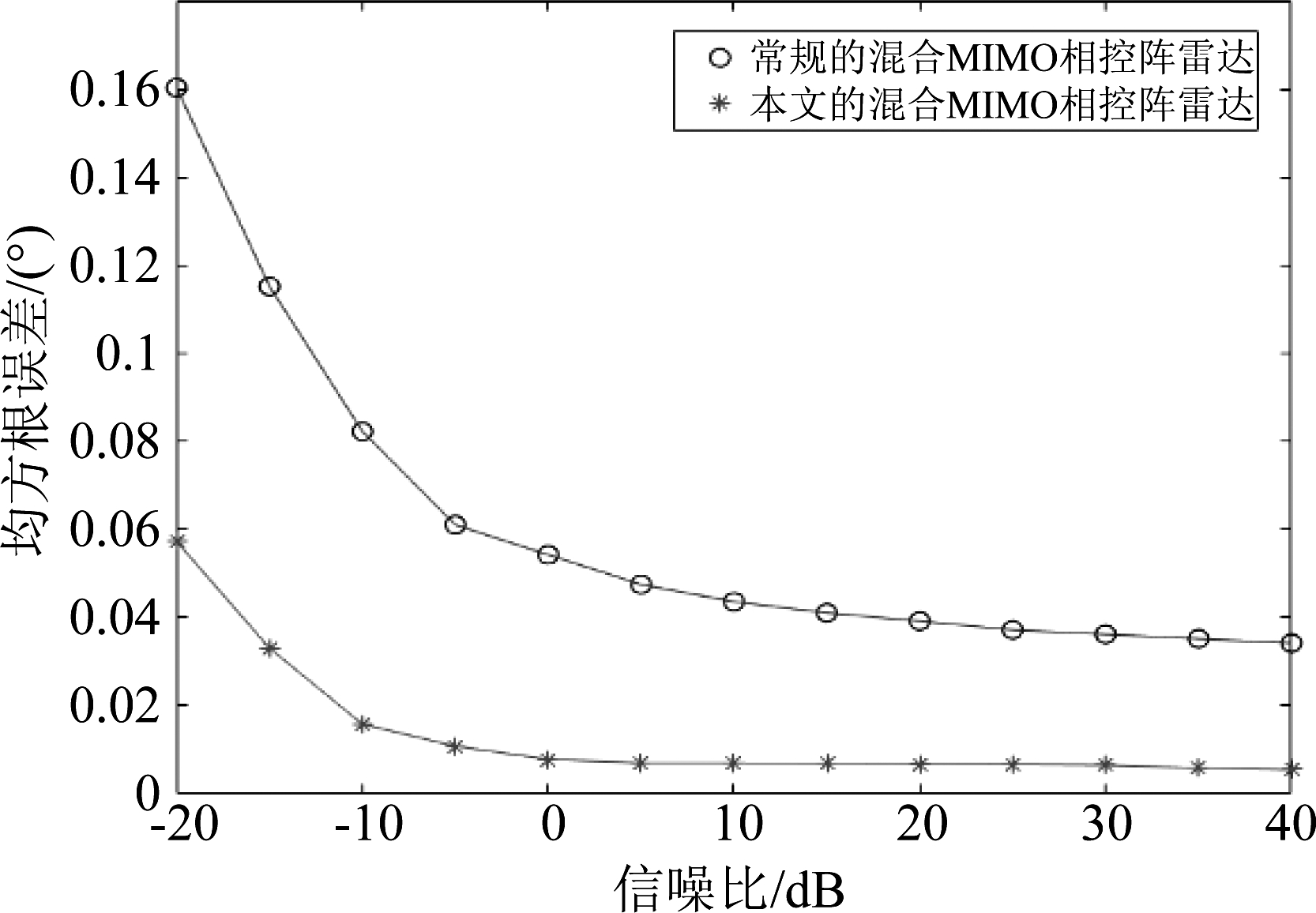
图6 RMSE对比图
Fig.6 RMSE comparison chart
可以看出:在信噪比-20 dB到40 dB的范围内,传统的混合MIMO相控阵雷达的RMSE值均高于本文提出的L形嵌套混合MIMO相控阵雷达。原因在于:“无孔”的差异阵列增大了雷达阵列的虚拟孔径,因此L形嵌套的混合MIMO 相控阵与传统阵列相比,在阵元数目以及空间目标相同的情况下, DOA估计效果更佳。综上所述,可以认为本文提出的L形嵌套的混合MIMO相控阵雷达设计方法,能够提高雷达阵列虚拟孔径,进而提高阵列自由度,实现更高数目的空间目标估计,获得更优的DOA估计性能。
6 结论
本文利用收发L形结构和嵌套阵的性质,提出了一种基于嵌套阵的L形混合MIMO相控阵雷达阵列设计方法,通过两个一维的线阵实现了二维混合MIMO相控阵雷达的功能。而且,由于嵌套阵形成的差异阵列是均匀密集分布的,我们推导出了阵列流形的矩阵形式,证明了与传统的混合MIMO相控阵雷达结构相比,我们提出的这种基于L形嵌套的混合MIMO相控阵雷达能够更好地扩展阵列孔径和自由度,且拥有更好的DOA估计性。
[1] Hassanien A, Vorobyov S A. Phased-MIMO radar: A Tradeoff Between Phased-Array and MIMO Radars[J]. IEEE Transactions on Signal Processing, 2010, 58(6): 3137-3151.
[2] Fishler E, Haimovich A, Blum R, et al. MIMO Radar: An Idea Whose Time Has Come[C]∥Radar Conference, 2004. Proceedings of the IEEE, 2004: 71-78.
[3] Li J, Stoica P. MIMO Radar with Colocated Antennas[J]. IEEE Signal Processing Magazine, 2007, 24(5): 106-114.
[4] Hassanien A, Vorobyov S A, Yoon Y S, et al. Two-Stage Based Design for Phased-MIMO Radar with Improved Coherent Transmit Processing Gain[C]∥Signal Processing Advances in Wireless Communications(SPAWC), 2014 IEEE 15th International Workshop on, 2014: 45- 49.
[5] Deligiannis A, Lambotharan S, Chambers J A. Beamforming for Fully-Overlapped Two-Dimensional Phased-MIMO radar[C]∥Radar Conference(RadarCon), 2015 IEEE, 2015: 0599- 0604.
[6] Liu C L, Vaidyanathan P P. Optimizing minimum redundancy arrays for robustness[C]∥2018 52nd Asilomar Conference on Signals, Systems, and Computers. IEEE, 2018: 79- 83.
[7] Kirschner A, Detlefsen J, Mees W. Spatial Smoothing for Coherent MIMO Radar Setups with Minimum Redundancy[C]∥Microwave Conference(GeMiC), 2016 German. IEEE, 2016: 255-258.
[8] Li J F, Jiang D F, Zhang X F. DOA Estimation Based on Combined Unitary ESPRIT for Coprime MIMO Radar[J]. IEEE Communications Letters, 2017, 21(1): 96-99.
[9] Liu C L, Vaidyanathan P P. Two-Dimensional Sparse Arrays with Hole-Free Coarray and Reduced Mutual Coupling[C]∥Signals, Systems and Computers, 2016 50th Asilomar Conference on. IEEE, 2016: 1508-1512.
[10]Raza A, Liu W, Shen Q. Thinned Coprime Array for Second-Order Difference Co-Array Generation With Reduced Mutual Coupling[J]. IEEE Transactions on Signal Processing, 2019, 67(8): 2052-2065.
[11]Piya P, Vaidyanathan P P. Nested array: A Novel Approach to Array Processing with Enhanced Degrees of Freedom[J]. IEEE Transactions on Signal Processing, 2010, 58(8): 4167- 4181.
[12]Piya P, Vaidyanathan P P. Nested Arrays in Two Dimensions, Part I: Geometrical Considerations[J]. IEEE Transactions on Signal Processing, 2012, 60(9): 4694- 4705.
[13]Liu C L, Vaidyanathan P P. Super nested arrays: Linear sparse arrays with reduced mutual coupling—Part I: Fundamentals[J]. IEEE Transactions on Signal Processing, 2016, 64(15): 3997- 4012.
[14]Liu C L, Vaidyanathan P P. Super nested arrays: Linear sparse arrays with reduced mutual coupling—Part II: High-order extensions[J]. IEEE Transactions on Signal Processing, 2016, 64(16): 4203- 4217.
[15]Mao L L, Li H B, Zhang Q F. Transmit Subaperturing for MIMO Radars with Nested Arrays[J]. Signal Processing, 2017, 134: 244-248.
[16]Yang M L, Sun L, Yuan X, et al. A New Nested MIMO Array With Increased Degrees of Freedom and Hole-Free Difference Coarray[J]. IEEE Signal Processing Letters, 2018, 25(1): 40- 44.
[17]陈璐, 毕大平, 潘继飞. 平移嵌套阵列稀疏贝叶斯学习角度估计算法[J]. 电子与信息学报, 2018, 40(5): 1173-1180.
Chen Lu, Bi Daping, Pan Jifei. A Direction of Arrial Estimation Algorithm for Translational Nested Array Besed on Sparse Bayesian Learning[J]. Journal of Electronics & Information Technology, 2018, 40(5): 1173-1180.(in Chinese)
[18]Zhu C L, Chen H, Shao H Z. Joint Phased-MIMO and Nested-Array Beamforming for Increased Degrees-of-Freedom[J]. International Journal of Antennas and Propagation, 2015: 1-11.
[19]刘帅琦, 王布宏, 李夏, 等. 二维嵌套混合 MIMO 相控阵雷达接收阵列设计[J]. 航空学报, 2018, 39(4): 173-181.
Liu Shuaiqi, Wang Buhong, Li Xia, et al. Design of Receiving Array of Two-Dimensional Nested Hybrid Phasd-MIMO Radar[J]. Acta Aeronautica et Astronautica Sinic, 2018, 39(4): 173-181.(in Chinese)
[20]Liu C L, Vaidyanathan P P. The Role of Difference Coarrays in Correlation Subspaces[C]∥Signals, Systems, and Computers, 2017 51st Asilomar Conference on. IEEE, 2017: 1173-1177.
[21]Alieldin A, Huang Y, Saad W M. Optimum Partitioning of a Phased-MIMO Radar Array Antenna[J]. IEEE Antennas and Wireless Propagation Letters, 2017, 16: 2287-2290.
[22]Liu C L, Vaidyanathan P P. Robustness of difference coarrays of sparse arrays to sensor failures—Part I: A theory motivated by coarray MUSIC[J]. IEEE Transactions on Signal Processing, 2019, 67(12): 3213-3226.
[23]徐峰, 薛珺亓, 杨小鹏. 相控阵 MIMO 雷达抗干扰波束形成算法[J]. 信号处理, 2017, 33(12): 1531-1535.
Xu Feng, Xue Junqi, Yang Xiaopeng. Phased-MIMO Radar Anti-jamming Beamforming Algorithm[J]. Journal of Signal Processing, 2017, 33(12): 1531-1535.(in Chinese)
