1 引言
舰船海底地震波是由舰船航行引起的振动、噪声和水体扰动以压力波的形式经流体介质传播到海底,进而引起海底介质的振动,在海底界面和海底以弹性波的形式向周围传播[1]。由于舰船地震波信号的成分集中于低频段,其具有受水文环境影响小、传播距离远、震动幅度大等特点,是近年来水雷引信中使用的较为新型的舰船物理场[2]。
目前,俄、美两国已经在水雷引信系统中使用舰船地震波场联合其他物理场对目标进行检测和识别,但出于保密,其相关技术并未公开报道。国内的研究主要集中于解释舰船海底地震波形成机理和传播规律上[3-5],例如,海军工程大学颜冰、卢再华等人分析了舰船地震波的形成机理,研究了其在不同海底介质中传播特性;中国科学院声学研究所张建民等人研究了海底不同介质参数对舰船地震波信号传播的影响[6-7];朱旭芳等人就舰船地震波信号的数值建模进行研究,获得一定的结果[8]。对于舰船地震波信号的应用,国内也取得一定研究成果,文献[9]中初步探讨了舰船地震波信号用于舰船目标检测的可行性,文献[10]基于舰船地震波信号的频域特点,利用短时傅里叶变换进行检测,而沈阳理工大学将海底地震波解释为Schulte波[11],利用该波特点对海底地震波信号进行识别。
舰船地震波的频率特性主要取决于舰船低频辐射声场,其中舰船辐射噪声主要是由舰船的机械噪声、螺旋桨噪声和水动力噪声组成。一般来说,目标船的辐射噪声,不仅会产生宽带的连续谱,也会产生具有窄带的线谱成分,其中线谱能量稳定,适合用来对舰船目标进行检测。舰船地震波信号具有类似的线谱特点,但是舰船地震波信号是一种非平稳信号,小波变换在分析非平稳信号时能获得比传统傅里叶变换更显著的效果,文献[12]中首次运用了小波变换对舰船地震波信号进行分析,只探讨了小波变化在特征提取中的优势,并未研究具体的舰船地震波信号检测算法。
因此,本文将根据舰船地震波的线谱特点,首先利用小波能量谱分析方法对信号进行处理,然后提出一种基于滑动小波能量谱的舰船地震波信号实时检测算法。
2 尺度-小波能量谱原理
设φ(t)为平方可积函数,即φ(t)∈L2(R),如果其傅里叶变换ψ(ω)满足容许条件:
![]()
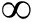
(1)
则φ(t)称为母小波[18],将φ(t)进行伸缩和平移变换,设其伸缩因子(尺度因子)为a,平移因子为b,可得到一组函数φa,b(t):
(2)
φa,b(t)称为小波基函数。
给定平方可积的信号f(t),则f(t)的连续小波变换定义为:
(3)
式中,a、b和t均是连续变量。
定义|WTf(a,b)|2为信号的尺度图,它是随尺度a与位移b的能量分布。根据小波变换系数的幅值平方在(a,b)平面上的加权积分等于信号在时域的总能量,有下式成立:
(4)
将![]() 看作(a,b)平面的能量密度函数,则:
看作(a,b)平面的能量密度函数,则:
(5)
E(a)=![]() |WTf(a,b)|2db
|WTf(a,b)|2db
(6)
式中,E(a)反映了信号的能量沿尺度方向的分布情况[12-13],定义为尺度-小波能量谱。
现对两种货船(记为A,B货船)实测的地震波信号进行尺度-小波能量谱求解,该数据是在汉江某处由地震波采集系统(采集加速度矢量)测量获得,试验时采样频率为460 Hz,周围无明显的工业噪声污染,测量目标为江上正在行进的货船,航速大约为10 kn,沿水流方向直线行驶。
如图1和图2为实测的地震波信号,从图中可知当舰船经过测量系统时,加速度有明显的幅度变化。文献[13]中对舰船地震波信号的时频进行分析,指出舰船地震波信号在垂直方向上的检测距离最远,频域线谱衰减时间长。因此,截取两艘货船az方向加速度数据中的一段,如图1(c)和图2(c)中的红色框中的一段数据,分别进行尺度-小波能量谱分析。
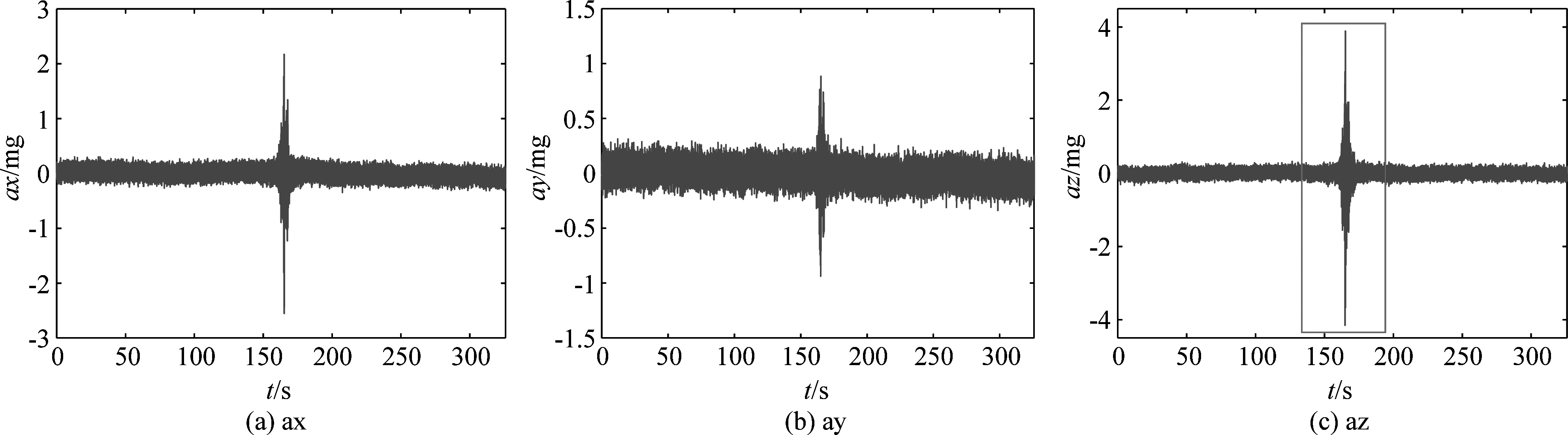
图1 实测A货船地震波数据
Fig.1 Three-axis measured A-cargo ship seismic wave data
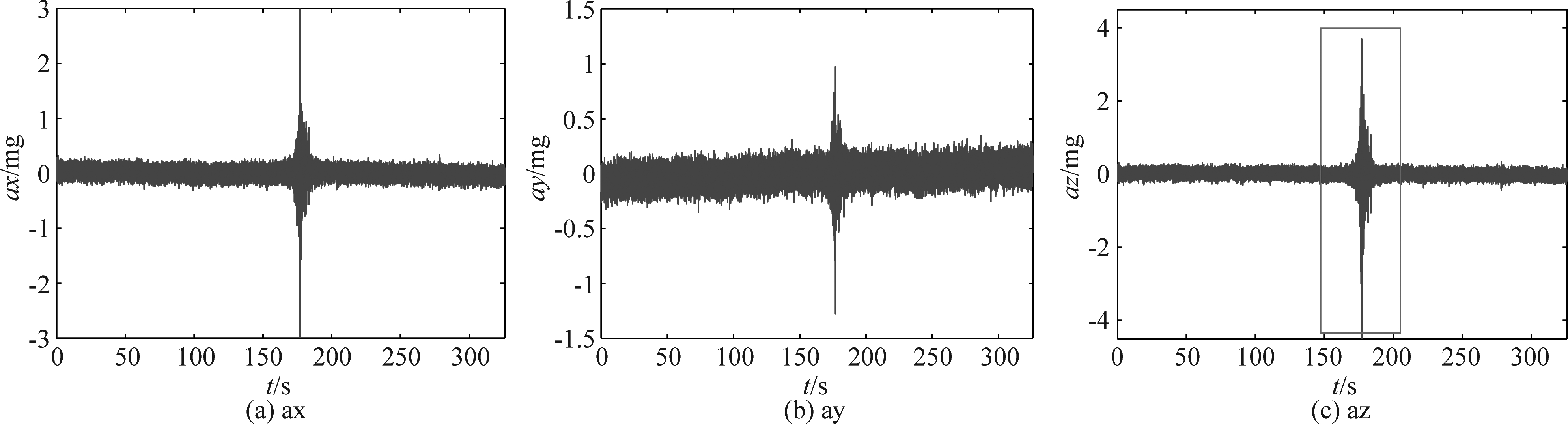
图2 实测B货船地震波数据
Fig.2 Three-axis measured B-cargo ship seismic wave data
采用Morlet小波基函数求解不同速度的舰船地震波小波能量谱,小波变换时尺度范围为1~128,步长为1,即a=j, j=1,2,……128,对az进行小波能量谱分析,得到结果如图3所示。

图3 两种货船尺度-小波能量谱
Fig.3 Two cargo ship scales-wavelet energy spectrum
从图3中可知,信号能量集中于6~15尺度之内,这符合舰船地震波信号的频域特性。因此,可以选取尺度6~15内的能量作为检测特征量。
3 基于滑动小波能量谱的实时检测算法
3.1 构造检测特征量
由上面分析可知,舰船海底地震波信号集中于尺度6~15之间,因此,可利用信号的这个特点构造检测特征量,对舰船目标进行检测。
构造检测特征量如下:
(7)
式中,Ei(a)为i时刻的尺度-小波能量谱,N1和N2为选取的特征尺度范围,当进行1~128尺度分解时,N1~N2为1~20。
3.2 实时检测算法
基于上述构造的特征量,利用滑动窗可获得滑动小波能量谱舰船地震波信号实时检测算法,检测时,设置检测阈值,当特征量连续多次大于检测阈值时,判断有信号出现,算法的原理框如图4所示。
图4 舰船地震波信号实时检测算法
Fig.4 The detection algorithm of seismic wave signal
算法的具体步骤如下:
(1)尺度-能量谱计算。利用滑动窗W截取一段数据,对该段数据求解尺度-小波能量谱
(8)
其中,
(9)
式中,m,n=1,2,…,N,N为采样点数,ΔT为采样间隔。
(2)特征提取。提取N1~N2尺度内的能量,按照式(8)、式(9)计算i时刻特征量。
(3)阈值确定。从初始时刻开始,选取本时刻i之前的K个特征量平均值作为基阈值U0(i),后期可根据实际情况利用阈值调整因子μ(>1)进行调整,即
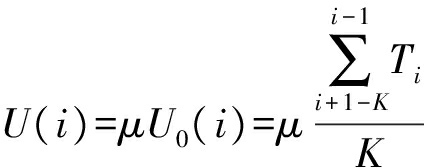
(10)
(4)目标检测。从初始时刻开始,若从i时刻起连续3次特征量大于阈值,即当Ti>Ui-1、Ti+1>Ui、且Ti+2>Ui+1时,则判定存在目标信号。
4 算例
4.1 实测算例
根据上述的地震波信号实时检测算法,对两种货船实测的数据进行试验,试验时按照算法步骤进行,其中数据滑动窗窗长N为1024、步长L为460,即每秒更新1次特征量,阈值调整窗口K为60,阈值调整参数μ为1.5。
检测的结果如图5~图6所示,图5为A货船的检测结果,图6为B货船检测结果,从两张图中可以看出,当目标接近测量系统时,特征量均发生较为明
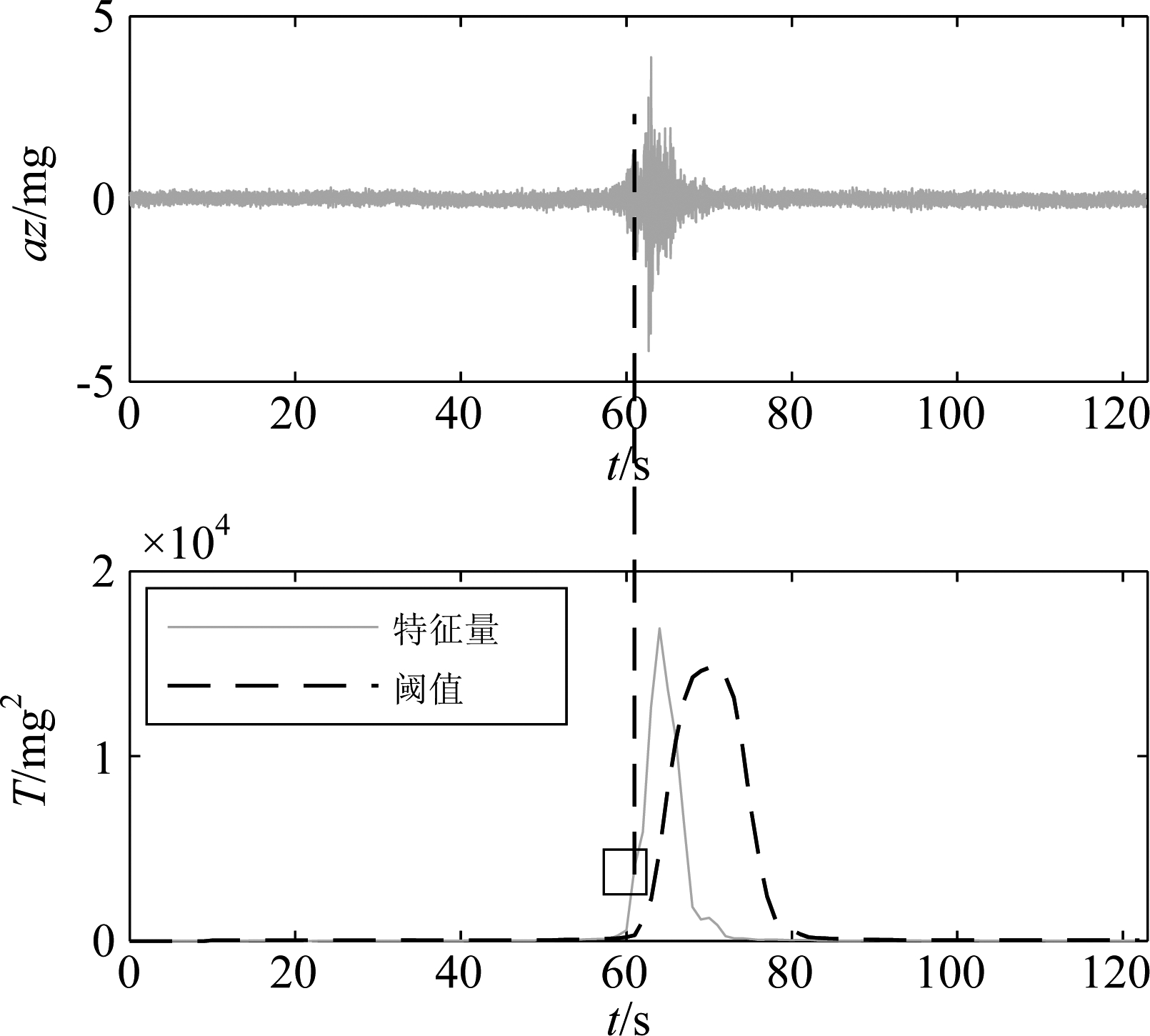
图5 A货船检测结果
Fig.5 The detection results of A cargo ship

图6 B货船检测结果
Fig.6 The detection results of B cargo ship
显的变化,两张图中的‘□’为信号检测到的时刻点,竖直虚线为检测点的对应时刻,A货船中心大约在64 s左右通过,B货船中心大约在66 s左右通过,从图5~图6中可知, A货船在61 s时检测到了目标,B货船在63 s时检测到了目标,检测时刻均在目标中心经过正横位置之前,且A货船在经过前3 s完成,B货船在前3 s完成,由试验时货船的速度大约为13 kn,换算获得检测的距离大约在20 m,该作用距离基本能够满足水雷的作战需求。
从上述结果可知,本文所提出的检测算法能够有效检测地震波信号,且其检测时刻点都在目标中心经过正横之前,具有较好的实时性。
4.2 仿真算例
4.1节中所用的实测数据信噪比较高,所以检测效果较为明显,而现实应用中信噪比往往无法控制,因此还需验证算法在低信噪比条件下的是否有效。由于实测时没有获得信噪比低的数据,现截取第1节中A货船Z方向上的一段实测数据叠加背景噪声代替低信噪比数据。
第2节中截取的Z方向上的数据长度为21 s,目标中心通过时刻大约在9 s处。现假设环境背景噪声的长度为180 s,将目标信号每隔10 s叠加到其中,可叠加6段目标信号。环境背景可用高斯白噪声代替,其大小根据设定的信噪比SNR来计算,信噪比SNR的计算公式为10log(信号时域峰-峰值/环境背景噪声峰-峰值)。
仿真时,将信噪比设置为-10 dB,如图7,为叠加前后的地震波信号,从图中可以看出,目标信号完全被淹没在背景噪声中。下面对仿真信号进行试验(检测参数按照3.1中设置)。
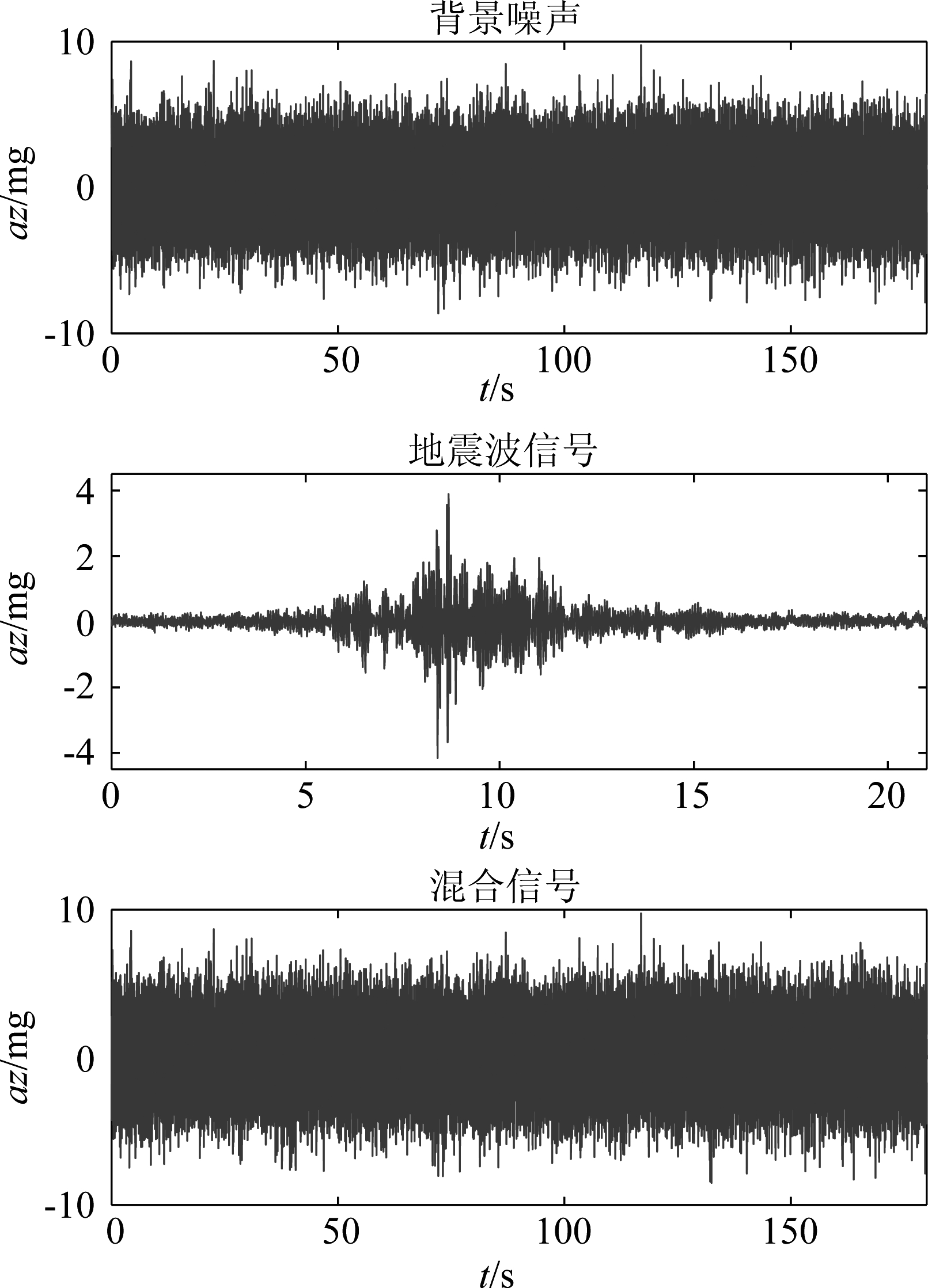
图7 仿真信号
Fig.7 Simulated signal
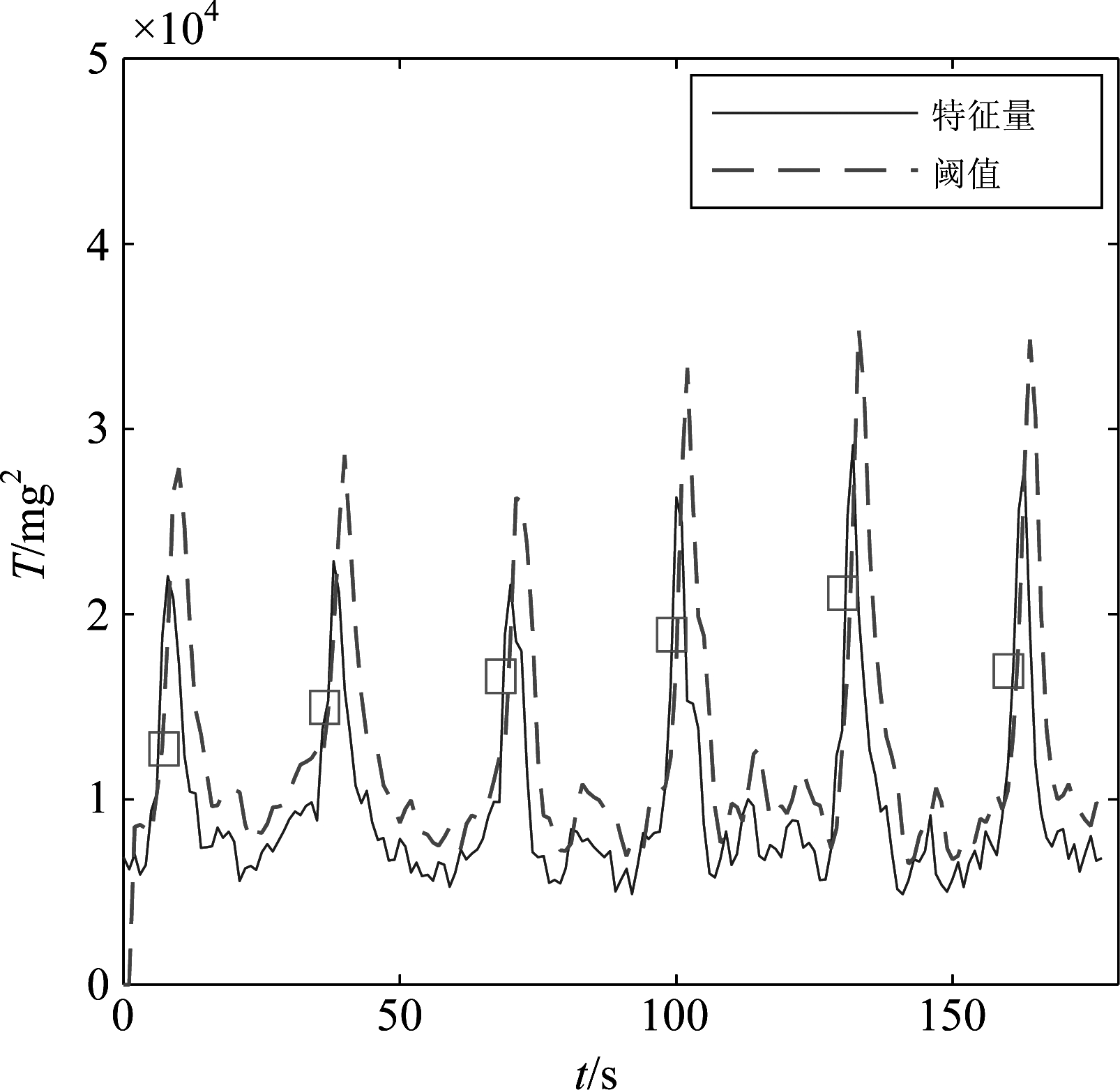
图8 仿真信号检测结果
Fig.8 The detection results of simulated signal
利用本文提出的检测算法进行检测,检测结果如图8所示,图中‘□’为检测点,从图中可以看出,在目标出现处特征量都有明显的变化,且算法能够检测到目标信号。表1中列出了检测点和目标中心通过时刻,从表1中可知,在目标中心通过之前就能够完成对目标的检测,具有较好的实时性。
为计算检测算法在低信噪比情况下的检测概率,现按表2中信噪比生成仿真数据,各信噪比数据段中存在100段目标信号。目前,公开文献中仅有文献[10]给出了具体检测算法,因此,同时用本文方法和文献中的方法进行检测,检测结果如表2所示,从表中可知,在信噪比为-20 dB时,信号的检测概率大约为85%,信噪比为-15 dB时检测概率大约
表1 仿真信号检测时间
Tab.1 The detection time of simulated signal
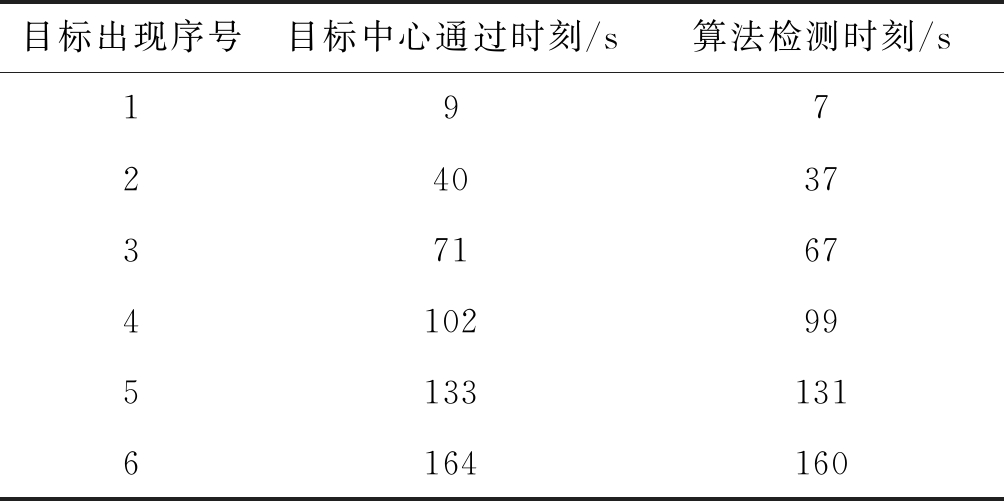
目标出现序号目标中心通过时刻/s算法检测时刻/s197240373716741029951331316164160
为96%,若信噪比大于-10 dB,检测概率为100%。对比文献[10]中的检测算法,可知,本文检测算法较该检测算法具有较大的提升,尤其是低信噪比时,如表2中SNR为-15 dB和-20 dB,本文算法检测概率能够达到96%和85%,而文献[10]中的算法检测概率极低,还容易出现虚警,造成这种结果的原因有两点:第一点是文献[10]中的算法是基于平稳信号傅里叶变换的时频信号分析,而目标地震波信号是一种非平稳信号;第二点是该算法中构造的检测特征量局限性问题,对应的检测阈值是人为的根据经验确定的,当背景信号发生改变时,由于其阈值是固定值,导致检测概率降低,虚警概率上升。
因此,由仿真结果可以判断,本文提出的检测地震波信号检测算法在较低的信噪比环境中仍具有较高的检测概率,较目前的检测算法具有较大的提升,在信噪比为-15 dB时,本文检测算法的检测概率是原来检测算法的检测概率的7.4倍。
表2 不同信噪比下的检测结果
Tab.2 The Detection results of different SNR
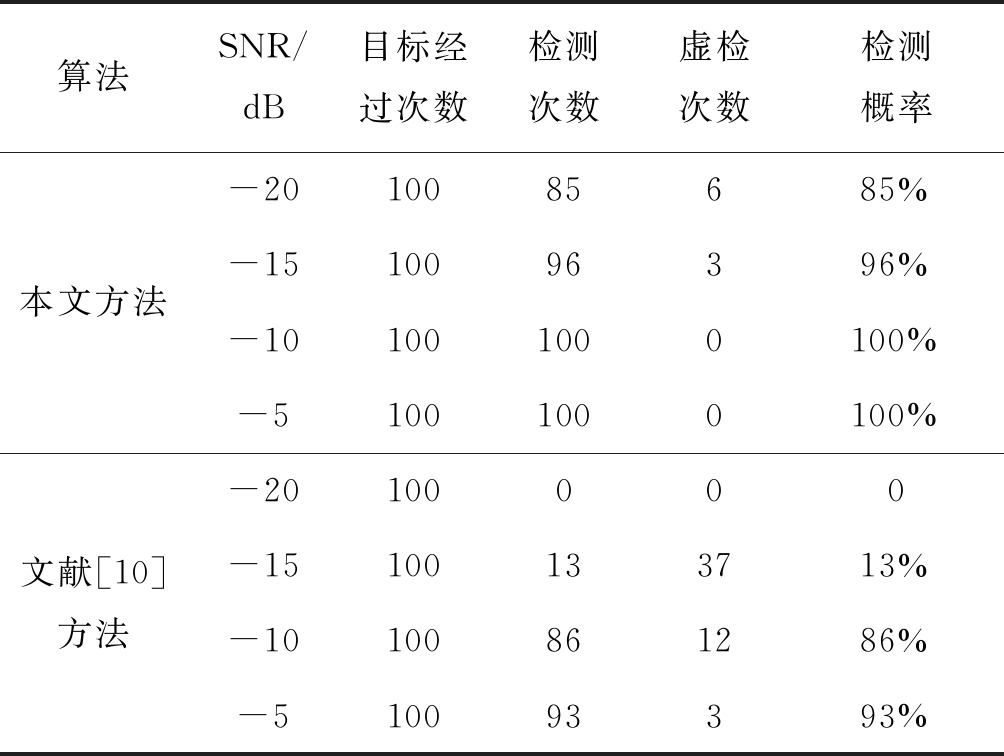
算法SNR/dB目标经过次数检测次数虚检次数检测概率本文方法-2010085685%-1510096396%-101001000100%-51001000100%文献[10]方法-20100000-15100133713%-10100861286%-510093393%
5 结论
本文利用舰船地震波信号的频域低频线谱信号特点,提出基于滑动小波能量谱的舰船地震波检测算法,重点研究地震波信号在尺度-小波谱中的特点和实时检测特征量提取。通过实测和仿真数据试验表明:舰船地震波信号在小波能量谱中具有较为明显的特点,能量集中在一段尺度之间;本文所提的地震波信号实时检测算法能够有效地实时对目标信号进行检测,且在信噪比为-15 dB时,检测概率达到96%,较原有的检测算法,本文方法在低信噪比情况下具有绝对的优势。
本文在验证检测算法和计算检测概率时,利用的是在汉江岸边所测数据,目标为普通的货船,对于应用于水雷中的地震波引信应该考虑接收的是舰船海底地震波信号。因此,为进一步验证算法,接下来将进行海底舰船目标检测试验。
[1] 孟路稳, 程广利, 陈亚男, 等. 舰船地震波传播机理及其在水雷引信中的应用研究[J]. 兵工学报, 2017, 38(2): 319-325.
Meng Luwen, Cheng Guangli, Chen Yanan, et al. On the Porpogation Mechanism of Ship Seismic Wave and Its Application in Mine Fuze[J]. Acta Armamentarii, 2017, 38(2): 319-325.(in Chinese)
[2] 董立, 张健, 郭策安, 等. 地震波引信设计方案的探讨[J]. 探测与控制学报, 2008, 30(5): 4- 6.
Dong Li, Zhang Jian, Guo Cean, et al. Research on design scheme for seismic wave fuze[J]. Journal of Detection&Control, 2008, 30(5): 4- 6.(in Chinese)
[3] 颜冰, 周伟, 龚沈光. 浅海地震波传播的简正波模型[J]. 武汉理工大学学报, 2006, 30(5): 804- 807.
Yan Bing, Zhou Wei, Gong Shenguang. A normal mode model for ocean seismo-acoustics in shallow water[J]. Wuhan University of Technology, 2006, 30(5): 804- 807.(in Chinese)
[4] 卢再华, 张志宏, 顾建农. 砂土底质浅水条件下实船地震波的检测试验[J]. 兵工学报, 2016, 37(3): 482- 488.
Lu Zaihua, Zhang Zhihong, Gu Jiannong. A detecting test of seismic waves caused by random ships in shallow water with sandy bottom[J]. Acta Armamentarii, 2016, 37(3): 482- 488.(in Chinese)
[5] 卢再华, 张志宏, 顾建农. 多孔介质水平分层海底低频地震波的数值模拟[J]. 兵工学报, 2014, 35(12): 2065-2071.
Lu Zaihua, Zhang Zhihong, Gu Jiannong. A numerical simulation of seismic wave caused by low frequency source in shallow sea with thick porous sediment by staggered-grid finite difference method[J]. Acta Armamentarii, 2014, 35(12): 2065-2071.(in Chinese)
[6] 李响, 颜冰. 舰船地震波场分析[J]. 噪声与振动控制, 2007(4): 120-122.
Li Xiang, Yan Bing. Wavelet Spectrum Analysis of Ship Seismic wave Field[J]. Noise and Vibration Control, 2007(4): 120-122.(in Chinese)
[7] 张建民, 安俊英. 海底衰减系数对舰船地震波的影响[J]. 声学与电子工程, 2018(4): 37- 40.
Zhang Jianmin,An Junying. The influence of attenuation coefficient of seafloor on seismic wave of ship[J].Acoustics and Electronics Engineering,2018(4):37- 40. (in Chinese)
[8] 朱旭芳, 颜冰, 马知远. 浅海舰船地震波场仿真中的边界处理[J]. 国防科技大学学报, 2018, 40(2): 85-90.
Zhu Xufang, Yan Bing, Ma Zhiyuan. Boundary disposing method of ship seismic wave field simulation in shallow sea[J]. Journal of National University of Defense Technology, 2018, 40(2). 85-90. (in Chinese)
[9] 陈云飞, 吕俊军, 于沨. 航行舰船地震波及其在水中目标探测中的应用[J]. 舰船科学技术, 2005, 27(3): 62- 66.
Chen Yunfei, Lü Junjun, Yu Feng.The ship induced seismic wave and it’s application in the underwater target detection[J]. Ship Science and Technology, 2005, 27(3): 62- 66.(in Chinese)
[10]马剑飞, 颜冰, 陈春行, 等. 基于RI-ALE-MUSIC的舰船地震波时频检测[J]. 振动与冲击, 2018, 37(13): 224-228.
Ma Jianfei, Yan Bing, Chen Chunhang, et al. Time-frequency detection for ship seismic wave based on RI-ALE-MUSIC[J]. Jouranl of Vibrantion and Shock, 2018, 37(13): 224-228.(in Chinese)
[11]邵雨新, 李环, 张自圃, 等. 浅海舰船地震波中Scholte波识别技术研究[J]. 沈阳理工大学学报, 2017, 36(3): 32-37.
Shao Yuxin, Li Huan, Zhang Zipu, et al. Research on Recognition of Scholte Wave in Shallow Sea Ship Seismic Wave[J]. Journal of Shenyang Ligong University, 2017, 36(3): 32-37.(in Chinese)
[12]李响, 颜冰. 小波谱在舰船地震波场分析中的应用[J]. 振动与冲击, 2008(4): 155-158, 177.
Li Xiang, Yan Bing. Application of wavelet spectrum and wavelet coherence in ship’s seismic-wave field[J]. Journal of Vibration & Shock, 2008(4): 155-158, 177.(in Chinese)
[13]Rioul O, Veterli M. Wavelet and signal processing[J]. IEEE SP MAG., 1991(10): 14-38.
[14]程军圣, 于德介, 杨宇, 等. 尺度-小波能量谱在滚动轴承故障诊断中的应用[J]. 振动工程学报, 2004, 17(1): 82- 85.
Cheng Junsheng, Yu Dejie, Yang Yu, et al. Application of Scale-Wavelet Power Spectrum to Fault Diagnosis of Rolling Bearings[J]. Journal of Vibration Engineering, 2004, 17(1): 82- 85.(in Chinese)


