1 引言
鉴于风电产业的快速发展,风电场作为一种高大、运动障碍物对气象雷达的影响越来越突出[1- 4]。风电场杂波可能造成附近气象雷达对气象目标的误检测与误识别。气象雷达风电场杂波的电磁散射特性计算对于风电场选址、气象雷达风电场杂波特征提取及抑制具有重要意义。
对于风轮机雷达回波的分析,国内外学者进行了大量研究。Balleri A等人通过实地测量获取风轮机雷达回波[5],现场测量能够得到最真实的数据,但无法控制风轮机的运动,只能用于特定环境下的风电场杂波电磁散射特性分析,无法实现不同场景下的风电场杂波散射特性的描述。俞一鸣等人通过缩比模型分析叶片的电磁散射特性[6-9],但模型制作过程较为繁琐,制作成本较高且实验重复性差。Angulo等人利用物理光学法推导出了适用于金属桅杆的解析模型[10],并认为叶片与桅杆的散射面积存在对应关系,进而运用桅杆RCS解析模型预估叶片RCS,该方法未考虑材质对风轮机叶片RCS的影响,且只考虑了雷达视线与叶片旋转面垂直时的情况,该结果对雷达视线照射角度要求较高,不能表征大多数照射情况下风电场杂波的电磁散射特性。何炜琨等人利用电磁分析软件求解简化圆柱叶片的雷达回波特性[11],并在此基础上建立了等比例放大的真实叶片解析模型,但该解析模型未考虑叶片材质及形状对风轮机叶片RCS的影响。
本文在风轮机圆柱桅杆及简化圆柱叶片电磁散射特性解析模型的基础上,考虑叶片翼型对其RCS的影响,建立风轮机真实叶片三维模型,利用数值拟合的方法建立风轮机简化叶片与对应真实叶片RCS差值的解析模型,基于两者差值及简化叶片解析模型,构建高保真的风轮机真实叶片电磁散射特性解析模型,并利用WSR- 88D气象雷达二次回波数据验证文中所给出的解析模型的有效性。
2 风轮机叶片电磁散射特性对其整体RCS的占比分析
对于风轮机而言,其RCS主要由叶片和桅杆两部分组成,两部分由于材料及结构差异导致后向散射特性差别较大,不同俯仰照射条件下叶片RCS占风轮机总RCS的比例不同。首先对风轮机的叶片及桅杆进行三维建模,其中桅杆长55 m,材质为金属,叶片长19.9 m,材质为玻璃纤维复合材料(相对介电常数为4),雷达频率为2.7 GHz。其次基于物理光学法计算其在不同照射条件下的RCS,对计算结果进行分析并计算叶片RCS占比。
由不同俯仰角风轮机叶片散射特性占比分析(图1)可以看出,当雷达视线俯仰角为90°时叶片对雷达影响“最大”,故后续对叶片建立解析模型时俯仰角选择90°(即考虑“最坏”的情况)。图2是叶片RCS在不同俯仰角时其RCS随方位角的变化,可以看出俯仰角为90°时其RCS较大,此时方位角在150°~240°范围(叶片前缘)内时叶片RCS较大且变化相对平缓,因此本文主要考虑雷达视线照射叶片前缘情况下风轮机叶片解析模型的建立。
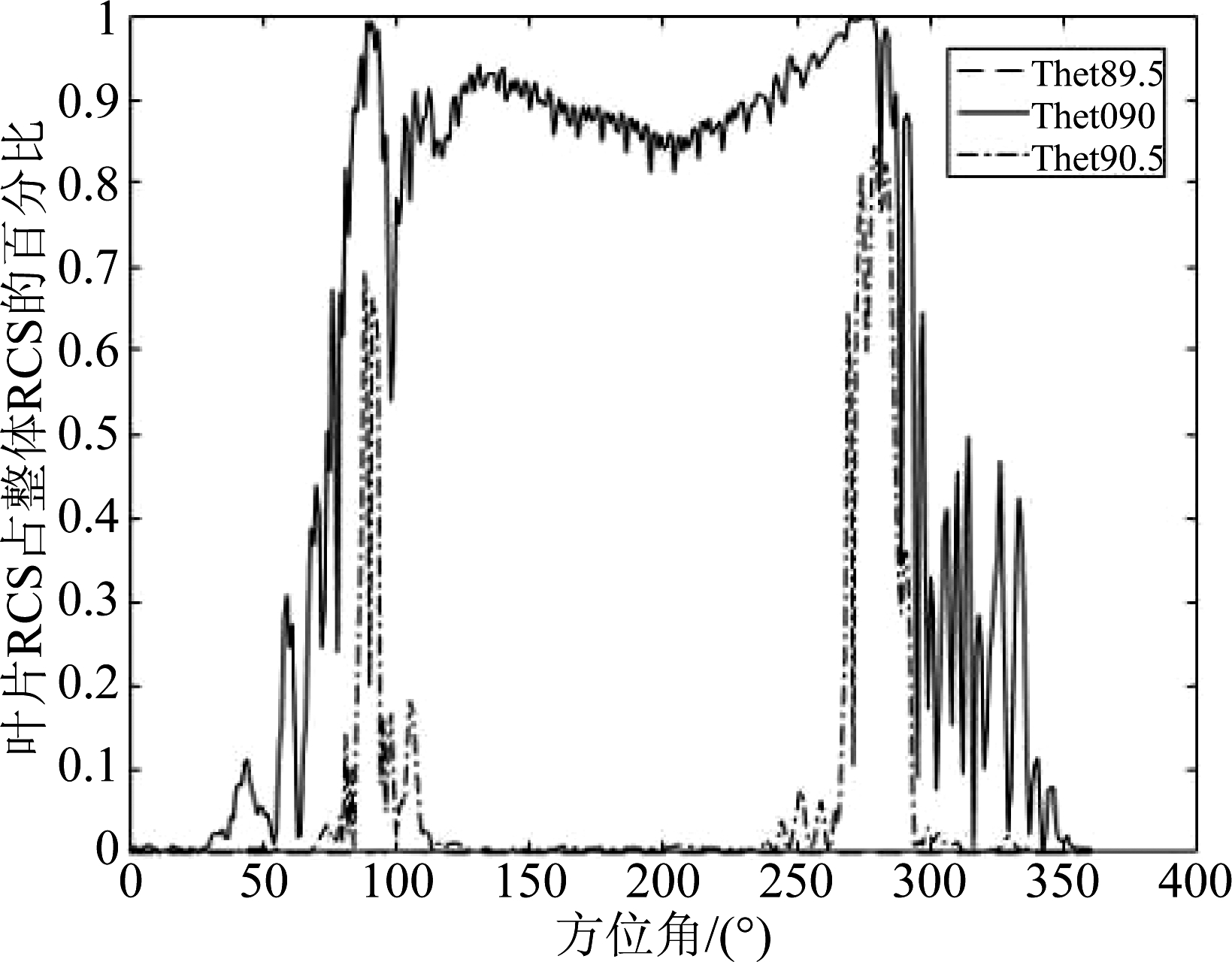
图1 不同俯仰角风轮机叶片散射特性占比分析
Fig.1 The proportion analysis of wind blade RCS with different pitch angles

图2 真实叶片RCS随方位角变化
Fig.2 RCS variation of real blade with azimuth angle
3 风轮机简化叶片解析模型的建立
由于叶片形状较为复杂,且不同厂家生产的风机叶片参数也存在一定差异,本文首先对简化圆柱叶片进行建模。在简化圆柱叶片模型建立时,其叶片长度等于真实叶片长,其截面直径为真实叶片的最大弦长。由简化圆柱叶片电磁特性的分析可知,叶片的RCS主要取决于叶片旋转面和雷达视线的相对位置,即与雷达照射的俯仰角及方位角有关。由于圆柱叶片散射特性的分析主要为后续真实叶片RCS的计算提供依据,故二者的雷达照射条件要保持一致,考虑雷达波束垂直照射风轮机叶片的一个边缘,即风轮机叶片RCS值最大的情况[11]。Grande O等人推导了此时理想圆柱导体RCS峰值解析公式[12],给出了理想圆柱导体RCS与其尺寸及雷达波长的关系。
在此基础上,通过改变雷达波长、风轮机叶片相对介电常数等参数,利用物理光学法计算不同介质简化圆柱叶片的RCS峰值,进而利用数值拟合对计算结果进行处理,可以得到简化圆柱叶片RCS与其材质、尺寸及雷达波长的关系,如式(1)所示[11]。
![]() ε2+0.04841*ε-0.06355)
ε2+0.04841*ε-0.06355)
(1)
式中,λ为雷达波长,r为圆柱叶片截面半径,H是叶片长度,ε是相对介电常数。
4 真实叶片模型的建立
为建立风轮机真实叶片模型,本文采用NACA- 4412翼型,分析叶片运行载荷并对其外形尺寸进行设计。基于坐标转换方法求出叶片各截面处的叶素坐标[13],利用UG建立叶片实体模型。UG在复杂曲线建模方面具有较大优势,其作为CAD产品设计中的主流软件,功能强大、设计过程快速方便,UG支持多种常用数据格式,如IGES,DXF/DWG,SAT等,可以很方便地与其他CAD设计软件和FEKO、ANSYS等电磁计算软件进行转换[14],因此本文通过UG使用叶素建模方法对风轮机叶片进行三维建模。
UG可以通过各叶素截面的三维坐标实现曲线三维建模。首先根据叶素截面三维坐标,在三维坐标系中建立点,其次将各离散点按序连成空间闭合曲线,得到叶素截面轮廓线,如图3所示。沿叶片展向也可以看出各叶素截面随扭转角的变化,如图4所示。
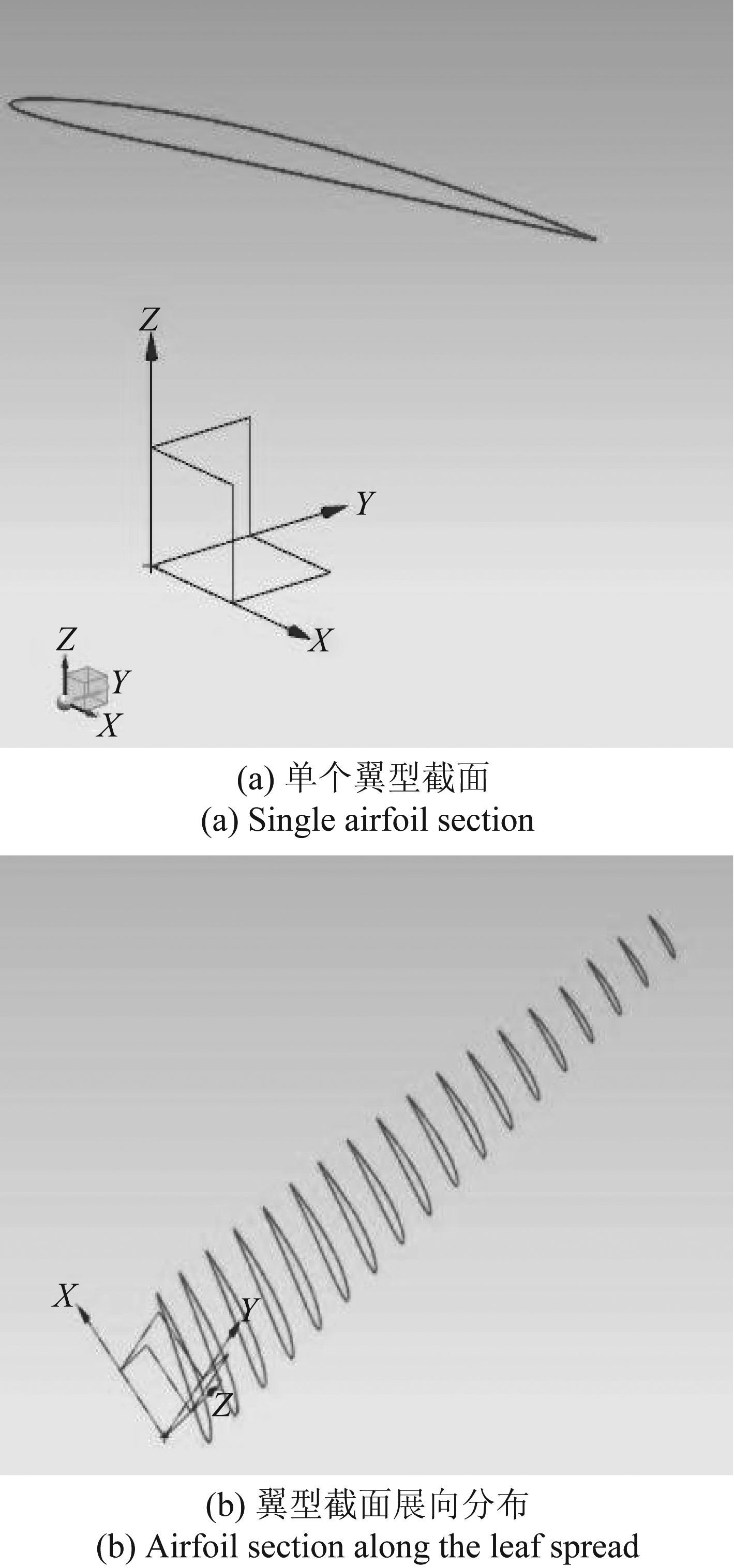
图3 翼型截面分布图
Fig.3 Airfoil section profile

图4 翼型截面随扭转角变化情况
Fig.4 Airfoil section changes with torsion angle
最后将上述各叶素截面轮廓线连起来生成实体,再对叶根处进行简化设计,得到单根叶片的三维模型,进而对单根叶片进行复制旋转得到风轮机叶片模型,如图5所示。将建模结果另存为IGES格式,将其导入FEKO等分析软件对其特性进行分析。

图5 真实叶片三维模型
Fig.5 Realistic blade 3D model
5 基于雷达散射截面积差值的真实叶片电磁散射特性解析模型
5.1 真实叶片与简化圆柱叶片雷达散射截面积差值
真实叶片的形状不规则,且不同型号的叶片参数相差较大,直接计算其RCS较为困难。考虑将圆柱叶片的电磁散射面积近似为矩形,其中矩形的长、宽分别等于圆柱叶片的叶长和截面直径,则圆柱叶片的散射面积可以表示为
Sm=2*r*H
(2)
式中,r为圆柱叶片截面半径,H为叶片长度。真实叶片电磁散射面积近似为三角形,三角形的高和底边分别为真实叶片长度及最大弦长。则真实叶片散射面积可表示为
(3)
依据圆柱叶片与真实叶片的对应关系,每一组叶片模型的面积差可表示为rH,考虑到真实叶片与简化叶片的面积差不一定完全被雷达照到,引入真实叶片的散射效率η,则该面积差可进一步写为
Sm-Sb=ηrH
(4)
式中,η取决于叶片扭曲Δβ,具体可表示为[10]
η=exp(-2.3Δβ)
(5)
Δβ是从叶根到尖端的总叶片扭曲,其取决于叶片长度和叶片的总体设计,在商用风轮机中,总叶片扭曲通常取为20°,在近似计算中η一般可以取0.5。
考虑雷达频率对RCS的影响,为此建立三组风轮机叶片模型进行分析,真实叶片参数与简化叶片参数一一对应,叶片长度对应相等,真实叶片最大弦长对应相应简化叶片的截面直径,叶片参数如表1中所示。利用物理光学法计算简化圆柱叶片和相应真实叶片的RCS,分析简化叶片与真实叶片雷达散射截面积差值随频率的变化,以文中三组模型为例,相对介电常数为4时,结果如图6所示。
由上述分析可以看出,简化叶片与真实叶片雷达散射特性的差值与叶片长度及雷达工作频率有关,会随着二者的增大而增大,为此本文考虑对上述散射特性差值进行数值拟合,将拟合结果与简化叶片RCS的解析模型相结合建立真实叶片RCS的解析模型。
表1 真实叶片模型参数
Tab.1 Model parameters of real blade
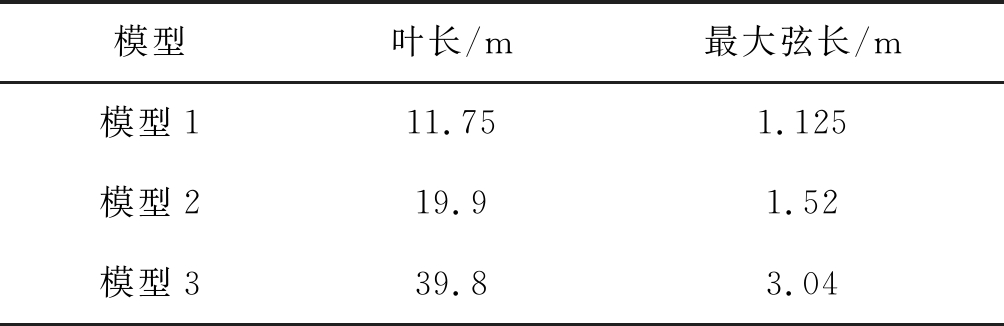
模型叶长/m最大弦长/m模型111.751.125模型219.91.52模型339.83.04

图6 雷达散射截面积差值随频率变化关系
Fig.6 Radar cross section variation with frequency
5.2 基于雷达散射截面积差值的真实叶片电磁散射特性解析模型
在简化叶片模型与真实叶片模型雷达散射截面积差值的基础上,进一步考虑叶片介电常数的影响。首先设置雷达频率,利用物理光学法计算不同介电常数时简化叶片与相应真实叶片的RCS数值,并将二者做差,以表1中第二组模型为例,当雷达照射频率为2.7GHz时,雷达散射截面积差值随相对介电常数的变化结果如表2所示。
表2 雷达散射截面积差值随相对介电常数的变化
Tab.2 Radar cross section variation with relative permittivity

介电常数23456差值/dB26.6030.5132.4233.6234.44
将差值数据导入数值拟合工具箱,利用多项式拟合模型,设定拟合阶次,得到雷达散射截面积差值的拟合结果,如式(6)所示。
![]() 4.560*10-3*ε2+7.39*10-4*ε-0.10415)
4.560*10-3*ε2+7.39*10-4*ε-0.10415)
(6)
其中, H表示真实叶片叶长,r等于叶片最大弦长的二分之一,ε为相对介电常数。则真实叶片的RCS可进一步写为
σr=σm-Δσ
(7)
其中,σm为简化圆柱叶片RCS,如式(1)所示。为验证上述真实叶片解析模型的准确性,利用物理光学法计算表1所示的三组真实叶片在2.7 GHz、4 GHz频率下的最大RCS,物理光学结果、解析模型计算结果与文献[11]计算结果如图7所示。由图7可以看出,雷达视线照射叶片前缘,即对应方位角在150°~240°范围内时,除极个别点外,本文解析模型与物理光学法得到的RCS差值基本控制在0~2 dB之间。

图7 真实叶片RCS峰值拟合结果
Fig.7 Peak RCS results of real blade
由图7可以看出,本文方法可以计算不同材质叶片在不同频率时的RCS,文献[11]给出的解析模型没有考虑叶片介电常数的影响,只给出了介电常数为4时等比例放大的真实叶片解析模型,可以看出文献方法只能在一定范围内估计叶片RCS,因其未考虑材质变化对叶片RCS的影响,本文解析模型的计算精度要高于文献计算的精度。
5.3 实测数据验证
采用美国WSR- 88D气象雷达风电场回波数据验证解析模型的合理性。选择分别位于美国德克萨斯州的KDYX气象雷达附近的Lone Star风电场和堪萨斯州的KDDC气象雷达附近的Dodge City风电场。通过谷歌地球可以获取雷达及风电场中部分风轮机所处位置的经纬度和地形高度等信息,在WSR- 88D Level II数据中提取包含高度、仰角及波束宽度等气象雷达的相关参数,由此可计算出风轮机与雷达之间的距离及相对位置,判断风轮机是否处于雷达视线范围内,并计算风轮机处于雷达视线范围内的长度。对于金属桅杆RCS的求解,文献[10]中已进行了比较详细的讨论,且得出金属桅杆RCS的求解公式(如式(8)所示)。将其与本文给出的解析模型相结合可估算出风电场中风轮机的RCS。
(8)
气象雷达方程[10]为
(9)
式中,Pr表示雷达接收信号功率,Pt表示雷达发射功率,θ0表示雷达波束宽度,K是一个与物质散射特性相关的常数,λ表示波长,τ表示雷达脉冲宽度,d表示目标与雷达之间的相对距离,Z表示雷达反射率因子。
在风电场中,风轮机间的距离一般为叶片旋转直径的3~5倍,对于主流2MW的风轮机而言该距离约为240~400 m,而WSR- 88D雷达距离分辨率为250 m,因此风轮机同时位于不同雷达分辨单元的概率较低,所以可将风轮机当做点目标进行考虑[15],点目标的雷达方程可写为
(10)
其中σ表示风轮机的RCS。由式(9)和式(10)可得到风轮机的雷达反射率因子[16]为
(11)
根据风轮机所处的经纬度等信息可在Level II数据中直接读取其所在区域的雷达反射率因子,将实际值与估计值进行比较,计算两者的差值,结果如图8所示。

图8 风电场雷达反射率因子计算结果验证
Fig.8 The verification of wind farm radar reflectivity factor results
由图8可以看出,与Level II数据对比,解析模型与实测风轮机RCS的误差基本控制在5 dB以内。同时也说明拟合方位角的范围选取是合适的,可以涵盖大部分的风轮机姿态。个别位置差值较大,误差主要由以下几个方面因素导致:
1)风轮机解析模型是在“理想条件”下求解其RCS,即不考虑其他电磁干扰,与实际风电场环境有一定偏差。
2)方位角的影响,解析模型考虑雷达视线照射风轮机前缘时的最大值,而在真实环境下雷达视线的方位角变化范围可能更大,方位角会对叶片RCS产生影响。
3)风电场中风轮机分布影响,解析模型计算时认为每个雷达分辨单元只存在一台风轮机,但在某些特殊照射角度下可能不止一台。
4)风电场中存在复杂的多径干扰情况,解析模型建立时未考虑多次反射的情况,可能导致计算值比实际值偏小。
5)风轮机与雷达间的地形地貌影响,如山脉或高大建筑物的遮挡。如Lone star风电场与其附近的KDYX雷达之间地势起伏不平,对雷达视线造成遮挡,导致解析模型求解值比实测值偏大(对应图8(a)中圆圈标记处)。而Dodge city风电场周边地势较为平坦,其与附近的KDDC雷达之间遮挡较少。
6 结论
本文在考虑叶片旋转平面与雷达视线夹角、风轮机叶片材料及几何形状的变化等复杂因素对风轮机散射特性影响的前提下建立圆柱简化叶片解析模型;其次,在真实叶片建模的基础上,分析气象雷达频段风轮机叶片电磁散射特性,给出风轮机简化叶片与相应真实叶片电磁散射的关系,并运用数值拟合的方法定量表征二者的差值,基于真实叶片与简化叶片雷达散射特性差值构建高保真风轮机真实叶片的解析模型,解决在兼顾运算效率及精度的前提下气象雷达频段的风电场杂波的精细建模问题。实验结果表明本文解析模型计算的结果与雷达实测结果误差基本控制在5 dB以内。解析模型的建立可以为风电场及雷达台站的规划选址提供判断依据,为风电场杂波特征提取及杂波抑制提供数据来源。
[1] 孙一琳. 2019年, 全球风电市场转型进行时[J]. 风能, 2019, 110(4): 70-72.
Sun Yilin. In 2019, when the global wind power market is undergoing transformation[J]. Wind Energy Magazine, 2019, 110(4): 70-72.(in Chinese)
[2] Seo B C, Krajewski W F, Mishra K V. Using the new dual-polarimetric capability of WSR- 88D to eliminate anomalous propagation and wind turbine effects in radar-rainfall[J]. Atmospheric Research, 2015, 153: 296-309.
[3] Norin L. Wind turbine impact on operational weather radar I/Q data: characterisation and filtering[J]. Atmospheric Measurement Techniques, 2017, 10(5): 1739-1753.
[4] 何炜琨, 郭双双, 王晓亮, 等. 基于奇异值分解的风电场杂波微动特征提取[J]. 电子测量与仪器学报, 2017, 31(4): 588-595.
He Weikun, Guo Shuangshuang, Wang Xiaoliang, et al. Micro-motion features extraction of wind farm echoes based on singular value decomposition[J]. Journal of Electronic Measurement and Instrumentation, 2017, 31(4): 588-595.(in Chinese)
[5] Balleri A , Al-Armaghany A , Griffiths H, et al. Measurements and analysis of the radar signature of a new wind turbine design at X-band[J]. IET Radar, Sonar & Navigation, 2013, 7(2): 1- 8.
[6] Zhang Y, Huston A, Palmer R D, et al. Using Scaled Models for Wind Turbine EM Scattering Characterization: Techniques and Experiments[J]. IEEE Transactions on Instrumentation and Measurement, 2011, 60(4): 1298-1306.
[7] 俞一鸣. 时频分析简介及应用[J]. 国外电子测量技术, 2015(6): 12-15.
Yu Yiming. Introduction and application of time-frequency analysis[J]. Foreign Electronic Measurement Technology, 2015(6): 12-15.(in Chinese)
[8] Li C J, Bhalla R, Ling H. Investigation of the Dynamic Radar Signatures of a Vertical-Axis Wind Turbine[J]. IEEE Antennas and Wireless Propagation Letters, 2015, 14: 763-766.
[9] 邹亮, 宫攀, 张黎, 等. 干式空心电抗器空间磁场缩比试验与模型简化[J]. 高电压技术, 2014, 40(6): 1675-1682.
Zou Liang, Gong Pan, Zhang Li, et al. Small-scale Experiment and Model Simplification of Space Magnetic Fields Around Air-core Reactors[J]. High Voltage Engineering, 2014, 40(6): 1675-1682.(in Chinese)
[10]Angulo I, Grande O, Jenn D, et al. Estimating reflectivity values from wind turbines for analyzing the potential impact on weather radar services[J]. Atmospheric Measurement Techniques, 2015, 8(5): 2183-2193.
[11]何炜琨, 汲超迪, 王晓亮, 等. 风轮机叶片雷达散射特性计算与解析式拟合[J]. 仪器仪表学报, 2017, 38(11): 2626-2633.
He Weikun, Ji Chaodi, Wang Xiaoliang, et al. Radar cross characteristics calculation and analytical formula fitting of wind turbine blade[J]. Chinese Journal of Scientific Instrument, 2017, 38(11): 2626-2633.(in Chinese)
[12]Grande O, Angulo I, Jenn D, et al. Analysis of wind turbines radar cross section for analyzing the potential impact on weather radars[C]∥2015 9th European Conference on Antennas and Propagation. Lisbon, Portugal: IEEE, 2015: 1-5.
[13]张涛, 刘胜. 后掠式叶片气动外形优化设计[J]. 液压与气动, 2019,(01):137-141.
Zhang Tao, Liu Sheng. Aerodynamic Shape Optimization Design of Backward Swept Blade[J]. Chinese Hydraulics & Pneumatics, 2019,(01):137-141.(in Chinese)
[14]Song F, Ni Y, Tan Z. Optimization Design, Modeling and Dynamic Analysis for Composite Wind Turbine Blade[J]. Procedia Engineering, 2011, 16(none): 369-375.
[15]李晓红, 谭维贤, 黄平平, 等. 基于极坐标格式算法的地基雷达数据处理方法[J]. 信号处理, 2019, 35(5): 926-932.
Li Xiaohong, Tan Weixian, Huang Pingping, et al. Ground-based Radar Data Processing Method Based on Polar Coordinate Format Algorithm[J]. Journal of Signal Processing, 2019, 35(5): 926-932.(in Chinese)
[16]Angulo I, De l V D, Cascón, I, et al. Impact analysis of wind farms on telecommunication services[J]. Renewable and Sustainable Energy Reviews, 2014, 32: 84-99.


