1 引言
线性调频(Linear Frequency Modulation,LFM)信号是雷达常用的信号形式之一,通过对信号时宽、带宽控制可同时获得高的距离分辨率和远作用距离[1]。为有效干扰LFM脉冲压缩体制雷达,数字射频存储装置(Digital Radio Frequency Memory, DRFM)广泛应用于雷达有源干扰系统,DRFM常用的工作方式为全脉冲读写,但对于收发分时工作体制干扰机,全脉冲读写导致干扰信号最小转发时延大于雷达脉冲宽度[2],生成的虚假目标距离上滞后真实目标。为解决该问题,干扰方通常利用LFM距离多普勒耦合特性,对假目标进行移频处理,使假目标导前真实目标,但移频假目标干扰转发一次仅能生成一个假目标,要达成对雷达的干扰压制效果需要进行多次转发。如何生成既能导前真实目标又能有效压制雷达的干扰样式,频谱弥散干扰[3](SMeared SPectrum jamming,SMSP)是一种有效的解决方案。频谱弥散干扰通过改变信号内部形式,转发一次即可在真实目标前后生成高密度梳状假目标群,达成对LFM脉冲压缩体制雷达欺骗兼压制干扰效果。围绕SMSP干扰抑制,文献[4]以双谱盒维数、信息维数为特征参数,利用支持向量机分类器进行回波类型识别,但自卫式干扰条件下,回波信号中包含真实目标回波,即使识别出回波类型,仍需要做进一步抑制处理。针对该问题,文献[5- 6]利用SMSP干扰与真实回波调频斜率上的差异,联合分数阶傅里叶变换(Fractional Fourier Transform, FRFT)和压缩感知(Compressive Sensing, CS)对抗SMSP干扰。其中,文献[5]利用短时傅里叶变换(Short Time Fourier Transform, STFT)估计干扰子信号调频斜率,进而构造分数阶信号-干扰联合字典,基于压缩感知算法重构真实目标回波,但受限于STFT时频分辨率,低干信比条件下干扰参数估计准确率较低,无法构造与干扰相匹配的联合字典。文献[6]分数阶域滤除部分干扰,在此基础上构造非重叠短时傅里叶矩阵稀疏重构真实目标回波,但由于在分数阶域设置了较大的遮盖带宽,滤波后剩余干扰较大,重构效果不够理想。
线性正则变换[7- 8](Linear Canonical Transform, LCT)作为分数阶傅里叶变换的广义形式,相比FRFT对信号时频平面的旋转,LCT可实现信号时频平面的旋转、拉伸和平移[9],随着相关理论和快速离散算法深入研究,已应用于参数估计[10]、时频滤波[11]、图像处理[12]等领域,本文将LCT应用于雷达抗干扰,以自卫式干扰条件下LFM脉冲压缩体制雷达对抗SMSP干扰为背景,利用雷达发射信号调频斜率已知的先验信息确定LCT参数矩阵,根据真实目标回波和干扰信号LCT特征差异,设计了两种LCT域干扰抑制方法,即窄带滤波法和基于LCT正交字典的稀疏重构法。仿真试验验证了所提方法的可行性和有效性。
2 真实目标回波与SMSP干扰LCT域特征分析
不考虑回波时延[4- 6],真实目标回波复数形式可表示为:
(1)
式中,σ为目标反射系数,T为脉冲宽度,B为信号带宽,k=B/T为调频斜率。SMSP干扰由N个子LFM信号延时拼接而成,其中第1个子信号可表示为:
(2)
式中,kj=Nk为子信号调频斜率。可以看出,子信号调频斜率为雷达发射信号调频斜率的N倍,时宽为雷达发射信号的1/N,带宽与雷达发射信号相同。对N个子信号进行延时拼接得到SMSP干扰为:
(3)
式中,Aj为SMSP干扰幅度。分析真实目标回波与干扰LCT域特征,当参数b≠0时,频率意义下的信号x(t)的LCT定义为[13]:
(4)
式中,A=[a,b;c,d]为参数矩阵,约束ad-bc=1,KA(u,t)为LCT变换核:
(5)
LCT核函数实质上是一组复包络为
初始频率为-u/b,调频斜率为a/b的LFM基信号,线性正则域由该组完备正交基表征。分析真实目标回波和SMSP干扰LCT域特征,令参数矩阵A中a、b满足a/b=-k,则真实目标回波LCT为:
(6)
同理,得到SMSP干扰第1个LFM子信号LCT为:
(7)
式(7)等效为求时宽为T/N,调频斜率为(N-1)k,带宽为B(N-1)/N的LFM信号的傅里叶变换,当该LFM信号满足较大的时宽带宽积时[1],式(7)可简化为:
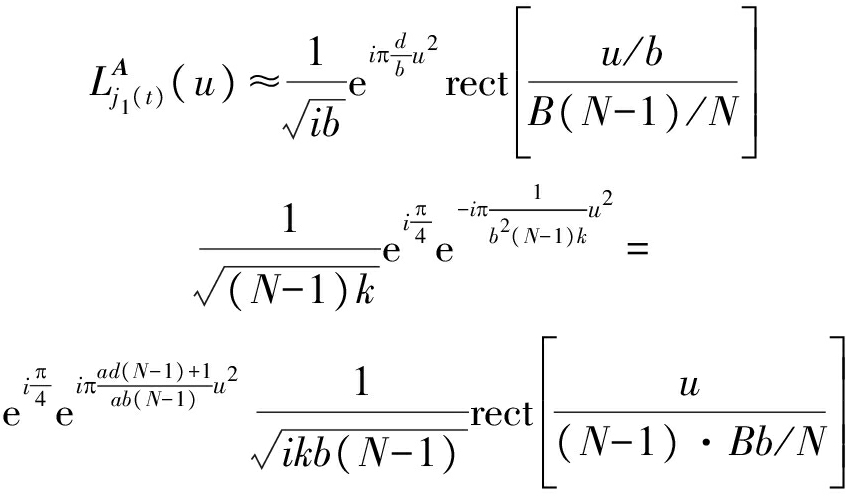
(8)
根据LCT时延性质[9],得到SMSP干扰LCT为:
(9)
由式(6)～式(9)可以看出,真实目标回波LCT为一辛格函数,峰值点u域位置为0,SMSP干扰第1个子信号LCT近似为矩形,N-1次平移叠加得到SMSP干扰LCT。分析真实目标LCT与SMSP干扰LCT幅度差异,令u=0,得到:
(10)
(11)
式中,N1=ceil(N/2),ceil表示向+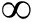
取整。令
得到:
(12)
式中,
为干信比(Jamming to Signal Ratio, JSR),D为雷达发射信号时宽带宽积。假设雷达发射信号脉冲宽度80 μs,带宽5 MHz,SMSP干扰子信号个数为5,根据式(12)得到临界JSR约为22.5 dB。由于SMSP干扰LCT不仅是子信号LCT的平移叠加,每个子信号LCT还存在相位调制,因此实际临界JSR会大于式(12)计算的临界值。综合式(6)～式(12)可以得到三个结论:一是真实目标回波、SMSP干扰参数矩阵下A的LCT均存在能量聚焦,区别在于不同的聚焦程度;二是真实目标回波LCT与SMSP干扰LCT幅度差异取决于JSR,当JSR满足式(12),真实目标回波LCT幅度高于干扰LCT幅度,峰值遮盖处理即提取真实目标回波;三是真实目标回波LCT与SMSP干扰LCT存在u域重叠,当JSR满足式(12),受干扰回波LCT峰值高于未受干扰回波LCT峰值,恢复信号幅度将大于真实目标回波。
3 SMSP干扰抑制方法
3.1 LCT域窄带滤波
第2节分析可知,当JSR满足式(12)时,真实目标回波LCT幅度高于SMSP干扰幅度,调整LCT参数矩阵使其满足a/b=-k,且ad-bc=1,对受干扰回波LCT域峰值遮盖,逆LCT处理即可提取真实目标回波。考虑到雷达信号处理的实时性要求,离散LCT应选择合适的快速算法。现有离散LCT快速算法主要包括直接离散DLCT、基分解DLCT、算子分解DLCT,对受干扰回波信号进行峰值遮盖处理要求DLCT应满足可逆性、低复杂度,且逼近连续LCT。文献[14]提出了一种针对纯离散数据的算子分解型DLCT,分解过程为:
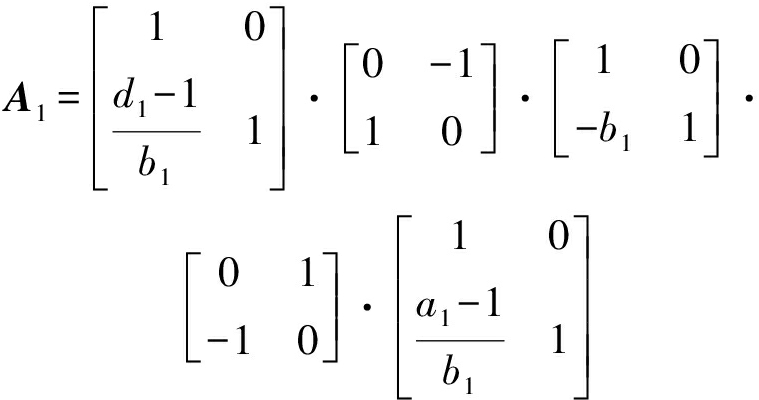
(13)
式中,参数矩阵A1=[a1,b1;c1,d1]=[a,b/Δt2/N1;cΔt2N1,d],N1为离散数据点数。该分解算法包含3次Chirp乘积、1次FFT、1次IFFT,计算复杂度O(NlogN),且无需过采样。
3.2 LCT域稀疏重构
第2节分析可知,真实目标回波在参数矩阵A下LCT为一个标准的辛格函数,LCT域稀疏度为1,根据压缩感知理论,构造合适的变换基,利用少量的观测值、观测矩阵,通过求解优化问题可高概率重构真实目标回波[5- 6]。算法实现的关键在于设计合适的变换基,本文采用Pei型直接离散DLCT[15]构造LCT正交字典,利用LCT正交字典设计变换基,具体步骤为:
步骤1 设计参数矩阵A,其元素满足a/b=-k,ad-bc=1。
步骤2 确定时域、LCT域采样间隔Δt、Δu和对应的采样点数2N+1、2M+1,对式(4)连续LCT离散化,得到:
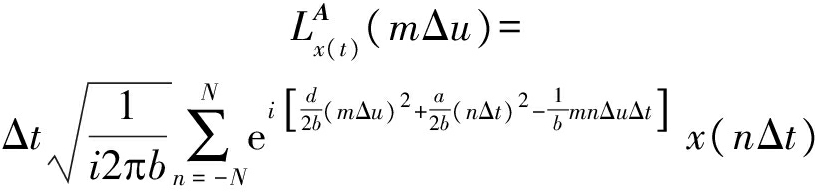
(14)
步骤3 上式可进一步表示为:
(15)
(16)
步骤4 为使KA(m,n)满足可逆性,要求:
(17)
步骤5 将式(17)带入(16),归一化处理得到:
(18)
(19)
步骤6 KA(m,n)即为本文构造的LCT正交字典,其共轭转置矩阵即为稀疏重构算法中的变换基。设计LCT正交字典仅需利用雷达发射信号先验信息,无需估计干扰参数。
4 仿真结果
4.1 参数设置与SMSP干扰
设雷达发射信号为LFM脉冲信号,脉宽80 μs,带宽5 MHz,采样频率25 MHz,真实目标为点目标,回波幅度为1 V,SMSP干扰子信号个数为5。真实目标回波、SMSP干扰时域波形和时频分布(利用STFT时频重排得到)如图1所示。可以看出,真实回波与SMSP干扰时域、频域完全重叠,且时频脊线存在交叉。对SMSP干扰进行脉冲压缩处理,图2对比移频干扰(移频量2.5 MHz)给出了SMSP脉冲压缩输出结果。可以看出,移频干扰经雷达匹配滤波器仅能输出1个导前真实目标的虚假目标,而SMSP干扰经匹配滤波输出高密度假目标群,且部分假目标导前真实目标。
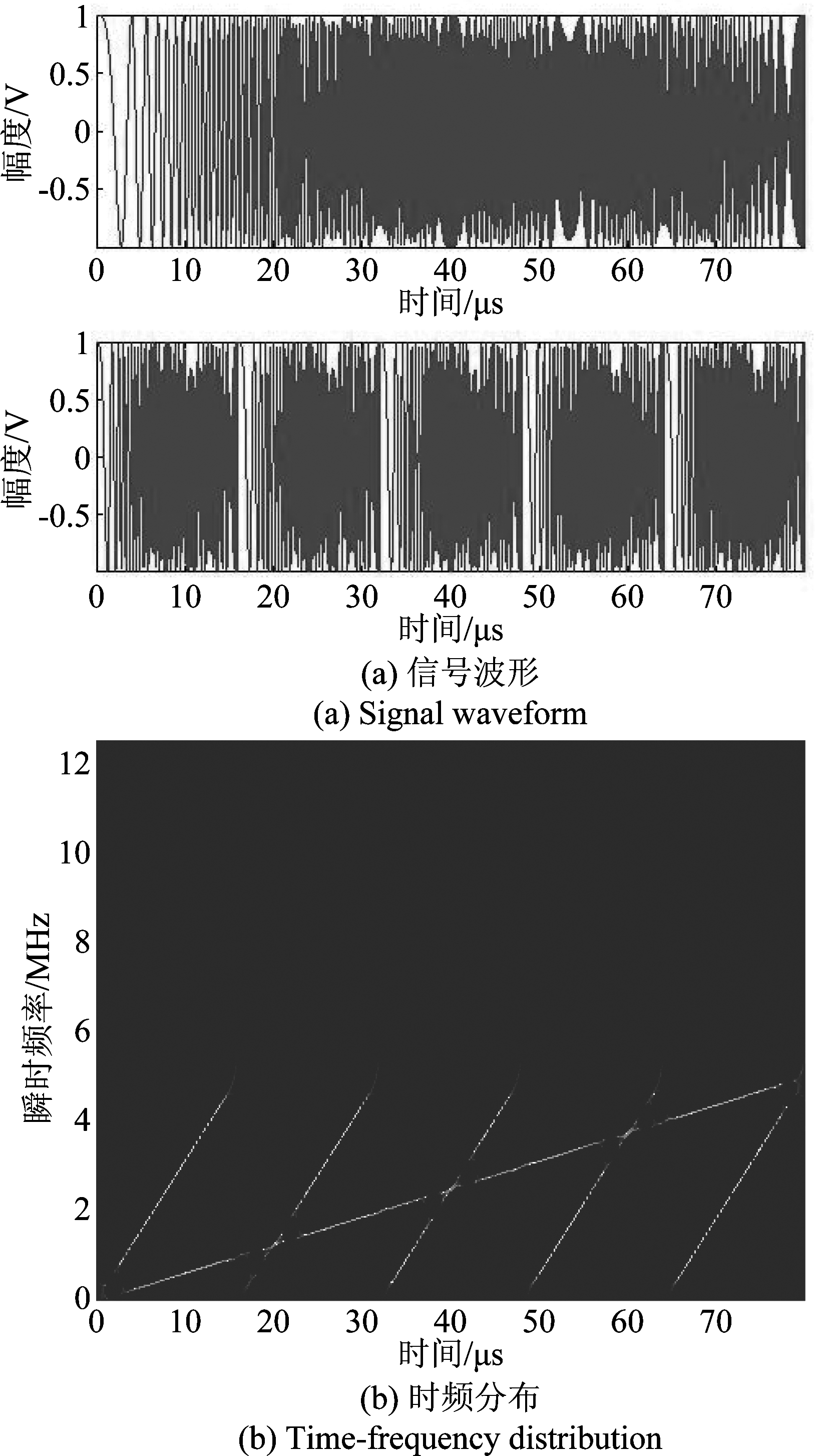
图1 真实目标回波、SMSP干扰时频特性
Fig.1 Time-frequency characteristics of the real target echo and SMSP jamming
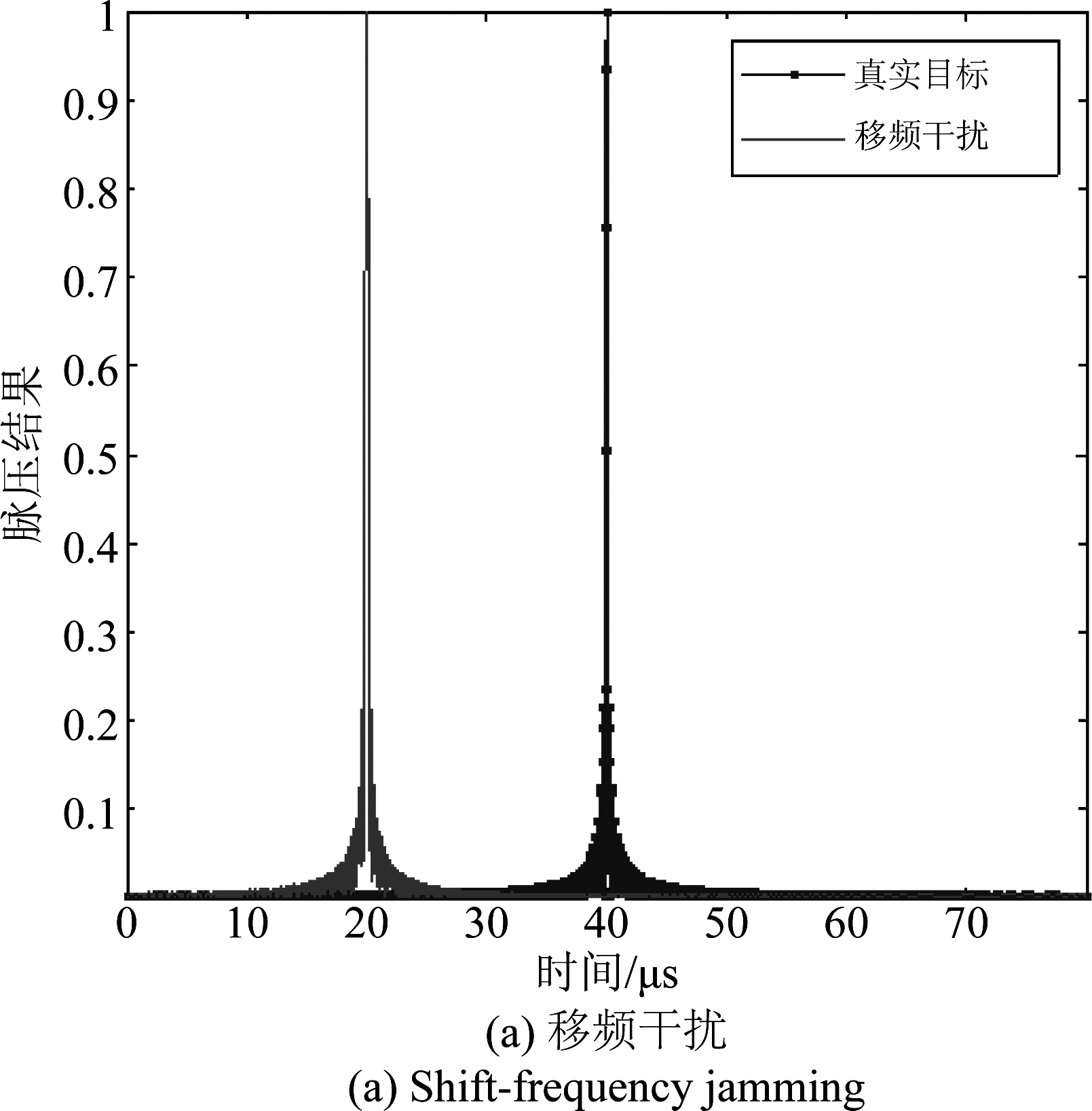
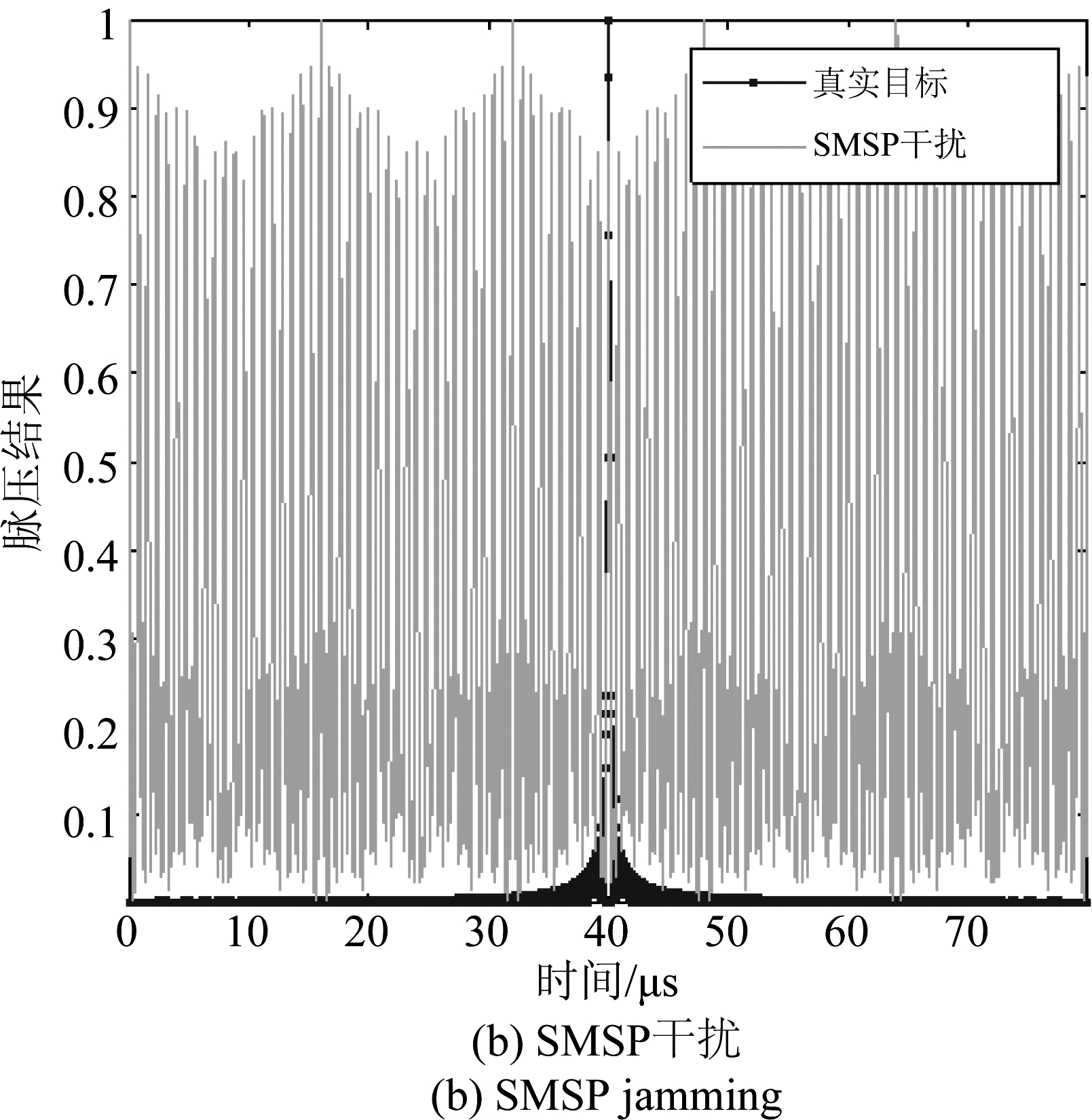
图2 干扰效果对比
Fig.2 Comparison of jamming effect
4.2 仿真实验1
4.2.1 可行性仿真分析
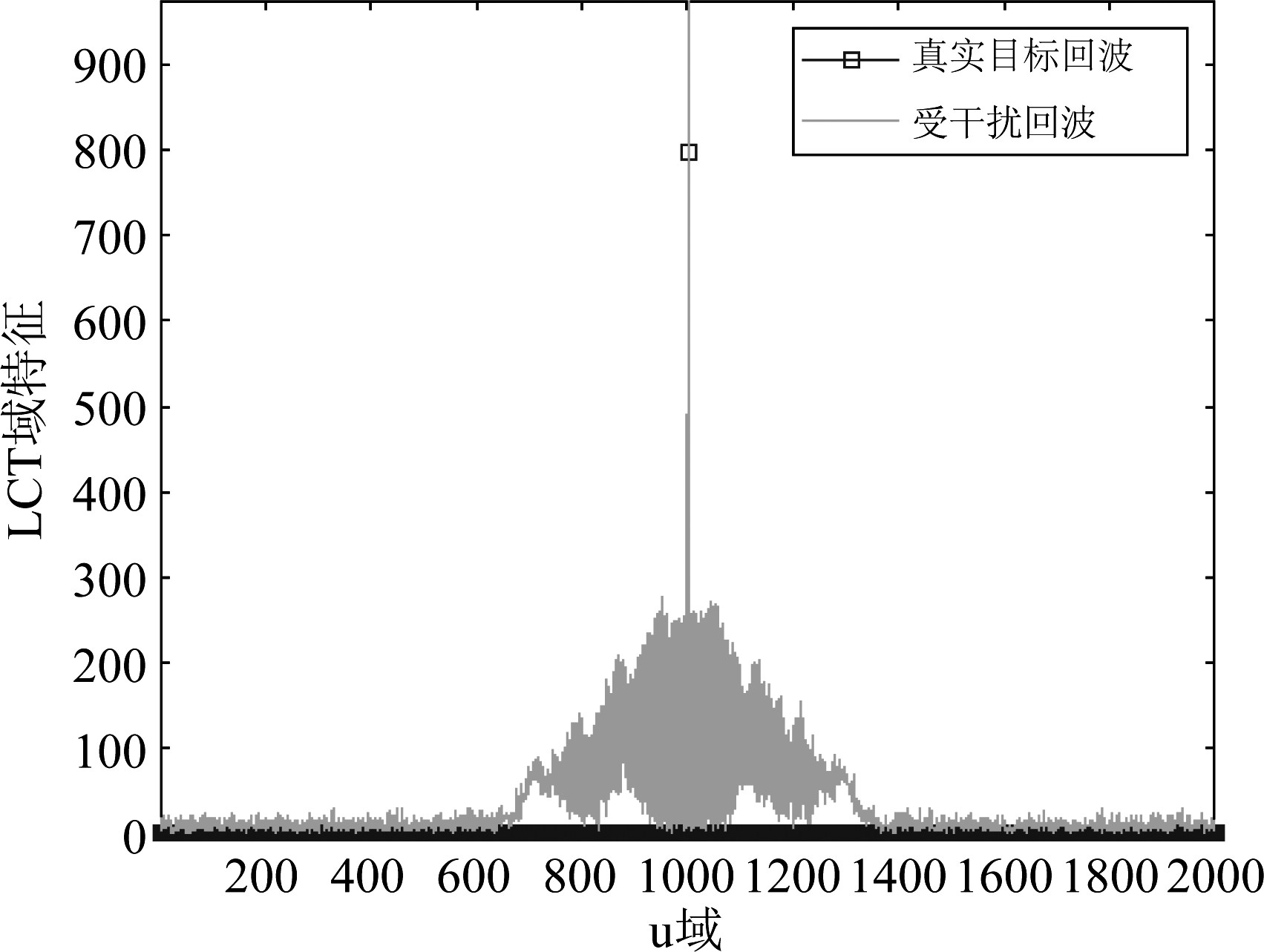
图3 受干扰回波信号LCT特性
Fig. 3 LCT characteristics of jammed echo
分析LCT窄带滤波抑制SMSP可行性,设信噪比(Signal to Noise Ratio, SNR)为0 dB、JSR为10 dB,令LCT参数矩阵A=[-k,1;0,-1/k],图3对比真实目标回波给出了受干扰回波LCT结果。可以看出,真实目标回波、SMSP干扰参数矩阵A下的LCT均存在能量聚焦,且部分重叠,导致受干扰回波LCT峰值点高于真实目标回波,与第2节理论分析一致。
利用宽度为5个LCT域采样点的矩形窗对受干扰回波LCT峰值遮盖处理,恢复信号时域波形如图4(a)所示,恢复信号与真实回波高度相似,且幅度大于真实目标回波。图4(b)给出了恢复信号脉冲压缩结果,虚假目标被有效抑制。
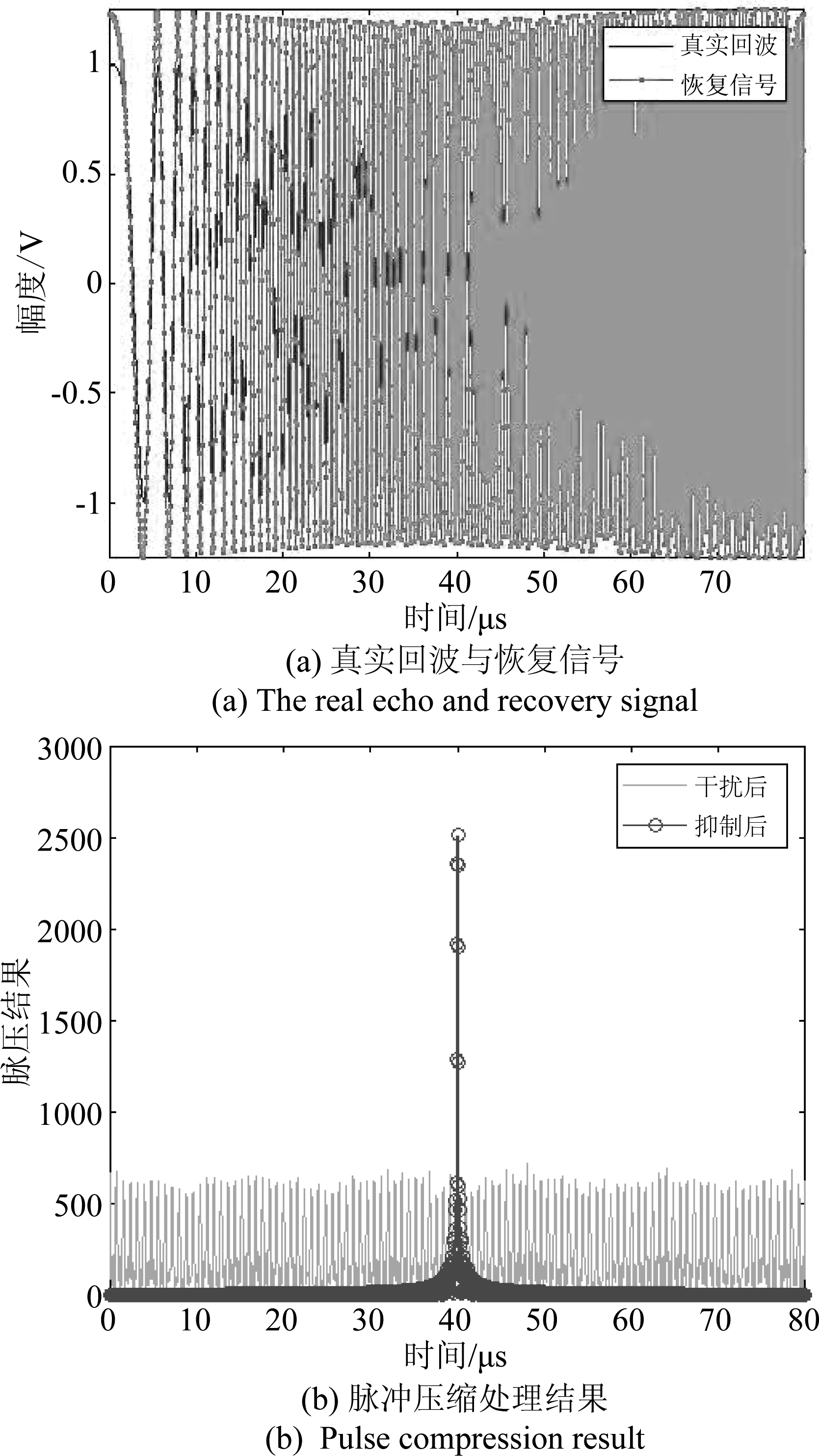
图4 干扰抑制效果
Fig. 4 Jamming suppression effect
4.2.2 干扰抑制效能
LCT域窄带滤波恢复信号与真实回波高度相似,幅度高于真实回波,因此可从恢复信号与真实回波相似程度、脉冲压缩后峰值差异评估算法对SMSP干扰抑制效能。皮尔逊相关系数[16](Pearson Correlation Coefficient,PCC)常用于分析两个随机变量的线性相关性,信号相似度越高,PCC越接近于1。同时,定义恢复信号与真实回波脉冲压缩后主瓣峰值比为PCMR=PCM1/PCM2(单位dB),其中PCM1为恢复信号脉冲压缩后主瓣峰值,PCM2为真实回波脉压后主瓣峰值。设JSR为10 dB,SNR取-5至15 dB,间隔1 dB,蒙特卡洛300次,图5(a)给出不同宽度遮盖窗下恢复信号与真实回波PCC随SNR变化曲线。设SNR为0 dB,JSR取0至30 dB,间隔1 dB,图5(b)给出了PCC随JSR变化曲线。两种仿真条件下,恢复信号与真实回波PCC均接近于1。同理,图6分别给出PCMR随SNR、JSR变化曲线,可以看出,PCMR均大于0 dB,说明恢复信号幅度大于真实回波幅度,JSR越大恢复信号幅度越大。综上分析,LCT窄带滤波法可提取SMSP干扰下的真实目标回波,恢复信号与真实恢复高度相似,且幅度大于真实回波,使得干扰成为“标的”。
4.3 仿真实验2
4.3.1 可行性仿真分析
分析LCT稀疏重构抑制SMSP可行性,按照3.2节步骤构造2000*2000的LCT正交字典,如图7所示。设SNR为0 dB、JSR为10 dB,压缩比(Sampling Ratio, SR)为2,测量矩阵为随机高斯矩阵,稀疏度为1,利用图7构造的正交字典,通过正交匹配追踪(Orthogonal Matching Pursuit, OMP)算法重构真实目标回波。图8对比真实目标回波,给出了重构信号时域波形和脉冲压缩处理结果。重构信号与真实回波高度相似,经脉冲压缩处理,虚假目标得到有效抑制。
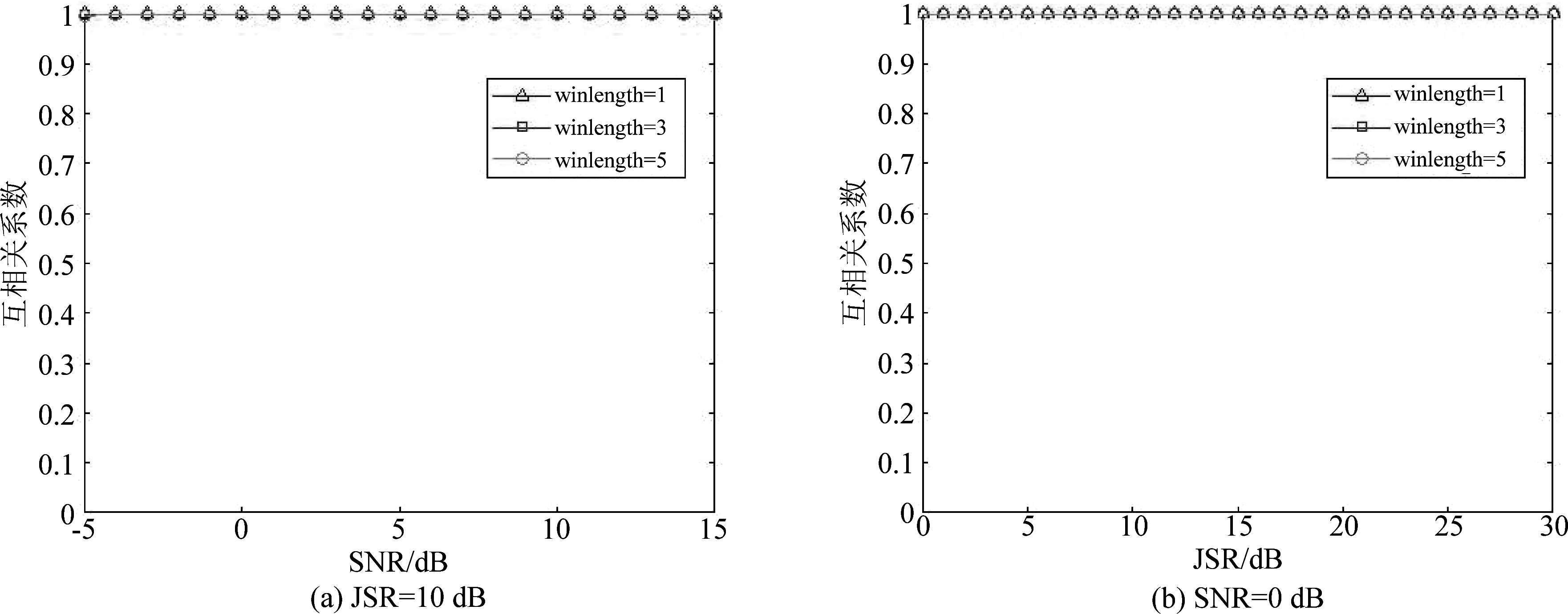
图5 PCC随SNR、JSR变化曲线
Fig.5 Curve of PCC with SNR and JSR
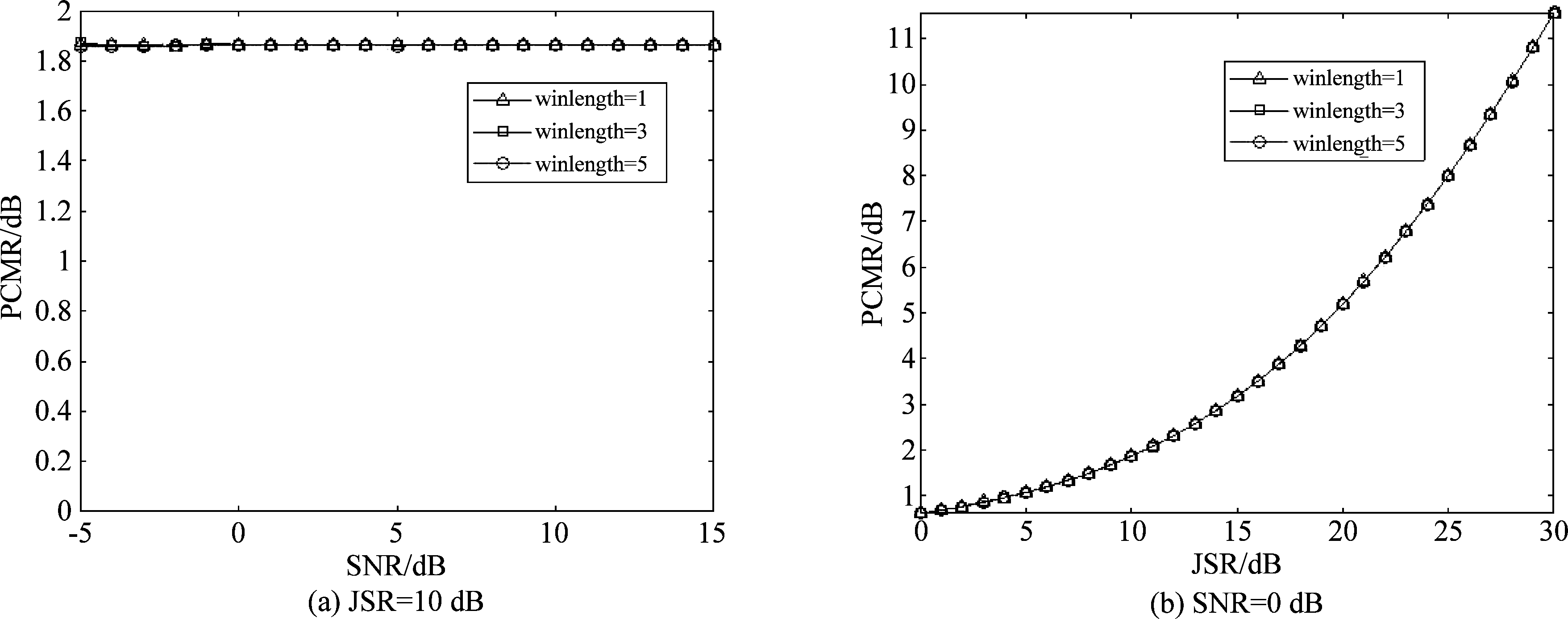
图6 PCMR随SNR、JSR变化曲线
Fig.6 Curve of PCMR with SNR and JSR
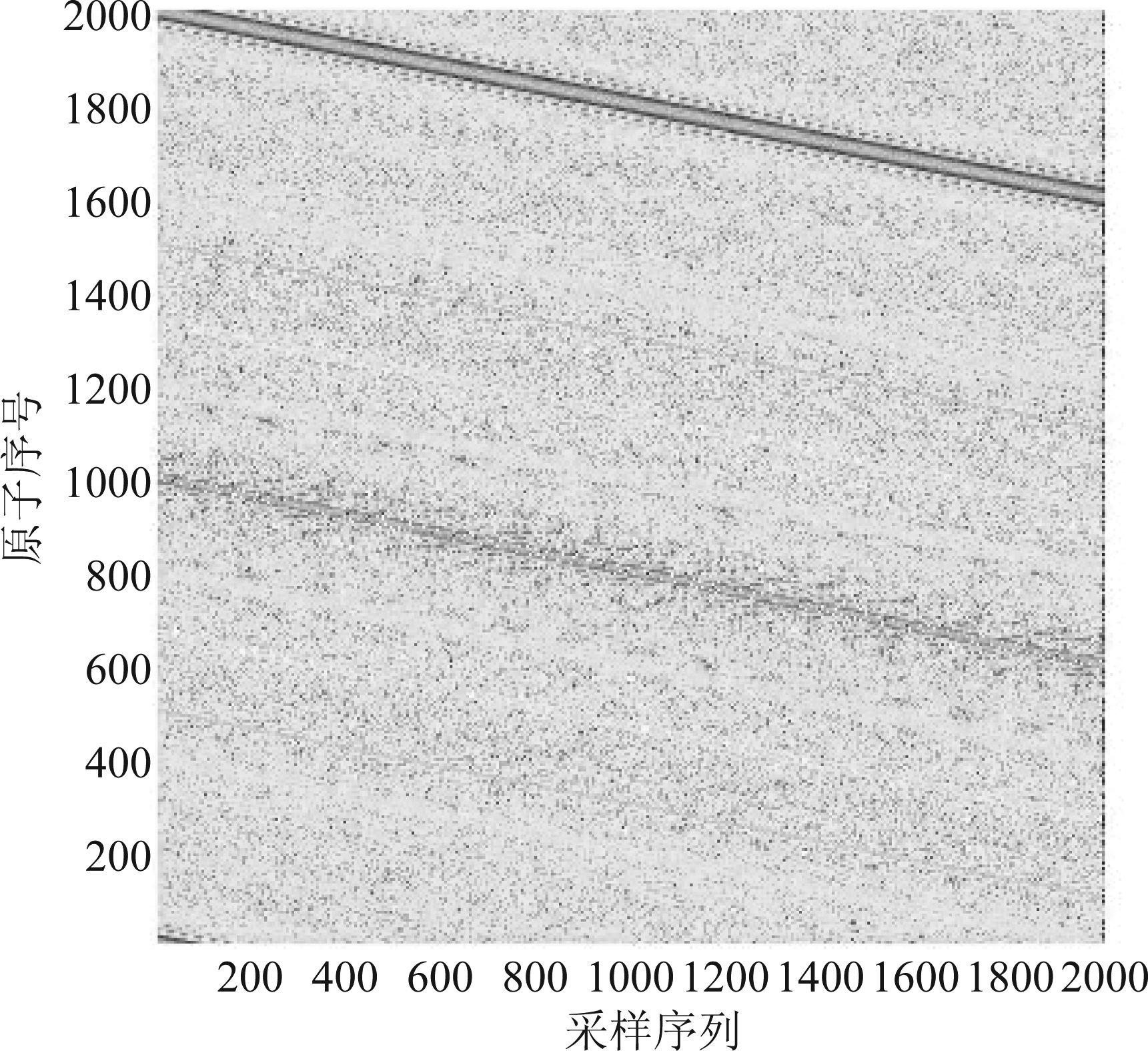
图7 LCT正交字典
Fig.7 LCT orthogonal dictionary
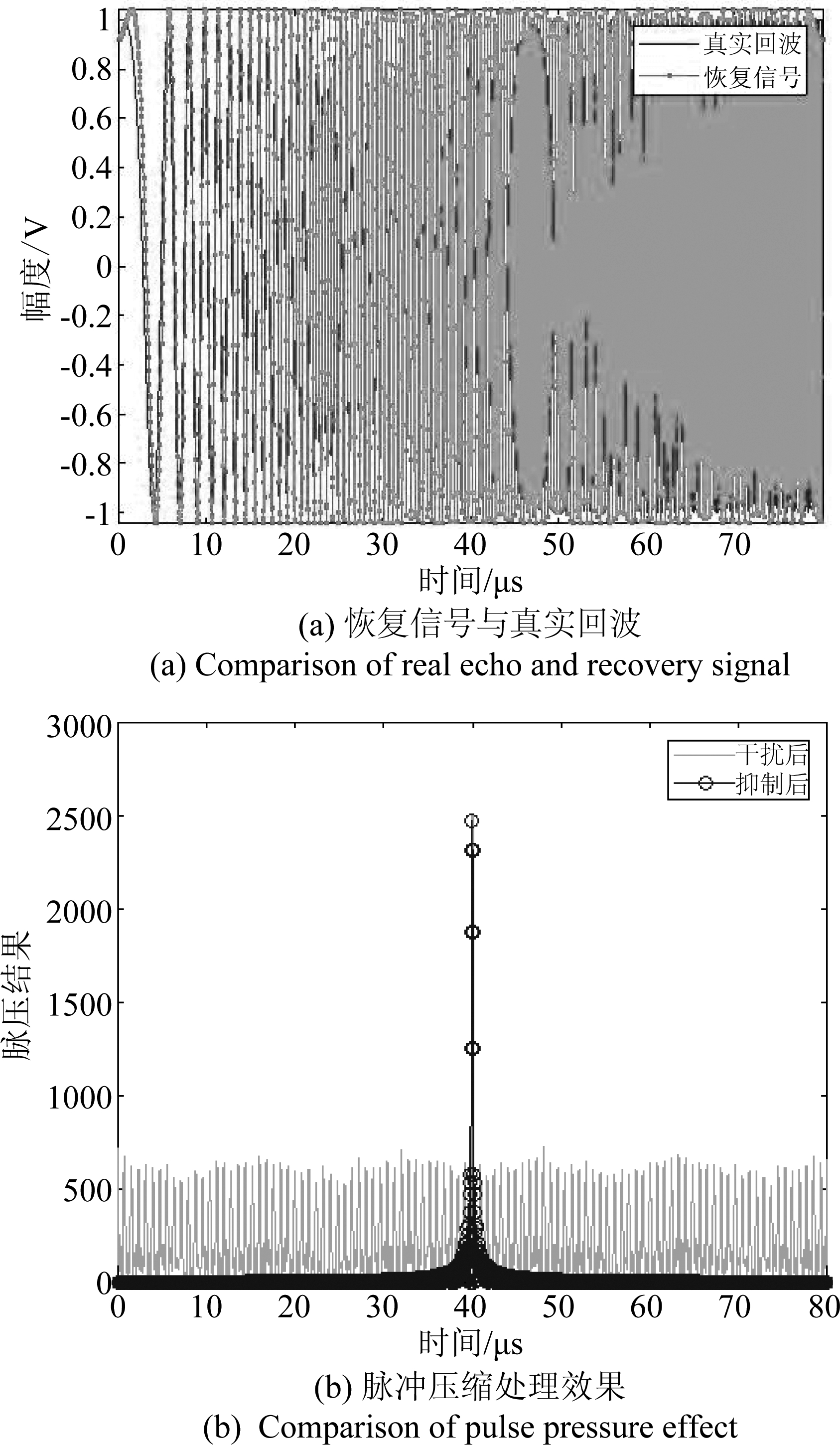
图8 干扰抑制效果
Fig.8 Jamming suppression effect
4.3.2 干扰抑制效能
SNR、JSR、蒙特卡洛次数同4.2.2节,图9～图10分别给出了3种不同压缩比条件下,重构信号与真实回波相关系数PCC、脉压主瓣峰值比PCMR随SNR和JSR变化曲线。图9可以看出,稀疏重构信号与真实回波PCC受JSR影响较大,当SNR等于0 dB,JSR小于20 dB时,PCC大于0.9,重构信号与真实回波相似度较高,当JSR大于20 dB时,相似度变差。分析原因是因为OMP算法沿用匹配追踪算法原子选取准则,通过逐次迭代,从正交字典中选择与信号(或余量)最匹配的原子进行稀疏逼近,当JSR增大到一定程度时,OMP获得的最“匹配”原子与真实回波并不匹配,影响了重构效果。图10可以看出,PCMR同样受JSR影响较大,当JSR小于20 dB时,PCMR大于0 dB,重构信号幅度大于真实回波幅度,当JSR大于20 dB时,PCMR迅速下降,且SR越大,下降速度越快。对比图5～图6可知,基于LCT正交字典稀疏重构抑制SMSP干扰方法受JSR影响程度大于LCT窄带滤波方法,当JSR大于20 dB时,已经难以恢复真实目标回波。
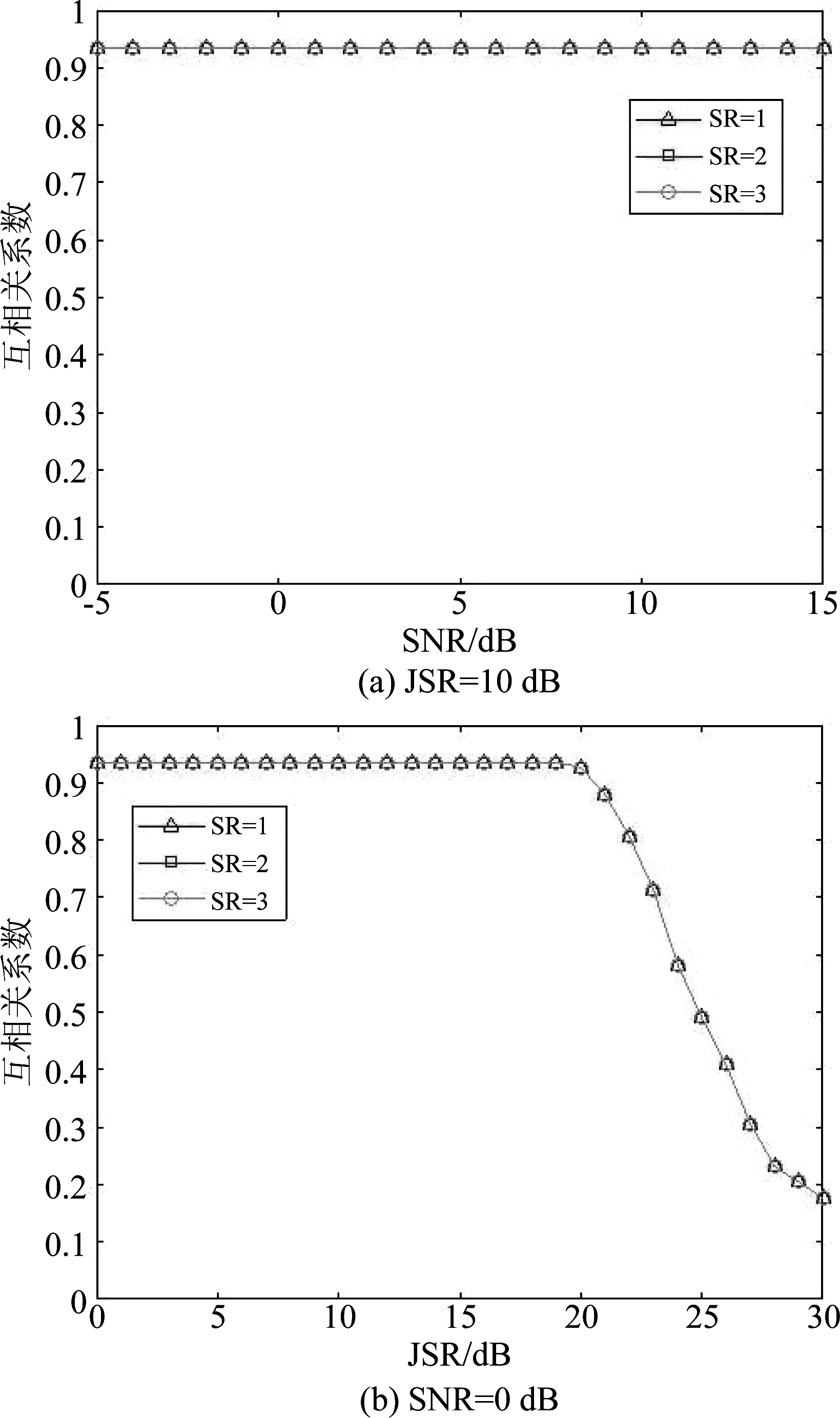
图9 PCC随SNR、JSR变化曲线
Fig.9 Curve of PCC with SNR and JSR
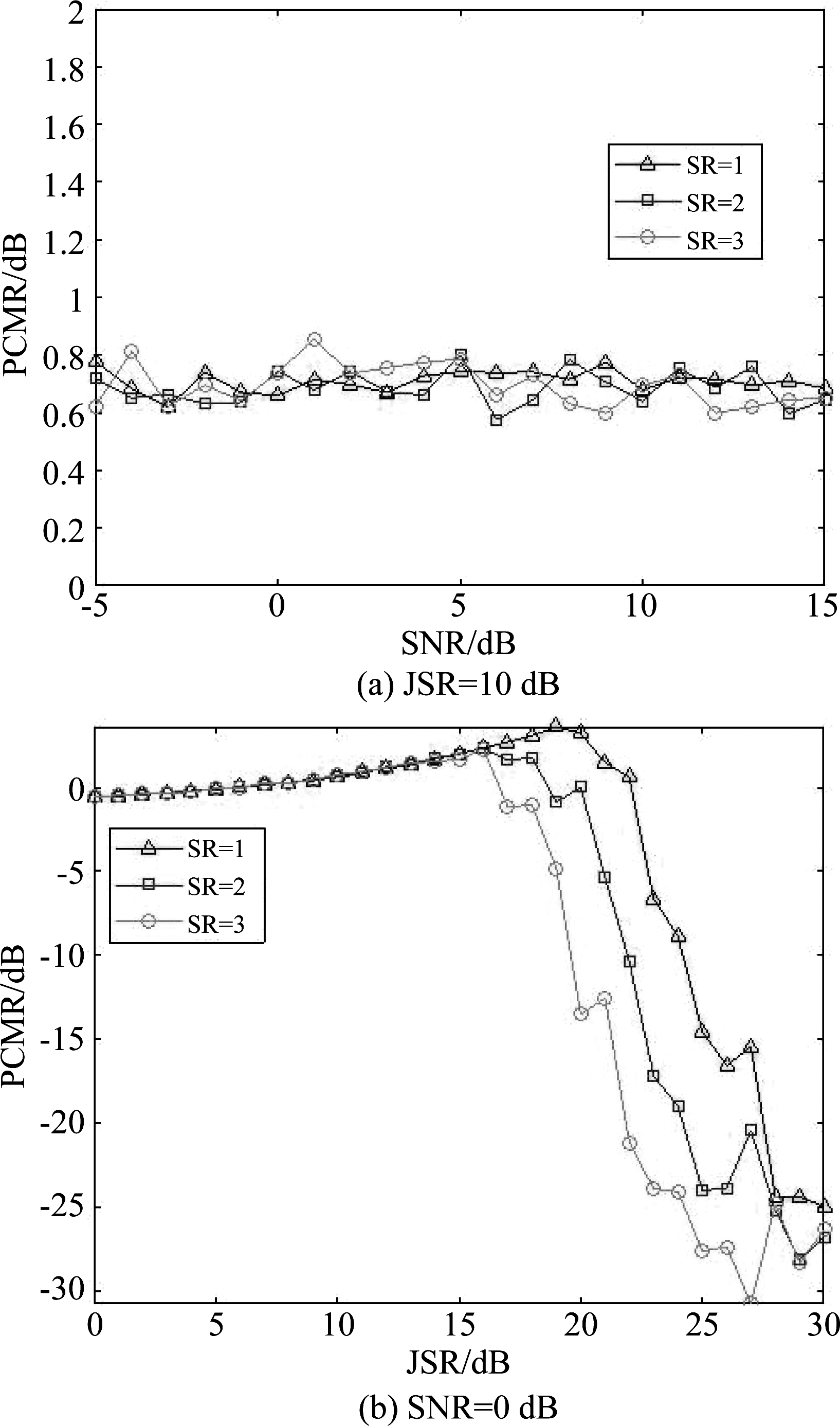
图10 PCMR随SNR、JSR变化曲线
Fig.10 Curve of PCMR with SNR and JSR
5 结论
基于DRFM生成的SMSP干扰由多个线性调频子信号延时拼接而成,经雷达匹配滤波输出高密度梳状假目标,干扰效能突出。围绕SMSP干扰抑制,本文利用雷达发射信号调频斜率先验信息确定LCT参数矩阵,根据真实目标回波与SMSP干扰LCT域特征差异,提出两种LCT域抑制SMSP干扰方法。仿真结果表明,LCT窄带滤波方法和基于LCT正交字典的稀疏重构方法均能达成不同程度的干扰抑制效能,相比稀疏重构方法,窄带滤波方法受干信比影响要小。文中仅利用了LCT对信号时频平面旋转特征分离真实回波与SMSP干扰信号,如何发挥LCT高自由度及对时频平面压缩、拉伸、平移特性,进一步分离目标回波与干扰信号,下一步仍需要做进一步的研究。
[1] Mark A R. 雷达信号处理基础[M]. 邢孟道，王彤，李真芳，等，译. 2版. 北京: 电子工业出版社, 2017: 139-140.
Mark A R. Fundamentals of radar signal processing[M]. Xing Mengdao, Wang Tong, Li Zhenfang, et al. translate. 2nd edn. Beijing: Publishing House of Electronics Industry, 2017: 139-140.(in Chinese)
[2] 赵国庆. 雷达对抗原理[M]. 2版. 西安: 西安电子科技大学出版社, 2012: 194-195.
Zhao Guoqing. Radar countermeasure principle[M]. 2nd edn. Xi’an: Xidian University Press, 2012: 194-195.(in Chinese)
[3] Sparrow M J, Cikalo J. ECM techniques to counter pulse compression radar[P]. United States Patent, 7081846, 2006.
[4] 杨少奇, 田波, 周瑞钊. 应用双谱分析和分形维数的雷达欺骗干扰识别[J]. 西安交通大学学报, 2016, 50(12): 128-135.
Yang Shaoqi, Tian Bo, Zhou Ruizhao. A jamming identification method against radar deception based on Bispectrum analysis and fractal dimension[J]. Journal of Xi’an Jiaotong University, 2016, 50(12): 128-135.(in Chinese)
[5] 赵杨, 尚朝轩, 韩壮志, 等. 分数阶傅里叶和压缩感知自适应抗频谱弥散干扰[J]. 电子与信息学报, 2019, 41(5): 1048-1053.
Zhao Yang, Shang Chaoxuan, Han Zhuangzhi, et al. Fractional Fourier Transform and Compressed Sensing adaptive countering smeared spectrum jamming[J]. Journal of Electronics & Information Technology, 2019, 41(5): 1048-1053.(in Chinese)
[6] 卢云龙, 李明, 曹润清, 等. 联合时频分布和压缩感知对抗频谱弥散干扰[J]. 电子与信息学报, 2016, 38(12): 3275-3281.
Lu Yunlong, Li Ming, Cao Ruiqing, et al. Jointing time-frequency distribution and compressed sensing for countering smeared spectrum jamming[J]. Journal of Electronics & Information Technology, 2016, 38(12): 3275-3281.(in Chinese)
[7] Collins S A. Lens-system diffraction integral written in terms of matrix optics[J]. Journal of the Optical Society of America, 1970, 60(9): 1168-1177.
[8] Moshinsky M, Quesne C. Linear Canonical Transformations and their unitary representations[J]. Journal of Mathematical Physics, 1971, 12(8): 1772-1780.
[9] 陶然, 齐林, 王越. 分数阶Fourier 变换的原理与应用[M]. 北京: 清华大学出版社, 2004: 433- 434.
Tao Ran, Qi Lin, Wang Yue. Theory and applications of the Fractional Fourier Transform[M]. Beijing: Tsinghua University Press, 2004: 433- 434.(in Chinese)
[10]Xu X N, Li B Z, Ma X L. Instantaneous frequency estimation based on the Linear Canonical Transform[J]. Journal of the Franklin Institute, 2012, 349(10): 3185-3193.
[11]向强, 秦开宇. 基于线性正则变换与短时傅里叶变换联合的时频分析方法[J]. 电子学报, 2011, 7(7): 1509-1513.
Xiang Qiang, Qin Kaiyu. A time frequency analysis method based on Linear Canonical Transform and Short-time Fourier Transform[J]. Acta Electronica Sinica, 2011, 7(7): 1509-1513.(in Chinese)
[12]Li Y, Sha X J, Wei D Y. Image scaling algorithm using multichannel sampling in the linear canonical transform domain[J]. Signal Image and Video Processing, 2014, 8(2): 197-204.
[13]孙艳楠, 李炳照, 陶然. 线性正则变换的离散化研究进展[J]. 光电工程, 2018, 45(6): 29- 49.
Sun Yannan, Li Bingzhao, Tao ran. Research progress on discretization of linear canonical transform[J]. Opto-Electronic Engineering, 2018, 45(6): 29- 49.(in Chinese)
[14]Pei S C, Huang S G. Fast discrete linear canonical transform based on CM-CC-CM decomposition and FFT[J]. IEEE Transactions on Signal Processing, 2016, 64(4): 855- 866.
[15]Pei S C, Ding J J. Close-form discrete fractional and affine Fourier transforms[J]. IEEE Transactions on Signal Processing, 2000, 48(5): 1338-1353.
[16]Ly A, Marsman M, Wagenmakers E J. Analytic posteriors for person’s correlation coefficient[J]. Statistica Neerlandica, 2018, 72(1): 4-13.
