表示天线之间的相位差,相邻两天线之间的时间延迟可以被明确地计算为
其中c表示光速。对于一个符号周期为Ts的单载波通信系统,其基带信号可以被表示为:随着全球移动通信用户和设备的不断增多,而无线通信频谱资源有限,用户已经不再满足于第四代(4G)移动通信的传输速率。第五代(5G)移动通信技术应运而生,3D MIMO(Three-Dimension Multiple-Input Multiple-Output)是5G通信中的关键技术之一,它可以同时调用天线端垂直维和水平维的天线自由度,产生更为精确的波束,并且它还能提高系统容量和传输效率[1]。5G通信的另一个关键技术就是毫米波技术,毫米波是指频率处于3～300 GHz之间的电磁波,它具有波束小、角分辨率高、隐蔽性好、抗干扰能力强等特点,可以有效地解决高速宽带无线接入问题,并且采用了毫米波技术的通信元件的体积小、重量轻,可以无缝应用到大规模MIMO技术中[2]。毫米波带宽是4G通信中LTE带宽的数千倍,保证了5G通信系统的超高速率和超连接数量,最近有文献指出毫米波通信技术可以和波束赋形技术相结合,单个微基站的波束覆盖的范围可达200米左右,在相同功耗条件下与传统的微小区的覆盖范围相似[3],同时文献[4]指出大规模天线阵列和波束赋形技术结合的毫米波通信系统在5G通信中有广阔的应用前景。毫米波通信毫米级的波长范围使得通信系统中的天线阵列可以密集排列,因此,毫米波通信技术非常适用于大规模3D MIMO通信系统。但如果在基站端为每一根天线配备RF(Radio Frequency)链路,对系统来说太过复杂,造成的成本消耗也令人无法接受,因此,毫米波通信技术还需要不断改进。毫米波通信技术和3D MIMO技术的优势点可以很好的互补结合,解决了当今通信频谱资源匮乏的难题同时又提高了通信系统的信道容量。
最近几年,研究毫米波大规模3D MIMO信道估计算法的很少,文献[5]利用了透镜天线阵列技术的能量聚焦特性减少了基站端所需的RF链路并且将3D信道转换到了空间波束信道。波束空间信道是稀疏的,文献[5]利用此稀疏特性提出了一种自适应的支持检测的信道估计算法,该算法的具体步骤是,先通过波束空间信道形成的特殊稀疏结构获得初始支撑集,然后根据波束空间信道在水平维和垂直维的功率扩散自适应地调整所获得的支撑集,在所有信道分量的支撑集都检测出来之后,就可以在低导频开销的情景下来进行信道估计研究。但文献[5]是在假设系统为窄带的前提下进行研究的,而大多数毫米波通信系统更可能是宽带的形式以实现高数据速率,因此文献[5]的研究具有局限性。但对于宽带毫米波通信系统,最近只有一些微小的成果。在文献[6]中,提出了一种基于同时正交匹配追踪(Simultaneous orthogonal matching pursuit, SOMP)的信道估计方案,具体地就是假设具有共同支撑集,即宽带波束空间信道在不同频率处的支撑集是相同的。文献[7]中提出了一种基于正交匹配追踪(orthogonal matching pursuit, OMP)的信道估计方案,它是先通过OMP算法独立地估计某些频率下的宽带波束空间信道的支撑集,然后组合这些支撑集以表示在所有频率下的共同支撑集。尽管这些信道估计算法的仿真结果都还不错,但它们都忽略了一个事实,就是在大规模MIMO中,发射的宽带信号将对大阵列孔径上的电磁波的物理传播延迟敏感,这被称之为空间宽带效应[8]。因此,文献[8]对具有空间宽带效应的大规模MIMO的信道估计进行了研究,给出了具有空间宽带效应的信道模型。但文献[8]的研究是建立在传统的2D MIMO系统的前提下,并未考虑更加实用的3D MIMO系统。基于此,本文研究了具有空间宽带效应的毫米波3D MIMO的信道估计,首先将空间宽带效应加入到了3D MIMO的基站天线端,然后得到具有空间宽带效应的毫米波3D MIMO信道模型,最后进行信道估计。
在介绍3D MIMO的空间宽带效应之前本节先介绍传统MIMO系统下的空间宽带效应,以前的学者提出的信道估计方案中的大规模MIMO信道模型大多数直接是从传统MIMO信道模型扩展出来的信道模型。然而,近期有学者发现对于大规模MIMO配置中的相同数据符号,在阵列孔径上存在着不可忽略的时间延迟,这种现象是大尺寸阵列天线的固有特性,被称之为空间宽带(选择)效应(Spatial-Wideband Effect)[9-10]。事实上,某些学者已经在雷达通信系统发现了这种现象,并且在阵列天线信号处理领域做了相应的研究[11-12]。但在现在的大规模MIMO通信系统中,人们往往会考虑由多径延迟扩展带来的频率选择效应,而忽略空间选择效应。因此,为了通信系统的准确性,频率选择效应和空间选择效应都应当考虑。当考虑了双宽带效应后,传统的大规模MIMO通信系统信道模型就不再适用了,需要重新制定新的大规模MIMO通信系统信道模型来凸显双宽带效应。
具体的空间宽带效应可以从图1中看出,为了示意图的方便性,本文考虑场源信号照射到具有N个单个方向的均匀线性阵列。设天线元件间的间距为d,载波波长为lc,载波频率为fc,y表示天线之间的相位差,相邻两天线之间的时间延迟可以被明确地计算为其中c表示光速。对于一个符号周期为Ts的单载波通信系统,其基带信号可以被表示为:
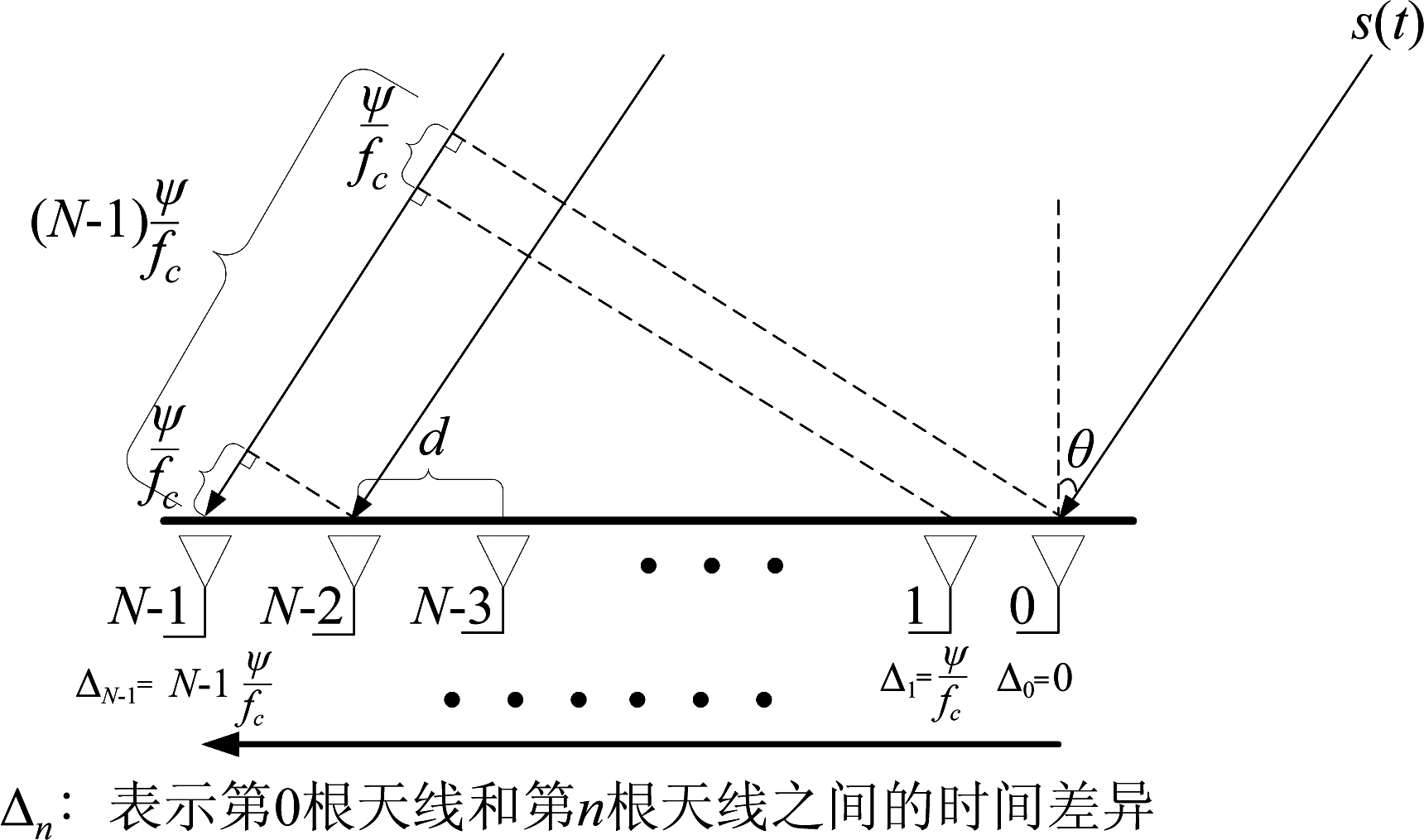
图1 线性阵列天线的空间宽带效应
Fig.1 Spatial wideband effect of linear array antenna
(1)
其中,g(t)为脉冲整形信号,s[i]为发送符号,相应的通带信号可被表示为
{s(t)ej2pfct},调制信号的带宽约为
在不失一般性的前提下,假设第一根天线与源信号完全同步并且接受到了信号{αs(t)ej2pfct},其中α表示复信道增益,那么其他天线接收到的信号将会是延迟后的{αs(t)ej2pfct}信号。
从图1可以看出,第0根天线和第n根天线之间的时间间隔为
第n根天线接收到的通带信号可以被表示为:
(2)
而其等效的基带接收信号可被表示为:
(3)
当基站端的天线数较少时,或者s(t)的传输带宽很窄,那么对于每根天线这样两种关系
和
成立。在这种情况下,基站端所有N根天线的接收信号可被表示为:
y(t)=[y0(t),y1(t),…,yn(t)]T=
αs(t)[1,e-j2py,…,e-j2p(N-1)y]Tαs(t)a(y)
(4)
其中,a(y)即为常见的指向角度θ的空间导向向量,等效基带信道向量将为h=αa(y),基带信道可被表示为[48]:
(5)
其中,L表示信道中的传输路径数,
表示第l条路径的到达角(DOA),tl表示相应的路径延迟,δ(·)表示狄拉克脉冲函数。需要强调的是,假设
的前提条件是符号周期Ts足够大或者基带信号s(t)的带宽足够窄,这是建立窄带信道模型的必要条件。但在宽带大规模MIMO系统中,天线数N往往会非常大且传输基带信号s(t)带宽也很大,在这种情况下上面所建立的关系不再成立,即
不再约等于
也会大于等于符号周期Ts,第n根天线接收到的传输符号和第0根天线上的不同。这种现象在阵列信号处理领域被称为空间宽带效应,且已经在雷达信号处理领域有了良好的研究,但是在无线通信领域很少被学者提及。
在毫米波大规模MIMO通信系统中窄带假设不再成立,传统的大规模MIMO通信系统信道模型[13]和其他从传统信道模型演化过来的信道模型不再适用,需要设计相应的信道模型,因为有数值表明,当基站端天线的数量或传输带宽变大时,不考虑空间宽带效应的算法的性能将会大大降低。在文献[14]中发现,随着系统带宽的增加,相控阵混合结构的性能会因为空间宽带效应而降低。
本文先考虑一个毫米波大规模MIMO通信系统,该系统中配备一个具有N根天线的均匀线性阵列的基站和K个随机单天线用户。本文将在OFDM方案中考虑双宽带效应,因为它适用于绝大部分宽带无线通信协议,OFDM子载波数量设为M。假设基站端和第k个用户之间有Lk个传输路径,τk,l,n表示第k个用户到第n根天线之间的第l个路径上的传输时间延迟。那么第k个用户到第n根天线的基带接收信号可被表示为:
(6)
其中,
表示相应的复信道增益,xk(t)表示第k个用户的传输信号,设第k用户的第l条路径的到达角为
从图1中可以得出:
(7)
为了更方便的表示,在下文设τk,l=τk,l,0。将式(7)代入式(6)中,得到:
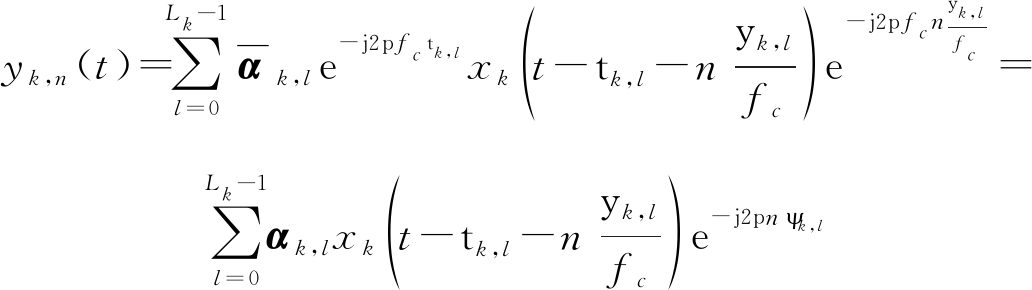
(8)
其中,
为等效信道增益。下一步能得出第k个用户和第n根天线之间的上行链路空间-时间信道模型为:
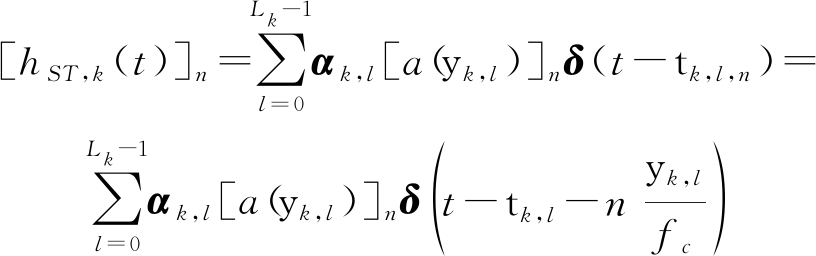
(9)
其中,a(y)[1,e-j2py,…,e-j2p(N-1)ψ]T,将式(9)进行连续时间傅里叶变换操作,得到第k个用户到第n根天线之间的上行链路空间-频域响应信道:
[hSF,k( f )]n=
[hST,k(t)]ne-j2pftdt=
(10)
将
表示OFDM中的子载波间隔,然后第m个子载波的空间-频率信道系数可被表示为[hSF,k(mη)]n,∀m∈Ι(M)。将所有N根天线的信道组合起来得到一个空间-频率信道矩阵:
Hκ=[hSF,k(0),hSF,k(η),…,hSF,k((M-1)η)]=
(11)
其中,符号“°”表示哈达玛乘操作并且
b(tk,l)[1,e-j2pηtk,l,…,e-j2p(M-1)ηtk,l]T∈CM×1
(12)
可以被看作为指向第k个用户上第l条路径延迟的频率域导向向量,Θ(yk,l)是一个N×M维的矩阵并且其第(n,m)个元素为:
[Θ(
k,l)]n,mexp(-j2pnmη
),
n∈Ι(N),m∈Ι(M)
(13)
以上是考虑空间和频率宽带效应(双宽带效应)而得出的更精确的大规模MIMO通信系统的信道模型,在这种情况下空间导向向量a(yk,l)和频域导向向量b(tk,l)以及相移矩阵Θ(yk,l)直接耦合。本文称式(11)为空间-频域宽带信道(双宽带信道),这是在基站端配备均匀线性天线的毫米波大规模MIMO通信系统情景下得到的。
在基站端配置均匀平面天线阵列情景下,即在毫米波大规模3D MIMO通信系统模型中,空间导向向量需要做一些改变,本文参考文献[5]的做法,设均匀平面天线阵列水平维有N1根天线,垂直维有N2根天线,总天线N=N1N2,再设其第k个用户的第l条路径的空间垂直角表示为
空间水平角表示为
则其空间导向向量为:
(14)
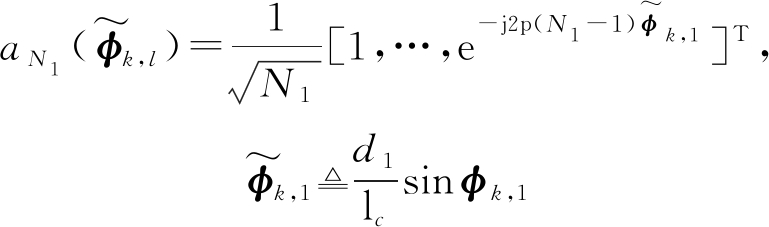
(15)
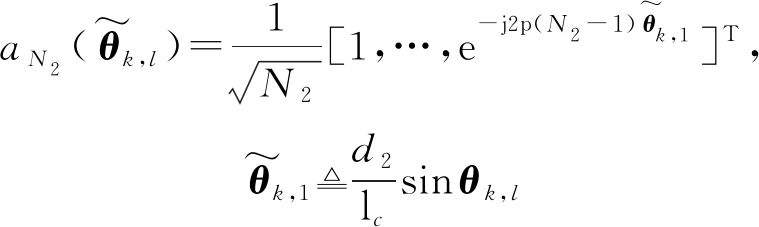
(16)
其中,φk,l为第k个用户的第l条路径的物理垂直角,θk,l为第k个用户的第l条路径的物理水平角,d1(d2)为天线元件间的间距,因为是均匀分布的平面天线阵列,所以有d=d1=d2。将式(14)代入进式(11),得到毫米波大规模3D MIMO通信系统的空间-频域信道模型:
(17)
均匀平面天线阵列有垂直维和水平维两个方向的入射角,因此相移矩阵需要重新设计。本文采用传统的均匀平面天线阵列入射角处理方式,Θ(φk,l,θk,l)为N×M的矩阵,和物理垂直角、物理水平角有关,矩阵中每项参数如下式所示:
n∈Ι(N),m∈Ι(M)
(18)
由式(18)可以看出角度域和延迟域以双重方式进行耦合,类似的二元性也出现在空间域和频域中,即它们各自的傅里叶变换中,具体如图2所示。角度域波束赋形和时域波束赋形可以通过加权空间域的天线和频域中的子载波来实现,另外角度-延迟域中每条路径的能量在角度和延迟尺度上扩散到相同的水平,本文将在下文以定理1给出。
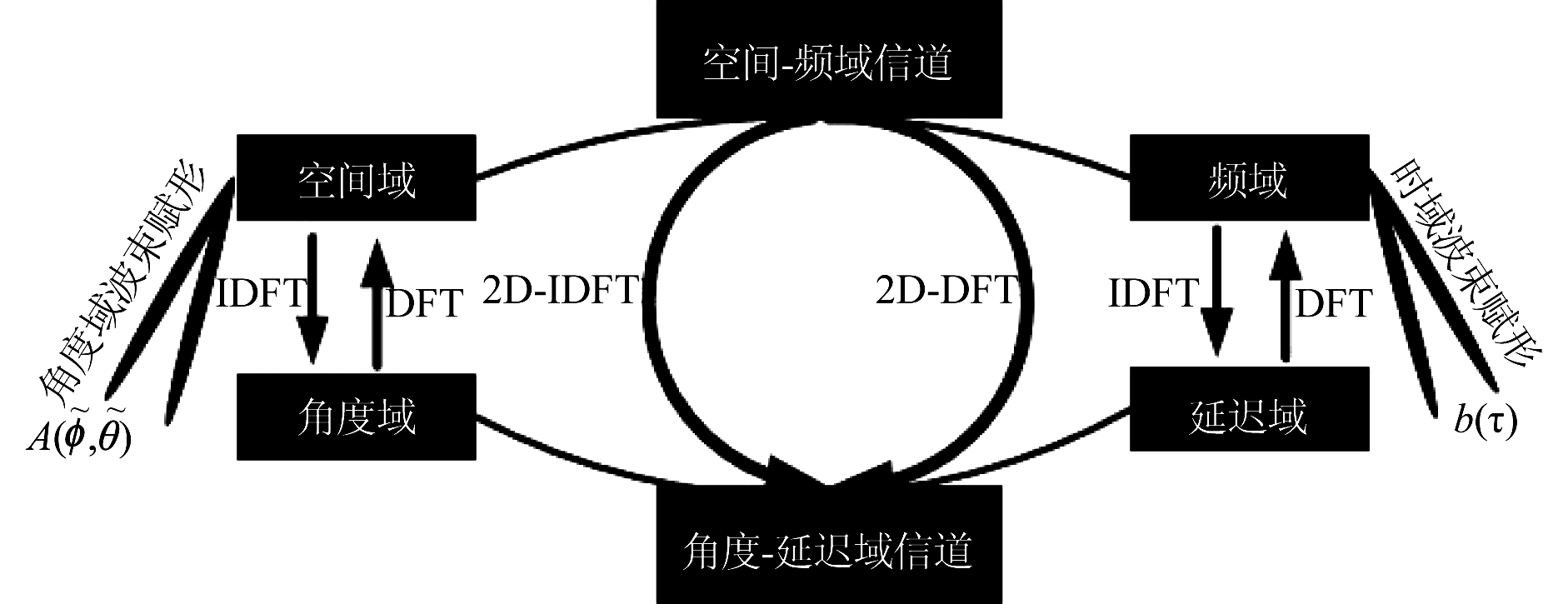
图2 角度域与延迟域以及它们的傅里叶变换
之间的对偶性:空间域和频域
Fig.2 Duality between the angle domain and the delay domain and their Fourier transform: spatial domain and frequency domain
本文给出的双宽带效应信道模型与传统信道模型最大的不同之处就在于多了相移矩阵Θ(φk,l,θk,l)的影响,即考虑了空间宽带效应的影响。因此在研究双宽带效应信道模型的特性之前,首先给出Θ(φk,l,θk,l)的渐进性质。
引理1 当N→
,M→时,如果条件
和
满足,那么Θ(φk,l,θk,l)的二维离散傅里叶逆变换为块稀疏矩阵,其中的非零元素都保持在正方形区域内,即
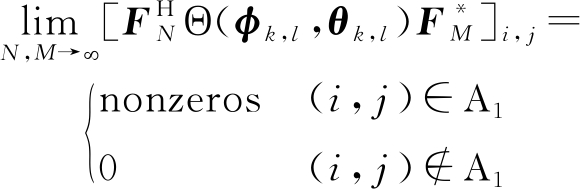
(19)
其中FN为归一化的N维DFT矩阵并且其第(i, j)项的值为
给出:
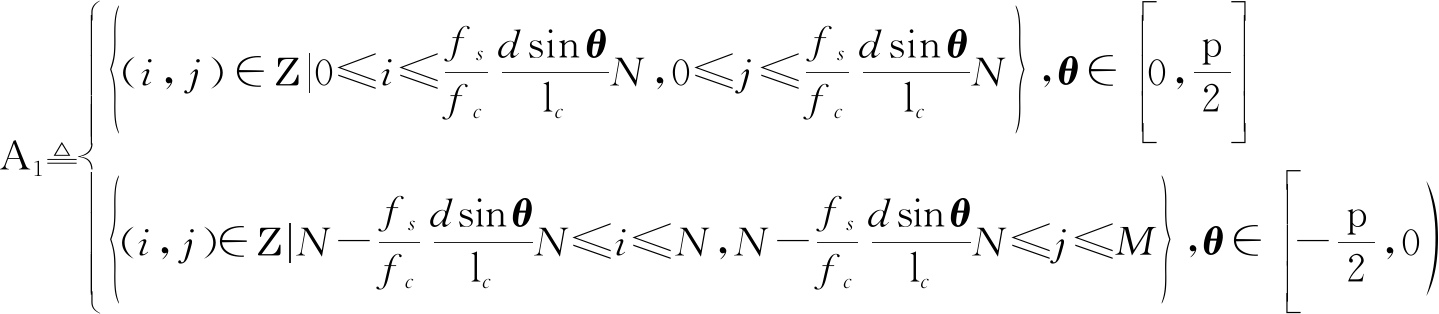
(20)
根据引理1本文可以给出定理1,如下所述。
定理1 当N→,M→时,转换到角度延迟域的信道
是一个稀疏矩阵并且只有Lk个非零区域,即每个区域对应其中的一条路径与传统的毫米波大规模3D MIMO通信系统信道相比,在角度延迟域的双宽带信道的表现完全不同,如果没有空间-宽带效应的影响,即相移矩阵Θ(φk,l,θk,l)不存在或为全1矩阵,每一条路径在角度延迟域信道表现为的冲激脉冲的形状。但在空间-宽带效应的影响下,引理1和定理1表明Θ(φk,l,θk,l)会将每条路径处的能量从脉冲形式的冲激形状扩散到方形区域,如图3和图4所示,N=256,M=128,d/lc=0.5, fc/fs=7。
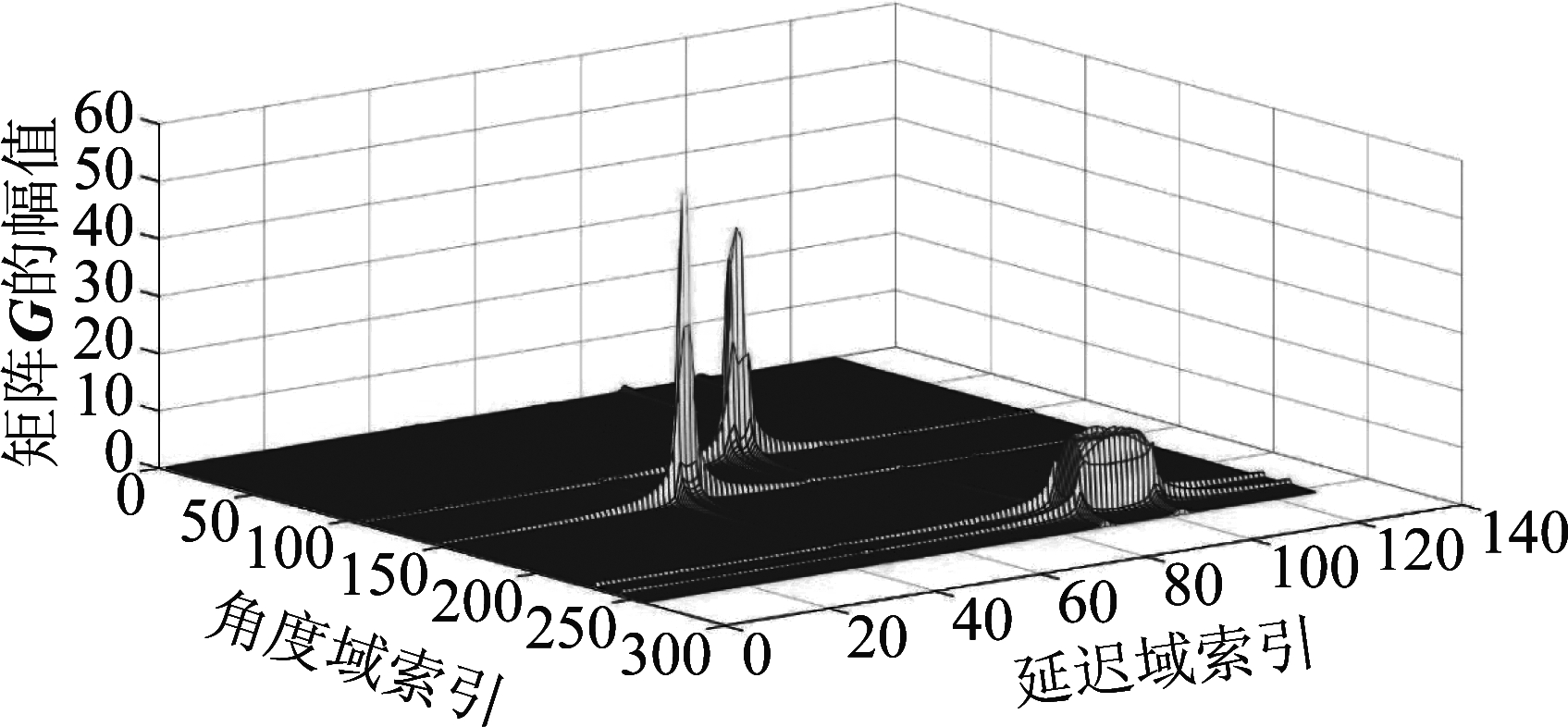
图3 角度延迟域的表面图
Fig.3 Surface map of the angular delay domain
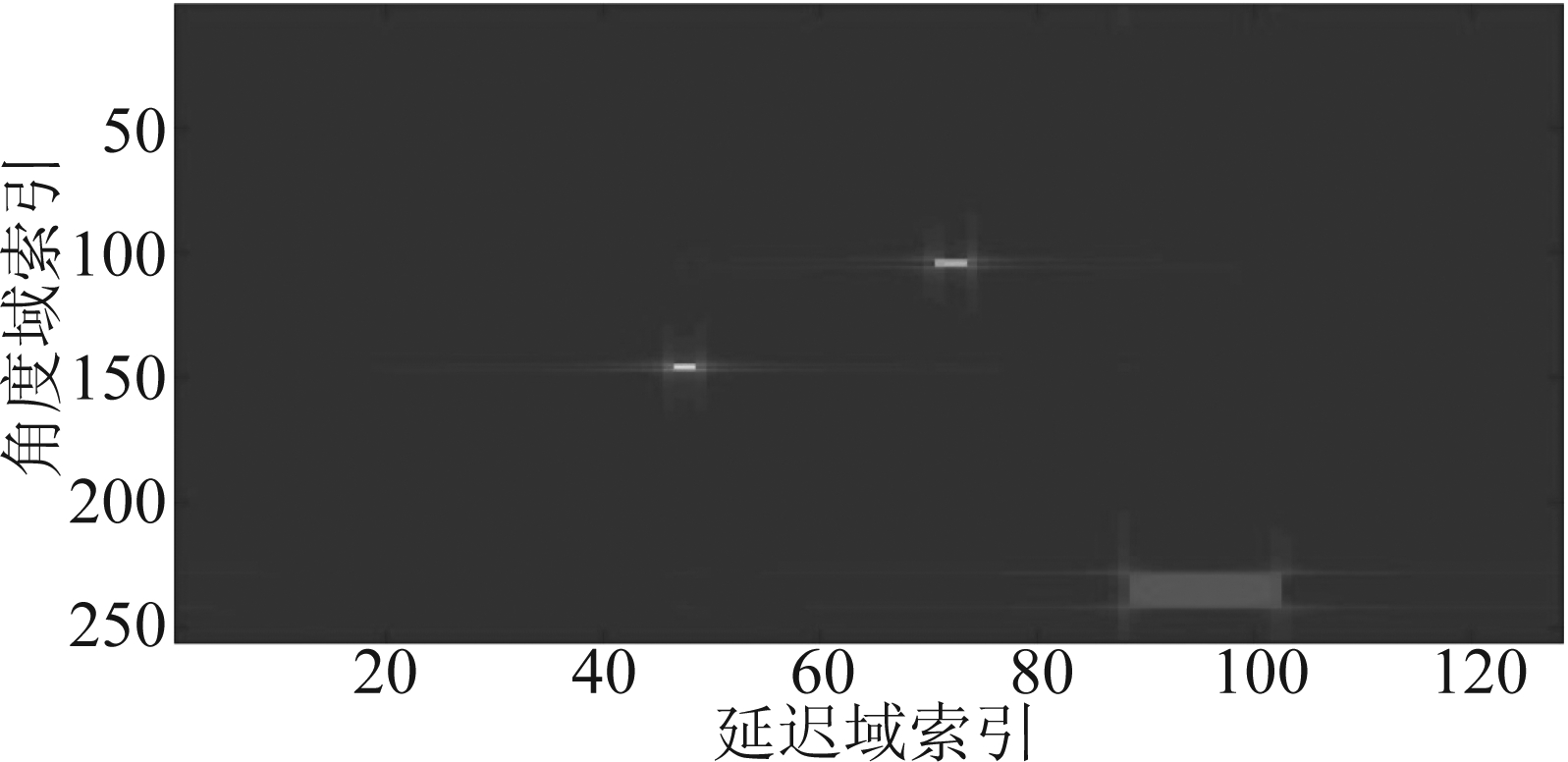
图4 角度延迟域的灰度图
Fig.4 Grayscale image of the angular delay domain
转换到角度延迟域的信道除了稀疏度高,它还有正交特性,将双宽带信道矩阵进行矢量化处理:
αk,l[vec(Θ(φk,l,θk,l))∘
(21)
定理2:当N→,M→时,下式成立:
(22)
从定理2可以看出,如果任意两个用户不共享相同的路径,则他们的信道向量渐进正交,这种现象被称之为角度延迟正交性,它表明不同位置的用户或同一位置但不在同一路径的用户的信道向量正交。通过利用这种特性,可以在没有导频污染的情况下进行信道估计方案的研究。
在经过上文的详细阐述,已经了解到毫米波大规模3D MIMO通信系统信道模型是传统3D MIMO通信系统信道模型的扩展,因此本文需要为此信道提出一个新的信道估计方案。首先对基站端的每根天线应用传统的MIMO最小二乘信道估计算法[15],将
表示为用户k到基站端的上行链路前导信道。从定理1中可以看出,物理垂直角φk,l、物理水平角θk,l和时间延迟tk,l参数隐藏在转换到角度延迟域中的信道矩阵
的非零区域中,但由于本文在处理均匀平面天线进行了克罗内克积操作处理,天线端的垂直角和水平角无法体现在角度延迟域的信道矩阵
中,但可以得到延迟参数,角度参数需要进一步处理。由于在实际场景中,N→,M→条件不会满足,因此将会出现功率泄露,即其中的非零区域将会扩散[16-17]。因此如果想要得到精确的参数数据,就需要通过更复杂的设计获得。
首先,给出角度旋转矩阵式(23)和延迟旋转矩阵式(24):
(23)
(24)
利用这两个矩阵就能得到角度延迟旋转矩阵:
(25)
对于每个用户能很容易的从角度延迟域信道矩阵中计算出其路径数量Lk,即非零区域的个数。从仿真图4中可以看出非零区域是一个方形区域,其横坐标是延迟域(子载波)的序号,纵坐标是角度域(天线元件)的序号。因此从中可以得到粗略的时间延迟
在得到了粗略的时间延迟后,可以利用下式来得到精确的时间延迟数据:
(26)
其中,U(a,b)被定义为点(a,b)的领域范围,在得到延迟数据后,再将向量化后的信道矩阵重构成能表现垂直角和水平角的信道矩阵。由于
即将均匀平面天线拉直为一个线性矩阵,通过下式(27)将
重构成隐藏物理垂直角和水平角的矩阵,如图5、图6所示。
(27)
类似的角度旋转矩阵如下所示:
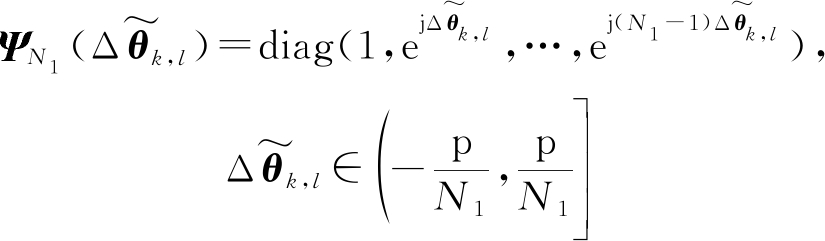
(28)
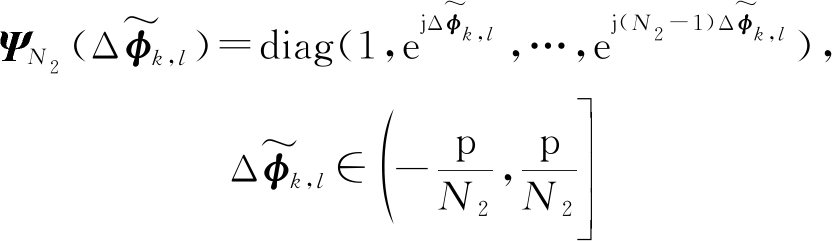
(29)
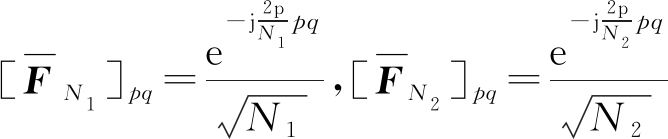
(30)
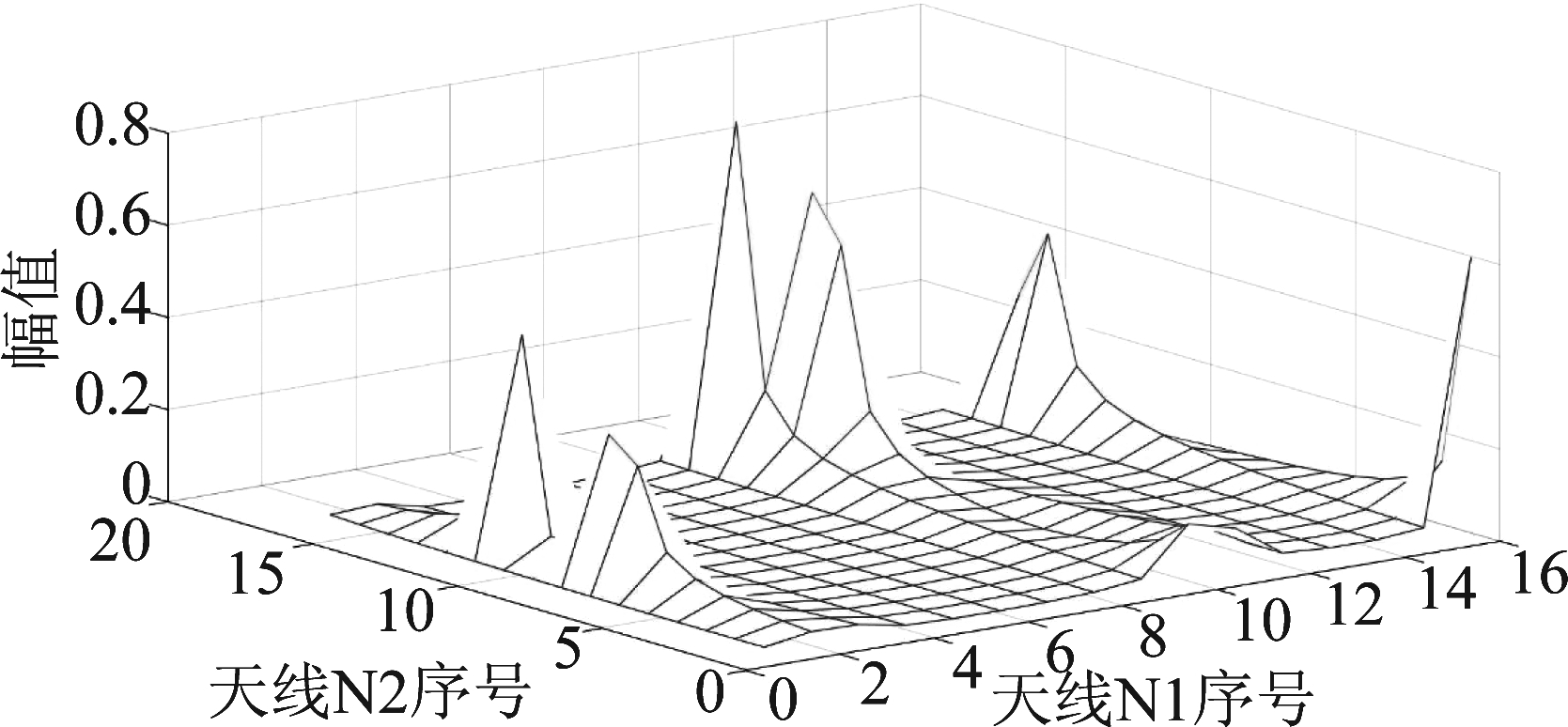
图5 重构的信道矩阵
Fig.5 Reconstructed channel matrix
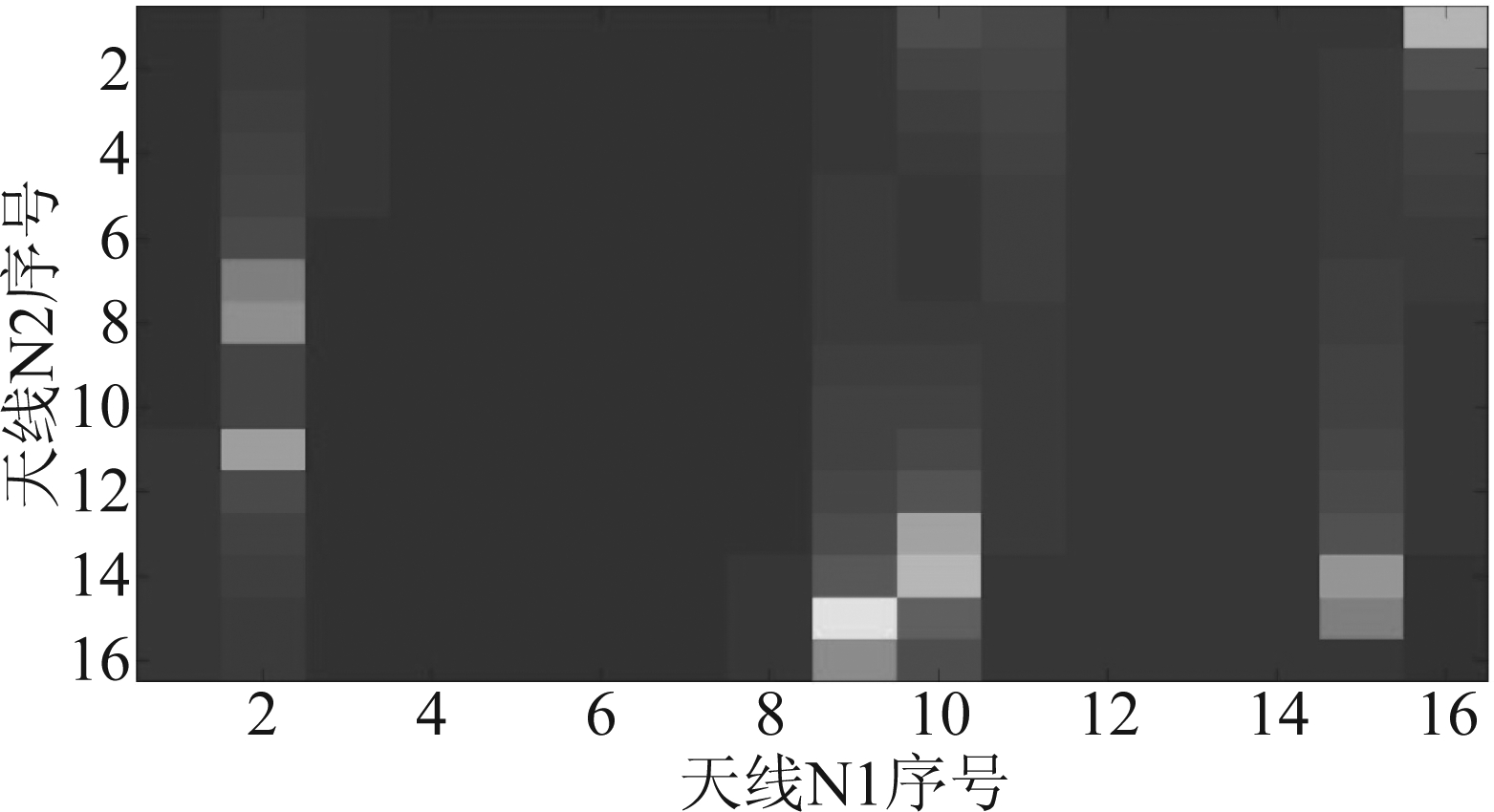
图6 重构的信道矩阵灰度图
Fig.6 Reconstructed channel matrix grayscale
下面再进行角度旋转操作
(31)
(32)
这样就得到了第k个用户的第l条路径上的水平角和垂直角,现在将其写入集合
中,在得到以上三个参数后,还需要估计信道增益αk,l的值。由定理2得知空间宽带效应特性允许具有不同角度延迟特征的用户通过相同的导频序列进行训练,并且不会导致任何导频污染。为了实现简单的信道估计算法,假设所有用户在训练块的所有子载波上发送导频“1”,于是基站端的所有天线接收到的上行链路信号为维度是N×M的矩阵:
(33)
为用户k的训练功率约束,WU为独立同分布的高斯白噪声矩阵,其内的每个元素呈
分布。
通过利用双宽带效应信道的角度延迟正交性和先前已经获得的集合Υl,每个用户的每条路径的信道增益可以被估计为:
(34)
现在信道的三个关键参数都已经获得,于是上行链路的估计信道可以被表示为:
(35)
以上就是整个信道估计方案的关键步骤流程。
本次的仿真场景为,基站端配备均匀平面矩阵,图7中水平方向和垂直方向的天线数都为N1=N2=16,天线间隔d设为载波波长的一半,载波频率fc=58 GHz,带宽设为fs=2 GHz,射频链路数NRF=8,用户数K=8并且每个用户都配备单根天线,均匀的分布在整个小区中。本文设每个用户的通信路径Lk=3,一个视距分量和两个非视距分量,垂直角和水平角在[-0.5,0.5]之间服从独立同分布的均匀分布,噪声为高斯白噪声且其中的每个元素服从分布。
图7是本文得到实验仿真结果,为了表现信道算法良好的性能,本文将其与LS(最小平方)算法,SOMP(同时正交匹配追踪)算法和OMP(正交匹配追踪)算法进行了比较。由图中可知,横坐标为信噪比SNR,纵坐标为归一化的最小均方误差NMSE。
(36)
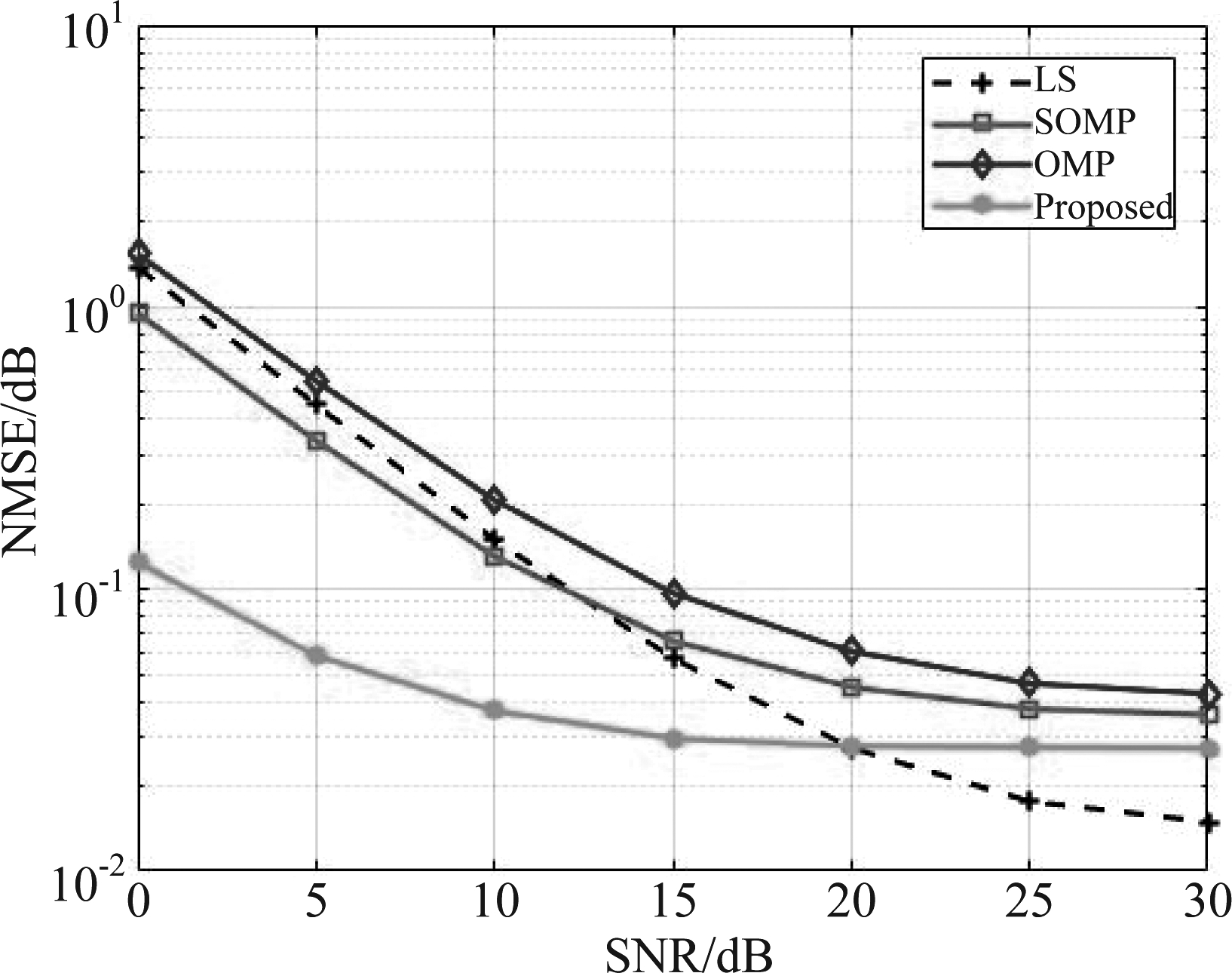
图7 不同信道估计算法的NMSE性能比较
Fig.7 Comparison of NMSE performance of different channel estimation algorithms
从图7中可以看出,在低信噪比区域(0～13 dB)本文所提出的算法较其他三种算法好,在整个信噪比区域本文的NMSE也比OMP与SOMP算法好,只有在(13～30 dB)区域本文的算法较LS算法略微有些不足,但本文的算法较其他所有算法步骤简单,这也是本文的优势所在。
本文分析了在宽带毫米波通信系统中常见的空间宽带效应以及它的特性,然后重新建模了毫米波大规模MIMO通信系统的信道,并且将其扩展到了基于透镜的3D MIMO通信系统中,然后利用双宽带效应的角度延迟域中的稀疏特性提出一种简单的信道估计方案,最后将该算法与其他传统信道估计算法通过仿真进行了对比分析,证明了本文提出的方案在低信噪比区域的优越性。
[1] Zheng K, Zhao L, Mei J, et al. Survey of Large-scale MIMO Systems[J]. IEEE Communications Surveys & Tutorials, 2015, 17(3): 1738-1760.
[2] 于彦彦. 毫米波MIMO中混合预编码技术的研究[D]. 南京邮电大学, 2018.
Yu Yanyan. Research on Mixed Precoding Technology in Millimeter Wave MIMO[D]. Nanjing University of Posts and Telecommunications, 2018.(in Chinese)
[3] Rangan S, Rappaport T S, Erkip E. Millimeter-Wave Cellular Wireless Networks: Potentials And Challenges[J]. Proceedings of the IEEE, 2014, 102(3): 366-385.
[4] Han S, Chih-Lin I, Xu Z, et al. Large-scale Antenna Systems with Hybrid Analog and Digital Beamforming for Millimeter Wave 5G[J]. IEEE Communications Magazine, 2015, 53(1): 186-194.
[5] Gao X, Dai L, Han S, et al. Beamspace Channel Estimation for 3D Lens-based Millimeter-wave Massive MIMO Systems[C]∥2016 8th International Conference on Wireless Communications & Signal Processing(WCSP). IEEE, 2016: 1-5.
[6] Gao Z, Hu C, Dai L, et al. Channel Estimation for Millimeter-wave Massive MIMO with Hybrid Precoding over Frequency-selective Fading Channels[J]. IEEE Communications Letters, 2016, 20(6): 1259-1262.
[7] Venugopal K, Alkhateeb A, Prelcic N G, et al. Channel Estimation for Hybrid Architecture-based Wideband Millimeter Wave Systems[J]. IEEE Journal on Selected Areas in Communications, 2017, 35(9): 1996-2009.
[8] Wang B, Gao F, Jin S, et al. Spatial-and Frequency-wideband Effects in Millimeter-wave Massive MIMO Systems[J]. IEEE Transactions on Signal Processing, 2018, 66(13): 3393-3406.
[9] Brady J H, Sayeed A M. Wideband Communication with High-dimensional Arrays: New Results and Transceiver Architectures[C]∥IEEE International Conference on Communication Workshop. IEEE, 2015: 1042-1047.
[10] Wang B, Gao F, Jin S, et al. Spatial-wideband Effect in Massive MIMO Systems[C]∥2017 23rd Asia-Pacific Conference on Communications(APCC). IEEE, 2017: 1- 6.
[11] Friedlander B, Weiss A J. Direction Finding for Wide-band Signals Using an Interpolated Array[J]. IEEE Transactions on Signal Processing, 2002, 41(4): 1618-1634.
[12] Yoon Y S, Kaplan L M, McClellan J H. TOPS: New DOA Estimator for Wideband Signals[J]. IEEE Transactions on Signal Processing, 2006, 54(6): 1977-1989.
[13] Ayach O E, Rajagopal S, Abu-Surra S, et al. Spatially Sparse Precoding in Millimeter Wave MIMO Systems[J]. IEEE Transactions on Wireless Communications, 2013, 13(3): 1499-1513.
[14] Zhang J, Huang X, Dyadyuk V, et al. Massive Hybrid Antenna Array for Millimeter-wave Cellular Communications[J]. IEEE Wireless Communications, 2015, 22(1): 79- 87.
[15] Barhumi I, Leus G, Moonen M. Optimal Training Design for MIMO OFDM Systems in Mobile Wireless Channels[J]. IEEE Transactions on Signal Processing, 2003, 51(6): 1615-1624.
[16] Xie H, Gao F, Zhang S, et al. A Unified Transmission Strategy for TDD/FDD Massive MIMO Systems with Spatial Basis Expansion Model[J]. IEEE Transactions on Vehicular Technology, 2016, 66(4): 3170-3184.
[17] Xie H, Gao F, Jin S. An Overview of Low-rank Channel Estimation for Massive MIMO Systems[J]. IEEE Access, 2016, 4: 7313-7321.
程 涛 男, 1992年生, 安徽芜湖人。南京邮电大学通信与信息工程学院硕士研究生。主要研究方向3D MIMO系统信道估计技术。
E-mail: 1216012020@njupt.edu.cn
李 汀 男, 1979 年生, 江苏扬州人。南京邮电大学通信与信息工程学院, 博士, 讲师, 研究方向为MIMO技术、3D MIMO技术、协作通信等。
E-mail: lit@njupt.edu.cn
季 薇 女, 1979年生, 江苏淮安人。南京邮电大学通信与信息工程学院副教授。主要研究方向为无线通信、机器学习。
E-mail: jiwei@njupt.edu.cn
梁 彦 女, 1979年生, 河北唐山人。南京邮电大学通信与信息工程学院, 讲师, 博士。主要研究方向为无线通信、信号处理。
E-mail: liangyan@njupt.edu.cn
李 飞 女, 1966 年生。南京邮电大学通信与信息工程学院教授、博士生导师。主要研究方向为量子智能计算、群智能和无线通信中的信号处理技术。
E-mail: lifei@njupt.edu.cn