在图像分析处理技术中,稀疏低秩[1]具有重要的研究意义。而目前存在的问题是,在稀疏性和低秩性之外,如何更进一步地去发掘和利用数据中潜在的本质结构,开发快速的、并行的新算法,既能够提高处理的精确度,又能够提升算法的效能。综合目前所提出的各种稀疏低秩的算法来看,较为常见且有效的评价办法就是其计算效率。基于此,本文提出了一种快速稀疏低秩鲁棒主成分分析算法,在不用考虑计算机处理能力的前提下,可以实现较好的处理效果,是一种较为高效的稀疏低秩算法[2- 6]。
在数字图像或视频的实际应用中,给定的数据矩阵D往往是低秩或近似低秩的,但存在随机幅值任意大但是分布稀疏的误差破坏了原有数据的低秩性,为了恢复矩阵D的低秩结构,可将矩阵D分解为两个矩阵之和,即
D=A+E
其中矩阵A和E未知,但A是低秩的。当矩阵E的元素服从独立同分布的高斯分布时,可用经典的PCA来获得最优的矩阵A,即求解下列最优化问题:
当E为稀疏的大噪声矩阵时,问题转化为双目标优化问题:
引入折中因子λ,将双目标优化问题转换为单目标优化问题:
表1是稀疏表示和矩阵低秩分解类比,从中可以看出其中的一些特征,围绕其可以开展很多相关研究[10-15]。
表1 稀疏表示和矩阵低秩分解类比
Tab.1 Sparse representation and matrix low rank decomposition analogy

Sparse VectorLow-Rank MatrixDegeneracy ofone signalcorrelated signalsMeasureℓ0 normx0rank(X)Convex Surrogateℓ1 normx1Nuclear normX*Compressed Sensingy=AxY=A(X)Error Correctiony=Ax+eY=A(X)+EDomain Transformyτ=Ax+eYτ=A(X)+EMixed StructuresY=A(X)+B(E)+Z
在这里使用混合规范[11-17]的办法,混合规范在遗传学,脑电图和信号处理等应用中的组相关性建模中具有非常重要的作用,如公式(1)所示:
(1)
其中A∈RM×N是具有非重叠组的混合规范应用于矩阵形式的数值,am∈RN代表不同的群体。
公式(1)主要贡献是提高计算效率,用于计算投影到l ,1。
,1。
公式(2)是目前最为先进的搜寻主成分的算法
![]()
s.t.‖X‖ ,1≤τ
,1≤τ
(2)
这个 l ,1的约束问题已经应用于图公式(3)将计算时间缩短了4~14倍。
,1的约束问题已经应用于图公式(3)将计算时间缩短了4~14倍。
(3)
公式(3)可以计算解决独立的问题,所以可以进行单因素解算。
(4)
当X(θ)=prox=·=p,1时,公式(5)满足傅里叶变换。
g(θ)=‖X(θ)‖p,1-τ
(5)
对于此解决方案,我们需要解决与“1-ball”密切相关的问题,它被定义为:
(6)
其中x,u∈R。
(7)
shrink(x,λ(τ))=sign(x)⊙max(|x|-λ(τ),0),λ(τ)是依赖于τ的收缩参数。有几种有效的算法来寻找这个收缩参数,如下式:
(8)
Steffensen的方法是拟牛顿根查找算法,当导数的解析表达式不可用时,该算法是有用的。缺点是需要两个功能评估,因此通常比牛顿法更优秀。给定函数f(x),Steffensen的原始迭代包括更新。
(9)
由于所涉及的所有分量都是正的,这是一个凸优化问题。对于每个部分,可以通过凸优化求得其局部最大值,即最优解。
(10)
对公式(10)凸优化求最优解得到下式:
![]()
subject to γ0∈X
(11)
由公式(9)求和,可以获得公式(10),整个算法流程如图1所示。下面介绍的所有测试都是使用运行在Intel i7-7700hq CPU(4核、3.50 GHz、16 GB RAM上的单线程Matlab代码计算的。
设x*是通过公式(11)求出的最小值,如果![]() 且
且![]() 则x*是其全局最小点,即
则x*是其全局最小点,即![]()
![]()
(12)
为了确保使用凸优化得到的解是最优解,将其与使用迭代法(公式(12))所得的解进行对比,发现凸优化是最佳解决方案。
接着公式(10)继续讨论,当γ(ij)∈R(ij),可以得到公式(13)
(13)

图1 算法伪代码
Fig.1 The pseudo code of the algorithm
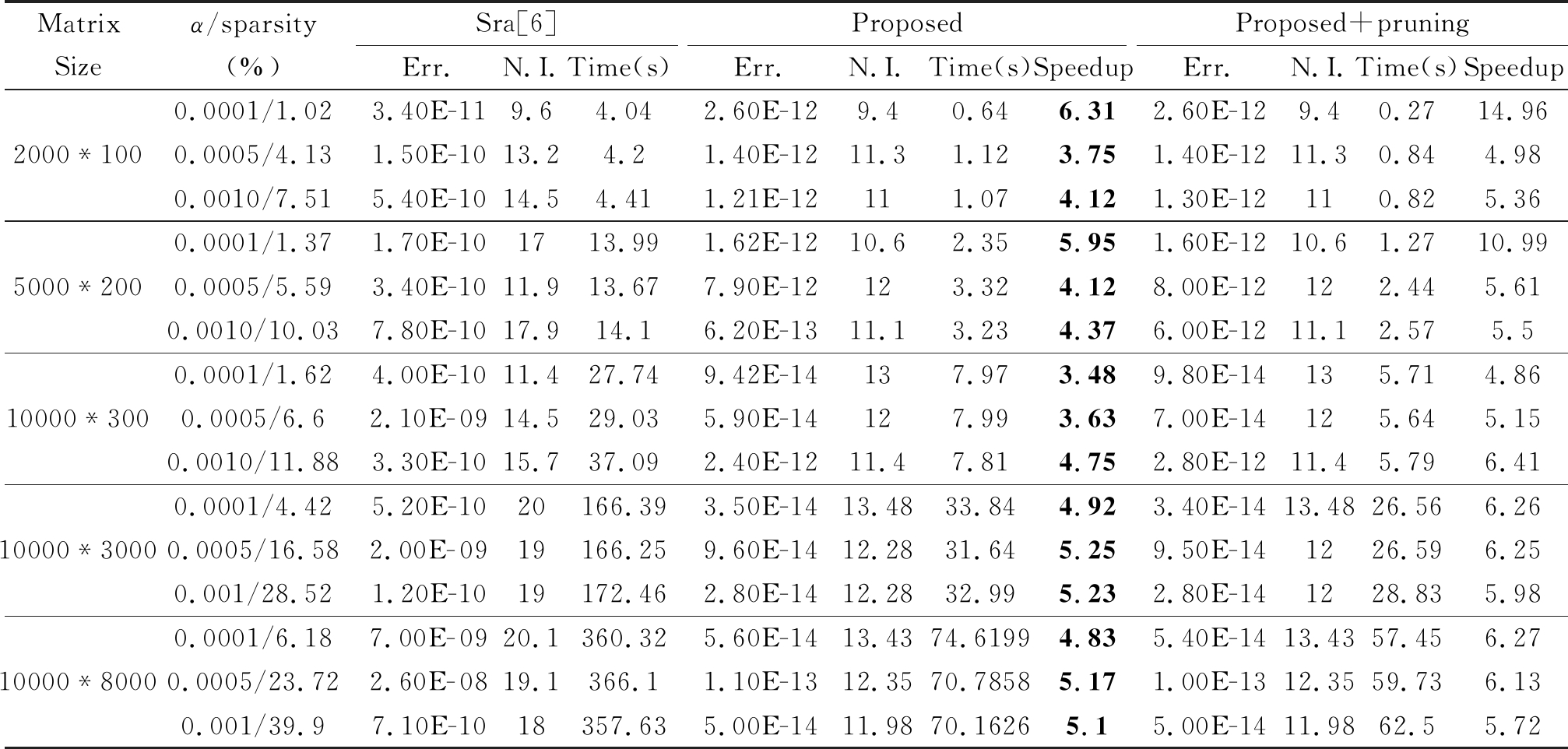
表2 对不同尺寸矩阵的模拟结果和三种测试方法进行了比较。
将错误(Err.),迭代次数(NI.)和它们的运行时间(Time(s))作为评价指标
Tab.2 Compares the simulation results of different size matrices with the three test methods.
Error (Err.), iteration times (NI.) And their running time (Time (s)) as an evaluation index
Matrix Sizeα/sparsity(%)Sra[6]Err.N.I.Time(s)ProposedErr.N.I.Time(s)SpeedupProposed+pruningErr.N.I.Time(s)Speedup2000*1000.0001/1.023.40E-119.64.042.60E-129.40.646.312.60E-129.40.2714.960.0005/4.131.50E-1013.24.21.40E-1211.31.123.751.40E-1211.30.844.980.0010/7.515.40E-1014.54.411.21E-12111.074.121.30E-12110.825.365000*2000.0001/1.371.70E-101713.991.62E-1210.62.355.951.60E-1210.61.2710.990.0005/5.593.40E-1011.913.677.90E-12123.324.128.00E-12122.445.610.0010/10.037.80E-1017.914.16.20E-1311.13.234.376.00E-1211.12.575.510000*3000.0001/1.624.00E-1011.427.749.42E-14137.973.489.80E-14135.714.860.0005/6.62.10E-0914.529.035.90E-14127.993.637.00E-14125.645.150.0010/11.883.30E-1015.737.092.40E-1211.47.814.752.80E-1211.45.796.4110000*30000.0001/4.425.20E-1020166.393.50E-1413.4833.844.923.40E-1413.4826.566.260.0005/16.582.00E-0919166.259.60E-1412.2831.645.259.50E-141226.596.250.001/28.521.20E-1019172.462.80E-1412.2832.995.232.80E-141228.835.9810000*80000.0001/6.187.00E-0920.1360.325.60E-1413.4374.61994.835.40E-1413.4357.456.270.0005/23.722.60E-0819.1366.11.10E-1312.3570.78585.171.00E-1312.3559.736.130.001/39.97.10E-1018357.635.00E-1411.9870.16265.15.00E-1411.9862.55.72
如表2所示,分别对不同尺寸矩阵的模拟结果和三种测试方法进行了比较。这三种方法分别是Sra,proposed以及proposed+pruning,Proposed就是本文的算法,可以看出将本文算法与pruning结合在不同的尺寸下,无论在错误(Err.),迭代次数(NI.)还是它们的运行时间(Time(s))上,都具有优势。
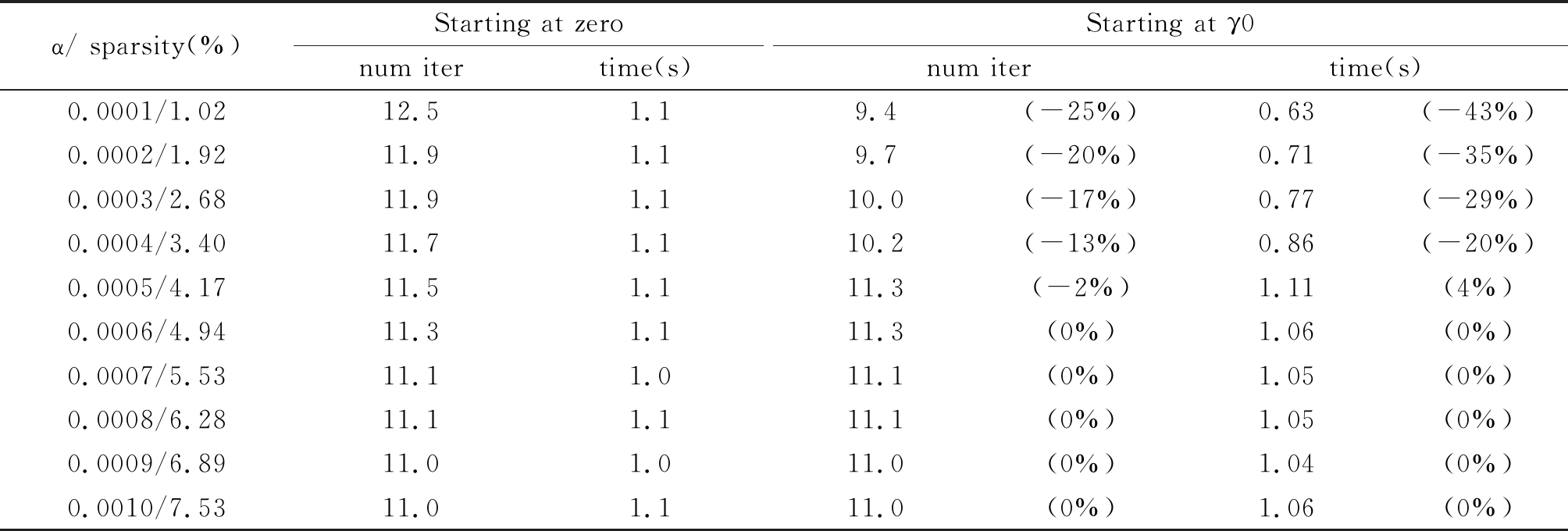
表3 算法对于初始点γ0的影响
Tab.3 The influence of the algorithm on the initial point γ0
α/ sparsity(%)Starting at zeronum itertime(s)Starting at γ0num itertime(s)0.0001/1.0212.51.19.4(-25%)0.63(-43%)0.0002/1.9211.91.19.7(-20%)0.71(-35%)0.0003/2.6811.91.110.0(-17%)0.77(-29%)0.0004/3.4011.71.110.2(-13%)0.86(-20%)0.0005/4.1711.51.111.3(-2%)1.11(4%)0.0006/4.9411.31.111.3(0%)1.06(0%)0.0007/5.5311.11.011.1(0%)1.05(0%)0.0008/6.2811.11.111.1(0%)1.05(0%)0.0009/6.8911.01.011.0(0%)1.04(0%)0.0010/7.5311.01.111.0(0%)1.06(0%)
如表3所示,可以看出算法从γ0点比从零点开始运算迭代次数最多可以下降25%,而时间减少了最多43%,可见算法在确定了γ0的条件下,性能更加优异。
公式(13)是当整个稀疏化矩阵带入到公式(10)中得到的式子。
为了验证改进算法的可实施性,进行了实例的测试,如图2是低秩矩阵图像去光照影响恢复的应用,通过本方法快速找到了显著性特征,并快速标注出来,然后通过去光照算法进行恢复。
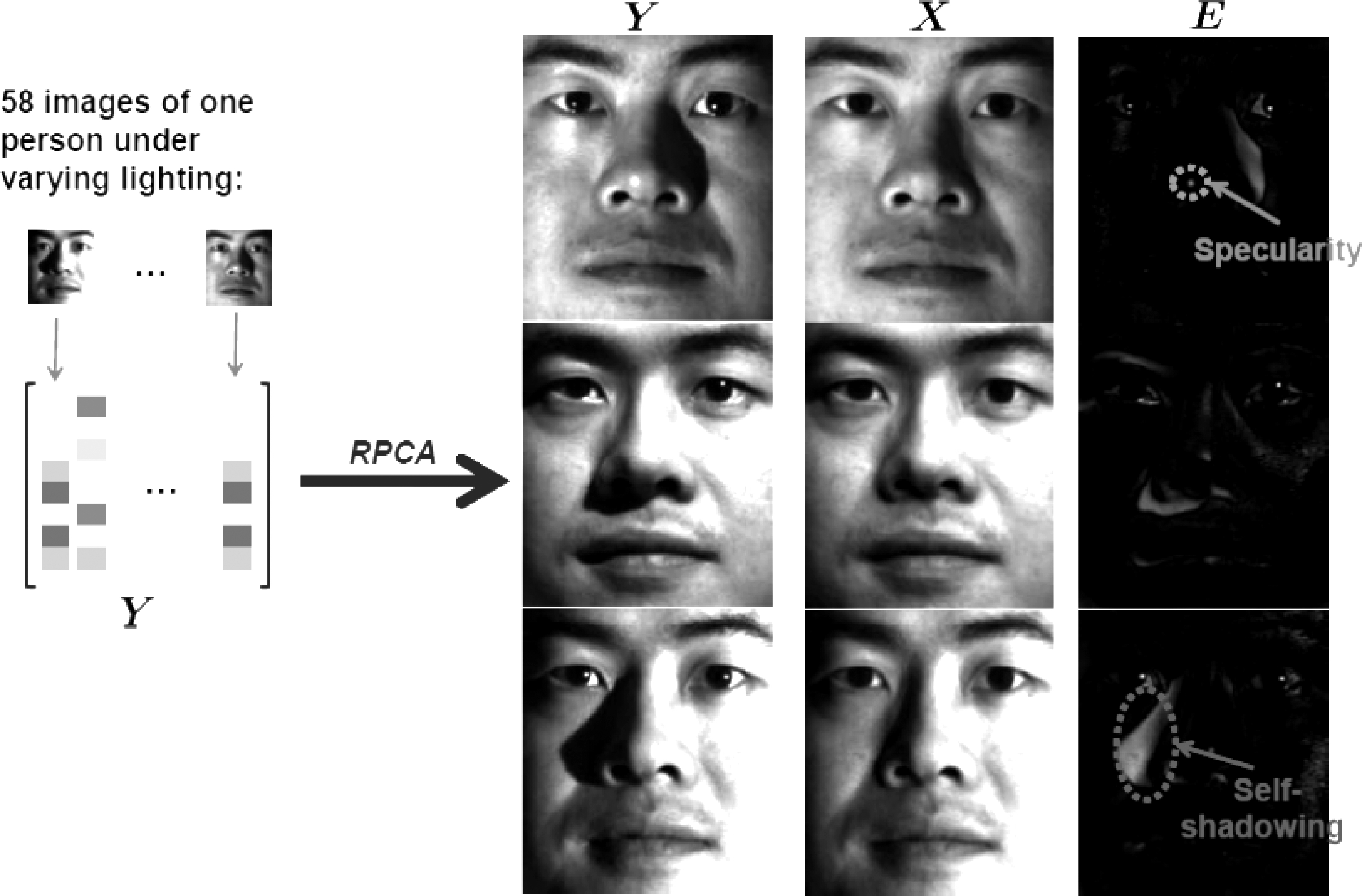
图2 图像去光照影响恢复
Fig.2 Image delighting affects restoration
图3是应用稀疏低秩特性最多的前景背景分离的应用,应用本算法可以通过提高运算速度对高帧率视频进行分析,解决了高帧率视频掉帧的问题,提高了效率。
如图4所示是本算法应用于图像去标签,其速率比目前最快的PCP算法快了10倍。

图3 背景建模
Fig.3 Background modeling
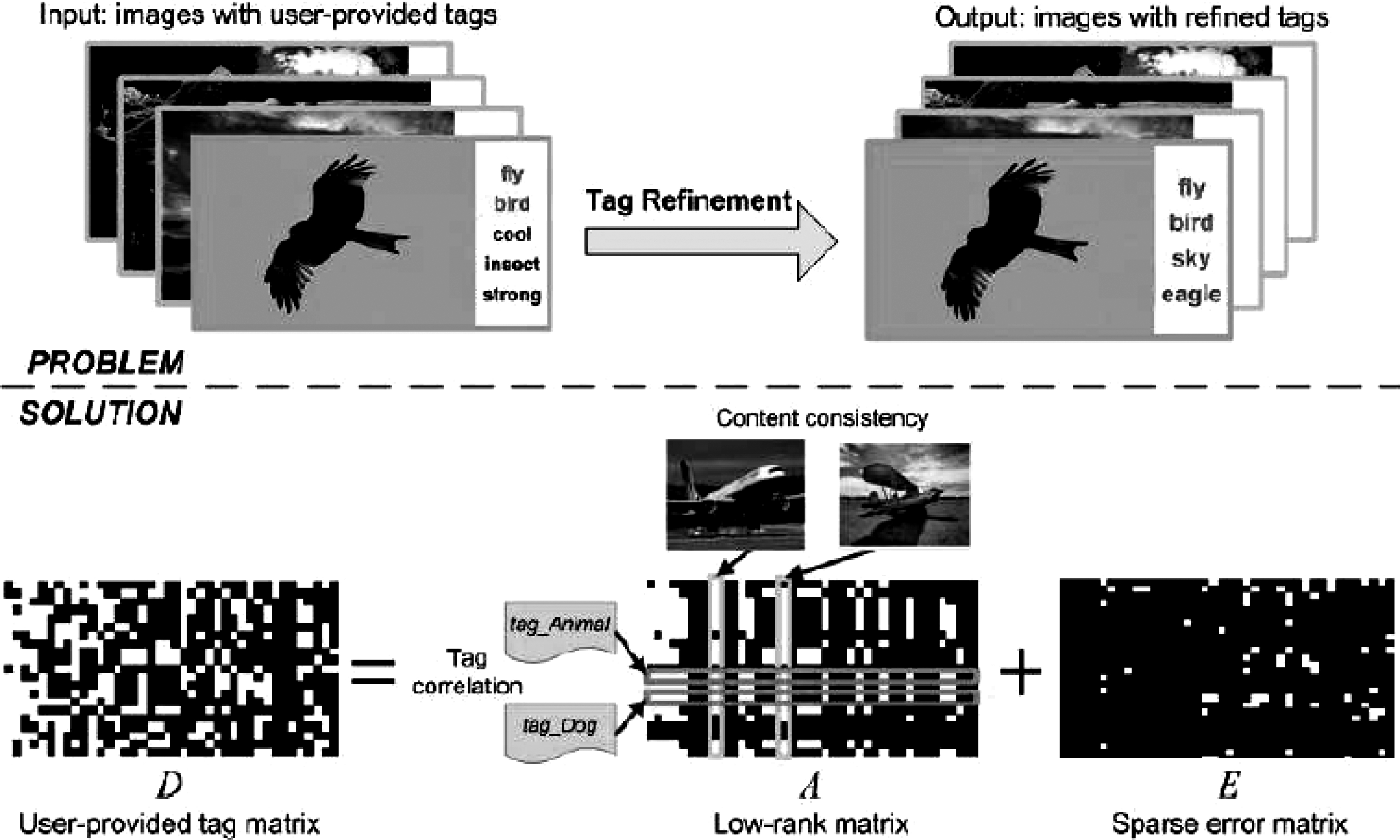
图4 图像去标签
Fig.4 Image untagging
表4 对不同尺寸图片和三个应用场景进行了比较。
将错误(Err.),迭代次数(NI.)和它们的运行时间(Time(s))作为评价指标
Tab.4 Compares pictures of different sizes with three application scenarios. Error (Err.), iteration times (NI.) And their running time (Time (s)) as an evaluation index
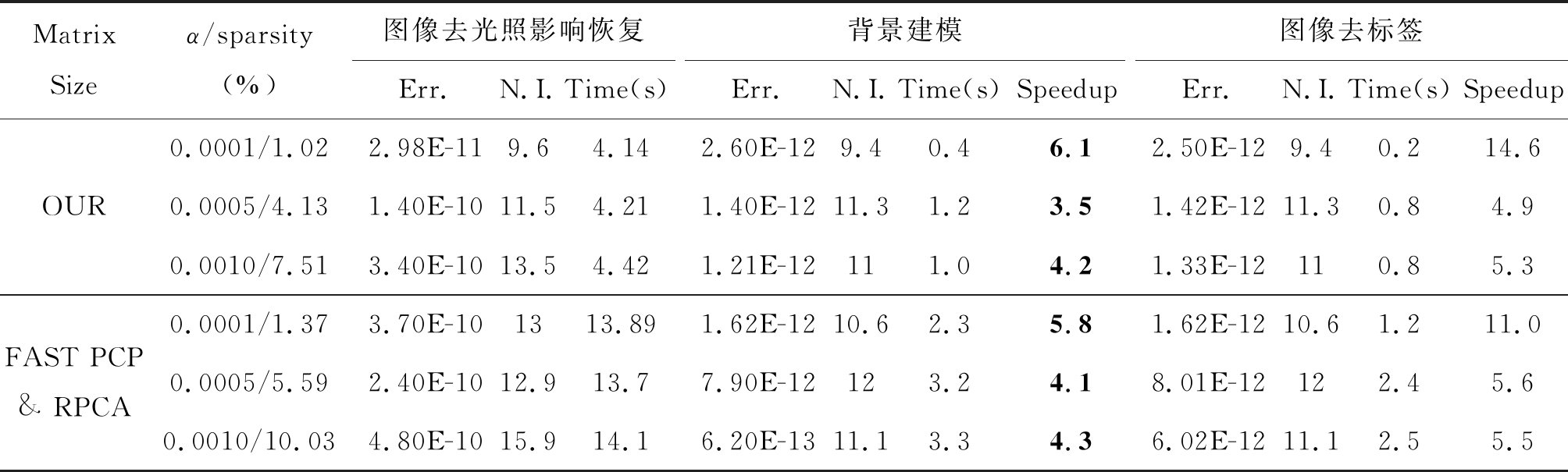
Matrix Sizeα/sparsity(%) 图像去光照影响恢复Err.N.I.Time(s)背景建模Err.N.I.Time(s)Speedup图像去标签Err.N.I.Time(s)SpeedupOUR0.0001/1.022.98E-119.64.142.60E-129.40.46.12.50E-129.40.214.60.0005/4.131.40E-1011.54.211.40E-1211.31.23.51.42E-1211.30.84.90.0010/7.513.40E-1013.54.421.21E-12111.04.21.33E-12110.85.3FAST PCP & RPCA0.0001/1.373.70E-101313.891.62E-1210.62.35.81.62E-1210.61.211.00.0005/5.592.40E-1012.913.77.90E-12123.24.18.01E-12122.45.60.0010/10.034.80E-1015.914.16.20E-1311.13.34.36.02E-1211.12.55.5
由表4可以看出,算法用于不同尺寸图片和三个应用场景上都比普通的FAST PCP & RPCA性能好的多。
快速稀疏低秩和鲁棒主成分分析(RPCA)的结合是比较快速、比较有效的稀疏低秩处理图像的方法,并且在无法保证计算机配置的情况下,其运算速度也是最快的,通过实验证明在大多数情况下,所提出的方法可以提供5~6倍左右的速度,最高可达10~14倍。 在稀疏条件下,解的精度至少比其他方法的水平高一个数量级,并且在多个应用测试中都取得了不错的效果。
[1] Fu H, Wang B, Liu H Z. Online RPCA on Background Modeling: Volume II[M]∥Proceedings of 2018 Chinese Intelligent Systems Conference, 2019.
[2] 孙志鹏, 王永丽, 王淑琴, 等. 视频背景分离中一种新的非凸秩近似的RPCA模型[J]. 山东科技大学学报: 自然科学版, 2019(4): 83-91.
Sun Zhipeng, Wang Yongli, Wang Shuqin, et al. A new non-convex-rank approximate RPCA model in video background separation[J]. Journal of Shandong University of Science and Technology: Natural Science Edition, 2019 (4): 83-91.(in Chinese)
[3] 曹锦纲, 杨国田, 杨锡运. 基于RPCA和视觉显著性的风机叶片表面缺陷检测[J]. 图学学报, 2019(4): 704-710.
Cao Jingang, Yang Guotian, Yang Xiyun. Surface defect detection of fan blade based on RPCA and visual significance[J]. Journal of Cartography, 2019(4): 704-710.(in Chinese)
[4] 叶学义, 罗宵晗, 王鹏, 等. 基于非凸低秩分解判别的叠加线性稀疏人脸识别[J]. 中国图象图形学报, 2019(8): 1327-1337.
Ye Xueyi, Lantern, Wang Peng, et al. Superimposed linear sparse face recognition based on non-convex low-rank decomposition[J]. China Image and Graphics, 2019 (8): 1327-1337.(in Chinese)
[5] 刘明君, 董增寿, 邵贵成. 基于改进的四叉树分解多聚焦图像融合算法研究[J]. 科技通报, 2019(4): 152-156.
Liu Mingjun, Dong Zengshou, Shao Guicheng. Research on multi-focus image fusion algorithm based on improved quadtree decomposition[J]. Science and Technology Bulletin, 2019 (4): 152-156.(in Chinese)
[6] Mikami S, Kawamura A, Iiguni Y. Residual drum sound estimation for RPCA singing voice extraction[C]∥Asia-pacific Signal & Information Processing Association Summit & Conference. IEEE, 2018.
[7] Wange S, Kewen X, Pu L. Regularized weighted incomplete robust principal component analysis method and its application in fitting trajectory of wireless sensor network nodes[J]. Journal of Computer Applications, 2018: 1709-1714+1720.
[8] Xu Y, Wu Z, Chanussot J, et al. Joint Reconstruction and Anomaly Detection From Compressive Hyperspectral Images Using Mahalanobis Distance-Regularized Tensor RPCA[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, PP(99): 1-12.
[9] Tian M, Wang X, Nie L, et al. Recognition of geochemical anomalies based on geographically weighted regression: A case study across the boundary areas of China and Mongolia[J]. Journal of Geochemical Exploration, 2018, 190.
[10] Shen Y, Xu H, Liu X. An alternating minimization method for robust principal component analysis[J]. Optimization Methods and Software, 2018(591): 1-26.
[11] Tao S, Li B, Li N, et al. A Novel Approach for Moving Window Size Selection utilizing recursive PCA[C]∥2018 Chinese Control Conference,2018. 7: 710-715.
[12] Qin K, Sun L, Liu B, et al. A Robust Change-Point Detection Method by Eliminating Sparse Noises from Time Series[C]∥2018 IEEE Third International Conference on Data Science in Cyberspace (DSC). IEEE, 2018.
[13] 于雯越, 安博文, 赵明. 基于光流法与RPCA的红外运动目标检测[J]. 现代计算机(专业版), 2018(23): 66-71.
Yu Wenyue, An Bowen, Zhao Ming. Infrared moving target detection based on optical flow method and RPCA[J]. Modern Computer (Professional Edition), 2018 (23): 66-71.(in Chinese)
[14] Sun W, Du Q. Graph-Regularized Fast and Robust Principal Component Analysis for Hyperspectral Band Selection[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, PP(99): 1-11.
[15] Jeong I Y, Lee K. Singing Voice Separation Using RPCA with Weighted $$l_{1$$-norm[C]∥International Conference on Latent Variable Analysis and Signal Separation. Springer, Cham, 2017.
[16] Javed S, Bouwmans T, Sultana M, et al. Moving Object Detection on RGB-D Videos Using Graph Regularized Spatiotemporal RPCA[C]∥International Conference on Image Analysis and Processing-2017. Springer, Cham, 2017.
[17] Tan C H, Chen J, Chau L P. Edge-preserving rain removal for light fiele images based on RPCA[C]∥2017 22nd International Conference on Digital Signal Processing (DSP). IEEE, 2017.
[18] 胡正平, 赵淑欢. 分辨性分解块稀疏表示遮挡人脸识别算法[J]. 信号处理, 2014, 30(2): 214-220.
Hu Zhengping, Zhao Shuhuan. The distinguishing decomposition block sparse means the blockface recognition algorithm [J].Journal of Signal Processing,2014, 30(2): 214-220. (in Chinese)
郑宝玉 男, 1945年生, 1969年和1981年分别获得南京邮电大学的学士学位和硕士学位。从那以后, 一直从事信号和信息处理的教学和研究。目前是南京邮电大学教授、博士生导师。研究领域涵盖了智能信号处理、无线网络和信号等领域。
E-mail:zby@njupt.edu.cn
李 昂 男, 1986年生, 安徽人。副教授, 博士, 正在参与在研国家自然科学基金面上项目2项, 主持省部级科研课题1项、市厅级科研项目2项, 发表学术论文近20篇, 其中SCI检索3篇, EI检索3篇, 申请发明专利2项, 实用新型专利2项, 近三年来开展了“机器学习专项研究与推广”、“5G网络关键技术”、“基于深度学习的基站视频识别分割”等研究。
E-mail: liang878@njust.edu.cn