近年来,大规模多输入多输出(Multiple-Input Multiple-Output,MIMO)引起了人们的广泛关注,大规模MIMO基站配备有数百个天线,可以同时服务于位于同一时频资源上的用户。具有高能效和高频谱效率的大规模MIMO是推动下一代通信进步的关键。
然而,大规模MIMO系统的性能高度依赖于估计的瞬时信道状态信息(Channel State Information,CSI)和预编码方法的准确性。现有的大多数预编码方法都基于精确的瞬时CSI估计,如经典的迫零(Zero-Forcing,ZF)和最大比传输(Maximal Ratio Transmission,MRT)方法。在频分双工(Frequency Division Duplexing,FDD)和时分双工(Time Division Duplexing,TDD)模式下,大规模MIMO系统中获得准确的瞬时CSI是一个巨大的挑战。在FDD模式下,由于基站天线较多,下行导频序列和上行信道反馈的开销都占用大量的时频资源,这使得FDD模式只支持低移动性和低频场景。在TDD模式下,由于下行链路瞬时CSI是通过估计基于信道互易性的上行链路CSI获得的,所以TDD模式被认为是大规模MIMO系统的一个推动因素[1]。然而,由于基带到射频链路的校准误差,下行链路瞬时CSI在实际中并不总是准确的。
相比之下,统计CSI如信道的协方差矩阵在相当长的时间内是静态和稳定的,这主要取决于天线参数和周围环境。文献[2]通过测量验证了统计CSI的长期稳定性,文献[3]中指出通过对信道样本进行长期反馈或平均可以很容易地获得稳定的信道统计CSI。因此,基站通常以很少的或没有反馈开销在非常慢的时间尺度上获取统计CSI。由于统计CSI的优势,已经引起了人们的兴趣,它被广泛应用于大规模MIMO系统。在文献[4]中,提出了新颖的双时间尺度混合模拟/数字预编码方案,以减少所需射频链的数量,其中模拟预编码器仅适用于统计CSI。通过利用统计CSI预编码方案减少了信道估计开销并且对估计延迟是鲁棒的。此外,在FDD的大规模MIMO系统中,为了减少下行导频和上行反馈开销,提出了两阶段预编码方法,其中统计CSI用于用户分组和降低分组间干扰[5]。此外,统计CSI也用于分层预编码的结构中,来减少小区间干扰[6- 8]。
可以看出,统计CSI在大多数现有预编码方案中被作为辅助信息,但仍然需要有效的用户瞬时CSI。然而,由于缺少正交导频序列,用户没有被分配导频,以及当前基站没有调度非活跃用户,会导致基站处没有用户的瞬时CSI。在这种情况下,由于瞬时CSI的缺失,基站不能利用任何天线阵列增益[9]。因此,研究基站如何在没有瞬时CSI的情况下与用户进行通信是非常重要的。统计CSI可以很容易地在基站处长期稳定地获得。因此,仅具有统计CSI的下行链路传输是合理的选择。然而,目前对仅有统计CSI的下行链路预编码方法的研究较为少见。文献[10]研究了单用户MIMO系统的最佳预编码方案。由于用户间的干扰,多用户情况下的研究主要集中在毫米波系统中的莱斯衰落信道[11]和两个单天线用户和两根天线的基站的简化情况[12-13]。而且,两用户情况下的预编码方法在用户的信道协方差矩阵上需要特殊的正交性,难以在数十个用户的大规模MIMO系统中实现。文献[14]提出了一种基于信噪比最大化度量的统计CSI统计波束成形方案,适用于大规模MIMO系统。文献[15]在2D MIMO中同时考虑了具有统计CSI和不完美瞬时CSI用户之间的相互干扰,但该方案没有利用3D MIMO信道的特性,具有较高的复杂度。
本文与文献[15]不同,考虑了在3D MIMO中基站同时服务于两种类型的用户。第一种类型被命名为未发送上行链路导频的S类用户,例如当前不活跃的用户,基站仅基于其统计CSI执行预编码。其余用户被命名为C类用户。然后,研究了在3D MIMO下混合利用S类用户的统计CSI和C类用户的瞬时CSI的下行链路传输的可行性。
考虑3D MIMO下行链路系统,基站配备M=NνNh根天线的均匀平面天线阵列,其中Nν和Nh分别为垂直与水平天线数。基站同时服务K个C类用户,N个S类用户,且用户数满足约束(K+N)≪M,系统模型如图1。
C类的第k个用户与S类的第n个用户的接收信号yC,k和yS,n可以表示为:
(1)
(2)
其中,gC,k=vec(HC,k)、gS,n=vec(HS,n)分别为第k个C类用户信道矩阵和第n个S类用户信道矩阵,wC,k、wS,n分别为第k个C类用户的预编码矩阵和第n个S类用户的预编码矩阵,xC,k、xS,n分别为第k个C类用户的发射信号和第n个S类用户的发射信号,且满足均值为零方差为1的复高斯随机分布,nC,k、nS,n为加性高斯白噪声。
本文采用3D MIMO窄带多路径信道模型[16],其可以被近似分解成水平导向矢量和垂直导向矢量的克罗内克积,即
(3)
其中,
为水平导向矢量,
为垂直导向矢量,
为路径数,
为第p条路径的大尺度衰落系数,
λ为波长,
为水平到达角,
为垂直到达角,D为天线间距取半个波长。
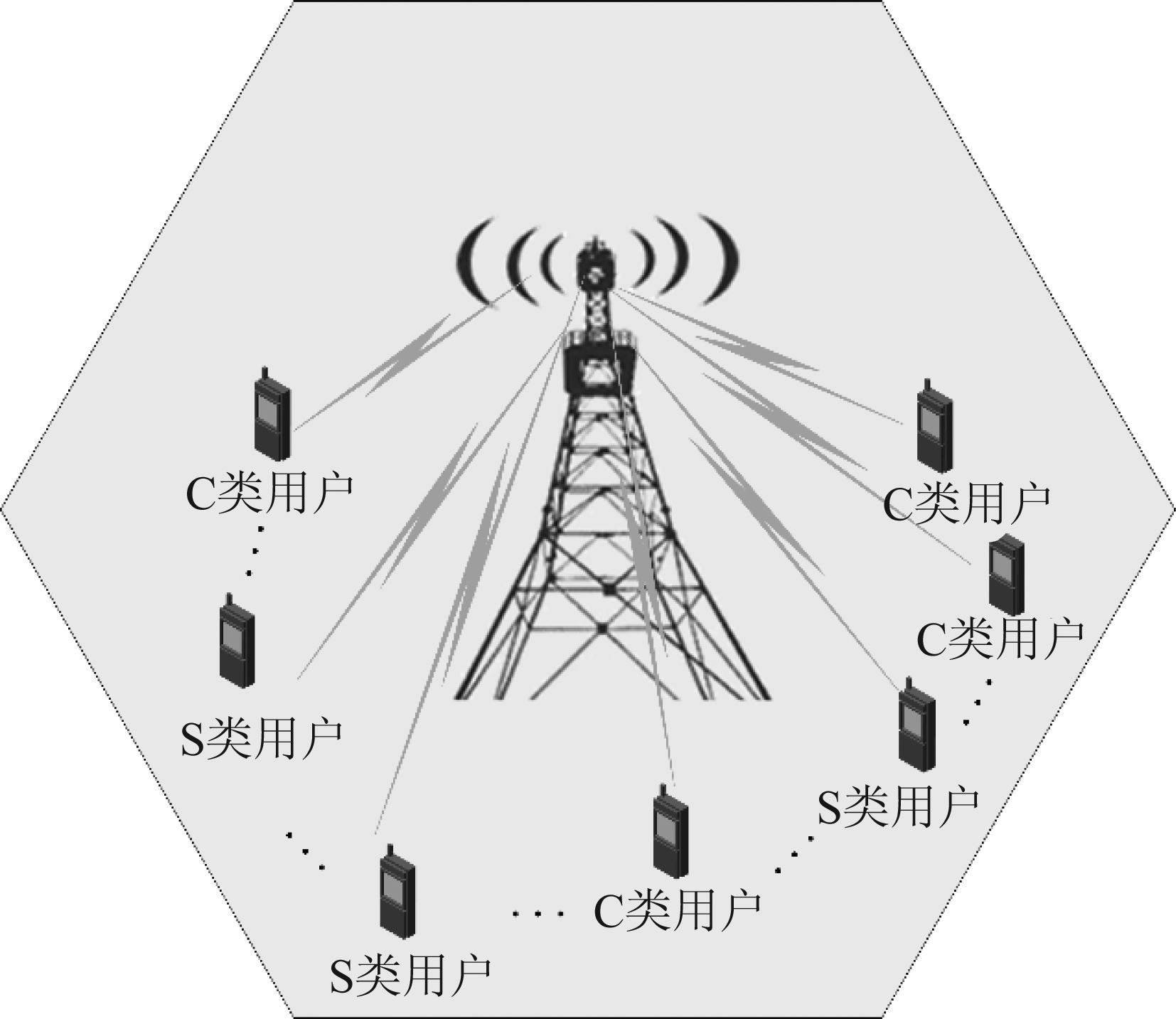
图1 系统模型
Fig.1 System model
假设基站有C类用户的瞬时CSI和S类用户的统计CSI。为了抑制C类用户和S类用户之间的相互干扰,本节提出了拓展的ZF预编码方案,目的是最小化基站的总发射功率。与文献[15]不同的是,本方案采用了3D MIMO的信道模型,充分利用了3D MIMO的信道的克罗内克积性质。
由于缺少S类用户的瞬时CSI,本文考虑抑制S类用户的平均干扰。基于ZF准则,考虑最小化基站总的发射功率,拓展的ZF方法的优化问题表达为
(4)
其中,GC=[gC,1,gC,2,...,gC,K]∈CM×K为所有C类用户的信道矩阵集合,WC=[wC,1,wC,2,…,wC,K]∈CM×K为所有C类用户预编码矩阵的集合,WS=[wS,1,wS,2,…,wS,N]∈CM×N为所有S类用户预编码矩阵的集合,ΦS,n为第n个S类用户的协方差矩阵。上式中第一约束条件是用来消除C类用户间的干扰,第二个约束是用来消除C类用户对S类用户的干扰,第三个约束是为了保证每个用户的接收信号功率为ρ,第四个约束是用来消除S类用户对C类用户的干扰,第五个约束条件是用来消除S类用户之间的干扰。
由于C类用户的预编码矩阵WC和S类用户的预编码矩阵wS,n,∀n=1,2,…,N在最优化问题中是独立的,可将最优化问题分解为两个子问题来处理。
基站对C类用户最小化发射功率最优化问题可以表述为:
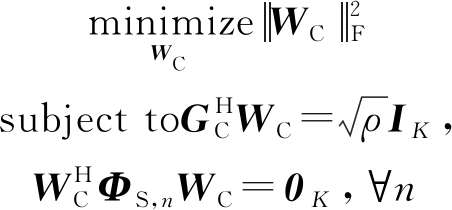
(5)
由于C类用户k的预编码矩阵wC,k可以写成水平预编码矩阵和垂直预编码矩阵的克罗内克积,即wC,k=wC,k,a⊗wC,k,e∈CNhNν×1。所以最优化问题公式(5)中的约束2可以改写为:
(wC,k,a⊗wC,k,e)H(ΦS,n,a⊗ΦS,n,e)
(wC,k,a⊗wC,k,e)=0,∀k,n
(6)
接着,由F范数的性质,=A⊗B=F==A=F·=B=F,可以推出:
=wC,k=F==wC,k,a⊗wC,k,e=F=
=wC,k,a=F·=wC,k,e=F
(7)
所以可将公式(5)的优化问题,转化为分别求解水平预编码的F范数与垂直预编码的F范数的平方的最小值,下面以求解水平预编码的F范数的平方的最小值为例,则最优化问题如下:
(8)
其中,WC,a=[wC,1,a,wC,2,a,…,wC,K,a]∈CNh×K为所有C类用户水平预编码的集合,GC,a=[hC,1,a,hC,2,a,...,hC,K,a]∈CNh×K为C类用户水平导向矢量的集合。令
由于ΦS,n,a为半正定矩阵,所以公式(8)的第二个约束
为一个非负的矢量。所以只要WC,a满足下面的约束
(9)
WC,a就能满足公式(8)的第二个约束。
接下来对ΦS,a进行奇异值分解,即
(10)
其中,U1,a为特征矢量酉矩阵,Λ1,a为对角矩阵,其特征值为降序排列。将公式(10)带入到公式(8)中的第二个约束条件中,定义
则公式(8)的约束二可以写为:
(11)
定义r1,a为ΦS,a的秩,所以对角矩阵Λ1,a前r1,a个特征值是非零的。为了满足约束(11),只要
的前r1,a行为维度为r1,a×K的零矩阵。所以可以写为:
(12)
根据酉矩阵的性质
且定义
将公式(8)的第一个约束写为:
(13)
将
分解成两个矩阵,即
其中
再利用公式(12)和公式(13),公式(8)的第一个约束可写为:
(14)
基于公式(12)可得,
所以公式(8)优化的问题可以简化为:
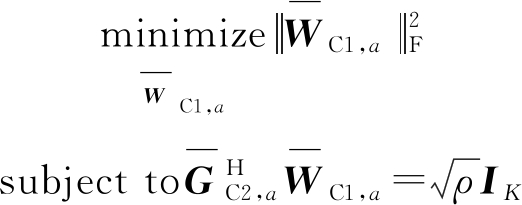
(15)
由于公式(15)的优化问题与ZF准则类似,基于线性代数的广义逆的性质,上述问题的最优解为:
(16)
所以,公式(8)最优化问题的解为:
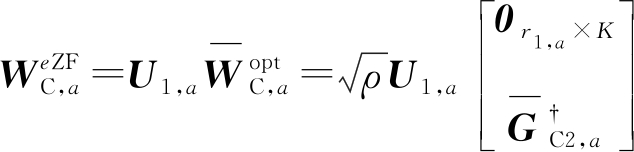
(17)
垂直预编码F范数的平方最小值的最优解同水平预编码的F范数的平方的最小值的最优解,即:
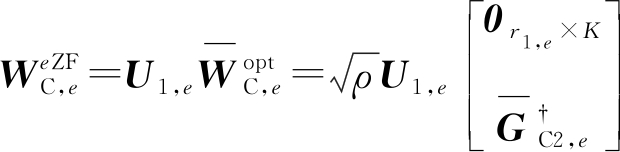
(18)
其中,U1,e为所有S类用户信道垂直协方差和ΦS,e的奇异值分解的特征矩阵,
从公式(9)可以看出,S类用户主要存在于r1,a维的子空间中。由于更大的天线规模,大规模3D MIMO系统具有比r1,a大得多的自由度。所以多余的自由度可用于抑制用户之间的干扰。C类用户可以避免对S类用户造成干扰,其代价是将阵列维度增益降低到Nh-r1,a。因此,相对于仅服务于C类用户的传统传输模式,C类用户的性能会受到损失。然而,当基站天线的数量足够大时,与Nh相比,r1,a变得可以忽略不计,并且可以减少C类用户的性能损失。
基站对S类用户最小化发射功率最优化问题可以表述为:
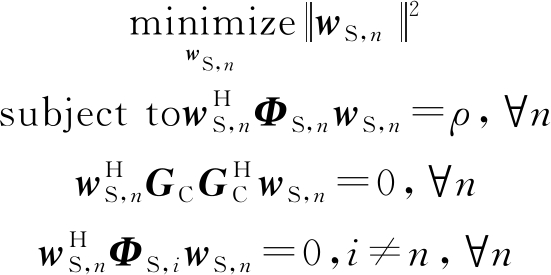
(19)
由于S类用户的预编码矩阵可以分解为水平预编码矩阵wS,n,a和垂直预编码矩阵wS,n,e的克罗内克积,即wS,n=wS,n,a⊗wS,n,e,同样的S类用户信道的协方差矩阵为ΦS,n=ΦS,n,a⊗ΦS,n,e,所以公式(19)最优化问题的约束条件可以写为:
(wS,n,a⊗wS,n,e)H(ΦS,n,a⊗ΦS,n,e)(wS,n,a⊗wS,n,e)=ρ,∀n
(wS,n,a⊗wS,n,e)H(hC,k,a⊗hC,k,e)(hC,k,a⊗hC,k,e)H
(wS,n,a⊗wS,n,e)=0,∀k,n
(wS,n,a⊗wS,n,e)H(ΦS,i,a⊗ΦS,i,e)(wS,n,a⊗wS,n,e)=0,
i≠n,∀n
(20)
利用克罗内克积的性质,上式可以进一步写为:
(21)
同C类用户的预编码方案一样,先考虑S类用户的水平预编码,则优化问题公式(19)的子问题为:
(22)
其中,GC,a=[hC,1,a,hC,2,a,…,hC,K,a]为C类用户水平天线阵列响应的集合。由于GC,a和ΦS,i,a,i≠n都是半正定的,所以公式(22)的第二和第三个约束可以合并写为:
(23)
定义
且Qn,a的秩表示为r2,a,对Qn,a进行奇异值分解可得:
(24)
同公式(9)到公式(11)处理一样,则可以得到:
(25)
令
然后将
分解为下面的形式
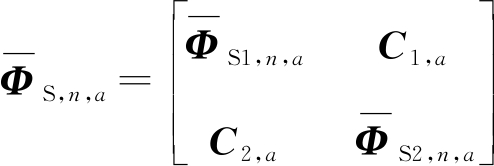
(26)
其中,
所以公式(12)的第一个约束条件进一步可以写为:
(27)
所以,公式(22)的优化问题可以化简为下面的形式:
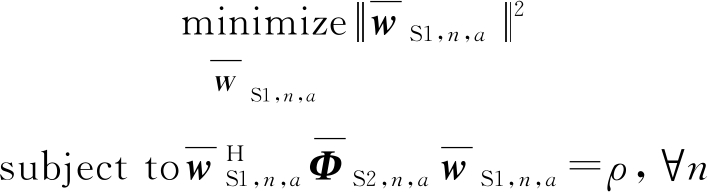
(28)
根据文献[15],其最优解为:
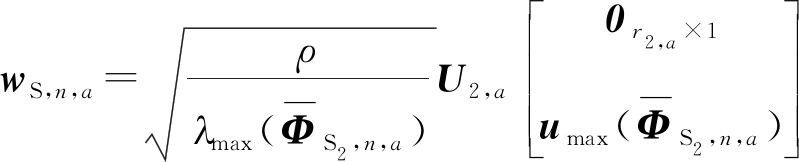
(29)
同理可得,其最优的垂直预编码为
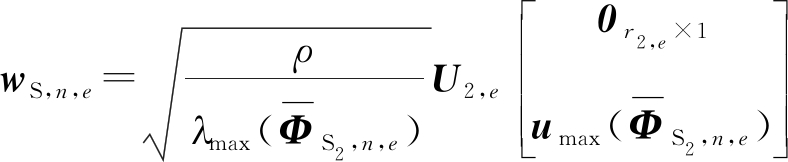
(30)
如公式(27)所示,S类的第n个用户必须牺牲部分有用信道统计信息以避免对其他用户造成干扰,这导致S类用户的平均接收信号功率降低。
为了验证本文所提出的用于3D MIMO系统的混合统计和瞬时CSI的下行链路预编码方案,并将该方案与文献[15]方案的性能进行比较,其中ρ=10 dB,S类用户信道的协方差矩阵为系统多次调度S类用户取得的平均值。仿真参数如表1。
表1 仿真参数
Tab.1 Simulation parameters
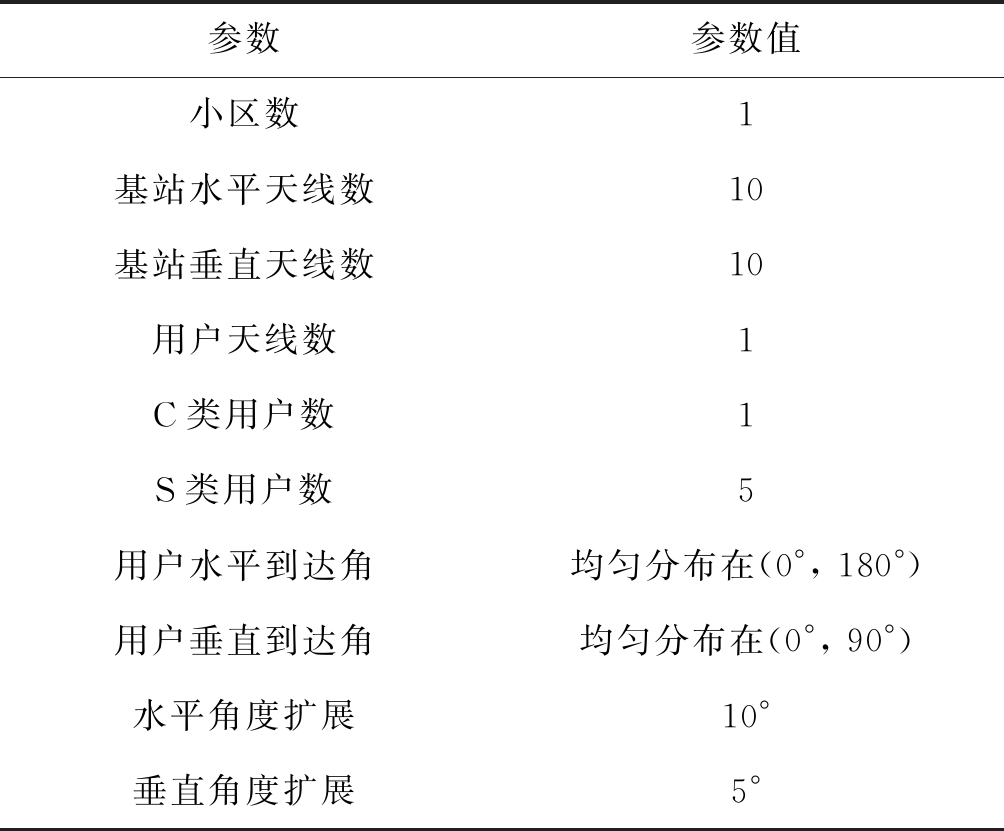
参数参数值小区数1基站水平天线数10基站垂直天线数10用户天线数1C类用户数1S类用户数5用户水平到达角均匀分布在(0°, 180°)用户垂直到达角均匀分布在(0°, 90°)水平角度扩展10°垂直角度扩展5°
图2比较了文献[15]方案、ZF预编码和本文所提方案的性能。从图2可知,在低SNR时各个方案的性能相近。文献[15]方案中的C类用户的性能与ZF预编码性能一样。本文所提方案中C类用户的平均可达速率接近文献[15]方案的C类用户,同时本文方案具有更低的复杂度。因为,本文考虑了天线垂直方向的自由度,利用文献[16]所提信道的近似分解,将3D MIMO信道近似为水平与垂直天线阵列矢量的克罗内克积,在水平与垂直维度分别计算最优预编码矩阵。相较于ZF方案,本文方案利用维度更低的水平与垂直阵列矢量;同时相较于文献[15]方案,本文方案将优化问题分解到水平与垂直维上分别求解,降低了计算的复杂度。但是,由于本文采用3D MIMO信道模型,S类用户信道的协方差矩阵分解为水平与垂直协方差矩阵的克罗内克积,相较于文献[15]的S类用户,牺牲了更多的有用信道信息来避免C类用户的干扰。因此,本文方案S类用户的平均速率低于文献[15]的S类用户。
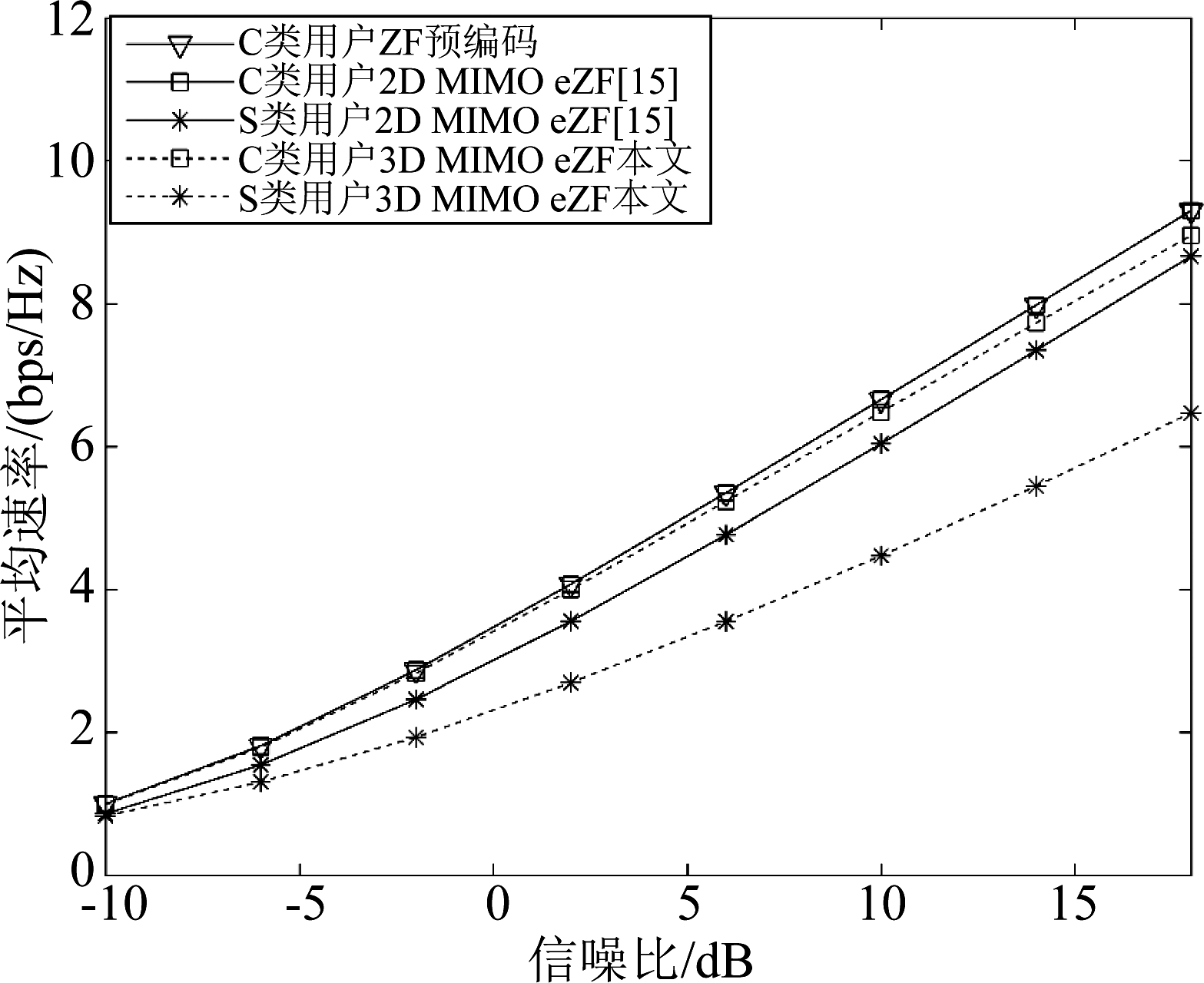
图2 三种方案性能比较图(Nν=10,Nh=10)
Fig.2 Performance comparison of three schemes (Nν=10,Nh=10)
图3显示了在水平与垂直天线数为20时三种方案的性能。从图3可知,本文方案的C类用户的平均速率和文献[15]以及ZF预编码相同。图2和图3可知,随着天线数,S类用户与C类用户平均可达速率的差距在减小。随着天线数增加,S类用户对C类用户的干扰减小;而当基站天线的数量足够大时,S类用户将不会影响C类用户的性能。
图4比较了系统中S类用户数量不同时,C类用户与S类用户的平均速率。从图中可以看出,随着S类用户数增加,C类用户与S类用户的平均速率都在下降。随着S类用户数增加,C类用户需要牺牲更多的有用信道信息来消除S类用户的干扰,所以C类用户平均速率下降的幅度要大于S类用户。
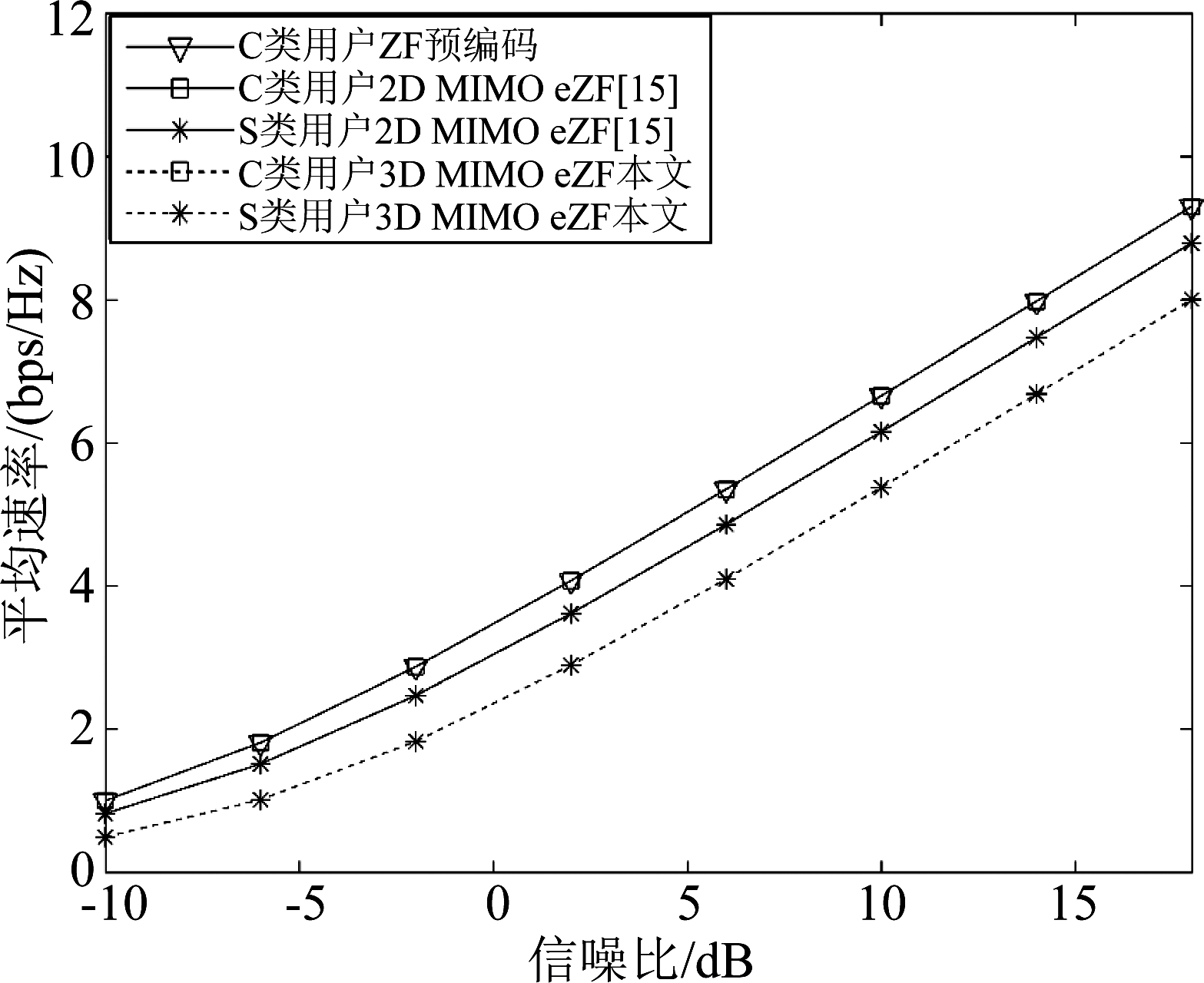
图3 三种方案性能比较图(Nν=20,Nh=20)
Fig.3 Performance comparison of three schemes (Nν=20,Nh=20)
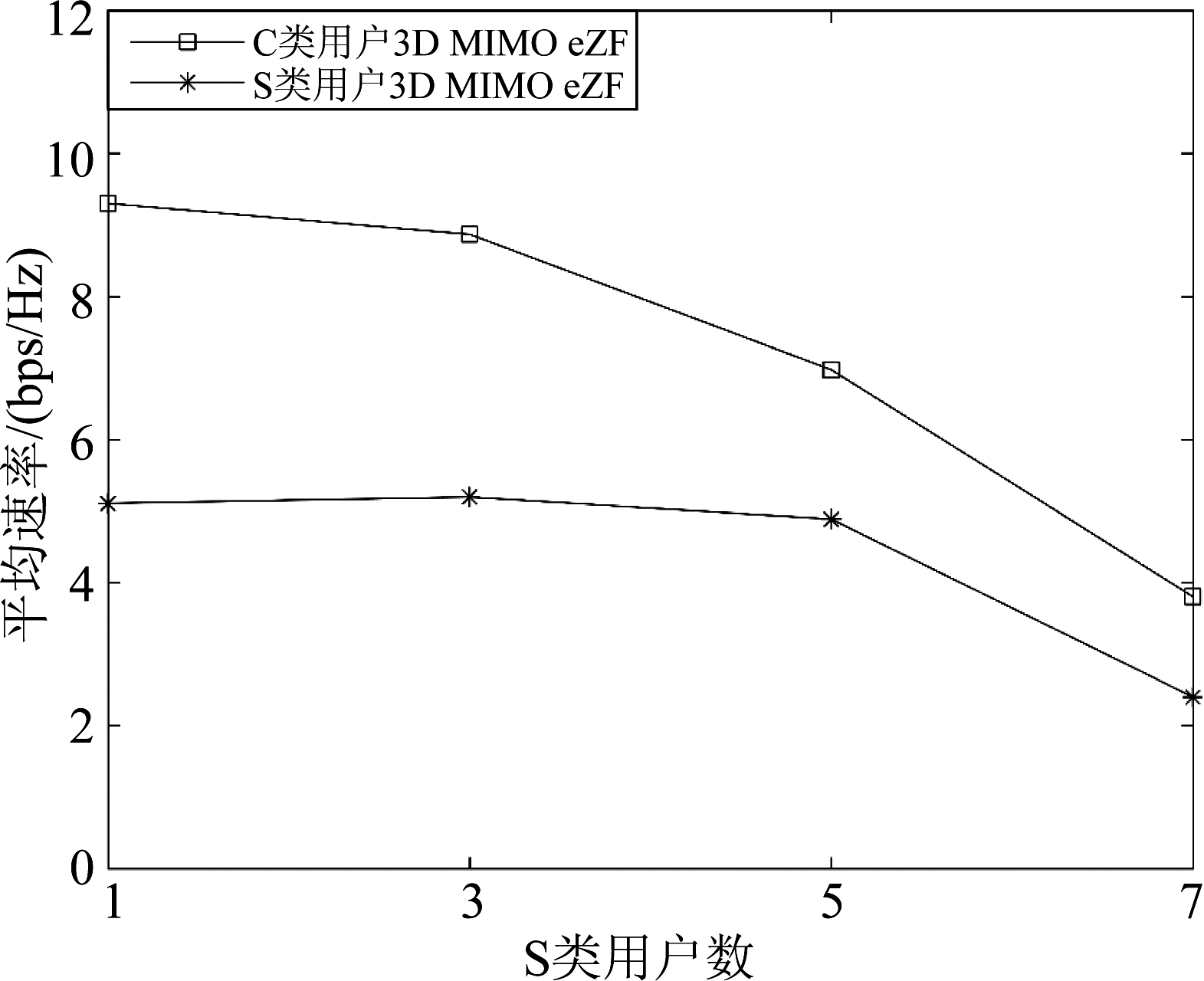
图4 不同S类用户数性能比较图(SNR=10 dB)
Fig.4 Performance comparison of different type-S users (SNR=10 dB)
本文分析了在3D MIMO中具有统计CSI和瞬时CSI用户并存的系统模型,考虑两类用户之间的相互干扰,以最小化基站总的发射功率为优化目标,提出了基于ZF准则的优化方法。利用3D MIMO窄带多路径信道模型的克罗内克积性质,将优化问题转化到水平维和垂直维上分别求解。相较于采用2D MIMO信道模型的方案,本文基于3D MIMO信道模型的方案极大地降低了复杂度,并有着良好的速率。
[1] Shen J, Zhang J, Letaief K B. Downlink user capacity of massive MIMO under pilot contamination[J]. IEEE Transactions on Wireless Communications, 2015, 14(6): 3183-3193.
[2] Viering I. Spatial long-term variation in urban, rural and indoor environments[J]. Proc 5th Meeting of COST273, 2002: 1-10.
[3] Mestre X. Improved estimation of eigenvalues and eigenvectors of covariance matrices using their sample estimates[J]. IEEE Transactions on Information Theory, 2008, 54(11): 5113-5129.
[4] Liu A, Lau V K N. Two stage constant-envelope precoding for low cost massive MIMO systems[J]. IEEE Transactions on Signal Processing, 2015, 64(2): 1-1.
[5] Chen J, Lau V K N. Two-tier precoding for FDD multi-cell massive MIMO time-varying interference networks[J]. IEEE Journal on Selected Areas in Communications, 2014, 32(6): 1230-1238.
[6] An L, Lau V. Hierarchical interference mitigation for massive MIMO cellular networks[J]. IEEE Transactions on Signal Processing, 2014, 62(18): 4786- 4797.
[7] Zhang J, Andrews J G. Adaptive spatial intercell interference cancellation in multicell wireless networks[J]. IEEE Journal on Selected Areas in Communications, 2010, 28(9): 1455-1468.
[8] Emil Björnson, Randa Z, David G, et al. Cooperative multicell precoding: rate region characterization and distributed strategies with instantaneous and statistical CSI[J]. IEEE Transactions on Signal Processing, 2010, 58(8): 4298- 4310.
[9] Bjornson E, Larsson E G, Marzetta T L. Massive MIMO: ten myths and one critical question[J]. IEEE Communications Magazine, 2016, 54(2): 114-123.
[10] Gao X, Jiang B, Li X, et al. Statistical eigenmode transmission over jointly-correlated MIMO channels[J]. IEEE Transactions on Information Theory, 2009.
[11] Jin S, Tan W, Matthaiou M, et al. Statistical eigenmode transmission for the MU-MIMO downlink in Rician fading[J]. IEEE Transactions on Wireless Communications, 2015, 14(12): 1-1.
[12] Wang J, Jin S, Gao X, et al. Statistical eigenmode-based SDMA for two-user downlink[J]. IEEE Transactions on Signal Processing, 2012, 60(10): 5371-5383.
[13] Raghavan V, Hanly S V, Veeravalli V V. Statistical beamforming on the Grassmann manifold for the two-user broadcast channel[J]. IEEE Transactions on Information Theory, 2013, 59(10): 6464- 6489.
[14] Zhang C, Huang Y, Jing Y, et al. Sum-rate analysis for massive MIMO downlink with joint statistical beamforming and user scheduling[J]. IEEE Transactions on Wireless Communications, 2017, 16(4): 2181-2194.
[15] Qiu S, Chen D, Luo K, et al. Downlink precoding with mixed statistical and imperfect instantaneous CSI for massive MIMO systems[J]. IEEE Transactions on Vehicular Technology, 2017: 1-1.
[16] Wang Z, Liu W, Qian C, et al. Two-dimensional precoding for 3-D massive MIMO[J]. IEEE Transactions on Vehicular Technology, 2017, 66(6): 5485-5490.
薛继实 男, 1993年生, 江苏盐城人。南京邮电大学通信与信息工程学院硕士研究生。主要研究方向3D MIMO系统干扰抑制技术。
E-mail: 1216012021@njupt.edu.cn
梁 彦 女, 1979年生, 河北唐山人。南京邮电大学通信与信息工程学院副教授, 硕士生导师。主要研究方向为无线通信、信号处理。
E-mail: liangyan@njupt.edu.cn
李 汀 男, 1979年生, 江苏扬州人。南京邮电大学通信与信息工程学院副教授, 硕士生导师。主要研究方向为MIMO技术、3D MIMO技术、协作通信。
E-mail: lit@njupt.edu.cn
季 薇 女, 1979年生, 江苏淮安人。南京邮电大学通信与信息工程学院副教授, 硕士生导师。主要研究方向无线通信、机器学习。
E-mail: jiwei@njupt.edu.cn
李 飞 女, 1966年生。南京邮电大学通信与信息工程学院教授, 博士生导师。主要研究方向为量子智能计算、群智能算法和无线通信中的信号处理算法。
E-mail: lifei@njupt.edu.cn