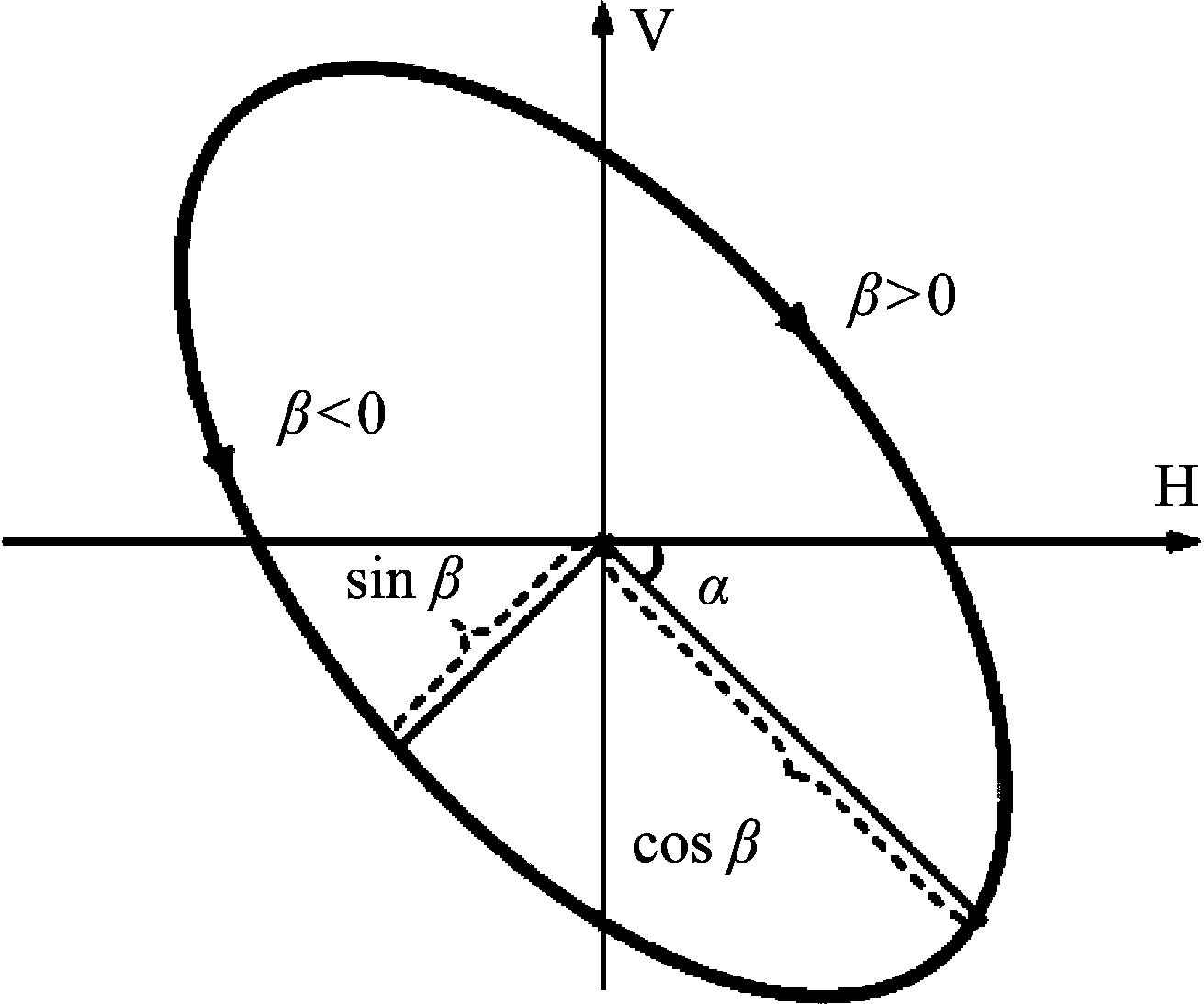
图1 极化椭圆
Fig.1 Polarization ellipse
智能天线可利用数字信号处理技术,产生空间定向波束,使主波束对准期望方向,零陷对准干扰信号的到达方向[1]。常规的智能天线通常使用相控天线阵列,其发射波束和接收波束则选择某一固定的极化方式,无法根据环境的先验信息实现自适应极化设计[2-3]。随着电磁环境的日益复杂,这种只使用空时自适应处理技术的智能天线很难满足设计需求,其性能改善也是相当有限。实际上,空间的电磁信号是矢量信号,完备的电磁信号应是一个六维的复矢量。传统的相控阵天线阵列仅能获得空间电磁信号一个场分量的信息,而极化天线阵列则使用了至少一对相互正交的偶极子天线接收电磁信号,可获得电磁信号的极化信息[4- 6]。如此可见,极化波束形成可选择设计匹配的极化状态来提高接收增益,也可选择与干扰信号的正交极化以减少干扰信号的影响[7- 8]。这里,可将使用极化阵列的智能天线称之为“极化智能天线”。考虑到极化波束形成优化是一个矢量优化问题,常规的最优化算法很难求解。大部分文献仅是针对某一特定的极化约束进行,而关于自适应极化设计的研究成果则相对比较少[9]。文献[10]的作者在总结传统的波束形成方法时,提到两种传统的方法,即均匀加权和切比雪夫加权方法。这两种方法虽然能够兼容零陷的设计,但无法再兼容自适应极化约束设计。2009年,在文献[11]中,Xiao J J等人提出了两种基于二阶锥规划(Second Order Core Programming, SOCP)的极化波束形成方法:第一种是主瓣极化约束以及指定旁瓣区域形成零点,第二种方法则分别主瓣极化约束和指定旁瓣区域进行极化约束设计。在此基础上,文献[12]首次将零点和极化约束进行叠加设计。在该文献中,所谓的“零点”仅是对某个方位角度而言,实现难度较容易但却很难应用。文献[13]的作者将零点进行展宽,实现了真正意义的零陷,并与正交极化进行叠加设计,并将其运用于极化相控阵雷达,推动了极化波束形成技术的进一步发展。但以上研究成果均基于均匀线阵而展开,并不适用现有的二维平面阵列天线结构。考虑到矢量波束优化问题的复杂性,二维极化波束形成并不是将简单一维数组转化为二维数组的过程,而是需要重新推导其优化模型,并寻求合适的求解器进行求解。
综上,在已有的基于均匀线阵的极化波束形成方法的基础上,本文以建立二维极化波束形成的矢量优化问题模型为突破,寻求使用SOCP的方法实现在二维观测平面实现主瓣区域的期望波束指向与极化匹配设计,以增强系统的接收增益和主瓣干扰的抑制能力;在旁瓣区域设定零陷凹面,与正交极化约束的叠加设计,以最大限度提高强干扰的抑制能力,进而提高了极化波束形成在极化智能天线实际工程中的适用性。
对于电磁波而言,极化(polarization)是指传播空间任意一点处电场的空间取向随时间变化的方式,可根据电场矢量端点随时间变化所形成的空间轨迹形状和旋向来描述。一般而言,电场矢量端点在波的传播横截面上随时间的变化轨迹为椭圆。假设存在单色的TEM(Transverse Electromagnetic Wave),即电矢量和磁矢量都与传播方向垂直,平面波沿z轴正半轴方向传播。该电磁波电场矢量的瞬时值可以表示为:
图1 极化椭圆
Fig.1 Polarization ellipse
由图1可见,极化椭圆的形状、倾斜角和旋向取决于水平通道和垂直通道的电场幅度比和相位差。倾斜角α、椭圆角率β和椭圆尺寸A三个参量是极化椭圆的唯一表征。倾斜角α表示以椭圆长轴与x轴正半轴方向的夹角,规定α∈[-p/2,p/2]。椭圆角率β定义为以椭圆长轴与短轴构成的直角三角形的最小内角,并约定左旋极化β取正值,右旋取负值。如此, β∈[-p/4,p/4]。椭圆尺寸定义为椭圆长轴与短轴构成直角三角形的斜边长,可得
来表示电磁波的能量。电场与极化椭圆参数之间的数学关系可表示为:
(1)
式(1)中,
为旋转矩阵,
为椭圆率矢量。
若忽略电磁波的能量,电磁波的极化状态可用参数对(α, β)进行表征,故可称之为极化状态的几何描述子。当β=0°时,表示线极化;当α=0°, β=0°时,表示水平极化;当α=90°, β=0°时,表示垂直极化。β=± p/4时表示圆极化。
假设有一电磁波信号沿r方向传播(r表示三维空间方位参数,即有方位角,俯仰角),方向r可表示为
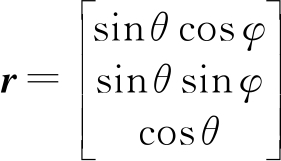
(2)
式(2)中θ∈[-p/2,p/2]为俯仰角,φ∈[0,2p]是方位角,定义
(3)
(4)
可构成一个右手坐标系,如图2所示。
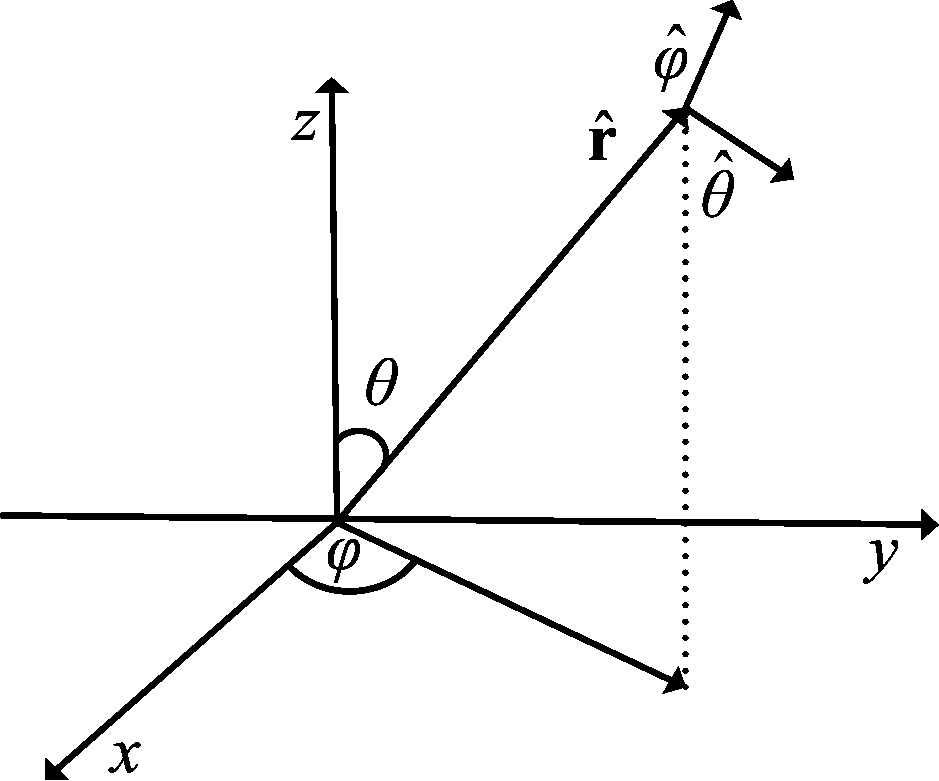
图2 坐标系统
Fig.2 The coordinate system
当电磁波沿r方向传播,电场传输方向垂直于磁场的传播方向,故电场和磁场在
限制的平面内。对每个偶极子产生一个激励,每个偶极子有如下响应:
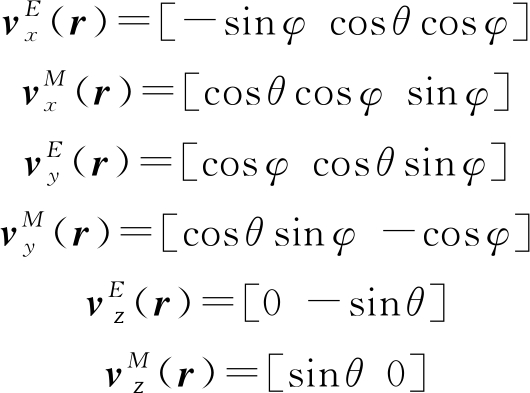
(5)
式(5)中
分别为电偶极子在
轴方向上的响应,
分别为磁偶极子在轴方向上的响应。对于一个由P个偶极子构成的极化天线,其阵元响应定义为V(r),假设在x轴上有一对电磁偶极子,那么阵元响应可以表示为
(6)
可将上述阵元响应分为水平分量和垂直分量,即
分量,用v(r;H)和v(r;V)表示,分别代表V(r)两列分量,即
V(r)=[v(r;H),v(r;V)]
(7)
考虑一个N×N极化矢量阵列,每个天线阵元由2个偶极子组成,分别用H和V表示水平和垂直方向上的偶极子,且其天线阵元激励相同,阵列的示意图如图3所示。
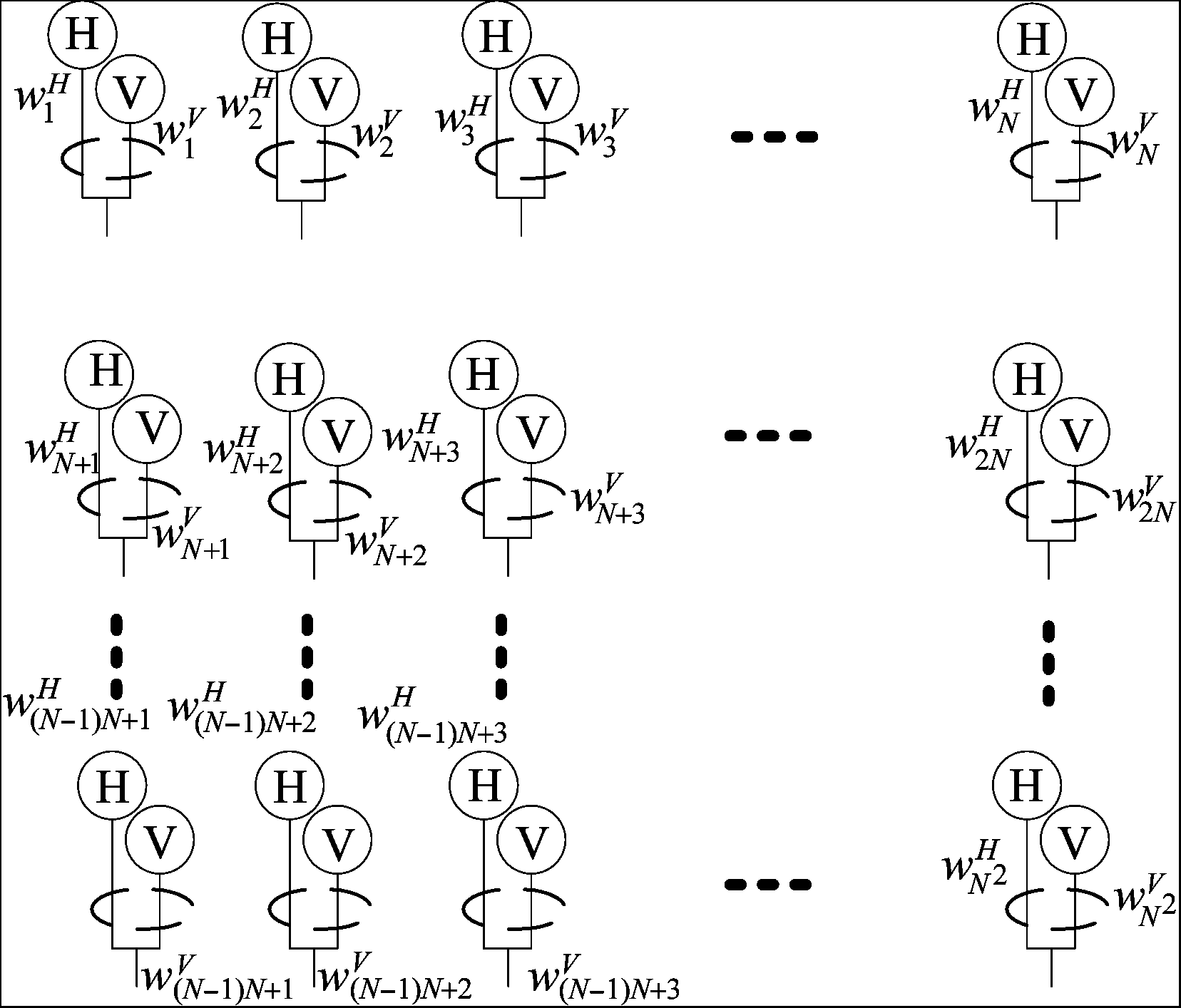
图3 平面极化天线阵列
Fig.3 Plane polarized antenna arrays
假设电磁波传播介质、阵元通道皆为理想状态,阵元间无电磁耦合。通过改变天线阵元的复权值可以得到期望波束。为了方便计算,本文将N×N个天线阵元的复加权值折合N2维列向量为
w=[wH,wV]T
(8)
可看出该复权值w的维数为2×N2。当波束指向方向为r时,阵因子F可表示为
F(r)=[e-jψ1(r),e-jψ2(r),…,e-jψN2(r)]T
(9)
式中ψn(r)=kr·xn,k为传播系数,定义为k=2p/λ,λ为波长,xn(1≤n≤N2)为阵元位置。由前述可知天线阵元响应为V(r),可进一步得到天线阵列响应为
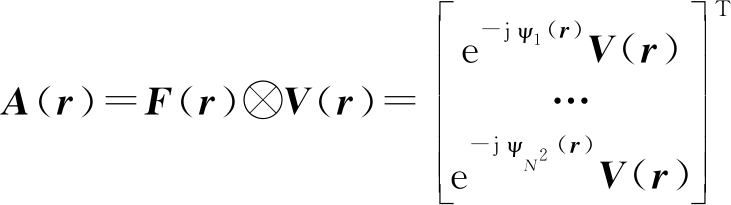
(10)
由式(10)可知,天线阵列响应分为水平和垂直分量,则式(10)可表示为
A(r;H)=F(r)⊗v(r;H)
A(r;V)=F(r)⊗v(r;V)
(11)
远场观察点的电场可表示为
E(r)=A(r)Tw
(12)
用E(r;H)和E(r;V)表示电场的水平和垂直分量,则
E(r;H)=A(r;H)TwH
(13)
E(r;V)=A(r;V)TwV
(14)
由于极化本身是由电场的水平和垂直分量的幅度比和相位差决定,可通过控制天线阵元的复权值来得到期望极化形式的波束。对于传统相控阵天线阵列来说,控制天线阵元复权值可以得到期望的方向图,但对于极化相控阵天线阵列来说,控制天线阵元复权值,不仅能得到期望方向图,还需要控制电磁波的极化状态。
首先,主瓣极化匹配设计能够很大程度提高接收增益,且避开与主瓣极化不同的干扰(如欺骗式干扰),进而提高系统的检测与跟踪性能;其次,强干扰一般来自于波束的旁瓣区域,故零陷或者极化控制的对象也是旁瓣区域某个特定区域。为了最大限度凸显干扰抑制的效果,本文将零陷凹面与极化约束进行叠加设计,即在控制主瓣区域的极化和能量的前提下,对所设计的零陷凹面进行极化约束。若零陷凹面的极化状态可选择为干扰信号的正交状态,这样的设计方式将大幅度提高强干扰的抑制能力。
基于以上,设平面极化阵列的每个阵元均由一对相互垂直的电偶极子的所组成,如图3所示,可得到期望的二维矢量波束为:
(1)主波束具有既定增益和期望的极化状态;
(2)峰值旁瓣水平最低;
(3)旁瓣指定区域(通常是指干扰或者电子设备存在的区域)设置具有极化约束的零陷凹面(设凹面的功率平均值为P)。
对上述要求进行问题建模,在最小峰值旁瓣准则下,可得到矢量波束优化问题的模型如式(15)所示。受限于阵列自由度,在某一区域或者某一点的完全零点是达不到的。在实际应用中,可以通过约束干扰区域Sd的功率W(rd)≤ε来达到抗干扰的目的,这里的ε≪1,∀rd∈Sd。
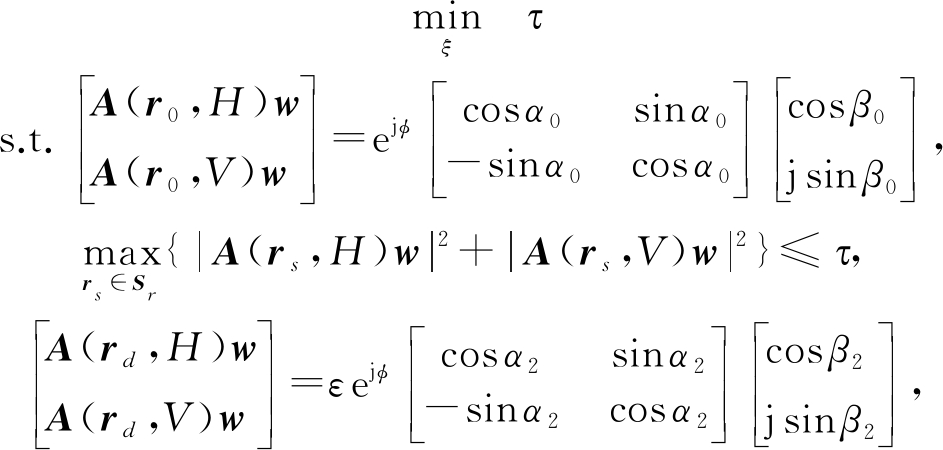
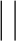A(rd,H)w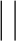2+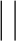A(rd,V)w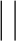2≤ε,rd∈Sd
(15)
将式(15)转化为两个标量的优化问题,得到两个方程,如式(16)和式(17)所示。
水平通道:
s.t. A(r0)w=ejφ(cos α0cos β0+jsin α0sin β0),
A(rd)w=εejφ(cos α2cos β2+jsin α2sin β2)
(16)
垂直通道:
s.t. A(r0)w=ejφ(-sin αcos β+jcos αsin β)A(rd)w=εejφ(-sin α2cos β2+jcos α2sin β2)
(17)
设零陷凹面范围Sd为以干扰信号来波方向(θp,φq)为中心的奇数维方阵,p和q为旁瓣零陷凹面在二维观测平面的坐标向量,p=(p-c,…,p-1,p,p+1,…,p+c),q=(q-c,…,q-1,q,q+1,…,q+c),c为常数。
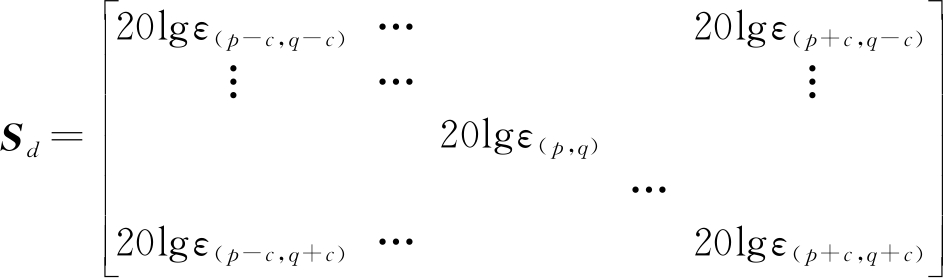
(18)
由式(16)、式(17)和式(18)可见,不同于均匀线阵的极化波束形成可使用传统的凸优化工具包CVX进行求解,二维极化波束形成的数据维度是多维,且数据量较大,故无法使用传统的CVX二阶锥规划求解器进行求解。本节考虑使用MOSEK求解器。这是因为优化问题建模的难易不仅在于线性和非线性,更是在凸与非凸进行区分,二阶锥的优化问题是自对偶。MOSEK的算法则具有这一特殊结构,较容易找到可行解。为了进一步评估算法的性能,本节对算法进行复杂度评估。首先建立N×N个天线阵元模型,时间复杂度为O(N2),假设采样点个数为M,建立极化阵列的导向矢量需要的时间复杂度为O(M2×N2),然后构造旁瓣零陷凹面矩阵需要的时间复杂度为O(M2),最后计算极化椭圆参数需要O(M2)。可估计基于SOCP的二维极化波束形成方法总体的时间复杂度为O(N2+2M2+M2×N2)。
为了进一步凸显方法的独创性,本节考虑两个仿真实例。其中,仿真1是基于均匀线阵极化波束形成的研究成果[10]。该成果主要是针对文献[11]进行创新性设计,即考虑主瓣极化约束的同时,将零陷与极化约束进行叠加设计以最大限度增大强干扰的抑制能力[14]。仿真2是对仿真1的矢量波束优化的问题模型进行二维建模与求解,最终实现了二维观测平面的零陷凹面与极化约束设计。
仿真1 基于均匀线阵的极化波束形成方法
假设阵列为ULA,阵元间距为半个波长,阵元个数为20,观测角度范围:θ∈[-90°,90°],限制半波束宽度为2°,主波束指向θ=0°,设定当波束在主瓣区域极化匹配椭圆参数对α=10°, β=20°,强干扰来自于方位[34
37°],其干扰的正交极化参数设定为(25°,35°)。在最大峰值旁瓣能量最小的准则下,对均匀线阵的极化波束形成算法进行仿真验证,并与文献[10]所列举的两种传统方法(均匀加权方法和切比雪夫加权)对比,得到以下仿真结果。
图4和图5分别表示基于SOCP方法的极化波束方向图和极化参数对(α, β)的优化值。图4中实线为基于SOCP的极化波束,虚线和点线分别为基于均匀加权和切比雪夫加权下的极化波束。无论均匀加权与切比雪夫加权,其零陷凹口深度、峰值旁瓣性能均好于基于SOCP的极化波束,仅牺牲一部分的主瓣宽度。然而对于干扰信号而言,这两种方法仅能在空域形成零点进行干扰抑制,无法兼容主瓣的极化匹配和零陷的正交极化设计。与前两者相比,基于SOCP的极化波束形成则能够在空域范围内能够进行自适应极化设计,意味着可进行主瓣极化匹配接收和旁瓣零陷的正交极化约束。在主瓣区域,极化波束实现了既定的主瓣增益(约-13 dB),在旁瓣区域,设计的零陷凹口满足了深度和宽度的需求,即凹口深度达到30 dB,凹口宽度为4°左右。如图5所示,两种传统方法无法实现自适应极化设计,换言之,只有固定的极化形式,而基于SOCP的极化波束形成则可根据先验信息,完成主瓣的极化匹配接收,零陷的极化正交可最大限度抑制强干扰。在主瓣区域,极化参数对(α, β)保持在(10°,20°)的平均值;在零陷区域,即[34
37°],可以看到极化参数对(α, β)也稳定在(25°,35°)上下。由此可见,整个观测角度内,主瓣和零陷凹面的极化状态均达到预设的要求,这也说明了极化波束形成方法的有效性。另外,在主瓣和零陷之外,两个极化椭圆参数的变化曲线却出现急剧变化的状态,这是因为零陷凹口对权值向量的影响,进而导致了对极化状态的影响,但非本文所关心,也不影响整体的性能。
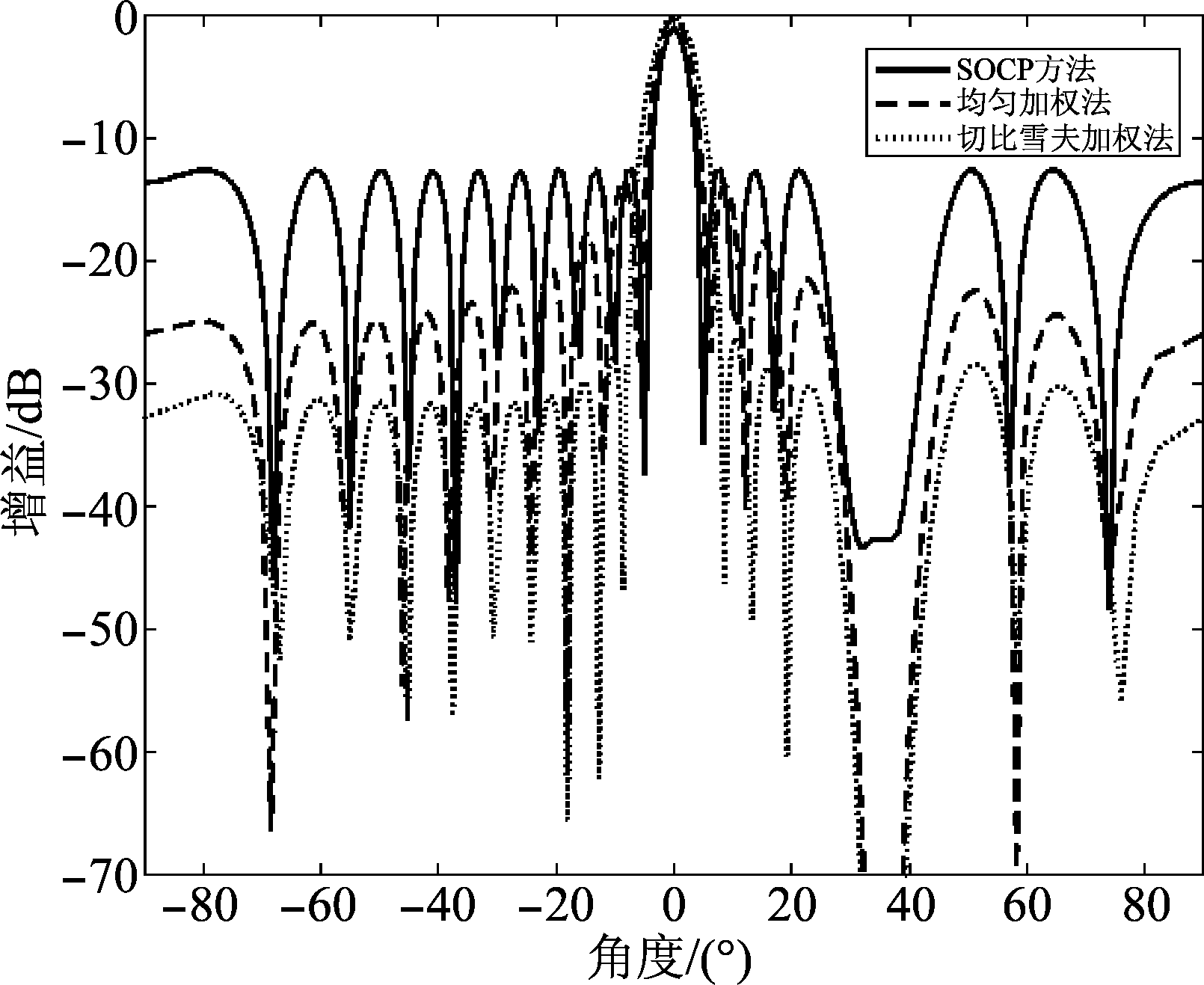
图4 极化波束方向图
Fig.4 Polarized beam patternt
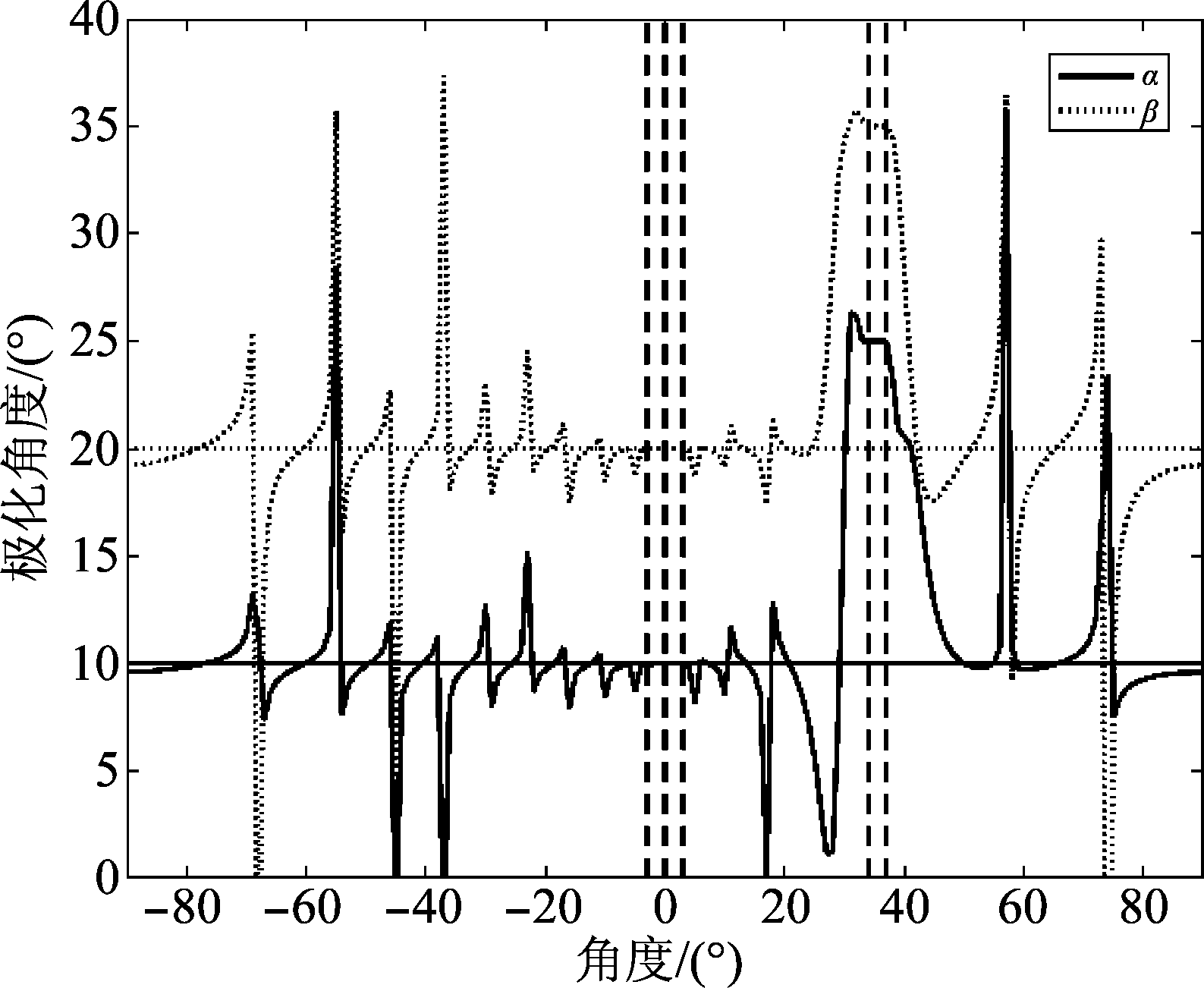
图5 优化的极化椭圆参数
Fig.5 The optimized polarization ellipse parameter
仿真2 基于二维面阵的极化波束形成方法
综合考虑阵元数目与波束的指向效果,本仿真实例使用一个10×10的极化平面阵列,阵元间距为半波长,阵元个数为100,观测角度θ∈[0°,90°],φ∈[0°,90°],设定主波束指向为(θ,φ)=(20°,20°),主瓣极化椭圆参数α=10°, β=20°,半波束宽度为2°,假设干扰信号来波方向为θ∈[60°:62°],φ∈[60°:62°],且椭圆极化参数α=65°, β=35°,那么设置的旁瓣凹面零陷坐标向量应为p=[60°,61°,62°],q=[60°,61°,62°],对应的凹面零陷极化椭圆参数为α=25°, β=35°,且凹面零陷深度门限为20·lg(ε)dB=-80 dB,即ε=0.0001,根据所推导的优化问题(16)和式(17),使用MOSEK求解器求出最优极化波束的极化状态矩阵,得到如图6～图9的仿真结果。
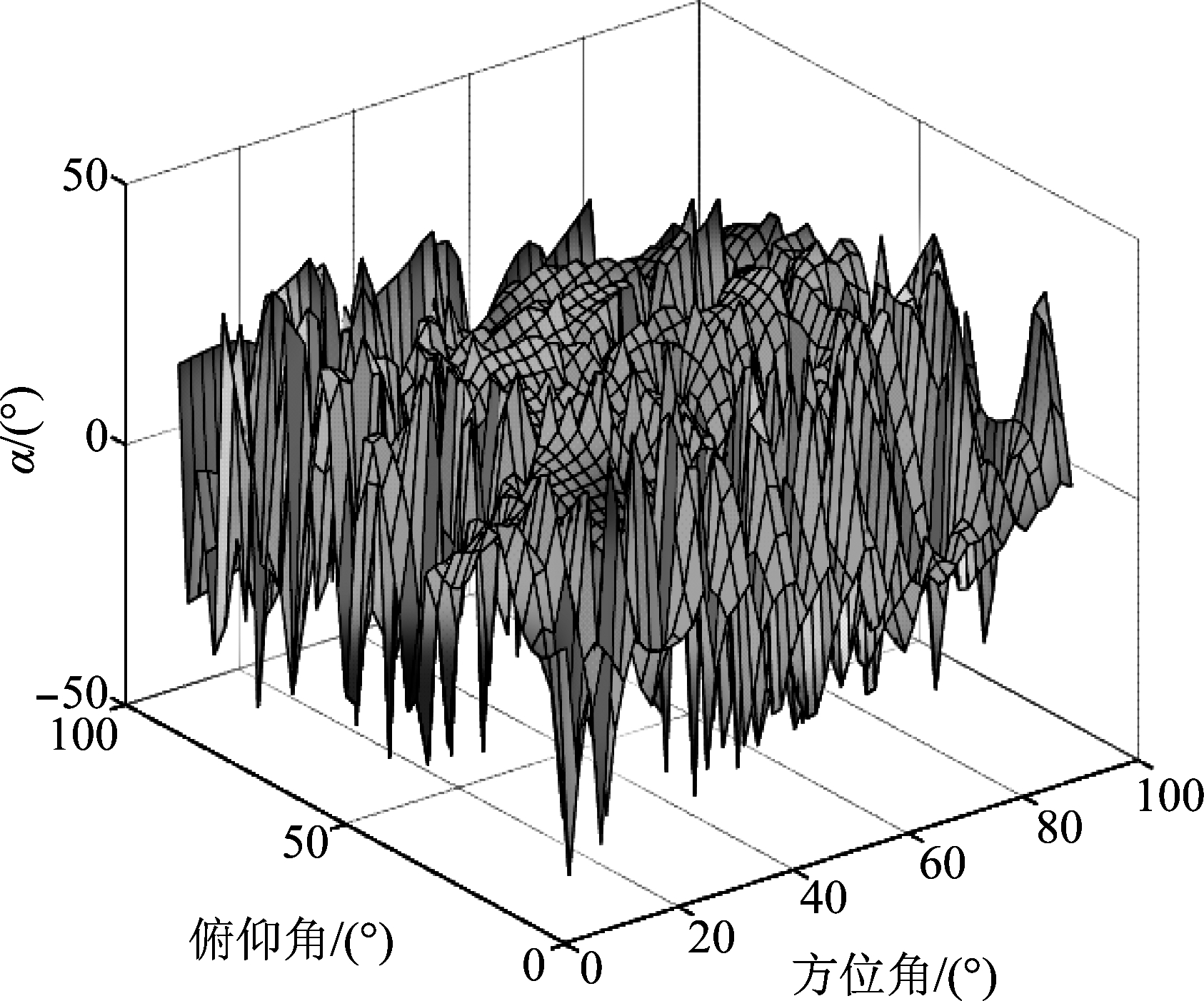
图6 极化椭圆参数α的曲面表示
Fig.6 The optimized polarization ellipse parameter surface
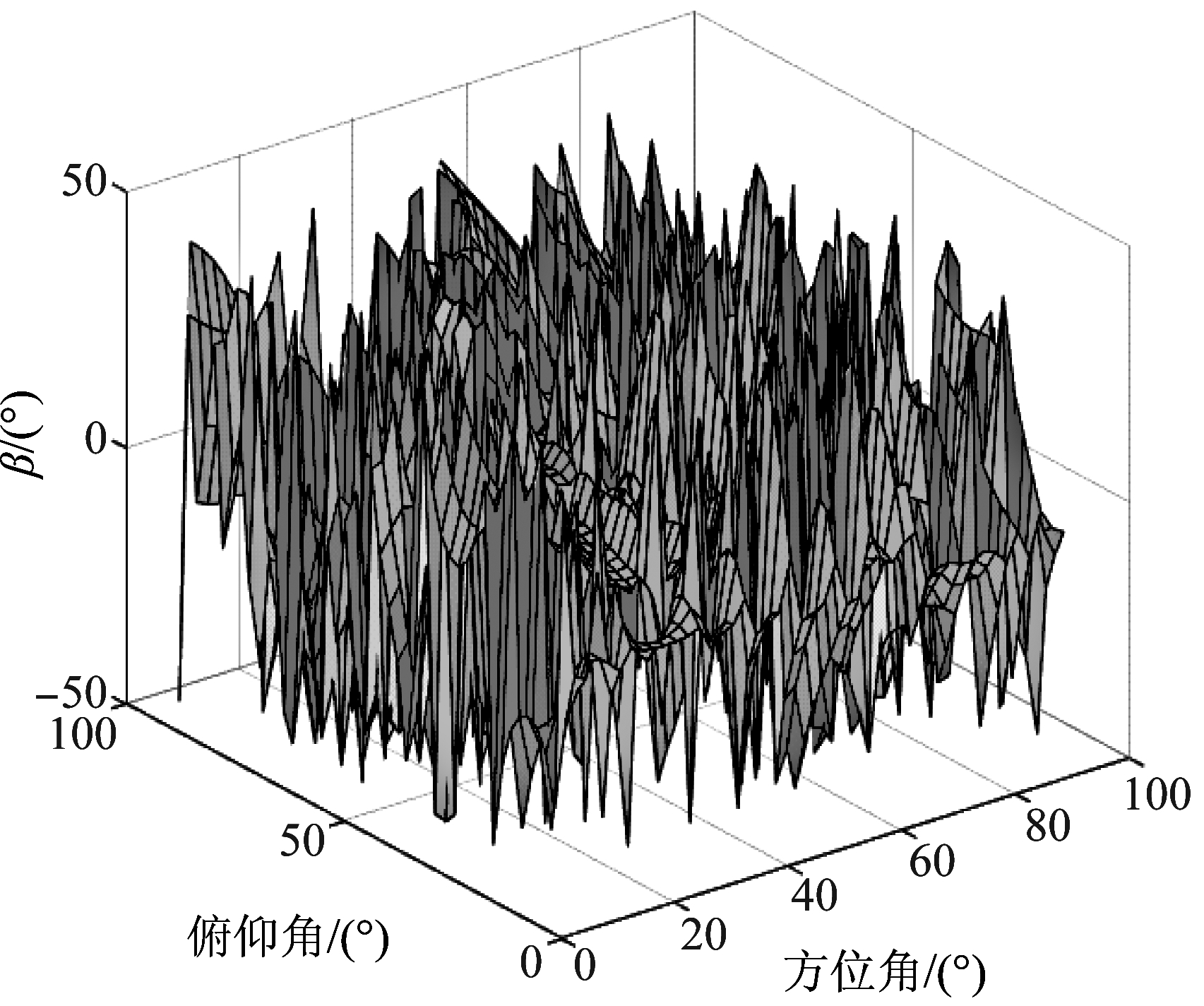
图7 极化椭圆参数β的曲面表示
Fig.7 The optimized polarization ellipse parameter surface
如图6和图7所示,极化椭圆参数α和β无法同时在一个三维空间进行表征,故分别由两个曲面进行表示。在主瓣和零陷区域,仍能大致看出α和β保持在一个平面。这说明了在主瓣和零陷区域,其自适应极化约束仍然是有效的,其平均值可由曲面的切线计算可得。
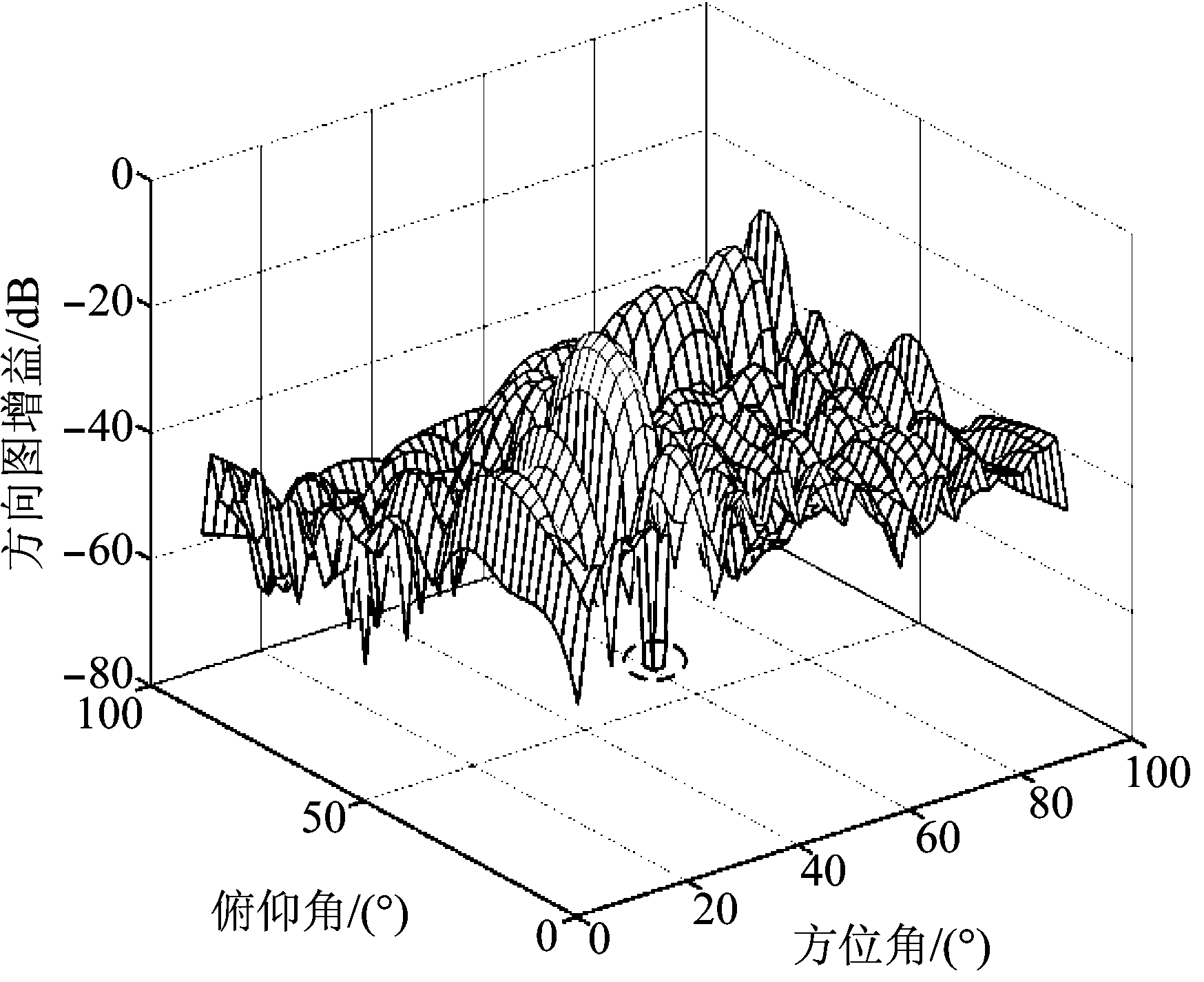
图8 具有零陷凹面的二维极化波束的三维表示
Fig.8 The 3-D representation of 2-D polarized beam with notch plane
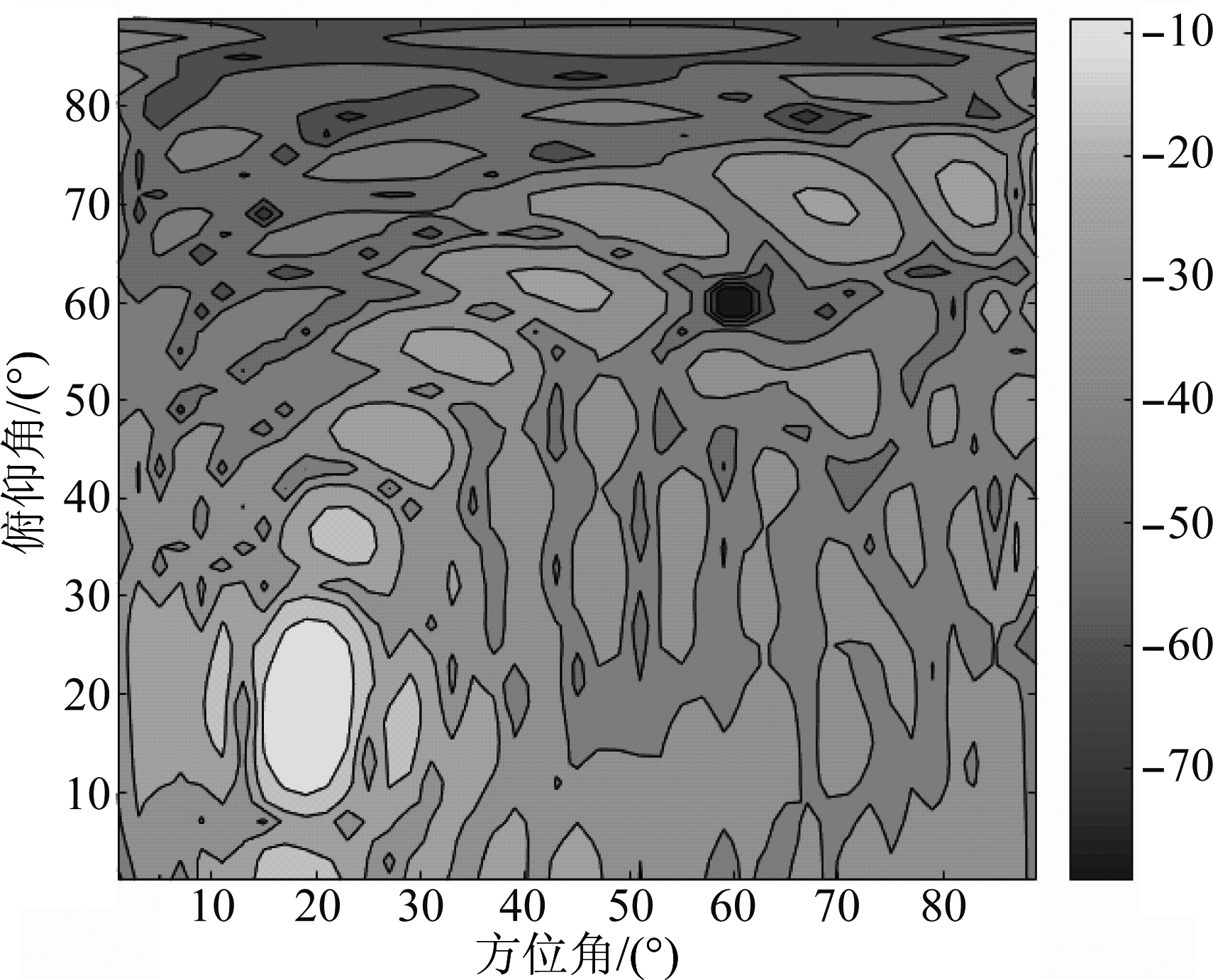
图9 具有零陷凹面的二维极化波束等高线表示
Fig.9 The contour representation of 2-D polarized beam with notch plane
图8和图9分别表示二维极化波束的三维显示及其对应的等高线图。由图8和图9可见,算法实现了主波束指向(θ,φ)=(20°,20°),并得到一个与期望零陷凹面位置相符合的零陷凹面。在二维观测平面内极化椭圆参数α与β的优化结果如图6和图7所示,当(θ,φ)=(20°,20°)时,主瓣的极化椭圆参数的平均值为α=10°, β=20°。当θ∈[60°,61°,62°],φ∈[60°,61°,62°]时,取图6和图7的切面,可得到零陷凹面的极化椭圆参数对的平均值为α=25°, β=35°,满足主瓣区域与零陷区域的极化自适应处理需求。
本文对极化智能天线的二维波束形成进行二维矢量优化问题建模,提出了一种基于二阶锥规划的波束形成方法,得到具有主瓣极化约束、零陷凹面极化约束的二维极化波束。仿真结果表明:本文所提出的方法既满足了空域主波束指向和零陷凹面设计的需求,也满足了主瓣和零陷凹面的极化约束要求,可有效提高了极化阵列的匹配接收和强干扰的抑制能力,进而提高了智能天线的整体性能。由于极化平面阵列阵元数目比较多,其设计成本必将相当昂贵,下一步将考虑对极化平面阵列的阵元进行稀疏优化,达到降低设计成本的目的。
[1] 赵瑞锋, 谈振辉, 蒋海林. 无线系统中的智能天线[J]. 电子学报, 2000, 28(12): 77- 80.
Zhao R F, Tan Z H, Jiang H L. Smart antennas for wireless Systems[J]. Acta Electronica Sinica, 2000, 28(12): 77- 82.(in Chinese)
[2] 沈建锋, 王宗欣. 智能天线中新的波束形成方法[J]. 电子学报, 2004, 32(3): 373-376.
Shen J F, Wang Z X. New Beamforming Methods in Smart Antenna[J]. Acta Electronica Sinica, 2004, 32(3): 373-376.(in Chinese)
[3] 刘力, 杨小鹏. 稳健的相干干扰抑制算法[J]. 信号处理, 2017, 33(12): 1555-1561.
Liu L,Yang X P. Robust Algorithm to Suppress Coherent Jamming[J]. Journal of Signal Processing, 2017, 32(12): 1555-1561.(in Chinese)
[4] 徐振海, 肖顺平, 张光义. 极化阵列天线的优势和应用前景[J]. 现代雷达, 2008, 30(2): 6-9.
Xu Z H, Xiao S P, Zhang G Y. Advantages and Applications of polarization sensitive array[J]. Modem Radar, 2008, 30(2): 6-9.(in Chinese)
[5] 董豹, 姚振东. 极化信息在智能天线技术中的应用[J]. 信号处理, 2002,18(6): 560-563.
Dong B, Yao Z D. Polarimetric Information Utilization in CDMA Cell Station Antenna[J]. Signal Processing, 2002, 18(6): 560-563.(in Chinese)
[6] 宁立跃, 杨小鹏. 多基地极化雷达主瓣干扰抑制算法[J]. 信号处理, 2017, 33(12): 1571-1577.
Ning L Y, Yang X P. Multi-base polarization Radar main-lobe interference suppression algorithm[J]. Journal of Signal Processing, 2017, 33(12): 1571-1577.(in Chinese)
[7] Xu Z, Liu Y, Li M, et al. Linearly Polarized Shaped Power Pattern Synthesis With Dynamic Range Ratio Control for Arbitrary Antenna Arrays[J]. IEEE Access, 2019, 7: 53621-53628.
[8] Jacob P, Madhukumar A S, Alphones A. Interference Mitigation through Cross Polarized Transmission in Femto-Macro Network[J]. IEEE Communications Letters, 2013, 17(10): 1940-1943.
[9] 吴迪军, 徐振海, 张亮, 等. 极化域空域联合匹配波束形成技术研究[J]. 电波科学学报, 2012, 27(1): 90-94.
Wu D J, Xu Z H, Zhang L, et al. Beamformer of polarized and spatial domains joint matching for polarization phased array radar[J]. Chinese Journal of Radio Science, 2012, 27(1): 90-94.(in Chinese)
[10] 闫敏. 极化相控阵天线阵列波束形成与极化合成技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2015.
Yan M. Research on beamforming and polarization synthesis for polarized phased array radar[D]. Harbin: Harbin Institute of Technology, 2015.(in Chinese)
[11] Xiao J J, Nehorai A. Optimal Polarized Beampattern Synthesis Using a Vector Antenna Array[J]. IEEE Transactions on Signal Processing, 2009, 57(2): 576-587.
[12] Wang P P, Liu J M, He Y L, et al. Arbitrary Cylindrical Vector Beam Generation Using Cross-Polarized Modulation[J]. IEEE Photonics Technology Letters, 2019, 31(11): 873- 876.
[13] 陈志坤, 乔晓林, 李风从. 基于极化波束形成的相控阵天线阵列导引头抗干扰技术研究[J]. 航空兵器, 2016(6):16-20.
Chen Z K, Qiao X L, Li F C. Research on anti-interference technology based on polarized beam synthesis[J]. Aero Weaponry, 2016(6): 16-20.(in Chinese)
[14] 陈志坤. MIMO雷达自适应波形设计与阵列优化研究[D]. 哈尔滨: 哈尔滨工业大学, 2017.
Chen Z K. Research on adaptive waveform design and array optimization for MIMO radar[D]. Harbin: Harbin Institute of Technology, 2017.(in Chinese)
陈志坤 男, 1982年生, 福建人。杭州电子科技大学讲师。主要研究方向为雷达、电子侦察技术等。
E-mail: czk@hdu.edu.cn
杜 康 男, 1996年生, 湖北人。杭州电子科技大学硕士研究生。主要研究方向包括阵列优化、波束形成。
E-mail: dk@hdu.edu.cn
彭冬亮 男, 1976年生, 山西人。杭州电子科技大学教授, 博士生导师。主要研究方向包括控制理论与控制工程、模式识别与智能系统(检测与估计、信息融合)、导航制导控制。
E-mail: dlpeng@hdu.edu.cn
申屠晗 男, 1984年生, 浙江人。杭州电子科技大学副教授。主要研究方向包括控制理论与控制工程(多传感器联合检测与跟踪、数据学习与反馈融合)。
E-mail: hanshentu@hdu.edu.cn
薛梦凡 女, 1990年生, 山西人。杭州电子科技大学讲师。主要研究方向包括信号处理、机器学习、目标识别、自主导航。
E-mail: xuemf@hdu.edu.cn